Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-12T22:10:53.337Z Has data issue: false hasContentIssue false
  • English
  • Français

BNS INVARIANTS AND ALGEBRAIC FIBRATIONS OF GROUP EXTENSIONS

Part of: Low-dimensional topology

Published online by Cambridge University Press:  21 September 2021

Stefan Friedl  and
Stefano Vidussi Open the ORCID record for Stefano Vidussi [Opens in a new window]
Stefan Friedl
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Germany (sfriedl@gmail.com)
Stefano Vidussi
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Germany (sfriedl@gmail.com) Department of Mathematics, University of California, Riverside, CA 92521, USA (svidussi@ucr.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finitely generated group that can be written as an extension

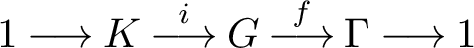$$ \begin{align*} 1 \longrightarrow K \stackrel{i}{\longrightarrow} G \stackrel{f}{\longrightarrow} \Gamma \longrightarrow 1 \end{align*} $$
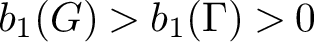where K is a finitely generated group. By a study of the Bieri–Neumann–Strebel (BNS) invariants we prove that if $b_1(G)> b_1(\Gamma ) > 0$ , then G algebraically fibres; that is, admits an epimorphism to 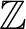$\Bbb {Z}$ with finitely generated kernel. 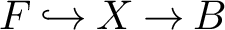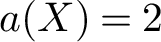An interesting case of this occurrence is when G is the fundamental group of a surface bundle over a surface $F \hookrightarrow X \rightarrow B$ with Albanese dimension $a(X) = 2$ . As an application, we show that if X has virtual Albanese dimension 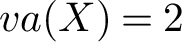$va(X) = 2$ and base and fibre have genus greater that 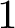$1$ , G is noncoherent. This answers for a broad class of bundles a question of J. Hillman ([9, Question 11(4)]). Finally, we show that there exist surface bundles over a surface whose BNS invariants have a structure that differs from that of Kodaira fibrations, determined by T. Delzant.

Keywords

Algebraic fibrationsgroups extensionsBieri-Neumann-Strebel invariants

MSC classification

Primary: 57M07: Topological methods in group theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 2 , March 2023 , pp. 985 - 999
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bieri, R., Neumann, W. and Strebel, R., A geometric invariant of discrete groups, Invent. Math. 90(3) (1987), 451–477.Google Scholar
Bieri, R. and Renz, B., Valuations on free resolutions and higher geometric invariants of groups, Comment. Math. Helv. 63(3) (1988), 464–497.Google Scholar
Bregman, C., On Kodaira fibrations with invariant cohomology, Geom. Topol. (to appear).Google Scholar
Catanese, F., Moduli and classification of irregular Kähler manifolds (and algebraic varieties) with Albanese general type fibrations, Invent. Math. 104 (1991), 263–289.CrossRefGoogle Scholar
Catanese, F., Fibred Kähler and quasi-projective groups, Adv. Geom. Suppl. (2003), S13–S27. Special issue dedicated to Adriano Barlotti.CrossRefGoogle Scholar
Delzant, T., L’invariant de Bieri Neumann Strebel des groupes fondamentaux des variétés kähleriennes, Math. Ann. 348 (2010), 119–125.CrossRefGoogle Scholar
Friedl, S. and Vidussi, S., On virtual algebraic fibrations of Kähler groups, Nagoya Math. J. 243 (2021), 42–60.CrossRefGoogle Scholar
Hillman, J., Four-manifolds, geometries and knots, Geom. Topol. Monogr. 5 (2002), 397 pp.Google Scholar
Hillman, J., Sections of surface bundles, Interactions between low-dimensional topology and mapping class groups, Geom. Topol. Monogr. 19 (2015), 1–19.Google Scholar
Johnson, D. L., Presentations of Groups. London Mathematical Society Student Texts, (Cambridge University Press, Cambridge, 1997).Google Scholar
Johnson, F. E. A., Surface fibrations and automorphisms of nonabelian extensions, Quart. J. Math. Oxford Ser. 44(2) (1993), 199–214.CrossRefGoogle Scholar
Koban, N. and Wong, P., The geometric invariants of certain group extensions with applications to twisted conjugacy, Topol. Appl. 193 (2015), 192–205.CrossRefGoogle Scholar
Kropholler, R. and Walsh, G., Incoherence and fibering of many free-by-free groups, Ann. Inst. Fourier (Grenoble) (to appear).Google Scholar
Morita, S., Characteristic classes of surface bundles, Invent. Math. 90(3) (1987), 551–577.CrossRefGoogle Scholar
Salter, N., Cup products, the Johnson homomorphism, and surface bundles over surfaces with multiple fiberings, Alg. Geom. Topol. 15 (2015), 3613–3652.CrossRefGoogle Scholar
Strebel, R., Notes on the Sigma invariants, Preprint, 2013, arXiv:1204.0214.Google Scholar