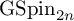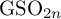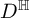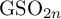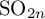Introduction
Inspired by conjectures of Langlands and Clozel’s work [Reference Clozel18] for the group
![]() $G = {\mathrm {GL}}_n$
, Buzzard–Gee [Reference Buzzard and Gee12, Conj. 5.16] formulate the following version of the Langlands correspondence (in one direction) for an arbitrary connected reductive group G over a number field F. Let
$G = {\mathrm {GL}}_n$
, Buzzard–Gee [Reference Buzzard and Gee12, Conj. 5.16] formulate the following version of the Langlands correspondence (in one direction) for an arbitrary connected reductive group G over a number field F. Let
![]() $\mathbb A_F$
denote the ring of adèles over F. Write
$\mathbb A_F$
denote the ring of adèles over F. Write
![]() $\widehat G$
(resp.
$\widehat G$
(resp.
![]() $^L G$
) for the Langlands dual group (resp. L-group) of G over
$^L G$
) for the Langlands dual group (resp. L-group) of G over
![]() $\overline {\mathbb {Q}}_{\ell }$
. When
$\overline {\mathbb {Q}}_{\ell }$
. When
![]() $g\in {}^L G(\overline {\mathbb {Q}}_{\ell })$
, let
$g\in {}^L G(\overline {\mathbb {Q}}_{\ell })$
, let
![]() $g_{\mathrm {ss}}$
denote its semisimple part.
$g_{\mathrm {ss}}$
denote its semisimple part.
Conjecture 1. Let
![]() $\ell $
be a prime number and fix an isomorphism
$\ell $
be a prime number and fix an isomorphism
![]() $\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
. Let
$\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
. Let
![]() $\pi $
be a cuspidal L-algebraic automorphic representation of
$\pi $
be a cuspidal L-algebraic automorphic representation of
![]() $G(\mathbb A_F)$
. Then there exists a Galois representation
$G(\mathbb A_F)$
. Then there exists a Galois representation
such that for all but finitely many primes
![]() ${{\mathfrak q}}$
of F (excluding
${{\mathfrak q}}$
of F (excluding
![]() ${{\mathfrak q}}|\ell $
and those such that
${{\mathfrak q}}|\ell $
and those such that
![]() $\pi _{{\mathfrak q}}$
are ramified), the
$\pi _{{\mathfrak q}}$
are ramified), the
![]() $\widehat G$
-conjugacy class of
$\widehat G$
-conjugacy class of
![]() $\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}} \in {}^L G(\overline {\mathbb {Q}}_{\ell })$
is the Satake parameter of
$\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}} \in {}^L G(\overline {\mathbb {Q}}_{\ell })$
is the Satake parameter of
![]() $\pi _{{\mathfrak q}}$
via
$\pi _{{\mathfrak q}}$
via
![]() $\iota $
.
$\iota $
.
The conjecture of Buzzard-Gee is more precise (and does not assume cuspidality). They describe the image of each complex conjugation element and
![]() $\ell $
-adic Hodge-theoretic properties of
$\ell $
-adic Hodge-theoretic properties of
![]() $\rho _{\pi }$
. Moreover, they predict [Reference Buzzard and Gee12, Conj. 5.17] that the compatibility holds at every
$\rho _{\pi }$
. Moreover, they predict [Reference Buzzard and Gee12, Conj. 5.17] that the compatibility holds at every
![]() ${{\mathfrak q}}$
coprime to
${{\mathfrak q}}$
coprime to
![]() $\ell $
such that
$\ell $
such that
![]() $\pi _{\mathfrak {q}}$
is unramified. In fact,
$\pi _{\mathfrak {q}}$
is unramified. In fact,
![]() $\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})$
, instead of its semisimple part, appears in their conjecture. While
$\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})$
, instead of its semisimple part, appears in their conjecture. While
![]() $\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})$
is expected to be always semisimple, this seems to be a problem of different nature and out of reach. Thus, we state the conjecture with
$\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})$
is expected to be always semisimple, this seems to be a problem of different nature and out of reach. Thus, we state the conjecture with
![]() $\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}}$
.
$\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}}$
.
For most recent results on Conjecture 1 for
![]() ${\mathrm {GL}}_n$
(in the regular case), we refer to [Reference Scholze71, Reference Harris, Lan, Taylor and Thorne35] and the references therein. Arthur’s endoscopic classification [Reference Arthur1] (see [Reference Mok62, Reference Kaletha, Minguez, Shin and White40] for unitary groups)Footnote 1 provides a crucial input for constructing Galois representations as in the conjecture for symplectic, special orthogonal and unitary groups by reducing the question to the case of general linear groups. When the group is
${\mathrm {GL}}_n$
(in the regular case), we refer to [Reference Scholze71, Reference Harris, Lan, Taylor and Thorne35] and the references therein. Arthur’s endoscopic classification [Reference Arthur1] (see [Reference Mok62, Reference Kaletha, Minguez, Shin and White40] for unitary groups)Footnote 1 provides a crucial input for constructing Galois representations as in the conjecture for symplectic, special orthogonal and unitary groups by reducing the question to the case of general linear groups. When the group is
![]() ${\mathrm {SO}}_{2n}$
, however, such an approach proves only a weaker local-global compatibility up to outer automorphisms (see (SO-i) in Theorem 6.5 below), falling short of proving Conjecture 1 (even under local hypotheses); we will return to this point as an application of our main theorem.
${\mathrm {SO}}_{2n}$
, however, such an approach proves only a weaker local-global compatibility up to outer automorphisms (see (SO-i) in Theorem 6.5 below), falling short of proving Conjecture 1 (even under local hypotheses); we will return to this point as an application of our main theorem.
Our goal is to prove Conjecture 1 for a quasi-split form
![]() $G^{*}$
of
$G^{*}$
of
![]() ${\mathrm {GSO}}_{2n}$
over a totally real field under certain local hypotheses, as a sequel to our work [Reference Kret and Shin50] where we proved the conjecture for
${\mathrm {GSO}}_{2n}$
over a totally real field under certain local hypotheses, as a sequel to our work [Reference Kret and Shin50] where we proved the conjecture for
![]() $\mathrm {GSp}_{2n}$
under similar local hypotheses. The group
$\mathrm {GSp}_{2n}$
under similar local hypotheses. The group
![]() ${\mathrm {GSO}}_{2n}$
is closely related to the classical group
${\mathrm {GSO}}_{2n}$
is closely related to the classical group
![]() ${\mathrm {SO}}_{2n}$
, just like
${\mathrm {SO}}_{2n}$
, just like
![]() $\mathrm {GSp}_{2n}$
is to
$\mathrm {GSp}_{2n}$
is to
![]() $\mathrm {Sp}_{2n}$
, but the similitude groups may well be regarded as non-classical groups. An important reason is that the Langlands dual groups of
$\mathrm {Sp}_{2n}$
, but the similitude groups may well be regarded as non-classical groups. An important reason is that the Langlands dual groups of
![]() ${\mathrm {GSO}}_{2n}$
and
${\mathrm {GSO}}_{2n}$
and
![]() $\mathrm {GSp}_{2n}$
, namely, the general spin groups
$\mathrm {GSp}_{2n}$
, namely, the general spin groups
![]() $\mathrm {GSpin}_{2n}$
and
$\mathrm {GSpin}_{2n}$
and
![]() $\mathrm {GSpin}_{2n+1}$
, do not admit standard embeddings (into general linear groups of proportional rank). This makes the problem both nontrivial and interesting. Furthermore, since the groups
$\mathrm {GSpin}_{2n+1}$
, do not admit standard embeddings (into general linear groups of proportional rank). This makes the problem both nontrivial and interesting. Furthermore, since the groups
![]() $\mathrm {GSp}_{2n}$
and
$\mathrm {GSp}_{2n}$
and
![]() ${\mathrm {GSO}}_{2n}$
appear as endoscopic groups of each other for varying n [Reference Xu81, Sect. 2.1], results for the one group likely have applications for the other, especially if one tries to prove cases of Conjecture 1 without local hypotheses.
${\mathrm {GSO}}_{2n}$
appear as endoscopic groups of each other for varying n [Reference Xu81, Sect. 2.1], results for the one group likely have applications for the other, especially if one tries to prove cases of Conjecture 1 without local hypotheses.
To be more precise, we set up some notation. Let F be a totally real number field, and
![]() $n \in \mathbb Z_{\geq 3}$
. Let
$n \in \mathbb Z_{\geq 3}$
. Let
![]() ${\mathrm {GSO}}_{2n}$
denote the connected split reductive group over F which is the identity component of the orthogonal similitude group
${\mathrm {GSO}}_{2n}$
denote the connected split reductive group over F which is the identity component of the orthogonal similitude group
![]() $\mathrm {GO}_{2n}$
. (See §2 below for an explicit definition.)
$\mathrm {GO}_{2n}$
. (See §2 below for an explicit definition.)
Our setup depends on the parity of n:
-
(n even)
 $E=F$
, and
$E=F$
, and
 $G^{*}={\mathrm {GSO}}_{2n}$
(the split form over F),
$G^{*}={\mathrm {GSO}}_{2n}$
(the split form over F), -
(n odd) E is a totally imaginary quadratic extension of F, and
 $G^{*}$
is a non-split quasi-split form of
$G^{*}$
is a non-split quasi-split form of
 ${\mathrm {GSO}}_{2n}$
relative to
${\mathrm {GSO}}_{2n}$
relative to
 $E/F$
(explicitly given as (8.4)).
$E/F$
(explicitly given as (8.4)).
We write
![]() ${\mathrm {GSO}}^{E/F}_{2n}$
for the F-group
${\mathrm {GSO}}^{E/F}_{2n}$
for the F-group
![]() $G^{*}$
in either case. The setup is naturally designed so that there are Shimura varieties for (an inner twist of)
$G^{*}$
in either case. The setup is naturally designed so that there are Shimura varieties for (an inner twist of)
![]() $\mathrm {Res}_{F/\mathbb {Q}} G^{*}$
. In particular,
$\mathrm {Res}_{F/\mathbb {Q}} G^{*}$
. In particular,
![]() $G^{*}(F_y)$
has discrete series at every infinite place y of F. (Indeed,
$G^{*}(F_y)$
has discrete series at every infinite place y of F. (Indeed,
![]() $G^{*}(F_y)$
has no discrete series if we swap the parity of n above.) There is a short exact sequence of F-groups
$G^{*}(F_y)$
has no discrete series if we swap the parity of n above.) There is a short exact sequence of F-groups
where
![]() ${\mathrm {SO}}^{E/F}_{2n}$
is a quasi-split form of
${\mathrm {SO}}^{E/F}_{2n}$
is a quasi-split form of
![]() ${\mathrm {SO}}_{2n}$
, defined similarly as
${\mathrm {SO}}_{2n}$
, defined similarly as
![]() ${\mathrm {GSO}}^{E/F}_{2n}$
, and
${\mathrm {GSO}}^{E/F}_{2n}$
, and
![]() $\mathrm {sim}$
denotes the similitude character. It is convenient to use the version of L-group relative to
$\mathrm {sim}$
denotes the similitude character. It is convenient to use the version of L-group relative to
![]() $E/F$
, with coefficients in either
$E/F$
, with coefficients in either
![]() ${\mathbb {C}}$
or
${\mathbb {C}}$
or
![]() $\overline {\mathbb {Q}}_{\ell }$
:
$\overline {\mathbb {Q}}_{\ell }$
:
where the nontrivial element of
![]() ${\mathrm {Gal}}(E/F)$
acts nontrivially on
${\mathrm {Gal}}(E/F)$
acts nontrivially on
![]() $\mathrm {GSpin}_{2n}$
. (This identifies
$\mathrm {GSpin}_{2n}$
. (This identifies
![]() $^L G^{*}$
with
$^L G^{*}$
with
![]() $\mathrm {GPin}_{2n}$
if
$\mathrm {GPin}_{2n}$
if
![]() $[E:F]=2$
.) An important feature of the (general) spin groups
$[E:F]=2$
.) An important feature of the (general) spin groups
![]() $\mathrm {GSpin}_m$
(
$\mathrm {GSpin}_m$
(
![]() $m \in \mathbb Z_{\geq 2}$
) is their spin representation
$m \in \mathbb Z_{\geq 2}$
) is their spin representation
![]() $\mathrm {spin}_m \colon \mathrm {GSpin}_m \rightarrow {\mathrm {GL}}_{2^{\lfloor m/2 \rfloor }}$
. In case m is even, this representation is reducible and splits up into a direct sum
$\mathrm {spin}_m \colon \mathrm {GSpin}_m \rightarrow {\mathrm {GL}}_{2^{\lfloor m/2 \rfloor }}$
. In case m is even, this representation is reducible and splits up into a direct sum
![]() $\mathrm {spin}_m = \mathrm {spin}_m^+ \oplus \mathrm {spin}_m^-$
of two irreducible representations of dimension
$\mathrm {spin}_m = \mathrm {spin}_m^+ \oplus \mathrm {spin}_m^-$
of two irreducible representations of dimension
![]() $2^{\lfloor m/2 \rfloor -1}$
. These representations
$2^{\lfloor m/2 \rfloor -1}$
. These representations
![]() $\mathrm {spin}_m^{\pm }$
are called the half-spin representations. Two other important representations are the standard representation and the spinor norm (see Lemma 3.1 for
$\mathrm {spin}_m^{\pm }$
are called the half-spin representations. Two other important representations are the standard representation and the spinor norm (see Lemma 3.1 for
![]() $\mathrm {pr}^{\circ }$
)
$\mathrm {pr}^{\circ }$
)
If m is odd,
![]() $\mathrm {spin}$
is faithful. In the even case
$\mathrm {spin}$
is faithful. In the even case
![]() $m = 2n$
, none of the representations
$m = 2n$
, none of the representations
![]() $\mathrm {spin}^+, \mathrm {spin}^-, \mathrm {std}$
or
$\mathrm {spin}^+, \mathrm {spin}^-, \mathrm {std}$
or
![]() $\mathcal N$
is faithful, but
$\mathcal N$
is faithful, but
![]() $\mathrm {spin}$
is faithful.
$\mathrm {spin}$
is faithful.
Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
. Consider the following hypotheses on
${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
. Consider the following hypotheses on
![]() $\pi $
, where
$\pi $
, where
![]() $|\mathrm {sim}|$
denotes the composite
$|\mathrm {sim}|$
denotes the composite
![]() ${\mathrm {GSO}}^{E/F}_{2n}(F\otimes _{\mathbb {Q}} {\mathbb R})\stackrel {\mathrm {sim}}{\rightarrow } (F\otimes {\mathbb R})^{\times } \stackrel {|\cdot |}{\rightarrow } {\mathbb R}^{\times }_{>0}$
:
${\mathrm {GSO}}^{E/F}_{2n}(F\otimes _{\mathbb {Q}} {\mathbb R})\stackrel {\mathrm {sim}}{\rightarrow } (F\otimes {\mathbb R})^{\times } \stackrel {|\cdot |}{\rightarrow } {\mathbb R}^{\times }_{>0}$
:
-
(St) There is a finite F-place
 ${{{\mathfrak q}}_{\mathrm {St}}}$
such that
${{{\mathfrak q}}_{\mathrm {St}}}$
such that
 $\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}$
is the Steinberg representation of
$\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}$
is the Steinberg representation of
 $G^{*}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
twisted by a character.
$G^{*}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
twisted by a character. -
(L-coh)
 $\pi _{\infty }|\mathrm {sim}|^{-n(n-1)/4}$
is
$\pi _{\infty }|\mathrm {sim}|^{-n(n-1)/4}$
is
 $\xi $
-cohomological for an irreducible algebraic representation
$\xi $
-cohomological for an irreducible algebraic representation
 $\xi =\otimes _{y:F\hookrightarrow {\mathbb {C}}} \xi _y$
of the group
$\xi =\otimes _{y:F\hookrightarrow {\mathbb {C}}} \xi _y$
of the group
 $(\mathrm {Res}_{F/\mathbb {Q}} G^{*}) \otimes _{\mathbb {Q}} {\mathbb {C}}\simeq \prod _{y:F\hookrightarrow {\mathbb {C}}} (G^{*}\otimes _{F,y}{\mathbb {C}})$
.
$(\mathrm {Res}_{F/\mathbb {Q}} G^{*}) \otimes _{\mathbb {Q}} {\mathbb {C}}\simeq \prod _{y:F\hookrightarrow {\mathbb {C}}} (G^{*}\otimes _{F,y}{\mathbb {C}})$
. -
(std-reg) The infinitesimal character of
 $\xi _y$
for every
$\xi _y$
for every
 $y:F\hookrightarrow {\mathbb {C}}$
, which is a regular Weyl group orbit in the Lie algebra of
$y:F\hookrightarrow {\mathbb {C}}$
, which is a regular Weyl group orbit in the Lie algebra of
 $\widehat {G}^{*}=\mathrm {GSpin}_{2n}({\mathbb {C}})$
, remains regular under the standard representation
$\widehat {G}^{*}=\mathrm {GSpin}_{2n}({\mathbb {C}})$
, remains regular under the standard representation
 $\mathrm {GSpin}_{2n}\rightarrow {\mathrm {GL}}_{2n}$
.
$\mathrm {GSpin}_{2n}\rightarrow {\mathrm {GL}}_{2n}$
.
In (L-coh), “
![]() $\xi $
-cohomological” means that the tensor product with
$\xi $
-cohomological” means that the tensor product with
![]() $\xi $
has nonvanishing relative Lie algebra cohomology in some degree (§1 below). Condition (L-coh) implies that
$\xi $
has nonvanishing relative Lie algebra cohomology in some degree (§1 below). Condition (L-coh) implies that
![]() $\pi $
is L-algebraic. The other two conditions should be superfluous as they do not appear in Conjecture 1. Condition (St) plays an essential role in our argument and would take significant new ideas and effort to get rid of. We assume (std-reg) for the reason that certain results for regular-algebraic self-dual cuspidal automorphic representations of
$\pi $
is L-algebraic. The other two conditions should be superfluous as they do not appear in Conjecture 1. Condition (St) plays an essential role in our argument and would take significant new ideas and effort to get rid of. We assume (std-reg) for the reason that certain results for regular-algebraic self-dual cuspidal automorphic representations of
![]() ${\mathrm {GL}}_N$
,
${\mathrm {GL}}_N$
,
![]() $N>2$
, are missing in the non-regular case. However, we need less than (std-reg) for our argument to work. The necessary input for us to proceed without (std-reg) is formulated as Hypothesis 6.11, which we expect to be quite nontrivial but within reach nonetheless. Thus, we assume either (std-reg) or Hypothesis 6.11 in the main theorem, hoping that (std-reg) will be removed as soon as the hypothesis is verified.
$N>2$
, are missing in the non-regular case. However, we need less than (std-reg) for our argument to work. The necessary input for us to proceed without (std-reg) is formulated as Hypothesis 6.11, which we expect to be quite nontrivial but within reach nonetheless. Thus, we assume either (std-reg) or Hypothesis 6.11 in the main theorem, hoping that (std-reg) will be removed as soon as the hypothesis is verified.
Let
![]() $S_{\mathrm {bad}} = S_{\mathrm {bad}}(\pi )$
denote the finite set of rational primes p such that either
$S_{\mathrm {bad}} = S_{\mathrm {bad}}(\pi )$
denote the finite set of rational primes p such that either
![]() $p=2$
, p ramifies in F, or
$p=2$
, p ramifies in F, or
![]() $\pi _{\mathfrak {q}}$
ramifies at a place
$\pi _{\mathfrak {q}}$
ramifies at a place
![]() ${{\mathfrak q}}$
of F above p. The following theorem assigns an
${{\mathfrak q}}$
of F above p. The following theorem assigns an
![]() $\ell $
-adic Galois representation to
$\ell $
-adic Galois representation to
![]() $\pi $
for each prime number
$\pi $
for each prime number
![]() $\ell $
and each isomorphism
$\ell $
and each isomorphism
![]() $\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
.
$\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
.
Theorem A. Assume that
![]() $\pi $
satisfies conditions (St) and (L-coh). If (std-reg) does not hold for
$\pi $
satisfies conditions (St) and (L-coh). If (std-reg) does not hold for
![]() $\pi $
, further assume Hypothesis 6.11 (for an
$\pi $
, further assume Hypothesis 6.11 (for an
![]() ${\mathrm {SO}}_{2n}(\mathbb A_F)$
-subrepresentation of
${\mathrm {SO}}_{2n}(\mathbb A_F)$
-subrepresentation of
![]() $\pi $
). Then there exists, up to
$\pi $
). Then there exists, up to
![]() $\widehat G$
-conjugation, a unique semisimple Galois representation attached to
$\widehat G$
-conjugation, a unique semisimple Galois representation attached to
![]() $\pi $
and
$\pi $
and
![]() $\iota $
$\iota $
such that the following hold.
-
(A1) For every prime
 ${{\mathfrak q}}$
of F not above
${{\mathfrak q}}$
of F not above
 $S_{\mathrm {bad}}\cup \{\ell \}$
,
$S_{\mathrm {bad}}\cup \{\ell \}$
,
 $\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
is
$\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
is
 $\widehat G^{*}$
-conjugate to
$\widehat G^{*}$
-conjugate to
 $\iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
, where
$\iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
, where
 $\phi _{\pi _{\mathfrak {q}}}$
is the unramified Langlands parameter of
$\phi _{\pi _{\mathfrak {q}}}$
is the unramified Langlands parameter of
 $\pi _{{\mathfrak q}}$
.
$\pi _{{\mathfrak q}}$
. -
(A2) The composition
corresponds to a cuspidal automorphic $$ \begin{align*}{\mathrm{Gal}}(\overline{F}/F) \overset {\rho_{\pi}} \to {}^L G^{*} \overset {\mathrm{pr}^{\circ}} \to {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}) \rtimes {\mathrm{Gal}}(E/F) \end{align*} $$
$$ \begin{align*}{\mathrm{Gal}}(\overline{F}/F) \overset {\rho_{\pi}} \to {}^L G^{*} \overset {\mathrm{pr}^{\circ}} \to {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}) \rtimes {\mathrm{Gal}}(E/F) \end{align*} $$
 ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation
 $\pi ^{\flat }$
contained in
$\pi ^{\flat }$
contained in
 $\pi $
in that
$\pi $
in that
 $\mathrm {pr}^{\circ }(\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}})$
is
$\mathrm {pr}^{\circ }(\rho _{\pi }(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}})$
is
 ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate to the Satake parameter of
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate to the Satake parameter of
 $\pi ^{\flat }_{\mathfrak {q}}$
via
$\pi ^{\flat }_{\mathfrak {q}}$
via
 $\iota $
at every
$\iota $
at every
 ${{\mathfrak q}}$
not above
${{\mathfrak q}}$
not above
 $S_{\mathrm {bad}}\cup \{\ell \}$
. Further, the composition corresponds to the central character of
$S_{\mathrm {bad}}\cup \{\ell \}$
. Further, the composition corresponds to the central character of $$ \begin{align*}{\mathrm{Gal}}(\overline{F}/F) \overset {\rho_{\pi}} \to {}^L G^{*} \overset {\mathcal N} \to {\mathrm{GL}}_1(\overline{\mathbb{Q}}_{\ell}) \end{align*} $$
$$ \begin{align*}{\mathrm{Gal}}(\overline{F}/F) \overset {\rho_{\pi}} \to {}^L G^{*} \overset {\mathcal N} \to {\mathrm{GL}}_1(\overline{\mathbb{Q}}_{\ell}) \end{align*} $$
 $\pi $
via class field theory and
$\pi $
via class field theory and
 $\iota $
.
$\iota $
.
-
(A3) For every
 ${{\mathfrak q}}|\ell $
, the representation
${{\mathfrak q}}|\ell $
, the representation
 $\rho _{\pi , {{\mathfrak q}}}$
is de Rham (in the sense that
$\rho _{\pi , {{\mathfrak q}}}$
is de Rham (in the sense that
 $r \circ \rho _{\pi ,{{\mathfrak q}}}$
is de Rham for all representations r of
$r \circ \rho _{\pi ,{{\mathfrak q}}}$
is de Rham for all representations r of
 $\widehat G^{*}$
). Moreover,
$\widehat G^{*}$
). Moreover,-
(a) The Hodge–Tate cocharacter of
 $\rho _{\pi , {{\mathfrak q}}}$
is explicitly determined by
$\rho _{\pi , {{\mathfrak q}}}$
is explicitly determined by
 $\xi $
. More precisely, for all
$\xi $
. More precisely, for all
 $y \colon F \to {\mathbb {C}}$
such that
$y \colon F \to {\mathbb {C}}$
such that
 $\iota y$
induces
$\iota y$
induces
 ${{\mathfrak q}}$
, we have
${{\mathfrak q}}$
, we have  $$ \begin{align*}\mu_{\mathrm{HT}}(\rho_{\pi, {{\mathfrak q}}}, \iota y) = \iota \mu_{\mathrm{Hodge}}(\xi_y) - \frac{n(n-1)}{4} \mathrm{sim}. \end{align*} $$
$$ \begin{align*}\mu_{\mathrm{HT}}(\rho_{\pi, {{\mathfrak q}}}, \iota y) = \iota \mu_{\mathrm{Hodge}}(\xi_y) - \frac{n(n-1)}{4} \mathrm{sim}. \end{align*} $$
(We still write
 $\mathrm {sim}$
to mean the cocharacter of
$\mathrm {sim}$
to mean the cocharacter of
 $\mathrm {GSpin}_{2n}$
dual to
$\mathrm {GSpin}_{2n}$
dual to
 $\mathrm {sim}:G^{*}\rightarrow \mathbb G_m$
. See §1 below for the Hodge–Tate and Hodge cocharacters
$\mathrm {sim}:G^{*}\rightarrow \mathbb G_m$
. See §1 below for the Hodge–Tate and Hodge cocharacters
 $\mu _{\mathrm {HT}}$
and
$\mu _{\mathrm {HT}}$
and
 $\mu _{\mathrm {Hodge}}$
.Footnote 2)
$\mu _{\mathrm {Hodge}}$
.Footnote 2) -
(b) If
 $\pi _{\mathfrak {q}}$
has nonzero invariants under a hyperspecial (resp. Iwahori) subgroup of
$\pi _{\mathfrak {q}}$
has nonzero invariants under a hyperspecial (resp. Iwahori) subgroup of
 $G^{*}(F_{\mathfrak {q}})$
, then either
$G^{*}(F_{\mathfrak {q}})$
, then either
 $\rho _{\pi , {{\mathfrak q}}}$
or a quadratic character twist is crystalline (resp. semistable).
$\rho _{\pi , {{\mathfrak q}}}$
or a quadratic character twist is crystalline (resp. semistable). -
(c) If
 $\ell \notin S_{\mathrm {bad}}$
, then
$\ell \notin S_{\mathrm {bad}}$
, then
 $\rho _{\pi , {{\mathfrak q}}}$
is crystalline.
$\rho _{\pi , {{\mathfrak q}}}$
is crystalline.
-
-
(A4) For every
 $v|\infty $
,
$v|\infty $
,
 $\rho _{\pi ,v}$
is odd (see §1 and Remark 12.6 below).
$\rho _{\pi ,v}$
is odd (see §1 and Remark 12.6 below). -
(A5) The Zariski closure of the image of
 $\rho _{\pi }({\mathrm {Gal}}(\overline {F}/E))$
in
$\rho _{\pi }({\mathrm {Gal}}(\overline {F}/E))$
in
 $\mathrm {PSO}_{2n}$
maps onto one of the following four subgroups of
$\mathrm {PSO}_{2n}$
maps onto one of the following four subgroups of
 $\mathrm {PSO}_{2n}$
:
$\mathrm {PSO}_{2n}$
:-
(a)
 $\mathrm {PSO}_{2n}$
,
$\mathrm {PSO}_{2n}$
, -
(b)
 $\mathrm {PSO}_{2n-1}$
(as a reducible subgroup),
$\mathrm {PSO}_{2n-1}$
(as a reducible subgroup), -
(c) the image of a principal
 $\mathrm {SL}_2$
in
$\mathrm {SL}_2$
in
 $\mathrm {PSO}_{2n}$
or
$\mathrm {PSO}_{2n}$
or -
(d) (only when
 $n=4$
)
$n=4$
)
 $G_2$
(embedded in
$G_2$
(embedded in
 ${\mathrm {SO}}_7 \subset \mathrm {PSO}_8$
) or
${\mathrm {SO}}_7 \subset \mathrm {PSO}_8$
) or
 ${\mathrm {SO}}_7$
(as an irreducible subgroup via the projective spin representation).
${\mathrm {SO}}_7$
(as an irreducible subgroup via the projective spin representation).
-
-
(A6) If
 $\rho ' \colon {\mathrm {Gal}}(\overline {F}/F) \to {}^L G^{*}$
is another semisimple Galois representation such that, for almost all finite F-places
$\rho ' \colon {\mathrm {Gal}}(\overline {F}/F) \to {}^L G^{*}$
is another semisimple Galois representation such that, for almost all finite F-places
 ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
 $\rho '$
and
$\rho '$
and
 $\rho _{\pi }$
are unramified, the semisimple parts
$\rho _{\pi }$
are unramified, the semisimple parts
 $\rho '(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
and
$\rho '(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
and
 $\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
are conjugate, then
$\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
are conjugate, then
 $\rho $
and
$\rho $
and
 $\rho '$
are conjugate.
$\rho '$
are conjugate.
Remark 0.1. The proof of the above theorem relies crucially on the main results of Arthur’s book [Reference Arthur1], which are currently conditional as explained in footnote 2. In particular, Theorem A, and in turn Theorems B, C and D, are conditional on the same results mentioned in this footnote.
As explained below Conjecture 1, the existence of Galois representations
in a weaker form is known for cuspidal automorphic representations
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (coh
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (coh
![]() $^{\circ }$
), (St
$^{\circ }$
), (St
![]() $^{\circ }$
) and (std-reg
$^{\circ }$
) and (std-reg
![]() $^{\circ }$
) (see Section 6 for these conditions), and possibly a larger class of representations though we have not worked it out. The main ingredients are Arthur’s transfer [Reference Arthur1, Thm. 1.5.2] from
$^{\circ }$
) (see Section 6 for these conditions), and possibly a larger class of representations though we have not worked it out. The main ingredients are Arthur’s transfer [Reference Arthur1, Thm. 1.5.2] from
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
to
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
to
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
, and collective results on the Langlands correspondence for
${\mathrm {GL}}_{2n}(\mathbb A_F)$
, and collective results on the Langlands correspondence for
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
in the self-dual case. Statements (SO-i)–(SO-v) of Theorem 6.5 below summarize what we know about
${\mathrm {GL}}_{2n}(\mathbb A_F)$
in the self-dual case. Statements (SO-i)–(SO-v) of Theorem 6.5 below summarize what we know about
![]() $\rho _{\pi ^{\flat }}$
. A main drawback of Theorem 6.5 is that the conjugacy class of each
$\rho _{\pi ^{\flat }}$
. A main drawback of Theorem 6.5 is that the conjugacy class of each
![]() $\rho _{\pi ^{\flat }}(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}}$
is determined only up to
$\rho _{\pi ^{\flat }}(\mathrm {Frob}_{{\mathfrak q}})_{\mathrm {ss}}$
is determined only up to
![]() $\mathrm {O}_{2n}$
-conjugacy, rather than
$\mathrm {O}_{2n}$
-conjugacy, rather than
![]() ${\mathrm {SO}}_{2n}$
-conjugacy.
${\mathrm {SO}}_{2n}$
-conjugacy.
Using Theorem A, we can upgrade Theorem 6.5 and remove this “outer” ambiguity (coming from the outer automorphism) as long as
![]() $\pi ^{\flat }$
can be extended to a cohomological representation
$\pi ^{\flat }$
can be extended to a cohomological representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
. If
${\mathrm {GSO}}_{2n}^{E/F}$
. If
![]() $\pi $
is
$\pi $
is
![]() $\xi $
-cohomological, then
$\xi $
-cohomological, then
![]() $\xi $
must satisfy condition (cent) of §9, so a necessary condition for such a cohomological extension to exist is the following condition (which is void for
$\xi $
must satisfy condition (cent) of §9, so a necessary condition for such a cohomological extension to exist is the following condition (which is void for
![]() $F=\mathbb {Q}$
):
$F=\mathbb {Q}$
):
-
(cent°) the central character
 $ \{\pm 1\}=\mu _2(F_y)\rightarrow {\mathbb {C}}^{\times }$
of
$ \{\pm 1\}=\mu _2(F_y)\rightarrow {\mathbb {C}}^{\times }$
of
 $\pi _y$
at each infinite place y of F is independent of y.
$\pi _y$
at each infinite place y of F is independent of y.
Theorem B. Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (cent
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (cent
![]() $^{\circ }$
), (coh
$^{\circ }$
), (coh
![]() $^{\circ }$
), (St
$^{\circ }$
), (St
![]() $^{\circ }$
) and (std-reg
$^{\circ }$
) and (std-reg
![]() $^{\circ }$
). Then Conjecture 1 holds (for every
$^{\circ }$
). Then Conjecture 1 holds (for every
![]() $\ell $
and
$\ell $
and
![]() $\iota $
). The associated Galois representation
$\iota $
). The associated Galois representation
![]() $\rho _{\pi ^{\flat }}$
is characterized uniquely up to
$\rho _{\pi ^{\flat }}$
is characterized uniquely up to
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
See Theorem 13.1 below for a precise and stronger statement. The crux of the argument lies in showing that
![]() $\pi ^{\flat }$
extends to an automorphic representation
$\pi ^{\flat }$
extends to an automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, satisfying conditions of Theorem A. As Theorem A has no outer ambiguity, this yields Theorem B.
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, satisfying conditions of Theorem A. As Theorem A has no outer ambiguity, this yields Theorem B.
Theorem B offers a new perspective on the local Langlands correspondence for quasi-split forms of
![]() ${\mathrm {SO}}_{2n}$
over p-adic fields. By localizing the theorem at finite places, we get a candidate for the correspondence, not just up to
${\mathrm {SO}}_{2n}$
over p-adic fields. By localizing the theorem at finite places, we get a candidate for the correspondence, not just up to
![]() $\mathrm {O}_{2n}$
-conjugacy as in [Reference Arthur1]. More precisely, let H denote a quasi-split form of
$\mathrm {O}_{2n}$
-conjugacy as in [Reference Arthur1]. More precisely, let H denote a quasi-split form of
![]() ${\mathrm {SO}}_{2n}$
over a p-adic field k, assumed to be split if n is even. Then we can find
${\mathrm {SO}}_{2n}$
over a p-adic field k, assumed to be split if n is even. Then we can find
![]() $E/F$
as above (depending on the parity of n) and a prime
$E/F$
as above (depending on the parity of n) and a prime
![]() ${{\mathfrak q}}$
of F such that
${{\mathfrak q}}$
of F such that
![]() $F_{\mathfrak {q}}\simeq k$
and
$F_{\mathfrak {q}}\simeq k$
and
![]() ${\mathrm {SO}}^{E/F}_{2n,{{\mathfrak q}}} \simeq H$
. If
${\mathrm {SO}}^{E/F}_{2n,{{\mathfrak q}}} \simeq H$
. If
![]() $\sigma $
is an irreducible discrete series representation of
$\sigma $
is an irreducible discrete series representation of
![]() $H(k)$
, then a candidate for the L-parameter for
$H(k)$
, then a candidate for the L-parameter for
![]() $\sigma $
is described by the following procedures.
$\sigma $
is described by the following procedures.
-
(1) Find
 $\pi ^{\flat }$
satisfying (cent
$\pi ^{\flat }$
satisfying (cent
 $^{\circ }$
), (coh
$^{\circ }$
), (coh
 $^{\circ }$
), (St
$^{\circ }$
), (St
 $^{\circ }$
) and (std-reg
$^{\circ }$
) and (std-reg
 $^{\circ }$
) such that
$^{\circ }$
) such that
 $\pi ^{\flat }_{\mathfrak {q}}\simeq \sigma $
.
$\pi ^{\flat }_{\mathfrak {q}}\simeq \sigma $
. -
(2) Obtain
 $\rho _{\pi ^{\flat }}$
from Theorem B (which relies on Theorem A).
$\rho _{\pi ^{\flat }}$
from Theorem B (which relies on Theorem A). -
(3) Take
 $\mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{\mathfrak {q}}}})$
, which can be viewed as an L-parameter for
$\mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{\mathfrak {q}}}})$
, which can be viewed as an L-parameter for
 $H(k)$
.
$H(k)$
.
The globalization in (1) is possible by a standard trace formula argument proving the limit multiplicity formula. See §1 below for the definition of WD. The L-parameter resulting from the above is in the
![]() $\mathrm {O}_{2n}$
-orbit of the L-parameter in [Reference Arthur1] by Theorem 6.5 (SO-i), but could a priori depend on various choices. It is an interesting problem to relate the global construction here to the purely local constructions by Kaletha [Reference Kaletha39, Reference Kaletha37] and Fargues–Scholze [Reference Fargues and Scholze24]. In fact, all this can be mimicked for
$\mathrm {O}_{2n}$
-orbit of the L-parameter in [Reference Arthur1] by Theorem 6.5 (SO-i), but could a priori depend on various choices. It is an interesting problem to relate the global construction here to the purely local constructions by Kaletha [Reference Kaletha39, Reference Kaletha37] and Fargues–Scholze [Reference Fargues and Scholze24]. In fact, all this can be mimicked for
![]() ${\mathrm {GSO}}_{2n}$
in place of
${\mathrm {GSO}}_{2n}$
in place of
![]() ${\mathrm {SO}}_{2n}$
, using Theorem A rather than Theorem B, so a similar question may be asked in the
${\mathrm {SO}}_{2n}$
, using Theorem A rather than Theorem B, so a similar question may be asked in the
![]() ${\mathrm {GSO}}_{2n}$
-case.
${\mathrm {GSO}}_{2n}$
-case.
As another application of Theorem A, we compute the automorphic multiplicities
![]() $m(\pi )$
for certain automorphic representations
$m(\pi )$
for certain automorphic representations
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
.
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
.
Theorem C. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (std-reg). Then we have
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (std-reg). Then we have
![]() $m(\pi ) = 1$
.
$m(\pi ) = 1$
.
To compute
![]() $m(\pi )$
for
$m(\pi )$
for
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
, we rely on Theorem A, Arthur’s multiplicity formula [Reference Arthur1] and a result of Bin Xu [Reference Xu81] to show that
${\mathrm {GSO}}_{2n}^{E/F}$
, we rely on Theorem A, Arthur’s multiplicity formula [Reference Arthur1] and a result of Bin Xu [Reference Xu81] to show that
![]() $m(\pi ) = m(\pi ^{\flat })$
for
$m(\pi ) = m(\pi ^{\flat })$
for
![]() $\pi ^{\flat } \subset \pi $
a well-chosen
$\pi ^{\flat } \subset \pi $
a well-chosen
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation. We remark that Arthur’s multiplicity formula computes multiplicities up to an outer automorphism orbit, but
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation. We remark that Arthur’s multiplicity formula computes multiplicities up to an outer automorphism orbit, but
![]() $m(\pi )$
in the theorem is the honest multiplicity.
$m(\pi )$
in the theorem is the honest multiplicity.
Our final application is meromorphic continuation of the (half) spin-L functions. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
unramified away from a finite set of places S. To make uniform statements, define a set
${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
unramified away from a finite set of places S. To make uniform statements, define a set
 $$ \begin{align} \mathfrak e :=\begin{cases} \{+,-\}, & \mbox{if}~n~\mbox{is even (thus}~E=F),\\ \{\emptyset\}, & \mbox{if}~n~\mbox{is odd (thus}~[E:F]=2),\\ \end{cases} \end{align} $$
$$ \begin{align} \mathfrak e :=\begin{cases} \{+,-\}, & \mbox{if}~n~\mbox{is even (thus}~E=F),\\ \{\emptyset\}, & \mbox{if}~n~\mbox{is odd (thus}~[E:F]=2),\\ \end{cases} \end{align} $$
with the understanding that
![]() $\mathrm {spin}^{\emptyset }=\mathrm {spin}$
. The partial (half-)spin L-function for
$\mathrm {spin}^{\emptyset }=\mathrm {spin}$
. The partial (half-)spin L-function for
![]() $\pi $
away from S is by definition
$\pi $
away from S is by definition
 $$ \begin{align} L^S(s,\pi,\mathrm{spin}^{\varepsilon}):=\prod_{\mathfrak{p}\notin S} \frac{1}{\det(1-q_{\mathfrak{p}}^{-s}\mathrm{spin}^{\varepsilon}(\phi_{\pi_{\mathfrak{p}}}(\mathrm{Frob}_{\mathfrak{p}})))},\qquad \varepsilon\in \mathfrak e, \end{align} $$
$$ \begin{align} L^S(s,\pi,\mathrm{spin}^{\varepsilon}):=\prod_{\mathfrak{p}\notin S} \frac{1}{\det(1-q_{\mathfrak{p}}^{-s}\mathrm{spin}^{\varepsilon}(\phi_{\pi_{\mathfrak{p}}}(\mathrm{Frob}_{\mathfrak{p}})))},\qquad \varepsilon\in \mathfrak e, \end{align} $$
where
![]() $q_{\mathfrak {p}} := \#(\mathcal O_F/\mathfrak {p})$
and
$q_{\mathfrak {p}} := \#(\mathcal O_F/\mathfrak {p})$
and
![]() $\phi _{\pi _{\mathfrak {p}}}$
is the unramified L-parameter of
$\phi _{\pi _{\mathfrak {p}}}$
is the unramified L-parameter of
![]() $\pi _{\mathfrak {p}}$
. Consider the following hypothesis for L-parameters
$\pi _{\mathfrak {p}}$
. Consider the following hypothesis for L-parameters
![]() $\phi _{\pi _y}$
at infinite places y.
$\phi _{\pi _y}$
at infinite places y.
-
(spin-reg)
 $\mathrm {spin}^{\varepsilon }(\phi _{\pi _y})$
is regular for every infinite place y of F and every
$\mathrm {spin}^{\varepsilon }(\phi _{\pi _y})$
is regular for every infinite place y of F and every
 $\varepsilon \in \mathfrak e$
.
$\varepsilon \in \mathfrak e$
.
When
![]() $n\ge 3$
, (spin-reg) implies (std-reg). This hypothesis ensures that
$n\ge 3$
, (spin-reg) implies (std-reg). This hypothesis ensures that
![]() $\mathrm {spin}^{\varepsilon }(\rho _{\pi })$
has distinct Hodge–Tate weights. Our construction and Theorem A allow us to apply the potential automorphy theorem of Barnet-Lamb–Gee–Geraghty–Taylor [Reference Barnet-Lamb, Gee, Geraghty and Taylor3] to the weakly compatible system of
$\mathrm {spin}^{\varepsilon }(\rho _{\pi })$
has distinct Hodge–Tate weights. Our construction and Theorem A allow us to apply the potential automorphy theorem of Barnet-Lamb–Gee–Geraghty–Taylor [Reference Barnet-Lamb, Gee, Geraghty and Taylor3] to the weakly compatible system of
![]() $\mathrm {spin}^{\varepsilon }(\rho _{\pi })$
(as
$\mathrm {spin}^{\varepsilon }(\rho _{\pi })$
(as
![]() $\ell $
and
$\ell $
and
![]() $\iota $
vary). Thereby, we obtain the following.
$\iota $
vary). Thereby, we obtain the following.
Theorem D. Assume
![]() $n\ge 3$
. Let
$n\ge 3$
. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (spin-reg). Then there exists a finite totally real extension
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (spin-reg). Then there exists a finite totally real extension
![]() $F'/F$
(which can be chosen to be disjoint from any prescribed finite extension of F in
$F'/F$
(which can be chosen to be disjoint from any prescribed finite extension of F in
![]() $\overline {F}$
) such that
$\overline {F}$
) such that
![]() $\mathrm {spin}^{\varepsilon }\circ \rho _{\pi }|_{{\mathrm {Gal}}(\overline {F}/F')}$
is automorphic for each
$\mathrm {spin}^{\varepsilon }\circ \rho _{\pi }|_{{\mathrm {Gal}}(\overline {F}/F')}$
is automorphic for each
![]() $\varepsilon \in \mathfrak e$
. More precisely, there exists a cuspidal automorphic representation
$\varepsilon \in \mathfrak e$
. More precisely, there exists a cuspidal automorphic representation
![]() $\Pi ^{\varepsilon }$
of
$\Pi ^{\varepsilon }$
of
![]() ${\mathrm {GL}}_{2^n/|\mathfrak e|}(\mathbb A_{F'})$
such that
${\mathrm {GL}}_{2^n/|\mathfrak e|}(\mathbb A_{F'})$
such that
-
• for each finite place
 ${{\mathfrak q}}'$
of
${{\mathfrak q}}'$
of
 $F'$
not above
$F'$
not above
 $S_{\mathrm {bad}}\cup \{\ell \}$
, the representation
$S_{\mathrm {bad}}\cup \{\ell \}$
, the representation
 $\iota ^{-1}\mathrm {spin}^{\varepsilon }\circ \rho _{\pi }|_{W_{F^{\prime }_{{{\mathfrak q}}'}}}$
is unramified and its Frobenius semisimplification is the Langlands parameter for
$\iota ^{-1}\mathrm {spin}^{\varepsilon }\circ \rho _{\pi }|_{W_{F^{\prime }_{{{\mathfrak q}}'}}}$
is unramified and its Frobenius semisimplification is the Langlands parameter for
 $\Pi ^{\varepsilon }_w$
,
$\Pi ^{\varepsilon }_w$
, -
• at each infinite place
 $y'$
of
$y'$
of
 $F'$
above a place y of F, we have
$F'$
above a place y of F, we have
 $\phi _{\Pi ^{\varepsilon }_{y'}}|_{W_{\mathbb {C}}}\simeq \mathrm {spin}^{\varepsilon }\circ \phi _{\pi _y}|_{W_{\mathbb {C}}}$
.
$\phi _{\Pi ^{\varepsilon }_{y'}}|_{W_{\mathbb {C}}}\simeq \mathrm {spin}^{\varepsilon }\circ \phi _{\pi _y}|_{W_{\mathbb {C}}}$
.
In particular, the partial spin L-function
![]() $L^S(s,\pi ,\mathrm {spin}^{\varepsilon })$
admits a meromorphic continuation and is holomorphic and nonzero in an explicit right half plane (e.g., in the region
$L^S(s,\pi ,\mathrm {spin}^{\varepsilon })$
admits a meromorphic continuation and is holomorphic and nonzero in an explicit right half plane (e.g., in the region
![]() $\Re (s)\ge 1$
if
$\Re (s)\ge 1$
if
![]() $\pi $
has unitary central character).
$\pi $
has unitary central character).
We now give a sketch of the argument for Theorem A. For simplicity, we put ourselves in the split case (when n is even) and assume
![]() $F = \mathbb {Q}$
to simplify notation. We also ignore all character twists and duals in the following sketch and keep the isomorphism
$F = \mathbb {Q}$
to simplify notation. We also ignore all character twists and duals in the following sketch and keep the isomorphism
![]() $\iota :{\mathbb {C}}\simeq \overline {\mathbb {Q}}_{\ell }$
implicit. (See the main text for correct twists and duals.)
$\iota :{\mathbb {C}}\simeq \overline {\mathbb {Q}}_{\ell }$
implicit. (See the main text for correct twists and duals.)
The basic idea is to construct
![]() $\rho _{\pi }$
and prove its expected properties by understanding what should be
$\rho _{\pi }$
and prove its expected properties by understanding what should be
![]() $\mathrm {spin}^+ \circ \rho _{\pi }$
,
$\mathrm {spin}^+ \circ \rho _{\pi }$
,
![]() $\mathrm {spin}^- \circ \rho _{\pi }$
,
$\mathrm {spin}^- \circ \rho _{\pi }$
,
![]() $\mathrm {std}\circ \rho _{\pi }$
and
$\mathrm {std}\circ \rho _{\pi }$
and
![]() $\mathcal N \circ \rho _{\pi }$
. One already has access to
$\mathcal N \circ \rho _{\pi }$
. One already has access to
![]() $\mathrm {std}\circ \rho _{\pi }$
via Arthur’s endoscopic classification and known instances of the global Langlands correspondence. The seemingly innocuous
$\mathrm {std}\circ \rho _{\pi }$
via Arthur’s endoscopic classification and known instances of the global Langlands correspondence. The seemingly innocuous
![]() $\mathcal N \circ \rho _{\pi }$
is not so trivial to combine with the other representations, but refer to the proof of Proposition 10.5. Most importantly, we realize
$\mathcal N \circ \rho _{\pi }$
is not so trivial to combine with the other representations, but refer to the proof of Proposition 10.5. Most importantly, we realize
![]() $\mathrm {spin}^+ \circ \rho _{\pi }$
and
$\mathrm {spin}^+ \circ \rho _{\pi }$
and
![]() $\mathrm {spin}^- \circ \rho _{\pi }$
in the cohomology of suitable Shimura varieties; this is the port of embarkation.
$\mathrm {spin}^- \circ \rho _{\pi }$
in the cohomology of suitable Shimura varieties; this is the port of embarkation.
In fact,
![]() $\rho _{\pi }$
would not be recovered from
$\rho _{\pi }$
would not be recovered from
![]() $\mathrm {spin}^+ \circ \rho _{\pi }$
,
$\mathrm {spin}^+ \circ \rho _{\pi }$
,
![]() $\mathrm {spin}^- \circ \rho _{\pi }$
,
$\mathrm {spin}^- \circ \rho _{\pi }$
,
![]() $\mathrm {std}\circ \rho _{\pi }$
and
$\mathrm {std}\circ \rho _{\pi }$
and
![]() $\mathcal N \circ \rho _{\pi }$
in general due to essential group-theoretic difficulties (e.g.,
$\mathcal N \circ \rho _{\pi }$
in general due to essential group-theoretic difficulties (e.g.,
![]() $\mathrm {GSpin}_{2n}$
is not acceptable in the sense of [Reference Larsen56, Reference Larsen55]), but condition (St) mitigates the matter. Another important role of (St) is to remove complexity associated with endoscopy.
$\mathrm {GSpin}_{2n}$
is not acceptable in the sense of [Reference Larsen56, Reference Larsen55]), but condition (St) mitigates the matter. Another important role of (St) is to remove complexity associated with endoscopy.
Our Shimura varieties are associated with an inner twist
![]() $G/\mathbb {Q}$
of the split group
$G/\mathbb {Q}$
of the split group
![]() ${\mathrm {GSO}}_{2n}$
(unique up to isomorphism) which splits at all primes
${\mathrm {GSO}}_{2n}$
(unique up to isomorphism) which splits at all primes
![]() $p \neq p_{\mathrm {St}}$
and whose derived subgroup is isomorphic to the quaternionic orthogonal group
$p \neq p_{\mathrm {St}}$
and whose derived subgroup is isomorphic to the quaternionic orthogonal group
![]() ${\mathrm {SO}}^{*}(2n)$
over
${\mathrm {SO}}^{*}(2n)$
over
![]() ${\mathbb R}$
(which is not isomorphic to
${\mathbb R}$
(which is not isomorphic to
![]() ${\mathrm {SO}}(a,b)$
for any signature
${\mathrm {SO}}(a,b)$
for any signature
![]() $a+b=2n$
). Concretely,
$a+b=2n$
). Concretely,
![]() $G({\mathbb R})$
is isomorphic to the group
$G({\mathbb R})$
is isomorphic to the group
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R})$
in §8 below.
${\mathrm {GSO}}_{2n}^J({\mathbb R})$
in §8 below.
The group G admits two abelian-type Shimura data
![]() $(G, X^{\varepsilon })$
with
$(G, X^{\varepsilon })$
with
![]() $\varepsilon \in \{+,-\}$
, corresponding to the two edges of the “fork” in the Dynkin diagram of type
$\varepsilon \in \{+,-\}$
, corresponding to the two edges of the “fork” in the Dynkin diagram of type
![]() $D_n$
(see Section 9). These two Shimura data are not isomorphic. (The analogous Shimura data are isomorphic via an outer automorphism when n is odd; see Lemma (ii) below. Even then, we distinguish the two data as the outer automorphism changes isomorphism classes of representations.)
$D_n$
(see Section 9). These two Shimura data are not isomorphic. (The analogous Shimura data are isomorphic via an outer automorphism when n is odd; see Lemma (ii) below. Even then, we distinguish the two data as the outer automorphism changes isomorphism classes of representations.)
Let
![]() $\pi $
be as in Theorem A. Using a trace formula argument, we transfer
$\pi $
be as in Theorem A. Using a trace formula argument, we transfer
![]() $\pi $
to a
$\pi $
to a
![]() $\xi $
-cohomological cuspidal automorphic representation
$\xi $
-cohomological cuspidal automorphic representation
![]() $\pi ^{\natural }$
of
$\pi ^{\natural }$
of
![]() $G(\mathbb A)$
with isomorphic unramified local components as
$G(\mathbb A)$
with isomorphic unramified local components as
![]() $\pi $
such that
$\pi $
such that
![]() $\pi ^{\natural }$
is Steinberg at a finite prime. Let
$\pi ^{\natural }$
is Steinberg at a finite prime. Let
![]() $\rho _{\pi }^{\mathrm {Sh},\varepsilon }$
be the
$\rho _{\pi }^{\mathrm {Sh},\varepsilon }$
be the
![]() ${\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-representation on the
${\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-representation on the
![]() $\pi ^{\natural ,\infty }$
-isotypical part of the (semisimplified) compact support cohomology of the
$\pi ^{\natural ,\infty }$
-isotypical part of the (semisimplified) compact support cohomology of the
![]() $\ell $
-adic local system
$\ell $
-adic local system
![]() ${\mathcal L}_{\xi }/\mathrm {Sh}(G, X^{\varepsilon })$
attached to
${\mathcal L}_{\xi }/\mathrm {Sh}(G, X^{\varepsilon })$
attached to
![]() $\xi $
. Conjecturally, the two representations
$\xi $
. Conjecturally, the two representations
![]() $\rho _{\pi }^{\mathrm {Sh},\varepsilon }$
should realize
$\rho _{\pi }^{\mathrm {Sh},\varepsilon }$
should realize
![]() $\mathrm {spin}^{\varepsilon } \circ \rho _{\pi }$
up to semi-simplification (and up to a twist and a multiplicity that we ignore in this introduction) in the non-endoscopic case. In particular, if
$\mathrm {spin}^{\varepsilon } \circ \rho _{\pi }$
up to semi-simplification (and up to a twist and a multiplicity that we ignore in this introduction) in the non-endoscopic case. In particular, if
![]() $\phi _{\pi _p} \colon W_{\mathbb {Q}_p}\rightarrow \mathrm {GSpin}_{2n}({\mathbb {C}})$
is the unramified L-parameter of
$\phi _{\pi _p} \colon W_{\mathbb {Q}_p}\rightarrow \mathrm {GSpin}_{2n}({\mathbb {C}})$
is the unramified L-parameter of
![]() $\pi _p$
at a prime
$\pi _p$
at a prime
![]() $p\neq \ell $
where
$p\neq \ell $
where
![]() $\pi _p$
is unramified, then
$\pi _p$
is unramified, then
![]() $\rho _{\pi }^{\mathrm {Sh},\varepsilon }|_{{\mathrm {Gal}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)}$
ought to be unramified and satisfy
$\rho _{\pi }^{\mathrm {Sh},\varepsilon }|_{{\mathrm {Gal}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)}$
ought to be unramified and satisfy
Employing Kisin’s results on the Langlands–Rapoport conjecture [Reference Kisin42] and the Langlands–Kottwitz method for Shimura varieties of abelian type in the forthcoming work of Kisin–Shin–Zhu [Reference Kisin, Shin and Zhu43], we prove (0.4) for almost all p.
Let
![]() $\pi ^{\flat } \subset \pi $
be an irreducible cuspidal automorphic
$\pi ^{\flat } \subset \pi $
be an irreducible cuspidal automorphic
![]() ${\mathrm {SO}}_{2n}(\mathbb A)$
-subrepresentation. From the aforementioned weaker version of Conjecture 1 for
${\mathrm {SO}}_{2n}(\mathbb A)$
-subrepresentation. From the aforementioned weaker version of Conjecture 1 for
![]() ${\mathrm {SO}}_{2n}$
, we construct (see Theorem 6.5 below)
${\mathrm {SO}}_{2n}$
, we construct (see Theorem 6.5 below)
such that
for all primes
![]() $p \neq \ell $
where
$p \neq \ell $
where
![]() $\pi ^{\flat }$
is unramified. Here,
$\pi ^{\flat }$
is unramified. Here,
![]() $\overset {\circ } \sim $
indicates
$\overset {\circ } \sim $
indicates
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy, and
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy, and
![]() $\mathrm {pr}^{\circ }:\mathrm {GSpin}_{2n} \twoheadrightarrow {\mathrm {SO}}_{2n}$
is the natural surjection.
$\mathrm {pr}^{\circ }:\mathrm {GSpin}_{2n} \twoheadrightarrow {\mathrm {SO}}_{2n}$
is the natural surjection.
We expect
![]() $\rho _{\pi }$
to lift
$\rho _{\pi }$
to lift
![]() $\rho _{\pi ^{\flat }}$
(up to outer automorphism) and to sit inside
$\rho _{\pi ^{\flat }}$
(up to outer automorphism) and to sit inside
![]() $\rho ^{\mathrm {Sh}}:=\rho ^{\mathrm {Sh},+}_{\pi }\oplus \rho ^{\mathrm {Sh},-}_{\pi }$
as illustrated below. By
$\rho ^{\mathrm {Sh}}:=\rho ^{\mathrm {Sh},+}_{\pi }\oplus \rho ^{\mathrm {Sh},-}_{\pi }$
as illustrated below. By
![]() $\overline {\mathrm {spin}}$
we mean the unique projective representation of
$\overline {\mathrm {spin}}$
we mean the unique projective representation of
![]() ${\mathrm {SO}}_{2n}$
that the projectivization of
${\mathrm {SO}}_{2n}$
that the projectivization of
![]() $\mathrm {spin}$
factors through.
$\mathrm {spin}$
factors through.

We deduce from (0.4) and (0.5) that the outer diagram commutes, after a conjugation if necessary. In fact, this is not straightforward because two
![]() $\mathrm {PGL}_{2^n}$
-valued Galois representations need not be conjugate even if they map each
$\mathrm {PGL}_{2^n}$
-valued Galois representations need not be conjugate even if they map each
![]() $\mathrm {Frob}_p$
into the same conjugacy class for almost all p. We get around the difficulty by using a classification of reductive subgroups of
$\mathrm {Frob}_p$
into the same conjugacy class for almost all p. We get around the difficulty by using a classification of reductive subgroups of
![]() ${\mathrm {SO}}_{2n}$
containing a regular unipotent element by Saxl–Seitz [Reference Saxl and Seitz70]. This is applicable since (St) tells us that the image of
${\mathrm {SO}}_{2n}$
containing a regular unipotent element by Saxl–Seitz [Reference Saxl and Seitz70]. This is applicable since (St) tells us that the image of
![]() $\rho _{\pi ^{\flat }}$
contains a regular unipotent element. As a consequence, the Zariski closure of the image of
$\rho _{\pi ^{\flat }}$
contains a regular unipotent element. As a consequence, the Zariski closure of the image of
![]() $\rho _{\pi ^{\flat }}$
is connected mod center. If it is connected, we have the commutativity of (0.6) after a conjugation, and it follows that there exists
$\rho _{\pi ^{\flat }}$
is connected mod center. If it is connected, we have the commutativity of (0.6) after a conjugation, and it follows that there exists
![]() $\rho _{\pi }$
completing the diagram. If the Zariski closure is connected only mod center, then we need a variant of (0.6) as explained in §10. A similar group-theoretic consideration shows that
$\rho _{\pi }$
completing the diagram. If the Zariski closure is connected only mod center, then we need a variant of (0.6) as explained in §10. A similar group-theoretic consideration shows that
![]() $\rho _{\pi }$
is characterized up to isomorphism by the images of Frobenius elements at almost all primes, cf. (A6) of Theorem A.
$\rho _{\pi }$
is characterized up to isomorphism by the images of Frobenius elements at almost all primes, cf. (A6) of Theorem A.
Having constructed
![]() $\rho _{\pi }$
, we verify that
$\rho _{\pi }$
, we verify that
![]() $\rho _{\pi }$
enjoys the expected properties. Let us focus here on (A1). By construction,
$\rho _{\pi }$
enjoys the expected properties. Let us focus here on (A1). By construction,
The key point is to refine this, or break the symmetry, by showing the same relation with
![]() $\mathrm {spin}^+$
and
$\mathrm {spin}^+$
and
![]() $\mathrm {spin}^-$
in place of
$\mathrm {spin}^-$
in place of
![]() $\mathrm {spin}$
(cf. proof of Proposition 10.5 below) with the help of (0.4). Roughly speaking, we are in a situation
$\mathrm {spin}$
(cf. proof of Proposition 10.5 below) with the help of (0.4). Roughly speaking, we are in a situation
and want to match the
![]() $+$
and
$+$
and
![]() $-$
parts. The problem is easy enough if
$-$
parts. The problem is easy enough if
![]() $\mathrm {spin}^+\rho _{\pi }\simeq \mathrm {spin}^-\rho _{\pi }$
, as there is little to distinguish. If
$\mathrm {spin}^+\rho _{\pi }\simeq \mathrm {spin}^-\rho _{\pi }$
, as there is little to distinguish. If
![]() $\mathrm {spin}^+\rho _{\pi }\not \simeq \mathrm {spin}^-\rho _{\pi }$
, then the idea is that the
$\mathrm {spin}^+\rho _{\pi }\not \simeq \mathrm {spin}^-\rho _{\pi }$
, then the idea is that the
![]() $+$
and
$+$
and
![]() $-$
parts do not overlap at sufficiently many places (by a Chebotarev type argument) to match the
$-$
parts do not overlap at sufficiently many places (by a Chebotarev type argument) to match the
![]() $+$
and
$+$
and
![]() $-$
parts unambiguously. If
$-$
parts unambiguously. If
![]() $\mathrm {spin}^+\rho _{\pi }$
or
$\mathrm {spin}^+\rho _{\pi }$
or
![]() $\mathrm {spin}^-\rho _{\pi }$
is irreducible, it is quite doable to promote this idea to a robust argument. In general, the smaller image of
$\mathrm {spin}^-\rho _{\pi }$
is irreducible, it is quite doable to promote this idea to a robust argument. In general, the smaller image of
![]() $\rho _{\pi }$
, the harder this problem becomes. However, in certain cases where the image is really small, such as contained in a principal
$\rho _{\pi }$
, the harder this problem becomes. However, in certain cases where the image is really small, such as contained in a principal
![]() $\mathrm {PGL}_2$
, the conjugacy classes
$\mathrm {PGL}_2$
, the conjugacy classes
![]() $\rho _{\pi }(\mathrm {Frob}_p)_{\mathrm {ss}}$
are stable under outer conjugation, and there is no distinction between inner and outer conjugacy. As we also have a classification of the Zariski closure of the possible images of
$\rho _{\pi }(\mathrm {Frob}_p)_{\mathrm {ss}}$
are stable under outer conjugation, and there is no distinction between inner and outer conjugacy. As we also have a classification of the Zariski closure of the possible images of
![]() $\rho _{\pi }$
, we can deal with each case via explicit group-theoretic computation. This finishes the sketch of proof for Theorem A.
$\rho _{\pi }$
, we can deal with each case via explicit group-theoretic computation. This finishes the sketch of proof for Theorem A.
Structure of the paper
The paper splits roughly into four parts consisting of Sections 1–8 (preparation), Sections 9–12 (the core argument), Sections 13–15 (applications) and the appendices. Let us go over these parts in more detail. In Sections 1–5, we define (variants of) orthogonal groups and spin groups along with subgroups containing regular unipotent elements and the outer automorphism. We define the spin groups and their spin representations through root data as well as Clifford algebras by fixing the underlying quadratic spaces, and we clarify the relationship between them. The root-theoretic approach is natural in the context of Langlands correspondence, whereas Clifford algebras have the advantage that various maps are determined and diagrams commute on the nose and not just up to conjugation. In Section 6, we construct Galois representations for certain cuspidal automorphic representations of quasi-split even orthogonal groups. This relies on Arthur’s book [Reference Arthur1] and the known construction of automorphic Galois representations, but a few extra steps are taken to get the information that we need later on. In particular, we study what happens to the Steinberg representation under Arthur’s transfer from
![]() ${\mathrm {SO}}_{2n}^{E/F}$
to
${\mathrm {SO}}_{2n}^{E/F}$
to
![]() ${\mathrm {GL}}_{2n}$
(this relies on Appendix B). In Section 7, we list a number of basic results on comparing representations of
${\mathrm {GL}}_{2n}$
(this relies on Appendix B). In Section 7, we list a number of basic results on comparing representations of
![]() ${\mathrm {SO}}_{2n}^{E/F}$
with those of
${\mathrm {SO}}_{2n}^{E/F}$
with those of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
. Section 8 discusses properties of the real points of
${\mathrm {GSO}}_{2n}^{E/F}$
. Section 8 discusses properties of the real points of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
and introduces certain global inner forms G of
${\mathrm {GSO}}_{2n}^{E/F}$
and introduces certain global inner forms G of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
. The core argument starts in Section 9, where we take the cohomology of Shimura varieties associated with two Shimura data
${\mathrm {GSO}}_{2n}^{E/F}$
. The core argument starts in Section 9, where we take the cohomology of Shimura varieties associated with two Shimura data
![]() $(G, X^{\pm })$
to find two Galois representations
$(G, X^{\pm })$
to find two Galois representations
![]() $\rho _{\pi }^{\mathrm {Sh}, \pm }$
attached to
$\rho _{\pi }^{\mathrm {Sh}, \pm }$
attached to
![]() $\pi $
as in the main theorem. In Section 10 we construct a
$\pi $
as in the main theorem. In Section 10 we construct a
![]() $\mathrm {GSpin}_{2n}$
-valued Galois representation
$\mathrm {GSpin}_{2n}$
-valued Galois representation
![]() $\rho _{\pi }$
of
$\rho _{\pi }$
of
![]() ${\mathrm {Gal}}(\overline {F}/E)$
from
${\mathrm {Gal}}(\overline {F}/E)$
from
![]() $\rho _{\pi }^{\mathrm {Sh}, \pm }$
and
$\rho _{\pi }^{\mathrm {Sh}, \pm }$
and
![]() $\rho _{\pi ^{\flat }}$
. This representation is not quite the one of Theorem A: The image of Frobenius under
$\rho _{\pi ^{\flat }}$
. This representation is not quite the one of Theorem A: The image of Frobenius under
![]() $\rho _{\pi }$
is controlled only outside an unspecified finite set of primes, and moreover,
$\rho _{\pi }$
is controlled only outside an unspecified finite set of primes, and moreover,
![]() $\rho _{\pi }$
should be extended to a representation of
$\rho _{\pi }$
should be extended to a representation of
![]() ${\mathrm {Gal}}(\overline {F}/F)$
. The two problems are resolved in Sections 11 and 12, respectively. We emphasize that neither of these arguments is formal: the first one relies on Bin Xu’s work [Reference Xu81] and the second on a subtle global argument. The proof of Theorem A is also completed in Section 12. Sections 13–15 present applications of our main theorem to the construction of Galois representations for
${\mathrm {Gal}}(\overline {F}/F)$
. The two problems are resolved in Sections 11 and 12, respectively. We emphasize that neither of these arguments is formal: the first one relies on Bin Xu’s work [Reference Xu81] and the second on a subtle global argument. The proof of Theorem A is also completed in Section 12. Sections 13–15 present applications of our main theorem to the construction of Galois representations for
![]() ${\mathrm {SO}}_{2n}^{E/F}$
, automorphic multiplicity and meromorphic continuation of (half)-spin L-functions.
${\mathrm {SO}}_{2n}^{E/F}$
, automorphic multiplicity and meromorphic continuation of (half)-spin L-functions.
1 Notation and preliminaries
We fix the following notation.
-
•
 $n \geq 3$
is an integer.Footnote 3
$n \geq 3$
is an integer.Footnote 3 -
• If k is a field,
 $\overline k$
denotes an algebraic closure of k.
$\overline k$
denotes an algebraic closure of k. -
• When X is a square matrix,
 $\mathscr {EV}(X)$
denotes the multi-set of eigenvalues of X.
$\mathscr {EV}(X)$
denotes the multi-set of eigenvalues of X. -
• When A is a multi-set with elements in a ring R with
 $r\in R$
, write
$r\in R$
, write
 $r\cdot A$
for the multi-set formed by the elements
$r\cdot A$
for the multi-set formed by the elements
 $ra \in A$
as a ranges over A. For
$ra \in A$
as a ranges over A. For
 $n\in \mathbb Z_{>0}$
, write
$n\in \mathbb Z_{>0}$
, write
 $A^{\oplus n}$
for the multi-set consisting of
$A^{\oplus n}$
for the multi-set consisting of
 $a\in A$
whose multiplicity in
$a\in A$
whose multiplicity in
 $A^n$
is n times that in A.
$A^n$
is n times that in A. -
• F is a number field. (In the main text, F is a totally real field with a distinguished embedding into
 ${\mathbb {C}}$
.)
${\mathbb {C}}$
.) -
•
 $\mathcal {O}_F$
is the ring of integers of F.
$\mathcal {O}_F$
is the ring of integers of F. -
•
 $\mathbb A_F$
is the ring of adèles of F,
$\mathbb A_F$
is the ring of adèles of F,
 $\mathbb A_F := (F \otimes {\mathbb R}) \times (F \otimes \widehat {\mathbb {Z}})$
.
$\mathbb A_F := (F \otimes {\mathbb R}) \times (F \otimes \widehat {\mathbb {Z}})$
. -
• If S is a finite set of F-places, then
 $\mathbb A_F^S \subset \mathbb A_F$
is the ring of adèles with trivial components at the places in S, and
$\mathbb A_F^S \subset \mathbb A_F$
is the ring of adèles with trivial components at the places in S, and
 $F_S := \prod _{v \in S} F_v$
;
$F_S := \prod _{v \in S} F_v$
;
 $F_{\infty }:=F\otimes _{\mathbb {Q}} {\mathbb R}$
.
$F_{\infty }:=F\otimes _{\mathbb {Q}} {\mathbb R}$
. -
• If
 ${{\mathfrak q}}$
is a finite F-place, we write
${{\mathfrak q}}$
is a finite F-place, we write
 $q_{{\mathfrak q}}$
for the cardinality of the residue field of
$q_{{\mathfrak q}}$
for the cardinality of the residue field of
 ${{\mathfrak q}}$
.
${{\mathfrak q}}$
. -
•
 $|\cdot |:\mathbb A_F^{\times } \rightarrow {\mathbb R}^{\times }_{>0}$
is the norm character on
$|\cdot |:\mathbb A_F^{\times } \rightarrow {\mathbb R}^{\times }_{>0}$
is the norm character on
 $\mathbb A_F^{\times }$
that is trivial on
$\mathbb A_F^{\times }$
that is trivial on
 $F^{\times }$
. Denote by
$F^{\times }$
. Denote by
 $|\cdot |_v:F_v^{\times } \rightarrow {\mathbb R}^{\times }_{>0}$
the restriction of
$|\cdot |_v:F_v^{\times } \rightarrow {\mathbb R}^{\times }_{>0}$
the restriction of
 $|\cdot |$
to the v-component. Our normalization is that
$|\cdot |$
to the v-component. Our normalization is that
 $|\cdot |_{{\mathfrak q}}$
sends a uniformizer of
$|\cdot |_{{\mathfrak q}}$
sends a uniformizer of
 $F_{\mathfrak {q}}$
to
$F_{\mathfrak {q}}$
to
 $q_{{\mathfrak q}}^{-1}$
, whereas
$q_{{\mathfrak q}}^{-1}$
, whereas
 $|\cdot |_v$
is the usual absolute value (resp. squared absolute value) when v is real (resp. complex).
$|\cdot |_v$
is the usual absolute value (resp. squared absolute value) when v is real (resp. complex). -
• If S is a set of prime numbers, we write
 $S^F$
for the set of F-places above S.
$S^F$
for the set of F-places above S. -
• If p is a prime number, then
 $F_p := F \otimes _{\mathbb {Q}} {\mathbb {Q}_p}$
.
$F_p := F \otimes _{\mathbb {Q}} {\mathbb {Q}_p}$
. -
•
 $\ell $
is a primenumber (typically different from p).
$\ell $
is a primenumber (typically different from p). -
•
 $\overline {\mathbb {Q}}_{\ell }$
is a fixed algebraic closure of
$\overline {\mathbb {Q}}_{\ell }$
is a fixed algebraic closure of
 $\mathbb {Q}_{\ell }$
, and
$\mathbb {Q}_{\ell }$
, and
 $\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
is an isomorphism.
$\iota \colon {\mathbb {C}} \overset \sim \to \overline {\mathbb {Q}}_{\ell }$
is an isomorphism. -
• For each prime number p, we fix the positive root
 $ p^{1/2} \in {\mathbb R}_{>0} \subset {\mathbb {C}}$
. From
$ p^{1/2} \in {\mathbb R}_{>0} \subset {\mathbb {C}}$
. From
 $\iota $
, we then obtain a choice for
$\iota $
, we then obtain a choice for
 $p^{1/2} \in \overline {\mathbb {Q}}_{\ell }$
. If q is a power of p, we obtain similarly a preferred choice
$p^{1/2} \in \overline {\mathbb {Q}}_{\ell }$
. If q is a power of p, we obtain similarly a preferred choice
 $q^{1/2}$
in
$q^{1/2}$
in
 $\overline {\mathbb {Q}}_{\ell }$
and in
$\overline {\mathbb {Q}}_{\ell }$
and in
 ${\mathbb {C}}$
.
${\mathbb {C}}$
. -
•
 $\Gamma =\Gamma _F:= {\mathrm {Gal}}(\overline {F}/F)$
is the absolute Galois group of F.
$\Gamma =\Gamma _F:= {\mathrm {Gal}}(\overline {F}/F)$
is the absolute Galois group of F. -
• For a finite extension E of F in
 $\overline {F}$
, write
$\overline {F}$
, write
 $\Gamma _E:={\mathrm {Gal}}(\overline {F}/E)$
and
$\Gamma _E:={\mathrm {Gal}}(\overline {F}/E)$
and
 $\Gamma _{E/F}:={\mathrm {Gal}}(E/F)$
.
$\Gamma _{E/F}:={\mathrm {Gal}}(E/F)$
. -
•
 $\Gamma _v = \Gamma _{F_v}:={\mathrm {Gal}}(\overline {F}_v/F_v)$
is (one of) the local Galois group(s) of F at the place v;
$\Gamma _v = \Gamma _{F_v}:={\mathrm {Gal}}(\overline {F}_v/F_v)$
is (one of) the local Galois group(s) of F at the place v;
 $W_{F_v} \subset \Gamma _v$
is the corresponding Weil group.
$W_{F_v} \subset \Gamma _v$
is the corresponding Weil group. -
• For each F-place v, choose an embedding
 $\iota _v:\overline {F} \hookrightarrow \overline {F}_v$
, which induces
$\iota _v:\overline {F} \hookrightarrow \overline {F}_v$
, which induces
 $\Gamma _v\hookrightarrow \Gamma $
that is canonical up to conjugation.
$\Gamma _v\hookrightarrow \Gamma $
that is canonical up to conjugation. -
•
 $\mathcal V_{\infty }:= \mathrm {Hom}_{\mathbb {Q}}(F, {\mathbb R})$
is the set of infinite places of F.
$\mathcal V_{\infty }:= \mathrm {Hom}_{\mathbb {Q}}(F, {\mathbb R})$
is the set of infinite places of F. -
•
 $c_y\in \Gamma $
is the complex conjugation (well-defined as a conjugacy class) induced by any embedding
$c_y\in \Gamma $
is the complex conjugation (well-defined as a conjugacy class) induced by any embedding
 $\overline {F}\hookrightarrow {\mathbb {C}}$
extending
$\overline {F}\hookrightarrow {\mathbb {C}}$
extending
 $y\in \mathcal V_{\infty }$
.
$y\in \mathcal V_{\infty }$
. -
• If S is a finite set of F-places, write
 $\Gamma _{F,S}$
for the Galois group
$\Gamma _{F,S}$
for the Galois group
 ${\mathrm {Gal}}(F(S)/F)$
where
${\mathrm {Gal}}(F(S)/F)$
where
 $F(S) \subset \overline {F}$
is the maximal extension of F that is unramified away from S. If S is a set of rational places, we write
$F(S) \subset \overline {F}$
is the maximal extension of F that is unramified away from S. If S is a set of rational places, we write
 $\Gamma _{F, S} := \Gamma _{F, S^F}$
.
$\Gamma _{F, S} := \Gamma _{F, S^F}$
. -
•
 $\mathrm {Frob}_{\mathfrak {q}}$
at a finite prime
$\mathrm {Frob}_{\mathfrak {q}}$
at a finite prime
 ${{\mathfrak q}}$
of F means the geometric Frobenius element in the quotient of
${{\mathfrak q}}$
of F means the geometric Frobenius element in the quotient of
 $\Gamma _{\mathfrak {q}}$
by the inertia subgroup, or the image thereof in
$\Gamma _{\mathfrak {q}}$
by the inertia subgroup, or the image thereof in
 $\Gamma _{F,S}$
. (The image in
$\Gamma _{F,S}$
. (The image in
 $\Gamma _{F,S}$
depends on the choice of
$\Gamma _{F,S}$
depends on the choice of
 $\iota _{\mathfrak {q}}$
, but its conjugacy class is independent of the choice.)
$\iota _{\mathfrak {q}}$
, but its conjugacy class is independent of the choice.) -
• When G is a connected reductive group over F, write
 $\widehat G$
and
$\widehat G$
and
 $^L G= \widehat G\rtimes \Gamma _F$
for the Langlands dual group and the L-group, respectively (with coefficients in
$^L G= \widehat G\rtimes \Gamma _F$
for the Langlands dual group and the L-group, respectively (with coefficients in
 ${\mathbb {C}}$
or
${\mathbb {C}}$
or
 $\overline {\mathbb {Q}}_{\ell }$
, depending on the context). If G splits over a finite extension
$\overline {\mathbb {Q}}_{\ell }$
, depending on the context). If G splits over a finite extension
 $E/F$
in
$E/F$
in
 $\overline {F}$
, then
$\overline {F}$
, then
 $\widehat G\rtimes \Gamma _{E/F}$
denotes the L-group with respect to
$\widehat G\rtimes \Gamma _{E/F}$
denotes the L-group with respect to
 $E/F$
. (Namely, such a semi-direct product is always understood with the L-action of
$E/F$
. (Namely, such a semi-direct product is always understood with the L-action of
 $\Gamma _{E/F}$
on
$\Gamma _{E/F}$
on
 $\widehat G$
.) Often we use
$\widehat G$
.) Often we use
 $^L G$
to mean
$^L G$
to mean
 $\widehat G\rtimes \Gamma _{E/F}$
.Footnote 4
$\widehat G\rtimes \Gamma _{E/F}$
.Footnote 4 -
• When H is a reductive group over
 $\overline {\mathbb {Q}}_{\ell }$
, we also use H to mean the topological group
$\overline {\mathbb {Q}}_{\ell }$
, we also use H to mean the topological group
 $H(\overline {\mathbb {Q}}_{\ell })$
by abuse of notation. This should be clear from the context and not leading to confusion.
$H(\overline {\mathbb {Q}}_{\ell })$
by abuse of notation. This should be clear from the context and not leading to confusion. -
• When F is a p-adic field and G is the set of F-points of a reductive group over F, we write
 $\mathrm {St}_G$
for the Steinberg representation of G (defined in [Reference Borel and Wallach8, X.4.6], for instance). Moreover, we write
$\mathrm {St}_G$
for the Steinberg representation of G (defined in [Reference Borel and Wallach8, X.4.6], for instance). Moreover, we write
 $\textbf {1}_G$
for the trivial representation of G. In certain cases, when G is clear, we write
$\textbf {1}_G$
for the trivial representation of G. In certain cases, when G is clear, we write
 $\mathrm {St} = \mathrm {St}_G$
or
$\mathrm {St} = \mathrm {St}_G$
or
 $\textbf {1} = \textbf {1}_G$
. We also sometimes write
$\textbf {1} = \textbf {1}_G$
. We also sometimes write
 $\mathrm {St}_n$
for
$\mathrm {St}_n$
for
 $\mathrm {St}_{{\mathrm {GL}}_n(F)}$
(in case F is clear from the context).
$\mathrm {St}_{{\mathrm {GL}}_n(F)}$
(in case F is clear from the context). -
• If G is an algebraic group, we write
 $Z(G)$
for its center.
$Z(G)$
for its center. -
• An inner twist of a reductive group G over a perfect field k means a reductive group
 $G'$
over k together with an isomorphism
$G'$
over k together with an isomorphism
 $i:G_{\overline k}\rightarrow G^{\prime }_{\overline k}$
such that the automorphism
$i:G_{\overline k}\rightarrow G^{\prime }_{\overline k}$
such that the automorphism
 $i^{-1}\sigma (i)$
of
$i^{-1}\sigma (i)$
of
 $G_{\overline k}$
is inner for every
$G_{\overline k}$
is inner for every
 $\sigma \in {\mathrm {Gal}}(\overline k/k)$
. There is an obvious notion of isomorphism for inner twists
$\sigma \in {\mathrm {Gal}}(\overline k/k)$
. There is an obvious notion of isomorphism for inner twists
 $(G',i)$
, cf. [Reference Kaletha38, 2.2]. We often say
$(G',i)$
, cf. [Reference Kaletha38, 2.2]. We often say
 $G'$
is an inner twist of G, keeping i implicit. If we forget i and only remember the k-group
$G'$
is an inner twist of G, keeping i implicit. If we forget i and only remember the k-group
 $G'$
and the existence of i, we refer to it as an inner form of G.
$G'$
and the existence of i, we refer to it as an inner form of G.
Fix G and
![]() $E/F$
as above. We introduce some notions on the Galois side. By an (
$E/F$
as above. We introduce some notions on the Galois side. By an (
![]() $\ell $
-adic) Galois representation of
$\ell $
-adic) Galois representation of
![]() $\Gamma _F$
(with values in
$\Gamma _F$
(with values in
![]() $\widehat G\rtimes \Gamma _{E/F}$
), we mean a continuous morphism
$\widehat G\rtimes \Gamma _{E/F}$
), we mean a continuous morphism
which factors through
![]() $\Gamma _{F,S}$
for some finite set S and commutes with the obvious projections onto
$\Gamma _{F,S}$
for some finite set S and commutes with the obvious projections onto
![]() $\Gamma _{E/F}$
. Similarly, we define a Galois representation with the source
$\Gamma _{E/F}$
. Similarly, we define a Galois representation with the source
![]() $\Gamma _{\mathfrak {q}}$
or with values in
$\Gamma _{\mathfrak {q}}$
or with values in
![]() $^L G(\overline {\mathbb {Q}}_{\ell })$
. Two Galois representations are considered isomorphic if they are conjugate by an element of
$^L G(\overline {\mathbb {Q}}_{\ell })$
. Two Galois representations are considered isomorphic if they are conjugate by an element of
![]() $\widehat {G}(\overline {\mathbb {Q}}_{\ell })$
. We say that
$\widehat {G}(\overline {\mathbb {Q}}_{\ell })$
. We say that
![]() $\rho $
as above is (totally) odd if for every real place y of F, the following holds: writing
$\rho $
as above is (totally) odd if for every real place y of F, the following holds: writing
![]() $\mathrm {Ad}$
for the adjoint action of
$\mathrm {Ad}$
for the adjoint action of
![]() $^L G$
on
$^L G$
on
![]() $\mathrm {Lie}\, G(\overline {\mathbb {Q}}_{\ell })$
, which preserves the Lie algebra of the derived subgroup
$\mathrm {Lie}\, G(\overline {\mathbb {Q}}_{\ell })$
, which preserves the Lie algebra of the derived subgroup
![]() $G_{\mathrm {der}}$
, the image of
$G_{\mathrm {der}}$
, the image of
![]() $c_y$
under the composite
$c_y$
under the composite
has trace equal to the rank of
![]() $\widehat G_{\mathrm {der}}$
. (Compare with [Reference Gross27].)
$\widehat G_{\mathrm {der}}$
. (Compare with [Reference Gross27].)
An
![]() $^L G$
-valued Weil–Deligne representation of
$^L G$
-valued Weil–Deligne representation of
![]() $W_{F_{\mathfrak {q}}}$
is a pair
$W_{F_{\mathfrak {q}}}$
is a pair
![]() $(r,N)$
consisting of a morphism
$(r,N)$
consisting of a morphism
which has open kernel on the inertia subgroup and commutes with the canonical projections onto
![]() $ \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
, and a nilpotent operator
$ \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
, and a nilpotent operator
![]() $N\in \mathrm {Lie}\, \widehat {G}(\overline {\mathbb {Q}}_{\ell })$
such that
$N\in \mathrm {Lie}\, \widehat {G}(\overline {\mathbb {Q}}_{\ell })$
such that
![]() $\mathrm {Ad} (r(w)) N= |w| N$
for
$\mathrm {Ad} (r(w)) N= |w| N$
for
![]() $w\in W_{F_{\mathfrak {q}}}$
, where
$w\in W_{F_{\mathfrak {q}}}$
, where
![]() $|\cdot |:W_{F_{\mathfrak {q}}}\rightarrow \|{{\mathfrak q}}\|^{\mathbb Z}$
is the homomorphism sending a geometric Frobenius element to
$|\cdot |:W_{F_{\mathfrak {q}}}\rightarrow \|{{\mathfrak q}}\|^{\mathbb Z}$
is the homomorphism sending a geometric Frobenius element to
![]() $\|{{\mathfrak q}}\|^{-1}$
; here,
$\|{{\mathfrak q}}\|^{-1}$
; here,
![]() $\|{{\mathfrak q}}\|\in \mathbb Z_{>0}$
denotes the norm of
$\|{{\mathfrak q}}\|\in \mathbb Z_{>0}$
denotes the norm of
![]() ${{\mathfrak q}}$
. The Frobenius-semisimplification
${{\mathfrak q}}$
. The Frobenius-semisimplification
![]() $(r^{\mathrm {ss}},N)$
is obtained by replacing r with its semisimplification. We say
$(r^{\mathrm {ss}},N)$
is obtained by replacing r with its semisimplification. We say
![]() $(r,N)$
is Frobenius-semisimple if
$(r,N)$
is Frobenius-semisimple if
![]() $r=r^{\mathrm {ss}}$
.
$r=r^{\mathrm {ss}}$
.
Let
![]() $\rho \colon \Gamma _F \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
be a Galois representation. Write
$\rho \colon \Gamma _F \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
be a Galois representation. Write
![]() ${\mathfrak p}$
for the prime of E induced by
${\mathfrak p}$
for the prime of E induced by
![]() $\iota _{\mathfrak {q}}:\overline {F} \hookrightarrow \overline {F}_{\mathfrak {q}}$
. Then the restriction (via
$\iota _{\mathfrak {q}}:\overline {F} \hookrightarrow \overline {F}_{\mathfrak {q}}$
. Then the restriction (via
![]() $\iota _{\mathfrak {q}}$
)
$\iota _{\mathfrak {q}}$
)
gives rise to an
![]() $^L G$
-valued Weil–Deligne representation, to be denoted by
$^L G$
-valued Weil–Deligne representation, to be denoted by
![]() $\mathrm {WD}(\rho |_{\Gamma _{F_{\mathfrak {q}}}})$
. The construction follows from the case of
$\mathrm {WD}(\rho |_{\Gamma _{F_{\mathfrak {q}}}})$
. The construction follows from the case of
![]() $G={\mathrm {GL}}_n$
by the Tannakian formalism via algebraic representations of
$G={\mathrm {GL}}_n$
by the Tannakian formalism via algebraic representations of
![]() $\widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
. (The case
$\widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
. (The case
![]() ${{\mathfrak q}}|\ell $
is more subtle than
${{\mathfrak q}}|\ell $
is more subtle than
![]() ${{\mathfrak q}}\nmid \ell $
. In the former case, a detailed explanation is given in the proof of [Reference Kret and Shin50, Lem. 3.2], where
${{\mathfrak q}}\nmid \ell $
. In the former case, a detailed explanation is given in the proof of [Reference Kret and Shin50, Lem. 3.2], where
![]() $\widehat G$
is denoted by H. In loc. cit.
$\widehat G$
is denoted by H. In loc. cit.
![]() $\Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
is trivial but the same argument extends.) When
$\Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
is trivial but the same argument extends.) When
![]() ${{\mathfrak q}}\nmid \ell $
, one can alternatively appeal to Grothendieck’s
${{\mathfrak q}}\nmid \ell $
, one can alternatively appeal to Grothendieck’s
![]() $\ell $
-adic monodromy theorem to construct
$\ell $
-adic monodromy theorem to construct
![]() $\mathrm {WD}(\rho |_{\Gamma _{F_{\mathfrak {q}}}})$
directly (without going through general linear groups).
$\mathrm {WD}(\rho |_{\Gamma _{F_{\mathfrak {q}}}})$
directly (without going through general linear groups).
A local L-parameter
![]() $\phi :W_{F_{\mathfrak {q}}} \times \mathrm {SL}(2)\rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
is associated with a Frobenius-semisimple
$\phi :W_{F_{\mathfrak {q}}} \times \mathrm {SL}(2)\rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E_{\mathfrak p}/F_{\mathfrak {q}}}$
is associated with a Frobenius-semisimple
![]() $^L G$
-valued Weil–Deligne representation
$^L G$
-valued Weil–Deligne representation
![]() $(r,N)$
given by the following recipe:
$(r,N)$
given by the following recipe:
 $$ \begin{align*}r(w) = \phi\left( w, \begin{pmatrix} |w|^{1/2} & 0 \\ 0 & |w|^{-1/2} \end{pmatrix} \right), \qquad \mbox{and}\qquad N = \phi\left( 1,\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \right). \end{align*} $$
$$ \begin{align*}r(w) = \phi\left( w, \begin{pmatrix} |w|^{1/2} & 0 \\ 0 & |w|^{-1/2} \end{pmatrix} \right), \qquad \mbox{and}\qquad N = \phi\left( 1,\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \right). \end{align*} $$
This induces a bijection on the sets of equivalence classes of such objects [Reference Gross and Reeder28, Prop. 2.2]. In practice (where only equivalence classes matter), we will use them interchangeably.
We introduce some further notation and conventions in representation theory. If
![]() $\pi $
is a representation on a complex vector space, then we set
$\pi $
is a representation on a complex vector space, then we set
![]() $\iota \pi :=\pi \otimes _{{\mathbb {C}},\iota } \overline {\mathbb {Q}}_{\ell }$
. Similarly, if
$\iota \pi :=\pi \otimes _{{\mathbb {C}},\iota } \overline {\mathbb {Q}}_{\ell }$
. Similarly, if
![]() $\phi $
is a local L-parameter of a connected reductive group G over a nonarchimedean local field so that
$\phi $
is a local L-parameter of a connected reductive group G over a nonarchimedean local field so that
![]() $\phi $
maps into
$\phi $
maps into
![]() $^L G({\mathbb {C}})$
, then
$^L G({\mathbb {C}})$
, then
![]() $\iota \phi $
is the parameter with values in
$\iota \phi $
is the parameter with values in
![]() $^L G(\overline {\mathbb {Q}}_{\ell })$
obtained from
$^L G(\overline {\mathbb {Q}}_{\ell })$
obtained from
![]() $\phi $
via
$\phi $
via
![]() $\iota $
. If G is a locally profinite group equipped with a Haar measure, then we write
$\iota $
. If G is a locally profinite group equipped with a Haar measure, then we write
![]() $\mathcal H(G)$
for the Hecke algebra of locally constant, complex valued functions with compact support. We write
$\mathcal H(G)$
for the Hecke algebra of locally constant, complex valued functions with compact support. We write
![]() $\mathcal H_{\overline {\mathbb {Q}}_{\ell }}(G)$
for the same algebra but now consisting of
$\mathcal H_{\overline {\mathbb {Q}}_{\ell }}(G)$
for the same algebra but now consisting of
![]() $\overline {\mathbb {Q}}_{\ell }$
-valued functions. We normalize every parabolic induction by the half power of the modulus character as in [Reference Bernstein and Zelevinsky7, 1.8], so that it preserves unitarity.
$\overline {\mathbb {Q}}_{\ell }$
-valued functions. We normalize every parabolic induction by the half power of the modulus character as in [Reference Bernstein and Zelevinsky7, 1.8], so that it preserves unitarity.
Let G be a real reductive group, K a maximal compact subgroup of
![]() $G({\mathbb R})$
, and
$G({\mathbb R})$
, and
![]() $\tilde K := K \cdot Z(G)({\mathbb R})$
. Let
$\tilde K := K \cdot Z(G)({\mathbb R})$
. Let
![]() $\xi $
be an irreducible algebraic representation of G over
$\xi $
be an irreducible algebraic representation of G over
![]() ${\mathbb {C}}$
. An irreducible admissible representation
${\mathbb {C}}$
. An irreducible admissible representation
![]() $\pi $
of
$\pi $
of
![]() $G({\mathbb R})$
is said to be
$G({\mathbb R})$
is said to be
![]() $\xi $
-cohomological if
$\xi $
-cohomological if
![]() $H^i(\mathrm {Lie}\, G({\mathbb {C}}),\tilde K, \pi \otimes _{\mathbb {C}} \xi )\neq 0$
for some
$H^i(\mathrm {Lie}\, G({\mathbb {C}}),\tilde K, \pi \otimes _{\mathbb {C}} \xi )\neq 0$
for some
![]() $i\ge 0$
. If this is the case, we assign a Hodge cocharacter over
$i\ge 0$
. If this is the case, we assign a Hodge cocharacter over
![]() ${\mathbb {C}}$
(well-defined up to
${\mathbb {C}}$
(well-defined up to
![]() $\widehat G$
-conjugacy) as in [Reference Kret and Shin50, Def 1.14]:
$\widehat G$
-conjugacy) as in [Reference Kret and Shin50, Def 1.14]:
Let L be a finite extension of
![]() $\mathbb {Q}_{\ell }$
. Let H be a possibly disconnected reductive group over
$\mathbb {Q}_{\ell }$
. Let H be a possibly disconnected reductive group over
![]() $\overline {\mathbb {Q}}_{\ell }$
(e.g., an L-group relative to a finite Galois extension), and
$\overline {\mathbb {Q}}_{\ell }$
(e.g., an L-group relative to a finite Galois extension), and
![]() $\rho \colon {\mathrm {Gal}}(\overline L/L)\rightarrow H(\overline {\mathbb {Q}}_{\ell })$
a continuous morphism. If
$\rho \colon {\mathrm {Gal}}(\overline L/L)\rightarrow H(\overline {\mathbb {Q}}_{\ell })$
a continuous morphism. If
![]() $\rho $
is Hodge–Tate with respect to each
$\rho $
is Hodge–Tate with respect to each
![]() $\mathbb {Q}_{\ell }$
-embedding
$\mathbb {Q}_{\ell }$
-embedding
![]() $i \colon L \hookrightarrow \overline {\mathbb {Q}}_{\ell }$
, we define a Hodge–Tate cocharacter over
$i \colon L \hookrightarrow \overline {\mathbb {Q}}_{\ell }$
, we define a Hodge–Tate cocharacter over
![]() $\overline {\mathbb {Q}}_{\ell }$
(well-defined up to H-conjugacy) as in [Reference Buzzard and Gee12, §2.4] (cf. [Reference Kret and Shin50, Def 1.10]):
$\overline {\mathbb {Q}}_{\ell }$
(well-defined up to H-conjugacy) as in [Reference Buzzard and Gee12, §2.4] (cf. [Reference Kret and Shin50, Def 1.10]):
We recall the following lemma that can be easily deduced from the Chebotarev density theorem, as it will be needed in §10. Let F be a number field. The density of a set S consisting of primes of F is defined to be the limit
![]() $d(S) = \lim _{n \to \infty } a_n(S) / a_n(F)$
, where
$d(S) = \lim _{n \to \infty } a_n(S) / a_n(F)$
, where
![]() $a_n(F)$
is the number of primes
$a_n(F)$
is the number of primes
![]() ${{\mathfrak q}}$
with bounded norm
${{\mathfrak q}}$
with bounded norm
![]() $\|{{\mathfrak q}}\| < n$
and
$\|{{\mathfrak q}}\| < n$
and
![]() $a_n(S)$
is the number of
$a_n(S)$
is the number of
![]() ${{\mathfrak q}} \in S$
with
${{\mathfrak q}} \in S$
with
![]() $\|{{\mathfrak q}}\| < n$
[Reference Serre72, Sect. I.2.2]. Depending on S, the limit
$\|{{\mathfrak q}}\| < n$
[Reference Serre72, Sect. I.2.2]. Depending on S, the limit
![]() $d(S)$
may or may not exist — in the former case, we say S has density
$d(S)$
may or may not exist — in the former case, we say S has density
![]() $d(S)$
, and otherwise we leave the density undefined.
$d(S)$
, and otherwise we leave the density undefined.
Lemma 1.1. Let S be a finite set of places of a number field F. Let
![]() $G/\overline {\mathbb {Q}}_{\ell }$
be a linear algebraic group and let
$G/\overline {\mathbb {Q}}_{\ell }$
be a linear algebraic group and let
![]() $r \colon \Gamma _{F,S} \to G(\overline {\mathbb {Q}}_{\ell })$
be a Galois representation with Zariski dense image. Let
$r \colon \Gamma _{F,S} \to G(\overline {\mathbb {Q}}_{\ell })$
be a Galois representation with Zariski dense image. Let
![]() $X \subset G$
be a closed subvariety that is invariant by G-conjugation and such that
$X \subset G$
be a closed subvariety that is invariant by G-conjugation and such that
![]() $\dim (X) < \dim (G)$
. Then the set of F-places
$\dim (X) < \dim (G)$
. Then the set of F-places
![]() ${{\mathfrak q}} \notin S$
with
${{\mathfrak q}} \notin S$
with
![]() $r(\mathrm {Frob}_{\mathfrak {q}}) \in X(\overline {\mathbb {Q}}_{\ell })$
has density
$r(\mathrm {Frob}_{\mathfrak {q}}) \in X(\overline {\mathbb {Q}}_{\ell })$
has density
![]() $0$
.
$0$
.
Proof. Let
![]() $\mu $
be the Haar measure on
$\mu $
be the Haar measure on
![]() $\Gamma _{S} = \Gamma _{F,S}$
with total volume
$\Gamma _{S} = \Gamma _{F,S}$
with total volume
![]() $1$
. We write X to also mean
$1$
. We write X to also mean
![]() $X(\overline {\mathbb {Q}}_{\ell })$
to simplify notation. Then
$X(\overline {\mathbb {Q}}_{\ell })$
to simplify notation. Then
![]() $Y = r^{-1}(X)$
is a closed subset of
$Y = r^{-1}(X)$
is a closed subset of
![]() $\Gamma _S$
(hence measurable) and stable under
$\Gamma _S$
(hence measurable) and stable under
![]() $\Gamma _S$
-conjugation. If we further have that
$\Gamma _S$
-conjugation. If we further have that
![]() $\mu (Y)=0$
, then the Chebotarev density theorem [Reference Serre72, I-8 Cor. 2b] implies that the set of places
$\mu (Y)=0$
, then the Chebotarev density theorem [Reference Serre72, I-8 Cor. 2b] implies that the set of places
![]() ${{\mathfrak q}} \notin S$
such that
${{\mathfrak q}} \notin S$
such that
![]() $\mathrm {Frob}_{{\mathfrak q}} \in Y$
has measure
$\mathrm {Frob}_{{\mathfrak q}} \in Y$
has measure
![]() $0$
, so we will be done.
$0$
, so we will be done.
So it suffices to prove that
![]() $\mu (Y) = 0$
. We induct on
$\mu (Y) = 0$
. We induct on
![]() $\dim (X)\in \{0,1,\ldots ,\dim (G)-1\}$
. We may assume that X is irreducible by induction. When
$\dim (X)\in \{0,1,\ldots ,\dim (G)-1\}$
. We may assume that X is irreducible by induction. When
![]() $\dim X=0$
, then X is a point and the preimage Y of X is a torsor under
$\dim X=0$
, then X is a point and the preimage Y of X is a torsor under
![]() $\ker (r)$
. We then have
$\ker (r)$
. We then have
![]() $\mathrm {vol}(Y) = \mathrm {vol}(\ker (r)) = 0$
, since
$\mathrm {vol}(Y) = \mathrm {vol}(\ker (r)) = 0$
, since
![]() $\ker (r)\subset \Gamma _S$
is a closed subgroup of infinite index by hypothesis. Now assume that the assertion is known whenever
$\ker (r)\subset \Gamma _S$
is a closed subgroup of infinite index by hypothesis. Now assume that the assertion is known whenever
![]() $\dim (X) < d$
and consider the case
$\dim (X) < d$
and consider the case
![]() $\dim (X)=d< \dim (G)$
. There exists an infinite sequence
$\dim (X)=d< \dim (G)$
. There exists an infinite sequence
![]() $\gamma _1, \gamma _2, \ldots \in \Gamma _S$
such that the subset
$\gamma _1, \gamma _2, \ldots \in \Gamma _S$
such that the subset
![]() $r(\gamma _i) X$
are mutually distinct. (If the choice were impossible after
$r(\gamma _i) X$
are mutually distinct. (If the choice were impossible after
![]() $i=r$
, then multiplication by
$i=r$
, then multiplication by
![]() $r(g)$
preserves
$r(g)$
preserves
![]() $\bigcup _{i<=r} r(\gamma _i) X$
for every
$\bigcup _{i<=r} r(\gamma _i) X$
for every
![]() $g\in \Gamma _S$
. This cannot happen because r has Zariski dense image, and the union has dimension
$g\in \Gamma _S$
. This cannot happen because r has Zariski dense image, and the union has dimension
![]() $d < \dim (G)$
.) Consider
$d < \dim (G)$
.) Consider
 $$ \begin{align*}\Gamma_S \supset \bigcup_{i=1}^{\infty} \gamma_i r^{-1}(X). \end{align*} $$
$$ \begin{align*}\Gamma_S \supset \bigcup_{i=1}^{\infty} \gamma_i r^{-1}(X). \end{align*} $$
The volume of
![]() $\Gamma _S$
is finite. Each term on the right-hand side is closed (so measurable), and the volumes of
$\Gamma _S$
is finite. Each term on the right-hand side is closed (so measurable), and the volumes of
![]() $\gamma _i r^{-1}(X)$
are all equal. We claim that their pairwise intersections have volume
$\gamma _i r^{-1}(X)$
are all equal. We claim that their pairwise intersections have volume
![]() $0$
. If this is true, then we deduce that
$0$
. If this is true, then we deduce that
![]() $\mathrm {vol} (\gamma _i r^{-1}(X)) = \mathrm {vol}( r^{-1}(X) ) =0$
, completing the proof.
$\mathrm {vol} (\gamma _i r^{-1}(X)) = \mathrm {vol}( r^{-1}(X) ) =0$
, completing the proof.
It remains to verify the claim. Observe that the intersection
maps into the intersection
![]() $r(\gamma _i)X \cap r(\gamma _j)X$
in G, which has dimension less than d, so indeed (*) has measure
$r(\gamma _i)X \cap r(\gamma _j)X$
in G, which has dimension less than d, so indeed (*) has measure
![]() $0$
by induction hypothesis. This completes the proof.
$0$
by induction hypothesis. This completes the proof.
We also record a lemma on projective algebraic representations, which will be useful later on.
Lemma 1.2. Let G be a connected simply-connected semi-simple group over
![]() ${\mathbb {C}}$
. Let
${\mathbb {C}}$
. Let
![]() $T \subset G$
be a maximal torus. Let
$T \subset G$
be a maximal torus. Let
![]() $r_1, r_2 \colon G \to \mathrm {PGL}_N$
be two projective representations whose restrictions to T are conjugate. Then
$r_1, r_2 \colon G \to \mathrm {PGL}_N$
be two projective representations whose restrictions to T are conjugate. Then
![]() $r_1, r_2$
are conjugate.
$r_1, r_2$
are conjugate.
Proof. We claim that any
![]() $r \colon G \to \mathrm {PGL}_N$
can be lifted to a representation
$r \colon G \to \mathrm {PGL}_N$
can be lifted to a representation
![]() $\widetilde {r} \colon G \to \mathrm {SL}_N$
. Let
$\widetilde {r} \colon G \to \mathrm {SL}_N$
. Let
![]() $H := (G \times _{\mathrm {PGL}_N} \mathrm {SL}_N)^0$
. Then
$H := (G \times _{\mathrm {PGL}_N} \mathrm {SL}_N)^0$
. Then
![]() $f \colon H \to G$
is a central isogeny and hence is an isomorphism as G is simply connected [Reference Milne61, Prop. 18.8]. The composition
$f \colon H \to G$
is a central isogeny and hence is an isomorphism as G is simply connected [Reference Milne61, Prop. 18.8]. The composition
![]() $G \to H \to \mathrm {SL}_N$
is the desired lift.
$G \to H \to \mathrm {SL}_N$
is the desired lift.
After conjugating, we may assume that
![]() $r_1|_T = r_2|_T$
. By the preceding paragraph, we can choose lifts
$r_1|_T = r_2|_T$
. By the preceding paragraph, we can choose lifts
![]() $\widetilde {r}_i$
of
$\widetilde {r}_i$
of
![]() $r_i$
for
$r_i$
for
![]() $i=1,2$
. Define a morphism of varieties
$i=1,2$
. Define a morphism of varieties
![]() $\chi :G \to \mathrm {SL}_N$
by
$\chi :G \to \mathrm {SL}_N$
by
![]() $\chi (g):=\widetilde {r}_1(g) \widetilde {r}_2(g)^{-1}$
. The image of
$\chi (g):=\widetilde {r}_1(g) \widetilde {r}_2(g)^{-1}$
. The image of
![]() $\chi |_T$
lies in
$\chi |_T$
lies in
![]() $\mu _N$
since
$\mu _N$
since
![]() $r_1|_T = r_2|_T$
. Hence, the image is trivial as T is connected, that is,
$r_1|_T = r_2|_T$
. Hence, the image is trivial as T is connected, that is,
![]() $\widetilde {r}_1|_T=\widetilde {r}_2|_T$
. Hence,
$\widetilde {r}_1|_T=\widetilde {r}_2|_T$
. Hence,
![]() $\widetilde {r}_1$
,
$\widetilde {r}_1$
,
![]() $\widetilde {r}_2$
are
$\widetilde {r}_2$
are
![]() ${\mathrm {GL}}_N$
-conjugate because the trace functions coincide on semisimple elements. It follows that
${\mathrm {GL}}_N$
-conjugate because the trace functions coincide on semisimple elements. It follows that
![]() $r_1$
,
$r_1$
,
![]() $r_2$
are
$r_2$
are
![]() $\mathrm {PGL}_N$
-conjugate.
$\mathrm {PGL}_N$
-conjugate.
2 Root data of
 ${\mathrm {GSO}}_{2n}$
and
${\mathrm {GSO}}_{2n}$
and
 $\mathrm {GSpin}_{2n}$
$\mathrm {GSpin}_{2n}$
Let
![]() $\mathrm {GO}_{2n}/\mathbb {Q}$
be the algebraic group such that for all
$\mathrm {GO}_{2n}/\mathbb {Q}$
be the algebraic group such that for all
![]() $\mathbb {Q}$
-algebras R, we have
$\mathbb {Q}$
-algebras R, we have
 $$ \begin{align} \mathrm{GO}_{2n}(R) = \left\lbrace g \in {\mathrm{GL}}_{2n}(R)\ \left| \ \exists\, \mathrm{sim}(g) \in R^{\times} \ \colon\ g{}^{\mathrm{t}} \cdot \left(\begin{matrix} & {1_n} \cr {1_n} & \end{matrix}\right) \ \cdot g = \mathrm{sim}(g) \cdot \left(\begin{matrix} & {1_n} \cr {1_n} & \end{matrix}\right) \right. \ \right\rbrace. \end{align} $$
$$ \begin{align} \mathrm{GO}_{2n}(R) = \left\lbrace g \in {\mathrm{GL}}_{2n}(R)\ \left| \ \exists\, \mathrm{sim}(g) \in R^{\times} \ \colon\ g{}^{\mathrm{t}} \cdot \left(\begin{matrix} & {1_n} \cr {1_n} & \end{matrix}\right) \ \cdot g = \mathrm{sim}(g) \cdot \left(\begin{matrix} & {1_n} \cr {1_n} & \end{matrix}\right) \right. \ \right\rbrace. \end{align} $$
(In the above formula,
![]() $1_n$
is the
$1_n$
is the
![]() $n\times n$
identity matrix.) The group
$n\times n$
identity matrix.) The group
![]() $\mathrm {GO}_{2n}$
is disconnected; its neutral component
$\mathrm {GO}_{2n}$
is disconnected; its neutral component
![]() ${\mathrm {GSO}}_{2n} \subset \mathrm {GO}_{2n}$
is defined by the condition
${\mathrm {GSO}}_{2n} \subset \mathrm {GO}_{2n}$
is defined by the condition
![]() $\det (g) = \mathrm {sim}(g)^n$
. The groups
$\det (g) = \mathrm {sim}(g)^n$
. The groups
![]() $\mathrm {GO}_{2n}$
,
$\mathrm {GO}_{2n}$
,
![]() ${\mathrm {GSO}}_{2n}$
are split and defined by a quadratic form of signature
${\mathrm {GSO}}_{2n}$
are split and defined by a quadratic form of signature
![]() $(n,n)$
. An element t of the diagonal torus
$(n,n)$
. An element t of the diagonal torus
![]() $\mathrm {T}_{{\mathrm {GSO}}} \subset {\mathrm {GSO}}_{2n}$
is of the form
$\mathrm {T}_{{\mathrm {GSO}}} \subset {\mathrm {GSO}}_{2n}$
is of the form
Hence,
![]() $\mathrm {T}_{{\mathrm {GSO}}} \simeq \mathbb {G}_{\mathrm {m}}^{n+1}$
by sending t to
$\mathrm {T}_{{\mathrm {GSO}}} \simeq \mathbb {G}_{\mathrm {m}}^{n+1}$
by sending t to
![]() $(t_0,t_1,\ldots ,t_n)$
. We identify
$(t_0,t_1,\ldots ,t_n)$
. We identify
![]() $X^{*}(\mathrm {T}_{{\mathrm {GSO}}}) = \bigoplus _{i=0}^n \mathbb Z \cdot e_i$
and
$X^{*}(\mathrm {T}_{{\mathrm {GSO}}}) = \bigoplus _{i=0}^n \mathbb Z \cdot e_i$
and
![]() $X_*(\mathrm {T}_{{\mathrm {GSO}}}) = \bigoplus _{i=0}^n \mathbb Z \cdot e^{*}_i$
accordingly. We let
$X_*(\mathrm {T}_{{\mathrm {GSO}}}) = \bigoplus _{i=0}^n \mathbb Z \cdot e^{*}_i$
accordingly. We let
![]() $\mathrm {B}_{\mathrm {GSO}}$
be the Borel subgroup of
$\mathrm {B}_{\mathrm {GSO}}$
be the Borel subgroup of
![]() ${\mathrm {GSO}}_{2n}$
of matrices of the form
${\mathrm {GSO}}_{2n}$
of matrices of the form
 $$ \begin{align} g = \left(\begin{matrix} A & {AB} \cr 0 & {c A^{\mathrm{t}, -1}} \end{matrix}\right) , \quad A \in B_{{\mathrm{GL}}_n}, \ B \in \mathrm{M}_n, \ B^{\mathrm{t}} = -B \quad \mathrm{and} \quad c = \mathrm{sim}(g), \end{align} $$
$$ \begin{align} g = \left(\begin{matrix} A & {AB} \cr 0 & {c A^{\mathrm{t}, -1}} \end{matrix}\right) , \quad A \in B_{{\mathrm{GL}}_n}, \ B \in \mathrm{M}_n, \ B^{\mathrm{t}} = -B \quad \mathrm{and} \quad c = \mathrm{sim}(g), \end{align} $$
where
![]() $B_{{\mathrm {GL}}_n} \subset {\mathrm {GL}}_n$
is the upper triangular Borel subgroup. (To see that
$B_{{\mathrm {GL}}_n} \subset {\mathrm {GL}}_n$
is the upper triangular Borel subgroup. (To see that
![]() $\mathrm {B}_{\mathrm {GSO}}$
is indeed a Borel subgroup, notice that any block matrix
$\mathrm {B}_{\mathrm {GSO}}$
is indeed a Borel subgroup, notice that any block matrix
![]() $g = {{\left ( \begin {smallmatrix} A & B \cr C & D \end {smallmatrix} \right )}}$
with
$g = {{\left ( \begin {smallmatrix} A & B \cr C & D \end {smallmatrix} \right )}}$
with
![]() $C = 0$
is of the above form if and only if
$C = 0$
is of the above form if and only if
![]() $g \in {\mathrm {GSO}}_{2n}$
, and moreover, the displayed group is solvable of dimension
$g \in {\mathrm {GSO}}_{2n}$
, and moreover, the displayed group is solvable of dimension
![]() $n^2 + 1$
).
$n^2 + 1$
).
We realize the split forms of even (special) orthogonal groups in
![]() $\mathrm {GO}_{2n}/\mathbb {Q}$
. Namely, we write
$\mathrm {GO}_{2n}/\mathbb {Q}$
. Namely, we write
![]() $\mathrm {O}_{2n}$
(resp.
$\mathrm {O}_{2n}$
(resp.
![]() ${\mathrm {SO}}_{2n}$
) for the subgroup of
${\mathrm {SO}}_{2n}$
) for the subgroup of
![]() $\mathrm {GO}_{2n}$
(resp.
$\mathrm {GO}_{2n}$
(resp.
![]() ${\mathrm {GSO}}_{2n}$
) where
${\mathrm {GSO}}_{2n}$
) where
![]() $\mathrm {sim}$
is trivial.
$\mathrm {sim}$
is trivial.
Lemma 2.1. The root datum of
![]() ${\mathrm {GSO}}_{2n}$
with respect to
${\mathrm {GSO}}_{2n}$
with respect to
![]() $\mathrm {B}_{\mathrm {GSO}}$
is described as follows.
$\mathrm {B}_{\mathrm {GSO}}$
is described as follows.
-
(i) The set of roots (resp. coroots) consists of
 $\pm (e_i - e_j)$
and
$\pm (e_i - e_j)$
and
 $\pm (e_i+e_j-e_0)$
(resp.
$\pm (e_i+e_j-e_0)$
(resp.
 $\pm (e_i^{*}-e_j^{*})$
and
$\pm (e_i^{*}-e_j^{*})$
and
 $\pm (e_i^{*}+e_j^{*})$
) with
$\pm (e_i^{*}+e_j^{*})$
) with
 $1\leq i<j\leq n$
.
$1\leq i<j\leq n$
. -
(ii) The positive roots are
 $\{e_i + e_j - e_0\}_{1\le i < j \leq n} \cup \{e_i - e_j\}_{1\le i<j\leq n}$
, and the positive coroots are
$\{e_i + e_j - e_0\}_{1\le i < j \leq n} \cup \{e_i - e_j\}_{1\le i<j\leq n}$
, and the positive coroots are
 $\{e^{*}_i \pm e^{*}_j\}_{1\le i < j \leq n}$
.
$\{e^{*}_i \pm e^{*}_j\}_{1\le i < j \leq n}$
. -
(iii) The simple roots are
 $\alpha _1 = e_1 - e_2$
,
$\alpha _1 = e_1 - e_2$
,
 $\ldots $
,
$\ldots $
,
 $\alpha _{n-1} = e_{n-1} - e_n$
, and
$\alpha _{n-1} = e_{n-1} - e_n$
, and
 $\alpha _n = e_{n-1} + e_n - e_0$
.
$\alpha _n = e_{n-1} + e_n - e_0$
. -
(iv) The simple coroots
 $\Delta ^{\vee }$
are
$\Delta ^{\vee }$
are
 $\alpha _1^{\vee } = e_1^{*} - e_2^{*}$
,
$\alpha _1^{\vee } = e_1^{*} - e_2^{*}$
,
 $\alpha _2^{\vee } = e_2^{*} - e_3^{*}$
,
$\alpha _2^{\vee } = e_2^{*} - e_3^{*}$
,
 $\ldots $
,
$\ldots $
,
 $\alpha _{n-1}^{\vee } = e_{n-1}^{*} - e_n^{*}$
and
$\alpha _{n-1}^{\vee } = e_{n-1}^{*} - e_n^{*}$
and
 $\alpha _n^{\vee } = e_{n-1}^{*} + e_n^{*}$
.
$\alpha _n^{\vee } = e_{n-1}^{*} + e_n^{*}$
.
Remark 2.2. The root datum of
![]() ${\mathrm {SO}}_{2n}$
is described similarly. Putting
${\mathrm {SO}}_{2n}$
is described similarly. Putting
![]() $\mathrm {T}_{{\mathrm {SO}}} := \mathrm {T}_{{\mathrm {GSO}}}\cap {\mathrm {SO}}_{2n}$
and
$\mathrm {T}_{{\mathrm {SO}}} := \mathrm {T}_{{\mathrm {GSO}}}\cap {\mathrm {SO}}_{2n}$
and
![]() $\mathrm {B}_{{\mathrm {SO}}} := \mathrm {B}_{\mathrm {GSO}} \cap {\mathrm {SO}}_{2n}$
, we have
$\mathrm {B}_{{\mathrm {SO}}} := \mathrm {B}_{\mathrm {GSO}} \cap {\mathrm {SO}}_{2n}$
, we have
![]() $\mathrm {T}_{{\mathrm {SO}}} = \{t\in \mathrm {T}_{{\mathrm {GSO}}} : t_0=1\}$
as well as
$\mathrm {T}_{{\mathrm {SO}}} = \{t\in \mathrm {T}_{{\mathrm {GSO}}} : t_0=1\}$
as well as
![]() $X^{*}(\mathrm {T}_{{\mathrm {SO}}})=\oplus _{i=1}^n e_i\cdot \mathbb Z$
and
$X^{*}(\mathrm {T}_{{\mathrm {SO}}})=\oplus _{i=1}^n e_i\cdot \mathbb Z$
and
![]() $X_*(\mathrm {T}_{{\mathrm {SO}}})=\oplus _{i=1}^n e_i^{*} \cdot \mathbb Z$
. To describe (positive or simple) roots and coroots, we only need to formally set
$X_*(\mathrm {T}_{{\mathrm {SO}}})=\oplus _{i=1}^n e_i^{*} \cdot \mathbb Z$
. To describe (positive or simple) roots and coroots, we only need to formally set
![]() $e_0=0$
in the lemma above.
$e_0=0$
in the lemma above.
Proof. The standard computation for
![]() ${\mathrm {SO}}_{2n}$
as in [Reference Fulton and Harris25, 18.1] can be easily adapted to
${\mathrm {SO}}_{2n}$
as in [Reference Fulton and Harris25, 18.1] can be easily adapted to
![]() ${\mathrm {GSO}}_{2n}$
.
${\mathrm {GSO}}_{2n}$
.
We define the following element (over any
![]() $\mathbb {Q}$
-algebra point of
$\mathbb {Q}$
-algebra point of
![]() $\mathrm {O}_{2n}$
)Footnote 5
$\mathrm {O}_{2n}$
)Footnote 5
 $$ \begin{align} \vartheta^{\circ} := -\left( \begin{array}{cc;{1pt/1pt}cc}1_{n-1} & & & \\ & 0 & & 1 \\ \hdashline[1pt/1pt] & & 1_{n-1} & \\ & 1& & 0 \end{array}\right)\in \mathrm{O}_{2n}. \end{align} $$
$$ \begin{align} \vartheta^{\circ} := -\left( \begin{array}{cc;{1pt/1pt}cc}1_{n-1} & & & \\ & 0 & & 1 \\ \hdashline[1pt/1pt] & & 1_{n-1} & \\ & 1& & 0 \end{array}\right)\in \mathrm{O}_{2n}. \end{align} $$
Since
![]() $\det (\vartheta ^{\circ }) = -1$
, we have
$\det (\vartheta ^{\circ }) = -1$
, we have
![]() $\vartheta ^{\circ } \notin {\mathrm {SO}}_{2n}$
. We write
$\vartheta ^{\circ } \notin {\mathrm {SO}}_{2n}$
. We write
![]() $\theta ^{\circ } \in \mathrm {Aut}({\mathrm {GSO}}_{2n})$
for the automorphism given by
$\theta ^{\circ } \in \mathrm {Aut}({\mathrm {GSO}}_{2n})$
for the automorphism given by
![]() $\vartheta ^{\circ }$
-conjugation.
$\vartheta ^{\circ }$
-conjugation.
Lemma 2.3. The automorphism
![]() $\theta ^{\circ }$
stabilizes
$\theta ^{\circ }$
stabilizes
![]() $\mathrm {B}_{\mathrm {GSO}}$
and
$\mathrm {B}_{\mathrm {GSO}}$
and
![]() $\mathrm {T}_{{\mathrm {GSO}}}$
and acts on
$\mathrm {T}_{{\mathrm {GSO}}}$
and acts on
![]() $\mathrm {T}_{{\mathrm {GSO}}}$
by
$\mathrm {T}_{{\mathrm {GSO}}}$
by
Furthermore,
![]() $\theta ^{\circ }(\alpha _i)= \alpha _i$
for
$\theta ^{\circ }(\alpha _i)= \alpha _i$
for
![]() $i < n-2$
,
$i < n-2$
,
![]() $\theta ^{\circ }(\alpha _{n-1}) = \alpha _n$
, and
$\theta ^{\circ }(\alpha _{n-1}) = \alpha _n$
, and
![]() $\theta ^{\circ }(\alpha _n) = \alpha _{n-1}$
.
$\theta ^{\circ }(\alpha _n) = \alpha _{n-1}$
.
Proof. By a direct computation,
![]() $\theta ^{\circ }( \mathrm {T}_{{\mathrm {GSO}}}) = \mathrm {T}_{{\mathrm {GSO}}}$
and
$\theta ^{\circ }( \mathrm {T}_{{\mathrm {GSO}}}) = \mathrm {T}_{{\mathrm {GSO}}}$
and
![]() $\theta ^{\circ }(\mathrm {B}_{\mathrm {GSO}}) = \mathrm {B}_{\mathrm {GSO}}$
. Since
$\theta ^{\circ }(\mathrm {B}_{\mathrm {GSO}}) = \mathrm {B}_{\mathrm {GSO}}$
. Since
![]() $\theta ^{\circ }$
only switches
$\theta ^{\circ }$
only switches
![]() $t_n$
and
$t_n$
and
![]() $t_{2n}=t_0 t_n^{-1}$
, its action on
$t_{2n}=t_0 t_n^{-1}$
, its action on
![]() $\mathrm {T}_{{\mathrm {GSO}}}$
is explicitly described as in the lemma. Thus,
$\mathrm {T}_{{\mathrm {GSO}}}$
is explicitly described as in the lemma. Thus,
![]() $\theta ^{\circ }(e_i)=e_i$
for
$\theta ^{\circ }(e_i)=e_i$
for
![]() $1\le i\le n-1$
and
$1\le i\le n-1$
and
![]() $\theta ^{\circ }(e_n)=e_0-e_n$
, from which the last assertion follows.
$\theta ^{\circ }(e_n)=e_0-e_n$
, from which the last assertion follows.
We define
![]() $\mathrm {GSpin}_{2n}$
to be the Langlands dual group
$\mathrm {GSpin}_{2n}$
to be the Langlands dual group
![]() $\widehat {{\mathrm {GSO}}_{2n}}$
over
$\widehat {{\mathrm {GSO}}_{2n}}$
over
![]() ${\mathbb {C}}$
(or later over
${\mathbb {C}}$
(or later over
![]() $\overline {\mathbb {Q}}_{\ell }$
via
$\overline {\mathbb {Q}}_{\ell }$
via
![]() $\iota :{\mathbb {C}}\simeq \overline {\mathbb {Q}}_{\ell }$
). That is,
$\iota :{\mathbb {C}}\simeq \overline {\mathbb {Q}}_{\ell }$
). That is,
![]() $\mathrm {GSpin}_{2n}$
is the connected reductive group over
$\mathrm {GSpin}_{2n}$
is the connected reductive group over
![]() ${\mathbb {C}}$
, equipped with a Borel subgroup
${\mathbb {C}}$
, equipped with a Borel subgroup
![]() $B_{\mathrm {GSpin}}$
and a maximal torus
$B_{\mathrm {GSpin}}$
and a maximal torus
![]() $\mathrm {T}_{\mathrm {GSpin}}$
, whose based root datum is dual to the one of
$\mathrm {T}_{\mathrm {GSpin}}$
, whose based root datum is dual to the one of
![]() ${\mathrm {GSO}}_{2n}$
that we described above. In particular,
${\mathrm {GSO}}_{2n}$
that we described above. In particular,
Via the identification
![]() $X^{*}(\mathrm {T}_{{\mathrm {GSO}}}) = \mathbb Z^{n+1}$
, we represent elements
$X^{*}(\mathrm {T}_{{\mathrm {GSO}}}) = \mathbb Z^{n+1}$
, we represent elements
![]() $s \in \mathrm {T}_{\mathrm {GSpin}}$
as
$s \in \mathrm {T}_{\mathrm {GSpin}}$
as
![]() $(s_0, s_1, \ldots , s_n)$
. In Section 3, we will also define an explicit model of
$(s_0, s_1, \ldots , s_n)$
. In Section 3, we will also define an explicit model of
![]() $\mathrm {GSpin}_{2n}$
over
$\mathrm {GSpin}_{2n}$
over
![]() $\mathbb {Q}$
using Clifford algebras.
$\mathbb {Q}$
using Clifford algebras.
Lemma 2.4. There is a unique
![]() $\theta \in \mathrm {Aut}(\mathrm {GSpin}_{2n})$
that fixes
$\theta \in \mathrm {Aut}(\mathrm {GSpin}_{2n})$
that fixes
![]() $\mathrm {T}_{\mathrm {GSpin}}$
and
$\mathrm {T}_{\mathrm {GSpin}}$
and
![]() $\mathrm {B}_{\mathrm {GSpin}}$
, switches
$\mathrm {B}_{\mathrm {GSpin}}$
, switches
![]() $\alpha _{n-1}^{\vee }$
and
$\alpha _{n-1}^{\vee }$
and
![]() $\alpha _n^{\vee }$
, leaves the other
$\alpha _n^{\vee }$
, leaves the other
![]() $\alpha _i^{\vee }$
invariant, and induces the trivial automorphism of the cocenter of
$\alpha _i^{\vee }$
invariant, and induces the trivial automorphism of the cocenter of
![]() $\mathrm {GSpin}_{2n}$
. We have
$\mathrm {GSpin}_{2n}$
. We have
![]() $\theta ^2 = 1$
, and on the torus
$\theta ^2 = 1$
, and on the torus
![]() $\mathrm {T}_{\mathrm {GSpin}}$
, the involution
$\mathrm {T}_{\mathrm {GSpin}}$
, the involution
![]() $\theta $
is given by
$\theta $
is given by
Proof. We have
![]() $\theta (e_i^{*} - e_{i+1}^{*}) = e_i^{*} - e_{i+1}^{*}$
(
$\theta (e_i^{*} - e_{i+1}^{*}) = e_i^{*} - e_{i+1}^{*}$
(
![]() $1 \leq i < n$
) and
$1 \leq i < n$
) and
![]() $\theta (e_{n-1}^{*} - e_n^{*}) = e_{n-1}^{*} + e_n^{*}$
. Thus,
$\theta (e_{n-1}^{*} - e_n^{*}) = e_{n-1}^{*} + e_n^{*}$
. Thus,
The center of
![]() ${\mathrm {GSO}}_{2n}$
is the image of
${\mathrm {GSO}}_{2n}$
is the image of
![]() $ \mathbb {G}_{\mathrm {m}} \owns z \mapsto (z^2, z, \ldots , z) \in \mathrm {T}_{{\mathrm {GSO}}}. $
The dual map is
$ \mathbb {G}_{\mathrm {m}} \owns z \mapsto (z^2, z, \ldots , z) \in \mathrm {T}_{{\mathrm {GSO}}}. $
The dual map is
Thus,
![]() $\theta (2e_0^{*} + e_1^{*} + \cdots + e_n^{*}) = 2e_0^{*} + e_1^{*} + \cdots + e_n^{*}$
, so
$\theta (2e_0^{*} + e_1^{*} + \cdots + e_n^{*}) = 2e_0^{*} + e_1^{*} + \cdots + e_n^{*}$
, so
![]() $\theta (2e_0^{*}) -e_n^{*} = 2e_0^{*} + e_n^{*}$
and
$\theta (2e_0^{*}) -e_n^{*} = 2e_0^{*} + e_n^{*}$
and
![]() $\theta (e_0^{*}) = e_0^{*} + e_n^{*}$
.
$\theta (e_0^{*}) = e_0^{*} + e_n^{*}$
.
Lemma 2.5. We have
![]() $Z(\mathrm {GSpin}_{2n})=\{(s_0,\ldots ,s_n):s_1=s_2=\cdots =s_n\in \{\pm 1\}\}$
, which is isomorphic to
$Z(\mathrm {GSpin}_{2n})=\{(s_0,\ldots ,s_n):s_1=s_2=\cdots =s_n\in \{\pm 1\}\}$
, which is isomorphic to
![]() $\mathbb {G}_{\mathrm {m}} \times \{\pm 1\}$
via
$\mathbb {G}_{\mathrm {m}} \times \{\pm 1\}$
via
![]() $(s_0,\ldots ,s_n)\mapsto (s_0,s_1)$
. In the latter coordinate,
$(s_0,\ldots ,s_n)\mapsto (s_0,s_1)$
. In the latter coordinate,
![]() $\theta (s_0,s_1) = (s_0s_1,s_1)$
.
$\theta (s_0,s_1) = (s_0s_1,s_1)$
.
Proof. Let
![]() $s \in \mathrm {T}_{\mathrm {GSpin}}$
. Then
$s \in \mathrm {T}_{\mathrm {GSpin}}$
. Then
![]() $s \in Z(\mathrm {GSpin}_{2n})$
if and only if
$s \in Z(\mathrm {GSpin}_{2n})$
if and only if
![]() $\alpha ^{\vee }(t) = 1$
for all
$\alpha ^{\vee }(t) = 1$
for all
![]() $\alpha ^{\vee } \in \Delta ^{\vee }$
. From Lemma 2.1(iii), we obtain
$\alpha ^{\vee } \in \Delta ^{\vee }$
. From Lemma 2.1(iii), we obtain
![]() $s_i/s_{i+1} = 1$
(
$s_i/s_{i+1} = 1$
(
![]() $i \leq n-1$
), and
$i \leq n-1$
), and
![]() $s_{n-1}s_n = 1$
. Hence,
$s_{n-1}s_n = 1$
. Hence,
![]() $s \in Z(\mathrm {GSpin}_{2n})$
if and only if
$s \in Z(\mathrm {GSpin}_{2n})$
if and only if
![]() $s_1 = \cdots = s_n \in \{\pm 1\}$
. By (2.5), we get
$s_1 = \cdots = s_n \in \{\pm 1\}$
. By (2.5), we get
![]() $\theta (s_0,s_1) = (s_0s_1,s_1)$
.
$\theta (s_0,s_1) = (s_0s_1,s_1)$
.
The Weyl group of
![]() ${\mathrm {GSO}}_{2n}$
(and
${\mathrm {GSO}}_{2n}$
(and
![]() $\mathrm {GSpin}_{2n}$
) is equal to
$\mathrm {GSpin}_{2n}$
) is equal to
![]() $\{\pm 1\}^{n, \prime } \rtimes \mathfrak S_n$
, where
$\{\pm 1\}^{n, \prime } \rtimes \mathfrak S_n$
, where
![]() $\{\pm 1\}^{n,\prime }$
is the group of
$\{\pm 1\}^{n,\prime }$
is the group of
![]() $a \in \{\pm 1\}^{n}$
such that
$a \in \{\pm 1\}^{n}$
such that
![]() $\prod _1^n a(i) = 1$
. The action of
$\prod _1^n a(i) = 1$
. The action of
![]() $\mathrm {W}_{{\mathrm {GSO}}}$
on
$\mathrm {W}_{{\mathrm {GSO}}}$
on
![]() $\mathrm {T}_{{\mathrm {GSO}}}$
is determined by
$\mathrm {T}_{{\mathrm {GSO}}}$
is determined by
 $$ \begin{align} \begin{cases} \sigma \cdot (t_0, t_1, \ldots, t_n) = (t_0, t_{\sigma(1)}, \ldots t_{\sigma(n)}) & \sigma \in \mathfrak S_n \cr a \cdot (t_0, t_1, \ldots, t_n) = (t_0, t_0 t_1^{-1}, t_0t_2^{-1}, t_3, \ldots, t_n) & a = (-1, -1, 1\ldots, 1) \in \{\pm 1\}^{n,\prime}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \sigma \cdot (t_0, t_1, \ldots, t_n) = (t_0, t_{\sigma(1)}, \ldots t_{\sigma(n)}) & \sigma \in \mathfrak S_n \cr a \cdot (t_0, t_1, \ldots, t_n) = (t_0, t_0 t_1^{-1}, t_0t_2^{-1}, t_3, \ldots, t_n) & a = (-1, -1, 1\ldots, 1) \in \{\pm 1\}^{n,\prime}. \end{cases} \end{align} $$
We define, for
![]() $\varepsilon \in \{\pm 1\}$
, the following cocharacter:
$\varepsilon \in \{\pm 1\}$
, the following cocharacter:
 $$ \begin{align} \mu_{\varepsilon} := \begin{cases} (1, 1, \ldots, 1, 1) & \mathrm{if } \varepsilon = (-1)^n \cr (1, 1, \ldots, 1, 0) & \mathrm{if } \varepsilon = (-1)^{n+1} \end{cases} \quad \in \mathbb Z^{n+1} = X_*(\mathrm{T}_{{\mathrm{GSO}}}) = X^{*}(\mathrm{T}_{\mathrm{GSpin}}). \end{align} $$
$$ \begin{align} \mu_{\varepsilon} := \begin{cases} (1, 1, \ldots, 1, 1) & \mathrm{if } \varepsilon = (-1)^n \cr (1, 1, \ldots, 1, 0) & \mathrm{if } \varepsilon = (-1)^{n+1} \end{cases} \quad \in \mathbb Z^{n+1} = X_*(\mathrm{T}_{{\mathrm{GSO}}}) = X^{*}(\mathrm{T}_{\mathrm{GSpin}}). \end{align} $$
Then
![]() $\mu _{\varepsilon }$
is a minuscule cocharacter of
$\mu _{\varepsilon }$
is a minuscule cocharacter of
![]() ${\mathrm {GSO}}_{2n}$
with
${\mathrm {GSO}}_{2n}$
with
![]() $\langle \alpha _i, \mu _{\varepsilon } \rangle = 1$
if and only if
$\langle \alpha _i, \mu _{\varepsilon } \rangle = 1$
if and only if
![]() $i = n$
(for
$i = n$
(for
![]() $\varepsilon = (-1)^n$
) and
$\varepsilon = (-1)^n$
) and
![]() $i = n-1$
(for
$i = n-1$
(for
![]() $\varepsilon = (-1)^{n+1}$
).
$\varepsilon = (-1)^{n+1}$
).
Definition 2.6. For
![]() $\varepsilon \in \{+,-\}$
, define the half-spin representation
$\varepsilon \in \{+,-\}$
, define the half-spin representation
![]() $\mathrm {spin}^{\varepsilon } = \mathrm {spin}^{\varepsilon }_{2n}$
to be the irreducible representation of
$\mathrm {spin}^{\varepsilon } = \mathrm {spin}^{\varepsilon }_{2n}$
to be the irreducible representation of
![]() $\mathrm {GSpin}_{2n}$
whose highest weight is equal to
$\mathrm {GSpin}_{2n}$
whose highest weight is equal to
![]() $\mu _{\varepsilon }$
in
$\mu _{\varepsilon }$
in
![]() $X^{*}(\mathrm {T}_{\mathrm {GSpin}})$
. By the spin representation of
$X^{*}(\mathrm {T}_{\mathrm {GSpin}})$
. By the spin representation of
![]() $\mathrm {GSpin}_{2n}$
, we mean
$\mathrm {GSpin}_{2n}$
, we mean
![]() $\mathrm {spin} := \mathrm {spin}^+ \oplus \mathrm {spin}^-$
.
$\mathrm {spin} := \mathrm {spin}^+ \oplus \mathrm {spin}^-$
.
These representations will be realized explicitly via Clifford algebras. Our sign convention is natural in that
![]() $\mathrm {spin}^+$
(resp.
$\mathrm {spin}^+$
(resp.
![]() $\mathrm {spin}^-$
) accounts for even (resp. odd) degree elements. See (4.2) and Lemma 4.1 below.
$\mathrm {spin}^-$
) accounts for even (resp. odd) degree elements. See (4.2) and Lemma 4.1 below.
The minuscule
![]() $\mu _{\varepsilon }$
has
$\mu _{\varepsilon }$
has
![]() $2^{n-1}$
translates under the Weyl group action. Thus, each half-spin representation has dimension
$2^{n-1}$
translates under the Weyl group action. Thus, each half-spin representation has dimension
![]() $2^{n-1}$
. More precisely, the weights of
$2^{n-1}$
. More precisely, the weights of
![]() $\mathrm {spin}^{(-1)^n}_{2n}$
are
$\mathrm {spin}^{(-1)^n}_{2n}$
are
 $$ \begin{align} \mathrm{T}_{\mathrm{GSpin}} \owns (s_0, s_1, \ldots, s_n) \mapsto \left( s_0 \prod_{i \in U} s_i \right)_{U \subset \{1, 2, \ldots, n\},\atop 2|\# U } \in \mathbb Z^{n+1} = X_*(\mathrm{T}_{{\mathrm{GSO}}}) = X^{*}(\mathrm{T}_{\mathrm{GSpin}}), \end{align} $$
$$ \begin{align} \mathrm{T}_{\mathrm{GSpin}} \owns (s_0, s_1, \ldots, s_n) \mapsto \left( s_0 \prod_{i \in U} s_i \right)_{U \subset \{1, 2, \ldots, n\},\atop 2|\# U } \in \mathbb Z^{n+1} = X_*(\mathrm{T}_{{\mathrm{GSO}}}) = X^{*}(\mathrm{T}_{\mathrm{GSpin}}), \end{align} $$
and
![]() $\mathrm {spin}^{(-1)^{n+1}}_{2n}$
has similar weights, except that the cardinality of U is now required to be odd. By computing the
$\mathrm {spin}^{(-1)^{n+1}}_{2n}$
has similar weights, except that the cardinality of U is now required to be odd. By computing the
![]() $\theta $
-action on weights, we verify that (see Lemma 4.4 for an explicit intertwiner)
$\theta $
-action on weights, we verify that (see Lemma 4.4 for an explicit intertwiner)
Lemma 2.7. The kernel
![]() $Z^{\varepsilon }$
of
$Z^{\varepsilon }$
of
![]() $\mathrm {spin}^{\varepsilon }$
is central in
$\mathrm {spin}^{\varepsilon }$
is central in
![]() $\mathrm {GSpin}_{2n}$
and finite of order
$\mathrm {GSpin}_{2n}$
and finite of order
![]() $2$
. The nontrivial element
$2$
. The nontrivial element
![]() $z_{\varepsilon }$
of
$z_{\varepsilon }$
of
![]() $Z^{\varepsilon }$
equals
$Z^{\varepsilon }$
equals
![]() $(\varepsilon , -1) \in \mathbb {G}_{\mathrm {m}} \times \{\pm 1\}$
. The spin representation of
$(\varepsilon , -1) \in \mathbb {G}_{\mathrm {m}} \times \{\pm 1\}$
. The spin representation of
![]() $\mathrm {GSpin}_{2n}$
is faithful.
$\mathrm {GSpin}_{2n}$
is faithful.
Proof. Since
![]() $\mathrm {GSpin}_{2n}$
is simple modulo the center, the kernel
$\mathrm {GSpin}_{2n}$
is simple modulo the center, the kernel
![]() $Z^{\varepsilon } \subset \mathrm {GSpin}_{2n}$
must be central. The central character is the restriction of
$Z^{\varepsilon } \subset \mathrm {GSpin}_{2n}$
must be central. The central character is the restriction of
![]() $\mu _{\varepsilon } \colon \mathrm {T}_{\mathrm {GSpin}} \to \mathbb {G}_{\mathrm {m}}$
to the center
$\mu _{\varepsilon } \colon \mathrm {T}_{\mathrm {GSpin}} \to \mathbb {G}_{\mathrm {m}}$
to the center
![]() $Z(\mathrm {GSpin}_{2n}) \subset \mathrm {T}_{\mathrm {GSpin}}$
. Let
$Z(\mathrm {GSpin}_{2n}) \subset \mathrm {T}_{\mathrm {GSpin}}$
. Let
![]() $s = (s_0, s_1, \ldots , s_n) = (a,b) \in Z(\mathrm {GSpin}_{2n}) \subset \mathrm {T}_{\mathrm {GSpin}}$
. Then (see proof of Lemma 2.5)
$s = (s_0, s_1, \ldots , s_n) = (a,b) \in Z(\mathrm {GSpin}_{2n}) \subset \mathrm {T}_{\mathrm {GSpin}}$
. Then (see proof of Lemma 2.5)
 $$ \begin{align} \mu_{\varepsilon}(s) = \begin{cases} s_0 s_1 \cdots s_n = ab^n& \mathrm{if } \varepsilon = (-1)^n \cr s_0 s_1 \cdots s_{n-1} = ab^{n-1}& \mathrm{if } \varepsilon = (-1)^{n+1}. \end{cases} \end{align} $$
$$ \begin{align} \mu_{\varepsilon}(s) = \begin{cases} s_0 s_1 \cdots s_n = ab^n& \mathrm{if } \varepsilon = (-1)^n \cr s_0 s_1 \cdots s_{n-1} = ab^{n-1}& \mathrm{if } \varepsilon = (-1)^{n+1}. \end{cases} \end{align} $$
The first assertion follows by considering the 4 different cases where n even or odd and
![]() $\varepsilon = \pm 1$
. For the second point, it suffices to observe that
$\varepsilon = \pm 1$
. For the second point, it suffices to observe that
![]() $Z^+ \cap Z^- = \{1\}$
.
$Z^+ \cap Z^- = \{1\}$
.
Later on, the following fact on
![]() ${\mathrm {SO}}_{2n-1}$
will be needed, so we record it here.
${\mathrm {SO}}_{2n-1}$
will be needed, so we record it here.
Lemma 2.8. Let
![]() $n \geq 3$
. Up to isomorphism the group
$n \geq 3$
. Up to isomorphism the group
![]() ${\mathrm {SO}}_{2n-1}$
has exactly one faithful representation of dimension
${\mathrm {SO}}_{2n-1}$
has exactly one faithful representation of dimension
![]() $2n$
, namely,
$2n$
, namely,
![]() $\mathrm {std}_{2n-1} \oplus \textbf {1}$
.
$\mathrm {std}_{2n-1} \oplus \textbf {1}$
.
Proof. We use the root system notation and conventions from [Reference Bourbaki10, Ch. 4, p. 253]. Assume
![]() $V_{\lambda }$
is a nontrivial irreducible representation of
$V_{\lambda }$
is a nontrivial irreducible representation of
![]() ${\mathrm {SO}}_{2n-1}$
with highest weight
${\mathrm {SO}}_{2n-1}$
with highest weight
![]() $\lambda \neq \omega _1$
. We show that
$\lambda \neq \omega _1$
. We show that
![]() $\dim (V_{\lambda })> 2n$
. Write
$\dim (V_{\lambda })> 2n$
. Write
![]() $\lambda = \sum _{i=1}^{n-1}x_i \omega _i$
with
$\lambda = \sum _{i=1}^{n-1}x_i \omega _i$
with
![]() $x_i \geq 0$
. If
$x_i \geq 0$
. If
![]() $x_i \neq 0$
for some i with
$x_i \neq 0$
for some i with
![]() $n - 1> i > 1$
, then
$n - 1> i > 1$
, then
![]() $\dim (V_{\lambda }) \geq \dim (V_{\omega _i})$
, and
$\dim (V_{\lambda }) \geq \dim (V_{\omega _i})$
, and
![]() $\dim (V_{\omega _i}) = \dim (\wedge ^i \mathrm {std})> 2n$
. We thus assume
$\dim (V_{\omega _i}) = \dim (\wedge ^i \mathrm {std})> 2n$
. We thus assume
![]() $\lambda = x_1 \omega _1 + x_{n-1} \omega _{n-1}$
. If
$\lambda = x_1 \omega _1 + x_{n-1} \omega _{n-1}$
. If
![]() $x_{n-1} = 0$
, then, as
$x_{n-1} = 0$
, then, as
![]() $\lambda \neq \omega _1$
, we have
$\lambda \neq \omega _1$
, we have
![]() $\dim (V_{\lambda }) \geq \dim (V_{2 \omega _1}) = (n-1)(2n+1)> 2n$
by the Weyl dimension formula. Assume
$\dim (V_{\lambda }) \geq \dim (V_{2 \omega _1}) = (n-1)(2n+1)> 2n$
by the Weyl dimension formula. Assume
![]() $x_{n-1} \neq 0$
. We cannot have
$x_{n-1} \neq 0$
. We cannot have
![]() $x_{n-1} = 1$
because then,
$x_{n-1} = 1$
because then,
![]() $V_{\lambda }$
does not descend to
$V_{\lambda }$
does not descend to
![]() ${\mathrm {SO}}_{2n-1}$
. Thus,
${\mathrm {SO}}_{2n-1}$
. Thus,
![]() $\dim (V_{\lambda }) \geq \dim (V_{2 \omega _{n-1}})$
, which equals
$\dim (V_{\lambda }) \geq \dim (V_{2 \omega _{n-1}})$
, which equals
![]() $10$
if
$10$
if
![]() $n= 3$
,
$n= 3$
,
![]() $35$
if
$35$
if
![]() $n = 4$
, and if
$n = 4$
, and if
![]() $n> 4$
, then
$n> 4$
, then
![]() $\dim (V_{2\omega _{n-1}}) \geq \dim (V_{\omega _{n-1}}) = 2^{n-1}> 2n$
.
$\dim (V_{2\omega _{n-1}}) \geq \dim (V_{\omega _{n-1}}) = 2^{n-1}> 2n$
.
3 Clifford algebras and Clifford groups
We recall how
![]() $\mathrm {GSpin}_{2n}$
is realized using the Clifford algebra, and we define a number of fundamental maps such as
$\mathrm {GSpin}_{2n}$
is realized using the Clifford algebra, and we define a number of fundamental maps such as
![]() $i_{\mathrm {std}} \colon \mathrm {GSpin}_{2n-1} \hookrightarrow \mathrm {GSpin}_{2n}$
and the projections from
$i_{\mathrm {std}} \colon \mathrm {GSpin}_{2n-1} \hookrightarrow \mathrm {GSpin}_{2n}$
and the projections from
![]() $\mathrm {GSpin}_{2n}$
to
$\mathrm {GSpin}_{2n}$
to
![]() ${\mathrm {GSO}}_{2n}$
and
${\mathrm {GSO}}_{2n}$
and
![]() ${\mathrm {SO}}_{2n}$
. We also give a concrete definition of outer automorphisms
${\mathrm {SO}}_{2n}$
. We also give a concrete definition of outer automorphisms
![]() $\theta $
of
$\theta $
of
![]() $\mathrm {GSpin}_{2n}$
and
$\mathrm {GSpin}_{2n}$
and
![]() $\theta ^{\circ }$
of
$\theta ^{\circ }$
of
![]() ${\mathrm {GSO}}_{2n}$
. Our main reference is [Reference Bass4], which introduces Clifford algebras over arbitrary commutative rings (with unity). Other useful references are [Reference Bourbaki9, §9] and [Reference Fulton and Harris25, §20].
${\mathrm {GSO}}_{2n}$
. Our main reference is [Reference Bass4], which introduces Clifford algebras over arbitrary commutative rings (with unity). Other useful references are [Reference Bourbaki9, §9] and [Reference Fulton and Harris25, §20].
Let V be a quadratic space over
![]() $\mathbb {Q}$
with quadratic form Q, giving rise to the groups
$\mathbb {Q}$
with quadratic form Q, giving rise to the groups
![]() $\mathrm {O}(V)$
,
$\mathrm {O}(V)$
,
![]() $\mathrm {GO}(V)$
,
$\mathrm {GO}(V)$
,
![]() ${\mathrm {SO}}(V)$
and
${\mathrm {SO}}(V)$
and
![]() ${\mathrm {GSO}}(V)$
. The Clifford algebra
${\mathrm {GSO}}(V)$
. The Clifford algebra
![]() $C(V)$
is a universal map
$C(V)$
is a universal map
![]() $V \to C(V)$
which is initial in the category of
$V \to C(V)$
which is initial in the category of
![]() $\mathbb {Q}$
-linear maps
$\mathbb {Q}$
-linear maps
![]() $f \colon V\to A$
into associative
$f \colon V\to A$
into associative
![]() $\mathbb {Q}$
-algebras A with unity
$\mathbb {Q}$
-algebras A with unity
![]() $1_A$
such that
$1_A$
such that
![]() $f(v)^2=Q(v)\cdot 1_A$
for all
$f(v)^2=Q(v)\cdot 1_A$
for all
![]() $v\in V$
. (See [Reference Bass4, (2.3)] or [Reference Bourbaki9, §9.1].)
$v\in V$
. (See [Reference Bass4, (2.3)] or [Reference Bourbaki9, §9.1].)
We define
![]() $\langle x, y \rangle := Q(x+y) - Q(x) - Q(y)$
for
$\langle x, y \rangle := Q(x+y) - Q(x) - Q(y)$
for
![]() $x,y \in V$
, and similarly,
$x,y \in V$
, and similarly,
![]() $\langle x, y \rangle = (x+y)^2 - x^2 - y^2$
for
$\langle x, y \rangle = (x+y)^2 - x^2 - y^2$
for
![]() $x,y \in C(V)$
. In particular,
$x,y \in C(V)$
. In particular,
![]() $\langle x, y \rangle $
measures if x and y anti-commute in
$\langle x, y \rangle $
measures if x and y anti-commute in
![]() $C(V)$
:
$C(V)$
:
The map
![]() $V\to C(V)$
induces a map
$V\to C(V)$
induces a map
![]() $V \to C(V)^{\mathrm {opp}}$
(sending each
$V \to C(V)^{\mathrm {opp}}$
(sending each
![]() $v\in V$
to the same element), where
$v\in V$
to the same element), where
![]() $C(V)^{\mathrm {opp}}$
is the opposite algebra. The latter factors through a unique
$C(V)^{\mathrm {opp}}$
is the opposite algebra. The latter factors through a unique
![]() $\mathbb {Q}$
-algebra map
$\mathbb {Q}$
-algebra map
![]() $\beta \colon C(V) \to C(V)^{\mathrm {opp}}$
. It is readily checked that
$\beta \colon C(V) \to C(V)^{\mathrm {opp}}$
. It is readily checked that
![]() $\beta ^2$
is the identity on
$\beta ^2$
is the identity on
![]() $C(V)$
. By the universal property,
$C(V)$
. By the universal property,
![]() $\beta $
is the unique involution of
$\beta $
is the unique involution of
![]() $C(V)$
that is the identity on V.
$C(V)$
that is the identity on V.
The universal property also yields a surjection from the tensor algebra
 $$ \begin{align*}\bigoplus_{d \in \mathbb Z_{\geq 0}} V^{\otimes d} \twoheadrightarrow C(V). \end{align*} $$
$$ \begin{align*}\bigoplus_{d \in \mathbb Z_{\geq 0}} V^{\otimes d} \twoheadrightarrow C(V). \end{align*} $$
Define
![]() $C^+ = C(V)^+$
(resp.
$C^+ = C(V)^+$
(resp.
![]() $C^- = C(V)^-$
) to be the image of
$C^- = C(V)^-$
) to be the image of
![]() $\oplus _{d \in \mathbb Z_{\geq 0}} V^{\otimes 2d}$
(resp.
$\oplus _{d \in \mathbb Z_{\geq 0}} V^{\otimes 2d}$
(resp.
![]() $\oplus _{d \in \mathbb Z_{\geq 0}} V^{\otimes 2d+1}$
) so that
$\oplus _{d \in \mathbb Z_{\geq 0}} V^{\otimes 2d+1}$
) so that
![]() $C(V) = C(V)^+ \oplus C(V)^-$
. In fact, the discussion of Clifford algebras so far works when V is replaced with a quadratic space on a module over an arbitrary commutative ring, in a way compatible with base change: in particular, if R is a (commutative)
$C(V) = C(V)^+ \oplus C(V)^-$
. In fact, the discussion of Clifford algebras so far works when V is replaced with a quadratic space on a module over an arbitrary commutative ring, in a way compatible with base change: in particular, if R is a (commutative)
![]() $\mathbb {Q}$
-algebra, then
$\mathbb {Q}$
-algebra, then
![]() $C(V\otimes _{\mathbb {Q}} R)=C(V)\otimes _{\mathbb {Q}} R$
[Reference Bourbaki9, §9.1, Prop 2]. By scalars in
$C(V\otimes _{\mathbb {Q}} R)=C(V)\otimes _{\mathbb {Q}} R$
[Reference Bourbaki9, §9.1, Prop 2]. By scalars in
![]() $C(V\otimes _{\mathbb {Q}} R)$
, we mean R times the multiplicative unity. We keep using
$C(V\otimes _{\mathbb {Q}} R)$
, we mean R times the multiplicative unity. We keep using
![]() $\beta $
to denote the main involution of
$\beta $
to denote the main involution of
![]() $C(V\otimes _{\mathbb {Q}} R)$
.
$C(V\otimes _{\mathbb {Q}} R)$
.
The Clifford group
![]() $\mathrm {GPin}(V)$
is the
$\mathrm {GPin}(V)$
is the
![]() $\mathbb {Q}$
-group such that for every
$\mathbb {Q}$
-group such that for every
![]() $\mathbb {Q}$
-algebra R,
$\mathbb {Q}$
-algebra R,
where homogeneity of x means that
![]() $x \in C(V\otimes _{\mathbb {Q}} R)^{\varepsilon }$
for some sign
$x \in C(V\otimes _{\mathbb {Q}} R)^{\varepsilon }$
for some sign
![]() $\varepsilon $
. The special Clifford group
$\varepsilon $
. The special Clifford group
![]() $\mathrm {GSpin}(V)$
is defined similarly with
$\mathrm {GSpin}(V)$
is defined similarly with
![]() $C^+$
in place of C. The embedding of invertible scalars in
$C^+$
in place of C. The embedding of invertible scalars in
![]() $C(V\otimes _{\mathbb {Q}} R)$
induces a central embedding
$C(V\otimes _{\mathbb {Q}} R)$
induces a central embedding
Since
![]() $x\beta (x)\in R$
for
$x\beta (x)\in R$
for
![]() $x\in C(V\otimes _{\mathbb {Q}} R)$
by [Reference Bass4, Prop 3.2.1 (a)], we have the spinor norm morphism
$x\in C(V\otimes _{\mathbb {Q}} R)$
by [Reference Bass4, Prop 3.2.1 (a)], we have the spinor norm morphism
over
![]() $\mathbb {Q}$
. (The involution in loc. cit. differs from our
$\mathbb {Q}$
. (The involution in loc. cit. differs from our
![]() $\beta $
by
$\beta $
by
![]() $C(-1_P)$
in their notation, so our
$C(-1_P)$
in their notation, so our
![]() $\mathcal N$
does not coincide with their N, but
$\mathcal N$
does not coincide with their N, but
![]() $\mathcal N$
and N have the same kernel.) Evidently, composing
$\mathcal N$
and N have the same kernel.) Evidently, composing
![]() $\mathcal N$
with (3.2) yields the squaring map.
$\mathcal N$
with (3.2) yields the squaring map.
Define
![]() $\mathrm {Spin}(V)$
by the following exact sequence of algebraic groups:
$\mathrm {Spin}(V)$
by the following exact sequence of algebraic groups:
Lemma 3.1. The following are true, where kernels and surjectivity are always meant in the category of algebraic groups over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
-
(i) The map
 $\mathrm {pr}^{\circ }=\mathrm {pr}^{\circ }_V \colon \mathrm {GPin}(V)\to \mathrm {O}(V),~ x \mapsto ( v\mapsto x v x^{-1})$
is surjective for
$\mathrm {pr}^{\circ }=\mathrm {pr}^{\circ }_V \colon \mathrm {GPin}(V)\to \mathrm {O}(V),~ x \mapsto ( v\mapsto x v x^{-1})$
is surjective for
 $\dim V$
even, and
$\dim V$
even, and
 $\mathrm {pr}^{\circ } \colon \mathrm {GPin}(V) \to {\mathrm {SO}}(V)$
is surjective when
$\mathrm {pr}^{\circ } \colon \mathrm {GPin}(V) \to {\mathrm {SO}}(V)$
is surjective when
 $\dim V$
is odd.
$\dim V$
is odd. -
(ii) We have
 $\ker (\mathrm {pr}^{\circ }) = \mathbb {G}_{\mathrm {m}}$
via (3.2).
$\ker (\mathrm {pr}^{\circ }) = \mathbb {G}_{\mathrm {m}}$
via (3.2). -
(iii)
 $\mathrm {pr} \colon \mathrm {GPin}(V) \to \mathrm {GO}(V),~ x \mapsto (v \mapsto x v \beta (x))$
is a surjection, and
$\mathrm {pr} \colon \mathrm {GPin}(V) \to \mathrm {GO}(V),~ x \mapsto (v \mapsto x v \beta (x))$
is a surjection, and
 $\mathrm {sim} \circ \mathrm {pr} = \mathcal N^2$
.
$\mathrm {sim} \circ \mathrm {pr} = \mathcal N^2$
. -
(iv) The map
 $\mathrm {pr}$
factors as
$\mathrm {pr}$
factors as
 $\mathrm {GPin}(V)\stackrel {(\mathrm {pr}^{\circ },\mathcal N)}{\longrightarrow } \mathrm {O}(V)\times {\mathrm {GL}}_1 \stackrel {\mathrm {mult.}}{\longrightarrow } \mathrm {GO}(V)$
, where the latter is the multiplication map. The map
$\mathrm {GPin}(V)\stackrel {(\mathrm {pr}^{\circ },\mathcal N)}{\longrightarrow } \mathrm {O}(V)\times {\mathrm {GL}}_1 \stackrel {\mathrm {mult.}}{\longrightarrow } \mathrm {GO}(V)$
, where the latter is the multiplication map. The map
 $(\mathrm {pr}^{\circ },\mathcal N)$
has kernel
$(\mathrm {pr}^{\circ },\mathcal N)$
has kernel
 $\mu _2$
(scalars
$\mu _2$
(scalars
 $\{\pm 1\}$
in
$\{\pm 1\}$
in
 $C(V)$
) and image
$C(V)$
) and image
 $\mathrm {O}(V)\times {\mathrm {GL}}_1$
(resp.
$\mathrm {O}(V)\times {\mathrm {GL}}_1$
(resp.
 ${\mathrm {SO}}(V)\times {\mathrm {GL}}_1$
) for n even (resp. odd).
${\mathrm {SO}}(V)\times {\mathrm {GL}}_1$
) for n even (resp. odd). -
(v) The multiplication map
 $\mathrm {Spin}(V)\times \mathbb G_m\rightarrow \mathrm {GSpin}(V)$
is a surjection with kernel
$\mathrm {Spin}(V)\times \mathbb G_m\rightarrow \mathrm {GSpin}(V)$
is a surjection with kernel
 $\{\pm (1,1)\}$
(diagonally embedded
$\{\pm (1,1)\}$
(diagonally embedded
 $\mu _2$
), where
$\mu _2$
), where
 $\{\pm 1\}\hookrightarrow \mathrm {Spin}(V)$
via (3.2).
$\{\pm 1\}\hookrightarrow \mathrm {Spin}(V)$
via (3.2).
Proof. (i) The surjectivity can be checked on field-valued points. This is proved in [Reference Bourbaki9, §9.5, Thm. 4].
(ii) As
![]() $V\subset C(V)$
generates the Clifford algebra, the identity
$V\subset C(V)$
generates the Clifford algebra, the identity
![]() $xvx^{-1}=v$
implies
$xvx^{-1}=v$
implies
![]() $xyx^{-1}=y$
for all
$xyx^{-1}=y$
for all
![]() $y\in C(V)$
, and the analogue holds for
$y\in C(V)$
, and the analogue holds for
![]() $C(V\otimes _{\mathbb {Q}} R)$
for
$C(V\otimes _{\mathbb {Q}} R)$
for
![]() $\mathbb {Q}$
-algebras R. Thus,
$\mathbb {Q}$
-algebras R. Thus,
![]() $\ker (\mathrm {pr}^{\circ })(R)$
consists of invertible elements in the center of
$\ker (\mathrm {pr}^{\circ })(R)$
consists of invertible elements in the center of
![]() $C(V\otimes _{\mathbb {Q}} R)$
. Let
$C(V\otimes _{\mathbb {Q}} R)$
. Let
![]() $W\subset V$
be an isotropic subspace. Then
$W\subset V$
be an isotropic subspace. Then
![]() $C(V\otimes _{\mathbb {Q}} R)\simeq \mathrm {End}(\bigwedge (W\otimes _{\mathbb {Q}} R))$
as super R-algebras by [Reference Bass4, (2.4) Thm.], so the center of
$C(V\otimes _{\mathbb {Q}} R)\simeq \mathrm {End}(\bigwedge (W\otimes _{\mathbb {Q}} R))$
as super R-algebras by [Reference Bass4, (2.4) Thm.], so the center of
![]() $C(V\otimes _{\mathbb {Q}} R)$
is R, implying that
$C(V\otimes _{\mathbb {Q}} R)$
is R, implying that
![]() $\ker (\mathrm {pr}^{\circ }) = \mathbb {G}_{\mathrm {m}}$
.
$\ker (\mathrm {pr}^{\circ }) = \mathbb {G}_{\mathrm {m}}$
.
(iii) We observe that
![]() $\mathrm {pr}(x)$
preserves V: as
$\mathrm {pr}(x)$
preserves V: as
![]() $x (V\otimes _{\mathbb {Q}} R) x^{-1} = V\otimes _{\mathbb {Q}} R$
and
$x (V\otimes _{\mathbb {Q}} R) x^{-1} = V\otimes _{\mathbb {Q}} R$
and
![]() $x\beta (x)\in R^{\times }$
imply that
$x\beta (x)\in R^{\times }$
imply that
![]() $x(V\otimes _{\mathbb {Q}} R)\beta (x)=V\otimes _{\mathbb {Q}} R$
. Moreover,
$x(V\otimes _{\mathbb {Q}} R)\beta (x)=V\otimes _{\mathbb {Q}} R$
. Moreover,
![]() $\mathrm {pr}(x)\in \mathrm {GO}(V)$
as
$\mathrm {pr}(x)\in \mathrm {GO}(V)$
as
Moreover,
![]() $\mathrm {pr}$
and
$\mathrm {pr}$
and
![]() $\mathrm {pr}^{\circ }$
coincide on
$\mathrm {pr}^{\circ }$
coincide on
![]() $\mathrm {Pin}(V)$
, so
$\mathrm {Pin}(V)$
, so
![]() $\mathrm {(S)O}(V)$
is in the image of
$\mathrm {(S)O}(V)$
is in the image of
![]() $\mathrm {pr}$
. However,
$\mathrm {pr}$
. However,
![]() $\mathcal N$
is seen to be surjective by considering scalar elements, telling us that the image of
$\mathcal N$
is seen to be surjective by considering scalar elements, telling us that the image of
![]() $\mathrm {pr}$
also contains
$\mathrm {pr}$
also contains
![]() $\mathbb {G}_{\mathrm {m}}$
(scalar matrices in
$\mathbb {G}_{\mathrm {m}}$
(scalar matrices in
![]() $\mathrm {GO}(V)$
). Since
$\mathrm {GO}(V)$
). Since
![]() $\mathbb {G}_{\mathrm {m}}$
and
$\mathbb {G}_{\mathrm {m}}$
and
![]() $\mathrm {(S)O}(V)$
generate
$\mathrm {(S)O}(V)$
generate
![]() $\mathrm {G(S)O}(V)$
, the surjectivity of
$\mathrm {G(S)O}(V)$
, the surjectivity of
![]() $\mathrm {pr}$
follows. The equality
$\mathrm {pr}$
follows. The equality
![]() $\mathrm {sim} \circ \mathrm {pr} = \mathcal N^2$
follows from (3.3).
$\mathrm {sim} \circ \mathrm {pr} = \mathcal N^2$
follows from (3.3).
(iv) The first part follows from
![]() $\mathrm {pr}(x)(v)=xv \beta (x)=xvx^{-1}x\beta (x)=\mathrm {pr}^{\circ }(x)(v) \mathcal N(x)$
when
$\mathrm {pr}(x)(v)=xv \beta (x)=xvx^{-1}x\beta (x)=\mathrm {pr}^{\circ }(x)(v) \mathcal N(x)$
when
![]() $x\in \mathrm {GPin}(V)$
and
$x\in \mathrm {GPin}(V)$
and
![]() $v\in V$
. The second part is easily seen from (i) and (ii).
$v\in V$
. The second part is easily seen from (i) and (ii).
(v) This readily follows from the preceding points.
If V is odd dimensional, then
![]() ${\mathrm {SO}}(V) \times \{\pm 1\} = \mathrm {O}(V)$
, and the group
${\mathrm {SO}}(V) \times \{\pm 1\} = \mathrm {O}(V)$
, and the group
![]() $\mathrm {GO}(V)$
is connected. For convenience, we define
$\mathrm {GO}(V)$
is connected. For convenience, we define
![]() ${\mathrm {GSO}}(V) := \mathrm {GO}(V)$
in this case. If
${\mathrm {GSO}}(V) := \mathrm {GO}(V)$
in this case. If
![]() $\dim (V)$
is even, then
$\dim (V)$
is even, then
![]() $\mathrm {O}(V)$
(resp.
$\mathrm {O}(V)$
(resp.
![]() $\mathrm {GO}(V)$
) has two connected components but does not admit a direct product decomposition into
$\mathrm {GO}(V)$
) has two connected components but does not admit a direct product decomposition into
![]() $\mathrm {O}(V)$
(resp.
$\mathrm {O}(V)$
(resp.
![]() ${\mathrm {GSO}}(V)$
) and
${\mathrm {GSO}}(V)$
) and
![]() $\{\pm 1\}$
.
$\{\pm 1\}$
.
Assume that we have an orthogonal sum decomposition
![]() $\varphi \colon W_1 \oplus W_2 \overset \sim \to V$
of nondegenerate quadratic spaces over
$\varphi \colon W_1 \oplus W_2 \overset \sim \to V$
of nondegenerate quadratic spaces over
![]() $\mathbb {Q}$
. As super algebras, we have ([Reference Bass4, (2.3)] or [Reference Bourbaki9, §9.3, Cor. 3, Cor. 4])
$\mathbb {Q}$
. As super algebras, we have ([Reference Bass4, (2.3)] or [Reference Bourbaki9, §9.3, Cor. 3, Cor. 4])
By definition, the algebra given by
![]() $\widehat \otimes $
on the left side has underlying vector space
$\widehat \otimes $
on the left side has underlying vector space
![]() $C(W_1) \otimes C(W_2)$
and product
$C(W_1) \otimes C(W_2)$
and product
if
![]() $a, c \in C(W_1)$
,
$a, c \in C(W_1)$
,
![]() $b, d \in C(W_2)$
are homogeneous elements of degree
$b, d \in C(W_2)$
are homogeneous elements of degree
![]() $k_a, k_b, k_c, k_d \in \mathbb Z/2\mathbb Z$
. The sign is there to make
$k_a, k_b, k_c, k_d \in \mathbb Z/2\mathbb Z$
. The sign is there to make
![]() $C_{\varphi }$
compatible with products since
$C_{\varphi }$
compatible with products since
![]() $bc=(-1)^{k_b k_c}cb$
in
$bc=(-1)^{k_b k_c}cb$
in
![]() $C(V)$
.
$C(V)$
.
In fact,
![]() $C_{\varphi }$
intertwines the involution
$C_{\varphi }$
intertwines the involution
![]() $\beta $
on
$\beta $
on
![]() $C(V)$
with the involution
$C(V)$
with the involution
for homogeneous elements
![]() $a\in C(W_1)$
,
$a\in C(W_1)$
,
![]() $b\in C(W_2)$
of degree
$b\in C(W_2)$
of degree
![]() $k_a, k_b \in \mathbb Z/2\mathbb Z$
, where
$k_a, k_b \in \mathbb Z/2\mathbb Z$
, where
![]() $\beta _1,\beta _2$
are the involutions of
$\beta _1,\beta _2$
are the involutions of
![]() $C(W_1)$
and
$C(W_1)$
and
![]() $C(W_2)$
(see below (3.1)). To verify that
$C(W_2)$
(see below (3.1)). To verify that
![]() $\beta $
is compatible with
$\beta $
is compatible with
![]() $\beta '$
, observe that
$\beta '$
, observe that
![]() $\beta $
on
$\beta $
on
![]() $C(V)$
restricts to
$C(V)$
restricts to
![]() $\beta _1,\beta _2$
via the obvious inclusions
$\beta _1,\beta _2$
via the obvious inclusions
![]() $C(W_1)\hookrightarrow C(V)$
and
$C(W_1)\hookrightarrow C(V)$
and
![]() $C(W_2)\hookrightarrow C(V)$
induced by
$C(W_2)\hookrightarrow C(V)$
induced by
![]() $W_1\subset V$
and
$W_1\subset V$
and
![]() $W_2\subset V$
(since
$W_2\subset V$
(since
![]() $\beta $
acts as the identity on both
$\beta $
acts as the identity on both
![]() $W_1$
and
$W_1$
and
![]() $W_2$
), and use the property that
$W_2$
), and use the property that
![]() $\beta _1$
,
$\beta _1$
,
![]() $\beta _2$
, and
$\beta _2$
, and
![]() $\beta $
are preserving degrees. It follows that
$\beta $
are preserving degrees. It follows that
Lemma 3.2. The mapping
![]() $C_{\varphi }$
induces a morphism
$C_{\varphi }$
induces a morphism
![]() $\mathrm {GSpin}(W_1) \times \mathrm {GSpin}(W_2) \to \mathrm {GSpin}(V)$
.
$\mathrm {GSpin}(W_1) \times \mathrm {GSpin}(W_2) \to \mathrm {GSpin}(V)$
.
Proof. We check that the image of
![]() $C_{\varphi }$
is in
$C_{\varphi }$
is in
![]() $\mathrm {GSpin}(V)$
. Let
$\mathrm {GSpin}(V)$
. Let
![]() $g \in \mathrm {GSpin}(W_1)$
,
$g \in \mathrm {GSpin}(W_1)$
,
![]() $h \in \mathrm {GSpin}(W_2)$
. Note that
$h \in \mathrm {GSpin}(W_2)$
. Note that
![]() $C_{\varphi }(g \widehat {\otimes }h)=gh \in C^+(V)$
. Let
$C_{\varphi }(g \widehat {\otimes }h)=gh \in C^+(V)$
. Let
![]() $w_1 + w_2 \in V$
with
$w_1 + w_2 \in V$
with
![]() $w_i \in W_i$
,
$w_i \in W_i$
,
![]() $i=1,2$
. To verify that
$i=1,2$
. To verify that
![]() $gh \in \mathrm {GSpin}(V)$
, since homogeneous elements of even degree commute with each other if they are perpendicular, we see that
$gh \in \mathrm {GSpin}(V)$
, since homogeneous elements of even degree commute with each other if they are perpendicular, we see that
Lemma 3.3. The diagram

commutes, where
![]() $i_{W_1, W_2}$
is the block diagonal embedding.
$i_{W_1, W_2}$
is the block diagonal embedding.
Proof. Immediate from the computation in the proof of the preceding lemma.
In later chapters, we will carry out explicit computations. It will then be convenient to work with fixed bases and quadratic forms. For this reason, we now fix quadratic forms on the vector spaces
![]() $V_{2n}={\mathbb {C}}^{2n}$
and
$V_{2n}={\mathbb {C}}^{2n}$
and
![]() $V_{2n-1}={\mathbb {C}}^{2n-1}$
. We take the following quadratic forms:
$V_{2n-1}={\mathbb {C}}^{2n-1}$
. We take the following quadratic forms:
 $$ \begin{align} Q_{2n} \colon x_1 x_{n+1} + x_2 x_{n+2} + \ldots + x_n x_{2n} & \mathrm{ on } {\mathbb{C}}^{2n} \cr Q_{2n-1} \colon y_1 y_{n+1} + \ldots + y_{n-2} y_{2n-2} + y_{2n-1}^2 & \mathrm{ on } {\mathbb{C}}^{2n-1}. \end{align} $$
$$ \begin{align} Q_{2n} \colon x_1 x_{n+1} + x_2 x_{n+2} + \ldots + x_n x_{2n} & \mathrm{ on } {\mathbb{C}}^{2n} \cr Q_{2n-1} \colon y_1 y_{n+1} + \ldots + y_{n-2} y_{2n-2} + y_{2n-1}^2 & \mathrm{ on } {\mathbb{C}}^{2n-1}. \end{align} $$
Using them, we write
![]() ${\mathrm {SO}}_{m}={\mathrm {SO}}(V_{m})$
,
${\mathrm {SO}}_{m}={\mathrm {SO}}(V_{m})$
,
![]() ${\mathrm {GSO}}_{m}={\mathrm {GSO}}(V_{m})$
, and likewise for
${\mathrm {GSO}}_{m}={\mathrm {GSO}}(V_{m})$
, and likewise for
![]() $\mathrm {O}_m$
,
$\mathrm {O}_m$
,
![]() $\mathrm {GO}_m$
, for
$\mathrm {GO}_m$
, for
![]() $m=2n$
and
$m=2n$
and
![]() $m=2n-1$
. This is identical to the convention of §2 for m even. Similarly, we write
$m=2n-1$
. This is identical to the convention of §2 for m even. Similarly, we write
![]() $\mathrm {pr}^{\circ }_{2n-1}=\mathrm {pr}^{\circ }_{V_{2n-1}}$
and
$\mathrm {pr}^{\circ }_{2n-1}=\mathrm {pr}^{\circ }_{V_{2n-1}}$
and
![]() $\mathrm {pr}^{\circ }_{2n}=\mathrm {pr}^{\circ }_{V_{2n}}$
.
$\mathrm {pr}^{\circ }_{2n}=\mathrm {pr}^{\circ }_{V_{2n}}$
.
Now we claim that
![]() $\mathrm {GSpin}(V_{2n})$
is isomorphic to
$\mathrm {GSpin}(V_{2n})$
is isomorphic to
![]() $\mathrm {GSpin}_{2n}$
of §8, that is, the Clifford algebra definition is compatible with the root-theoretic definition as the Langlands dual of
$\mathrm {GSpin}_{2n}$
of §8, that is, the Clifford algebra definition is compatible with the root-theoretic definition as the Langlands dual of
![]() ${\mathrm {GSO}}_{2n}$
. (An analogous argument shows that
${\mathrm {GSO}}_{2n}$
. (An analogous argument shows that
![]() $\mathrm {GSpin}_{2n-1}$
is dual to
$\mathrm {GSpin}_{2n-1}$
is dual to
![]() $\mathrm {GSp}_{2n-2}$
.) As this is a routine exercise, we only sketch the argument. First,
$\mathrm {GSp}_{2n-2}$
.) As this is a routine exercise, we only sketch the argument. First,
![]() $\mathrm {pr}^{\circ }$
restricts to a connected double covering
$\mathrm {pr}^{\circ }$
restricts to a connected double covering
![]() $\mathrm {Spin}(V_{m})\rightarrow {\mathrm {SO}}(V_{m})$
([Reference Fulton and Harris25, Prop. 20.38]), which must then be the unique (up to isomorphism) simply connected covering. This determines the root datum of
$\mathrm {Spin}(V_{m})\rightarrow {\mathrm {SO}}(V_{m})$
([Reference Fulton and Harris25, Prop. 20.38]), which must then be the unique (up to isomorphism) simply connected covering. This determines the root datum of
![]() $\mathrm {Spin}(V_{m})$
. From this, we compute the root datum of
$\mathrm {Spin}(V_{m})$
. From this, we compute the root datum of
![]() $\mathrm {GSpin}(V_m)$
via the central isogeny
$\mathrm {GSpin}(V_m)$
via the central isogeny
![]() $\mathrm {Spin}(V_{m})\times \mathbb G_m\rightarrow \mathrm {GSpin}(V_m)$
of Lemma 3.1. Finally, when
$\mathrm {Spin}(V_{m})\times \mathbb G_m\rightarrow \mathrm {GSpin}(V_m)$
of Lemma 3.1. Finally, when
![]() $m=2n$
, we deduce that the outcome is dual to the root datum of
$m=2n$
, we deduce that the outcome is dual to the root datum of
![]() ${\mathrm {GSO}}_{2n}$
in Lemma 2.1. Therefore,
${\mathrm {GSO}}_{2n}$
in Lemma 2.1. Therefore,
![]() $\mathrm {GSpin}(V_{2n})$
is isomorphic to
$\mathrm {GSpin}(V_{2n})$
is isomorphic to
![]() $\mathrm {GSpin}_{2n}$
of §8. Henceforth, we identify
$\mathrm {GSpin}_{2n}$
of §8. Henceforth, we identify
In fact, we may and will choose
![]() $\mathrm {B}_{\mathrm {GSpin}}$
and
$\mathrm {B}_{\mathrm {GSpin}}$
and
![]() $\mathrm {T}_{\mathrm {GSpin}}$
to be the preimages of
$\mathrm {T}_{\mathrm {GSpin}}$
to be the preimages of
![]() $\mathrm {B}_{{\mathrm {SO}}}$
and
$\mathrm {B}_{{\mathrm {SO}}}$
and
![]() $\mathrm {T}_{{\mathrm {SO}}}$
via
$\mathrm {T}_{{\mathrm {SO}}}$
via
![]() $\mathrm {pr}^{\circ }: \mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. We fix pinnings of
$\mathrm {pr}^{\circ }: \mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. We fix pinnings of
![]() $\mathrm {GSpin}_{2n}$
,
$\mathrm {GSpin}_{2n}$
,
![]() ${\mathrm {GSO}}_{2n}$
, and
${\mathrm {GSO}}_{2n}$
, and
![]() ${\mathrm {SO}}_{2n}$
(which are
${\mathrm {SO}}_{2n}$
(which are
![]() $\Gamma _F$
-equivariant if
$\Gamma _F$
-equivariant if
![]() $(V_{2n},Q_{2n})$
is defined over F) compatibly via
$(V_{2n},Q_{2n})$
is defined over F) compatibly via
![]() $\mathrm {pr}$
and
$\mathrm {pr}$
and
![]() $\mathrm {pr}^{\circ }$
.
$\mathrm {pr}^{\circ }$
.
Lemma 3.4. Via (3.5), the central embedding of scalar matrices
![]() $\mathrm {cent}^{\circ }:\mathbb G_m\rightarrow {\mathrm {GSO}}_{2n}$
and
$\mathrm {cent}^{\circ }:\mathbb G_m\rightarrow {\mathrm {GSO}}_{2n}$
and
![]() $\mathrm {sim}:{\mathrm {GSO}}_{2n}\rightarrow \mathbb G_m$
are dual to
$\mathrm {sim}:{\mathrm {GSO}}_{2n}\rightarrow \mathbb G_m$
are dual to
![]() $\mathcal N:\mathrm {GSpin}_{2n}\rightarrow \mathbb G_m$
and the central embedding
$\mathcal N:\mathrm {GSpin}_{2n}\rightarrow \mathbb G_m$
and the central embedding
![]() $\mathrm {cent}:\mathbb G_m\rightarrow \mathrm {GSpin}_{2n}$
of (3.2), respectively.
$\mathrm {cent}:\mathbb G_m\rightarrow \mathrm {GSpin}_{2n}$
of (3.2), respectively.
Remark 3.5. The dual map of
![]() $\mathrm {cent}^{\circ }$
was made explicit in (2.7). According to the present lemma, (2.7) gives an explicit formula for
$\mathrm {cent}^{\circ }$
was made explicit in (2.7). According to the present lemma, (2.7) gives an explicit formula for
![]() $\mathcal N$
restricted to
$\mathcal N$
restricted to
![]() $T_{\mathrm {GSpin}}$
.
$T_{\mathrm {GSpin}}$
.
Proof. Write
![]() $Z^0$
for the identity component of the center of
$Z^0$
for the identity component of the center of
![]() $\mathrm {GSpin}_{2n}$
, consisting of
$\mathrm {GSpin}_{2n}$
, consisting of
![]() $(s_0,1,\ldots ,1)$
with
$(s_0,1,\ldots ,1)$
with
![]() $s_0\in {\mathbb G}_m$
in the notation of Lemma 2.5. The dual of
$s_0\in {\mathbb G}_m$
in the notation of Lemma 2.5. The dual of
![]() $\mathrm {sim}:{\mathrm {GSO}}_{2n}\rightarrow {\mathbb G}_m$
is calculated as the central cocharacter
$\mathrm {sim}:{\mathrm {GSO}}_{2n}\rightarrow {\mathbb G}_m$
is calculated as the central cocharacter
![]() $\mathbb G_m\rightarrow Z^0\subset \mathrm {GSpin}_{2n}$
,
$\mathbb G_m\rightarrow Z^0\subset \mathrm {GSpin}_{2n}$
,
![]() $z\mapsto (z,1,\ldots ,1)$
. The inclusion
$z\mapsto (z,1,\ldots ,1)$
. The inclusion
![]() $\mathrm {cent}:\mathbb G_m\rightarrow \mathrm {GSpin}_{2n}$
identifies
$\mathrm {cent}:\mathbb G_m\rightarrow \mathrm {GSpin}_{2n}$
identifies
![]() $\mathbb G_m$
with
$\mathbb G_m$
with
![]() $Z^0$
. Thus, cent is dual to
$Z^0$
. Thus, cent is dual to
![]() $\mathrm {sim}$
.
$\mathrm {sim}$
.
Both
![]() $\mathcal N\circ \mathrm {cent}$
and
$\mathcal N\circ \mathrm {cent}$
and
![]() $\mathrm {sim}\circ \mathrm {cent}^{\circ }$
are the squaring map on
$\mathrm {sim}\circ \mathrm {cent}^{\circ }$
are the squaring map on
![]() $\mathbb G_m$
. Using the hat symbol to denote a dual morphism, we see that
$\mathbb G_m$
. Using the hat symbol to denote a dual morphism, we see that
and that they are all equal to the squaring map. It follows that
![]() $\mathcal N$
is dual to
$\mathcal N$
is dual to
![]() $\mathrm {cent}^{\circ }$
.
$\mathrm {cent}^{\circ }$
.
We have the morphism of quadratic spaces
Indeed,
![]() $Q_{2n} \varphi = Q_{2n-1}$
as readily checked. We have the complementary embedding:
$Q_{2n} \varphi = Q_{2n-1}$
as readily checked. We have the complementary embedding:
 $$ \begin{align*}\varphi' \colon {\mathbb{C}} \to {\mathbb{C}}^{2n}, \quad u \mapsto x, \quad \mathrm{where} \quad \begin{cases} x_k = 0 & k \neq n,\ 2n \cr x_k = (-1)^{k/n} u & \mathrm{if}\ k = n\ \mathrm{or}\ k = 2n. \end{cases} \end{align*} $$
$$ \begin{align*}\varphi' \colon {\mathbb{C}} \to {\mathbb{C}}^{2n}, \quad u \mapsto x, \quad \mathrm{where} \quad \begin{cases} x_k = 0 & k \neq n,\ 2n \cr x_k = (-1)^{k/n} u & \mathrm{if}\ k = n\ \mathrm{or}\ k = 2n. \end{cases} \end{align*} $$
Write
![]() $U := \varphi '({\mathbb {C}})=(e_n-e_{2n})\cdot {\mathbb {C}}$
for the image. The induced quadratic form on U is then
$U := \varphi '({\mathbb {C}})=(e_n-e_{2n})\cdot {\mathbb {C}}$
for the image. The induced quadratic form on U is then
![]() $a\cdot (e_n-e_{2n})\mapsto -a^2$
. This gives us an orthogonal decomposition of quadratic spaces
$a\cdot (e_n-e_{2n})\mapsto -a^2$
. This gives us an orthogonal decomposition of quadratic spaces
![]() ${\mathbb {C}}^{2n} = {\mathbb {C}}^{2n-1} \widehat {\oplus } U$
. Let
${\mathbb {C}}^{2n} = {\mathbb {C}}^{2n-1} \widehat {\oplus } U$
. Let
![]() $\mathrm {PO}_m$
denote the adjoint group of
$\mathrm {PO}_m$
denote the adjoint group of
![]() $\mathrm {O}_m$
. The decomposition induces morphisms (cf. Lemmas 3.2, 3.3)
$\mathrm {O}_m$
. The decomposition induces morphisms (cf. Lemmas 3.2, 3.3)
 $$ \begin{align} i_{\mathrm{std}} &:= C_{\varphi, \varphi'} \colon \mathrm{GSpin}_{2n-1} \times \mathrm{GSpin}_1 \to \mathrm{GSpin}_{2n}, \cr i_{\mathrm{std}}^{\circ} &:= i_{{\mathbb{C}}^{2n-1}, {\mathbb{C}}} \colon \mathrm{O}_{2n-1} \times \mathrm{O}_1 \to \mathrm{O}_{2n},~~\mbox{and} \cr \overline {i_{\mathrm{std}}} &:= \mathrm{PO}_{2n-1} \to \mathrm{PO}_{2n}, \end{align} $$
$$ \begin{align} i_{\mathrm{std}} &:= C_{\varphi, \varphi'} \colon \mathrm{GSpin}_{2n-1} \times \mathrm{GSpin}_1 \to \mathrm{GSpin}_{2n}, \cr i_{\mathrm{std}}^{\circ} &:= i_{{\mathbb{C}}^{2n-1}, {\mathbb{C}}} \colon \mathrm{O}_{2n-1} \times \mathrm{O}_1 \to \mathrm{O}_{2n},~~\mbox{and} \cr \overline {i_{\mathrm{std}}} &:= \mathrm{PO}_{2n-1} \to \mathrm{PO}_{2n}, \end{align} $$
where
![]() $\overline {i_{\mathrm {std}}}$
is induced from
$\overline {i_{\mathrm {std}}}$
is induced from
![]() $i_{\mathrm {std}} \colon \mathrm {GSpin}_{2n-1} \times \mathrm {GSpin}_1 \to \mathrm {GSpin}_{2n} \twoheadrightarrow \mathrm {PSO}_{2n}\subset \mathrm {PO}_{2n}$
. By Lemma 3.3, we have
$i_{\mathrm {std}} \colon \mathrm {GSpin}_{2n-1} \times \mathrm {GSpin}_1 \to \mathrm {GSpin}_{2n} \twoheadrightarrow \mathrm {PSO}_{2n}\subset \mathrm {PO}_{2n}$
. By Lemma 3.3, we have
![]() $\mathrm {pr}^{\circ } \circ i_{\mathrm {std}}=i_{\mathrm {std}}^{\circ }\circ (\mathrm {pr}^{\circ }_{2n-1}\times \mathrm {pr}^{\circ }_{U})$
.
$\mathrm {pr}^{\circ } \circ i_{\mathrm {std}}=i_{\mathrm {std}}^{\circ }\circ (\mathrm {pr}^{\circ }_{2n-1}\times \mathrm {pr}^{\circ }_{U})$
.
Let
![]() $1_{2n-1}, 1_U$
denote the identity map on
$1_{2n-1}, 1_U$
denote the identity map on
![]() ${\mathbb {C}}^{2n-1},U$
. Then (cf. (2.4))
${\mathbb {C}}^{2n-1},U$
. Then (cf. (2.4))
 $$ \begin{align*} i_{\mathrm{std}}^{\circ}(-1_{2n-1}, 1_U) =-\left( \begin{array}{cc;{1pt/1pt}cc}1_{n-1} & & & \\ & 0 & & 1 \\ \hdashline[1pt/1pt] & & 1_{n-1} & \\ & 1& & 0 \end{array}\right) = \vartheta^{\circ} \in \mathrm{O}_{2n}. \end{align*} $$
$$ \begin{align*} i_{\mathrm{std}}^{\circ}(-1_{2n-1}, 1_U) =-\left( \begin{array}{cc;{1pt/1pt}cc}1_{n-1} & & & \\ & 0 & & 1 \\ \hdashline[1pt/1pt] & & 1_{n-1} & \\ & 1& & 0 \end{array}\right) = \vartheta^{\circ} \in \mathrm{O}_{2n}. \end{align*} $$
Fix
![]() $\sqrt {-1}\in \mathbb G_m=Z(\mathrm {GPin}_{2n})$
. Define
$\sqrt {-1}\in \mathbb G_m=Z(\mathrm {GPin}_{2n})$
. Define
Lemma 3.6. We have
-
(i)
 $\mathrm {pr}^{\circ }_{2n}(\vartheta ) = \vartheta ^{\circ }$
and
$\mathrm {pr}^{\circ }_{2n}(\vartheta ) = \vartheta ^{\circ }$
and
 $\vartheta ^2 = 1$
.
$\vartheta ^2 = 1$
. -
(ii) The conjugation action of
 $\vartheta $
(resp.
$\vartheta $
(resp.
 $\vartheta ^{\circ }$
) fixes the subgroup
$\vartheta ^{\circ }$
) fixes the subgroup
 $i_{\mathrm {std}}(\mathrm {GSpin}_{2n-1}\times \mathrm {GSpin}_1) \subset \mathrm {GSpin}_{2n}$
via
$i_{\mathrm {std}}(\mathrm {GSpin}_{2n-1}\times \mathrm {GSpin}_1) \subset \mathrm {GSpin}_{2n}$
via
 $i_{\mathrm {std}}$
(resp.
$i_{\mathrm {std}}$
(resp.
 ${\mathrm {SO}}_{2n-1}\times {\mathrm {SO}}_1 \subset {\mathrm {SO}}_{2n}$
via
${\mathrm {SO}}_{2n-1}\times {\mathrm {SO}}_1 \subset {\mathrm {SO}}_{2n}$
via
 $i^{\circ }_{\mathrm {std}}$
) and induces the identity automorphism on that subgroup.
$i^{\circ }_{\mathrm {std}}$
) and induces the identity automorphism on that subgroup. -
(iii) The conjugation action of
 $\vartheta $
(resp.
$\vartheta $
(resp.
 $\vartheta ^{\circ }$
) defines the outer automorphism
$\vartheta ^{\circ }$
) defines the outer automorphism
 $\theta $
of
$\theta $
of
 $\mathrm {GSpin}_{2n}$
(resp.
$\mathrm {GSpin}_{2n}$
(resp.
 $\theta ^{\circ }$
of
$\theta ^{\circ }$
of
 ${\mathrm {GSO}}_{2n}$
) in Lemmas 2.3 and 2.4.
${\mathrm {GSO}}_{2n}$
) in Lemmas 2.3 and 2.4.
Proof. (i) Let
![]() $w_1\in {\mathbb {C}}^{2n-1}$
and
$w_1\in {\mathbb {C}}^{2n-1}$
and
![]() $w_2:=e_n-e_{2n}\in U$
. All of
$w_2:=e_n-e_{2n}\in U$
. All of
![]() $w_1,w_2,\vartheta $
have degree 1 in
$w_1,w_2,\vartheta $
have degree 1 in
![]() $C({\mathbb {C}}^{2n})$
. In either
$C({\mathbb {C}}^{2n})$
. In either
![]() $C({\mathbb {C}}^{2n})$
or
$C({\mathbb {C}}^{2n})$
or
![]() $C(U)$
, we have
$C(U)$
, we have
![]() $w_2^2=Q_{2n}(w_2)=-1$
and
$w_2^2=Q_{2n}(w_2)=-1$
and
![]() $\vartheta ^2=-w_2^2 = 1$
. Thus,
$\vartheta ^2=-w_2^2 = 1$
. Thus,
![]() $\vartheta w_1 \vartheta ^{-1}=-w_1\vartheta \vartheta ^{-1}=-w_1$
and
$\vartheta w_1 \vartheta ^{-1}=-w_1\vartheta \vartheta ^{-1}=-w_1$
and
![]() $\vartheta w_2 \vartheta ^{-1}= w_2$
. Hence,
$\vartheta w_2 \vartheta ^{-1}= w_2$
. Hence,
![]() $\mathrm {pr}^{\circ }_{2n}(\vartheta ) = \vartheta ^{\circ }$
.
$\mathrm {pr}^{\circ }_{2n}(\vartheta ) = \vartheta ^{\circ }$
.
(ii) This is obvious for
![]() $\vartheta ^{\circ }$
. The conjugation by
$\vartheta ^{\circ }$
. The conjugation by
![]() $\vartheta $
is the identity on
$\vartheta $
is the identity on
![]() $C^+({\mathbb {C}}^{2n-1})$
and
$C^+({\mathbb {C}}^{2n-1})$
and
![]() $C^+(U)$
, since
$C^+(U)$
, since
![]() $\vartheta \perp {\mathbb {C}}^{2n-1}$
and
$\vartheta \perp {\mathbb {C}}^{2n-1}$
and
![]() $C^+(U)$
is commutative, respectively. The assertion for
$C^+(U)$
is commutative, respectively. The assertion for
![]() $\vartheta $
follows.
$\vartheta $
follows.
(iii) This is true by definition for
![]() $\theta ^{\circ }$
. Since
$\theta ^{\circ }$
. Since
![]() $\theta $
and the conjugation by
$\theta $
and the conjugation by
![]() $\vartheta $
act trivially on the center of
$\vartheta $
act trivially on the center of
![]() $\mathrm {GSpin}_{2n}$
, it suffices to check that their actions are identical on the adjoint group. This reduces to the fact that
$\mathrm {GSpin}_{2n}$
, it suffices to check that their actions are identical on the adjoint group. This reduces to the fact that
![]() $\theta ^{\circ }$
is given by the
$\theta ^{\circ }$
is given by the
![]() $\vartheta ^{\circ }$
-conjugation, as
$\vartheta ^{\circ }$
-conjugation, as
![]() $\theta $
and
$\theta $
and
![]() $\theta ^{\circ }$
(resp.
$\theta ^{\circ }$
(resp.
![]() $\vartheta $
and
$\vartheta $
and
![]() $\vartheta ^{\circ }$
) induce the same action on the adjoint group (thanks to part (i)).
$\vartheta ^{\circ }$
) induce the same action on the adjoint group (thanks to part (i)).
We have fixed pinnings of
![]() $\mathrm {GSpin}_{2n}$
,
$\mathrm {GSpin}_{2n}$
,
![]() ${\mathrm {GSO}}_{2n}$
and
${\mathrm {GSO}}_{2n}$
and
![]() ${\mathrm {SO}}_{2n}$
compatibly via
${\mathrm {SO}}_{2n}$
compatibly via
![]() $\mathrm {pr}$
. They are fixed by
$\mathrm {pr}$
. They are fixed by
![]() $\theta \in \mathrm {Aut}(\mathrm {GSpin}_{2n})$
and
$\theta \in \mathrm {Aut}(\mathrm {GSpin}_{2n})$
and
![]() $\theta ^{\circ }\in \mathrm {Aut}({\mathrm {GSO}}_{2n})$
. It is easy to see that
$\theta ^{\circ }\in \mathrm {Aut}({\mathrm {GSO}}_{2n})$
. It is easy to see that
![]() $\theta $
and
$\theta $
and
![]() $\theta ^{\circ }$
induce automorphisms of based root data, which correspond to each other via duality of the two based root data. Thus, letting
$\theta ^{\circ }$
induce automorphisms of based root data, which correspond to each other via duality of the two based root data. Thus, letting
![]() $E/F$
be a quadratic extension of fields of characteristic 0, and
$E/F$
be a quadratic extension of fields of characteristic 0, and
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
an outer form of
${\mathrm {GSO}}_{2n}^{E/F}$
an outer form of
![]() ${\mathrm {GSO}}_{2n}$
over F with respect to the Galois action
${\mathrm {GSO}}_{2n}$
over F with respect to the Galois action
![]() $\Gamma _{E/F}=\{1,c\}\stackrel {\sim }{\to } \{1,\theta \}$
, we can identify
$\Gamma _{E/F}=\{1,c\}\stackrel {\sim }{\to } \{1,\theta \}$
, we can identify
where the semi-direct product is given by
![]() $c g c^{-1} = \theta (g)$
. (Of course,
$c g c^{-1} = \theta (g)$
. (Of course,
![]() $c=c^{-1}$
.) The second identification above is via
$c=c^{-1}$
.) The second identification above is via
![]() $c\mapsto \vartheta $
. Similarly, for
$c\mapsto \vartheta $
. Similarly, for
![]() ${\mathrm {SO}}_{2n}^{E/F}$
an outer form of
${\mathrm {SO}}_{2n}^{E/F}$
an outer form of
![]() ${\mathrm {SO}}_{2n}$
with respect to
${\mathrm {SO}}_{2n}$
with respect to
![]() $\Gamma _{E/F}=\{1,c\}\stackrel {\sim }{\to } \{1,\theta ^{\circ }\}$
, we have
$\Gamma _{E/F}=\{1,c\}\stackrel {\sim }{\to } \{1,\theta ^{\circ }\}$
, we have
Let us describe the center
![]() $Z(\mathrm {Spin}_{2n})$
of
$Z(\mathrm {Spin}_{2n})$
of
![]() $\mathrm {Spin}_{2n}=\mathrm {Spin}(V_{2n})$
explicitly as this is going to be useful for classifying inner twists of (quasi-split forms of)
$\mathrm {Spin}_{2n}=\mathrm {Spin}(V_{2n})$
explicitly as this is going to be useful for classifying inner twists of (quasi-split forms of)
![]() ${\mathrm {SO}}_{2n}$
and
${\mathrm {SO}}_{2n}$
and
![]() ${\mathrm {GSO}}_{2n}$
in §8. In what follows, we identify
${\mathrm {GSO}}_{2n}$
in §8. In what follows, we identify
![]() $Z(\mathrm {GSpin}_{2n})=\{(s_0,s_1)\,:\,s_0\in \mathbb G_m,~s_1\in \{\pm 1\}\}$
as in Lemma 2.5 and write
$Z(\mathrm {GSpin}_{2n})=\{(s_0,s_1)\,:\,s_0\in \mathbb G_m,~s_1\in \{\pm 1\}\}$
as in Lemma 2.5 and write
![]() $1,-1$
for
$1,-1$
for
![]() $(1,1),(1,-1)\in Z(\mathrm {GSpin}_{2n})$
.
$(1,1),(1,-1)\in Z(\mathrm {GSpin}_{2n})$
.
Lemma 3.7. Let
![]() $\zeta _4$
be a primitive fourth root of unity. Recall the elements
$\zeta _4$
be a primitive fourth root of unity. Recall the elements
![]() $z_{\pm }$
defined in Lemma 2.7. Then we have
$z_{\pm }$
defined in Lemma 2.7. Then we have
![]() $Z(\mathrm {Spin}_{2n}) \subset Z(\mathrm {GSpin}_{2n})$
via
$Z(\mathrm {Spin}_{2n}) \subset Z(\mathrm {GSpin}_{2n})$
via
![]() $\mathrm {T}_{\mathrm {Spin}}\subset T_{\mathrm {GSpin}}$
explained above, and the following are true.
$\mathrm {T}_{\mathrm {Spin}}\subset T_{\mathrm {GSpin}}$
explained above, and the following are true.
-
(i) If
 $n $
is even,
$n $
is even,
 $Z(\mathrm {Spin}_{2n})=\{1,-1,z_+,z_-\}$
and is isomorphic to
$Z(\mathrm {Spin}_{2n})=\{1,-1,z_+,z_-\}$
and is isomorphic to
 $(\mathbb Z/2\mathbb Z)^2$
. If n is odd,
$(\mathbb Z/2\mathbb Z)^2$
. If n is odd,
 $Z(\mathrm {Spin}_{2n})=\{1,-1,\zeta ,-\zeta =\zeta ^{-1}\}$
and is isomorphic to
$Z(\mathrm {Spin}_{2n})=\{1,-1,\zeta ,-\zeta =\zeta ^{-1}\}$
and is isomorphic to
 $\mathbb Z/4\mathbb Z$
, where
$\mathbb Z/4\mathbb Z$
, where
 $\zeta =(\zeta _4,-1)$
.
$\zeta =(\zeta _4,-1)$
. -
(ii) The action of
 $\theta $
is trivial on
$\theta $
is trivial on
 $\{1,-1\}$
and permuting
$\{1,-1\}$
and permuting
 $\{z_+,z_-\}$
(resp.
$\{z_+,z_-\}$
(resp.
 $\{\zeta ,-\zeta \}$
).
$\{\zeta ,-\zeta \}$
).
Proof. We have
![]() $Z(\mathrm {Spin}_{2n})=Z(\mathrm {GSpin}_{2n}) \cap \mathrm {Spin}_{2n}= \{z\in Z(\mathrm {GSpin}_{2n}): \mathcal N(z)=1\}$
, where
$Z(\mathrm {Spin}_{2n})=Z(\mathrm {GSpin}_{2n}) \cap \mathrm {Spin}_{2n}= \{z\in Z(\mathrm {GSpin}_{2n}): \mathcal N(z)=1\}$
, where
![]() $\mathcal N$
is described by (2.7) (Remark 3.5). It follows from Lemma 2.5 that
$\mathcal N$
is described by (2.7) (Remark 3.5). It follows from Lemma 2.5 that
which is alternatively described as in (i). Assertion (ii) is also clear from that lemma.
4 The spin representations
We recollect how to construct the spin representations via Clifford algebras, and we show that they coincide with the highest weight representations in Section 2. We also check some compatibility of maps that will become handy.
Consider the quadratic space
![]() $V_{2n} := {\mathbb {C}}^{2n}$
from (3.4) with standard basis
$V_{2n} := {\mathbb {C}}^{2n}$
from (3.4) with standard basis
![]() $\{e_1,..,e_{2n}\}$
and quadratic form
$\{e_1,..,e_{2n}\}$
and quadratic form
![]() $Q_{2n}$
. Define
$Q_{2n}$
. Define
![]() $W_{2n} := \oplus _{i=1}^n {\mathbb {C}} e_i$
and
$W_{2n} := \oplus _{i=1}^n {\mathbb {C}} e_i$
and
![]() $W^{\prime }_{2n} := \oplus _{i=n+1}^{2n} {\mathbb {C}} e_i$
. We often omit the subscript
$W^{\prime }_{2n} := \oplus _{i=n+1}^{2n} {\mathbb {C}} e_i$
. We often omit the subscript
![]() $2n$
to lighten notation, when there is no danger of confusion. Since W is isotropic, we obtain a morphism
$2n$
to lighten notation, when there is no danger of confusion. Since W is isotropic, we obtain a morphism
![]() $\bigwedge W \overset \sim \to C(W) \hookrightarrow C(V)$
. Through this injection, we view
$\bigwedge W \overset \sim \to C(W) \hookrightarrow C(V)$
. Through this injection, we view
![]() $\bigwedge W$
as a subspace of
$\bigwedge W$
as a subspace of
![]() $C(V)$
. The space
$C(V)$
. The space
![]() $\bigwedge W$
carries an
$\bigwedge W$
carries an
![]() $C(V)$
-module structure
$C(V)$
-module structure
that is uniquely characterized by the following:
-
•
 $w \in W \subset V$
acts through left multiplication,
$w \in W \subset V$
acts through left multiplication, -
• and
 $w' \in W' \subset V$
acts as (4.1)on
$w' \in W' \subset V$
acts as (4.1)on $$ \begin{align} w' (w_1 \wedge w_2 \wedge \cdots \wedge w_r) = \sum_{i=1}^r (-1)^{i+1} \langle w', w_i \rangle (w_1 \wedge w_2 \wedge \cdots \wedge \widehat {w_i} \wedge \cdots \wedge w_r) \end{align} $$
$$ \begin{align} w' (w_1 \wedge w_2 \wedge \cdots \wedge w_r) = \sum_{i=1}^r (-1)^{i+1} \langle w', w_i \rangle (w_1 \wedge w_2 \wedge \cdots \wedge \widehat {w_i} \wedge \cdots \wedge w_r) \end{align} $$
 $w_1 \wedge \cdots \wedge w_r \in \bigwedge ^r W \subset \bigwedge W$
.
$w_1 \wedge \cdots \wedge w_r \in \bigwedge ^r W \subset \bigwedge W$
.
The subspaces
![]() ${\bigwedge }^+ W := \bigwedge _{i \in 2\mathbb Z_{\geq 0}} W$
and
${\bigwedge }^+ W := \bigwedge _{i \in 2\mathbb Z_{\geq 0}} W$
and
![]() ${\bigwedge }^- W := \bigwedge _{i \in 1+2\mathbb Z_{\geq 0}} W$
of
${\bigwedge }^- W := \bigwedge _{i \in 1+2\mathbb Z_{\geq 0}} W$
of
![]() $\bigwedge W$
are stable under
$\bigwedge W$
are stable under
![]() $C^+(V)$
. By restriction, we obtain the spin representations
$C^+(V)$
. By restriction, we obtain the spin representations
We recall that the representations
![]() $\mathrm {spin}^{\pm }$
are irreducible. In (4.5) and (4.6) below, we will choose (ordered) bases for
$\mathrm {spin}^{\pm }$
are irreducible. In (4.5) and (4.6) below, we will choose (ordered) bases for
![]() $ \bigwedge W$
and
$ \bigwedge W$
and
![]() $ \bigwedge ^{\pm } W$
coming from
$ \bigwedge ^{\pm } W$
coming from
![]() $\{e_1,\ldots ,e_n\}$
to view
$\{e_1,\ldots ,e_n\}$
to view
![]() $\mathrm {spin}$
and
$\mathrm {spin}$
and
![]() $\mathrm {spin}^{\pm }$
as
$\mathrm {spin}^{\pm }$
as
![]() ${\mathrm {GL}}_{2^n}$
and
${\mathrm {GL}}_{2^n}$
and
![]() ${\mathrm {GL}}_{2^{n-1}}$
-valued representations, respectively. We had another definition of
${\mathrm {GL}}_{2^{n-1}}$
-valued representations, respectively. We had another definition of
![]() $\mathrm {spin}^{\varepsilon }$
as the representation with highest weight
$\mathrm {spin}^{\varepsilon }$
as the representation with highest weight
![]() $\mu _{\varepsilon }$
(Definition 2.6),
$\mu _{\varepsilon }$
(Definition 2.6),
![]() $\varepsilon \in \{+,-\}$
. Let us check that the two definitions coincide via (3.5).
$\varepsilon \in \{+,-\}$
. Let us check that the two definitions coincide via (3.5).
Lemma 4.1. The highest weight of the half-spin representation
![]() $\mathrm {spin}^{\varepsilon }$
of
$\mathrm {spin}^{\varepsilon }$
of
![]() $\mathrm {GSpin}_{2n}$
on
$\mathrm {GSpin}_{2n}$
on
![]() $\bigwedge ^{\varepsilon } W$
is equal to
$\bigwedge ^{\varepsilon } W$
is equal to
![]() $\mu _{\varepsilon }$
.
$\mu _{\varepsilon }$
.
Proof. We may compare
![]() $\mu _{\varepsilon }$
and the highest weight of
$\mu _{\varepsilon }$
and the highest weight of
![]() $\mathrm {spin}^{\varepsilon }$
after pulling back along
$\mathrm {spin}^{\varepsilon }$
after pulling back along
![]() $\mathrm {Spin}_{2n}\times \mathbb G_m\twoheadrightarrow \mathrm {GSpin}_{2n}$
. They coincide on
$\mathrm {Spin}_{2n}\times \mathbb G_m\twoheadrightarrow \mathrm {GSpin}_{2n}$
. They coincide on
![]() $\mathrm {Spin}_{2n}$
by [Reference Fulton and Harris25, Prop. 20.15] and evidently restrict to the weight 1 character on
$\mathrm {Spin}_{2n}$
by [Reference Fulton and Harris25, Prop. 20.15] and evidently restrict to the weight 1 character on
![]() $\mathbb G_m$
. The lemma follows.
$\mathbb G_m$
. The lemma follows.
Let us introduce a bilinear pairing on
![]() $\bigwedge W$
which is invariant under the spin representation up to scalars. Let
$\bigwedge W$
which is invariant under the spin representation up to scalars. Let
![]() $\mathrm {pr}_n: \bigwedge W\rightarrow {\mathbb {C}}$
denote the projection onto
$\mathrm {pr}_n: \bigwedge W\rightarrow {\mathbb {C}}$
denote the projection onto
![]() $\bigwedge ^n W$
, identified with
$\bigwedge ^n W$
, identified with
![]() ${\mathbb {C}}$
via
${\mathbb {C}}$
via
![]() $e_1\wedge \cdots \wedge e_n \mapsto 1$
. Write
$e_1\wedge \cdots \wedge e_n \mapsto 1$
. Write
![]() $\tau : \bigwedge W\stackrel {\sim }{\to } \bigwedge W$
for the
$\tau : \bigwedge W\stackrel {\sim }{\to } \bigwedge W$
for the
![]() ${\mathbb {C}}$
-linear anti-automorphism
${\mathbb {C}}$
-linear anti-automorphism
![]() $w_1\wedge \cdots \wedge w_r \mapsto w_r \wedge \cdots \wedge w_1$
for
$w_1\wedge \cdots \wedge w_r \mapsto w_r \wedge \cdots \wedge w_1$
for
![]() $r\ge 1$
and
$r\ge 1$
and
![]() $w_1,\ldots ,w_r\in W$
. Define
$w_1,\ldots ,w_r\in W$
. Define
We write
![]() $\mathrm {spin}^{\vee }$
and
$\mathrm {spin}^{\vee }$
and
![]() $\mathrm {spin}^{\varepsilon ,\vee }$
for the dual representations of
$\mathrm {spin}^{\varepsilon ,\vee }$
for the dual representations of
![]() $\mathrm {spin}$
and
$\mathrm {spin}$
and
![]() $\mathrm {spin}^{\varepsilon }$
. By the preceding lemma, the highest weight of
$\mathrm {spin}^{\varepsilon }$
. By the preceding lemma, the highest weight of
![]() $\mathrm {spin}^{\varepsilon ,\vee }$
is in the Weyl group orbit of
$\mathrm {spin}^{\varepsilon ,\vee }$
is in the Weyl group orbit of
![]() $(\mu _{\varepsilon })^{-1}$
.
$(\mu _{\varepsilon })^{-1}$
.
Lemma 4.2. The pairing
![]() $(\!(~,~)\!)$
is nondegenerate; it is alternating if
$(\!(~,~)\!)$
is nondegenerate; it is alternating if
![]() $n\equiv 2,3~(\mathrm {mod}~4)$
and symmetric if
$n\equiv 2,3~(\mathrm {mod}~4)$
and symmetric if
![]() $n\equiv 0,1~(\mathrm {mod}~4)$
. The restriction of
$n\equiv 0,1~(\mathrm {mod}~4)$
. The restriction of
![]() $(\!(~,~)\!)$
to each of
$(\!(~,~)\!)$
to each of
![]() $\bigwedge ^+ W$
and
$\bigwedge ^+ W$
and
![]() $\bigwedge ^- W$
is nondegenerate if n is even, and identically zero if n is odd. We have
$\bigwedge ^- W$
is nondegenerate if n is even, and identically zero if n is odd. We have
In particular, we have
![]() $\mathrm {spin}^{\varepsilon } \simeq \mathrm {spin}^{(-1)^n \varepsilon ,\vee } \otimes \mathcal N$
.
$\mathrm {spin}^{\varepsilon } \simeq \mathrm {spin}^{(-1)^n \varepsilon ,\vee } \otimes \mathcal N$
.
Proof. The first two assertions are elementary and left to the reader. The last assertion follows from the rest. For the equality (4.3), we claim that
Since
![]() $\mathrm {GPin}_{2n}\subset C(V)$
, this implies (4.3) as
$\mathrm {GPin}_{2n}\subset C(V)$
, this implies (4.3) as
It remains to prove the claim. The proof of (4.4) reduces to the case
![]() $c\in V$
, then to the two cases
$c\in V$
, then to the two cases
![]() $c\in W$
and
$c\in W$
and
![]() $c\in W'$
by linearity. In both cases, (4.4) follows from the explicit description of the
$c\in W'$
by linearity. In both cases, (4.4) follows from the explicit description of the
![]() $C(V)$
-action as in (4.1). Indeed, (4.4) is obvious if
$C(V)$
-action as in (4.1). Indeed, (4.4) is obvious if
![]() $c\in W$
. When
$c\in W$
. When
![]() $c\in W'$
, it is enough to show that for
$c\in W'$
, it is enough to show that for
![]() $0\le r,s\le n$
,
$0\le r,s\le n$
,
![]() $1\le i_1<\cdots <i_r\le n$
,
$1\le i_1<\cdots <i_r\le n$
,
![]() $1\le j_1<\cdots <j_s\le n$
, and
$1\le j_1<\cdots <j_s\le n$
, and
![]() $1\le k\le n$
,
$1\le k\le n$
,
(This implies (4.4) by taking
![]() $\mathrm {pr}_n$
.) The equality is simply
$\mathrm {pr}_n$
.) The equality is simply
![]() $0=0$
unless
$0=0$
unless
![]() $k=r_0=s_0$
for some
$k=r_0=s_0$
for some
![]() $1\le r_0\le r$
and
$1\le r_0\le r$
and
![]() $1\le s_0\le s$
. In the latter case, the equality boils down to
$1\le s_0\le s$
. In the latter case, the equality boils down to
 $$ \begin{align*}&(-1)^{r_0+1} e_{i_r}\wedge \cdots \wedge \widehat{e}_{i_{r_0}}\wedge \cdots \wedge e_{i_1}\wedge e_{j_1}\wedge \cdots \wedge e_{j_s} \\&\quad= (-1)^{s_0+1} e_{i_r}\wedge \cdots \wedge e_{i_1}\wedge e_{j_1}\wedge \cdots \wedge \widehat{e}_{j_{s_0}} \wedge \cdots \wedge e_{j_s},\end{align*} $$
$$ \begin{align*}&(-1)^{r_0+1} e_{i_r}\wedge \cdots \wedge \widehat{e}_{i_{r_0}}\wedge \cdots \wedge e_{i_1}\wedge e_{j_1}\wedge \cdots \wedge e_{j_s} \\&\quad= (-1)^{s_0+1} e_{i_r}\wedge \cdots \wedge e_{i_1}\wedge e_{j_1}\wedge \cdots \wedge \widehat{e}_{j_{s_0}} \wedge \cdots \wedge e_{j_s},\end{align*} $$
which is clear. The proof is complete.
We also discuss the odd case. Equip
![]() $V_{2n-1}={\mathbb {C}}^{2n-1}$
with standard basis
$V_{2n-1}={\mathbb {C}}^{2n-1}$
with standard basis
![]() $\{f_1,\ldots ,f_{2n-1}\}$
and quadratic form
$\{f_1,\ldots ,f_{2n-1}\}$
and quadratic form
![]() $Q_{2n-1}$
of (3.4). As in [Reference Fulton and Harris25, p.306], we decompose
$Q_{2n-1}$
of (3.4). As in [Reference Fulton and Harris25, p.306], we decompose
where
![]() $W_{2n-1}:=\oplus _{i=1}^{n-1} {\mathbb {C}} f_i$
,
$W_{2n-1}:=\oplus _{i=1}^{n-1} {\mathbb {C}} f_i$
,
![]() $W_{2n-1}':=\oplus _{i=n}^{2n-2} {\mathbb {C}} f_i$
, and
$W_{2n-1}':=\oplus _{i=n}^{2n-2} {\mathbb {C}} f_i$
, and
![]() $U_{2n-1}:={\mathbb {C}} f_{2n-1}$
. Again, we omit the subscript
$U_{2n-1}:={\mathbb {C}} f_{2n-1}$
. Again, we omit the subscript
![]() $2n-1$
when it is clear from the context. Then W and
$2n-1$
when it is clear from the context. Then W and
![]() $W'$
are
$W'$
are
![]() $(n-1)$
-dimensional isotropic subspaces, and U is a line perpendicular to them. As in the even case, each of
$(n-1)$
-dimensional isotropic subspaces, and U is a line perpendicular to them. As in the even case, each of
![]() $\bigwedge W $
and
$\bigwedge W $
and
![]() $\bigwedge ^{\pm } W$
can be viewed as a subspace of
$\bigwedge ^{\pm } W$
can be viewed as a subspace of
![]() $C(V)$
and has a unique structure of left
$C(V)$
and has a unique structure of left
![]() $C(V)$
-module where
$C(V)$
-module where
-
•
 $w \in W \subset V$
acts on
$w \in W \subset V$
acts on
 $\bigwedge W$
through left multiplication,
$\bigwedge W$
through left multiplication, -
•
 $w' \in W' \subset V$
acts as in (4.1) (cf. [Reference Fulton and Harris25, 20.16]),
$w' \in W' \subset V$
acts as in (4.1) (cf. [Reference Fulton and Harris25, 20.16]), -
•
 $f_{2n-1}$
acts trivially on
$f_{2n-1}$
acts trivially on
 $\bigwedge ^+ W$
and as
$\bigwedge ^+ W$
and as
 $-1$
on
$-1$
on
 $\bigwedge ^- W$
.
$\bigwedge ^- W$
.
Consider the bijection
 $$ \begin{align*}\psi \colon \bigwedge W_{2n-1} \overset \sim \to {\bigwedge}^+ W_{2n}, \quad w_1 \wedge \cdots \wedge w_r \mapsto \begin{cases} w_1 \wedge \cdots \wedge w_r \wedge e_n, & r \mathrm{ \ odd} \cr w_1 \wedge \cdots \wedge w_r, & r \mathrm{ \ even}. \end{cases} \end{align*} $$
$$ \begin{align*}\psi \colon \bigwedge W_{2n-1} \overset \sim \to {\bigwedge}^+ W_{2n}, \quad w_1 \wedge \cdots \wedge w_r \mapsto \begin{cases} w_1 \wedge \cdots \wedge w_r \wedge e_n, & r \mathrm{ \ odd} \cr w_1 \wedge \cdots \wedge w_r, & r \mathrm{ \ even}. \end{cases} \end{align*} $$
Lemma 4.3. For all
![]() $g \in \mathrm {GSpin}_{2n-1}$
and all
$g \in \mathrm {GSpin}_{2n-1}$
and all
![]() $w \in \bigwedge W_{2n-1}$
, we have
$w \in \bigwedge W_{2n-1}$
, we have
![]() $i_{\mathrm {std}}(g) \psi (w) = \psi (g w)$
, where
$i_{\mathrm {std}}(g) \psi (w) = \psi (g w)$
, where
![]() $i_{\mathrm {std}}(g)$
and g act by
$i_{\mathrm {std}}(g)$
and g act by
![]() $\mathrm {spin}^+$
of
$\mathrm {spin}^+$
of
![]() $\mathrm {GSpin}_{2n}$
and
$\mathrm {GSpin}_{2n}$
and
![]() $\mathrm {spin}$
of
$\mathrm {spin}$
of
![]() $\mathrm {GSpin}_{2n-1}$
, respectively.
$\mathrm {GSpin}_{2n-1}$
, respectively.
Proof. We keep writing
![]() $W=W_{2n-1}$
,
$W=W_{2n-1}$
,
![]() $W'=W^{\prime }_{2n-1}$
,
$W'=W^{\prime }_{2n-1}$
,
![]() $U=U_{2n-1}$
. We identify
$U=U_{2n-1}$
. We identify
![]() $V_{2n}=(W\oplus U^1 \oplus W'\oplus U^2$
via
$V_{2n}=(W\oplus U^1 \oplus W'\oplus U^2$
via
![]() $W_{2n}=W\oplus U^1$
and
$W_{2n}=W\oplus U^1$
and
![]() $W^{\prime }_{2n}=W'\oplus U^2$
with
$W^{\prime }_{2n}=W'\oplus U^2$
with
![]() $U^1={\mathbb {C}} e_n$
and
$U^1={\mathbb {C}} e_n$
and
![]() $U^2={\mathbb {C}} e_{2n}$
, mapping the basis of W (resp.
$U^2={\mathbb {C}} e_{2n}$
, mapping the basis of W (resp.
![]() $W'$
) onto the first
$W'$
) onto the first
![]() $n-1$
elements in the basis of
$n-1$
elements in the basis of
![]() $W_{2n}$
(resp.
$W_{2n}$
(resp.
![]() $W^{\prime }_{2n}$
). This also gives the embedding
$W^{\prime }_{2n}$
). This also gives the embedding
![]() $V_{2n-1}\subset V_{2n}$
, with U diagonally embedded in
$V_{2n-1}\subset V_{2n}$
, with U diagonally embedded in
![]() $U^1\oplus U^2$
(so
$U^1\oplus U^2$
(so
![]() $f_{2n-1}$
maps to
$f_{2n-1}$
maps to
![]() $e_n+e_{2n}$
), as in the formula below (3.4).
$e_n+e_{2n}$
), as in the formula below (3.4).
There is an obvious embedding
![]() $\iota ^+: \bigwedge W \hookrightarrow \bigwedge (W\oplus U^1)$
. We also have
$\iota ^+: \bigwedge W \hookrightarrow \bigwedge (W\oplus U^1)$
. We also have
![]() $\iota ^-:\bigwedge W \hookrightarrow \bigwedge (W\oplus U^1)$
by
$\iota ^-:\bigwedge W \hookrightarrow \bigwedge (W\oplus U^1)$
by
![]() $(\cdot )\wedge e_n$
. Both
$(\cdot )\wedge e_n$
. Both
![]() $\iota ^+$
and
$\iota ^+$
and
![]() $\iota ^-$
are
$\iota ^-$
are
![]() $C(W\oplus W')$
-equivariant, by using that left and right multiplications commute and that
$C(W\oplus W')$
-equivariant, by using that left and right multiplications commute and that
![]() $e_n$
is orthogonal to
$e_n$
is orthogonal to
![]() $W\oplus W'$
. Furthermore,
$W\oplus W'$
. Furthermore,
![]() $\iota ^-$
intertwines the
$\iota ^-$
intertwines the
![]() $f_{2n-1}$
-action on
$f_{2n-1}$
-action on
![]() $\bigwedge ^- W$
, which is by multiplication by
$\bigwedge ^- W$
, which is by multiplication by
![]() $-1$
, and the
$-1$
, and the
![]() $e_n+e_{2n}$
-action on
$e_n+e_{2n}$
-action on
![]() $\bigwedge ^+ (W\oplus U^1)$
, since
$\bigwedge ^+ (W\oplus U^1)$
, since
![]() $w\wedge e_n=-e_n\wedge w$
if
$w\wedge e_n=-e_n\wedge w$
if
![]() $w\in \bigwedge ^- W$
and since
$w\in \bigwedge ^- W$
and since
![]() $W\perp e_{2n}$
with respect to
$W\perp e_{2n}$
with respect to
![]() $Q_{2n}$
.
$Q_{2n}$
.
Now we claim that
![]() $\psi $
is
$\psi $
is
![]() $C^+(W\oplus W'\oplus U)$
-equivariant, which implies the lemma by restricting from
$C^+(W\oplus W'\oplus U)$
-equivariant, which implies the lemma by restricting from
![]() $C^+(W\oplus W'\oplus U)$
to
$C^+(W\oplus W'\oplus U)$
to
![]() $\mathrm {GSpin}_{2n-1}$
. It suffices to verify equivariance of
$\mathrm {GSpin}_{2n-1}$
. It suffices to verify equivariance of
![]() $\psi $
under
$\psi $
under
![]() $C^+(W\oplus W')$
and
$C^+(W\oplus W')$
and
![]() $C^-(W\oplus W')\otimes f_{2n-1}$
. But
$C^-(W\oplus W')\otimes f_{2n-1}$
. But
![]() $\psi $
is
$\psi $
is
![]() $\iota ^+$
on
$\iota ^+$
on
![]() $\bigwedge ^+ W$
and
$\bigwedge ^+ W$
and
![]() $\iota ^-$
on
$\iota ^-$
on
![]() $\bigwedge ^- W$
. Thus, the claim is deduced by putting together the equivariance in the preceding paragraph.
$\bigwedge ^- W$
. Thus, the claim is deduced by putting together the equivariance in the preceding paragraph.
Lemma 4.4. Let
![]() $\vartheta \in \mathrm {GPin}_{2n}$
be the element from (3.7). We have
$\vartheta \in \mathrm {GPin}_{2n}$
be the element from (3.7). We have
![]() ${\bigwedge }^+ W_{2n} \overset \sim \to {\bigwedge }^- W_{2n}$
,
${\bigwedge }^+ W_{2n} \overset \sim \to {\bigwedge }^- W_{2n}$
,
![]() $x \mapsto \vartheta x$
. We have
$x \mapsto \vartheta x$
. We have
![]() $\mathrm {spin}^+\circ \theta =\mathrm {spin}^-$
via this isomorphism (i.e.,
$\mathrm {spin}^+\circ \theta =\mathrm {spin}^-$
via this isomorphism (i.e.,
![]() $\vartheta (\mathrm {spin}^+(g) x) = \mathrm {spin}^-(\theta (g)) \vartheta x$
for each
$\vartheta (\mathrm {spin}^+(g) x) = \mathrm {spin}^-(\theta (g)) \vartheta x$
for each
![]() $g\in \mathrm {GSpin}_{2n}$
).
$g\in \mathrm {GSpin}_{2n}$
).
Proof. Henceforth, we omit the symbol
![]() $\wedge $
for the wedge product in
$\wedge $
for the wedge product in
![]() $W_{2n}$
. Consider
$W_{2n}$
. Consider
![]() $v = e_{k_1} \cdots e_{k_r} \in {\bigwedge }^+ W_{2n}$
, with
$v = e_{k_1} \cdots e_{k_r} \in {\bigwedge }^+ W_{2n}$
, with
![]() $k_1 < k_2 < \ldots < k_r$
and r is even. Then
$k_1 < k_2 < \ldots < k_r$
and r is even. Then
where
![]() $e_{2n}$
acts by (4.1). Thus, the isomorphism follows from the following computations.
$e_{2n}$
acts by (4.1). Thus, the isomorphism follows from the following computations.
 $$ \begin{align*} e_{n} e_{k_1} \cdots e_{k_r} & = \begin{cases} 0, & k_r = n, \cr e_{k_1}\cdots e_{k_r} e_n, & k_r \neq n, \end{cases} \cr e_{2n} e_{k_1} \cdots e_{k_r} & = \sum_{i=1}^r (-1)^{i+1} \langle e_{2n}, e_{k_i} \rangle e_{k_1} \cdots \widehat{e_{k_i}} \cdots e_{k_r} = \begin{cases} - e_{k_1} \cdots e_{k_{r-1}}, & k_r = n, \cr 0, & k_r \neq n. \end{cases} \end{align*} $$
$$ \begin{align*} e_{n} e_{k_1} \cdots e_{k_r} & = \begin{cases} 0, & k_r = n, \cr e_{k_1}\cdots e_{k_r} e_n, & k_r \neq n, \end{cases} \cr e_{2n} e_{k_1} \cdots e_{k_r} & = \sum_{i=1}^r (-1)^{i+1} \langle e_{2n}, e_{k_i} \rangle e_{k_1} \cdots \widehat{e_{k_i}} \cdots e_{k_r} = \begin{cases} - e_{k_1} \cdots e_{k_{r-1}}, & k_r = n, \cr 0, & k_r \neq n. \end{cases} \end{align*} $$
The last assertion comes down to showing that
![]() $\vartheta g x= \theta (g) \vartheta x$
, where
$\vartheta g x= \theta (g) \vartheta x$
, where
![]() $\vartheta g, \theta (g) \vartheta \in C(V)$
act through the
$\vartheta g, \theta (g) \vartheta \in C(V)$
act through the
![]() $C(V)$
-module structure on
$C(V)$
-module structure on
![]() $x\in \bigwedge W_{2n}$
. But this is clear since
$x\in \bigwedge W_{2n}$
. But this is clear since
![]() $\theta (g)=\vartheta g \vartheta ^{-1}$
.
$\theta (g)=\vartheta g \vartheta ^{-1}$
.
Consider the basis
![]() $\{b_U\}$
of
$\{b_U\}$
of
![]() $\bigwedge W_{2n}$
, with
$\bigwedge W_{2n}$
, with
where
![]() $U = \{k_1 < k_2 < \cdots < k_r\}$
ranges over the subsets of
$U = \{k_1 < k_2 < \cdots < k_r\}$
ranges over the subsets of
![]() $\{1, 2, \ldots , n\}$
. The U of even size form a basis for
$\{1, 2, \ldots , n\}$
. The U of even size form a basis for
![]() ${\bigwedge }^+ W_{2n}$
, and the U with odd size form a basis for
${\bigwedge }^+ W_{2n}$
, and the U with odd size form a basis for
![]() ${\bigwedge }^- W_{2n}$
. Order the
${\bigwedge }^- W_{2n}$
. Order the
![]() $b_U$
for U odd, and the
$b_U$
for U odd, and the
![]() $b_U$
for U even, in such a way that the ordering of
$b_U$
for U even, in such a way that the ordering of
![]() $\{b_U\}_{|U|:\mathrm {even}}$
corresponds to that of
$\{b_U\}_{|U|:\mathrm {even}}$
corresponds to that of
![]() $\{b_U\}_{|U|:\mathrm {odd}}$
via
$\{b_U\}_{|U|:\mathrm {odd}}$
via
![]() $b_U\mapsto \vartheta b_U/\sqrt {-1}$
. Then these orderings of the
$b_U\mapsto \vartheta b_U/\sqrt {-1}$
. Then these orderings of the
![]() $b_U$
give us two identifications
$b_U$
give us two identifications
such that the following proposition holds.
Proposition 4.5. The following diagram commutes

5 Some special subgroups of
 $\mathrm {GSpin}_{2n}$
$\mathrm {GSpin}_{2n}$
In this section, the base field of all algebraic groups is an algebraically closed field of characteristic 0 such as
![]() ${\mathbb {C}}$
or
${\mathbb {C}}$
or
![]() $\overline {\mathbb {Q}}_{\ell }$
. We begin with principal morphisms for
$\overline {\mathbb {Q}}_{\ell }$
. We begin with principal morphisms for
![]() $\mathrm {GSpin}_{2n-1}$
and
$\mathrm {GSpin}_{2n-1}$
and
![]() $\mathrm {GSpin}_{2n}$
. (See [Reference Patrikis64, Sect. 7] and [Reference Gross29, Reference Serre73] for general discussions.) The following notation will be convenient for us. Denote by
$\mathrm {GSpin}_{2n}$
. (See [Reference Patrikis64, Sect. 7] and [Reference Gross29, Reference Serre73] for general discussions.) The following notation will be convenient for us. Denote by
the product of the central embedding
![]() $\mathbb G_m\hookrightarrow \mathrm {GSpin}_{2n-1}$
and a fixed principal
$\mathbb G_m\hookrightarrow \mathrm {GSpin}_{2n-1}$
and a fixed principal
![]() $\mathrm {SL}_2$
-mapping. Note that
$\mathrm {SL}_2$
-mapping. Note that
![]() $j_{\mathrm {reg}}$
has the following kernel:Footnote 6
$j_{\mathrm {reg}}$
has the following kernel:Footnote 6
 $$ \begin{align*}\begin{cases} \langle (-1, \left( \begin{smallmatrix} {-1} & 0 \cr 0 & {-1} \end{smallmatrix} \right) )\rangle, & \mathrm{if}\,~n(n-1)/2 \,\mathrm{ is \ odd},\\ \langle (1, \left( \begin{smallmatrix} {-1} & 0 \cr 0 & {-1} \end{smallmatrix} \right) )\rangle, & \mathrm{if}\,~n(n-1)/2 \,\mathrm{ The \ following \ are \ true:is \ even}. \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} \langle (-1, \left( \begin{smallmatrix} {-1} & 0 \cr 0 & {-1} \end{smallmatrix} \right) )\rangle, & \mathrm{if}\,~n(n-1)/2 \,\mathrm{ is \ odd},\\ \langle (1, \left( \begin{smallmatrix} {-1} & 0 \cr 0 & {-1} \end{smallmatrix} \right) )\rangle, & \mathrm{if}\,~n(n-1)/2 \,\mathrm{ The \ following \ are \ true:is \ even}. \end{cases} \end{align*} $$
We write
![]() $G_{\mathrm {pri}} \subset \mathrm {GSpin}_{2n-1}$
for the image of
$G_{\mathrm {pri}} \subset \mathrm {GSpin}_{2n-1}$
for the image of
![]() $j_{\mathrm {reg}}$
. The group
$j_{\mathrm {reg}}$
. The group
![]() $G_{\mathrm {pri}}$
is isomorphic to
$G_{\mathrm {pri}}$
is isomorphic to
![]() ${\mathrm {GL}}_2$
if
${\mathrm {GL}}_2$
if
![]() $n(n+1)/2$
is odd, and to
$n(n+1)/2$
is odd, and to
![]() $\mathbb {G}_{\mathrm {m}} \times \mathrm {PGL}_2$
otherwise. Using
$\mathbb {G}_{\mathrm {m}} \times \mathrm {PGL}_2$
otherwise. Using
![]() $i_{\mathrm {std}}$
from (3.6), we define
$i_{\mathrm {std}}$
from (3.6), we define
The map
![]() $\mathrm {pr}^{\circ }\circ i_{\mathrm {reg}}: \mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_2 \to {\mathrm {SO}}_{2n}$
factors through
$\mathrm {pr}^{\circ }\circ i_{\mathrm {reg}}: \mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_2 \to {\mathrm {SO}}_{2n}$
factors through
![]() $\mathrm {PGL}_2\rightarrow {\mathrm {SO}}_{2n}$
, to be denoted
$\mathrm {PGL}_2\rightarrow {\mathrm {SO}}_{2n}$
, to be denoted
![]() $i^{\circ }_{\mathrm {reg}}$
, via the natural projection from
$i^{\circ }_{\mathrm {reg}}$
, via the natural projection from
![]() $\mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_2 \rightarrow \mathrm {PGL}_2$
(trivial on the
$\mathbb {G}_{\mathrm {m}} \times \mathrm {SL}_2 \rightarrow \mathrm {PGL}_2$
(trivial on the
![]() $\mathbb {G}_{\mathrm {m}}$
-factor). We see that the preimage of
$\mathbb {G}_{\mathrm {m}}$
-factor). We see that the preimage of
![]() $i^{\circ }_{\mathrm {reg}}(\mathrm {PGL}_2)$
in
$i^{\circ }_{\mathrm {reg}}(\mathrm {PGL}_2)$
in
![]() $\mathrm {GSpin}_{2n}$
is
$\mathrm {GSpin}_{2n}$
is
![]() $i_{\mathrm {std}}(G_{\mathrm {pri}})$
. Denote by
$i_{\mathrm {std}}(G_{\mathrm {pri}})$
. Denote by
![]() $\overline {j_{\mathrm {reg}}}:\mathrm {PGL}_2\to \mathrm {PSO}_{2n-1}$
the map induced by
$\overline {j_{\mathrm {reg}}}:\mathrm {PGL}_2\to \mathrm {PSO}_{2n-1}$
the map induced by
![]() $j_{\mathrm {reg}}$
on the adjoint groups.Footnote 7 We also introduce the map
$j_{\mathrm {reg}}$
on the adjoint groups.Footnote 7 We also introduce the map
Recall that we have fixed earlier the group
![]() ${\mathrm {SO}}_8$
in (2.1) (cf. below (2.3)). Let
${\mathrm {SO}}_8$
in (2.1) (cf. below (2.3)). Let
![]() $T_{\mathrm {GSpin}_7} \subset \mathrm {GSpin}_7$
be as in [Reference Kret and Shin50, §Notation] and put
$T_{\mathrm {GSpin}_7} \subset \mathrm {GSpin}_7$
be as in [Reference Kret and Shin50, §Notation] and put
![]() $T_{\mathrm {Spin}_7} = T_{\mathrm {GSpin}_7} \cap \mathrm {Spin}_7$
.
$T_{\mathrm {Spin}_7} = T_{\mathrm {GSpin}_7} \cap \mathrm {Spin}_7$
.
We will now fix a convenient basis for
![]() $X_*(T_{\mathrm {Spin}_7})$
. We have
$X_*(T_{\mathrm {Spin}_7})$
. We have
![]() $X_*(T_{\mathrm {GSpin}_7}) = X^{*}(T_{\mathrm {GSp}_6}) = \bigoplus _{i=0}^3 \mathbb Z e_i$
, the center
$X_*(T_{\mathrm {GSpin}_7}) = X^{*}(T_{\mathrm {GSp}_6}) = \bigoplus _{i=0}^3 \mathbb Z e_i$
, the center
![]() $Z_{\mathrm {GSp}_6} \subset T_{\mathrm {GSp}_6}$
equals
$Z_{\mathrm {GSp}_6} \subset T_{\mathrm {GSp}_6}$
equals
![]() $\{(t^2, t, t, t) | t \in \mathbb {G}_{\mathrm {m}}\}$
(use the roots
$\{(t^2, t, t, t) | t \in \mathbb {G}_{\mathrm {m}}\}$
(use the roots
![]() $\alpha _i$
listed in [loc. cit., p.10]), and so
$\alpha _i$
listed in [loc. cit., p.10]), and so
![]() $X^{*}(T_{\mathrm {GSp}_6}) \to X^{*}(Z_{\mathrm {GSp}_6})$
identifies with
$X^{*}(T_{\mathrm {GSp}_6}) \to X^{*}(Z_{\mathrm {GSp}_6})$
identifies with
![]() $\mathbb Z^4 \to \mathbb Z$
,
$\mathbb Z^4 \to \mathbb Z$
,
![]() $(x_i) \mapsto 2a_0 + a_1 + a_2 + a_3$
. Thus,
$(x_i) \mapsto 2a_0 + a_1 + a_2 + a_3$
. Thus,
![]() $X_*(T_{\mathrm {Spin}_7}) = \{ (a_i)\in \mathbb Z^4\, |\, 2a_0 + a_1 + a_2 + a_3 = 0\}$
. By projecting
$X_*(T_{\mathrm {Spin}_7}) = \{ (a_i)\in \mathbb Z^4\, |\, 2a_0 + a_1 + a_2 + a_3 = 0\}$
. By projecting
![]() $(a_i)\in \mathbb Z^4$
onto
$(a_i)\in \mathbb Z^4$
onto
![]() $(a_1, a_2, a_3)$
, we obtain
$(a_1, a_2, a_3)$
, we obtain
We write
![]() $T_{{\mathrm {SO}}_8} \subset {\mathrm {SO}}_8$
for the maximal torus corresponding to (2.2) (so with
$T_{{\mathrm {SO}}_8} \subset {\mathrm {SO}}_8$
for the maximal torus corresponding to (2.2) (so with
![]() $t_0 = 1$
). The spin representation of
$t_0 = 1$
). The spin representation of
![]() $\mathrm {Spin}_7$
is orthogonal ([Reference Kret and Shin50, Lem. 0.1]), yielding an embedding
$\mathrm {Spin}_7$
is orthogonal ([Reference Kret and Shin50, Lem. 0.1]), yielding an embedding
![]() $\mathrm {spin}^{\circ \prime } : \mathrm {Spin}_7\hookrightarrow {\mathrm {SO}}(q)$
, for some quadratic form q in
$\mathrm {spin}^{\circ \prime } : \mathrm {Spin}_7\hookrightarrow {\mathrm {SO}}(q)$
, for some quadratic form q in
![]() $8$
variables. We fix an isomorphism
$8$
variables. We fix an isomorphism
![]() $u \colon {\mathrm {SO}}(q) \overset \sim \to {\mathrm {SO}}_8$
, in such a way that the composition
$u \colon {\mathrm {SO}}(q) \overset \sim \to {\mathrm {SO}}_8$
, in such a way that the composition
maps
![]() $T_{\mathrm {Spin}_7}$
into
$T_{\mathrm {Spin}_7}$
into
![]() $T_{{\mathrm {SO}}_8}$
and such that
$T_{{\mathrm {SO}}_8}$
and such that
for some choice of numbering
![]() $\tau ^j=(\tau ^j_1,\tau ^j_2,\tau ^j_3)\in \{\pm 1\}^3$
for
$\tau ^j=(\tau ^j_1,\tau ^j_2,\tau ^j_3)\in \{\pm 1\}^3$
for
![]() $j=1,...,8$
, such that
$j=1,...,8$
, such that
![]() $\tau ^j = -\tau ^{j + 4}$
for
$\tau ^j = -\tau ^{j + 4}$
for
![]() $j=1,2,3, 4$
. In (5.2), the embedding
$j=1,2,3, 4$
. In (5.2), the embedding
![]() $X_*(T_{{\mathrm {SO}}_8}) \subset \mathbb Z^8$
comes from (2.2).
$X_*(T_{{\mathrm {SO}}_8}) \subset \mathbb Z^8$
comes from (2.2).
We write
![]() $\overline {\mathrm {spin}^{\circ }}:\mathrm {Spin}_7\hookrightarrow \mathrm {PSO}_8$
for the projectivization of
$\overline {\mathrm {spin}^{\circ }}:\mathrm {Spin}_7\hookrightarrow \mathrm {PSO}_8$
for the projectivization of
![]() $\mathrm {spin}^{\circ }$
. Fixing a non-isotropic line in the underlying 8-dimensional space, the stabilizer of the line in
$\mathrm {spin}^{\circ }$
. Fixing a non-isotropic line in the underlying 8-dimensional space, the stabilizer of the line in
![]() $\mathrm {Spin}_7$
is isomorphic to a group of type
$\mathrm {Spin}_7$
is isomorphic to a group of type
![]() $G_2$
, cf. [Reference Gross and Savin31, p.169, Prop. 2.2(4)]. Thereby, we obtain an embedding
$G_2$
, cf. [Reference Gross and Savin31, p.169, Prop. 2.2(4)]. Thereby, we obtain an embedding
![]() $j_{\mathrm {spin}} \colon G_2\hookrightarrow \mathrm {Spin}_7$
. Alternatively, an embedding
$j_{\mathrm {spin}} \colon G_2\hookrightarrow \mathrm {Spin}_7$
. Alternatively, an embedding
![]() $G_2\hookrightarrow \mathrm {Spin}_7$
can be constructed using the octonion algebra [Reference Chenevier16, Sect. 2.5]. The conjugacy class of
$G_2\hookrightarrow \mathrm {Spin}_7$
can be constructed using the octonion algebra [Reference Chenevier16, Sect. 2.5]. The conjugacy class of
![]() $j_{\mathrm {spin}}$
is unique (thus independent of choices) by [loc. cit., Proposition 2.11]. Denote by
$j_{\mathrm {spin}}$
is unique (thus independent of choices) by [loc. cit., Proposition 2.11]. Denote by
the composite
![]() $i_{\mathrm {std}}\circ j_{\mathrm {spin}}$
. The restriction of
$i_{\mathrm {std}}\circ j_{\mathrm {spin}}$
. The restriction of
![]() $\mathrm {spin}^{\varepsilon }:\mathrm {Spin}_8\rightarrow {\mathrm {GL}}_8$
via
$\mathrm {spin}^{\varepsilon }:\mathrm {Spin}_8\rightarrow {\mathrm {GL}}_8$
via
![]() $i_{\mathrm {spin}}$
is isomorphic to
$i_{\mathrm {spin}}$
is isomorphic to
![]() $\mathbf {1}\oplus \mathrm {std}$
, where
$\mathbf {1}\oplus \mathrm {std}$
, where
![]() $\mathbf {1}$
and
$\mathbf {1}$
and
![]() $\mathrm {std}$
are the trivial and the unique irreducible 7-dimensional representation of
$\mathrm {std}$
are the trivial and the unique irreducible 7-dimensional representation of
![]() $G_2$
, respectively. (This is easy to see by dimension counting, as the other irreducible representations have dimension
$G_2$
, respectively. (This is easy to see by dimension counting, as the other irreducible representations have dimension
![]() $\ge 14$
.)
$\ge 14$
.)
Lemma 5.1. The representation
![]() $\mathrm {spin}^{\circ }:\mathrm {Spin}_7\hookrightarrow {\mathrm {SO}}_8$
is
$\mathrm {spin}^{\circ }:\mathrm {Spin}_7\hookrightarrow {\mathrm {SO}}_8$
is
![]() $\mathrm {O}_8$
-conjugate to
$\mathrm {O}_8$
-conjugate to
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
but not locally conjugate (thus not conjugate) as an
$\theta ^{\circ } \mathrm {spin}^{\circ }$
but not locally conjugate (thus not conjugate) as an
![]() ${\mathrm {SO}}_8$
-valued representation. In fact, there exists an open dense subset
${\mathrm {SO}}_8$
-valued representation. In fact, there exists an open dense subset
![]() $U \subset \mathrm {Spin}_7$
such that
$U \subset \mathrm {Spin}_7$
such that
![]() $\mathrm {spin}^{\circ } t$
and
$\mathrm {spin}^{\circ } t$
and
![]() $\theta ^{\circ } \mathrm {spin}^{\circ } t$
are not conjugate for any
$\theta ^{\circ } \mathrm {spin}^{\circ } t$
are not conjugate for any
![]() $t \in U$
. Moreover,
$t \in U$
. Moreover,
![]() $\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
and
$\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
and
![]() $\theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
are not
$\theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
are not
![]() ${\mathrm {SO}}_8$
-conjugate. The analogous assertion holds for
${\mathrm {SO}}_8$
-conjugate. The analogous assertion holds for
![]() $\overline {\mathrm {spin}}:{\mathrm {SO}}_7\hookrightarrow \mathrm {PSO}_8$
.
$\overline {\mathrm {spin}}:{\mathrm {SO}}_7\hookrightarrow \mathrm {PSO}_8$
.
Proof. Evidently,
![]() $\mathrm {spin}^{\circ }$
and
$\mathrm {spin}^{\circ }$
and
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
are
$\theta ^{\circ } \mathrm {spin}^{\circ }$
are
![]() $\mathrm {O}_8$
-conjugate since
$\mathrm {O}_8$
-conjugate since
![]() $\theta ^{\circ } = {\mathrm {Int}}(\vartheta ^{\circ })$
with
$\theta ^{\circ } = {\mathrm {Int}}(\vartheta ^{\circ })$
with
![]() $\vartheta ^{\circ }\in \mathrm {O}_8$
. Let
$\vartheta ^{\circ }\in \mathrm {O}_8$
. Let
![]() $T_{{\mathrm {GL}}_8} \subset {\mathrm {GL}}_8$
be the diagonal torus. Let
$T_{{\mathrm {GL}}_8} \subset {\mathrm {GL}}_8$
be the diagonal torus. Let
![]() $\Omega _{\mathrm {Spin}_7},\Omega _{{\mathrm {SO}}_8},\Omega _{{\mathrm {GL}}_8}$
denote the Weyl groups corresponding to
$\Omega _{\mathrm {Spin}_7},\Omega _{{\mathrm {SO}}_8},\Omega _{{\mathrm {GL}}_8}$
denote the Weyl groups corresponding to
![]() $T_{\mathrm {Spin}_7},T_{{\mathrm {SO}}_8},T_{{\mathrm {GL}}_8}$
. In view of the weights of the spin representation [Reference Fulton and Harris25, Prop. 20.20], we know that
$T_{\mathrm {Spin}_7},T_{{\mathrm {SO}}_8},T_{{\mathrm {GL}}_8}$
. In view of the weights of the spin representation [Reference Fulton and Harris25, Prop. 20.20], we know that
(The
![]() $\Omega _{{\mathrm {GL}}_8}$
-orbit of 8-tuples is simply an unordered 8-tuple.) When
$\Omega _{{\mathrm {GL}}_8}$
-orbit of 8-tuples is simply an unordered 8-tuple.) When
![]() $\varepsilon _1 a_1 + \varepsilon _2 a_2 + \varepsilon _3 a_3$
are all distinct, the right-hand side breaks up into exactly two
$\varepsilon _1 a_1 + \varepsilon _2 a_2 + \varepsilon _3 a_3$
are all distinct, the right-hand side breaks up into exactly two
![]() $\Omega _{{\mathrm {SO}}_8}$
-orbits, which are permuted by
$\Omega _{{\mathrm {SO}}_8}$
-orbits, which are permuted by
![]() $\theta ^{\circ }$
. Similarly, if
$\theta ^{\circ }$
. Similarly, if
![]() $U_T$
is the open dense subset of
$U_T$
is the open dense subset of
![]() $T_{\mathrm {Spin}_7}$
consisting of
$T_{\mathrm {Spin}_7}$
consisting of
![]() $t = (t_1, t_2, t_3) \in T_{\mathrm {Spin}_7}$
with
$t = (t_1, t_2, t_3) \in T_{\mathrm {Spin}_7}$
with
![]() $t^{\varepsilon _1}_1,t_2^{\varepsilon _2},t_3^{\varepsilon _3}$
all distinct, then
$t^{\varepsilon _1}_1,t_2^{\varepsilon _2},t_3^{\varepsilon _3}$
all distinct, then
![]() $\mathrm {spin}^{\circ }(t)$
and
$\mathrm {spin}^{\circ }(t)$
and
![]() $\theta ^{\circ }(\mathrm {spin}^{\circ }(t))$
are not
$\theta ^{\circ }(\mathrm {spin}^{\circ }(t))$
are not
![]() ${\mathrm {SO}}_8$
-conjugate. This implies the existence of U as in the lemma by taking U to be the set of regular semisimple elements whose conjugacy classes meet
${\mathrm {SO}}_8$
-conjugate. This implies the existence of U as in the lemma by taking U to be the set of regular semisimple elements whose conjugacy classes meet
![]() $U_T$
.
$U_T$
.
Now assume that
![]() $\mathrm {spin}^{\circ }(\mathrm {Spin}_7) = g \theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7) g^{-1}$
for some
$\mathrm {spin}^{\circ }(\mathrm {Spin}_7) = g \theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7) g^{-1}$
for some
![]() $g \in {\mathrm {SO}}_8$
. Then the composition
$g \in {\mathrm {SO}}_8$
. Then the composition
![]() $c_g = \mathrm {spin}^{\circ , -1} \circ \mathrm {Int}_g \circ \theta ^{\circ } \mathrm {spin}^{\circ }$
is an automorphism of
$c_g = \mathrm {spin}^{\circ , -1} \circ \mathrm {Int}_g \circ \theta ^{\circ } \mathrm {spin}^{\circ }$
is an automorphism of
![]() $\mathrm {Spin}_7$
, which is hence inner and of the form
$\mathrm {Spin}_7$
, which is hence inner and of the form
![]() $x \mapsto hxh^{-1}$
for some
$x \mapsto hxh^{-1}$
for some
![]() $h \in \mathrm {Spin}_7$
. Thus,
$h \in \mathrm {Spin}_7$
. Thus,
![]() $\mathrm {spin}^{\circ }$
and
$\mathrm {spin}^{\circ }$
and
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
are conjugate by
$\theta ^{\circ } \mathrm {spin}^{\circ }$
are conjugate by
![]() $g^{-1} \mathrm {spin}^{\circ }(h)$
, a contradiction. Thus,
$g^{-1} \mathrm {spin}^{\circ }(h)$
, a contradiction. Thus,
![]() $\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
and
$\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
and
![]() $\theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
are not
$\theta ^{\circ }\mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
are not
![]() ${\mathrm {SO}}_8$
-conjugate. The projective analogue for
${\mathrm {SO}}_8$
-conjugate. The projective analogue for
![]() $\overline {\mathrm {spin}} \colon {\mathrm {SO}}_7\hookrightarrow \mathrm {PSO}_8$
also follows.
$\overline {\mathrm {spin}} \colon {\mathrm {SO}}_7\hookrightarrow \mathrm {PSO}_8$
also follows.
Lemma 5.2. Write
![]() $H := \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7)) \subset \mathrm {Spin}_8$
. The restriction of
$H := \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7)) \subset \mathrm {Spin}_8$
. The restriction of
![]() $\mathrm {spin}^{\varepsilon }$
to H is irreducible if and only if
$\mathrm {spin}^{\varepsilon }$
to H is irreducible if and only if
![]() $\varepsilon = -$
. More precisely, we have
$\varepsilon = -$
. More precisely, we have
![]() $\overline {\mathrm {spin}^+} \circ \mathrm {spin}^{\circ } \simeq \overline {\mathrm {std} \oplus \textbf {1}}$
and
$\overline {\mathrm {spin}^+} \circ \mathrm {spin}^{\circ } \simeq \overline {\mathrm {std} \oplus \textbf {1}}$
and
![]() $\overline {\mathrm {spin}^-} \circ \mathrm {spin}^{\circ } \simeq \overline {\mathrm {spin}^{\circ }}$
.
$\overline {\mathrm {spin}^-} \circ \mathrm {spin}^{\circ } \simeq \overline {\mathrm {spin}^{\circ }}$
.
Proof. We compute the composition
![]() $\overline {\mathrm {spin}^{\varepsilon }} \circ \mathrm {spin}^{\circ } \colon \mathrm {Spin}_7 \overset {\mathrm {spin}^{\circ }} \to {\mathrm {SO}}_8 \to \mathrm {PSO}_8 \overset { \overline {\mathrm {spin}^{\varepsilon }}} \to \mathrm {PGL}_8$
on
$\overline {\mathrm {spin}^{\varepsilon }} \circ \mathrm {spin}^{\circ } \colon \mathrm {Spin}_7 \overset {\mathrm {spin}^{\circ }} \to {\mathrm {SO}}_8 \to \mathrm {PSO}_8 \overset { \overline {\mathrm {spin}^{\varepsilon }}} \to \mathrm {PGL}_8$
on
![]() $T_{\mathrm {Spin}_7}$
. For
$T_{\mathrm {Spin}_7}$
. For
![]() $a \in X_*(T_{\mathrm {Spin}_7})$
,
$a \in X_*(T_{\mathrm {Spin}_7})$
,
![]() $\mathrm {spin}^{\circ }(a)$
is given by (5.2), and for
$\mathrm {spin}^{\circ }(a)$
is given by (5.2), and for
![]() $b \in X_*(T_{{\mathrm {SO}}_8}) = \mathbb Z^4$
, we have
$b \in X_*(T_{{\mathrm {SO}}_8}) = \mathbb Z^4$
, we have
![]() $\overline {\mathrm {spin}^{\varepsilon }}(b) = (\tfrac 12 (\tau _1 b_1 + \tau _2 b_2 + \tau _3 b_3 + \tau _4 b_4))_{\tau \in \{\pm 1\}^4, \prod _{i=1}^4 \tau _i = \varepsilon }$
(both up to the Weyl group actions). From this, it follows that
$\overline {\mathrm {spin}^{\varepsilon }}(b) = (\tfrac 12 (\tau _1 b_1 + \tau _2 b_2 + \tau _3 b_3 + \tau _4 b_4))_{\tau \in \{\pm 1\}^4, \prod _{i=1}^4 \tau _i = \varepsilon }$
(both up to the Weyl group actions). From this, it follows that
![]() $\overline {\mathrm {spin}^{\varepsilon }} \circ \mathrm {spin}^{\circ } |_{T_{\mathrm {Spin}_7}}$
is conjugated to
$\overline {\mathrm {spin}^{\varepsilon }} \circ \mathrm {spin}^{\circ } |_{T_{\mathrm {Spin}_7}}$
is conjugated to
![]() $\overline {\mathrm {std} \oplus \textbf {1}}|_{T_{\mathrm {Spin}_7}}$
and
$\overline {\mathrm {std} \oplus \textbf {1}}|_{T_{\mathrm {Spin}_7}}$
and
![]() $\overline {\mathrm {spin}^{\circ }}|_{T_{\mathrm {Spin}_7}}$
for
$\overline {\mathrm {spin}^{\circ }}|_{T_{\mathrm {Spin}_7}}$
for
![]() $\varepsilon =+$
and
$\varepsilon =+$
and
![]() $\varepsilon = -$
, respectively. The lemma now follows from Lemma 1.2.
$\varepsilon = -$
, respectively. The lemma now follows from Lemma 1.2.
Lemma 5.3. Let
![]() $n \geq 3$
and
$n \geq 3$
and
![]() $H \subsetneq {\mathrm {SO}}_{2n}$
be a proper connected reductive subgroup containing a regular unipotent element. Then H is isomorphic to a quotient of
$H \subsetneq {\mathrm {SO}}_{2n}$
be a proper connected reductive subgroup containing a regular unipotent element. Then H is isomorphic to a quotient of
![]() $\mathrm {Spin}_{2n-1}$
,
$\mathrm {Spin}_{2n-1}$
,
![]() $\mathrm {SL}_2$
or
$\mathrm {SL}_2$
or
![]() $G_2$
(the last can occur only if
$G_2$
(the last can occur only if
![]() $n = 4$
).
$n = 4$
).
Proof. We begin with some preliminaries. When G is a reductive group, write
![]() $\Sigma (G)$
for the set of maximal proper connected reductive subgroups M of G that contain a regular unipotent element of G. From [Reference Saxl and Seitz70, Thms. A,B], we have the following:Footnote 8
$\Sigma (G)$
for the set of maximal proper connected reductive subgroups M of G that contain a regular unipotent element of G. From [Reference Saxl and Seitz70, Thms. A,B], we have the following:Footnote 8
-
(a) Case
 $G \simeq {\mathrm {SO}}_{2n}$
(
$G \simeq {\mathrm {SO}}_{2n}$
(
 $n \geq 3$
), then every
$n \geq 3$
), then every
 $M \in \Sigma (G)$
is isomorphic to a quotient of
$M \in \Sigma (G)$
is isomorphic to a quotient of
 $\mathrm {Spin}_{2n-1}$
.
$\mathrm {Spin}_{2n-1}$
. -
(b) Case
 $G \simeq {\mathrm {SO}}_{2n-1}$
(
$G \simeq {\mathrm {SO}}_{2n-1}$
(
 $n \geq 3$
,
$n \geq 3$
,
 $n \neq 4$
), then every
$n \neq 4$
), then every
 $M \in \Sigma (G)$
is isomorphic to a quotient of
$M \in \Sigma (G)$
is isomorphic to a quotient of
 $\mathrm {SL}_2$
.
$\mathrm {SL}_2$
. -
(c) Case
 $G \simeq {\mathrm {SO}}_7$
, then every
$G \simeq {\mathrm {SO}}_7$
, then every
 $M \in \Sigma (G)$
is isomorphic to
$M \in \Sigma (G)$
is isomorphic to
 $G_2$
.
$G_2$
. -
(d) Case
 $G \simeq G_2$
, then every
$G \simeq G_2$
, then every
 $M \in \Sigma (G)$
is isomorphic to a quotient of
$M \in \Sigma (G)$
is isomorphic to a quotient of
 $\mathrm {SL}_2$
.
$\mathrm {SL}_2$
.
We prove the following claim: If H is a connected reductive subgroup of some connected reductive group G (over
![]() ${\mathbb {C}}$
or
${\mathbb {C}}$
or
![]() $\overline {\mathbb {Q}}_{\ell }$
), such that H contains a regular unipotent element u of G, then u is also regular unipotent in H. To see this, write
$\overline {\mathbb {Q}}_{\ell }$
), such that H contains a regular unipotent element u of G, then u is also regular unipotent in H. To see this, write
![]() $B_u \subset G$
for the unique Borel subgroup that contains u. Now let
$B_u \subset G$
for the unique Borel subgroup that contains u. Now let
![]() $B_0 \owns u$
be a Borel subgroup of H that contains u. Then
$B_0 \owns u$
be a Borel subgroup of H that contains u. Then
![]() $B_0$
is a connected solvable subgroup of G and hence is contained in a Borel subgroup
$B_0$
is a connected solvable subgroup of G and hence is contained in a Borel subgroup
![]() $B_1$
of G. As
$B_1$
of G. As
![]() $u \in B_1$
, we must have
$u \in B_1$
, we must have
![]() $B_1 = B_u$
. Hence,
$B_1 = B_u$
. Hence,
![]() $B_0 \subset B_u \cap H$
. Since
$B_0 \subset B_u \cap H$
. Since
![]() $(B_u \cap H)^0$
is connected solvable and contains
$(B_u \cap H)^0$
is connected solvable and contains
![]() $B_0$
, we must have
$B_0$
, we must have
![]() $(B_u \cap H)^0= B_0$
by maximality of
$(B_u \cap H)^0= B_0$
by maximality of
![]() $B_0$
. This shows that in H, the element u is contained in exactly one Borel subgroup. Therefore,
$B_0$
. This shows that in H, the element u is contained in exactly one Borel subgroup. Therefore,
![]() $u \in H$
is regular unipotent.
$u \in H$
is regular unipotent.
Now let H be as in the statement of the lemma. Let
![]() $u \in H$
be regular unipotent in
$u \in H$
be regular unipotent in
![]() ${\mathrm {SO}}_{2n}$
. Let
${\mathrm {SO}}_{2n}$
. Let
![]() $M \in \Sigma ({\mathrm {SO}}_{2n})$
such that
$M \in \Sigma ({\mathrm {SO}}_{2n})$
such that
![]() $H \subset M$
. If
$H \subset M$
. If
![]() $H = M$
, we are done by (a) above. So assume
$H = M$
, we are done by (a) above. So assume
![]() $H \neq M$
. Again by (a), M is a quotient of
$H \neq M$
. Again by (a), M is a quotient of
![]() $\mathrm {Spin}_{2n-1}$
, and hence
$\mathrm {Spin}_{2n-1}$
, and hence
![]() $M_{\mathrm {ad}} \simeq {\mathrm {SO}}_{2n-1}$
. Then
$M_{\mathrm {ad}} \simeq {\mathrm {SO}}_{2n-1}$
. Then
![]() $H_{\mathrm {ad}}$
maps to
$H_{\mathrm {ad}}$
maps to
![]() ${\mathrm {SO}}_{2n-1}$
(since the center of H commutes with u, it is contained in
${\mathrm {SO}}_{2n-1}$
(since the center of H commutes with u, it is contained in
![]() $Z_{{\mathrm {SO}}_{2n}}$
by [Reference Springer75, Thm. 4.11] and thus also in
$Z_{{\mathrm {SO}}_{2n}}$
by [Reference Springer75, Thm. 4.11] and thus also in
![]() $Z_M$
), and by the claim, we can find an
$Z_M$
), and by the claim, we can find an
![]() $M' \in \Sigma ({\mathrm {SO}}_{2n-1})$
that contains the image of
$M' \in \Sigma ({\mathrm {SO}}_{2n-1})$
that contains the image of
![]() $H_{\mathrm {ad}}$
in
$H_{\mathrm {ad}}$
in
![]() ${\mathrm {SO}}_{2n-1}$
. If
${\mathrm {SO}}_{2n-1}$
. If
![]() $H_{\mathrm {ad}} = M'$
, we are done by (b) or (c) if
$H_{\mathrm {ad}} = M'$
, we are done by (b) or (c) if
![]() $n = 4$
. If
$n = 4$
. If
![]() $H_{\mathrm {ad}} \neq M'$
, then again
$H_{\mathrm {ad}} \neq M'$
, then again
![]() $M'$
is either
$M'$
is either
![]() $G_2$
or a quotient of
$G_2$
or a quotient of
![]() $\mathrm {SL}_2$
, and we can argue similarly.
$\mathrm {SL}_2$
, and we can argue similarly.
If H is an algebraic group, we write
![]() $\Upsilon (H)$
for the set of
$\Upsilon (H)$
for the set of
![]() ${\mathrm {SO}}_{2n}$
-conjugacy classes of morphisms
${\mathrm {SO}}_{2n}$
-conjugacy classes of morphisms
![]() $H \to {\mathrm {SO}}_{2n}$
that have a regular unipotent element in their image. By abuse of notation, we often identify
$H \to {\mathrm {SO}}_{2n}$
that have a regular unipotent element in their image. By abuse of notation, we often identify
![]() $\Upsilon (H)$
with a set of representatives for the conjugacy classes.
$\Upsilon (H)$
with a set of representatives for the conjugacy classes.
Lemma 5.4. We have
 $$ \begin{align*} \Upsilon(\mathrm{Spin}_{2n-1}) &= \left\lbrace {i^{\circ}_{\mathrm{std}}} \colon \mathrm{Spin}_{2n-1} \to {\mathrm{SO}}_{2n} \right\rbrace & (n \geq 3, n \neq 4) \cr \Upsilon(\mathrm{Spin}_7) &= \left\lbrace {i^{\circ}_{\mathrm{std}}}, \mathrm{spin}^{\circ}, \theta^{\circ} \mathrm{spin}^{\circ} \colon \mathrm{Spin}_7 \to {\mathrm{SO}}_8 \right\rbrace & (n = 4) \cr \Upsilon(\mathrm{SL}_2) &= \{ i_{\mathrm{reg}} \colon \mathrm{SL}_2 \to {\mathrm{SO}}_{2n}\} & (n \geq 3) \cr \Upsilon(G_2) &= \{ {i_{\mathrm{spin}}} \colon G_2 \to {\mathrm{SO}}_8\} & (n=4). \end{align*} $$
$$ \begin{align*} \Upsilon(\mathrm{Spin}_{2n-1}) &= \left\lbrace {i^{\circ}_{\mathrm{std}}} \colon \mathrm{Spin}_{2n-1} \to {\mathrm{SO}}_{2n} \right\rbrace & (n \geq 3, n \neq 4) \cr \Upsilon(\mathrm{Spin}_7) &= \left\lbrace {i^{\circ}_{\mathrm{std}}}, \mathrm{spin}^{\circ}, \theta^{\circ} \mathrm{spin}^{\circ} \colon \mathrm{Spin}_7 \to {\mathrm{SO}}_8 \right\rbrace & (n = 4) \cr \Upsilon(\mathrm{SL}_2) &= \{ i_{\mathrm{reg}} \colon \mathrm{SL}_2 \to {\mathrm{SO}}_{2n}\} & (n \geq 3) \cr \Upsilon(G_2) &= \{ {i_{\mathrm{spin}}} \colon G_2 \to {\mathrm{SO}}_8\} & (n=4). \end{align*} $$
Proof. Let
![]() $f \colon H \to {\mathrm {SO}}_{2n}$
be a morphism with a regular unipotent element in its image, where H is one of the 4 groups in the lemma.
$f \colon H \to {\mathrm {SO}}_{2n}$
be a morphism with a regular unipotent element in its image, where H is one of the 4 groups in the lemma.
Case
![]() $H = \mathrm {Spin}_{2n-1}$
. We have
$H = \mathrm {Spin}_{2n-1}$
. We have
![]() $\ker (f) \subset \{\pm 1\}$
. Assume first
$\ker (f) \subset \{\pm 1\}$
. Assume first
![]() $\ker (f) = \{\pm 1\}$
. Then
$\ker (f) = \{\pm 1\}$
. Then
![]() $r := \mathrm {std} \circ f$
,
$r := \mathrm {std} \circ f$
,
![]() $r' := \mathrm {std} \circ {i^{\circ }_{\mathrm {std}}}$
are two faithful representations of dimension
$r' := \mathrm {std} \circ {i^{\circ }_{\mathrm {std}}}$
are two faithful representations of dimension
![]() $2n$
. By Lemma 2.8, r and
$2n$
. By Lemma 2.8, r and
![]() $r'$
are isomorphic. By acceptability of
$r'$
are isomorphic. By acceptability of
![]() $\mathrm {O}_{2n}$
, we find a
$\mathrm {O}_{2n}$
, we find a
![]() $g \in \mathrm {O}_{2n}$
that conjugates r to
$g \in \mathrm {O}_{2n}$
that conjugates r to
![]() $r'$
[Reference Kret and Shin50, Prop. B.1]. The element g might have negative determinant. In this case, we can replace g by
$r'$
[Reference Kret and Shin50, Prop. B.1]. The element g might have negative determinant. In this case, we can replace g by
![]() $g \cdot \vartheta ^{\circ }$
, as
$g \cdot \vartheta ^{\circ }$
, as
![]() $\vartheta ^{\circ }$
centralizes
$\vartheta ^{\circ }$
centralizes
![]() $i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
by Lemma 3.6(ii).
$i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
by Lemma 3.6(ii).
Now assume
![]() $\ker (f) = 1$
. Then
$\ker (f) = 1$
. Then
![]() $r = \mathrm {std} \circ f$
is a faithful
$r = \mathrm {std} \circ f$
is a faithful
![]() $2n$
-dimensional representation of
$2n$
-dimensional representation of
![]() $\mathrm {Spin}_{2n-1}$
. The smallest such representation by dimension is the spin representation, and therefore,
$\mathrm {Spin}_{2n-1}$
. The smallest such representation by dimension is the spin representation, and therefore,
![]() $2^{n-1} \leq 2n$
, and
$2^{n-1} \leq 2n$
, and
![]() $n \leq 4$
. We distinguish in subcases
$n \leq 4$
. We distinguish in subcases
![]() $n = 3$
or
$n = 3$
or
![]() $n = 4$
:
$n = 4$
:
(When
![]() $n = 3$
.) We show that this subcase
$n = 3$
.) We show that this subcase
![]() $(H = \mathrm {Spin}_{2n-1},\ker (f)=1,n=3)$
does not occur. Assume
$(H = \mathrm {Spin}_{2n-1},\ker (f)=1,n=3)$
does not occur. Assume
![]() $f \colon \mathrm {Spin}_5 \to {\mathrm {SO}}_6$
is injective with a regular unipotent element in its image. Recall
$f \colon \mathrm {Spin}_5 \to {\mathrm {SO}}_6$
is injective with a regular unipotent element in its image. Recall
![]() ${\mathrm {SO}}_6 \simeq \mathrm {SL}_4/\{\pm 1\}$
. Write
${\mathrm {SO}}_6 \simeq \mathrm {SL}_4/\{\pm 1\}$
. Write
![]() $\widetilde {H} \subset \mathrm {SL}_4$
for the pre-image of
$\widetilde {H} \subset \mathrm {SL}_4$
for the pre-image of
![]() $f(\mathrm {Spin}_5)$
in
$f(\mathrm {Spin}_5)$
in
![]() $\mathrm {SL}_4$
. Let
$\mathrm {SL}_4$
. Let
![]() $M \subset \mathrm {SL}_4$
be a proper maximal connected reductive subgroup of
$M \subset \mathrm {SL}_4$
be a proper maximal connected reductive subgroup of
![]() $\mathrm {SL}_4$
that contains H. Then M is isomorphic to
$\mathrm {SL}_4$
that contains H. Then M is isomorphic to
![]() $\mathrm {Sp}_4$
by [Reference Saxl and Seitz70, Thm. B]. By dimension consideration, we must have
$\mathrm {Sp}_4$
by [Reference Saxl and Seitz70, Thm. B]. By dimension consideration, we must have
![]() $\widetilde {H} = M$
. In particular, the image of f in
$\widetilde {H} = M$
. In particular, the image of f in
![]() $\mathrm {SL}_4/\{\pm 1\}$
must be isomorphic to
$\mathrm {SL}_4/\{\pm 1\}$
must be isomorphic to
![]() $\mathrm {PSp}_4$
. Hence,
$\mathrm {PSp}_4$
. Hence,
![]() $\mathrm {Spin}_5 \overset \sim \to \mathrm {PSp}_4$
, a contradiction.
$\mathrm {Spin}_5 \overset \sim \to \mathrm {PSp}_4$
, a contradiction.
(When
![]() $n = 4$
.) We want to classify all conjugacy classes of injections
$n = 4$
.) We want to classify all conjugacy classes of injections
![]() $f \colon \mathrm {Spin}_7 \to {\mathrm {SO}}_8$
with a regular unipotent element in their image. In this case, they do exist, as
$f \colon \mathrm {Spin}_7 \to {\mathrm {SO}}_8$
with a regular unipotent element in their image. In this case, they do exist, as
![]() $\mathrm {spin}^{\circ }$
is an example. The representations
$\mathrm {spin}^{\circ }$
is an example. The representations
![]() $\mathrm {std} \circ f$
and
$\mathrm {std} \circ f$
and
![]() $\mathrm {std} \circ \mathrm {spin}^{\circ }$
are both faithful representations of
$\mathrm {std} \circ \mathrm {spin}^{\circ }$
are both faithful representations of
![]() $\mathrm {Spin}_7$
of dimension
$\mathrm {Spin}_7$
of dimension
![]() $8$
. Hence, they are isomorphic. By acceptability of
$8$
. Hence, they are isomorphic. By acceptability of
![]() $\mathrm {O}_8$
, there exists a
$\mathrm {O}_8$
, there exists a
![]() $g \in \mathrm {O}_8$
that conjugates f to
$g \in \mathrm {O}_8$
that conjugates f to
![]() $\mathrm {spin}^{\circ }$
. This implies that f is
$\mathrm {spin}^{\circ }$
. This implies that f is
![]() ${\mathrm {SO}}_8$
-conjugate to either
${\mathrm {SO}}_8$
-conjugate to either
![]() $\mathrm {spin}^{\circ }$
or
$\mathrm {spin}^{\circ }$
or
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
. By Lemma 5.1, the representations
$\theta ^{\circ } \mathrm {spin}^{\circ }$
. By Lemma 5.1, the representations
![]() $\mathrm {spin}^{\circ }$
and
$\mathrm {spin}^{\circ }$
and
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
are not
$\theta ^{\circ } \mathrm {spin}^{\circ }$
are not
![]() ${\mathrm {SO}}_8$
-conjugate. Observe finally that
${\mathrm {SO}}_8$
-conjugate. Observe finally that
![]() $\ker ( i^{\circ }_{\mathrm {std}}) = \{\pm 1\}$
while
$\ker ( i^{\circ }_{\mathrm {std}}) = \{\pm 1\}$
while
![]() $\mathrm {spin}^{\circ }$
and
$\mathrm {spin}^{\circ }$
and
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
are injective. Hence,
$\theta ^{\circ } \mathrm {spin}^{\circ }$
are injective. Hence,
![]() $i^{\circ }_{\mathrm {std}}$
is not conjugate to either
$i^{\circ }_{\mathrm {std}}$
is not conjugate to either
![]() $\mathrm {spin}^{\circ }$
or
$\mathrm {spin}^{\circ }$
or
![]() $\theta ^{\circ } \mathrm {spin}^{\circ }$
. This verifies the description of
$\theta ^{\circ } \mathrm {spin}^{\circ }$
. This verifies the description of
![]() $ \Upsilon (\mathrm {Spin}_7)$
in the lemma.
$ \Upsilon (\mathrm {Spin}_7)$
in the lemma.
Case
![]() $H = \mathrm {SL}_2$
. We want to classify the morphisms
$H = \mathrm {SL}_2$
. We want to classify the morphisms
![]() $f \colon \mathrm {SL}_2 \to {\mathrm {SO}}_{2n}$
with a regular unipotent element in the image. In fact, such a morphism is called the “principal morphism” in the literature, and it is well-known that it is unique up to conjugacy. However, we could not find a precise reference, so we give some detail for a general connected reductive group G.
$f \colon \mathrm {SL}_2 \to {\mathrm {SO}}_{2n}$
with a regular unipotent element in the image. In fact, such a morphism is called the “principal morphism” in the literature, and it is well-known that it is unique up to conjugacy. However, we could not find a precise reference, so we give some detail for a general connected reductive group G.
We first note that the natural map
![]() $\mathrm {Hom}(\mathrm {SL}_2, G) \to \mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
, equivariant for the adjoint action of G, is a bijection. To construct the inverse, let
$\mathrm {Hom}(\mathrm {SL}_2, G) \to \mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
, equivariant for the adjoint action of G, is a bijection. To construct the inverse, let
![]() $g \in \mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
. The composition
$g \in \mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
. The composition
![]() ${\mathrm {Rep}}(G) \to {\mathrm {Rep}}(\mathrm {Lie}\,(G)) \to {\mathrm {Rep}}(\mathrm {Lie}\,(\mathrm {SL}_2)) {\overset {\sim } \leftarrow } {\mathrm {Rep}}(\mathrm {SL}_2)$
is a
${\mathrm {Rep}}(G) \to {\mathrm {Rep}}(\mathrm {Lie}\,(G)) \to {\mathrm {Rep}}(\mathrm {Lie}\,(\mathrm {SL}_2)) {\overset {\sim } \leftarrow } {\mathrm {Rep}}(\mathrm {SL}_2)$
is a
![]() $\otimes $
-functor preserving the underlying vector spaces, where the last arrow is an equivalence (e.g., see [Reference Bourbaki11, VIII.1.5]). Thus, the composition arises from a morphism of groups
$\otimes $
-functor preserving the underlying vector spaces, where the last arrow is an equivalence (e.g., see [Reference Bourbaki11, VIII.1.5]). Thus, the composition arises from a morphism of groups
![]() $f \colon \mathrm {SL}_2 \to G$
by [Reference Deligne, Milne and Cycles21, Cor. 2.9], and one checks directly that
$f \colon \mathrm {SL}_2 \to G$
by [Reference Deligne, Milne and Cycles21, Cor. 2.9], and one checks directly that
![]() $g \mapsto f$
and
$g \mapsto f$
and
![]() $f \mapsto \mathrm {Lie}\,(f)$
are inverse to each other. By the Jacobson–Morozov lemma,
$f \mapsto \mathrm {Lie}\,(f)$
are inverse to each other. By the Jacobson–Morozov lemma,
![]() $\mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
is in bijection with the set of nilpotent elements in
$\mathrm {Hom}(\mathrm {Lie}\,(\mathrm {SL}_2), \mathrm {Lie}\,(G))$
is in bijection with the set of nilpotent elements in
![]() $\mathrm {Lie}\,(G)$
via
$\mathrm {Lie}\,(G)$
via
![]() $g \mapsto g\left ( \begin {smallmatrix} 0 & 1 \cr 0 & 0 \end {smallmatrix} \right ) $
. Above, we consider f such that
$g \mapsto g\left ( \begin {smallmatrix} 0 & 1 \cr 0 & 0 \end {smallmatrix} \right ) $
. Above, we consider f such that
![]() $f\left ( \begin {smallmatrix} 1 & 1 \cr 0 & 1 \end {smallmatrix} \right ) $
is regular unipotent; thus,
$f\left ( \begin {smallmatrix} 1 & 1 \cr 0 & 1 \end {smallmatrix} \right ) $
is regular unipotent; thus,
![]() $g \left ( \begin {smallmatrix} 0 & 1 \cr 0 & 0 \end {smallmatrix} \right ) $
is regular nilpotent in
$g \left ( \begin {smallmatrix} 0 & 1 \cr 0 & 0 \end {smallmatrix} \right ) $
is regular nilpotent in
![]() $\mathrm {Lie}\,(G)$
and hence unique up to conjugacy. The same statement follows for f then as well.
$\mathrm {Lie}\,(G)$
and hence unique up to conjugacy. The same statement follows for f then as well.
Case
![]() $H = G_2$
and
$H = G_2$
and
![]() $n = 4$
. Let
$n = 4$
. Let
![]() $f \colon G_2 \to {\mathrm {SO}}_8$
be a morphism with a regular unipotent element in its image. Recall
$f \colon G_2 \to {\mathrm {SO}}_8$
be a morphism with a regular unipotent element in its image. Recall
![]() $i_{\mathrm {spin}} \colon G_2 \to \mathrm {Spin}_8$
from (5.3); it induces a morphism
$i_{\mathrm {spin}} \colon G_2 \to \mathrm {Spin}_8$
from (5.3); it induces a morphism
![]() $\overline {i_{\mathrm {spin}}} \colon G_2 \to {\mathrm {SO}}_8$
. The representations
$\overline {i_{\mathrm {spin}}} \colon G_2 \to {\mathrm {SO}}_8$
. The representations
![]() $\mathrm {std} \circ f$
and
$\mathrm {std} \circ f$
and
![]() $\mathrm {std} \circ \overline {i_{\mathrm {spin}}}$
are both faithful and of dimension
$\mathrm {std} \circ \overline {i_{\mathrm {spin}}}$
are both faithful and of dimension
![]() $8$
and hence isomorphic (they are both isomorphic to
$8$
and hence isomorphic (they are both isomorphic to
![]() $r_7 \oplus \textbf {1}$
, where
$r_7 \oplus \textbf {1}$
, where
![]() $r_7$
is the unique representation of
$r_7$
is the unique representation of
![]() $G_2$
of dimension
$G_2$
of dimension
![]() $7$
). By
$7$
). By
![]() $O_8$
-acceptability, we can find a
$O_8$
-acceptability, we can find a
![]() $g \in O_8$
such that
$g \in O_8$
such that
![]() $f = g \overline {i_{\mathrm {spin}}} g^{-1}$
. If
$f = g \overline {i_{\mathrm {spin}}} g^{-1}$
. If
![]() $\det (g) = 1$
, we are done. The element
$\det (g) = 1$
, we are done. The element
![]() $\vartheta ^{\circ } \in O_8$
centralizes the subgroup
$\vartheta ^{\circ } \in O_8$
centralizes the subgroup
![]() ${\mathrm {SO}}_{2n-1}$
. The map
${\mathrm {SO}}_{2n-1}$
. The map
![]() $i_{\mathrm {spin}}$
factors over the map
$i_{\mathrm {spin}}$
factors over the map
![]() $j_{\mathrm {spin}} \colon G_2 \to \mathrm {Spin}_7$
(see above (5.3)). In particular,
$j_{\mathrm {spin}} \colon G_2 \to \mathrm {Spin}_7$
(see above (5.3)). In particular,
![]() $\vartheta ^{\circ }{i_{\mathrm {spin}}} \vartheta ^{\circ , -1} = \overline {i_{\mathrm {spin}}}$
, and we can replace g by
$\vartheta ^{\circ }{i_{\mathrm {spin}}} \vartheta ^{\circ , -1} = \overline {i_{\mathrm {spin}}}$
, and we can replace g by
![]() $g \vartheta ^{\circ }$
.
$g \vartheta ^{\circ }$
.
Proposition 5.5. Let
![]() $n\ge 3$
. Let
$n\ge 3$
. Let
![]() $\overline H \subset \mathrm {PSO}_{2n}$
be a (possibly disconnected) reductive subgroup (over
$\overline H \subset \mathrm {PSO}_{2n}$
be a (possibly disconnected) reductive subgroup (over
![]() ${\mathbb {C}}$
or
${\mathbb {C}}$
or
![]() $\overline {\mathbb {Q}}_{\ell }$
) containing a regular unipotent element. Up to conjugation by an element of
$\overline {\mathbb {Q}}_{\ell }$
) containing a regular unipotent element. Up to conjugation by an element of
![]() $\mathrm {PSO}_{2n}$
, the following holds (in particular,
$\mathrm {PSO}_{2n}$
, the following holds (in particular,
![]() $\overline H$
is connected in all cases):
$\overline H$
is connected in all cases):
-
(i) if
 $n\neq 4$
, then
$n\neq 4$
, then
 $\overline H = \mathrm {PSO}_{2n}$
,
$\overline H = \mathrm {PSO}_{2n}$
,
 $\overline H=\overline {i_{\mathrm {std}}}(\mathrm {PSO}_{2n-1})$
or
$\overline H=\overline {i_{\mathrm {std}}}(\mathrm {PSO}_{2n-1})$
or
 $\overline H=\overline {i_{\mathrm {reg}}}(\mathrm {PGL}_2)$
;
$\overline H=\overline {i_{\mathrm {reg}}}(\mathrm {PGL}_2)$
; -
(ii) if
 $n=4$
, then
$n=4$
, then
 $\overline H$
is either as in (1),
$\overline H$
is either as in (1),
 $\overline H=\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
$\overline H=\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
 $\overline H=\overline {\theta ^{\circ }\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
or
$\overline H=\overline {\theta ^{\circ }\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
or
 $\overline H = \overline {i_{\mathrm {spin}}}(G_2)$
.
$\overline H = \overline {i_{\mathrm {spin}}}(G_2)$
.
If
![]() $H \subset {\mathrm {SO}}_{2n}$
is a (possibly disconnected) reductive subgroup containing a regular unipotent element, then
$H \subset {\mathrm {SO}}_{2n}$
is a (possibly disconnected) reductive subgroup containing a regular unipotent element, then
![]() $H^0\subset H\subset H^0\cdot Z({\mathrm {SO}}_{2n})$
and
$H^0\subset H\subset H^0\cdot Z({\mathrm {SO}}_{2n})$
and
![]() $H^0$
surjects onto
$H^0$
surjects onto
![]() $\overline H\subset \mathrm {PSO}_{2n}$
as in the list above. (See the proof for the list of possible
$\overline H\subset \mathrm {PSO}_{2n}$
as in the list above. (See the proof for the list of possible
![]() $H^0$
.)
$H^0$
.)
Proof. We first focus on the classification of reductive subgroups
![]() $H \subset {\mathrm {SO}}_{2n}$
containing a regular unipotent element. If
$H \subset {\mathrm {SO}}_{2n}$
containing a regular unipotent element. If
![]() $H = {\mathrm {SO}}_{2n}$
, there is nothing to do, so we assume H is proper. By Lemma 5.3, the group
$H = {\mathrm {SO}}_{2n}$
, there is nothing to do, so we assume H is proper. By Lemma 5.3, the group
![]() $H^0$
is isomorphic to a quotient of
$H^0$
is isomorphic to a quotient of
![]() $\mathrm {Spin}_{2n-1}, G_2$
or
$\mathrm {Spin}_{2n-1}, G_2$
or
![]() $\mathrm {SL}_2$
. Using Lemma 5.4, we conjugate so that
$\mathrm {SL}_2$
. Using Lemma 5.4, we conjugate so that
![]() $f \colon H^0 \hookrightarrow {\mathrm {SO}}_8$
is one of the maps listed in that lemma. So
$f \colon H^0 \hookrightarrow {\mathrm {SO}}_8$
is one of the maps listed in that lemma. So
-
(a) When
 $n \neq 4$
, f equals
$n \neq 4$
, f equals
 $\overline {i^{\circ }_{\mathrm {std}}}$
or
$\overline {i^{\circ }_{\mathrm {std}}}$
or
 $i_{\mathrm {reg}}$
.
$i_{\mathrm {reg}}$
. -
(b) When
 $n = 4$
, f equals
$n = 4$
, f equals
 $\overline {i^{\circ }_{\mathrm {std}}}$
,
$\overline {i^{\circ }_{\mathrm {std}}}$
,
 $i_{\mathrm {reg}}$
,
$i_{\mathrm {reg}}$
,
 $\overline {i_{\mathrm {spin}}}$
,
$\overline {i_{\mathrm {spin}}}$
,
 $\mathrm {spin}^{\circ }$
or
$\mathrm {spin}^{\circ }$
or
 $\theta ^{\circ } \mathrm {spin}^{\circ }$
.
$\theta ^{\circ } \mathrm {spin}^{\circ }$
.
From this list, we see that if
![]() $\mathrm {std}(H^0)$
is reducible (so
$\mathrm {std}(H^0)$
is reducible (so
![]() $f \neq \mathrm {spin}^{\circ }, \theta ^{\circ } \mathrm {spin}^{\circ }$
), then
$f \neq \mathrm {spin}^{\circ }, \theta ^{\circ } \mathrm {spin}^{\circ }$
), then
![]() $\mathrm {std}(H)$
is contained in a parabolic subgroup of
$\mathrm {std}(H)$
is contained in a parabolic subgroup of
![]() ${\mathrm {GL}}_{2n}$
with Levi component
${\mathrm {GL}}_{2n}$
with Levi component
![]() ${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
. By reductivity,
${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
. By reductivity,
![]() $\mathrm {std}(H)$
is contained in
$\mathrm {std}(H)$
is contained in
![]() ${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
, and it is an irreducible subgroup. We see that
${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
, and it is an irreducible subgroup. We see that
![]() $H^0\subset H^+:=i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z({\mathrm {SO}}_{2n})$
, and by Schur’s lemma, the centralizer of
$H^0\subset H^+:=i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z({\mathrm {SO}}_{2n})$
, and by Schur’s lemma, the centralizer of
![]() $H^0$
in
$H^0$
in
![]() $H^+$
is
$H^+$
is
![]() $Z({\mathrm {SO}}_{2n})$
. Since
$Z({\mathrm {SO}}_{2n})$
. Since
![]() $H^0$
has no nontrivial outer automorphism, the conjugation by each
$H^0$
has no nontrivial outer automorphism, the conjugation by each
![]() $h\in H$
on
$h\in H$
on
![]() $H^0$
is an inner automorphism. Thus, there exists
$H^0$
is an inner automorphism. Thus, there exists
![]() $h'\in H^0$
such that
$h'\in H^0$
such that
![]() $h' h^{-1}$
centralizes
$h' h^{-1}$
centralizes
![]() $H^0$
. It follows that
$H^0$
. It follows that
![]() $H\subset H^0\times Z({\mathrm {SO}}_{2n})$
. If
$H\subset H^0\times Z({\mathrm {SO}}_{2n})$
. If
![]() $\mathrm {std}(H^0) \subset {\mathrm {GL}}_{2n}$
is irreducible, the centralizer of
$\mathrm {std}(H^0) \subset {\mathrm {GL}}_{2n}$
is irreducible, the centralizer of
![]() $H^0$
in
$H^0$
in
![]() ${\mathrm {SO}}_{2n}$
is
${\mathrm {SO}}_{2n}$
is
![]() $ Z({\mathrm {SO}}_{2n})$
again by Schur’s lemma, with no nontrivial outer automorphism for
$ Z({\mathrm {SO}}_{2n})$
again by Schur’s lemma, with no nontrivial outer automorphism for
![]() $H^0$
. As in the reducible case, we deduce
$H^0$
. As in the reducible case, we deduce
![]() $H^0\subset H\subset H^0\times Z({\mathrm {SO}}_{2n})$
.
$H^0\subset H\subset H^0\times Z({\mathrm {SO}}_{2n})$
.
Finally, if a reductive subgroup
![]() $\overline H \subset \mathrm {PSO}_{2n}$
contains a regular unipotent element, then so does its preimage H in
$\overline H \subset \mathrm {PSO}_{2n}$
contains a regular unipotent element, then so does its preimage H in
![]() ${\mathrm {SO}}_{2n}$
. By the previous argument, we may conjugate so that
${\mathrm {SO}}_{2n}$
. By the previous argument, we may conjugate so that
![]() $H^0$
is of type (a) or (b), and moreover, we find
$H^0$
is of type (a) or (b), and moreover, we find
![]() $H^0\subset H\subset H^0\times Z({\mathrm {SO}}_{2n})$
. In particular,
$H^0\subset H\subset H^0\times Z({\mathrm {SO}}_{2n})$
. In particular,
![]() $\overline H$
is connected and of the type listed in (i) and (ii).
$\overline H$
is connected and of the type listed in (i) and (ii).
In the next lemma, and also in the later sections, the following group will play a role:
Recall
![]() $z^{\varepsilon } \in Z(\mathrm {GSpin}_{2n})$
is such that
$z^{\varepsilon } \in Z(\mathrm {GSpin}_{2n})$
is such that
![]() $\langle z^{\varepsilon } \rangle = \ker (\mathrm {spin}^{\varepsilon })$
. We have
$\langle z^{\varepsilon } \rangle = \ker (\mathrm {spin}^{\varepsilon })$
. We have
![]() $H_{2n-1} = \mathrm {GSpin}_{2n-1} \times \langle z^+ \rangle $
. By projecting, we obtain a quadratic character
$H_{2n-1} = \mathrm {GSpin}_{2n-1} \times \langle z^+ \rangle $
. By projecting, we obtain a quadratic character
such that the composition
![]() $\mathrm {spin}^{\varepsilon } \circ \kappa $
is trivial if
$\mathrm {spin}^{\varepsilon } \circ \kappa $
is trivial if
![]() $\varepsilon = +$
and otherwise equal to the composition
$\varepsilon = +$
and otherwise equal to the composition
In the definition of
![]() $\kappa $
, we could have also used
$\kappa $
, we could have also used
![]() $z^-$
; in that case, the convention would be slightly different. But notice that
$z^-$
; in that case, the convention would be slightly different. But notice that
![]() $\kappa _0$
does not depend on this choice as this character is simply the canonical map of
$\kappa _0$
does not depend on this choice as this character is simply the canonical map of
![]() $H_{2n-1}$
onto its component group. Observe also that
$H_{2n-1}$
onto its component group. Observe also that
![]() $\theta $
acts trivially on
$\theta $
acts trivially on
![]() $\mathrm {GSpin}_{2n-1}$
and on
$\mathrm {GSpin}_{2n-1}$
and on
![]() $z^+$
via
$z^+$
via
![]() $z^+ \mapsto -z^+$
. This gives the simple formula
$z^+ \mapsto -z^+$
. This gives the simple formula
Lemma 5.6. Let
![]() $r \colon \Gamma \to \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
be a semisimple representation containing a regular unipotent element in its image. Let
$r \colon \Gamma \to \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
be a semisimple representation containing a regular unipotent element in its image. Let
![]() $\chi \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
be a character and
$\chi \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
be a character and
![]() $\varepsilon \in \{+,-\}$
.
$\varepsilon \in \{+,-\}$
.
-
(i) If
 $\chi \otimes \mathrm {spin}^{\varepsilon } (r) \simeq \mathrm {spin}^{\varepsilon } (r)$
, then
$\chi \otimes \mathrm {spin}^{\varepsilon } (r) \simeq \mathrm {spin}^{\varepsilon } (r)$
, then
 $\chi = 1$
.
$\chi = 1$
. -
(ii) If
 $\chi \otimes \mathrm {spin}^+ (r) \simeq \mathrm {spin}^- (r)$
, then r has image in the group
$\chi \otimes \mathrm {spin}^+ (r) \simeq \mathrm {spin}^- (r)$
, then r has image in the group
 $H_{2n-1} \subset \mathrm {GSpin}_{2n}$
up to conjugation, and
$H_{2n-1} \subset \mathrm {GSpin}_{2n}$
up to conjugation, and
 $\chi $
is equal to
$\chi $
is equal to
 $\kappa _0 \circ r$
.
$\kappa _0 \circ r$
. -
(iii) If
 $\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}(r)$
for two characters
$\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}(r)$
for two characters
 $\chi ^{\pm } \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
, then
$\chi ^{\pm } \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
, then
 $\chi ^{\pm }$
are both trivial, or r has image in
$\chi ^{\pm }$
are both trivial, or r has image in
 $H_{2n-1}$
up to conjugation and
$H_{2n-1}$
up to conjugation and
 $\chi ^+ = \chi ^- = \kappa _0 \circ r$
.
$\chi ^+ = \chi ^- = \kappa _0 \circ r$
.
Proof. (i) Write
![]() $\overline r \colon \Gamma \to \mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
for the projectivization of r. By Proposition 5.5, we can distinguish between two cases for the Zariski closure of the image of
$\overline r \colon \Gamma \to \mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
for the projectivization of r. By Proposition 5.5, we can distinguish between two cases for the Zariski closure of the image of
![]() $\overline r$
in
$\overline r$
in
![]() $\mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. If the Zariski closure of
$\mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. If the Zariski closure of
![]() $\overline r$
is either
$\overline r$
is either
![]() $\mathrm {PSO}_{2n}$
or
$\mathrm {PSO}_{2n}$
or
![]() $\overline {i_{\mathrm {std}}}(\mathrm {PSO}_{2n-1})$
, then
$\overline {i_{\mathrm {std}}}(\mathrm {PSO}_{2n-1})$
, then
![]() $\mathrm {spin}^{\varepsilon } r$
is strongly irreducible, and the statement follows from [Reference Kret and Shin50, Lem. 4.8(i)]. In the remaining cases, the Zariski closure of
$\mathrm {spin}^{\varepsilon } r$
is strongly irreducible, and the statement follows from [Reference Kret and Shin50, Lem. 4.8(i)]. In the remaining cases, the Zariski closure of
![]() $\mathrm {Im}(\overline r)$
is
$\mathrm {Im}(\overline r)$
is
![]() $\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
$\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
![]() $\overline {\theta ^{\circ } \mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
$\overline {\theta ^{\circ } \mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
,
![]() $\overline {i_{\mathrm {reg}}}(\mathrm {PGL}_2)$
or
$\overline {i_{\mathrm {reg}}}(\mathrm {PGL}_2)$
or
![]() $i_{\mathrm {spin}}(G_2)$
. In the last two of these,
$i_{\mathrm {spin}}(G_2)$
. In the last two of these,
![]() $\mathrm {Im}(\overline r)\subset \overline {i_{\mathrm {std}}}({\mathrm {SO}}_{2n-1}(\overline {\mathbb {Q}}_{\ell }))$
, so
$\mathrm {Im}(\overline r)\subset \overline {i_{\mathrm {std}}}({\mathrm {SO}}_{2n-1}(\overline {\mathbb {Q}}_{\ell }))$
, so
![]() $\mathrm {Im}(r)$
is contained in
$\mathrm {Im}(r)$
is contained in
![]() $\overline {\mathbb {Q}}_{\ell }$
-points of
$\overline {\mathbb {Q}}_{\ell }$
-points of
![]() $H_{2n-1}$
(which is the preimage of
$H_{2n-1}$
(which is the preimage of
![]() $i_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
in
$i_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
in
![]() $\mathrm {GSpin}_{2n}$
). Then we show
$\mathrm {GSpin}_{2n}$
). Then we show
![]() $\chi =1$
by the argument exactly as in Cases (i), (ii), (iv) in the proof of [Reference Kret and Shin50, Lem. 5.1, Prop. 5.2], noting that
$\chi =1$
by the argument exactly as in Cases (i), (ii), (iv) in the proof of [Reference Kret and Shin50, Lem. 5.1, Prop. 5.2], noting that
![]() $\mathrm {spin}^{\varepsilon }$
restricts to
$\mathrm {spin}^{\varepsilon }$
restricts to
![]() $\mathrm {spin}$
on
$\mathrm {spin}$
on
![]() $\mathrm {GSpin}_{2n-1}$
by Proposition 4.5. Finally, if the Zariski closure of the image is
$\mathrm {GSpin}_{2n-1}$
by Proposition 4.5. Finally, if the Zariski closure of the image is
![]() $\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
(resp.
$\overline {\mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
(resp.
![]() $\overline {\theta ^{\circ } \mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
), then
$\overline {\theta ^{\circ } \mathrm {spin}^{\circ }}({\mathrm {SO}}_7)$
), then
![]() $\overline {\mathrm {spin}^{\varepsilon }} \circ \overline r$
is irreducible if
$\overline {\mathrm {spin}^{\varepsilon }} \circ \overline r$
is irreducible if
![]() $\varepsilon = -$
(resp.
$\varepsilon = -$
(resp.
![]() $\varepsilon = +$
) and isomorphic to
$\varepsilon = +$
) and isomorphic to
![]() $\mathrm {std} \oplus \textbf {1}$
if
$\mathrm {std} \oplus \textbf {1}$
if
![]() $\varepsilon = +$
(resp.
$\varepsilon = +$
(resp.
![]() $\varepsilon = -$
) by Lemma 5.2. In particular, the representation
$\varepsilon = -$
) by Lemma 5.2. In particular, the representation
![]() $\mathrm {spin}^{\varepsilon } r$
satisfies the conditions of [Reference Kret and Shin50, Prop. 4.9], and so
$\mathrm {spin}^{\varepsilon } r$
satisfies the conditions of [Reference Kret and Shin50, Prop. 4.9], and so
![]() $\chi = 1$
in this case as well.
$\chi = 1$
in this case as well.
(ii) If the Zariski closure of the image of r contains
![]() $\mathrm {Spin}_{2n}$
, then (ii) cannot occur. Thus, r has either image in
$\mathrm {Spin}_{2n}$
, then (ii) cannot occur. Thus, r has either image in
![]() $H_{2n-1}$
, or it has image in
$H_{2n-1}$
, or it has image in
![]() $\mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
. In the latter case,
$\mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
. In the latter case,
![]() $\mathrm {spin}^- r$
is strongly irreducible while
$\mathrm {spin}^- r$
is strongly irreducible while
![]() $\mathrm {spin}^+ r$
is not by Lemma 5.2, which is a contradiction. Thus,
$\mathrm {spin}^+ r$
is not by Lemma 5.2, which is a contradiction. Thus,
![]() $\mathrm {Im}(r) \subset H_{2n-1}$
. For
$\mathrm {Im}(r) \subset H_{2n-1}$
. For
![]() $g \in H_{2n-1}$
, we have
$g \in H_{2n-1}$
, we have
Put
![]() $t = \kappa _0 \circ r$
. Then
$t = \kappa _0 \circ r$
. Then
![]() $t \otimes \mathrm {spin}^+r \simeq \mathrm {spin}^- r$
and
$t \otimes \mathrm {spin}^+r \simeq \mathrm {spin}^- r$
and
![]() $t \chi ^{-1} \otimes \mathrm {spin}^+ r \simeq \mathrm {spin}^+ r$
, and
$t \chi ^{-1} \otimes \mathrm {spin}^+ r \simeq \mathrm {spin}^+ r$
, and
![]() $t = \chi $
by (i).
$t = \chi $
by (i).
(iii) Write H for the Zariski closure of the image of r. By the proof of (i), we see that either
![]() $\mathrm {Spin}_{2n} \subset H$
, or
$\mathrm {Spin}_{2n} \subset H$
, or
![]() $H \subset H_{2n-1}$
or
$H \subset H_{2n-1}$
or
![]() $H \subset \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
up to conjugation. Assume that
$H \subset \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
up to conjugation. Assume that
![]() $H \not \subset H_{2n-1}$
(even after conjugation), so that
$H \not \subset H_{2n-1}$
(even after conjugation), so that
![]() $\mathrm {Spin}_{2n} \subset H$
or
$\mathrm {Spin}_{2n} \subset H$
or
![]() $H \subset \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
. In this case, we need to show that
$H \subset \mathrm {pr}^{-1}(\mathrm {spin}^{\circ }(\mathrm {Spin}_7))$
. In this case, we need to show that
![]() $\chi ^+=\chi ^-=1$
. Suppose
$\chi ^+=\chi ^-=1$
. Suppose
![]() $\chi ^-\neq 1$
to the contrary. Since
$\chi ^-\neq 1$
to the contrary. Since
![]() $\mathrm {spin}^-(r)$
is strongly irreducible by assumption on H (cf. Lemma 5.2), we have
$\mathrm {spin}^-(r)$
is strongly irreducible by assumption on H (cf. Lemma 5.2), we have
by [Reference Kret and Shin50, Lem. 4.8(i)]. In particular,
![]() $\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r)\overset \sim \to \mathrm {spin}(r)$
induces an isomorphism
$\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r)\overset \sim \to \mathrm {spin}(r)$
induces an isomorphism
![]() $\chi ^- \otimes \mathrm {spin}^-(r) \overset \sim \to \mathrm {ker}(\mathrm {spin}(r) \twoheadrightarrow \mathrm {spin}^-(r)) = \mathrm {spin}^+(r)$
. As
$\chi ^- \otimes \mathrm {spin}^-(r) \overset \sim \to \mathrm {ker}(\mathrm {spin}(r) \twoheadrightarrow \mathrm {spin}^-(r)) = \mathrm {spin}^+(r)$
. As
![]() $H \not \subset H_{2n-1}$
, this contradicts (ii). Therefore,
$H \not \subset H_{2n-1}$
, this contradicts (ii). Therefore,
![]() $\chi ^- = 1$
. From
$\chi ^- = 1$
. From
![]() $\chi ^+ \mathrm {spin}^+ r \oplus \chi ^- \mathrm {spin}^- r \cong \mathrm {spin}(r)$
, we then obtain
$\chi ^+ \mathrm {spin}^+ r \oplus \chi ^- \mathrm {spin}^- r \cong \mathrm {spin}(r)$
, we then obtain
![]() $\chi ^+ \mathrm {spin}^+ r \cong \mathrm {spin}^+r$
, which implies
$\chi ^+ \mathrm {spin}^+ r \cong \mathrm {spin}^+r$
, which implies
![]() $\chi ^+ = 1$
by item (i).
$\chi ^+ = 1$
by item (i).
Now assume
![]() $H \subset H_{2n-1}$
up to conjugation. We obtain a character
$H \subset H_{2n-1}$
up to conjugation. We obtain a character
![]() $t = \kappa _0 \circ r \colon \Gamma \to \{\pm 1\}$
. Write
$t = \kappa _0 \circ r \colon \Gamma \to \{\pm 1\}$
. Write
![]() $\Gamma _0 := \ker (t)$
. We have
$\Gamma _0 := \ker (t)$
. We have
![]() $\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}^+(r) \oplus \mathrm {spin}^-(r)$
. By Proposition 4.5, we have
$\chi ^+ \mathrm {spin}^+(r) \oplus \chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}^+(r) \oplus \mathrm {spin}^-(r)$
. By Proposition 4.5, we have
![]() $\mathrm {spin}^+(r|_{\Gamma _0}) \simeq \mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
, where
$\mathrm {spin}^+(r|_{\Gamma _0}) \simeq \mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
, where
![]() $\mathrm {spin}_{2n-1}$
denotes the spin representation of
$\mathrm {spin}_{2n-1}$
denotes the spin representation of
![]() $\mathrm {GSpin}_{2n-1}$
. By the proof of [Reference Kret and Shin50, Prop. 5.1],
$\mathrm {GSpin}_{2n-1}$
. By the proof of [Reference Kret and Shin50, Prop. 5.1],
![]() $\mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
decomposes as a direct sum
$\mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
decomposes as a direct sum
![]() $r_1^{e_1} \oplus \cdots \oplus r_k^{e_k}$
, such that
$r_1^{e_1} \oplus \cdots \oplus r_k^{e_k}$
, such that
![]() $k, e_i \in \mathbb Z_{\geq 1}$
,
$k, e_i \in \mathbb Z_{\geq 1}$
,
![]() $r_i$
is irreducible, and
$r_i$
is irreducible, and
![]() $\dim (r_i) \neq \dim (r_j)$
for
$\dim (r_i) \neq \dim (r_j)$
for
![]() $i \neq j$
. Moreover, the projective image of
$i \neq j$
. Moreover, the projective image of
![]() $\mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
in
$\mathrm {spin}_{2n-1}(r|_{\Gamma _0})$
in
![]() $\mathrm {PGL}_{2^{n-1}}$
is Zariski connected. This implies that the
$\mathrm {PGL}_{2^{n-1}}$
is Zariski connected. This implies that the
![]() $r_i$
are strongly irreducible
$r_i$
are strongly irreducible
![]() $\Gamma _0$
-representations [Proposition 4.8(ii), loc. cit.].
$\Gamma _0$
-representations [Proposition 4.8(ii), loc. cit.].
Suppose
![]() $\chi ^-|_{\Gamma _0} \neq 1$
. We again claim that (5.8) holds. To see this, assume
$\chi ^-|_{\Gamma _0} \neq 1$
. We again claim that (5.8) holds. To see this, assume
![]() $f \colon \chi ^- \otimes \mathrm {spin}^-(r) \to \mathrm {spin}^-(r)$
is a nontrivial
$f \colon \chi ^- \otimes \mathrm {spin}^-(r) \to \mathrm {spin}^-(r)$
is a nontrivial
![]() $\Gamma _0$
-morphism. Since the
$\Gamma _0$
-morphism. Since the
![]() $\dim (r_i)$
are distinct, the morphism f induces an isomorphism from
$\dim (r_i)$
are distinct, the morphism f induces an isomorphism from
![]() $\chi ^- \otimes r_1$
to one of the copies of
$\chi ^- \otimes r_1$
to one of the copies of
![]() $r_1$
in
$r_1$
in
![]() $\mathrm {spin}^-(r)$
. Since
$\mathrm {spin}^-(r)$
. Since
![]() $r_1$
is strongly irreducible by [Proposition 4.8(i), loc. cit.], this implies
$r_1$
is strongly irreducible by [Proposition 4.8(i), loc. cit.], this implies
![]() $\chi ^-|_{\Gamma _0} = 1$
. Thus,
$\chi ^-|_{\Gamma _0} = 1$
. Thus,
![]() $\chi ^- \in \{t, 1\}$
.
$\chi ^- \in \{t, 1\}$
.
Arguing with
![]() $+$
instead of
$+$
instead of
![]() $-$
, we find similarly
$-$
, we find similarly
![]() $\chi ^+ \in \{t, 1\}$
. If
$\chi ^+ \in \{t, 1\}$
. If
![]() $\chi ^+ = 1$
, then we have
$\chi ^+ = 1$
, then we have
which implies
![]() $\chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}^-(r)$
, and thus
$\chi ^- \mathrm {spin}^-(r) \simeq \mathrm {spin}^-(r)$
, and thus
![]() $\chi ^- = 1$
by (i). By the same argument, if
$\chi ^- = 1$
by (i). By the same argument, if
![]() $\chi ^- = 1$
, then
$\chi ^- = 1$
, then
![]() $\chi ^+ = 1$
. Thus,
$\chi ^+ = 1$
. Thus,
![]() $\chi ^+ = \chi ^-$
. The statement follows.
$\chi ^+ = \chi ^-$
. The statement follows.
Lemma 5.7. Let
![]() $\gamma , \gamma ' \in \mathrm {GSpin}_{2n}$
be two semi-simple elements. Then
$\gamma , \gamma ' \in \mathrm {GSpin}_{2n}$
be two semi-simple elements. Then
![]() $\gamma , \gamma '$
are
$\gamma , \gamma '$
are
![]() $\mathrm {GPin}_{2n}$
-conjugate if and only if they are conjugate in the representations
$\mathrm {GPin}_{2n}$
-conjugate if and only if they are conjugate in the representations
![]() $\mathcal N, \mathrm {std}$
and
$\mathcal N, \mathrm {std}$
and
![]() $\mathrm {spin}$
.
$\mathrm {spin}$
.
Proof. This follows from [Reference Kret and Shin50, §1] and the fact that
![]() $\mathrm {GPin}_{2n}$
has
$\mathrm {GPin}_{2n}$
has
![]() $\{\mathrm {std},\mathcal N,\mathrm {spin}\}$
as a fundamental set in the sense thereof, which follows from the fact that
$\{\mathrm {std},\mathcal N,\mathrm {spin}\}$
as a fundamental set in the sense thereof, which follows from the fact that
![]() $\{\mathrm {std},\mathcal N,\mathrm {spin}^+,\mathrm {spin}^-\}$
is a fundamental set for
$\{\mathrm {std},\mathcal N,\mathrm {spin}^+,\mathrm {spin}^-\}$
is a fundamental set for
![]() $\mathrm {GSpin}_{2n}$
as checked therein.
$\mathrm {GSpin}_{2n}$
as checked therein.
Proposition 5.8. Let
![]() $E/F$
be a quadratic extension of characteristic zero fields. Let H be one of the following algebraic groups
$E/F$
be a quadratic extension of characteristic zero fields. Let H be one of the following algebraic groups
where
![]() $\Gamma _{E/F}$
acts through
$\Gamma _{E/F}$
acts through
![]() $\theta ^{\circ }$
or
$\theta ^{\circ }$
or
![]() $\theta $
in the semi-direct products. We write
$\theta $
in the semi-direct products. We write
![]() $H^0$
for the neutral component of H. Let
$H^0$
for the neutral component of H. Let
be semisimple Galois representations such that
-
•
 $r_1$
and
$r_1$
and
 $r_2$
are locally conjugate and
$r_2$
are locally conjugate and -
• the Zariski closure of
 $r_1(\Gamma )$
contains a regular unipotent element.
$r_1(\Gamma )$
contains a regular unipotent element.
Then
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are
$r_2$
are
![]() $H^0$
-conjugate.
$H^0$
-conjugate.
Proof. For simplicity, we abbreviate
![]() $H(\overline {\mathbb {Q}}_{\ell })$
as H if there is no danger of confusion.
$H(\overline {\mathbb {Q}}_{\ell })$
as H if there is no danger of confusion.
The case
![]() $H = {\mathrm {SO}}_{2n}$
. Write
$H = {\mathrm {SO}}_{2n}$
. Write
![]() $\overline r_1,\overline r_2:\Gamma \rightarrow \mathrm {PSO}_{2n}$
for the projectivizations of
$\overline r_1,\overline r_2:\Gamma \rightarrow \mathrm {PSO}_{2n}$
for the projectivizations of
![]() $r_1,r_2$
. Write
$r_1,r_2$
. Write
![]() $I_i$
for the Zariski closure of
$I_i$
for the Zariski closure of
![]() $\overline r_i(\Gamma )$
in
$\overline r_i(\Gamma )$
in
![]() $\mathrm {PSO}_{2n}$
, for
$\mathrm {PSO}_{2n}$
, for
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $\mathrm {O}_{2n}$
is acceptable [Reference Kret and Shin50, Prop. B.1],
$\mathrm {O}_{2n}$
is acceptable [Reference Kret and Shin50, Prop. B.1],
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are conjugate by an element of
$r_2$
are conjugate by an element of
![]() $w\in \mathrm {O}_{2n}$
(i.e.,
$w\in \mathrm {O}_{2n}$
(i.e.,
![]() $r_2=w r_1 w^{-1}$
). In particular, the Zariski closure of
$r_2=w r_1 w^{-1}$
). In particular, the Zariski closure of
![]() $r_2(\Gamma )$
also contains a regular unipotent element. We are done if
$r_2(\Gamma )$
also contains a regular unipotent element. We are done if
![]() $w\in {\mathrm {SO}}_{2n}$
, so we may assume that
$w\in {\mathrm {SO}}_{2n}$
, so we may assume that
![]() $w\notin {\mathrm {SO}}_{2n}$
henceforth.
$w\notin {\mathrm {SO}}_{2n}$
henceforth.
There are now three cases by Proposition 5.5: either (A)
![]() $I_1=\mathrm {PSO}_{2n}$
, (B)
$I_1=\mathrm {PSO}_{2n}$
, (B)
![]() $I_1$
is
$I_1$
is
![]() ${\mathrm {SO}}_{2n-1}$
,
${\mathrm {SO}}_{2n-1}$
,
![]() $\mathrm {PGL}_2$
, or
$\mathrm {PGL}_2$
, or
![]() $G_2$
(the last case when
$G_2$
(the last case when
![]() $n=4$
) or (C)
$n=4$
) or (C)
![]() $n=4$
and
$n=4$
and
![]() $I_1$
is
$I_1$
is
![]() $\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
or
$\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
or
![]() $\theta ^{\circ }\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
.
$\theta ^{\circ }\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
.
Case (A). Since
![]() $r_1$
has Zariski dense image in
$r_1$
has Zariski dense image in
![]() ${\mathrm {SO}}_{2n}$
, there exists
${\mathrm {SO}}_{2n}$
, there exists
![]() ${{\mathfrak q}}$
such that
${{\mathfrak q}}$
such that
![]() $r_1(\mathrm {Frob}_{\mathfrak {q}})$
and
$r_1(\mathrm {Frob}_{\mathfrak {q}})$
and
![]() $w r_1(\mathrm {Frob}_{\mathfrak {q}}) w^{-1}$
are not outer conjugate by Lemma 1.1. This contradicts
$w r_1(\mathrm {Frob}_{\mathfrak {q}}) w^{-1}$
are not outer conjugate by Lemma 1.1. This contradicts
![]() $r_2(\mathrm {Frob}_{\mathfrak {q}})=w r_1(\mathrm {Frob}_{\mathfrak {q}}) w^{-1}$
since
$r_2(\mathrm {Frob}_{\mathfrak {q}})=w r_1(\mathrm {Frob}_{\mathfrak {q}}) w^{-1}$
since
![]() $w\in \mathrm {O}_{2n}\backslash {\mathrm {SO}}_{2n}$
.
$w\in \mathrm {O}_{2n}\backslash {\mathrm {SO}}_{2n}$
.
Case (B). The image of
![]() $r_1$
is contained in
$r_1$
is contained in
![]() $i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z_{{\mathrm {SO}}_{2n}}$
, which is centralized by
$i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z_{{\mathrm {SO}}_{2n}}$
, which is centralized by
![]() $\vartheta ^{\circ }\in \mathrm {O}_{2n}\backslash {\mathrm {SO}}_{2n}$
. Since
$\vartheta ^{\circ }\in \mathrm {O}_{2n}\backslash {\mathrm {SO}}_{2n}$
. Since
![]() $\vartheta ^{\circ }$
and w belong to the same
$\vartheta ^{\circ }$
and w belong to the same
![]() ${\mathrm {SO}}_{2n}$
-coset, it follows that
${\mathrm {SO}}_{2n}$
-coset, it follows that
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are
$r_2$
are
![]() ${\mathrm {SO}}_{2n}$
-conjugate.
${\mathrm {SO}}_{2n}$
-conjugate.
Case (C). Without loss of generality, we may assume
![]() $I_1=\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
. Since
$I_1=\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
. Since
![]() $r_1={\mathrm {Int}}(w)\circ r_2$
for
$r_1={\mathrm {Int}}(w)\circ r_2$
for
![]() $w\in \mathrm {O}_{8}\backslash {\mathrm {SO}}_{8}$
, we see that
$w\in \mathrm {O}_{8}\backslash {\mathrm {SO}}_{8}$
, we see that
![]() $I_2$
is
$I_2$
is
![]() $\mathrm {PSO}_8$
-conjugate to
$\mathrm {PSO}_8$
-conjugate to
![]() $\theta ^{\circ }\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
.
$\theta ^{\circ }\overline {\mathrm {spin}}({\mathrm {SO}}_7)$
.
We claim that this case does not arise. By assumption,
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are locally conjugate representations with values in
$r_2$
are locally conjugate representations with values in
![]() ${\mathrm {SO}}_8$
.
${\mathrm {SO}}_8$
.
We may assume, after replacing
![]() $r_2$
with a suitable
$r_2$
with a suitable
![]() ${\mathrm {SO}}_8$
-conjugate, that
${\mathrm {SO}}_8$
-conjugate, that
![]() $r_1(\gamma ) = \theta ^{\circ } r_2(\gamma )$
for all
$r_1(\gamma ) = \theta ^{\circ } r_2(\gamma )$
for all
![]() $\gamma \in \Gamma $
. There exists a representation
$\gamma \in \Gamma $
. There exists a representation
![]() $\widetilde {r} \colon \Gamma \to \mathrm {Spin}_7$
such that
$\widetilde {r} \colon \Gamma \to \mathrm {Spin}_7$
such that
![]() $r_1(\gamma ) = \mathrm {spin}(\widetilde {r}(\gamma ))$
,
$r_1(\gamma ) = \mathrm {spin}(\widetilde {r}(\gamma ))$
,
![]() $r_2(\gamma ) = \theta ^{\circ } \mathrm {spin}(\widetilde {r}(\gamma ))$
. However, by Lemma 1.1, there exists an F-place
$r_2(\gamma ) = \theta ^{\circ } \mathrm {spin}(\widetilde {r}(\gamma ))$
. However, by Lemma 1.1, there exists an F-place
![]() ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
![]() $\widetilde {r}$
is unramified and
$\widetilde {r}$
is unramified and
![]() $\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}) \in U$
with U is as in Lemma 5.1. Then
$\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}) \in U$
with U is as in Lemma 5.1. Then
![]() $\mathrm {spin}(\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}))$
and
$\mathrm {spin}(\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}))$
and
![]() $\theta ^{\circ } \mathrm {spin}(\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}))$
are not
$\theta ^{\circ } \mathrm {spin}(\widetilde {r}(\mathrm {Frob}_{{\mathfrak q}}))$
are not
![]() ${\mathrm {SO}}_8$
-conjugate. This contradicts the assumption that
${\mathrm {SO}}_8$
-conjugate. This contradicts the assumption that
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are locally conjugate. The claim is proved.
$r_2$
are locally conjugate. The claim is proved.
The case
![]() $H = {\mathrm {SO}}_{2n} \rtimes \Gamma _{E/F}$
. By the preceding case, we may assume that
$H = {\mathrm {SO}}_{2n} \rtimes \Gamma _{E/F}$
. By the preceding case, we may assume that
![]() $r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
. (Strictly speaking, we proved the
$r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
. (Strictly speaking, we proved the
![]() ${\mathrm {SO}}_{2n}$
-case for
${\mathrm {SO}}_{2n}$
-case for
![]() $\Gamma =\Gamma _F$
, but the proof goes through without change for
$\Gamma =\Gamma _F$
, but the proof goes through without change for
![]() $\Gamma _E$
.) Since
$\Gamma _E$
.) Since
![]() ${\mathrm {SO}}_{2n} \rtimes \Gamma _{E/F}\simeq \mathrm {O}_{2n}$
via
${\mathrm {SO}}_{2n} \rtimes \Gamma _{E/F}\simeq \mathrm {O}_{2n}$
via
![]() $g\rtimes c\mapsto g\vartheta ^{\circ }$
, we identify the two groups. In particular, H is acceptable, so there exists
$g\rtimes c\mapsto g\vartheta ^{\circ }$
, we identify the two groups. In particular, H is acceptable, so there exists
![]() $w\in \mathrm {O}_{2n}$
such that
$w\in \mathrm {O}_{2n}$
such that
![]() $r_2=w r_1 w^{-1}$
. We are done if
$r_2=w r_1 w^{-1}$
. We are done if
![]() $w\in {\mathrm {SO}}_{2n}$
, so assume that
$w\in {\mathrm {SO}}_{2n}$
, so assume that
![]() $w\notin {\mathrm {SO}}_{2n}$
. Depending on the projective image of
$w\notin {\mathrm {SO}}_{2n}$
. Depending on the projective image of
![]() $r_1|_{\Gamma _E}$
, we have Cases (A), (B), (C) as above. The arguments there tell us that Cases (A) and (C) are impossible when
$r_1|_{\Gamma _E}$
, we have Cases (A), (B), (C) as above. The arguments there tell us that Cases (A) and (C) are impossible when
![]() $w\notin {\mathrm {SO}}_{2n}$
. In Case (B), we know
$w\notin {\mathrm {SO}}_{2n}$
. In Case (B), we know
![]() $r_1(\Gamma _E)$
is contained in
$r_1(\Gamma _E)$
is contained in
![]() $i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z_{{\mathrm {SO}}_{2n}}$
. The normalizer of the latter in
$i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})\times Z_{{\mathrm {SO}}_{2n}}$
. The normalizer of the latter in
![]() $\mathrm {O}_{2n}$
is
$\mathrm {O}_{2n}$
is
![]() $\mathrm {O}_{2n-1}\times \mathrm {O}_1$
(embedded in
$\mathrm {O}_{2n-1}\times \mathrm {O}_1$
(embedded in
![]() $\mathrm {O}_{2n}$
via
$\mathrm {O}_{2n}$
via
![]() $i^{\circ }_{\mathrm {std}}$
), which is centralized by
$i^{\circ }_{\mathrm {std}}$
), which is centralized by
![]() $\vartheta ^{\circ }$
. Hence, if we write
$\vartheta ^{\circ }$
. Hence, if we write
![]() $w=w_0\vartheta ^{\circ }$
with
$w=w_0\vartheta ^{\circ }$
with
![]() $w_0 \in {\mathrm {SO}}_{2n}$
, then
$w_0 \in {\mathrm {SO}}_{2n}$
, then
![]() $r_2=w_0 r_1 w_0^{-1}$
. Namely,
$r_2=w_0 r_1 w_0^{-1}$
. Namely,
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are
$r_2$
are
![]() $H^0$
-conjugate.
$H^0$
-conjugate.
The
![]() $\mathbf {GSpin}_{\boldsymbol{2n}}$
-case. Write
$\mathbf {GSpin}_{\boldsymbol{2n}}$
-case. Write
![]() $r_1^{\circ },r_2^{\circ }$
for the composition of
$r_1^{\circ },r_2^{\circ }$
for the composition of
![]() $r_1,r_2$
with
$r_1,r_2$
with
![]() $\mathrm {pr}^{\circ } :\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. Then
$\mathrm {pr}^{\circ } :\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. Then
![]() $r_1^{\circ }$
and
$r_1^{\circ }$
and
![]() $r_2^{\circ }$
are conjugate by the
$r_2^{\circ }$
are conjugate by the
![]() ${\mathrm {SO}}_{2n}$
-case treated above. Hence, we may assume that
${\mathrm {SO}}_{2n}$
-case treated above. Hence, we may assume that
![]() $r_2=\chi r_1$
with a continuous character
$r_2=\chi r_1$
with a continuous character
![]() $\chi :\Gamma \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$
, where
$\chi :\Gamma \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$
, where
![]() $\overline {\mathbb {Q}}_{\ell }^{\times }=\ker (\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n})$
via Lemma 3.1 (ii). Since
$\overline {\mathbb {Q}}_{\ell }^{\times }=\ker (\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n})$
via Lemma 3.1 (ii). Since
![]() $r_1$
and
$r_1$
and
![]() $\chi \otimes r_1$
are locally conjugate by the initial assumption, we have
$\chi \otimes r_1$
are locally conjugate by the initial assumption, we have
It follows from Lemma 5.6 that
![]() $\chi =1$
.
$\chi =1$
.
The
![]() $\mathbf {GSpin}_{\boldsymbol{2n}}\ \boldsymbol{\rtimes}\ \boldsymbol{\Gamma}_{\boldsymbol{E/F}}$
-case. By the
$\mathbf {GSpin}_{\boldsymbol{2n}}\ \boldsymbol{\rtimes}\ \boldsymbol{\Gamma}_{\boldsymbol{E/F}}$
-case. By the
![]() $\mathrm {GSpin}_{2n}$
-case above, we may assume that
$\mathrm {GSpin}_{2n}$
-case above, we may assume that
![]() $r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
. Writing
$r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
. Writing
![]() $r_i^{\circ }:=\mathrm {pr}^{\circ } \circ r_i$
for
$r_i^{\circ }:=\mathrm {pr}^{\circ } \circ r_i$
for
![]() $i=1,2$
, we have
$i=1,2$
, we have
![]() $r^{\circ }_1|_{\Gamma _E}=r^{\circ }_2|_{\Gamma _E}$
. By the preceding argument, we deduce that
$r^{\circ }_1|_{\Gamma _E}=r^{\circ }_2|_{\Gamma _E}$
. By the preceding argument, we deduce that
![]() $r^{\circ }_1=r^{\circ }_2$
. However,
$r^{\circ }_1=r^{\circ }_2$
. However,
![]() $r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
implies that
$r_1|_{\Gamma _E}=r_2|_{\Gamma _E}$
implies that
![]() $r_1 = r_2$
or
$r_1 = r_2$
or
![]() $r_1 = r_2\otimes \chi $
by Example A.6, with
$r_1 = r_2\otimes \chi $
by Example A.6, with
![]() $\chi $
as in that example. If
$\chi $
as in that example. If
![]() $r_1=r_2$
, then we are done so suppose
$r_1=r_2$
, then we are done so suppose
![]() $r_1= r_2\otimes \chi $
. Then
$r_1= r_2\otimes \chi $
. Then
![]() $r^{\circ }_1 = r^{\circ }_2\otimes \chi _{E/F}$
for
$r^{\circ }_1 = r^{\circ }_2\otimes \chi _{E/F}$
for
![]() $\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}=\{\pm 1\}$
. Set
$\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}=\{\pm 1\}$
. Set
![]() $R_i:=\mathrm {std}\circ r^{\circ }_i$
for
$R_i:=\mathrm {std}\circ r^{\circ }_i$
for
![]() $i=1,2$
, so that
$i=1,2$
, so that
![]() $R_1 = R_2\otimes \chi _{E/F}$
. Since
$R_1 = R_2\otimes \chi _{E/F}$
. Since
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are locally conjugate, the
$r_2$
are locally conjugate, the
![]() ${\mathrm {GL}}_{2n}$
-valued representations
${\mathrm {GL}}_{2n}$
-valued representations
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are locally conjugate and thus conjugate. So
$R_2$
are locally conjugate and thus conjugate. So
![]() $R_1\simeq R_1\otimes \chi _{E/F}$
. By [Reference Kret and Shin50, Lem. 4.8],
$R_1\simeq R_1\otimes \chi _{E/F}$
. By [Reference Kret and Shin50, Lem. 4.8],
![]() $R_1$
is not strongly irreducible. Considering the projective image of
$R_1$
is not strongly irreducible. Considering the projective image of
![]() $r_1|_{\Gamma _E}$
as in the
$r_1|_{\Gamma _E}$
as in the
![]() ${\mathrm {SO}}_{2n}$
-case above, we see that Case (A) is excluded and only Case (B) or (C) occurs. In either case, again because
${\mathrm {SO}}_{2n}$
-case above, we see that Case (A) is excluded and only Case (B) or (C) occurs. In either case, again because
![]() $R_1$
is not strongly irreducible, the only possibility is that
$R_1$
is not strongly irreducible, the only possibility is that
![]() $R_1|_{\Gamma _E}$
decomposes into two strongly irreducible representations of dimensions
$R_1|_{\Gamma _E}$
decomposes into two strongly irreducible representations of dimensions
![]() $(2n-1)$
and 1. Then it is easy to see that
$(2n-1)$
and 1. Then it is easy to see that
![]() $R_1=R^{\prime }_1\oplus R^{\prime \prime }_1$
already on
$R_1=R^{\prime }_1\oplus R^{\prime \prime }_1$
already on
![]() $\Gamma _F$
, with strongly irreducible
$\Gamma _F$
, with strongly irreducible
![]() $R^{\prime }_1$
and
$R^{\prime }_1$
and
![]() $R^{\prime \prime }_1$
of dimensions
$R^{\prime \prime }_1$
of dimensions
![]() $(2n-1)$
and 1. It follows from
$(2n-1)$
and 1. It follows from
![]() $R_1\simeq R_1\otimes \chi _{E/F}$
that
$R_1\simeq R_1\otimes \chi _{E/F}$
that
![]() $R^{\prime }_1\simeq R^{\prime }_1\otimes \chi _{E/F}$
(and similarly for
$R^{\prime }_1\simeq R^{\prime }_1\otimes \chi _{E/F}$
(and similarly for
![]() $R^{\prime \prime }_1$
), but this contradicts strong irreducibility of
$R^{\prime \prime }_1$
), but this contradicts strong irreducibility of
![]() $R^{\prime }_1$
[Reference Kret and Shin50, Lem. 4.8].
$R^{\prime }_1$
[Reference Kret and Shin50, Lem. 4.8].
6 On
 ${\mathrm {SO}}_{2n}$
-valued Galois representations
${\mathrm {SO}}_{2n}$
-valued Galois representations
In this section, we construct Galois representations associated with automorphic representations of even orthogonal groups over a totally real field F. More precisely, we will derive a weaker version of Conjecture 1 for such groups from the literature. Let either
-
•
 $E=F$
or
$E=F$
or -
• E be a CM quadratic extension of F.
In the latter case, write c for the nontrivial element of
![]() $\Gamma _{E/F}:={\mathrm {Gal}}(E/F)$
. Write
$\Gamma _{E/F}:={\mathrm {Gal}}(E/F)$
. Write
![]() ${\mathrm {SO}}_{2n}^{E/F}$
for the split group
${\mathrm {SO}}_{2n}^{E/F}$
for the split group
![]() ${\mathrm {SO}}_{2n}$
if
${\mathrm {SO}}_{2n}$
if
![]() $E=F$
, and the quasi-split outer form of
$E=F$
, and the quasi-split outer form of
![]() ${\mathrm {SO}}_{2n}$
over F relative to
${\mathrm {SO}}_{2n}$
over F relative to
![]() $E/F$
otherwise. To be precise, in the latter case,
$E/F$
otherwise. To be precise, in the latter case,
for F-algebras R, and
![]() ${\mathrm {SO}}^{E/F}_{2n}$
is the connected component where
${\mathrm {SO}}^{E/F}_{2n}$
is the connected component where
![]() $\det (g)=1$
. We can extend the standard embedding
$\det (g)=1$
. We can extend the standard embedding
![]() $\mathrm {std}:{\mathrm {SO}}_{2n}({\mathbb {C}})\hookrightarrow {\mathrm {GL}}_{2n}({\mathbb {C}})$
to a map (still denoted
$\mathrm {std}:{\mathrm {SO}}_{2n}({\mathbb {C}})\hookrightarrow {\mathrm {GL}}_{2n}({\mathbb {C}})$
to a map (still denoted
![]() $\mathrm {std}$
)
$\mathrm {std}$
)
whose image is
![]() ${\mathrm {SO}}_{2n}({\mathbb {C}})$
if
${\mathrm {SO}}_{2n}({\mathbb {C}})$
if
![]() $E=F$
and
$E=F$
and
![]() $\mathrm {O}_{2n}({\mathbb {C}})$
if
$\mathrm {O}_{2n}({\mathbb {C}})$
if
![]() $E\neq F$
. More precisely, when
$E\neq F$
. More precisely, when
![]() $E\neq F$
, we fix the extended map
$E\neq F$
, we fix the extended map
![]() $\mathrm {std}$
by requiring
$\mathrm {std}$
by requiring
![]() $c\mapsto \vartheta ^{\circ }$
. (We defined
$c\mapsto \vartheta ^{\circ }$
. (We defined
![]() $\mathrm {O}_{2n}$
explicitly in the last section, and
$\mathrm {O}_{2n}$
explicitly in the last section, and
![]() $\vartheta ^{\circ }$
was given in (2.4).)
$\vartheta ^{\circ }$
was given in (2.4).)
Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
. The following will be key assumptions on
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
. The following will be key assumptions on
![]() $\pi ^{\flat }$
. (Recall from §1 that
$\pi ^{\flat }$
. (Recall from §1 that
![]() $ \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
denotes the Steinberg representation.)
$ \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
denotes the Steinberg representation.)
-
(coh°)
 $\pi ^{\flat }_{\infty }$
is cohomological for an irreducible algebraic representation
$\pi ^{\flat }_{\infty }$
is cohomological for an irreducible algebraic representation
 $\xi ^{\flat } = \otimes _{y \in \mathcal V_{\infty }} \xi _y^{\flat }$
of
$\xi ^{\flat } = \otimes _{y \in \mathcal V_{\infty }} \xi _y^{\flat }$
of
 ${\mathrm {SO}}^{E/F}_{2n, F \otimes {\mathbb {C}}}$
.
${\mathrm {SO}}^{E/F}_{2n, F \otimes {\mathbb {C}}}$
. -
(St°) There exists a prime
 ${{{\mathfrak q}}_{\mathrm {St}}}$
of F such that
${{{\mathfrak q}}_{\mathrm {St}}}$
of F such that
 $\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}^{\flat } \simeq \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
up to a character twist.
$\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}^{\flat } \simeq \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
up to a character twist.
Condition (coh
![]() $^{\circ }$
) implies that the infinitesimal character of
$^{\circ }$
) implies that the infinitesimal character of
![]() $\xi ^{\flat }_y$
is given by
$\xi ^{\flat }_y$
is given by
![]() $\rho _{{\mathrm {SO}}}+\lambda (\xi _y^{\flat })$
at each
$\rho _{{\mathrm {SO}}}+\lambda (\xi _y^{\flat })$
at each
![]() $y\in \mathcal V_{\infty }$
; see [Reference Borel and Wallach8, Thm. I.5.3]. In particular,
$y\in \mathcal V_{\infty }$
; see [Reference Borel and Wallach8, Thm. I.5.3]. In particular,
![]() $\pi ^{\flat }$
is C-algebraic in the sense of Buzzard–Gee [Reference Buzzard and Gee12, Lem. 7.2.2], and thus also L-algebraic as the half sum of positive (co)roots is integral for
$\pi ^{\flat }$
is C-algebraic in the sense of Buzzard–Gee [Reference Buzzard and Gee12, Lem. 7.2.2], and thus also L-algebraic as the half sum of positive (co)roots is integral for
![]() ${\mathrm {SO}}^{E/F}_{2n}$
. In (St
${\mathrm {SO}}^{E/F}_{2n}$
. In (St
![]() $^{\circ }$
), characters of
$^{\circ }$
), characters of
![]() ${\mathrm {SO}}^{E/F}_{2n}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
are exactly the characters factoring through the cokernel of
${\mathrm {SO}}^{E/F}_{2n}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
are exactly the characters factoring through the cokernel of
![]() $\mathrm {Spin}^{E/F}_{2n}(F_{{{\mathfrak q}}_{\mathrm {St}}})\rightarrow {\mathrm {SO}}^{E/F}_{2n}(F_{{{\mathfrak q}}_{\mathrm {St}}})$
. (This is a special case of the general fact [Reference Kret and Shin49, Cor. 2.3.3].) Such characters are in a natural bijection with characters of
$\mathrm {Spin}^{E/F}_{2n}(F_{{{\mathfrak q}}_{\mathrm {St}}})\rightarrow {\mathrm {SO}}^{E/F}_{2n}(F_{{{\mathfrak q}}_{\mathrm {St}}})$
. (This is a special case of the general fact [Reference Kret and Shin49, Cor. 2.3.3].) Such characters are in a natural bijection with characters of
![]() $F_{{{\mathfrak q}}_{\mathrm {St}}}^{\times }/(F_{{{\mathfrak q}}_{\mathrm {St}}}^{\times })^2 \simeq H^1(F_{{{{\mathfrak q}}_{\mathrm {St}}}}, \{\pm 1\})$
.
$F_{{{\mathfrak q}}_{\mathrm {St}}}^{\times }/(F_{{{\mathfrak q}}_{\mathrm {St}}}^{\times })^2 \simeq H^1(F_{{{{\mathfrak q}}_{\mathrm {St}}}}, \{\pm 1\})$
.
Write
![]() $\mathrm {T}_{{\mathrm {SO}}} := \mathrm {T}_{{\mathrm {GSO}}} \cap {\mathrm {SO}}_{2n}$
over
$\mathrm {T}_{{\mathrm {SO}}} := \mathrm {T}_{{\mathrm {GSO}}} \cap {\mathrm {SO}}_{2n}$
over
![]() ${\mathbb {C}}$
and choose the Borel subgroup containing
${\mathbb {C}}$
and choose the Borel subgroup containing
![]() $T_{{\mathrm {SO}}}$
in
$T_{{\mathrm {SO}}}$
in
![]() ${\mathrm {SO}}^{E/F}_{2n}$
as in the preceding section. For each
${\mathrm {SO}}^{E/F}_{2n}$
as in the preceding section. For each
![]() $y\in \mathcal V_{\infty }$
, the highest weight of
$y\in \mathcal V_{\infty }$
, the highest weight of
![]() $\xi _y^{\flat }$
gives rise to a dominant cocharacter
$\xi _y^{\flat }$
gives rise to a dominant cocharacter
![]() $\lambda (\xi _y^{\flat })\in X_*(\mathrm {T}_{{\mathrm {SO}}})$
. Let
$\lambda (\xi _y^{\flat })\in X_*(\mathrm {T}_{{\mathrm {SO}}})$
. Let
![]() $\phi _{\pi ^{\flat }_y}:W_{F_y}\rightarrow {}^L {\mathrm {SO}}_{2n}^{E/F}$
denote the L-parameter of
$\phi _{\pi ^{\flat }_y}:W_{F_y}\rightarrow {}^L {\mathrm {SO}}_{2n}^{E/F}$
denote the L-parameter of
![]() $\pi ^{\flat }_y$
assigned by [Reference Langlands53]. Recall
$\pi ^{\flat }_y$
assigned by [Reference Langlands53]. Recall
![]() $\mathrm {std}:{\mathrm {SO}}_{2n}\hookrightarrow {\mathrm {GL}}_{2n}$
denotes the standard embedding. We also consider the following conditions:
$\mathrm {std}:{\mathrm {SO}}_{2n}\hookrightarrow {\mathrm {GL}}_{2n}$
denotes the standard embedding. We also consider the following conditions:
-
(std-reg°)
 $\ \ \mathrm {std}\circ \phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
is regular (i.e., the centralizer group in
$\ \ \mathrm {std}\circ \phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
is regular (i.e., the centralizer group in
 ${\mathrm {GL}}_{2n}({\mathbb {C}})$
is a torus) for every
${\mathrm {GL}}_{2n}({\mathbb {C}})$
is a torus) for every
 $y\in \mathcal V_{\infty }$
.
$y\in \mathcal V_{\infty }$
. -
(disc-∞) If n is odd, then
 $[E:F]=2$
. If n is even, then
$[E:F]=2$
. If n is even, then
 $E=F$
.
$E=F$
.
Since E is either F or a CM quadratic extension of F, condition (disc-
![]() $\infty $
) is equivalent to requiring
$\infty $
) is equivalent to requiring
![]() ${\mathrm {SO}}^{E/F}_{2n}(F_y)$
to admit discrete series at all infinite places y of F (or equivalently, to admit compact maximal tori). Condition (std-reg
${\mathrm {SO}}^{E/F}_{2n}(F_y)$
to admit discrete series at all infinite places y of F (or equivalently, to admit compact maximal tori). Condition (std-reg
![]() $^{\circ }$
), when (coh
$^{\circ }$
), when (coh
![]() $^{\circ }$
) is imposed, amounts to requiring that
$^{\circ }$
) is imposed, amounts to requiring that
![]() $\mathrm {std} \circ (\rho _{{\mathrm {SO}}} +\lambda (\xi ^{\flat }_y))$
should be a regular cocharacter of
$\mathrm {std} \circ (\rho _{{\mathrm {SO}}} +\lambda (\xi ^{\flat }_y))$
should be a regular cocharacter of
![]() ${\mathrm {GL}}_{2n}$
for every
${\mathrm {GL}}_{2n}$
for every
![]() $y\in \mathcal V_{\infty }$
, since
$y\in \mathcal V_{\infty }$
, since
![]() $\phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
encodes the infinitesimal character of
$\phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
encodes the infinitesimal character of
![]() $\pi _y$
according to [Reference Vogan78, Prop. 7.4].
$\pi _y$
according to [Reference Vogan78, Prop. 7.4].
When v is a prime of F, write
![]() $\phi _{\pi ^{\flat }_v} \colon W_{F_{\mathfrak {q}}} \rightarrow {}^L {\mathrm {SO}}^{E/F}_{2n}$
for the L-parameter of
$\phi _{\pi ^{\flat }_v} \colon W_{F_{\mathfrak {q}}} \rightarrow {}^L {\mathrm {SO}}^{E/F}_{2n}$
for the L-parameter of
![]() $\pi ^{\flat }_v$
as given by [Reference Arthur1, Thm 1.5.1]. (By the Langlands quotient theorem,
$\pi ^{\flat }_v$
as given by [Reference Arthur1, Thm 1.5.1]. (By the Langlands quotient theorem,
![]() $\pi ^{\flat }_v$
is the unique quotient of an induced representation from a character twist of a tempered representation on a Levi subgroup. Apply Arthur’s theorem to this tempered representation.) Note that
$\pi ^{\flat }_v$
is the unique quotient of an induced representation from a character twist of a tempered representation on a Levi subgroup. Apply Arthur’s theorem to this tempered representation.) Note that
![]() $\phi _{\pi ^{\flat }_v}$
is well-defined only up to
$\phi _{\pi ^{\flat }_v}$
is well-defined only up to
![]() $\mathrm {O}_{2n}({\mathbb {C}})$
-conjugacy in loc. cit. (This does not matter for the statement of (SO-i) in Theorem 6.5 below.)
$\mathrm {O}_{2n}({\mathbb {C}})$
-conjugacy in loc. cit. (This does not matter for the statement of (SO-i) in Theorem 6.5 below.)
Let
![]() $\mathrm {Unr}(\pi ^{\flat })$
denote the set of finite primes
$\mathrm {Unr}(\pi ^{\flat })$
denote the set of finite primes
![]() ${{\mathfrak q}}$
of F such that
${{\mathfrak q}}$
of F such that
![]() ${{\mathfrak q}}$
is unramified in E and
${{\mathfrak q}}$
is unramified in E and
![]() $\pi ^{\flat }_{\mathfrak {q}}$
is unramified. In this case, the unramified L-parameter
$\pi ^{\flat }_{\mathfrak {q}}$
is unramified. In this case, the unramified L-parameter
![]() $\phi _{\pi ^{\flat }_{\mathfrak {q}}}$
is determined (up to
$\phi _{\pi ^{\flat }_{\mathfrak {q}}}$
is determined (up to
![]() $\mathrm {SO}_{2n}({\mathbb {C}})$
-conjugacy, not just up to outer automorphism) by the Satake isomorphism.
$\mathrm {SO}_{2n}({\mathbb {C}})$
-conjugacy, not just up to outer automorphism) by the Satake isomorphism.
Thanks to Arthur, we can lift
![]() $\pi ^{\flat }$
to an automorphic representation of
$\pi ^{\flat }$
to an automorphic representation of
![]() ${\mathrm {GL}}_{2n}$
as follows. The Hecke character
${\mathrm {GL}}_{2n}$
as follows. The Hecke character
![]() $F^{\times }\backslash \mathbb A_F^{\times } \rightarrow \{\pm 1\}$
corresponding to the Galois character
$F^{\times }\backslash \mathbb A_F^{\times } \rightarrow \{\pm 1\}$
corresponding to the Galois character
![]() $\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}=\{\pm 1\}$
is still denoted
$\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}=\{\pm 1\}$
is still denoted
![]() $\chi _{E/F}$
. Let
$\chi _{E/F}$
. Let
![]() $\chi _{E/F,{{\mathfrak q}}}$
denote its local component at
$\chi _{E/F,{{\mathfrak q}}}$
denote its local component at
![]() ${{\mathfrak q}}$
.
${{\mathfrak q}}$
.
Proposition 6.1 (Arthur)
Assume that
![]() $\pi ^{\flat }$
satisfies (St
$\pi ^{\flat }$
satisfies (St
![]() $^{\circ }$
). Then there exists a self-dual automorphic representation
$^{\circ }$
). Then there exists a self-dual automorphic representation
![]() $\pi ^{\sharp }$
of
$\pi ^{\sharp }$
of
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
, which is either cuspidal or the isobaric sum of two cuspidal self-dual representations of
${\mathrm {GL}}_{2n}(\mathbb A_F)$
, which is either cuspidal or the isobaric sum of two cuspidal self-dual representations of
![]() ${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
![]() ${\mathrm {GL}}_1(\mathbb A_F)$
, such that
${\mathrm {GL}}_1(\mathbb A_F)$
, such that
-
(Ar1)
 $\pi ^{\sharp }_{\mathfrak {q}}$
is unramified at every
$\pi ^{\sharp }_{\mathfrak {q}}$
is unramified at every
 ${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
.
${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
. -
(Ar2)
 $\pi ^{\sharp }_{{{{\mathfrak q}}_{\mathrm {St}}}} \simeq \mathrm {St}_{2n-1} \boxplus \chi _{E/F,{{{\mathfrak q}}_{\mathrm {St}}}}$
up to a quadratic character of
$\pi ^{\sharp }_{{{{\mathfrak q}}_{\mathrm {St}}}} \simeq \mathrm {St}_{2n-1} \boxplus \chi _{E/F,{{{\mathfrak q}}_{\mathrm {St}}}}$
up to a quadratic character of
 ${\mathrm {GL}}_{2n}(\mathbb A_F)$
.
${\mathrm {GL}}_{2n}(\mathbb A_F)$
. -
(Ar3)
 $\phi _{\pi ^{\sharp }_v} \simeq \mathrm {std} \circ \phi _{\pi ^{\flat }_v}$
at every F-place v.
$\phi _{\pi ^{\sharp }_v} \simeq \mathrm {std} \circ \phi _{\pi ^{\flat }_v}$
at every F-place v.
If
![]() $\pi ^{\flat }$
satisfies both (St
$\pi ^{\flat }$
satisfies both (St
![]() $^{\circ }$
) and (coh
$^{\circ }$
) and (coh
![]() $^{\circ }$
), then we furthermore have
$^{\circ }$
), then we furthermore have
-
(Ar4)
 $\pi ^{\sharp }_y$
and
$\pi ^{\sharp }_y$
and
 $\pi ^{\flat }_y$
are tempered for all infinite F-places y.
$\pi ^{\flat }_y$
are tempered for all infinite F-places y.
If
![]() $\pi ^{\flat }$
has properties (coh
$\pi ^{\flat }$
has properties (coh
![]() $^{\circ }$
), (St
$^{\circ }$
), (St
![]() $^{\circ }$
), and (std-reg
$^{\circ }$
), and (std-reg
![]() $^{\circ }$
), then the following strengthening holds:
$^{\circ }$
), then the following strengthening holds:
-
(Ar4)+
 $\pi ^{\sharp }_v$
and
$\pi ^{\sharp }_v$
and
 $\pi ^{\flat }_v$
are tempered for all F-places v.
$\pi ^{\flat }_v$
are tempered for all F-places v.
Remark 6.2. In fact, (Ar1) is implied by (Ar3) since
![]() $\phi _{\pi ^{\flat }_{\mathfrak {q}}}$
is an unramified parameter at every
$\phi _{\pi ^{\flat }_{\mathfrak {q}}}$
is an unramified parameter at every
![]() ${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
, but we state (Ar1) to make (SO-ii) below more transparent.
${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
, but we state (Ar1) to make (SO-ii) below more transparent.
Proof. Consider
![]() $\pi ^{\flat }$
satisfying (St
$\pi ^{\flat }$
satisfying (St
![]() $^{\circ }$
). For notational convenience, we assume
$^{\circ }$
). For notational convenience, we assume
![]() $\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}^{\flat } \simeq \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
(not just up to a quadratic character twist) as the general case works in the same way. By [Reference Arthur1, Thm. 1.5.2] (using the notation there),Footnote 9 we have a formal global parameter
$\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}^{\flat } \simeq \mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
(not just up to a quadratic character twist) as the general case works in the same way. By [Reference Arthur1, Thm. 1.5.2] (using the notation there),Footnote 9 we have a formal global parameter
![]() $\psi $
(as in [Reference Arthur1, 1.4]) such that
$\psi $
(as in [Reference Arthur1, 1.4]) such that
![]() $\pi ^{\flat }_v$
appears as a subquotient of a member of the packet
$\pi ^{\flat }_v$
appears as a subquotient of a member of the packet
![]() $\tilde {\Pi }(\psi _v)$
at every place v of F, where
$\tilde {\Pi }(\psi _v)$
at every place v of F, where
![]() $\psi _v$
denotes the localization of
$\psi _v$
denotes the localization of
![]() $\psi $
at v as in loc. cit. (A priori, members of
$\psi $
at v as in loc. cit. (A priori, members of
![]() $\tilde {\Pi }(\psi _v)$
may be reducible due to possible failure of the generalized Ramanujan conjecture. Only from the argument below it follows that
$\tilde {\Pi }(\psi _v)$
may be reducible due to possible failure of the generalized Ramanujan conjecture. Only from the argument below it follows that
![]() $\psi $
is a generic parameter (i.e., its
$\psi $
is a generic parameter (i.e., its
![]() ${\mathrm {SU}}(2)$
-part is trivial). Then
${\mathrm {SU}}(2)$
-part is trivial). Then
![]() $\tilde {\Pi }(\psi _v)$
consists of irreducible representations by [Reference Xu81, Appendix A].)
$\tilde {\Pi }(\psi _v)$
consists of irreducible representations by [Reference Xu81, Appendix A].)
Since
![]() $\mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
appears as a subquotient of a member of
$\mathrm {St}_{{\mathrm {SO}},{{{\mathfrak q}}_{\mathrm {St}}}}$
appears as a subquotient of a member of
![]() $\tilde {\Pi }(\psi _{{{{\mathfrak q}}_{\mathrm {St}}}})$
, Proposition B.1 implies that
$\tilde {\Pi }(\psi _{{{{\mathfrak q}}_{\mathrm {St}}}})$
, Proposition B.1 implies that
![]() $\psi _{{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \psi _{\mathrm {St},{{{\mathfrak q}}_{\mathrm {St}}}}$
, where
$\psi _{{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \psi _{\mathrm {St},{{{\mathfrak q}}_{\mathrm {St}}}}$
, where
![]() $\psi _{\mathrm {St}}$
is defined above that proposition. Thus,
$\psi _{\mathrm {St}}$
is defined above that proposition. Thus,
where
![]() $\psi _{\mathrm {St}_{2n-1},{{{\mathfrak q}}_{\mathrm {St}}}}$
(resp.
$\psi _{\mathrm {St}_{2n-1},{{{\mathfrak q}}_{\mathrm {St}}}}$
(resp.
![]() $\psi _{\mathbf 1,{{{\mathfrak q}}_{\mathrm {St}}}}$
) denotes the A-parameter for the Steinberg (resp. trivial) representation
$\psi _{\mathbf 1,{{{\mathfrak q}}_{\mathrm {St}}}}$
) denotes the A-parameter for the Steinberg (resp. trivial) representation
![]() $\mathrm {St}_{2n-1}$
of
$\mathrm {St}_{2n-1}$
of
![]() ${\mathrm {GL}}_{2n-1}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
(resp.
${\mathrm {GL}}_{2n-1}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
(resp.
![]() ${\mathrm {GL}}_{1}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
). It follows that either
${\mathrm {GL}}_{1}(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
). It follows that either
![]() $\psi =\pi ^{\#}$
or
$\psi =\pi ^{\#}$
or
![]() $\psi =\pi ^{\#}_1\boxplus \pi ^{\#}_2$
, where
$\psi =\pi ^{\#}_1\boxplus \pi ^{\#}_2$
, where
![]() $\pi ^{\#}$
,
$\pi ^{\#}$
,
![]() $\pi ^{\#}_1$
, and
$\pi ^{\#}_1$
, and
![]() $\pi ^{\#}_2$
are cuspidal self-dual automorphic representations of
$\pi ^{\#}_2$
are cuspidal self-dual automorphic representations of
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
,
${\mathrm {GL}}_{2n}(\mathbb A_F)$
,
![]() ${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
![]() ${\mathrm {GL}}_1(\mathbb A_F)$
, respectively. In the second case, we take
${\mathrm {GL}}_1(\mathbb A_F)$
, respectively. In the second case, we take
![]() $\pi ^{\#}$
to be the isobaric sum of
$\pi ^{\#}$
to be the isobaric sum of
![]() $\pi ^{\#}_1$
and
$\pi ^{\#}_1$
and
![]() $\pi ^{\#}_2$
. Now (Ar2) follows from (6.3). We define
$\pi ^{\#}_2$
. Now (Ar2) follows from (6.3). We define
![]() $\phi _{{\mathfrak q}}\in \tilde {\Phi }({\mathrm {SO}}^{E/F}_{2n,F_{\mathfrak {q}}})$
as the restriction of
$\phi _{{\mathfrak q}}\in \tilde {\Phi }({\mathrm {SO}}^{E/F}_{2n,F_{\mathfrak {q}}})$
as the restriction of
![]() $\psi _{{\mathfrak q}}\in \tilde {\Psi }({\mathrm {SO}}^{E/F}_{2n,F_{\mathfrak {q}}})$
from
$\psi _{{\mathfrak q}}\in \tilde {\Psi }({\mathrm {SO}}^{E/F}_{2n,F_{\mathfrak {q}}})$
from
![]() ${\mathcal L}_{F_{\mathfrak {q}}}\times {\mathrm {SU}}(2)$
to
${\mathcal L}_{F_{\mathfrak {q}}}\times {\mathrm {SU}}(2)$
to
![]() ${\mathcal L}_{F_{\mathfrak {q}}}$
. Then Properties (Ar1) and (Ar3) with
${\mathcal L}_{F_{\mathfrak {q}}}$
. Then Properties (Ar1) and (Ar3) with
![]() $\phi _{\mathfrak {q}}$
in place of
$\phi _{\mathfrak {q}}$
in place of
![]() $\phi _{\pi _{\mathfrak {q}}^{\flat }}$
are part of Arthur’s result already cited.
$\phi _{\pi _{\mathfrak {q}}^{\flat }}$
are part of Arthur’s result already cited.
To complete the proof of (Ar1) and (Ar3), it suffices to verify that
![]() $\phi _v = \phi _{\pi _v^{\flat }}$
in
$\phi _v = \phi _{\pi _v^{\flat }}$
in
![]() $\tilde {\Phi }(G_{F_v})$
. In the notation of [Reference Arthur1] (between Theorems 1.5.1 and 1.5.2),
$\tilde {\Phi }(G_{F_v})$
. In the notation of [Reference Arthur1] (between Theorems 1.5.1 and 1.5.2),
![]() $\phi _v$
gives rise to
$\phi _v$
gives rise to
-
• a
 $F_v$
-rational parabolic subgroup
$F_v$
-rational parabolic subgroup
 $P_v\subset G_{F_v}$
with a Levi factor
$P_v\subset G_{F_v}$
with a Levi factor
 $M_v$
,
$M_v$
, -
• a bounded parameter
 $\phi _{M_v}\in \tilde {\Phi }(M_v)$
,
$\phi _{M_v}\in \tilde {\Phi }(M_v)$
, -
• a point
 $\lambda $
in the open chamber for
$\lambda $
in the open chamber for
 $P_v$
in
$P_v$
in
 $X_*(M_v)_{F_v}\otimes _{\mathbb {Z}} {\mathbb R}$
,
$X_*(M_v)_{F_v}\otimes _{\mathbb {Z}} {\mathbb R}$
,
such that
![]() $\phi _v$
comes from the
$\phi _v$
comes from the
![]() $\lambda $
-twist
$\lambda $
-twist
![]() $\phi _{M_v,\lambda }$
of
$\phi _{M_v,\lambda }$
of
![]() $\phi _{M_v}$
. (This is the counterpart of the Langlands quotient construction for L-parameters.) The statement of [Reference Arthur1, Thm. 1.5.2] tells us that
$\phi _{M_v}$
. (This is the counterpart of the Langlands quotient construction for L-parameters.) The statement of [Reference Arthur1, Thm. 1.5.2] tells us that
![]() $\pi ^{\flat }_v$
is a subrepresentation of the normalized induction
$\pi ^{\flat }_v$
is a subrepresentation of the normalized induction
![]() $\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
for some
$\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
for some
![]() $\sigma _v\in \tilde {\Pi }(M_v)$
, where
$\sigma _v\in \tilde {\Pi }(M_v)$
, where
![]() $\sigma _{v,\lambda }$
denotes the
$\sigma _{v,\lambda }$
denotes the
![]() $\lambda $
-twist of
$\lambda $
-twist of
![]() $\sigma _v$
, since
$\sigma _v$
, since
![]() $\pi ^{\flat }_v$
appears in the packet of
$\pi ^{\flat }_v$
appears in the packet of
![]() $\psi _v$
in loc. cit. According to the same theorem,
$\psi _v$
in loc. cit. According to the same theorem,
![]() $\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
must be completely reducible since it appears in the
$\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
must be completely reducible since it appears in the
![]() $L^2$
-discrete spectrum. This means that
$L^2$
-discrete spectrum. This means that
![]() $\pi ^{\flat }_v$
is irreducible and the Langlands quotient of
$\pi ^{\flat }_v$
is irreducible and the Langlands quotient of
![]() $\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
(thus,
$\mathrm {Ind}^{G(F_v)}_{P_v(F_v)}(\sigma _{v,\lambda })$
(thus,
![]() $\pi ^{\flat }_v$
is isomorphic to the latter). Since the formation of Langlands parametrization is compatible with the Langlands quotient, it follows that
$\pi ^{\flat }_v$
is isomorphic to the latter). Since the formation of Langlands parametrization is compatible with the Langlands quotient, it follows that
![]() $\phi _v$
is the L-parameter of
$\phi _v$
is the L-parameter of
![]() $\pi _v^{\flat }$
, namely, that
$\pi _v^{\flat }$
, namely, that
![]() $\phi _v=\phi _{\pi _v^{\flat }}$
.
$\phi _v=\phi _{\pi _v^{\flat }}$
.
It remains to check (Ar4) and (Ar4)+. Assume (coh
![]() $^{\circ }$
) in addition to (St
$^{\circ }$
) in addition to (St
![]() $^{\circ }$
). Thanks to (Ar3),
$^{\circ }$
). Thanks to (Ar3),
![]() $\pi ^{\#}$
is L-algebraic since L-algebraicity is preserved by
$\pi ^{\#}$
is L-algebraic since L-algebraicity is preserved by
![]() $\mathrm {std}$
. Applying [Reference Clozel18, Lem. 4.9] to
$\mathrm {std}$
. Applying [Reference Clozel18, Lem. 4.9] to
![]() $\pi ^{\#}\otimes |\det |^{1/2}$
if
$\pi ^{\#}\otimes |\det |^{1/2}$
if
![]() $\pi ^{\#}$
is cuspidal, and
$\pi ^{\#}$
is cuspidal, and
![]() $\pi ^{\#}_1$
and
$\pi ^{\#}_1$
and
![]() $\pi ^{\#}_2$
otherwise, to deduce that
$\pi ^{\#}_2$
otherwise, to deduce that
![]() $\pi ^{\#}_v$
is essentially tempered at all
$\pi ^{\#}_v$
is essentially tempered at all
![]() $y|\infty $
. Since
$y|\infty $
. Since
![]() $\pi ^{\#}$
is self-dual,
$\pi ^{\#}$
is self-dual,
![]() $\pi ^{\#}_y$
are a fortiori tempered. Now suppose furthermore that
$\pi ^{\#}_y$
are a fortiori tempered. Now suppose furthermore that
![]() $\pi ^{\flat }_y$
has property (std-reg
$\pi ^{\flat }_y$
has property (std-reg
![]() $^{\circ }$
). Then
$^{\circ }$
). Then
![]() $\pi ^{\#}$
is regular L-algebraic. Arguing as above but applying [Reference Caraiani13, Thm. 1.2] to
$\pi ^{\#}$
is regular L-algebraic. Arguing as above but applying [Reference Caraiani13, Thm. 1.2] to
![]() $\pi ^{\#}$
at finite places, in place of [Reference Clozel18, Lem. 4.9] at infinite places, we deduce (Ar4)+. Finally, whenever
$\pi ^{\#}$
at finite places, in place of [Reference Clozel18, Lem. 4.9] at infinite places, we deduce (Ar4)+. Finally, whenever
![]() $\pi ^{\#}_v$
is tempered (for finite or infinite v), this implies that
$\pi ^{\#}_v$
is tempered (for finite or infinite v), this implies that
![]() $\psi _v$
is bounded and hence that
$\psi _v$
is bounded and hence that
![]() $\pi ^{\flat }_v$
is tempered by [Reference Arthur1, Thm. 1.5.1].
$\pi ^{\flat }_v$
is tempered by [Reference Arthur1, Thm. 1.5.1].
Corollary 6.3. Assume (disc-
![]() $\infty $
). If
$\infty $
). If
![]() $\pi ^{\flat }$
satisfies (St
$\pi ^{\flat }$
satisfies (St
![]() $^{\circ }$
) and (coh
$^{\circ }$
) and (coh
![]() $^{\circ }$
), then
$^{\circ }$
), then
![]() $\pi ^{\flat }_y$
is a discrete series representation for every infinite place y.
$\pi ^{\flat }_y$
is a discrete series representation for every infinite place y.
Proof. The condition (disc-
![]() $\infty $
) guarantees that
$\infty $
) guarantees that
![]() ${\mathrm {SO}}_{2n}^{E/F}(F_y)$
contains an elliptic maximal torus at infinite places y so that it admits discrete series. In this case, a tempered
${\mathrm {SO}}_{2n}^{E/F}(F_y)$
contains an elliptic maximal torus at infinite places y so that it admits discrete series. In this case, a tempered
![]() $\xi $
-cohomological representation is a discrete series representation by [Reference Borel and Wallach8, Thm. III.5.1]. Thus, the corollary follows from (Ar4) of the preceding proposition.
$\xi $
-cohomological representation is a discrete series representation by [Reference Borel and Wallach8, Thm. III.5.1]. Thus, the corollary follows from (Ar4) of the preceding proposition.
Under the assumptions of the corollary, let us describe
![]() $\phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
explicitly. Fix an
$\phi _{\pi ^{\flat }_y}|_{W_{\overline {F}_y}}$
explicitly. Fix an
![]() ${\mathbb R}$
-isomorphism
${\mathbb R}$
-isomorphism
![]() $\overline {F}_y\simeq {\mathbb {C}}$
once and for all, so that we can identify
$\overline {F}_y\simeq {\mathbb {C}}$
once and for all, so that we can identify
![]() $W_{\overline {F}_y}={\mathbb {C}}^{\times }$
. We noted that the infinitesimal character of
$W_{\overline {F}_y}={\mathbb {C}}^{\times }$
. We noted that the infinitesimal character of
![]() $\xi ^{\flat }_y$
is
$\xi ^{\flat }_y$
is
![]() $\rho _{{\mathrm {SO}}}+\lambda (\xi _y^{\flat })$
. The half sum of positive coroots
$\rho _{{\mathrm {SO}}}+\lambda (\xi _y^{\flat })$
. The half sum of positive coroots
![]() $\rho _{{\mathrm {SO}}}\in X_*(\mathrm {T}_{{\mathrm {SO}}})$
is equal to
$\rho _{{\mathrm {SO}}}\in X_*(\mathrm {T}_{{\mathrm {SO}}})$
is equal to
![]() $(n-1)e_1+(n-2)e_2+\cdots +e_{n-1}$
. It follows from the construction of discrete series L-packets in [Reference Langlands53, p.134] that possibly after
$(n-1)e_1+(n-2)e_2+\cdots +e_{n-1}$
. It follows from the construction of discrete series L-packets in [Reference Langlands53, p.134] that possibly after
![]() ${\mathrm {SO}}^{E/F}_{2n}({\mathbb {C}})$
-conjugation, we have
${\mathrm {SO}}^{E/F}_{2n}({\mathbb {C}})$
-conjugation, we have
Continue to assume (St
![]() $^{\circ }$
) and (coh
$^{\circ }$
) and (coh
![]() $^{\circ }$
) for
$^{\circ }$
) for
![]() $\pi ^{\flat }$
as well as (disc-
$\pi ^{\flat }$
as well as (disc-
![]() $\infty $
). We noted that
$\infty $
). We noted that
![]() $\pi ^{\flat }$
is L-algebraic thanks to (coh
$\pi ^{\flat }$
is L-algebraic thanks to (coh
![]() $^{\circ }$
). Then Conjecture 1 predicts the existence of an
$^{\circ }$
). Then Conjecture 1 predicts the existence of an
![]() $^L {\mathrm {SO}}^{E/F}_{2n}$
-valued Galois representation attached to
$^L {\mathrm {SO}}^{E/F}_{2n}$
-valued Galois representation attached to
![]() $\pi ^{\flat }$
. When (std-reg
$\pi ^{\flat }$
. When (std-reg
![]() $^{\circ }$
) is also assumed, Theorem 6.5 below proves the conjecture modulo outer automorphisms in that (SO-i) is weaker than what is predicted. (This is to be upgraded by (SO-i+) in §13; also see Remark 13.2.) The proof is carried out by reducing to the known results for
$^{\circ }$
) is also assumed, Theorem 6.5 below proves the conjecture modulo outer automorphisms in that (SO-i) is weaker than what is predicted. (This is to be upgraded by (SO-i+) in §13; also see Remark 13.2.) The proof is carried out by reducing to the known results for
![]() $\pi ^{\#}$
on
$\pi ^{\#}$
on
![]() ${\mathrm {GL}}_{2n}$
. We will get to the theorem after observing that (disc-
${\mathrm {GL}}_{2n}$
. We will get to the theorem after observing that (disc-
![]() $\infty $
) is automatically satisfied under the additional hypothesis (std-reg
$\infty $
) is automatically satisfied under the additional hypothesis (std-reg
![]() $^{\circ }$
); this observation is related to (SO-v) of the theorem.
$^{\circ }$
); this observation is related to (SO-v) of the theorem.
Lemma 6.4. Suppose there exists a cuspidal automorphic representation
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
such that (St
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
such that (St
![]() $^{\circ }$
),(coh
$^{\circ }$
),(coh
![]() $^{\circ }$
) and (std-reg
$^{\circ }$
) and (std-reg
![]() $^{\circ }$
) hold. Then (disc-
$^{\circ }$
) hold. Then (disc-
![]() $\infty $
) is satisfied.Footnote 10
$\infty $
) is satisfied.Footnote 10
Proof. For each
![]() $y\in \mathcal V_{\infty }$
, Proposition 6.1 tells us that
$y\in \mathcal V_{\infty }$
, Proposition 6.1 tells us that
![]() $\phi _{\pi ^{\flat }_y}$
is tempered. From this and (coh
$\phi _{\pi ^{\flat }_y}$
is tempered. From this and (coh
![]() $^{\circ }$
), we obtain a decomposition of the form
$^{\circ }$
), we obtain a decomposition of the form
where
![]() $\chi _{a_i}: {\mathbb {C}}^{\times } \rightarrow {\mathbb {C}}^{\times }$
is given by
$\chi _{a_i}: {\mathbb {C}}^{\times } \rightarrow {\mathbb {C}}^{\times }$
is given by
![]() $z\mapsto (z/\overline z)^{a_i} $
using the identification
$z\mapsto (z/\overline z)^{a_i} $
using the identification
![]() $W_{\overline {F}_y}={\mathbb {C}}^{\times }$
above, and
$W_{\overline {F}_y}={\mathbb {C}}^{\times }$
above, and
![]() $\omega _{i'}$
is a quadratic character of
$\omega _{i'}$
is a quadratic character of
![]() $W_{F_y}$
. (In fact,
$W_{F_y}$
. (In fact,
![]() $a_i$
are mutually distinct.) By the dimension reason,
$a_i$
are mutually distinct.) By the dimension reason,
![]() $|I'|$
is even. However, (std-reg
$|I'|$
is even. However, (std-reg
![]() $^{\circ }$
) implies that
$^{\circ }$
) implies that
![]() $|I'|\le 1$
. Hence,
$|I'|\le 1$
. Hence,
![]() $I'$
is empty and
$I'$
is empty and
![]() $|I|=n$
. Now the image of
$|I|=n$
. Now the image of
![]() $j\in W_{F_y}$
in
$j\in W_{F_y}$
in
![]() ${\mathrm {GL}}_{2n}({\mathbb {C}})$
under
${\mathrm {GL}}_{2n}({\mathbb {C}})$
under
![]() $\mathrm {std}\circ \phi _{\pi ^{\flat }_y}$
has determinant
$\mathrm {std}\circ \phi _{\pi ^{\flat }_y}$
has determinant
![]() $(-1)^n$
since the determinant of j is
$(-1)^n$
since the determinant of j is
![]() $-1$
in each induced representation. In view of (6.2), we deduce that
$-1$
in each induced representation. In view of (6.2), we deduce that
![]() $E=F$
if n is even and
$E=F$
if n is even and
![]() $E\neq F$
otherwise. That is, (disc-
$E\neq F$
otherwise. That is, (disc-
![]() $\infty $
) holds true.
$\infty $
) holds true.
Theorem 6.5. Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (coh
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (coh
![]() $^{\circ }$
), (St
$^{\circ }$
), (St
![]() $^{\circ }$
) and (std-reg
$^{\circ }$
) and (std-reg
![]() $^{\circ }$
). Then there exists a semisimple Galois representation (depending on
$^{\circ }$
). Then there exists a semisimple Galois representation (depending on
![]() $\iota $
)
$\iota $
)
whose restriction to
![]() $\Gamma _{F_{\mathfrak {q}}}$
at every F-place
$\Gamma _{F_{\mathfrak {q}}}$
at every F-place
![]() ${{\mathfrak q}}|\ell $
is potentially semistable, such that the following hold. Here,
${{\mathfrak q}}|\ell $
is potentially semistable, such that the following hold. Here,
![]() $\overset {\circ } \sim $
means
$\overset {\circ } \sim $
means
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy.
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy.
-
(SO-i) For every finite F-place
 ${{\mathfrak q}}$
(including
${{\mathfrak q}}$
(including
 ${{\mathfrak q}}|\ell $
), in the convention of §1, we have
${{\mathfrak q}}|\ell $
), in the convention of §1, we have  $$ \begin{align*}\iota \phi_{\pi^{\flat}_{\mathfrak{q}}} \overset {\circ} \sim \mathrm{WD}(\rho_{\pi^{\flat}}|_{\Gamma_{F_{\mathfrak{q}}}})^{\mathrm{F-ss}}. \end{align*} $$
$$ \begin{align*}\iota \phi_{\pi^{\flat}_{\mathfrak{q}}} \overset {\circ} \sim \mathrm{WD}(\rho_{\pi^{\flat}}|_{\Gamma_{F_{\mathfrak{q}}}})^{\mathrm{F-ss}}. \end{align*} $$
-
(SO-ii) Let
 ${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
. If
${{\mathfrak q}} \in \mathrm {Unr}(\pi ^{\flat })$
. If
 ${{\mathfrak q}} \nmid \ell $
, then
${{\mathfrak q}} \nmid \ell $
, then
 $\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is unramified at
$\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is unramified at
 ${{\mathfrak q}}$
, and for all eigenvalues
${{\mathfrak q}}$
, and for all eigenvalues
 $\alpha $
of
$\alpha $
of
 $\mathrm {std}(\rho _{\pi ^{\flat }}(\mathrm {Frob}_{\mathfrak {q}}))_{\mathrm {ss}}$
and all embeddings
$\mathrm {std}(\rho _{\pi ^{\flat }}(\mathrm {Frob}_{\mathfrak {q}}))_{\mathrm {ss}}$
and all embeddings
 $\overline {\mathbb {Q}}_{\ell } \hookrightarrow {\mathbb {C}}$
we have
$\overline {\mathbb {Q}}_{\ell } \hookrightarrow {\mathbb {C}}$
we have
 $|\alpha | = 1$
.
$|\alpha | = 1$
. -
(SO-iii) For each
 ${{\mathfrak q}} | \ell $
, and for each
${{\mathfrak q}} | \ell $
, and for each
 $y \colon F \hookrightarrow {\mathbb {C}}$
such that
$y \colon F \hookrightarrow {\mathbb {C}}$
such that
 $\iota y$
induces
$\iota y$
induces
 ${{\mathfrak q}}$
, we have
${{\mathfrak q}}$
, we have
 $\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y) \overset {\circ } \sim \iota \mu _{\mathrm {Hodge}}(\xi ^{\flat }, y)$
.
$\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y) \overset {\circ } \sim \iota \mu _{\mathrm {Hodge}}(\xi ^{\flat }, y)$
. -
(SO-iv) If
 $\pi ^{\flat }_{\mathfrak {q}}$
is unramified at
$\pi ^{\flat }_{\mathfrak {q}}$
is unramified at
 ${{\mathfrak q}} | \ell $
, then
${{\mathfrak q}} | \ell $
, then
 $\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is crystalline. If
$\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is crystalline. If
 $\pi ^{\flat }_{\mathfrak {q}}$
has a nonzero Iwahori fixed vector at
$\pi ^{\flat }_{\mathfrak {q}}$
has a nonzero Iwahori fixed vector at
 ${{\mathfrak q}} | \ell $
, then
${{\mathfrak q}} | \ell $
, then
 $\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is semistable.
$\rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is semistable. -
(SO-v)
 $\rho _{\pi ^{\flat }}$
is totally odd. More explicitly, for each real place y of F and the corresponding complex conjugation
$\rho _{\pi ^{\flat }}$
is totally odd. More explicitly, for each real place y of F and the corresponding complex conjugation
 $c_y\in \Gamma _F$
(well-defined up to conjugacy),
$c_y\in \Gamma _F$
(well-defined up to conjugacy),  $$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim \begin{cases} {\mathrm{diag}}(\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2},\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), & n:\mbox{even},\\ {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1) \rtimes c, & n:\mbox{odd}. \end{cases}. \end{align*} $$
$$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim \begin{cases} {\mathrm{diag}}(\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2},\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), & n:\mbox{even},\\ {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1) \rtimes c, & n:\mbox{odd}. \end{cases}. \end{align*} $$
Condition (SO-i) characterizes
![]() $\rho _{\pi ^{\flat }}$
uniquely up to
$\rho _{\pi ^{\flat }}$
uniquely up to
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
Remark 6.6. Since
![]() $\pi ^{\flat }_{\infty }$
is a discrete series representation, the conjugation by
$\pi ^{\flat }_{\infty }$
is a discrete series representation, the conjugation by
![]() $\phi _{\pi ^{\flat }_y}(j)$
on
$\phi _{\pi ^{\flat }_y}(j)$
on
![]() $\mathrm {T}_{{\mathrm {SO}}}$
is the inverse map, where j denotes the usual element of the real Weil group. Thus, (SO-v) and (6.4) imply Buzzard–Gee’s prediction on the image of complex conjugation in [Reference Buzzard and Gee12, Conj. 3.2.1, 3.2.2]. When n is odd, we also observe that (SO-v) is equivalent to
$\mathrm {T}_{{\mathrm {SO}}}$
is the inverse map, where j denotes the usual element of the real Weil group. Thus, (SO-v) and (6.4) imply Buzzard–Gee’s prediction on the image of complex conjugation in [Reference Buzzard and Gee12, Conj. 3.2.1, 3.2.2]. When n is odd, we also observe that (SO-v) is equivalent to
 $$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},a,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},a^{-1}) \rtimes c,\quad \forall a\in \overline{\mathbb{Q}}_{\ell}^{\times}. \end{align*} $$
$$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},a,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},a^{-1}) \rtimes c,\quad \forall a\in \overline{\mathbb{Q}}_{\ell}^{\times}. \end{align*} $$
Remark 6.7. Without (St
![]() $^{\circ }$
), an analogous theorem can be proved only under (coh
$^{\circ }$
), an analogous theorem can be proved only under (coh
![]() $^{\circ }$
) and (std-reg), but in a weaker and less precise form. The strategy is similar: transfer
$^{\circ }$
) and (std-reg), but in a weaker and less precise form. The strategy is similar: transfer
![]() $\pi ^{\flat }$
to a regular algebraic automorphic representation of
$\pi ^{\flat }$
to a regular algebraic automorphic representation of
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
, which is an isobaric sum of cuspidal self-dual automorphic representations, and apply the known results on associating Galois representations.
${\mathrm {GL}}_{2n}(\mathbb A_F)$
, which is an isobaric sum of cuspidal self-dual automorphic representations, and apply the known results on associating Galois representations.
Proof of Theorem 6.5
Let
![]() $\pi ^{\#}$
be as in Proposition 6.1 so that
$\pi ^{\#}$
be as in Proposition 6.1 so that
-
Case 1:
 $\pi ^{\#}$
is cuspidal or
$\pi ^{\#}$
is cuspidal or -
Case 2:
 $\pi ^{\#}=\pi ^{\#}_1\boxplus \pi ^{\#}_2$
, with
$\pi ^{\#}=\pi ^{\#}_1\boxplus \pi ^{\#}_2$
, with
 $\pi ^{\#}_1$
(resp.
$\pi ^{\#}_1$
(resp.
 $\pi ^{\#}_2$
) a cuspidal automorphic representation of
$\pi ^{\#}_2$
) a cuspidal automorphic representation of
 ${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
(resp.
${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
(resp.
 ${\mathrm {GL}}_1(\mathbb A_F)$
).
${\mathrm {GL}}_1(\mathbb A_F)$
).
As in the proof there, we know that
![]() $\pi ^{\#}$
is L-algebraic.
$\pi ^{\#}$
is L-algebraic.
In Case 1, consider the C-algebraic twist
![]() $\Pi := \pi ^{\sharp } \otimes |\det |^{(1 - 2n)/2}$
, which is regular by (std-reg), and essentially self-dual (“essentially” means up to a character twist). Applying the well-known construction of Galois representations (see [Reference Barnet-Lamb, Gee, Geraghty and Taylor3, Thm. 2.1.1] for a summary and further references) to
$\Pi := \pi ^{\sharp } \otimes |\det |^{(1 - 2n)/2}$
, which is regular by (std-reg), and essentially self-dual (“essentially” means up to a character twist). Applying the well-known construction of Galois representations (see [Reference Barnet-Lamb, Gee, Geraghty and Taylor3, Thm. 2.1.1] for a summary and further references) to
![]() $\Pi $
, we obtain a semisimple Galois representation (recall
$\Pi $
, we obtain a semisimple Galois representation (recall
![]() $\Gamma =\Gamma _F$
by convention)
$\Gamma =\Gamma _F$
by convention)
satisfying the obvious analogues of properties (SO-i) through (SO-iv) for
![]() ${\mathrm {GL}}_{2n}$
, with
${\mathrm {GL}}_{2n}$
, with
![]() $\rho _{\Pi }$
and
$\rho _{\Pi }$
and
![]() ${\mathrm {GL}}_{2n}$
in place of
${\mathrm {GL}}_{2n}$
in place of
![]() $\rho _{\pi ^{\flat }}$
and
$\rho _{\pi ^{\flat }}$
and
![]() $\mathrm {O}_{2n}$
; call these analogues (GL-i), …, (GL-iv). By “obvious”, we mean, for instance, that (GL-ii) is about the eigenvalues of
$\mathrm {O}_{2n}$
; call these analogues (GL-i), …, (GL-iv). By “obvious”, we mean, for instance, that (GL-ii) is about the eigenvalues of
![]() $\rho _{\Pi }(\mathrm {Frob}_{\mathfrak {q}})$
having absolute value 1. We also spell out (GL-i), which states that
$\rho _{\Pi }(\mathrm {Frob}_{\mathfrak {q}})$
having absolute value 1. We also spell out (GL-i), which states that
In particular, for all
![]() ${{\mathfrak q}}\in \mathrm {Unr}(\pi ^{\flat })$
, since
${{\mathfrak q}}\in \mathrm {Unr}(\pi ^{\flat })$
, since
![]() $\Pi _{\mathfrak {q}}$
is unramified by (Ar1), we see that
$\Pi _{\mathfrak {q}}$
is unramified by (Ar1), we see that
![]() $\rho _{\Pi }$
is unramified at
$\rho _{\Pi }$
is unramified at
![]() ${{\mathfrak q}}$
as well and that
${{\mathfrak q}}$
as well and that
Since each
![]() $\pi ^{\#}_{\mathfrak {q}}$
is self-dual, we see that
$\pi ^{\#}_{\mathfrak {q}}$
is self-dual, we see that
![]() $\rho _{\Pi }$
is self-dual. By (Ar2) and (6.5) at
$\rho _{\Pi }$
is self-dual. By (Ar2) and (6.5) at
![]() ${{\mathfrak q}} ={{{\mathfrak q}}_{\mathrm {St}}}$
as well as semisimplicity of
${{\mathfrak q}} ={{{\mathfrak q}}_{\mathrm {St}}}$
as well as semisimplicity of
![]() $\rho _{\Pi }$
, we see that either
$\rho _{\Pi }$
, we see that either
-
•
 $\rho _{\Pi }$
is irreducible, or
$\rho _{\Pi }$
is irreducible, or -
•
 $\rho _{\Pi }=\rho _1\oplus \rho _2$
for self-dual irreducible subrepresentations
$\rho _{\Pi }=\rho _1\oplus \rho _2$
for self-dual irreducible subrepresentations
 $\rho _1$
and
$\rho _1$
and
 $\rho _2$
with
$\rho _2$
with
 $\dim \rho _1 = n-1$
and
$\dim \rho _1 = n-1$
and
 $\dim \rho _2 = 1$
.
$\dim \rho _2 = 1$
.
Either way, it follows from [Reference Bellaïche and Chenevier6, Cor. 1.3] that every irreducible constituent of
![]() $\rho _{\Pi }$
is orthogonal in the sense of loc. cit. (As we are in Case 1, apply their corollary with
$\rho _{\Pi }$
is orthogonal in the sense of loc. cit. (As we are in Case 1, apply their corollary with
![]() $\eta = |\cdot |^{2n-1}$
, in which case
$\eta = |\cdot |^{2n-1}$
, in which case
![]() $\eta _{\lambda }(c) = -1$
in their notation.)
$\eta _{\lambda }(c) = -1$
in their notation.)
Now we turn to Case 2. Take
![]() $\Pi _1 := \pi ^{\#}_1|\det |^{1-n}$
and
$\Pi _1 := \pi ^{\#}_1|\det |^{1-n}$
and
![]() $\Pi _2 := \pi ^{\#}_2$
. Each of
$\Pi _2 := \pi ^{\#}_2$
. Each of
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
is cuspidal, regular C-algebraic and essentially self-dual, so the same construction yields
$\Pi _2$
is cuspidal, regular C-algebraic and essentially self-dual, so the same construction yields
![]() $\rho _{\Pi _1}$
and
$\rho _{\Pi _1}$
and
![]() $\rho _{\Pi _2}$
, which are
$\rho _{\Pi _2}$
, which are
![]() $2n-1$
and
$2n-1$
and
![]() $1$
-dimensional, respectively. Then put
$1$
-dimensional, respectively. Then put
![]() $\rho _{\Pi } := \rho _{\Pi _1} \oplus \rho _{\Pi _2}$
. As before, (GL-i), …, (GL-iv) hold true for
$\rho _{\Pi } := \rho _{\Pi _1} \oplus \rho _{\Pi _2}$
. As before, (GL-i), …, (GL-iv) hold true for
![]() $\rho _{\Pi }$
. Moreover, an argument as in Case 1 shows that
$\rho _{\Pi }$
. Moreover, an argument as in Case 1 shows that
![]() $\rho _{\Pi _1}$
and
$\rho _{\Pi _1}$
and
![]() $\rho _{\Pi _2}$
are self-dual and orthogonal. It follows from (Ar2) and (6.5) at
$\rho _{\Pi _2}$
are self-dual and orthogonal. It follows from (Ar2) and (6.5) at
![]() $v={{{\mathfrak q}}_{\mathrm {St}}}$
that
$v={{{\mathfrak q}}_{\mathrm {St}}}$
that
![]() $\rho _{\Pi _1}$
and
$\rho _{\Pi _1}$
and
![]() $\rho _{\Pi _2}$
are irreducible.
$\rho _{\Pi _2}$
are irreducible.
From here on, we treat the two cases together. Since
![]() $\rho _{\Pi }$
is self-dual and orthogonal, after conjugating
$\rho _{\Pi }$
is self-dual and orthogonal, after conjugating
![]() $\rho _{\Pi }$
by an element of
$\rho _{\Pi }$
by an element of
![]() ${\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
, we can ensure that
${\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
, we can ensure that
![]() $\rho _{\Pi }(\Gamma )\subset \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Write
$\rho _{\Pi }(\Gamma )\subset \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Write
for the
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-valued representation that
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-valued representation that
![]() $\rho _{\Pi }$
factors through. (In case
$\rho _{\Pi }$
factors through. (In case
![]() $\rho _{\Pi }$
is reducible, we even have
$\rho _{\Pi }$
is reducible, we even have
![]() $\rho _{\Pi }(\Gamma )\subset (\mathrm {O}_{2n-1}\times \mathrm {O}_1)(\overline {\mathbb {Q}}_{\ell })$
.) Let us check that this is the desired Galois representation and deduce properties (SO-i) through (SO-v) from (GL-i) through (GL-iv).
$\rho _{\Pi }(\Gamma )\subset (\mathrm {O}_{2n-1}\times \mathrm {O}_1)(\overline {\mathbb {Q}}_{\ell })$
.) Let us check that this is the desired Galois representation and deduce properties (SO-i) through (SO-v) from (GL-i) through (GL-iv).
We start with the case
![]() $E=F$
. Then
$E=F$
. Then
![]() $\phi _{\pi ^{\flat }_v}(\mathrm {Frob}_{\mathfrak {q}})\in {\mathrm {SO}}_{2n}({\mathbb {C}})$
in (6.6), so we deduce via the Chebotarev density theorem that
$\phi _{\pi ^{\flat }_v}(\mathrm {Frob}_{\mathfrak {q}})\in {\mathrm {SO}}_{2n}({\mathbb {C}})$
in (6.6), so we deduce via the Chebotarev density theorem that
![]() $\rho _{\pi ^{\flat }}$
has image in
$\rho _{\pi ^{\flat }}$
has image in
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Note that (GL-ii) is the same statement as (SO-ii). The Hodge-theoretic properties at
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Note that (GL-ii) is the same statement as (SO-ii). The Hodge-theoretic properties at
![]() $\ell $
in (SO-iii) and (SO-iv) may be checked after composing with a faithful representation, so these properties hold. One sees from [Reference Kret and Shin50, Appendix B] (for
$\ell $
in (SO-iii) and (SO-iv) may be checked after composing with a faithful representation, so these properties hold. One sees from [Reference Kret and Shin50, Appendix B] (for
![]() $\mathrm {O}_{2n}$
) that (GL-i) implies (SO-i). (Alternatively, one can appeal to [Reference Gan, Gross and Prasad26, Thm. 8.1].) The assertion on the cocharacters in (SO-iii) also follows (GL-iii) that the two cocharacters become conjugate in
$\mathrm {O}_{2n}$
) that (GL-i) implies (SO-i). (Alternatively, one can appeal to [Reference Gan, Gross and Prasad26, Thm. 8.1].) The assertion on the cocharacters in (SO-iii) also follows (GL-iii) that the two cocharacters become conjugate in
![]() ${\mathrm {GL}}_{2n}$
.
${\mathrm {GL}}_{2n}$
.
We now prove (SO-v), namely, that
![]() $\rho _{\pi ^{\flat }}$
is totally odd. The following claim
$\rho _{\pi ^{\flat }}$
is totally odd. The following claim
-
(E) The element
 $\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))\in {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has eigenvalues
$\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))\in {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has eigenvalues
 $1$
and
$1$
and
 $-1$
with multiplicity n each, for every
$-1$
with multiplicity n each, for every
 $y\in \mathcal V_{\infty }$
$y\in \mathcal V_{\infty }$
follows from [Reference Caraiani and Le Hung14] (in fact, it can also be deduced from Taïbi’s theorem [Reference Taïbi76, Thm. 6.3.4] when
![]() $\pi ^{\sharp }$
is cuspidal, and from Taylor [Reference Taylor77, Prop. A] when
$\pi ^{\sharp }$
is cuspidal, and from Taylor [Reference Taylor77, Prop. A] when
![]() $\pi ^{\sharp }$
is not cuspidal).
$\pi ^{\sharp }$
is not cuspidal).
As
![]() $\rho _{\pi ^{\flat }}(c_y)\in {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has order 2, we have
$\rho _{\pi ^{\flat }}(c_y)\in {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has order 2, we have
 $$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{a_y},\underbrace{-1,\ldots,-1}_{b_y},\underbrace{1,\ldots,1}_{a_y},\underbrace{-1,\ldots,-1}_{b_y}),\quad a_y+b_y=n, \quad a_y,b_y\in \mathbb Z_{\ge0}. \end{align*} $$
$$ \begin{align*}\rho_{\pi^{\flat}}(c_y)\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{a_y},\underbrace{-1,\ldots,-1}_{b_y},\underbrace{1,\ldots,1}_{a_y},\underbrace{-1,\ldots,-1}_{b_y}),\quad a_y+b_y=n, \quad a_y,b_y\in \mathbb Z_{\ge0}. \end{align*} $$
So (E) implies that
![]() $a_y=b_y$
; this is possible as n is even, which follows from Lemma 6.4 and the running assumption that
$a_y=b_y$
; this is possible as n is even, which follows from Lemma 6.4 and the running assumption that
![]() $E=F$
. Now one computes the adjoint action of
$E=F$
. Now one computes the adjoint action of
![]() $\rho _{\pi ^{\flat }}(c_y)$
on
$\rho _{\pi ^{\flat }}(c_y)$
on
![]() $\mathrm {Lie}\, {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
to be
$\mathrm {Lie}\, {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
to be
![]() $-n$
. (A similar computation is done in the proof of [Reference Kret and Shin50, Lem. 1.9] for
$-n$
. (A similar computation is done in the proof of [Reference Kret and Shin50, Lem. 1.9] for
![]() $\mathrm {GSp}_{2n}$
.) Thus,
$\mathrm {GSp}_{2n}$
.) Thus,
![]() $\rho _{\pi ^{\flat }}$
is totally odd.
$\rho _{\pi ^{\flat }}$
is totally odd.
It remains to treat the case
![]() $E\neq F$
. In this case, the standard embedding
$E\neq F$
. In this case, the standard embedding
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F} \hookrightarrow {\mathrm {GL}}_{2n}$
identifies
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F} \hookrightarrow {\mathrm {GL}}_{2n}$
identifies
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F} \stackrel {\sim }{\to } \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. The composition of
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F} \stackrel {\sim }{\to } \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. The composition of
![]() $\rho _{\pi ^{\flat }}$
with this isomorphism is still to be denoted by
$\rho _{\pi ^{\flat }}$
with this isomorphism is still to be denoted by
![]() $\rho _{\pi ^{\flat }}$
. Since
$\rho _{\pi ^{\flat }}$
. Since
![]() $\phi _{\pi ^{\flat }_{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}}) \in \mathrm {O}_{2n}({\mathbb {C}})\backslash {\mathrm {SO}}_{2n}({\mathbb {C}})$
(resp.
$\phi _{\pi ^{\flat }_{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}}) \in \mathrm {O}_{2n}({\mathbb {C}})\backslash {\mathrm {SO}}_{2n}({\mathbb {C}})$
(resp.
![]() $\phi _{\pi ^{\flat }_y}(\mathrm {Frob}_{\mathfrak {q}})\in {\mathrm {SO}}_{2n}({\mathbb {C}})$
) in (6.6) when
$\phi _{\pi ^{\flat }_y}(\mathrm {Frob}_{\mathfrak {q}})\in {\mathrm {SO}}_{2n}({\mathbb {C}})$
) in (6.6) when
![]() ${{\mathfrak q}}$
is inert (resp. split) in E by the unramified Langlands correspondence, we see that
${{\mathfrak q}}$
is inert (resp. split) in E by the unramified Langlands correspondence, we see that
commutes with the natural projections onto
![]() $\Gamma _{E/F}$
. (By continuity, it suffices to check the commutativity on Frobenius conjugacy classes.) Thus,
$\Gamma _{E/F}$
. (By continuity, it suffices to check the commutativity on Frobenius conjugacy classes.) Thus,
![]() $\rho _{\pi ^{\flat }}$
is a Galois representation valued in
$\rho _{\pi ^{\flat }}$
is a Galois representation valued in
![]() ${}^L ({\mathrm {SO}}^{E/F}_{2n})$
. Properties (SO-i) through (SO-iv) follow from (GL-i) through (GL-iv) in the same way as for the
${}^L ({\mathrm {SO}}^{E/F}_{2n})$
. Properties (SO-i) through (SO-iv) follow from (GL-i) through (GL-iv) in the same way as for the
![]() $E=F$
case.
$E=F$
case.
We now prove (SO-v). The argument for claim (E) still applies, and since n is odd by Lemma 6.4, we have
 $$ \begin{align} &\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{\frac{n-1}{2}}, \underbrace{-1,\ldots,-1}_{\frac{n+1}{2}},\underbrace{1,\ldots,1}_{\frac{n-1}{2}}, \underbrace{-1,\ldots,-1}_{\frac{n+1}{2}})\cdot \mathrm{std}(c) \quad\mbox{in}~~{\mathrm{GL}}_{2n}(\overline{\mathbb{Q}}_{\ell}). \end{align} $$
$$ \begin{align} &\sim {\mathrm{diag}}(\underbrace{1,\ldots,1}_{\frac{n-1}{2}}, \underbrace{-1,\ldots,-1}_{\frac{n+1}{2}},\underbrace{1,\ldots,1}_{\frac{n-1}{2}}, \underbrace{-1,\ldots,-1}_{\frac{n+1}{2}})\cdot \mathrm{std}(c) \quad\mbox{in}~~{\mathrm{GL}}_{2n}(\overline{\mathbb{Q}}_{\ell}). \end{align} $$
(Recall that
![]() $\mathrm {std}(c)=\vartheta ^{\circ }$
is the
$\mathrm {std}(c)=\vartheta ^{\circ }$
is the
![]() $2n\times 2n$
permutation matrix switching n and
$2n\times 2n$
permutation matrix switching n and
![]() $2n$
.) Therefore,
$2n$
.) Therefore,
 $$ \begin{align*}\rho_{\pi^{\flat}}(c_y)~\sim~{\mathrm{diag}}(\underbrace{1,\ldots,1}_{\frac{n-1}{2}},\underbrace{-1,\ldots,-1}_{\frac{n+1}{2}},\underbrace{1,\ldots,1}_{\frac{n-1}{2}},\underbrace{-1,\ldots,-1}_{\frac{n+1}{2}}) \rtimes c\quad\mbox{in}~~{}^L {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}). \end{align*} $$
$$ \begin{align*}\rho_{\pi^{\flat}}(c_y)~\sim~{\mathrm{diag}}(\underbrace{1,\ldots,1}_{\frac{n-1}{2}},\underbrace{-1,\ldots,-1}_{\frac{n+1}{2}},\underbrace{1,\ldots,1}_{\frac{n-1}{2}},\underbrace{-1,\ldots,-1}_{\frac{n+1}{2}}) \rtimes c\quad\mbox{in}~~{}^L {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}). \end{align*} $$
From this, it follows that the adjoint action of
![]() $\rho _{\pi ^{\flat }}(c_y)$
on
$\rho _{\pi ^{\flat }}(c_y)$
on
![]() $\mathrm {Lie}\, {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has trace equal to
$\mathrm {Lie}\, {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
has trace equal to
![]() $-n$
. Hence,
$-n$
. Hence,
![]() $\rho _{\pi ^{\flat }}$
is totally odd.
$\rho _{\pi ^{\flat }}$
is totally odd.
The following corollary allows us to apply Proposition 5.5 to identify the Zariski closure of the image of
![]() $\rho _{\pi ^{\flat }}$
.
$\rho _{\pi ^{\flat }}$
.
Corollary 6.8. In the setup of Theorem 6.5, the image of
![]() $\rho _{\pi ^{\flat }}$
(thus also
$\rho _{\pi ^{\flat }}$
(thus also
![]() $\rho _{\pi ^{\flat }}(\Gamma _E)$
contains a regular unipotent element of
$\rho _{\pi ^{\flat }}(\Gamma _E)$
contains a regular unipotent element of
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
.
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
.
Proof. Suppose that
![]() ${{{\mathfrak q}}_{\mathrm {St}}}\nmid \ell $
. Then
${{{\mathfrak q}}_{\mathrm {St}}}\nmid \ell $
. Then
![]() $\iota \phi _{\pi ^{\flat }_{{{\mathfrak q}}_{\mathrm {St}}}}\overset {\circ } \sim \mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}})^{\mathrm {F-ss}}$
by (SO-i), where the two sides are compared through [Reference Gross and Reeder28, Prop. 2.2] by the convention of §1. Since
$\iota \phi _{\pi ^{\flat }_{{{\mathfrak q}}_{\mathrm {St}}}}\overset {\circ } \sim \mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}})^{\mathrm {F-ss}}$
by (SO-i), where the two sides are compared through [Reference Gross and Reeder28, Prop. 2.2] by the convention of §1. Since
![]() $\phi _{\pi ^{\flat }_{{{\mathfrak q}}_{\mathrm {St}}}}$
contains a regular unipotent element in the image, so does
$\phi _{\pi ^{\flat }_{{{\mathfrak q}}_{\mathrm {St}}}}$
contains a regular unipotent element in the image, so does
![]() $\mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}})$
. Therefore,
$\mathrm {WD}(\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}})$
. Therefore,
![]() $\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}}$
has a regular unipotent in the image. If
$\rho _{\pi ^{\flat }}|_{\Gamma _{F_{{\mathfrak q}}}}$
has a regular unipotent in the image. If
![]() ${{{\mathfrak q}}_{\mathrm {St}}}|\ell $
, then the same is shown following the argument of [Reference Kret and Shin50, Lem. 3.2].
${{{\mathfrak q}}_{\mathrm {St}}}|\ell $
, then the same is shown following the argument of [Reference Kret and Shin50, Lem. 3.2].
The next corollary is solely about automorphic representations but proved by means of Galois representations. Interestingly, we do not know how to derive it within the theory of automorphic forms. The corollary is not needed in this paper, as (disc-
![]() $\infty $
) will be imposed in the main case of interest.
$\infty $
) will be imposed in the main case of interest.
Corollary 6.9. Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (coh
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying (coh
![]() $^{\circ }$
), (St
$^{\circ }$
), (St
![]() $^{\circ }$
), and (std-reg
$^{\circ }$
), and (std-reg
![]() $^{\circ }$
). If (disc-
$^{\circ }$
). If (disc-
![]() $\infty $
) is false (i.e., n is odd and
$\infty $
) is false (i.e., n is odd and
![]() $E=F$
, or n is even and
$E=F$
, or n is even and
![]() $[E:F]=2$
), then
$[E:F]=2$
), then
![]() $\pi ^{\#}$
in Proposition 6.1 (the functorial lift of
$\pi ^{\#}$
in Proposition 6.1 (the functorial lift of
![]() $\pi ^{\flat }$
to
$\pi ^{\flat }$
to
![]() ${\mathrm {GL}}_{2n}$
) is the isobaric sum of cuspidal self-dual automorphic representations of
${\mathrm {GL}}_{2n}$
) is the isobaric sum of cuspidal self-dual automorphic representations of
![]() ${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
${\mathrm {GL}}_{2n-1}(\mathbb A_F)$
and
![]() ${\mathrm {GL}}_1(\mathbb A_F)$
.
${\mathrm {GL}}_1(\mathbb A_F)$
.
Proof. Fix a real place y of F. Up to conjugation, we may assume that
where the latter
![]() $c_y$
means its image in
$c_y$
means its image in
![]() $\Gamma _{E/F}$
; so
$\Gamma _{E/F}$
; so
![]() $\mathrm {std}(c_y)=1$
if
$\mathrm {std}(c_y)=1$
if
![]() $E=F$
and
$E=F$
and
![]() $\mathrm {std}(c_y)=\vartheta ^{\circ }$
if
$\mathrm {std}(c_y)=\vartheta ^{\circ }$
if
![]() $[E:F] = 2$
. The proof of Theorem 6.5 shows that
$[E:F] = 2$
. The proof of Theorem 6.5 shows that
![]() $\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))\in {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is odd for every real place y. That is,
$\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))\in {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is odd for every real place y. That is,
![]() $\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))$
has each of the eigenvalues 1 and
$\mathrm {std}(\rho _{\pi ^{\flat }}(c_y))$
has each of the eigenvalues 1 and
![]() $-1$
with multiplicity n. It is elementary to see that this is impossible when (disc-
$-1$
with multiplicity n. It is elementary to see that this is impossible when (disc-
![]() $\infty $
) is false. Indeed, if n is odd and
$\infty $
) is false. Indeed, if n is odd and
![]() $E=F$
, then the number of
$E=F$
, then the number of
![]() $1$
’s on the diagonal of
$1$
’s on the diagonal of
![]() $\rho _{\pi ^{\flat }}(c_y)$
is obviously even (so cannot equal n). If n is even and
$\rho _{\pi ^{\flat }}(c_y)$
is obviously even (so cannot equal n). If n is even and
![]() $[E:F]=2$
, this is elementary linear algebra.
$[E:F]=2$
, this is elementary linear algebra.
Remark 6.10. The corollary suggests that in that setup,
![]() $\pi ^{\flat }$
should come from an automorphic representation on
$\pi ^{\flat }$
should come from an automorphic representation on
![]() $\mathrm {Sp}_{2n-2}(\mathbb A_F)$
, where
$\mathrm {Sp}_{2n-2}(\mathbb A_F)$
, where
![]() $\mathrm {Sp}_{2n-2}$
is viewed as a twisted endoscopic group for
$\mathrm {Sp}_{2n-2}$
is viewed as a twisted endoscopic group for
![]() ${\mathrm {SO}}^{E/F}_{2n}$
(see the paragraph containing (1.2.5) in [Reference Arthur1]).
${\mathrm {SO}}^{E/F}_{2n}$
(see the paragraph containing (1.2.5) in [Reference Arthur1]).
If we assume (coh
![]() $^{\circ }$
) and (St
$^{\circ }$
) and (St
![]() $^{\circ }$
) but not (std-reg
$^{\circ }$
) but not (std-reg
![]() $^{\circ }$
), then some expected properties to be needed in our arguments are not known. We formulate them as a hypothesis so that our results become unconditional once the hypothesis is verified. (In the preceding arguments in this section, (std-reg
$^{\circ }$
), then some expected properties to be needed in our arguments are not known. We formulate them as a hypothesis so that our results become unconditional once the hypothesis is verified. (In the preceding arguments in this section, (std-reg
![]() $^{\circ }$
) allowed us to apply the results on the Ramanujan conjecture and construction of automorphic Galois representations for regular algebraic cuspidal automorphic representations of
$^{\circ }$
) allowed us to apply the results on the Ramanujan conjecture and construction of automorphic Galois representations for regular algebraic cuspidal automorphic representations of
![]() ${\mathrm {GL}}_n$
which are self-dual.)
${\mathrm {GL}}_n$
which are self-dual.)
Hypothesis 6.11. Assume (disc-
![]() $\infty $
). When
$\infty $
). When
![]() $\pi ^{\flat }$
satisfies (coh
$\pi ^{\flat }$
satisfies (coh
![]() $^{\circ }$
) and (St
$^{\circ }$
) and (St
![]() $^{\circ }$
) but not (std-reg
$^{\circ }$
) but not (std-reg
![]() $^{\circ }$
), the following hold true.
$^{\circ }$
), the following hold true.
-
(1)
 $\pi ^{\flat }_{\mathfrak {q}}$
is tempered at every finite prime
$\pi ^{\flat }_{\mathfrak {q}}$
is tempered at every finite prime
 ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
 $\pi ^{\flat }_{\mathfrak {q}}$
is unramified.
$\pi ^{\flat }_{\mathfrak {q}}$
is unramified. -
(2) There exists a semisimple Galois representation
 $\rho _{\pi ^{\flat }}:\Gamma _F \rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
satisfying (SO-i) at every
$\rho _{\pi ^{\flat }}:\Gamma _F \rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
satisfying (SO-i) at every
 ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
 $\pi ^{\flat }_{\mathfrak {q}}$
is unramified as well as (SO-iii), (SO-iv) and (SO-v). Moreover,
$\pi ^{\flat }_{\mathfrak {q}}$
is unramified as well as (SO-iii), (SO-iv) and (SO-v). Moreover,
 $\rho _{\pi ^{\flat }}(\Gamma _F)$
contains a regular unipotent element.
$\rho _{\pi ^{\flat }}(\Gamma _F)$
contains a regular unipotent element.
The hypothesis readily implies (SO-ii) for
![]() $\rho _{\pi ^{\flat }}$
. We expect that this hypothesis is accessible via suitable orthogonal Shimura varieties. If one is only interested in constructing the
$\rho _{\pi ^{\flat }}$
. We expect that this hypothesis is accessible via suitable orthogonal Shimura varieties. If one is only interested in constructing the
![]() $\mathrm {GSpin}_{2n}$
-valued representation
$\mathrm {GSpin}_{2n}$
-valued representation
![]() $\rho _{\pi }$
without proving its
$\rho _{\pi }$
without proving its
![]() $\ell $
-adic Hodge-theoretic properties, then (SO-iii) and (SO-iv) may be dropped from the hypothesis.
$\ell $
-adic Hodge-theoretic properties, then (SO-iii) and (SO-iv) may be dropped from the hypothesis.
Remark 6.12. Corollary 6.8 (or the above hypothesis, if (std-reg
![]() $^{\circ }$
) fails) tells us that the Zariski closure of
$^{\circ }$
) fails) tells us that the Zariski closure of
![]() $\rho _{\pi ^{\flat }}(\Gamma _F)$
belongs to the list of subgroups of
$\rho _{\pi ^{\flat }}(\Gamma _F)$
belongs to the list of subgroups of
![]() ${\mathrm {SO}}_{2n}$
in Proposition 5.5. In the list, the
${\mathrm {SO}}_{2n}$
in Proposition 5.5. In the list, the
![]() $\mathrm {PGL}_2$
,
$\mathrm {PGL}_2$
,
![]() $G_2$
and
$G_2$
and
![]() $\mathrm {PSO}_{2n-1}$
cases can only occur when (std-reg
$\mathrm {PSO}_{2n-1}$
cases can only occur when (std-reg
![]() $^{\circ }$
) is not satisfied. Since
$^{\circ }$
) is not satisfied. Since
![]() $\mathrm {PGL}_2$
and
$\mathrm {PGL}_2$
and
![]() $G_2$
are contained in
$G_2$
are contained in
![]() $\mathrm {PSO}_{2n-1}$
(up to conjugation), we only need to observe this for
$\mathrm {PSO}_{2n-1}$
(up to conjugation), we only need to observe this for
![]() $\mathrm {PSO}_{2n-1}$
. In this case,
$\mathrm {PSO}_{2n-1}$
. In this case,
![]() $\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y)$
of Theorem 6.5 must factor through
$\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y)$
of Theorem 6.5 must factor through
![]() $i^{\circ }_{std}:{\mathrm {SO}}_{2n-1}\hookrightarrow {\mathrm {SO}}_{2n}$
and thus cannot be regular as a cocharacter of
$i^{\circ }_{std}:{\mathrm {SO}}_{2n-1}\hookrightarrow {\mathrm {SO}}_{2n}$
and thus cannot be regular as a cocharacter of
![]() ${\mathrm {GL}}_{2n}$
. By (SO-iii) of the theorem,
${\mathrm {GL}}_{2n}$
. By (SO-iii) of the theorem,
![]() $\mathrm {std}(\mu _{\mathrm {Hodge}}(\xi ^{\flat },y))$
is not regular either, contradicting (std-reg
$\mathrm {std}(\mu _{\mathrm {Hodge}}(\xi ^{\flat },y))$
is not regular either, contradicting (std-reg
![]() $^{\circ }$
).
$^{\circ }$
).
7 Extension and restriction
In this section, we study how the local conditions (St), (coh) on a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(introduced in the introduction and §10 respectively) compare to conditions (
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(introduced in the introduction and §10 respectively) compare to conditions (
![]() $\mathrm {St}^{\circ }$
), (
$\mathrm {St}^{\circ }$
), (
![]() $\mathrm {Coh}^{\circ }$
) on an irreducible
$\mathrm {Coh}^{\circ }$
) on an irreducible
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation (given in §6).
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
-subrepresentation (given in §6).
Lemma 7.1. Let
![]() ${{\mathfrak q}}$
be a finite place of F. Let
${{\mathfrak q}}$
be a finite place of F. Let
![]() $\pi $
be an irreducible admissible representation of
$\pi $
be an irreducible admissible representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
, and let
${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
, and let
![]() $\pi ^{\flat } \subset \pi $
be an irreducible
$\pi ^{\flat } \subset \pi $
be an irreducible
![]() ${\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
-subrepresentation. Then
${\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
-subrepresentation. Then
![]() $\pi $
is a character twist of the Steinberg representation of
$\pi $
is a character twist of the Steinberg representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
if and only if
${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
if and only if
![]() $\pi ^{\flat }$
is a character twist of the Steinberg representation of
$\pi ^{\flat }$
is a character twist of the Steinberg representation of
![]() ${\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
.
${\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
.
Proof. Write
![]() $G = {\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
and
$G = {\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
and
![]() $G_0 = {\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
. To lighten notation, when H is an algebraic group over
$G_0 = {\mathrm {SO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
. To lighten notation, when H is an algebraic group over
![]() $F_{{\mathfrak q}}$
, we still write H for
$F_{{\mathfrak q}}$
, we still write H for
![]() $H(F_{{\mathfrak q}})$
in this proof when there is no danger of confusion.
$H(F_{{\mathfrak q}})$
in this proof when there is no danger of confusion.
(
![]() $\Rightarrow $
) Let
$\Rightarrow $
) Let
![]() $P \subset G$
be a parabolic subgroup, and write
$P \subset G$
be a parabolic subgroup, and write
![]() $C_P$
for the space of smooth functions on
$C_P$
for the space of smooth functions on
![]() $P \backslash G$
. Fixing a Borel subgroup B and taking
$P \backslash G$
. Fixing a Borel subgroup B and taking
![]() $P \supset B$
, we may view
$P \supset B$
, we may view
![]() $C_P \subset C_B$
as those functions on
$C_P \subset C_B$
as those functions on
![]() $G/B$
that are P-invariant. These spaces
$G/B$
that are P-invariant. These spaces
![]() $C_P$
define a (non-linear) filtration on
$C_P$
define a (non-linear) filtration on
![]() $C_B$
, and the Steinberg representation
$C_B$
, and the Steinberg representation
![]() $\mathrm {St}_G$
is the quotient of
$\mathrm {St}_G$
is the quotient of
![]() $C_B$
generated by all subrepresentations
$C_B$
generated by all subrepresentations
![]() $C_P$
with
$C_P$
with
![]() $P \subset G$
proper [Reference Borel and Wallach8, X.4.6]. There is a natural bijection between the parabolic subgroups of G with those of
$P \subset G$
proper [Reference Borel and Wallach8, X.4.6]. There is a natural bijection between the parabolic subgroups of G with those of
![]() $G_0$
by
$G_0$
by
![]() $P\mapsto P_0 := P\cap G_0$
. Applying loc. cit. now to
$P\mapsto P_0 := P\cap G_0$
. Applying loc. cit. now to
![]() $G_0$
, we take
$G_0$
, we take
![]() $B_0 := G_0 \cap B$
and consider the spaces
$B_0 := G_0 \cap B$
and consider the spaces
![]() $C_{B_0} \supset C_{P_0}$
for
$C_{B_0} \supset C_{P_0}$
for
![]() $B_0 \subset P_0 \subsetneq G_0$
and
$B_0 \subset P_0 \subsetneq G_0$
and
![]() $\mathrm {St}_{G_0}$
as before. The inclusion
$\mathrm {St}_{G_0}$
as before. The inclusion
![]() $G_0\hookrightarrow G$
induces an isomorphism
$G_0\hookrightarrow G$
induces an isomorphism
![]() $P_0 \backslash G_0 \overset \sim \to P \backslash G$
for each parabolic P (injectivity is clear; surjectivity can be seen by using the Bruhat decomposition, for instance). Thereby, we have a
$P_0 \backslash G_0 \overset \sim \to P \backslash G$
for each parabolic P (injectivity is clear; surjectivity can be seen by using the Bruhat decomposition, for instance). Thereby, we have a
![]() $G_0$
-equivariant filtration-preserving isomorphism
$G_0$
-equivariant filtration-preserving isomorphism
![]() $C_B\overset \sim \to C_{B_0}$
restricting to
$C_B\overset \sim \to C_{B_0}$
restricting to
![]() $C_P\overset \sim \to C_{P_0}$
for each P. Therefore,
$C_P\overset \sim \to C_{P_0}$
for each P. Therefore,
![]() $\mathrm {St}_G|_{G_0} \simeq \mathrm {St}_{G_0}$
.
$\mathrm {St}_G|_{G_0} \simeq \mathrm {St}_{G_0}$
.
(
![]() $\Leftarrow $
) Write
$\Leftarrow $
) Write
![]() $G' = \mathrm {GSpin}_{2n}^{E/F}(F_{\mathfrak {q}})$
and
$G' = \mathrm {GSpin}_{2n}^{E/F}(F_{\mathfrak {q}})$
and
![]() $G_0' = \mathrm {Spin}_{2n}^{E/F}(F_{\mathfrak {q}})$
. By abuse of notation, write
$G_0' = \mathrm {Spin}_{2n}^{E/F}(F_{\mathfrak {q}})$
. By abuse of notation, write
![]() $G_0/G^{\prime }_0:=\mathrm {coker}(\mathrm {pr}:G^{\prime }_0\rightarrow G_0)$
and likewise for
$G_0/G^{\prime }_0:=\mathrm {coker}(\mathrm {pr}:G^{\prime }_0\rightarrow G_0)$
and likewise for
![]() $G/G'$
. These are finite abelian groups. We claim that every smooth character
$G/G'$
. These are finite abelian groups. We claim that every smooth character
![]() $G_0 \to {\mathbb {C}}^{\times }$
extends to a smooth character
$G_0 \to {\mathbb {C}}^{\times }$
extends to a smooth character
![]() $G \to {\mathbb {C}}^{\times }$
. Since such characters factor through
$G \to {\mathbb {C}}^{\times }$
. Since such characters factor through
![]() $G_0/G^{\prime }_0$
and
$G_0/G^{\prime }_0$
and
![]() $G/G'$
, respectively (see e.g., [Reference Kret and Shin49, Cor. 2.6]) the claim would follow once we verify that
$G/G'$
, respectively (see e.g., [Reference Kret and Shin49, Cor. 2.6]) the claim would follow once we verify that
![]() $G_0/G^{\prime }_0\rightarrow G/G'$
is injective. So let
$G_0/G^{\prime }_0\rightarrow G/G'$
is injective. So let
![]() $g_0\in G_0$
and suppose that
$g_0\in G_0$
and suppose that
![]() $g_0=\mathrm {pr}(g)$
for
$g_0=\mathrm {pr}(g)$
for
![]() $g\in G'$
. Then
$g\in G'$
. Then
![]() $1=\mathrm {sim}(g_0)=\mathrm {sim}(\mathrm {pr}(g))=\mathcal N(g)^2$
by Lemma 3.1 (iii). If
$1=\mathrm {sim}(g_0)=\mathrm {sim}(\mathrm {pr}(g))=\mathcal N(g)^2$
by Lemma 3.1 (iii). If
![]() $\mathcal N(g)=-1$
, then we replace g with
$\mathcal N(g)=-1$
, then we replace g with
![]() $zg$
using
$zg$
using
![]() $z\in Z_{\mathrm {GSpin}}$
such that
$z\in Z_{\mathrm {GSpin}}$
such that
![]() $\mathcal N(z)=-1$
and
$\mathcal N(z)=-1$
and
![]() $\mathrm {pr}(z)=1$
(in the coordinates of Lemma 2.5, choose
$\mathrm {pr}(z)=1$
(in the coordinates of Lemma 2.5, choose
![]() $z=(1,-1)$
if n is odd, and
$z=(1,-1)$
if n is odd, and
![]() $z=(\zeta _4,-1)$
if n is even); so we may assume that
$z=(\zeta _4,-1)$
if n is even); so we may assume that
![]() $\mathcal N(g)=1$
. But this means that
$\mathcal N(g)=1$
. But this means that
![]() $g_0$
is trivial in
$g_0$
is trivial in
![]() $G_0/G^{\prime }_0$
. The claim has been proved.
$G_0/G^{\prime }_0$
. The claim has been proved.
Thanks to the claim, we may assume
![]() $\pi ^{\flat } = \mathrm {St}_{G_0}$
after twisting by a character. Since
$\pi ^{\flat } = \mathrm {St}_{G_0}$
after twisting by a character. Since
![]() $\pi |_{G_0}$
contains
$\pi |_{G_0}$
contains
![]() $\mathrm {St}_{G_0}$
, we can twist
$\mathrm {St}_{G_0}$
, we can twist
![]() $\pi $
such that the central character of
$\pi $
such that the central character of
![]() $\pi $
is trivial. (The central character is a character
$\pi $
is trivial. (The central character is a character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }/\{\pm 1\}$
, so there exists a smooth character
$F^{\times }/\{\pm 1\}$
, so there exists a smooth character
![]() $\chi ^{1/2}:F^{\times }\rightarrow {\mathbb {C}}^{\times }$
whose square is
$\chi ^{1/2}:F^{\times }\rightarrow {\mathbb {C}}^{\times }$
whose square is
![]() $\chi $
. Then we twist by
$\chi $
. Then we twist by
![]() $\mathrm {sim} \circ \chi ^{-1/2}$
.) By assumption,
$\mathrm {sim} \circ \chi ^{-1/2}$
.) By assumption,
where the first equality is from the implication (
![]() $\Rightarrow $
) and the second from the triviality of central characters. By Frobenius reciprocity, this realizes
$\Rightarrow $
) and the second from the triviality of central characters. By Frobenius reciprocity, this realizes
![]() $\pi $
as a constituent of
$\pi $
as a constituent of
![]() $\mathrm {Ind}^G_{Z(G)G_0} \mathrm {St}_G$
, which is the direct sum of twists of
$\mathrm {Ind}^G_{Z(G)G_0} \mathrm {St}_G$
, which is the direct sum of twists of
![]() $\mathrm {St}_G$
by characters of the finite abelian group
$\mathrm {St}_G$
by characters of the finite abelian group
![]() $G/Z(G)G_0$
.
$G/Z(G)G_0$
.
Let y be a real place of F so that
![]() $E_y/F_y={\mathbb {C}}/{\mathbb R}$
if n is odd and
$E_y/F_y={\mathbb {C}}/{\mathbb R}$
if n is odd and
![]() $E_y=F_y={\mathbb R}$
if n is even.
$E_y=F_y={\mathbb R}$
if n is even.
Lemma 7.2. Let
![]() $\pi $
be an irreducible admissible representation of
$\pi $
be an irreducible admissible representation of
![]() ${\mathrm {GSO}}_{2n}^{E_y/F_y}(F_y)$
with central character
${\mathrm {GSO}}_{2n}^{E_y/F_y}(F_y)$
with central character
![]() $\omega _{\pi }$
. Let
$\omega _{\pi }$
. Let
![]() $\pi ^{\flat }$
be an irreducible
$\pi ^{\flat }$
be an irreducible
![]() ${\mathrm {SO}}_{2n}^{E_y/F_y}(F_y)$
-subrepresentation. Let
${\mathrm {SO}}_{2n}^{E_y/F_y}(F_y)$
-subrepresentation. Let
![]() $\xi $
be an irreducible algebraic representation of
$\xi $
be an irreducible algebraic representation of
![]() ${\mathrm {GSO}}_{2n}^{E_y/F_y}$
, and
${\mathrm {GSO}}_{2n}^{E_y/F_y}$
, and
![]() $\xi ^{\flat }$
its pullback to
$\xi ^{\flat }$
its pullback to
![]() ${\mathrm {SO}}_{2n}^{E_y/F_y}$
. Then,
${\mathrm {SO}}_{2n}^{E_y/F_y}$
. Then,
-
(1) The representation
 $\pi $
is essentially unitary if and only if
$\pi $
is essentially unitary if and only if
 $\pi ^{\flat }$
is unitary.
$\pi ^{\flat }$
is unitary. -
(2) The representation
 $\pi $
is a discrete series representation if and only if
$\pi $
is a discrete series representation if and only if
 $\pi ^{\flat }$
is a discrete series representation.
$\pi ^{\flat }$
is a discrete series representation. -
(3) Assume
 $\pi $
is essentially unitary. Then
$\pi $
is essentially unitary. Then
 $\pi $
is
$\pi $
is
 $\xi $
-cohomological if and only if
$\xi $
-cohomological if and only if
 $\pi ^{\flat }$
is
$\pi ^{\flat }$
is
 $\xi ^{\flat }$
-cohomological and
$\xi ^{\flat }$
-cohomological and
 $\omega _{\pi }=\omega _{\xi }^{-1}$
, where
$\omega _{\pi }=\omega _{\xi }^{-1}$
, where
 $\omega _{\xi }$
is the central character of
$\omega _{\xi }$
is the central character of
 $\xi $
on
$\xi $
on
 $Z({\mathrm {GSO}}_{2n}^{E_y/F_y})(F_y)$
$Z({\mathrm {GSO}}_{2n}^{E_y/F_y})(F_y)$
Proof. Write
![]() $G = {\mathrm {GSO}}_{2n}^{E_y/F_y}(F_y)$
,
$G = {\mathrm {GSO}}_{2n}^{E_y/F_y}(F_y)$
,
![]() $G_0 = {\mathrm {SO}}_{2n}^{E_y/F_y}(F_y)$
and
$G_0 = {\mathrm {SO}}_{2n}^{E_y/F_y}(F_y)$
and
![]() $F_y^{\times }\subset G$
for the image of
$F_y^{\times }\subset G$
for the image of
![]() $\mathbb G_m(F_y)$
.
$\mathbb G_m(F_y)$
.
(1) The “only if” direction is obvious. For the “if” direction, assume
![]() $\pi ^{\flat }$
is unitary. We may assume
$\pi ^{\flat }$
is unitary. We may assume
![]() $\omega _{\pi } = 1$
. Choose a Hermitian form
$\omega _{\pi } = 1$
. Choose a Hermitian form
![]() $h( \cdot ,\cdot )$
on
$h( \cdot ,\cdot )$
on
![]() $\pi $
, extending the
$\pi $
, extending the
![]() $G_0$
-equivariant one on
$G_0$
-equivariant one on
![]() $\pi ^{\flat }$
. Choose representatives
$\pi ^{\flat }$
. Choose representatives
![]() $\{g_1, \ldots , g_r\}$
for the quotient
$\{g_1, \ldots , g_r\}$
for the quotient
![]() $G/F_y^{\times } G_0$
and define
$G/F_y^{\times } G_0$
and define
![]() $h'(\cdot , \cdot ) = \sum _{i=1}^r h(g_i \cdot , g_i \cdot )$
. Then
$h'(\cdot , \cdot ) = \sum _{i=1}^r h(g_i \cdot , g_i \cdot )$
. Then
![]() $h'(\cdot , \cdot )$
is a G-equivariant Hermitian form on
$h'(\cdot , \cdot )$
is a G-equivariant Hermitian form on
![]() $\pi $
.
$\pi $
.
(2) This follows directly from the characterization of discrete series representations through square-integrability (modulo center) of their matrix coefficients.
(3) This is implied by the fact that a unitary representation is cohomological if and only if its central character and infinitesimal character coincide with those of an algebraic representation. The “only if” direction is true without the unitarity condition by [Reference Borel and Wallach8, Thm. I.5.3.(ii)]. We explain the “if” direction in the case of interest. (This argument adapts to the general case.) For
![]() $G_0$
, this follows from [Reference Salamanca-Riba69, Thm. 1.8], which applies to connected semisimple real Lie groups. The case of G follows from that of
$G_0$
, this follows from [Reference Salamanca-Riba69, Thm. 1.8], which applies to connected semisimple real Lie groups. The case of G follows from that of
![]() $G_0$
, by applying [Reference Borel and Wallach8, Cor. I.6.6] to
$G_0$
, by applying [Reference Borel and Wallach8, Cor. I.6.6] to
![]() $\pi \otimes \xi $
by taking H there to be
$\pi \otimes \xi $
by taking H there to be
![]() $Z(G)$
, and similarly to
$Z(G)$
, and similarly to
![]() $(\pi |_{G_0})\otimes \xi ^{\flat }$
with
$(\pi |_{G_0})\otimes \xi ^{\flat }$
with
![]() $H=Z(G_0)$
.
$H=Z(G_0)$
.
8 Certain forms of
 ${\mathrm {GSO}}_{2n}$
and outer automorphisms
${\mathrm {GSO}}_{2n}$
and outer automorphisms
In this section, we introduce a certain form of the split group
![]() ${\mathrm {GSO}}_{2n}$
over a totally real field F, to be used to construct Shimura varieties. We start by considering real groups. Let
${\mathrm {GSO}}_{2n}$
over a totally real field F, to be used to construct Shimura varieties. We start by considering real groups. Let
![]() $\mathrm {GO}_{2n}^{\mathrm {cpt}}, \mathrm {O}_{2n}^{\mathrm {cpt}}, {\mathrm {SO}}_{2n}^{\mathrm {cpt}}, \mathrm {PSO}_{2n}^{\mathrm {cpt}}$
and
$\mathrm {GO}_{2n}^{\mathrm {cpt}}, \mathrm {O}_{2n}^{\mathrm {cpt}}, {\mathrm {SO}}_{2n}^{\mathrm {cpt}}, \mathrm {PSO}_{2n}^{\mathrm {cpt}}$
and
![]() ${\mathrm {GSO}}_{2n}^{\mathrm {cpt}}$
be the various versions of the orthogonal group defined by the quadratic form
${\mathrm {GSO}}_{2n}^{\mathrm {cpt}}$
be the various versions of the orthogonal group defined by the quadratic form
![]() $x_1^2 + x_2^2 + \cdots + x_{2n}^2$
on
$x_1^2 + x_2^2 + \cdots + x_{2n}^2$
on
![]() ${\mathbb R}^{2n}$
. Consider the matrix
${\mathbb R}^{2n}$
. Consider the matrix
![]() $J = \left ( \begin {smallmatrix} 0 & {-1_n} \cr {1_n} & 0 \end {smallmatrix} \right ) \in {\mathrm {SO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
. We define the group
$J = \left ( \begin {smallmatrix} 0 & {-1_n} \cr {1_n} & 0 \end {smallmatrix} \right ) \in {\mathrm {SO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
. We define the group
![]() ${\mathrm {GSO}}_{2n}^J$
over
${\mathrm {GSO}}_{2n}^J$
over
![]() ${\mathbb R}$
to be the inner form of
${\mathbb R}$
to be the inner form of
![]() ${\mathrm {GSO}}_{2n,{\mathbb R}}^{\mathrm {cpt}}$
obtained by conjugating the
${\mathrm {GSO}}_{2n,{\mathbb R}}^{\mathrm {cpt}}$
obtained by conjugating the
![]() ${\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})$
-action by J (using that
${\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})$
-action by J (using that
![]() $J^2$
is central). Namely, for all
$J^2$
is central). Namely, for all
![]() ${\mathbb R}$
-algebras R, we have
${\mathbb R}$
-algebras R, we have
For
![]() $g \in {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb {C}} \otimes _{{\mathbb R}} R)$
, we have
$g \in {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb {C}} \otimes _{{\mathbb R}} R)$
, we have
![]() $g^{\mathrm {t}} J \overline g = \mathrm {sim}(g) J$
if and only if
$g^{\mathrm {t}} J \overline g = \mathrm {sim}(g) J$
if and only if
![]() $J \overline g J^{-1} = g$
, and thus
$J \overline g J^{-1} = g$
, and thus
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R})$
is the group of matrices
${\mathrm {GSO}}_{2n}^J({\mathbb R})$
is the group of matrices
![]() $g \in {\mathrm {GL}}_{2n}({\mathbb {C}})$
preserving the forms
$g \in {\mathrm {GL}}_{2n}({\mathbb {C}})$
preserving the forms
 $$ \begin{align} \begin{cases} x_1^2 + x_2^2 + \cdots + x_{2n}^2 \cr -x_1 \overline x_{n+1} + x_{n+1} \overline x_1 - x_2 \overline x_{n+2} + x_{n+2} \overline x_2 - \cdots - x_n \overline x_{2n} + x_{2n} \overline x_n \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} x_1^2 + x_2^2 + \cdots + x_{2n}^2 \cr -x_1 \overline x_{n+1} + x_{n+1} \overline x_1 - x_2 \overline x_{n+2} + x_{n+2} \overline x_2 - \cdots - x_n \overline x_{2n} + x_{2n} \overline x_n \end{cases} \end{align} $$
up to the scalar
![]() $\mathrm {sim}(g) \in {\mathbb R}^{\times }$
(the scalar is required to be the same for both forms), and such that g satisfies the condition
$\mathrm {sim}(g) \in {\mathbb R}^{\times }$
(the scalar is required to be the same for both forms), and such that g satisfies the condition
![]() $\det (g) = \mathrm {sim}(g)^n$
.
$\det (g) = \mathrm {sim}(g)^n$
.
Similarly, we define the inner forms
![]() $\mathrm {GO}_{2n}^J, {\mathrm {SO}}_{2n}^J, \mathrm {O}_{2n}^J, \mathrm {PSO}_{2n}^J$
of
$\mathrm {GO}_{2n}^J, {\mathrm {SO}}_{2n}^J, \mathrm {O}_{2n}^J, \mathrm {PSO}_{2n}^J$
of
![]() $\mathrm {GO}_{2n}^{\mathrm {cpt}}, {\mathrm {SO}}_{2n}^{\mathrm {cpt}}, \mathrm {O}_{2n}^{\mathrm {cpt}}, \mathrm {PSO}_{2n}^{\mathrm {cpt}}$
. Then
$\mathrm {GO}_{2n}^{\mathrm {cpt}}, {\mathrm {SO}}_{2n}^{\mathrm {cpt}}, \mathrm {O}_{2n}^{\mathrm {cpt}}, \mathrm {PSO}_{2n}^{\mathrm {cpt}}$
. Then
![]() ${\mathrm {SO}}_{2n}^J({\mathbb R})$
is the real Lie group which is often denoted
${\mathrm {SO}}_{2n}^J({\mathbb R})$
is the real Lie group which is often denoted
![]() ${\mathrm {SO}}^{*}(2n)$
in the literature (e.g., [Reference Helgason36, Sect. X.2, p.445]). Note that
${\mathrm {SO}}^{*}(2n)$
in the literature (e.g., [Reference Helgason36, Sect. X.2, p.445]). Note that
![]() ${\mathrm {SO}}_{2n}^J({\mathbb R})$
is not isomorphic to any of the classical groups
${\mathrm {SO}}_{2n}^J({\mathbb R})$
is not isomorphic to any of the classical groups
![]() ${\mathrm {SO}}(p, q)$
, where
${\mathrm {SO}}(p, q)$
, where
![]() $2n = p + q$
(see [Reference Knapp44, thm 6.105(c)]). The group
$2n = p + q$
(see [Reference Knapp44, thm 6.105(c)]). The group
![]() ${\mathrm {SO}}(p, q)$
with
${\mathrm {SO}}(p, q)$
with
![]() $2n = p + q$
is quasi-split if and only if
$2n = p + q$
is quasi-split if and only if
![]() $|n-p|\le 1$
, giving rise to two classes of inner twists (recall that
$|n-p|\le 1$
, giving rise to two classes of inner twists (recall that
![]() ${\mathrm {SO}}(p, q)$
and
${\mathrm {SO}}(p, q)$
and
![]() ${\mathrm {SO}}(p', q')$
lie in the same class if and only if
${\mathrm {SO}}(p', q')$
lie in the same class if and only if
![]() $p \equiv p' \mod 2$
). The group
$p \equiv p' \mod 2$
). The group
![]() ${\mathrm {SO}}^J_{2n}$
, and hence the group
${\mathrm {SO}}^J_{2n}$
, and hence the group
![]() ${\mathrm {GSO}}^J_{2n}$
, is not quasi-split since
${\mathrm {GSO}}^J_{2n}$
, is not quasi-split since
![]() ${\mathrm {SO}}^J_{2n}$
is not isomorphic to any group of the form
${\mathrm {SO}}^J_{2n}$
is not isomorphic to any group of the form
![]() ${\mathrm {SO}}(p, q)$
.
${\mathrm {SO}}(p, q)$
.
We pin down the isomorphisms
 $$ \begin{align} C_X \colon {\mathrm{GSO}}_{2n}^{\mathrm{cpt}}({\mathbb{C}}) & \overset \sim \to {\mathrm{GSO}}_{2n}({\mathbb{C}}), \quad g \mapsto X^{-1} g X, \quad X = \left( \begin{smallmatrix} 1 & 1 \cr i & {-i} \end{smallmatrix} \right) , \cr {\mathrm{GSO}}_{2n}^{\mathrm{cpt}}({\mathbb{C}}) & \overset \sim \to {\mathrm{GSO}}_{2n}^J({\mathbb{C}}), \quad g \mapsto (g, J^{-1} g J) \in {\mathrm{GSO}}_{2n}^{\mathrm{cmpt}}({\mathbb{C}})^2 ={\mathrm{GSO}}_{2n}^{\mathrm{cmpt}}({\mathbb{C}} \otimes_{{\mathbb R}} {\mathbb{C}}). \end{align} $$
$$ \begin{align} C_X \colon {\mathrm{GSO}}_{2n}^{\mathrm{cpt}}({\mathbb{C}}) & \overset \sim \to {\mathrm{GSO}}_{2n}({\mathbb{C}}), \quad g \mapsto X^{-1} g X, \quad X = \left( \begin{smallmatrix} 1 & 1 \cr i & {-i} \end{smallmatrix} \right) , \cr {\mathrm{GSO}}_{2n}^{\mathrm{cpt}}({\mathbb{C}}) & \overset \sim \to {\mathrm{GSO}}_{2n}^J({\mathbb{C}}), \quad g \mapsto (g, J^{-1} g J) \in {\mathrm{GSO}}_{2n}^{\mathrm{cmpt}}({\mathbb{C}})^2 ={\mathrm{GSO}}_{2n}^{\mathrm{cmpt}}({\mathbb{C}} \otimes_{{\mathbb R}} {\mathbb{C}}). \end{align} $$
Lemma 8.1.
-
(i) The group
 ${\mathrm {GSO}}^J_{2n}$
is an inner form of the split group
${\mathrm {GSO}}^J_{2n}$
is an inner form of the split group
 ${\mathrm {GSO}}(n,n)$
over
${\mathrm {GSO}}(n,n)$
over
 ${\mathbb R}$
if n is even, and an outer form otherwise.
${\mathbb R}$
if n is even, and an outer form otherwise. -
(ii) Explicitly,
 $$ \begin{align*} \mathrm{GO}_{2n}^J({\mathbb R}) =\left\lbrace \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \in {\mathrm{GL}}_{2n}({\mathbb{C}}) \left| \begin{matrix} A, B \in \mathrm{M}_n({\mathbb{C}})\ \mathrm{ such \ that} \cr A^t A + \overline B^t \overline B = \lambda \cdot 1_n \mathrm{ (where }\ \lambda = \mathrm{sim}(g) \in {\mathbb R}^{\times}) \cr A^t B = \overline B^t \overline A\end{matrix}\right.\right\rbrace. \end{align*} $$
$$ \begin{align*} \mathrm{GO}_{2n}^J({\mathbb R}) =\left\lbrace \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \in {\mathrm{GL}}_{2n}({\mathbb{C}}) \left| \begin{matrix} A, B \in \mathrm{M}_n({\mathbb{C}})\ \mathrm{ such \ that} \cr A^t A + \overline B^t \overline B = \lambda \cdot 1_n \mathrm{ (where }\ \lambda = \mathrm{sim}(g) \in {\mathbb R}^{\times}) \cr A^t B = \overline B^t \overline A\end{matrix}\right.\right\rbrace. \end{align*} $$
-
(iii) The following are true:
-
(a) The groups
 ${\mathrm {SO}}^J_{2n}({\mathbb R})$
and
${\mathrm {SO}}^J_{2n}({\mathbb R})$
and
 $\mathrm {O}^J_{2n}({\mathbb R})$
are connected and equal to each other.
$\mathrm {O}^J_{2n}({\mathbb R})$
are connected and equal to each other. -
(b) The map
 $\mathrm {sim} \colon \mathrm {GO}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective;
$\mathrm {sim} \colon \mathrm {GO}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective;
 $\mathrm {sim} \colon {\mathrm {GSO}}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective if and only if n is even.
$\mathrm {sim} \colon {\mathrm {GSO}}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective if and only if n is even. -
(c) We have
 ${\mathrm {GSO}}_{2n}^J({\mathbb R}) = \mathrm {GO}^J_{2n}({\mathbb R})$
if and only if n is even.
${\mathrm {GSO}}_{2n}^J({\mathbb R}) = \mathrm {GO}^J_{2n}({\mathbb R})$
if and only if n is even. -
(d) If n is even (resp. odd), then
 $|\pi _0({\mathrm {GSO}}^J_{2n}({\mathbb R}))|$
equals 2 (resp. 1).
$|\pi _0({\mathrm {GSO}}^J_{2n}({\mathbb R}))|$
equals 2 (resp. 1).
-
-
(iv) The mapping
for $$ \begin{align*}\theta^J \colon {\mathrm{GSO}}_{2n}^J({\mathbb R}) \to {\mathrm{GSO}}_{2n}^J({\mathbb R}), \quad g = \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \mapsto T g T^{-1} = \left( \begin{smallmatrix} A & {-B} \cr {\overline B} & {\overline A} \end{smallmatrix} \right) \end{align*} $$
$$ \begin{align*}\theta^J \colon {\mathrm{GSO}}_{2n}^J({\mathbb R}) \to {\mathrm{GSO}}_{2n}^J({\mathbb R}), \quad g = \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \mapsto T g T^{-1} = \left( \begin{smallmatrix} A & {-B} \cr {\overline B} & {\overline A} \end{smallmatrix} \right) \end{align*} $$
 $T = i \cdot \left ( \begin {smallmatrix} 0 & 1 \cr 1 & 0 \end {smallmatrix} \right ) \in \mathrm {GO}_{2n}^J({\mathbb R})$
is an automorphism of
$T = i \cdot \left ( \begin {smallmatrix} 0 & 1 \cr 1 & 0 \end {smallmatrix} \right ) \in \mathrm {GO}_{2n}^J({\mathbb R})$
is an automorphism of
 ${\mathrm {GSO}}_{2n}^J$
over
${\mathrm {GSO}}_{2n}^J$
over
 ${\mathbb R}$
. It is outer if and only if n is odd.
${\mathbb R}$
. It is outer if and only if n is odd.
-
(v) The group
 ${\mathrm {SO}}_{2n}^J$
(resp.
${\mathrm {SO}}_{2n}^J$
(resp.
 ${\mathrm {GSO}}_{2n}^J$
) has a nontrivial outer automorphism defined over
${\mathrm {GSO}}_{2n}^J$
) has a nontrivial outer automorphism defined over
 ${\mathbb R}$
that acts trivially on the center if and only if n is odd.
${\mathbb R}$
that acts trivially on the center if and only if n is odd. -
(vi) The groups
 ${\mathrm {SO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
and
${\mathrm {SO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
and
 ${\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
are connected.
${\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
are connected.
Proof. (i). The group
![]() ${\mathrm {SO}}_{2n}^J$
is an inner form of
${\mathrm {SO}}_{2n}^J$
is an inner form of
![]() ${\mathrm {SO}}_{2n,{\mathbb R}}^{\mathrm {cpt}}$
, and the compact form lies in the split inner class if and only if n is even.
${\mathrm {SO}}_{2n,{\mathbb R}}^{\mathrm {cpt}}$
, and the compact form lies in the split inner class if and only if n is even.
(ii). Let
![]() $g = \left ( \begin {smallmatrix} A & B \cr C & D \end {smallmatrix} \right ) \in {\mathrm {GL}}_{2n}({\mathbb {C}})$
. Write
$g = \left ( \begin {smallmatrix} A & B \cr C & D \end {smallmatrix} \right ) \in {\mathrm {GL}}_{2n}({\mathbb {C}})$
. Write
![]() $\lambda = \mathrm {sim}(g)$
. We compute
$\lambda = \mathrm {sim}(g)$
. We compute
 $$ \begin{align*} & J \overline g = g J \Leftrightarrow \left( \begin{smallmatrix} 0 & {-1} \cr 1 & 0 \end{smallmatrix} \right) \left( \begin{smallmatrix} {\overline A} & {\overline B} \cr {\overline C} & {\overline D} \end{smallmatrix} \right) = \left( \begin{smallmatrix} A & B \cr C & D \end{smallmatrix} \right) \left( \begin{smallmatrix} 0 & {-1} \cr 1 & 0 \end{smallmatrix} \right) \Leftrightarrow \left( \begin{smallmatrix} {-\overline C} & {-\overline D} \cr {\overline A} & {\overline B} \end{smallmatrix} \right) = \left( \begin{smallmatrix} B & {-A} \cr D & {-C} \end{smallmatrix} \right) \Leftrightarrow g = \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \cr &\left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) ^t \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) = \lambda \left( \begin{smallmatrix} 1 & 0 \cr 0 & 1 \end{smallmatrix} \right) \Leftrightarrow \lambda \left( \begin{smallmatrix} 1 & 0 \cr 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix} {A^t} & {-\overline B^t} \cr {B^t} & {\overline A^t} \end{smallmatrix} \right) \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) = \left( \begin{smallmatrix} {A^tA + \overline B^t \overline B} & {A^tB - \overline B^t \overline A} \cr {B^tA-\overline A^t \overline B} & {B^tB + \overline A^t \overline A} \end{smallmatrix} \right). \end{align*} $$
$$ \begin{align*} & J \overline g = g J \Leftrightarrow \left( \begin{smallmatrix} 0 & {-1} \cr 1 & 0 \end{smallmatrix} \right) \left( \begin{smallmatrix} {\overline A} & {\overline B} \cr {\overline C} & {\overline D} \end{smallmatrix} \right) = \left( \begin{smallmatrix} A & B \cr C & D \end{smallmatrix} \right) \left( \begin{smallmatrix} 0 & {-1} \cr 1 & 0 \end{smallmatrix} \right) \Leftrightarrow \left( \begin{smallmatrix} {-\overline C} & {-\overline D} \cr {\overline A} & {\overline B} \end{smallmatrix} \right) = \left( \begin{smallmatrix} B & {-A} \cr D & {-C} \end{smallmatrix} \right) \Leftrightarrow g = \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) \cr &\left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) ^t \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) = \lambda \left( \begin{smallmatrix} 1 & 0 \cr 0 & 1 \end{smallmatrix} \right) \Leftrightarrow \lambda \left( \begin{smallmatrix} 1 & 0 \cr 0 & 1 \end{smallmatrix} \right) = \left( \begin{smallmatrix} {A^t} & {-\overline B^t} \cr {B^t} & {\overline A^t} \end{smallmatrix} \right) \left( \begin{smallmatrix} A & B \cr {-\overline B} & {\overline A} \end{smallmatrix} \right) = \left( \begin{smallmatrix} {A^tA + \overline B^t \overline B} & {A^tB - \overline B^t \overline A} \cr {B^tA-\overline A^t \overline B} & {B^tB + \overline A^t \overline A} \end{smallmatrix} \right). \end{align*} $$
These identities are equivalent to the stated conditions on g.
(iii.a) By [Reference Zhang83, Cor. 6.3],
![]() $\det \left ( \begin {smallmatrix} A & B \cr {-\overline B} & {\overline A} \end {smallmatrix} \right ) \geq 0$
for all
$\det \left ( \begin {smallmatrix} A & B \cr {-\overline B} & {\overline A} \end {smallmatrix} \right ) \geq 0$
for all
![]() $A, B \in \mathrm {M}_n({\mathbb {C}})$
. By Lemma 8.1(ii), any
$A, B \in \mathrm {M}_n({\mathbb {C}})$
. By Lemma 8.1(ii), any
![]() $g \in \mathrm {O}_{2n}^J({\mathbb R})$
has
$g \in \mathrm {O}_{2n}^J({\mathbb R})$
has
![]() $\det (g) \geq 0$
and thus
$\det (g) \geq 0$
and thus
![]() $\det (g) = 1$
. Thus,
$\det (g) = 1$
. Thus,
![]() $\mathrm {O}_{2n}^J({\mathbb R}) = \mathrm {SO}_{2n}^J({\mathbb R})$
. By [Reference Knapp44, prop I.1.145], the group
$\mathrm {O}_{2n}^J({\mathbb R}) = \mathrm {SO}_{2n}^J({\mathbb R})$
. By [Reference Knapp44, prop I.1.145], the group
![]() ${\mathrm {SO}}_{2n}^J({\mathbb R})$
(and hence
${\mathrm {SO}}_{2n}^J({\mathbb R})$
(and hence
![]() $\mathrm {O}_{2n}^J({\mathbb R})$
) is connected.
$\mathrm {O}_{2n}^J({\mathbb R})$
) is connected.
(iii.b) By restricting to the center, we see that the image of the similitudes factor contains
![]() ${\mathbb R}^{\times }_{>0}$
in all stated cases. The element
${\mathbb R}^{\times }_{>0}$
in all stated cases. The element
![]() $g = \left ( \begin {smallmatrix} A & 0 \cr 0 & {\overline A} \end {smallmatrix} \right ) $
with
$g = \left ( \begin {smallmatrix} A & 0 \cr 0 & {\overline A} \end {smallmatrix} \right ) $
with
![]() $A = i 1_n$
lies in
$A = i 1_n$
lies in
![]() $\mathrm {GO}_{2n}^J({\mathbb R})$
and has
$\mathrm {GO}_{2n}^J({\mathbb R})$
and has
![]() $\mathrm {sim}(g) = -1$
, proving the first part. Since
$\mathrm {sim}(g) = -1$
, proving the first part. Since
![]() $\det (g) = 1$
, we have
$\det (g) = 1$
, we have
![]() $g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
if n is even, proving the second part in that case. Assume for a contradiction that
$g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
if n is even, proving the second part in that case. Assume for a contradiction that
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective when n is odd. Take some
${\mathrm {GSO}}_{2n}^J({\mathbb R}) \to {\mathbb R}^{\times }$
is surjective when n is odd. Take some
![]() $g' \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
with
$g' \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
with
![]() $\mathrm {sim}(g') = -1$
. Then
$\mathrm {sim}(g') = -1$
. Then
![]() $\mathrm {sim}(gg') = 1$
, thus
$\mathrm {sim}(gg') = 1$
, thus
![]() $gg' \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
and hence
$gg' \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
and hence
![]() $g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
: Contradiction.
$g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
: Contradiction.
(iii.c) For n odd, the element
![]() $g = \left ( \begin {smallmatrix} A & 0 \cr 0 & {\overline A} \end {smallmatrix}\right )$
from (iii.b) shows
$g = \left ( \begin {smallmatrix} A & 0 \cr 0 & {\overline A} \end {smallmatrix}\right )$
from (iii.b) shows
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R}) \neq \mathrm {GO}_{2n}^J({\mathbb R})$
. Assume n even. If
${\mathrm {GSO}}_{2n}^J({\mathbb R}) \neq \mathrm {GO}_{2n}^J({\mathbb R})$
. Assume n even. If
![]() $h \in \mathrm {GO}_{2n}^J({\mathbb R})$
, choose
$h \in \mathrm {GO}_{2n}^J({\mathbb R})$
, choose
![]() $g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
with
$g \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
with
![]() $\mathrm {sim}(g) = \mathrm {sim}(h)^{-1}$
using (iii.b). Then
$\mathrm {sim}(g) = \mathrm {sim}(h)^{-1}$
using (iii.b). Then
![]() $hg \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
and hence also
$hg \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
and hence also
![]() $h \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
. Thus,
$h \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
. Thus,
![]() $\mathrm {GO}_{2n}^J({\mathbb R}) = {\mathrm {GSO}}_{2n}^J({\mathbb R})$
.
$\mathrm {GO}_{2n}^J({\mathbb R}) = {\mathrm {GSO}}_{2n}^J({\mathbb R})$
.
(iii.d) Write
![]() $c := \# \pi _0({\mathrm {GSO}}_{2n}^J({\mathbb R})) $
. As
$c := \# \pi _0({\mathrm {GSO}}_{2n}^J({\mathbb R})) $
. As
![]() $\mathrm {H}^1({\mathbb R}, \mu _2)$
has
$\mathrm {H}^1({\mathbb R}, \mu _2)$
has
![]() $2$
elements, we have
$2$
elements, we have
![]() $c \leq 2$
. If n is even, then
$c \leq 2$
. If n is even, then
![]() $\mathrm {sim}$
is surjective and hence
$\mathrm {sim}$
is surjective and hence
![]() $c \geq 2$
and
$c \geq 2$
and
![]() $c = 2$
. If n is odd, we have
$c = 2$
. If n is odd, we have
![]() ${\mathbb R}^{\times }_{>0} \times {\mathrm {SO}}_{2n}^J({\mathbb R}) \overset \sim \to {\mathrm {GSO}}_{2n}^J({\mathbb R})$
; hence
${\mathbb R}^{\times }_{>0} \times {\mathrm {SO}}_{2n}^J({\mathbb R}) \overset \sim \to {\mathrm {GSO}}_{2n}^J({\mathbb R})$
; hence
![]() $c =1$
.
$c =1$
.
(iv) We have
![]() $T^t T = -1$
and
$T^t T = -1$
and
![]() $J \overline T J^{-1} = J$
, so indeed,
$J \overline T J^{-1} = J$
, so indeed,
![]() $T \in \mathrm {GO}_{2n}^J({\mathbb R})$
. As
$T \in \mathrm {GO}_{2n}^J({\mathbb R})$
. As
![]() $\mathrm {sim}(T) = -1$
and
$\mathrm {sim}(T) = -1$
and
![]() $\det (T) = i^{2n}(-1)^n = 1$
, we have
$\det (T) = i^{2n}(-1)^n = 1$
, we have
![]() $\mathrm {sim}(T)^n \neq \det (T)$
if and only if n is odd.
$\mathrm {sim}(T)^n \neq \det (T)$
if and only if n is odd.
(v) By the example in (iv), we may assume n even. Any
![]() ${\mathbb R}$
-automorphism
${\mathbb R}$
-automorphism
![]() $\theta \in \mathrm {Aut}({\mathrm {GSO}}_{2n}^J)$
acting trivially on the center is given by
$\theta \in \mathrm {Aut}({\mathrm {GSO}}_{2n}^J)$
acting trivially on the center is given by
![]() $\theta \colon g \mapsto Y g Y^{-1}$
for some
$\theta \colon g \mapsto Y g Y^{-1}$
for some
![]() $Y \in \mathrm {GO}_{2n}^J({\mathbb {C}})$
. Replacing Y with
$Y \in \mathrm {GO}_{2n}^J({\mathbb {C}})$
. Replacing Y with
![]() $tY$
for some
$tY$
for some
![]() $t \in {\mathbb {C}}^{\times }$
, we may assume that
$t \in {\mathbb {C}}^{\times }$
, we may assume that
![]() $\mathrm {sim}(Y) = 1$
(as
$\mathrm {sim}(Y) = 1$
(as
![]() $\theta $
does not change, it is still defined over
$\theta $
does not change, it is still defined over
![]() ${\mathbb R}$
). Write
${\mathbb R}$
). Write
![]() $\sigma \colon \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}}) \to \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}})$
for the automorphism
$\sigma \colon \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}}) \to \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}})$
for the automorphism
![]() $g \mapsto J \overline g J^{-1}$
, so that
$g \mapsto J \overline g J^{-1}$
, so that
![]() $\mathrm {GO}_{2n}^J({\mathbb R}) = \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}})^{\sigma = \mathrm {id}}$
. As
$\mathrm {GO}_{2n}^J({\mathbb R}) = \mathrm {GO}_{2n}^{\mathrm {cpt}}({\mathbb {C}})^{\sigma = \mathrm {id}}$
. As
![]() $\theta $
is defined over
$\theta $
is defined over
![]() ${\mathbb R}$
,
${\mathbb R}$
,
and therefore,
![]() $YJ \cdot \overline g \cdot J^{-1} Y^{-1} = J \overline Y \cdot \overline g \cdot \overline Y^{-1} J^{-1}$
, so
$YJ \cdot \overline g \cdot J^{-1} Y^{-1} = J \overline Y \cdot \overline g \cdot \overline Y^{-1} J^{-1}$
, so
![]() $\overline Y^{-1} J^{-1} YJ \cdot \overline g = \overline g \cdot \overline Y^{-1} J^{-1} Y J$
. Thus,
$\overline Y^{-1} J^{-1} YJ \cdot \overline g = \overline g \cdot \overline Y^{-1} J^{-1} Y J$
. Thus,
We have
![]() $Y^t Y = 1$
, so we compute as follows using
$Y^t Y = 1$
, so we compute as follows using
![]() $J^t J=1$
:
$J^t J=1$
:
Therefore,
![]() $\lambda \in \{\pm 1\}$
. If
$\lambda \in \{\pm 1\}$
. If
![]() $\lambda = 1$
, then
$\lambda = 1$
, then
![]() $Y \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
, and
$Y \in \mathrm {O}_{2n}^J({\mathbb R}) = {\mathrm {SO}}_{2n}^J({\mathbb R})$
, and
![]() $\theta $
is inner. If
$\theta $
is inner. If
![]() $\lambda = -1$
, then
$\lambda = -1$
, then
![]() $\sigma (Y) = -Y$
so
$\sigma (Y) = -Y$
so
![]() $iY \in \mathrm {GO}_{2n}^J({\mathbb R}) = {\mathrm {GSO}}_{2n}^J({\mathbb R})$
(n is even). Thus,
$iY \in \mathrm {GO}_{2n}^J({\mathbb R}) = {\mathrm {GSO}}_{2n}^J({\mathbb R})$
(n is even). Thus,
![]() $\theta = (g \mapsto (iy)g(iY)^{-1})$
is inner.
$\theta = (g \mapsto (iy)g(iY)^{-1})$
is inner.
(vi) It is standard that
![]() ${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
is connected. Let us show that
${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
is connected. Let us show that
![]() ${\mathrm {GSO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
is connected from this. The multiplication map
${\mathrm {GSO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
is connected from this. The multiplication map
![]() ${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})\times {\mathbb R}^{\times } \rightarrow {\mathrm {GSO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
has connected image since
${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})\times {\mathbb R}^{\times } \rightarrow {\mathrm {GSO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
has connected image since
![]() ${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
meets both connected components of
${\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb R})$
meets both connected components of
![]() ${\mathbb R}^{\times }$
. So we will be done if we check the surjectivity. This is equivalent to the injectivity of
${\mathbb R}^{\times }$
. So we will be done if we check the surjectivity. This is equivalent to the injectivity of
![]() $H^1({\mathbb R},\{\pm 1\})\rightarrow H^1({\mathbb R},{\mathrm {SO}}^{\mathrm {cpt}}_{2n}\times {\mathrm {GL}}_1)$
, which follows from the fact that there is no
$H^1({\mathbb R},\{\pm 1\})\rightarrow H^1({\mathbb R},{\mathrm {SO}}^{\mathrm {cpt}}_{2n}\times {\mathrm {GL}}_1)$
, which follows from the fact that there is no
![]() $g\in {\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb {C}})$
with
$g\in {\mathrm {SO}}^{\mathrm {cpt}}_{2n}({\mathbb {C}})$
with
![]() $g^{-1} \overline {g}=-1$
. (Via
$g^{-1} \overline {g}=-1$
. (Via
![]() $h=\sqrt {-1} g$
, the latter is equivalent to non-existence of
$h=\sqrt {-1} g$
, the latter is equivalent to non-existence of
![]() $h\in {\mathrm {GL}}_{2n}({\mathbb R})$
with
$h\in {\mathrm {GL}}_{2n}({\mathbb R})$
with
![]() $h ^t h=-1$
, which is clear.)
$h ^t h=-1$
, which is clear.)
Now we turn to the global setup. Let n and
![]() $E/F$
be as in §6 and impose condition (disc-
$E/F$
be as in §6 and impose condition (disc-
![]() $\infty $
) from now on. In analogy with the
$\infty $
) from now on. In analogy with the
![]() ${\mathrm {SO}}_{2n}$
-case, we introduce a quasi-split form
${\mathrm {SO}}_{2n}$
-case, we introduce a quasi-split form
![]() $G^{*}$
of
$G^{*}$
of
![]() ${\mathrm {GSO}}_{2n}$
over F. If n is even, we have
${\mathrm {GSO}}_{2n}$
over F. If n is even, we have
![]() $E=F$
and take the split form
$E=F$
and take the split form
![]() $G^{*} := {\mathrm {GSO}}_{2n,F}$
(or simply written as
$G^{*} := {\mathrm {GSO}}_{2n,F}$
(or simply written as
![]() ${\mathrm {GSO}}_{2n}$
). If n is odd, then
${\mathrm {GSO}}_{2n}$
). If n is odd, then
![]() $E/F$
is a totally imaginary quadratic extension. In this case, let
$E/F$
is a totally imaginary quadratic extension. In this case, let
![]() $G^{*}$
be the quasi-split form
$G^{*}$
be the quasi-split form
![]() ${\mathrm {GSO}}^{E/F}_{2n,F}$
of
${\mathrm {GSO}}^{E/F}_{2n,F}$
of
![]() ${\mathrm {GSO}}_{2n,F}$
(up to F-automorphism) given by the 1-cocycle
${\mathrm {GSO}}_{2n,F}$
(up to F-automorphism) given by the 1-cocycle
![]() ${\mathrm {Gal}}(E/F)\rightarrow \mathrm {Aut}({\mathrm {GSO}}_{2n,E})$
sending the nontrivial element to
${\mathrm {Gal}}(E/F)\rightarrow \mathrm {Aut}({\mathrm {GSO}}_{2n,E})$
sending the nontrivial element to
![]() $\theta ^{\circ }={\mathrm {Int}}(\vartheta ^{\circ })$
. Since
$\theta ^{\circ }={\mathrm {Int}}(\vartheta ^{\circ })$
. Since
![]() $\vartheta ^{\circ }\in \mathrm {O}_{2n}(E)$
, this cocycle comes from the
$\vartheta ^{\circ }\in \mathrm {O}_{2n}(E)$
, this cocycle comes from the
![]() $\mathrm {Aut}({\mathrm {SO}}_{2n,E})$
-valued cocycle determining
$\mathrm {Aut}({\mathrm {SO}}_{2n,E})$
-valued cocycle determining
![]() ${\mathrm {SO}}^{E/F}_{2n}$
as an outer form of
${\mathrm {SO}}^{E/F}_{2n}$
as an outer form of
![]() ${\mathrm {SO}}_{2n}$
; thus, we have
${\mathrm {SO}}_{2n}$
; thus, we have
![]() ${\mathrm {SO}}^{E/F}_{2n}\hookrightarrow {\mathrm {GSO}}^{E/F}_{2n}$
. Concretely, in analogy with (6.1),
${\mathrm {SO}}^{E/F}_{2n}\hookrightarrow {\mathrm {GSO}}^{E/F}_{2n}$
. Concretely, in analogy with (6.1),
 $$ \begin{align} {\mathrm{GSO}}^{E/F}_{2n}(R) = \left\{g \in {\mathrm{GL}}_{2n}(E \otimes_F R)\ \left|\ \begin{array}{c} \mathrm{there \ exists}~\lambda\in R^{\times}~\mathrm{such \ that} \\ c(g) = \vartheta^{\circ} g \vartheta^{\circ}, ~ g^t \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right) g = \lambda \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right), ~\det(g) = \lambda^n \end{array} \right.\right\}, \end{align} $$
$$ \begin{align} {\mathrm{GSO}}^{E/F}_{2n}(R) = \left\{g \in {\mathrm{GL}}_{2n}(E \otimes_F R)\ \left|\ \begin{array}{c} \mathrm{there \ exists}~\lambda\in R^{\times}~\mathrm{such \ that} \\ c(g) = \vartheta^{\circ} g \vartheta^{\circ}, ~ g^t \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right) g = \lambda \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right), ~\det(g) = \lambda^n \end{array} \right.\right\}, \end{align} $$
and
![]() $\mathrm {GO}^{E/F}_{2n}(R)$
is defined by removing the condition
$\mathrm {GO}^{E/F}_{2n}(R)$
is defined by removing the condition
![]() $\det (g) = \lambda ^n$
.
$\det (g) = \lambda ^n$
.
We write
![]() $G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
for both parities of n, understanding that
$G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
for both parities of n, understanding that
![]() $E=F$
if n is even, for a streamlined exposition. In both cases, we have an exact sequence
$E=F$
if n is even, for a streamlined exposition. In both cases, we have an exact sequence
where the similitude map
![]() ${\mathrm {GSO}}^{E/F}_{2n} \rightarrow \mathbb G_m$
is the usual one if
${\mathrm {GSO}}^{E/F}_{2n} \rightarrow \mathbb G_m$
is the usual one if
![]() $E=F$
, and
$E=F$
, and
![]() $g\mapsto \lambda $
in (8.4) if
$g\mapsto \lambda $
in (8.4) if
![]() $E\neq F$
. Note that
$E\neq F$
. Note that
![]() $\widehat {G^{*}_{\mathrm {ad}}}$
is isomorphic to
$\widehat {G^{*}_{\mathrm {ad}}}$
is isomorphic to
![]() $\mathrm {Spin}_{2n}({\mathbb {C}})$
, on which
$\mathrm {Spin}_{2n}({\mathbb {C}})$
, on which
![]() $\Gamma $
acts trivially (resp. nontrivially via
$\Gamma $
acts trivially (resp. nontrivially via
![]() ${\mathrm {Gal}}(E/F)$
as
${\mathrm {Gal}}(E/F)$
as
![]() $\{1,\theta \}$
) if n is even (resp. odd).
$\{1,\theta \}$
) if n is even (resp. odd).
Write
![]() $(\cdot )^D$
for the Pontryagin dual of a locally compact abelian group. Let v be a place of F. By [Reference Kottwitz46, Thm 1.2], we have a mapFootnote 11
$(\cdot )^D$
for the Pontryagin dual of a locally compact abelian group. Let v be a place of F. By [Reference Kottwitz46, Thm 1.2], we have a mapFootnote 11
which is an isomorphism if v is a finite place (but not if v is infinite).
Lemma 8.2. We have
 $$ \begin{align*}Z(\widehat{G^{*}_{\mathrm{ad}}})^{\Gamma_v} \simeq \begin{cases} (\mu_2)^2, & n \mathrm{ \ is \ even}, \cr \mu_2, & n \mathrm{ \ is \ odd}, v \mathrm{ \ is \ non-split \ in }\ {E}/F, \cr \mu_4, & n \mathrm{ \ is \ odd}, v \mathrm{ \ is \ split \ in }\ {E}/F. \end{cases} \end{align*} $$
$$ \begin{align*}Z(\widehat{G^{*}_{\mathrm{ad}}})^{\Gamma_v} \simeq \begin{cases} (\mu_2)^2, & n \mathrm{ \ is \ even}, \cr \mu_2, & n \mathrm{ \ is \ odd}, v \mathrm{ \ is \ non-split \ in }\ {E}/F, \cr \mu_4, & n \mathrm{ \ is \ odd}, v \mathrm{ \ is \ split \ in }\ {E}/F. \end{cases} \end{align*} $$
Proof. This follows from Lemma 3.7.
By [Reference Kottwitz46, Prop. 2.6] and the Hasse principle from [Reference Platonov and Rapinchuk68, Thm. 6.22], we have an exact sequence of pointed sets
Since
![]() $Z(\widehat {G^{*}_{\mathrm {ad}}})$
is finite, we may forget
$Z(\widehat {G^{*}_{\mathrm {ad}}})$
is finite, we may forget
![]() $\pi _0(\cdot )$
in (8.6) and the proof of the lemma below. From now until the end of §9, we fix a finite place
$\pi _0(\cdot )$
in (8.6) and the proof of the lemma below. From now until the end of §9, we fix a finite place
![]() ${{{\mathfrak q}}_{\mathrm {St}}}$
and an infinite place
${{{\mathfrak q}}_{\mathrm {St}}}$
and an infinite place
![]() $y_{\infty }$
of F.
$y_{\infty }$
of F.
Lemma 8.3. Let
![]() ${{{\mathfrak q}}_{\mathrm {St}}}$
(resp.
${{{\mathfrak q}}_{\mathrm {St}}}$
(resp.
![]() $y_{\infty }$
) be a fixed finite (resp. infinite) place of F. There exists an inner twist G of
$y_{\infty }$
) be a fixed finite (resp. infinite) place of F. There exists an inner twist G of
![]() $G^{*}$
such that for all F-places
$G^{*}$
such that for all F-places
![]() $v \neq {{{\mathfrak q}}_{\mathrm {St}}}$
, we have
$v \neq {{{\mathfrak q}}_{\mathrm {St}}}$
, we have
 $$ \begin{align} G_v \simeq \begin{cases} {\mathrm{GSO}}^J_{2n,F_v} & v = y_{\infty} \cr {\mathrm{GSO}}^{\mathrm{cpt}}_{2n, F_v} & v \in \mathcal V_{\infty} \backslash \{y_{\infty}\} \cr G^{*}_{F_v} & v \notin \mathcal V_{\infty}\cup \{{{{\mathfrak q}}_{\mathrm{St}}}\}. \end{cases} \end{align} $$
$$ \begin{align} G_v \simeq \begin{cases} {\mathrm{GSO}}^J_{2n,F_v} & v = y_{\infty} \cr {\mathrm{GSO}}^{\mathrm{cpt}}_{2n, F_v} & v \in \mathcal V_{\infty} \backslash \{y_{\infty}\} \cr G^{*}_{F_v} & v \notin \mathcal V_{\infty}\cup \{{{{\mathfrak q}}_{\mathrm{St}}}\}. \end{cases} \end{align} $$
This inner twist G is unique up to isomorphism if either n is even or
![]() ${{{\mathfrak q}}_{\mathrm {St}}}$
is non-split in
${{{\mathfrak q}}_{\mathrm {St}}}$
is non-split in
![]() $E/F$
; otherwise, there are two choices for G. (Recall the notion of inner twist from §1.)
$E/F$
; otherwise, there are two choices for G. (Recall the notion of inner twist from §1.)
Proof. Put
By duality, the inclusion
![]() $Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma } \subset Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v}$
induces a surjection
$Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma } \subset Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v}$
induces a surjection
![]() $(Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v})^D \twoheadrightarrow (Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma })^D$
. Hence, we can choose some invariant
$(Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v})^D \twoheadrightarrow (Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma })^D$
. Hence, we can choose some invariant
![]() $\widetilde {a_{{{{\mathfrak q}}_{\mathrm {St}}}}} \in (Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v})^D$
mapping to the expression on the right-hand side of (8.8). Let
$\widetilde {a_{{{{\mathfrak q}}_{\mathrm {St}}}}} \in (Z(\widehat {G^{*}_{\mathrm {ad}}})^{\Gamma _v})^D$
mapping to the expression on the right-hand side of (8.8). Let
![]() $G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
be the inner twist of
$G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
be the inner twist of
![]() $G^{*}$
over
$G^{*}$
over
![]() $F_{{{{\mathfrak q}}_{\mathrm {St}}}}$
corresponding to
$F_{{{{\mathfrak q}}_{\mathrm {St}}}}$
corresponding to
![]() $\widetilde {a_{{{\mathfrak q}}_{\mathrm {St}}}}$
. Then, by (8.6), the collection of local inner twists
$\widetilde {a_{{{\mathfrak q}}_{\mathrm {St}}}}$
. Then, by (8.6), the collection of local inner twists
![]() $\{G_v\}_{\mathrm {places } v}$
comes from a global inner twist
$\{G_v\}_{\mathrm {places } v}$
comes from a global inner twist
![]() $G/F$
, unique up to isomorphism. Conversely, any G as in the lemma satisfies
$G/F$
, unique up to isomorphism. Conversely, any G as in the lemma satisfies
![]() $\alpha _{{{{\mathfrak q}}_{\mathrm {St}}}}(G)=a_{{{{\mathfrak q}}_{\mathrm {St}}}}$
by (8.6). Therefore, the number of choices for G equals the number of choices for
$\alpha _{{{{\mathfrak q}}_{\mathrm {St}}}}(G)=a_{{{{\mathfrak q}}_{\mathrm {St}}}}$
by (8.6). Therefore, the number of choices for G equals the number of choices for
![]() $\widetilde {a_{{{{\mathfrak q}}_{\mathrm {St}}}}}$
, which can be computed using Lemma 8.2.
$\widetilde {a_{{{{\mathfrak q}}_{\mathrm {St}}}}}$
, which can be computed using Lemma 8.2.
Remark 8.4. The group
![]() $G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
in the lemma is never quasi-split, regardless of the parity of
$G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
in the lemma is never quasi-split, regardless of the parity of
![]() $[F:\mathbb {Q}]$
. It is always a unitary group for a Hermitian form over a quaternion algebra. This corresponds to the “
$[F:\mathbb {Q}]$
. It is always a unitary group for a Hermitian form over a quaternion algebra. This corresponds to the “
![]() $d=2$
case” in [Reference Arthur1, §9.1]. In this case, the rank of
$d=2$
case” in [Reference Arthur1, §9.1]. In this case, the rank of
![]() $G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is roughly
$G_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is roughly
![]() $n/2$
(see [Reference Arthur1] for precise information).
$n/2$
(see [Reference Arthur1] for precise information).
9 Shimura varieties of type D corresponding to
 $\mathbf {spin}^{\boldsymbol{\pm} }$
$\mathbf {spin}^{\boldsymbol{\pm} }$
We continue in the same global setup, with an inner form G of a quasi-split form
![]() $G^{*}$
of
$G^{*}$
of
![]() ${\mathrm {GSO}}_{2n}$
over a totally real field F, depending on the fixed places
${\mathrm {GSO}}_{2n}$
over a totally real field F, depending on the fixed places
![]() ${{{\mathfrak q}}_{\mathrm {St}}}$
and
${{{\mathfrak q}}_{\mathrm {St}}}$
and
![]() $y_{\infty }$
of F. We are going to construct Shimura data associated with
$y_{\infty }$
of F. We are going to construct Shimura data associated with
![]() $\mathrm {Res}_{F/\mathbb {Q}}G$
by giving an
$\mathrm {Res}_{F/\mathbb {Q}}G$
by giving an
![]() ${\mathbb R}$
-morphism
${\mathbb R}$
-morphism
![]() ${\mathbb S}:=\mathrm {Res}_{{\mathbb {C}}/{\mathbb R}}\mathbb G_m \rightarrow (\mathrm {Res}_{F/\mathbb {Q}}G)\otimes _{\mathbb {Q}} {\mathbb R}$
. Our running assumption (disc-
${\mathbb S}:=\mathrm {Res}_{{\mathbb {C}}/{\mathbb R}}\mathbb G_m \rightarrow (\mathrm {Res}_{F/\mathbb {Q}}G)\otimes _{\mathbb {Q}} {\mathbb R}$
. Our running assumption (disc-
![]() $\infty $
) is clearly a necessary condition for the existence of such Shimura data. We define
$\infty $
) is clearly a necessary condition for the existence of such Shimura data. We define
 $$ \begin{align*} h_{(-1)^n} \colon {\mathbb S} \to {\mathrm{GSO}}_{2n}^J, &\quad x + yi \mapsto \left(\begin{matrix} {x1_{n}} & {y1_{n}} \cr {-y1_{n}} & {x1_{n}} \end{matrix}\right) \cr h_{(-1)^{n+1}} \colon {\mathbb S} \to {\mathrm{GSO}}_{2n}^J, &\quad x + y i \mapsto \left(\begin{matrix} {x 1_n} & {{\mathrm{diag}}(y 1_{n-1}, -y)} \cr {{\mathrm{diag}}(-y1_{n-1}, y)} & {x 1_n} \end{matrix}\right). \end{align*} $$
$$ \begin{align*} h_{(-1)^n} \colon {\mathbb S} \to {\mathrm{GSO}}_{2n}^J, &\quad x + yi \mapsto \left(\begin{matrix} {x1_{n}} & {y1_{n}} \cr {-y1_{n}} & {x1_{n}} \end{matrix}\right) \cr h_{(-1)^{n+1}} \colon {\mathbb S} \to {\mathrm{GSO}}_{2n}^J, &\quad x + y i \mapsto \left(\begin{matrix} {x 1_n} & {{\mathrm{diag}}(y 1_{n-1}, -y)} \cr {{\mathrm{diag}}(-y1_{n-1}, y)} & {x 1_n} \end{matrix}\right). \end{align*} $$
We will often omit
![]() $1_n$
in the cases similar to the above if a matrix is clearly
$1_n$
in the cases similar to the above if a matrix is clearly
![]() $2n\times 2n$
in the context.
$2n\times 2n$
in the context.
By slight abuse of notation, we write
![]() $\mathrm {Ad}$
for either the natural map from
$\mathrm {Ad}$
for either the natural map from
![]() ${\mathrm {GSO}}_{2n}^J\rightarrow {\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
or the adjoint representation of
${\mathrm {GSO}}_{2n}^J\rightarrow {\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
or the adjoint representation of
![]() ${\mathrm {GSO}}_{2n}^J$
on
${\mathrm {GSO}}_{2n}^J$
on
![]() $\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J$
.
$\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J$
.
Lemma 9.1. Let
![]() $\varepsilon \in \{+,-\}$
and put
$\varepsilon \in \{+,-\}$
and put
![]() $K_{\varepsilon } := \mathrm {Cent}_{{\mathrm {GSO}}_{2n}^J({\mathbb R})}(h_{\varepsilon })$
. The following hold.
$K_{\varepsilon } := \mathrm {Cent}_{{\mathrm {GSO}}_{2n}^J({\mathbb R})}(h_{\varepsilon })$
. The following hold.
-
(i) In the representation of
 ${\mathbb {C}}^{\times }$
on
${\mathbb {C}}^{\times }$
on
 $\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J({\mathbb {C}})$
via
$\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J({\mathbb {C}})$
via
 $\mathrm {Ad} \circ h_{\varepsilon }$
, only the characters
$\mathrm {Ad} \circ h_{\varepsilon }$
, only the characters
 $z \mapsto z^{-1} \overline z$
,
$z \mapsto z^{-1} \overline z$
,
 $z \mapsto 1$
and
$z \mapsto 1$
and
 $z \mapsto z \overline z^{-1}$
appear.
$z \mapsto z \overline z^{-1}$
appear. -
(ii) The involution on
 ${\mathrm {GSO}}^J_{2n,\mathrm {ad}}$
given by
${\mathrm {GSO}}^J_{2n,\mathrm {ad}}$
given by
 $\mathrm {Ad}\ h_{\varepsilon }(i)$
is a Cartan involution.
$\mathrm {Ad}\ h_{\varepsilon }(i)$
is a Cartan involution. -
(iii)
 $K_+$
and
$K_+$
and
 $K_-$
are
$K_-$
are
 ${\mathrm {GSO}}_{2n}^J({\mathbb R})$
-conjugate.
${\mathrm {GSO}}_{2n}^J({\mathbb R})$
-conjugate.
Proof. For (i) and (ii), we only treat the case of
![]() $\varepsilon =(-1)^n$
as the argument for
$\varepsilon =(-1)^n$
as the argument for
![]() $-\varepsilon $
is the same. Let
$-\varepsilon $
is the same. Let
![]() $z = x+yi \in {\mathbb {C}}^{\times }$
and consider the left-multiplication action of the matrix
$z = x+yi \in {\mathbb {C}}^{\times }$
and consider the left-multiplication action of the matrix
![]() $h_{\varepsilon }(x + iy)= \left ( \begin {smallmatrix} x & y \cr {-y} & x \end {smallmatrix} \right )$
on
$h_{\varepsilon }(x + iy)= \left ( \begin {smallmatrix} x & y \cr {-y} & x \end {smallmatrix} \right )$
on
![]() $\mathrm {M}_{2n}({\mathbb {C}})$
. The matrix
$\mathrm {M}_{2n}({\mathbb {C}})$
. The matrix
![]() $\left ( \begin {smallmatrix} x & y \cr {-y} & x \end {smallmatrix} \right )$
is conjugate to
$\left ( \begin {smallmatrix} x & y \cr {-y} & x \end {smallmatrix} \right )$
is conjugate to
![]() $\left ( \begin {smallmatrix} {x+yi} & {} \cr {} & {x-yi} \end {smallmatrix} \right ) $
via
$\left ( \begin {smallmatrix} {x+yi} & {} \cr {} & {x-yi} \end {smallmatrix} \right ) $
via
![]() $\left ( \begin {smallmatrix} 1 & 1 \cr i & {-i} \end {smallmatrix} \right )$
. Hence, only the characters
$\left ( \begin {smallmatrix} 1 & 1 \cr i & {-i} \end {smallmatrix} \right )$
. Hence, only the characters
![]() $z \overline z^{-1}$
,
$z \overline z^{-1}$
,
![]() $\overline z z^{-1}$
and
$\overline z z^{-1}$
and
![]() $1$
appear in the representation of
$1$
appear in the representation of
![]() ${\mathbb S}$
on
${\mathbb S}$
on
![]() $\mathrm {M}_{2n}({\mathbb {C}})$
via conjugation by
$\mathrm {M}_{2n}({\mathbb {C}})$
via conjugation by
![]() $h_{\varepsilon }(x + iy)$
. Since
$h_{\varepsilon }(x + iy)$
. Since
![]() $\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J({\mathbb R})$
is contained in
$\mathrm {Lie}\, {\mathrm {GSO}}_{2n}^J({\mathbb R})$
is contained in
![]() $\mathrm {M}_{2n}({\mathbb {C}})$
via the standard representation, (i) is true for
$\mathrm {M}_{2n}({\mathbb {C}})$
via the standard representation, (i) is true for
![]() $h_{\varepsilon }(z)$
. Since
$h_{\varepsilon }(z)$
. Since
![]() $J^{-1} = h_{\varepsilon }(i)$
, the inner form of
$J^{-1} = h_{\varepsilon }(i)$
, the inner form of
![]() ${\mathrm {GSO}}_{2n}^J$
defined by
${\mathrm {GSO}}_{2n}^J$
defined by
![]() $h_{\varepsilon }(i)$
is the compact-modulo-center form
$h_{\varepsilon }(i)$
is the compact-modulo-center form
![]() ${\mathrm {GSO}}_{2n, {\mathbb R}}^{\mathrm {cpt}}$
, so part (ii) follows.
${\mathrm {GSO}}_{2n, {\mathbb R}}^{\mathrm {cpt}}$
, so part (ii) follows.
Let us prove (iii). Write
![]() $\overline h_{\varepsilon }:=\mathrm {Ad}\circ h_{\varepsilon }$
. Clearly,
$\overline h_{\varepsilon }:=\mathrm {Ad}\circ h_{\varepsilon }$
. Clearly,
![]() $\mathrm {Ad}(K_{\varepsilon })\subset \mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
. The Lie algebra
$\mathrm {Ad}(K_{\varepsilon })\subset \mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
. The Lie algebra
![]() $\mathrm {Lie}(K_{\varepsilon })$
(resp. the Lie algebra of
$\mathrm {Lie}(K_{\varepsilon })$
(resp. the Lie algebra of
![]() $\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
) is the
$\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
) is the
![]() $(0,0)$
part of
$(0,0)$
part of
![]() $\mathrm {Lie}({\mathrm {GSO}}_{2n}^J)$
(resp.
$\mathrm {Lie}({\mathrm {GSO}}_{2n}^J)$
(resp.
![]() $\mathrm {Lie}({\mathrm {GSO}}_{2n,\mathrm {ad}}^J)$
) via
$\mathrm {Lie}({\mathrm {GSO}}_{2n,\mathrm {ad}}^J)$
) via
![]() $h_{\varepsilon }$
, in the sense of [Reference Deligne20]. In particular,
$h_{\varepsilon }$
, in the sense of [Reference Deligne20]. In particular,
is surjective. Therefore,
![]() $\mathrm {Ad}(K_{\varepsilon })\supset \mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })^0$
. Since
$\mathrm {Ad}(K_{\varepsilon })\supset \mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })^0$
. Since
![]() $\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
is connected by [Reference Deligne20, proof of Prop. 1.2.7], we have
$\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
is connected by [Reference Deligne20, proof of Prop. 1.2.7], we have
![]() $\mathrm {Ad}(K_{\varepsilon })=\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
. The latter is the identity component of a maximal compact subgroup of
$\mathrm {Ad}(K_{\varepsilon })=\mathrm {Cent}_{{\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})}(\overline h_{\varepsilon })$
. The latter is the identity component of a maximal compact subgroup of
![]() ${\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})$
by loc. cit. so
${\mathrm {GSO}}_{2n,\mathrm {ad}}^J({\mathbb R})$
by loc. cit. so
![]() $\mathrm {Ad}(K_-)$
and
$\mathrm {Ad}(K_-)$
and
![]() $\mathrm {Ad}(K_+)$
are conjugate in
$\mathrm {Ad}(K_+)$
are conjugate in
![]() ${\mathrm {GSO}}_{2n, \mathrm {ad}}^J({\mathbb R})$
. Since
${\mathrm {GSO}}_{2n, \mathrm {ad}}^J({\mathbb R})$
. Since
![]() $K_{\varepsilon }=\mathrm {Ad}^{-1}(\mathrm {Ad}(K_{\varepsilon }))$
and since
$K_{\varepsilon }=\mathrm {Ad}^{-1}(\mathrm {Ad}(K_{\varepsilon }))$
and since
![]() $\mathrm {Ad}\colon {\mathrm {GSO}}_{2n}^J \to {\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
is surjective on real points by Hilbert 90, we lift a conjugating element to see that
$\mathrm {Ad}\colon {\mathrm {GSO}}_{2n}^J \to {\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
is surjective on real points by Hilbert 90, we lift a conjugating element to see that
![]() $K_+$
and
$K_+$
and
![]() $K_-$
are conjugate in
$K_-$
are conjugate in
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R})$
.
${\mathrm {GSO}}_{2n}^J({\mathbb R})$
.
Recall the cocharacters
![]() $\mu _+, \mu _-$
from (2.9), which are outer conjugate as
$\mu _+, \mu _-$
from (2.9), which are outer conjugate as
![]() $\mu _+ = \vartheta ^{\circ } \mu _- (\vartheta ^{\circ })^{-1}$
(but not inner, cf. (2.8)).
$\mu _+ = \vartheta ^{\circ } \mu _- (\vartheta ^{\circ })^{-1}$
(but not inner, cf. (2.8)).
Lemma 9.2. Let
![]() $\varepsilon \in \{+,-\}$
.
$\varepsilon \in \{+,-\}$
.
-
(i) Consider the inclusion of
 ${\mathbb {C}}^{\times }$
in
${\mathbb {C}}^{\times }$
in
 $({\mathbb {C}} \otimes _{{\mathbb R}} {\mathbb {C}})^{\times } = ({\mathbb {C}}^{\times })^{{\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})}$
indexed by the identity
$({\mathbb {C}} \otimes _{{\mathbb R}} {\mathbb {C}})^{\times } = ({\mathbb {C}}^{\times })^{{\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})}$
indexed by the identity
 $\mathrm {id}_{{\mathbb {C}}/{\mathbb R}} \in {\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})$
. Then
$\mathrm {id}_{{\mathbb {C}}/{\mathbb R}} \in {\mathrm {Gal}}({\mathbb {C}}/{\mathbb R})$
. Then
 $C_X h_{\varepsilon ,{\mathbb {C}}}|_{{\mathbb {C}}^{\times }} = \mu _{\varepsilon }$
.
$C_X h_{\varepsilon ,{\mathbb {C}}}|_{{\mathbb {C}}^{\times }} = \mu _{\varepsilon }$
. -
(ii) The complex conjugate morphism
 $z \mapsto h_{\varepsilon }(\overline z)$
is
$z \mapsto h_{\varepsilon }(\overline z)$
is
 ${\mathrm {GSO}}_{2n}^J({\mathbb R})$
-conjugate to
${\mathrm {GSO}}_{2n}^J({\mathbb R})$
-conjugate to
 $h_{(-1)^{n}\varepsilon }$
.
$h_{(-1)^{n}\varepsilon }$
.
Proof. In the proof, put
![]() $\varepsilon =(-1)^n$
. (i). Recall
$\varepsilon =(-1)^n$
. (i). Recall
![]() $C_X$
from (8.3), which induces
$C_X$
from (8.3), which induces
![]() ${\mathrm {GSO}}_{2n}^J({\mathbb R})\hookrightarrow {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb {C}}) \stackrel {C_X}{\simeq } {\mathrm {GSO}}_{2n}({\mathbb {C}})$
. The morphism
${\mathrm {GSO}}_{2n}^J({\mathbb R})\hookrightarrow {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb {C}}) \stackrel {C_X}{\simeq } {\mathrm {GSO}}_{2n}({\mathbb {C}})$
. The morphism
![]() $C_X h_{\varepsilon }$
equals
$C_X h_{\varepsilon }$
equals
![]() $x+yi \mapsto \left ( \begin {smallmatrix} {x+yi} & 0 \cr 0 & {x-yi} \end {smallmatrix} \right )$
. The holomorphic part of this morphism is
$x+yi \mapsto \left ( \begin {smallmatrix} {x+yi} & 0 \cr 0 & {x-yi} \end {smallmatrix} \right )$
. The holomorphic part of this morphism is
![]() $z \mapsto \left ( \begin {smallmatrix} z & 0 \cr 0 & 1 \end {smallmatrix} \right )$
, which is
$z \mapsto \left ( \begin {smallmatrix} z & 0 \cr 0 & 1 \end {smallmatrix} \right )$
, which is
![]() $\mu _{\varepsilon }$
. Then
$\mu _{\varepsilon }$
. Then
![]() $h_{\varepsilon } = \vartheta ^{\circ } h_{-\varepsilon } \vartheta ^{\circ }$
, where
$h_{\varepsilon } = \vartheta ^{\circ } h_{-\varepsilon } \vartheta ^{\circ }$
, where
![]() $\vartheta ^{\circ }$
is as in (2.4). Write
$\vartheta ^{\circ }$
is as in (2.4). Write
![]() $\vartheta ^c = \left ( \begin {smallmatrix} {-1_{2n-1}} & 0 \cr 0 & {1} \end {smallmatrix} \right )$
. Note that
$\vartheta ^c = \left ( \begin {smallmatrix} {-1_{2n-1}} & 0 \cr 0 & {1} \end {smallmatrix} \right )$
. Note that
![]() $C_X(\vartheta ^c) = \vartheta ^{\circ }$
, so
$C_X(\vartheta ^c) = \vartheta ^{\circ }$
, so
![]() $\vartheta ^c$
-conjugation becomes
$\vartheta ^c$
-conjugation becomes
![]() $\vartheta ^{\circ }$
-conjugation under
$\vartheta ^{\circ }$
-conjugation under
![]() $C_X$
. As
$C_X$
. As
![]() $\vartheta ^{\circ }$
swaps
$\vartheta ^{\circ }$
swaps
![]() $\mu _{\varepsilon }$
and
$\mu _{\varepsilon }$
and
![]() $\mu _{-\varepsilon }$
, we obtain
$\mu _{-\varepsilon }$
, we obtain
![]() $C_X h_{-\varepsilon }|_{{\mathbb {C}}^{\times }} = \mu _{-\varepsilon }$
.
$C_X h_{-\varepsilon }|_{{\mathbb {C}}^{\times }} = \mu _{-\varepsilon }$
.
(ii). Write
![]() $z = x + yi \in {\mathbb {C}}$
. We compute
$z = x + yi \in {\mathbb {C}}$
. We compute
 $$ \begin{align*}h_{\varepsilon}(\overline z) = \left(\begin{matrix} x & {-y} \cr y & x \end{matrix}\right) = T h_{\varepsilon}(z) T^{-1}, \end{align*} $$
$$ \begin{align*}h_{\varepsilon}(\overline z) = \left(\begin{matrix} x & {-y} \cr y & x \end{matrix}\right) = T h_{\varepsilon}(z) T^{-1}, \end{align*} $$
where
![]() $T = i \left ( \begin {smallmatrix} 0 & 1 \cr 1 & 0 \end {smallmatrix} \right ) \in \mathrm {GO}_{2n}^J({\mathbb R})$
. By Lemma 8.1(iv),
$T = i \left ( \begin {smallmatrix} 0 & 1 \cr 1 & 0 \end {smallmatrix} \right ) \in \mathrm {GO}_{2n}^J({\mathbb R})$
. By Lemma 8.1(iv),
![]() $T \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
if n is even, which proves (ii) in that case. For n odd, the above identity shows
$T \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
if n is even, which proves (ii) in that case. For n odd, the above identity shows
![]() $z\mapsto h_{\varepsilon }(\overline z)$
and
$z\mapsto h_{\varepsilon }(\overline z)$
and
![]() $h_{\varepsilon }$
are conjugate under an outer automorphism. Thus, by (i), the cocharacter attached to
$h_{\varepsilon }$
are conjugate under an outer automorphism. Thus, by (i), the cocharacter attached to
![]() $h_{\varepsilon }(\overline z)$
is conjugate to
$h_{\varepsilon }(\overline z)$
is conjugate to
![]() $\mu _{-\varepsilon }$
.
$\mu _{-\varepsilon }$
.
By Lemma 9.1, the conditions of [Reference Deligne20, Prop. 1.2.2] on
![]() $(\mathrm {PSO}_{2n}^J, h_{\pm }(z))$
and
$(\mathrm {PSO}_{2n}^J, h_{\pm }(z))$
and
![]() $(\mathrm {PSO}_{2n}^J, h_{\pm }(\overline {z}))$
are satisfied. By this proposition, there exists a
$(\mathrm {PSO}_{2n}^J, h_{\pm }(\overline {z}))$
are satisfied. By this proposition, there exists a
![]() $g \in \mathrm {PSO}_{2n}^J({\mathbb {C}})$
that conjugates
$g \in \mathrm {PSO}_{2n}^J({\mathbb {C}})$
that conjugates
![]() $(\mathrm {PSO}_{2n, {\mathbb R}}^J, h_{\varepsilon }(\overline z))$
to
$(\mathrm {PSO}_{2n, {\mathbb R}}^J, h_{\varepsilon }(\overline z))$
to
![]() $(\mathrm {PSO}_{2n, {\mathbb R}}^J, h_{-\varepsilon }(z))$
. This implies that for all
$(\mathrm {PSO}_{2n, {\mathbb R}}^J, h_{-\varepsilon }(z))$
. This implies that for all
![]() $x \in \mathrm {PSO}_{2n}^J({\mathbb {C}})$
, we have
$x \in \mathrm {PSO}_{2n}^J({\mathbb {C}})$
, we have
![]() $g \overline x g^{-1} = \overline {g x g^{-1}}$
. Thus, also
$g \overline x g^{-1} = \overline {g x g^{-1}}$
. Thus, also
![]() $\overline g ^{-1} g \overline x = \overline x \overline g^{-1} g$
and
$\overline g ^{-1} g \overline x = \overline x \overline g^{-1} g$
and
![]() $\overline g^{-1} g \in Z(\mathrm {PSO}_{2n}^J({\mathbb {C}})) = \{1\}$
, and thus
$\overline g^{-1} g \in Z(\mathrm {PSO}_{2n}^J({\mathbb {C}})) = \{1\}$
, and thus
![]() $\overline g = g$
, which means
$\overline g = g$
, which means
![]() $g \in \mathrm {PSO}_{2n}^J({\mathbb R})$
. By Hilbert 90, we may lift g to an element
$g \in \mathrm {PSO}_{2n}^J({\mathbb R})$
. By Hilbert 90, we may lift g to an element
![]() $\widetilde {g} \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
. Then the map
$\widetilde {g} \in {\mathrm {GSO}}_{2n}^J({\mathbb R})$
. Then the map
![]() ${\mathbb {C}}^{\times } \owns z \mapsto \chi (z) := h^{-1}_{\varepsilon }(\overline z) \widetilde {g} h_{-\varepsilon }(z) \widetilde {g}^{-1}$
is a continuous homomorphism to
${\mathbb {C}}^{\times } \owns z \mapsto \chi (z) := h^{-1}_{\varepsilon }(\overline z) \widetilde {g} h_{-\varepsilon }(z) \widetilde {g}^{-1}$
is a continuous homomorphism to
![]() $Z({\mathrm {GSO}}_{2n}^J({\mathbb R})) = {\mathbb R}^{\times }$
. It suffices to show that
$Z({\mathrm {GSO}}_{2n}^J({\mathbb R})) = {\mathbb R}^{\times }$
. It suffices to show that
![]() $\chi $
is trivial. The subgroup
$\chi $
is trivial. The subgroup
![]() $\chi (U(1)) \subset {\mathbb R}^{\times }$
is connected and compact and hence trivial. Since
$\chi (U(1)) \subset {\mathbb R}^{\times }$
is connected and compact and hence trivial. Since
![]() $h_{\varepsilon }$
and
$h_{\varepsilon }$
and
![]() $h_{-\varepsilon }$
agree and are central on
$h_{-\varepsilon }$
agree and are central on
![]() ${\mathbb R}^{\times } \subset {\mathbb {C}}^{\times }$
, we have
${\mathbb R}^{\times } \subset {\mathbb {C}}^{\times }$
, we have
![]() $\chi ({\mathbb R}^{\times })=\{1\}$
as well. So
$\chi ({\mathbb R}^{\times })=\{1\}$
as well. So
![]() $\chi $
is trivial as desired. The proof for
$\chi $
is trivial as desired. The proof for
![]() $h_{-\varepsilon }$
is similar.
$h_{-\varepsilon }$
is similar.
Let G be as in Lemma 8.3. Let
![]() $X^{\varepsilon }$
be the
$X^{\varepsilon }$
be the
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb R})$
-conjugacy class of the morphism
$(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb R})$
-conjugacy class of the morphism
where the nontrivial component corresponds to the place
![]() $y_{\infty }$
. Then
$y_{\infty }$
. Then
![]() $\mu ^{\varepsilon } = (\mu _{\varepsilon }, 1, \ldots , 1) \in X_*((\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathbb {C}}) = X_*({\mathrm {GSO}}_{2n,{\mathbb {C}}})^{\mathcal V_{\infty }}$
is the cocharacter attached to
$\mu ^{\varepsilon } = (\mu _{\varepsilon }, 1, \ldots , 1) \in X_*((\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathbb {C}}) = X_*({\mathrm {GSO}}_{2n,{\mathbb {C}}})^{\mathcal V_{\infty }}$
is the cocharacter attached to
![]() $h_{\varepsilon }$
, in the same way as in Lemma 9.2 (i). The reflex field of
$h_{\varepsilon }$
, in the same way as in Lemma 9.2 (i). The reflex field of
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
means the field of definition for the conjugacy class of
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
means the field of definition for the conjugacy class of
![]() $\mu ^{\varepsilon }$
, as a subfield of
$\mu ^{\varepsilon }$
, as a subfield of
![]() ${\mathbb {C}}$
.
${\mathbb {C}}$
.
Lemma 9.3. Let
![]() $\varepsilon \in \{\pm 1\}$
. Then
$\varepsilon \in \{\pm 1\}$
. Then
-
(i) The pair
 $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is a Shimura datum of abelian type.
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is a Shimura datum of abelian type. -
(ii) The Shimura data
 $(\mathrm {Res}_{F/\mathbb {Q}} G, X^+)$
and
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^+)$
and
 $(\mathrm {Res}_{F/\mathbb {Q}} G, X^-)$
are isomorphic only if n is odd.
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^-)$
are isomorphic only if n is odd. -
(iii) If
 $F \neq \mathbb {Q}$
, the Shimura varieties attached to
$F \neq \mathbb {Q}$
, the Shimura varieties attached to
 $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
are projective.
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
are projective. -
(iv) The reflex field of the datum
 $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is equal to E, equipped with an embedding
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is equal to E, equipped with an embedding
 $x_{\infty }: E\hookrightarrow {\mathbb {C}}$
extending
$x_{\infty }: E\hookrightarrow {\mathbb {C}}$
extending
 $y_{\infty }:F\hookrightarrow {\mathbb {C}}$
.
$y_{\infty }:F\hookrightarrow {\mathbb {C}}$
.
Remark 9.4. About (i): When
![]() $F=\mathbb {Q}$
, the Shimura datum
$F=\mathbb {Q}$
, the Shimura datum
![]() $(G, X^{\varepsilon })$
can be shown to be of Hodge type, but we do not need this fact. About (ii): If n is odd and
$(G, X^{\varepsilon })$
can be shown to be of Hodge type, but we do not need this fact. About (ii): If n is odd and
![]() ${{{\mathfrak q}}_{\mathrm {St}}}$
is inert in
${{{\mathfrak q}}_{\mathrm {St}}}$
is inert in
![]() $E/F$
, then one can show that
$E/F$
, then one can show that
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G, X^+) \simeq (\mathrm {Res}_{F/\mathbb {Q}} G, X^-)$
.
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^+) \simeq (\mathrm {Res}_{F/\mathbb {Q}} G, X^-)$
.
Proof. (i) Clearly,
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathrm {ad}}$
has no compact factor defined over
$(\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathrm {ad}}$
has no compact factor defined over
![]() $\mathbb {Q}$
, which is one of Deligne’s axioms of Shimura datum [Reference Deligne20, 2.1]. The remaining two axioms follow from Lemma 9.1, and hence,
$\mathbb {Q}$
, which is one of Deligne’s axioms of Shimura datum [Reference Deligne20, 2.1]. The remaining two axioms follow from Lemma 9.1, and hence,
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is a Shimura datum. In the terminology of loc. cit.,
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is a Shimura datum. In the terminology of loc. cit.,
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is of type
$(\mathrm {Res}_{F/\mathbb {Q}} G, X^{\varepsilon })$
is of type
![]() $D^{\mathbb H}$
. By [Reference Deligne20, Prop. 2.3.10], a datum
$D^{\mathbb H}$
. By [Reference Deligne20, Prop. 2.3.10], a datum
![]() $(G', X')$
of type
$(G', X')$
of type
![]() $D^{\mathbb H}$
is of abelian type if the derived group of
$D^{\mathbb H}$
is of abelian type if the derived group of
![]() $G^{\prime }_{{\mathbb {C}}}$
is (a product of)
$G^{\prime }_{{\mathbb {C}}}$
is (a product of)
![]() ${\mathrm {SO}}_{2n,{\mathbb {C}}}$
. (Not all Shimura data of type
${\mathrm {SO}}_{2n,{\mathbb {C}}}$
. (Not all Shimura data of type
![]() $D^{\mathbb H}$
are of abelian type.)
$D^{\mathbb H}$
are of abelian type.)
(ii) If n is even, then every automorphism of
![]() $(G_{F_{y_{\infty }}})_{\mathrm {ad}}$
(isomorphic to
$(G_{F_{y_{\infty }}})_{\mathrm {ad}}$
(isomorphic to
![]() ${\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
) is inner by Lemma 8.1 (v). However, it follows from Lemma 9.2 (i) that no inner automorphism of
${\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
) is inner by Lemma 8.1 (v). However, it follows from Lemma 9.2 (i) that no inner automorphism of
![]() ${\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
takes
${\mathrm {GSO}}_{2n,\mathrm {ad}}^J$
takes
![]() $\mathrm {Ad}\circ h_+$
to
$\mathrm {Ad}\circ h_+$
to
![]() $\mathrm {Ad}\circ h_-$
, since
$\mathrm {Ad}\circ h_-$
, since
![]() $\mathrm {Ad}\circ \mu _+$
to
$\mathrm {Ad}\circ \mu _+$
to
![]() $\mathrm {Ad}\circ \mu _-$
are not conjugate by
$\mathrm {Ad}\circ \mu _-$
are not conjugate by
![]() ${\mathrm {GSO}}_{2n,\mathrm {ad}}({\mathbb {C}})$
. Hence, no automorphism of
${\mathrm {GSO}}_{2n,\mathrm {ad}}({\mathbb {C}})$
. Hence, no automorphism of
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G)_{{\mathbb R}}$
(thus also of
$(\mathrm {Res}_{F/\mathbb {Q}} G)_{{\mathbb R}}$
(thus also of
![]() $\mathrm {Res}_{F/\mathbb {Q}} G$
) carries
$\mathrm {Res}_{F/\mathbb {Q}} G$
) carries
![]() $X^+$
onto
$X^+$
onto
![]() $X^-$
.
$X^-$
.
(iii) If
![]() $F \neq \mathbb {Q}$
, there exists some real place
$F \neq \mathbb {Q}$
, there exists some real place
![]() $y_{\infty }' \in \mathcal V_{\infty }$
of F different from
$y_{\infty }' \in \mathcal V_{\infty }$
of F different from
![]() $y_{\infty }$
. Since
$y_{\infty }$
. Since
![]() $G_{y_{\infty }'}$
is compact modulo center,
$G_{y_{\infty }'}$
is compact modulo center,
![]() $\mathrm {Res}_{F/\mathbb {Q}}G$
is anisotropic modulo center over
$\mathrm {Res}_{F/\mathbb {Q}}G$
is anisotropic modulo center over
![]() $\mathbb {Q}$
. Hence, the associated Shimura varieties are projective by Bailey-Borel [Reference Baily and Borel2, Thm. 1].
$\mathbb {Q}$
. Hence, the associated Shimura varieties are projective by Bailey-Borel [Reference Baily and Borel2, Thm. 1].
(iv) Assume that n is odd (thus,
![]() $[E:F]=2$
). Suppose that
$[E:F]=2$
). Suppose that
![]() $\sigma \in \mathrm {Aut}({\mathbb {C}}/\mathbb {Q})$
stabilizes the conjugacy class of
$\sigma \in \mathrm {Aut}({\mathbb {C}}/\mathbb {Q})$
stabilizes the conjugacy class of
![]() $\mu ^{\varepsilon }$
. Since
$\mu ^{\varepsilon }$
. Since
![]() $\sigma (\mu ^{\varepsilon }) \sim \mu ^{\varepsilon }$
, we have
$\sigma (\mu ^{\varepsilon }) \sim \mu ^{\varepsilon }$
, we have
![]() $\sigma (y_{\infty }) = y_{\infty }$
, so
$\sigma (y_{\infty }) = y_{\infty }$
, so
![]() $\sigma \in \mathrm {Aut}({\mathbb {C}}/F)$
with respect to
$\sigma \in \mathrm {Aut}({\mathbb {C}}/F)$
with respect to
![]() $y_{\infty }:F\hookrightarrow {\mathbb {C}}$
. If
$y_{\infty }:F\hookrightarrow {\mathbb {C}}$
. If
![]() $\sigma $
has nontrivial image in
$\sigma $
has nontrivial image in
![]() ${\mathrm {Gal}}(E/F)$
, then Lemma 9.2 (ii) tells us that
${\mathrm {Gal}}(E/F)$
, then Lemma 9.2 (ii) tells us that
![]() $\sigma (\mu ^{\varepsilon }) \sim (\mu _{-\varepsilon }, 1, \ldots , 1)$
, which is not
$\sigma (\mu ^{\varepsilon }) \sim (\mu _{-\varepsilon }, 1, \ldots , 1)$
, which is not
![]() ${\mathrm {GSO}}_{2n}({\mathbb {C}})$
-conjugate to
${\mathrm {GSO}}_{2n}({\mathbb {C}})$
-conjugate to
![]() $\mu ^{\varepsilon }$
. Thus,
$\mu ^{\varepsilon }$
. Thus,
![]() $\sigma $
is trivial on E (embedded in
$\sigma $
is trivial on E (embedded in
![]() ${\mathbb {C}}$
extending
${\mathbb {C}}$
extending
![]() $y_{\infty }$
). Conversely, if
$y_{\infty }$
). Conversely, if
![]() $\sigma \in \mathrm {Aut}({\mathbb {C}}/E)$
, then
$\sigma \in \mathrm {Aut}({\mathbb {C}}/E)$
, then
![]() $\sigma (\mu ^{\varepsilon }) = \mu ^{\varepsilon }$
. Hence, the reflex field is E. When n is even (thus
$\sigma (\mu ^{\varepsilon }) = \mu ^{\varepsilon }$
. Hence, the reflex field is E. When n is even (thus
![]() $E=F$
), the preceding argument shows that the reflex field is F.
$E=F$
), the preceding argument shows that the reflex field is F.
We introduce the following notation. Let
![]() $\varepsilon \in \{+,-\}$
.
$\varepsilon \in \{+,-\}$
.
-
• Taking an algebraic closure of E in
 ${\mathbb {C}}$
via
${\mathbb {C}}$
via
 $x_{\infty }:E\hookrightarrow {\mathbb {C}}$
, we fix
$x_{\infty }:E\hookrightarrow {\mathbb {C}}$
, we fix
 $\overline {F}=\overline E\hookrightarrow {\mathbb {C}}$
.
$\overline {F}=\overline E\hookrightarrow {\mathbb {C}}$
. -
• We fix an isomorphism
 $G \otimes _F \mathbb A_F^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}} \simeq G^{*} \otimes _F \mathbb A_F^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}}$
.
$G \otimes _F \mathbb A_F^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}} \simeq G^{*} \otimes _F \mathbb A_F^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}}$
. -
• Z is the center of G.
-
•
 $\xi =\otimes _{y|\infty } \xi _y$
is an irreducible algebraic representation of
$\xi =\otimes _{y|\infty } \xi _y$
is an irreducible algebraic representation of
 $(\mathrm {Res}_{F/\mathbb {Q}}G)\times _{\mathbb {Q}} {\mathbb {C}}=\prod _{y|\infty }G\times _{F,y} {\mathbb {C}}$
.
$(\mathrm {Res}_{F/\mathbb {Q}}G)\times _{\mathbb {Q}} {\mathbb {C}}=\prod _{y|\infty }G\times _{F,y} {\mathbb {C}}$
. -
•
 $\Pi _{\xi }^{G(F_{\infty })}$
is the set of isomorphism classes of (irreducible) discrete series representations of
$\Pi _{\xi }^{G(F_{\infty })}$
is the set of isomorphism classes of (irreducible) discrete series representations of
 $G(F_{\infty })$
which have the same infinitesimal and central characters as
$G(F_{\infty })$
which have the same infinitesimal and central characters as
 $\xi ^{\vee }$
.
$\xi ^{\vee }$
. -
•
 $K_{\infty }^{\varepsilon }$
is the centralizer of
$K_{\infty }^{\varepsilon }$
is the centralizer of
 $h^{\varepsilon }$
in
$h^{\varepsilon }$
in
 $(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb R})=G(F_{\infty })$
.
$(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb R})=G(F_{\infty })$
. -
• For irreducible admissible representations
 $\tau _{\infty }$
of
$\tau _{\infty }$
of
 $G(F_{\infty })$
, put (9.2)
$G(F_{\infty })$
, put (9.2) $$ \begin{align} \mathrm{ep}^{\varepsilon}(\tau_{\infty} \otimes \xi): = \sum_{i=1}^{n(n-1)} (-1)^i \dim \mathrm{H}^i(\mathrm{Lie}\, G(F_{\infty}), K_{\infty}^{\varepsilon}; \tau_{\infty} \otimes \xi). \end{align} $$
$$ \begin{align} \mathrm{ep}^{\varepsilon}(\tau_{\infty} \otimes \xi): = \sum_{i=1}^{n(n-1)} (-1)^i \dim \mathrm{H}^i(\mathrm{Lie}\, G(F_{\infty}), K_{\infty}^{\varepsilon}; \tau_{\infty} \otimes \xi). \end{align} $$
Let
![]() $\pi ^{\natural }$
be a cuspidal automorphic representation of
$\pi ^{\natural }$
be a cuspidal automorphic representation of
![]() $G(\mathbb A_F)$
such that
$G(\mathbb A_F)$
such that
-
•
 $\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is a Steinberg representation up to a character twist,
$\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is a Steinberg representation up to a character twist, -
•
 $\pi ^{\natural }$
is
$\pi ^{\natural }$
is
 $\xi $
-cohomological.
$\xi $
-cohomological.
The latter condition implies via (the proof of) [Reference Kret and Shin50, Lem. 7.1] the following condition:
-
(cent) There exists an integer
 $w \in \mathbb Z$
, called the central weight of
$w \in \mathbb Z$
, called the central weight of
 $\xi $
, such that for every infinite F-place
$\xi $
, such that for every infinite F-place
 $y|\infty $
, the central character of
$y|\infty $
, the central character of
 $\xi _y$
is of the form
$\xi _y$
is of the form
 $x \mapsto x^w$
.
$x \mapsto x^w$
.
We also make the following assumption:
-
(temp)
 $\pi ^{\natural }_{{\mathfrak q}}$
is essentially tempered at every finite F-place
$\pi ^{\natural }_{{\mathfrak q}}$
is essentially tempered at every finite F-place
 ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
 $\pi _{{\mathfrak q}}$
is unramified.
$\pi _{{\mathfrak q}}$
is unramified.
This may seem strong, but (temp) will be satisfied in practice; see the paragraph above (10.4). Let
![]() $A(\pi ^{\natural })$
be the set of (isomorphism classes of) cuspidal automorphic representations
$A(\pi ^{\natural })$
be the set of (isomorphism classes of) cuspidal automorphic representations
![]() $\tau $
of
$\tau $
of
![]() $G(\mathbb A_F)$
such that
$G(\mathbb A_F)$
such that
-
(i)
 $\tau _{{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}\otimes \delta $
for an unramified character
$\tau _{{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}\otimes \delta $
for an unramified character
 $\delta $
of the group
$\delta $
of the group
 $G(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
,
$G(F_{{{{\mathfrak q}}_{\mathrm {St}}}})$
, -
(ii)
 $\tau ^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \pi ^{\natural , \infty , {{{\mathfrak q}}_{\mathrm {St}}}}$
and
$\tau ^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}\simeq \pi ^{\natural , \infty , {{{\mathfrak q}}_{\mathrm {St}}}}$
and -
(iii)
 $\tau _{\infty }$
is
$\tau _{\infty }$
is
 $\xi $
-cohomological.
$\xi $
-cohomological.
By (temp),
![]() $\tau _{{\mathfrak q}}$
is essentially tempered at every
$\tau _{{\mathfrak q}}$
is essentially tempered at every
![]() ${{\mathfrak q}}$
where
${{\mathfrak q}}$
where
![]() $\pi _{{\mathfrak q}}$
is unramified. Define
$\pi _{{\mathfrak q}}$
is unramified. Define
 $$ \begin{align} a^{\varepsilon}(\pi^{\natural}) := (-1)^{n(n-1)/2} N^{-1}_{\infty} \sum_{\tau \in A(\pi^{\natural})} m(\tau) \cdot \mathrm{ep}^{\varepsilon}(\tau_{\infty} \otimes \xi) \in \mathbb{Q}, \end{align} $$
$$ \begin{align} a^{\varepsilon}(\pi^{\natural}) := (-1)^{n(n-1)/2} N^{-1}_{\infty} \sum_{\tau \in A(\pi^{\natural})} m(\tau) \cdot \mathrm{ep}^{\varepsilon}(\tau_{\infty} \otimes \xi) \in \mathbb{Q}, \end{align} $$
where
![]() $m(\tau )$
is the multiplicity of
$m(\tau )$
is the multiplicity of
![]() $\tau $
in the discrete automorphic spectrum of G, and
$\tau $
in the discrete automorphic spectrum of G, and
 $$ \begin{align} N_{\infty} := |\Pi_{\xi}^{G(F_{\infty})}| \cdot |\pi_0(G(F_{\infty})/Z(F_{\infty}))| = \begin{cases} 2^{n-1} \cdot 2, & \mbox{if}~n~\mbox{is~even},\\ 2^{n-1} , & \mbox{if}~n~\mbox{is~odd}. \end{cases} \end{align} $$
$$ \begin{align} N_{\infty} := |\Pi_{\xi}^{G(F_{\infty})}| \cdot |\pi_0(G(F_{\infty})/Z(F_{\infty}))| = \begin{cases} 2^{n-1} \cdot 2, & \mbox{if}~n~\mbox{is~even},\\ 2^{n-1} , & \mbox{if}~n~\mbox{is~odd}. \end{cases} \end{align} $$
Here,
![]() $|\pi _0(G(F_{\infty })/Z(F_{\infty }))|\in \{1,2\}$
depending on the parity of n from Lemma 8.1 (iii), (vi).
$|\pi _0(G(F_{\infty })/Z(F_{\infty }))|\in \{1,2\}$
depending on the parity of n from Lemma 8.1 (iii), (vi).
Lemma 9.5. The groups
![]() $K_{\infty }^+$
and
$K_{\infty }^+$
and
![]() $K_{\infty }^-$
are
$K_{\infty }^-$
are
![]() $G(F_{\infty })$
-conjugate. In particular,
$G(F_{\infty })$
-conjugate. In particular,
![]() $a^-(\pi ^{\natural }) = a^+(\pi ^{\natural })$
.
$a^-(\pi ^{\natural }) = a^+(\pi ^{\natural })$
.
Henceforth, we will write
![]() $a(\pi ^{\natural })\in \mathbb {Q}$
for the common value of
$a(\pi ^{\natural })\in \mathbb {Q}$
for the common value of
![]() $a^{\varepsilon }(\pi ^{\natural })$
.
$a^{\varepsilon }(\pi ^{\natural })$
.
Proof. The
![]() $y_{\infty }$
-components of
$y_{\infty }$
-components of
![]() $K_{\infty }^{\varepsilon }$
is
$K_{\infty }^{\varepsilon }$
is
![]() $K_{\varepsilon }$
, which are conjugate to each other by Lemma 9.1. The components of
$K_{\varepsilon }$
, which are conjugate to each other by Lemma 9.1. The components of
![]() $K_{\infty }^{\varepsilon }$
at the other real places y equal
$K_{\infty }^{\varepsilon }$
at the other real places y equal
![]() $G(F_y)\simeq {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
, which is connected. Therefore,
$G(F_y)\simeq {\mathrm {GSO}}_{2n}^{\mathrm {cpt}}({\mathbb R})$
, which is connected. Therefore,
![]() $K_{\infty }^+$
and
$K_{\infty }^+$
and
![]() $K_{\infty }^-$
are connected and
$K_{\infty }^-$
are connected and
![]() $G(F_{\infty })$
-conjugate. It then follows that
$G(F_{\infty })$
-conjugate. It then follows that
![]() $\mathrm {ep}^+(\tau _{\infty } \otimes \xi ) = \mathrm {ep}^-(\tau _{\infty } \otimes \xi )$
for all
$\mathrm {ep}^+(\tau _{\infty } \otimes \xi ) = \mathrm {ep}^-(\tau _{\infty } \otimes \xi )$
for all
![]() $\tau _{\infty }$
. Thus,
$\tau _{\infty }$
. Thus,
![]() $a^+(\pi ^{\natural }) = a^-(\pi ^{\natural })$
.
$a^+(\pi ^{\natural }) = a^-(\pi ^{\natural })$
.
Since condition (cent) holds, we can attach to
![]() $\xi $
a lisse
$\xi $
a lisse
![]() $\overline {\mathbb {Q}}_{\ell }$
-sheaf
$\overline {\mathbb {Q}}_{\ell }$
-sheaf
![]() ${\mathcal L}_{\iota \xi }$
on
${\mathcal L}_{\iota \xi }$
on
![]() $\mathrm {Sh}^{\varepsilon }_K$
as in [Reference Kret and Shin50, below Lem. 7.1] and [Reference Carayol15, Sect. 2.1, 2.1.4]. We have a canonical model
$\mathrm {Sh}^{\varepsilon }_K$
as in [Reference Kret and Shin50, below Lem. 7.1] and [Reference Carayol15, Sect. 2.1, 2.1.4]. We have a canonical model
![]() $\mathrm {Sh}^{\varepsilon }_{K}$
over E for each neat open compact subgroup
$\mathrm {Sh}^{\varepsilon }_{K}$
over E for each neat open compact subgroup
![]() $K\subset G(\mathbb A_F^{\infty })$
(see [Reference Pink66, §0] for the definition of neat subgroups) and a distinguished embedding
$K\subset G(\mathbb A_F^{\infty })$
(see [Reference Pink66, §0] for the definition of neat subgroups) and a distinguished embedding
![]() $E\subset \overline {F}$
(compatible with
$E\subset \overline {F}$
(compatible with
![]() $E\subset {\mathbb {C}}$
and the fixed embedding
$E\subset {\mathbb {C}}$
and the fixed embedding
![]() $\overline {F}\hookrightarrow {\mathbb {C}}$
). We take the limit over K of the étale cohomology of with compact support
$\overline {F}\hookrightarrow {\mathbb {C}}$
). We take the limit over K of the étale cohomology of with compact support
equipped with commuting linear actions of
![]() $\Gamma _E={\mathrm {Gal}}(\overline {F}/E)$
and
$\Gamma _E={\mathrm {Gal}}(\overline {F}/E)$
and
![]() $G(\mathbb A_F^{\infty })$
. The two groups act continuously and admissibly, respectively. Write
$G(\mathbb A_F^{\infty })$
. The two groups act continuously and admissibly, respectively. Write
![]() $\mathrm {H}_{\mathrm {c}}^i(\mathrm {Sh}_K^{\varepsilon }, {\mathcal L}_{\iota \xi })^{\mathrm {ss}}$
for the semisimplification as a
$\mathrm {H}_{\mathrm {c}}^i(\mathrm {Sh}_K^{\varepsilon }, {\mathcal L}_{\iota \xi })^{\mathrm {ss}}$
for the semisimplification as a
![]() $\Gamma _E\times G(\mathbb A_F^{\infty })$
-module. (No semisimplification is necessary for the
$\Gamma _E\times G(\mathbb A_F^{\infty })$
-module. (No semisimplification is necessary for the
![]() $ G(\mathbb A_F^{\infty })$
-action if
$ G(\mathbb A_F^{\infty })$
-action if
![]() $F\neq \mathbb {Q}$
, in which case
$F\neq \mathbb {Q}$
, in which case
![]() $\mathrm {Sh}_K^{\varepsilon }$
is projective. This can be seen from the semisimplicity of the discrete
$\mathrm {Sh}_K^{\varepsilon }$
is projective. This can be seen from the semisimplicity of the discrete
![]() $L^2$
-automorphic spectrum via Matsushima’s formula.)
$L^2$
-automorphic spectrum via Matsushima’s formula.)
We construct Galois representations of
![]() $\Gamma _E$
by taking the
$\Gamma _E$
by taking the
![]() $\iota \tau ^{\infty }$
-isotypic part in the cohomology as follows. We consider
$\iota \tau ^{\infty }$
-isotypic part in the cohomology as follows. We consider
![]() $\tau _1,\tau _2\in A(\pi ^{\natural })$
are equivalent and write
$\tau _1,\tau _2\in A(\pi ^{\natural })$
are equivalent and write
![]() $\tau _1\sim \tau _2$
if
$\tau _1\sim \tau _2$
if
![]() $\tau _1^{\infty }\simeq \tau _2^{\infty }$
. Let
$\tau _1^{\infty }\simeq \tau _2^{\infty }$
. Let
![]() $A(\pi ^{\natural })/{\sim }$
denote the set of (representatives for) equivalence classes. Let
$A(\pi ^{\natural })/{\sim }$
denote the set of (representatives for) equivalence classes. Let
![]() $\tau \in A(\pi ^{\natural })$
. Define
$\tau \in A(\pi ^{\natural })$
. Define
 $$ \begin{align} \rho_{\pi^{\natural}}^{\mathrm{Sh}, \varepsilon}:=(-1)^{n(n-1)/2} \sum_{\tau \in A(\pi^{\natural})/\sim} \sum_{i=0}^{n(n-1)} (-1)^i \mathrm{H}_c^i(\mathrm{Sh}^{\varepsilon}, {\mathcal L}_{\xi})[\iota\tau^{\infty}]. \end{align} $$
$$ \begin{align} \rho_{\pi^{\natural}}^{\mathrm{Sh}, \varepsilon}:=(-1)^{n(n-1)/2} \sum_{\tau \in A(\pi^{\natural})/\sim} \sum_{i=0}^{n(n-1)} (-1)^i \mathrm{H}_c^i(\mathrm{Sh}^{\varepsilon}, {\mathcal L}_{\xi})[\iota\tau^{\infty}]. \end{align} $$
A priori
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
is an alternating sum of semisimple representations of
$\rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
is an alternating sum of semisimple representations of
![]() $\Gamma _E$
and thus a virtual representation (but see Theorem 9.6 below). Fix a neat open compact subgroup
$\Gamma _E$
and thus a virtual representation (but see Theorem 9.6 below). Fix a neat open compact subgroup
 $$ \begin{align*}K = \prod_{{{\mathfrak q}} \nmid \infty} K_{\mathfrak{q}} \subset G(\mathbb A_F^{\infty})\quad\mbox{such~that}\quad(\pi^{\natural, \infty})^ K \neq 0, \end{align*} $$
$$ \begin{align*}K = \prod_{{{\mathfrak q}} \nmid \infty} K_{\mathfrak{q}} \subset G(\mathbb A_F^{\infty})\quad\mbox{such~that}\quad(\pi^{\natural, \infty})^ K \neq 0, \end{align*} $$
and also such that
![]() $K_{{\mathfrak q}}$
is hyperspecial whenever
$K_{{\mathfrak q}}$
is hyperspecial whenever
![]() $\pi ^{\natural }_{{\mathfrak q}}$
(or equivalently
$\pi ^{\natural }_{{\mathfrak q}}$
(or equivalently
![]() $\pi _{{\mathfrak q}}$
) is unramified. Let
$\pi _{{\mathfrak q}}$
) is unramified. Let
![]() $S_{\mathrm {bad}}$
be the set of rational primes p for which either
$S_{\mathrm {bad}}$
be the set of rational primes p for which either
-
•
 $p=2$
,
$p=2$
, -
•
 $\mathrm {Res}_{F/\mathbb {Q}} G$
is ramified over
$\mathrm {Res}_{F/\mathbb {Q}} G$
is ramified over
 $\mathbb {Q}_p$
or
$\mathbb {Q}_p$
or -
•
 $K_p = \prod _{{{\mathfrak q}}|p} K_{\mathfrak {q}}$
is not hyperspecial.
$K_p = \prod _{{{\mathfrak q}}|p} K_{\mathfrak {q}}$
is not hyperspecial.
We write
![]() $S^F_{\mathrm {bad}}$
(resp.
$S^F_{\mathrm {bad}}$
(resp.
![]() $S^E_{\mathrm {bad}}$
) for the F-places (resp.
$S^E_{\mathrm {bad}}$
) for the F-places (resp.
![]() ${E}$
-places) above
${E}$
-places) above
![]() $S_{\mathrm {bad}}$
. We apply the Langlands–Kottwitz method at level K to compute the image of Frobenius elements under
$S_{\mathrm {bad}}$
. We apply the Langlands–Kottwitz method at level K to compute the image of Frobenius elements under
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
at almost all primes.
$\rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
at almost all primes.
Theorem 9.6. Consider
![]() $\pi ^{\natural }$
satisfying condition (temp); see below (9.2). There exists a finite set of rational primes S containing
$\pi ^{\natural }$
satisfying condition (temp); see below (9.2). There exists a finite set of rational primes S containing
![]() $S_{\mathrm {bad}}$
, such that for all
$S_{\mathrm {bad}}$
, such that for all
![]() ${\mathfrak p}$
not above S and all sufficiently large integers j (with the lower bound for j depending on
${\mathfrak p}$
not above S and all sufficiently large integers j (with the lower bound for j depending on
![]() ${\mathfrak p}$
), writing
${\mathfrak p}$
), writing
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
, we have
${{\mathfrak q}}:={\mathfrak p}\cap F$
, we have
Moreover, the summand of (9.6) is nonzero only if
![]() $i=n(n-1)/2$
. In particular, the virtual representation
$i=n(n-1)/2$
. In particular, the virtual representation
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is a true semisimple representation.
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is a true semisimple representation.
Proof. We mimic the proof of [Reference Kret and Shin50, Prop. 8.2] closely. Note that our
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
corresponds to
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
corresponds to
![]() $\rho _2^{\mathrm {shim}}$
there. Another difference is that we use S to denote a set of primes of
$\rho _2^{\mathrm {shim}}$
there. Another difference is that we use S to denote a set of primes of
![]() $\mathbb {Q}$
(not F or E). It is enough to find S as in the theorem for each
$\mathbb {Q}$
(not F or E). It is enough to find S as in the theorem for each
![]() $\varepsilon $
separately, as we can take the union of the set for each of
$\varepsilon $
separately, as we can take the union of the set for each of
![]() $+$
and
$+$
and
![]() $-$
(and take the maximum of lower bounds for j). We suppose that
$-$
(and take the maximum of lower bounds for j). We suppose that
![]() $F\neq \mathbb {Q}$
so that our Shimura varieties are proper. The case
$F\neq \mathbb {Q}$
so that our Shimura varieties are proper. The case
![]() $F=\mathbb {Q}$
will be addressed at the end of proof.
$F=\mathbb {Q}$
will be addressed at the end of proof.
Let
![]() $f_{\infty }= N_{\infty }^{-1} f_{\xi }$
, where
$f_{\infty }= N_{\infty }^{-1} f_{\xi }$
, where
![]() $f_{\xi }$
is the Euler-Poincaré (a.k.a. Lefschetz) function for
$f_{\xi }$
is the Euler-Poincaré (a.k.a. Lefschetz) function for
![]() $\xi $
on
$\xi $
on
![]() $G(F_{\infty })$
as recalled in [Reference Kret and Shin50, Appendix A]. Then
$G(F_{\infty })$
as recalled in [Reference Kret and Shin50, Appendix A]. Then
 $$ \begin{align*}\mathrm{Tr}\, \tau_{\infty}(f_{\infty})=N_{\infty}^{-1} \mathrm{ep}^{\varepsilon}(\tau_{\infty}\otimes\xi)=N_{\infty}^{-1}\sum_{i = 0}^{\infty} (-1)^i \dim \mathrm{H}^i(\mathfrak g, K^{\varepsilon}_{\infty}; \tau_{\infty} \otimes \xi). \end{align*} $$
$$ \begin{align*}\mathrm{Tr}\, \tau_{\infty}(f_{\infty})=N_{\infty}^{-1} \mathrm{ep}^{\varepsilon}(\tau_{\infty}\otimes\xi)=N_{\infty}^{-1}\sum_{i = 0}^{\infty} (-1)^i \dim \mathrm{H}^i(\mathfrak g, K^{\varepsilon}_{\infty}; \tau_{\infty} \otimes \xi). \end{align*} $$
Choose a decomposable Hecke operator
![]() $f^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}=\prod _{{{\mathfrak q}}\neq {{{\mathfrak q}}_{\mathrm {St}}}} f_{\mathfrak {q}} \in \mathcal H(G(\mathbb A^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}_F)// K^{{{{\mathfrak q}}_{\mathrm {St}}}})$
such that for all automorphic representations
$f^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}=\prod _{{{\mathfrak q}}\neq {{{\mathfrak q}}_{\mathrm {St}}}} f_{\mathfrak {q}} \in \mathcal H(G(\mathbb A^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}}_F)// K^{{{{\mathfrak q}}_{\mathrm {St}}}})$
such that for all automorphic representations
![]() $\tau $
of
$\tau $
of
![]() $G(\mathbb A_F)$
with
$G(\mathbb A_F)$
with
![]() $\tau ^{\infty ,K} \neq 0$
and
$\tau ^{\infty ,K} \neq 0$
and
![]() $\mathrm {Tr}\, \tau _{\infty }(f_{\infty }) \neq 0$
, we have
$\mathrm {Tr}\, \tau _{\infty }(f_{\infty }) \neq 0$
, we have
 $$ \begin{align*}\mathrm{Tr}\,\tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}}(f^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}}) = \begin{cases} 1 & \mathrm{if \ } \tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}} \simeq \pi^{\natural,\infty,{{{\mathfrak q}}_{\mathrm{St}}}} \cr 0 & \mathrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\mathrm{Tr}\,\tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}}(f^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}}) = \begin{cases} 1 & \mathrm{if \ } \tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}} \simeq \pi^{\natural,\infty,{{{\mathfrak q}}_{\mathrm{St}}}} \cr 0 & \mathrm{otherwise.} \end{cases} \end{align*} $$
This is possible since there are only finitely many such
![]() $\tau $
(one of which is
$\tau $
(one of which is
![]() $\pi ^{\natural }$
). Let
$\pi ^{\natural }$
). Let
![]() $f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
be a Lefschetz function from [Reference Kret and Shin50, Eq. (A.4)]. There exists a finite set of primes
$f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
be a Lefschetz function from [Reference Kret and Shin50, Eq. (A.4)]. There exists a finite set of primes
![]() $\Sigma \supset S_{\mathrm {bad}}\cup \{\ell \}$
such that
$\Sigma \supset S_{\mathrm {bad}}\cup \{\ell \}$
such that
![]() $f_{{\mathfrak p}'}$
is the characteristic function of
$f_{{\mathfrak p}'}$
is the characteristic function of
![]() $K_{{\mathfrak p}'}$
(which is hyperspecial) for every
$K_{{\mathfrak p}'}$
(which is hyperspecial) for every
![]() ${\mathfrak p}'$
not above
${\mathfrak p}'$
not above
![]() $\Sigma $
. We fix
$\Sigma $
. We fix
![]() $\Sigma $
and
$\Sigma $
and
![]() $f^{\infty }=\prod _{v\nmid \infty } f_v$
as above.
$f^{\infty }=\prod _{v\nmid \infty } f_v$
as above.
In the rest of the proof, we fix an E-prime
![]() ${\mathfrak p}$
not above
${\mathfrak p}$
not above
![]() $\Sigma \cup \{\ell \}$
. Write
$\Sigma \cup \{\ell \}$
. Write
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
, and p for the rational prime below
${{\mathfrak q}}:={\mathfrak p}\cap F$
, and p for the rational prime below
![]() ${\mathfrak p}$
. To apply the Langlands–Kottwitz method, we need an integral model for
${\mathfrak p}$
. To apply the Langlands–Kottwitz method, we need an integral model for
![]() $\mathrm {Sh}^{\varepsilon }_K$
over
$\mathrm {Sh}^{\varepsilon }_K$
over
![]() $\mathcal O_{E_{{\mathfrak p}}}$
. Thus, we choose an isomorphism
$\mathcal O_{E_{{\mathfrak p}}}$
. Thus, we choose an isomorphism
![]() $\iota _p:{\mathbb {C}}\stackrel {\sim }{\to } \overline {\mathbb {Q}}_p$
such that the valuation on
$\iota _p:{\mathbb {C}}\stackrel {\sim }{\to } \overline {\mathbb {Q}}_p$
such that the valuation on
![]() $\overline {\mathbb {Q}}_p$
restricts to the
$\overline {\mathbb {Q}}_p$
restricts to the
![]() ${\mathfrak p}$
-adic valuation via
${\mathfrak p}$
-adic valuation via
![]() $\iota _p x_{\infty }: E\hookrightarrow \overline {\mathbb {Q}}_p$
. (Recall
$\iota _p x_{\infty }: E\hookrightarrow \overline {\mathbb {Q}}_p$
. (Recall
![]() $x_{\infty }$
from Lemma 9.3 (iv).) The
$x_{\infty }$
from Lemma 9.3 (iv).) The
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)(\overline {\mathbb {Q}}_p)$
-conjugacy class of
$(\mathrm {Res}_{F/\mathbb {Q}}G)(\overline {\mathbb {Q}}_p)$
-conjugacy class of
![]() $\iota _p \mu :\mathbb G_m\rightarrow (\mathrm {Res}_{F/\mathbb {Q}}G)_{\overline {\mathbb {Q}}_p}$
is defined over
$\iota _p \mu :\mathbb G_m\rightarrow (\mathrm {Res}_{F/\mathbb {Q}}G)_{\overline {\mathbb {Q}}_p}$
is defined over
![]() $E_{\mathfrak p}$
.
$E_{\mathfrak p}$
.
For
![]() $j\in \mathbb Z_{\ge 1}$
, let
$j\in \mathbb Z_{\ge 1}$
, let
![]() $f^{(j)}_p$
, denote the function in the unramified Hecke algebra of
$f^{(j)}_p$
, denote the function in the unramified Hecke algebra of
![]() $G(F_p)$
constructed in [Reference Kottwitz47, §7] for the endoscopic group
$G(F_p)$
constructed in [Reference Kottwitz47, §7] for the endoscopic group
![]() $H=G^{*}$
, which is isomorphic to G over
$H=G^{*}$
, which is isomorphic to G over
![]() $F_p=F\otimes _{\mathbb {Q}} \mathbb {Q}_p$
. (This is the function
$F_p=F\otimes _{\mathbb {Q}} \mathbb {Q}_p$
. (This is the function
![]() $h_p$
in loc. cit. We take s and
$h_p$
in loc. cit. We take s and
![]() $t_i$
’s on p.179 there to be trivial, so that
$t_i$
’s on p.179 there to be trivial, so that
![]() $h_p$
is the image of
$h_p$
is the image of
![]() $\phi _j$
under the standard base change map on p.180.) The L-group for
$\phi _j$
under the standard base change map on p.180.) The L-group for
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)_{E_{{\mathfrak p}}}$
(with coefficients in
$(\mathrm {Res}_{F/\mathbb {Q}}G)_{E_{{\mathfrak p}}}$
(with coefficients in
![]() ${\mathbb {C}}$
) can be identified as
${\mathbb {C}}$
) can be identified as
 $$ \begin{align*}^L (\mathrm{Res}_{F/\mathbb{Q}}G)_{E_{{\mathfrak p}}} = \Big(\prod_{\sigma\in \mathrm{Hom}(F,\overline{\mathbb{Q}}_p)} \widehat G \Big) \rtimes \Gamma_{E_{{\mathfrak p}}},\end{align*} $$
$$ \begin{align*}^L (\mathrm{Res}_{F/\mathbb{Q}}G)_{E_{{\mathfrak p}}} = \Big(\prod_{\sigma\in \mathrm{Hom}(F,\overline{\mathbb{Q}}_p)} \widehat G \Big) \rtimes \Gamma_{E_{{\mathfrak p}}},\end{align*} $$
where
![]() $\Gamma _{E_{{\mathfrak p}}}$
acts trivially on the factor for
$\Gamma _{E_{{\mathfrak p}}}$
acts trivially on the factor for
![]() $\sigma =\iota _p y_{\infty }$
. (The Galois action may permute the other factors via its natural action on
$\sigma =\iota _p y_{\infty }$
. (The Galois action may permute the other factors via its natural action on
![]() $\mathrm {Hom}(F,\overline {\mathbb {Q}}_p)$
, but this does not matter to us.) The representation of
$\mathrm {Hom}(F,\overline {\mathbb {Q}}_p)$
, but this does not matter to us.) The representation of
![]() $^L (\mathrm {Res}_{F/\mathbb {Q}}G)_{E_{{\mathfrak p}}}$
of highest weight
$^L (\mathrm {Res}_{F/\mathbb {Q}}G)_{E_{{\mathfrak p}}}$
of highest weight
![]() $\iota _p \mu $
is the representation
$\iota _p \mu $
is the representation
![]() $(\mathrm {spin}^{\varepsilon },1,\ldots ,1)$
. Here,
$(\mathrm {spin}^{\varepsilon },1,\ldots ,1)$
. Here,
![]() $\mathrm {spin}^{\varepsilon }$
is on the factor for
$\mathrm {spin}^{\varepsilon }$
is on the factor for
![]() $\sigma =\iota _p y_{\infty }$
, where we identify
$\sigma =\iota _p y_{\infty }$
, where we identify
(in the ambient group
![]() ${\mathrm {GL}}_{2n}(E\otimes _F \overline {\mathbb {Q}}_p)\simeq {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_p)\times {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_p)$
of the left-hand side, we project onto the
${\mathrm {GL}}_{2n}(E\otimes _F \overline {\mathbb {Q}}_p)\simeq {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_p)\times {\mathrm {GL}}_{2n}(\overline {\mathbb {Q}}_p)$
of the left-hand side, we project onto the
![]() $\iota _p x_{\infty }$
-component) and thus identify
$\iota _p x_{\infty }$
-component) and thus identify
![]() $\widehat G=\mathrm {GSpin}_{2n}$
on the
$\widehat G=\mathrm {GSpin}_{2n}$
on the
![]() $\iota _p y_{\infty }$
-component. Now let
$\iota _p y_{\infty }$
-component. Now let
![]() $\tau _p=\prod _{{{\mathfrak q}}'|p} \tau _{{{\mathfrak q}}'} $
be an unramified representation of
$\tau _p=\prod _{{{\mathfrak q}}'|p} \tau _{{{\mathfrak q}}'} $
be an unramified representation of
![]() $G(F_p)=(\mathrm {Res}_{F/\mathbb {Q}}G)(\mathbb {Q}_p)=\prod _{{{\mathfrak q}}'|p} G(F_{{{\mathfrak q}}'})$
, and denote by
$G(F_p)=(\mathrm {Res}_{F/\mathbb {Q}}G)(\mathbb {Q}_p)=\prod _{{{\mathfrak q}}'|p} G(F_{{{\mathfrak q}}'})$
, and denote by
![]() $\phi _{\tau _p}:W_{\mathbb {Q}_p}\rightarrow {}^L (\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathbb {Q}_p}$
its L-parameter. Then the
$\phi _{\tau _p}:W_{\mathbb {Q}_p}\rightarrow {}^L (\mathrm {Res}_{F/\mathbb {Q}} G)_{\mathbb {Q}_p}$
its L-parameter. Then the
![]() $\iota _p y_{\infty }$
-component of
$\iota _p y_{\infty }$
-component of
![]() $\phi _{\tau _p}|_{W_{E_{\mathfrak p}}}$
is given by
$\phi _{\tau _p}|_{W_{E_{\mathfrak p}}}$
is given by
![]() $\phi _{\tau _{{\mathfrak q}}}|_{W_{E_{\mathfrak p}}}$
. All in all, we can explicate [Reference Kottwitz45, (2.2.1)] in our setup asFootnote 12
$\phi _{\tau _{{\mathfrak q}}}|_{W_{E_{\mathfrak p}}}$
. All in all, we can explicate [Reference Kottwitz45, (2.2.1)] in our setup asFootnote 12
As in the proof of [Reference Kret and Shin50, Prop. 8.2] (where our
![]() $f^{(j)}_p$
is denoted by
$f^{(j)}_p$
is denoted by
![]() $h^{G^{*}}_p$
), the Lefschetz functions
$h^{G^{*}}_p$
), the Lefschetz functions
![]() $f_{\infty }$
and
$f_{\infty }$
and
![]() $f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
allow us to simplify the stabilized Langlands-Kottwitz formula [Reference Kisin, Shin and Zhu43, Thm. 8.3.11] (recalled in [Reference Kret and Shin50, Thm. 7.3]) and obtain a simple stabilization of the trace formula for G; the outcomes are formulas (8.8) and (8.9) of [Reference Kret and Shin50]. Combining them, we obtain
$f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
allow us to simplify the stabilized Langlands-Kottwitz formula [Reference Kisin, Shin and Zhu43, Thm. 8.3.11] (recalled in [Reference Kret and Shin50, Thm. 7.3]) and obtain a simple stabilization of the trace formula for G; the outcomes are formulas (8.8) and (8.9) of [Reference Kret and Shin50]. Combining them, we obtain
Note that
![]() $f_p$
is the characteristic function of the hyperspecial subgroup
$f_p$
is the characteristic function of the hyperspecial subgroup
![]() $K_p=\prod _{{\mathfrak p}|p} K_{\mathfrak p}$
. Following the argument from Equation (8.10) to (8.13) in [Reference Kret and Shin50], we compute
$K_p=\prod _{{\mathfrak p}|p} K_{\mathfrak p}$
. Following the argument from Equation (8.10) to (8.13) in [Reference Kret and Shin50], we compute
Let us show that
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is a true representation by showing that only the middle degree cohomology contributes to
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is a true representation by showing that only the middle degree cohomology contributes to
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
. Since the canonical smooth integral model of
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
. Since the canonical smooth integral model of
![]() $\mathrm {Sh}_K^{\varepsilon }$
constructed by Kisin is proper as shown in [Reference Youcis82, Thm. 2.1.29] (extending the analogous result for Hodge-type Shimura varieties by Madapusi Pera [Reference Madapusi Pera58, Cor. 4.1.7]), the action of
$\mathrm {Sh}_K^{\varepsilon }$
constructed by Kisin is proper as shown in [Reference Youcis82, Thm. 2.1.29] (extending the analogous result for Hodge-type Shimura varieties by Madapusi Pera [Reference Madapusi Pera58, Cor. 4.1.7]), the action of
![]() $\mathrm {Frob}_{\mathfrak p}$
on
$\mathrm {Frob}_{\mathfrak p}$
on
![]() $\mathrm {H}_c^i(\mathrm {Sh}_K, {\mathcal L}_{\xi })$
is pure of weight
$\mathrm {H}_c^i(\mathrm {Sh}_K, {\mathcal L}_{\xi })$
is pure of weight
![]() $-w+i$
by [Reference Deligne22, Cor. 3.3.6] since
$-w+i$
by [Reference Deligne22, Cor. 3.3.6] since
![]() ${\mathcal L}_{\xi }$
is pure of weight
${\mathcal L}_{\xi }$
is pure of weight
![]() $-w$
[Reference Pink67, §5.4, Prop. 5.6.2]. (To obtain purity from Pink’s result, we enlarge the set S if necessary; cf. [Reference Morel63, 1.3], especially the proof of (7) in Proposition 1.3.4 there.) The argument for Part (2) of [Reference Kret and Shin50, Lem. 8.1] (replacing Lemma 2.7 in the proof therein with our condition (temp)) implies that
$-w$
[Reference Pink67, §5.4, Prop. 5.6.2]. (To obtain purity from Pink’s result, we enlarge the set S if necessary; cf. [Reference Morel63, 1.3], especially the proof of (7) in Proposition 1.3.4 there.) The argument for Part (2) of [Reference Kret and Shin50, Lem. 8.1] (replacing Lemma 2.7 in the proof therein with our condition (temp)) implies that
![]() $\tau _{\mathfrak {q}}|\mathrm {sim}|^{w/2} = \pi ^{\natural }_{\mathfrak {q}}|\mathrm {sim}|^{w/2}$
is tempered and unitary. Combining with (9.10), we conclude that
$\tau _{\mathfrak {q}}|\mathrm {sim}|^{w/2} = \pi ^{\natural }_{\mathfrak {q}}|\mathrm {sim}|^{w/2}$
is tempered and unitary. Combining with (9.10), we conclude that
![]() $\mathrm {H}_c^i(\mathrm {Sh}^{\varepsilon }, {\mathcal L}_{\xi })[\iota \tau ^{\infty }]=0$
unless
$\mathrm {H}_c^i(\mathrm {Sh}^{\varepsilon }, {\mathcal L}_{\xi })[\iota \tau ^{\infty }]=0$
unless
![]() $i=n(n-1)/2$
.
$i=n(n-1)/2$
.
Finally, the case
![]() $F=\mathbb {Q}$
is handled via intersection cohomology as in the proof of [Reference Kret and Shin50, Prop. 8.2]. Thus, we content ourselves with giving a sketch. For each
$F=\mathbb {Q}$
is handled via intersection cohomology as in the proof of [Reference Kret and Shin50, Prop. 8.2]. Thus, we content ourselves with giving a sketch. For each
![]() $\tau \in A(\pi ^{\natural })$
, one observes as in [Reference Kret and Shin50, Lem. 8.1] that
$\tau \in A(\pi ^{\natural })$
, one observes as in [Reference Kret and Shin50, Lem. 8.1] that
![]() $\mathrm {H}_c^i(\mathrm {Sh}^{\varepsilon }, {\mathcal L}_{\xi })[\iota \tau ^{\infty }]$
is isomorphic to the
$\mathrm {H}_c^i(\mathrm {Sh}^{\varepsilon }, {\mathcal L}_{\xi })[\iota \tau ^{\infty }]$
is isomorphic to the
![]() $\iota \tau ^{\infty }$
-isotypic part of the intersection cohomology as
$\iota \tau ^{\infty }$
-isotypic part of the intersection cohomology as
![]() $\Gamma _E$
-representations. The point is that
$\Gamma _E$
-representations. The point is that
![]() $\tau ^{\infty }$
does not appear in any parabolic induction of an automorphic representation on a proper Levi subgroup of
$\tau ^{\infty }$
does not appear in any parabolic induction of an automorphic representation on a proper Levi subgroup of
![]() $G(\mathbb A)$
. (If it does appear, then restricting
$G(\mathbb A)$
. (If it does appear, then restricting
![]() $\tau $
from
$\tau $
from
![]() $G(\mathbb A)$
to its derived subgroup
$G(\mathbb A)$
to its derived subgroup
![]() $G^{\mathrm {der}}(\mathbb A)$
and transferring to the quasi-split inner form
$G^{\mathrm {der}}(\mathbb A)$
and transferring to the quasi-split inner form
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A)$
via [Reference Kret and Shin50, Prop. 6.3], we would have a cohomological automorphic representation
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A)$
via [Reference Kret and Shin50, Prop. 6.3], we would have a cohomological automorphic representation
![]() $\tau ^{\flat }$
of
$\tau ^{\flat }$
of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A)$
with a Steinberg component up to a twist that appears as a constituent in a parabolically induced representation. Then the Arthur parameter for
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A)$
with a Steinberg component up to a twist that appears as a constituent in a parabolically induced representation. Then the Arthur parameter for
![]() $\tau ^{\flat }$
cannot have the shape described in Proposition 6.1, leading to a contradiction.) The rest of the proof of [Reference Kret and Shin50, Prop. 8.2] carries over, via the analogue of part 2 of [Reference Kret and Shin50, Lem. 8.1] (the latter is justified using condition (temp) in our case), bearing in mind that the middle degree is
$\tau ^{\flat }$
cannot have the shape described in Proposition 6.1, leading to a contradiction.) The rest of the proof of [Reference Kret and Shin50, Prop. 8.2] carries over, via the analogue of part 2 of [Reference Kret and Shin50, Lem. 8.1] (the latter is justified using condition (temp) in our case), bearing in mind that the middle degree is
![]() $n(n-1)/2$
for us (which was
$n(n-1)/2$
for us (which was
![]() $n(n+1)/2$
for the group
$n(n+1)/2$
for the group
![]() $\mathrm {GSp}_{2n}$
).
$\mathrm {GSp}_{2n}$
).
Corollary 9.7. Let
![]() $\pi ^{\natural }$
be as above. If
$\pi ^{\natural }$
be as above. If
![]() $\tau \in A(\pi ^{\natural })$
, then
$\tau \in A(\pi ^{\natural })$
, then
-
(1)
 $\tau _{\infty }$
belongs to the discrete series L-packet
$\tau _{\infty }$
belongs to the discrete series L-packet
 $\Pi ^{G(F_{\infty })}_{\xi }$
,
$\Pi ^{G(F_{\infty })}_{\xi }$
, -
(2)
 $\tau ^{\infty }\tau ^{\prime }_{\infty }\in A(\pi ^{\natural })$
and
$\tau ^{\infty }\tau ^{\prime }_{\infty }\in A(\pi ^{\natural })$
and
 $m(\tau )=m(\tau ^{\infty }\tau ^{\prime }_{\infty })$
for all
$m(\tau )=m(\tau ^{\infty }\tau ^{\prime }_{\infty })$
for all
 $\tau ^{\prime }_{\infty }\in \Pi ^{G(F_{\infty })}_{\xi }$
.
$\tau ^{\prime }_{\infty }\in \Pi ^{G(F_{\infty })}_{\xi }$
.
Moreover,
![]() $a(\pi ^{\natural })=\sum _{\tau \in A(\pi ^{\natural })/\sim } m(\tau )\in \mathbb Z_{>0}$
.
$a(\pi ^{\natural })=\sum _{\tau \in A(\pi ^{\natural })/\sim } m(\tau )\in \mathbb Z_{>0}$
.
Proof. This is the exact analogue of [Reference Kret and Shin50, Cor. 8.4, Cor. 8.5] and the same proof applies. (Since
![]() $a(\pi ^{\natural })=a^+(\pi ^{\natural })=a^-(\pi ^{\natural })$
, we adapt the argument there to either
$a(\pi ^{\natural })=a^+(\pi ^{\natural })=a^-(\pi ^{\natural })$
, we adapt the argument there to either
![]() $\varepsilon \in \{+,-\}$
to compute.)
$\varepsilon \in \{+,-\}$
to compute.)
Proposition 9.8. Assume that
![]() $F\neq \mathbb {Q}$
. Let
$F\neq \mathbb {Q}$
. Let
![]() $x_{\infty }:E\hookrightarrow {\mathbb {C}}$
and
$x_{\infty }:E\hookrightarrow {\mathbb {C}}$
and
![]() $y_{\infty }:F\hookrightarrow {\mathbb {C}}$
be as in Lemma 9.3. Then
$y_{\infty }:F\hookrightarrow {\mathbb {C}}$
be as in Lemma 9.3. Then
Proof. We start by setting up some notation. Let
![]() ${\mathfrak p}$
be a prime of E above
${\mathfrak p}$
be a prime of E above
![]() $\ell $
, and
$\ell $
, and
![]() $\sigma : E\hookrightarrow \overline {\mathbb {Q}}_{\ell }$
an embedding inducing the
$\sigma : E\hookrightarrow \overline {\mathbb {Q}}_{\ell }$
an embedding inducing the
![]() ${\mathfrak p}$
-adic valuation on E. Let r be a de Rham Galois representation of
${\mathfrak p}$
-adic valuation on E. Let r be a de Rham Galois representation of
![]() $\Gamma _E$
on a
$\Gamma _E$
on a
![]() $\overline {\mathbb {Q}}_{\ell }$
-vector space. Write
$\overline {\mathbb {Q}}_{\ell }$
-vector space. Write
![]() $D_{\mathrm {dR},\sigma }(r)$
for the filtered
$D_{\mathrm {dR},\sigma }(r)$
for the filtered
![]() $\overline {\mathbb {Q}}_{\ell }$
-vector space associated with
$\overline {\mathbb {Q}}_{\ell }$
-vector space associated with
![]() $r|_{\Gamma _{E_{{\mathfrak p}}}}$
with respect to
$r|_{\Gamma _{E_{{\mathfrak p}}}}$
with respect to
![]() $\sigma $
(as on p.99 of [Reference Harris and Taylor33]). Define
$\sigma $
(as on p.99 of [Reference Harris and Taylor33]). Define
![]() $\mathrm {HT}_{\sigma }(r)$
to be the multi-set containing each
$\mathrm {HT}_{\sigma }(r)$
to be the multi-set containing each
![]() $j\in \mathbb Z$
with multiplicity
$j\in \mathbb Z$
with multiplicity
![]() $\dim \mathrm {gr}^j (D_{\mathrm {dR},\sigma }(r))$
. (So the cardinality of
$\dim \mathrm {gr}^j (D_{\mathrm {dR},\sigma }(r))$
. (So the cardinality of
![]() $\mathrm {HT}_{\sigma }(r)$
equals
$\mathrm {HT}_{\sigma }(r)$
equals
![]() $\dim r$
.) When
$\dim r$
.) When
![]() $a\in \mathbb Z_{>0}$
and A is a multi-set, we write
$a\in \mathbb Z_{>0}$
and A is a multi-set, we write
![]() $ A^{\oplus a}$
to denote the multi-set such that the multiplicity of each element in
$ A^{\oplus a}$
to denote the multi-set such that the multiplicity of each element in
![]() $A^{\oplus a}$
is a times that in A.
$A^{\oplus a}$
is a times that in A.
Write
![]() $\lambda (\xi )=\{\lambda (\xi _y)\}_{y|\infty }$
for the highest weight of
$\lambda (\xi )=\{\lambda (\xi _y)\}_{y|\infty }$
for the highest weight of
![]() $\xi =\otimes _{y|\infty } \xi _y$
. In the basis of §2 for
$\xi =\otimes _{y|\infty } \xi _y$
. In the basis of §2 for
![]() $X^{*}(\mathrm {T}_{{\mathrm {GSO}}})=X_*(\mathrm {T}_{\mathrm {GSpin}})=\mathbb Z^{n+1}$
, we write
$X^{*}(\mathrm {T}_{{\mathrm {GSO}}})=X_*(\mathrm {T}_{\mathrm {GSpin}})=\mathbb Z^{n+1}$
, we write
![]() $\xi _{y_{\infty }}$
and the half sum of positive roots
$\xi _{y_{\infty }}$
and the half sum of positive roots
![]() $\rho $
for
$\rho $
for
![]() ${\mathrm {GSO}}_{2n}$
as
${\mathrm {GSO}}_{2n}$
as
 $$ \begin{align*} \lambda(\xi_{y_{\infty}}) &= (a_0,a_1,\ldots,a_n) ,\qquad a_1\ge a_2\ge \cdots \ge |a_n|\ge 0, \\ \rho &= (-n(n-1)/4,n-1,n-2,\ldots,1,0). \end{align*} $$
$$ \begin{align*} \lambda(\xi_{y_{\infty}}) &= (a_0,a_1,\ldots,a_n) ,\qquad a_1\ge a_2\ge \cdots \ge |a_n|\ge 0, \\ \rho &= (-n(n-1)/4,n-1,n-2,\ldots,1,0). \end{align*} $$
Let
![]() $\mathscr P^{\varepsilon }(n)$
denote the collection of subsets of
$\mathscr P^{\varepsilon }(n)$
denote the collection of subsets of
![]() $\{1,2,\ldots ,n\}$
whose cardinality has the same parity as n if
$\{1,2,\ldots ,n\}$
whose cardinality has the same parity as n if
![]() $\varepsilon =(-1)^n$
and different parity if
$\varepsilon =(-1)^n$
and different parity if
![]() $\varepsilon =(-1)^{n+1}$
. Put
$\varepsilon =(-1)^{n+1}$
. Put
 $$ \begin{align*} (b_0,b_1,\ldots,b_n)&:=(a_0-\tfrac{n(n-1)}{2},a_1+n-1,a_2+n-2,\ldots,a_{n-1}+1,a_n)\\ &=\lambda(\xi_{y_{\infty}})+\rho - (n(n-1)/4,0,0,\ldots,0), \end{align*} $$
$$ \begin{align*} (b_0,b_1,\ldots,b_n)&:=(a_0-\tfrac{n(n-1)}{2},a_1+n-1,a_2+n-2,\ldots,a_{n-1}+1,a_n)\\ &=\lambda(\xi_{y_{\infty}})+\rho - (n(n-1)/4,0,0,\ldots,0), \end{align*} $$
which equals
![]() $\mu _{\mathrm {Hodge}}(\xi _{x_{\infty }}) - \frac {n(n-1)}{4} \mathrm {sim}$
. Via the description of weights in the representation
$\mu _{\mathrm {Hodge}}(\xi _{x_{\infty }}) - \frac {n(n-1)}{4} \mathrm {sim}$
. Via the description of weights in the representation
![]() $\mathrm {spin}^{\varepsilon }$
in (2.10) (which gives the weights in
$\mathrm {spin}^{\varepsilon }$
in (2.10) (which gives the weights in
![]() $\mathrm {spin}^{\varepsilon ,\vee }$
), the proposition amounts to the assertion that
$\mathrm {spin}^{\varepsilon ,\vee }$
), the proposition amounts to the assertion that
 $$ \begin{align} \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon}) = \Big\{ -b_0 - \sum_{i\in I} b_i \,\Big|\, I\in \mathscr P^{\varepsilon}(n) \Big\}^{\oplus a(\pi^{\natural})} = \Big\{ -a_0 - \sum_{i\in I} a_i +\sum_{i\notin I} (n-i)\,\Big|\, I\in \mathscr P^{\varepsilon}(n) \Big\}^{\oplus a(\pi^{\natural})}. \end{align} $$
$$ \begin{align} \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon}) = \Big\{ -b_0 - \sum_{i\in I} b_i \,\Big|\, I\in \mathscr P^{\varepsilon}(n) \Big\}^{\oplus a(\pi^{\natural})} = \Big\{ -a_0 - \sum_{i\in I} a_i +\sum_{i\notin I} (n-i)\,\Big|\, I\in \mathscr P^{\varepsilon}(n) \Big\}^{\oplus a(\pi^{\natural})}. \end{align} $$
We prove this assertion using a result from [Reference Lan, Liu and Zhu52]. Let us introduce some more notation. Write
![]() $\mathrm {Sh}^{\varepsilon }_{K}({\mathbb {C}})$
for the complex manifold obtained from
$\mathrm {Sh}^{\varepsilon }_{K}({\mathbb {C}})$
for the complex manifold obtained from
![]() $\mathrm {Sh}^{\varepsilon }_{K}$
by base change along
$\mathrm {Sh}^{\varepsilon }_{K}$
by base change along
![]() $x_{\infty }:E\hookrightarrow {\mathbb {C}}$
, and
$x_{\infty }:E\hookrightarrow {\mathbb {C}}$
, and
![]() ${\mathcal L}_{\xi }^{\mathrm {top}}$
for the topological local system on
${\mathcal L}_{\xi }^{\mathrm {top}}$
for the topological local system on
![]() $\mathrm {Sh}^{\varepsilon }_{K}({\mathbb {C}})$
coming from
$\mathrm {Sh}^{\varepsilon }_{K}({\mathbb {C}})$
coming from
![]() $\xi $
. Writing
$\xi $
. Writing
![]() $K^{\varepsilon }$
(Lemma 9.1) as
$K^{\varepsilon }$
(Lemma 9.1) as
![]() $K^{\varepsilon }=\prod _{y} K^{\varepsilon }_{y}$
, we have
$K^{\varepsilon }=\prod _{y} K^{\varepsilon }_{y}$
, we have
![]() $K^{\varepsilon }_{y_{\infty }}=K_{\varepsilon }$
and
$K^{\varepsilon }_{y_{\infty }}=K_{\varepsilon }$
and
![]() $K^{\varepsilon }_{y}=G(F_y)\simeq {\mathrm {GSO}}^{\mathrm {cpt}}_{2n}(F_y)$
for
$K^{\varepsilon }_{y}=G(F_y)\simeq {\mathrm {GSO}}^{\mathrm {cpt}}_{2n}(F_y)$
for
![]() $y\neq y_{\infty }$
. Restricting
$y\neq y_{\infty }$
. Restricting
![]() $h^{\varepsilon }_{{\mathbb {C}}}$
to the first factor of
$h^{\varepsilon }_{{\mathbb {C}}}$
to the first factor of
![]() ${\mathbb S}_{\mathbb {C}} = \mathbb G_{m,{\mathbb {C}}}\times \mathbb G_{m,{\mathbb {C}}}$
(labeled by the identity
${\mathbb S}_{\mathbb {C}} = \mathbb G_{m,{\mathbb {C}}}\times \mathbb G_{m,{\mathbb {C}}}$
(labeled by the identity
![]() ${\mathbb {C}}\rightarrow {\mathbb {C}}$
, not the complex conjugation), we obtain a cocharacter
${\mathbb {C}}\rightarrow {\mathbb {C}}$
, not the complex conjugation), we obtain a cocharacter
![]() $\mathbb G_{m,{\mathbb {C}}}\rightarrow K^{\varepsilon }_{{\mathbb {C}}}$
, which we denote by
$\mathbb G_{m,{\mathbb {C}}}\rightarrow K^{\varepsilon }_{{\mathbb {C}}}$
, which we denote by
![]() $\mu ^{\varepsilon }$
; this is consistent with the definition of
$\mu ^{\varepsilon }$
; this is consistent with the definition of
![]() $\mu ^{\varepsilon }$
below (9.1). We also have a parabolic subgroup
$\mu ^{\varepsilon }$
below (9.1). We also have a parabolic subgroup
![]() $Q\subset (\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}$
with Levi component
$Q\subset (\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}$
with Levi component
![]() $K^{\varepsilon }_{{\mathbb {C}}}$
as [Reference Faltings23, p.57] (such that the Borel embedding goes into
$K^{\varepsilon }_{{\mathbb {C}}}$
as [Reference Faltings23, p.57] (such that the Borel embedding goes into
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb {C}})/Q$
). Fix an elliptic maximal torus
$(\mathrm {Res}_{F/\mathbb {Q}}G)({\mathbb {C}})/Q$
). Fix an elliptic maximal torus
![]() $T_{\infty }\subset K^{\varepsilon }$
and a Borel subgroup
$T_{\infty }\subset K^{\varepsilon }$
and a Borel subgroup
![]() $B\subset (\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}$
contained in Q such that B contains
$B\subset (\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}$
contained in Q such that B contains
![]() $T_{\infty }$
. Let
$T_{\infty }$
. Let
![]() $R^+$
denote the set of positive roots of
$R^+$
denote the set of positive roots of
![]() $T_{\infty }$
in B. By
$T_{\infty }$
in B. By
![]() $R^-$
we denote the set of roots of
$R^-$
we denote the set of roots of
![]() $T_{\infty }$
in the opposite Borel subgroup. Write
$T_{\infty }$
in the opposite Borel subgroup. Write
![]() $\Omega $
for the Weyl group of
$\Omega $
for the Weyl group of
![]() $T_{\infty ,{\mathbb {C}}}$
in
$T_{\infty ,{\mathbb {C}}}$
in
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)_{\mathbb {C}}$
, and
$(\mathrm {Res}_{F/\mathbb {Q}}G)_{\mathbb {C}}$
, and
![]() $\Omega _{\mathrm {nc}}$
for the subset of
$\Omega _{\mathrm {nc}}$
for the subset of
![]() $\omega \in \Omega $
such that
$\omega \in \Omega $
such that
![]() $\omega \lambda $
is
$\omega \lambda $
is
![]() $B\cap K^{\varepsilon }_{{\mathbb {C}}}$
-dominant whenever
$B\cap K^{\varepsilon }_{{\mathbb {C}}}$
-dominant whenever
![]() $\lambda \in X^{*}(T_{\infty })$
is B-dominant. Let
$\lambda \in X^{*}(T_{\infty })$
is B-dominant. Let
![]() $\Omega _{\mathrm {c}}$
denote the Weyl group of
$\Omega _{\mathrm {c}}$
denote the Weyl group of
![]() $T_{\infty ,{\mathbb {C}}}$
in
$T_{\infty ,{\mathbb {C}}}$
in
![]() $K^{\varepsilon }_{\mathbb {C}}$
. The inclusion
$K^{\varepsilon }_{\mathbb {C}}$
. The inclusion
![]() $\Omega _{\mathrm {nc}}\subset \Omega $
induces a canonical bijection
$\Omega _{\mathrm {nc}}\subset \Omega $
induces a canonical bijection
![]() $\Omega _{\mathrm {nc}}\simeq \Omega /\Omega _{\mathrm {c}}$
. We parametrize members of the discrete series L-packet
$\Omega _{\mathrm {nc}}\simeq \Omega /\Omega _{\mathrm {c}}$
. We parametrize members of the discrete series L-packet
![]() $\Pi ^{G(F_{\infty })}_{\xi }$
as
$\Pi ^{G(F_{\infty })}_{\xi }$
as
![]() $\{ \pi (\omega ) | \omega \in \Omega _{\mathrm {nc}}\}$
following [Reference Harris34, 3.3]. (Our
$\{ \pi (\omega ) | \omega \in \Omega _{\mathrm {nc}}\}$
following [Reference Harris34, 3.3]. (Our
![]() $\pi (\omega )$
is
$\pi (\omega )$
is
![]() $\pi (\omega \lambda ,\omega R^+)$
in their notation.) Even though
$\pi (\omega \lambda ,\omega R^+)$
in their notation.) Even though
![]() $Q,T_{\infty },B,\Omega _c$
depend on
$Q,T_{\infty },B,\Omega _c$
depend on
![]() $\varepsilon $
(since they do on
$\varepsilon $
(since they do on
![]() $K^{\varepsilon }$
), we suppress it from the notation for simplicity.
$K^{\varepsilon }$
), we suppress it from the notation for simplicity.
Write
![]() $\rho _G\in X^{*}(T)$
for the half sum of all roots in
$\rho _G\in X^{*}(T)$
for the half sum of all roots in
![]() $R^+$
, and define
$R^+$
, and define
![]() $\omega \star \lambda _0:=\omega (\lambda _0+\rho _G)-\rho _G$
for
$\omega \star \lambda _0:=\omega (\lambda _0+\rho _G)-\rho _G$
for
![]() $\lambda _0\in X^{*}(T_{\infty })$
. Every irreducible representation
$\lambda _0\in X^{*}(T_{\infty })$
. Every irreducible representation
![]() $V_{\lambda _0}$
of
$V_{\lambda _0}$
of
![]() $K^{\varepsilon }_{\mathbb {C}}$
of highest weight
$K^{\varepsilon }_{\mathbb {C}}$
of highest weight
![]() $\lambda _0\in X^{*}(T_{\infty })$
gives rise to an automorphic vector bundle, to be denoted by
$\lambda _0\in X^{*}(T_{\infty })$
gives rise to an automorphic vector bundle, to be denoted by
![]() $\mathcal E_{\lambda _0}$
. Write
$\mathcal E_{\lambda _0}$
. Write
![]() $\lambda =\lambda (\xi )\in X^{*}(T_{\infty })$
for the B-dominant highest weight of
$\lambda =\lambda (\xi )\in X^{*}(T_{\infty })$
for the B-dominant highest weight of
![]() $\xi $
.
$\xi $
.
For a finite multi-set A, write
![]() $\mathrm {mult}(a|A)\in \mathbb Z_{\ge 0}$
for the multiplicity of a in A. For each
$\mathrm {mult}(a|A)\in \mathbb Z_{\ge 0}$
for the multiplicity of a in A. For each
![]() $j\in \mathbb Z$
, define
$j\in \mathbb Z$
, define
![]() $\Omega _{\mathrm {nc}}(j)$
to be the set of
$\Omega _{\mathrm {nc}}(j)$
to be the set of
![]() $\omega \in \Omega _{\mathrm {nc}}$
such that the composition
$\omega \in \Omega _{\mathrm {nc}}$
such that the composition
![]() $\mathbb G_m \stackrel {(\mu ^{\varepsilon })^{-1}}{\rightarrow } T_{\infty ,{\mathbb {C}}}\stackrel {\omega \star \lambda }{\rightarrow } \mathbb G_m$
equals
$\mathbb G_m \stackrel {(\mu ^{\varepsilon })^{-1}}{\rightarrow } T_{\infty ,{\mathbb {C}}}\stackrel {\omega \star \lambda }{\rightarrow } \mathbb G_m$
equals
![]() $z\mapsto z^j$
. Then,
$z\mapsto z^j$
. Then,
 $$ \begin{align*} &\mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon})\big) \nonumber\\ &= \sum_{\tau\in A(\pi^{\natural})/\sim} \mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(H^{n(n-1)/2}(\mathrm{Sh}^{\varepsilon},{\mathcal L}_{\xi})[\iota \tau^{\infty}]\big) \quad \mbox{by Theorem 9.6 and (9.6)},\nonumber\\ &= \sum_{\tau\in A(\pi^{\natural})/\sim} \sum_{\omega\in \Omega_{\mathrm{nc}}(j)} \dim H^{\frac{n(n-1)}{2}-l(\omega)}(\mathrm{Sh}^{\epsilon}({\mathbb{C}}),\mathcal E_{\omega\star \lambda})[\tau^{\infty}], \quad \mbox{by [52, Theorem 6.2.9]}. \end{align*} $$
$$ \begin{align*} &\mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon})\big) \nonumber\\ &= \sum_{\tau\in A(\pi^{\natural})/\sim} \mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(H^{n(n-1)/2}(\mathrm{Sh}^{\varepsilon},{\mathcal L}_{\xi})[\iota \tau^{\infty}]\big) \quad \mbox{by Theorem 9.6 and (9.6)},\nonumber\\ &= \sum_{\tau\in A(\pi^{\natural})/\sim} \sum_{\omega\in \Omega_{\mathrm{nc}}(j)} \dim H^{\frac{n(n-1)}{2}-l(\omega)}(\mathrm{Sh}^{\epsilon}({\mathbb{C}}),\mathcal E_{\omega\star \lambda})[\tau^{\infty}], \quad \mbox{by [52, Theorem 6.2.9]}. \end{align*} $$
From [Reference Harris34, §3], we have an isomorphism of
![]() $G(\mathbb A_F^{\infty })$
-modules:
$G(\mathbb A_F^{\infty })$
-modules:
For each
![]() $\tau \in A(\pi ^{\natural })$
, we pass to the
$\tau \in A(\pi ^{\natural })$
, we pass to the
![]() $\tau ^{\infty }$
-isotypic parts (with notation as in (9.5)) to obtain
$\tau ^{\infty }$
-isotypic parts (with notation as in (9.5)) to obtain
where the sum runs over irreducible unitary representations of
![]() $G(F_{\infty })$
. By [Reference Harris34, Prop. 4.4.12], if the cohomology on the right-hand side is nonzero, then
$G(F_{\infty })$
. By [Reference Harris34, Prop. 4.4.12], if the cohomology on the right-hand side is nonzero, then
![]() $\tau ^{\prime }_{\infty }$
is
$\tau ^{\prime }_{\infty }$
is
![]() $\xi $
-cohomological, so
$\xi $
-cohomological, so
![]() $\tau ^{\infty }\otimes \tau ^{\prime }_{\infty }\in A(\pi ^{\infty })$
. It follows from Corollary 9.7 that
$\tau ^{\infty }\otimes \tau ^{\prime }_{\infty }\in A(\pi ^{\infty })$
. It follows from Corollary 9.7 that
![]() $\tau ^{\prime }_{\infty }\in \Pi ^{G(F_{\infty })}_{\infty }$
and that
$\tau ^{\prime }_{\infty }\in \Pi ^{G(F_{\infty })}_{\infty }$
and that
![]() $ m(\tau ^{\infty }\otimes \tau ^{\prime }_{\infty })=m(\tau )$
. Moreover, [Reference Harris34, Thm. 3.4] implies that
$ m(\tau ^{\infty }\otimes \tau ^{\prime }_{\infty })=m(\tau )$
. Moreover, [Reference Harris34, Thm. 3.4] implies that
![]() $H^{k} (\mathrm {Lie}\, Q, K^{\varepsilon },\tau ^{\prime }_{\infty }\otimes V_{\omega \star \lambda })$
is nonzero for a unique
$H^{k} (\mathrm {Lie}\, Q, K^{\varepsilon },\tau ^{\prime }_{\infty }\otimes V_{\omega \star \lambda })$
is nonzero for a unique
![]() $\tau ^{\prime }_{\infty }$
, in which case the cohomology is one-dimensional. We use this to resume the computation of
$\tau ^{\prime }_{\infty }$
, in which case the cohomology is one-dimensional. We use this to resume the computation of
![]() $ \mathrm {mult}(j \,|\, \mathrm {HT}_{\iota x_{\infty }}(\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }))$
and obtain
$ \mathrm {mult}(j \,|\, \mathrm {HT}_{\iota x_{\infty }}(\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }))$
and obtain
 $$ \begin{align*}\mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon})\big) = \sum_{\tau\in A(\pi^{\natural})/\sim} \sum_{\omega\in \Omega_{\mathrm{nc}}(j)} m(\tau) = a(\pi^{\natural}) \cdot |\Omega_{\mathrm{nc}}(j)|. \end{align*} $$
$$ \begin{align*}\mathrm{mult}\big(j \,|\, \mathrm{HT}_{\iota x_{\infty}}(\rho_{\pi^{\natural}}^{\mathrm{Sh},\varepsilon})\big) = \sum_{\tau\in A(\pi^{\natural})/\sim} \sum_{\omega\in \Omega_{\mathrm{nc}}(j)} m(\tau) = a(\pi^{\natural}) \cdot |\Omega_{\mathrm{nc}}(j)|. \end{align*} $$
To conclude (9.11), it remains to prove the following claim: that
![]() $| \Omega _{\mathrm {nc}}(j)|$
is precisely the number of ways j can be written as
$| \Omega _{\mathrm {nc}}(j)|$
is precisely the number of ways j can be written as
![]() $-a_0 - \sum _{i\in I} a_i +\sum _{i\notin I} (n-i)$
with
$-a_0 - \sum _{i\in I} a_i +\sum _{i\notin I} (n-i)$
with
![]() $I\in \mathscr P^{\varepsilon }(n)$
.
$I\in \mathscr P^{\varepsilon }(n)$
.
As a preparation, we fix an isomorphism between the pairs
![]() $(T_{\infty ,{\mathbb {C}}},B)$
and
$(T_{\infty ,{\mathbb {C}}},B)$
and
![]() $(\mathrm {T}_{{\mathrm {GSO}}},B_{{\mathrm {GSO}}})$
induced by an inner twist
$(\mathrm {T}_{{\mathrm {GSO}}},B_{{\mathrm {GSO}}})$
induced by an inner twist
![]() $(\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}\simeq (\mathrm {Res}_{F/\mathbb {Q}}G^{*})_{{\mathbb {C}}}$
. So the Weyl action of
$(\mathrm {Res}_{F/\mathbb {Q}}G)_{{\mathbb {C}}}\simeq (\mathrm {Res}_{F/\mathbb {Q}}G^{*})_{{\mathbb {C}}}$
. So the Weyl action of
![]() $\Omega $
is identified with the
$\Omega $
is identified with the
![]() $W_{{\mathrm {GSO}}}$
-action in (2.8), while
$W_{{\mathrm {GSO}}}$
-action in (2.8), while
![]() $\Omega _{\mathrm {c}}$
is identified with
$\Omega _{\mathrm {c}}$
is identified with
![]() $\mathfrak {S}_n$
therein if
$\mathfrak {S}_n$
therein if
![]() $\varepsilon =(-1)^n$
. (If
$\varepsilon =(-1)^n$
. (If
![]() $\varepsilon =(-1)^{n+1}$
, then
$\varepsilon =(-1)^{n+1}$
, then
![]() $\Omega _{\mathrm {c}}$
is the
$\Omega _{\mathrm {c}}$
is the
![]() $\theta ^{\circ }$
-conjugate of
$\theta ^{\circ }$
-conjugate of
![]() $\mathfrak {S}_n$
.) For a subset
$\mathfrak {S}_n$
.) For a subset
![]() $I\subset \{1,...,n\}$
, let
$I\subset \{1,...,n\}$
, let
![]() $\omega ^{\prime }_I$
denote the action on
$\omega ^{\prime }_I$
denote the action on
![]() $(t_0,t_1,\ldots ,t_n)\in X^{*}(\mathrm {T}_{{\mathrm {GSO}}})$
by
$(t_0,t_1,\ldots ,t_n)\in X^{*}(\mathrm {T}_{{\mathrm {GSO}}})$
by
![]() $t_i\mapsto t_i$
for
$t_i\mapsto t_i$
for
![]() $i\in I$
,
$i\in I$
,
![]() $t_i\mapsto -t_i$
for
$t_i\mapsto -t_i$
for
![]() $i\notin I$
, and
$i\notin I$
, and
![]() $t_0\mapsto t_0+\sum _{i\in I} t_i$
. Then
$t_0\mapsto t_0+\sum _{i\in I} t_i$
. Then
![]() $\omega ^{\prime }_I\in \Omega $
if and only if
$\omega ^{\prime }_I\in \Omega $
if and only if
![]() $n-|I|$
is even.
$n-|I|$
is even.
Let us prove the claim, starting with the case
![]() $\varepsilon =(-1)^n$
. Then
$\varepsilon =(-1)^n$
. Then
![]() $n-|I|$
is even for each
$n-|I|$
is even for each
![]() $I\in \mathscr P^{\varepsilon }(n)$
. Write
$I\in \mathscr P^{\varepsilon }(n)$
. Write
![]() $\omega _I\in \Omega _{\mathrm {nc}}$
for the unique intersection of the
$\omega _I\in \Omega _{\mathrm {nc}}$
for the unique intersection of the
![]() $\Omega _{\mathrm {c}}$
-orbit of
$\Omega _{\mathrm {c}}$
-orbit of
![]() $\omega _I$
with
$\omega _I$
with
![]() $\Omega _{\mathrm {nc}}$
. We have bijections
$\Omega _{\mathrm {nc}}$
. We have bijections
Since
![]() $\varepsilon =(-1)^n$
, we have from (2.9)
$\varepsilon =(-1)^n$
, we have from (2.9)
a priori up to the
![]() $\Omega _{\mathrm {c}}$
-action, but
$\Omega _{\mathrm {c}}$
-action, but
![]() $\mu ^{\varepsilon }$
is
$\mu ^{\varepsilon }$
is
![]() $\Omega _{\mathrm {c}}$
-invariant. From this, we compute for
$\Omega _{\mathrm {c}}$
-invariant. From this, we compute for
![]() $\lambda =(a_0,a_1,\ldots ,a_n)\in X^{*}(T_{\infty })\simeq X^{*}(\mathrm {T}_{{\mathrm {GSO}}})$
:
$\lambda =(a_0,a_1,\ldots ,a_n)\in X^{*}(T_{\infty })\simeq X^{*}(\mathrm {T}_{{\mathrm {GSO}}})$
:
 $$ \begin{align*}(\omega_I \star \lambda)\circ (\mu^{\varepsilon})^{-1} = (\omega^{\prime}_I \star \lambda)\circ (\mu^{\varepsilon})^{-1} = -a_0 - \sum_{i\in I}(a_i+n-i) + \sum_{\mathrm{all}~i} (n-i)= -a_0-\sum_{i\in I}a_i + \sum_{i\notin I} (n-i). \end{align*} $$
$$ \begin{align*}(\omega_I \star \lambda)\circ (\mu^{\varepsilon})^{-1} = (\omega^{\prime}_I \star \lambda)\circ (\mu^{\varepsilon})^{-1} = -a_0 - \sum_{i\in I}(a_i+n-i) + \sum_{\mathrm{all}~i} (n-i)= -a_0-\sum_{i\in I}a_i + \sum_{i\notin I} (n-i). \end{align*} $$
Thus, the claim for
![]() $\varepsilon =(-1)^n$
follows.
$\varepsilon =(-1)^n$
follows.
Keep
![]() $\varepsilon =(-1)^n$
and let us prove the claim for
$\varepsilon =(-1)^n$
and let us prove the claim for
![]() $P^{-\varepsilon }(n)$
. Since
$P^{-\varepsilon }(n)$
. Since
![]() $n-|I|$
is odd, we no longer have
$n-|I|$
is odd, we no longer have
![]() $\omega ^{\prime }_I\in \Omega $
but instead have
$\omega ^{\prime }_I\in \Omega $
but instead have
![]() $\omega ^{\prime \prime }_I:=\theta ^{\circ }\omega ^{\prime }_I = \omega ^{\prime }_I \theta ^{\circ } \in \Omega $
. Replacing
$\omega ^{\prime \prime }_I:=\theta ^{\circ }\omega ^{\prime }_I = \omega ^{\prime }_I \theta ^{\circ } \in \Omega $
. Replacing
![]() $\omega ^{\prime }_I$
with
$\omega ^{\prime }_I$
with
![]() $\omega ^{\prime \prime }_I$
in the previous paragraph, we obtain
$\omega ^{\prime \prime }_I$
in the previous paragraph, we obtain
![]() $\omega _I$
and analogous bijections
$\omega _I$
and analogous bijections
It follows from
![]() $\mu ^{-\varepsilon }=\theta ^{\circ } \mu ^{\varepsilon }$
and
$\mu ^{-\varepsilon }=\theta ^{\circ } \mu ^{\varepsilon }$
and
![]() $\Omega _{\mathrm {c}}$
-invariance of
$\Omega _{\mathrm {c}}$
-invariance of
![]() $\mu ^{\varepsilon }$
that
$\mu ^{\varepsilon }$
that
The proof is now done since the computation of
![]() $(\omega ^{\prime }_I \star \lambda )\circ (\mu ^{\varepsilon })^{-1}$
in the preceding case goes through verbatim.
$(\omega ^{\prime }_I \star \lambda )\circ (\mu ^{\varepsilon })^{-1}$
in the preceding case goes through verbatim.
10 Construction of
 $\mathbf {GSpin}_{\boldsymbol{2n}}$
-valued Galois representations
$\mathbf {GSpin}_{\boldsymbol{2n}}$
-valued Galois representations
We continue in the setting of §8 and §9. The goal of this section is to attach
![]() $\mathrm {GSpin}_{2n}$
-valued Galois representations of
$\mathrm {GSpin}_{2n}$
-valued Galois representations of
![]() $\Gamma _{E}$
to the automorphic representations of
$\Gamma _{E}$
to the automorphic representations of
![]() $G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
under consideration. The main input comes from the cohomology of Shimura varieties studied in the last section. Write
$G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
under consideration. The main input comes from the cohomology of Shimura varieties studied in the last section. Write
![]() $\mathrm {std} \colon \mathrm {GSpin}_{2n} \hookrightarrow {\mathrm {GL}}_{2n}$
for the composite of
$\mathrm {std} \colon \mathrm {GSpin}_{2n} \hookrightarrow {\mathrm {GL}}_{2n}$
for the composite of
![]() $\mathrm {pr} \colon \mathrm {GSpin}_{2n}\rightarrow {\mathrm {GSO}}_{2n}$
and the inclusion
$\mathrm {pr} \colon \mathrm {GSpin}_{2n}\rightarrow {\mathrm {GSO}}_{2n}$
and the inclusion
![]() ${\mathrm {GSO}}_{2n}\subset {\mathrm {GL}}_{2n}$
.
${\mathrm {GSO}}_{2n}\subset {\mathrm {GL}}_{2n}$
.
Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $G^{*}(\mathbb A_F)$
. Let
$G^{*}(\mathbb A_F)$
. Let
![]() $\phi _{\pi _y}$
denote the L-parameter of
$\phi _{\pi _y}$
denote the L-parameter of
![]() $\pi _y$
for
$\pi _y$
for
![]() $y\in \mathcal V_{\infty }$
. Throughout this section, we assume that
$y\in \mathcal V_{\infty }$
. Throughout this section, we assume that
-
(St) for some finite F-place
 ${{{\mathfrak q}}_{\mathrm {St}}}$
, the local representation
${{{\mathfrak q}}_{\mathrm {St}}}$
, the local representation
 $\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}$
is isomorphic to the Steinberg representation up to a character twist,
$\pi _{{{{\mathfrak q}}_{\mathrm {St}}}}$
is isomorphic to the Steinberg representation up to a character twist, -
(coh) the representation
 $\pi _{\infty }$
is cohomological for some representation
$\pi _{\infty }$
is cohomological for some representation
 $\xi $
of
$\xi $
of
 $(\mathrm {Res}_{F/\mathbb {Q}}G^{*})\otimes _{\mathbb {Q}} {\mathbb {C}}$
(then
$(\mathrm {Res}_{F/\mathbb {Q}}G^{*})\otimes _{\mathbb {Q}} {\mathbb {C}}$
(then
 $\xi $
satisfies condition (cent) by [Reference Kret and Shin50, Lem. 7.1] as before).
$\xi $
satisfies condition (cent) by [Reference Kret and Shin50, Lem. 7.1] as before).
Choose
![]() $\pi ^{\flat }$
a cuspidal automorphic representation of
$\pi ^{\flat }$
a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
contained in
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
contained in
![]() $\pi |_{{\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)}$
(see [Reference Labesse and Schwermer51]). We observe that
$\pi |_{{\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)}$
(see [Reference Labesse and Schwermer51]). We observe that
![]() $\pi ^{\flat }$
satisfies conditions (St
$\pi ^{\flat }$
satisfies conditions (St
![]() $^{\circ }$
) and (coh
$^{\circ }$
) and (coh
![]() $^{\circ }$
) of §6 thanks to Lemma 7.1 and 7.2. Consider the following analogue of (std-reg
$^{\circ }$
) of §6 thanks to Lemma 7.1 and 7.2. Consider the following analogue of (std-reg
![]() $^{\circ }$
) for
$^{\circ }$
) for
![]() $\pi $
:
$\pi $
:
-
(std-reg)
 $\mathrm {std}\circ \phi _{\pi _y}|_{W_{\overline {F}_y}}$
is regular at every
$\mathrm {std}\circ \phi _{\pi _y}|_{W_{\overline {F}_y}}$
is regular at every
 $y\in \mathcal V_{\infty }$
.
$y\in \mathcal V_{\infty }$
.
In addition to (St) and (coh), the following is also assumed throughout:
-
• Either (std-reg) holds for
 $\pi $
, or Hypothesis 6.11 is true for
$\pi $
, or Hypothesis 6.11 is true for
 $\pi ^{\flat }$
.
$\pi ^{\flat }$
.
So Hypothesis 6.11 comes into play only when (std-reg) does not hold.
Condition (std-reg) is equivalent to the one given in the introduction via local Langlands for real groups (e.g., see [Reference Buzzard and Gee12, §2.3]). If (std-reg) is imposed on
![]() $\pi $
, then (std-reg
$\pi $
, then (std-reg
![]() $^{\circ }$
) follows from (coh
$^{\circ }$
) follows from (coh
![]() $^{\circ }$
). By [Reference Langlands53, §3, (iv)], we have that
$^{\circ }$
). By [Reference Langlands53, §3, (iv)], we have that
![]() $\phi _{\pi ^{\flat },y}=\mathrm {pr}^{\circ }\circ \phi _{\pi ,y}$
at each
$\phi _{\pi ^{\flat },y}=\mathrm {pr}^{\circ }\circ \phi _{\pi ,y}$
at each
![]() $y\in \mathcal V_{\infty }$
. We can also see (std-reg
$y\in \mathcal V_{\infty }$
. We can also see (std-reg
![]() $^{\circ }$
) from this and (std-reg).
$^{\circ }$
) from this and (std-reg).
Lemma 10.1. In addition to (St) and (coh) for
![]() $\pi $
, assume either (std-reg) for
$\pi $
, assume either (std-reg) for
![]() $\pi $
or Hypothesis 6.11 for
$\pi $
or Hypothesis 6.11 for
![]() $\pi ^{\flat }$
. Then
$\pi ^{\flat }$
. Then
![]() $\pi ^{\flat }$
is tempered at all places, and
$\pi ^{\flat }$
is tempered at all places, and
![]() $\pi $
is essentially tempered at all places.
$\pi $
is essentially tempered at all places.
Proof. This follows from Proposition 6.1 if (std-reg) holds. Otherwise, the same proposition implies
![]() $\pi ^{\flat }$
is tempered at infinite places, and Hypothesis 6.11 asserts that
$\pi ^{\flat }$
is tempered at infinite places, and Hypothesis 6.11 asserts that
![]() $\pi ^{\flat }$
is tempered at finite places. The last assertion easily follows from the temperedness of
$\pi ^{\flat }$
is tempered at finite places. The last assertion easily follows from the temperedness of
![]() $\pi ^{\flat }$
. (See the proof of [Reference Kret and Shin50, Lem. 2.7].)
$\pi ^{\flat }$
. (See the proof of [Reference Kret and Shin50, Lem. 2.7].)
The right-hand side of (8.4) is easily extended to a model of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
over
${\mathrm {GSO}}_{2n}^{E/F}$
over
![]() $\mathcal O_{F}$
(by replacing
$\mathcal O_{F}$
(by replacing
![]() $E,F$
with
$E,F$
with
![]() $\mathcal O_E,\mathcal O_F$
). Similarly, we have a model of
$\mathcal O_E,\mathcal O_F$
). Similarly, we have a model of
![]() ${\mathrm {SO}}_{2n}^{E/F}$
closed in the model of
${\mathrm {SO}}_{2n}^{E/F}$
closed in the model of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
, defined by the condition
${\mathrm {GSO}}_{2n}^{E/F}$
, defined by the condition
![]() $\lambda =1$
. At each F-prime
$\lambda =1$
. At each F-prime
![]() ${{\mathfrak q}}$
not above
${{\mathfrak q}}$
not above
![]() $2$
and unramified in E, we have the hyperspecial group
$2$
and unramified in E, we have the hyperspecial group
![]() $H_{{\mathfrak q}}:={\mathrm {GSO}}_{2n}^{E/F}(\mathcal O_{F_{\mathfrak {q}}})$
, whose intersection with
$H_{{\mathfrak q}}:={\mathrm {GSO}}_{2n}^{E/F}(\mathcal O_{F_{\mathfrak {q}}})$
, whose intersection with
![]() ${\mathrm {SO}}_{2n}^{E/F}(F_{{\mathfrak q}})$
is the hyperspecial subgroup
${\mathrm {SO}}_{2n}^{E/F}(F_{{\mathfrak q}})$
is the hyperspecial subgroup
![]() $H_{0,{{\mathfrak q}}}:={\mathrm {SO}}_{2n}^{E/F}(\mathcal O_{F_{{\mathfrak q}}})$
in the latter. We will fix these choices of hyperspecial subgroups for
$H_{0,{{\mathfrak q}}}:={\mathrm {SO}}_{2n}^{E/F}(\mathcal O_{F_{{\mathfrak q}}})$
in the latter. We will fix these choices of hyperspecial subgroups for
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
and
${\mathrm {GSO}}_{2n}^{E/F}$
and
![]() ${\mathrm {SO}}_{2n}^{E/F}$
. At each
${\mathrm {SO}}_{2n}^{E/F}$
. At each
![]() ${{\mathfrak q}}\in \mathrm {Unr}(\pi )$
(so that
${{\mathfrak q}}\in \mathrm {Unr}(\pi )$
(so that
![]() $\pi _v^{H_{{\mathfrak q}}}$
is nontrivial), we can thus find an irreducible
$\pi _v^{H_{{\mathfrak q}}}$
is nontrivial), we can thus find an irreducible
![]() ${\mathrm {SO}}_{2n}^{E/F}(F_{{\mathfrak q}})$
-subrepresentation in
${\mathrm {SO}}_{2n}^{E/F}(F_{{\mathfrak q}})$
-subrepresentation in
![]() $\pi _v$
with nonzero
$\pi _v$
with nonzero
![]() $H_{0,{{\mathfrak q}}}$
-fixed vectors. Consequently, after translating
$H_{0,{{\mathfrak q}}}$
-fixed vectors. Consequently, after translating
![]() $\pi ^{\flat }$
inside of
$\pi ^{\flat }$
inside of
![]() $\pi $
by a suitable
$\pi $
by a suitable
![]() $g \in {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, we may assume that
$g \in {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, we may assume that
![]() $\pi ^{\flat }_{{\mathfrak q}}$
is unramified at every
$\pi ^{\flat }_{{\mathfrak q}}$
is unramified at every
![]() ${{\mathfrak q}}$
not above
${{\mathfrak q}}$
not above
![]() $S_{\mathrm {bad}}$
(with respect to the hyperspecial subgroups above).
$S_{\mathrm {bad}}$
(with respect to the hyperspecial subgroups above).
Thanks to Theorem 6.5 if (std-reg) is assumed, or instead by Hypothesis 6.11, we have a Galois representation
whose restriction to
![]() $\Gamma _{E,S_{\mathrm {bad}}}$
satisfies, writing
$\Gamma _{E,S_{\mathrm {bad}}}$
satisfies, writing
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
for each
${{\mathfrak q}}:={\mathfrak p}\cap F$
for each
![]() ${\mathfrak p}$
,
${\mathfrak p}$
,
for all
![]() ${E}$
-places
${E}$
-places
![]() ${\mathfrak p} \notin S^E_{\mathrm {bad}}$
. Here,
${\mathfrak p} \notin S^E_{\mathrm {bad}}$
. Here,
![]() $\overset {\circ } \sim $
indicates
$\overset {\circ } \sim $
indicates
![]() $\mathrm {O}_{2n}$
-conjugacy (instead of
$\mathrm {O}_{2n}$
-conjugacy (instead of
![]() ${\mathrm {SO}}_{2n}$
-conjugacy).
${\mathrm {SO}}_{2n}$
-conjugacy).
Let
![]() $H\subset {\mathrm {SO}}_{2n}$
denote the Zariski closure of the image of
$H\subset {\mathrm {SO}}_{2n}$
denote the Zariski closure of the image of
![]() $\rho _{\pi ^{\flat }} \colon \Gamma _{E,S_{\mathrm {bad}}}\rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. By Proposition 5.5, either H is connected or
$\rho _{\pi ^{\flat }} \colon \Gamma _{E,S_{\mathrm {bad}}}\rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. By Proposition 5.5, either H is connected or
![]() $H=H^0\times Z({\mathrm {SO}}_{2n})$
. Therefore, via
$H=H^0\times Z({\mathrm {SO}}_{2n})$
. Therefore, via
![]() $\{\pm 1\}=Z({\mathrm {SO}}_{2n})$
, we can find a Galois character
$\{\pm 1\}=Z({\mathrm {SO}}_{2n})$
, we can find a Galois character
such that the product morphism
![]() $\eta \rho _{\pi ^{\flat }}$
has Zariski dense image in
$\eta \rho _{\pi ^{\flat }}$
has Zariski dense image in
![]() $H^0$
. In particular, if
$H^0$
. In particular, if
![]() $H^0 = H$
, we take
$H^0 = H$
, we take
![]() $\eta = 1$
. We define the character
$\eta = 1$
. We define the character
to be the character so that the composition
![]() $\widetilde {\eta } \colon \Gamma _{E, S_{\mathrm {bad}}} \to \langle z^+ \rangle \overset \sim \to _{\mathrm {pr}^{\circ }} \{\pm 1\}$
is equal to
$\widetilde {\eta } \colon \Gamma _{E, S_{\mathrm {bad}}} \to \langle z^+ \rangle \overset \sim \to _{\mathrm {pr}^{\circ }} \{\pm 1\}$
is equal to
![]() $\eta $
.
$\eta $
.
Recall that G is an inner form of
![]() $G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
giving rise to the Shimura data
$G^{*}={\mathrm {GSO}}^{E/F}_{2n}$
giving rise to the Shimura data
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G,X^{\pm })$
studied earlier. By [Reference Kret and Shin50, Prop. 6.3], there exists a cuspidal automorphic representation
$(\mathrm {Res}_{F/\mathbb {Q}} G,X^{\pm })$
studied earlier. By [Reference Kret and Shin50, Prop. 6.3], there exists a cuspidal automorphic representation
![]() $\pi ^{\natural }$
of
$\pi ^{\natural }$
of
![]() $G(\mathbb A_F)$
such that
$G(\mathbb A_F)$
such that
-
•
 $\pi ^{\natural }_{{{\mathfrak q}}'} \simeq \pi _{{{\mathfrak q}}'}$
at every finite prime
$\pi ^{\natural }_{{{\mathfrak q}}'} \simeq \pi _{{{\mathfrak q}}'}$
at every finite prime
 ${{\mathfrak q}}'$
where
${{\mathfrak q}}'$
where
 $\pi _{{{\mathfrak q}}'}$
is unramified (we have
$\pi _{{{\mathfrak q}}'}$
is unramified (we have
 $G_{{{\mathfrak q}}'}\simeq G^{*}_{{{\mathfrak q}}'}$
at such
$G_{{{\mathfrak q}}'}\simeq G^{*}_{{{\mathfrak q}}'}$
at such
 ${{\mathfrak q}}'$
),
${{\mathfrak q}}'$
), -
•
 $\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is a character twist of the Steinberg representation,
$\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
is a character twist of the Steinberg representation, -
•
 $\pi ^{\natural }_{\infty }$
is
$\pi ^{\natural }_{\infty }$
is
 $\xi $
-cohomological.
$\xi $
-cohomological.
The first condition and Lemma 10.1 imply that
![]() $\pi ^{\natural }$
satisfies condition (temp) of §9. Theorem 9.6 yields semisimple representations
$\pi ^{\natural }$
satisfies condition (temp) of §9. Theorem 9.6 yields semisimple representations
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
of
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
of
![]() $\Gamma _{E,S}$
for
$\Gamma _{E,S}$
for
![]() $\varepsilon \in \{\pm 1\}$
such that its dual
$\varepsilon \in \{\pm 1\}$
such that its dual
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon ,\vee }$
has the following property:
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon ,\vee }$
has the following property:
where S is a finite set of rational primes containing
![]() $S_{\mathrm {bad}}$
, large enough, so that Theorem 9.6 holds for both
$S_{\mathrm {bad}}$
, large enough, so that Theorem 9.6 holds for both
![]() $\varepsilon = +$
and
$\varepsilon = +$
and
![]() $\varepsilon = -$
. We define
$\varepsilon = -$
. We define
![]() $\rho _{\pi }^{\mathrm {Sh}, \varepsilon } := \rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
for
$\rho _{\pi }^{\mathrm {Sh}, \varepsilon } := \rho _{\pi ^{\natural }}^{\mathrm {Sh}, \varepsilon }$
for
![]() $\varepsilon \in \{\pm \}$
(which depends not on the choice of
$\varepsilon \in \{\pm \}$
(which depends not on the choice of
![]() $\pi ^{\natural }$
but only on
$\pi ^{\natural }$
but only on
![]() $\pi $
by (10.4)), and
$\pi $
by (10.4)), and
Then
![]() $\widetilde {\rho }^{\mathrm {Sh},\vee }_{\pi }$
is a
$\widetilde {\rho }^{\mathrm {Sh},\vee }_{\pi }$
is a
![]() $\Gamma _{E,S}$
-representation of dimension
$\Gamma _{E,S}$
-representation of dimension
![]() $a_{\pi } 2^n$
, where
$a_{\pi } 2^n$
, where
![]() $a_{\pi } := a(\pi ^{\natural })$
. We set
$a_{\pi } := a(\pi ^{\natural })$
. We set
when the input is a
![]() $\mathrm {GSpin}_{2n}$
-valued Galois representation or a local L-parameter, and write
$\mathrm {GSpin}_{2n}$
-valued Galois representation or a local L-parameter, and write
![]() $\widetilde {\mathrm {spin}}^{a}(\cdot )$
for the a-fold self-direct sum of
$\widetilde {\mathrm {spin}}^{a}(\cdot )$
for the a-fold self-direct sum of
![]() $\widetilde {\mathrm {spin}}(\cdot )$
. (So
$\widetilde {\mathrm {spin}}(\cdot )$
. (So
![]() $\widetilde {\mathrm {spin}}=\mathrm {spin}$
if
$\widetilde {\mathrm {spin}}=\mathrm {spin}$
if
![]() $\eta =1$
.) We have
$\eta =1$
.) We have
Then
![]() $\rho ^{\mathrm {Sh},\vee }_{\pi }$
,
$\rho ^{\mathrm {Sh},\vee }_{\pi }$
,
![]() $\widetilde {\rho }^{\mathrm {Sh},\vee }_{\pi }$
are a
$\widetilde {\rho }^{\mathrm {Sh},\vee }_{\pi }$
are a
![]() $\Gamma _{E,S}$
-representation of dimension
$\Gamma _{E,S}$
-representation of dimension
![]() $a_{\pi } 2^n$
, where
$a_{\pi } 2^n$
, where
![]() $a_{\pi } := a(\pi ^{\natural })$
.
$a_{\pi } := a(\pi ^{\natural })$
.
When
![]() $*$
is a map (resp. an element), we use
$*$
is a map (resp. an element), we use
![]() $\overline {*}$
to denote the composition with the adjoint map (resp. the image under the adjoint map) that is clear from the context.
$\overline {*}$
to denote the composition with the adjoint map (resp. the image under the adjoint map) that is clear from the context.
Proposition 10.2. There exists a continuous semisimple representation
(with C standing for a cohomological normalization) such that we have
Proof. Consider the diagram

At each prime
![]() ${\mathfrak p}$
of E not above S, we obtain from (10.1) that
${\mathfrak p}$
of E not above S, we obtain from (10.1) that
 $$ \begin{align} & \overline {\mathrm{spin}^{a_{\pi}}} ( (\eta \rho_{\pi^{\flat}})(\mathrm{Frob}_{\mathfrak p})_{\mathrm{ss}}) \sim \iota \overline {\mathrm{spin}^{a_{\pi}}}((\eta \phi_{\pi_{\mathfrak{q}}^{\flat}})(\mathrm{Frob}_{\mathfrak p})) \nonumber\\ & = \iota \overline { \mathrm{spin}^{a_{\pi}}((\tilde{\eta}\phi_{\pi_{\mathfrak{q}}^{\flat}})(\mathrm{Frob}_{\mathfrak p})) } \sim \overline{\widetilde{\rho}_{\pi}^{\mathrm{Sh},\vee}(\mathrm{Frob}_{\mathfrak p})_{\mathrm{ss}}} \in \mathrm{PGL}_{a_{\pi} 2^n}(\overline{\mathbb{Q}}_{\ell}). \end{align} $$
$$ \begin{align} & \overline {\mathrm{spin}^{a_{\pi}}} ( (\eta \rho_{\pi^{\flat}})(\mathrm{Frob}_{\mathfrak p})_{\mathrm{ss}}) \sim \iota \overline {\mathrm{spin}^{a_{\pi}}}((\eta \phi_{\pi_{\mathfrak{q}}^{\flat}})(\mathrm{Frob}_{\mathfrak p})) \nonumber\\ & = \iota \overline { \mathrm{spin}^{a_{\pi}}((\tilde{\eta}\phi_{\pi_{\mathfrak{q}}^{\flat}})(\mathrm{Frob}_{\mathfrak p})) } \sim \overline{\widetilde{\rho}_{\pi}^{\mathrm{Sh},\vee}(\mathrm{Frob}_{\mathfrak p})_{\mathrm{ss}}} \in \mathrm{PGL}_{a_{\pi} 2^n}(\overline{\mathbb{Q}}_{\ell}). \end{align} $$
Recall that
![]() $\eta \rho _{\pi ^{\flat }}$
has connected image. So (10.9) implies, via [Reference Kret and Shin50, Prop. 4.6, Ex. 4.7], the existence of
$\eta \rho _{\pi ^{\flat }}$
has connected image. So (10.9) implies, via [Reference Kret and Shin50, Prop. 4.6, Ex. 4.7], the existence of
![]() $g \in {\mathrm {GL}}_{a_{\pi } 2^{n}}(\overline {\mathbb {Q}}_{\ell })$
such that
$g \in {\mathrm {GL}}_{a_{\pi } 2^{n}}(\overline {\mathbb {Q}}_{\ell })$
such that
Replace
![]() $\widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee }$
by
$\widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee }$
by
![]() $g^{-1} \widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee } g$
so that
$g^{-1} \widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee } g$
so that
![]() $\overline {\widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee }} = \overline {\mathrm {spin}^{a_{\pi }}}( \eta \rho _{\pi ^{\flat }})$
. From Diagram (10.8), we deduce that
$\overline {\widetilde {\rho }_{\pi }^{\mathrm {Sh},\vee }} = \overline {\mathrm {spin}^{a_{\pi }}}( \eta \rho _{\pi ^{\flat }})$
. From Diagram (10.8), we deduce that
where
![]() $\mathrm {GSpin}_{2n}$
is viewed as a subgroup of
$\mathrm {GSpin}_{2n}$
is viewed as a subgroup of
![]() ${\mathrm {GL}}_{a_{\pi } 2^n}$
via
${\mathrm {GL}}_{a_{\pi } 2^n}$
via
![]() $\mathrm {spin}^{a_{\pi }}$
. That is, there exists a representation
$\mathrm {spin}^{a_{\pi }}$
. That is, there exists a representation
![]() $\widetilde {\rho }_{\pi }^C \colon \Gamma _{{E},S} \to \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
such that
$\widetilde {\rho }_{\pi }^C \colon \Gamma _{{E},S} \to \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
such that
Define
![]() $\rho _{\pi }^C:=\tilde {\eta } \widetilde {\rho }_{\pi }^C$
. Then it follows that
$\rho _{\pi }^C:=\tilde {\eta } \widetilde {\rho }_{\pi }^C$
. Then it follows that
Thanks to (10.1) and (10.5),
![]() $\rho _{\pi }^C$
satisfies (10.7) and (10.6). The proof is complete.
$\rho _{\pi }^C$
satisfies (10.7) and (10.6). The proof is complete.
Remark 10.3. The bottom row in (10.8) cannot be replaced with
![]() $\mathrm {PSO}_{2n}$
. (If it did, since
$\mathrm {PSO}_{2n}$
. (If it did, since
![]() $\overline \rho _{\pi ^{\flat }}$
has connected image in
$\overline \rho _{\pi ^{\flat }}$
has connected image in
![]() $\mathrm {PSO}_{2n}$
by Proposition 5.5, the argument above would work without introducing the
$\mathrm {PSO}_{2n}$
by Proposition 5.5, the argument above would work without introducing the
![]() $\eta $
-twist.) For instance, observe that
$\eta $
-twist.) For instance, observe that
![]() $\mathrm {GSpin}_{2n} \stackrel {\mathrm {spin}}{\longrightarrow } {\mathrm {GL}}_{2^{n}} \rightarrow \mathrm {PGL}_{2^{n}}$
does not factor through
$\mathrm {GSpin}_{2n} \stackrel {\mathrm {spin}}{\longrightarrow } {\mathrm {GL}}_{2^{n}} \rightarrow \mathrm {PGL}_{2^{n}}$
does not factor through
![]() $\mathrm {PSO}_{2n}$
since
$\mathrm {PSO}_{2n}$
since
![]() $\mathrm {spin}^+$
and
$\mathrm {spin}^+$
and
![]() $\mathrm {spin}^-$
have different central characters.
$\mathrm {spin}^-$
have different central characters.
We can refine (10.6) by separating
![]() $\mathrm {spin}^+$
and
$\mathrm {spin}^+$
and
![]() $\mathrm {spin}^-$
, which is a key intermediate step towards the main theorem. Our argument is quite delicate and sensitive to the underlying group-theoretic structures.
$\mathrm {spin}^-$
, which is a key intermediate step towards the main theorem. Our argument is quite delicate and sensitive to the underlying group-theoretic structures.
Proposition 10.4. Up to replacing
![]() $\rho _{\pi }^C$
by
$\rho _{\pi }^C$
by
![]() $\eta \theta (\rho _{\pi }^C)$
if necessary, we have the following. For every
$\eta \theta (\rho _{\pi }^C)$
if necessary, we have the following. For every
![]() ${\mathfrak p} \notin S^E$
and
${\mathfrak p} \notin S^E$
and
![]() $\varepsilon \in \{+,-\}$
,
$\varepsilon \in \{+,-\}$
,
where we write
![]() ${{\mathfrak q}}$
for the prime of F below
${{\mathfrak q}}$
for the prime of F below
![]() ${\mathfrak p}$
.
${\mathfrak p}$
.
Proof. Recall from §1 that we often write
![]() $G_0$
to mean
$G_0$
to mean
![]() $G_0(\overline {\mathbb {Q}}_{\ell })$
when
$G_0(\overline {\mathbb {Q}}_{\ell })$
when
![]() $G_0$
is a reductive group over
$G_0$
is a reductive group over
![]() $\overline {\mathbb {Q}}_{\ell }$
. Moreover, we assume
$\overline {\mathbb {Q}}_{\ell }$
. Moreover, we assume
![]() ${\mathfrak p} \notin S^E$
throughout, without repeating this condition.
${\mathfrak p} \notin S^E$
throughout, without repeating this condition.
The assertion (10.11) follows from (10.7) (and it is invariant under conjugation by an element of
![]() $\mathrm {GPin}_{2n}$
). The main thing to prove is (10.10). For simplicity, write
$\mathrm {GPin}_{2n}$
). The main thing to prove is (10.10). For simplicity, write
![]() $\rho :=\rho _{\pi }^C$
,
$\rho :=\rho _{\pi }^C$
,
![]() $\check \rho ^{\mathrm {Sh}, \varepsilon } := \rho _{\pi }^{\mathrm {Sh}, \varepsilon ,\vee }$
,
$\check \rho ^{\mathrm {Sh}, \varepsilon } := \rho _{\pi }^{\mathrm {Sh}, \varepsilon ,\vee }$
,
![]() $\rho ^{\circ }:=\mathrm {pr}^{\circ }\rho _{\pi }^C$
, and
$\rho ^{\circ }:=\mathrm {pr}^{\circ }\rho _{\pi }^C$
, and
![]() $a:=a_{\pi }$
. From (10.5) and (10.6), we have
$a:=a_{\pi }$
. From (10.5) and (10.6), we have
Write
![]() $Z:=Z(\mathrm {GSpin}_{2n})$
and H for the Zariski closure of
$Z:=Z(\mathrm {GSpin}_{2n})$
and H for the Zariski closure of
![]() $\mathrm {im}(\rho ^{\circ })$
in
$\mathrm {im}(\rho ^{\circ })$
in
![]() ${\mathrm {SO}}_{2n}$
. Then H contains a regular unipotent element by Corollary 6.8. We divide into two cases based on Proposition 5.5.
${\mathrm {SO}}_{2n}$
. Then H contains a regular unipotent element by Corollary 6.8. We divide into two cases based on Proposition 5.5.
Case 1. Assume
![]() $\mathrm {spin}^{\varepsilon }\rho _{\pi }^C$
is irreducible for
$\mathrm {spin}^{\varepsilon }\rho _{\pi }^C$
is irreducible for
![]() $\varepsilon = -$
. This happens when
$\varepsilon = -$
. This happens when
![]() $H^0$
is
$H^0$
is
![]() ${\mathrm {SO}}_{2n}$
,
${\mathrm {SO}}_{2n}$
,
![]() $i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
, or
$i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
, or
![]() $n = 4$
and
$n = 4$
and
![]() $H^0 = \mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
(possibly after conjugation in
$H^0 = \mathrm {spin}^{\circ }(\mathrm {Spin}_7)$
(possibly after conjugation in
![]() $\mathrm {GSpin}_{2n}$
). In the first two subcases,
$\mathrm {GSpin}_{2n}$
). In the first two subcases,
![]() $\mathrm {spin}^+ \rho $
is also irreducible; for irreducibility in the third case, see Lemma 5.2.
$\mathrm {spin}^+ \rho $
is also irreducible; for irreducibility in the third case, see Lemma 5.2.
If
![]() $\mathrm {spin}^+ \rho \simeq \eta \otimes \mathrm {spin}^- \rho $
, then it is clear from (10.12) that
$\mathrm {spin}^+ \rho \simeq \eta \otimes \mathrm {spin}^- \rho $
, then it is clear from (10.12) that
![]() $\check \rho ^{\mathrm {Sh},+}\simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}\simeq (\mathrm {spin}^+\rho )^{\oplus a} \simeq (\eta \otimes \mathrm {spin}^-\rho )^{\oplus a}$
. So the proposition follows from Theorem 9.6.
$\check \rho ^{\mathrm {Sh},+}\simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}\simeq (\mathrm {spin}^+\rho )^{\oplus a} \simeq (\eta \otimes \mathrm {spin}^-\rho )^{\oplus a}$
. So the proposition follows from Theorem 9.6.
Henceforth, assume that
![]() $\mathrm {spin}^+ \rho \not \simeq \eta \otimes \mathrm {spin}^- \rho $
.
$\mathrm {spin}^+ \rho \not \simeq \eta \otimes \mathrm {spin}^- \rho $
.
We claim that
![]() $\mathrm {spin}^-\rho (\gamma )_{\mathrm {ss}}$
is regular in
$\mathrm {spin}^-\rho (\gamma )_{\mathrm {ss}}$
is regular in
![]() ${\mathrm {GL}}_{2^{n-1}}$
on a density 1 set of
${\mathrm {GL}}_{2^{n-1}}$
on a density 1 set of
![]() $\gamma \in \Gamma $
. Define
$\gamma \in \Gamma $
. Define
![]() $X^-$
to be the subset of
$X^-$
to be the subset of
![]() $h\in H(\overline {\mathbb {Q}}_{\ell })$
such that the semisimple part of
$h\in H(\overline {\mathbb {Q}}_{\ell })$
such that the semisimple part of
![]() $\overline {\mathrm {spin}}^-(h)$
is non-regular in
$\overline {\mathrm {spin}}^-(h)$
is non-regular in
![]() $\mathrm {PGL}_{2^{n-1}}$
. Then
$\mathrm {PGL}_{2^{n-1}}$
. Then
![]() $X^-$
is Zariski-closed and conjugation-invariant in H. To show
$X^-$
is Zariski-closed and conjugation-invariant in H. To show
![]() $H\neq X^-$
, let
$H\neq X^-$
, let
![]() $\tilde H\subset \mathrm {GSpin}_{2n}$
be the preimage of H, so that
$\tilde H\subset \mathrm {GSpin}_{2n}$
be the preimage of H, so that
![]() $\tilde H^0$
equals
$\tilde H^0$
equals
![]() $\mathrm {Spin}_{2n}$
,
$\mathrm {Spin}_{2n}$
,
![]() $i_{\mathrm {std}}(\mathrm {Spin}_{2n-1})$
, or
$i_{\mathrm {std}}(\mathrm {Spin}_{2n-1})$
, or
![]() $\overline {\mathrm {spin}}(\mathrm {Spin}_7)$
in the three cases, respectively. Then the restriction of
$\overline {\mathrm {spin}}(\mathrm {Spin}_7)$
in the three cases, respectively. Then the restriction of
![]() $\mathrm {spin}^-$
via
$\mathrm {spin}^-$
via
![]() $\tilde H^0 \hookrightarrow \mathrm {GSpin}_{2n}$
is an irreducible representation with distinct weight vectors. (When
$\tilde H^0 \hookrightarrow \mathrm {GSpin}_{2n}$
is an irreducible representation with distinct weight vectors. (When
![]() $\tilde H^0=i_{\mathrm {std}}(\mathrm {Spin}_{2n-1})$
, the restriction is the spin representation of
$\tilde H^0=i_{\mathrm {std}}(\mathrm {Spin}_{2n-1})$
, the restriction is the spin representation of
![]() $\mathrm {Spin}_{2n-1}$
by Proposition 4.5.) So some element
$\mathrm {Spin}_{2n-1}$
by Proposition 4.5.) So some element
![]() $h_0$
of
$h_0$
of
![]() $\tilde H^0$
maps to a regular element of
$\tilde H^0$
maps to a regular element of
![]() ${\mathrm {GL}}_{2^{n-1}}$
under
${\mathrm {GL}}_{2^{n-1}}$
under
![]() $\mathrm {spin}^-$
. It follows that some element of
$\mathrm {spin}^-$
. It follows that some element of
![]() $H^0$
maps to a regular element of
$H^0$
maps to a regular element of
![]() $\mathrm {PGL}_{2^{n-1}}$
. We know that
$\mathrm {PGL}_{2^{n-1}}$
. We know that
![]() $\widetilde {H}$
is a subgroup of
$\widetilde {H}$
is a subgroup of
![]() $Z(\mathrm {GSpin}_{2n})\widetilde {H} \subset \mathrm {GSpin}_{2n}$
, thus by multiplying
$Z(\mathrm {GSpin}_{2n})\widetilde {H} \subset \mathrm {GSpin}_{2n}$
, thus by multiplying
![]() $h_0$
by elements in the center, we obtain in each connected component of H an element with regular image in
$h_0$
by elements in the center, we obtain in each connected component of H an element with regular image in
![]() ${\mathrm {GL}}_{2^{n-1}}$
. In particular, for each connected component C of H, we have
${\mathrm {GL}}_{2^{n-1}}$
. In particular, for each connected component C of H, we have
![]() $X^- \cap C \neq C$
, and thus
$X^- \cap C \neq C$
, and thus
![]() $\dim X^- <\dim H$
. Therefore, the set of
$\dim X^- <\dim H$
. Therefore, the set of
![]() $\gamma $
such that
$\gamma $
such that
![]() $\rho ^{\circ }(\gamma )\notin X^-$
has density 1 according to Lemma 1.1, and in this case,
$\rho ^{\circ }(\gamma )\notin X^-$
has density 1 according to Lemma 1.1, and in this case,
![]() $\overline {\mathrm {spin}^-\rho (\gamma )_{\mathrm {ss}}}=\overline {\mathrm {spin}^-}(\rho ^{\circ }(\gamma )_{\mathrm {ss}})$
is regular. The claim is verified.
$\overline {\mathrm {spin}^-\rho (\gamma )_{\mathrm {ss}}}=\overline {\mathrm {spin}^-}(\rho ^{\circ }(\gamma )_{\mathrm {ss}})$
is regular. The claim is verified.
Given a square matrix g, let
![]() $\mathscr {EV}(g)$
for the multi-set of its eigenvalues. Since
$\mathscr {EV}(g)$
for the multi-set of its eigenvalues. Since
![]() $\mathrm {spin}^+ \rho \not \simeq \eta \otimes \mathrm {spin}^- \rho $
, there exists
$\mathrm {spin}^+ \rho \not \simeq \eta \otimes \mathrm {spin}^- \rho $
, there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
-
•
 $\mathrm {spin}^- \rho (\gamma )$
has distinct eigenvalues,
$\mathrm {spin}^- \rho (\gamma )$
has distinct eigenvalues, -
•
 $\mathscr {EV}(\eta (\gamma ) \mathrm {spin}^- \rho (\gamma ))\neq \mathscr {EV}(\mathrm {spin}^+ \rho (\gamma ))$
.
$\mathscr {EV}(\eta (\gamma ) \mathrm {spin}^- \rho (\gamma ))\neq \mathscr {EV}(\mathrm {spin}^+ \rho (\gamma ))$
.
In particular, there exists an eigenvalue
![]() $\alpha $
of
$\alpha $
of
![]() $\eta (\gamma ) \mathrm {spin}^- \rho (\gamma )$
which is not an eigenvalue of
$\eta (\gamma ) \mathrm {spin}^- \rho (\gamma )$
which is not an eigenvalue of
![]() $\mathrm {spin}^+ \rho (\gamma )$
. Then
$\mathrm {spin}^+ \rho (\gamma )$
. Then
![]() $\alpha $
appears as an eigenvalue with multiplicity a on the right-hand side of (10.12). We know from Theorem 9.6 that each eigenvalue of
$\alpha $
appears as an eigenvalue with multiplicity a on the right-hand side of (10.12). We know from Theorem 9.6 that each eigenvalue of
![]() $\check \rho ^{\mathrm {Sh},+}(\gamma )$
and
$\check \rho ^{\mathrm {Sh},+}(\gamma )$
and
![]() $\eta (\gamma )\check \rho ^{\mathrm {Sh},-}(\gamma )$
appears with multiplicity divisible by a. Thus,
$\eta (\gamma )\check \rho ^{\mathrm {Sh},-}(\gamma )$
appears with multiplicity divisible by a. Thus,
![]() $\alpha $
is an eigenvalue of either
$\alpha $
is an eigenvalue of either
![]() $\check \rho ^{\mathrm {Sh},+}(\gamma )$
or
$\check \rho ^{\mathrm {Sh},+}(\gamma )$
or
![]() $\eta (\gamma ) \check \rho ^{\mathrm {Sh},-}(\gamma )$
, but not both. This implies, together with Theorem 9.6 and the irreducibility of
$\eta (\gamma ) \check \rho ^{\mathrm {Sh},-}(\gamma )$
, but not both. This implies, together with Theorem 9.6 and the irreducibility of
![]() $\mathrm {spin}^-\rho $
, that (i)
$\mathrm {spin}^-\rho $
, that (i)
![]() $(\eta \otimes \mathrm {spin}^-\rho )^{\oplus a} \simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}$
and
$(\eta \otimes \mathrm {spin}^-\rho )^{\oplus a} \simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}$
and
![]() $(\mathrm {spin}^+ \rho )^{\oplus a} \simeq \check \rho ^{\mathrm {Sh},+}$
, or (ii)
$(\mathrm {spin}^+ \rho )^{\oplus a} \simeq \check \rho ^{\mathrm {Sh},+}$
, or (ii)
![]() $(\eta \otimes \mathrm {spin}^-\rho )^{\oplus a} \simeq \check \rho ^{\mathrm {Sh},+}$
and
$(\eta \otimes \mathrm {spin}^-\rho )^{\oplus a} \simeq \check \rho ^{\mathrm {Sh},+}$
and
![]() $(\mathrm {spin}^+\rho )^{\oplus a}\simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}$
. In case (i), Equation (10.10) follows from Theorem 9.6. If (ii) occurs, replace
$(\mathrm {spin}^+\rho )^{\oplus a}\simeq \eta \otimes \check \rho ^{\mathrm {Sh},-}$
. In case (i), Equation (10.10) follows from Theorem 9.6. If (ii) occurs, replace
![]() $\rho $
with
$\rho $
with
![]() $\eta \otimes (\vartheta \rho \vartheta ^{-1})$
, where
$\eta \otimes (\vartheta \rho \vartheta ^{-1})$
, where
![]() $\vartheta \in \mathrm {GPin}_{2n}$
is as in (3.7). (Here,
$\vartheta \in \mathrm {GPin}_{2n}$
is as in (3.7). (Here,
![]() $\mathrm {im}(\eta )=\{\pm 1\}$
is viewed as the subgroup of
$\mathrm {im}(\eta )=\{\pm 1\}$
is viewed as the subgroup of
![]() $\ker (\mathrm {pr}^{\circ })=\mathbb G_m$
.) Then equations (10.6) and (10.7) are still true (as
$\ker (\mathrm {pr}^{\circ })=\mathbb G_m$
.) Then equations (10.6) and (10.7) are still true (as
![]() $\mathrm {pr}^{\circ }(\eta ) = 1$
). Hence, if we run the current proof again, we will be in Case 1(i). We are done in Case 1.
$\mathrm {pr}^{\circ }(\eta ) = 1$
). Hence, if we run the current proof again, we will be in Case 1(i). We are done in Case 1.
Case 2. We now assume
![]() $H^0 \subset i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
, which covers the cases
$H^0 \subset i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
, which covers the cases
![]() $H^0 = i^{\circ }_{\mathrm {reg}}(\mathrm {PGL}_2)$
,
$H^0 = i^{\circ }_{\mathrm {reg}}(\mathrm {PGL}_2)$
,
![]() $H^0 = i^{\circ }_{\mathrm {std}}(G_2)$
and
$H^0 = i^{\circ }_{\mathrm {std}}(G_2)$
and
![]() $n = 4$
. By Proposition 5.5, we have
$n = 4$
. By Proposition 5.5, we have
![]() $H \subset H^0 Z({\mathrm {SO}}_{2n})$
, and
$H \subset H^0 Z({\mathrm {SO}}_{2n})$
, and
![]() $\rho $
has image in the group
$\rho $
has image in the group
![]() $H_{2n-1}$
from (5.4). By (10.2),
$H_{2n-1}$
from (5.4). By (10.2),
![]() $\eta \rho ^{\circ }$
has dense image in
$\eta \rho ^{\circ }$
has dense image in
![]() $H^0$
, and by (10.3),
$H^0$
, and by (10.3),
![]() $\widetilde {\rho }$
has image in
$\widetilde {\rho }$
has image in
![]() $\mathrm {GSpin}_{2n-1} \subset H_{2n-1}$
. In particular,
$\mathrm {GSpin}_{2n-1} \subset H_{2n-1}$
. In particular,
![]() $\eta $
is equal to
$\eta $
is equal to
![]() $\kappa _0 \circ \rho $
, with
$\kappa _0 \circ \rho $
, with
![]() $\kappa _0$
from (5.6). From (5.7), we obtain
$\kappa _0$
from (5.6). From (5.7), we obtain
where we write
![]() $\rho _{\mathfrak {p}} := \rho (\mathrm {Frob}_{\mathfrak {p}})_{\mathrm {ss}}$
and
$\rho _{\mathfrak {p}} := \rho (\mathrm {Frob}_{\mathfrak {p}})_{\mathrm {ss}}$
and
![]() $\eta _{\mathfrak {p}} := \eta (\mathrm {Frob}_{\mathfrak {p}})$
. Similarly, we write
$\eta _{\mathfrak {p}} := \eta (\mathrm {Frob}_{\mathfrak {p}})$
. Similarly, we write
![]() $\widetilde {\eta }_{\mathfrak {p}} := \widetilde {\eta }(\mathrm {Frob}_{\mathfrak {p}})$
and
$\widetilde {\eta }_{\mathfrak {p}} := \widetilde {\eta }(\mathrm {Frob}_{\mathfrak {p}})$
and
![]() $\phi _{\mathfrak {p}} := \iota q_{\mathfrak {p}}^{-n(n-1)/4} \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {p}})$
. We claim
$\phi _{\mathfrak {p}} := \iota q_{\mathfrak {p}}^{-n(n-1)/4} \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {p}})$
. We claim
By Equation (10.1), we have
![]() $\mathrm {pr}^{\circ } \rho _{\mathfrak {p}} \overset {\circ } \sim \mathrm {pr}^{\circ } \phi _{\mathfrak {p}} \in {\mathrm {SO}}_{2n}$
. Multiplying
$\mathrm {pr}^{\circ } \rho _{\mathfrak {p}} \overset {\circ } \sim \mathrm {pr}^{\circ } \phi _{\mathfrak {p}} \in {\mathrm {SO}}_{2n}$
. Multiplying
![]() $\eta $
, we obtain
$\eta $
, we obtain
![]() $\mathrm {pr}^{\circ }(\widetilde {\eta }_{\mathfrak {p}} \phi _p) \overset {\circ } \sim \mathrm {pr}^{\circ }(\widetilde {\eta }_p \rho _{\mathfrak {p}})$
. By assumption,
$\mathrm {pr}^{\circ }(\widetilde {\eta }_{\mathfrak {p}} \phi _p) \overset {\circ } \sim \mathrm {pr}^{\circ }(\widetilde {\eta }_p \rho _{\mathfrak {p}})$
. By assumption,
![]() $\mathrm {pr}^{\circ }(\widetilde {\eta }_p \rho _{\mathfrak {p}}) \in i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
. Hence,
$\mathrm {pr}^{\circ }(\widetilde {\eta }_p \rho _{\mathfrak {p}}) \in i^{\circ }_{\mathrm {std}}({\mathrm {SO}}_{2n-1})$
. Hence,
![]() $\widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}} = g x g^{-1}$
for some
$\widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}} = g x g^{-1}$
for some
![]() $g\in \mathrm {GPin}_{2n}$
and
$g\in \mathrm {GPin}_{2n}$
and
![]() $x \in i_{\mathrm {std}}(\mathrm {GSpin}_{2n-1})$
. We have
$x \in i_{\mathrm {std}}(\mathrm {GSpin}_{2n-1})$
. We have
![]() $\theta (x) = x$
, and thus,
$\theta (x) = x$
, and thus,
As
![]() $\theta (g) g^{-1} \in \mathrm {GSpin}_{2n}$
, this implies that
$\theta (g) g^{-1} \in \mathrm {GSpin}_{2n}$
, this implies that
![]() $\theta (\widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}}) \sim \widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}}$
. Since
$\theta (\widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}}) \sim \widetilde {\eta }_{\mathfrak {p}} \phi _{\mathfrak {p}}$
. Since
![]() $\theta (\widetilde {\eta }_{\mathfrak {p}}) = \eta _{\mathfrak {p}} \widetilde {\eta }_{\mathfrak {p}}$
, (10.14) follows.
$\theta (\widetilde {\eta }_{\mathfrak {p}}) = \eta _{\mathfrak {p}} \widetilde {\eta }_{\mathfrak {p}}$
, (10.14) follows.
In (10.6), we established
which implies by (10.13) and (10.14)
![]() $\mathrm {spin}^{+, \oplus 2}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{+, \oplus 2}(\phi _{\mathfrak {p}})$
. It follows that
$\mathrm {spin}^{+, \oplus 2}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{+, \oplus 2}(\phi _{\mathfrak {p}})$
. It follows that
![]() $\mathrm {spin}^{+}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{+}(\phi _{\mathfrak {p}})$
, Similarly, we deduce
$\mathrm {spin}^{+}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{+}(\phi _{\mathfrak {p}})$
, Similarly, we deduce
![]() $ \mathrm {spin}^{-}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{-}(\phi _{\mathfrak {p}})$
.
$ \mathrm {spin}^{-}(\rho _{\mathfrak {p}}) \sim \mathrm {spin}^{-}(\phi _{\mathfrak {p}})$
.
From now on, we replace, if necessary,
![]() $\rho _{\pi }^C$
by
$\rho _{\pi }^C$
by
![]() $\eta \theta (\rho _{\pi }^C)$
so that the conclusion of Proposition 10.4 holds for
$\eta \theta (\rho _{\pi }^C)$
so that the conclusion of Proposition 10.4 holds for
![]() $\rho _{\pi }^C$
.
$\rho _{\pi }^C$
.
Proposition 10.5. We have that (writing
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
)
${{\mathfrak q}}:={\mathfrak p}\cap F$
)
Proof. We first establish the claim that
![]() $\chi _{\ell }^{n(n-1)/2} \iota \omega _{\pi } = \mathcal N\rho _{\pi }^C$
, where
$\chi _{\ell }^{n(n-1)/2} \iota \omega _{\pi } = \mathcal N\rho _{\pi }^C$
, where
![]() $\chi _{\ell }$
is the cyclotomic character and we view
$\chi _{\ell }$
is the cyclotomic character and we view
![]() $\omega _{\pi }$
as a Galois character via class field theory. In view of Lemma 5.6(i), it suffices to check that
$\omega _{\pi }$
as a Galois character via class field theory. In view of Lemma 5.6(i), it suffices to check that
By Lemma 4.2, we have
Let
![]() ${\mathfrak p} \notin S^E$
, and write shorthand
${\mathfrak p} \notin S^E$
, and write shorthand
![]() $\rho _{\mathfrak {p}} := \rho ^C_{\pi }(\mathrm {Frob}_{{\mathfrak p}})_{\mathrm {ss}}$
and
$\rho _{\mathfrak {p}} := \rho ^C_{\pi }(\mathrm {Frob}_{{\mathfrak p}})_{\mathrm {ss}}$
and
![]() $\phi _{\mathfrak {p}} := \iota q_{\mathfrak {p}}^{-n(n-1)/4}\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak p})$
. We apply (10.10) and compute using Lemma 4.2 again (but now locally)
$\phi _{\mathfrak {p}} := \iota q_{\mathfrak {p}}^{-n(n-1)/4}\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak p})$
. We apply (10.10) and compute using Lemma 4.2 again (but now locally)
We now appeal to functoriality of the Satake isomorphism (unramified local Langlands correspondence) with respect to
![]() $\mathbb {G}_{\mathrm {m}} \hookrightarrow {\mathrm {GSO}}_{2n}$
(dual to
$\mathbb {G}_{\mathrm {m}} \hookrightarrow {\mathrm {GSO}}_{2n}$
(dual to
![]() $\mathcal N:\mathrm {GSpin}_{2n}\rightarrow \mathbb {G}_{\mathrm {m}}$
), to get
$\mathcal N:\mathrm {GSpin}_{2n}\rightarrow \mathbb {G}_{\mathrm {m}}$
), to get
![]() $\mathcal N(\phi _{\mathfrak {p}}) = \chi _{\ell }^{n(n-1)/2}(\mathrm {Frob}_{\mathfrak {p}}) \iota \omega _{\pi }(\mathrm {Frob}_p)$
. Therefore,
$\mathcal N(\phi _{\mathfrak {p}}) = \chi _{\ell }^{n(n-1)/2}(\mathrm {Frob}_{\mathfrak {p}}) \iota \omega _{\pi }(\mathrm {Frob}_p)$
. Therefore,
Comparing with (10.17), we obtain (10.16). At this point, we have established that
 $$ \begin{align} \mathrm{spin}^{\varepsilon} \rho_{\mathfrak p} &\sim \mathrm{spin}^{\varepsilon} \phi_{{\mathfrak p}} \in {\mathrm{GL}}_{2^{n-1}}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(Proposition \ 10.4),} \cr \mathrm{pr}^{\circ} \rho_{\mathfrak p} & \overset {\circ} \sim \mathrm{pr}^{\circ} \phi_{{\mathfrak p}} \in {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(Proposition \ 10.4),} \cr \mathcal N \rho_{\mathfrak p} & = \mathcal N\phi_{{\mathfrak p}} \in \mathbb{G}_{\mathrm{m}}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(claim \ above)}. \end{align} $$
$$ \begin{align} \mathrm{spin}^{\varepsilon} \rho_{\mathfrak p} &\sim \mathrm{spin}^{\varepsilon} \phi_{{\mathfrak p}} \in {\mathrm{GL}}_{2^{n-1}}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(Proposition \ 10.4),} \cr \mathrm{pr}^{\circ} \rho_{\mathfrak p} & \overset {\circ} \sim \mathrm{pr}^{\circ} \phi_{{\mathfrak p}} \in {\mathrm{SO}}_{2n}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(Proposition \ 10.4),} \cr \mathcal N \rho_{\mathfrak p} & = \mathcal N\phi_{{\mathfrak p}} \in \mathbb{G}_{\mathrm{m}}(\overline{\mathbb{Q}}_{\ell}) & \mathrm{(claim \ above)}. \end{align} $$
By [Reference Kret and Shin50, Lem. 1.1, table], a semi-simple element
![]() $\gamma $
of
$\gamma $
of
![]() $\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is determined up to conjugacy by the conjugacy classes of
$\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is determined up to conjugacy by the conjugacy classes of
![]() $\mathrm {spin}^+\gamma , \mathrm {spin}^-\gamma \in {\mathrm {GL}}_{2^{n-1}}$
,
$\mathrm {spin}^+\gamma , \mathrm {spin}^-\gamma \in {\mathrm {GL}}_{2^{n-1}}$
,
![]() $\mathrm {std} \gamma \in {\mathrm {GL}}_{2n}$
and
$\mathrm {std} \gamma \in {\mathrm {GL}}_{2n}$
and
![]() $\mathcal N\gamma \in \mathbb {G}_{\mathrm {m}}$
. We complete the proof by noting that the two sides of (10.15) become conjugate under
$\mathcal N\gamma \in \mathbb {G}_{\mathrm {m}}$
. We complete the proof by noting that the two sides of (10.15) become conjugate under
![]() $\mathrm {spin}^+$
,
$\mathrm {spin}^+$
,
![]() $\mathrm {spin}^-$
,
$\mathrm {spin}^-$
,
![]() $\mathrm {std}$
and
$\mathrm {std}$
and
![]() $\mathcal N$
by (10.19).
$\mathcal N$
by (10.19).
11 Compatibility at unramified places
We continue in the setup of §10 with the same running assumptions. We determined the image of Frobenius under
![]() $\rho _{\pi }^C$
at each prime away from some finite set S. Now we compute the image at the finite places
$\rho _{\pi }^C$
at each prime away from some finite set S. Now we compute the image at the finite places
![]() ${\mathfrak p} \nmid \ell $
above
${\mathfrak p} \nmid \ell $
above
![]() $S \backslash S_{\mathrm {bad}}$
. The argument follows that of [Reference Kret and Shin50, §10], but there are new technical difficulties due to half-spin representations and the automorphism
$S \backslash S_{\mathrm {bad}}$
. The argument follows that of [Reference Kret and Shin50, §10], but there are new technical difficulties due to half-spin representations and the automorphism
![]() $\theta $
.
$\theta $
.
Proposition 11.1. Let
![]() ${\mathfrak p}$
be a prime of E not lying above
${\mathfrak p}$
be a prime of E not lying above
![]() $S_{\mathrm {bad}} \cup \{\ell \}$
. Then
$S_{\mathrm {bad}} \cup \{\ell \}$
. Then
![]() $\rho ^C_{\pi }$
is unramified at
$\rho ^C_{\pi }$
is unramified at
![]() ${\mathfrak p}$
. Moreover, writing
${\mathfrak p}$
. Moreover, writing
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
,
${{\mathfrak q}}:={\mathfrak p}\cap F$
,
Proof. Fix
![]() ${\mathfrak p}$
as in the statement. Let p denote the prime of
${\mathfrak p}$
as in the statement. Let p denote the prime of
![]() $\mathbb {Q}$
below
$\mathbb {Q}$
below
![]() ${\mathfrak p}$
. Let
${\mathfrak p}$
. Let
![]() $\pi ^{\natural }$
be a transfer of
$\pi ^{\natural }$
be a transfer of
![]() $\pi $
from
$\pi $
from
![]() $G^{*}(\mathbb A_F)$
to
$G^{*}(\mathbb A_F)$
to
![]() $G(\mathbb A_F)$
as in the paragraph above (10.4). Let
$G(\mathbb A_F)$
as in the paragraph above (10.4). Let
![]() $B(\pi ^{\natural })$
be the set of cuspidal automorphic representations
$B(\pi ^{\natural })$
be the set of cuspidal automorphic representations
![]() $\tau $
of
$\tau $
of
![]() $G(\mathbb A_F)$
such that
$G(\mathbb A_F)$
such that
-
•
 $\tau _{{{{\mathfrak q}}_{\mathrm {St}}}}$
and
$\tau _{{{{\mathfrak q}}_{\mathrm {St}}}}$
and
 $\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
are isomorphic up to a twist by an unramified character,
$\pi ^{\natural }_{{{{\mathfrak q}}_{\mathrm {St}}}}$
are isomorphic up to a twist by an unramified character, -
•
 $\tau ^{\infty , {{{\mathfrak q}}_{\mathrm {St}}},p}$
and
$\tau ^{\infty , {{{\mathfrak q}}_{\mathrm {St}}},p}$
and
 $\pi ^{\natural , \infty , {{{\mathfrak q}}_{\mathrm {St}}},p}$
are isomorphic,
$\pi ^{\natural , \infty , {{{\mathfrak q}}_{\mathrm {St}}},p}$
are isomorphic, -
•
 $\tau _p$
is unramified,
$\tau _p$
is unramified, -
•
 $\tau _{\infty }$
is
$\tau _{\infty }$
is
 $\xi $
-cohomological.
$\xi $
-cohomological.
We define an equivalence relation
![]() $\approx $
on the set
$\approx $
on the set
![]() $B(\pi ^{\natural })$
by declaring that
$B(\pi ^{\natural })$
by declaring that
![]() $\tau _1\approx \tau _2$
if and only if
$\tau _1\approx \tau _2$
if and only if
![]() $\tau _2 \in A(\tau _1)$
. (Recall the definition of
$\tau _2 \in A(\tau _1)$
. (Recall the definition of
![]() $A(\tau _1)$
from above (9.3); notice that
$A(\tau _1)$
from above (9.3); notice that
![]() $\tau _1 \approx \tau _2$
if and only if
$\tau _1 \approx \tau _2$
if and only if
![]() $\tau _{1, {{\mathfrak q}}} \simeq \tau _{2,{{\mathfrak q}}}$
.) To simplify notation, we will write B for a set of representatives for
$\tau _{1, {{\mathfrak q}}} \simeq \tau _{2,{{\mathfrak q}}}$
.) To simplify notation, we will write B for a set of representatives for
![]() $B(\pi ^{\natural })/{\approx }$
.
$B(\pi ^{\natural })/{\approx }$
.
For
![]() $\varepsilon \in \{+,-\}$
, define (true) representations of
$\varepsilon \in \{+,-\}$
, define (true) representations of
![]() $\Gamma _{E}$
by
$\Gamma _{E}$
by
![]() $\rho ^{\mathrm {Sh}, \varepsilon }_B:=\sum _{\tau \in B} \rho ^{\mathrm {Sh},\varepsilon }_{\tau }$
(see Theorem 9.6). Put
$\rho ^{\mathrm {Sh}, \varepsilon }_B:=\sum _{\tau \in B} \rho ^{\mathrm {Sh},\varepsilon }_{\tau }$
(see Theorem 9.6). Put
![]() $b(\pi ^{\natural }) := \sum _{\tau \in B} a(\tau )\in \mathbb Z_{>0}$
. Since
$b(\pi ^{\natural }) := \sum _{\tau \in B} a(\tau )\in \mathbb Z_{>0}$
. Since
![]() $\rho _{\tau }^{\mathrm {Sh},\varepsilon ,\vee }$
satisfies (10.4) for each
$\rho _{\tau }^{\mathrm {Sh},\varepsilon ,\vee }$
satisfies (10.4) for each
![]() $\tau \in B$
, we deduce the following on the dual of
$\tau \in B$
, we deduce the following on the dual of
![]() $\rho ^{\mathrm {Sh}, \varepsilon }_B$
by comparing the images of Frobenius conjugacy classes at all but finitely many places via (10.4) and (10.10):
$\rho ^{\mathrm {Sh}, \varepsilon }_B$
by comparing the images of Frobenius conjugacy classes at all but finitely many places via (10.4) and (10.10):
We adapt the argument of Theorem 9.6. Consider the function f on
![]() $G(\mathbb A_F)$
of the form
$G(\mathbb A_F)$
of the form
![]() $f = f_{\infty } f_{{{{\mathfrak q}}_{\mathrm {St}}}} \textbf {1}_{K_p} f^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}, p}$
, where
$f = f_{\infty } f_{{{{\mathfrak q}}_{\mathrm {St}}}} \textbf {1}_{K_p} f^{\infty , {{{\mathfrak q}}_{\mathrm {St}}}, p}$
, where
![]() $f_{\infty }$
and
$f_{\infty }$
and
![]() $f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
are as in that argument, and
$f_{{{{\mathfrak q}}_{\mathrm {St}}}}$
are as in that argument, and
![]() $f^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}, p}$
is such that, for all automorphic representations
$f^{\infty ,{{{\mathfrak q}}_{\mathrm {St}}}, p}$
is such that, for all automorphic representations
![]() $\tau $
of
$\tau $
of
![]() $G(\mathbb A_F)$
with
$G(\mathbb A_F)$
with
![]() $(\tau ^{\infty })^K \neq 0$
and
$(\tau ^{\infty })^K \neq 0$
and
![]() $\mathrm {Tr}\, \tau _{\infty }(f_{\infty }) \neq 0$
, we have
$\mathrm {Tr}\, \tau _{\infty }(f_{\infty }) \neq 0$
, we have
 $$ \begin{align} \mathrm{Tr}\, \tau^{\infty, {{{\mathfrak q}}_{\mathrm{St}}}, p }(f^{\infty, {{{\mathfrak q}}_{\mathrm{St}}}, p }) = \begin{cases} 1 & \mathrm{if \ } \tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}, p} \simeq \pi^{\natural,\infty,{{{\mathfrak q}}_{\mathrm{St}}},p}, \cr 0 & \mathrm{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \mathrm{Tr}\, \tau^{\infty, {{{\mathfrak q}}_{\mathrm{St}}}, p }(f^{\infty, {{{\mathfrak q}}_{\mathrm{St}}}, p }) = \begin{cases} 1 & \mathrm{if \ } \tau^{\infty,{{{\mathfrak q}}_{\mathrm{St}}}, p} \simeq \pi^{\natural,\infty,{{{\mathfrak q}}_{\mathrm{St}}},p}, \cr 0 & \mathrm{otherwise.} \end{cases} \end{align} $$
Arguing as in Theorem 9.6, we obtain
Define
![]() $\rho _B^{\mathrm {Sh}} := \rho _B^{\mathrm {Sh}, +} \oplus \rho _B^{\mathrm {Sh},-}$
. Applying (11.3) for both
$\rho _B^{\mathrm {Sh}} := \rho _B^{\mathrm {Sh}, +} \oplus \rho _B^{\mathrm {Sh},-}$
. Applying (11.3) for both
![]() $\varepsilon = \pm $
and taking the sum, we obtain
$\varepsilon = \pm $
and taking the sum, we obtain
Since Xu [Reference Xu81, Thm. 1.8] describes global L-packets for (not only
![]() $\mathrm {GSp}_{2n}$
but) quasi-split forms of
$\mathrm {GSp}_{2n}$
but) quasi-split forms of
![]() ${\mathrm {GSO}}_{2n}$
, the argument for [Reference Kret and Shin50, Lem. 10.2] goes through unchanged, except Corollary 9.7 replaces [Reference Kret and Shin50, Cor. 8.4]. This argument shows that
${\mathrm {GSO}}_{2n}$
, the argument for [Reference Kret and Shin50, Lem. 10.2] goes through unchanged, except Corollary 9.7 replaces [Reference Kret and Shin50, Cor. 8.4]. This argument shows that
![]() $\pi ^{\natural }$
and
$\pi ^{\natural }$
and
![]() $\tau \otimes \omega $
belong to the same global packet in Xu’s paper for an automorphic quadratic character
$\tau \otimes \omega $
belong to the same global packet in Xu’s paper for an automorphic quadratic character
![]() $\omega \colon {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F) \to {\mathbb {C}}^{\times }$
. Since each member of the packet in [Reference Xu81] is a
$\omega \colon {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F) \to {\mathbb {C}}^{\times }$
. Since each member of the packet in [Reference Xu81] is a
![]() $\theta $
-orbit of representations, this tells us that either
$\theta $
-orbit of representations, this tells us that either
![]() $\pi ^{\natural }_x \simeq \tau _x \otimes \omega _x$
or
$\pi ^{\natural }_x \simeq \tau _x \otimes \omega _x$
or
![]() $\theta (\pi _x^{\natural }) \simeq \tau _x \otimes \omega _x$
at almost all places x (where both
$\theta (\pi _x^{\natural }) \simeq \tau _x \otimes \omega _x$
at almost all places x (where both
![]() $\pi ^{\natural }_x$
,
$\pi ^{\natural }_x$
,
![]() $\tau _x$
, and
$\tau _x$
, and
![]() $\omega _x$
are unramified). Since
$\omega _x$
are unramified). Since
![]() $\pi ^{\natural }_x\simeq \tau _x$
at almost all x,
$\pi ^{\natural }_x\simeq \tau _x$
at almost all x,
Let us define characters
![]() $\chi ^{\varepsilon }:\Gamma _E\rightarrow \{\pm 1\}$
from
$\chi ^{\varepsilon }:\Gamma _E\rightarrow \{\pm 1\}$
from
![]() $\omega $
via
$\omega $
via
![]() $\mathrm {spin}^{\varepsilon }$
as follows. Via class field theory and Galois cohomology (applying [Reference Lapid and Mao54, Lem. A.1] to
$\mathrm {spin}^{\varepsilon }$
as follows. Via class field theory and Galois cohomology (applying [Reference Lapid and Mao54, Lem. A.1] to
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
; see also [Reference Waldspurger79]), we assign to
${\mathrm {GSO}}_{2n}^{E/F}$
; see also [Reference Waldspurger79]), we assign to
![]() $\omega $
the continuous character
$\omega $
the continuous character
whose restriction to
![]() $W_E$
factors through a character
$W_E$
factors through a character
![]() $c \colon \Gamma _E \to Z(\mathrm {GSpin}_{2n})$
. We then define
$c \colon \Gamma _E \to Z(\mathrm {GSpin}_{2n})$
. We then define
![]() $\chi ^{\varepsilon } := \mathrm {spin}^{\varepsilon }(c)$
. We deduce
$\chi ^{\varepsilon } := \mathrm {spin}^{\varepsilon }(c)$
. We deduce
by using (11.5) to verify that the semisimplfication of the image of Frobenius matches at almost all places.
By Lemma 5.6(iii), we have
![]() $\chi ^+ = \chi ^-$
. Set
$\chi ^+ = \chi ^-$
. Set
![]() $\chi :=\chi ^+$
. The same lemma tells us that
$\chi :=\chi ^+$
. The same lemma tells us that
![]() $\chi = 1$
or that
$\chi = 1$
or that
![]() $\rho _{\pi }^C$
has image in the group
$\rho _{\pi }^C$
has image in the group
![]() $H_{2n-1}$
from (5.4) and
$H_{2n-1}$
from (5.4) and
![]() $\chi = \kappa _0 \circ \rho _{\pi }^C$
.
$\chi = \kappa _0 \circ \rho _{\pi }^C$
.
First case. Suppose that
![]() $\chi = 1$
for every
$\chi = 1$
for every
![]() $\tau \in B$
. Then, for each
$\tau \in B$
. Then, for each
![]() $\tau \in B$
, there is some
$\tau \in B$
, there is some
![]() $l \in \mathbb Z/2\mathbb Z$
, and we have
$l \in \mathbb Z/2\mathbb Z$
, and we have
As l does not depend on
![]() $\varepsilon $
, we obtain from (11.4) that
$\varepsilon $
, we obtain from (11.4) that
Thus,
![]() $\rho ^{\mathrm {Sh}}_B(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}\sim \iota q_{\mathfrak p}^{n(n-1)/4} i_{b(\pi ^{\natural })}\circ \mathrm {spin}^{\vee }(\phi _{\pi _{\mathfrak {q}}})(\mathrm {Frob}_{\mathfrak p})$
. Comparing the dual of this with (11.1), we deduce that
$\rho ^{\mathrm {Sh}}_B(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}\sim \iota q_{\mathfrak p}^{n(n-1)/4} i_{b(\pi ^{\natural })}\circ \mathrm {spin}^{\vee }(\phi _{\pi _{\mathfrak {q}}})(\mathrm {Frob}_{\mathfrak p})$
. Comparing the dual of this with (11.1), we deduce that
Since we also know the conjugacy relation with
![]() $\mathrm {std}$
and
$\mathrm {std}$
and
![]() $\mathcal N$
in place of
$\mathcal N$
in place of
![]() $\mathrm {spin}$
from (10.11) and Proposition 10.5 (and the argument at (10.16) in its proof), we use Lemma 5.7 to conclude that
$\mathrm {spin}$
from (10.11) and Proposition 10.5 (and the argument at (10.16) in its proof), we use Lemma 5.7 to conclude that
If
![]() $k = 0$
, then (11.7) implies the theorem. So we assume
$k = 0$
, then (11.7) implies the theorem. So we assume
![]() $k = 1$
in the rest of the argument.
$k = 1$
in the rest of the argument.
We now distinguish between those
![]() $\tau \in B$
according to whether or not their Satake parameter at
$\tau \in B$
according to whether or not their Satake parameter at
![]() ${{\mathfrak q}}$
becomes conjugate to that of
${{\mathfrak q}}$
becomes conjugate to that of
![]() $\pi $
under
$\pi $
under
![]() $\mathrm {spin}^+$
and
$\mathrm {spin}^+$
and
![]() $\mathrm {spin}^-$
: Write
$\mathrm {spin}^-$
: Write
and
![]() $B_{\mathrm {bad}} := B - B_{\mathrm {good}}$
. Thus, (11.3) implies
$B_{\mathrm {bad}} := B - B_{\mathrm {good}}$
. Thus, (11.3) implies
 $$ \begin{align} q_{\mathfrak p}^{-jn(n-1)/4} \iota^{-1} b(\pi^{\natural}) \mathrm{Tr}\, \mathrm{spin}^{\varepsilon}(\rho_{\pi}^C)(\mathrm{Frob}_{\mathfrak p}^j) & = \sum_{\tau \in B_{\mathrm{good}}} a(\tau) \mathrm{Tr}\,(\mathrm{spin}^{\varepsilon}(\phi_{\pi_{\mathfrak{q}}}))(\mathrm{Frob}_{\mathfrak p}^j) \cr & + \sum_{\tau \in B_{\mathrm{bad}}} a(\tau) \mathrm{Tr}\,(\mathrm{spin}^{-\varepsilon}(\phi_{\pi_{\mathfrak{q}}}))(\mathrm{Frob}_{\mathfrak p}^j). \end{align} $$
$$ \begin{align} q_{\mathfrak p}^{-jn(n-1)/4} \iota^{-1} b(\pi^{\natural}) \mathrm{Tr}\, \mathrm{spin}^{\varepsilon}(\rho_{\pi}^C)(\mathrm{Frob}_{\mathfrak p}^j) & = \sum_{\tau \in B_{\mathrm{good}}} a(\tau) \mathrm{Tr}\,(\mathrm{spin}^{\varepsilon}(\phi_{\pi_{\mathfrak{q}}}))(\mathrm{Frob}_{\mathfrak p}^j) \cr & + \sum_{\tau \in B_{\mathrm{bad}}} a(\tau) \mathrm{Tr}\,(\mathrm{spin}^{-\varepsilon}(\phi_{\pi_{\mathfrak{q}}}))(\mathrm{Frob}_{\mathfrak p}^j). \end{align} $$
Equation (11.7) and (11.9) imply that
![]() $\mathrm {spin}^{ - \varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b(\pi ^{\natural })} \simeq \mathrm {spin}^{\varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b_0} \oplus \mathrm {spin}^{-\varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b_1}$
, as
$\mathrm {spin}^{ - \varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b(\pi ^{\natural })} \simeq \mathrm {spin}^{\varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b_0} \oplus \mathrm {spin}^{-\varepsilon }(\phi _{\pi _{\mathfrak {q}}})^{b_1}$
, as
![]() $W_{E_{\mathfrak p}}$
-representations, where
$W_{E_{\mathfrak p}}$
-representations, where
![]() $b_0 = \sum _{\tau \in B_{\mathrm {good}}} a(\tau )$
,
$b_0 = \sum _{\tau \in B_{\mathrm {good}}} a(\tau )$
,
![]() $b_1 = \sum _{\tau \in B_{\mathrm {bad}}} a(\tau )$
and
$b_1 = \sum _{\tau \in B_{\mathrm {bad}}} a(\tau )$
and
![]() $b(\pi ^{\natural }) = b_0 + b_1$
. Thus,
$b(\pi ^{\natural }) = b_0 + b_1$
. Thus,
As
![]() $\pi ^{\natural }$
contributes to
$\pi ^{\natural }$
contributes to
![]() $B_{\mathrm {good}}$
, we have
$B_{\mathrm {good}}$
, we have
![]() $b_0 = b(\pi ^{\natural }) - b_1> 0$
. Thus,
$b_0 = b(\pi ^{\natural }) - b_1> 0$
. Thus,
![]() $\mathrm {spin}^{-\varepsilon }(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^{\varepsilon }(\phi _{\pi _{\mathfrak {q}}})$
, and
$\mathrm {spin}^{-\varepsilon }(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^{\varepsilon }(\phi _{\pi _{\mathfrak {q}}})$
, and
![]() $\phi _{\pi _{\mathfrak {q}}} \sim \theta \phi _{\pi _{\mathfrak {q}}}$
, in which case the proposition follows from (11.7). Here, we applied Lemma 1.1 of [Reference Kret and Shin50] and the fact that
$\phi _{\pi _{\mathfrak {q}}} \sim \theta \phi _{\pi _{\mathfrak {q}}}$
, in which case the proposition follows from (11.7). Here, we applied Lemma 1.1 of [Reference Kret and Shin50] and the fact that
![]() $\mathrm {spin}^{\pm }$
,
$\mathrm {spin}^{\pm }$
,
![]() $\mathrm {std}$
,
$\mathrm {std}$
,
![]() $\mathcal N$
are fundamental representations (see table above Lemma 1.1 in [loc. cit]).
$\mathcal N$
are fundamental representations (see table above Lemma 1.1 in [loc. cit]).
Second case. Suppose that
![]() $\chi \neq 1$
for some
$\chi \neq 1$
for some
![]() $\tau \in B$
. As explained, then
$\tau \in B$
. As explained, then
![]() $\rho _{\pi }^C$
has image in the group
$\rho _{\pi }^C$
has image in the group
![]() $H_{2n-1}$
from (5.4). We obtain from (11.4) and (11.1) that
$H_{2n-1}$
from (5.4). We obtain from (11.4) and (11.1) that
 $$ \begin{align} \iota^{-1} b(\pi^{\natural}) \mathrm{Tr}\, & \left( \mathrm{spin}(\rho_{\pi}^C) \oplus \chi \mathrm{spin}(\rho_{\pi}^C) \right)(\mathrm{Frob}_{\mathfrak p}^j) = \cr &= \sum_{\tau\in B} a(\tau) (1+ \chi(\mathrm{Frob}_{\mathfrak p})^j)q_{\mathfrak p}^{jn(n-1)/4}\mathrm{Tr}\,(\mathrm{spin}(\phi_{\tau_{\mathfrak{q}}}(\mathrm{Frob}_{\mathfrak p})^j)). \end{align} $$
$$ \begin{align} \iota^{-1} b(\pi^{\natural}) \mathrm{Tr}\, & \left( \mathrm{spin}(\rho_{\pi}^C) \oplus \chi \mathrm{spin}(\rho_{\pi}^C) \right)(\mathrm{Frob}_{\mathfrak p}^j) = \cr &= \sum_{\tau\in B} a(\tau) (1+ \chi(\mathrm{Frob}_{\mathfrak p})^j)q_{\mathfrak p}^{jn(n-1)/4}\mathrm{Tr}\,(\mathrm{spin}(\phi_{\tau_{\mathfrak{q}}}(\mathrm{Frob}_{\mathfrak p})^j)). \end{align} $$
For each
![]() $\tau \in B$
, there exist
$\tau \in B$
, there exist
![]() $a, b \in \mathbb Z/2\mathbb Z$
such that for both
$a, b \in \mathbb Z/2\mathbb Z$
such that for both
![]() $\varepsilon \in \{\pm 1\}$
, we have
$\varepsilon \in \{\pm 1\}$
, we have
![]() $ \mathrm {spin}^{\varepsilon }(\phi _{\tau _{\mathfrak p}}) \simeq \chi ^{b} \mathrm {spin}^{(-1)^{a}\varepsilon }(\phi _{\pi _{\mathfrak p}}). $
Thus, we have
$ \mathrm {spin}^{\varepsilon }(\phi _{\tau _{\mathfrak p}}) \simeq \chi ^{b} \mathrm {spin}^{(-1)^{a}\varepsilon }(\phi _{\pi _{\mathfrak p}}). $
Thus, we have
as
![]() $W_{E_{{\mathfrak p}}}$
-representations. In particular, on the right-hand side of (11.11), we may replace
$W_{E_{{\mathfrak p}}}$
-representations. In particular, on the right-hand side of (11.11), we may replace
![]() $\phi _{\tau _{\mathfrak p}}$
by
$\phi _{\tau _{\mathfrak p}}$
by
![]() $\phi _{\pi _{\mathfrak p}}$
. We have
$\phi _{\pi _{\mathfrak p}}$
. We have
![]() $\chi \mathrm {spin}^+(\rho _{\pi }^C) \simeq \mathrm {spin}^-(\rho _{\pi }^C)$
by Lemma 5.6(ii) and so
$\chi \mathrm {spin}^+(\rho _{\pi }^C) \simeq \mathrm {spin}^-(\rho _{\pi }^C)$
by Lemma 5.6(ii) and so
![]() $ \chi \mathrm {spin}(\rho _{\pi }^C) \simeq \mathrm {spin}(\rho _{\pi }^C)$
. By removing the multiplicity
$ \chi \mathrm {spin}(\rho _{\pi }^C) \simeq \mathrm {spin}(\rho _{\pi }^C)$
. By removing the multiplicity
![]() $b(\pi ^{\natural })$
on both sides of (11.11), we thus find that
$b(\pi ^{\natural })$
on both sides of (11.11), we thus find that
We claim that, in fact, also
![]() $\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
. If true, (11.12) would imply that
$\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
. If true, (11.12) would imply that
We check the claim. As
![]() $\mathrm {pr}^{\circ }$
surjects
$\mathrm {pr}^{\circ }$
surjects
![]() $Z(\mathrm {GSpin}_{2n})$
onto
$Z(\mathrm {GSpin}_{2n})$
onto
![]() $Z({\mathrm {SO}}_{2n})$
, we see that
$Z({\mathrm {SO}}_{2n})$
, we see that
![]() $\mathrm {pr}^{\circ }$
induces an isomorphism from the component group of
$\mathrm {pr}^{\circ }$
induces an isomorphism from the component group of
![]() $H_{2n-1}$
to the component group of
$H_{2n-1}$
to the component group of
![]() $H_{2n-1}^{\circ } = {\mathrm {SO}}_{2n-1} Z({\mathrm {SO}}_{2n})$
. Consequently,
$H_{2n-1}^{\circ } = {\mathrm {SO}}_{2n-1} Z({\mathrm {SO}}_{2n})$
. Consequently,
![]() $\chi $
(which equals
$\chi $
(which equals
![]() $\kappa _0 \circ \rho _{\pi }^C$
by Lemma 5.6(iii)) is equal to the composition
$\kappa _0 \circ \rho _{\pi }^C$
by Lemma 5.6(iii)) is equal to the composition
We know that
![]() $\mathrm {pr}^{\circ }(\phi _{\pi _{{\mathfrak q}}}(\mathrm {Frob}_{\mathfrak p})) \overset {\circ } \sim \mathrm {pr}^{\circ }(\rho _{\pi }^C(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}) \in {\mathrm {SO}}_{2n}$
since they become conjugate after applying
$\mathrm {pr}^{\circ }(\phi _{\pi _{{\mathfrak q}}}(\mathrm {Frob}_{\mathfrak p})) \overset {\circ } \sim \mathrm {pr}^{\circ }(\rho _{\pi }^C(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}) \in {\mathrm {SO}}_{2n}$
since they become conjugate after applying
![]() $\mathrm {std}$
. Therefore,
$\mathrm {std}$
. Therefore,
![]() $\chi |_{W_{E_{\mathfrak p}}}$
equals
$\chi |_{W_{E_{\mathfrak p}}}$
equals
and hence equals
![]() $W_{E_{\mathfrak p}} \overset {\phi _{\pi _{{\mathfrak q}}}} \to H_{2n-1} \twoheadrightarrow \{\pm 1\}$
(the argument is similar to the one below (10.14)), which, in turn, implies that
$W_{E_{\mathfrak p}} \overset {\phi _{\pi _{{\mathfrak q}}}} \to H_{2n-1} \twoheadrightarrow \{\pm 1\}$
(the argument is similar to the one below (10.14)), which, in turn, implies that
![]() $\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
. Hence, the claim is proved, and (11.13) holds true as observed above.
$\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
. Hence, the claim is proved, and (11.13) holds true as observed above.
We thus find (11.7) again. If
![]() $k = 0$
in that equation, we are done. Now assume
$k = 0$
in that equation, we are done. Now assume
![]() $k = 1$
. Define
$k = 1$
. Define
![]() $B_{\mathrm {good}}, B_{\mathrm {bad}}$
as in (11.8). As
$B_{\mathrm {good}}, B_{\mathrm {bad}}$
as in (11.8). As
![]() $\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
, it follows from (11.6) that for each
$\chi \mathrm {spin}^+(\phi _{\pi _{\mathfrak {q}}}) \simeq \mathrm {spin}^-(\phi _{\pi _{\mathfrak {q}}})$
, it follows from (11.6) that for each
![]() $\tau \in B_{\mathrm {bad}}$
, we have
$\tau \in B_{\mathrm {bad}}$
, we have
![]() $\mathrm {spin}^{\varepsilon }(\phi _{\tau _{\mathfrak {q}}}) \simeq \mathrm {spin}^{-\varepsilon }(\phi _{\pi _{{\mathfrak q}}})$
for both signs
$\mathrm {spin}^{\varepsilon }(\phi _{\tau _{\mathfrak {q}}}) \simeq \mathrm {spin}^{-\varepsilon }(\phi _{\pi _{{\mathfrak q}}})$
for both signs
![]() $\varepsilon \in \{\pm 1\}$
. Thus, we obtain (11.9) with
$\varepsilon \in \{\pm 1\}$
. Thus, we obtain (11.9) with
![]() $\# B_{\mathrm {good}}> 0$
again. By the same argument as in (11.10), we deduce that
$\# B_{\mathrm {good}}> 0$
again. By the same argument as in (11.10), we deduce that
![]() $\phi _{\pi _{\mathfrak {q}}} \sim \theta \phi _{\pi _{\mathfrak {q}}}$
, in which case the proposition follows from (11.7).
$\phi _{\pi _{\mathfrak {q}}} \sim \theta \phi _{\pi _{\mathfrak {q}}}$
, in which case the proposition follows from (11.7).
12 The main theorem
In this section, we prove Theorem A (Theorem 12.5), the main result of this paper. Before doing this, we switch the normalization for
![]() $\pi $
from (coh) to (L-coh), and extend the Galois action from
$\pi $
from (coh) to (L-coh), and extend the Galois action from
![]() $\Gamma _E$
to
$\Gamma _E$
to
![]() $\Gamma _F$
.
$\Gamma _F$
.
As in Theorem A, let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $G^{*}(\mathbb A_F)$
satisfying (St) and (L-coh). Fix a cuspidal automorphic representation
$G^{*}(\mathbb A_F)$
satisfying (St) and (L-coh). Fix a cuspidal automorphic representation
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
which embeds in
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
which embeds in
![]() $\pi |_{{\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)}$
as it is possible by [Reference Labesse and Schwermer51]. Assume either (std-reg) for
$\pi |_{{\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)}$
as it is possible by [Reference Labesse and Schwermer51]. Assume either (std-reg) for
![]() $\pi $
or Hypothesis 6.11 for an
$\pi $
or Hypothesis 6.11 for an
![]() ${\mathrm {SO}}_{2n}(\mathbb A_F)$
-subrepresentation
${\mathrm {SO}}_{2n}(\mathbb A_F)$
-subrepresentation
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() $\pi $
. Define
$\pi $
. Define
![]() $\tilde \pi :=\pi |\mathrm {sim}|^{-n(n-1)/4}$
. Then
$\tilde \pi :=\pi |\mathrm {sim}|^{-n(n-1)/4}$
. Then
![]() $\tilde \pi $
is
$\tilde \pi $
is
![]() $\xi $
-cohomological and will play the role of
$\xi $
-cohomological and will play the role of
![]() $\pi $
in Sections 10 and 11. Naturally,
$\pi $
in Sections 10 and 11. Naturally,
![]() $\pi ^{\flat }$
is a subrepresentation of
$\pi ^{\flat }$
is a subrepresentation of
![]() $\tilde {\pi }|_{{\mathrm {SO}}_{2n}(\mathbb A_F)}$
since
$\tilde {\pi }|_{{\mathrm {SO}}_{2n}(\mathbb A_F)}$
since
![]() $|\mathrm {sim}|$
is trivial when restricted to
$|\mathrm {sim}|$
is trivial when restricted to
![]() ${\mathrm {SO}}_{2n}(\mathbb A_F)$
.
${\mathrm {SO}}_{2n}(\mathbb A_F)$
.
Let
![]() $S^F$
(resp.
$S^F$
(resp.
![]() $S^E$
) be the finite set of places of F (resp. E) above
$S^E$
) be the finite set of places of F (resp. E) above
![]() $S:=S_{\mathrm {bad}}\cup \{\ell \}$
. Fix an infinite place
$S:=S_{\mathrm {bad}}\cup \{\ell \}$
. Fix an infinite place
![]() $y_{\infty }\in \mathcal V_{\infty }$
and also fix a finite place
$y_{\infty }\in \mathcal V_{\infty }$
and also fix a finite place
![]() ${{\mathfrak q}}$
as in (St). (Recall that the group G, Shimura varieties, and the resulting
${{\mathfrak q}}$
as in (St). (Recall that the group G, Shimura varieties, and the resulting
![]() $\mathrm {GSpin}_{2n}$
-valued Galois representations in earlier sections depend on the choice of
$\mathrm {GSpin}_{2n}$
-valued Galois representations in earlier sections depend on the choice of
![]() $y_{\infty }$
and
$y_{\infty }$
and
![]() ${{\mathfrak q}}$
.) From Propositions 10.2 and 11.1, we obtain
${{\mathfrak q}}$
.) From Propositions 10.2 and 11.1, we obtain
such that for every
![]() ${\mathfrak p}\notin S^E$
, writing
${\mathfrak p}\notin S^E$
, writing
![]() ${{\mathfrak q}} := {\mathfrak p}|_F$
, we have
${{\mathfrak q}} := {\mathfrak p}|_F$
, we have
Let us explain the definition of
![]() $\rho _{\pi }$
on
$\rho _{\pi }$
on
![]() $\Gamma _{F,S}$
. If n is even (thus
$\Gamma _{F,S}$
. If n is even (thus
![]() $E=F$
), then we simply take
$E=F$
), then we simply take
![]() $\rho _{\pi }:=\rho ^C_{\tilde \pi }$
. In case n is odd (so
$\rho _{\pi }:=\rho ^C_{\tilde \pi }$
. In case n is odd (so
![]() $[E:F]=2$
), write
$[E:F]=2$
), write
![]() $c_{y_{\infty }} \in \Gamma $
for the complex conjugation corresponding to
$c_{y_{\infty }} \in \Gamma $
for the complex conjugation corresponding to
![]() $y_{\infty }$
(canonical up to conjugacy). In order to apply Lemma A.1, we check
$y_{\infty }$
(canonical up to conjugacy). In order to apply Lemma A.1, we check
Lemma 12.1. When n is odd, we have
![]() ${}^{c_{y_{\infty }}} \rho ^C_{\tilde \pi }\simeq \theta \circ \rho ^C_{\tilde \pi }$
.
${}^{c_{y_{\infty }}} \rho ^C_{\tilde \pi }\simeq \theta \circ \rho ^C_{\tilde \pi }$
.
Proof. In light of Proposition 5.8, it is enough to check this locally, namely, that
for almost all primes
![]() ${\mathfrak p}$
of E. For each
${\mathfrak p}$
of E. For each
![]() ${\mathfrak p}$
, write
${\mathfrak p}$
, write
![]() ${{\mathfrak q}}:={\mathfrak p}\cap F$
. Firstly, if
${{\mathfrak q}}:={\mathfrak p}\cap F$
. Firstly, if
![]() ${{\mathfrak q}}$
splits in E as
${{\mathfrak q}}$
splits in E as
![]() ${\mathfrak p} c({\mathfrak p})$
, then we use (12.1) to deduce that
${\mathfrak p} c({\mathfrak p})$
, then we use (12.1) to deduce that
(To see the third conjugacy relation, we argue as follows. From (8.4), we see that an element of
![]() ${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
has the form
${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
has the form
![]() $(g,\theta (g))$
with
$(g,\theta (g))$
with
![]() $g\in {\mathrm {GSO}}_{2n,E_{{\mathfrak p}}}$
and that
$g\in {\mathrm {GSO}}_{2n,E_{{\mathfrak p}}}$
and that
![]() ${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
is isomorphic to
${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
is isomorphic to
![]() ${\mathrm {GSO}}_{2n,E_{{\mathfrak p}}}$
and
${\mathrm {GSO}}_{2n,E_{{\mathfrak p}}}$
and
![]() ${\mathrm {GSO}}_{2n,E_{c({\mathfrak p})}}$
by the projection map onto the first and second components, respectively. Likewise, the dual group of
${\mathrm {GSO}}_{2n,E_{c({\mathfrak p})}}$
by the projection map onto the first and second components, respectively. Likewise, the dual group of
![]() ${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
is naturally the subgroup of
${\mathrm {GSO}}^{E/F}_{2n,F_{\mathfrak {q}}}$
is naturally the subgroup of
![]() $\mathrm {GSpin}_{2n}\times \mathrm {GSpin}_{2n}$
consisting of elements of the form
$\mathrm {GSpin}_{2n}\times \mathrm {GSpin}_{2n}$
consisting of elements of the form
![]() $(g,\theta (g))$
, the two components corresponding to
$(g,\theta (g))$
, the two components corresponding to
![]() ${\mathfrak p}$
and
${\mathfrak p}$
and
![]() $c({\mathfrak p})$
. It follows that
$c({\mathfrak p})$
. It follows that
![]() $\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{c({\mathfrak p})}) \sim \theta (\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{{\mathfrak p}}))$
.)
$\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{c({\mathfrak p})}) \sim \theta (\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{{\mathfrak p}}))$
.)
Secondly, if
![]() ${{\mathfrak q}}$
is inert in E, then
${{\mathfrak q}}$
is inert in E, then
![]() $c_{y_{\infty }} \mathrm {Frob}_{\mathfrak p} c_{y_{\infty }}^{-1}\sim \mathrm {Frob}_{\mathfrak p}$
. Thus, we need to check that the conjugacy class of
$c_{y_{\infty }} \mathrm {Frob}_{\mathfrak p} c_{y_{\infty }}^{-1}\sim \mathrm {Frob}_{\mathfrak p}$
. Thus, we need to check that the conjugacy class of
![]() $\rho ^C_{\tilde \pi }(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}$
is
$\rho ^C_{\tilde \pi }(\mathrm {Frob}_{\mathfrak p})_{\mathrm {ss}}$
is
![]() $\theta $
-invariant. Writing
$\theta $
-invariant. Writing
![]() $\theta (\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{{\mathfrak q}}))=s\rtimes c\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
,
$\theta (\phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{{\mathfrak q}}))=s\rtimes c\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
,
This implies the desired
![]() $\theta $
-invariance via (12.1). The proof is complete.
$\theta $
-invariance via (12.1). The proof is complete.
We are assuming that n is odd. By Lemmas 12.1 and A.1, we extend
![]() $\rho ^C_{\tilde \pi }$
to a Galois representation to be denoted
$\rho ^C_{\tilde \pi }$
to a Galois representation to be denoted
![]() $\rho _{\pi }$
:
$\rho _{\pi }$
:
There are two choices up to conjugacy (Example A.6). We choose one arbitrarily and possibly modify the choice below.
We return to treating both parities of n. We fixed
![]() $\pi ^{\flat }$
above. Theorem 6.5, or Hypothesis 6.11 if (std-reg) is not assumed, supplies us with
$\pi ^{\flat }$
above. Theorem 6.5, or Hypothesis 6.11 if (std-reg) is not assumed, supplies us with
such that
![]() $\rho _{\pi ^{\flat }}(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}\overset {\circ } \sim \iota \phi _{\pi ^{\flat }_{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
for
$\rho _{\pi ^{\flat }}(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}\overset {\circ } \sim \iota \phi _{\pi ^{\flat }_{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
for
![]() ${{\mathfrak q}},{\mathfrak p}$
as above. Thanks to (12.1) and the unramified Langlands functoriality with respect to
${{\mathfrak q}},{\mathfrak p}$
as above. Thanks to (12.1) and the unramified Langlands functoriality with respect to
![]() ${\mathrm {SO}}_{2n}\rightarrow {\mathrm {GSO}}^{E/F}_{2n}$
(whose dual morphism is
${\mathrm {SO}}_{2n}\rightarrow {\mathrm {GSO}}^{E/F}_{2n}$
(whose dual morphism is
![]() $\mathrm {pr}^{\circ }$
),
$\mathrm {pr}^{\circ }$
),
Thus, the conjugacy classes at the left and right ends are
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate, under the identification
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate, under the identification
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}= \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Since
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}= \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. Since
![]() $\mathrm {O}_{2n}$
is acceptable,
$\mathrm {O}_{2n}$
is acceptable,
![]() $\rho _{\pi ^{\flat }}|_{\Gamma _{E,S}}$
and
$\rho _{\pi ^{\flat }}|_{\Gamma _{E,S}}$
and
![]() $\mathrm {pr}^{\circ }\circ \rho _{\pi }|_{\Gamma _{E,S}}$
are
$\mathrm {pr}^{\circ }\circ \rho _{\pi }|_{\Gamma _{E,S}}$
are
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate. Replacing
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate. Replacing
![]() $\rho _{\pi ^{\flat }}$
by an
$\rho _{\pi ^{\flat }}$
by an
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate, we may and will assume that
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate, we may and will assume that
without disturbing the validity of (SO-i) through (SO-v) in Theorem 6.5. When n is odd, we take an extra step as follows. Observe that
![]() $\rho _{\pi ^{\flat }}$
and
$\rho _{\pi ^{\flat }}$
and
![]() $\mathrm {pr}^{\circ }\circ \rho _{\pi }$
are two
$\mathrm {pr}^{\circ }\circ \rho _{\pi }$
are two
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
-valued representations of
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
-valued representations of
![]() $\Gamma _{F,S}$
extending (12.3). If they are not equal, then
$\Gamma _{F,S}$
extending (12.3). If they are not equal, then
![]() $\mathrm {pr}^{\circ }\circ \rho _{\pi }=\rho _{\pi ^{\flat }}\otimes \chi _{E/F}$
by Example A.5 with
$\mathrm {pr}^{\circ }\circ \rho _{\pi }=\rho _{\pi ^{\flat }}\otimes \chi _{E/F}$
by Example A.5 with
![]() $\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
. Then we go back to (12.2) and replace
$\chi _{E/F}:\Gamma _F\twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
. Then we go back to (12.2) and replace
![]() $\rho _{\pi }$
with
$\rho _{\pi }$
with
![]() $\rho _{\pi }\otimes \chi $
, where
$\rho _{\pi }\otimes \chi $
, where
![]() $\chi $
is as in Example A.6; this does not affect the discussion between (12.2) and here. Since
$\chi $
is as in Example A.6; this does not affect the discussion between (12.2) and here. Since
![]() $\mathrm {pr}^{\circ }\circ \chi =\chi _{E/F}$
, this ensures that
$\mathrm {pr}^{\circ }\circ \chi =\chi _{E/F}$
, this ensures that
As in §2, let
![]() $(s_0,s_1,\ldots ,s_n)\in (\overline {\mathbb {Q}}_{\ell }^{\times })^{n+1}$
denote an element of
$(s_0,s_1,\ldots ,s_n)\in (\overline {\mathbb {Q}}_{\ell }^{\times })^{n+1}$
denote an element of
![]() $T_{\mathrm {GSpin}}(\overline {\mathbb {Q}}_{\ell })\subset \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. This element maps to
$T_{\mathrm {GSpin}}(\overline {\mathbb {Q}}_{\ell })\subset \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. This element maps to
![]() ${\mathrm {diag}}(s_1,\ldots ,s_n,s_1^{-1},\ldots ,s_n^{-1})\in {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
under
${\mathrm {diag}}(s_1,\ldots ,s_n,s_1^{-1},\ldots ,s_n^{-1})\in {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
under
![]() $\mathrm {pr}^{\circ }$
, and maps to
$\mathrm {pr}^{\circ }$
, and maps to
![]() $s_0^2s_1s_2\cdots s_n$
under the spinor norm
$s_0^2s_1s_2\cdots s_n$
under the spinor norm
![]() $\mathcal N$
.
$\mathcal N$
.
Lemma 12.2. At every infinite place y of F, the following are
![]() $\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate:
$\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate:
 $$ \begin{align} \rho_{\pi}(c_y)\sim \begin{cases} (a,\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), ~~a\in \{\pm 1\},& n:\mathrm{even},\\ (1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1)\rtimes c, & n:\mathrm{odd}. \end{cases} \end{align} $$
$$ \begin{align} \rho_{\pi}(c_y)\sim \begin{cases} (a,\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), ~~a\in \{\pm 1\},& n:\mathrm{even},\\ (1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1)\rtimes c, & n:\mathrm{odd}. \end{cases} \end{align} $$
where the right-hand side lies in
![]() $\mathrm {T}_{\mathrm {GSpin}}(\overline {\mathbb {Q}}_{\ell }) \rtimes {\mathrm {Gal}}(E/F)$
.
$\mathrm {T}_{\mathrm {GSpin}}(\overline {\mathbb {Q}}_{\ell }) \rtimes {\mathrm {Gal}}(E/F)$
.
Proof. In light of (12.3) (which is valid for both odd and even n as discussed above) and Theorem 6.5 (SO-v) (or Hypothesis 6.11) which describes
![]() $\rho _{\pi ^{\flat }}(c_y)$
, the following are
$\rho _{\pi ^{\flat }}(c_y)$
, the following are
![]() $\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate:
$\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugate:
 $$ \begin{align*}\mathrm{pr}^{\circ}(\rho_{\pi}(c_y)) \sim \begin{cases} {\mathrm{diag}}(\underbrace{1,\ldots,1}_{n/2}, \underbrace{-1,\ldots,-1}_{n/2},\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), & n:\mbox{even},\\ {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2}, \underbrace{-1,\ldots,-1}_{(n-1)/2},1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1) \rtimes \theta, & n:\mbox{odd}. \end{cases} \end{align*} $$
$$ \begin{align*}\mathrm{pr}^{\circ}(\rho_{\pi}(c_y)) \sim \begin{cases} {\mathrm{diag}}(\underbrace{1,\ldots,1}_{n/2}, \underbrace{-1,\ldots,-1}_{n/2},\underbrace{1,\ldots,1}_{n/2},\underbrace{-1,\ldots,-1}_{n/2}), & n:\mbox{even},\\ {\mathrm{diag}}(\underbrace{1,\ldots,1}_{(n-1)/2}, \underbrace{-1,\ldots,-1}_{(n-1)/2},1,\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},1) \rtimes \theta, & n:\mbox{odd}. \end{cases} \end{align*} $$
Therefore,
![]() $\rho _{\pi }(c_y)$
is a lift of the right-hand side (up to
$\rho _{\pi }(c_y)$
is a lift of the right-hand side (up to
![]() $\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy) via
$\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy) via
![]() $\mathrm {pr}^{\circ }$
. Moreover,
$\mathrm {pr}^{\circ }$
. Moreover,
![]() $\rho _{\pi }(c_y)^2=\rho _{\pi }(c_y^2)=1$
. We claim that these two conditions imply (12.4).
$\rho _{\pi }(c_y)^2=\rho _{\pi }(c_y^2)=1$
. We claim that these two conditions imply (12.4).
This is straightforward when n is even. Now suppose that n is odd. Evidently the right-hand side of (12.4) satisfies the two conditions. Any other lift of order 2 can only differ (possibly after conjugation) from the right-hand side of (12.4) by scalars
![]() $\{\pm 1\}$
. (Use Lemma 3.1 (ii) and the order two condition.) This implies (12.4) since every
$\{\pm 1\}$
. (Use Lemma 3.1 (ii) and the order two condition.) This implies (12.4) since every
![]() $g\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes c$
is conjugate to
$g\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes c$
is conjugate to
![]() $-g$
; indeed,
$-g$
; indeed,
![]() $-g= \zeta g \zeta ^{-1}$
if
$-g= \zeta g \zeta ^{-1}$
if
![]() $\zeta \in Z_{\mathrm {Spin}}(\overline {\mathbb {Q}}_{\ell })$
is an element of order 4, noting that
$\zeta \in Z_{\mathrm {Spin}}(\overline {\mathbb {Q}}_{\ell })$
is an element of order 4, noting that
![]() $\theta (\zeta )=\zeta ^{-1}$
.
$\theta (\zeta )=\zeta ^{-1}$
.
Let
![]() $\omega _{\pi }: F^{\times } \backslash \mathbb A_F^{\times } \rightarrow {\mathbb {C}}^{\times }$
denote the central character of
$\omega _{\pi }: F^{\times } \backslash \mathbb A_F^{\times } \rightarrow {\mathbb {C}}^{\times }$
denote the central character of
![]() $\pi $
. By abuse of notation, we still write
$\pi $
. By abuse of notation, we still write
![]() $\omega _{\pi }$
(depending on the choice of
$\omega _{\pi }$
(depending on the choice of
![]() $\iota $
) for the
$\iota $
) for the
![]() $\ell $
-adic character of
$\ell $
-adic character of
![]() $\Gamma _F$
corresponding to
$\Gamma _F$
corresponding to
![]() $\omega _{\pi }$
via class field theory (as in [Reference Harris and Taylor33, pp.20–21]). To make
$\omega _{\pi }$
via class field theory (as in [Reference Harris and Taylor33, pp.20–21]). To make
![]() $\omega _{\pi }$
explicit, recall that
$\omega _{\pi }$
explicit, recall that
![]() $\tilde \pi =\pi |\mathrm {sim}|^{-n(n-1)/4}$
is
$\tilde \pi =\pi |\mathrm {sim}|^{-n(n-1)/4}$
is
![]() $\xi $
-cohomological. By condition (cent), the central character of
$\xi $
-cohomological. By condition (cent), the central character of
![]() $\xi $
is
$\xi $
is
![]() $z\mapsto z^w$
on
$z\mapsto z^w$
on
![]() $F_y^{\times }$
at every real place y of F, for an integer w independent of y. Therefore, (recalling
$F_y^{\times }$
at every real place y of F, for an integer w independent of y. Therefore, (recalling
![]() $\mathrm {sim}$
is the squaring map on the center)
$\mathrm {sim}$
is the squaring map on the center)
Then
![]() $\omega _{\pi } |\cdot |^{w-n(n-1)/4}$
is a finite-order Hecke character which is
$\omega _{\pi } |\cdot |^{w-n(n-1)/4}$
is a finite-order Hecke character which is
![]() $\mathrm {sgn}^w$
at every real place. Hence,
$\mathrm {sgn}^w$
at every real place. Hence,
![]() $\omega _{\pi }=\chi _{\mathrm {cyc}}^{-w+n(n-1)/2} \chi _0$
, where
$\omega _{\pi }=\chi _{\mathrm {cyc}}^{-w+n(n-1)/2} \chi _0$
, where
![]() $\chi _{\mathrm {cyc}}$
is the
$\chi _{\mathrm {cyc}}$
is the
![]() $\ell $
-adic cyclotomic character, and
$\ell $
-adic cyclotomic character, and
![]() $\chi _0$
a finite-order character with
$\chi _0$
a finite-order character with
![]() $\chi _0(c_y)=(-1)^w$
at each real place y. The upshot is that
$\chi _0(c_y)=(-1)^w$
at each real place y. The upshot is that
We are ready to upgrade (12.1) to a compatibility at places of F for odd n (thus,
![]() $[E:F]=2$
).
$[E:F]=2$
).
Corollary 12.3. We have
![]() $\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
. Moreover, at every finite place
$\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
. Moreover, at every finite place
![]() ${{\mathfrak q}}$
of F not above
${{\mathfrak q}}$
of F not above
![]() $S_{\mathrm {bad}}\cup \{\ell \}$
,
$S_{\mathrm {bad}}\cup \{\ell \}$
,
Remark 12.4. The corollary is certainly not automatic from (12.1) since the unramified base change from
![]() $G^{*}(F_{\mathfrak {q}})$
to
$G^{*}(F_{\mathfrak {q}})$
to
![]() $G^{*}(E_{\mathfrak p})$
is not injective when
$G^{*}(E_{\mathfrak p})$
is not injective when
![]() ${{\mathfrak q}}$
does not split in E. Curiously, our proof crucially relies on the image of complex conjugation. We have not found a local or global proof only using properties at finite places.
${{\mathfrak q}}$
does not split in E. Curiously, our proof crucially relies on the image of complex conjugation. We have not found a local or global proof only using properties at finite places.
Proof. Via the unramified Langlands functoriality with respect to the central embedding
![]() $\mathbb G_m\hookrightarrow {\mathrm {GSO}}_{2n}^{E/F}$
, (12.1) implies that
$\mathbb G_m\hookrightarrow {\mathrm {GSO}}_{2n}^{E/F}$
, (12.1) implies that
![]() $\mathcal N\circ \rho _{\pi }|_{\Gamma _E}=\omega _{\pi }|_{\Gamma _E}$
. If n is even, then
$\mathcal N\circ \rho _{\pi }|_{\Gamma _E}=\omega _{\pi }|_{\Gamma _E}$
. If n is even, then
![]() $E=F$
, so there is no more to prove as the latter assertion is already true by (12.1).
$E=F$
, so there is no more to prove as the latter assertion is already true by (12.1).
Henceforth, assume that n is odd (so
![]() $[E:F]=2$
). Then either
$[E:F]=2$
). Then either
![]() $\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
or
$\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
or
![]() $\mathcal N\circ \rho _{\pi } = \omega _{\pi }\otimes \chi _{E/F}$
, where
$\mathcal N\circ \rho _{\pi } = \omega _{\pi }\otimes \chi _{E/F}$
, where
![]() $\chi _{E/F}\colon \Gamma _F \twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
. To exclude the latter case, let y be a real place of F. We have
$\chi _{E/F}\colon \Gamma _F \twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
. To exclude the latter case, let y be a real place of F. We have
![]() $\mathcal N(\rho _{\pi }(c_y))=(-1)^{(n-1)/2}$
from Lemma 12.2, and
$\mathcal N(\rho _{\pi }(c_y))=(-1)^{(n-1)/2}$
from Lemma 12.2, and
![]() $\omega _{\pi }(c_y)=(-1)^{n(n-1)/2}$
from (12.5), but clearly,
$\omega _{\pi }(c_y)=(-1)^{n(n-1)/2}$
from (12.5), but clearly,
![]() $\chi _{E/F}(c_y)=-1$
. Then the only possibility is that
$\chi _{E/F}(c_y)=-1$
. Then the only possibility is that
![]() $\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
.
$\mathcal N\circ \rho _{\pi } = \omega _{\pi }$
.
We prove the second assertion. If
![]() ${{\mathfrak q}}$
splits in E, this follows immediately from (12.1) for
${{\mathfrak q}}$
splits in E, this follows immediately from (12.1) for
![]() $\rho _{\pi }|_{\Gamma _{E,S}}$
. Henceforth, assume that
$\rho _{\pi }|_{\Gamma _{E,S}}$
. Henceforth, assume that
![]() ${{\mathfrak q}}$
is inert in E. We have seen that
${{\mathfrak q}}$
is inert in E. We have seen that
![]() $\mathrm {pr}^{\circ }\circ \rho _{\pi }|_{\Gamma _{E,S}}=\rho _{\pi ^{\flat }}|_{\Gamma _{E,S}}$
. Theorem 6.5 (SO-i) (or Hypothesis 6.11) tells us that
$\mathrm {pr}^{\circ }\circ \rho _{\pi }|_{\Gamma _{E,S}}=\rho _{\pi ^{\flat }}|_{\Gamma _{E,S}}$
. Theorem 6.5 (SO-i) (or Hypothesis 6.11) tells us that
(Note that the outer automorphism ambiguity disappears as it is absorbed by the
![]() ${\mathrm {SO}}_{2n}$
-conjugacy on the nontrivial coset of
${\mathrm {SO}}_{2n}$
-conjugacy on the nontrivial coset of
![]() ${\mathrm {SO}}_{2n}\rtimes \Gamma _{E/F}$
; since
${\mathrm {SO}}_{2n}\rtimes \Gamma _{E/F}$
; since
![]() ${{\mathfrak q}}$
is inert in E, the image of
${{\mathfrak q}}$
is inert in E, the image of
![]() $\mathrm {Frob}_{\mathfrak {q}}$
in
$\mathrm {Frob}_{\mathfrak {q}}$
in
![]() $\Gamma _{E/F}$
is nontrivial.) Therefore,
$\Gamma _{E/F}$
is nontrivial.) Therefore,
![]() $\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}\sim z \iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
for some
$\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}\sim z \iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
for some
![]() $z\in \overline {\mathbb {Q}}_{\ell }^{\times }$
. Taking the spinor norm,
$z\in \overline {\mathbb {Q}}_{\ell }^{\times }$
. Taking the spinor norm,
It follows that
![]() $z\in \{\pm 1\}$
. Since every
$z\in \{\pm 1\}$
. Since every
![]() $g\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes c$
is conjugate to
$g\in \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes c$
is conjugate to
![]() $-g$
(proof of Lemma 12.2), we conclude that
$-g$
(proof of Lemma 12.2), we conclude that
![]() $\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
is conjugate to
$\rho _{\pi }(\mathrm {Frob}_{\mathfrak {q}})_{\mathrm {ss}}$
is conjugate to
![]() $\iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
.
$\iota \phi _{\pi _{\mathfrak {q}}}(\mathrm {Frob}_{\mathfrak {q}})$
.
Theorem 12.5. Theorem A is true.
Proof. Let
![]() $\pi $
be as in the theorem. We fix an automorphic representation
$\pi $
be as in the theorem. We fix an automorphic representation
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
in
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
in
![]() $\pi |_{{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)}$
, take
$\pi |_{{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)}$
, take
![]() $\rho _{\pi ^{\flat }}:\Gamma _F\rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
to be as in Theorem 6.5, or Hypothesis 6.11 if (std-reg) is false, and define
$\rho _{\pi ^{\flat }}:\Gamma _F\rightarrow {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
to be as in Theorem 6.5, or Hypothesis 6.11 if (std-reg) is false, and define
such that
![]() $\rho _{\pi ^{\flat }}=\mathrm {pr}^{\circ }\circ \rho _{\pi }$
as explained at the start of this section. We can inflate
$\rho _{\pi ^{\flat }}=\mathrm {pr}^{\circ }\circ \rho _{\pi }$
as explained at the start of this section. We can inflate
![]() $\rho _{\pi }$
to a representation
$\rho _{\pi }$
to a representation
![]() $\Gamma _F \rightarrow \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{F}$
of Theorem A, but we work with
$\Gamma _F \rightarrow \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{F}$
of Theorem A, but we work with
![]() $\rho _{\pi }$
in the form of (12.6) as this is harmless for verifying the theorem.
$\rho _{\pi }$
in the form of (12.6) as this is harmless for verifying the theorem.
The equality
![]() $\rho _{\pi ^{\flat }}=\mathrm {pr}^{\circ }\circ \rho _{\pi }$
and Corollary 12.3 imply (A2). Corollary 12.3 exactly gives (A1). Item (A4) is straightforward from Lemma 12.2. To see (A5), note that the image of
$\rho _{\pi ^{\flat }}=\mathrm {pr}^{\circ }\circ \rho _{\pi }$
and Corollary 12.3 imply (A2). Corollary 12.3 exactly gives (A1). Item (A4) is straightforward from Lemma 12.2. To see (A5), note that the image of
![]() $\rho _{\pi }$
in
$\rho _{\pi }$
in
![]() $\mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is the same as the image of
$\mathrm {PSO}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is the same as the image of
![]() $\rho _{\pi ^{\flat }}$
in the same group. The Zariski closure of the image is (possibly disconnected and) reductive since
$\rho _{\pi ^{\flat }}$
in the same group. The Zariski closure of the image is (possibly disconnected and) reductive since
![]() $\rho _{\pi ^{\flat }}$
is semisimple and contains a regular unipotent element by Corollary 6.8. Hence, (A5) is implied by Proposition 5.5. Now
$\rho _{\pi ^{\flat }}$
is semisimple and contains a regular unipotent element by Corollary 6.8. Hence, (A5) is implied by Proposition 5.5. Now
![]() $\rho _{\pi }$
also contains a regular unipotent in the image, so (A6) and the uniqueness of
$\rho _{\pi }$
also contains a regular unipotent in the image, so (A6) and the uniqueness of
![]() $\rho _{\pi }$
up to conjugacy are consequences of Proposition 5.8.
$\rho _{\pi }$
up to conjugacy are consequences of Proposition 5.8.
It remains to verify (A3). We begin with part (b). If
![]() $\pi _{\mathfrak {q}}$
has nonzero invariants under a hyperspecial (resp. Iwahori) subgroup, then
$\pi _{\mathfrak {q}}$
has nonzero invariants under a hyperspecial (resp. Iwahori) subgroup, then
![]() $\pi ^{\flat }_{\mathfrak {q}}$
and
$\pi ^{\flat }_{\mathfrak {q}}$
and
![]() $\omega _{\pi ,{{\mathfrak q}}}$
enjoy the same property. Therefore, (b) follows from (A2) and Theorem 6.5 (SO-iv). To prove part (c), write
$\omega _{\pi ,{{\mathfrak q}}}$
enjoy the same property. Therefore, (b) follows from (A2) and Theorem 6.5 (SO-iv). To prove part (c), write
![]() ${\mathfrak p}$
for a place of E above
${\mathfrak p}$
for a place of E above
![]() ${{\mathfrak q}}$
. Since
${{\mathfrak q}}$
. Since
![]() ${\mathfrak p}$
is unramified over E, it suffices to check that
${\mathfrak p}$
is unramified over E, it suffices to check that
![]() $\rho _{\pi }|_{\Gamma _E}$
is crystalline at
$\rho _{\pi }|_{\Gamma _E}$
is crystalline at
![]() ${\mathfrak p}$
. Moreover, we may assume that
${\mathfrak p}$
. Moreover, we may assume that
![]() $F\neq \mathbb {Q}$
by the automorphic base change of [Reference Kret and Shin50, Prop. 6.6] and (A6). (If
$F\neq \mathbb {Q}$
by the automorphic base change of [Reference Kret and Shin50, Prop. 6.6] and (A6). (If
![]() $F=\mathbb {Q}$
, then replace F with a real quadratic field
$F=\mathbb {Q}$
, then replace F with a real quadratic field
![]() $F'$
in which
$F'$
in which
![]() $\ell $
is split, and E with
$\ell $
is split, and E with
![]() $EF'$
. By (A6),
$EF'$
. By (A6),
![]() $\rho _{\pi }|_{\Gamma _{F'}}\simeq \rho _{\pi _{F'}}$
, where
$\rho _{\pi }|_{\Gamma _{F'}}\simeq \rho _{\pi _{F'}}$
, where
![]() $\pi _{F'}$
is the base change of
$\pi _{F'}$
is the base change of
![]() $\pi $
to
$\pi $
to
![]() $F'$
constructed in loc. cit. Thus, the question is now about
$F'$
constructed in loc. cit. Thus, the question is now about
![]() $\rho _{\pi _{F'}}$
.) Now that
$\rho _{\pi _{F'}}$
.) Now that
![]() $F\neq \mathbb {Q}$
, the Shimura varieties in §9 are proper, and
$F\neq \mathbb {Q}$
, the Shimura varieties in §9 are proper, and
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is crystalline at all places above
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},\varepsilon }$
is crystalline at all places above
![]() $\ell $
by [Reference Lovering57]. Since
$\ell $
by [Reference Lovering57]. Since
![]() $\mathrm {spin}\circ \rho _{\pi }|_{\Gamma _E}$
embeds in
$\mathrm {spin}\circ \rho _{\pi }|_{\Gamma _E}$
embeds in
![]() $\rho _{\pi ^{\natural }}^{\mathrm {Sh},+}\oplus \rho _{\pi ^{\natural }}^{\mathrm {Sh},-}$
(which is isomorphic to the
$\rho _{\pi ^{\natural }}^{\mathrm {Sh},+}\oplus \rho _{\pi ^{\natural }}^{\mathrm {Sh},-}$
(which is isomorphic to the
![]() $a(\pi ^{\natural })$
-fold direct sum of
$a(\pi ^{\natural })$
-fold direct sum of
![]() $\mathrm {spin}\circ \rho _{\pi }$
), and since
$\mathrm {spin}\circ \rho _{\pi }$
), and since
![]() $\mathrm {spin}$
is faithful, we deduce that
$\mathrm {spin}$
is faithful, we deduce that
![]() $\rho _{\pi }|_{\Gamma _E}$
is crystalline at
$\rho _{\pi }|_{\Gamma _E}$
is crystalline at
![]() ${\mathfrak p}$
as desired.
${\mathfrak p}$
as desired.
Finally, we prove (A3), part (a). We first claim that if two cocharacters
![]() $\mu _1,\mu _2\in X_*(T_{\mathrm {GSpin}})$
become conjugate after composition with each of
$\mu _1,\mu _2\in X_*(T_{\mathrm {GSpin}})$
become conjugate after composition with each of
![]() $\mathrm {spin}^{+,\vee }$
,
$\mathrm {spin}^{+,\vee }$
,
![]() $\mathrm {spin}^{-,\vee }$
,
$\mathrm {spin}^{-,\vee }$
,
![]() $\mathrm {std}^{\circ }$
and
$\mathrm {std}^{\circ }$
and
![]() $\mathcal N$
, then
$\mathcal N$
, then
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
are
$\mu _2$
are
![]() $\mathrm {GSpin}_{2n}$
-conjugate. To see this, note that a semi-simple conjugacy class
$\mathrm {GSpin}_{2n}$
-conjugate. To see this, note that a semi-simple conjugacy class
![]() $\gamma $
in
$\gamma $
in
![]() $\mathrm {GSpin}_{2n}({\mathbb {C}})$
is determined by the conjugacy classes
$\mathrm {GSpin}_{2n}({\mathbb {C}})$
is determined by the conjugacy classes
![]() $\mathrm {spin}^{\pm }(\gamma )$
,
$\mathrm {spin}^{\pm }(\gamma )$
,
![]() $\mathcal N(\gamma )$
and
$\mathcal N(\gamma )$
and
![]() $\mathrm {std}(\gamma )$
by [Reference Kret and Shin50, Lem. 1.3] (thus also determined by
$\mathrm {std}(\gamma )$
by [Reference Kret and Shin50, Lem. 1.3] (thus also determined by
![]() $\mathrm {spin}^{\pm ,\vee }(\gamma )$
,
$\mathrm {spin}^{\pm ,\vee }(\gamma )$
,
![]() $\mathcal N(\gamma )$
and
$\mathcal N(\gamma )$
and
![]() $\mathrm {std}(\gamma )$
) and the table above Lemma 1.1 therein. The same statement holds for the cocharacters via the Weyl group-equivariant isomorphism
$\mathrm {std}(\gamma )$
) and the table above Lemma 1.1 therein. The same statement holds for the cocharacters via the Weyl group-equivariant isomorphism
![]() $X_*(T_{\mathrm {GSpin}}) \otimes _{\mathbb Z} {\mathbb {C}}^{\times } \to T_{\mathrm {GSpin}}({\mathbb {C}})$
, proving the claim.
$X_*(T_{\mathrm {GSpin}}) \otimes _{\mathbb Z} {\mathbb {C}}^{\times } \to T_{\mathrm {GSpin}}({\mathbb {C}})$
, proving the claim.
Our second claim is that for every
![]() $y:F\hookrightarrow {\mathbb {C}}$
,
$y:F\hookrightarrow {\mathbb {C}}$
,
Accept this for now. The representations
![]() $\mathrm {std}^{\circ }$
and
$\mathrm {std}^{\circ }$
and
![]() $\mathcal N$
factor over the isogeny
$\mathcal N$
factor over the isogeny
![]() $(\mathcal N,\mathrm {pr}^{\circ }):\mathrm {GSpin}_{2n}\rightarrow \mathbb {G}_{\mathrm {m}}\times {\mathrm {SO}}_{2n}$
, so it follows easily from (A2) and Theorem 6.5 (SO-iii) that (12.7) holds with
$(\mathcal N,\mathrm {pr}^{\circ }):\mathrm {GSpin}_{2n}\rightarrow \mathbb {G}_{\mathrm {m}}\times {\mathrm {SO}}_{2n}$
, so it follows easily from (A2) and Theorem 6.5 (SO-iii) that (12.7) holds with
![]() $\mathrm {std}^{\circ }$
and
$\mathrm {std}^{\circ }$
and
![]() $\mathcal N$
in place of
$\mathcal N$
in place of
![]() $\mathrm {spin}^{\varepsilon }$
. Thus, we can conclude by the first claim.
$\mathrm {spin}^{\varepsilon }$
. Thus, we can conclude by the first claim.
To complete the proof of (A3)(a), we check the second claim (12.7). A base-change argument as in the preceding paragraph allows us to assume that
![]() $F\neq \mathbb {Q}$
. Recall that we chose an embedding
$F\neq \mathbb {Q}$
. Recall that we chose an embedding
![]() $y_{\infty }:F\hookrightarrow {\mathbb {C}}$
in the definition of G and the Shimura data
$y_{\infty }:F\hookrightarrow {\mathbb {C}}$
in the definition of G and the Shimura data
![]() $(\mathrm {Res}_{F/\mathbb {Q}} G,X^{\varepsilon })$
. It follows from Proposition 9.8 (applicable as
$(\mathrm {Res}_{F/\mathbb {Q}} G,X^{\varepsilon })$
. It follows from Proposition 9.8 (applicable as
![]() $F\neq \mathbb {Q}$
) that
$F\neq \mathbb {Q}$
) that
We can repeat the construction from the beginning of §12 up to now, with
![]() $y:F\hookrightarrow {\mathbb {C}}$
in place of
$y:F\hookrightarrow {\mathbb {C}}$
in place of
![]() $y_{\infty }$
. Write
$y_{\infty }$
. Write
![]() $\rho _{\pi }(y):\Gamma _F\rightarrow \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
for the resulting Galois representation. From (A1) and (A6) of Theorem A (which have already been verified) to
$\rho _{\pi }(y):\Gamma _F\rightarrow \mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })\rtimes \Gamma _{E/F}$
for the resulting Galois representation. From (A1) and (A6) of Theorem A (which have already been verified) to
![]() $\rho _{\pi }$
and
$\rho _{\pi }$
and
![]() $\rho _{\pi }(y)$
, we deduce that
$\rho _{\pi }(y)$
, we deduce that
![]() $\rho _{\pi }\simeq \rho _{\pi }(y)$
. Applying Proposition 9.8 to
$\rho _{\pi }\simeq \rho _{\pi }(y)$
. Applying Proposition 9.8 to
![]() $\rho _{\pi }(y)$
, we see that (12.8) holds with y in place of
$\rho _{\pi }(y)$
, we see that (12.8) holds with y in place of
![]() $y_{\infty }$
.
$y_{\infty }$
.
Now the left-hand side of (12.8) equals
![]() $\mathrm {spin}^{\varepsilon ,\vee }\circ \mu _{\mathrm {HT}}( \rho _{\pi } ,\iota y)$
by construction of Hodge–Tate cocharacters, so we are done with proving (12.7) as desired.
$\mathrm {spin}^{\varepsilon ,\vee }\circ \mu _{\mathrm {HT}}( \rho _{\pi } ,\iota y)$
by construction of Hodge–Tate cocharacters, so we are done with proving (12.7) as desired.
Remark 12.6. Lemma 12.2 tells us that
![]() $\rho _{\pi }$
is totally odd. Our result also shows that
$\rho _{\pi }$
is totally odd. Our result also shows that
![]() $\rho _{\pi }(c_y)$
is as predicted by [Reference Buzzard and Gee12, Conj. 3.2.1, 3.2.2] for every infinite place y of F. Indeed, as explained in §6 of their paper, their conjectures are compatible with the functoriality. Considering the L-morphism
$\rho _{\pi }(c_y)$
is as predicted by [Reference Buzzard and Gee12, Conj. 3.2.1, 3.2.2] for every infinite place y of F. Indeed, as explained in §6 of their paper, their conjectures are compatible with the functoriality. Considering the L-morphism
![]() $^L {\mathrm {GSO}}_{2n}^{E/F} \rightarrow {}^L {\mathrm {SO}}_{2n}^{E/F}$
dual to the inclusion
$^L {\mathrm {GSO}}_{2n}^{E/F} \rightarrow {}^L {\mathrm {SO}}_{2n}^{E/F}$
dual to the inclusion
![]() ${\mathrm {SO}}_{2n}^{E/F} \hookrightarrow {\mathrm {GSO}}_{2n}^{E/F}$
, we reduce the question to the case of
${\mathrm {SO}}_{2n}^{E/F} \hookrightarrow {\mathrm {GSO}}_{2n}^{E/F}$
, we reduce the question to the case of
![]() ${\mathrm {SO}}_{2n}^{E/F}$
in view of the characterization of
${\mathrm {SO}}_{2n}^{E/F}$
in view of the characterization of
![]() $\rho _{\pi }(c_y)$
in terms of
$\rho _{\pi }(c_y)$
in terms of
![]() $\mathrm {pr}^{\circ }(\rho _{\pi _{\pi }}(c_y))$
. The latter is conjugate to
$\mathrm {pr}^{\circ }(\rho _{\pi _{\pi }}(c_y))$
. The latter is conjugate to
![]() $\rho _{\pi ^{\flat }}$
, which is as conjectured by loc. cit. by Remark 6.6.
$\rho _{\pi ^{\flat }}$
, which is as conjectured by loc. cit. by Remark 6.6.
Remark 12.7. It was easier to determine the Hodge–Tate cocharacter in the
![]() $\mathrm {GSp}$
-case [Reference Kret and Shin50], thanks to the absence of nontrivial outer automorphisms. In particular, we did not need to prove the analogue of Proposition 9.8. Compare with the proof of Theorem 9.1 (iii.a’) of loc. cit.
$\mathrm {GSp}$
-case [Reference Kret and Shin50], thanks to the absence of nontrivial outer automorphisms. In particular, we did not need to prove the analogue of Proposition 9.8. Compare with the proof of Theorem 9.1 (iii.a’) of loc. cit.
13 Refinement for
 ${\mathrm {SO}}_{2n}$
-valued Galois representations
${\mathrm {SO}}_{2n}$
-valued Galois representations
As an application of our results, we improve upon Theorem 6.5 in this section by removing the outer ambiguity in the images of Frobenius conjugacy classes.
Let
![]() $E/F$
be a quadratic CM extension of F in case n is odd, and
$E/F$
be a quadratic CM extension of F in case n is odd, and
![]() $E := F$
for n even. Let
$E := F$
for n even. Let
![]() ${\mathrm {SO}}_{2n}^{E/F}$
be the corresponding group defined above (6.2). If
${\mathrm {SO}}_{2n}^{E/F}$
be the corresponding group defined above (6.2). If
![]() $\pi ^{\flat }$
(resp.
$\pi ^{\flat }$
(resp.
![]() $\pi $
) is an automorphic representation of
$\pi $
) is an automorphic representation of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
(resp.
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
(resp.
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
), we write
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
), we write
![]() $S_{\mathrm {bad}}(\pi ^{\flat })$
(resp
$S_{\mathrm {bad}}(\pi ^{\flat })$
(resp
![]() $S_{\mathrm {bad}}(\pi )$
) for the set of rational prime numbers p, such that
$S_{\mathrm {bad}}(\pi )$
) for the set of rational prime numbers p, such that
![]() $p = 2$
, p ramifies in E, or
$p = 2$
, p ramifies in E, or
![]() $\pi ^{\flat }_p$
(resp.
$\pi ^{\flat }_p$
(resp.
![]() $\pi _p$
) is a ramified representation. For other notation, we refer to Section 1.
$\pi _p$
) is a ramified representation. For other notation, we refer to Section 1.
In order to extend a given cohomological representation
![]() $\pi ^{\flat }$
of
$\pi ^{\flat }$
of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
to a cohomological representation
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
to a cohomological representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, the following condition on the central character
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
, the following condition on the central character
![]() $\omega _{\pi ^{\flat }}\colon \mu _2(F) \backslash \mu _2(\mathbb A_F) \to {\mathbb {C}}^{\times }$
is necessary in view of condition (cent) of §9. (If
$\omega _{\pi ^{\flat }}\colon \mu _2(F) \backslash \mu _2(\mathbb A_F) \to {\mathbb {C}}^{\times }$
is necessary in view of condition (cent) of §9. (If
![]() $\pi $
is
$\pi $
is
![]() $\xi $
-cohomological with
$\xi $
-cohomological with
![]() $w\in \mathbb Z$
as in (cent), then all
$w\in \mathbb Z$
as in (cent), then all
![]() $\omega _{\pi ^{\flat },y}$
are trivial, resp. nontrivial, according as w is even, resp. odd.)
$\omega _{\pi ^{\flat },y}$
are trivial, resp. nontrivial, according as w is even, resp. odd.)
-
(cent°) The sign character
 $\omega _{\pi ^{\flat },y}: \mu _2(F_y)=\{\pm 1\} \to {\mathbb {C}}^{\times }$
does not depend on
$\omega _{\pi ^{\flat },y}: \mu _2(F_y)=\{\pm 1\} \to {\mathbb {C}}^{\times }$
does not depend on
 $y|\infty $
.
$y|\infty $
.
Theorem 13.1. Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying
${\mathrm {SO}}^{E/F}_{2n}(\mathbb A_F)$
satisfying
![]() $(\mathrm {cent}^{\circ })$
,
$(\mathrm {cent}^{\circ })$
,
![]() $(\mathrm {coh}^{\circ })$
,
$(\mathrm {coh}^{\circ })$
,
![]() $(\mathrm {St}^{\circ })$
and
$(\mathrm {St}^{\circ })$
and
![]() $(\mathrm {std-reg}^{\circ }$
) of §6. Then there exists a semisimple Galois representation (depending on
$(\mathrm {std-reg}^{\circ }$
) of §6. Then there exists a semisimple Galois representation (depending on
![]() $\iota $
)
$\iota $
)
satisfying (SO-i)–(SO-v) as in Theorem 6.5 as well as the following.
-
(SO-i+) For every finite prime
 ${{\mathfrak q}}$
of F not above
${{\mathfrak q}}$
of F not above
 $S_{\mathrm {bad}}(\pi ^{\flat }) \cup \{\ell \}$
, as
$S_{\mathrm {bad}}(\pi ^{\flat }) \cup \{\ell \}$
, as $$ \begin{align*}\iota \phi_{\pi^{\flat}_{\mathfrak{q}}} \sim \mathrm{WD}(\rho_{\pi^{\flat}}|_{\Gamma_{F_{\mathfrak{q}}}})^{\mathrm{F-ss}}, \end{align*} $$
$$ \begin{align*}\iota \phi_{\pi^{\flat}_{\mathfrak{q}}} \sim \mathrm{WD}(\rho_{\pi^{\flat}}|_{\Gamma_{F_{\mathfrak{q}}}})^{\mathrm{F-ss}}, \end{align*} $$
 ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-parameters.
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-parameters.
-
(SO-iii+) For every
 ${{\mathfrak q}} | \ell $
, the representation
${{\mathfrak q}} | \ell $
, the representation
 $ \rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is potentially semistable. For each
$ \rho _{\pi ^{\flat }, {{\mathfrak q}}}$
is potentially semistable. For each
 $y \colon F \hookrightarrow {\mathbb {C}}$
such that
$y \colon F \hookrightarrow {\mathbb {C}}$
such that
 $\iota y$
induces
$\iota y$
induces
 ${{\mathfrak q}}$
, we have
${{\mathfrak q}}$
, we have
 $\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y) \sim \iota \mu _{\mathrm {Hodge}}(\xi ^{\flat }, y)$
.
$\mu _{\mathrm {HT}}(\rho _{\pi ^{\flat },{{\mathfrak q}}},\iota y) \sim \iota \mu _{\mathrm {Hodge}}(\xi ^{\flat }, y)$
.
Condition (SO-i+) characterizes
![]() $\rho _{\pi ^{\flat }}$
uniquely up to
$\rho _{\pi ^{\flat }}$
uniquely up to
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugation.
Remark 13.2. Statement (SO-i+) is stronger than (SO-i) in that the statement is up to
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy, but also weaker as it excludes the places above
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy, but also weaker as it excludes the places above
![]() $S_{\mathrm {bad}}(\pi ^{\flat }) \cup \{\ell \}$
. Clearly, (SO-iii+) strengthens (SO-iii). If we drop (std-reg
$S_{\mathrm {bad}}(\pi ^{\flat }) \cup \{\ell \}$
. Clearly, (SO-iii+) strengthens (SO-iii). If we drop (std-reg
![]() $^{\circ }$
) from the assumption, then the theorem can be proved by the same argument, but conditionally on Hypothesis 6.11.
$^{\circ }$
) from the assumption, then the theorem can be proved by the same argument, but conditionally on Hypothesis 6.11.
Proof of Theorem 13.1
We have
![]() $\mu _2 = Z({\mathrm {SO}}_{2n}^{E/F})$
. We claim that the central character
$\mu _2 = Z({\mathrm {SO}}_{2n}^{E/F})$
. We claim that the central character
![]() $\omega _{\pi ^{\flat }}$
extends (via
$\omega _{\pi ^{\flat }}$
extends (via
![]() $\mu _2(\mathbb A_F)\subset \mathbb A_F^{\times }$
) to a Hecke character
$\mu _2(\mathbb A_F)\subset \mathbb A_F^{\times }$
) to a Hecke character
such that
![]() $\chi _y(z)=z^w$
at every infinite place y, where
$\chi _y(z)=z^w$
at every infinite place y, where
![]() $w=0$
(resp.
$w=0$
(resp.
![]() $w=1$
) if
$w=1$
) if
![]() $\omega _{\pi ^{\flat },y}$
is trivial (resp. nontrivial) at every
$\omega _{\pi ^{\flat },y}$
is trivial (resp. nontrivial) at every
![]() $y|\infty $
.
$y|\infty $
.
To prove the claim, let
![]() $E'$
be a quadratic CM extension of F. We start by extending
$E'$
be a quadratic CM extension of F. We start by extending
![]() $\omega _{\pi ^{\flat }}$
to a (unitary) Hecke character
$\omega _{\pi ^{\flat }}$
to a (unitary) Hecke character
![]() $\chi ':F^{\times } \backslash \mathbb A_F^{\times } \to {\mathbb {C}}^{\times }$
whose infinite components are trivial if
$\chi ':F^{\times } \backslash \mathbb A_F^{\times } \to {\mathbb {C}}^{\times }$
whose infinite components are trivial if
![]() $w=0$
and the sign character if
$w=0$
and the sign character if
![]() $w=1$
. If
$w=1$
. If
![]() $w=0$
, then such a
$w=0$
, then such a
![]() $\chi '$
exists since
$\chi '$
exists since
![]() $\mu _2(F)\mu _2(F_{\infty })\backslash \mu _2(\mathbb A_F)$
is a closed subgroup of
$\mu _2(F)\mu _2(F_{\infty })\backslash \mu _2(\mathbb A_F)$
is a closed subgroup of
![]() $\overline {F^{\times } F_{\infty }^{\times }}\backslash \mathbb A_F^{\times } $
, where the bar means the closure in
$\overline {F^{\times } F_{\infty }^{\times }}\backslash \mathbb A_F^{\times } $
, where the bar means the closure in
![]() $\mathbb A_F^{\times }$
. If
$\mathbb A_F^{\times }$
. If
![]() $w=1$
, consider the quadratic Hecke character
$w=1$
, consider the quadratic Hecke character
![]() $\chi _{E'/F}$
associated with
$\chi _{E'/F}$
associated with
![]() $E'/F$
via class field theory. Then
$E'/F$
via class field theory. Then
![]() $\omega _{\pi ^{\flat }}(\chi _{E'/F}|_{\mu _2(\mathbb A_F)})$
extends to a Hecke character with trivial components at
$\omega _{\pi ^{\flat }}(\chi _{E'/F}|_{\mu _2(\mathbb A_F)})$
extends to a Hecke character with trivial components at
![]() $\infty $
by the
$\infty $
by the
![]() $w=0$
case. Multiplying
$w=0$
case. Multiplying
![]() $\chi _{E'/F}$
, we obtain a desired choice of
$\chi _{E'/F}$
, we obtain a desired choice of
![]() $\chi '$
. Whether
$\chi '$
. Whether
![]() $w=0$
or
$w=0$
or
![]() $w=1$
, we now see that
$w=1$
, we now see that
![]() $\chi :=\chi ' |\cdot |^w$
has desired components at
$\chi :=\chi ' |\cdot |^w$
has desired components at
![]() $\infty $
, where
$\infty $
, where
![]() $|\cdot |$
is the absolute value character on
$|\cdot |$
is the absolute value character on
![]() $\mathbb A_F^{\times }$
. The claim is proved.
$\mathbb A_F^{\times }$
. The claim is proved.
Consider the multiplication map
![]() $f \colon {\mathrm {GL}}_1\times {\mathrm {SO}}_{2n}^{E/F} \to {\mathrm {GSO}}_{2n}^{E/F}$
. Let
$f \colon {\mathrm {GL}}_1\times {\mathrm {SO}}_{2n}^{E/F} \to {\mathrm {GSO}}_{2n}^{E/F}$
. Let
![]() $\xi ^{\flat }$
be such that
$\xi ^{\flat }$
be such that
![]() $\pi ^{\flat }$
is
$\pi ^{\flat }$
is
![]() $\xi ^{\flat }$
-cohomological. Write
$\xi ^{\flat }$
-cohomological. Write
![]() $\varsigma $
for the algebraic character
$\varsigma $
for the algebraic character
![]() $z \mapsto z^w$
of
$z \mapsto z^w$
of
![]() ${\mathrm {GL}}_1$
over F. Then
${\mathrm {GL}}_1$
over F. Then
![]() $(\varsigma , \xi ^{\flat })$
descends to an algebraic representation
$(\varsigma , \xi ^{\flat })$
descends to an algebraic representation
![]() $\xi $
of
$\xi $
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
via f.
${\mathrm {GSO}}_{2n}^{E/F}$
via f.
Let us extend
![]() $\pi ^{\flat }$
to an irreducible admissible
$\pi ^{\flat }$
to an irreducible admissible
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
-representation, by decomposing
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
-representation, by decomposing
![]() $\pi ^{\flat } = \otimes _v' \pi _v^{\flat }$
and taking an irreducible subrepresentation
$\pi ^{\flat } = \otimes _v' \pi _v^{\flat }$
and taking an irreducible subrepresentation
![]() $\pi _v$
of
$\pi _v$
of
which is semisimple [Reference Xu80, pp.1832–1833]. Take
![]() $\pi _v$
to be unramified for almost all v, and define
$\pi _v$
to be unramified for almost all v, and define
![]() $\pi := \otimes _v' \pi _v$
. Lemma 5.4 of [Reference Xu81] states that
$\pi := \otimes _v' \pi _v$
. Lemma 5.4 of [Reference Xu81] states that
 $$ \begin{align*}\sum_{\omega \in X/YX(\pi)} m(\pi \otimes \omega) = \sum_{g \in {\mathrm{GSO}}_{2n}^{E/F}(\mathbb A_F)/\widetilde{G}(\pi) {\mathrm{GSO}}_{2n}^{E/F}(F)} m\big((\pi^{\flat})^g\big), \end{align*} $$
$$ \begin{align*}\sum_{\omega \in X/YX(\pi)} m(\pi \otimes \omega) = \sum_{g \in {\mathrm{GSO}}_{2n}^{E/F}(\mathbb A_F)/\widetilde{G}(\pi) {\mathrm{GSO}}_{2n}^{E/F}(F)} m\big((\pi^{\flat})^g\big), \end{align*} $$
where X is the set of characters of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)/{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F) Z({\mathrm {GSO}}_{2n}^{E/F})(\mathbb A_F)$
, and
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)/{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F) Z({\mathrm {GSO}}_{2n}^{E/F})(\mathbb A_F)$
, and
![]() $\omega $
in the formula is represented by such characters. We refer to loc. cit. for some undefined notation that is not important for us but content ourselves with pointing out that both sides are finite sums. Since
$\omega $
in the formula is represented by such characters. We refer to loc. cit. for some undefined notation that is not important for us but content ourselves with pointing out that both sides are finite sums. Since
![]() $m(\pi ^{\flat })>0$
, the right-hand side is positive. Thus, the left-hand side is positive, and thus we may (and do) twist
$m(\pi ^{\flat })>0$
, the right-hand side is positive. Thus, the left-hand side is positive, and thus we may (and do) twist
![]() $\pi $
so that it is discrete automorphic.
$\pi $
so that it is discrete automorphic.
We now check that
![]() $\pi $
satisfies the conditions of Theorem A. Since
$\pi $
satisfies the conditions of Theorem A. Since
![]() $\pi ^{\flat }_{\infty }$
is
$\pi ^{\flat }_{\infty }$
is
![]() $\xi ^{\flat }$
-cohomological, by construction,
$\xi ^{\flat }$
-cohomological, by construction,
![]() $\pi _{\infty }$
is cohomological according to Lemma 7.2. By Lemma 7.1,
$\pi _{\infty }$
is cohomological according to Lemma 7.2. By Lemma 7.1,
![]() $\pi $
satisfies (St), thus also cuspidal. Condition (std-reg) is implied by (std-reg
$\pi $
satisfies (St), thus also cuspidal. Condition (std-reg) is implied by (std-reg
![]() $^{\circ }$
) on
$^{\circ }$
) on
![]() $\pi ^{\flat }$
. Hence, we have a Galois representation
$\pi ^{\flat }$
. Hence, we have a Galois representation
such that for every finite F-place
![]() ${{\mathfrak q}}$
not above
${{\mathfrak q}}$
not above
![]() $S_{\mathrm {bad}}(\pi ) \cup \{\ell \}$
,
$S_{\mathrm {bad}}(\pi ) \cup \{\ell \}$
,
As in the preceding section, we can arrange that
![]() $\rho _{\pi ^{\flat }} = \mathrm {pr}^{\circ } \circ \rho _{\pi }$
(not just up to outer automorphism). The Satake parameter of
$\rho _{\pi ^{\flat }} = \mathrm {pr}^{\circ } \circ \rho _{\pi }$
(not just up to outer automorphism). The Satake parameter of
![]() $\pi ^{\flat }_{\mathfrak {q}}$
is equal to the composition of the Satake parameter of
$\pi ^{\flat }_{\mathfrak {q}}$
is equal to the composition of the Satake parameter of
![]() $\pi _{\mathfrak {q}}$
with the natural surjection (cf. [Reference Xu81, Lem. 5.2])
$\pi _{\mathfrak {q}}$
with the natural surjection (cf. [Reference Xu81, Lem. 5.2])
In particular, (SO-i+) follows from (13.1) for the places not above
![]() $S_{\mathrm {bad}}(\pi ) \cup \{\ell \}$
. Similarly, (SO-iii+) follows from Theorem A (A3)(a).
$S_{\mathrm {bad}}(\pi ) \cup \{\ell \}$
. Similarly, (SO-iii+) follows from Theorem A (A3)(a).
At this point, we have not yet completely proved (SO-i+), as the inclusion
![]() $S_{\mathrm {bad}}(\pi ^{\flat }) \subset S_{\mathrm {bad}}(\pi )$
is strict in general. Thus, it remains to treat
$S_{\mathrm {bad}}(\pi ^{\flat }) \subset S_{\mathrm {bad}}(\pi )$
is strict in general. Thus, it remains to treat
![]() ${{\mathfrak q}}$
above a prime
${{\mathfrak q}}$
above a prime
![]() $p \in S_{\mathrm {bad}}(\pi ) \backslash S_{\mathrm {bad}}(\pi ^{\flat })$
. Consider for n odd (resp. even) the obvious hyperspecial subgroup (recall
$p \in S_{\mathrm {bad}}(\pi ) \backslash S_{\mathrm {bad}}(\pi ^{\flat })$
. Consider for n odd (resp. even) the obvious hyperspecial subgroup (recall
![]() ${{\mathfrak q}} \nmid 2$
)
${{\mathfrak q}} \nmid 2$
)
 $$ \begin{align*} K_{{\mathfrak q}} := \begin{cases} \{(g, \lambda) \in {\mathrm{GL}}_{2n}(\mathcal O_E \otimes_{\mathcal O_F} \mathcal O_{F_{\mathfrak{q}}}) \times \mathcal O_{F_{\mathfrak{q}}}^{\times} \ |\ \overline g = \vartheta^{\circ} g \vartheta^{\circ}, g^t \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix}\right) g = \lambda \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right), \det(g) = \lambda^n\} \cr\mathrm{resp.} \cr \left\lbrace (g, \lambda) \in {\mathrm{GL}}_{2n}(\mathcal O_{F_{\mathfrak{q}}}) \times \mathcal O_{F_{\mathfrak{q}}}^{\times} \ \left| \ g{}^{\mathrm{t}} \cdot \left( \begin{smallmatrix} {} & {1_n} \cr {1_n} & {} \end{smallmatrix} \right) \ \ \cdot g = \lambda \cdot \left( \begin{smallmatrix} {} & {1_n} \cr {1_n} & {} \end{smallmatrix} \right), \det(g) = \lambda^n \right. \ \right\rbrace\end{cases} \end{align*} $$
$$ \begin{align*} K_{{\mathfrak q}} := \begin{cases} \{(g, \lambda) \in {\mathrm{GL}}_{2n}(\mathcal O_E \otimes_{\mathcal O_F} \mathcal O_{F_{\mathfrak{q}}}) \times \mathcal O_{F_{\mathfrak{q}}}^{\times} \ |\ \overline g = \vartheta^{\circ} g \vartheta^{\circ}, g^t \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix}\right) g = \lambda \left( \begin{smallmatrix} 0 & {1_n} \cr {1_n} & 0 \end{smallmatrix} \right), \det(g) = \lambda^n\} \cr\mathrm{resp.} \cr \left\lbrace (g, \lambda) \in {\mathrm{GL}}_{2n}(\mathcal O_{F_{\mathfrak{q}}}) \times \mathcal O_{F_{\mathfrak{q}}}^{\times} \ \left| \ g{}^{\mathrm{t}} \cdot \left( \begin{smallmatrix} {} & {1_n} \cr {1_n} & {} \end{smallmatrix} \right) \ \ \cdot g = \lambda \cdot \left( \begin{smallmatrix} {} & {1_n} \cr {1_n} & {} \end{smallmatrix} \right), \det(g) = \lambda^n \right. \ \right\rbrace\end{cases} \end{align*} $$
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
. Define
${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
. Define
![]() $K_{0{{\mathfrak q}}}$
to be the kernel of the similitudes mapping
$K_{0{{\mathfrak q}}}$
to be the kernel of the similitudes mapping
![]() $K_{\mathfrak {q}} \to \mathcal O_{F_{\mathfrak {q}}}^{\times }$
,
$K_{\mathfrak {q}} \to \mathcal O_{F_{\mathfrak {q}}}^{\times }$
,
![]() $(g, \lambda ) \mapsto \lambda $
. Then
$(g, \lambda ) \mapsto \lambda $
. Then
![]() $\pi _{\mathfrak {q}}$
is a ramified representation of
$\pi _{\mathfrak {q}}$
is a ramified representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
but has nonzero
${\mathrm {GSO}}_{2n}^{E/F}(F_{\mathfrak {q}})$
but has nonzero
![]() $K_{0{{\mathfrak q}}}$
-fixed vectors, on which
$K_{0{{\mathfrak q}}}$
-fixed vectors, on which
![]() $K_{\mathfrak {q}}$
acts through nontrivial characters of
$K_{\mathfrak {q}}$
acts through nontrivial characters of
![]() $K_{\mathfrak {q}} / K_{0{{\mathfrak q}}}\simeq \mathcal O_{F_{\mathfrak {q}}}^{\times }$
. We fix one such character
$K_{\mathfrak {q}} / K_{0{{\mathfrak q}}}\simeq \mathcal O_{F_{\mathfrak {q}}}^{\times }$
. We fix one such character
![]() $\chi ^0_{\mathfrak {q}}$
of
$\chi ^0_{\mathfrak {q}}$
of
![]() $K_{\mathfrak {q}}$
and do this at every
$K_{\mathfrak {q}}$
and do this at every
![]() ${{\mathfrak q}}$
above p. Now we globalize
${{\mathfrak q}}$
above p. Now we globalize
![]() $\{\chi ^0_{\mathfrak {q}}\}_{{{\mathfrak q}}|p}$
to a Hecke character
$\{\chi ^0_{\mathfrak {q}}\}_{{{\mathfrak q}}|p}$
to a Hecke character
![]() $\chi :F^{\times }\backslash \mathbb A_F^{\times }\rightarrow {\mathbb {C}}^{\times }$
whose restriction to each
$\chi :F^{\times }\backslash \mathbb A_F^{\times }\rightarrow {\mathbb {C}}^{\times }$
whose restriction to each
![]() $\mathcal O_{F_{\mathfrak {q}}}^{\times }$
is
$\mathcal O_{F_{\mathfrak {q}}}^{\times }$
is
![]() $\chi ^0_{{\mathfrak q}}$
and whose archimedean components are trivial. (This is possible by [Reference Clozel, Harris and Taylor17, Lem. 4.1.1].) Define
$\chi ^0_{{\mathfrak q}}$
and whose archimedean components are trivial. (This is possible by [Reference Clozel, Harris and Taylor17, Lem. 4.1.1].) Define
![]() $\pi ' := \pi \otimes \chi ^{-1}$
. Then
$\pi ' := \pi \otimes \chi ^{-1}$
. Then
![]() $\pi '$
also satisfies the conditions of Theorem A. Moreover,
$\pi '$
also satisfies the conditions of Theorem A. Moreover,
![]() $p \notin S_{\mathrm {bad}}(\pi ')$
by construction. Therefore, (13.1) is true at each
$p \notin S_{\mathrm {bad}}(\pi ')$
by construction. Therefore, (13.1) is true at each
![]() ${{\mathfrak q}}|p$
, with
${{\mathfrak q}}|p$
, with
![]() $\pi '$
in place of
$\pi '$
in place of
![]() $\pi $
. Then (SO-i+) for
$\pi $
. Then (SO-i+) for
![]() ${{\mathfrak q}}$
follows as before.
${{\mathfrak q}}$
follows as before.
14 Automorphic multiplicity one
Let
![]() $E/F$
be a quadratic CM extension of F in case n is odd, and
$E/F$
be a quadratic CM extension of F in case n is odd, and
![]() $E := F$
for n even. Let
$E := F$
for n even. Let
![]() ${\mathrm {SO}}_{2n}^{E/F}$
and
${\mathrm {SO}}_{2n}^{E/F}$
and
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
be as before. If
${\mathrm {GSO}}_{2n}^{E/F}$
be as before. If
![]() $\pi $
(resp.
$\pi $
(resp.
![]() $\pi ^{\flat }$
) is an automorphic representation of
$\pi ^{\flat }$
) is an automorphic representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(resp.
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(resp.
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
), we write
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
), we write
![]() $m(\pi )$
(resp.
$m(\pi )$
(resp.
![]() $m(\pi ^{\flat })$
) for its automorphic multiplicity. In this section, we will show that
$m(\pi ^{\flat })$
) for its automorphic multiplicity. In this section, we will show that
![]() $m(\pi ^{\flat })$
and
$m(\pi ^{\flat })$
and
![]() $m(\pi )$
are
$m(\pi )$
are
![]() $1$
for certain classes of automorphic representations of
$1$
for certain classes of automorphic representations of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
and
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
and
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(and some inner forms of those groups). To do this, we combine our results with Arthur’s result on multiplicities for
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
(and some inner forms of those groups). To do this, we combine our results with Arthur’s result on multiplicities for
![]() ${\mathrm {SO}}_{2n}^{E/F}$
and with Xu’s result on multiplicities for
${\mathrm {SO}}_{2n}^{E/F}$
and with Xu’s result on multiplicities for
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
.
${\mathrm {GSO}}_{2n}^{E/F}$
.
Let
![]() $\pi ^{\flat }$
be a discrete automorphic representation of
$\pi ^{\flat }$
be a discrete automorphic representation of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
. Arthur gives in the discussion below [Reference Arthur1, Thm. 1.5.2] the following result towards the computation of
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
. Arthur gives in the discussion below [Reference Arthur1, Thm. 1.5.2] the following result towards the computation of
![]() $m(\pi ^{\flat })$
. Let
$m(\pi ^{\flat })$
. Let
![]() $\psi = \psi _1 \boxplus \cdots \boxplus \psi _r$
be the global (formal) parameter of
$\psi = \psi _1 \boxplus \cdots \boxplus \psi _r$
be the global (formal) parameter of
![]() $\pi ^{\flat }$
[Reference Arthur1, §1.4] (cf. Section 6). Technically,
$\pi ^{\flat }$
[Reference Arthur1, §1.4] (cf. Section 6). Technically,
![]() $\psi $
is an automorphic representation
$\psi $
is an automorphic representation
![]() $\pi ^{\sharp }$
of
$\pi ^{\sharp }$
of
![]() ${\mathrm {GL}}_{2n}(\mathbb A_F)$
given as an isobaric sum of discrete automorphic representations
${\mathrm {GL}}_{2n}(\mathbb A_F)$
given as an isobaric sum of discrete automorphic representations
![]() $\pi _i^{\sharp }$
of
$\pi _i^{\sharp }$
of
![]() ${\mathrm {GL}}_{n_i}(\mathbb A_F)$
, with
${\mathrm {GL}}_{n_i}(\mathbb A_F)$
, with
![]() $\pi _i^{\sharp }$
representing the formal parameter
$\pi _i^{\sharp }$
representing the formal parameter
![]() $\psi _i$
. In terms of these parameters, Arthur proves a decomposition of the form
$\psi _i$
. In terms of these parameters, Arthur proves a decomposition of the form
 $$ \begin{align*}\mathrm{L}^2_{\mathrm{disc}}\big({\mathrm{SO}}_{2n}^{E/F}(F)\backslash {\mathrm{SO}}_{2n}^{E/F}(\mathbb A_F)\big) \overset \sim \to \bigoplus_{\psi \in \widetilde{\Psi}_2({\mathrm{SO}}_{2n}^{E/F}) } \bigoplus_{\tau \in \widetilde{\Pi}_{\psi}(\varepsilon_{\psi})} m_{\psi} \tau \end{align*} $$
$$ \begin{align*}\mathrm{L}^2_{\mathrm{disc}}\big({\mathrm{SO}}_{2n}^{E/F}(F)\backslash {\mathrm{SO}}_{2n}^{E/F}(\mathbb A_F)\big) \overset \sim \to \bigoplus_{\psi \in \widetilde{\Psi}_2({\mathrm{SO}}_{2n}^{E/F}) } \bigoplus_{\tau \in \widetilde{\Pi}_{\psi}(\varepsilon_{\psi})} m_{\psi} \tau \end{align*} $$
as an
![]() $\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
-Hecke module. It takes us too far afield to recall all the notation here, but we emphasize that
$\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
-Hecke module. It takes us too far afield to recall all the notation here, but we emphasize that
![]() $\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
is the restricted tensor product of the local algebras
$\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
is the restricted tensor product of the local algebras
![]() $\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F}(F_v))$
consisting of
$\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F}(F_v))$
consisting of
![]() $\theta ^{\circ }$
-invariant functions [Reference Arthur1, before (1.5.3)]. Similarly, the local packet
$\theta ^{\circ }$
-invariant functions [Reference Arthur1, before (1.5.3)]. Similarly, the local packet
![]() $\widetilde {\Pi }_{\psi _v}(\varepsilon _{\psi })$
consists of
$\widetilde {\Pi }_{\psi _v}(\varepsilon _{\psi })$
consists of
![]() $\theta ^{\circ }$
-orbits of representations.
$\theta ^{\circ }$
-orbits of representations.
Assume
![]() $\pi ^{\flat } \not \simeq \pi ^{\flat } \circ \theta ^{\circ }$
for the moment. Both
$\pi ^{\flat } \not \simeq \pi ^{\flat } \circ \theta ^{\circ }$
for the moment. Both
![]() $\pi ^{\flat }$
and
$\pi ^{\flat }$
and
![]() $\pi ^{\flat } \circ \theta ^{\circ }$
map to the same global parameter
$\pi ^{\flat } \circ \theta ^{\circ }$
map to the same global parameter
![]() $\psi $
and are isomorphic as
$\psi $
and are isomorphic as
![]() $\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
-modules. Arthur proves
$\widetilde {\mathcal {H}}({\mathrm {SO}}_{2n}^{E/F})$
-modules. Arthur proves
![]() $m_{\psi } \leq 2$
for all
$m_{\psi } \leq 2$
for all
![]() $\psi $
. Thus,
$\psi $
. Thus,
However,
![]() $\theta ^{\circ }$
acts on
$\theta ^{\circ }$
acts on
![]() $\mathrm {L}^2_{\mathrm {disc}}({\mathrm {SO}}_{2n}^{E/F}(F)\backslash {\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F))$
, so if
$\mathrm {L}^2_{\mathrm {disc}}({\mathrm {SO}}_{2n}^{E/F}(F)\backslash {\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F))$
, so if
![]() $\pi ^{\flat }$
appears, then
$\pi ^{\flat }$
appears, then
![]() $\pi ^{\flat } \circ \theta ^{\circ }$
also appears. Hence,
$\pi ^{\flat } \circ \theta ^{\circ }$
also appears. Hence,
![]() $m(\pi ^{\flat }), m(\pi ^{\flat } \circ \theta ^{\circ }) \geq 1$
, forcing
$m(\pi ^{\flat }), m(\pi ^{\flat } \circ \theta ^{\circ }) \geq 1$
, forcing
![]() $m(\pi ^{\flat }) = 1$
and
$m(\pi ^{\flat }) = 1$
and
![]() $m(\pi ^{\flat } \circ \theta ^{\circ }) = 1$
.
$m(\pi ^{\flat } \circ \theta ^{\circ }) = 1$
.
From now on, we impose the assumption (std-reg
![]() ${}^{\circ }$
) on
${}^{\circ }$
) on
![]() $\pi ^{\flat }$
. At the infinite F-places v, the infinitesimal character of
$\pi ^{\flat }$
. At the infinite F-places v, the infinitesimal character of
![]() $\pi ^{\flat }_v$
is then not fixed by
$\pi ^{\flat }_v$
is then not fixed by
![]() $\theta ^{\circ }$
. In particular,
$\theta ^{\circ }$
. In particular,
![]() $\pi ^{\flat } \not \simeq \pi ^{\flat } \circ \theta ^{\circ }$
. By the preceding paragraph, we have
$\pi ^{\flat } \not \simeq \pi ^{\flat } \circ \theta ^{\circ }$
. By the preceding paragraph, we have
![]() $m(\pi ^{\flat }) = 1$
,
$m(\pi ^{\flat }) = 1$
,
![]() $m(\pi ^{\flat } \circ \theta ^{\circ }) = 1$
and
$m(\pi ^{\flat } \circ \theta ^{\circ }) = 1$
and
![]() $m_{\psi } = 2$
.
$m_{\psi } = 2$
.
Proposition 14.1. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (std-reg). Then
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
satisfying (L-coh), (St) and (std-reg). Then
![]() $m(\pi ) = 1$
.
$m(\pi ) = 1$
.
Proof (cf. [Reference Kret and Shin50, Thm. 12.1])
Let
![]() $\pi ^{\flat }$
be a cuspidal automorphic representation of
$\pi ^{\flat }$
be a cuspidal automorphic representation of
![]() ${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
contained in
${\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
contained in
![]() $\pi $
. Then
$\pi $
. Then
![]() $\pi ^{\flat }$
satisfies (coh
$\pi ^{\flat }$
satisfies (coh
![]() $^{\circ }$
) and (St
$^{\circ }$
) and (St
![]() $^{\circ }$
) as explained at the start of §10. Let
$^{\circ }$
) as explained at the start of §10. Let
![]() $Y(\pi )$
be the set of continuous characters
$Y(\pi )$
be the set of continuous characters
![]() $\omega \colon {\mathrm {GSO}}_{2n}^{E/F} (\mathbb A_F) \to {\mathbb {C}}^{\times }$
which are trivial on the subgroup
$\omega \colon {\mathrm {GSO}}_{2n}^{E/F} (\mathbb A_F) \to {\mathbb {C}}^{\times }$
which are trivial on the subgroup
![]() ${\mathrm {GSO}}_{2n}^{E/F}(F)\mathbb A_F^{\times }{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
of
${\mathrm {GSO}}_{2n}^{E/F}(F)\mathbb A_F^{\times }{\mathrm {SO}}_{2n}^{E/F}(\mathbb A_F)$
of
![]() ${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
and such that
${\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
and such that
![]() $\pi \simeq \pi \otimes \omega $
. Xu [Reference Xu81, Prop. 1.7] proves that
$\pi \simeq \pi \otimes \omega $
. Xu [Reference Xu81, Prop. 1.7] proves that
where
![]() $\widetilde {\psi }$
is the global parameter of
$\widetilde {\psi }$
is the global parameter of
![]() $\pi $
as defined in [Reference Xu81, Sect. 3] (
$\pi $
as defined in [Reference Xu81, Sect. 3] (
![]() $\widetilde {\psi }$
is denoted
$\widetilde {\psi }$
is denoted
![]() $\widetilde {\phi }$
there), and
$\widetilde {\phi }$
there), and
![]() $\alpha ({\mathcal S}_{\phi })$
will not be important for us.
$\alpha ({\mathcal S}_{\phi })$
will not be important for us.
We claim that
![]() $Y(\pi ) = \{\mathbf {1}\}$
in (14.2). Let
$Y(\pi ) = \{\mathbf {1}\}$
in (14.2). Let
![]() $\omega \in Y(\pi )$
and let
$\omega \in Y(\pi )$
and let
![]() $\chi \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
be the corresponding character via class field theory. As
$\chi \colon \Gamma \to \overline {\mathbb {Q}}_{\ell }^{\times }$
be the corresponding character via class field theory. As
![]() $\chi \rho _{\pi }$
and
$\chi \rho _{\pi }$
and
![]() $\rho _{\pi }$
have conjugate Frobenius images at almost all places, we obtain
$\rho _{\pi }$
have conjugate Frobenius images at almost all places, we obtain
![]() $\chi \rho _{\pi } \simeq \rho _{\pi }$
by Proposition 5.8, and thus
$\chi \rho _{\pi } \simeq \rho _{\pi }$
by Proposition 5.8, and thus
![]() $\chi = 1$
by Lemma 5.6. Hence,
$\chi = 1$
by Lemma 5.6. Hence,
![]() $Y(\pi ) =\{\mathbf {1}\}$
.
$Y(\pi ) =\{\mathbf {1}\}$
.
Let
![]() $\psi $
denote the Arthur parameter of
$\psi $
denote the Arthur parameter of
![]() $\pi ^{\flat }$
. In [Reference Xu81, Cor. 5.10], Xu states that
$\pi ^{\flat }$
. In [Reference Xu81, Cor. 5.10], Xu states that
![]() $m_{\widetilde {\psi }} = m_{\psi } / \# \Sigma _Y(\pi )$
, where
$m_{\widetilde {\psi }} = m_{\psi } / \# \Sigma _Y(\pi )$
, where
![]() $\Sigma _Y(\pi ) := \Sigma _0 / \Sigma _0(\pi , Y)$
, where
$\Sigma _Y(\pi ) := \Sigma _0 / \Sigma _0(\pi , Y)$
, where
![]() $\Sigma _0$
is the
$\Sigma _0$
is the
![]() $2$
-group
$2$
-group
![]() $\{1, \theta \}$
, and
$\{1, \theta \}$
, and
![]() $\Sigma _0(\pi , Y)$
is the group of
$\Sigma _0(\pi , Y)$
is the group of
![]() $\theta ' \in \Sigma _0$
such that
$\theta ' \in \Sigma _0$
such that
![]() $\pi \otimes \omega \simeq \pi ^{\theta '}$
for some
$\pi \otimes \omega \simeq \pi ^{\theta '}$
for some
![]() $\omega \in Y(\pi )$
. We saw below (14.1) that
$\omega \in Y(\pi )$
. We saw below (14.1) that
![]() $m_{\psi } = 2$
. It is enough to check that
$m_{\psi } = 2$
. It is enough to check that
![]() $\# \Sigma _Y(\pi ) = 2$
, which would imply
$\# \Sigma _Y(\pi ) = 2$
, which would imply
![]() $m_{\widetilde {\psi }} =1$
. As
$m_{\widetilde {\psi }} =1$
. As
![]() $Y(\pi ) =\{\mathbf {1}\}$
, this reduces to
$Y(\pi ) =\{\mathbf {1}\}$
, this reduces to
![]() $\pi \not \simeq \pi ^{\theta }$
. Again by (std-reg), the infinitesimal character of
$\pi \not \simeq \pi ^{\theta }$
. Again by (std-reg), the infinitesimal character of
![]() $\pi _v$
for
$\pi _v$
for
![]() $v | \infty $
is not fixed by
$v | \infty $
is not fixed by
![]() $\theta $
, so this is indeed true.
$\theta $
, so this is indeed true.
Let G be the inner form of
![]() ${\mathrm {GSO}}_{2n}^{E/F}$
which was constructed in (8.7) and used in our Shimura data. We close this section with computing automorphic multiplicities for this G. In particular, we prove that the multiplicities
${\mathrm {GSO}}_{2n}^{E/F}$
which was constructed in (8.7) and used in our Shimura data. We close this section with computing automorphic multiplicities for this G. In particular, we prove that the multiplicities
![]() $a(\cdot )$
appearing in Section 9 are in fact equal to
$a(\cdot )$
appearing in Section 9 are in fact equal to
![]() $1$
.
$1$
.
Proposition 14.2. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() $G({\mathbb A}_F)$
, satisfying (coh), (St) and (str-reg). Then
$G({\mathbb A}_F)$
, satisfying (coh), (St) and (str-reg). Then
![]() $m(\pi ) = 1$
.
$m(\pi ) = 1$
.
Proof. The proof is the same as the argument for [Reference Kret and Shin50, Thm. 12.2]. The main point is that automorphic representations
![]() $\tau ^{*}$
of
$\tau ^{*}$
of
![]() $G^{*}(\mathbb A_F)= {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
contributing to the analogue of [loc. cit., Equation (12.2)] have automorphic multiplicity
$G^{*}(\mathbb A_F)= {\mathrm {GSO}}_{2n}^{E/F}(\mathbb A_F)$
contributing to the analogue of [loc. cit., Equation (12.2)] have automorphic multiplicity
![]() $1$
. Notice that [Reference Xu81, Thm. 1.8] may be used again, together with the existence of Galois representations (our Theorem A), to prove that for all
$1$
. Notice that [Reference Xu81, Thm. 1.8] may be used again, together with the existence of Galois representations (our Theorem A), to prove that for all
![]() $\pi ^{*}$
and
$\pi ^{*}$
and
![]() $\tau ^{*}$
contributing to [Reference Kret and Shin50, Eq. (12.2)], we have
$\tau ^{*}$
contributing to [Reference Kret and Shin50, Eq. (12.2)], we have
![]() $\tau ^{*}_{{{{\mathfrak q}}_{\mathrm {St}}}} \simeq \pi ^{*}_{{{{\mathfrak q}}_{\mathrm {St}}}}$
.
$\tau ^{*}_{{{{\mathfrak q}}_{\mathrm {St}}}} \simeq \pi ^{*}_{{{{\mathfrak q}}_{\mathrm {St}}}}$
.
15 Meromorphic continuation of spin L-functions
Let
![]() $n\in \mathbb Z_{\ge 3}$
, and
$n\in \mathbb Z_{\ge 3}$
, and
![]() $\mathfrak e$
be as in (0.2). Let
$\mathfrak e$
be as in (0.2). Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
unramified away from a finite set of places S satisfying (St), (L-coh) and (spin-reg). This implies (std-reg) for
${\mathrm {GSO}}^{E/F}_{2n}(\mathbb A_F)$
unramified away from a finite set of places S satisfying (St), (L-coh) and (spin-reg). This implies (std-reg) for
![]() $\pi $
. Indeed, if the image of
$\pi $
. Indeed, if the image of
![]() $(s_0,s_1,\ldots ,s_n)\in T_{\mathrm {GSpin}}$
under
$(s_0,s_1,\ldots ,s_n)\in T_{\mathrm {GSpin}}$
under
![]() $\mathrm {spin}^{\varepsilon }$
is regular for some
$\mathrm {spin}^{\varepsilon }$
is regular for some
![]() $\varepsilon \in \mathfrak e$
, then
$\varepsilon \in \mathfrak e$
, then
![]() $s_1,\ldots ,s_n$
must be mutually distinct, as the weights in
$s_1,\ldots ,s_n$
must be mutually distinct, as the weights in
![]() $\mathrm {spin}^{\varepsilon }$
are described as the Weyl orbit(s) of (2.9).
$\mathrm {spin}^{\varepsilon }$
are described as the Weyl orbit(s) of (2.9).
Proposition 15.1. Assume that
![]() $\pi $
satisfies (St), (L-coh) and (spin-reg). Let
$\pi $
satisfies (St), (L-coh) and (spin-reg). Let
![]() $n\in \mathbb Z_{\ge 3}$
. There exist a number field
$n\in \mathbb Z_{\ge 3}$
. There exist a number field
![]() $M_{\pi }$
and a semisimple representation
$M_{\pi }$
and a semisimple representation
for each finite place
![]() $\lambda $
of
$\lambda $
of
![]() $M_{\pi }$
such that the following hold for every
$M_{\pi }$
such that the following hold for every
![]() $\varepsilon \in \mathfrak e$
. (Write
$\varepsilon \in \mathfrak e$
. (Write
![]() $\ell $
for the rational prime below
$\ell $
for the rational prime below
![]() $\lambda $
.)
$\lambda $
.)
-
(1) At each place
 ${{\mathfrak q}}$
of F not above
${{\mathfrak q}}$
of F not above
 $S_{\mathrm {bad}}\cup \{\ell \}$
, we have
$S_{\mathrm {bad}}\cup \{\ell \}$
, we have  $$ \begin{align*}\mathrm{char}(R^{\varepsilon}_{\pi,\lambda}(\mathrm{Frob}_{\mathfrak{q}}))=\mathrm{char}(\mathrm{spin}^{\varepsilon}(\iota\phi_{\pi_{\mathfrak{q}}}(\mathrm{Frob}_{\mathfrak{q}})))\in M_{\pi}[X].\end{align*} $$
$$ \begin{align*}\mathrm{char}(R^{\varepsilon}_{\pi,\lambda}(\mathrm{Frob}_{\mathfrak{q}}))=\mathrm{char}(\mathrm{spin}^{\varepsilon}(\iota\phi_{\pi_{\mathfrak{q}}}(\mathrm{Frob}_{\mathfrak{q}})))\in M_{\pi}[X].\end{align*} $$
-
(2)
 $R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}}$
is de Rham for every
$R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}}$
is de Rham for every
 ${{\mathfrak q}}|\ell $
. Moreover, it is crystalline if
${{\mathfrak q}}|\ell $
. Moreover, it is crystalline if
 $\pi _v$
is unramified and
$\pi _v$
is unramified and
 ${{\mathfrak q}}\notin S^F_{\mathrm {bad}}$
.
${{\mathfrak q}}\notin S^F_{\mathrm {bad}}$
. -
(3) For each
 ${{\mathfrak q}}|\ell $
and each
${{\mathfrak q}}|\ell $
and each
 $y:F\hookrightarrow {\mathbb {C}}$
such that
$y:F\hookrightarrow {\mathbb {C}}$
such that
 $\iota y$
induces
$\iota y$
induces
 ${{\mathfrak q}}$
, we have
${{\mathfrak q}}$
, we have
 $\mu _{\mathrm {HT}}(R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}},\iota y)=\iota (\mathrm {spin}^{\varepsilon }\circ \mu _{\mathrm {Hodge}}(\phi _{\pi _y}))$
. In particular,
$\mu _{\mathrm {HT}}(R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}},\iota y)=\iota (\mathrm {spin}^{\varepsilon }\circ \mu _{\mathrm {Hodge}}(\phi _{\pi _y}))$
. In particular,
 $\mu _{\mathrm {HT}}(R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}},\iota y)$
is a regular cocharacter for each y.
$\mu _{\mathrm {HT}}(R^{\varepsilon }_{\pi ,\lambda }|_{\Gamma _{\mathfrak {q}}},\iota y)$
is a regular cocharacter for each y. -
(4)
 $R^{\varepsilon }_{\pi ,\lambda }$
is pure.
$R^{\varepsilon }_{\pi ,\lambda }$
is pure. -
(5)
 $R^{\varepsilon }_{\pi ,\lambda }$
maps into
$R^{\varepsilon }_{\pi ,\lambda }$
maps into
 $\mathrm {GSp}_{2^n/|\mathfrak e|}(\overline {M}_{\pi ,\lambda })$
if
$\mathrm {GSp}_{2^n/|\mathfrak e|}(\overline {M}_{\pi ,\lambda })$
if
 $n\equiv 2,3~(\mathrm {mod}~4)$
(resp.
$n\equiv 2,3~(\mathrm {mod}~4)$
(resp.
 $\mathrm {GO}_{2^n/|\mathfrak e|}(\overline {M}_{\pi ,\lambda })$
if
$\mathrm {GO}_{2^n/|\mathfrak e|}(\overline {M}_{\pi ,\lambda })$
if
 $n\equiv 0,1~(\mathrm {mod}~4)$
) for a nondegenerate alternating (resp. symmetric) pairing on the underlying
$n\equiv 0,1~(\mathrm {mod}~4)$
) for a nondegenerate alternating (resp. symmetric) pairing on the underlying
 $2^{n}/|\mathfrak e|$
-dimensional space over
$2^{n}/|\mathfrak e|$
-dimensional space over
 $\overline {M}_{\pi ,\lambda }$
. The multiplier character
$\overline {M}_{\pi ,\lambda }$
. The multiplier character
 $\mu ^{\varepsilon }_{\lambda }:\Gamma \rightarrow {\mathrm {GL}}_{1}(\overline {M}_{\pi ,\lambda })$
(so that
$\mu ^{\varepsilon }_{\lambda }:\Gamma \rightarrow {\mathrm {GL}}_{1}(\overline {M}_{\pi ,\lambda })$
(so that
 $R^{\varepsilon }_{\pi ,\lambda }\simeq (R^{\varepsilon }_{\pi ,\lambda })^{\vee }\otimes \mu ^{\varepsilon }_{\lambda }$
) is totally of sign
$R^{\varepsilon }_{\pi ,\lambda }\simeq (R^{\varepsilon }_{\pi ,\lambda })^{\vee }\otimes \mu ^{\varepsilon }_{\lambda }$
) is totally of sign
 $(-1)^{n(n-1)/2}$
and associated with
$(-1)^{n(n-1)/2}$
and associated with
 $\omega _{\pi }$
via class field theory and
$\omega _{\pi }$
via class field theory and
 $\iota _{\lambda }$
.
$\iota _{\lambda }$
.
Proof. Let M be the field of definition of
![]() $\xi $
, which is a finite extension of
$\xi $
, which is a finite extension of
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() ${\mathbb {C}}$
. We can choose
${\mathbb {C}}$
. We can choose
![]() $M_{\pi }$
to be the field of definition for the
$M_{\pi }$
to be the field of definition for the
![]() $\pi ^{\infty }$
-isotypic part in the (compact support) Betti cohomology of
$\pi ^{\infty }$
-isotypic part in the (compact support) Betti cohomology of
![]() $H^{\bullet }(\mathrm {Sh}^+({\mathbb {C}}),{\mathcal L}_{\xi })\oplus H^{\bullet }(\mathrm {Sh}^-({\mathbb {C}}),{\mathcal L}_{\xi })$
with M-coefficient. Then
$H^{\bullet }(\mathrm {Sh}^+({\mathbb {C}}),{\mathcal L}_{\xi })\oplus H^{\bullet }(\mathrm {Sh}^-({\mathbb {C}}),{\mathcal L}_{\xi })$
with M-coefficient. Then
![]() $M_{\pi }$
is a finite extension of M in
$M_{\pi }$
is a finite extension of M in
![]() ${\mathbb {C}}$
. For each prime
${\mathbb {C}}$
. For each prime
![]() $\ell $
and a finite place
$\ell $
and a finite place
![]() $\lambda $
of
$\lambda $
of
![]() $M_{\pi }$
above
$M_{\pi }$
above
![]() $\ell $
, extend
$\ell $
, extend
![]() $M\hookrightarrow {\mathbb {C}}$
to an isomorphism
$M\hookrightarrow {\mathbb {C}}$
to an isomorphism
![]() $\overline M_{\pi ,\lambda }\simeq {\mathbb {C}}$
. Identifying
$\overline M_{\pi ,\lambda }\simeq {\mathbb {C}}$
. Identifying
![]() $\overline M_{\pi ,\lambda }\simeq \overline {\mathbb {Q}}_{\ell }$
, we have
$\overline M_{\pi ,\lambda }\simeq \overline {\mathbb {Q}}_{\ell }$
, we have
![]() $\iota _{\lambda }:{\mathbb {C}}\stackrel {\sim }{\to } \overline {\mathbb {Q}}_{\ell }$
. Take
$\iota _{\lambda }:{\mathbb {C}}\stackrel {\sim }{\to } \overline {\mathbb {Q}}_{\ell }$
. Take
Then (1), (2) and (3) follow from (A2) and (A3) of Theorem A, respectively. Part (4) follows from (SO-ii) of Theorem 6.5 via (A2). The first part of (5) holds true since
![]() $\mathrm {spin}^{\varepsilon }: \mathrm {GSpin}_{2n}\rightarrow {\mathrm {GL}}_{2^{n-1}}$
is an irreducible representation preserving a nondegenerate symplectic (resp. symmetric) pairing up to scalar if n is 2 (resp. 0) mod 4, and since
$\mathrm {spin}^{\varepsilon }: \mathrm {GSpin}_{2n}\rightarrow {\mathrm {GL}}_{2^{n-1}}$
is an irreducible representation preserving a nondegenerate symplectic (resp. symmetric) pairing up to scalar if n is 2 (resp. 0) mod 4, and since
![]() $\mathrm {spin}: \mathrm {GPin}_{2n}\rightarrow {\mathrm {GL}}_{2^{n}}$
is irreducible and preserves a nondegenerate symplectic (resp. symmetric) pairing up to scalar if n is 3 (resp. 1) mod 4. Indeed, the irreducibility is standard and the rest follows from Lemma 4.2 (with the pairing given as in the lemma). Lemma 4.2 also tells us that
$\mathrm {spin}: \mathrm {GPin}_{2n}\rightarrow {\mathrm {GL}}_{2^{n}}$
is irreducible and preserves a nondegenerate symplectic (resp. symmetric) pairing up to scalar if n is 3 (resp. 1) mod 4. Indeed, the irreducibility is standard and the rest follows from Lemma 4.2 (with the pairing given as in the lemma). Lemma 4.2 also tells us that
![]() $\mu ^{\varepsilon }_{\lambda }=\mathcal N\circ \rho _{\pi ,\iota _{\lambda }}$
. By (A2),
$\mu ^{\varepsilon }_{\lambda }=\mathcal N\circ \rho _{\pi ,\iota _{\lambda }}$
. By (A2),
![]() $\omega _{\pi }=\mathcal N\circ \rho _{\pi ,\iota _{\lambda }}$
so
$\omega _{\pi }=\mathcal N\circ \rho _{\pi ,\iota _{\lambda }}$
so
![]() $\mu ^{\varepsilon }_{\lambda }$
is associated with
$\mu ^{\varepsilon }_{\lambda }$
is associated with
![]() $\omega _{\pi }$
. As in the proof of part 5 of [Reference Kret and Shin50, Prop. 13.1],
$\omega _{\pi }$
. As in the proof of part 5 of [Reference Kret and Shin50, Prop. 13.1],
![]() $\omega _{\pi } \otimes |\cdot |^{n(n-1)/2}$
corresponds to an even Galois character of
$\omega _{\pi } \otimes |\cdot |^{n(n-1)/2}$
corresponds to an even Galois character of
![]() $\Gamma $
. (We change
$\Gamma $
. (We change
![]() $n(n+1)/2$
in [Reference Kret and Shin50] to
$n(n+1)/2$
in [Reference Kret and Shin50] to
![]() $n(n-1)/2$
here due to the difference in the definition of (L-coh).) It follows that
$n(n-1)/2$
here due to the difference in the definition of (L-coh).) It follows that
![]() $\mu _{\lambda ,y}(c_y)=(-1)^{n(n-1)/2}$
for every
$\mu _{\lambda ,y}(c_y)=(-1)^{n(n-1)/2}$
for every
![]() $y|\infty $
.
$y|\infty $
.
Now we apply potential automorphy results to the weakly compatible system of
![]() $R^{\varepsilon }_{\pi ,\lambda }$
.
$R^{\varepsilon }_{\pi ,\lambda }$
.
Theorem 15.2. Theorem D is true.
Proof. This follows from [Reference Patrikis and Taylor65, Thm. A], which can be applied to the weakly compatible system
![]() $\{R^{\varepsilon }_{\pi ,\lambda }\}$
thanks to the preceding proposition.
$\{R^{\varepsilon }_{\pi ,\lambda }\}$
thanks to the preceding proposition.
Remark 15.3. We cannot appeal to the potential automorphy as in [Reference Barnet-Lamb, Gee, Geraghty and Taylor3, Thm. A], as
![]() $R^{\varepsilon }_{\pi ,\lambda }$
may be reducible. The point of [Reference Patrikis and Taylor65] is to replace the irreducibility hypothesis with a purity hypothesis (guaranteed by (iv) of Proposition 15.1). We take advantage of this.
$R^{\varepsilon }_{\pi ,\lambda }$
may be reducible. The point of [Reference Patrikis and Taylor65] is to replace the irreducibility hypothesis with a purity hypothesis (guaranteed by (iv) of Proposition 15.1). We take advantage of this.
Appendix A Extending a Galois representation
Here we investigate the problem of extending a
![]() $\widehat G$
-valued Galois representation to an
$\widehat G$
-valued Galois representation to an
![]() $^L G$
-valued representation over a quadratic extension.
$^L G$
-valued representation over a quadratic extension.
We freely use the notation and terminology of §1. Let E be a CM quadratic extension over a totally real field F in an algebraic closure
![]() $\overline {F}$
. Set
$\overline {F}$
. Set
![]() $\Gamma =\Gamma _F:={\mathrm {Gal}}(\overline {F}/F)$
,
$\Gamma =\Gamma _F:={\mathrm {Gal}}(\overline {F}/F)$
,
![]() $\Gamma _E:={\mathrm {Gal}}(\overline {F}/E)$
, and
$\Gamma _E:={\mathrm {Gal}}(\overline {F}/E)$
, and
![]() $\Gamma _{E/F}:={\mathrm {Gal}}(E/F)=\{1,c\}$
. Let G be a quasi-split group over F which splits over E. Let
$\Gamma _{E/F}:={\mathrm {Gal}}(E/F)=\{1,c\}$
. Let G be a quasi-split group over F which splits over E. Let
![]() $\theta \in \mathrm {Aut}(\widehat G)$
denote the action of c on
$\theta \in \mathrm {Aut}(\widehat G)$
denote the action of c on
![]() $\widehat G$
(with respect to a pinning over F). By
$\widehat G$
(with respect to a pinning over F). By
![]() $\widehat G(\overline {\mathbb {Q}}_{\ell }) \rtimes \Gamma _{E/F}$
, we mean the L-group relative to
$\widehat G(\overline {\mathbb {Q}}_{\ell }) \rtimes \Gamma _{E/F}$
, we mean the L-group relative to
![]() $E/F$
, namely, the semi-direct product such that
$E/F$
, namely, the semi-direct product such that
![]() $c g c = \theta (g)$
for
$c g c = \theta (g)$
for
![]() $g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
.
$g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
.
Fix an infinite place y of F. Write
![]() $c_y\in \Gamma _F$
for the corresponding complex conjugation (well-defined up to conjugacy). Let
$c_y\in \Gamma _F$
for the corresponding complex conjugation (well-defined up to conjugacy). Let
![]() $\rho ': \Gamma _E\rightarrow \widehat G(\overline {\mathbb {Q}}_{\ell })$
be a Galois representation. Define
$\rho ': \Gamma _E\rightarrow \widehat G(\overline {\mathbb {Q}}_{\ell })$
be a Galois representation. Define
(Of course,
![]() $c^{-1}_y=c_y$
.) We will sometimes impose the following hypotheses.
$c^{-1}_y=c_y$
.) We will sometimes impose the following hypotheses.
-
(H1)
 $\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))=Z(\widehat G)$
.
$\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))=Z(\widehat G)$
. -
(H2) The map
 $Z(\widehat G)\rightarrow Z(\widehat G)^{\theta }$
given by
$Z(\widehat G)\rightarrow Z(\widehat G)^{\theta }$
given by
 $z\mapsto z\theta (z)$
is a surjection on
$z\mapsto z\theta (z)$
is a surjection on
 $\overline {\mathbb {Q}}_{\ell }$
-points.
$\overline {\mathbb {Q}}_{\ell }$
-points.
Lemma A.1. Consider the following statements.
-
(1)
 $\rho '$
extends to some
$\rho '$
extends to some
 $\rho :\Gamma _F\rightarrow \widehat G(\overline {\mathbb {Q}}_{\ell }) \rtimes \Gamma _{E/F}$
.
$\rho :\Gamma _F\rightarrow \widehat G(\overline {\mathbb {Q}}_{\ell }) \rtimes \Gamma _{E/F}$
. -
(2)
 $^{c_y}\rho '\simeq \theta \circ \rho '$
.
$^{c_y}\rho '\simeq \theta \circ \rho '$
. -
(3) there exists
 $g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
such that
$g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
such that
 $g\theta (g)=1$
and
$g\theta (g)=1$
and
 $\rho '(c_y \gamma c_y^{-1})=g \theta (\rho '(\gamma ))g^{-1}$
for every
$\rho '(c_y \gamma c_y^{-1})=g \theta (\rho '(\gamma ))g^{-1}$
for every
 $\gamma \in \Gamma _E$
.
$\gamma \in \Gamma _E$
.
Then (3)
![]() $\Leftrightarrow $
(1)
$\Leftrightarrow $
(1)
![]() $\Rightarrow $
(2). In particular, if
$\Rightarrow $
(2). In particular, if
![]() $\rho $
is as in (1), then the element g such that
$\rho $
is as in (1), then the element g such that
![]() $\rho (c_y)=g\rtimes c$
enjoys the property of (3). If (H1) and (H2) are satisfied, then we also have (2)
$\rho (c_y)=g\rtimes c$
enjoys the property of (3). If (H1) and (H2) are satisfied, then we also have (2)
![]() $\Rightarrow $
(3), so all three statements are equivalent.
$\Rightarrow $
(3), so all three statements are equivalent.
Remark A.2. We recommend [Reference Bellaïche and Chenevier5, Section A.11] as a useful guide to similar ideas.
Remark A.3. Often, (2) is the condition to verify to extend a Galois representation, as we did in Lemma 12.1 of this paper.
Proof. (3)
![]() $\Leftrightarrow $
(1): First we show (3)
$\Leftrightarrow $
(1): First we show (3)
![]() $\Rightarrow $
(1). Define
$\Rightarrow $
(1). Define
![]() $\rho $
by
$\rho $
by
![]() $\rho |_{\Gamma _E}:=\rho '$
and
$\rho |_{\Gamma _E}:=\rho '$
and
![]() $\rho (\gamma c_ y):=\rho '(\gamma )g c$
(
$\rho (\gamma c_ y):=\rho '(\gamma )g c$
(
![]() $\gamma \in \Gamma _E$
). Then
$\gamma \in \Gamma _E$
). Then
 $$ \begin{align*}\rho(c_ y ^2)&=gc gc = g\theta(g)=1,\\[7pt]\rho(c_ y \gamma c_ y ^{-1}) &= {}^{c_ y} \rho'(\gamma) = g \theta(\rho'(\gamma))g^{-1}, \end{align*} $$
$$ \begin{align*}\rho(c_ y ^2)&=gc gc = g\theta(g)=1,\\[7pt]\rho(c_ y \gamma c_ y ^{-1}) &= {}^{c_ y} \rho'(\gamma) = g \theta(\rho'(\gamma))g^{-1}, \end{align*} $$
and using this, one checks that
![]() $\rho $
is a homomorphism on the entire
$\rho $
is a homomorphism on the entire
![]() $\Gamma $
. A similar computation shows (1)
$\Gamma $
. A similar computation shows (1)
![]() $\Rightarrow $
(3) for g such that
$\Rightarrow $
(3) for g such that
![]() $\rho (c_y)=g\rtimes c$
.
$\rho (c_y)=g\rtimes c$
.
(1)
![]() $\Rightarrow $
(2): Write
$\Rightarrow $
(2): Write
![]() $\rho (c_y)=gc$
with
$\rho (c_y)=gc$
with
![]() $g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
. For every
$g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
. For every
![]() $\gamma \in \Gamma _E$
,
$\gamma \in \Gamma _E$
,
(2)
![]() $\Rightarrow $
(3), assuming (H1) and (H2): There exists
$\Rightarrow $
(3), assuming (H1) and (H2): There exists
![]() $g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
such that
$g\in \widehat G(\overline {\mathbb {Q}}_{\ell })$
such that
Putting
![]() $c_ y \gamma c^{-1}_ y $
in place of
$c_ y \gamma c^{-1}_ y $
in place of
![]() $\gamma $
, we obtain
$\gamma $
, we obtain
Hence,
![]() $g\theta (g)\in Z(\widehat G)$
as
$g\theta (g)\in Z(\widehat G)$
as
![]() $\mathrm {Cent}_{\widehat G}(\rho ')=Z(\widehat G)$
by (H1). As a central element,
$\mathrm {Cent}_{\widehat G}(\rho ')=Z(\widehat G)$
by (H1). As a central element,
namely,
![]() $g\theta (g)\in Z(\widehat G)^{\theta }$
. By (H2),
$g\theta (g)\in Z(\widehat G)^{\theta }$
. By (H2),
![]() $g\theta (g)=z\theta (z)$
for some
$g\theta (g)=z\theta (z)$
for some
![]() $z\in Z(\widehat G)$
. Replacing g with
$z\in Z(\widehat G)$
. Replacing g with
![]() $gz^{-1}$
, we can arrange that
$gz^{-1}$
, we can arrange that
This does not affect (A.1), so we are done.
Lemma A.4. Assume (H1). Then the set of
![]() $\widehat {G}$
-conjugacy classes of extensions of
$\widehat {G}$
-conjugacy classes of extensions of
![]() $\rho '$
to
$\rho '$
to
![]() $\Gamma $
is an
$\Gamma $
is an
![]() $H^1(\Gamma _{E/F},Z(\widehat G))$
-torsor if nonempty.
$H^1(\Gamma _{E/F},Z(\widehat G))$
-torsor if nonempty.
Proof. Fix an extension
![]() $\rho _0$
of
$\rho _0$
of
![]() $\rho '$
, which exists by Lemma A.1. If
$\rho '$
, which exists by Lemma A.1. If
![]() $\rho $
is another extension of
$\rho $
is another extension of
![]() $\rho '$
, then set
$\rho '$
, then set
![]() $z:=\rho _0(c_y)\rho (c_y)^{-1}$
. Writing
$z:=\rho _0(c_y)\rho (c_y)^{-1}$
. Writing
![]() $\rho _0(c_y)=g_0 \rtimes c$
and
$\rho _0(c_y)=g_0 \rtimes c$
and
![]() $\rho (c_y)=g\rtimes c$
, we have
$\rho (c_y)=g\rtimes c$
, we have
![]() $z g= g_0$
, and both
$z g= g_0$
, and both
![]() $g_0,g$
satisfy the condition of Lemma A.1 (3). It follows that z centralizes
$g_0,g$
satisfy the condition of Lemma A.1 (3). It follows that z centralizes
![]() $\theta (\mathrm {im}(\rho '))$
, hence
$\theta (\mathrm {im}(\rho '))$
, hence
![]() $z\in Z(\widehat G)$
, and also that
$z\in Z(\widehat G)$
, and also that
![]() $z\theta (z)=1$
. Thus, z defines a
$z\theta (z)=1$
. Thus, z defines a
![]() $Z(\widehat G)$
-valued 1-cocycle on
$Z(\widehat G)$
-valued 1-cocycle on
![]() $\Gamma _{E/F}$
, and by reversing the process, such a cocycle determines an extension of
$\Gamma _{E/F}$
, and by reversing the process, such a cocycle determines an extension of
![]() $\rho '$
.
$\rho '$
.
Let
![]() $\rho _z$
be the extension given by
$\rho _z$
be the extension given by
![]() $z\in Z(\widehat G)$
such that
$z\in Z(\widehat G)$
such that
![]() $z\theta (z)=1$
. It remains to show that
$z\theta (z)=1$
. It remains to show that
![]() $\rho _z\sim \rho _0$
if and only if
$\rho _z\sim \rho _0$
if and only if
![]() $z=\theta (x)/x$
for some
$z=\theta (x)/x$
for some
![]() $x\in Z(\widehat G)$
. If
$x\in Z(\widehat G)$
. If
![]() $\rho _z\sim \rho _0$
, then
$\rho _z\sim \rho _0$
, then
![]() $\rho _z=\mathrm {Int}(x) \rho _0$
for some
$\rho _z=\mathrm {Int}(x) \rho _0$
for some
![]() $x\in \widehat G$
. By (H1),
$x\in \widehat G$
. By (H1),
![]() $x\in Z(\widehat G)$
. Evaluating at
$x\in Z(\widehat G)$
. Evaluating at
![]() $c_y$
, we obtain
$c_y$
, we obtain
![]() $z^{-1}\rho _0(c_y)= x \rho _0(c_y) x^{-1}$
. Therefore,
$z^{-1}\rho _0(c_y)= x \rho _0(c_y) x^{-1}$
. Therefore,
![]() $z=\theta (x)/x$
. The converse direction is shown similarly by arguing backward.
$z=\theta (x)/x$
. The converse direction is shown similarly by arguing backward.
We illustrate assumptions (H1), (H2), and the lemmas in the following examples.
Example A.5. Consider
![]() $\widehat G={\mathrm {SO}}_{2n}$
(
$\widehat G={\mathrm {SO}}_{2n}$
(
![]() $n\ge 3$
) with
$n\ge 3$
) with
![]() $\theta $
being the conjugation by
$\theta $
being the conjugation by
![]() $\vartheta ^{\circ }\in \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })-{\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
as in (2.4). Assume that
$\vartheta ^{\circ }\in \mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })-{\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
as in (2.4). Assume that
![]() $\mathrm {im}(\rho ')$
contains a regular unipotent of
$\mathrm {im}(\rho ')$
contains a regular unipotent of
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. In this case,
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
. In this case,
![]() $Z(\widehat G)=Z(\widehat G)^{\theta } = \{\pm 1\}$
. Then (H2) is trivially false but (H1) is true. To see this, by assumption,
$Z(\widehat G)=Z(\widehat G)^{\theta } = \{\pm 1\}$
. Then (H2) is trivially false but (H1) is true. To see this, by assumption,
![]() $\mathrm {std}\circ \rho '$
is either irreducible or the direct sum of an irreducible
$\mathrm {std}\circ \rho '$
is either irreducible or the direct sum of an irreducible
![]() $(2n-1)$
-dimensional representation and a character. In the former case, (H1) is clear by Schur’s lemma. In the latter case, again by Schur’s lemma, a centralizer of
$(2n-1)$
-dimensional representation and a character. In the former case, (H1) is clear by Schur’s lemma. In the latter case, again by Schur’s lemma, a centralizer of
![]() $\mathrm {im}(\rho ')$
in
$\mathrm {im}(\rho ')$
in
![]() ${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is contained in
${\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
is contained in
![]() $(\begin {smallmatrix} a \cdot 1_{2n-1} & 0 \\ 0 & b \end {smallmatrix})$
with
$(\begin {smallmatrix} a \cdot 1_{2n-1} & 0 \\ 0 & b \end {smallmatrix})$
with
![]() $a,b\in \{\pm 1\}$
up to
$a,b\in \{\pm 1\}$
up to
![]() $\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy. Since the determinant equals 1, we deduce that
$\mathrm {O}_{2n}(\overline {\mathbb {Q}}_{\ell })$
-conjugacy. Since the determinant equals 1, we deduce that
![]() $a=b$
(i.e., the centralizer belongs to
$a=b$
(i.e., the centralizer belongs to
![]() $Z(\widehat G)$
).
$Z(\widehat G)$
).
We easily compute
![]() $Z^1(\Gamma _{E/F},Z(\widehat G))=H^1(\Gamma _{E/F},Z(\widehat G))\simeq \mathbb Z/2\mathbb Z$
, the nontrivial element sending c to
$Z^1(\Gamma _{E/F},Z(\widehat G))=H^1(\Gamma _{E/F},Z(\widehat G))\simeq \mathbb Z/2\mathbb Z$
, the nontrivial element sending c to
![]() $-1$
. In fact, if
$-1$
. In fact, if
![]() $\rho $
extends
$\rho $
extends
![]() $\rho '$
in the setup of the preceding lemmas, the other extension is easily described as
$\rho '$
in the setup of the preceding lemmas, the other extension is easily described as
![]() $\rho \otimes \chi _{E/F}$
, where
$\rho \otimes \chi _{E/F}$
, where
![]() $\chi _{E/F}:\Gamma \twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
.
$\chi _{E/F}:\Gamma \twoheadrightarrow \Gamma _{E/F}\stackrel {\sim }{\to } \{\pm 1\}$
.
Example A.6. The main case of interest for us is when
-
•
 $\widehat G=\mathrm {GSpin}_{2n}$
(
$\widehat G=\mathrm {GSpin}_{2n}$
(
 $n\ge 3$
) ,
$n\ge 3$
) , -
•
 $\theta $
is the conjugation by an element of
$\theta $
is the conjugation by an element of
 $\mathrm {GPin}_{2n}(\overline {\mathbb {Q}}_{\ell })-\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
,
$\mathrm {GPin}_{2n}(\overline {\mathbb {Q}}_{\ell })-\mathrm {GSpin}_{2n}(\overline {\mathbb {Q}}_{\ell })$
, -
•
 $\mathrm {im}(\rho ')$
contains a regular unipotent.
$\mathrm {im}(\rho ')$
contains a regular unipotent.
Since
![]() $Z(\widehat G)^{\theta }=\mathbb G_m$
(identified with invertible scalars in the Clifford algebra underlying
$Z(\widehat G)^{\theta }=\mathbb G_m$
(identified with invertible scalars in the Clifford algebra underlying
![]() $\widehat G$
as a
$\widehat G$
as a
![]() $\mathrm {GSpin}$
group; see §3), assumption (H2) is satisfied. (The squaring map
$\mathrm {GSpin}$
group; see §3), assumption (H2) is satisfied. (The squaring map
![]() $\mathbb G_m\rightarrow \mathbb G_m$
is clearly surjective on
$\mathbb G_m\rightarrow \mathbb G_m$
is clearly surjective on
![]() $\overline {\mathbb {Q}}_{\ell }$
-points.) To check (H1),
$\overline {\mathbb {Q}}_{\ell }$
-points.) To check (H1),
![]() $\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))$
is contained in the preimage of
$\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))$
is contained in the preimage of
![]() $\mathrm {Cent}_{{\mathrm {SO}}_{2n}}(\mathrm {im}(\rho ^{\prime ,\circ }))$
via
$\mathrm {Cent}_{{\mathrm {SO}}_{2n}}(\mathrm {im}(\rho ^{\prime ,\circ }))$
via
![]() $\mathrm {pr}^{\circ }:\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. Since the latter centralizer is
$\mathrm {pr}^{\circ }:\mathrm {GSpin}_{2n}\rightarrow {\mathrm {SO}}_{2n}$
. Since the latter centralizer is
![]() $\{\pm 1\}\subset {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
, we see that
$\{\pm 1\}\subset {\mathrm {SO}}_{2n}(\overline {\mathbb {Q}}_{\ell })$
, we see that
![]() $\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))\subset \mathrm {pr}^{\prime ,-1}(\{\pm 1\}) = Z(\widehat G)$
.
$\mathrm {Cent}_{\widehat G}(\mathrm {im}(\rho '))\subset \mathrm {pr}^{\prime ,-1}(\{\pm 1\}) = Z(\widehat G)$
.
In the coordinates for
![]() $Z(\widehat G)$
of Lemma 2.5,
$Z(\widehat G)$
of Lemma 2.5,
![]() $Z^1(\Gamma _{E/F},Z(\widehat G))=\{(s_0,s_1): s_1\in \{\pm 1\},~s_1=s_0^2\}\simeq \mu _4$
, of which coboundaries are
$Z^1(\Gamma _{E/F},Z(\widehat G))=\{(s_0,s_1): s_1\in \{\pm 1\},~s_1=s_0^2\}\simeq \mu _4$
, of which coboundaries are
![]() $\{(\pm 1,1)\}\simeq \mu _2$
. (The first identification is given by taking the image of c.) Hence,
$\{(\pm 1,1)\}\simeq \mu _2$
. (The first identification is given by taking the image of c.) Hence,
![]() $H^1(\Gamma _{E/F},Z(\widehat G))\simeq \mathbb Z/2\mathbb Z$
. Let
$H^1(\Gamma _{E/F},Z(\widehat G))\simeq \mathbb Z/2\mathbb Z$
. Let
![]() $\zeta =(\zeta _4,-1)\in Z(\widehat G)$
, where
$\zeta =(\zeta _4,-1)\in Z(\widehat G)$
, where
![]() $\zeta _4$
is a primitive fourth root of unity, cf. Lemma 3.7. If
$\zeta _4$
is a primitive fourth root of unity, cf. Lemma 3.7. If
![]() $\rho $
is an extension of
$\rho $
is an extension of
![]() $\rho '$
, then the other extension (up to
$\rho '$
, then the other extension (up to
![]() $\widehat G$
-conjugacy) is described as
$\widehat G$
-conjugacy) is described as
![]() $\rho \otimes \chi $
, where
$\rho \otimes \chi $
, where
![]() $\chi :\Gamma \rightarrow Z(\widehat G)\rtimes \{1,c\}$
is inflated from
$\chi :\Gamma \rightarrow Z(\widehat G)\rtimes \{1,c\}$
is inflated from
![]() $\Gamma _{E/F}\stackrel {\sim }{\to } \{1,\zeta \rtimes c\}$
. Notice that
$\Gamma _{E/F}\stackrel {\sim }{\to } \{1,\zeta \rtimes c\}$
. Notice that
![]() $\mathrm {pr}^{\circ }\circ \chi =\chi _{E/F}$
, for
$\mathrm {pr}^{\circ }\circ \chi =\chi _{E/F}$
, for
![]() $\chi _{E/F}$
as in the preceding example.
$\chi _{E/F}$
as in the preceding example.
Example A.7. When studying Galois representations arising from automorphic representations on a unitary group
![]() $U_n$
in n variables, two target groups appear in the literature: the group
$U_n$
in n variables, two target groups appear in the literature: the group
![]() $\mathcal {G}_n$
in [Reference Clozel, Harris and Taylor17, §2.1] and the C-group of
$\mathcal {G}_n$
in [Reference Clozel, Harris and Taylor17, §2.1] and the C-group of
![]() $U_n$
in [Reference Buzzard and Gee12]; the two are isogenous as explained in [Reference Buzzard and Gee12, §8.3]. The latter is the L-group of a
$U_n$
in [Reference Buzzard and Gee12]; the two are isogenous as explained in [Reference Buzzard and Gee12, §8.3]. The latter is the L-group of a
![]() $\mathbb G_m$
-extension of
$\mathbb G_m$
-extension of
![]() $U_n$
; it does not satisfy (H2). The former is not an L-group but still a semi-direct product
$U_n$
; it does not satisfy (H2). The former is not an L-group but still a semi-direct product
![]() $({\mathrm {GL}}_n\times {\mathrm {GL}}_1)\rtimes \Gamma _{E/F}$
, with
$({\mathrm {GL}}_n\times {\mathrm {GL}}_1)\rtimes \Gamma _{E/F}$
, with
![]() $c(g,\mu )=(\mu g^{-t},\mu )$
for an anti-diagonal matrix
$c(g,\mu )=(\mu g^{-t},\mu )$
for an anti-diagonal matrix
![]() $\Phi _n\in {\mathrm {GL}}_n$
. As such, the discussion in this appendix goes through for
$\Phi _n\in {\mathrm {GL}}_n$
. As such, the discussion in this appendix goes through for
![]() $\mathcal {G}_n$
. An easy computation shows that
$\mathcal {G}_n$
. An easy computation shows that
![]() $\mathcal {G}_n$
satisfies (H2) and that
$\mathcal {G}_n$
satisfies (H2) and that
![]() $H^1(\Gamma _{E/F},Z({\mathrm {GL}}_n\times {\mathrm {GL}}_1))=\{1\}$
for the given Galois action. Thus, provided that
$H^1(\Gamma _{E/F},Z({\mathrm {GL}}_n\times {\mathrm {GL}}_1))=\{1\}$
for the given Galois action. Thus, provided that
![]() $\rho '$
satisfies (H1) (e.g., if
$\rho '$
satisfies (H1) (e.g., if
![]() $\rho '$
is irreducible), an extension of
$\rho '$
is irreducible), an extension of
![]() $\rho '$
exists if and only if
$\rho '$
exists if and only if
![]() $^{c_y}\rho '\simeq \theta \circ \rho '$
, and the extension is unique up to conjugacy. Compare this with [Reference Clozel, Harris and Taylor17, Lem. 2.1.4] (which allows a general coefficient field of characteristic
$^{c_y}\rho '\simeq \theta \circ \rho '$
, and the extension is unique up to conjugacy. Compare this with [Reference Clozel, Harris and Taylor17, Lem. 2.1.4] (which allows a general coefficient field of characteristic
![]() $0$
).
$0$
).
Appendix B On local A-packets of even special orthogonal groups
In this appendix, we study the A-packets of the trivial and Steinberg representations of quasi-split forms of
![]() ${\mathrm {SO}}_{2n}$
, with
${\mathrm {SO}}_{2n}$
, with
![]() $n\ge 3$
, often following the notation and formulation of [Reference Arthur1].
$n\ge 3$
, often following the notation and formulation of [Reference Arthur1].
Let F be a finite extension of
![]() $\mathbb {Q}_p$
. Suppose that
$\mathbb {Q}_p$
. Suppose that
![]() $E=F$
or that E is a quadratic extension of F. Let
$E=F$
or that E is a quadratic extension of F. Let
![]() $\chi _{E/F}:F^{\times } \rightarrow \{\pm 1\}$
denote the quadratic character associated with
$\chi _{E/F}:F^{\times } \rightarrow \{\pm 1\}$
denote the quadratic character associated with
![]() $E/F$
via class field theory. Let
$E/F$
via class field theory. Let
![]() $G := {\mathrm {SO}}^{E/F}_{2n}$
denote the quasi-split form of the split group
$G := {\mathrm {SO}}^{E/F}_{2n}$
denote the quasi-split form of the split group
![]() ${\mathrm {SO}}_{2n}$
over F twisted by
${\mathrm {SO}}_{2n}$
over F twisted by
![]() $\chi _{E/F}$
. Write
$\chi _{E/F}$
. Write
![]() $\tilde {\mathrm {Out}}_{2n}(G):=\mathrm {O}_{2n}({\mathbb {C}})/{\mathrm {SO}}_{2n}({\mathbb {C}})$
for the outer automorphism group of
$\tilde {\mathrm {Out}}_{2n}(G):=\mathrm {O}_{2n}({\mathbb {C}})/{\mathrm {SO}}_{2n}({\mathbb {C}})$
for the outer automorphism group of
![]() ${\mathrm {SO}}_{2n}({\mathbb {C}})$
. Denote by
${\mathrm {SO}}_{2n}({\mathbb {C}})$
. Denote by
![]() $\mathbf {1}$
and
$\mathbf {1}$
and
![]() $\mathrm {St}$
the trivial and Steinberg representations of
$\mathrm {St}$
the trivial and Steinberg representations of
![]() $G(F)$
. We aim to identify local A-packets containing
$G(F)$
. We aim to identify local A-packets containing
![]() $\mathbf {1}$
or
$\mathbf {1}$
or
![]() $\mathrm {St}$
.
$\mathrm {St}$
.
Let
![]() ${\mathcal L}_F:=W_F\times {\mathrm {SU}}(2)$
denote the local Langlands group. Let
${\mathcal L}_F:=W_F\times {\mathrm {SU}}(2)$
denote the local Langlands group. Let
![]() $|\cdot |:W_F\rightarrow {\mathbb R}^{\times }_{>0}$
denote the absolute value character sending a geometric Frobenius element to the inverse of the residue cardinality of F. By abuse, keep writing
$|\cdot |:W_F\rightarrow {\mathbb R}^{\times }_{>0}$
denote the absolute value character sending a geometric Frobenius element to the inverse of the residue cardinality of F. By abuse, keep writing
![]() $|\cdot |$
for its pullback to
$|\cdot |$
for its pullback to
![]() ${\mathcal L}_F$
via projection.
${\mathcal L}_F$
via projection.
Denote by
![]() $\Psi ^+(G)$
the set of isomorphism classes of extended A-parameters, that is, continuous morphisms
$\Psi ^+(G)$
the set of isomorphism classes of extended A-parameters, that is, continuous morphisms
![]() $\psi :{\mathcal L}_{F}\times {\mathrm {SU}}(2)\rightarrow {}^L G$
such that
$\psi :{\mathcal L}_{F}\times {\mathrm {SU}}(2)\rightarrow {}^L G$
such that
![]() $\psi |_{{\mathcal L}_F}$
is an L-parameter. (Two A-parameters are considered isomorphic if they are in the same
$\psi |_{{\mathcal L}_F}$
is an L-parameter. (Two A-parameters are considered isomorphic if they are in the same
![]() $\widehat G$
-orbit.) An extended A-parameter
$\widehat G$
-orbit.) An extended A-parameter
![]() $\psi \in \Psi ^+(G)$
gives rise to an L-parameter:
$\psi \in \Psi ^+(G)$
gives rise to an L-parameter:
Write
![]() $\Psi (G)$
for the subset of
$\Psi (G)$
for the subset of
![]() $\Psi ^+(G)$
consisting of
$\Psi ^+(G)$
consisting of
![]() $\psi \in \Psi ^+(G)$
such that the image of
$\psi \in \Psi ^+(G)$
such that the image of
![]() $\psi ({\mathcal L}_F)$
in
$\psi ({\mathcal L}_F)$
in
![]() ${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
is bounded. (Such a property is
${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
is bounded. (Such a property is
![]() $\widehat G$
-invariant.) The set of
$\widehat G$
-invariant.) The set of
![]() $\tilde {\mathrm {Out}}_{2n}(G)$
-orbits in
$\tilde {\mathrm {Out}}_{2n}(G)$
-orbits in
![]() $\Psi ^+(G)$
(resp.
$\Psi ^+(G)$
(resp.
![]() $\Psi (G)$
) is denoted by
$\Psi (G)$
) is denoted by
![]() $\tilde {\Psi }^+(G)$
(resp.
$\tilde {\Psi }^+(G)$
(resp.
![]() $\tilde {\Psi }(G)$
). The group
$\tilde {\Psi }(G)$
). The group
![]() ${\mathcal L}_F \times {\mathrm {SU}}(2)$
admits the involution permuting the two
${\mathcal L}_F \times {\mathrm {SU}}(2)$
admits the involution permuting the two
![]() ${\mathrm {SU}}(2)$
-components (acting as the identity on
${\mathrm {SU}}(2)$
-components (acting as the identity on
![]() $W_F$
). This involution induces an involution
$W_F$
). This involution induces an involution
We say
![]() $\psi \in \tilde {\Psi }^+(G)$
is square-integrable if
$\psi \in \tilde {\Psi }^+(G)$
is square-integrable if
![]() $g\psi g^{-1}=\psi $
for at most finitely many elements
$g\psi g^{-1}=\psi $
for at most finitely many elements
![]() $g\in \widehat G$
. Then
$g\in \widehat G$
. Then
![]() $\psi $
lies in
$\psi $
lies in
![]() $\tilde {\Psi }(G)$
. To see this, let
$\tilde {\Psi }(G)$
. To see this, let
![]() $w\in W_F$
be a lift of (geometric) Frobenius. Then
$w\in W_F$
be a lift of (geometric) Frobenius. Then
![]() $\psi (w)^m$
centralizes the image of
$\psi (w)^m$
centralizes the image of
![]() $\psi $
for some
$\psi $
for some
![]() $m\in \mathbb Z_{\ge 1}$
as in [Reference Deligne19, proof of Lem. 8.4.3]. It follows that, replacing m with a suitable multiple,
$m\in \mathbb Z_{\ge 1}$
as in [Reference Deligne19, proof of Lem. 8.4.3]. It follows that, replacing m with a suitable multiple,
![]() $\psi (w)^m$
has trivial image in
$\psi (w)^m$
has trivial image in
![]() ${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
. Write
${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
. Write
![]() $I_F\subset W_F$
for the inertia subgroup. Since
$I_F\subset W_F$
for the inertia subgroup. Since
![]() $I_F\times {\mathrm {SU}}(2)\times {\mathrm {SU}}(2)\subset {\mathcal L}_F\times {\mathrm {SU}}(2)$
has already bounded image in
$I_F\times {\mathrm {SU}}(2)\times {\mathrm {SU}}(2)\subset {\mathcal L}_F\times {\mathrm {SU}}(2)$
has already bounded image in
![]() ${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
under
${\mathrm {SO}}_{2n}({\mathbb {C}})\rtimes \Gamma _{E/F}$
under
![]() $\psi $
, we see that
$\psi $
, we see that
![]() $\psi \in \Psi (G)$
. Denote by
$\psi \in \Psi (G)$
. Denote by
![]() $\Psi _2(G)$
the subset of
$\Psi _2(G)$
the subset of
![]() $\Psi (G)$
consisting of square-integrable members.
$\Psi (G)$
consisting of square-integrable members.
Define
![]() $\psi _{\mathrm {triv}} \colon {\mathcal L}_F \times {\mathrm {SU}}(2) \to {}^L G$
as follows. On
$\psi _{\mathrm {triv}} \colon {\mathcal L}_F \times {\mathrm {SU}}(2) \to {}^L G$
as follows. On
![]() ${\mathcal L}_F$
, it is the composite map
${\mathcal L}_F$
, it is the composite map
![]() ${\mathcal L}_F\twoheadrightarrow W_F \twoheadrightarrow \Gamma _{E/F}\subset {}^L G$
through the natural projections. On
${\mathcal L}_F\twoheadrightarrow W_F \twoheadrightarrow \Gamma _{E/F}\subset {}^L G$
through the natural projections. On
![]() ${\mathrm {SU}}(2)$
(outside
${\mathrm {SU}}(2)$
(outside
![]() ${\mathcal L}_F$
),
${\mathcal L}_F$
),
![]() $\psi _{\mathrm {triv}}$
is a principal embedding
$\psi _{\mathrm {triv}}$
is a principal embedding
![]() $i_{\mathrm {pri}} \colon {\mathrm {SU}}(2) \to \widehat G$
that is
$i_{\mathrm {pri}} \colon {\mathrm {SU}}(2) \to \widehat G$
that is
![]() $\theta ^{\circ }$
-invariant (i.e.,
$\theta ^{\circ }$
-invariant (i.e.,
![]() $i_{\mathrm {pri}}$
commutes with the L-action of
$i_{\mathrm {pri}}$
commutes with the L-action of
![]() $\Gamma _{E/F}$
on
$\Gamma _{E/F}$
on
![]() $\widehat G$
). (Such an
$\widehat G$
). (Such an
![]() $i_{\mathrm {pri}}$
into
$i_{\mathrm {pri}}$
into
![]() $\widehat G$
can be realized as the
$\widehat G$
can be realized as the
![]() ${\mathrm {SU}}(2)$
-representation
${\mathrm {SU}}(2)$
-representation
![]() ${\mathrm {Sym}}^{2n-2}\oplus \mathbf {1}$
into
${\mathrm {Sym}}^{2n-2}\oplus \mathbf {1}$
into
![]() ${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
, where the latter is identified with the centralizer of the element
${\mathrm {GL}}_{2n-1}\times {\mathrm {GL}}_1$
, where the latter is identified with the centralizer of the element
![]() $\vartheta ^{\circ }\in {\mathrm {GL}}_{2n}$
from §3. Write
$\vartheta ^{\circ }\in {\mathrm {GL}}_{2n}$
from §3. Write
![]() $\psi _{\mathrm {St}}:=\widehat \psi _{\mathrm {triv}}$
. Then
$\psi _{\mathrm {St}}:=\widehat \psi _{\mathrm {triv}}$
. Then
![]() $\psi _{\mathrm {triv}},\psi _{\mathrm {St}}\in \Psi (G)$
and they are
$\psi _{\mathrm {triv}},\psi _{\mathrm {St}}\in \Psi (G)$
and they are
![]() $\tilde {\mathrm {Out}}_{2n}(G)$
-stable.
$\tilde {\mathrm {Out}}_{2n}(G)$
-stable.
To every
![]() $\psi \in \tilde {\Psi }(G)$
, Arthur [Reference Arthur1, Thm. 1.5.1] assigned an A-packet
$\psi \in \tilde {\Psi }(G)$
, Arthur [Reference Arthur1, Thm. 1.5.1] assigned an A-packet
![]() $\tilde {\Pi }(\psi )$
, which is a certain finite multi-set consisting of
$\tilde {\Pi }(\psi )$
, which is a certain finite multi-set consisting of
![]() $\tilde {\mathrm {Out}}_{2n}(G)$
-orbits of irreducible unitary representations of
$\tilde {\mathrm {Out}}_{2n}(G)$
-orbits of irreducible unitary representations of
![]() $G(F)$
. Below loc. cit. he also defines
$G(F)$
. Below loc. cit. he also defines
![]() $\tilde {\Pi }(\psi )$
for
$\tilde {\Pi }(\psi )$
for
![]() $\psi \in \tilde {\Psi }^+(G)$
, consisting of
$\psi \in \tilde {\Psi }^+(G)$
, consisting of
![]() $\tilde {\mathrm {Out}}_{2n}(G)$
-orbits of parabolically induced representations of
$\tilde {\mathrm {Out}}_{2n}(G)$
-orbits of parabolically induced representations of
![]() $G(F)$
(which need not be irreducible or unitary).
$G(F)$
(which need not be irreducible or unitary).
By a globalization
![]() $(\dot E/\dot F,{{\mathfrak q}},\dot G)$
of
$(\dot E/\dot F,{{\mathfrak q}},\dot G)$
of
![]() $(E/F,G)$
as above, we mean an extension of number fields
$(E/F,G)$
as above, we mean an extension of number fields
![]() $\dot E/\dot F$
, a finite place
$\dot E/\dot F$
, a finite place
![]() ${{\mathfrak q}}$
, and a quasi-split form
${{\mathfrak q}}$
, and a quasi-split form
![]() $\dot G$
of the split
$\dot G$
of the split
![]() ${\mathrm {SO}}_{2n}$
over
${\mathrm {SO}}_{2n}$
over
![]() $\dot F$
such that
$\dot F$
such that
![]() $\dot E_{\mathfrak {q}}\simeq E$
,
$\dot E_{\mathfrak {q}}\simeq E$
,
![]() $\dot F_{\mathfrak {q}} \simeq F$
and
$\dot F_{\mathfrak {q}} \simeq F$
and
![]() $\dot G_{\mathfrak {q}} \simeq G$
. It is an elementary fact that such a globalization always exists. Recall that a (formal) global parameter
$\dot G_{\mathfrak {q}} \simeq G$
. It is an elementary fact that such a globalization always exists. Recall that a (formal) global parameter
![]() $\dot \psi \in \tilde {\Psi }(\dot G)$
gives rise to a parameter
$\dot \psi \in \tilde {\Psi }(\dot G)$
gives rise to a parameter
![]() $\dot \psi _v\in \tilde \Psi ^+(\dot G_{\dot F_v})$
and a packet
$\dot \psi _v\in \tilde \Psi ^+(\dot G_{\dot F_v})$
and a packet
![]() $\tilde \Pi (\dot \psi _v)$
at each place v of
$\tilde \Pi (\dot \psi _v)$
at each place v of
![]() $\dot F$
.
$\dot F$
.
Proposition B.1. Let
![]() $\psi \in \tilde \Psi ^+(G)$
. The following are true.
$\psi \in \tilde \Psi ^+(G)$
. The following are true.
-
(1)
 $\tilde {\Pi }(\psi _{\mathrm {triv}})=\{\mathbf {1}\}$
and
$\tilde {\Pi }(\psi _{\mathrm {triv}})=\{\mathbf {1}\}$
and
 $\tilde {\Pi }(\psi _{\mathrm {St}})=\{\mathrm {St}\}$
.
$\tilde {\Pi }(\psi _{\mathrm {St}})=\{\mathrm {St}\}$
. -
(2) Assume
 $\psi \in \tilde \Psi (G)$
. If
$\psi \in \tilde \Psi (G)$
. If
 $\mathbf {1}$
(resp.
$\mathbf {1}$
(resp.
 $\mathrm {St}$
) is a member of
$\mathrm {St}$
) is a member of
 $\tilde {\Pi }(\psi )$
, then
$\tilde {\Pi }(\psi )$
, then
 $\psi =\psi _{\mathrm {triv}}$
(resp.
$\psi =\psi _{\mathrm {triv}}$
(resp.
 $\psi =\psi _{\mathrm {St}}$
).
$\psi =\psi _{\mathrm {St}}$
). -
(3) Assume that
 $\psi =\dot \psi _{{\mathfrak q}}\in \tilde \Psi ^+(G)$
for global data
$\psi =\dot \psi _{{\mathfrak q}}\in \tilde \Psi ^+(G)$
for global data
 $(\dot E/\dot F,{{\mathfrak q}},\dot G)$
and
$(\dot E/\dot F,{{\mathfrak q}},\dot G)$
and
 $\dot \psi $
as above. If
$\dot \psi $
as above. If
 $\mathbf {1}$
(resp.
$\mathbf {1}$
(resp.
 $\mathrm {St}$
) is a subquotient of a member of
$\mathrm {St}$
) is a subquotient of a member of
 $\tilde {\Pi }(\psi )$
, then
$\tilde {\Pi }(\psi )$
, then
 $\psi =\psi _{\mathrm {triv}}$
(resp.
$\psi =\psi _{\mathrm {triv}}$
(resp.
 $\psi =\psi _{\mathrm {St}}$
).
$\psi =\psi _{\mathrm {St}}$
).
Remark B.2. We use (3) in the main text. Part (3) would be subsumed by (2) if the generalized Ramanujan conjecture for general linear groups was known, cf. proof of (3) below.
Proof. (1) According to [Reference Arthur1, Lem. 7.1.1] (and the discussion following it), the involution
![]() $\psi \mapsto \widehat \psi $
changes members of A-packets by the Aubert involution, which carries
$\psi \mapsto \widehat \psi $
changes members of A-packets by the Aubert involution, which carries
![]() $\mathbf {1}$
to
$\mathbf {1}$
to
![]() $\mathrm {St}$
and vice versa. So it suffices to treat the case of
$\mathrm {St}$
and vice versa. So it suffices to treat the case of
![]() $\psi =\psi _{\mathrm {triv}}$
.
$\psi =\psi _{\mathrm {triv}}$
.
We know that
![]() ${\mathcal S}_{\psi }=\{1\}$
and that the L-packet
${\mathcal S}_{\psi }=\{1\}$
and that the L-packet
![]() $\tilde {\Pi }(\phi _{\psi })$
embeds in
$\tilde {\Pi }(\phi _{\psi })$
embeds in
![]() $\tilde {\Pi }(\psi )$
. Hence,
$\tilde {\Pi }(\psi )$
. Hence,
![]() $\tilde {\Pi }(\psi )=\tilde {\Pi }(\phi _{\psi })$
and it is a singleton. Clearly,
$\tilde {\Pi }(\psi )=\tilde {\Pi }(\phi _{\psi })$
and it is a singleton. Clearly,
![]() $\phi _{\psi }$
is a spherical parameter in the sense of [Reference Arthur1, §6.1]. Hence,
$\phi _{\psi }$
is a spherical parameter in the sense of [Reference Arthur1, §6.1]. Hence,
![]() $\Pi (\phi _{\psi })$
contains the irreducible spherical representation corresponding to
$\Pi (\phi _{\psi })$
contains the irreducible spherical representation corresponding to
![]() $\phi _{\psi }$
via the spherical local Langlands correspondence recalled in loc. cit.
Footnote 13
$\phi _{\psi }$
via the spherical local Langlands correspondence recalled in loc. cit.
Footnote 13
Hence it boils down to observing that
![]() $\phi _{\psi _{\mathrm {triv}}}$
corresponds to
$\phi _{\psi _{\mathrm {triv}}}$
corresponds to
![]() $\mathbf {1}$
. (This is easy to see from the fact that
$\mathbf {1}$
. (This is easy to see from the fact that
![]() $\mathbf {1}$
is a subquotient of
$\mathbf {1}$
is a subquotient of
![]() $\mathrm {Ind}^G_B(\delta _B^{-1/2})$
.)
$\mathrm {Ind}^G_B(\delta _B^{-1/2})$
.)
(2)
![]() $\Rightarrow $
(3). Before proving (2), let us assume (2) and verify (3) for each
$\Rightarrow $
(3). Before proving (2), let us assume (2) and verify (3) for each
![]() $(E/F,G)$
. We fix a Borel subgroup B and a maximal torus T of G over F such that
$(E/F,G)$
. We fix a Borel subgroup B and a maximal torus T of G over F such that
![]() $T\subset B$
. Since
$T\subset B$
. Since
![]() $\psi $
comes from a global parameter,
$\psi $
comes from a global parameter,
![]() $\psi |_{{\mathcal L}_F}$
is constrained by what local components of cuspidal automorphic representations of general linear groups can be. Following the same observations as in [Reference Xu81, App. A], we can express
$\psi |_{{\mathcal L}_F}$
is constrained by what local components of cuspidal automorphic representations of general linear groups can be. Following the same observations as in [Reference Xu81, App. A], we can express
![]() $\psi $
concretely as follows:
$\psi $
concretely as follows:
 $$ \begin{align*}\psi = \psi_{G_-} \oplus \bigoplus_{i=1}^r ( |\cdot|^{a_i} \psi_i \oplus |\cdot|^{-a_i} \psi_i^{\vee}),\qquad 0<a_r<\cdots < a_1<1/2, \end{align*} $$
$$ \begin{align*}\psi = \psi_{G_-} \oplus \bigoplus_{i=1}^r ( |\cdot|^{a_i} \psi_i \oplus |\cdot|^{-a_i} \psi_i^{\vee}),\qquad 0<a_r<\cdots < a_1<1/2, \end{align*} $$
where
![]() $\psi _{G_-}\in \tilde {\Psi }({\mathrm {SO}}^{E/F}_{2n_-})$
and
$\psi _{G_-}\in \tilde {\Psi }({\mathrm {SO}}^{E/F}_{2n_-})$
and
![]() $\psi _i\in \Psi ({\mathrm {GL}}_{n_i})$
such that
$\psi _i\in \Psi ({\mathrm {GL}}_{n_i})$
such that
![]() $n_-+\sum _{i=1}^r n_i = n$
, and if we take
$n_-+\sum _{i=1}^r n_i = n$
, and if we take
 $$ \begin{align} M={\mathrm{SO}}^{E/F}_{2n_-}\times \prod_{i=1}^r {\mathrm{GL}}_{n_i} \end{align} $$
$$ \begin{align} M={\mathrm{SO}}^{E/F}_{2n_-}\times \prod_{i=1}^r {\mathrm{GL}}_{n_i} \end{align} $$
to be a Levi subgroup of a standard parabolic subgroup P, we have
(Namely,
![]() $\psi _M$
is not just an “extended” parameter of M.) Actually in loc. cit., a weaker inequality
$\psi _M$
is not just an “extended” parameter of M.) Actually in loc. cit., a weaker inequality
![]() $a_r\le \cdots \le a_1$
holds for the exponents, but this is because he wants
$a_r\le \cdots \le a_1$
holds for the exponents, but this is because he wants
![]() $\psi _i$
to be simple parameters. We only require
$\psi _i$
to be simple parameters. We only require
![]() $\psi _i$
to be bounded parameters, so the simple parameters with the same exponent will go into a single
$\psi _i$
to be bounded parameters, so the simple parameters with the same exponent will go into a single
![]() $\psi _i$
in our case.
$\psi _i$
in our case.
Our goal is to show that
![]() $M=G$
. Indeed, it would immediately imply that
$M=G$
. Indeed, it would immediately imply that
![]() $\psi $
belongs to
$\psi $
belongs to
![]() $\tilde {\Psi }(G)$
(not just
$\tilde {\Psi }(G)$
(not just
![]() $\tilde {\Psi }^+(G)$
) so we can conclude by (2). If
$\tilde {\Psi }^+(G)$
) so we can conclude by (2). If
![]() $M\neq G$
(i.e., if
$M\neq G$
(i.e., if
![]() $r\ge 1$
), we will show a contradiction.
$r\ge 1$
), we will show a contradiction.
By construction (see [Reference Arthur1, §1.5]), the packet
![]() $\tilde {\Pi }(\psi )$
consists of (
$\tilde {\Pi }(\psi )$
consists of (
![]() $\mathrm {Out}_{2n}(G)$
-orbits of) the normalized induced representations
$\mathrm {Out}_{2n}(G)$
-orbits of) the normalized induced representations
for
![]() $\sigma $
in the A-packet
$\sigma $
in the A-packet
![]() $\Pi (\psi _M)$
for M, where the character
$\Pi (\psi _M)$
for M, where the character
![]() $\chi :M(F)\rightarrow {\mathbb {C}}^{\times }$
is defined to be trivial on
$\chi :M(F)\rightarrow {\mathbb {C}}^{\times }$
is defined to be trivial on
![]() ${\mathrm {SO}}^{E/F}_{2n_-}(F)$
and
${\mathrm {SO}}^{E/F}_{2n_-}(F)$
and
![]() $|\det |^{a_i}$
on
$|\det |^{a_i}$
on
![]() ${\mathrm {GL}}_{n_i}(F)$
.
${\mathrm {GL}}_{n_i}(F)$
.
Now suppose that
![]() $\mathbf {1}$
or
$\mathbf {1}$
or
![]() $\mathrm {St}$
is a subquotient of a member of
$\mathrm {St}$
is a subquotient of a member of
![]() $\tilde {\Pi }(\psi )$
. Then for some
$\tilde {\Pi }(\psi )$
. Then for some
![]() $\sigma \in \Pi (\psi _M)$
, the irreducible subquotients of (B.2) have the supercuspidal support
$\sigma \in \Pi (\psi _M)$
, the irreducible subquotients of (B.2) have the supercuspidal support
![]() $(T,\delta _B^{-1/2})$
, which is the supercuspidal support of both
$(T,\delta _B^{-1/2})$
, which is the supercuspidal support of both
![]() $\mathbf {1}$
and
$\mathbf {1}$
and
![]() $\mathrm {St}$
(up to the Weyl group action). Write
$\mathrm {St}$
(up to the Weyl group action). Write
![]() $\sigma =\sigma _-\otimes (\otimes _{i=1}^r \sigma _i)$
according to (B.1). Then
$\sigma =\sigma _-\otimes (\otimes _{i=1}^r \sigma _i)$
according to (B.1). Then
![]() $\sigma $
is a subquotient of a principal series representation. The unitary representation
$\sigma $
is a subquotient of a principal series representation. The unitary representation
![]() $\sigma _i$
of
$\sigma _i$
of
![]() ${\mathrm {GL}}_{n_i}(F)$
corresponds to an A-parameter in
${\mathrm {GL}}_{n_i}(F)$
corresponds to an A-parameter in
![]() $\Psi ({\mathrm {GL}}_{n_i})$
, so it has the form
$\Psi ({\mathrm {GL}}_{n_i})$
, so it has the form
where
![]() $\chi _{i,j}$
is a unitary character, and
$\chi _{i,j}$
is a unitary character, and
![]() $\boxplus $
denotes the operation corresponding to the direct sum under the local Langlands correspondence. If we write
$\boxplus $
denotes the operation corresponding to the direct sum under the local Langlands correspondence. If we write
![]() $T={\mathrm {SO}}^{E/F}_{2n_{0}}\times \prod _{k=1}^{n-n_0} {\mathrm {GL}}_1$
(if
$T={\mathrm {SO}}^{E/F}_{2n_{0}}\times \prod _{k=1}^{n-n_0} {\mathrm {GL}}_1$
(if
![]() $E=F$
, then
$E=F$
, then
![]() $n_0=0$
; otherwise
$n_0=0$
; otherwise
![]() $n_0=1$
), then accordingly (up to the Weyl action)
$n_0=1$
), then accordingly (up to the Weyl action)
However, (B.3) tells us that the supercuspidal support of (B.2) is represented by a character
of
![]() $T(F)$
such that each
$T(F)$
such that each
![]() $\chi _{i,j}|\cdot |^{e_{i,j}+a_i}$
appears in the multi-set
$\chi _{i,j}|\cdot |^{e_{i,j}+a_i}$
appears in the multi-set
![]() $\{\varsigma _k\}$
. Comparing the two supports, we must have that
$\{\varsigma _k\}$
. Comparing the two supports, we must have that
![]() $e_{i,j}+a_i\in \tfrac {1}{2}\mathbb Z$
since the half-integrality of exponents is invariant under the Weyl action. However, this is impossible since
$e_{i,j}+a_i\in \tfrac {1}{2}\mathbb Z$
since the half-integrality of exponents is invariant under the Weyl action. However, this is impossible since
![]() $e_{i,j}\in \tfrac {1}{2}\mathbb Z$
and
$e_{i,j}\in \tfrac {1}{2}\mathbb Z$
and
![]() $0<a_i<\tfrac {1}{2}$
(and the index set for
$0<a_i<\tfrac {1}{2}$
(and the index set for
![]() $i,j$
is nonempty). This proves that
$i,j$
is nonempty). This proves that
![]() $M=G$
as desired.
$M=G$
as desired.
(2) As in the proof of (1), it is enough to consider the case
![]() $\mathbf {1}\in \tilde {\Pi }(\psi )$
by Aubert involution. We deduce
$\mathbf {1}\in \tilde {\Pi }(\psi )$
by Aubert involution. We deduce
![]() $\psi =\psi _{\mathrm {triv}}$
by dividing into two cases.
$\psi =\psi _{\mathrm {triv}}$
by dividing into two cases.
Case 1: when G is unramified. Let
![]() $s_{\psi }\in \widehat G$
denote the image of
$s_{\psi }\in \widehat G$
denote the image of
![]() $-1\in {\mathrm {SU}}(2)$
(outside
$-1\in {\mathrm {SU}}(2)$
(outside
![]() ${\mathcal L}_F$
) under
${\mathcal L}_F$
) under
![]() $\psi $
. Let us show that
$\psi $
. Let us show that
![]() $\psi |_{W_F}$
is unramified, using the fact that
$\psi |_{W_F}$
is unramified, using the fact that
![]() $\tilde {\Pi }(\psi )$
contains an unramified representation, namely,
$\tilde {\Pi }(\psi )$
contains an unramified representation, namely,
![]() $\mathbf {1}$
. In fact, we induct on rank for unramified even special orthogonal groups to prove the unique existence of an unramified representation in
$\mathbf {1}$
. In fact, we induct on rank for unramified even special orthogonal groups to prove the unique existence of an unramified representation in
![]() $\tilde {\Pi }(\psi )$
, where we allow more general
$\tilde {\Pi }(\psi )$
, where we allow more general
![]() $\psi \in \tilde {\Psi }(G)$
, for the moment, which are unramified on
$\psi \in \tilde {\Psi }(G)$
, for the moment, which are unramified on
![]() $W_F$
. The base case of induction is obvious. Next, we recall the character identities from [Reference Arthur1, Thm. 2.2.1], which have the form (cf. the second and last displayed formulas in the proof of [Reference Marshall and Shin59, Lem. 5.4] for the analogues for unitary groups)
$W_F$
. The base case of induction is obvious. Next, we recall the character identities from [Reference Arthur1, Thm. 2.2.1], which have the form (cf. the second and last displayed formulas in the proof of [Reference Marshall and Shin59, Lem. 5.4] for the analogues for unitary groups)
 $$ \begin{align} \sum_{\sigma\in \tilde{\Pi}(\psi)} 1_K(\sigma)&= \tilde{1}_{K^{2n}}(\tilde{\pi}_{\psi^{2n}}),\qquad \mbox{if}~ s_{\psi}\in Z(\widehat G), \end{align} $$
$$ \begin{align} \sum_{\sigma\in \tilde{\Pi}(\psi)} 1_K(\sigma)&= \tilde{1}_{K^{2n}}(\tilde{\pi}_{\psi^{2n}}),\qquad \mbox{if}~ s_{\psi}\in Z(\widehat G), \end{align} $$
 $$ \begin{align} \sum_{\sigma\in \tilde{\Pi}(\psi)} 1_K(\sigma) &= 1_{K'}(\psi'),\qquad \mbox{if}~ s_{\psi}\notin Z(\widehat G), \end{align} $$
$$ \begin{align} \sum_{\sigma\in \tilde{\Pi}(\psi)} 1_K(\sigma) &= 1_{K'}(\psi'),\qquad \mbox{if}~ s_{\psi}\notin Z(\widehat G), \end{align} $$
where the setup and notation are as in [Reference Arthur1]. We partly explain the notation.
-
•
 $\psi ^{2n}$
is the A-parameter for
$\psi ^{2n}$
is the A-parameter for
 ${\mathrm {GL}}_{2n}$
obtained from
${\mathrm {GL}}_{2n}$
obtained from
 $\psi $
via the standard embedding.
$\psi $
via the standard embedding. -
•
 $\tilde {\pi }_{\psi ^{2n}}$
is the unique representation of
$\tilde {\pi }_{\psi ^{2n}}$
is the unique representation of
 ${\mathrm {GL}}_{2n}(F)$
in the A-packet of
${\mathrm {GL}}_{2n}(F)$
in the A-packet of
 $\psi ^{2n}$
.
$\psi ^{2n}$
. -
• When
 $s_{\psi }\notin Z(\widehat G)$
, we can find an unramified endoscopic group
$s_{\psi }\notin Z(\widehat G)$
, we can find an unramified endoscopic group
 $G'$
such that
$G'$
such that
 $(G',s_{\psi })$
is part of an elliptic endoscopic datum for G. (In particular,
$(G',s_{\psi })$
is part of an elliptic endoscopic datum for G. (In particular,
 $\widehat G'$
is a connected centralizer of
$\widehat G'$
is a connected centralizer of
 $s_{\psi }$
in
$s_{\psi }$
in
 $\widehat G$
.) Then
$\widehat G$
.) Then
 $G'$
is a product of two even special orthogonal groups [Reference Arthur1, p.14];
$G'$
is a product of two even special orthogonal groups [Reference Arthur1, p.14];
 $\psi '$
is a parameter on
$\psi '$
is a parameter on
 $G'$
giving rise to
$G'$
giving rise to
 $\psi $
.
$\psi $
. -
•
 $K^{2n}$
, K,
$K^{2n}$
, K,
 $K'$
are hyperspecial subgroups of
$K'$
are hyperspecial subgroups of
 ${\mathrm {GL}}_{2n}(F)$
,
${\mathrm {GL}}_{2n}(F)$
,
 $G(F)$
,
$G(F)$
,
 $G'(F)$
, respectively.
$G'(F)$
, respectively. -
•
 $\tilde {1}_{K^{2n}}(\tilde {\pi }_{\psi ^{2n}})$
is a twisted trace.
$\tilde {1}_{K^{2n}}(\tilde {\pi }_{\psi ^{2n}})$
is a twisted trace.
The existence of an unramified member in
![]() $\tilde {\Pi }(\psi )$
tells us that the left-hand side is nonzero. The resulting nonvanishing of the right-hand side implies
$\tilde {\Pi }(\psi )$
tells us that the left-hand side is nonzero. The resulting nonvanishing of the right-hand side implies
![]() $\psi |_{W_F}$
is unramified: if
$\psi |_{W_F}$
is unramified: if
![]() $s_{\psi }\in Z(\widehat G)$
, then
$s_{\psi }\in Z(\widehat G)$
, then
![]() $\tilde {\pi }_{\psi ^{2n}}$
is unramified from (B.4) so this follows; if
$\tilde {\pi }_{\psi ^{2n}}$
is unramified from (B.4) so this follows; if
![]() $s_{\psi }\notin Z(\widehat G)$
, we conclude by induction via (B.5).
$s_{\psi }\notin Z(\widehat G)$
, we conclude by induction via (B.5).
We have shown
![]() $\psi |_{W_F}$
to be unramified. Next, we observe that
$\psi |_{W_F}$
to be unramified. Next, we observe that
![]() $\tilde {\Pi }(\psi )$
contains a unique unramified representation by a similar induction. If
$\tilde {\Pi }(\psi )$
contains a unique unramified representation by a similar induction. If
![]() $s_{\psi }\in Z(\widehat G)$
, then this is true because the right-hand side of (B.4) is
$s_{\psi }\in Z(\widehat G)$
, then this is true because the right-hand side of (B.4) is
![]() $1$
in the normalization of loc. cit. If
$1$
in the normalization of loc. cit. If
![]() $s_{\psi }\notin Z(\widehat G)$
, this follows since the right-hand side of (B.5) is equal to
$s_{\psi }\notin Z(\widehat G)$
, this follows since the right-hand side of (B.5) is equal to
![]() $1$
by induction hypothesis.
$1$
by induction hypothesis.
As in the proof of (1), we have the embedding
![]() $\tilde {\Pi }(\phi _{\psi })\hookrightarrow \tilde {\Pi }(\psi )$
. Since
$\tilde {\Pi }(\phi _{\psi })\hookrightarrow \tilde {\Pi }(\psi )$
. Since
![]() $\phi _{\psi }$
is unramified,
$\phi _{\psi }$
is unramified,
![]() $\tilde {\Pi }(\phi _{\psi })$
contains an unramified representation. Now we appeal to the special property that
$\tilde {\Pi }(\phi _{\psi })$
contains an unramified representation. Now we appeal to the special property that
![]() $\mathbf {1}\in \tilde {\Pi }(\psi )$
. By the uniqueness shown above,
$\mathbf {1}\in \tilde {\Pi }(\psi )$
. By the uniqueness shown above,
![]() $\mathbf {1}\in \tilde {\Pi }(\psi )$
belongs to
$\mathbf {1}\in \tilde {\Pi }(\psi )$
belongs to
![]() $\tilde {\Pi }(\phi _{\psi })$
. Therefore,
$\tilde {\Pi }(\phi _{\psi })$
. Therefore,
![]() $\phi _{\psi }$
is the (unramified) L-parameter of
$\phi _{\psi }$
is the (unramified) L-parameter of
![]() $\mathbf {1}$
. It follows that
$\mathbf {1}$
. It follows that
![]() $\psi =\psi _{\mathrm {triv}}$
.
$\psi =\psi _{\mathrm {triv}}$
.
Case 2: when G is ramified. Although it might be possible to give a local proof, our strategy is to make use of Case 1 via globalization. Our first claim is that
![]() $\psi \in \tilde {\Psi }_2(G)$
if
$\psi \in \tilde {\Psi }_2(G)$
if
![]() $\mathbf {1}\in \tilde {\Pi }(\psi )$
. If the claim was false, then there exists a proper Levi subgroup M of G such that
$\mathbf {1}\in \tilde {\Pi }(\psi )$
. If the claim was false, then there exists a proper Levi subgroup M of G such that
![]() $\psi $
is the image of some
$\psi $
is the image of some
![]() $\psi _M\in \tilde {\Psi }_2(M)$
. According to Arthur’s construction of
$\psi _M\in \tilde {\Psi }_2(M)$
. According to Arthur’s construction of
![]() $\tilde {\Pi }(\psi )$
(see [Reference Arthur1, Prop. 2.4.3]),
$\tilde {\Pi }(\psi )$
(see [Reference Arthur1, Prop. 2.4.3]),
![]() $\mathbf {1}$
(as well as the other members of
$\mathbf {1}$
(as well as the other members of
![]() $\tilde {\Pi }(G)$
) appears as a subquotient of a parabolic induction
$\tilde {\Pi }(G)$
) appears as a subquotient of a parabolic induction
![]() $\mathrm {Ind}_P^G(\sigma )$
, where P is a parabolic subgroup of G with Levi factor M, and
$\mathrm {Ind}_P^G(\sigma )$
, where P is a parabolic subgroup of G with Levi factor M, and
![]() $\sigma \in \tilde {\Pi }(\psi _M)$
. Since
$\sigma \in \tilde {\Pi }(\psi _M)$
. Since
![]() $\sigma $
is unitary,
$\sigma $
is unitary,
![]() $\mathrm {Ind}_P^G(\sigma )$
is also unitary and thus semisimple. From this and Frobenius reciprocity,
$\mathrm {Ind}_P^G(\sigma )$
is also unitary and thus semisimple. From this and Frobenius reciprocity,
where
![]() $\mathrm {Jac}^G_P$
denotes the normalized Jacquet module with respect to P. Since
$\mathrm {Jac}^G_P$
denotes the normalized Jacquet module with respect to P. Since
![]() $\mathrm {Jac}^G_P \mathbf {1}=\delta _P^{-1/2}$
is a non-unitary character, this is a contradiction. The claim is proved.
$\mathrm {Jac}^G_P \mathbf {1}=\delta _P^{-1/2}$
is a non-unitary character, this is a contradiction. The claim is proved.
As
![]() $\psi \in \tilde {\Psi }_2(G)$
, we may mimic [Reference Arthur1, Prop. 7.2.1] to globalize
$\psi \in \tilde {\Psi }_2(G)$
, we may mimic [Reference Arthur1, Prop. 7.2.1] to globalize
![]() $(E/F,G,\psi )$
to
$(E/F,G,\psi )$
to
![]() $(\dot E/\dot F,\dot G,\dot \psi )$
with
$(\dot E/\dot F,\dot G,\dot \psi )$
with
![]() $\dot \psi \in \tilde {\Psi }_2(\dot G)$
such that the latter triple specializes to
$\dot \psi \in \tilde {\Psi }_2(\dot G)$
such that the latter triple specializes to
![]() $(E/F,G,\psi )$
at
$(E/F,G,\psi )$
at
![]() ${\mathfrak q}$
, and
${\mathfrak q}$
, and
![]() ${\mathcal S}_{\dot \psi }\stackrel {\sim }{\to }{\mathcal S}_{\psi }$
. We may further arrange (possibly by choosing a new globalization) that there exists another prime
${\mathcal S}_{\dot \psi }\stackrel {\sim }{\to }{\mathcal S}_{\psi }$
. We may further arrange (possibly by choosing a new globalization) that there exists another prime
![]() ${\mathfrak q}'\neq {\mathfrak q}$
such that
${\mathfrak q}'\neq {\mathfrak q}$
such that
![]() $(\dot E/\dot F,\dot G,\dot \psi )$
specializes to
$(\dot E/\dot F,\dot G,\dot \psi )$
specializes to
![]() $(E/F,G,\psi )$
at
$(E/F,G,\psi )$
at
![]() ${\mathfrak q}'$
as well. Since
${\mathfrak q}'$
as well. Since
![]() $\textbf {1}\in \tilde {\Pi }(\psi )=\tilde {\Pi }(\dot \psi _{\mathfrak {q}})$
, we can find a discrete automorphic representation
$\textbf {1}\in \tilde {\Pi }(\psi )=\tilde {\Pi }(\dot \psi _{\mathfrak {q}})$
, we can find a discrete automorphic representation
![]() $\dot \pi $
such that
$\dot \pi $
such that
![]() $\dot \pi _{\mathfrak {q}}\simeq \textbf {1}$
by Arthur’s multiplicity formula [Reference Arthur1, Thm. 1.5.2]. (Let
$\dot \pi _{\mathfrak {q}}\simeq \textbf {1}$
by Arthur’s multiplicity formula [Reference Arthur1, Thm. 1.5.2]. (Let
![]() $\chi :{\mathcal S}_{\psi }\rightarrow {\mathbb {C}}^{\times }$
denote the character corresponding to
$\chi :{\mathcal S}_{\psi }\rightarrow {\mathbb {C}}^{\times }$
denote the character corresponding to
![]() $\textbf {1}$
in [Reference Arthur1, Thm. 1.5.1]. We can find
$\textbf {1}$
in [Reference Arthur1, Thm. 1.5.1]. We can find
![]() $\dot \pi \in \tilde {\Pi }_{\dot \psi }$
such that
$\dot \pi \in \tilde {\Pi }_{\dot \psi }$
such that
![]() $\dot \pi _{\mathfrak {q}}=\textbf {1}$
,
$\dot \pi _{\mathfrak {q}}=\textbf {1}$
,
![]() $\dot \pi _{v}$
corresponds to the trivial character of
$\dot \pi _{v}$
corresponds to the trivial character of
![]() ${\mathcal S}_{\dot \psi }$
at
${\mathcal S}_{\dot \psi }$
at
![]() $v\neq {\mathfrak q},{\mathfrak q}'$
, and
$v\neq {\mathfrak q},{\mathfrak q}'$
, and
![]() $\dot \pi _{{\mathfrak q}'}$
corresponds to
$\dot \pi _{{\mathfrak q}'}$
corresponds to
![]() $\epsilon _{\dot \psi }\chi ^{-1}$
. Then
$\epsilon _{\dot \psi }\chi ^{-1}$
. Then
![]() $\dot \pi \in \tilde {\Pi }_{\dot \psi }(\epsilon _{\dot \psi })$
by the choices.) As
$\dot \pi \in \tilde {\Pi }_{\dot \psi }(\epsilon _{\dot \psi })$
by the choices.) As
![]() $\dot \pi _{\mathfrak {q}}=\textbf {1}$
, it follows from [Reference Kim, Shin and Templier41, Lem 6.2] that
$\dot \pi _{\mathfrak {q}}=\textbf {1}$
, it follows from [Reference Kim, Shin and Templier41, Lem 6.2] that
![]() $\dot \pi $
is one-dimensional (up to outer automorphism).
$\dot \pi $
is one-dimensional (up to outer automorphism).
Then
![]() $\dot \pi _v$
is trivial on the image of
$\dot \pi _v$
is trivial on the image of
![]() $\mathrm {Spin}^{E/F}_{2n}(F_v)$
by [Reference Kret and Shin49, §2.3] for each finite place v. By bounding the Galois cohomology of
$\mathrm {Spin}^{E/F}_{2n}(F_v)$
by [Reference Kret and Shin49, §2.3] for each finite place v. By bounding the Galois cohomology of
![]() $\mu _2=\ker (\mathrm {Spin}^{E/F}_{2n}\rightarrow {\mathrm {SO}}^{E/F}_{2n})$
uniformly across all finite places, we see that
$\mu _2=\ker (\mathrm {Spin}^{E/F}_{2n}\rightarrow {\mathrm {SO}}^{E/F}_{2n})$
uniformly across all finite places, we see that
![]() $\dot \pi $
is a finite order character. This implies that there exists a finite prime
$\dot \pi $
is a finite order character. This implies that there exists a finite prime
![]() $\mathfrak {p}\neq {\mathfrak q},{\mathfrak q}'$
such that
$\mathfrak {p}\neq {\mathfrak q},{\mathfrak q}'$
such that
![]() $\dot G$
is unramified at
$\dot G$
is unramified at
![]() $\mathfrak {p}$
and that
$\mathfrak {p}$
and that
![]() $\dot \pi _{\mathfrak {p}}=\mathbf {1}$
. Hence,
$\dot \pi _{\mathfrak {p}}=\mathbf {1}$
. Hence,
![]() $\dot \psi _{\mathfrak {p}}$
is determined by part (3); in particular,
$\dot \psi _{\mathfrak {p}}$
is determined by part (3); in particular,
![]() $\dot \psi _{\mathfrak {p}}|_{{\mathrm {SU}}(2)}$
(outside
$\dot \psi _{\mathfrak {p}}|_{{\mathrm {SU}}(2)}$
(outside
![]() ${\mathcal L}_F$
) is principal. (Part (3) is applicable to
${\mathcal L}_F$
) is principal. (Part (3) is applicable to
![]() $\dot \psi _{\mathfrak {p}}$
thanks to Case 1 above combined with our proof of (2)
$\dot \psi _{\mathfrak {p}}$
thanks to Case 1 above combined with our proof of (2)
![]() $\Rightarrow $
(3) for unramified groups.) Thus, the
$\Rightarrow $
(3) for unramified groups.) Thus, the
![]() ${\mathrm {SU}}(2)$
-part of
${\mathrm {SU}}(2)$
-part of
![]() $\dot \psi $
is
$\dot \psi $
is
![]() ${\mathrm {Sym}}^{2n-2}\oplus \textbf {1}$
, and the same is true for
${\mathrm {Sym}}^{2n-2}\oplus \textbf {1}$
, and the same is true for
![]() $\psi =\dot \psi _{\mathfrak p}$
. Therefore,
$\psi =\dot \psi _{\mathfrak p}$
. Therefore,
for quadratic characters
![]() $\chi _1,\chi _2:W_F\rightarrow \{\pm 1\}$
. This tells us that
$\chi _1,\chi _2:W_F\rightarrow \{\pm 1\}$
. This tells us that
![]() ${\mathcal S}_{\psi }=\{1\}$
. As the dual parameter is tempered, we see, using compatibility with the Aubert involution, that
${\mathcal S}_{\psi }=\{1\}$
. As the dual parameter is tempered, we see, using compatibility with the Aubert involution, that
![]() $\tilde {\Pi }(\psi )$
is a singleton and coincides with
$\tilde {\Pi }(\psi )$
is a singleton and coincides with
![]() $\tilde {\Pi }(\phi _{\psi })$
. The latter is the Langlands quotient of the principal series arising from
$\tilde {\Pi }(\phi _{\psi })$
. The latter is the Langlands quotient of the principal series arising from
![]() $\phi _{\psi }$
(which factors through the L-group of a minimal Levi). However,
$\phi _{\psi }$
(which factors through the L-group of a minimal Levi). However,
![]() $\textbf {1}\in \tilde {\Pi }(\psi )$
by hypothesis. We conclude that
$\textbf {1}\in \tilde {\Pi }(\psi )$
by hypothesis. We conclude that
![]() $\psi =\psi _{\mathrm {triv}}$
.
$\psi =\psi _{\mathrm {triv}}$
.
Acknowledgements
We are very grateful for an anonymous referee for his or her comments and suggestions. SWS is partially supported by NSF grant DMS-1802039 and NSF RTG grant DMS-1646385. AK is partially supported by an NWO VENI and an NWO VIDI grant.
Competing interests
The authors have no competing interest to declare.