In the present note, which is introductory to the following paper, closed expressions, suitable for computational purposes, are found for the sums of the series

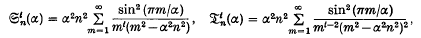
where α > 1, t = 1, 2, 3, …, and n is a positive integer. In each case a recurrent relation is found giving the values of 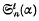and 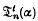for t > 2 in terms of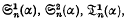 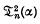and the series Θκ(α) (κ = 1, 2, …, t), where

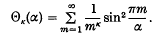
When κ is even the last series is expressed in closed form in terms of the Bernoullian polynomial φκ(l/α) and, when κ is odd and α is rational, a closed form is found involving the polygamma function Ψ(κ)(z), where 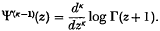The general expressions for 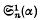and 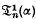involve Ψ(z) and Ψ′(z) when α is rational, but for special values of α they reduce to a form independent of the Ψ-function. 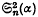and 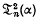are independent of n and are expressible as simple rational functions of α.