We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
Wilson's cloud method, provides a means of measuring the ranges of β-rays which is free from any uncertainties arising from the scattering of the rays, and for this reason it is an invaluable method for obtaining the true rate of loss of energy of β-rays as they traverse matter. Thetrue rate of loss of energy or ‘stopping power’ is defined as the quantity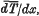 
, where 
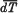is the mean energy lost by β-rays of energy T in travelling a distance dx measured along their paths. The cloud method of course enables one to observe only the total ranges of β-particles, and in deducing the stopping power from the mean range it is necessary to bear in mind that owing to ‘straggling,’ which in the case of β-rays is large, the differential coefficient 
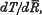, where 
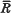is the mean range of particles of energy T, is not exactly the same as the stopping power 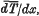. 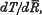is however the quantity which the cloud method enables us to observe. It is the purpose of this note to consider the exact relation between these two quantities so that the information provided by the cloud method may be rigorously interpreted.
* This can be done without increasing the probability of ‘double’ collisions. For if n be the total number of particles the average number which suffer single collisions, in which the energy lost lies between Q and Q + dQ, is ø (Q) dQdx × n and is proportional to ndx. The number which suffer double collisions is
and is proportional to n (dx)2. It follows that by choosing dx sufficiently small the former may be made as large as we please without affecting the latter.
* If, in observing R, ‘tracks’ with ‘branches’ greater than a certain length are omitted then the effective value of M is less than T and the correction is correspondingly less.
