Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kataoka, Norisato
2001.
Note on distribution of units of real quadratic number fields.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 77,
Issue. 10,
Kitaoka, Yoshiyuki
2001.
Distribution of Units of a Cubic Field with Negative Discriminant.
Journal of Number Theory,
Vol. 91,
Issue. 2,
p.
318.
Ichimura, Humio
2001.
Note on the ring of integers of a Kummer extension of prime degree. IV.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 77,
Issue. 6,
Chen, Yen-Mei J
2002.
On Primitive Roots of One-Dimensional Tori.
Journal of Number Theory,
Vol. 93,
Issue. 1,
p.
23.
Kataoka, Norisato
2003.
The distribution of prime ideals in a real quadratic field with units having a given index in the residue class field.
Journal of Number Theory,
Vol. 101,
Issue. 2,
p.
349.
Kitaoka, Yoshiyuki
2004.
Distribution of units of algebraic number fields with only one fundamental unit.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 80,
Issue. 6,
Kitaoka, Yoshiyuki
2004.
Galois Theory and Modular Forms.
Vol. 11,
Issue. ,
p.
287.
Kitaoka, Yoshiyuki
2004.
Ray class field of prime conductor of a real quadratic field.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 80,
Issue. 6,
Chen, Yen-Mei J.
and
Yu, Jing
2005.
On primitive points of elliptic curves with complex multiplication.
Journal of Number Theory,
Vol. 114,
Issue. 1,
p.
66.
KITAOKA, Yoshiyuki
2006.
Distribution of units of a cubic abelian field modulo prime numbers.
Journal of the Mathematical Society of Japan,
Vol. 58,
Issue. 2,
Breuer, Florian
2021.
Multiplicative orders of Gauss periods and the arithmetic of real quadratic fields.
Finite Fields and Their Applications,
Vol. 73,
Issue. ,
p.
101848.




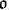
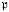 ) the subgroup represented by
) the subgroup represented by 