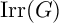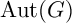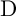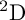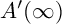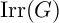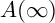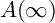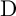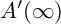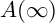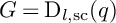1 Introduction
After the classification of finite simple groups and with the knowledge on their representations having also greatly expanded in the last decades, it seems overdue to determine for each quasisimple group G the action of its outer automorphism group
![]() $\mathrm {Out}(G)$
on its set of irreducible (complex) characters
$\mathrm {Out}(G)$
on its set of irreducible (complex) characters
![]() $\mathrm {Irr}(G)$
. This is important in order to use our results on representations of simple groups to get theorems about arbitrary finite groups. A crucial example is the McKay conjecture asserting
$\mathrm {Irr}(G)$
. This is important in order to use our results on representations of simple groups to get theorems about arbitrary finite groups. A crucial example is the McKay conjecture asserting
for p a prime, X a finite group, P one of its Sylow p-subgroups, and
![]() $\mathrm {Irr}_{p'}(X)$
the set of irreducible characters of X of degree prime to p. It is fairly clear that once this is solved for a normal subgroup Y of X, the next step to deduce something for X is to determine the action of X on at least
$\mathrm {Irr}_{p'}(X)$
the set of irreducible characters of X of degree prime to p. It is fairly clear that once this is solved for a normal subgroup Y of X, the next step to deduce something for X is to determine the action of X on at least
![]() $\mathrm {Irr}_{p'}(Y)$
. The McKay conjecture has been reduced to a so-called inductive McKay condition about quasisimple groups by Isaacs–Malle–Navarro [Reference Isaacs, Malle and NavarroIMN], and the first requirement is an Out
$\mathrm {Irr}_{p'}(Y)$
. The McKay conjecture has been reduced to a so-called inductive McKay condition about quasisimple groups by Isaacs–Malle–Navarro [Reference Isaacs, Malle and NavarroIMN], and the first requirement is an Out
![]() $(X)$
-equivariant bijection realizing McKay’s equality. Knowing the action of
$(X)$
-equivariant bijection realizing McKay’s equality. Knowing the action of
![]() $\mathrm {Out}(G)$
on
$\mathrm {Out}(G)$
on
![]() $\mathrm {Irr}(G)$
for all quasisimple groups G would also have applications to other conjectures about characters with similar reductions such as the Alperin–McKay conjecture or the Dade conjecture (see [Reference SpäthS5], [Reference SpäthS6]) or even conjectures about modular characters (see [Reference Navarro and TiepNT11]) through the unitriangularity of decomposition matrices (see [Reference Brunat, Dudas and TaylorBDT]).
$\mathrm {Irr}(G)$
for all quasisimple groups G would also have applications to other conjectures about characters with similar reductions such as the Alperin–McKay conjecture or the Dade conjecture (see [Reference SpäthS5], [Reference SpäthS6]) or even conjectures about modular characters (see [Reference Navarro and TiepNT11]) through the unitriangularity of decomposition matrices (see [Reference Brunat, Dudas and TaylorBDT]).
For alternating and sporadic groups, the action of
![]() $\mathrm {Out}(G)$
on
$\mathrm {Out}(G)$
on
![]() $\mathrm {Irr}(G)$
is easy to deduce from the available description of
$\mathrm {Irr}(G)$
is easy to deduce from the available description of
![]() $\mathrm {Irr}(G)$
. When G is the universal covering group of a finite simple group of Lie type, this is a question in [Reference Geck and MalleGM, §A.9]. Previous research on the subject has left open only the case of groups of type
$\mathrm {Irr}(G)$
. When G is the universal covering group of a finite simple group of Lie type, this is a question in [Reference Geck and MalleGM, §A.9]. Previous research on the subject has left open only the case of groups of type
![]() $\mathrm {D}$
(see [Reference Cabanes and SpäthCS4, 2.5]). The present paper is the first part of a solution to that problem. A second part [Reference SpäthS7] will finish the determination of
$\mathrm {D}$
(see [Reference Cabanes and SpäthCS4, 2.5]). The present paper is the first part of a solution to that problem. A second part [Reference SpäthS7] will finish the determination of
![]() $\mathrm {Irr}(G)$
as an
$\mathrm {Irr}(G)$
as an
![]() $\mathrm {Out}(G)$
-set. The splitting is due to the quite different methods used here and in [Reference SpäthS7]. A third part will focus on applications to the McKay conjecture [Reference SpäthS8].
$\mathrm {Out}(G)$
-set. The splitting is due to the quite different methods used here and in [Reference SpäthS7]. A third part will focus on applications to the McKay conjecture [Reference SpäthS8].
In order to be more specific about intermediate goals and results, let us introduce some notation. Let
![]() $G={{\mathbf G}}^F$
for
$G={{\mathbf G}}^F$
for
![]() $F\colon {{\mathbf G}}\to {{\mathbf G}}$
be a Frobenius endomorphism of a simply connected simple algebraic group
$F\colon {{\mathbf G}}\to {{\mathbf G}}$
be a Frobenius endomorphism of a simply connected simple algebraic group
![]() ${{\mathbf G}}$
. Upon choosing an F-stable maximal torus and a Borel subgroup containing it, one can define a group E of so-called field and graph automorphisms of G. One can also define a reductive group
${{\mathbf G}}$
. Upon choosing an F-stable maximal torus and a Borel subgroup containing it, one can define a group E of so-called field and graph automorphisms of G. One can also define a reductive group
![]() $\widetilde {\mathbf G}$
realizing a regular embedding for
$\widetilde {\mathbf G}$
realizing a regular embedding for
![]() ${{\mathbf G}}$
, that is,
${{\mathbf G}}$
, that is,
![]() ${{\mathbf G}}=[\widetilde {\mathbf G} ,\widetilde {\mathbf G}]$
with connected
${{\mathbf G}}=[\widetilde {\mathbf G} ,\widetilde {\mathbf G}]$
with connected
![]() ${\mathrm {Z}} (\widetilde {\mathbf G})$
and also assume that F extends to a Frobenius endomorphism of
${\mathrm {Z}} (\widetilde {\mathbf G})$
and also assume that F extends to a Frobenius endomorphism of
![]() $\widetilde {\mathbf G}$
with E also acting on
$\widetilde {\mathbf G}$
with E also acting on
![]() ${{\widetilde G}}:=\widetilde {\mathbf G}^F$
. Then
${{\widetilde G}}:=\widetilde {\mathbf G}^F$
. Then
![]() $\mathrm {Aut}(G)$
is induced by the direct product
$\mathrm {Aut}(G)$
is induced by the direct product
![]() ${{\widetilde G}}\rtimes E$
(see, e.g., [Reference Gorenstein, Lyons and SolomonGLS, 2.5.12]).
${{\widetilde G}}\rtimes E$
(see, e.g., [Reference Gorenstein, Lyons and SolomonGLS, 2.5.12]).
The determination of the action of
![]() ${{\widetilde G}}\rtimes E$
on
${{\widetilde G}}\rtimes E$
on
![]() $\mathrm {Irr}(G)$
mostly relies on establishing that
$\mathrm {Irr}(G)$
mostly relies on establishing that
![]() ${{\widetilde G}}$
-orbits and E-orbits are somehow transversal. More precisely, one aims at showing the following property:
${{\widetilde G}}$
-orbits and E-orbits are somehow transversal. More precisely, one aims at showing the following property:
![]() $A'({\infty })$
: There exists an E-stable
$A'({\infty })$
: There exists an E-stable
![]() ${{\widetilde G}}$
-transversal in
${{\widetilde G}}$
-transversal in
![]() $\mathrm {Irr}(G)$
.
$\mathrm {Irr}(G)$
.
This, combined with the present knowledge of
![]() $\mathrm {Irr}({{\widetilde G}})$
, is enough to determine
$\mathrm {Irr}({{\widetilde G}})$
, is enough to determine
![]() $\mathrm {Irr}(G)$
as an
$\mathrm {Irr}(G)$
as an
![]() $\mathrm {Out}(G)$
-set (see [Reference Cabanes and SpäthCS4, 2.5]). However, in order to deduce any valuable statement about representations of almost-simple groups, it is also important to answer extendibility questions. For instance, a difficult theorem of Lusztig essentially focusing on the case of type
$\mathrm {Out}(G)$
-set (see [Reference Cabanes and SpäthCS4, 2.5]). However, in order to deduce any valuable statement about representations of almost-simple groups, it is also important to answer extendibility questions. For instance, a difficult theorem of Lusztig essentially focusing on the case of type
![]() $\mathrm {D}$
shows that any element of
$\mathrm {D}$
shows that any element of
![]() $\mathrm {Irr}(G)$
extends to its stabilizer in
$\mathrm {Irr}(G)$
extends to its stabilizer in
![]() ${{\widetilde G}}$
(see [Reference LusztigL2], [Reference LusztigL3]). This notably leads to the determination of the action of E on the set of
${{\widetilde G}}$
(see [Reference LusztigL2], [Reference LusztigL3]). This notably leads to the determination of the action of E on the set of
![]() ${{\widetilde G}}$
-orbits in
${{\widetilde G}}$
-orbits in
![]() $\mathrm {Irr} (G)$
.
$\mathrm {Irr} (G)$
.
The following strengthening of
![]() $A'({\infty })$
was introduced in [Reference SpäthS4] in order to check the inductive McKay condition for the defining characteristic.
$A'({\infty })$
was introduced in [Reference SpäthS4] in order to check the inductive McKay condition for the defining characteristic.
![]() $A({\infty })$
: There exists an E-stable
$A({\infty })$
: There exists an E-stable
![]() ${{\widetilde G}}$
-transversal
${{\widetilde G}}$
-transversal
![]() $\mathbb T$
in
$\mathbb T$
in
![]() $\mathrm {Irr}(G)$
and any
$\mathrm {Irr}(G)$
and any
![]() $\chi \in \mathbb T$
extends to an irreducible character of its stabilizer
$\chi \in \mathbb T$
extends to an irreducible character of its stabilizer
![]() $G\rtimes E_{\chi }$
.
$G\rtimes E_{\chi }$
.
The aim of the present paper and its sequel [Reference SpäthS7] is to prove
![]() $A({\infty })$
for G of type
$A({\infty })$
for G of type
![]() $\mathrm {D}$
and
$\mathrm {D}$
and
![]() $^2\mathrm {D}$
. In the present paper, G will be indeed some
$^2\mathrm {D}$
. In the present paper, G will be indeed some
![]() $\mathrm {D}_{ l, \mathrm {sc}}(q)$
(
$\mathrm {D}_{ l, \mathrm {sc}}(q)$
(
![]() $l\geq 4$
, q a power of an odd prime); the case of twisted types
$l\geq 4$
, q a power of an odd prime); the case of twisted types
![]() $^2\mathrm {D}$
will also be deduced in [Reference SpäthS7].
$^2\mathrm {D}$
will also be deduced in [Reference SpäthS7].
Our main theorem here can be seen as showing that a putative counterexample to
![]() $A({\infty })$
with minimal l still satisfies
$A({\infty })$
with minimal l still satisfies
![]() $A'({\infty })$
.
$A'({\infty })$
.
Theorem A. Let
![]() $G= \mathrm {D}_{l,sc}(q)$
(
$G= \mathrm {D}_{l,sc}(q)$
(
![]() $l\geq 4$
, q a power of an odd prime), and let
$l\geq 4$
, q a power of an odd prime), and let
![]() ${\widetilde G}$
and E as above (see also Notation 2.2). If any
${\widetilde G}$
and E as above (see also Notation 2.2). If any
![]() $\mathrm {D}_{l',sc}(q)$
for
$\mathrm {D}_{l',sc}(q)$
for
![]() $4\leq l'<l$
satisfies
$4\leq l'<l$
satisfies
![]() $A({\infty })$
, then G satisfies
$A({\infty })$
, then G satisfies
![]() $A'({\infty })$
.
$A'({\infty })$
.
More precisely, we assume Hypothesis 2.14, that is, that condition A
![]() $(\infty )$
holds for the cuspidal characters of any
$(\infty )$
holds for the cuspidal characters of any
![]() $G'=\mathrm {D}_{l',sc}(q)$
with
$G'=\mathrm {D}_{l',sc}(q)$
with
![]() $4\leq l'<l$
.
$4\leq l'<l$
.
Our proof uses as a starting point a theorem of Malle [Reference Malle and SpäthMal2] showing the existence part
![]() $A'({\infty })$
of the above statement for cuspidal characters. Then, our strategy is through the parametrization of
$A'({\infty })$
of the above statement for cuspidal characters. Then, our strategy is through the parametrization of
![]() $\mathrm {Irr}(G)$
given by Harish-Chandra theory. In particular, we take the standard Levi supplement
$\mathrm {Irr}(G)$
given by Harish-Chandra theory. In particular, we take the standard Levi supplement
![]() ${{\mathbf L}}$
of an F-stable parabolic subgroup
${{\mathbf L}}$
of an F-stable parabolic subgroup
![]() ${\mathbf P}$
containing our chosen Borel subgroup and consider parabolic induction R
${\mathbf P}$
containing our chosen Borel subgroup and consider parabolic induction R
![]() $^{{\mathbf G}}_{{{\mathbf L}}}\lambda $
of cuspidal characters
$^{{\mathbf G}}_{{{\mathbf L}}}\lambda $
of cuspidal characters
![]() $\lambda \in \mathrm {Irr}_{cusp} ({{\mathbf L}}^F)$
.
$\lambda \in \mathrm {Irr}_{cusp} ({{\mathbf L}}^F)$
.
An essential ingredient of that parametrization is the deep theorem by Lusztig and Geck (see [Reference LusztigL
Reference Bonnafé1, 8.6] and [Reference GeckG, Cor. 2]) that any
![]() $\lambda \in \mathrm {Irr}_{cusp} ({{\mathbf L}}^F)$
extends to its stabilizer in
$\lambda \in \mathrm {Irr}_{cusp} ({{\mathbf L}}^F)$
extends to its stabilizer in
![]() $N:={\mathrm {N}}_{{{\mathbf G}}}({{\mathbf L}})^F$
. In order to put that parametrization to use for our purpose of tracking automorphism actions, it is important to find an equivariant version of that statement. This does not seem possible from the available proofs, so we devise a new one in this paper, showing namely with the same notation for
$N:={\mathrm {N}}_{{{\mathbf G}}}({{\mathbf L}})^F$
. In order to put that parametrization to use for our purpose of tracking automorphism actions, it is important to find an equivariant version of that statement. This does not seem possible from the available proofs, so we devise a new one in this paper, showing namely with the same notation for
![]() $G= \mathrm {D}_{l,sc}(q)$
,
$G= \mathrm {D}_{l,sc}(q)$
,
![]() ${{\widetilde G}}$
,
${{\widetilde G}}$
,
![]() ${{\mathbf L}}$
, N, E.
${{\mathbf L}}$
, N, E.
Theorem B. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}({{\mathbf L}}^F)$
. Assume Hypothesis 2.14 holds for
$\lambda \in \mathrm {Irr}_{cusp}({{\mathbf L}}^F)$
. Assume Hypothesis 2.14 holds for
![]() $\mathrm {D}_{l',sc}(q)$
(
$\mathrm {D}_{l',sc}(q)$
(
![]() $4\leq l'<l$
). Then some
$4\leq l'<l$
). Then some
![]() ${({\mathrm {Z}}(\widetilde {\mathbf G}){{\mathbf L}})}^F$
-conjugate
${({\mathrm {Z}}(\widetilde {\mathbf G}){{\mathbf L}})}^F$
-conjugate
![]() $\lambda _0$
of
$\lambda _0$
of
![]() $\lambda $
has an
$\lambda $
has an
![]() $(N{\mathrm {N}}_E({{\mathbf L}}))_{\lambda _0} $
-stable extension to
$(N{\mathrm {N}}_E({{\mathbf L}}))_{\lambda _0} $
-stable extension to
![]() $N_{\lambda _0}$
.
$N_{\lambda _0}$
.
Studying the group structure of N, our proof uses essentially the Steinberg relations for the structure of G, not its realization as spin group, making probably more uniform a case-by-case but effective proof of Geck–Lusztig’s theorem for other quasisimple groups of Lie type (see [Reference Brough and SpäthBS, 4.3] and [Reference CarterCSS, 4.13] for types A and C).
We should point out that the above extendibility property is part of the following wider problem where
![]() $({{\mathbf H}} ,F)$
is a reductive group defined over a finite field and F is its associated Frobenius endomorphism.
$({{\mathbf H}} ,F)$
is a reductive group defined over a finite field and F is its associated Frobenius endomorphism.
(P) Let
![]() ${\mathbf S}$
be an F-stable torus of
${\mathbf S}$
be an F-stable torus of
![]() ${{\mathbf H}}$
. Does every
${{\mathbf H}}$
. Does every
![]() $\psi \in \mathrm {Irr}({\mathrm {C}}_{{{\mathbf H}}}({\mathbf S})^F)$
extend to its stabilizer in
$\psi \in \mathrm {Irr}({\mathrm {C}}_{{{\mathbf H}}}({\mathbf S})^F)$
extend to its stabilizer in
![]() ${\mathrm {N}}_{{{\mathbf H}}}({\mathbf S})^F$
?
${\mathrm {N}}_{{{\mathbf H}}}({\mathbf S})^F$
?
This was answered in the affirmative in the case where
![]() ${\mathbf S}$
is a Sylow d-torus (
${\mathbf S}$
is a Sylow d-torus (
![]() $d\geq 1$
) in the sense of [Reference MaslowskiMT, 25.6] (see [Reference SpäthS1], [Reference SpäthS2], [Reference SpäthS3]). Lusztig’s theorem on the case where
$d\geq 1$
) in the sense of [Reference MaslowskiMT, 25.6] (see [Reference SpäthS1], [Reference SpäthS2], [Reference SpäthS3]). Lusztig’s theorem on the case where
![]() ${\mathbf S}$
is split and
${\mathbf S}$
is split and
![]() $\psi $
is cuspidal was important in [Reference LusztigL1] to turn Deligne–Lusztig theory into a parametrization of
$\psi $
is cuspidal was important in [Reference LusztigL1] to turn Deligne–Lusztig theory into a parametrization of
![]() $\mathrm {Irr}({{\mathbf H}}^F)$
when
$\mathrm {Irr}({{\mathbf H}}^F)$
when
![]() ${{\mathbf H}}$
has connected center. It seems that even partial answers to (P) have quite interesting applications (see also [Reference BonnaféB1, §15] and [Reference MalleMal1, 2.9]).
${{\mathbf H}}$
has connected center. It seems that even partial answers to (P) have quite interesting applications (see also [Reference BonnaféB1, §15] and [Reference MalleMal1, 2.9]).
Let for now
![]() $\mathrm {Irr}_{cusp}(N)$
be the set of characters of N whose restriction to L is a sum of cuspidal characters. Theorem B then can be seen as the starting point of a specific parametrization of
$\mathrm {Irr}_{cusp}(N)$
be the set of characters of N whose restriction to L is a sum of cuspidal characters. Theorem B then can be seen as the starting point of a specific parametrization of
![]() $\mathrm {Irr}_{cusp}(N)$
bearing similarities with the parametrizations of characters of normalizers of Sylow d-tori given in the author’s work just mentioned but with a special emphasis on outer automorphism actions.
$\mathrm {Irr}_{cusp}(N)$
bearing similarities with the parametrizations of characters of normalizers of Sylow d-tori given in the author’s work just mentioned but with a special emphasis on outer automorphism actions.
Through preparations gathered at the start of the paper and similar to a method developed in [Reference Malle and TestermanMS] where
![]() ${{\mathbf L}}$
was a torus, our main goal Theorem A reduces to a weak analogue of it for
${{\mathbf L}}$
was a torus, our main goal Theorem A reduces to a weak analogue of it for
![]() $\mathrm {Irr}_{cusp}(N)$
. This is Theorem 6.1. It is checked through a strategy prescribed by Clifford theory. In particular, this entails a quite detailed analysis of the relative Weyl groups
$\mathrm {Irr}_{cusp}(N)$
. This is Theorem 6.1. It is checked through a strategy prescribed by Clifford theory. In particular, this entails a quite detailed analysis of the relative Weyl groups
and their various embeddings related to
![]() ${{\widetilde G}}$
and E.
${{\widetilde G}}$
and E.
1.1 Structure of the paper
In §2, we recall notation on quasisimple groups of Lie type, their automorphisms, and the conditions
![]() $A({\infty })$
and
$A({\infty })$
and
![]() $A'({\infty })$
. Then we collect the basic facts about cuspidal characters and Harish-Chandra theory for finite groups of Lie type. This leads to Theorem 2.8, which sums up the methods from [Reference Malle and TestermanMS] to establish condition
$A'({\infty })$
. Then we collect the basic facts about cuspidal characters and Harish-Chandra theory for finite groups of Lie type. This leads to Theorem 2.8, which sums up the methods from [Reference Malle and TestermanMS] to establish condition
![]() $A({\infty })$
through Harish-Chandra theory. This is roughly the road map for the rest of the paper, in particular splitting the task into two halves that will be addressed in §§3 and 4 and §§6 and 7.
$A({\infty })$
through Harish-Chandra theory. This is roughly the road map for the rest of the paper, in particular splitting the task into two halves that will be addressed in §§3 and 4 and §§6 and 7.
The rest of the paper is specific to type
![]() $\mathrm {D}$
(untwisted) in odd characteristic. After recalling a method from [Reference CarterCSS] for constructing extensions, the main objective of §§3 and 4 is Theorem B. Section 3 is a description of certain group theoretical aspects of the groups
$\mathrm {D}$
(untwisted) in odd characteristic. After recalling a method from [Reference CarterCSS] for constructing extensions, the main objective of §§3 and 4 is Theorem B. Section 3 is a description of certain group theoretical aspects of the groups
![]() $L:={{\mathbf L}}^F$
and N, using also the classic embedding
$L:={{\mathbf L}}^F$
and N, using also the classic embedding
![]() ${{\mathbf G}}\leq \overline {{\mathbf G}}$
of type
${{\mathbf G}}\leq \overline {{\mathbf G}}$
of type
![]() $\mathrm {D}_l$
into type
$\mathrm {D}_l$
into type
![]() $\mathrm B_l$
. The root system
$\mathrm B_l$
. The root system
![]() $\Phi '$
of
$\Phi '$
of
![]() ${{\mathbf L}}$
is the direct product of irreducible root systems of types
${{\mathbf L}}$
is the direct product of irreducible root systems of types
![]() $\mathrm A$
and
$\mathrm A$
and
![]() $\mathrm {D}$
. Roughly speaking, the factors of type
$\mathrm {D}$
. Roughly speaking, the factors of type
![]() $\mathrm A_{d-1}$
form a root system
$\mathrm A_{d-1}$
form a root system
![]() $\Phi _d$
and the factor of type
$\Phi _d$
and the factor of type
![]() $\mathrm {D}$
gives
$\mathrm {D}$
gives
![]() $\Phi _{-1}$
. Along the way, we introduce a set
$\Phi _{-1}$
. Along the way, we introduce a set
![]() $\mathbb D$
determining the types occurring as factors of
$\mathbb D$
determining the types occurring as factors of
![]() $\Phi '$
. This description will be used in the whole paper. For each
$\Phi '$
. This description will be used in the whole paper. For each
![]() $d\in \mathbb D$
, we describe a normal inclusion
$d\in \mathbb D$
, we describe a normal inclusion
![]() $H_d\lhd V_d\leq \overline {N}:={\mathrm {N}}_{\overline {{\mathbf G}}}({{\mathbf L}})^F$
, where
$H_d\lhd V_d\leq \overline {N}:={\mathrm {N}}_{\overline {{\mathbf G}}}({{\mathbf L}})^F$
, where
![]() $H_d=L\cap V_d$
is an elementary abelian
$H_d=L\cap V_d$
is an elementary abelian
![]() $2$
-group and
$2$
-group and
![]() $L{\left\langle V_d\mid d\in {\mathbb D}\right\rangle } =\overline {N}$
. This normal inclusion
$L{\left\langle V_d\mid d\in {\mathbb D}\right\rangle } =\overline {N}$
. This normal inclusion
![]() $H_d\lhd V_d$
concentrates the equivariant extendibility problem we have to solve.
$H_d\lhd V_d$
concentrates the equivariant extendibility problem we have to solve.
In §4, we draw the consequences of the structure of N in terms of characters. One has to take care of all the factors involved and deal with the inclusion in type
![]() $\mathrm B$
, which provides the graph automorphism specific to type
$\mathrm B$
, which provides the graph automorphism specific to type
![]() $\mathrm {D}$
. Concerning the diagonal automorphisms, we avoid choosing a regular embedding
$\mathrm {D}$
. Concerning the diagonal automorphisms, we avoid choosing a regular embedding
![]() ${{\widetilde G}}$
and instead consider inclusions
${{\widetilde G}}$
and instead consider inclusions
![]() $L\lhd \mathcal L^{-1}(Z)\cap {{\mathbf L}}$
where
$L\lhd \mathcal L^{-1}(Z)\cap {{\mathbf L}}$
where
![]() $Z\leq {\mathrm {Z}}({{\mathbf G}})$
and
$Z\leq {\mathrm {Z}}({{\mathbf G}})$
and
![]() $\mathcal L$
is the Lang map
$\mathcal L$
is the Lang map
![]() $x\mapsto x^{-1}F(x)$
on
$x\mapsto x^{-1}F(x)$
on
![]() ${{\mathbf G}}$
.
${{\mathbf G}}$
.
Theorem B being proved, we study in §5 how automorphisms act on cuspidal characters in types
![]() $\mathrm A$
and
$\mathrm A$
and
![]() $\mathrm {D}$
, making use in the latter case of Malle’s theorem [Reference Malle and SpäthMal2] mentioned above and some results about semisimple characters already used in the study of the McKay conjecture for the defining characteristic (see [Reference MalleMas, §8]).
$\mathrm {D}$
, making use in the latter case of Malle’s theorem [Reference Malle and SpäthMal2] mentioned above and some results about semisimple characters already used in the study of the McKay conjecture for the defining characteristic (see [Reference MalleMas, §8]).
In §6, the most technical of the paper, the objective is to prove Theorem 6.1, showing that
![]() $\mathrm {Irr}_{cusp}(N)$
satisfies a version of
$\mathrm {Irr}_{cusp}(N)$
satisfies a version of
![]() $A({\infty })$
. As already shown in §2, this translates into requirements on
$A({\infty })$
. As already shown in §2, this translates into requirements on
![]() $\mathrm {Irr}(N_{\lambda }/L)$
, the characters of the relative Weyl group
$\mathrm {Irr}(N_{\lambda }/L)$
, the characters of the relative Weyl group
![]() $W(\lambda )$
associated with a cuspidal character
$W(\lambda )$
associated with a cuspidal character
![]() $\lambda $
of L. The comparison of the action of diagonal versus graph-field automorphisms on
$\lambda $
of L. The comparison of the action of diagonal versus graph-field automorphisms on
![]() $\mathrm {Irr}_{cusp}(N)$
relates with the induced action of related characters of relative Weyl groups. The proof splits naturally into the various cases for the stabilizer of
$\mathrm {Irr}_{cusp}(N)$
relates with the induced action of related characters of relative Weyl groups. The proof splits naturally into the various cases for the stabilizer of
![]() $\lambda $
in
$\lambda $
in
![]() $L\cap \mathcal L^{-1}({\mathrm {Z}}({{\mathbf G}}))/L$
. This leads to Propositions 6.28 and 6.35 describing the situation in the two main cases. In the proofs, graph-field automorphisms are taken care of by embedding the relative Weyl group
$L\cap \mathcal L^{-1}({\mathrm {Z}}({{\mathbf G}}))/L$
. This leads to Propositions 6.28 and 6.35 describing the situation in the two main cases. In the proofs, graph-field automorphisms are taken care of by embedding the relative Weyl group
![]() $W(\lambda )$
into overgroups
$W(\lambda )$
into overgroups
![]() $K(\lambda )$
and
$K(\lambda )$
and
![]() $\widehat K(\lambda )$
(see Notation 6.4) for field automorphisms and the embedding into type
$\widehat K(\lambda )$
(see Notation 6.4) for field automorphisms and the embedding into type
![]() $\mathrm B$
for the graph automorphism of order 2.
$\mathrm B$
for the graph automorphism of order 2.
In §7, we essentially put together all the material of the preceding section to establish Theorem 6.1 and with some extra effort Theorem A.
2 Basic considerations
We first gather here some notation around characters, recall Condition
![]() $A(\infty )$
, and give a rephrasement that provides alternative approaches for the proof of Theorem A. In §2.2, we collect relevant results from Harish-Chandra theory. We conclude with general considerations on cuspidal characters in §2.3.
$A(\infty )$
, and give a rephrasement that provides alternative approaches for the proof of Theorem A. In §2.2, we collect relevant results from Harish-Chandra theory. We conclude with general considerations on cuspidal characters in §2.3.
2.1 Notation and Condition
 $A(\infty )$
$A(\infty )$
In general, we follow the notation about characters as introduced in [Reference IsaacsI]. Additionally, we use some terminology from [Reference SpäthS1], [Reference SpäthS2], [Reference SpäthS3] that is recalled in the following paragraph.
Notation 2.1. Let
![]() $X\lhd Y$
be finite groups, and let
$X\lhd Y$
be finite groups, and let
![]() $\mathbb {T}\subseteq \mathrm {Irr}(X)$
. An extension map with respect to
$\mathbb {T}\subseteq \mathrm {Irr}(X)$
. An extension map with respect to
![]() $X\lhd Y$
for
$X\lhd Y$
for
![]() $\mathbb {T}$
is a map
$\mathbb {T}$
is a map
![]() $\Lambda :\mathbb {T}\longrightarrow \coprod _{X\leq I \leq Y } \mathrm {Irr}(I)$
such that every
$\Lambda :\mathbb {T}\longrightarrow \coprod _{X\leq I \leq Y } \mathrm {Irr}(I)$
such that every
![]() $\lambda \in \mathbb {T}$
is mapped to an extension of
$\lambda \in \mathbb {T}$
is mapped to an extension of
![]() $\lambda $
to
$\lambda $
to
![]() ${Y_{\lambda }}$
, the inertia subgroup of
${Y_{\lambda }}$
, the inertia subgroup of
![]() $\lambda $
in Y. We say that maximal extendibility holds with respect to
$\lambda $
in Y. We say that maximal extendibility holds with respect to
![]() $X\lhd Y$
for
$X\lhd Y$
for
![]() $\mathbb {T}$
if such an extension map exists (see also [Reference Cabanes and SpäthCS2, Def. 5.7]). In such a case, the map can be chosen Y-equivariant, provided
$\mathbb {T}$
if such an extension map exists (see also [Reference Cabanes and SpäthCS2, Def. 5.7]). In such a case, the map can be chosen Y-equivariant, provided
![]() $\mathbb {T}$
is Y-stable (see [Reference Cabanes and SpäthCS2, Th. 4.1]). Whenever
$\mathbb {T}$
is Y-stable (see [Reference Cabanes and SpäthCS2, Th. 4.1]). Whenever
![]() $\mathbb {T}=\mathrm {Irr}(X)$
, we omit to mention
$\mathbb {T}=\mathrm {Irr}(X)$
, we omit to mention
![]() $\mathbb {T}$
. For
$\mathbb {T}$
. For
![]() $\lambda \in \mathrm {Irr}(X)$
and
$\lambda \in \mathrm {Irr}(X)$
and
![]() $\psi \in \mathrm {Irr}(Y)$
, we write
$\psi \in \mathrm {Irr}(Y)$
, we write
![]() ${\lambda ^Y}$
for the character induced to Y and
${\lambda ^Y}$
for the character induced to Y and
![]() ${\psi \rceil _X}$
for the restricted character. For any generalized character
${\psi \rceil _X}$
for the restricted character. For any generalized character
![]() $\kappa $
, we denote by
$\kappa $
, we denote by
![]() ${\mathrm {Irr}(\kappa )}$
the set of (irreducible) constituents of
${\mathrm {Irr}(\kappa )}$
the set of (irreducible) constituents of
![]() $\kappa $
. If
$\kappa $
. If
![]() $\sigma \in \mathrm {Aut}(X)$
and
$\sigma \in \mathrm {Aut}(X)$
and
![]() $\lambda \in \mathrm {Irr}(X)$
, we write
$\lambda \in \mathrm {Irr}(X)$
, we write
![]() ${\lambda ^{\sigma }}= \,^{\sigma ^{-1} }\lambda $
for the character with
${\lambda ^{\sigma }}= \,^{\sigma ^{-1} }\lambda $
for the character with
![]() $\,^{\sigma ^{-1}} \lambda (x)= \lambda ^{\sigma }(x)=\lambda (\sigma (x))$
for
$\,^{\sigma ^{-1}} \lambda (x)= \lambda ^{\sigma }(x)=\lambda (\sigma (x))$
for
![]() $x\in X$
.
$x\in X$
.
If two subgroups
![]() $H_1,H_2\leq Y$
satisfy
$H_1,H_2\leq Y$
satisfy
![]() $[H_1,H_2]=1$
, and
$[H_1,H_2]=1$
, and
![]() $\lambda _i\in \mathrm {Irr}(H_i)$
for
$\lambda _i\in \mathrm {Irr}(H_i)$
for
![]() $i=1, 2$
with
$i=1, 2$
with
![]() $\mathrm {Irr}({\left. \lambda _1\right\rceil _{{H_1\cap H_2}}})=\mathrm {Irr}({\left. \lambda _2\right\rceil _{{H_1\cap H_2}}})$
, then there exists a unique character
$\mathrm {Irr}({\left. \lambda _1\right\rceil _{{H_1\cap H_2}}})=\mathrm {Irr}({\left. \lambda _2\right\rceil _{{H_1\cap H_2}}})$
, then there exists a unique character
![]() $\phi \in \mathrm {Irr}({\left\langle H_1,H_2 \right\rangle })$
with
$\phi \in \mathrm {Irr}({\left\langle H_1,H_2 \right\rangle })$
with
![]() $\mathrm {Irr}({\left. \phi \right\rceil _{{H_i}}})=\{\lambda _i\}$
according to [Reference Isaacs, Malle and NavarroIMN, §5] and we write
$\mathrm {Irr}({\left. \phi \right\rceil _{{H_i}}})=\{\lambda _i\}$
according to [Reference Isaacs, Malle and NavarroIMN, §5] and we write
![]() ${\lambda _1\cdot \lambda _2}$
for this character. Let
${\lambda _1\cdot \lambda _2}$
for this character. Let
![]() $\mathbb I$
be a finite set, and let Z, H, and
$\mathbb I$
be a finite set, and let Z, H, and
![]() $H_i$
(
$H_i$
(
![]() $i\in \mathbb I$
) be finite groups with
$i\in \mathbb I$
) be finite groups with
![]() $Z\leq H_i\leq H$
. If
$Z\leq H_i\leq H$
. If
![]() $[H_i,H_{i'}]=1$
, for every
$[H_i,H_{i'}]=1$
, for every
![]() $i,i'\in \mathbb I$
with
$i,i'\in \mathbb I$
with
![]() $i\neq i'$
and
$i\neq i'$
and
![]() $H_i\cap {\left\langle H_{j}\mid j\in \mathbb I\setminus \{i\}\right\rangle } =Z$
, we consider
$H_i\cap {\left\langle H_{j}\mid j\in \mathbb I\setminus \{i\}\right\rangle } =Z$
, we consider
![]() $ {\left\langle H_{i}\mid i\in \mathbb I\right\rangle } \leq H$
the central product of the groups
$ {\left\langle H_{i}\mid i\in \mathbb I\right\rangle } \leq H$
the central product of the groups
![]() $H_i$
. Given
$H_i$
. Given
![]() $\nu \in \mathrm {Irr}(Z)$
and
$\nu \in \mathrm {Irr}(Z)$
and
![]() $\lambda _i\in \mathrm {Irr}(H_i\mid \nu )$
, we denote by
$\lambda _i\in \mathrm {Irr}(H_i\mid \nu )$
, we denote by
![]() ${\odot _{i \in \mathbb I}\lambda _i}\in \mathrm {Irr}({\left\langle H_{i}\mid i\in \mathbb I\right\rangle } )$
the character
${\odot _{i \in \mathbb I}\lambda _i}\in \mathrm {Irr}({\left\langle H_{i}\mid i\in \mathbb I\right\rangle } )$
the character
![]() $\phi \in \mathrm {Irr}({\left\langle H_{i}\mid i\in \mathbb I\right\rangle })$
with
$\phi \in \mathrm {Irr}({\left\langle H_{i}\mid i\in \mathbb I\right\rangle })$
with
![]() $\mathrm {Irr}({\left. \phi \right\rceil _{{H_i}}})=\{\lambda _i\}$
for every
$\mathrm {Irr}({\left. \phi \right\rceil _{{H_i}}})=\{\lambda _i\}$
for every
![]() $i\in \mathbb I$
(see also [Reference Isaacs, Malle and NavarroIMN, §5]).
$i\in \mathbb I$
(see also [Reference Isaacs, Malle and NavarroIMN, §5]).
Next, we introduce the groups and automorphisms considered in the following.
Notation 2.2 (Simple groups of Lie type)
Let
![]() ${{\mathbf G}}$
be a simple linear algebraic group of simply connected type over an algebraic closure
${{\mathbf G}}$
be a simple linear algebraic group of simply connected type over an algebraic closure
![]() ${{\mathbb {F}}}$
of
${{\mathbb {F}}}$
of
![]() ${\mathbb {F}}_p$
for p a prime. Additionally, let
${\mathbb {F}}_p$
for p a prime. Additionally, let
![]() $ F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be a Frobenius endomorphism defining an
$ F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be a Frobenius endomorphism defining an
![]() ${\mathbb {F}}_q$
-structure on
${\mathbb {F}}_q$
-structure on
![]() ${{\mathbf G}}$
for q, a power of p. The automorphisms of
${{\mathbf G}}$
for q, a power of p. The automorphisms of
![]() ${{{{\mathbf G}}^F}}$
are restrictions to
${{{{\mathbf G}}^F}}$
are restrictions to
![]() ${{{{\mathbf G}}^F}}$
of bijective endomorphisms of
${{{{\mathbf G}}^F}}$
of bijective endomorphisms of
![]() ${{\mathbf G}}$
commuting to F (see [Reference Gorenstein, Lyons and SolomonGLS, §1.15]), so it makes sense to consider stabilizers
${{\mathbf G}}$
commuting to F (see [Reference Gorenstein, Lyons and SolomonGLS, §1.15]), so it makes sense to consider stabilizers
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})_{{\mathbf H}}$
for F-stable subgroups
$\mathrm {Aut}({{{{\mathbf G}}^F}})_{{\mathbf H}}$
for F-stable subgroups
![]() ${{\mathbf H}}\leq {{\mathbf G}}$
. Let
${{\mathbf H}}\leq {{\mathbf G}}$
. Let
![]() ${{\mathbf T}_0}$
be an F-stable maximally split torus, and let
${{\mathbf T}_0}$
be an F-stable maximally split torus, and let
![]() ${{\mathbf B}}$
be an F-stable Borel subgroup of
${{\mathbf B}}$
be an F-stable Borel subgroup of
![]() ${{\mathbf G}}$
with
${{\mathbf G}}$
with
![]() ${\mathbf T}_0\subseteq {\mathbf B}$
and
${\mathbf T}_0\subseteq {\mathbf B}$
and
![]() ${{\mathbf N}_0}:={\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)$
. According to [Reference MaslowskiMT, Th. 24.11], the group
${{\mathbf N}_0}:={\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)$
. According to [Reference MaslowskiMT, Th. 24.11], the group
![]() $ G:={{{{\mathbf G}}^F}}$
has a split
$ G:={{{{\mathbf G}}^F}}$
has a split
![]() $BN$
-pair with respect to
$BN$
-pair with respect to
![]() $ B:={\mathbf B}^F$
,
$ B:={\mathbf B}^F$
,
![]() $ {T_0}:={\mathbf T}_0^F$
, and
$ {T_0}:={\mathbf T}_0^F$
, and
![]() ${N_0}:={\mathbf N}_0^F$
. Let
${N_0}:={\mathbf N}_0^F$
. Let
![]() ${E({{{{\mathbf G}}^F}})}$
, often just
${E({{{{\mathbf G}}^F}})}$
, often just
![]() $ E$
, be the subgroup of
$ E$
, be the subgroup of
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})_{({\mathbf B},{\mathbf T}_0)}$
generated by the restrictions to
$\mathrm {Aut}({{{{\mathbf G}}^F}})_{({\mathbf B},{\mathbf T}_0)}$
generated by the restrictions to
![]() ${{{{\mathbf G}}^F}}$
of graph automorphisms and some Frobenius endomorphism
${{{{\mathbf G}}^F}}$
of graph automorphisms and some Frobenius endomorphism
![]() ${F_0}$
stabilizing
${F_0}$
stabilizing
![]() ${\mathbf T}_0$
and
${\mathbf T}_0$
and
![]() ${\mathbf B}$
as in [Reference Gorenstein, Lyons and SolomonGLS, Th. 2.5.1] and [Reference Cabanes and SpäthCS4, §2.A].
${\mathbf B}$
as in [Reference Gorenstein, Lyons and SolomonGLS, Th. 2.5.1] and [Reference Cabanes and SpäthCS4, §2.A].
Let
![]() ${{{\mathbf G}}\leq \widetilde {{\mathbf G}}}$
be a regular embedding, that is, a closed inclusion of algebraic groups with
${{{\mathbf G}}\leq \widetilde {{\mathbf G}}}$
be a regular embedding, that is, a closed inclusion of algebraic groups with
![]() ${\widetilde {{\mathbf G}}}=\operatorname Z( \widetilde {\mathbf G}){{\mathbf G}}$
and connected
${\widetilde {{\mathbf G}}}=\operatorname Z( \widetilde {\mathbf G}){{\mathbf G}}$
and connected
![]() $\operatorname Z( \widetilde {{\mathbf G}})$
. Then
$\operatorname Z( \widetilde {{\mathbf G}})$
. Then
![]() ${\widetilde {\mathbf T}_0}:=\operatorname Z(\widetilde {\mathbf G}){\mathbf T}_0$
is a maximal torus of
${\widetilde {\mathbf T}_0}:=\operatorname Z(\widetilde {\mathbf G}){\mathbf T}_0$
is a maximal torus of
![]() $\widetilde {{\mathbf G}}$
. Let
$\widetilde {{\mathbf G}}$
. Let
![]() ${\widetilde {T}_0}:=\widetilde {\mathbf T}_0^F$
. Assume that
${\widetilde {T}_0}:=\widetilde {\mathbf T}_0^F$
. Assume that
![]() $F:\widetilde {\mathbf G}\rightarrow \widetilde {\mathbf G}$
is a Frobenius endomorphism extending the one of
$F:\widetilde {\mathbf G}\rightarrow \widetilde {\mathbf G}$
is a Frobenius endomorphism extending the one of
![]() ${{\mathbf G}}$
(see also [Reference Malle and TestermanMS, §2]). Then
${{\mathbf G}}$
(see also [Reference Malle and TestermanMS, §2]). Then
![]() $\widetilde {\mathbf G}^F$
has again a split
$\widetilde {\mathbf G}^F$
has again a split
![]() $BN$
-pair with respect to the groups
$BN$
-pair with respect to the groups
![]() ${\widetilde B}:= \widetilde {T}_0 B$
and
${\widetilde B}:= \widetilde {T}_0 B$
and
![]() ${{\widetilde N}^{\prime }_0}:=\widetilde {T}_0 N_0$
(see [Reference MaslowskiMT, Th. 24.11]). Often the action of
${{\widetilde N}^{\prime }_0}:=\widetilde {T}_0 N_0$
(see [Reference MaslowskiMT, Th. 24.11]). Often the action of
![]() $\widetilde N^{\prime }_0$
on
$\widetilde N^{\prime }_0$
on
![]() ${{\mathbf G}}$
will be studied via the group
${{\mathbf G}}$
will be studied via the group
![]() ${\widetilde N_0}:=\{x\in {\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)\mid x^{-1} F(x) \in \operatorname Z({{\mathbf G}})\}$
, which will be shown to induce the same automorphisms on
${\widetilde N_0}:=\{x\in {\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)\mid x^{-1} F(x) \in \operatorname Z({{\mathbf G}})\}$
, which will be shown to induce the same automorphisms on
![]() ${{\mathbf G}}$
(see Remark 2.16).
${{\mathbf G}}$
(see Remark 2.16).
Via the convention given in [Reference Malle and TestermanMS, §2],
![]() $E({{{{\mathbf G}}^F}})$
also acts on
$E({{{{\mathbf G}}^F}})$
also acts on
![]() $\widetilde {\mathbf G}^F$
and the semi-direct product
$\widetilde {\mathbf G}^F$
and the semi-direct product
![]() $\widetilde {\mathbf G}^F\rtimes E({{{{\mathbf G}}^F}})$
induces on
$\widetilde {\mathbf G}^F\rtimes E({{{{\mathbf G}}^F}})$
induces on
![]() ${{{{\mathbf G}}^F}}$
the whole automorphism group
${{{{\mathbf G}}^F}}$
the whole automorphism group
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})$
.
$\mathrm {Aut}({{{{\mathbf G}}^F}})$
.
We recall the conditions
![]() ${A(\infty )} $
and
${A(\infty )} $
and
![]() ${A'(\infty )}$
from [Reference Cabanes and SpäthCS4, Def. 2.2].
${A'(\infty )}$
from [Reference Cabanes and SpäthCS4, Def. 2.2].
Condition 2.3 (On stabilizers of irreducible characters of
 ${{{{\mathbf G}}^F}}$
)
${{{{\mathbf G}}^F}}$
)
-
A(∞): There exists some E-stable
 ${{{\widetilde {\mathbf G}}^F}}$
-transversal
${{{\widetilde {\mathbf G}}^F}}$
-transversal
 $\mathbb {T}$
in
$\mathbb {T}$
in
 $\mathrm {Irr}({{{{\mathbf G}}^F}})$
, such that every
$\mathrm {Irr}({{{{\mathbf G}}^F}})$
, such that every
 $\chi \in \mathbb {T}$
extends to
$\chi \in \mathbb {T}$
extends to
 ${{{{\mathbf G}}^F}} E_{\chi }$
.
${{{{\mathbf G}}^F}} E_{\chi }$
. -
A ′(∞): There exists some E-stable
 ${{{\widetilde {\mathbf G}}^F}}$
-transversal
${{{\widetilde {\mathbf G}}^F}}$
-transversal
 $\mathbb {T}$
in
$\mathbb {T}$
in
 $\mathrm {Irr}({{{{\mathbf G}}^F}})$
.
$\mathrm {Irr}({{{{\mathbf G}}^F}})$
.
Condition
![]() $A'(\infty )$
implies a weak version of [Reference SpäthS4, Assum. 2.12(v)].
$A'(\infty )$
implies a weak version of [Reference SpäthS4, Assum. 2.12(v)].
Lemma 2.4. Let
![]() ${\widetilde Y}$
and
${\widetilde Y}$
and
![]() ${\widetilde X}$
be two subgroups of a group Z with
${\widetilde X}$
be two subgroups of a group Z with
![]() ${\widetilde X}\lhd Z$
and
${\widetilde X}\lhd Z$
and
![]() $Z={\widetilde Y} {\widetilde X}$
. For
$Z={\widetilde Y} {\widetilde X}$
. For
![]() $X:={\widetilde X}\cap {\widetilde Y}$
, let
$X:={\widetilde X}\cap {\widetilde Y}$
, let
![]() $\mathcal M\subseteq \mathrm {Irr}(X)$
be Z-stable. Then the following are equivalent:
$\mathcal M\subseteq \mathrm {Irr}(X)$
be Z-stable. Then the following are equivalent:
-
(i) There is a
 ${\widetilde Y}$
-stable
${\widetilde Y}$
-stable
 ${\widetilde X}$
-transversal
${\widetilde X}$
-transversal
 ${\mathcal M}_0$
in
${\mathcal M}_0$
in
 $\mathcal M$
.
$\mathcal M$
. -
(ii) Every
 $\zeta '\in \mathcal M$
is
$\zeta '\in \mathcal M$
is
 ${\widetilde X}$
-conjugate to some
${\widetilde X}$
-conjugate to some
 $\zeta $
such that
$\zeta $
such that
 $( {\widetilde X} {\widetilde Y})_{\zeta }= {\widetilde X}_{\zeta } {\widetilde Y}_{\zeta }$
.
$( {\widetilde X} {\widetilde Y})_{\zeta }= {\widetilde X}_{\zeta } {\widetilde Y}_{\zeta }$
. -
(iii) Every
 $\zeta '\in {\mathcal M}$
satisfies
$\zeta '\in {\mathcal M}$
satisfies
 $( {\widetilde X}{\widetilde Y} )_{\zeta '}=({\widetilde Y}^x)_{\zeta '} {\widetilde X}_{\zeta '}$
for some
$( {\widetilde X}{\widetilde Y} )_{\zeta '}=({\widetilde Y}^x)_{\zeta '} {\widetilde X}_{\zeta '}$
for some
 $x\in {\widetilde X}$
.
$x\in {\widetilde X}$
.
Proof. This follows from [Reference CarterCSS, Rem. 3.3].
2.2 Action of
 $\mathrm {Aut}(G)$
on Harish-Chandra-induced characters
$\mathrm {Aut}(G)$
on Harish-Chandra-induced characters
Using a detailed analysis of Harish-Chandra induction, the results of [Reference Malle and TestermanMS] describe the action of
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})$
in terms of cuspidal characters and their relative Weyl groups. The action is expressed in terms of the labels given by Howlett–Lehrer theory.
$\mathrm {Aut}({{{{\mathbf G}}^F}})$
in terms of cuspidal characters and their relative Weyl groups. The action is expressed in terms of the labels given by Howlett–Lehrer theory.
Notation 2.5. Let
![]() $ L$
be a standard Levi subgroup of G with respect to B and
$ L$
be a standard Levi subgroup of G with respect to B and
![]() $T_0$
, that is,
$T_0$
, that is,
![]() $L={{\mathbf L}}^F$
for some standard Levi subgroup
$L={{\mathbf L}}^F$
for some standard Levi subgroup
![]() ${{{\mathbf L}}}$
of
${{{\mathbf L}}}$
of
![]() ${{\mathbf G}}$
such that
${{\mathbf G}}$
such that
![]() ${\mathbf T}_0\leq {{\mathbf L}}$
and
${\mathbf T}_0\leq {{\mathbf L}}$
and
![]() ${{\mathbf L}} {\mathbf B}$
is an F-stable parabolic subgroup. We set
${{\mathbf L}} {\mathbf B}$
is an F-stable parabolic subgroup. We set
![]() $ N:={\mathrm {N}}_{{\mathbf G}}({{\mathbf L}})^F$
,
$ N:={\mathrm {N}}_{{\mathbf G}}({{\mathbf L}})^F$
,
![]() $ W:=N/L$
, and we abbreviate
$ W:=N/L$
, and we abbreviate
We write
![]() ${\mathrm {Irr}_{cusp}(L)}$
for the set of cuspidal characters of L as defined in [Reference Cabanes and EnguehardC, 9.1] and
${\mathrm {Irr}_{cusp}(L)}$
for the set of cuspidal characters of L as defined in [Reference Cabanes and EnguehardC, 9.1] and
![]() ${\mathrm {Irr}_{cusp}(N)}:=\bigcup _{\lambda \in \mathrm {Irr}_{cusp}(L)}\mathrm {Irr}(\lambda ^N)$
. Let us denote by
${\mathrm {Irr}_{cusp}(N)}:=\bigcup _{\lambda \in \mathrm {Irr}_{cusp}(L)}\mathrm {Irr}(\lambda ^N)$
. Let us denote by
![]() ${\operatorname {R}_L^G}$
the Harish-Chandra induction from L to G. For
${\operatorname {R}_L^G}$
the Harish-Chandra induction from L to G. For
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
, let
$\lambda \in \mathrm {Irr}_{cusp}(L)$
, let
(sometimes denoted as
![]() ${\mathcal E(G,(L,\lambda ))}$
in the literature). Let also
${\mathcal E(G,(L,\lambda ))}$
in the literature). Let also
![]() ${\mathrm {Irr}(G\mid (L,\mathbb {T}))}:=\bigcup _{\lambda \in \mathbb {T}}\mathrm {Irr}(G\mid (L,\lambda ))$
for
${\mathrm {Irr}(G\mid (L,\mathbb {T}))}:=\bigcup _{\lambda \in \mathbb {T}}\mathrm {Irr}(G\mid (L,\lambda ))$
for
![]() $\mathbb {T}\subseteq \mathrm {Irr}_{cusp}(L)$
.
$\mathbb {T}\subseteq \mathrm {Irr}_{cusp}(L)$
.
2.6. Let
![]() ${\mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}}$
be the subgroup of
${\mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}}$
be the subgroup of
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})$
generated by the automorphisms of
$\mathrm {Aut}({{{{\mathbf G}}^F}})$
generated by the automorphisms of
![]() ${{{{\mathbf G}}^F}}$
induced by N and
${{{{\mathbf G}}^F}}$
induced by N and
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})_{({\mathbf B}{{\mathbf L}},{{\mathbf L}})}$
. Note
$\mathrm {Aut}({{{{\mathbf G}}^F}})_{({\mathbf B}{{\mathbf L}},{{\mathbf L}})}$
. Note
![]() $E_L\leq \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
. According to Howlett–Lehrer theory (see [Reference Cabanes and EnguehardC, §10]), fixing an extension
$E_L\leq \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
. According to Howlett–Lehrer theory (see [Reference Cabanes and EnguehardC, §10]), fixing an extension
![]() $\widetilde {\lambda }\in \mathrm {Irr}(N_{\lambda })$
of
$\widetilde {\lambda }\in \mathrm {Irr}(N_{\lambda })$
of
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
defines a unique labeling of
$\lambda \in \mathrm {Irr}_{cusp}(L)$
defines a unique labeling of
![]() $\mathrm {Irr}(G\mid (L,\lambda ))$
by
$\mathrm {Irr}(G\mid (L,\lambda ))$
by
![]() $\mathrm {Irr}(W(\lambda ))$
where
$\mathrm {Irr}(W(\lambda ))$
where
![]() ${W(\lambda )}:=N_{\lambda }/L$
. We write
${W(\lambda )}:=N_{\lambda }/L$
. We write
![]() ${\operatorname {R}_L^G(\lambda )_{\eta }}$
for the character of
${\operatorname {R}_L^G(\lambda )_{\eta }}$
for the character of
![]() $\mathrm {Irr}(G\mid (L,\lambda ))$
associated with
$\mathrm {Irr}(G\mid (L,\lambda ))$
associated with
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
via the extension
$\eta \in \mathrm {Irr}(W(\lambda ))$
via the extension
![]() $\widetilde {\lambda }$
.
$\widetilde {\lambda }$
.
Accordingly, the parametrization of
![]() $\mathrm {Irr}(G\mid (L,\mathrm {Irr}_{cusp}(L)))$
depends on an extension map
$\mathrm {Irr}(G\mid (L,\mathrm {Irr}_{cusp}(L)))$
depends on an extension map
![]() ${\Lambda _L}$
with respect to
${\Lambda _L}$
with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathrm {Irr}_{cusp}(L)$
. For
$\mathrm {Irr}_{cusp}(L)$
. For
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
, let
$\lambda \in \mathrm {Irr}_{cusp}(L)$
, let
![]() ${R(\lambda )}\lhd W(\lambda )$
be defined as in [Reference Cabanes and EnguehardC, Prop. 10.6.3]. If
${R(\lambda )}\lhd W(\lambda )$
be defined as in [Reference Cabanes and EnguehardC, Prop. 10.6.3]. If
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
and
$\lambda \in \mathrm {Irr}_{cusp}(L)$
and
![]() $\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
, let
$\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
, let
![]() ${\delta _{\lambda ,\sigma }}$
be the unique linear character of
${\delta _{\lambda ,\sigma }}$
be the unique linear character of
![]() $W(^{\sigma }\lambda )$
satisfying
$W(^{\sigma }\lambda )$
satisfying
We only use the formula with some simplifying assumptions on
![]() $R(\lambda )$
and
$R(\lambda )$
and
![]() $\delta _{\lambda ,\sigma }$
.
$\delta _{\lambda ,\sigma }$
.
Theorem 2.7 (Malle–Späth [Reference Malle and TestermanMS, Ths. 4.6 and 4.7])
Let
![]() $\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
and
$\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
and
![]() $\Lambda _L$
be an N-equivariant extension map with respect to
$\Lambda _L$
be an N-equivariant extension map with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathrm {Irr}_{cusp}(L)$
. Assume that
$\mathrm {Irr}_{cusp}(L)$
. Assume that
![]() $\operatorname {R}_L^G(\lambda )_{\eta }$
(
$\operatorname {R}_L^G(\lambda )_{\eta }$
(
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
,
$\lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
) is defined using
$\eta \in \mathrm {Irr}(W(\lambda ))$
) is defined using
![]() $\Lambda _L$
and
$\Lambda _L$
and
Then
![]() $^{\sigma }(\operatorname {R}_L^G(\lambda )_{\eta })= \operatorname {R}_L^G({}^{\sigma }\lambda )_{^{\sigma }\eta \delta _{\lambda ,\sigma }^{-1}}$
for every
$^{\sigma }(\operatorname {R}_L^G(\lambda )_{\eta })= \operatorname {R}_L^G({}^{\sigma }\lambda )_{^{\sigma }\eta \delta _{\lambda ,\sigma }^{-1}}$
for every
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
.
$\eta \in \mathrm {Irr}(W(\lambda ))$
.
In §5 of [Reference Malle and TestermanMS], the analog of Theorem A was proved for characters in
![]() $\mathrm {Irr}(G \mid (T_0, \mathrm {Irr}_{cusp}(T_0))$
by studying
$\mathrm {Irr}(G \mid (T_0, \mathrm {Irr}_{cusp}(T_0))$
by studying
![]() $\mathrm {Irr}_{cusp}({\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)^F)$
. For other standard Levi subgroups, the strategy from [Reference Malle and TestermanMS] leads naturally to the following statement where we focus on a single L and its stabilizer in E. Sections 3–6 will ensure the assumptions for the groups from Notation 2.2 whenever
$\mathrm {Irr}_{cusp}({\mathrm {N}}_{{\mathbf G}}({\mathbf T}_0)^F)$
. For other standard Levi subgroups, the strategy from [Reference Malle and TestermanMS] leads naturally to the following statement where we focus on a single L and its stabilizer in E. Sections 3–6 will ensure the assumptions for the groups from Notation 2.2 whenever
![]() ${{{{\mathbf G}}^F}} =\mathrm {D}_{ l, \mathrm {sc}}(q)$
.
${{{{\mathbf G}}^F}} =\mathrm {D}_{ l, \mathrm {sc}}(q)$
.
Theorem 2.8. Let
![]() ${\widetilde {L}'}:=\widetilde {T}_0 L$
,
${\widetilde {L}'}:=\widetilde {T}_0 L$
,
![]() ${\widetilde N'}:=\widetilde {T}_0 N$
and
${\widetilde N'}:=\widetilde {T}_0 N$
and
![]() ${\widehat N}:=NE_L$
. Assume that there exist:
${\widehat N}:=NE_L$
. Assume that there exist:
-
(i) an
 $\widehat N$
-stable
$\widehat N$
-stable
 ${\widetilde {L}'}$
-transversal
${\widetilde {L}'}$
-transversal
 $\mathbb {T}$
in
$\mathbb {T}$
in
 $\mathrm {Irr}_{cusp}(L)$
, an N-equivariant extension map
$\mathrm {Irr}_{cusp}(L)$
, an N-equivariant extension map
 $\Lambda _{L, \mathbb {T}}$
with respect to
$\Lambda _{L, \mathbb {T}}$
with respect to
 $L\lhd N$
for
$L\lhd N$
for
 $\mathbb {T}$
such that any
$\mathbb {T}$
such that any
 $\lambda \in \mathbb {T}$
satisfies Equation (2.2); and
$\lambda \in \mathbb {T}$
satisfies Equation (2.2); and -
(ii) some
 $E_L$
-stable
$E_L$
-stable
 ${\widetilde N'}$
-transversal in
${\widetilde N'}$
-transversal in
 $\mathrm {Irr}_{cusp}(N)$
.
$\mathrm {Irr}_{cusp}(N)$
.
Then there exists an
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde {\mathbf G}^F$
-transversal in
$\widetilde {\mathbf G}^F$
-transversal in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
.
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
.
For the proof of Theorem 2.8, we parametrize
![]() $\mathrm {Irr}_{cusp}(N)$
via a set
$\mathrm {Irr}_{cusp}(N)$
via a set
![]() $\mathcal P(L)$
using an extension map
$\mathcal P(L)$
using an extension map
![]() $\Lambda _L$
with respect to
$\Lambda _L$
with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathrm {Irr}_{cusp}(L)$
deduced from
$\mathrm {Irr}_{cusp}(L)$
deduced from
![]() $\Lambda _{L, \mathbb {T}}$
.
$\Lambda _{L, \mathbb {T}}$
.
Notation 2.9. Assume that
![]() $\mathbb {T}$
is an
$\mathbb {T}$
is an
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() ${\widetilde {L}'}$
-transversal in
${\widetilde {L}'}$
-transversal in
![]() $\mathrm {Irr}_{cusp}(L)$
. For each
$\mathrm {Irr}_{cusp}(L)$
. For each
![]() $\lambda \in \mathbb {T}$
, we denote by
$\lambda \in \mathbb {T}$
, we denote by
![]() ${\mathcal O}_{\lambda }$
its N-orbit in
${\mathcal O}_{\lambda }$
its N-orbit in
![]() $\mathrm {Irr}_{cusp}(L)$
. Note
$\mathrm {Irr}_{cusp}(L)$
. Note
![]() ${\mathcal O}_{\lambda }\subseteq \mathrm {Irr}_{cusp}(L)$
. Let
${\mathcal O}_{\lambda }\subseteq \mathrm {Irr}_{cusp}(L)$
. Let
![]() $M(\lambda )\subseteq {\widetilde {L}'}$
be a set of representatives of the
$M(\lambda )\subseteq {\widetilde {L}'}$
be a set of representatives of the
![]() ${\widetilde {L}'}_{\lambda }$
-cosets in
${\widetilde {L}'}_{\lambda }$
-cosets in
![]() $\widetilde {L}'$
. We define an extension map
$\widetilde {L}'$
. We define an extension map
![]() $\Lambda _{L}$
on
$\Lambda _{L}$
on
![]() ${\mathcal O}_{\lambda }$
by
${\mathcal O}_{\lambda }$
by
Hence,
![]() $\Lambda _L$
is defined, but depends on the choice of
$\Lambda _L$
is defined, but depends on the choice of
![]() $M(\lambda )$
. The map
$M(\lambda )$
. The map
![]() $\Lambda _L': \mathrm {Irr}_{cusp}(L)\longrightarrow \coprod _{L\leq I \leq N} \mathrm {Irr}(I)$
with
$\Lambda _L': \mathrm {Irr}_{cusp}(L)\longrightarrow \coprod _{L\leq I \leq N} \mathrm {Irr}(I)$
with
![]() $\Lambda _L'(\mu ):={\left. \Lambda _L(\mu )\right\rceil _{{N_{\widetilde {\mu }}}}}$
for every
$\Lambda _L'(\mu ):={\left. \Lambda _L(\mu )\right\rceil _{{N_{\widetilde {\mu }}}}}$
for every
![]() $\mu \in \mathrm {Irr}_{cusp}(L)$
is well defined, where
$\mu \in \mathrm {Irr}_{cusp}(L)$
is well defined, where
![]() $\widetilde {\mu }\in \mathrm {Irr}({\widetilde {L}'}_{\mu })$
is an extension of
$\widetilde {\mu }\in \mathrm {Irr}({\widetilde {L}'}_{\mu })$
is an extension of
![]() $\mu $
. In contrast to
$\mu $
. In contrast to
![]() $\Lambda _L$
, we see that
$\Lambda _L$
, we see that
![]() $\Lambda _L'$
is independent of the choice of
$\Lambda _L'$
is independent of the choice of
![]() $M(\lambda )$
. Observe that
$M(\lambda )$
. Observe that
![]() $[N/L, {\widetilde {L}'}/L]=1$
. The map
$[N/L, {\widetilde {L}'}/L]=1$
. The map
![]() $\Lambda _L'$
is even
$\Lambda _L'$
is even
![]() $\widehat N {\widetilde {L}'}$
-equivariant since
$\widehat N {\widetilde {L}'}$
-equivariant since
![]() $\Lambda _L$
is N-equivariant and
$\Lambda _L$
is N-equivariant and
![]() $\Lambda _{L,\mathbb {T}}$
is
$\Lambda _{L,\mathbb {T}}$
is
![]() $\widehat N$
-equivariant.
$\widehat N$
-equivariant.
We write
![]() ${\mathcal P '(L)}$
for the set of pairs
${\mathcal P '(L)}$
for the set of pairs
![]() $(\lambda ,\eta )$
with
$(\lambda ,\eta )$
with
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
and
$\lambda \in \mathrm {Irr}_{cusp}(L)$
and
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
. The groups N and W act naturally via conjugation on
$\eta \in \mathrm {Irr}(W(\lambda ))$
. The groups N and W act naturally via conjugation on
![]() ${\mathcal P ' (L)}$
. We denote by
${\mathcal P ' (L)}$
. We denote by
![]() ${\mathcal P(L)}$
the set of N-orbits in
${\mathcal P(L)}$
the set of N-orbits in
![]() $\mathcal P '(L)$
and by
$\mathcal P '(L)$
and by
![]() ${\overline {(\lambda ,\eta )}}$
the N-orbit containing
${\overline {(\lambda ,\eta )}}$
the N-orbit containing
![]() $(\lambda ,\eta )$
. Since L is mostly clear from the context, we omit it, writing
$(\lambda ,\eta )$
. Since L is mostly clear from the context, we omit it, writing
![]() ${\mathcal P '}$
and
${\mathcal P '}$
and
![]() ${\mathcal P}$
.
${\mathcal P}$
.
The parametrization of
![]() $\mathrm {Irr}_{cusp}(N)$
is given by the following.
$\mathrm {Irr}_{cusp}(N)$
is given by the following.
Proposition 2.10. Let
![]() $\Lambda _{L}$
,
$\Lambda _{L}$
,
![]() $\mathcal P '$
, and
$\mathcal P '$
, and
![]() $\mathcal P$
be as in 2.8 and 2.9.
$\mathcal P$
be as in 2.8 and 2.9.
-
(a) Then the map
is a well-defined bijection. $$ \begin{align*}\Upsilon: \mathcal P \longrightarrow \mathrm{Irr}_{cusp}(N) {\text{ with }} \overline{(\lambda,\eta)}\longmapsto (\Lambda_L(\lambda )\eta)^N\end{align*} $$
$$ \begin{align*}\Upsilon: \mathcal P \longrightarrow \mathrm{Irr}_{cusp}(N) {\text{ with }} \overline{(\lambda,\eta)}\longmapsto (\Lambda_L(\lambda )\eta)^N\end{align*} $$
-
(b)
 $^{\sigma }\Upsilon (\overline {(\lambda ,\eta )})=\Upsilon (\overline {(^{\sigma }\lambda ,{}^{\sigma }\eta \delta _{\lambda ,\sigma })})$
for every
$^{\sigma }\Upsilon (\overline {(\lambda ,\eta )})=\Upsilon (\overline {(^{\sigma }\lambda ,{}^{\sigma }\eta \delta _{\lambda ,\sigma })})$
for every
 $\sigma \in \mathrm {Aut}(G)_{L,\mathrm {HC} }$
and
$\sigma \in \mathrm {Aut}(G)_{L,\mathrm {HC} }$
and
 $\overline {(\lambda ,\eta )}\in \mathcal P$
, where
$\overline {(\lambda ,\eta )}\in \mathcal P$
, where
 $\delta _{\lambda ,\sigma }\in \mathrm {Irr}(W(^{\sigma }\lambda ))$
is as given in 2.6.
$\delta _{\lambda ,\sigma }\in \mathrm {Irr}(W(^{\sigma }\lambda ))$
is as given in 2.6.
Proof. Clifford theory together with Gallagher’s lemma [Reference IsaacsI, 6.17] proves part (a). The definition of
![]() $\delta _{\lambda ,\sigma }$
in Equation (2.1) from 2.6 leads to part (b).
$\delta _{\lambda ,\sigma }$
in Equation (2.1) from 2.6 leads to part (b).
In combination with Theorem 2.7, we obtain a proof of Theorem 2.8.
Proof of Theorem 2.8
For the application of Theorem 2.7, we have to ensure that under our assumptions, Equation (2.2) holds for characters
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
. For every
$\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
. For every
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
, the character
$\lambda \in \mathrm {Irr}_{cusp}(L)$
, the character
![]() $\Lambda _L(\lambda )$
is an extension of
$\Lambda _L(\lambda )$
is an extension of
![]() $\Lambda _L'(\lambda )$
. Accordingly,
$\Lambda _L'(\lambda )$
. Accordingly,
![]() $\delta _{\lambda ,\sigma }$
defined as the unique linear character of
$\delta _{\lambda ,\sigma }$
defined as the unique linear character of
![]() $W(^{\sigma } \lambda )$
such that
$W(^{\sigma } \lambda )$
such that
![]() $^{\sigma }\Lambda _L(\lambda )=\Lambda _L(^{\sigma }\lambda )\delta _{\lambda ,\sigma }$
satisfies as well
$^{\sigma }\Lambda _L(\lambda )=\Lambda _L(^{\sigma }\lambda )\delta _{\lambda ,\sigma }$
satisfies as well
![]() ${\left. {}^{\sigma }\Lambda _L(\lambda )\right\rceil _{{N_{\widetilde {\lambda }^{\sigma } }}}} ={\left. \Lambda _L(^{\sigma }\lambda )\, \, \delta _{\lambda ,\sigma }\right\rceil _{{N_{\widetilde {\lambda } ^{\sigma } }}}}$
. Since
${\left. {}^{\sigma }\Lambda _L(\lambda )\right\rceil _{{N_{\widetilde {\lambda }^{\sigma } }}}} ={\left. \Lambda _L(^{\sigma }\lambda )\, \, \delta _{\lambda ,\sigma }\right\rceil _{{N_{\widetilde {\lambda } ^{\sigma } }}}}$
. Since
![]() $\Lambda _L'(\lambda )$
is
$\Lambda _L'(\lambda )$
is
![]() ${\widetilde N'} E_L$
-equivariant, we see that
${\widetilde N'} E_L$
-equivariant, we see that
![]() ${\left. \delta _{\lambda ,\sigma }\right\rceil _{{N_{\widetilde {\lambda } ^{\sigma } }}}}$
is trivial. Accordingly,
${\left. \delta _{\lambda ,\sigma }\right\rceil _{{N_{\widetilde {\lambda } ^{\sigma } }}}}$
is trivial. Accordingly,
![]() $\ker (\delta _{\lambda ,\sigma })\geq N_{^{\sigma } \widetilde {\lambda }}/L$
for every
$\ker (\delta _{\lambda ,\sigma })\geq N_{^{\sigma } \widetilde {\lambda }}/L$
for every
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
and
$\lambda \in \mathrm {Irr}_{cusp}(L)$
and
![]() $\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
where
$\sigma \in \mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
where
![]() $\widetilde {\lambda }$
denotes an extension of
$\widetilde {\lambda }$
denotes an extension of
![]() $\lambda $
to
$\lambda $
to
![]() ${\widetilde {L}'}_{\lambda }$
. Recall
${\widetilde {L}'}_{\lambda }$
. Recall
![]() $W(^{\sigma } \widetilde {\lambda })=N_{^{\sigma } \widetilde {\lambda }}/L$
. In combination with the inclusion
$W(^{\sigma } \widetilde {\lambda })=N_{^{\sigma } \widetilde {\lambda }}/L$
. In combination with the inclusion
![]() $R(^{\sigma } \lambda ) \leq W(^{\sigma } \widetilde {\lambda }) $
from [Reference CarterCSS, Lem. 4.14], we obtain the required containment (2.2).
$R(^{\sigma } \lambda ) \leq W(^{\sigma } \widetilde {\lambda }) $
from [Reference CarterCSS, Lem. 4.14], we obtain the required containment (2.2).
Via Harish-Chandra induction, the map
is well defined according to [Reference Malle and TestermanMS, Th. 4.7] and bijective. Hence,
![]() $\Upsilon '\circ \Upsilon ^{-1}$
is a bijection between
$\Upsilon '\circ \Upsilon ^{-1}$
is a bijection between
![]() $\mathrm {Irr}_{cusp}(N)$
and
$\mathrm {Irr}_{cusp}(N)$
and
![]() $\mathrm {Irr}( G\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Via
$\mathrm {Irr}( G\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Via
![]() $\Upsilon $
and
$\Upsilon $
and
![]() $\Upsilon '$
, the group
$\Upsilon '$
, the group
![]() $\mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
and hence
$\mathrm {Aut}({{{{\mathbf G}}^F}})_{L,{\mathrm {HC}}}$
and hence
![]() ${\widetilde N'} E_L$
act on
${\widetilde N'} E_L$
act on
![]() $\mathcal P$
. By the description of this action given in Theorem 2.7 and Proposition 2.10, these actions coincide. Hence,
$\mathcal P$
. By the description of this action given in Theorem 2.7 and Proposition 2.10, these actions coincide. Hence,
![]() $\Upsilon '\circ \Upsilon ^{-1}$
is
$\Upsilon '\circ \Upsilon ^{-1}$
is
![]() ${\widetilde N'} E_L$
-equivariant. By Assumption 2.8
(ii), every
${\widetilde N'} E_L$
-equivariant. By Assumption 2.8
(ii), every
![]() $\psi _0\in \mathrm {Irr}_{cusp}(N)$
has an
$\psi _0\in \mathrm {Irr}_{cusp}(N)$
has an
![]() ${\widetilde {L}'}$
-conjugate
${\widetilde {L}'}$
-conjugate
![]() $\psi $
such that
$\psi $
such that
![]() $({\widetilde N'}E_L )_{\psi }= {\widetilde N'}_{\psi } (E_L)_{\psi } $
. Hence, every
$({\widetilde N'}E_L )_{\psi }= {\widetilde N'}_{\psi } (E_L)_{\psi } $
. Hence, every
![]() $\chi _0\in \mathrm {Irr}(G\mid (L,\mathrm {Irr}_{cusp}(L)))$
has an
$\chi _0\in \mathrm {Irr}(G\mid (L,\mathrm {Irr}_{cusp}(L)))$
has an
![]() $\widetilde N'$
-conjugate
$\widetilde N'$
-conjugate
![]() $\chi $
with
$\chi $
with
![]() $(\widetilde {\mathbf G}^F E_L)_{\chi }=G(\widetilde N' E_L )_{\chi }=G(\widetilde N^{\prime }_{\chi }) (E_L)_{\chi }=\widetilde {\mathbf G}^F_{\chi } (E_L)_{\chi } $
. This implies the statement (see Lemma 2.4).
$(\widetilde {\mathbf G}^F E_L)_{\chi }=G(\widetilde N' E_L )_{\chi }=G(\widetilde N^{\prime }_{\chi }) (E_L)_{\chi }=\widetilde {\mathbf G}^F_{\chi } (E_L)_{\chi } $
. This implies the statement (see Lemma 2.4).
In the following sections, we verify the assumptions of Theorem 2.8: We prove Assumption 2.8
(ii), that is, that every
![]() $\psi \in \mathrm {Irr}_{cusp}(N)$
is
$\psi \in \mathrm {Irr}_{cusp}(N)$
is
![]() ${\widetilde {L}'}$
-conjugate to some
${\widetilde {L}'}$
-conjugate to some
![]() $\psi _0$
with
$\psi _0$
with
![]() $({\widetilde N'}E_L)_{\psi _0}={\widetilde N'}_{\psi _0} (E_L)_{\psi _0}$
, and prove the existence of an extension map as required in Assumption 2.8
(i). Note that by Lusztig [Reference LusztigL1] and Geck [Reference GeckG], an extension map exists. Their proofs are indirect, and we do not see how the required properties can be deduced from their proofs. In later sections, we give an independent explicit construction of the required extension map.
$({\widetilde N'}E_L)_{\psi _0}={\widetilde N'}_{\psi _0} (E_L)_{\psi _0}$
, and prove the existence of an extension map as required in Assumption 2.8
(i). Note that by Lusztig [Reference LusztigL1] and Geck [Reference GeckG], an extension map exists. Their proofs are indirect, and we do not see how the required properties can be deduced from their proofs. In later sections, we give an independent explicit construction of the required extension map.
2.3 Action on characters of normalizers of Levi subgroups
In the following, we discuss some basic considerations that will be applied to ensure Assumption 2.8
(ii). In the case where
![]() $L=T_0$
, Assumption 2.8
(ii) holds, whenever the underlying group
$L=T_0$
, Assumption 2.8
(ii) holds, whenever the underlying group
![]() ${{{{\mathbf G}}^F}}$
is of simply connected type (see [Reference Malle and TestermanMS, Proof of Cor. 5.3]). The assumption on the characters
${{{{\mathbf G}}^F}}$
is of simply connected type (see [Reference Malle and TestermanMS, Proof of Cor. 5.3]). The assumption on the characters
![]() $\mathrm {Irr}_{cusp}(N)$
is very similar to the results [Reference Cabanes and SpäthCS2, Prop. 5.13], [Reference Cabanes and SpäthCS3, Th. 5.1], and [Reference Cabanes and SpäthCS4, 5.E] on
$\mathrm {Irr}_{cusp}(N)$
is very similar to the results [Reference Cabanes and SpäthCS2, Prop. 5.13], [Reference Cabanes and SpäthCS3, Th. 5.1], and [Reference Cabanes and SpäthCS4, 5.E] on
![]() $\mathrm {Irr}({\mathrm {N}}_{{\mathbf H}}({\mathbf S})^F)$
for Sylow
$\mathrm {Irr}({\mathrm {N}}_{{\mathbf H}}({\mathbf S})^F)$
for Sylow
![]() $\Phi _d$
-tori
$\Phi _d$
-tori
![]() ${\mathbf S}$
of
${\mathbf S}$
of
![]() $({{\mathbf H}},F)$
, where
$({{\mathbf H}},F)$
, where
![]() ${{\mathbf H}}$
is a simple simply connected group of type different from
${{\mathbf H}}$
is a simple simply connected group of type different from
![]() $\mathrm {D}_l$
and d is a positive integer. The proof there relies on [, Th. 4.3], and we use here a similar strategy. The following proposition gives the road map for the verification of Assumption 2.8
(ii).
$\mathrm {D}_l$
and d is a positive integer. The proof there relies on [, Th. 4.3], and we use here a similar strategy. The following proposition gives the road map for the verification of Assumption 2.8
(ii).
We set
![]() ${W(\phi )}=N_{\phi }/L$
for every
${W(\phi )}=N_{\phi }/L$
for every
![]() $L\leq M\leq \widetilde {T}_0L$
and
$L\leq M\leq \widetilde {T}_0L$
and
![]() $\phi \in \mathrm {Irr}(M)$
.
$\phi \in \mathrm {Irr}(M)$
.
Proposition 2.11. Let
![]() $\widehat N$
,
$\widehat N$
,
![]() $\widetilde {L}'=\widetilde {T}_0L$
be as in Theorem 2.8,
$\widetilde {L}'=\widetilde {T}_0L$
be as in Theorem 2.8,
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\Lambda _{L,\mathbb {T}}$
as in Assumption 2.8
(i), and
$\Lambda _{L,\mathbb {T}}$
as in Assumption 2.8
(i), and
![]() $\Upsilon $
from Proposition 2.10. Let
$\Upsilon $
from Proposition 2.10. Let
![]() $\lambda \in \mathbb {T} $
,
$\lambda \in \mathbb {T} $
,
![]() $\widetilde {\lambda } \in \mathrm {Irr}(\widetilde {L}^{\prime }_ \lambda \mid \lambda )$
,
$\widetilde {\lambda } \in \mathrm {Irr}(\widetilde {L}^{\prime }_ \lambda \mid \lambda )$
,
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
, and
$\eta \in \mathrm {Irr}(W(\lambda ))$
, and
![]() $\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
. We set
$\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
. We set
![]() ${{\widehat W}}:=\widehat N/L =NE_L/L$
and
${{\widehat W}}:=\widehat N/L =NE_L/L$
and
![]() ${\widehat K(\lambda )}:=\widehat W_{\lambda }$
. If
${\widehat K(\lambda )}:=\widehat W_{\lambda }$
. If
![]() $\eta $
is
$\eta $
is
![]() $\widehat K(\lambda )_{\eta _0}$
-stable, then
$\widehat K(\lambda )_{\eta _0}$
-stable, then
We adapt the arguments from the proof of [Reference Cabanes and SpäthCS3, Th. 4.3], where
![]() $\eta $
is assumed to be
$\eta $
is assumed to be
![]() ${\mathrm {N}}_{W\rtimes E_L}(W(\widetilde {\lambda }))_{\eta _0}$
-stable. Note that
${\mathrm {N}}_{W\rtimes E_L}(W(\widetilde {\lambda }))_{\eta _0}$
-stable. Note that
![]() $\widehat K(\lambda )$
normalizes
$\widehat K(\lambda )$
normalizes
![]() $W(\lambda )$
, but this group is in general different from
$W(\lambda )$
, but this group is in general different from
![]() ${\mathrm {N}}_{W\rtimes E_L}(W(\widetilde {\lambda }))$
.
${\mathrm {N}}_{W\rtimes E_L}(W(\widetilde {\lambda }))$
.
Proof. Recall
![]() $\psi =\Upsilon (\overline {(\lambda ,\eta )})=(\Lambda _{L,\mathbb {T}}(\lambda )\eta )^N$
. By the assumptions on
$\psi =\Upsilon (\overline {(\lambda ,\eta )})=(\Lambda _{L,\mathbb {T}}(\lambda )\eta )^N$
. By the assumptions on
![]() $\mathbb {T}$
,
$\mathbb {T}$
,
![]() $(\widehat N {\widetilde {L}'})_{\lambda }=\widehat N_{\lambda } {\widetilde {L}'}_{\lambda }$
for every
$(\widehat N {\widetilde {L}'})_{\lambda }=\widehat N_{\lambda } {\widetilde {L}'}_{\lambda }$
for every
![]() $\lambda \in \mathbb {T}$
.
$\lambda \in \mathbb {T}$
.
Let
![]() $\widetilde {\lambda }\in \mathrm {Irr}({\widetilde {L}'}_{\lambda }\mid \lambda )$
and
$\widetilde {\lambda }\in \mathrm {Irr}({\widetilde {L}'}_{\lambda }\mid \lambda )$
and
![]() $\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
. According to [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11],
$\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
. According to [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11],
![]() $\widetilde {\lambda }$
is an extension of
$\widetilde {\lambda }$
is an extension of
![]() $\lambda $
. The group
$\lambda $
. The group
![]() ${\widetilde {L}'}_{\lambda }/(L\operatorname Z({{\widetilde G}}))$
acts by multiplication with linear characters of
${\widetilde {L}'}_{\lambda }/(L\operatorname Z({{\widetilde G}}))$
acts by multiplication with linear characters of
![]() $W(\lambda )/W(\widetilde {\lambda })$
on
$W(\lambda )/W(\widetilde {\lambda })$
on
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. Computing the action of
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. Computing the action of
![]() $W(\lambda )/W(\widetilde {\lambda })$
on
$W(\lambda )/W(\widetilde {\lambda })$
on
![]() $\mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
shows that the action of
$\mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
shows that the action of
![]() $\widetilde {L}^{\prime }_{\lambda }/L$
on
$\widetilde {L}^{\prime }_{\lambda }/L$
on
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is transitive. Hence, the characters
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is transitive. Hence, the characters
![]() $\{ (\Lambda _L(\lambda )\eta ')^N \mid \eta '\in \mathrm {Irr}(W(\lambda )\mid \eta _0)\}$
are the
$\{ (\Lambda _L(\lambda )\eta ')^N \mid \eta '\in \mathrm {Irr}(W(\lambda )\mid \eta _0)\}$
are the
![]() ${\widetilde {L}'}_{\lambda }$
-conjugates of
${\widetilde {L}'}_{\lambda }$
-conjugates of
![]() $\psi $
.
$\psi $
.
Let
![]() $l\in {\widetilde {L}'}$
and
$l\in {\widetilde {L}'}$
and
![]() $\widehat n\in \widehat N$
with
$\widehat n\in \widehat N$
with
![]() $\psi ^{l}=(\psi )^{\widehat n}$
. Note that
$\psi ^{l}=(\psi )^{\widehat n}$
. Note that
![]() $\psi ^{\widehat n}\in \mathrm {Irr}(N\mid \mathbb {T})$
since
$\psi ^{\widehat n}\in \mathrm {Irr}(N\mid \mathbb {T})$
since
![]() $\mathbb {T}$
is
$\mathbb {T}$
is
![]() $\widehat N$
-stable. Then
$\widehat N$
-stable. Then
![]() $\mathrm {Irr}({\left. \psi ^{l}\right\rceil _{{L}}})$
is the N-orbit of
$\mathrm {Irr}({\left. \psi ^{l}\right\rceil _{{L}}})$
is the N-orbit of
![]() $\lambda ^{l}$
. Recall
$\lambda ^{l}$
. Recall
![]() $\mathbb {T}$
is an
$\mathbb {T}$
is an
![]() $\widetilde {L}'$
-transversal. If
$\widetilde {L}'$
-transversal. If
![]() $l\notin {\widetilde {L}'}_{\lambda }$
, then
$l\notin {\widetilde {L}'}_{\lambda }$
, then
![]() $\lambda ^{l}\neq \lambda $
and
$\lambda ^{l}\neq \lambda $
and
![]() $\lambda ^{l}\notin \mathbb {T}$
, in particular
$\lambda ^{l}\notin \mathbb {T}$
, in particular
![]() $\psi ^{l}\notin \mathrm {Irr}(N\mid \mathbb {T})$
. This implies
$\psi ^{l}\notin \mathrm {Irr}(N\mid \mathbb {T})$
. This implies
![]() $l\in {\widetilde {L}'}_{\lambda }$
and
$l\in {\widetilde {L}'}_{\lambda }$
and
![]() $\psi ^{l}=(\Lambda _L(\lambda )\eta \nu )^N$
for some linear character
$\psi ^{l}=(\Lambda _L(\lambda )\eta \nu )^N$
for some linear character
![]() $\nu $
of
$\nu $
of
![]() $\mathrm {Irr}(W(\lambda )/W(\widetilde {\lambda }))$
. Accordingly,
$\mathrm {Irr}(W(\lambda )/W(\widetilde {\lambda }))$
. Accordingly,
![]() $(\psi )^{\widehat n}\in \mathrm {Irr}(N\mid \lambda )$
and hence
$(\psi )^{\widehat n}\in \mathrm {Irr}(N\mid \lambda )$
and hence
![]() $(\psi )^{\widehat n}=(\psi )^{\widehat n'}$
for some
$(\psi )^{\widehat n}=(\psi )^{\widehat n'}$
for some
![]() $\widehat n'\in \widehat N_{\lambda }$
. Note that
$\widehat n'\in \widehat N_{\lambda }$
. Note that
The equality
![]() $\psi ^{l}=\psi ^{\widehat n'}$
implies
$\psi ^{l}=\psi ^{\widehat n'}$
implies
![]() $\eta ^{\widehat n'}=\eta \nu $
and hence
$\eta ^{\widehat n'}=\eta \nu $
and hence
![]() $\widehat n' L\in W(\lambda ) \widehat K(\lambda )_{\eta _0}$
. As
$\widehat n' L\in W(\lambda ) \widehat K(\lambda )_{\eta _0}$
. As
![]() $\eta $
is
$\eta $
is
![]() $\widehat K(\lambda )_{\eta _0}$
-stable,
$\widehat K(\lambda )_{\eta _0}$
-stable,
![]() $\eta ^{\widehat n'}=\eta $
and hence
$\eta ^{\widehat n'}=\eta $
and hence
![]() $\psi ^{\widehat n'}=\psi $
. This shows
$\psi ^{\widehat n'}=\psi $
. This shows
![]() $(\widehat N {\widetilde {L}'} )_{\psi }=\widehat N_{\psi } {\widetilde {L}'}_{\psi }$
.
$(\widehat N {\widetilde {L}'} )_{\psi }=\widehat N_{\psi } {\widetilde {L}'}_{\psi }$
.
The above proposition allows us to prove the following result showing how to construct an
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() $\widetilde {L}'$
-transversal in
$\widetilde {L}'$
-transversal in
![]() $\mathrm {Irr}_{cusp}(N)$
.
$\mathrm {Irr}_{cusp}(N)$
.
Proposition 2.12. In the situation of Lemma 2.8, assume that:
-
(i)
 $(\widehat N {\widetilde {L}'})_{\lambda }=\widehat N_{\lambda } {\widetilde {L}'}_{\lambda }$
for every
$(\widehat N {\widetilde {L}'})_{\lambda }=\widehat N_{\lambda } {\widetilde {L}'}_{\lambda }$
for every
 $\lambda \in \mathbb {T}$
,
$\lambda \in \mathbb {T}$
, -
(ii) there exists an
 $\widehat N$
-equivariant extension map
$\widehat N$
-equivariant extension map
 $\Lambda _{L,\mathbb {T}}$
with respect to
$\Lambda _{L,\mathbb {T}}$
with respect to
 $L\lhd N$
for
$L\lhd N$
for
 $\mathbb {T}$
, and
$\mathbb {T}$
, and -
(iii) for every
 $\lambda \in \mathbb {T}$
,
$\lambda \in \mathbb {T}$
,
 $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
, and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
, and
 $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
 $\widehat K(\lambda )_{\eta _0}$
-stable
$\widehat K(\lambda )_{\eta _0}$
-stable
 $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
Let
![]() $\overline {\mathbb {T}}\subseteq \mathrm {Irr}_{cusp}(L)$
be the set of characters that are
$\overline {\mathbb {T}}\subseteq \mathrm {Irr}_{cusp}(L)$
be the set of characters that are
![]() ${\widetilde {L}'}$
-conjugate to one in
${\widetilde {L}'}$
-conjugate to one in
![]() $\mathbb {T}$
. Then there exists some
$\mathbb {T}$
. Then there exists some
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() ${\widetilde {L}'}$
-transversal in
${\widetilde {L}'}$
-transversal in
![]() $\mathrm {Irr}(N\mid \overline {\mathbb {T}})$
.
$\mathrm {Irr}(N\mid \overline {\mathbb {T}})$
.
Proof. By the assumptions, there exists
![]() $\mathcal P_1 \subseteq \mathcal P$
such that:
$\mathcal P_1 \subseteq \mathcal P$
such that:
-
• if
 $\overline {(\lambda ,\eta )} \in \mathcal P_1$
, then
$\overline {(\lambda ,\eta )} \in \mathcal P_1$
, then
 $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
 $\eta $
is
$\eta $
is
 $\widehat K(\lambda )_{\eta _0}$
-stable for some
$\widehat K(\lambda )_{\eta _0}$
-stable for some
 $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
 $\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
; and
$\eta _0\in \mathrm {Irr}({\left. \eta \right\rceil _{{W(\widetilde {\lambda })}}})$
; and -
• for each
 $\lambda \in \mathbb {T}$
,
$\lambda \in \mathbb {T}$
,
 $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
 $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
 $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
with
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
with
 $\overline { (\lambda ,\eta )}\in \mathcal P_1$
.
$\overline { (\lambda ,\eta )}\in \mathcal P_1$
.
Proposition 2.11 tells us that the characters
![]() $\Upsilon (\mathcal P_1)$
can form part of an
$\Upsilon (\mathcal P_1)$
can form part of an
![]() $E_L$
-stable
$E_L$
-stable
![]() ${\widetilde {L}'}$
-transversal.
${\widetilde {L}'}$
-transversal.
According to Proposition 2.10, for every
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, the group
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, the group
![]() ${\widetilde {L}'}_{\lambda }$
acts transitively on the set
${\widetilde {L}'}_{\lambda }$
acts transitively on the set
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. Since for each
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. Since for each
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
there exists some
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
such that
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
such that
![]() $\overline { (\lambda ,\eta )}\in \mathcal P_1$
, each
$\overline { (\lambda ,\eta )}\in \mathcal P_1$
, each
![]() ${\widetilde {L}'}$
-orbit has a nonempty intersection with
${\widetilde {L}'}$
-orbit has a nonempty intersection with
![]() $\Upsilon (\mathcal P_1)$
. This implies that every character in
$\Upsilon (\mathcal P_1)$
. This implies that every character in
![]() $\Upsilon (\mathcal P_1)$
has the property required (see Lemma 2.4).
$\Upsilon (\mathcal P_1)$
has the property required (see Lemma 2.4).
2.4 Reminder on cuspidal characters
The considerations of §2.2 explain how the action of automorphisms on non-cuspidal characters depends on the underlying cuspidal character and a character of the relative Weyl group associated with a cuspidal pair. For the proof of Theorem A, we require some general results on cuspidal characters that we collect here. By a theorem of Malle, stabilizers of cuspidal characters coincide with those of semisimple characters (see [Reference BonnaféB1, 15.A] for a definition of semisimple characters).
Theorem 2.13. Let
![]() ${{\mathbf H}}$
be a simply connected simple linear algebraic group with an
${{\mathbf H}}$
be a simply connected simple linear algebraic group with an
![]() ${\mathbb {F}}_q$
-structure given by a Frobenius map
${\mathbb {F}}_q$
-structure given by a Frobenius map
![]() $F:{{\mathbf H}}\rightarrow {{\mathbf H}}$
. Let
$F:{{\mathbf H}}\rightarrow {{\mathbf H}}$
. Let
![]() ${{\mathbf H}} \longrightarrow \widetilde {{\mathbf H}}$
be a regular embedding, and let
${{\mathbf H}} \longrightarrow \widetilde {{\mathbf H}}$
be a regular embedding, and let
![]() $E({{{{\mathbf H}}}^F})$
be a group of automorphisms of
$E({{{{\mathbf H}}}^F})$
be a group of automorphisms of
![]() ${{{{\mathbf H}}}^F}$
generated by graph and field automorphisms as in 2.2. Then there exists some
${{{{\mathbf H}}}^F}$
generated by graph and field automorphisms as in 2.2. Then there exists some
![]() $E({{{{\mathbf H}}}^F})$
-stable
$E({{{{\mathbf H}}}^F})$
-stable
![]() $\widetilde {{\mathbf H}}^F$
-transversal in
$\widetilde {{\mathbf H}}^F$
-transversal in
![]() $\mathrm {Irr}_{cusp}( {{\mathbf H}}^F)$
.
$\mathrm {Irr}_{cusp}( {{\mathbf H}}^F)$
.
Proof. We abbreviate
![]() $E({{{{\mathbf H}}}^F})$
as E. Let
$E({{{{\mathbf H}}}^F})$
as E. Let
![]() $\chi \in \mathrm {Irr}_{cusp}({{\mathbf H}}^F)$
. According to Lemma 2.4, it is sufficient to prove that
$\chi \in \mathrm {Irr}_{cusp}({{\mathbf H}}^F)$
. According to Lemma 2.4, it is sufficient to prove that
![]() $\chi $
has some
$\chi $
has some
![]() $\widetilde {{\mathbf H}}^F$
-conjugate
$\widetilde {{\mathbf H}}^F$
-conjugate
![]() $\chi _0$
with
$\chi _0$
with
![]() $(\widetilde {{\mathbf H}}^F E)_{\chi _0}= \widetilde {{\mathbf H}}^F_{\chi _0} E_{\chi _0}$
. By [Reference Malle and SpäthMal2, Th. 1], there exists a semisimple character
$(\widetilde {{\mathbf H}}^F E)_{\chi _0}= \widetilde {{\mathbf H}}^F_{\chi _0} E_{\chi _0}$
. By [Reference Malle and SpäthMal2, Th. 1], there exists a semisimple character
![]() $\rho $
of
$\rho $
of
![]() ${{{{\mathbf H}}}^F}$
, such that
${{{{\mathbf H}}}^F}$
, such that
![]() $\rho $
and
$\rho $
and
![]() $\chi $
have the same stabilizer. By [Reference SpäthS4, Proof of 3.4(c)], the semisimple character
$\chi $
have the same stabilizer. By [Reference SpäthS4, Proof of 3.4(c)], the semisimple character
![]() $\rho $
has some
$\rho $
has some
![]() $(\widetilde {{\mathbf H}})^F$
-conjugate
$(\widetilde {{\mathbf H}})^F$
-conjugate
![]() $\rho _0$
with
$\rho _0$
with
![]() $(\widetilde {{\mathbf H}}^F E)_{\rho _0}= \widetilde {{\mathbf H}}^F_{\rho _0} E_{\rho _0}$
.
$(\widetilde {{\mathbf H}}^F E)_{\rho _0}= \widetilde {{\mathbf H}}^F_{\rho _0} E_{\rho _0}$
.
In our considerations on
![]() $\mathrm {D}_{l,sc}(q)$
, we assume the following for all
$\mathrm {D}_{l,sc}(q)$
, we assume the following for all
![]() $4\leq l'<l$
, which amounts to
$4\leq l'<l$
, which amounts to
![]() $A(\infty )$
for cuspidal characters in rank
$A(\infty )$
for cuspidal characters in rank
![]() $<l$
. This was called
$<l$
. This was called
![]() $A_{\mathrm {cusp}}$
in our Introduction. In [Reference SpäthS7], we will see that it is actually always satisfied.
$A_{\mathrm {cusp}}$
in our Introduction. In [Reference SpäthS7], we will see that it is actually always satisfied.
Hypothesis 2.14 (Extension of cuspidal characters of
 $\mathrm {D}_{l',sc}(q)$
)
$\mathrm {D}_{l',sc}(q)$
)
Let
![]() ${{\mathbf H}}$
be a simply connected simple group of type
${{\mathbf H}}$
be a simply connected simple group of type
![]() $\mathrm {D}_{l'}$
(
$\mathrm {D}_{l'}$
(
![]() $l'\geq 4$
), and let
$l'\geq 4$
), and let
![]() $F:{{\mathbf H}}\rightarrow {{\mathbf H}}$
a standard Frobenius endomorphism. Then there exists some
$F:{{\mathbf H}}\rightarrow {{\mathbf H}}$
a standard Frobenius endomorphism. Then there exists some
![]() $E({{{{\mathbf H}}}^F})$
-stable
$E({{{{\mathbf H}}}^F})$
-stable
![]() $\widetilde {{\mathbf H}}^F$
-transversal
$\widetilde {{\mathbf H}}^F$
-transversal
![]() $\mathbb {T}$
in
$\mathbb {T}$
in
![]() $\mathrm {Irr}_{cusp}({{\mathbf H}}^F)$
such that every
$\mathrm {Irr}_{cusp}({{\mathbf H}}^F)$
such that every
![]() $\chi \in \mathbb {T}$
extends to
$\chi \in \mathbb {T}$
extends to
![]() ${{\mathbf H}}^FE({{{{\mathbf H}}}^F})_{\chi }$
.
${{\mathbf H}}^FE({{{{\mathbf H}}}^F})_{\chi }$
.
The following facts are well known (see also [Reference BonnaféB1, 12.1]).
Lemma 2.15. Let
![]() ${{\mathbf G}}$
be a simply connected simple group with Frobenius endomorphism
${{\mathbf G}}$
be a simply connected simple group with Frobenius endomorphism
![]() $F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
,
$F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
,
![]() ${{\mathbf L}}$
an F-stable Levi subgroup of
${{\mathbf L}}$
an F-stable Levi subgroup of
![]() ${{\mathbf G}}$
,
${{\mathbf G}}$
,
![]() $L:={{\mathbf L}}^F$
,
$L:={{\mathbf L}}^F$
,
![]() $L_0:=[{{\mathbf L}},{{\mathbf L}}]^F$
, and
$L_0:=[{{\mathbf L}},{{\mathbf L}}]^F$
, and
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
.
$\lambda \in \mathrm {Irr}_{cusp}(L)$
.
-
(a) Then
 $\mathrm {Irr}({\left. \lambda \right\rceil _{{L_0}}}) \subseteq \mathrm {Irr}_{cusp}(L_0)$
.
$\mathrm {Irr}({\left. \lambda \right\rceil _{{L_0}}}) \subseteq \mathrm {Irr}_{cusp}(L_0)$
. -
(b) If
 $[{{\mathbf L}},{{\mathbf L}}]$
is a central product of F-stable semisimple groups
$[{{\mathbf L}},{{\mathbf L}}]$
is a central product of F-stable semisimple groups
 ${{\mathbf H}}_1$
and
${{\mathbf H}}_1$
and
 ${{\mathbf H}}_2$
, then
${{\mathbf H}}_2$
, then
 $\mathrm {Irr}({\left. \lambda \right\rceil _{{{{\mathbf H}}_1^F}}}) \subseteq \mathrm {Irr}_{cusp}({{\mathbf H}}_1^F)$
.
$\mathrm {Irr}({\left. \lambda \right\rceil _{{{{\mathbf H}}_1^F}}}) \subseteq \mathrm {Irr}_{cusp}({{\mathbf H}}_1^F)$
. -
(c) Let
 $ \widetilde {{\mathbf G}}$
be a reductive group with
$ \widetilde {{\mathbf G}}$
be a reductive group with
 ${\mathbb {F}}_q$
-structure given by
${\mathbb {F}}_q$
-structure given by
 $F:\widetilde {\mathbf G}\rightarrow \widetilde {\mathbf G}$
extending F already defined on
$F:\widetilde {\mathbf G}\rightarrow \widetilde {\mathbf G}$
extending F already defined on
 ${{\mathbf G}}$
and such that
${{\mathbf G}}$
and such that
 $[\widetilde {{\mathbf G}} , \widetilde {{\mathbf G}}]={{\mathbf G}} $
, then every
$[\widetilde {{\mathbf G}} , \widetilde {{\mathbf G}}]={{\mathbf G}} $
, then every
 $\widetilde {\lambda }\in \mathrm {Irr}((\operatorname Z(\widetilde {\mathbf G}){{\mathbf L}})^F\mid \lambda )$
is cuspidal.
$\widetilde {\lambda }\in \mathrm {Irr}((\operatorname Z(\widetilde {\mathbf G}){{\mathbf L}})^F\mid \lambda )$
is cuspidal.
Proof. For a finite group H with a split BN-pair of characteristic p, a given
![]() $\chi \in \mathrm {Irr} (H)$
is cuspidal if and only if the corresponding representation space has no nonzero fixed point under any O
$\chi \in \mathrm {Irr} (H)$
is cuspidal if and only if the corresponding representation space has no nonzero fixed point under any O
![]() $_p(P)$
for any proper parabolic subgroup P of H. It is then clear that for any
$_p(P)$
for any proper parabolic subgroup P of H. It is then clear that for any
![]() $H'\lhd H$
with
$H'\lhd H$
with
![]() $p'$
-index, one has
$p'$
-index, one has
![]() $\chi \in \mathrm {Irr}_{cusp} (H)$
if and only if
$\chi \in \mathrm {Irr}_{cusp} (H)$
if and only if
![]() ${\left. \chi \right\rceil _{{H'}}}$
has a cuspidal irreducible component (and then all are). This gives (a) and (c). For (b), note that
${\left. \chi \right\rceil _{{H'}}}$
has a cuspidal irreducible component (and then all are). This gives (a) and (c). For (b), note that
![]() ${{\mathbf H}}_1\cap {{\mathbf H}}_2$
is a group of semi-simple elements, so that the O
${{\mathbf H}}_1\cap {{\mathbf H}}_2$
is a group of semi-simple elements, so that the O
![]() $_p(P)$
’s as above for
$_p(P)$
’s as above for
![]() $H:={{\mathbf L}}_0^F$
are direct products of corresponding subgroups of
$H:={{\mathbf L}}_0^F$
are direct products of corresponding subgroups of
![]() ${{\mathbf H}}_1^F$
and
${{\mathbf H}}_1^F$
and
![]() ${{\mathbf H}}_2^F$
.
${{\mathbf H}}_2^F$
.
Remark 2.16.
-
(a) Let
 ${{\mathbf G}}$
be a simply connected simple group, and let
${{\mathbf G}}$
be a simply connected simple group, and let
 $\widetilde {{\mathbf G}}$
be a connected algebraic group with
$\widetilde {{\mathbf G}}$
be a connected algebraic group with
 $\widetilde {{\mathbf G}}={{\mathbf G}} \operatorname Z(\widetilde {{\mathbf G}})$
. Let
$\widetilde {{\mathbf G}}={{\mathbf G}} \operatorname Z(\widetilde {{\mathbf G}})$
. Let
 $F:\widetilde {{\mathbf G}}\rightarrow \widetilde {\mathbf G}$
be a Frobenius endomorphism stabilizing
$F:\widetilde {{\mathbf G}}\rightarrow \widetilde {\mathbf G}$
be a Frobenius endomorphism stabilizing
 ${{\mathbf G}}$
. Then
${{\mathbf G}}$
. Then
 $x\in \widetilde {\mathbf G}^F$
can be written as
$x\in \widetilde {\mathbf G}^F$
can be written as
 $x=gz$
with
$x=gz$
with
 $g\in {{\mathbf G}}$
and
$g\in {{\mathbf G}}$
and
 $z\in \operatorname Z(\widetilde {\mathbf G})$
, such that
$z\in \operatorname Z(\widetilde {\mathbf G})$
, such that
 $g^{-1}F(g)=z F(z^{-1})$
. If
$g^{-1}F(g)=z F(z^{-1})$
. If
 ${\mathcal L}:{{\mathbf G}}\rightarrow {{\mathbf G}}$
is defined by
${\mathcal L}:{{\mathbf G}}\rightarrow {{\mathbf G}}$
is defined by
 $g\mapsto g^{-1}F(g)$
and
$g\mapsto g^{-1}F(g)$
and
 ${{\widetilde G}}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
, we see where
${{\widetilde G}}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
, we see where $$ \begin{align*}{{{\widetilde{\mathbf G}}^F}} \leq {\widetilde G}. \widetilde Z,\end{align*} $$
$$ \begin{align*}{{{\widetilde{\mathbf G}}^F}} \leq {\widetilde G}. \widetilde Z,\end{align*} $$
 $\widetilde Z:=\{z\in \operatorname Z(\widetilde {\mathbf G})\mid F(z)\in z\operatorname Z({{\mathbf G}}) \}$
. Note that
$\widetilde Z:=\{z\in \operatorname Z(\widetilde {\mathbf G})\mid F(z)\in z\operatorname Z({{\mathbf G}}) \}$
. Note that
 ${\widetilde G}$
by its construction is independent of the choice of
${\widetilde G}$
by its construction is independent of the choice of
 $\widetilde {\mathbf G}$
. We also have
$\widetilde {\mathbf G}$
. We also have
 ${\widetilde G}={\operatorname N}_{{{\mathbf G}}}({{\mathbf G}}^F)$
as an easy consequence of [Reference BonnaféB1, Lem. 6.1].
${\widetilde G}={\operatorname N}_{{{\mathbf G}}}({{\mathbf G}}^F)$
as an easy consequence of [Reference BonnaféB1, Lem. 6.1].
-
(b) From now on, we assume additionally that
 $\operatorname Z(\widetilde {\mathbf G})$
is connected. Then the (outer) automorphisms of
$\operatorname Z(\widetilde {\mathbf G})$
is connected. Then the (outer) automorphisms of
 ${{{{\mathbf G}}^F}}$
induced by conjugation by some element
${{{{\mathbf G}}^F}}$
induced by conjugation by some element
 $g\in {\widetilde G}$
are called diagonal automorphisms and they are parametrized by
$g\in {\widetilde G}$
are called diagonal automorphisms and they are parametrized by
 $\mathcal L(g) [\operatorname Z({{\mathbf G}}),F]\in \operatorname Z({{\mathbf G}})/ [\operatorname Z({{\mathbf G}}),F]$
(see also [Reference Geck and MalleGM, 1.5.12]).
$\mathcal L(g) [\operatorname Z({{\mathbf G}}),F]\in \operatorname Z({{\mathbf G}})/ [\operatorname Z({{\mathbf G}}),F]$
(see also [Reference Geck and MalleGM, 1.5.12]).Note the difference with the convention used in the introduction where
 ${{\widetilde G}}$
was used to abbreviate
${{\widetilde G}}$
was used to abbreviate
 $\widetilde {\mathbf G}^F$
. We still clearly have
$\widetilde {\mathbf G}^F$
. We still clearly have
 ${{\widetilde G}}/\operatorname Z({{{{\mathbf G}}^F}})=\widetilde {\mathbf G}^F/\operatorname Z(\widetilde {\mathbf G}^F)$
.
${{\widetilde G}}/\operatorname Z({{{{\mathbf G}}^F}})=\widetilde {\mathbf G}^F/\operatorname Z(\widetilde {\mathbf G}^F)$
.
This allows the following conclusion for the above group
![]() ${\widetilde G}$
.
${\widetilde G}$
.
Theorem 2.17. Maximal extendibility holds with respect to
![]() ${{\mathbf G}}^F \lhd {\widetilde G}$
.
${{\mathbf G}}^F \lhd {\widetilde G}$
.
Proof. Let
![]() $\widetilde {\mathbf G}$
be a group with connected centre, such that there exists a regular embedding
$\widetilde {\mathbf G}$
be a group with connected centre, such that there exists a regular embedding
![]() ${{\mathbf G}}\rightarrow \widetilde {\mathbf G}$
that is also an
${{\mathbf G}}\rightarrow \widetilde {\mathbf G}$
that is also an
![]() ${\mathbb {F}}_q$
-morphism as in 2.2. Then, according to a theorem of Lusztig (see [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11]), maximal extendibility holds with respect to
${\mathbb {F}}_q$
-morphism as in 2.2. Then, according to a theorem of Lusztig (see [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11]), maximal extendibility holds with respect to
![]() ${{{{\mathbf G}}^F}}\lhd {{{\widetilde {\mathbf G}}^F}}$
, and
${{{{\mathbf G}}^F}}\lhd {{{\widetilde {\mathbf G}}^F}}$
, and
![]() $\chi $
has an extension
$\chi $
has an extension
![]() $\widetilde {\chi }$
to
$\widetilde {\chi }$
to
![]() ${{{\widetilde {\mathbf G}}^F}}_{\chi }$
. According to the above,
${{{\widetilde {\mathbf G}}^F}}_{\chi }$
. According to the above,
![]() ${{{\widetilde {\mathbf G}}^F}}\leq {\widetilde G}. \widetilde Z$
. Clearly,
${{{\widetilde {\mathbf G}}^F}}\leq {\widetilde G}. \widetilde Z$
. Clearly,
![]() $\widetilde {\chi }$
extends to
$\widetilde {\chi }$
extends to
![]() ${{{\widetilde {\mathbf G}}^F}}_{\chi }\widetilde Z$
since
${{{\widetilde {\mathbf G}}^F}}_{\chi }\widetilde Z$
since
![]() $\widetilde Z$
is abelian and
$\widetilde Z$
is abelian and
![]() $[\widetilde Z, {{{\widetilde {\mathbf G}}^F}}]=1$
. Now, we see that
$[\widetilde Z, {{{\widetilde {\mathbf G}}^F}}]=1$
. Now, we see that
![]() ${{{\widetilde {\mathbf G}}^F}}_{\chi }\widetilde Z={\widetilde G}_{\chi } \widetilde Z$
and hence
${{{\widetilde {\mathbf G}}^F}}_{\chi }\widetilde Z={\widetilde G}_{\chi } \widetilde Z$
and hence
![]() $\chi $
extends to
$\chi $
extends to
![]() ${\widetilde G}_{\chi }$
as well.
${\widetilde G}_{\chi }$
as well.
Proposition 2.18. In the situation of Remark 2.16, let
![]() ${{\mathbf K}}\leq {{\mathbf G}}$
be an F-stable reductive subgroup with
${{\mathbf K}}\leq {{\mathbf G}}$
be an F-stable reductive subgroup with
![]() ${\mathbf T}_0\leq {{\mathbf K}}$
. Let
${\mathbf T}_0\leq {{\mathbf K}}$
. Let
![]() $\widetilde {{\mathbf K}}:={{\mathbf K}} \operatorname Z(\widetilde {{\mathbf G}})$
and
$\widetilde {{\mathbf K}}:={{\mathbf K}} \operatorname Z(\widetilde {{\mathbf G}})$
and
![]() $\widetilde K:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {{\mathbf K}}$
. Let
$\widetilde K:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {{\mathbf K}}$
. Let
![]() $\chi \in \mathrm {Irr}({{{{\mathbf K}}^F}})$
,
$\chi \in \mathrm {Irr}({{{{\mathbf K}}^F}})$
,
![]() $\widetilde {\chi }\in \mathrm {Irr}(\widetilde {{\mathbf K}}^F \mid \chi )$
, and
$\widetilde {\chi }\in \mathrm {Irr}(\widetilde {{\mathbf K}}^F \mid \chi )$
, and
![]() $\nu \in \mathrm {Irr}({\left. \widetilde {\chi }\right\rceil _{{\operatorname Z(\widetilde {{\mathbf G}}^F)}}})$
. As said above,
$\nu \in \mathrm {Irr}({\left. \widetilde {\chi }\right\rceil _{{\operatorname Z(\widetilde {{\mathbf G}}^F)}}})$
. As said above,
![]() $\chi $
extends to
$\chi $
extends to
![]() $\widetilde {{\mathbf K}}^F_{\chi }$
. Let
$\widetilde {{\mathbf K}}^F_{\chi }$
. Let
![]() $\gamma \in E({{{{\mathbf G}}^F}})_{(\chi ,{{\mathbf K}})}$
and
$\gamma \in E({{{{\mathbf G}}^F}})_{(\chi ,{{\mathbf K}})}$
and
![]() $\mu \in \mathrm {Irr}(\widetilde {{\mathbf K}}^F/{{{{\mathbf K}}^F}})$
with
$\mu \in \mathrm {Irr}(\widetilde {{\mathbf K}}^F/{{{{\mathbf K}}^F}})$
with
![]() $\widetilde {\chi }^{\gamma }=\widetilde {\chi }\mu $
. Then the following are equivalent:
$\widetilde {\chi }^{\gamma }=\widetilde {\chi }\mu $
. Then the following are equivalent:
-
(i)
 $\chi $
has a
$\chi $
has a
 $\gamma $
-stable extension to
$\gamma $
-stable extension to
 $\widetilde K _{\chi }$
.
$\widetilde K _{\chi }$
. -
(ii) For
 $\widetilde Z':=\mathcal L(\widetilde K_{\chi })$
, there exists some extension
$\widetilde Z':=\mathcal L(\widetilde K_{\chi })$
, there exists some extension
 $\widetilde {\nu }\in \mathrm {Irr}(\widetilde Z')$
of
$\widetilde {\nu }\in \mathrm {Irr}(\widetilde Z')$
of
 $\nu $
such that
$\nu $
such that
 $\mu (tz)= \widetilde {\nu } (z)^{-1} (\widetilde {\nu }^{\gamma } (z){}) $
for every
$\mu (tz)= \widetilde {\nu } (z)^{-1} (\widetilde {\nu }^{\gamma } (z){}) $
for every
 $t\in \widetilde K_{\chi }$
and
$t\in \widetilde K_{\chi }$
and
 $z \in \widetilde Z'$
with
$z \in \widetilde Z'$
with
 $tz\in \widetilde {{\mathbf K}}^F_{\chi }$
.
$tz\in \widetilde {{\mathbf K}}^F_{\chi }$
.
Proof. We prove the statement only in the case where
![]() ${{\mathbf K}}={{\mathbf G}}$
. The results transfer to a general
${{\mathbf K}}={{\mathbf G}}$
. The results transfer to a general
![]() ${{\mathbf K}}$
as only the quotient groups are relevant to our considerations. Let
${{\mathbf K}}$
as only the quotient groups are relevant to our considerations. Let
![]() $\widetilde {\chi }$
be a
$\widetilde {\chi }$
be a
![]() $\gamma $
-stable extension to
$\gamma $
-stable extension to
![]() ${\widetilde G}_{\chi }$
, then there exists an extension
${\widetilde G}_{\chi }$
, then there exists an extension
![]() $\widetilde {\nu }\in \mathrm {Irr}(\widetilde Z')$
of
$\widetilde {\nu }\in \mathrm {Irr}(\widetilde Z')$
of
![]() $\nu $
such that
$\nu $
such that
![]() $\widetilde {\chi }:=({\left. \widetilde {\chi }.\widetilde {\nu }\right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\chi }}}})^{{{{\widetilde {\mathbf G}}^F}}}$
. We observe
$\widetilde {\chi }:=({\left. \widetilde {\chi }.\widetilde {\nu }\right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\chi }}}})^{{{{\widetilde {\mathbf G}}^F}}}$
. We observe
![]() $(\widetilde {\chi }.\widetilde {\nu })^{\gamma }=\widetilde {\chi }.\widetilde {\nu }^{\gamma }$
. This leads to the given formula for
$(\widetilde {\chi }.\widetilde {\nu })^{\gamma }=\widetilde {\chi }.\widetilde {\nu }^{\gamma }$
. This leads to the given formula for
![]() $\mu $
in (ii).
$\mu $
in (ii).
For the other direction, let
![]() $\chi _0$
be the extension of
$\chi _0$
be the extension of
![]() $\chi $
to
$\chi $
to
![]() $\widetilde {{\mathbf G}}^F_{\chi }$
such that
$\widetilde {{\mathbf G}}^F_{\chi }$
such that
![]() $\widetilde {\chi }=\chi _0^{\widetilde {\mathbf G}^F}$
. Then
$\widetilde {\chi }=\chi _0^{\widetilde {\mathbf G}^F}$
. Then
![]() $\chi _0^{\gamma }=\chi _0{\left. \mu \right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\chi }}}}$
and
$\chi _0^{\gamma }=\chi _0{\left. \mu \right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\chi }}}}$
and
![]() $ \chi _0.\widetilde {\nu }$
is an extension of
$ \chi _0.\widetilde {\nu }$
is an extension of
![]() $\chi $
to
$\chi $
to
![]() $\widetilde {{\mathbf G}}_{\chi }^F\widetilde Z'={\widetilde G}_{\chi } \widetilde Z'$
. The character
$\widetilde {{\mathbf G}}_{\chi }^F\widetilde Z'={\widetilde G}_{\chi } \widetilde Z'$
. The character
![]() $\widehat {\chi }:={\left. (\chi _0.\widetilde {\nu })\right\rceil _{{{\widetilde G}_{\chi }}}}$
satisfies
$\widehat {\chi }:={\left. (\chi _0.\widetilde {\nu })\right\rceil _{{{\widetilde G}_{\chi }}}}$
satisfies
There is some
![]() $\kappa \in \mathrm {Irr}({\widetilde G}_{\chi }/{{\mathbf G}}^F)$
with
$\kappa \in \mathrm {Irr}({\widetilde G}_{\chi }/{{\mathbf G}}^F)$
with
![]() $\widetilde {\chi } ^{\gamma }=\widetilde {\chi } \kappa $
. According to [Reference IsaacsI, (6.17)], the above equality of characters implies
$\widetilde {\chi } ^{\gamma }=\widetilde {\chi } \kappa $
. According to [Reference IsaacsI, (6.17)], the above equality of characters implies
![]() $\kappa (t)\widetilde {\nu }^{\gamma } (z)(\widetilde {\nu } (z))^{-1}= \mu (tz)$
, whenever
$\kappa (t)\widetilde {\nu }^{\gamma } (z)(\widetilde {\nu } (z))^{-1}= \mu (tz)$
, whenever
![]() $t\in {\widetilde G}_{\chi }$
and
$t\in {\widetilde G}_{\chi }$
and
![]() $z\in \widetilde Z'$
with
$z\in \widetilde Z'$
with
![]() $tz\in \widetilde {{\mathbf G}}^F_{\chi }$
. By the assumption on
$tz\in \widetilde {{\mathbf G}}^F_{\chi }$
. By the assumption on
![]() $\mu $
and
$\mu $
and
![]() $\widetilde {\nu }$
, this leads to
$\widetilde {\nu }$
, this leads to
![]() $\kappa =1$
. Then
$\kappa =1$
. Then
![]() $\chi $
has a
$\chi $
has a
![]() $\gamma $
-stable extension to
$\gamma $
-stable extension to
![]() ${\widetilde G}_{\chi }$
.
${\widetilde G}_{\chi }$
.
For later, we restate
![]() $A(\infty )$
for groups of type
$A(\infty )$
for groups of type
![]() $\mathrm A$
(see [Reference Cabanes and SpäthCS2]).
$\mathrm A$
(see [Reference Cabanes and SpäthCS2]).
Proposition 2.19. Let
![]() $G=\operatorname {SL}_n(q)$
,
$G=\operatorname {SL}_n(q)$
,
![]() ${\widetilde G}:=\operatorname {GL}_n(q)$
, and write
${\widetilde G}:=\operatorname {GL}_n(q)$
, and write
![]() ${E(\operatorname {SL}_n(q))} $
for the group of field and graph automorphisms of G and
${E(\operatorname {SL}_n(q))} $
for the group of field and graph automorphisms of G and
![]() ${\widetilde G}$
with regard to the usual BN-pair.
${\widetilde G}$
with regard to the usual BN-pair.
-
(a) Then there exists an
 $E(\operatorname {SL}_n(q))$
-stable
$E(\operatorname {SL}_n(q))$
-stable
 $\operatorname {GL}_n(q)$
-transversal
$\operatorname {GL}_n(q)$
-transversal
 $\mathbb {T}$
in
$\mathbb {T}$
in
 $\mathrm {Irr}(\operatorname {SL}_n(q))$
, such that every
$\mathrm {Irr}(\operatorname {SL}_n(q))$
, such that every
 $\chi \in \mathbb {T}$
extends to
$\chi \in \mathbb {T}$
extends to
 $\operatorname {SL}_n(q)E(\operatorname {SL}_n(q))_{\chi }$
.
$\operatorname {SL}_n(q)E(\operatorname {SL}_n(q))_{\chi }$
. -
(b) Let
 $\gamma '$
be the automorphism of
$\gamma '$
be the automorphism of
 $\operatorname {SL}_n(q)$
given by transpose-inverse, and let
$\operatorname {SL}_n(q)$
given by transpose-inverse, and let
 $E'(\operatorname {SL}_n(q))\leq \mathrm {Aut}(\operatorname {SL}_n(q))$
be the subgroup generated by
$E'(\operatorname {SL}_n(q))\leq \mathrm {Aut}(\operatorname {SL}_n(q))$
be the subgroup generated by
 $\gamma '$
and the field automorphisms described above. Then
$\gamma '$
and the field automorphisms described above. Then
 $E'(\operatorname {SL}_n(q))$
is abelian and there exists an
$E'(\operatorname {SL}_n(q))$
is abelian and there exists an
 $E'(\operatorname {SL}_n(q))$
-stable
$E'(\operatorname {SL}_n(q))$
-stable
 $\operatorname {GL}_n(q)$
-transversal
$\operatorname {GL}_n(q)$
-transversal
 $\mathbb {T}$
in
$\mathbb {T}$
in
 $\mathrm {Irr}(\operatorname {SL}_n(q))$
, such that every
$\mathrm {Irr}(\operatorname {SL}_n(q))$
, such that every
 $\chi \in \mathbb {T}$
extends to
$\chi \in \mathbb {T}$
extends to
 $\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))_{\chi }$
.
$\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))_{\chi }$
.
Proof. Part (a) follows from [Reference Cabanes and SpäthCS2, Th. 4.1] using Lemma 2.4.
Let
![]() $\gamma \in E(\operatorname {SL}_n(q))$
be the graph automorphism. Following the considerations in [Reference Cabanes and SpäthCS2, 3.2], we see that
$\gamma \in E(\operatorname {SL}_n(q))$
be the graph automorphism. Following the considerations in [Reference Cabanes and SpäthCS2, 3.2], we see that
![]() $\gamma '$
and
$\gamma '$
and
![]() $v_0\gamma $
induce the same automorphism of
$v_0\gamma $
induce the same automorphism of
![]() $\operatorname {SL}_n(q)$
, where
$\operatorname {SL}_n(q)$
, where
![]() $v_0\in \operatorname {SL}_n(p)$
is defined as in [Reference Cabanes and SpäthCS2, 3.2] and p is the prime dividing q. This proves that
$v_0\in \operatorname {SL}_n(p)$
is defined as in [Reference Cabanes and SpäthCS2, 3.2] and p is the prime dividing q. This proves that
![]() $\mathbb {T}$
is also
$\mathbb {T}$
is also
![]() $E'(\operatorname {SL}_n(q))$
-stable. For part (b), we have to prove that every
$E'(\operatorname {SL}_n(q))$
-stable. For part (b), we have to prove that every
![]() $\chi \in \mathbb {T}$
extends to its inertia group in
$\chi \in \mathbb {T}$
extends to its inertia group in
![]() $\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))$
. This statement is clear whenever
$\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))$
. This statement is clear whenever
![]() $E'(\operatorname {SL}_n(q))_{\chi }$
is cyclic (see [Reference IsaacsI, (9.12)]). If for
$E'(\operatorname {SL}_n(q))_{\chi }$
is cyclic (see [Reference IsaacsI, (9.12)]). If for
![]() $\chi \in \mathbb {T}$
the group
$\chi \in \mathbb {T}$
the group
![]() $E'(\operatorname {SL}_n(q))_{\chi }$
is noncyclic, we see
$E'(\operatorname {SL}_n(q))_{\chi }$
is noncyclic, we see
![]() $\gamma '\in E'(\operatorname {SL}_n(q))_{\chi }$
. Let
$\gamma '\in E'(\operatorname {SL}_n(q))_{\chi }$
. Let
![]() $F_{q'}\in E'(\operatorname {SL}_n(q))$
be a field automorphism such that
$F_{q'}\in E'(\operatorname {SL}_n(q))$
be a field automorphism such that
![]() $E'(\operatorname {SL}_n(q))_{\chi } ={\left\langle F_{q'},\gamma '\right\rangle }$
. By (a), there exists some
$E'(\operatorname {SL}_n(q))_{\chi } ={\left\langle F_{q'},\gamma '\right\rangle }$
. By (a), there exists some
![]() $\gamma $
-stable extension of
$\gamma $
-stable extension of
![]() $\chi $
to
$\chi $
to
![]() $G{\left\langle F_{q'}\right\rangle }$
. This extension is then also
$G{\left\langle F_{q'}\right\rangle }$
. This extension is then also
![]() $\gamma '$
and hence
$\gamma '$
and hence
![]() $\gamma v_0$
-stable as
$\gamma v_0$
-stable as
![]() $[v_0,F_{q'}]=1$
. From this, we deduce that
$[v_0,F_{q'}]=1$
. From this, we deduce that
![]() $\chi $
extends to
$\chi $
extends to
![]() $\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))_{\chi }$
.
$\operatorname {SL}_n(q)E'(\operatorname {SL}_n(q))_{\chi }$
.
3 The Levi subgroup and its normalizer
In this and the following section, we reprove with quite different methods that for every standard Levi subgroup L of
![]() $\mathrm {D}_{l,\mathrm {sc}}(q)$
, every
$\mathrm {D}_{l,\mathrm {sc}}(q)$
, every
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
extends to its stabilizer inside
$\lambda \in \mathrm {Irr}_{cusp}(L)$
extends to its stabilizer inside
![]() ${\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
, which follows from the mentioned results by Geck and Lusztig. For
${\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
, which follows from the mentioned results by Geck and Lusztig. For
![]() $E({{{{\mathbf G}}^F}})\leq \mathrm {Aut}({{{{\mathbf G}}^F}})$
from §2.2, we construct a
$E({{{{\mathbf G}}^F}})\leq \mathrm {Aut}({{{{\mathbf G}}^F}})$
from §2.2, we construct a
![]() $\widetilde {T}$
-transversal
$\widetilde {T}$
-transversal
![]() $\mathbb {T}$
of
$\mathbb {T}$
of
![]() $\mathrm {Irr}_{cusp}(L)$
and an
$\mathrm {Irr}_{cusp}(L)$
and an
![]() $N\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}(L)$
-equivariant extension map with respect to
$N\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}(L)$
-equivariant extension map with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Theorem 3.1. Let L be a standard Levi subgroup of
![]() ${{{{\mathbf G}}^F}}=\mathrm {D}_{l,sc}(q)$
. Let
${{{{\mathbf G}}^F}}=\mathrm {D}_{l,sc}(q)$
. Let
![]() $E_L:=\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}(L)$
, N,
$E_L:=\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}(L)$
, N,
![]() $\widehat N:=NE_L$
and
$\widehat N:=NE_L$
and
![]() ${\widetilde {L}'}:=\widetilde {T}_0 L$
be associated with L as in 2.8. If
${\widetilde {L}'}:=\widetilde {T}_0 L$
be associated with L as in 2.8. If
![]() $\mathrm {D}_{l',sc}(q)$
is a direct factor of
$\mathrm {D}_{l',sc}(q)$
is a direct factor of
![]() $[L,L]$
, then assume Hypothesis 2.14 holds for
$[L,L]$
, then assume Hypothesis 2.14 holds for
![]() $\mathrm {D}_{l',sc}(q)$
. Then:
$\mathrm {D}_{l',sc}(q)$
. Then:
-
(a) There exists an
 $\widehat N$
-stable
$\widehat N$
-stable
 ${\widetilde {L}'}$
-transversal
${\widetilde {L}'}$
-transversal
 $\mathbb {T}\subseteq \mathrm {Irr}_{cusp}(L)$
.
$\mathbb {T}\subseteq \mathrm {Irr}_{cusp}(L)$
. -
(b) There exists an
 $\widehat N$
-equivariant extension map
$\widehat N$
-equivariant extension map
 ${\Lambda _{L\lhd N}}$
with respect to
${\Lambda _{L\lhd N}}$
with respect to
 $L\lhd N$
for
$L\lhd N$
for
 $\mathbb {T}$
.
$\mathbb {T}$
.
This implies Theorem B and ensures Assumptions (i) and (ii) of Proposition 2.12. In [Reference Brough and SpäthBS, Th. 4.3] and [Reference CarterCSS, Prop. 4.13], the analogous result was shown in the case where
![]() ${{\mathbf G}}$
is of type
${{\mathbf G}}$
is of type
![]() $\mathrm A_l$
or
$\mathrm A_l$
or
![]() $\mathrm C_l$
. The interested reader may notice that without assuming Hypothesis 2.14 for smaller ranks, the proof we give implies a version of the theorem without the equivariance statement.
$\mathrm C_l$
. The interested reader may notice that without assuming Hypothesis 2.14 for smaller ranks, the proof we give implies a version of the theorem without the equivariance statement.
Like in the proofs given in [Reference Brough and SpäthBS] and [Reference CarterCSS], we essentially apply the following statement providing an extension map for nonlinear characters.
Proposition 3.2 [Reference CarterCSS, Prop. 4.1]
Let
![]() $K\lhd M$
be finite groups, let the group D act on M, stabilizing K, and let
$K\lhd M$
be finite groups, let the group D act on M, stabilizing K, and let
![]() $\mathbb {K}\subseteq \mathrm {Irr}(K)$
be
$\mathbb {K}\subseteq \mathrm {Irr}(K)$
be
![]() $MD$
-stable. Assume that there exist D-stable subgroups
$MD$
-stable. Assume that there exist D-stable subgroups
![]() ${K_0}$
and V of M such that:
${K_0}$
and V of M such that:
-
(i) the groups satisfy:
-
(i.1)
 $K={K_0} (K\cap V) $
and
$K={K_0} (K\cap V) $
and
 $H:= K\cap V \leq \operatorname Z(K)$
,
$H:= K\cap V \leq \operatorname Z(K)$
, -
(i.2)
 $M=KV$
;
$M=KV$
;
-
-
(ii) for
 $\mathbb {K}_0:=\bigcup _{\lambda \in \mathbb {K}}\mathrm {Irr}({\left. \lambda \right\rceil _{{{K_0}}}})$
, there exist:
$\mathbb {K}_0:=\bigcup _{\lambda \in \mathbb {K}}\mathrm {Irr}({\left. \lambda \right\rceil _{{{K_0}}}})$
, there exist:-
(ii.1) a
 $VD$
-equivariant extension map
$VD$
-equivariant extension map
 $\Lambda _0$
with respect to
$\Lambda _0$
with respect to
 $H\lhd V$
; and
$H\lhd V$
; and -
(ii.2) an
 $\epsilon (V)D$
-equivariant extension map
$\epsilon (V)D$
-equivariant extension map
 $\Lambda _{\epsilon }$
with respect to
$\Lambda _{\epsilon }$
with respect to
 ${K_0}\lhd {K_0}\rtimes \epsilon (V)$
for
${K_0}\lhd {K_0}\rtimes \epsilon (V)$
for
 $\mathbb {K}_0$
, where
$\mathbb {K}_0$
, where
 ${\epsilon }\colon V\to V/H$
denotes the canonical epimorphism.
${\epsilon }\colon V\to V/H$
denotes the canonical epimorphism.
-
Then there exists an
![]() $MD$
-equivariant extension map with respect to
$MD$
-equivariant extension map with respect to
![]() $K\lhd M$
for
$K\lhd M$
for
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
In this section, we construct the set
![]() $\mathbb {T}$
for Theorem 3.1(a) and introduce groups H, K,
$\mathbb {T}$
for Theorem 3.1(a) and introduce groups H, K,
![]() ${K_0}$
(see Lemma 3.11), M, D, and V (in Corollary 3.23) for a later application of Proposition 3.2 in the proof of Theorem 3.1
(b). Here, we show that the groups introduced satisfy the group-theoretic assumptions made in 3.2
(i). Afterward, in §4, we ensure the character-theoretic assumptions, namely 3.2
(ii) in order to prove Theorem 3.1
(b).
${K_0}$
(see Lemma 3.11), M, D, and V (in Corollary 3.23) for a later application of Proposition 3.2 in the proof of Theorem 3.1
(b). Here, we show that the groups introduced satisfy the group-theoretic assumptions made in 3.2
(i). Afterward, in §4, we ensure the character-theoretic assumptions, namely 3.2
(ii) in order to prove Theorem 3.1
(b).
3.1 Subgroups of the Levi subgroup L
As a first step, we dissect the root system of
![]() ${{\mathbf L}}$
and introduce subgroups of L with those new root systems. For a nonnegative integer i, let
${{\mathbf L}}$
and introduce subgroups of L with those new root systems. For a nonnegative integer i, let
![]() ${\underline {i}}:=\{1,\ldots , i\}$
. For computations with elements of
${\underline {i}}:=\{1,\ldots , i\}$
. For computations with elements of
![]() ${{\mathbf G}}$
, we use the Steinberg generators satisfying the Chevalley relations together with an explicit embedding of
${{\mathbf G}}$
, we use the Steinberg generators satisfying the Chevalley relations together with an explicit embedding of
![]() $\mathrm {D}_{l,sc}({\mathbb {F}}) $
into
$\mathrm {D}_{l,sc}({\mathbb {F}}) $
into
![]() $\mathrm B_{l,sc}({\mathbb {F}}) $
.
$\mathrm B_{l,sc}({\mathbb {F}}) $
.
Notation 3.3 (The groups
 ${{\mathbf G}}$
and
${{\mathbf G}}$
and
 ${\overline {\mathbf G}}$
, roots, and generators)
${\overline {\mathbf G}}$
, roots, and generators)
In this and the following section, we assume that the simply connected simple group
![]() ${{\mathbf G}}$
from 2.2 is of type
${{\mathbf G}}$
from 2.2 is of type
![]() $\mathrm {D}_l$
(
$\mathrm {D}_l$
(
![]() $l\geq 4$
) over
$l\geq 4$
) over
![]() ${\mathbb {F}}$
the algebraic closure of
${\mathbb {F}}$
the algebraic closure of
![]() ${\mathbb {F}}_p$
for
${\mathbb {F}}_p$
for
![]() $ p$
some odd prime. Hence,
$ p$
some odd prime. Hence,
![]() ${{\mathbf G}}\cong \mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
. Denote
${{\mathbf G}}\cong \mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
. Denote
![]() ${\underline {l}}:=\{1,\dots ,l\}$
. Let
${\underline {l}}:=\{1,\dots ,l\}$
. Let
![]() $ \Phi :=\{\pm e_i\pm e_j\mid i,j\in {\underline {l}},\, i\neq j \}$
be the root system of
$ \Phi :=\{\pm e_i\pm e_j\mid i,j\in {\underline {l}},\, i\neq j \}$
be the root system of
![]() ${{\mathbf G}}$
with simple roots
${{\mathbf G}}$
with simple roots
![]() ${{\alpha }_2}:=e_2+e_1$
,
${{\alpha }_2}:=e_2+e_1$
,
![]() ${{\alpha }_1}=e_2-e_1$
and
${{\alpha }_1}=e_2-e_1$
and
![]() ${{\alpha }_i}:=e_i-e_{i-1}$
(
${{\alpha }_i}:=e_i-e_{i-1}$
(
![]() $i\geq 3$
),
$i\geq 3$
),
(see [Reference Gorenstein, Lyons and SolomonGLS, Rem. 1.8.8]), where the set
![]() $\{{e_i}\}_{i\in {\underline {l}}}$
is an orthonormal basis of
$\{{e_i}\}_{i\in {\underline {l}}}$
is an orthonormal basis of
![]() $\mathbb R^l$
whose scalar product is denoted by
$\mathbb R^l$
whose scalar product is denoted by
![]() ${(x,y)}$
. The Chevalley generators
${(x,y)}$
. The Chevalley generators
![]() ${\mathbf x _{\alpha }(t)}$
,
${\mathbf x _{\alpha }(t)}$
,
![]() ${\mathbf {n}_{\alpha }(t')}$
and
${\mathbf {n}_{\alpha }(t')}$
and
![]() ${{\mathbf h} _{\alpha }(t')}$
(
${{\mathbf h} _{\alpha }(t')}$
(
![]() ${\alpha }\in \Phi $
,
${\alpha }\in \Phi $
,
![]() $t,t'\in {\mathbb {F}}$
with
$t,t'\in {\mathbb {F}}$
with
![]() $t'\neq 0$
) together with the Chevalley relations describe the group structure of
$t'\neq 0$
) together with the Chevalley relations describe the group structure of
![]() ${{\mathbf G}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, Th. 1.12.1]).
${{\mathbf G}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, Th. 1.12.1]).
Let
![]() ${\overline \Phi }:=\{\pm e_i,\,\pm e_i\pm e_j\mid i,j\in {\underline {l}},\, i\neq j \}$
,
${\overline \Phi }:=\{\pm e_i,\,\pm e_i\pm e_j\mid i,j\in {\underline {l}},\, i\neq j \}$
,
![]() ${{\overline {\mathbf G}}}:=\mathrm B_{l,sc}({\mathbb {F}})$
with Chevalley generators
${{\overline {\mathbf G}}}:=\mathrm B_{l,sc}({\mathbb {F}})$
with Chevalley generators
![]() $\overline {\mathbf x }_{\alpha }(t)$
,
$\overline {\mathbf x }_{\alpha }(t)$
,
![]() $\overline {\mathbf {n}} _{\alpha }(t')$
and
$\overline {\mathbf {n}} _{\alpha }(t')$
and
![]() $\overline {\mathbf {h}} _{\alpha }(t')$
(
$\overline {\mathbf {h}} _{\alpha }(t')$
(
![]() ${\alpha }\in \overline \Phi $
,
${\alpha }\in \overline \Phi $
,
![]() $t,t'\in {\mathbb {F}}$
with
$t,t'\in {\mathbb {F}}$
with
![]() $t'\neq 0$
). Assume that the structure constants of
$t'\neq 0$
). Assume that the structure constants of
![]() ${{\mathbf G}}$
and
${{\mathbf G}}$
and
![]() $\overline {{\mathbf G}}$
are chosen such that
$\overline {{\mathbf G}}$
are chosen such that
![]() $\mathbf x _{\alpha }(t)\mapsto \overline {\mathbf {x}} _{\alpha }(t)$
(
$\mathbf x _{\alpha }(t)\mapsto \overline {\mathbf {x}} _{\alpha }(t)$
(
![]() ${\alpha }\in \Phi $
,
${\alpha }\in \Phi $
,
![]() $t\in {\mathbb {F}}$
) defines an embedding
$t\in {\mathbb {F}}$
) defines an embedding
![]() $\iota _{\mathrm {D}}:{{\mathbf G}}\rightarrow \overline {{\mathbf G}}$
. For simplicity of notation, we write
$\iota _{\mathrm {D}}:{{\mathbf G}}\rightarrow \overline {{\mathbf G}}$
. For simplicity of notation, we write
![]() $ \mathbf x _{\alpha }(t)$
,
$ \mathbf x _{\alpha }(t)$
,
![]() $ \mathbf {n}_{\alpha }(t')=\mathbf x _{\alpha }(t')\mathbf x _{-{\alpha }}(-t'{}^{-1})\mathbf x _{\alpha }(t')$
, and
$ \mathbf {n}_{\alpha }(t')=\mathbf x _{\alpha }(t')\mathbf x _{-{\alpha }}(-t'{}^{-1})\mathbf x _{\alpha }(t')$
, and
![]() $ {\mathbf h} _{\alpha }(t')=\mathbf {n}_{\alpha }(t')\mathbf {n}_{\alpha }(1)^{-1}$
for the generators of
$ {\mathbf h} _{\alpha }(t')=\mathbf {n}_{\alpha }(t')\mathbf {n}_{\alpha }(1)^{-1}$
for the generators of
![]() ${\overline {\mathbf G}}$
and thus identify
${\overline {\mathbf G}}$
and thus identify
![]() ${{\mathbf G}}$
with the corresponding subgroup of
${{\mathbf G}}$
with the corresponding subgroup of
![]() ${\overline {\mathbf G}}$
. This is possible according to [Reference SpäthS2, 10.1] (see also [Reference Malle and TestermanMS, 2.Reference Cabanes and EnguehardC]). Among the relations between Chevalley generators, the following will be the most useful to us. For
${\overline {\mathbf G}}$
. This is possible according to [Reference SpäthS2, 10.1] (see also [Reference Malle and TestermanMS, 2.Reference Cabanes and EnguehardC]). Among the relations between Chevalley generators, the following will be the most useful to us. For
![]() $a,b\in {\mathbb R}^l\setminus \{0\}$
, recall
$a,b\in {\mathbb R}^l\setminus \{0\}$
, recall
![]() ${\langle a,b\rangle }= 2(a,b)/(b,b)$
. Let
${\langle a,b\rangle }= 2(a,b)/(b,b)$
. Let
![]() ${\alpha },\beta \in \overline {\Phi }$
,
${\alpha },\beta \in \overline {\Phi }$
,
![]() $t\in {\mathbb {F}}$
,
$t\in {\mathbb {F}}$
,
![]() $t'\in {\mathbb {F}^{\times }}$
. Then
$t'\in {\mathbb {F}^{\times }}$
. Then
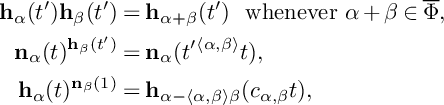 $$ \begin{align*} {\mathbf h} _{\alpha}(t'){\mathbf h}_{\beta}(t')&={\mathbf h} _{{\alpha}+\beta}(t')\ \ \text{whenever } {\alpha}+\beta\in\overline{\Phi},\\ \mathbf{n}_{\alpha}(t)^{{\mathbf h} _{\beta}(t')}&=\mathbf{n}_{\alpha}(t'{}^{{\left\langle {\alpha},\beta\right\rangle}}t), \\ {\mathbf h} _{\alpha}(t)^{\mathbf{n}_{\beta}(1)}&={\mathbf h} _{{\alpha}-{\left\langle {\alpha},\beta\right\rangle}\beta}(c_{{\alpha},\beta}t), \end{align*} $$
$$ \begin{align*} {\mathbf h} _{\alpha}(t'){\mathbf h}_{\beta}(t')&={\mathbf h} _{{\alpha}+\beta}(t')\ \ \text{whenever } {\alpha}+\beta\in\overline{\Phi},\\ \mathbf{n}_{\alpha}(t)^{{\mathbf h} _{\beta}(t')}&=\mathbf{n}_{\alpha}(t'{}^{{\left\langle {\alpha},\beta\right\rangle}}t), \\ {\mathbf h} _{\alpha}(t)^{\mathbf{n}_{\beta}(1)}&={\mathbf h} _{{\alpha}-{\left\langle {\alpha},\beta\right\rangle}\beta}(c_{{\alpha},\beta}t), \end{align*} $$
where the first line is from [Reference Gorenstein, Lyons and SolomonGLS, 1.12.1(e)], the second is easy from [Reference Gorenstein, Lyons and SolomonGLS, 1.12.1(g)], and the third, along with the definition of
![]() $c_{{\alpha },\beta }\in \{\pm 1\}$
, is from [Reference Gorenstein, Lyons and SolomonGLS, 1.12.1(i)].
$c_{{\alpha },\beta }\in \{\pm 1\}$
, is from [Reference Gorenstein, Lyons and SolomonGLS, 1.12.1(i)].
Definition 3.4. Let
![]() ${{\mathbf X}_{{\alpha }}}:={\left\langle \mathbf x _{{\alpha }}(t)\mid t \in {\mathbb {F}}\right\rangle }$
for
${{\mathbf X}_{{\alpha }}}:={\left\langle \mathbf x _{{\alpha }}(t)\mid t \in {\mathbb {F}}\right\rangle }$
for
![]() ${\alpha }\in \overline \Phi $
,
${\alpha }\in \overline \Phi $
,
![]() ${\mathbf T}:={\left\langle {\mathbf h} _{\alpha }(t')\mid {\alpha }\in \Phi , t'\in {\mathbb {F}}^{\times }\right\rangle }$
, and
${\mathbf T}:={\left\langle {\mathbf h} _{\alpha }(t')\mid {\alpha }\in \Phi , t'\in {\mathbb {F}}^{\times }\right\rangle }$
, and
![]() ${\overline {\mathbf T}}:={\left\langle {\mathbf h} _{\alpha }(t')\mid {\alpha }\in \overline {\Phi }, t'\in {\mathbb {F}}^{\times }\right\rangle }$
. Note
${\overline {\mathbf T}}:={\left\langle {\mathbf h} _{\alpha }(t')\mid {\alpha }\in \overline {\Phi }, t'\in {\mathbb {F}}^{\times }\right\rangle }$
. Note
![]() ${\mathbf T}=\overline {\mathbf T}$
is the image of the map
${\mathbf T}=\overline {\mathbf T}$
is the image of the map
with kernel
![]() $\{ (t^{\prime }_1,\dots ,t^{\prime }_l)\in \{ \pm 1\} ^l \mid t^{\prime }_1\dots t^{\prime }_l=1 \}$
(see also [Reference SpäthS2, 10.1]). The group
$\{ (t^{\prime }_1,\dots ,t^{\prime }_l)\in \{ \pm 1\} ^l \mid t^{\prime }_1\dots t^{\prime }_l=1 \}$
(see also [Reference SpäthS2, 10.1]). The group
![]() ${\mathbf T}$
can be chosen as the group
${\mathbf T}$
can be chosen as the group
![]() ${\mathbf T}_0$
from 2.2 and
${\mathbf T}_0$
from 2.2 and
![]() ${\mathbf T}{\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Delta \right\rangle }$
as the group
${\mathbf T}{\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Delta \right\rangle }$
as the group
![]() ${\mathbf B}$
.
${\mathbf B}$
.
Denoting
![]() ${h_0}={\mathbf h} _{e_1}(-1)$
, one has
${h_0}={\mathbf h} _{e_1}(-1)$
, one has
![]() $\operatorname Z(\overline {{\mathbf G}})={\left\langle h_0\right\rangle }$
of order 2 (see [Reference Gorenstein, Lyons and SolomonGLS, 1.12.6]) with
$\operatorname Z(\overline {{\mathbf G}})={\left\langle h_0\right\rangle }$
of order 2 (see [Reference Gorenstein, Lyons and SolomonGLS, 1.12.6]) with
![]() $\overline {{\mathbf G}}/{\left\langle h_0\right\rangle } ={\operatorname {SO}_{2l+1}({\mathbb {F}})}\geq {\operatorname {SO}_{2l}({\mathbb {F}})}={{\mathbf G}}/{\left\langle h_0\right\rangle }$
.
$\overline {{\mathbf G}}/{\left\langle h_0\right\rangle } ={\operatorname {SO}_{2l+1}({\mathbb {F}})}\geq {\operatorname {SO}_{2l}({\mathbb {F}})}={{\mathbf G}}/{\left\langle h_0\right\rangle }$
.
For every positive integer i, let
![]() $ {F_{p^i}}:{\overline {\mathbf G}} \rightarrow {\overline {\mathbf G}}$
be the Frobenius endomorphism given by
$ {F_{p^i}}:{\overline {\mathbf G}} \rightarrow {\overline {\mathbf G}}$
be the Frobenius endomorphism given by
![]() $\mathbf x _{{\alpha }}(t)\mapsto \mathbf x _{\alpha }(t^{p^i})$
for
$\mathbf x _{{\alpha }}(t)\mapsto \mathbf x _{\alpha }(t^{p^i})$
for
![]() $t\in {\mathbb {F}}$
and
$t\in {\mathbb {F}}$
and
![]() ${\alpha }\in \overline {\Phi }$
. We write
${\alpha }\in \overline {\Phi }$
. We write
![]() ${\gamma }$
for the graph automorphism of
${\gamma }$
for the graph automorphism of
![]() ${{\mathbf G}}$
given by
${{\mathbf G}}$
given by
![]() $\mathbf x _{{\epsilon }{\alpha }}(t)\mapsto \mathbf x _{{\epsilon }\gamma _0({\alpha })}(t)$
for
$\mathbf x _{{\epsilon }{\alpha }}(t)\mapsto \mathbf x _{{\epsilon }\gamma _0({\alpha })}(t)$
for
![]() $t\in {\mathbb {F}}$
,
$t\in {\mathbb {F}}$
,
![]() ${\epsilon }\in \{\pm 1\}$
and
${\epsilon }\in \{\pm 1\}$
and
![]() ${\alpha }\in \Delta $
, where
${\alpha }\in \Delta $
, where
![]() ${\gamma _0}$
denotes the symmetry of the Dynkin diagram of
${\gamma _0}$
denotes the symmetry of the Dynkin diagram of
![]() $\Delta $
of order
$\Delta $
of order
![]() $2$
with
$2$
with
![]() ${\alpha }_2 \mapsto {\alpha }_1$
. If
${\alpha }_2 \mapsto {\alpha }_1$
. If
![]() $l=4$
, we denote by
$l=4$
, we denote by
![]() ${\gamma _3}$
the graph automorphism of
${\gamma _3}$
the graph automorphism of
![]() ${{\mathbf G}}$
induced by the symmetry of the Dynkin diagram of
${{\mathbf G}}$
induced by the symmetry of the Dynkin diagram of
![]() $\Delta $
with order
$\Delta $
with order
![]() $3$
sending
$3$
sending
![]() ${\alpha }_2 \mapsto {\alpha }_1$
and
${\alpha }_2 \mapsto {\alpha }_1$
and
![]() ${\alpha }_1\mapsto {\alpha }_4$
. We assume that
${\alpha }_1\mapsto {\alpha }_4$
. We assume that
![]() $ F=F_{q}$
for
$ F=F_{q}$
for
![]() $ q:=p^f$
, where
$ q:=p^f$
, where
![]() $ f$
is a positive integer. Note that the group
$ f$
is a positive integer. Note that the group
![]() $E({{{{\mathbf G}}^F}})$
from 2.2 satisfies accordingly
$E({{{{\mathbf G}}^F}})$
from 2.2 satisfies accordingly
![]() ${E({{{{\mathbf G}}^F}})}={\left\langle {\left. F_p\right\rceil _{{{{{{\mathbf G}}^F}}}}},{\left. \gamma \right\rceil _{{{{{{\mathbf G}}^F}}}}}\right\rangle }$
whenever
${E({{{{\mathbf G}}^F}})}={\left\langle {\left. F_p\right\rceil _{{{{{{\mathbf G}}^F}}}}},{\left. \gamma \right\rceil _{{{{{{\mathbf G}}^F}}}}}\right\rangle }$
whenever
![]() $l\geq 5$
; otherwise,
$l\geq 5$
; otherwise,
![]() $l=4$
and
$l=4$
and
![]() $E({{{{\mathbf G}}^F}})={\left\langle {\left. F_p\right\rceil _{{{{{{\mathbf G}}^F}}}}}, {\left. \gamma \right\rceil _{{{{{{\mathbf G}}^F}}}}},{\left. \gamma _3\right\rceil _{{{{{{\mathbf G}}^F}}}}}\right\rangle }$
.
$E({{{{\mathbf G}}^F}})={\left\langle {\left. F_p\right\rceil _{{{{{{\mathbf G}}^F}}}}}, {\left. \gamma \right\rceil _{{{{{{\mathbf G}}^F}}}}},{\left. \gamma _3\right\rceil _{{{{{{\mathbf G}}^F}}}}}\right\rangle }$
.
We recall that the graph automorphism
![]() $\gamma $
of
$\gamma $
of
![]() ${{\mathbf G}}$
is induced by an element of
${{\mathbf G}}$
is induced by an element of
![]() ${\overline {\mathbf G}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, 2.7] for the corresponding statement in classical groups). Let
${\overline {\mathbf G}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, 2.7] for the corresponding statement in classical groups). Let
![]() $\varpi \in {\mathbb {F}}^{\times }$
such that
$\varpi \in {\mathbb {F}}^{\times }$
such that
![]() $\varpi ^2=-1$
. By [Reference SpäthS2, 10.1] (see also [Reference Malle and TestermanMS, 2.Reference Cabanes and EnguehardC]), the automorphism
$\varpi ^2=-1$
. By [Reference SpäthS2, 10.1] (see also [Reference Malle and TestermanMS, 2.Reference Cabanes and EnguehardC]), the automorphism
![]() $\gamma $
of
$\gamma $
of
![]() ${{\mathbf G}}$
is induced by conjugating with
${{\mathbf G}}$
is induced by conjugating with
![]() $\mathbf {n} _{e_1}(\varpi )\in {\overline {\mathbf G}}$
.
$\mathbf {n} _{e_1}(\varpi )\in {\overline {\mathbf G}}$
.
Notation 3.5. Let
![]() ${{\mathbf L}}$
be a Levi subgroup of
${{\mathbf L}}$
be a Levi subgroup of
![]() ${{\mathbf G}}$
such that
${{\mathbf G}}$
such that
![]() ${\mathbf B} {{\mathbf L}}$
is a parabolic subgroup of
${\mathbf B} {{\mathbf L}}$
is a parabolic subgroup of
![]() ${{\mathbf G}}$
and
${{\mathbf G}}$
and
![]() ${\mathbf T}\subseteq {{\mathbf L}}$
. Let
${\mathbf T}\subseteq {{\mathbf L}}$
. Let
![]() $ L:={{\mathbf L}}^F$
, and let
$ L:={{\mathbf L}}^F$
, and let
![]() ${\Phi '}$
be the root system of
${\Phi '}$
be the root system of
![]() ${{\mathbf L}}$
, that is,
${{\mathbf L}}$
, that is,
![]() ${{\mathbf L}}={\mathbf T}{\left\langle \left.{\mathbf X}_ {\alpha }\vphantom {{\alpha }\in \Phi '}\hskip .1em\right.\mid {\alpha }\in \Phi ' \right\rangle }$
. As
${{\mathbf L}}={\mathbf T}{\left\langle \left.{\mathbf X}_ {\alpha }\vphantom {{\alpha }\in \Phi '}\hskip .1em\right.\mid {\alpha }\in \Phi ' \right\rangle }$
. As
![]() $\Phi '$
is a parabolic root subsystem of
$\Phi '$
is a parabolic root subsystem of
![]() $\Phi $
, it has as basis
$\Phi $
, it has as basis
![]() ${\Delta '}= \Delta \cap \Phi '$
. We assume that one of the following holds:
${\Delta '}= \Delta \cap \Phi '$
. We assume that one of the following holds:
-
(i)
 $\Delta '\subseteq \{ e_2-e_1, e_3-e_2, \ldots , e_l-e_{l-1}\}$
, or
$\Delta '\subseteq \{ e_2-e_1, e_3-e_2, \ldots , e_l-e_{l-1}\}$
, or -
(ii)
 $\{ e_2-e_1, e_2+e_1\}\subseteq \Delta '$
.
$\{ e_2-e_1, e_2+e_1\}\subseteq \Delta '$
.
Recall that a split Levi subgroup of
![]() ${{\mathbf G}}$
containing
${{\mathbf G}}$
containing
![]() ${\mathbf T}$
is called standard if it is generated by
${\mathbf T}$
is called standard if it is generated by
![]() ${\mathbf T}$
and the
${\mathbf T}$
and the
![]() ${\mathbf X}_{{\alpha }}$
’s such that
${\mathbf X}_{{\alpha }}$
’s such that
![]() ${\alpha }\in \pm \Delta '$
for some subset
${\alpha }\in \pm \Delta '$
for some subset
![]() $\Delta '\subseteq \Delta $
. Recall that
$\Delta '\subseteq \Delta $
. Recall that
![]() $\gamma $
swaps
$\gamma $
swaps
![]() $e_2-e_1$
and
$e_2-e_1$
and
![]() $ e_2+e_1$
while fixing the other elements of
$ e_2+e_1$
while fixing the other elements of
![]() $\Delta $
. Then any subset
$\Delta $
. Then any subset
![]() $\Delta '\subseteq \Delta $
is such that
$\Delta '\subseteq \Delta $
is such that
![]() $\Delta '$
or
$\Delta '$
or
![]() $\gamma (\Delta ')$
satisfies 3.5
(i) or 3.5
(ii). We then get that
$\gamma (\Delta ')$
satisfies 3.5
(i) or 3.5
(ii). We then get that
![]() ${{\mathbf L}}$
can be assumed to satisfy Notation 3.5.
${{\mathbf L}}$
can be assumed to satisfy Notation 3.5.
Lemma 3.6. Every standard Levi subgroup of
![]() ${{\mathbf G}}$
containing
${{\mathbf G}}$
containing
![]() ${\mathbf T}$
is
${\mathbf T}$
is
![]() ${\left\langle \gamma \right\rangle }$
-conjugate to a standard Levi subgroup whose root system has a basis
${\left\langle \gamma \right\rangle }$
-conjugate to a standard Levi subgroup whose root system has a basis
![]() $\Delta '\subseteq \Delta $
satisfying 3.5
(i) or 3.5
(ii).
$\Delta '\subseteq \Delta $
satisfying 3.5
(i) or 3.5
(ii).
3.7 (Decomposing
 $\Phi '$
)
$\Phi '$
)
In the following, we decompose
![]() $\Phi '$
into smaller root systems, which are the disjoint union of irreducible root systems of the same type. By
$\Phi '$
into smaller root systems, which are the disjoint union of irreducible root systems of the same type. By
![]() ${{\mathsf {type}}(\Psi )}$
, we denote the type of the root system
${{\mathsf {type}}(\Psi )}$
, we denote the type of the root system
![]() $\Psi $
. Whenever
$\Psi $
. Whenever
![]() $\Psi $
is a subset of
$\Psi $
is a subset of
![]() $\overline {\Phi }$
, we also denote by
$\overline {\Phi }$
, we also denote by
![]() ${W_{\Psi }}$
the subgroup of N
${W_{\Psi }}$
the subgroup of N
![]() $_{\overline {\mathbf G}} ({\mathbf T})/{\mathbf T}$
generated by reflections defined by elements of
$_{\overline {\mathbf G}} ({\mathbf T})/{\mathbf T}$
generated by reflections defined by elements of
![]() $\Psi $
.
$\Psi $
.
Since
![]() $\Phi '$
is a parabolic root subsystem of
$\Phi '$
is a parabolic root subsystem of
![]() $\Phi $
,
$\Phi $
,
![]() $\Phi '$
decomposes as a disjoint union of indecomposable root systems of types
$\Phi '$
decomposes as a disjoint union of indecomposable root systems of types
![]() $\mathrm {D}$
and
$\mathrm {D}$
and
![]() $\mathrm A$
, that are called components of
$\mathrm A$
, that are called components of
![]() $\Phi '$
.
$\Phi '$
.
If
![]() $\Delta '$
satisfies Assumption 3.5
(i), let
$\Delta '$
satisfies Assumption 3.5
(i), let
![]() ${\Phi _{d}}$
be the union of the components of
${\Phi _{d}}$
be the union of the components of
![]() $\Phi '$
of type
$\Phi '$
of type
![]() $\mathrm A_{d-1}$
(
$\mathrm A_{d-1}$
(
![]() $d\geq 2$
). If
$d\geq 2$
). If
![]() $\Delta '$
satisfies Assumption 3.5
(ii), let
$\Delta '$
satisfies Assumption 3.5
(ii), let
![]() ${\Phi _{-1}}$
be the union of components of
${\Phi _{-1}}$
be the union of components of
![]() $\Phi '$
that have a nontrivial intersection with
$\Phi '$
that have a nontrivial intersection with
![]() $\{ e_2-e_1, e_1+e_2\}$
and let
$\{ e_2-e_1, e_1+e_2\}$
and let
![]() $\Phi _{d}$
be the union of components of
$\Phi _{d}$
be the union of components of
![]() $\Phi ' \setminus \Phi _{-1}$
of type
$\Phi ' \setminus \Phi _{-1}$
of type
![]() $\mathrm A_{d-1}$
(
$\mathrm A_{d-1}$
(
![]() $d\geq 2$
). If
$d\geq 2$
). If
![]() $\Delta '$
satisfies Assumption 3.5
(ii),
$\Delta '$
satisfies Assumption 3.5
(ii),
![]() ${\mathsf {type}}(\Phi _{{-1}})\in \{\mathrm A_3,\mathrm A_1\times \mathrm A_1, \mathrm {D}_m \mid m\geq 4\}$
.
${\mathsf {type}}(\Phi _{{-1}})\in \{\mathrm A_3,\mathrm A_1\times \mathrm A_1, \mathrm {D}_m \mid m\geq 4\}$
.
Let
![]() ${\mathbb D '}$
be the set of integers d such that
${\mathbb D '}$
be the set of integers d such that
![]() $\Phi _d$
is defined and nonempty, that is,
$\Phi _d$
is defined and nonempty, that is,
![]() $\operatorname {SL}_d({\mathbb {F}})$
is a summand of
$\operatorname {SL}_d({\mathbb {F}})$
is a summand of
![]() $[{{\mathbf L}},{{\mathbf L}}]$
. Then
$[{{\mathbf L}},{{\mathbf L}}]$
. Then
![]() $\Phi '=\bigsqcup _{d\in \mathbb D'} \Phi _d$
, a disjoint union.
$\Phi '=\bigsqcup _{d\in \mathbb D'} \Phi _d$
, a disjoint union.
Recall that
![]() $W_{\overline \Phi }$
, the group generated by the reflections along the roots of
$W_{\overline \Phi }$
, the group generated by the reflections along the roots of
![]() $\overline \Phi $
coincides with
$\overline \Phi $
coincides with
![]() $W_0:=\overline N_0/T_0$
, can be identified with the permutations of
$W_0:=\overline N_0/T_0$
, can be identified with the permutations of
![]() ${\underline {l}}\cup -{\underline {l}}$
that commute with the sign change, and hence acts on
${\underline {l}}\cup -{\underline {l}}$
that commute with the sign change, and hence acts on
![]() ${\underline {l}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, Rem. 1.8.8]).
${\underline {l}}$
(see [Reference Gorenstein, Lyons and SolomonGLS, Rem. 1.8.8]).
3.8 (Orbits of
 $W_{\Phi '}$
on
$W_{\Phi '}$
on
 ${\underline {l}}$
)
${\underline {l}}$
)
Let
![]() ${\mathcal O}$
be the set of orbits of
${\mathcal O}$
be the set of orbits of
![]() $W_{\Phi '}$
on
$W_{\Phi '}$
on
![]() ${\underline {l}}$
, let
${\underline {l}}$
, let
![]() ${{\mathcal O}_1}\subseteq {\mathcal O}$
be the set of singletons in
${{\mathcal O}_1}\subseteq {\mathcal O}$
be the set of singletons in
![]() ${\mathcal O}$
, and let
${\mathcal O}$
, and let
![]() ${{\mathcal O}_d}$
be the set of orbits of
${{\mathcal O}_d}$
be the set of orbits of
![]() $W_{\Phi _d}$
on
$W_{\Phi _d}$
on
![]() ${\underline {l}}$
contained in
${\underline {l}}$
contained in
![]() ${\mathcal O}\setminus {\mathcal O}_1$
, whenever
${\mathcal O}\setminus {\mathcal O}_1$
, whenever
![]() $d\in \mathbb D'$
. We define
$d\in \mathbb D'$
. We define
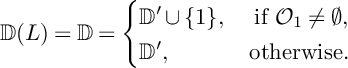 $$ \begin{align*} {\mathbb D(L)}=\mathbb D&=\begin{cases} \mathbb D'\cup \{1\},& \text{ if }{\mathcal O}_1\neq \emptyset,\\ \mathbb D',&\, \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathbb D(L)}=\mathbb D&=\begin{cases} \mathbb D'\cup \{1\},& \text{ if }{\mathcal O}_1\neq \emptyset,\\ \mathbb D',&\, \text{otherwise}. \end{cases} \end{align*} $$
For
![]() $d\in \mathbb D \setminus \{-1\}$
, let
$d\in \mathbb D \setminus \{-1\}$
, let
![]() ${a_d}:=|{\mathcal O}_d|$
and note that
${a_d}:=|{\mathcal O}_d|$
and note that
![]() $|I|=d$
for any
$|I|=d$
for any
![]() $I\in {\mathcal O}_d$
.
$I\in {\mathcal O}_d$
.
For
![]() $I\subseteq {\underline {l}}$
, let
$I\subseteq {\underline {l}}$
, let
![]() ${\Phi _I}:=\Phi '\cap {\left\langle \left.e_k\vphantom {k\in I}\hskip .1em\right.\mid k\in I \right\rangle }$
and
${\Phi _I}:=\Phi '\cap {\left\langle \left.e_k\vphantom {k\in I}\hskip .1em\right.\mid k\in I \right\rangle }$
and
![]() ${\overline {\Phi }_I}:=\overline \Phi \cap {\left\langle \left.e_k\vphantom {k\in I}\hskip .1em\right.\mid k\in I \right\rangle }$
. For
${\overline {\Phi }_I}:=\overline \Phi \cap {\left\langle \left.e_k\vphantom {k\in I}\hskip .1em\right.\mid k\in I \right\rangle }$
. For
![]() $d\in \mathbb D$
, let
$d\in \mathbb D$
, let
![]() ${J_d}:=\bigcup _{o\in {\mathcal O}_d}o$
, and
${J_d}:=\bigcup _{o\in {\mathcal O}_d}o$
, and
![]() ${\overline {\Phi }_d}:= \overline {\Phi }_{J_d}$
.
${\overline {\Phi }_d}:= \overline {\Phi }_{J_d}$
.
Next, we introduce groups K,
![]() ${K_0}$
, and H that will later be proved to satisfy Assumption 3.2
(i) with a group M.
${K_0}$
, and H that will later be proved to satisfy Assumption 3.2
(i) with a group M.
Notation 3.9 (Subgroups of
 ${{\mathbf L}}$
and L)
${{\mathbf L}}$
and L)
Let
![]() $\varpi \in {\mathbb {F}}^{\times }$
and
$\varpi \in {\mathbb {F}}^{\times }$
and
![]() $h_0$
as in Definition 3.4. Define
$h_0$
as in Definition 3.4. Define
![]() ${{\mathbf h} _I(t)}:=\prod _{i\in I}{\mathbf h} _{e_i}(t)$
for
${{\mathbf h} _I(t)}:=\prod _{i\in I}{\mathbf h} _{e_i}(t)$
for
![]() $I\subseteq {\underline {l}}$
and
$I\subseteq {\underline {l}}$
and
![]() $t\in {\mathbb {F}}^{\times }$
. For
$t\in {\mathbb {F}}^{\times }$
. For
![]() $I\in {\mathcal O}$
, let
$I\in {\mathcal O}$
, let
![]() ${{{\mathbf G}_{I}}}={\left\langle \left.{\mathbf X}_{\alpha }\vphantom {{\alpha } \in \Phi _I}\hskip .1em\right.\mid {\alpha } \in \Phi _I \right\rangle }$
and
${{{\mathbf G}_{I}}}={\left\langle \left.{\mathbf X}_{\alpha }\vphantom {{\alpha } \in \Phi _I}\hskip .1em\right.\mid {\alpha } \in \Phi _I \right\rangle }$
and
![]() $ {G_I}:={{\mathbf G}}_I^F$
. Note that for
$ {G_I}:={{\mathbf G}}_I^F$
. Note that for
![]() $I\in {\mathcal O}_1$
, the group
$I\in {\mathcal O}_1$
, the group
![]() ${{\mathbf G}_{I}}$
is trivial. Let
${{\mathbf G}_{I}}$
is trivial. Let
![]() ${H_0}:={\left\langle h_0,{\mathbf h} _{e_i}(\varpi ){\mathbf h} _{e_{i'}}(-\varpi )\mid i,i'\in {\underline {l}}\right\rangle } ={\left\langle h_{\alpha }(-1)\mid \alpha \in \Phi \right\rangle }$
. For
${H_0}:={\left\langle h_0,{\mathbf h} _{e_i}(\varpi ){\mathbf h} _{e_{i'}}(-\varpi )\mid i,i'\in {\underline {l}}\right\rangle } ={\left\langle h_{\alpha }(-1)\mid \alpha \in \Phi \right\rangle }$
. For
![]() $d\in \mathbb D$
, let
$d\in \mathbb D$
, let
![]() ${{\widetilde H}_d}:={\left\langle h_0, {\mathbf h} _I(\varpi ) \mid I\in {\mathcal O}_d\right\rangle }$
,
${{\widetilde H}_d}:={\left\langle h_0, {\mathbf h} _I(\varpi ) \mid I\in {\mathcal O}_d\right\rangle }$
,
![]() ${H_d}:={\left\langle h_0, {\mathbf h} _I(\varpi ) {\mathbf h} _{I'}(-\varpi )\mid I,I'\in {\mathcal O}_d\right\rangle }$
and
${H_d}:={\left\langle h_0, {\mathbf h} _I(\varpi ) {\mathbf h} _{I'}(-\varpi )\mid I,I'\in {\mathcal O}_d\right\rangle }$
and
Lemma 3.10. Let
![]() ${\mathbb D_{\mathrm {even}}}:= \mathbb D \cap 2\mathbb {Z}$
and
${\mathbb D_{\mathrm {even}}}:= \mathbb D \cap 2\mathbb {Z}$
and
![]() ${\mathbb D_{\mathrm {odd}}}:= \mathbb D\setminus \mathbb D_{\mathrm {even}}$
. If
${\mathbb D_{\mathrm {odd}}}:= \mathbb D\setminus \mathbb D_{\mathrm {even}}$
. If
![]() ${ H_{\epsilon }}:={\left\langle \widetilde H_d\mid d\in \mathbb D_{\epsilon }\right\rangle }\cap H_0$
for
${ H_{\epsilon }}:={\left\langle \widetilde H_d\mid d\in \mathbb D_{\epsilon }\right\rangle }\cap H_0$
for
![]() ${\epsilon }\in \{ {\mathrm {odd}},{\mathrm {even}}\}$
, then
${\epsilon }\in \{ {\mathrm {odd}},{\mathrm {even}}\}$
, then
![]() $H=H_{\mathrm {even}}. H_{\mathrm {odd}}$
.
$H=H_{\mathrm {even}}. H_{\mathrm {odd}}$
.
Proof. An element
![]() $t\in {\mathbf T}$
can be written as
$t\in {\mathbf T}$
can be written as
![]() $\prod _{i=1}^l{\mathbf h} _{e_i}(t_i)$
(
$\prod _{i=1}^l{\mathbf h} _{e_i}(t_i)$
(
![]() $t_i\in {\mathbb {F}}^{\times }$
). We have
$t_i\in {\mathbb {F}}^{\times }$
). We have
![]() $t\in H_0$
if
$t\in H_0$
if
![]() $t_i\in {\left\langle \varpi \right\rangle }$
and
$t_i\in {\left\langle \varpi \right\rangle }$
and
![]() $\prod _{i=1}^l t_i^2=1$
. In particular,
$\prod _{i=1}^l t_i^2=1$
. In particular,
![]() ${\mathbf h} _I(\varpi )\in H_0$
if and only if
${\mathbf h} _I(\varpi )\in H_0$
if and only if
![]() $|I|$
even. This implies
$|I|$
even. This implies
![]() $H_d\leq H_0$
whenever
$H_d\leq H_0$
whenever
![]() $2\mid d$
. On the other hand,
$2\mid d$
. On the other hand,
![]() $\widetilde H_d\not \leq H_0$
for every
$\widetilde H_d\not \leq H_0$
for every
![]() $d\in \mathbb D_{\mathrm {odd}}$
.
$d\in \mathbb D_{\mathrm {odd}}$
.
With this notation,
![]() $\operatorname Z({{\mathbf G}})={\left\langle h_0, {\mathbf h} _{{\underline {l}}} (\varpi )\right\rangle }$
(see [Reference Gorenstein, Lyons and SolomonGLS, Table 1.12.6]).
$\operatorname Z({{\mathbf G}})={\left\langle h_0, {\mathbf h} _{{\underline {l}}} (\varpi )\right\rangle }$
(see [Reference Gorenstein, Lyons and SolomonGLS, Table 1.12.6]).
Lemma 3.11.
![]() $H\leq \operatorname Z({{\mathbf L}})$
.
$H\leq \operatorname Z({{\mathbf L}})$
.
Proof. We see that
![]() $[{\mathbf h} _I(\varpi ), {{\mathbf G}}_I]=1$
by the Chevalley relations and this implies the statement by the definition of H.
$[{\mathbf h} _I(\varpi ), {{\mathbf G}}_I]=1$
by the Chevalley relations and this implies the statement by the definition of H.
The groups
![]() ${{K_0}}:={\left\langle G_I\mid I \in {\mathcal O}\right\rangle }$
and
${{K_0}}:={\left\langle G_I\mid I \in {\mathcal O}\right\rangle }$
and
![]() $ K:={K_0} H$
then satisfy Assumption 3.2(i.1) for H.
$ K:={K_0} H$
then satisfy Assumption 3.2(i.1) for H.
To understand later the action of
![]() ${\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
on
${\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
on
![]() $\mathrm {Irr}(K)$
, we analyze the structure of L by introducing several subgroups.
$\mathrm {Irr}(K)$
, we analyze the structure of L by introducing several subgroups.
3.12 (Structure of
 ${{\mathbf L}}$
)
${{\mathbf L}}$
)
We note that the Levi subgroup
![]() ${{\mathbf L}}$
satisfies
${{\mathbf L}}$
satisfies
![]() ${{\mathbf L}}={\mathbf T} {\left\langle {{\mathbf G}}_I\mid I\in {\mathcal O}\right\rangle }$
. Let
${{\mathbf L}}={\mathbf T} {\left\langle {{\mathbf G}}_I\mid I\in {\mathcal O}\right\rangle }$
. Let
![]() ${{\mathbf T}_I}:={\left\langle \left.{\mathbf h} _{e_i}(t)\vphantom {i\in I, t \in {\mathbb {F}}^{\times }}\hskip .1em\right.\mid i\in I, t \in {\mathbb {F}}^{\times } \right\rangle }$
for
${{\mathbf T}_I}:={\left\langle \left.{\mathbf h} _{e_i}(t)\vphantom {i\in I, t \in {\mathbb {F}}^{\times }}\hskip .1em\right.\mid i\in I, t \in {\mathbb {F}}^{\times } \right\rangle }$
for
![]() $I\in {\mathcal O}$
. For
$I\in {\mathcal O}$
. For
![]() $I,I'\in {\mathcal O}$
with
$I,I'\in {\mathcal O}$
with
![]() $I\neq I'$
, we see that no nontrivial linear combination of a root in
$I\neq I'$
, we see that no nontrivial linear combination of a root in
![]() $\Phi _I$
and one in
$\Phi _I$
and one in
![]() $\Phi _{I'}$
is a root in
$\Phi _{I'}$
is a root in
![]() $\Phi $
as well. Therefore,
$\Phi $
as well. Therefore,
![]() $[{{\mathbf G}}_I,{{\mathbf G}}_{I'}]=1$
according to Chevalley’s commutator formula. By the Steinberg relations, we see
$[{{\mathbf G}}_I,{{\mathbf G}}_{I'}]=1$
according to Chevalley’s commutator formula. By the Steinberg relations, we see
![]() $[{{\mathbf G}}_I,{\mathbf T}_{I'}]=1$
. The group
$[{{\mathbf G}}_I,{\mathbf T}_{I'}]=1$
. The group
![]() ${{\mathbf G}}_I$
is either trivial or a simply connected simple group unless
${{\mathbf G}}_I$
is either trivial or a simply connected simple group unless
![]() $I= {\mathcal O}_{-1}$
and
$I= {\mathcal O}_{-1}$
and
![]() ${\mathsf {type}}(\Phi _{-1})= \mathrm A_1\times \mathrm A_1$
. Accordingly,
${\mathsf {type}}(\Phi _{-1})= \mathrm A_1\times \mathrm A_1$
. Accordingly,
![]() $[{{\mathbf L}},{{\mathbf L}}]={\left\langle {{\mathbf G}}_I\mid I\in {\mathcal O}\right\rangle }$
.
$[{{\mathbf L}},{{\mathbf L}}]={\left\langle {{\mathbf G}}_I\mid I\in {\mathcal O}\right\rangle }$
.
We observe that
![]() ${{\mathbf G}}_I\cap {\mathbf T}\leq {\mathbf T}_I$
and computations with the coroot lattices prove that
${{\mathbf G}}_I\cap {\mathbf T}\leq {\mathbf T}_I$
and computations with the coroot lattices prove that
![]() ${\mathbf T}$
is the central product of the groups
${\mathbf T}$
is the central product of the groups
![]() ${\mathbf T}_I$
(
${\mathbf T}_I$
(
![]() $I\in {\mathcal O}$
) over
$I\in {\mathcal O}$
) over
![]() ${\left\langle h_0\right\rangle }$
. This implies that
${\left\langle h_0\right\rangle }$
. This implies that
![]() ${{\mathbf L}}$
is the central product of the groups
${{\mathbf L}}$
is the central product of the groups
![]() ${{\mathbf L}}_I$
(
${{\mathbf L}}_I$
(
![]() $I\in {\mathcal O}$
) where
$I\in {\mathcal O}$
) where
![]() ${{{\mathbf L}}_I}:={\mathbf T}_I {{\mathbf G}}_I$
.
${{{\mathbf L}}_I}:={\mathbf T}_I {{\mathbf G}}_I$
.
Analogously, we see that
![]() ${{\mathbf L}}$
is the central product of the groups
${{\mathbf L}}$
is the central product of the groups
![]() ${{\mathbf L}}_d$
(
${{\mathbf L}}_d$
(
![]() $d\in \mathbb D$
) over the group
$d\in \mathbb D$
) over the group
![]() ${\left\langle h_0\right\rangle }$
, where
${\left\langle h_0\right\rangle }$
, where
![]() ${{{\mathbf L}}_d}:={\left\langle {{\mathbf L}}_I\mid I\in {\mathcal O}_d\right\rangle }$
.
${{{\mathbf L}}_d}:={\left\langle {{\mathbf L}}_I\mid I\in {\mathcal O}_d\right\rangle }$
.
The structure of
![]() ${{\mathbf L}}$
studied above implies the following results on L. Recall
${{\mathbf L}}$
studied above implies the following results on L. Recall
![]() ${K_0}:={\left\langle G_I\mid I \in {\mathcal O}\right\rangle }$
from Lemma 3.11.
${K_0}:={\left\langle G_I\mid I \in {\mathcal O}\right\rangle }$
from Lemma 3.11.
Lemma 3.13. Recall
![]() $\mathcal L:{{\mathbf G}}\rightarrow {{\mathbf G}}$
the Lang map defined by
$\mathcal L:{{\mathbf G}}\rightarrow {{\mathbf G}}$
the Lang map defined by
![]() $g\mapsto g^{-1} F(g)$
, let
$g\mapsto g^{-1} F(g)$
, let
![]() ${\widehat L}:={{\mathbf L}}\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
, and let
${\widehat L}:={{\mathbf L}}\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
, and let
![]() ${\widetilde {L}}:={{\mathbf L}}\cap \mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
.
${\widetilde {L}}:={{\mathbf L}}\cap \mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
.
-
(a) If
 ${L_I}:={{\mathbf L}}_I^F$
for every
${L_I}:={{\mathbf L}}_I^F$
for every
 $I\in {\mathcal O}$
and
$I\in {\mathcal O}$
and
 ${L_0}:={\left\langle \left.L_I\vphantom {I \in {\mathcal O}}\hskip .1em\right.\mid I \in {\mathcal O} \right\rangle }$
, then
${L_0}:={\left\langle \left.L_I\vphantom {I \in {\mathcal O}}\hskip .1em\right.\mid I \in {\mathcal O} \right\rangle }$
, then
 $L_0\lhd L$
.
$L_0\lhd L$
. -
(b) Let
 $I\in {\mathcal O}$
and
$I\in {\mathcal O}$
and
 ${\widehat L_I}:={{\mathbf L}}_I\cap \widehat L$
. Then
${\widehat L_I}:={{\mathbf L}}_I\cap \widehat L$
. Then
 $\widehat L_I={\left\langle L_I, t_I\right\rangle }$
for every
$\widehat L_I={\left\langle L_I, t_I\right\rangle }$
for every
 $t_I\in {\mathbf T}_I\cap \mathcal L^{-1}(h_0)$
. We assume chosen such a
$t_I\in {\mathbf T}_I\cap \mathcal L^{-1}(h_0)$
. We assume chosen such a
 $t_I$
for each
$t_I$
for each
 $I\in {\mathcal O}$
.
$I\in {\mathcal O}$
.The group
 ${\widehat L}$
is the central product of
${\widehat L}$
is the central product of
 $\widehat L_I$
(
$\widehat L_I$
(
 $I\in {\mathcal O}$
) and for
$I\in {\mathcal O}$
) and for
 $d\in \mathbb D$
,
$d\in \mathbb D$
,
 ${\widehat L_d}:=\widehat L\cap {{\mathbf L}}_d$
is the central product of
${\widehat L_d}:=\widehat L\cap {{\mathbf L}}_d$
is the central product of
 $\widehat L_I$
(
$\widehat L_I$
(
 $I\in {\mathcal O}_d$
).
$I\in {\mathcal O}_d$
). -
(c)
 $L= {\left\langle {{\mathbf L}}_I^F, t_I t_{I'}\mid I, I'\in {\mathcal O}\right\rangle }$
.
$L= {\left\langle {{\mathbf L}}_I^F, t_I t_{I'}\mid I, I'\in {\mathcal O}\right\rangle }$
. -
(d)
 ${K_0}$
is the direct product of all
${K_0}$
is the direct product of all
 $G_I$
,
$G_I$
,
 ${K_0}\lhd \widetilde {L}$
and
${K_0}\lhd \widetilde {L}$
and
 $\widetilde {L}/{K_0}$
is abelian.
$\widetilde {L}/{K_0}$
is abelian. -
(e) If
 ${\zeta }\in {\mathbb {F}}^{\times } $
with
${\zeta }\in {\mathbb {F}}^{\times } $
with
 $\zeta ^{(q-1)_2}=\varpi $
and
$\zeta ^{(q-1)_2}=\varpi $
and
 $t_{Q,2}:={\mathbf h} _Q(\zeta )$
for every
$t_{Q,2}:={\mathbf h} _Q(\zeta )$
for every
 $Q\subseteq {\underline {l}}$
, then
$Q\subseteq {\underline {l}}$
, then
 $\widetilde {L}=\widehat L {\left\langle t_{{\underline {l}},2}\right\rangle }$
.
$\widetilde {L}=\widehat L {\left\langle t_{{\underline {l}},2}\right\rangle }$
.
The arguments of Remark 2.16 show that
![]() $\widetilde {L}'$
from 2.8 and
$\widetilde {L}'$
from 2.8 and
![]() $\widetilde {L}$
induce the same automorphisms on
$\widetilde {L}$
induce the same automorphisms on
![]() ${{\mathbf G}}$
.
${{\mathbf G}}$
.
Proof. Recall that
![]() ${{\mathbf L}}$
is the central product of the groups
${{\mathbf L}}$
is the central product of the groups
![]() ${{\mathbf L}}_I$
, where each
${{\mathbf L}}_I$
, where each
![]() ${{\mathbf L}}_I$
is F-stable. Every
${{\mathbf L}}_I$
is F-stable. Every
![]() $x\in {{\mathbf L}}$
can be written as
$x\in {{\mathbf L}}$
can be written as
![]() $\prod _ {I \in {\mathcal O}} x_I$
with
$\prod _ {I \in {\mathcal O}} x_I$
with
![]() $x_I \in {{\mathbf L}}_I$
. Clearly,
$x_I \in {{\mathbf L}}_I$
. Clearly,
![]() $x\in L$
if and only if
$x\in L$
if and only if
![]() $\mathcal L(x)=1$
. We see that
$\mathcal L(x)=1$
. We see that
![]() $\mathcal L(x)=\prod _{I \in {\mathcal O}}\mathcal L(x_I)$
by the structure of
$\mathcal L(x)=\prod _{I \in {\mathcal O}}\mathcal L(x_I)$
by the structure of
![]() $\mathcal L$
and hence
$\mathcal L$
and hence
![]() $x\in L$
implies
$x\in L$
implies
![]() $\mathcal L(x_I)\in {\left\langle h_0\right\rangle }$
. The group
$\mathcal L(x_I)\in {\left\langle h_0\right\rangle }$
. The group
![]() $L_0$
is the group of elements
$L_0$
is the group of elements
![]() $\prod _ {I \in {\mathcal O}} x_I$
with
$\prod _ {I \in {\mathcal O}} x_I$
with
![]() $x_I\in L_I:={{\mathbf L}}_I^F$
. The group
$x_I\in L_I:={{\mathbf L}}_I^F$
. The group
![]() $\widehat L:= \mathcal L({\left\langle h_0\right\rangle } ) \cap {{\mathbf L}}$
is the group of elements
$\widehat L:= \mathcal L({\left\langle h_0\right\rangle } ) \cap {{\mathbf L}}$
is the group of elements
![]() $\prod x_I$
with
$\prod x_I$
with
![]() $x_I\in {{\mathbf L}}_I$
and
$x_I\in {{\mathbf L}}_I$
and
![]() $\mathcal L(x_I )\in {\left\langle h_0\right\rangle }$
. Hence,
$\mathcal L(x_I )\in {\left\langle h_0\right\rangle }$
. Hence,
![]() $\widehat L $
is the central product of
$\widehat L $
is the central product of
![]() $\widehat L_I$
(
$\widehat L_I$
(
![]() $I\in {\mathcal O}$
) over
$I\in {\mathcal O}$
) over
![]() ${\left\langle h_0\right\rangle }$
. Clearly,
${\left\langle h_0\right\rangle }$
. Clearly,
![]() $ L_0 \lhd \widehat L$
,
$ L_0 \lhd \widehat L$
,
![]() $\widehat L_I={\left\langle L_I,t_I\right\rangle }$
and
$\widehat L_I={\left\langle L_I,t_I\right\rangle }$
and
![]() $L=L_0 {\left\langle t_I t_{I'}\mid I, I' \in {\mathcal O}\right\rangle }$
. This ensures the parts (a)–(c).
$L=L_0 {\left\langle t_I t_{I'}\mid I, I' \in {\mathcal O}\right\rangle }$
. This ensures the parts (a)–(c).
Part (d) follows from the fact that
![]() ${{\mathbf L}}/{\left\langle {{\mathbf G}}_I\mid I \in {\mathcal O}\right\rangle }$
is isomorphic to a quotient of
${{\mathbf L}}/{\left\langle {{\mathbf G}}_I\mid I \in {\mathcal O}\right\rangle }$
is isomorphic to a quotient of
![]() ${\mathbf T}$
and hence abelian. For part (e), we observe
${\mathbf T}$
and hence abelian. For part (e), we observe
![]() $\mathcal L({\mathbf h} _Q(\zeta ))= {\mathbf h} _Q(\varpi )$
for every
$\mathcal L({\mathbf h} _Q(\zeta ))= {\mathbf h} _Q(\varpi )$
for every
![]() $Q\subseteq {\underline {l}}$
and recall that
$Q\subseteq {\underline {l}}$
and recall that
![]() $\operatorname Z({{\mathbf G}})={\left\langle h_0,{\mathbf h} _{{\underline {l}}}(\varpi )\right\rangle }$
.
$\operatorname Z({{\mathbf G}})={\left\langle h_0,{\mathbf h} _{{\underline {l}}}(\varpi )\right\rangle }$
.
3.2 The structure of
 $N/L$
$N/L$
We analyze
![]() $N:={\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
and
$N:={\mathrm {N}}_{{{{\mathbf G}}^F}}({{\mathbf L}})$
and
![]() $\overline N:={\operatorname N}_{{{{\overline {\mathbf G}}^F}}}({\mathbf L})$
. In the following, we identify
$\overline N:={\operatorname N}_{{{{\overline {\mathbf G}}^F}}}({\mathbf L})$
. In the following, we identify
![]() $W_{\overline \Phi }$
with certain permutation groups
$W_{\overline \Phi }$
with certain permutation groups
![]() ${\mathcal {S}}_{\pm \underline l}$
via the action on
${\mathcal {S}}_{\pm \underline l}$
via the action on
![]() $\{\pm e_i\mid i \in {\underline {l}}\}$
and
$\{\pm e_i\mid i \in {\underline {l}}\}$
and
![]() $W_{\Phi }$
with
$W_{\Phi }$
with
![]() ${\mathcal {S}}_{\pm {\underline {l}}}^{\mathrm {D}}$
. We generalize the notation of those permutation groups in order to describe
${\mathcal {S}}_{\pm {\underline {l}}}^{\mathrm {D}}$
. We generalize the notation of those permutation groups in order to describe
![]() $N/L$
.
$N/L$
.
Notation 3.14 (Young-like subgroups,
 ${\mathcal {S}}_M$
and
${\mathcal {S}}_M$
and
 ${\mathcal {Y}}_J$
)
${\mathcal {Y}}_J$
)
Let M be a set. Given a map
![]() $\|. \|: M\rightarrow \mathbb {Z}$
with
$\|. \|: M\rightarrow \mathbb {Z}$
with
![]() $m\mapsto \| m\|$
, we define
$m\mapsto \| m\|$
, we define
![]() ${\mathcal {S}}_M$
to be the group of bijections
${\mathcal {S}}_M$
to be the group of bijections
![]() $\pi : M\rightarrow M $
with
$\pi : M\rightarrow M $
with
![]() $\|\pi (m)\|=\|m\|$
for every
$\|\pi (m)\|=\|m\|$
for every
![]() $m\in M$
and we write
$m\in M$
and we write
![]() ${{\mathcal {S}}_{\pm M}}$
for the bijections
${{\mathcal {S}}_{\pm M}}$
for the bijections
![]() $\pi : \{ \pm 1\}\times M \rightarrow \{ \pm 1\}\times M$
satisfying
$\pi : \{ \pm 1\}\times M \rightarrow \{ \pm 1\}\times M$
satisfying
![]() $\pi (-1,m)= (-\epsilon , m')$
and
$\pi (-1,m)= (-\epsilon , m')$
and
![]() $\|m\|=\|m'\|$
, whenever
$\|m\|=\|m'\|$
, whenever
![]() $m, m'\in M$
with
$m, m'\in M$
with
![]() $\pi (1,m)=({\epsilon },m')$
. When no map
$\pi (1,m)=({\epsilon },m')$
. When no map
![]() $\|.\|$
is specified, we assume it is a constant map.
$\|.\|$
is specified, we assume it is a constant map.
In order to denote the elements of
![]() ${\mathcal {S}}_M$
and
${\mathcal {S}}_M$
and
![]() ${\mathcal {S}}_{\pm M}$
, we fix a bijection
${\mathcal {S}}_{\pm M}$
, we fix a bijection
![]() $f:M \rightarrow \{1,\ldots , |M|\}$
. This induces a canonical embedding
$f:M \rightarrow \{1,\ldots , |M|\}$
. This induces a canonical embedding
![]() $\iota : {\mathcal {S}}_M \rightarrow {\mathcal {S}}_{\underline {{|M|}}}$
and an embedding
$\iota : {\mathcal {S}}_M \rightarrow {\mathcal {S}}_{\underline {{|M|}}}$
and an embedding
![]() $\iota _{\pm }: {\mathcal {S}}_{\pm M}\rightarrow {\mathcal {S}}_{\pm \underline {|M|}}$
. For r pairwise distinct elements
$\iota _{\pm }: {\mathcal {S}}_{\pm M}\rightarrow {\mathcal {S}}_{\pm \underline {|M|}}$
. For r pairwise distinct elements
![]() $m_1, m_2,\ldots , m_r\in M$
, we write
$m_1, m_2,\ldots , m_r\in M$
, we write
![]() $(m_1,m_2,\ldots , m_r)\in {\mathcal {S}}_M$
for the element
$(m_1,m_2,\ldots , m_r)\in {\mathcal {S}}_M$
for the element
![]() $\iota ^{-1}(f(m_1), f(m_2),\ldots , f(m_r))$
. Via
$\iota ^{-1}(f(m_1), f(m_2),\ldots , f(m_r))$
. Via
![]() $\iota _{\pm }$
, we obtain also a cycle notation for elements of
$\iota _{\pm }$
, we obtain also a cycle notation for elements of
![]() ${\mathcal {S}}_{\pm M}$
.
${\mathcal {S}}_{\pm M}$
.
If J is a partition of M, we write
![]() $J\vdash M$
for short. For
$J\vdash M$
for short. For
![]() $J\vdash M$
, we set
$J\vdash M$
, we set
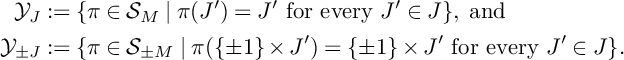 $$ \begin{align*} {{\mathcal{Y}}_J}&:=\{ \pi \in{\mathcal{S}}_M\mid \pi(J')=J' \text{ for every }J'\in J \}, {\text{ and }} \\ {{\mathcal{Y}}_{\pm J}}&:=\{ \pi \in{\mathcal{S}}_{\pm M}\mid \pi(\{\pm 1\}\times J')= \{\pm 1\}\times J' \text{ for every }J'\in J \}. \end{align*} $$
$$ \begin{align*} {{\mathcal{Y}}_J}&:=\{ \pi \in{\mathcal{S}}_M\mid \pi(J')=J' \text{ for every }J'\in J \}, {\text{ and }} \\ {{\mathcal{Y}}_{\pm J}}&:=\{ \pi \in{\mathcal{S}}_{\pm M}\mid \pi(\{\pm 1\}\times J')= \{\pm 1\}\times J' \text{ for every }J'\in J \}. \end{align*} $$
Let
![]() $M_{odd}:=\{ m\in M \mid \| m\| \text { odd }\}$
and
$M_{odd}:=\{ m\in M \mid \| m\| \text { odd }\}$
and
We use the above notation for permutation groups on the set
![]() ${\mathcal O}$
from 3.8.
${\mathcal O}$
from 3.8.
Definition 3.15. Let
![]() ${\|. \|}: {\mathcal O} \longrightarrow \mathbb {Z}$
be given by
${\|. \|}: {\mathcal O} \longrightarrow \mathbb {Z}$
be given by
![]() $\|I\|=d$
for every
$\|I\|=d$
for every
![]() $I\in {\mathcal O}_d$
, and let
$I\in {\mathcal O}_d$
, and let
![]() ${\mathcal {S}}_{\pm {\mathcal O}}$
,
${\mathcal {S}}_{\pm {\mathcal O}}$
,
![]() ${\mathcal {S}}^{\mathrm {D}}_{\pm {\mathcal O}}$
, and
${\mathcal {S}}^{\mathrm {D}}_{\pm {\mathcal O}}$
, and
![]() ${\mathcal {S}}_{ {\mathcal O}}$
be the permutation groups on
${\mathcal {S}}_{ {\mathcal O}}$
be the permutation groups on
![]() ${\mathcal O}$
defined as in 3.14 with respect to
${\mathcal O}$
defined as in 3.14 with respect to
![]() $\|.\|$
.
$\|.\|$
.
Recall that we have chosen a maximal torus
![]() ${\mathbf T}$
of
${\mathbf T}$
of
![]() ${{\mathbf G}}$
and that
${{\mathbf G}}$
and that
![]() ${{\mathbf L}}$
is a standard Levi subgroup of
${{\mathbf L}}$
is a standard Levi subgroup of
![]() ${{\mathbf G}}$
with
${{\mathbf G}}$
with
![]() ${\mathbf T}\subseteq {{\mathbf L}}$
(see 3.3 and 3.5). For
${\mathbf T}\subseteq {{\mathbf L}}$
(see 3.3 and 3.5). For
![]() ${\overline {\mathbf N}_0}:={\mathrm {N}}_{\overline {\mathbf G}}({\mathbf T})$
, we identify the Weyl group
${\overline {\mathbf N}_0}:={\mathrm {N}}_{\overline {\mathbf G}}({\mathbf T})$
, we identify the Weyl group
![]() $\overline {\mathbf N}_0/{\mathbf T}$
with
$\overline {\mathbf N}_0/{\mathbf T}$
with
![]() ${\mathcal {S}}_{\pm {\underline {l}}}$
, the epimorphism
${\mathcal {S}}_{\pm {\underline {l}}}$
, the epimorphism
![]() ${\rho _{{\mathbf T}}}: \overline {\mathbf N}_0\longrightarrow {\mathcal {S}}_{\pm {\underline {l}}}$
is given by
${\rho _{{\mathbf T}}}: \overline {\mathbf N}_0\longrightarrow {\mathcal {S}}_{\pm {\underline {l}}}$
is given by
With this notation, we can compute the relative Weyl group of L in G. Recall
![]() $N:={\mathrm {N}}_{{\mathbf G}}({{\mathbf L}})^F$
.
$N:={\mathrm {N}}_{{\mathbf G}}({{\mathbf L}})^F$
.
Proposition 3.16. Let
![]() ${N_0}:={\mathrm {N}}_{{{{{\mathbf G}}^F}}}({\mathbf T})$
,
${N_0}:={\mathrm {N}}_{{{{{\mathbf G}}^F}}}({\mathbf T})$
,
![]() ${{\overline N}_0}:={\mathrm {N}}_{{{{\overline {\mathbf G}}^F}}}({\mathbf T})$
, and
${{\overline N}_0}:={\mathrm {N}}_{{{{\overline {\mathbf G}}^F}}}({\mathbf T})$
, and
![]() ${\overline N}:={\mathrm {N}}_{{{{\overline {\mathbf G}}^F}}}({{\mathbf L}})$
. Then
${\overline N}:={\mathrm {N}}_{{{{\overline {\mathbf G}}^F}}}({{\mathbf L}})$
. Then
Proof. According to the considerations in [Reference Cabanes and EnguehardC, 9.2],
![]() $\rho _{{\mathbf T}}(N\cap N_0)/\rho _{{\mathbf T}}(L\cap N_0)\cong \operatorname {N}_{\overline W_0} (W_{\Phi '})/W_{\Phi '}$
, where
$\rho _{{\mathbf T}}(N\cap N_0)/\rho _{{\mathbf T}}(L\cap N_0)\cong \operatorname {N}_{\overline W_0} (W_{\Phi '})/W_{\Phi '}$
, where
![]() ${\overline W_0}:=\overline N_0/\overline T_0$
. We then make routine considerations inside
${\overline W_0}:=\overline N_0/\overline T_0$
. We then make routine considerations inside
![]() $\overline W_0$
(see, e.g., [Reference HowlettH]). Note that
$\overline W_0$
(see, e.g., [Reference HowlettH]). Note that
![]() $\operatorname {N}_{\overline W_0} (W_{\Phi '})=\operatorname {Stab}_{\overline W_0}(\Phi ')=W_{\Phi '}\operatorname {Stab}_{\overline W_0}(\Delta ')$
.
$\operatorname {N}_{\overline W_0} (W_{\Phi '})=\operatorname {Stab}_{\overline W_0}(\Phi ')=W_{\Phi '}\operatorname {Stab}_{\overline W_0}(\Delta ')$
.
From the definition of
![]() $\Phi _{-1}$
, one can check that
$\Phi _{-1}$
, one can check that
![]() $\operatorname {Stab}_{\overline W_0}(\Delta ')$
stabilizes
$\operatorname {Stab}_{\overline W_0}(\Delta ')$
stabilizes
![]() $\Phi _{-1}\cap \Delta '$
. This implies that
$\Phi _{-1}\cap \Delta '$
. This implies that
![]() $\operatorname {Stab}_{\overline W_0}(\Delta ')$
stabilizes
$\operatorname {Stab}_{\overline W_0}(\Delta ')$
stabilizes
![]() $\Phi _d\cap \Delta '$
for every
$\Phi _d\cap \Delta '$
for every
![]() $d\in \mathbb D$
, and
$d\in \mathbb D$
, and
We have
![]() $\operatorname {N}_{\overline W_0} (W_{\Phi '})=W_{\overline {\Phi }_1}\times \prod _{d\in \mathbb D}\operatorname {Stab}_{W_{\overline \Phi _{d}}}(\Phi _{d})= \operatorname {Stab}_{W_{\overline \Phi _{-1}}}(\Phi _{-1})\times W_{\overline \Phi _1}\times \prod _{\stackrel {d\in \mathbb D}{d>1}} \operatorname {Stab}_{W_{\overline \Phi _d}} (\Phi _d)$
with
$\operatorname {N}_{\overline W_0} (W_{\Phi '})=W_{\overline {\Phi }_1}\times \prod _{d\in \mathbb D}\operatorname {Stab}_{W_{\overline \Phi _{d}}}(\Phi _{d})= \operatorname {Stab}_{W_{\overline \Phi _{-1}}}(\Phi _{-1})\times W_{\overline \Phi _1}\times \prod _{\stackrel {d\in \mathbb D}{d>1}} \operatorname {Stab}_{W_{\overline \Phi _d}} (\Phi _d)$
with
and
for
![]() $d\in \mathbb D$
with
$d\in \mathbb D$
with
![]() $d>1$
. Hence,
$d>1$
. Hence,
![]() $\rho _{{\mathbf T}}( N \cap N_0)/\rho _{{\mathbf T}}(L\cap N_0)\cong {\mathcal {S}}_{\pm {\mathcal O}}^{\mathrm {D}}$
.
$\rho _{{\mathbf T}}( N \cap N_0)/\rho _{{\mathbf T}}(L\cap N_0)\cong {\mathcal {S}}_{\pm {\mathcal O}}^{\mathrm {D}}$
.
By the proof, we see that
![]() ${\mathcal {S}}_{\pm {\mathcal O}}$
corresponds to
${\mathcal {S}}_{\pm {\mathcal O}}$
corresponds to
![]() $\operatorname {Stab}_{\overline W_0}(\Phi '\cap \Delta )$
and hence there exists some embedding of
$\operatorname {Stab}_{\overline W_0}(\Phi '\cap \Delta )$
and hence there exists some embedding of
![]() ${\mathcal {S}}_{\pm {\mathcal O}}$
into
${\mathcal {S}}_{\pm {\mathcal O}}$
into
![]() ${\mathcal {S}}_{\pm {\underline {l}}}$
. We fix some more notation to describe explicitly the permutations in
${\mathcal {S}}_{\pm {\underline {l}}}$
. We fix some more notation to describe explicitly the permutations in
![]() ${\mathcal {S}}_{\pm {\underline {l}}}$
corresponding to
${\mathcal {S}}_{\pm {\underline {l}}}$
corresponding to
![]() $\operatorname {Stab}_{\overline W_0}(\Delta ')$
.
$\operatorname {Stab}_{\overline W_0}(\Delta ')$
.
Notation 3.17. For
![]() $d\in \mathbb D\setminus \{-1\}$
, we fix orderings on
$d\in \mathbb D\setminus \{-1\}$
, we fix orderings on
![]() ${\mathcal O}_d$
and the sets
${\mathcal O}_d$
and the sets
![]() $I\in {\mathcal O}_d$
: we write
$I\in {\mathcal O}_d$
: we write
![]() ${I_{d,j}}$
(
${I_{d,j}}$
(
![]() $ j \in \underline { a_d}$
) for the sets in
$ j \in \underline { a_d}$
) for the sets in
![]() ${\mathcal O}_d $
and
${\mathcal O}_d $
and
![]() ${I_{d,j}(k)}\in I_{d,j}$
(
${I_{d,j}(k)}\in I_{d,j}$
(
![]() $ j \in \underline { a_d}$
,
$ j \in \underline { a_d}$
,
![]() $k \in \underline d$
) for the elements of
$k \in \underline d$
) for the elements of
![]() $I_{d,j}$
.
$I_{d,j}$
.
For each
![]() $ k\in \underline d$
, let
$ k\in \underline d$
, let
![]() $f_k^{(d)}: {\underline {l}}\longrightarrow {\underline {l}}$
be a bijection such that
$f_k^{(d)}: {\underline {l}}\longrightarrow {\underline {l}}$
be a bijection such that
![]() $f_k^{(d)}(j)=I_{d,j}(k)$
for every
$f_k^{(d)}(j)=I_{d,j}(k)$
for every
![]() $j\in \underline {a_d}$
and
$j\in \underline {a_d}$
and
![]() $f_k^{(d)}$
has the maximal number of fixed points. Then
$f_k^{(d)}$
has the maximal number of fixed points. Then
![]() ${f_k^{(d)}}$
defines an element of
${f_k^{(d)}}$
defines an element of
![]() ${\mathcal {S}}_{\pm {\underline {l}}}$
without sign changes, that we also denote by
${\mathcal {S}}_{\pm {\underline {l}}}$
without sign changes, that we also denote by
![]() $f_k^{(d)}$
by abuse of notation.
$f_k^{(d)}$
by abuse of notation.
In the following, we use that for every
![]() $Q\subseteq {\underline {l}}$
,
$Q\subseteq {\underline {l}}$
,
![]() ${\mathcal {S}}_{\pm Q}$
can be seen naturally as a subgroup of
${\mathcal {S}}_{\pm Q}$
can be seen naturally as a subgroup of
![]() ${\mathcal {S}}_{\pm {\underline {l}}}$
.
${\mathcal {S}}_{\pm {\underline {l}}}$
.
Lemma 3.18.
-
(a) Let
 $d\in \mathbb D\setminus \{-1\}$
and
$d\in \mathbb D\setminus \{-1\}$
and
 ${\overline {\kappa }_d}:{\mathcal {S}}_{\pm \underline {a_d}}\rightarrow {\mathcal {S}}_{\pm J_d}$
be given by
${\overline {\kappa }_d}:{\mathcal {S}}_{\pm \underline {a_d}}\rightarrow {\mathcal {S}}_{\pm J_d}$
be given by
 $\pi \mapsto \prod _{k \in \underline d } \pi ^{f_k^{(d)}}$
the latter a product of conjugates of
$\pi \mapsto \prod _{k \in \underline d } \pi ^{f_k^{(d)}}$
the latter a product of conjugates of
 $\pi $
in
$\pi $
in
 ${\mathcal {S}}_{\pm {\underline {l}}}$
. Then
${\mathcal {S}}_{\pm {\underline {l}}}$
. Then
 $\overline {\kappa }_d$
is injective and
$\overline {\kappa }_d$
is injective and
 $\operatorname {Stab}_{{\mathcal {S}}_{\pm J_d}}(\Phi _d) =W_{\Phi _d} \rtimes \overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
$\operatorname {Stab}_{{\mathcal {S}}_{\pm J_d}}(\Phi _d) =W_{\Phi _d} \rtimes \overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
-
(b) If
 $-1\in \mathbb D$
, let
$-1\in \mathbb D$
, let
 ${\overline \kappa _{-1}}: {\mathcal {S}}_{\pm \underline {1}}\rightarrow {\mathcal {S}}_{\pm J_{-1}}$
be the morphism with
${\overline \kappa _{-1}}: {\mathcal {S}}_{\pm \underline {1}}\rightarrow {\mathcal {S}}_{\pm J_{-1}}$
be the morphism with
 $\overline \kappa _{-1}({\mathcal {S}}_{\pm \underline {1}})= {\left\langle (1,-1)\right\rangle }$
. Let
$\overline \kappa _{-1}({\mathcal {S}}_{\pm \underline {1}})= {\left\langle (1,-1)\right\rangle }$
. Let
 ${\overline W_d}:=\overline \kappa _d({\mathcal {S}}_{\pm \underline {a_d}})$
and
${\overline W_d}:=\overline \kappa _d({\mathcal {S}}_{\pm \underline {a_d}})$
and
 ${W^{\circ }(L)}:= \prod _{d\in \mathbb D} \overline W_d$
. Then
${W^{\circ }(L)}:= \prod _{d\in \mathbb D} \overline W_d$
. Then
 $\operatorname {Stab}_{\overline W_0}(\Phi ')= W_{\Phi '} W^{\circ }(L)$
.
$\operatorname {Stab}_{\overline W_0}(\Phi ')= W_{\Phi '} W^{\circ }(L)$
.
Proof. For (a), we observe that the sets
![]() $\bigcup _{j\in {\underline {a_d}} }I_{d,j}(k)$
(
$\bigcup _{j\in {\underline {a_d}} }I_{d,j}(k)$
(
![]() $k\in \underline d)$
form a partition of
$k\in \underline d)$
form a partition of
![]() $J_d$
. This implies that the groups
$J_d$
. This implies that the groups
![]() ${\mathcal {S}}_{\pm \underline {a_d}}^{f_k^{(d)}}$
and
${\mathcal {S}}_{\pm \underline {a_d}}^{f_k^{(d)}}$
and
![]() ${\mathcal {S}}_{\pm \underline {a_d}}^{f_{k'}^{(d)}}$
commute and are disjoint. We see that
${\mathcal {S}}_{\pm \underline {a_d}}^{f_{k'}^{(d)}}$
commute and are disjoint. We see that
![]() $\overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
stabilizes
$\overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
stabilizes
![]() ${\mathcal O}_d$
. This proves (a). Part (b) is clear from the definitions.
${\mathcal O}_d$
. This proves (a). Part (b) is clear from the definitions.
We can choose
![]() $I_{d,j}(k)$
(
$I_{d,j}(k)$
(
![]() $d\in \mathbb D\setminus \{\pm 1\}$
,
$d\in \mathbb D\setminus \{\pm 1\}$
,
![]() $j\in {\underline {a_d}}$
, and
$j\in {\underline {a_d}}$
, and
![]() $k\in \underline d$
) such that
$k\in \underline d$
) such that
![]() $e_{I_{d,j}(k+1)}-e_{I_{d,j}(k)}\in \Delta '$
for every
$e_{I_{d,j}(k+1)}-e_{I_{d,j}(k)}\in \Delta '$
for every
![]() $j\in \underline {a_d}$
and
$j\in \underline {a_d}$
and
![]() $k\in \underline {d-1}$
. With this choice,
$k\in \underline {d-1}$
. With this choice,
![]() $\overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
stabilizes
$\overline {\kappa }_d({\mathcal {S}}_{\pm \underline {a_d}})$
stabilizes
![]() $\Delta '$
and hence coincides with
$\Delta '$
and hence coincides with
![]() $\operatorname {Stab}_{\overline W_{\overline \Phi _d}}(\Delta ')$
.
$\operatorname {Stab}_{\overline W_{\overline \Phi _d}}(\Delta ')$
.
3.3 A supplement of L in
 $\overline N$
$\overline N$
In the following, we determine a supplement
![]() $\overline V\leq \overline N_0$
with
$\overline V\leq \overline N_0$
with
![]() $\overline N=L \overline V$
and
$\overline N=L \overline V$
and
![]() $\rho _{{\mathbf T}}(\overline V)= W^{\circ }(L)$
where
$\rho _{{\mathbf T}}(\overline V)= W^{\circ }(L)$
where
![]() $W^{\circ }(L)$
is the group from Lemma 3.18. We construct the group
$W^{\circ }(L)$
is the group from Lemma 3.18. We construct the group
![]() $\overline V$
using extended Weyl groups
$\overline V$
using extended Weyl groups
![]() $\overline V^{\prime }_{Weyl}$
(see 3.19). Extended Weyl groups are known to be supplements of
$\overline V^{\prime }_{Weyl}$
(see 3.19). Extended Weyl groups are known to be supplements of
![]() $ T_0$
in
$ T_0$
in
![]() $\overline N_0$
.
$\overline N_0$
.
In a first step, we define for every
![]() $d\in \mathbb D$
a subgroup
$d\in \mathbb D$
a subgroup
![]() $\overline V_d\leq {\overline N}_0$
with
$\overline V_d\leq {\overline N}_0$
with
![]() $\rho _{{\mathbf T}}(\overline V_d)=\overline {\kappa }_d({\mathcal {S}}_{\pm a_d})$
. We construct
$\rho _{{\mathbf T}}(\overline V_d)=\overline {\kappa }_d({\mathcal {S}}_{\pm a_d})$
. We construct
![]() $\kappa _d$
, a lifting of
$\kappa _d$
, a lifting of
![]() $\overline \kappa _d$
via
$\overline \kappa _d$
via
![]() $\rho _{{\mathbf T}}$
. This construction will later simplify some arguments by providing a tool to transfer results from [Reference Malle and TestermanMS].
$\rho _{{\mathbf T}}$
. This construction will later simplify some arguments by providing a tool to transfer results from [Reference Malle and TestermanMS].
By definition, the group
![]() $\overline {\mathbf N}_0$
is an extension of
$\overline {\mathbf N}_0$
is an extension of
![]() $\overline W_0$
by
$\overline W_0$
by
![]() ${\mathbf T}$
. It has proved to be more convenient to work with an extension of
${\mathbf T}$
. It has proved to be more convenient to work with an extension of
![]() $\overline W_0$
by an elementary abelian
$\overline W_0$
by an elementary abelian
![]() $2$
-group, the extended Weyl group (introduced first by Tits), here denoted by
$2$
-group, the extended Weyl group (introduced first by Tits), here denoted by
![]() $\overline V^{\prime }_{Weyl}$
. (Note that if
$\overline V^{\prime }_{Weyl}$
. (Note that if
![]() $2\mid q$
, the group
$2\mid q$
, the group
![]() $\overline {\mathbf N}_0$
is the semi-direct product of
$\overline {\mathbf N}_0$
is the semi-direct product of
![]() ${\mathbf T}$
and a group isomorphic to the Weyl group.) In consideration of Definition 3.4, we work here with the group
${\mathbf T}$
and a group isomorphic to the Weyl group.) In consideration of Definition 3.4, we work here with the group
![]() $\overline V_0$
, a
$\overline V_0$
, a
![]() ${\mathbf T}$
-conjugate of
${\mathbf T}$
-conjugate of
![]() $V^{\prime }_{Weyl}$
. Then the graph automorphism of
$V^{\prime }_{Weyl}$
. Then the graph automorphism of
![]() $ G$
is induced by an element of
$ G$
is induced by an element of
![]() $\overline V_0$
(see Definition 3.4).
$\overline V_0$
(see Definition 3.4).
Notation 3.19 (The groups
 $\overline V_0$
,
$\overline V_0$
,
 $\overline V_I$
, and
$\overline V_I$
, and
 $V_I$
)
$V_I$
)
The group
![]() ${V^{\prime }_{Weyl}}:={\left\langle \left.\overline {\mathbf {n}}_i'\vphantom { i\in {\underline {l}}}\hskip .1em\right.\mid i\in {\underline {l}} \right\rangle }$
with
${V^{\prime }_{Weyl}}:={\left\langle \left.\overline {\mathbf {n}}_i'\vphantom { i\in {\underline {l}}}\hskip .1em\right.\mid i\in {\underline {l}} \right\rangle }$
with
![]() $\overline {\mathbf {n}}_1':=\mathbf {n}_{e_1}(1)$
and
$\overline {\mathbf {n}}_1':=\mathbf {n}_{e_1}(1)$
and
![]() $\overline {\mathbf {n}}_i':=\mathbf {n}_{{\alpha }_i}(-1)$
, where
$\overline {\mathbf {n}}_i':=\mathbf {n}_{{\alpha }_i}(-1)$
, where
![]() ${\alpha }_i= e_i-e_{i-1}$
(
${\alpha }_i= e_i-e_{i-1}$
(
![]() $2\leq i\leq l$
) is known as the extended Weyl group of type
$2\leq i\leq l$
) is known as the extended Weyl group of type
![]() $\mathrm B_l$
.
$\mathrm B_l$
.
Let
![]() $\zeta _8\in {\mathbb {F}}$
with
$\zeta _8\in {\mathbb {F}}$
with
![]() $\zeta _8^2=\varpi $
. The group
$\zeta _8^2=\varpi $
. The group
![]() ${\overline V_0}:=(V^{\prime }_{Weyl})^{{\mathbf h} _{\underline l}(\zeta _8)} $
is accordingly generated by
${\overline V_0}:=(V^{\prime }_{Weyl})^{{\mathbf h} _{\underline l}(\zeta _8)} $
is accordingly generated by
![]() ${{\overline {\mathbf n}}_1}:=(\overline {\mathbf {n}} _1')^{{\mathbf h} _{\underline l}(\zeta _8)}=\mathbf {n}_{e_1}(\varpi )$
and
${{\overline {\mathbf n}}_1}:=(\overline {\mathbf {n}} _1')^{{\mathbf h} _{\underline l}(\zeta _8)}=\mathbf {n}_{e_1}(\varpi )$
and
![]() ${\overline {\mathbf n}_i}:=(\overline {\mathbf {n}} _i')^{{\mathbf h} _{\underline l}(\zeta _8)}=\mathbf {n} _{{\alpha }_i}(-1)$
. The group
${\overline {\mathbf n}_i}:=(\overline {\mathbf {n}} _i')^{{\mathbf h} _{\underline l}(\zeta _8)}=\mathbf {n} _{{\alpha }_i}(-1)$
. The group
![]() $\overline V_0$
satisfies
$\overline V_0$
satisfies
![]() $\overline V_0 \cap \overline T_0=H_0$
where
$\overline V_0 \cap \overline T_0=H_0$
where
![]() $H_0$
is defined as
$H_0$
is defined as
![]() ${\left\langle {\mathbf h} _{{\alpha }}(-1)\mid {\alpha }\in \Phi \right\rangle }$
in 3.19. According to Definition 3.4,
${\left\langle {\mathbf h} _{{\alpha }}(-1)\mid {\alpha }\in \Phi \right\rangle }$
in 3.19. According to Definition 3.4,
![]() $\overline {\mathbf {n}}_1\in \overline V_0$
and
$\overline {\mathbf {n}}_1\in \overline V_0$
and
![]() $\gamma $
induce the same automorphism of
$\gamma $
induce the same automorphism of
![]() ${{\mathbf G}}$
.
${{\mathbf G}}$
.
For
![]() $I\subseteq \underline l$
, we set
$I\subseteq \underline l$
, we set
Let
![]() ${\widetilde H_I}:={\left\langle {\mathbf h} _{e_i}(\varpi )\mid i \in I\right\rangle }$
and
${\widetilde H_I}:={\left\langle {\mathbf h} _{e_i}(\varpi )\mid i \in I\right\rangle }$
and
![]() ${\widetilde H_0}:=\widetilde H_{\underline {l}}$
.
${\widetilde H_0}:=\widetilde H_{\underline {l}}$
.
3.20 (Facts around
 $H_I\lhd \overline V_I$
)
$H_I\lhd \overline V_I$
)
Maximal extendibility holds with respect to
![]() $H_I\lhd \overline V_I$
, since those groups are conjugate to those considered in [Reference Malle and TestermanMS, Prop. 3.8] for the case where the underlying root system is of type
$H_I\lhd \overline V_I$
, since those groups are conjugate to those considered in [Reference Malle and TestermanMS, Prop. 3.8] for the case where the underlying root system is of type
![]() $\mathrm B_{|I|}$
. For
$\mathrm B_{|I|}$
. For
![]() ${H_I}:={\left\langle h_0,{\mathbf h} _{\pm e_i\pm e_{i'}}(-1)\mid i,i'\in I\right\rangle }$
, we obtain
${H_I}:={\left\langle h_0,{\mathbf h} _{\pm e_i\pm e_{i'}}(-1)\mid i,i'\in I\right\rangle }$
, we obtain
![]() $\overline V_I\cap {\mathbf T}=H_I$
.
$\overline V_I\cap {\mathbf T}=H_I$
.
For disjoint sets
![]() $I,I'\subseteq {\underline {l}}$
, the Steinberg relations imply
$I,I'\subseteq {\underline {l}}$
, the Steinberg relations imply
We introduce maps
![]() $\kappa _d: \widetilde H_{{\underline {a_d}}}V_{\underline {a_d}}\longrightarrow \widetilde H_0\overline V_0$
with
$\kappa _d: \widetilde H_{{\underline {a_d}}}V_{\underline {a_d}}\longrightarrow \widetilde H_0\overline V_0$
with
![]() $\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
for the canonical epimorphism
$\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
for the canonical epimorphism
![]() $ {\rho _{{\underline {a_d}}}: \overline V_{{\underline {a_d}}}\longrightarrow {\mathcal {S}}_{\pm {\underline {a_d}}}}$
.
$ {\rho _{{\underline {a_d}}}: \overline V_{{\underline {a_d}}}\longrightarrow {\mathcal {S}}_{\pm {\underline {a_d}}}}$
.
The following defines a lift of
![]() $\overline W_d:=\overline \kappa _d({\mathcal {S}}_{\pm a_d})$
that is a subgroup of
$\overline W_d:=\overline \kappa _d({\mathcal {S}}_{\pm a_d})$
that is a subgroup of
![]() $\overline V_0$
. In 3.17, we introduced the elements
$\overline V_0$
. In 3.17, we introduced the elements
![]() $f_k^{(d)}\in {\mathcal {S}}_{\pm {\underline {l}}}$
(
$f_k^{(d)}\in {\mathcal {S}}_{\pm {\underline {l}}}$
(
![]() $d\in \mathbb D\setminus \{-1\}$
,
$d\in \mathbb D\setminus \{-1\}$
,
![]() $k \in {\underline {a_d}}$
) without sign changes.
$k \in {\underline {a_d}}$
) without sign changes.
Lemma 3.21. Let
![]() $d\in \mathbb D\setminus \{-1\}$
,
$d\in \mathbb D\setminus \{-1\}$
,
![]() $m_k^{(d)}\in \overline V\cap \rho _{\mathbf T}^{-1}(f_k^{(d)})$
(
$m_k^{(d)}\in \overline V\cap \rho _{\mathbf T}^{-1}(f_k^{(d)})$
(
![]() $k\in \underline d$
), and
$k\in \underline d$
), and
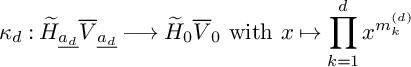 $$ \begin{align*}{\kappa_d} : \widetilde H_{{\underline{a_d}}}\overline V_{{\underline{a_d}}} \longrightarrow \widetilde H_{0} \overline V_{0} \text{ with } x\mapsto \prod_{k=1}^d x ^{m_k^{(d)}}\end{align*} $$
$$ \begin{align*}{\kappa_d} : \widetilde H_{{\underline{a_d}}}\overline V_{{\underline{a_d}}} \longrightarrow \widetilde H_{0} \overline V_{0} \text{ with } x\mapsto \prod_{k=1}^d x ^{m_k^{(d)}}\end{align*} $$
for a fixed order in
![]() $\underline d$
. Set
$\underline d$
. Set
![]() ${\overline V_d}:= {\left\langle \kappa _d(\overline V_{{\underline {a_d}}})\right\rangle }$
. Then:
${\overline V_d}:= {\left\langle \kappa _d(\overline V_{{\underline {a_d}}})\right\rangle }$
. Then:
-
(a)
 ${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a morphism of groups;
${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a morphism of groups; -
(b)
 $\kappa _d(v^x)=\kappa _d(v)^{\kappa _d(x)}$
for every
$\kappa _d(v^x)=\kappa _d(v)^{\kappa _d(x)}$
for every
 $x\in \overline V_{{\underline {a_d}}}$
and
$x\in \overline V_{{\underline {a_d}}}$
and
 $v\in V_{{\underline {a_d}}}$
;
$v\in V_{{\underline {a_d}}}$
; -
(c)
 $\kappa _d(H_{\underline {a_d}})={\left\langle h_0^d,{\mathbf h} _{I}(\varpi ) {\mathbf h} _{I'}(-\varpi )\mid I,I'\in {\mathcal O}_d\right\rangle }\leq H_d$
;
$\kappa _d(H_{\underline {a_d}})={\left\langle h_0^d,{\mathbf h} _{I}(\varpi ) {\mathbf h} _{I'}(-\varpi )\mid I,I'\in {\mathcal O}_d\right\rangle }\leq H_d$
; -
(d)
 $\kappa _d(\widetilde H_{{\underline {a_d}}})= {\left\langle h_0^d,{\mathbf h} _{I}(\varpi ) \mid I\in {\mathcal O}_d\right\rangle }$
;
$\kappa _d(\widetilde H_{{\underline {a_d}}})= {\left\langle h_0^d,{\mathbf h} _{I}(\varpi ) \mid I\in {\mathcal O}_d\right\rangle }$
; -
(e)
 $\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
for the canonical epimorphism
$\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
for the canonical epimorphism
 $\rho _{\underline {a_d}}:\overline V_{\underline {a_d}}\longrightarrow {\mathcal {S}}_{\pm {\underline {a_d}}}$
, in particular
$\rho _{\underline {a_d}}:\overline V_{\underline {a_d}}\longrightarrow {\mathcal {S}}_{\pm {\underline {a_d}}}$
, in particular
 $\rho _{{\mathbf T}}(\overline V_d)=\overline W_d= \kappa _d({\mathcal {S}}_{\pm a_d})$
.
$\rho _{{\mathbf T}}(\overline V_d)=\overline W_d= \kappa _d({\mathcal {S}}_{\pm a_d})$
.
Proof. The sets
![]() $J_d(k):=f_k^{(d)}({\underline {a_d}})$
form a partition of
$J_d(k):=f_k^{(d)}({\underline {a_d}})$
form a partition of
![]() $J_d$
. For
$J_d$
. For
![]() $x\in V_{{\underline {a_d}}}$
, we see
$x\in V_{{\underline {a_d}}}$
, we see
![]() $x^{m_k^{(d)}}\in V_{J_d(k)}$
and hence
$x^{m_k^{(d)}}\in V_{J_d(k)}$
and hence
![]() ${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is independent of the order chosen in
${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is independent of the order chosen in
![]() $\underline d$
. Then
$\underline d$
. Then
![]() ${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a diagonal embedding of
${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a diagonal embedding of
![]() $V_{{\underline {a_d}}}$
into the central product of the groups
$V_{{\underline {a_d}}}$
into the central product of the groups
![]() $V_{J_d(k)}$
(
$V_{J_d(k)}$
(
![]() $k\in \underline d$
) over
$k\in \underline d$
) over
![]() ${\left\langle h_0\right\rangle }$
. This implies that
${\left\langle h_0\right\rangle }$
. This implies that
![]() ${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a morphism of groups. This proves (a).
${\left. \kappa _d\right\rceil _{{V_{\underline {a_d}}}}}$
is a morphism of groups. This proves (a).
By part (a), it is enough to prove part (b) for
![]() $x=\overline {\mathbf {n}} _1$
and
$x=\overline {\mathbf {n}} _1$
and
![]() $v\in \{\overline {\mathbf {n}}_2^{\overline {\mathbf {n}}_1}, \overline {\mathbf {n}}_2, \overline {\mathbf {n}}_3,\ldots , \overline {\mathbf {n}}_{a_d}\} $
, since
$v\in \{\overline {\mathbf {n}}_2^{\overline {\mathbf {n}}_1}, \overline {\mathbf {n}}_2, \overline {\mathbf {n}}_3,\ldots , \overline {\mathbf {n}}_{a_d}\} $
, since
![]() $V_{{\underline {a_d}} }$
is generated by
$V_{{\underline {a_d}} }$
is generated by
![]() $\{\overline {\mathbf {n}}_2^{\overline {\mathbf {n}}_1}, \overline {\mathbf {n}}_2, \overline {\mathbf {n}}_3,\ldots , \overline {\mathbf {n}}_{a_d}\}$
. The equation
$\{\overline {\mathbf {n}}_2^{\overline {\mathbf {n}}_1}, \overline {\mathbf {n}}_2, \overline {\mathbf {n}}_3,\ldots , \overline {\mathbf {n}}_{a_d}\}$
. The equation
![]() $\kappa _d(\overline {\mathbf {n}}_i^{\overline {\mathbf {n}} _1})=\kappa _d(\overline {\mathbf {n}}_i)^{\kappa _d(\overline {\mathbf {n}} _1)}$
for
$\kappa _d(\overline {\mathbf {n}}_i^{\overline {\mathbf {n}} _1})=\kappa _d(\overline {\mathbf {n}}_i)^{\kappa _d(\overline {\mathbf {n}} _1)}$
for
![]() $i\geq 3$
is clear since no nontrivial linear combination of those roots is a root. Computations show
$i\geq 3$
is clear since no nontrivial linear combination of those roots is a root. Computations show
![]() $\kappa _d(\overline {\mathbf {n}}_2^{\overline {\mathbf {n}} _1})=\kappa _d(\overline {\mathbf {n}}_2)^{\kappa _d(\overline {\mathbf {n}} _1)}$
and hence part (b).
$\kappa _d(\overline {\mathbf {n}}_2^{\overline {\mathbf {n}} _1})=\kappa _d(\overline {\mathbf {n}}_2)^{\kappa _d(\overline {\mathbf {n}} _1)}$
and hence part (b).
For part (c), we note that
![]() $\ker ({\left. \kappa _d\right\rceil _{{H_{\underline {a_d}}}}})= {\left\langle h_0^{d-1}\right\rangle }$
. The equation
$\ker ({\left. \kappa _d\right\rceil _{{H_{\underline {a_d}}}}})= {\left\langle h_0^{d-1}\right\rangle }$
. The equation
![]() $\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
in (e) follows from
$\rho _{{\mathbf T}}\circ \kappa _d=\overline \kappa _d\circ \rho _{{\underline {a_d}}}$
in (e) follows from
![]() $\rho _{{\mathbf T}}(m_k^{(d)})=f_k^{(d)}$
.
$\rho _{{\mathbf T}}(m_k^{(d)})=f_k^{(d)}$
.
Recall that the group H from Notation 3.9 is a subgroup associated with
![]() ${{\mathbf L}}$
. To understand the above construction, we consider the following statement.
${{\mathbf L}}$
. To understand the above construction, we consider the following statement.
Theorem 3.22. If
![]() $-1\in \mathbb D$
, set
$-1\in \mathbb D$
, set
![]() ${\overline V_{-1}}:= {\left\langle H_{-1},\overline {\mathbf {n}}_1\right\rangle }$
. Let
${\overline V_{-1}}:= {\left\langle H_{-1},\overline {\mathbf {n}}_1\right\rangle }$
. Let
![]() ${\overline V}:= H{\left\langle \left.\overline V_d\vphantom {d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
and
${\overline V}:= H{\left\langle \left.\overline V_d\vphantom {d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
and
![]() ${V_{\mathrm {D}}}:=\overline V\cap {{\mathbf G}}$
.
${V_{\mathrm {D}}}:=\overline V\cap {{\mathbf G}}$
.
-
(a)
 $N=L V_{\mathrm {D}}$
.
$N=L V_{\mathrm {D}}$
. -
(b) If
 $\gamma \in E_L$
, then
$\gamma \in E_L$
, then
 $\overline {\mathbf {n}}_1\in \overline V$
.
$\overline {\mathbf {n}}_1\in \overline V$
.
Proof. Because of
![]() $\rho _{{\mathbf T}}(\overline V_d)=\overline W_d$
, we see
$\rho _{{\mathbf T}}(\overline V_d)=\overline W_d$
, we see
![]() $\rho _{{\mathbf T}}(\overline V)= W^{\circ }(L)$
. Clearly,
$\rho _{{\mathbf T}}(\overline V)= W^{\circ }(L)$
. Clearly,
![]() $V_{\mathrm {D}}\leq N$
. Additionally, we see that
$V_{\mathrm {D}}\leq N$
. Additionally, we see that
![]() $\overline V$
normalizes L and
$\overline V$
normalizes L and
![]() ${{\mathbf L}}$
by definition. If
${{\mathbf L}}$
by definition. If
![]() ${{\mathbf L}}$
is
${{\mathbf L}}$
is
![]() $\gamma $
-stable, then
$\gamma $
-stable, then
![]() $\overline {\mathbf {n}}_1\in \overline V$
. According to Definition 3.4,
$\overline {\mathbf {n}}_1\in \overline V$
. According to Definition 3.4,
![]() $\overline {\mathbf {n}}_1$
and
$\overline {\mathbf {n}}_1$
and
![]() $\gamma $
induce the same automorphism of
$\gamma $
induce the same automorphism of
![]() ${{\mathbf G}}$
.
${{\mathbf G}}$
.
Corollary 3.23. The groups K,
![]() ${K_0}$
, and H from Notation 3.9 and Lemma 3.11 together with
${K_0}$
, and H from Notation 3.9 and Lemma 3.11 together with
![]() ${V}:=V_{\mathrm {D}}$
,
${V}:=V_{\mathrm {D}}$
,
![]() ${M}:=KV$
, and
${M}:=KV$
, and
![]() ${D}:=E_L$
satisfy Assumption 3.2
(i).
${D}:=E_L$
satisfy Assumption 3.2
(i).
Proof. According to Lemma 3.11,
![]() $K=HK_0$
and
$K=HK_0$
and
![]() $H\leq \operatorname Z(K)$
. This is Assumption 3.2(i.1). The equality
$H\leq \operatorname Z(K)$
. This is Assumption 3.2(i.1). The equality
![]() $M=KV$
follows from the definition of M. In order to prove
$M=KV$
follows from the definition of M. In order to prove
![]() $H=V\cap K$
, we show
$H=V\cap K$
, we show
![]() $\overline V_d\cap {{\mathbf L}}\leq H_d$
for every
$\overline V_d\cap {{\mathbf L}}\leq H_d$
for every
![]() $d\in \mathbb D$
. Since
$d\in \mathbb D$
. Since
![]() $\overline V_d \leq \overline V_0$
by construction and
$\overline V_d \leq \overline V_0$
by construction and
![]() $\overline V_d:={\left\langle \kappa _d(\overline V_{{\underline {a_d}}})\right\rangle }=\overline W_d$
, we observe that
$\overline V_d:={\left\langle \kappa _d(\overline V_{{\underline {a_d}}})\right\rangle }=\overline W_d$
, we observe that
![]() $\kappa _d(H_{{\underline {a_d}}})\leq H_d$
according to Lemma 3.21(c).
$\kappa _d(H_{{\underline {a_d}}})\leq H_d$
according to Lemma 3.21(c).
By the construction,
![]() $V_{\mathrm {D}}$
is
$V_{\mathrm {D}}$
is
![]() $\overline V{\left\langle F_p \right\rangle }$
-stable and hence
$\overline V{\left\langle F_p \right\rangle }$
-stable and hence
![]() $E_L$
-stable. By the construction, we also see that
$E_L$
-stable. By the construction, we also see that
![]() $K_0$
and
$K_0$
and
![]() $V_{\mathrm {D}}$
are D-stable.
$V_{\mathrm {D}}$
are D-stable.
4 Extending cuspidal characters of Levi subgroups
This section now focuses on the character theory of our groups. We ensure the character-theoretic Assumption 3.2
(ii) and apply Proposition 3.2 in the proof of Theorem 3.1
(b). We analyze the action of
![]() $\overline V$
on
$\overline V$
on
![]() ${K_0}$
and consider subgroups of
${K_0}$
and consider subgroups of
![]() $\overline N$
and L associated with each
$\overline N$
and L associated with each
![]() $d\in \mathbb D$
. For every
$d\in \mathbb D$
. For every
![]() $d\in \mathbb D$
, we define subgroups
$d\in \mathbb D$
, we define subgroups
![]() $K_{0,d}$
and
$K_{0,d}$
and
![]() $K_d$
and study them separately for
$K_d$
and study them separately for
![]() $d=1$
,
$d=1$
,
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $d=-1$
.
$d=-1$
.
4.1 The inclusion
 $H_1 \lhd \overline V_{1}$
$H_1 \lhd \overline V_{1}$
We recall here some results on the extended Weyl groups. If
![]() $1\in \mathbb D$
, then
$1\in \mathbb D$
, then
![]() $H_1\cong H_{J_1}$
and
$H_1\cong H_{J_1}$
and
![]() $\overline V_1\cong \overline V_{J_1}$
for the group
$\overline V_1\cong \overline V_{J_1}$
for the group
![]() $\overline V_{J_1}$
from 3.19. (Recall
$\overline V_{J_1}$
from 3.19. (Recall
![]() $J_d=\bigcup _{I\in {\mathcal O}_d} I$
for
$J_d=\bigcup _{I\in {\mathcal O}_d} I$
for
![]() $d\in \mathbb D$
[see Notation 3.9].) We set
$d\in \mathbb D$
[see Notation 3.9].) We set
![]() $K_{0,1}:=1$
and
$K_{0,1}:=1$
and
![]() $K_1:=H_1$
. In order to apply Proposition 3.2, we investigate the Clifford theory for
$K_1:=H_1$
. In order to apply Proposition 3.2, we investigate the Clifford theory for
![]() $H_1\lhd \overline V_1$
. The results are also relevant for studying
$H_1\lhd \overline V_1$
. The results are also relevant for studying
![]() $H_d\lhd \overline V_d$
for
$H_d\lhd \overline V_d$
for
![]() $d\geq 1$
.
$d\geq 1$
.
Proposition 4.1. Let
![]() $l'\leq l$
be some positive integer,
$l'\leq l$
be some positive integer,
![]() $\widetilde H':=\widetilde H_{\underline {l'}}$
,
$\widetilde H':=\widetilde H_{\underline {l'}}$
,
![]() $H':=\widetilde H'\cap H_0$
,
$H':=\widetilde H'\cap H_0$
,
![]() $\overline V':=\overline V_{\underline {l'}}$
, and
$\overline V':=\overline V_{\underline {l'}}$
, and
![]() $\rho ':\overline V'\rightarrow {\mathcal {S}}_{\pm {\underline {l}}'}$
the canonical epimorphism.
$\rho ':\overline V'\rightarrow {\mathcal {S}}_{\pm {\underline {l}}'}$
the canonical epimorphism.
-
(a) Maximal extendibility holds with respect to
 $H'\lhd \overline V'$
.
$H'\lhd \overline V'$
. -
(b) Let
 $\lambda \in \mathrm {Irr}(H')$
with
$\lambda \in \mathrm {Irr}(H')$
with
 $h_0\notin \ker (\lambda )$
. Then some
$h_0\notin \ker (\lambda )$
. Then some
 $\overline V'$
-conjugate
$\overline V'$
-conjugate
 $\lambda '$
of
$\lambda '$
of
 $\lambda $
has an extension
$\lambda $
has an extension
 $\widetilde {\lambda }'$
to
$\widetilde {\lambda }'$
to
 $\widetilde H'$
such that
$\widetilde H'$
such that
 $\rho '(\overline V^{\prime }_{\widetilde {\lambda }'})={\mathcal {S}}_{l'}$
and
$\rho '(\overline V^{\prime }_{\widetilde {\lambda }'})={\mathcal {S}}_{l'}$
and
 $\overline V^{\prime }_{\lambda }=\overline V^{\prime }_{\widetilde {\lambda }}{\left\langle c \right\rangle }$
for some
$\overline V^{\prime }_{\lambda }=\overline V^{\prime }_{\widetilde {\lambda }}{\left\langle c \right\rangle }$
for some
 $c\in \overline V'$
with
$c\in \overline V'$
with
 $\rho _{{\mathbf T}}(c)=\prod _{i\in \underline {l'}}(i,-i)$
.
$\rho _{{\mathbf T}}(c)=\prod _{i\in \underline {l'}}(i,-i)$
.
Proof. By [Reference Malle and TestermanMS, Prop. 3.10], maximal extendibility holds with respect to
![]() $ H'\lhd \overline V'$
. Note that
$ H'\lhd \overline V'$
. Note that
![]() $\overline V'$
coincides with the group
$\overline V'$
coincides with the group
![]() $\overline V^t$
considered in [Reference Malle and TestermanMS]. This proves part (a).
$\overline V^t$
considered in [Reference Malle and TestermanMS]. This proves part (a).
Let
![]() $\lambda \in \mathrm {Irr}(H')$
with
$\lambda \in \mathrm {Irr}(H')$
with
![]() $\lambda (h_0)=-1$
and
$\lambda (h_0)=-1$
and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H'\mid \lambda )$
. Note that
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H'\mid \lambda )$
. Note that
![]() $\widetilde H'$
is the
$\widetilde H'$
is the
![]() $l'$
-fold central product of the cyclic groups
$l'$
-fold central product of the cyclic groups
![]() ${\left\langle {\mathbf h} _{e_i}(\varpi )\right\rangle }$
(
${\left\langle {\mathbf h} _{e_i}(\varpi )\right\rangle }$
(
![]() $i\in \underline {l'}$
) over
$i\in \underline {l'}$
) over
![]() ${\left\langle h_0\right\rangle }$
. The group
${\left\langle h_0\right\rangle }$
. The group
![]() $\overline V$
acts by permutation and inversion on the factors. It is then easy to see that some
$\overline V$
acts by permutation and inversion on the factors. It is then easy to see that some
![]() $\overline V'$
-conjugate
$\overline V'$
-conjugate
![]() $\lambda '$
of
$\lambda '$
of
![]() $\lambda $
has an extension
$\lambda $
has an extension
![]() $\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde H')$
such that
$\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde H')$
such that
The other extension of
![]() $\lambda '$
to
$\lambda '$
to
![]() $\widetilde H$
is
$\widetilde H$
is
![]() $(\widetilde {\lambda }')^{-1}$
. Observe that
$(\widetilde {\lambda }')^{-1}$
. Observe that
![]() $(\widetilde {\lambda }')^2$
is the character with kernel
$(\widetilde {\lambda }')^2$
is the character with kernel
![]() $H'$
. (Recall
$H'$
. (Recall
![]() $\widetilde H'/H'\cong \mathrm C_2$
and hence there is exactly one character with this property.) The element
$\widetilde H'/H'\cong \mathrm C_2$
and hence there is exactly one character with this property.) The element
![]() $c\in \overline V'$
with
$c\in \overline V'$
with
![]() $\rho '(c)=\prod _{i=1}^{l'} (i,-i)$
satisfies
$\rho '(c)=\prod _{i=1}^{l'} (i,-i)$
satisfies
![]() $(\widetilde {\lambda }')^{c}=(\widetilde {\lambda }')^{-1}$
and hence
$(\widetilde {\lambda }')^{c}=(\widetilde {\lambda }')^{-1}$
and hence
![]() $\overline V^{\prime }_{\lambda '}=\overline V^{\prime }_{\widetilde {\lambda }'} {\left\langle c\right\rangle }$
. According to (a), there exists some extension
$\overline V^{\prime }_{\lambda '}=\overline V^{\prime }_{\widetilde {\lambda }'} {\left\langle c\right\rangle }$
. According to (a), there exists some extension
![]() $\phi _0$
of
$\phi _0$
of
![]() $\lambda '$
to
$\lambda '$
to
![]() $\overline V_{\lambda '}$
. Then
$\overline V_{\lambda '}$
. Then
![]() ${\left. \phi _0\right\rceil _{{V_{\widetilde {\lambda }'}}}}$
and
${\left. \phi _0\right\rceil _{{V_{\widetilde {\lambda }'}}}}$
and
![]() $\widetilde {\lambda }'$
determine a common extension
$\widetilde {\lambda }'$
determine a common extension
![]() $\phi $
to
$\phi $
to
![]() $\widetilde H'\overline V^{\prime }_{\widetilde {\lambda }'}$
(see [Reference SpäthS3, 4.1(a)]). By this construction,
$\widetilde H'\overline V^{\prime }_{\widetilde {\lambda }'}$
(see [Reference SpäthS3, 4.1(a)]). By this construction,
![]() ${\left. \phi \right\rceil _{{\overline V^{\prime }_{\widetilde {\lambda }}}}}$
is c-stable.
${\left. \phi \right\rceil _{{\overline V^{\prime }_{\widetilde {\lambda }}}}}$
is c-stable.
4.2 The inclusion
 $K_{d}\lhd K_{d} \overline V_d$
for
$K_{d}\lhd K_{d} \overline V_d$
for
 $d\geq 2$
$d\geq 2$
In the following, we investigate the groups
![]() ${K_d}:=H_d{\left\langle G_I\mid I\in {\mathcal O}_d\right\rangle }$
and
${K_d}:=H_d{\left\langle G_I\mid I\in {\mathcal O}_d\right\rangle }$
and
![]() $K_d \overline V_d$
for
$K_d \overline V_d$
for
![]() $d\in \mathbb D\setminus \{\pm 1\}$
, where
$d\in \mathbb D\setminus \{\pm 1\}$
, where
![]() ${{\mathbf G}}_I={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Phi _I\right\rangle }$
and
${{\mathbf G}}_I={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Phi _I\right\rangle }$
and
![]() $G_I={{\mathbf G}_{I}}^F$
(see Notation 3.9 and Lemma 3.13).
$G_I={{\mathbf G}_{I}}^F$
(see Notation 3.9 and Lemma 3.13).
Lemma 4.2. Let
![]() $I\in {\mathcal O}\setminus (\{J_{-1}\} \cup {\mathcal O}_1)$
and
$I\in {\mathcal O}\setminus (\{J_{-1}\} \cup {\mathcal O}_1)$
and
![]() ${{\mathbf Z}_I}:= {\mathbf h} _I({\mathbb {F}}^{\times })$
. Then:
${{\mathbf Z}_I}:= {\mathbf h} _I({\mathbb {F}}^{\times })$
. Then:
-
(a)
 ${{\mathbf G}_{I}}\cong \operatorname {SL}_{|I|}({\mathbb {F}})$
and
${{\mathbf G}_{I}}\cong \operatorname {SL}_{|I|}({\mathbb {F}})$
and
 $G_I\cong \operatorname {SL}_{|I|}( q)$
;
$G_I\cong \operatorname {SL}_{|I|}( q)$
; -
(b)
 ${{\mathbf L}}_I= {{\mathbf G}_{I}}.{\mathbf Z}_I$
,
${{\mathbf L}}_I= {{\mathbf G}_{I}}.{\mathbf Z}_I$
,
 ${{\mathbf L}}_I/{\left\langle h_0\right\rangle }\cong \operatorname {GL}_{|I|}({\mathbb {F}})$
and
${{\mathbf L}}_I/{\left\langle h_0\right\rangle }\cong \operatorname {GL}_{|I|}({\mathbb {F}})$
and
 $|{{\mathbf G}_{I}}\cap {\mathbf Z}_I|=\frac {{|I|_{p'}}}{\gcd (2,|I|)}$
; and
$|{{\mathbf G}_{I}}\cap {\mathbf Z}_I|=\frac {{|I|_{p'}}}{\gcd (2,|I|)}$
; and -
(c)
 $L_I\cong \operatorname {GL}_{|I|}(q)$
if
$L_I\cong \operatorname {GL}_{|I|}(q)$
if
 $2\nmid |I|$
.
$2\nmid |I|$
.
Proof. By the assumptions,
![]() $d:=|I|\geq 1$
and
$d:=|I|\geq 1$
and
![]() $\Phi _I$
is a root system of type
$\Phi _I$
is a root system of type
![]() $\mathrm A_{d}$
. One has
$\mathrm A_{d}$
. One has
![]() ${{\mathbf G}_{I}}=[{\mathbf T}{{\mathbf G}}_I,{\mathbf T}{{\mathbf G}}_I]$
where
${{\mathbf G}_{I}}=[{\mathbf T}{{\mathbf G}}_I,{\mathbf T}{{\mathbf G}}_I]$
where
![]() ${\mathbf T}{{\mathbf G}}_I$
is a Levi subgroup, so
${\mathbf T}{{\mathbf G}}_I$
is a Levi subgroup, so
![]() ${{\mathbf G}}_I$
is simply connected
${{\mathbf G}}_I$
is simply connected
![]() $\cong \operatorname {SL}_{|I|}({\mathbb {F}})$
by [Reference MaslowskiMT, 12.14]. Note
$\cong \operatorname {SL}_{|I|}({\mathbb {F}})$
by [Reference MaslowskiMT, 12.14]. Note
![]() $I\neq J_{-1}$
. This gives (a).
$I\neq J_{-1}$
. This gives (a).
Any element of
![]() ${\mathbf T}_I$
can be written as
${\mathbf T}_I$
can be written as
![]() $\prod _{i\in I}{\mathbf h} _{e_i}(t_i)$
for some
$\prod _{i\in I}{\mathbf h} _{e_i}(t_i)$
for some
![]() $t_i\in {\mathbb {F}}^{\times }$
. Let
$t_i\in {\mathbb {F}}^{\times }$
. Let
![]() $\kappa \in {\mathbb {F}}$
with
$\kappa \in {\mathbb {F}}$
with
![]() $\kappa ^{|I|}=\prod _{i\in I} t_i$
and fix
$\kappa ^{|I|}=\prod _{i\in I} t_i$
and fix
![]() $j\in I$
. Then, by the Chevalley relations in
$j\in I$
. Then, by the Chevalley relations in
![]() $\overline {{\mathbf G}}$
,
$\overline {{\mathbf G}}$
,
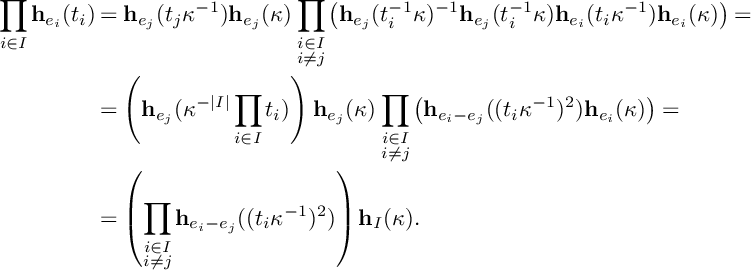 $$ \begin{align*} \prod_{i\in I}{\mathbf h} _{e_i}(t_i)&= {\mathbf h} _{e_j}(t_j\kappa^{-1}) {\mathbf h} _{e_j}(\kappa) \, \prod_{\substack{i\in I\\ i\neq j }}\left ( {\mathbf h} _{e_j}(t_i^{-1}\kappa)^{-1} {\mathbf h} _{e_j}(t_i^{-1}\kappa) {\mathbf h} _{e_i}(t_i\kappa^{-1}) {\mathbf h} _{e_i}(\kappa) \right )= \\ &=\left( {\mathbf h} _{e_j}( \kappa^{-|I|} \prod_{i\in I}t_i)\right) \, {\mathbf h} _{e_j}(\kappa) \, \prod_{\substack{i\in I\\i\neq j }}\left ( {\mathbf h} _{e_i-e_j}((t_i\kappa^{-1})^2) {\mathbf h} _{e_i}(\kappa) \right )=\\ &= \left (\prod_{\substack{i\in I\\ i\neq j } }{\mathbf h} _{e_i-e_j}((t_i\kappa^{-1})^2) \right ) {\mathbf h} _{I}(\kappa). \end{align*} $$
$$ \begin{align*} \prod_{i\in I}{\mathbf h} _{e_i}(t_i)&= {\mathbf h} _{e_j}(t_j\kappa^{-1}) {\mathbf h} _{e_j}(\kappa) \, \prod_{\substack{i\in I\\ i\neq j }}\left ( {\mathbf h} _{e_j}(t_i^{-1}\kappa)^{-1} {\mathbf h} _{e_j}(t_i^{-1}\kappa) {\mathbf h} _{e_i}(t_i\kappa^{-1}) {\mathbf h} _{e_i}(\kappa) \right )= \\ &=\left( {\mathbf h} _{e_j}( \kappa^{-|I|} \prod_{i\in I}t_i)\right) \, {\mathbf h} _{e_j}(\kappa) \, \prod_{\substack{i\in I\\i\neq j }}\left ( {\mathbf h} _{e_i-e_j}((t_i\kappa^{-1})^2) {\mathbf h} _{e_i}(\kappa) \right )=\\ &= \left (\prod_{\substack{i\in I\\ i\neq j } }{\mathbf h} _{e_i-e_j}((t_i\kappa^{-1})^2) \right ) {\mathbf h} _{I}(\kappa). \end{align*} $$
Accordingly,
![]() ${\mathbf T}_I=({\mathbf T}_I\cap {{\mathbf G}_{I}}) {\mathbf Z}_I$
. We note that
${\mathbf T}_I=({\mathbf T}_I\cap {{\mathbf G}_{I}}) {\mathbf Z}_I$
. We note that
![]() ${{\mathbf G}_{I}}\cong \operatorname {SL}_{|I|}( {\mathbb {F}})$
and
${{\mathbf G}_{I}}\cong \operatorname {SL}_{|I|}( {\mathbb {F}})$
and
![]() $G_I\cong \operatorname {SL}_{|I|}( q)$
as F acts on
$G_I\cong \operatorname {SL}_{|I|}( q)$
as F acts on
![]() ${{\mathbf G}_{I}}$
as standard Frobenius endomorphism. By the Chevalley relations,
${{\mathbf G}_{I}}$
as standard Frobenius endomorphism. By the Chevalley relations,
![]() ${\mathbf Z}_I\leq {\operatorname C}_{{\mathbf L}}({\mathbf G}_{I})$
and
${\mathbf Z}_I\leq {\operatorname C}_{{\mathbf L}}({\mathbf G}_{I})$
and
![]() ${{\mathbf L}}_I={\mathbf T}_I {{\mathbf G}_{I}}= {\mathbf Z}_I {{\mathbf G}_{I}}$
.
${{\mathbf L}}_I={\mathbf T}_I {{\mathbf G}_{I}}= {\mathbf Z}_I {{\mathbf G}_{I}}$
.
The calculations above show that an element of
![]() ${\mathbf Z}_I\cap {{\mathbf G}_{I}}$
can be written as
${\mathbf Z}_I\cap {{\mathbf G}_{I}}$
can be written as
![]() $\prod _{i\in I}{\mathbf h} _{e_i}(t)$
with
$\prod _{i\in I}{\mathbf h} _{e_i}(t)$
with
![]() $t^{|I|}=1$
. For
$t^{|I|}=1$
. For
![]() $d\in \mathbb D_{{\mathrm {even}}}$
, the element
$d\in \mathbb D_{{\mathrm {even}}}$
, the element
![]() $\prod _{i=1}^l{\mathbf h} _{e_i}(-1)$
is trivial and hence
$\prod _{i=1}^l{\mathbf h} _{e_i}(-1)$
is trivial and hence
![]() $|{\mathbf Z}_I\cap {{\mathbf G}_{I}}|=\frac {|I|_{p'}} {\gcd (2,|I|_{p'})}$
.
$|{\mathbf Z}_I\cap {{\mathbf G}_{I}}|=\frac {|I|_{p'}} {\gcd (2,|I|_{p'})}$
.
If
![]() $2\mid d $
, then with similar considerations as above, we see
$2\mid d $
, then with similar considerations as above, we see
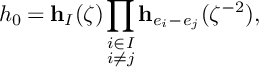 $$ \begin{align} h_0&= {\mathbf h} _I(\zeta) \prod_{\substack{i\in I\\i\neq j }} {\mathbf h} _{e_i-e_j}(\zeta^{-2}),\end{align} $$
$$ \begin{align} h_0&= {\mathbf h} _I(\zeta) \prod_{\substack{i\in I\\i\neq j }} {\mathbf h} _{e_i-e_j}(\zeta^{-2}),\end{align} $$
where
![]() $\zeta \in {\mathbb {F}}^{\times }$
has order
$\zeta \in {\mathbb {F}}^{\times }$
has order
![]() $2|I|_2$
. This implies that
$2|I|_2$
. This implies that
![]() ${{\mathbf L}}_I/{\left\langle h_0\right\rangle }$
is the central product of the one-dimensional torus
${{\mathbf L}}_I/{\left\langle h_0\right\rangle }$
is the central product of the one-dimensional torus
![]() ${\mathbf Z}_I/{\left\langle h_0\right\rangle }$
with
${\mathbf Z}_I/{\left\langle h_0\right\rangle }$
with
![]() ${{\mathbf G}}_I/{\left\langle h_0\right\rangle }$
over
${{\mathbf G}}_I/{\left\langle h_0\right\rangle }$
over
![]() $\operatorname Z({{\mathbf G}}_I)$
. Accordingly,
$\operatorname Z({{\mathbf G}}_I)$
. Accordingly,
![]() ${{\mathbf L}}_I/{\left\langle h_0\right\rangle } \cong \operatorname {GL}_{|I|}({\mathbb {F}})$
.
${{\mathbf L}}_I/{\left\langle h_0\right\rangle } \cong \operatorname {GL}_{|I|}({\mathbb {F}})$
.
For odd d, this implies analogously
![]() $ {{\mathbf L}}_I\cong \operatorname {GL}_d({\mathbb {F}})$
and
$ {{\mathbf L}}_I\cong \operatorname {GL}_d({\mathbb {F}})$
and
![]() $L_I\cong \operatorname {GL}_d(q)$
. This is the statement in (b) and (c). We could also have argued on Levi subgroups of
$L_I\cong \operatorname {GL}_d(q)$
. This is the statement in (b) and (c). We could also have argued on Levi subgroups of
![]() ${{\mathbf G}}/{\left\langle h_0\right\rangle }=\text {SO}_{2l}({\mathbb {F}})$
.
${{\mathbf G}}/{\left\langle h_0\right\rangle }=\text {SO}_{2l}({\mathbb {F}})$
.
Next, we study how
![]() $\widetilde {L}$
acts on
$\widetilde {L}$
acts on
![]() ${K_{0,d}}$
, which includes the action induced by
${K_{0,d}}$
, which includes the action induced by
![]() $t_I$
(
$t_I$
(
![]() $I\in {\mathcal O}$
) and
$I\in {\mathcal O}$
) and
![]() $t_{{\underline {l}},2}$
from Lemma 3.13. Recall that
$t_{{\underline {l}},2}$
from Lemma 3.13. Recall that
![]() $\widehat L_I:={{\mathbf L}}_I\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
satisfies
$\widehat L_I:={{\mathbf L}}_I\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
satisfies
![]() $\widehat L_I={\left\langle L_I,t_I\right\rangle }$
for some
$\widehat L_I={\left\langle L_I,t_I\right\rangle }$
for some
![]() $t_I\in {\mathbf T}_I\cap \mathcal L^{-1}(h_0)$
, and
$t_I\in {\mathbf T}_I\cap \mathcal L^{-1}(h_0)$
, and
![]() $\mathcal L^{-1}({\mathbf h} _{\underline {l}}(\varpi ))\cap {{\mathbf L}} = {\left\langle \widehat L,t_{{\underline {l}},2}\right\rangle }$
with
$\mathcal L^{-1}({\mathbf h} _{\underline {l}}(\varpi ))\cap {{\mathbf L}} = {\left\langle \widehat L,t_{{\underline {l}},2}\right\rangle }$
with
![]() $t_{{\underline {l}},2}={\mathbf h} _{\underline {l}}(\zeta )$
. According to Remark 2.16)(b), diagonal automorphisms of
$t_{{\underline {l}},2}={\mathbf h} _{\underline {l}}(\zeta )$
. According to Remark 2.16)(b), diagonal automorphisms of
![]() $G_I$
are parametrized by
$G_I$
are parametrized by
![]() $\operatorname Z({{\mathbf G}_{I}}) /[\operatorname Z({{\mathbf G}_{I}}) ,F]$
.
$\operatorname Z({{\mathbf G}_{I}}) /[\operatorname Z({{\mathbf G}_{I}}) ,F]$
.
Lemma 4.3. Let
![]() $I\in {\mathcal O}\setminus ({\mathcal O}_1\cup \{J_{-1}\})$
.
$I\in {\mathcal O}\setminus ({\mathcal O}_1\cup \{J_{-1}\})$
.
-
(a) If
 $2\nmid |I|$
, then
$2\nmid |I|$
, then
 $\widehat L_I= L_I{\operatorname C}_{{\mathbf T}_I}(L_I) $
, in particular
$\widehat L_I= L_I{\operatorname C}_{{\mathbf T}_I}(L_I) $
, in particular
 $t_{I}$
from Lemma 3.13(b) can be chosen such that
$t_{I}$
from Lemma 3.13(b) can be chosen such that
 $t_I\in {\operatorname C}_{{\mathbf T}_I}(L_I)$
.
$t_I\in {\operatorname C}_{{\mathbf T}_I}(L_I)$
. -
(b) For
 $2\mid |I|$
, the element
$2\mid |I|$
, the element
 ${t_{I}}$
induces on
${t_{I}}$
induces on
 $G_I$
a diagonal automorphism corresponding to
$G_I$
a diagonal automorphism corresponding to
 $g[\operatorname Z({{\mathbf G}_{I}}),F]$
with
$g[\operatorname Z({{\mathbf G}_{I}}),F]$
with
 $g\in \operatorname Z({{\mathbf G}_{I}})$
of order
$g\in \operatorname Z({{\mathbf G}_{I}})$
of order
 $|\operatorname Z({{\mathbf G}_{I}})|_2$
.
$|\operatorname Z({{\mathbf G}_{I}})|_2$
. -
(c)
 ${t_{{\underline {l}},2}} \in {\operatorname C}_{\widetilde {L}}(L_I)$
.
${t_{{\underline {l}},2}} \in {\operatorname C}_{\widetilde {L}}(L_I)$
.
Proof. Keep
![]() $d:=|I|$
. According to the theorem of Lang, we can choose
$d:=|I|$
. According to the theorem of Lang, we can choose
![]() $t_I\in {\mathbf T}_I$
such that
$t_I\in {\mathbf T}_I$
such that
![]() ${t_I}^{-1}F(t_I)=h_0$
as
${t_I}^{-1}F(t_I)=h_0$
as
![]() ${\mathbf T}_I$
is connected.
${\mathbf T}_I$
is connected.
If
![]() $2\nmid |I|$
, we see that
$2\nmid |I|$
, we see that
![]() $h_0={\mathbf h} _I(-1)$
and hence
$h_0={\mathbf h} _I(-1)$
and hence
![]() $h_0\in {\mathbf Z}_I$
. Since
$h_0\in {\mathbf Z}_I$
. Since
![]() ${\mathbf Z}_I$
is again connected
${\mathbf Z}_I$
is again connected
![]() $t_I$
can be chosen in
$t_I$
can be chosen in
![]() $\operatorname Z({{\mathbf L}}_I)$
, whence (a).
$\operatorname Z({{\mathbf L}}_I)$
, whence (a).
Following (4.1),
![]() $h_0=z_1z_2$
for some
$h_0=z_1z_2$
for some
![]() $z_1\in {\mathbf Z}_I$
and
$z_1\in {\mathbf Z}_I$
and
![]() $z_2\in \operatorname Z({{\mathbf G}_{I}})$
. Here,
$z_2\in \operatorname Z({{\mathbf G}_{I}})$
. Here,
![]() $z_2$
is an element of order
$z_2$
is an element of order
![]() $|I|_2=d_2$
. Then the element
$|I|_2=d_2$
. Then the element
![]() $t_I$
can be analogously written as
$t_I$
can be analogously written as
![]() $zg$
with
$zg$
with
![]() $z\in \operatorname Z({{\mathbf G}}_I)$
and
$z\in \operatorname Z({{\mathbf G}}_I)$
and
![]() $g\in {{\mathbf G}}$
such that
$g\in {{\mathbf G}}$
such that
![]() $\mathcal L(z)=z_1$
and
$\mathcal L(z)=z_1$
and
![]() $\mathcal L(g)=z_2$
. As g induces on
$\mathcal L(g)=z_2$
. As g induces on
![]() ${{\mathbf G}}$
a diagonal automorphism associated with
${{\mathbf G}}$
a diagonal automorphism associated with
![]() $z_2 [\operatorname Z({{\mathbf G}_{I}}),F]$
, the element
$z_2 [\operatorname Z({{\mathbf G}_{I}}),F]$
, the element
![]() $t_I\in \widetilde {{\mathbf G}_{I}}$
with
$t_I\in \widetilde {{\mathbf G}_{I}}$
with
![]() $x^{-1}F(x)=h_0$
induces the same diagonal automorphism. This gives (b).
$x^{-1}F(x)=h_0$
induces the same diagonal automorphism. This gives (b).
The element
![]() $t_{{\underline {l}},2}={\mathbf h} _{{\underline {l}}}(\zeta )$
from Lemma 3.13(e) centralizes
$t_{{\underline {l}},2}={\mathbf h} _{{\underline {l}}}(\zeta )$
from Lemma 3.13(e) centralizes
![]() ${{\mathbf G}_{I}}$
since the Weyl group of
${{\mathbf G}_{I}}$
since the Weyl group of
![]() ${{\mathbf G}}_I$
centralizes
${{\mathbf G}}_I$
centralizes
![]() $t_{{\underline {l}},2}$
.
$t_{{\underline {l}},2}$
.
Recall the groups
![]() ${\widetilde H_d}={\left\langle \left.h_0,{\mathbf h} _I(\varpi )\vphantom {I\in {\mathcal O}_d}\hskip .1em\right.\mid I\in {\mathcal O}_d \right\rangle }$
,
${\widetilde H_d}={\left\langle \left.h_0,{\mathbf h} _I(\varpi )\vphantom {I\in {\mathcal O}_d}\hskip .1em\right.\mid I\in {\mathcal O}_d \right\rangle }$
,
![]() ${H_0}={\left\langle {\mathbf h} _{\alpha }(-1)\mid {\alpha } \in \Phi \right\rangle }$
, and
${H_0}={\left\langle {\mathbf h} _{\alpha }(-1)\mid {\alpha } \in \Phi \right\rangle }$
, and
![]() ${{H_d}}=\widetilde H_d \cap H_{0}$
defined in Notation 3.9 for every
${{H_d}}=\widetilde H_d \cap H_{0}$
defined in Notation 3.9 for every
![]() $d\in \mathbb D$
. Using the groups
$d\in \mathbb D$
. Using the groups
![]() $G_I$
from Lemma 3.13, let
$G_I$
from Lemma 3.13, let
![]() ${K_{0,d}}:= {\left\langle \left.G_I\vphantom {I \in {\mathcal O}_d}\hskip .1em\right.\mid I \in {\mathcal O}_d \right\rangle }$
and
${K_{0,d}}:= {\left\langle \left.G_I\vphantom {I \in {\mathcal O}_d}\hskip .1em\right.\mid I \in {\mathcal O}_d \right\rangle }$
and
![]() ${K_d}:=H_dK_{0,d}$
. If
${K_d}:=H_dK_{0,d}$
. If
![]() $\mathbb D=\{d\}$
, then
$\mathbb D=\{d\}$
, then
![]() ${K_0}=K_{0,d} $
and
${K_0}=K_{0,d} $
and
![]() $K=K_d$
. As
$K=K_d$
. As
![]() $\overline V_d\cap K_d\leq {\mathrm {C}}_{{{\mathbf L}}}({{\mathbf G}}_I)$
as a consequence of Lemma 3.11, there is a well-defined action of
$\overline V_d\cap K_d\leq {\mathrm {C}}_{{{\mathbf L}}}({{\mathbf G}}_I)$
as a consequence of Lemma 3.11, there is a well-defined action of
![]() $\overline V_d/H_d$
on
$\overline V_d/H_d$
on
![]() $K_d$
.
$K_d$
.
Lemma 4.4 (The action of
 $V_d$
on
$V_d$
on
 $K_{0,d}$
)
$K_{0,d}$
)
Let
![]() $d\in \mathbb D$
. Let
$d\in \mathbb D$
. Let
![]() ${\epsilon _d}: \overline V_d\rightarrow \overline V_d/H_d$
be the canonical morphism and
${\epsilon _d}: \overline V_d\rightarrow \overline V_d/H_d$
be the canonical morphism and
![]() ${\overline {\mathbf {n}}_1^{(d)}} :=\kappa _d(\overline {\mathbf {n}}_1)$
. Then:
${\overline {\mathbf {n}}_1^{(d)}} :=\kappa _d(\overline {\mathbf {n}}_1)$
. Then:
-
(a)
 $K_{0,d}\rtimes {\epsilon }(\overline V_d) \cong (G_{I_{d,1}} \rtimes {\left\langle {\epsilon }(\overline {\mathbf {n}}_1^{(d)})\right\rangle })\wr {\mathcal {S}}_{a_d}$
.
$K_{0,d}\rtimes {\epsilon }(\overline V_d) \cong (G_{I_{d,1}} \rtimes {\left\langle {\epsilon }(\overline {\mathbf {n}}_1^{(d)})\right\rangle })\wr {\mathcal {S}}_{a_d}$
. -
(b) Then
 $\overline {\mathbf {n}} _1^{(d)}$
induces the graph automorphism transpose-inverse on
$\overline {\mathbf {n}} _1^{(d)}$
induces the graph automorphism transpose-inverse on
 $G_{I_{d,1}}$
.
$G_{I_{d,1}}$
. -
(c) If
 $2 \nmid d$
,
$2 \nmid d$
,
 $\overline {\mathbf {n}} _1^{(d)}$
induces on
$\overline {\mathbf {n}} _1^{(d)}$
induces on
 $L_{I_{d,1}}$
a product of a nontrivial graph and an inner automorphism via the isomorphism
$L_{I_{d,1}}$
a product of a nontrivial graph and an inner automorphism via the isomorphism
 $L_{I_{d,1}}\cong \operatorname {GL}_d(q)$
from Lemma 4.2(c).
$L_{I_{d,1}}\cong \operatorname {GL}_d(q)$
from Lemma 4.2(c).
Proof. Part (a) follows from the Steinberg presentation.
For part (b), we see that
![]() $G_{I_{d,1}}^{\overline {\mathbf {n}} _1^{(d)}}=G_{I_{d,1}}$
and
$G_{I_{d,1}}^{\overline {\mathbf {n}} _1^{(d)}}=G_{I_{d,1}}$
and
![]() $G_{I_{d,1}}\cap {\left\langle h_0\right\rangle }=\{1\}$
from the Chevalley relations. We compute the action of
$G_{I_{d,1}}\cap {\left\langle h_0\right\rangle }=\{1\}$
from the Chevalley relations. We compute the action of
![]() $\overline {\mathbf {n}} _1^{(d)}$
on
$\overline {\mathbf {n}} _1^{(d)}$
on
![]() $G_{I_{d,1}}$
in the quotient
$G_{I_{d,1}}$
in the quotient
![]() $G/{\left\langle h_0\right\rangle }$
or
$G/{\left\langle h_0\right\rangle }$
or
![]() $G_{I_{d,1}} \times {\left\langle h_0\right\rangle }/{\left\langle {h_0}\right\rangle }$
, respectively. In [Reference Gorenstein, Lyons and SolomonGLS, 2.7], the group
$G_{I_{d,1}} \times {\left\langle h_0\right\rangle }/{\left\langle {h_0}\right\rangle }$
, respectively. In [Reference Gorenstein, Lyons and SolomonGLS, 2.7], the group
![]() ${{\mathbf G}}/{\left\langle h_0\right\rangle }$
and its Steinberg generators are given explicitly as subgroup and elements of
${{\mathbf G}}/{\left\langle h_0\right\rangle }$
and its Steinberg generators are given explicitly as subgroup and elements of
![]() $\operatorname {SO}_{2l}(q)$
. The element
$\operatorname {SO}_{2l}(q)$
. The element
![]() $\overline {\mathbf {n}} _1^{(d)}$
acts on
$\overline {\mathbf {n}} _1^{(d)}$
acts on
![]() ${{\mathbf G}}_{I_{d,1}}{\left\langle h_0\right\rangle }/{\left\langle h_0\right\rangle }$
by transpose-inverse via
${{\mathbf G}}_{I_{d,1}}{\left\langle h_0\right\rangle }/{\left\langle h_0\right\rangle }$
by transpose-inverse via
![]() $G_{I_{d,1}}\cong \operatorname {SL}_d(q)$
. Computations in that group show part (b).
$G_{I_{d,1}}\cong \operatorname {SL}_d(q)$
. Computations in that group show part (b).
The element
![]() $\overline {\mathbf {n}} _1^{(d)}$
acts by inversion on
$\overline {\mathbf {n}} _1^{(d)}$
acts by inversion on
![]() ${\mathbf Z}_{I_{d,1}}$
and hence
${\mathbf Z}_{I_{d,1}}$
and hence
![]() $\overline {\mathbf {n}} _1^{(d)}$
satisfies the statement in part (c) as
$\overline {\mathbf {n}} _1^{(d)}$
satisfies the statement in part (c) as
![]() ${{\mathbf L}}_{I_{d,1}}={{\mathbf G}}_{I_{d,1}}{\mathbf Z}_ {I_{d,1}}$
.
${{\mathbf L}}_{I_{d,1}}={{\mathbf G}}_{I_{d,1}}{\mathbf Z}_ {I_{d,1}}$
.
Next, we study an analog of
![]() $\widetilde {L}$
from Lemma 3.13 associated with
$\widetilde {L}$
from Lemma 3.13 associated with
![]() $d\in \mathbb D$
, that is defined using the Lang map
$d\in \mathbb D$
, that is defined using the Lang map
![]() $\mathcal L$
from there. Note that
$\mathcal L$
from there. Note that
![]() ${\mathbf h} _{\underline {l}}(\varpi )\notin {\mathbf T}_{J_d}$
whenever
${\mathbf h} _{\underline {l}}(\varpi )\notin {\mathbf T}_{J_d}$
whenever
![]() $\mathbb D\neq \{d\}$
, but
$\mathbb D\neq \{d\}$
, but
![]() ${\mathbf h} _{\underline {l}}(\varpi )= \prod _{d\in \mathbb D}{\mathbf h} _{J_d}(\varpi )$
.
${\mathbf h} _{\underline {l}}(\varpi )= \prod _{d\in \mathbb D}{\mathbf h} _{J_d}(\varpi )$
.
Proposition 4.5. Let
![]() $d\in \mathbb D\setminus \{\pm 1\}$
, let
$d\in \mathbb D\setminus \{\pm 1\}$
, let
![]() ${\epsilon }_{d}: \overline V_{d}\longrightarrow \overline V_{d}/H_{d}$
be as in Lemma 4.4, let
${\epsilon }_{d}: \overline V_{d}\longrightarrow \overline V_{d}/H_{d}$
be as in Lemma 4.4, let
![]() ${\widetilde {T}_d}:={\mathbf T}_{J_d}\cap \mathcal L^{-1}({\left\langle h_0, {\mathbf h} _{J_d}(\varpi )\right\rangle })$
, and let
${\widetilde {T}_d}:={\mathbf T}_{J_d}\cap \mathcal L^{-1}({\left\langle h_0, {\mathbf h} _{J_d}(\varpi )\right\rangle })$
, and let
![]() $\widetilde {L}_{d}:= \widetilde {T}_d K_{0,d} $
. Then:
$\widetilde {L}_{d}:= \widetilde {T}_d K_{0,d} $
. Then:
-
(a) There exists some
 $\overline V_{d}{\left\langle F_p \right\rangle }$
-stable
$\overline V_{d}{\left\langle F_p \right\rangle }$
-stable
 $\widetilde {L}_{d}$
-transversal
$\widetilde {L}_{d}$
-transversal
 ${\mathbb {T}^{\circ }_{d}}$
in
${\mathbb {T}^{\circ }_{d}}$
in
 $\mathrm {Irr}_{cusp}(K_{0,d} )$
.
$\mathrm {Irr}_{cusp}(K_{0,d} )$
. -
(b) There exists an
 ${\epsilon }_{d}(\overline V_{d})\times {\left\langle F_p \right\rangle }$
-equivariant extension map
${\epsilon }_{d}(\overline V_{d})\times {\left\langle F_p \right\rangle }$
-equivariant extension map
 ${\Lambda _{\epsilon _d}}$
with respect to
${\Lambda _{\epsilon _d}}$
with respect to
 $K_{0,d} \lhd K_{0,d}\rtimes {\epsilon }_{d}(V_{d}) $
for
$K_{0,d} \lhd K_{0,d}\rtimes {\epsilon }_{d}(V_{d}) $
for
 $\mathbb {T}^{\circ }_{d}$
.
$\mathbb {T}^{\circ }_{d}$
. -
(c) Maximal extendibility holds with respect to
 ${K_{0,d}}\lhd \widetilde {L}_{d}$
and
${K_{0,d}}\lhd \widetilde {L}_{d}$
and
 $K_{d}\lhd \widetilde {L}_{d}$
.
$K_{d}\lhd \widetilde {L}_{d}$
.
For the proof of part (b), we require a strengthening of a result on wreath products that can, for example, be found in [Reference KlupschK, Th. 2.10].
Lemma 4.6. Let
![]() $X\rtimes Y$
be a finite group, and let A be a group of automorphisms of
$X\rtimes Y$
be a finite group, and let A be a group of automorphisms of
![]() $X\rtimes Y$
, stabilizing X, Y and some
$X\rtimes Y$
, stabilizing X, Y and some
![]() $\mathbb {K}\subseteq \mathrm {Irr}(X)$
. Let a be a positive integer. Note that A acts on
$\mathbb {K}\subseteq \mathrm {Irr}(X)$
. Let a be a positive integer. Note that A acts on
![]() $X^a\lhd (X\rtimes Y)\wr {\mathcal {S}}_a$
by diagonally acting on
$X^a\lhd (X\rtimes Y)\wr {\mathcal {S}}_a$
by diagonally acting on
![]() $(X\rtimes Y)^a$
and trivially on
$(X\rtimes Y)^a$
and trivially on
![]() ${\mathcal {S}}_a$
. In this context, we write then
${\mathcal {S}}_a$
. In this context, we write then
![]() $\Delta A$
for that group. If there exists an
$\Delta A$
for that group. If there exists an
![]() $(X\rtimes Y)\rtimes A$
-equivariant extension map with respect to
$(X\rtimes Y)\rtimes A$
-equivariant extension map with respect to
![]() $X\lhd X\rtimes Y$
for
$X\lhd X\rtimes Y$
for
![]() $\mathbb {K}$
, then there exists an
$\mathbb {K}$
, then there exists an
![]() $((X\rtimes Y)\wr {\mathcal {S}}_a)\rtimes \Delta A$
-equivariant extension map with respect to
$((X\rtimes Y)\wr {\mathcal {S}}_a)\rtimes \Delta A$
-equivariant extension map with respect to
![]() $X^a\lhd (X\rtimes Y)\wr {\mathcal {S}}_a$
for
$X^a\lhd (X\rtimes Y)\wr {\mathcal {S}}_a$
for
![]() $\mathbb {K}^a:=\{\chi _1\otimes \cdots \otimes \chi _a\mid \chi _i\in \mathbb {K} \}$
.
$\mathbb {K}^a:=\{\chi _1\otimes \cdots \otimes \chi _a\mid \chi _i\in \mathbb {K} \}$
.
Proof. This follows by the considerations in the proof of [Reference KlupschK, Th. 2.10] using the construction of representations of wreath products given in [Reference NavarroN, 10.1].
Proof of Proposition 4.5
Let
![]() $I_1:=I_{d,1}$
. Via the isomorphism
$I_1:=I_{d,1}$
. Via the isomorphism
![]() $G_{I_1}\cong \operatorname {SL}_d(q)$
from Lemma 4.2, the
$G_{I_1}\cong \operatorname {SL}_d(q)$
from Lemma 4.2, the
![]() $E(\operatorname {SL}_d(q))$
-stable
$E(\operatorname {SL}_d(q))$
-stable
![]() $\operatorname {GL}_d(q)$
-transversal in
$\operatorname {GL}_d(q)$
-transversal in
![]() $\mathrm {Irr}(\operatorname {SL}_d(q))$
from Proposition 2.19(b) determines a subset
$\mathrm {Irr}(\operatorname {SL}_d(q))$
from Proposition 2.19(b) determines a subset
![]() $\mathbb {T}_{I_1}\subseteq \mathrm {Irr}_{cusp}(G_{I_1})$
. According to Lemma 4.4
(b), this set is
$\mathbb {T}_{I_1}\subseteq \mathrm {Irr}_{cusp}(G_{I_1})$
. According to Lemma 4.4
(b), this set is
![]() $\overline {\mathbf {n}}_1^{(d)}$
-stable. The
$\overline {\mathbf {n}}_1^{(d)}$
-stable. The
![]() $E(\operatorname {SL}_d(q))$
-stable
$E(\operatorname {SL}_d(q))$
-stable
![]() $\operatorname {GL}_d(q)$
-transversal in
$\operatorname {GL}_d(q)$
-transversal in
![]() $\mathrm {Irr}(\operatorname {SL}_d(q))$
can even be chosen such that each character extends to its inertia group in
$\mathrm {Irr}(\operatorname {SL}_d(q))$
can even be chosen such that each character extends to its inertia group in
![]() $\operatorname {SL}_d(q)\rtimes E(\operatorname {SL}_d(q))$
. Accordingly, maximal extendibility holds with respect to
$\operatorname {SL}_d(q)\rtimes E(\operatorname {SL}_d(q))$
. Accordingly, maximal extendibility holds with respect to
![]() $G_{I_1}\lhd G_{I_1}\rtimes {\left\langle F_p,\epsilon _d(\overline {\mathbf {n}} _1^{(d)})\right\rangle }$
for
$G_{I_1}\lhd G_{I_1}\rtimes {\left\langle F_p,\epsilon _d(\overline {\mathbf {n}} _1^{(d)})\right\rangle }$
for
![]() $\mathbb {T}_{I_1}$
.
$\mathbb {T}_{I_1}$
.
Note that
![]() $\mathbb {T}_{I_1}$
is
$\mathbb {T}_{I_1}$
is
![]() ${\mathrm {N}}_{\overline V_d}(G_{I_1})$
-stable, as
${\mathrm {N}}_{\overline V_d}(G_{I_1})$
-stable, as
![]() ${\mathrm {N}}_{\overline V_d}(G_{I_1})$
acts as
${\mathrm {N}}_{\overline V_d}(G_{I_1})$
acts as
![]() ${\left\langle \overline {\mathbf {n}}_1^{d}\right\rangle }$
. Accordingly, via conjugation with elements of
${\left\langle \overline {\mathbf {n}}_1^{d}\right\rangle }$
. Accordingly, via conjugation with elements of
![]() $\overline V_d$
, the set
$\overline V_d$
, the set
![]() $\mathbb {T}_{I_1}$
determines characters
$\mathbb {T}_{I_1}$
determines characters
![]() $\mathbb {T}_{I}\subseteq \mathrm {Irr}_{cusp}(G_I)$
for every
$\mathbb {T}_{I}\subseteq \mathrm {Irr}_{cusp}(G_I)$
for every
![]() $I\in {\mathcal O}_d$
. Recall that by Lemma 3.13(d), the group
$I\in {\mathcal O}_d$
. Recall that by Lemma 3.13(d), the group
![]() ${K_0}$
is the direct product of the groups
${K_0}$
is the direct product of the groups
![]() $G_I$
(
$G_I$
(
![]() $I\in {\mathcal O}$
). Analogously,
$I\in {\mathcal O}$
). Analogously,
![]() $K_{0,d}$
is the direct product of the groups
$K_{0,d}$
is the direct product of the groups
![]() $G_I$
(
$G_I$
(
![]() $I\in {\mathcal O}_d$
).
$I\in {\mathcal O}_d$
).
The product
![]() $\mathbb {T}_d^{\circ }$
of these characters
$\mathbb {T}_d^{\circ }$
of these characters
![]() $\prod _{I\in {\mathcal O}_d}\mathbb {T}_I$
defines a
$\prod _{I\in {\mathcal O}_d}\mathbb {T}_I$
defines a
![]() $\overline V_d {\left\langle F_p \right\rangle }$
-stable set in
$\overline V_d {\left\langle F_p \right\rangle }$
-stable set in
![]() $\mathrm {Irr}_{cusp}(K_{0,d})$
. By this construction,
$\mathrm {Irr}_{cusp}(K_{0,d})$
. By this construction,
![]() $\mathbb {T}_d^{\circ }$
is
$\mathbb {T}_d^{\circ }$
is
![]() $\overline V_d{\left\langle F_p \right\rangle }$
-stable. Following the description of the action of
$\overline V_d{\left\langle F_p \right\rangle }$
-stable. Following the description of the action of
![]() $\widetilde {L}$
on
$\widetilde {L}$
on
![]() ${K_{0,d}}$
given in Lemma 4.3, we see that
${K_{0,d}}$
given in Lemma 4.3, we see that
![]() $\mathbb {T}^{\circ }_d$
is an
$\mathbb {T}^{\circ }_d$
is an
![]() $\widetilde {L}_d$
-transversal in
$\widetilde {L}_d$
-transversal in
![]() $\mathrm {Irr}_{cusp}(K_{0,d})$
. This proves part (a).
$\mathrm {Irr}_{cusp}(K_{0,d})$
. This proves part (a).
Recall
![]() $K_{0,d} \rtimes {\epsilon }_d(\overline V_d) \cong \left (G_{I_1}\rtimes {\left\langle {\epsilon }(\overline {\mathbf {n}} _1^{(d)})\right\rangle }\right )\wr {\mathcal {S}}_{a_d}$
from Lemma 4.4. As stated above, maximal extendibility holds with respect to
$K_{0,d} \rtimes {\epsilon }_d(\overline V_d) \cong \left (G_{I_1}\rtimes {\left\langle {\epsilon }(\overline {\mathbf {n}} _1^{(d)})\right\rangle }\right )\wr {\mathcal {S}}_{a_d}$
from Lemma 4.4. As stated above, maximal extendibility holds with respect to
![]() $G_{I_1}\lhd G_{I_1}\rtimes {\left\langle F_p,\epsilon (\overline {\mathbf {n}} _1^{(d)})\right\rangle }$
for
$G_{I_1}\lhd G_{I_1}\rtimes {\left\langle F_p,\epsilon (\overline {\mathbf {n}} _1^{(d)})\right\rangle }$
for
![]() $\mathbb {T}_{I_1}$
. According to Lemma 4.6, this implies by the choice of
$\mathbb {T}_{I_1}$
. According to Lemma 4.6, this implies by the choice of
![]() $\mathbb {T}^{\circ }_d$
that there is an
$\mathbb {T}^{\circ }_d$
that there is an
![]() ${\epsilon }_{d}(\overline V_{d}){\left\langle F_p \right\rangle }$
-equivariant extension map
${\epsilon }_{d}(\overline V_{d}){\left\langle F_p \right\rangle }$
-equivariant extension map
![]() $\Lambda _{{\epsilon }_d}$
with respect to
$\Lambda _{{\epsilon }_d}$
with respect to
![]() $K_{0,d} \lhd K_{0,d} \rtimes {\epsilon }_{d}(V_{d}) $
for
$K_{0,d} \lhd K_{0,d} \rtimes {\epsilon }_{d}(V_{d}) $
for
![]() $\mathbb {T}^{\circ }_{d}$
.
$\mathbb {T}^{\circ }_{d}$
.
According to Theorem 2.17, maximal extendibility holds with respect to
![]() $G_I\lhd {\widetilde G}_I$
where
$G_I\lhd {\widetilde G}_I$
where
![]() ${\widetilde G}_I:={{\mathbf G}}_I \cap \mathcal L^{-1}(\operatorname Z({{\mathbf G}_{I}}))$
. Additionally,
${\widetilde G}_I:={{\mathbf G}}_I \cap \mathcal L^{-1}(\operatorname Z({{\mathbf G}_{I}}))$
. Additionally,
![]() $[{{\mathbf G}}_I,{\mathbf Z}_I]=1$
for
$[{{\mathbf G}}_I,{\mathbf Z}_I]=1$
for
![]() ${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
from Lemma 4.2. We observe that
${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
from Lemma 4.2. We observe that
![]() $\widetilde {L}_d\leq {\left\langle {\widetilde G}_I\mid I\in {\mathcal O}_d\right\rangle } {\left\langle {\mathbf Z}_I\mid I\in {\mathcal O}_d\right\rangle }$
, even more precisely
$\widetilde {L}_d\leq {\left\langle {\widetilde G}_I\mid I\in {\mathcal O}_d\right\rangle } {\left\langle {\mathbf Z}_I\mid I\in {\mathcal O}_d\right\rangle }$
, even more precisely
where
![]() $\widehat Z_I:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}_I)\cap {\mathbf Z}_I)\cap {\mathbf Z}_I$
. We see that maximal extendibility holds with respect to
$\widehat Z_I:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}_I)\cap {\mathbf Z}_I)\cap {\mathbf Z}_I$
. We see that maximal extendibility holds with respect to
![]() $K_{0,d} \lhd {\left\langle {\widetilde G}_I\mid I\in {\mathcal O}_d\right\rangle } {\left\langle \widehat Z_I\mid I\in {\mathcal O}_d\right\rangle }$
. Hence, maximal extendibility holds with respect to
$K_{0,d} \lhd {\left\langle {\widetilde G}_I\mid I\in {\mathcal O}_d\right\rangle } {\left\langle \widehat Z_I\mid I\in {\mathcal O}_d\right\rangle }$
. Hence, maximal extendibility holds with respect to
![]() $K_{0,d} \lhd \widetilde {L}_d $
and
$K_{0,d} \lhd \widetilde {L}_d $
and
![]() $K_d\lhd \widetilde {L}_d$
, as
$K_d\lhd \widetilde {L}_d$
, as
![]() $\widetilde {L}_d/{K_{0,d}}$
is abelian.
$\widetilde {L}_d/{K_{0,d}}$
is abelian.
Lemma 4.7. Let
![]() $d\in \mathbb D \setminus \{\pm 1\}$
.
$d\in \mathbb D \setminus \{\pm 1\}$
.
-
(a) Maximal extendibility holds with respect to
 $H_d\lhd \overline V_d$
.
$H_d\lhd \overline V_d$
. -
(b) If
 $2\nmid d$
,
$2\nmid d$
,
 $\lambda \in \mathrm {Irr}(H_d)$
with
$\lambda \in \mathrm {Irr}(H_d)$
with
 $\lambda (h_0)=-1$
, and
$\lambda (h_0)=-1$
, and
 $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H_d|\lambda )$
, then
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H_d|\lambda )$
, then
 $(\overline V_d)_{\widetilde {\lambda }}\leq V_{\mathrm {D}}$
and
$(\overline V_d)_{\widetilde {\lambda }}\leq V_{\mathrm {D}}$
and
 $(\overline V_d)_{\lambda }=(\overline V_d)_{\widetilde {\lambda }}{\left\langle c_d\right\rangle }$
for some
$(\overline V_d)_{\lambda }=(\overline V_d)_{\widetilde {\lambda }}{\left\langle c_d\right\rangle }$
for some
 $c_d\in \overline V_d$
.
$c_d\in \overline V_d$
.
Proof. Recall that by [Reference Malle and TestermanMS, Prop. 3.8] maximal extendibility holds with respect to
![]() $ H_{{\underline {a_d}}}\lhd \overline V_{{\underline {a_d}}}$
. Via the map
$ H_{{\underline {a_d}}}\lhd \overline V_{{\underline {a_d}}}$
. Via the map
![]() $\kappa _d: \overline V_{{\underline {a_d}}}\longrightarrow \overline V_d$
from Lemma 3.21, the maximal extendibility with respect to
$\kappa _d: \overline V_{{\underline {a_d}}}\longrightarrow \overline V_d$
from Lemma 3.21, the maximal extendibility with respect to
![]() $H_{{\underline {a_d}}}\lhd \overline V_{{\underline {a_d}}}$
gives a
$H_{{\underline {a_d}}}\lhd \overline V_{{\underline {a_d}}}$
gives a
![]() $\overline V_d$
-equivariant extension map for
$\overline V_d$
-equivariant extension map for
![]() $\kappa _d(H_{\underline {a_d}})\lhd \kappa _d(V_{\underline {a_d}})$
. This implies part (a) according to [Reference SpäthS2, 4.1(a)].
$\kappa _d(H_{\underline {a_d}})\lhd \kappa _d(V_{\underline {a_d}})$
. This implies part (a) according to [Reference SpäthS2, 4.1(a)].
In part (b), we assume
![]() $2\nmid d$
and hence
$2\nmid d$
and hence
![]() $\kappa _d(H_{\underline {a_d}})=H_d$
. The character
$\kappa _d(H_{\underline {a_d}})=H_d$
. The character
![]() $\lambda \in \mathrm {Irr}(H_d)$
with
$\lambda \in \mathrm {Irr}(H_d)$
with
![]() $\lambda (h_0)=-1$
corresponds via
$\lambda (h_0)=-1$
corresponds via
![]() $\kappa _d$
to some
$\kappa _d$
to some
![]() $\lambda _0\in \mathrm {Irr}(H_{{\underline {a_d}}})$
with
$\lambda _0\in \mathrm {Irr}(H_{{\underline {a_d}}})$
with
![]() $\lambda _0(h_0)=-1$
. Proposition 4.1(b) implies that via
$\lambda _0(h_0)=-1$
. Proposition 4.1(b) implies that via
![]() $\kappa _d$
there is some
$\kappa _d$
there is some
![]() $\overline V_d$
-conjugate
$\overline V_d$
-conjugate
![]() $\lambda '$
of
$\lambda '$
of
![]() $\lambda $
with
$\lambda $
with
![]() $\rho _{{\mathbf T}}(\overline V_{\widetilde {\lambda }'})={\mathcal {S}}_{{\mathcal O}_d}$
for any
$\rho _{{\mathbf T}}(\overline V_{\widetilde {\lambda }'})={\mathcal {S}}_{{\mathcal O}_d}$
for any
![]() $\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde H_d\mid \lambda ')$
and
$\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde H_d\mid \lambda ')$
and
![]() $(\overline V_{d})_{\lambda '}=\overline V_{\widetilde {\lambda }'}{\left\langle c^{\prime }_d\right\rangle }$
for some
$(\overline V_{d})_{\lambda '}=\overline V_{\widetilde {\lambda }'}{\left\langle c^{\prime }_d\right\rangle }$
for some
![]() $c^{\prime }_d\in \mathrm {Irr}(\overline V_d)$
with
$c^{\prime }_d\in \mathrm {Irr}(\overline V_d)$
with
![]() $\rho _{{\mathbf T}}(c^{\prime }_d)=\prod _{i\in J_d}(i,-i)$
. We observe that
$\rho _{{\mathbf T}}(c^{\prime }_d)=\prod _{i\in J_d}(i,-i)$
. We observe that
![]() $(\overline V_d)_{\widetilde {\lambda }'}\leq V_{\mathrm {D}}$
. Because of
$(\overline V_d)_{\widetilde {\lambda }'}\leq V_{\mathrm {D}}$
. Because of
![]() $V_{\mathrm {D}}\lhd \overline V$
, this implies
$V_{\mathrm {D}}\lhd \overline V$
, this implies
![]() $(\overline V_d)_{\widetilde {\lambda }}\leq V_{\mathrm {D}}$
and
$(\overline V_d)_{\widetilde {\lambda }}\leq V_{\mathrm {D}}$
and
![]() $(\overline V_d)_{\lambda }=(\overline V_d)_{\widetilde {\lambda }} {\left\langle c_d\right\rangle }$
for some
$(\overline V_d)_{\lambda }=(\overline V_d)_{\widetilde {\lambda }} {\left\langle c_d\right\rangle }$
for some
![]() $c_d\in \overline V_d$
. This proves part (b).
$c_d\in \overline V_d$
. This proves part (b).
4.3 Consideration of
 $K_{-1}\lhd K_{-1}\overline V_{-1}$
$K_{-1}\lhd K_{-1}\overline V_{-1}$
The group structure of
![]() $G_{J_{-1}}$
depends on
$G_{J_{-1}}$
depends on
![]() ${\mathsf {type}}(\Phi _{-1})$
. By its definition,
${\mathsf {type}}(\Phi _{-1})$
. By its definition,
![]() ${\mathsf {type}}(\Phi _{-1})\in \{\mathrm A_1\times \mathrm A_1, \mathrm A_3, \mathrm {D}_{|J_{-1}|}\}$
. For the application of Proposition 3.2, we prove the following statement. Recall
${\mathsf {type}}(\Phi _{-1})\in \{\mathrm A_1\times \mathrm A_1, \mathrm A_3, \mathrm {D}_{|J_{-1}|}\}$
. For the application of Proposition 3.2, we prove the following statement. Recall
![]() $\overline V_{-1}={\left\langle \mathbf {n}_{e_1}(\varpi ), h_0\right\rangle }$
,
$\overline V_{-1}={\left\langle \mathbf {n}_{e_1}(\varpi ), h_0\right\rangle }$
,
![]() $\widetilde H_{-1}={\left\langle {\mathbf h} _{J_{-1}}(\varpi ), h_0\right\rangle }$
,
$\widetilde H_{-1}={\left\langle {\mathbf h} _{J_{-1}}(\varpi ), h_0\right\rangle }$
,
![]() $H_{-1}=\widetilde H_{-1}\cap H_0$
, and
$H_{-1}=\widetilde H_{-1}\cap H_0$
, and
![]() $G_{J_{-1}}={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Phi _{-1}\right\rangle }^F$
. As before, we set
$G_{J_{-1}}={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Phi _{-1}\right\rangle }^F$
. As before, we set
![]() ${K_{0,-1}}:=G_{J_{-1}}$
and
${K_{0,-1}}:=G_{J_{-1}}$
and
![]() ${K_{-1}}:=H_{-1}G_{J_{-1}}$
.
${K_{-1}}:=H_{-1}G_{J_{-1}}$
.
Proposition 4.8. Assume Hypothesis 2.14 holds for
![]() ${{\mathbf G}}_{J_{-1}}^F$
if
${{\mathbf G}}_{J_{-1}}^F$
if
![]() $\Phi _{-1}$
is of type
$\Phi _{-1}$
is of type
![]() $\mathrm {D}$
. Let
$\mathrm {D}$
. Let
![]() ${\epsilon _{-1}}:\overline V_{-1}\longrightarrow \overline V_{-1}/H_{-1}$
be the canonical epimorphism, and let
${\epsilon _{-1}}:\overline V_{-1}\longrightarrow \overline V_{-1}/H_{-1}$
be the canonical epimorphism, and let
![]() $\widetilde {L}_{-1}:= ({{\mathbf G}}_{J_{-1}}{\mathbf T}_{J_{-1}})\cap \mathcal L^{-1}({\left\langle h_0, {\mathbf h} _{J_{-1}}(\varpi )\right\rangle })$
. Then:
$\widetilde {L}_{-1}:= ({{\mathbf G}}_{J_{-1}}{\mathbf T}_{J_{-1}})\cap \mathcal L^{-1}({\left\langle h_0, {\mathbf h} _{J_{-1}}(\varpi )\right\rangle })$
. Then:
-
(a) There exists some
 $\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
$\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
 $\widetilde {L}_{-1}$
-transversal
$\widetilde {L}_{-1}$
-transversal
 ${\mathbb {T}_{-1}^{\circ }}$
in
${\mathbb {T}_{-1}^{\circ }}$
in
 $\mathrm {Irr}_{cusp}(K_{0,-1})$
.
$\mathrm {Irr}_{cusp}(K_{0,-1})$
. -
(b) There exists an
 ${\epsilon }_{-1}(\overline V_{-1}){\left\langle F_p \right\rangle }$
-equivariant extension map
${\epsilon }_{-1}(\overline V_{-1}){\left\langle F_p \right\rangle }$
-equivariant extension map
 ${\Lambda _{\epsilon _{-1}}}$
with respect to
${\Lambda _{\epsilon _{-1}}}$
with respect to
 $K_{0,-1} \lhd K_{0,-1}\rtimes {\epsilon }_{-1}(\overline V_{-1}) $
for
$K_{0,-1} \lhd K_{0,-1}\rtimes {\epsilon }_{-1}(\overline V_{-1}) $
for
 $\mathbb {T}^{\circ }_{-1}$
.
$\mathbb {T}^{\circ }_{-1}$
. -
(c) Maximal extendibility holds with respect to
 $K_{0,-1}\lhd \widetilde {L}_{-1}$
and
$K_{0,-1}\lhd \widetilde {L}_{-1}$
and
 $K_{-1}\lhd \widetilde {L}_{-1}$
.
$K_{-1}\lhd \widetilde {L}_{-1}$
.
Proof. As in the proof of Lemma 3.13, we see that
![]() $\widetilde {L}_{-1}=T_{-1}{G_{J_{-1}}} {\left\langle t_{J_{-1}}, t_{J_{-1},2}\right\rangle }$
, where
$\widetilde {L}_{-1}=T_{-1}{G_{J_{-1}}} {\left\langle t_{J_{-1}}, t_{J_{-1},2}\right\rangle }$
, where
![]() $T_{-1}:={\mathbf T}_{J_{-1}}^F$
,
$T_{-1}:={\mathbf T}_{J_{-1}}^F$
,
![]() $\zeta \in {\mathbb {F}}^{\times }$
with
$\zeta \in {\mathbb {F}}^{\times }$
with
![]() $\zeta ^{(q-1)_2}=\varpi $
,
$\zeta ^{(q-1)_2}=\varpi $
,
![]() ${t_{J_{-1}}}:={\mathbf h} _{e_1}(\zeta ^2)$
and
${t_{J_{-1}}}:={\mathbf h} _{e_1}(\zeta ^2)$
and
![]() ${t_{J_{-1},2}}:={\mathbf h} _{J_{-1}}(\zeta )$
. Note that the action of
${t_{J_{-1},2}}:={\mathbf h} _{J_{-1}}(\zeta )$
. Note that the action of
![]() $\widetilde {L}$
on
$\widetilde {L}$
on
![]() $G_{J_{-1}}$
coincides with the one of
$G_{J_{-1}}$
coincides with the one of
![]() ${\left\langle T_{{-1}}, t_{J_{-1}}, t_{J_{-1},2}\right\rangle }$
up to inner automorphisms. By the definition of
${\left\langle T_{{-1}}, t_{J_{-1}}, t_{J_{-1},2}\right\rangle }$
up to inner automorphisms. By the definition of
![]() $G_{J_{-1}}$
, we see
$G_{J_{-1}}$
, we see
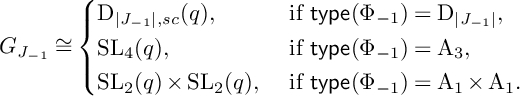 $$\begin{align*}G_{J_{-1}}\cong \begin{cases} \mathrm{D}_{|J_{-1}|,sc}(q),& \text{ if } {\mathsf {type}}(\Phi_{-1})=\mathrm{D}_{|J_{-1}|},\\ \operatorname{SL}_4(q), & \text{ if } {\mathsf {type}}(\Phi_{-1})=\mathrm A_3,\\ \operatorname{SL}_2(q)\times \operatorname{SL}_2(q),&\text{ if }{\mathsf {type}}(\Phi_{-1})=\mathrm A_1\times \mathrm A_1. \end{cases}\end{align*}$$
$$\begin{align*}G_{J_{-1}}\cong \begin{cases} \mathrm{D}_{|J_{-1}|,sc}(q),& \text{ if } {\mathsf {type}}(\Phi_{-1})=\mathrm{D}_{|J_{-1}|},\\ \operatorname{SL}_4(q), & \text{ if } {\mathsf {type}}(\Phi_{-1})=\mathrm A_3,\\ \operatorname{SL}_2(q)\times \operatorname{SL}_2(q),&\text{ if }{\mathsf {type}}(\Phi_{-1})=\mathrm A_1\times \mathrm A_1. \end{cases}\end{align*}$$
Assume
![]() ${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{l_{-1}}$
with
${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{l_{-1}}$
with
![]() $l_{-1}:=|J_{-1}|$
and
$l_{-1}:=|J_{-1}|$
and
![]() $l_{-1}>3$
. Then
$l_{-1}>3$
. Then
![]() $T_{-1}\leq G_{J_{-1}}$
. The elements
$T_{-1}\leq G_{J_{-1}}$
. The elements
![]() $t_{J_{-1}}$
and
$t_{J_{-1}}$
and
![]() $t_{J_{-1},2}$
act as diagonal automorphisms on
$t_{J_{-1},2}$
act as diagonal automorphisms on
![]() $G_{J_{-1}}$
. Part (a) follows from Theorem 2.13. By Hypothesis 2.14, we can choose a
$G_{J_{-1}}$
. Part (a) follows from Theorem 2.13. By Hypothesis 2.14, we can choose a
![]() $\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
$\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
![]() $\widetilde {L}_{-1}$
-transversal
$\widetilde {L}_{-1}$
-transversal
![]() $\mathbb {T}^{\circ }_{-1}$
in
$\mathbb {T}^{\circ }_{-1}$
in
![]() $\mathrm {Irr}_{cusp}(K_{0,-1})$
such that maximal extendibility holds with respect to
$\mathrm {Irr}_{cusp}(K_{0,-1})$
such that maximal extendibility holds with respect to
![]() $K_{0,-1}\lhd K_{0,-1}\rtimes {\left\langle \gamma , F_p\right\rangle }$
for
$K_{0,-1}\lhd K_{0,-1}\rtimes {\left\langle \gamma , F_p\right\rangle }$
for
![]() $\mathbb {T}_{-1}$
. Note that
$\mathbb {T}_{-1}$
. Note that
![]() $K_{0,-1}\rtimes {\left\langle \gamma , F_p\right\rangle }=K_{0,-1}\rtimes ({\epsilon }_{-1}(\overline V_{-1})\times {\left\langle F_p \right\rangle })$
. By this choice, we see that an extension map
$K_{0,-1}\rtimes {\left\langle \gamma , F_p\right\rangle }=K_{0,-1}\rtimes ({\epsilon }_{-1}(\overline V_{-1})\times {\left\langle F_p \right\rangle })$
. By this choice, we see that an extension map
![]() $\Lambda _{{\epsilon }_1}$
as required in part (b) exists. Note that the actions on
$\Lambda _{{\epsilon }_1}$
as required in part (b) exists. Note that the actions on
![]() $G_{J_{-1}}$
induced by
$G_{J_{-1}}$
induced by
![]() $\gamma $
and
$\gamma $
and
![]() $\mathbf {n}_{e_1}(\varpi )$
coincide by 3.3. According to Theorem 2.17, maximal extendibility holds with respect to
$\mathbf {n}_{e_1}(\varpi )$
coincide by 3.3. According to Theorem 2.17, maximal extendibility holds with respect to
![]() $G_{J_{-1}}\lhd \widetilde {L}_{-1}$
. This proves part (c) in the case where
$G_{J_{-1}}\lhd \widetilde {L}_{-1}$
. This proves part (c) in the case where
![]() ${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{l_{-1}}$
with
${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{l_{-1}}$
with
![]() $l_{-1}>3$
.
$l_{-1}>3$
.
Assume
![]() ${\mathsf {type}}(\Phi _{-1})=\mathrm A_1\times \mathrm A_1$
, then
${\mathsf {type}}(\Phi _{-1})=\mathrm A_1\times \mathrm A_1$
, then
![]() $t_{J_{-1}}$
induces on both factors a noninner diagonal automorphism, while
$t_{J_{-1}}$
induces on both factors a noninner diagonal automorphism, while
![]() $t_{J_{-1},2}$
induces a noninner diagonal automorphism only on one factor, since
$t_{J_{-1},2}$
induces a noninner diagonal automorphism only on one factor, since
![]() $h_0={\mathbf h} _{e_2-e_1}(-1){\mathbf h} _{e_1+e_2}(-1)$
and
$h_0={\mathbf h} _{e_2-e_1}(-1){\mathbf h} _{e_1+e_2}(-1)$
and
![]() ${\mathbf h} _{e_1}(\varpi ) {\mathbf h} _{e_2}(\varpi )= {\mathbf h} _{e_1+e_2}(-1)$
. Clearly,
${\mathbf h} _{e_1}(\varpi ) {\mathbf h} _{e_2}(\varpi )= {\mathbf h} _{e_1+e_2}(-1)$
. Clearly,
![]() $\overline V_{-1}$
acts by permutation of the two factors. Let
$\overline V_{-1}$
acts by permutation of the two factors. Let
![]() $\mathbb {T}(\operatorname {SL}_2(q))$
be an
$\mathbb {T}(\operatorname {SL}_2(q))$
be an
![]() ${\left\langle F_p \right\rangle }$
-stable
${\left\langle F_p \right\rangle }$
-stable
![]() $\operatorname {GL}_2(q)$
-transversal in
$\operatorname {GL}_2(q)$
-transversal in
![]() $\mathrm {Irr}_{cusp}(\operatorname {SL}_2(q))$
(see Proposition 2.19). Then
$\mathrm {Irr}_{cusp}(\operatorname {SL}_2(q))$
(see Proposition 2.19). Then
![]() $\mathbb {T}^{\circ }_{-1}:=\mathbb {T}(\operatorname {SL}_2(q))\times \mathbb {T}(\operatorname {SL}_2(q))$
is a
$\mathbb {T}^{\circ }_{-1}:=\mathbb {T}(\operatorname {SL}_2(q))\times \mathbb {T}(\operatorname {SL}_2(q))$
is a
![]() $\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
$\overline V_{-1}{\left\langle F_p \right\rangle }$
-stable
![]() $\widetilde {L}_{-1}$
-transversal in
$\widetilde {L}_{-1}$
-transversal in
![]() $\mathrm {Irr}_{cusp}(G_{J_{-1}})$
. This proves part (a) in that case. Part (b) follows from the fact that
$\mathrm {Irr}_{cusp}(G_{J_{-1}})$
. This proves part (a) in that case. Part (b) follows from the fact that
![]() $K_{0,-1}\rtimes {\epsilon }_{-1}(\overline V_{-1})\cong \operatorname {SL}_2(q)\wr \mathrm C_2$
(see also Lemma 4.6). Part (c) follows again from the fact that
$K_{0,-1}\rtimes {\epsilon }_{-1}(\overline V_{-1})\cong \operatorname {SL}_2(q)\wr \mathrm C_2$
(see also Lemma 4.6). Part (c) follows again from the fact that
![]() $ \widetilde {L}_{-1}$
is
$ \widetilde {L}_{-1}$
is
![]() $(\widehat {\operatorname {SL}}_2(q))^2$
, where
$(\widehat {\operatorname {SL}}_2(q))^2$
, where
Assume
![]() ${\mathsf {type}}(\Phi _{-1})=\mathrm A_3$
. Recall
${\mathsf {type}}(\Phi _{-1})=\mathrm A_3$
. Recall
![]() ${\alpha }_2=e_2+e_1$
,
${\alpha }_2=e_2+e_1$
,
![]() ${\alpha }_1=e_2-e_1$
, and
${\alpha }_1=e_2-e_1$
, and
![]() ${\alpha }_i:=e_i-e_{i-1}$
(
${\alpha }_i:=e_i-e_{i-1}$
(
![]() $i\geq 3$
) for the simple roots in
$i\geq 3$
) for the simple roots in
![]() $\Delta $
. In this case,
$\Delta $
. In this case,
![]() $G_{J_{-1}}\cong \operatorname {SL}_4(q)$
and
$G_{J_{-1}}\cong \operatorname {SL}_4(q)$
and
![]() $\mathbf {n}_{e_1}(\varpi )$
acts on
$\mathbf {n}_{e_1}(\varpi )$
acts on
![]() $G_{J_{-1}}$
as a nontrivial graph automorphism. In order to see the automorphisms induced by
$G_{J_{-1}}$
as a nontrivial graph automorphism. In order to see the automorphisms induced by
![]() $t_{J_{-1}}$
and
$t_{J_{-1}}$
and
![]() $t_{J_{-1},2}$
, we use again the equation
$t_{J_{-1},2}$
, we use again the equation
![]() $h_0={\mathbf h} _{{\alpha }_1}(-1){\mathbf h} _{{\alpha }_2}(-1)$
and additionally the equation
$h_0={\mathbf h} _{{\alpha }_1}(-1){\mathbf h} _{{\alpha }_2}(-1)$
and additionally the equation
This implies that
![]() $t_{J_{-1}}$
induces on
$t_{J_{-1}}$
induces on
![]() $G_{J_{-1}}$
some noninner diagonal automorphism of
$G_{J_{-1}}$
some noninner diagonal automorphism of
![]() $\operatorname {SL}_4(q)$
corresponding via the Lang map (see Remark 2.16
(b)) to the central involution, while
$\operatorname {SL}_4(q)$
corresponding via the Lang map (see Remark 2.16
(b)) to the central involution, while
![]() $t_{J_{-1},2}$
induces a diagonal automorphism of
$t_{J_{-1},2}$
induces a diagonal automorphism of
![]() $\operatorname {SL}_4(q)$
associated with a generator of the center. Let
$\operatorname {SL}_4(q)$
associated with a generator of the center. Let
![]() $E(\operatorname {SL}_4(q))$
be the subgroup of
$E(\operatorname {SL}_4(q))$
be the subgroup of
![]() $\mathrm {Aut}(\operatorname {SL}_4(q))$
from Proposition 2.19. According to Proposition 2.19(a), there exists a
$\mathrm {Aut}(\operatorname {SL}_4(q))$
from Proposition 2.19. According to Proposition 2.19(a), there exists a
![]() $\operatorname {GL}_4(q)$
-transversal
$\operatorname {GL}_4(q)$
-transversal
![]() $\mathbb {T}(\operatorname {SL}_4(q))$
in
$\mathbb {T}(\operatorname {SL}_4(q))$
in
![]() $\mathrm {Irr}(\operatorname {SL}_4(q))$
, that is stable under the group
$\mathrm {Irr}(\operatorname {SL}_4(q))$
, that is stable under the group
![]() $E(\operatorname {SL}_4(q))$
generated by graph and field automorphisms of
$E(\operatorname {SL}_4(q))$
generated by graph and field automorphisms of
![]() $\operatorname {SL}_4(q)$
and such that maximal extendibility holds with respect to
$\operatorname {SL}_4(q)$
and such that maximal extendibility holds with respect to
![]() $\operatorname {SL}_4(q)\lhd \operatorname {SL}_4(q)\rtimes E(\operatorname {SL}_4(q))$
for
$\operatorname {SL}_4(q)\lhd \operatorname {SL}_4(q)\rtimes E(\operatorname {SL}_4(q))$
for
![]() $\mathbb {T}(\operatorname {SL}_4(q))$
. This choice guarantees part (b). As
$\mathbb {T}(\operatorname {SL}_4(q))$
. This choice guarantees part (b). As
![]() $\widetilde {L}_{-1}/G_{J_{-1}}$
is cyclic, part (c) holds in that case, as well.
$\widetilde {L}_{-1}/G_{J_{-1}}$
is cyclic, part (c) holds in that case, as well.
Recall
![]() ${\widetilde H_1}:={\left\langle h_0, {\mathbf h} _{J_{-1}}(\varpi )\right\rangle }$
.
${\widetilde H_1}:={\left\langle h_0, {\mathbf h} _{J_{-1}}(\varpi )\right\rangle }$
.
Lemma 4.9.
-
(a) There exists some
 $\overline V_{-1}$
-equivariant extension map
$\overline V_{-1}$
-equivariant extension map
 $\Lambda _{0,-1}$
with respect to
$\Lambda _{0,-1}$
with respect to
 $H_{-1}\lhd \overline V_{-1}$
.
$H_{-1}\lhd \overline V_{-1}$
. -
(b) If
 $\lambda \in \mathrm {Irr}(H_{-1})$
with
$\lambda \in \mathrm {Irr}(H_{-1})$
with
 $\lambda (h_0)=-1$
and
$\lambda (h_0)=-1$
and
 $\widetilde {\lambda } \in \mathrm {Irr}(\widetilde H_{-1}\mid \lambda )$
, then
$\widetilde {\lambda } \in \mathrm {Irr}(\widetilde H_{-1}\mid \lambda )$
, then
 $(\overline V_{-1})_{\widetilde {\lambda }}=H_{-1}$
.
$(\overline V_{-1})_{\widetilde {\lambda }}=H_{-1}$
.
Proof. As
![]() $\overline V_{-1}/H_{-1}$
is cyclic, there exists an extension map as required in (a). For the proof of (b), note that the equality
$\overline V_{-1}/H_{-1}$
is cyclic, there exists an extension map as required in (a). For the proof of (b), note that the equality
![]() $[\overline {\mathbf {n}}_1,{\mathbf h} _{J_{-1}}(\varpi )]=h_0$
implies
$[\overline {\mathbf {n}}_1,{\mathbf h} _{J_{-1}}(\varpi )]=h_0$
implies
![]() $\widetilde {\lambda }^{\overline {\mathbf {n}}_1}\neq \widetilde {\lambda }$
as
$\widetilde {\lambda }^{\overline {\mathbf {n}}_1}\neq \widetilde {\lambda }$
as
![]() $\widetilde {\lambda }(h_0)=-1$
.
$\widetilde {\lambda }(h_0)=-1$
.
4.4 Proof of Theorem B
We now finish the proof of Theorem 3.1 and therefore Theorem B. The above allows us now to verify the character-theoretic assumptions from Proposition 3.2 for the groups K,
![]() ${K_0}$
,
${K_0}$
,
![]() ${K_{0,d}}$
, and
${K_{0,d}}$
, and
![]() $V_{\mathrm {D}}$
, introduced in Lemma 3.11 and Theorem 3.22. From the definitions of
$V_{\mathrm {D}}$
, introduced in Lemma 3.11 and Theorem 3.22. From the definitions of
![]() $K_{0,d}$
before Lemma 4.4, we see
$K_{0,d}$
before Lemma 4.4, we see
![]() ${K_0}={\left\langle \left.{K_{0,d}}\vphantom { d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
, even more
${K_0}={\left\langle \left.{K_{0,d}}\vphantom { d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
, even more
![]() ${K_0}$
is the central product of the groups
${K_0}$
is the central product of the groups
![]() ${K_{0,d}}$
(
${K_{0,d}}$
(
![]() $d\in \mathbb D$
).
$d\in \mathbb D$
).
By abuse of notation, we write
![]() $\mathrm {Irr}_{cusp}(K)$
for
$\mathrm {Irr}_{cusp}(K)$
for
![]() $\bigcup _{\chi \in \mathrm {Irr}_{cusp}(L)}\mathrm {Irr}({\left. \chi \right\rceil _{K}})\subseteq \mathrm {Irr}(K)$
.
$\bigcup _{\chi \in \mathrm {Irr}_{cusp}(L)}\mathrm {Irr}({\left. \chi \right\rceil _{K}})\subseteq \mathrm {Irr}(K)$
.
Proposition 4.10. There exists a
![]() $\overline V{\left\langle F_p \right\rangle }$
-stable
$\overline V{\left\langle F_p \right\rangle }$
-stable
![]() $\widetilde {L}$
-transversal
$\widetilde {L}$
-transversal
![]() ${\mathbb K_0}$
in
${\mathbb K_0}$
in
![]() $\mathrm {Irr}_{cusp}({K_0})$
. Moreover
$\mathrm {Irr}_{cusp}({K_0})$
. Moreover
![]() ${\mathbb K}:=\mathrm {Irr}(K\mid \mathbb {K}_0)$
and
${\mathbb K}:=\mathrm {Irr}(K\mid \mathbb {K}_0)$
and
![]() ${\mathbb T}=\mathrm {Irr}(L\mid \mathbb {K})$
are
${\mathbb T}=\mathrm {Irr}(L\mid \mathbb {K})$
are
![]() $NE_L$
-stable
$NE_L$
-stable
![]() $\widetilde {L}$
-transversals in
$\widetilde {L}$
-transversals in
![]() $\mathrm {Irr}_{cusp}(K)$
and
$\mathrm {Irr}_{cusp}(K)$
and
![]() $\mathrm {Irr}_{cusp}(L)$
, respectively.
$\mathrm {Irr}_{cusp}(L)$
, respectively.
Note that this implies Theorem 3.1(a).
Proof. For
![]() $d\in \mathbb D\setminus \{1\} $
, let
$d\in \mathbb D\setminus \{1\} $
, let
![]() $\mathbb {T}_d^{\circ }$
be the
$\mathbb {T}_d^{\circ }$
be the
![]() $\overline V_d {\left\langle F_p \right\rangle }$
-stable
$\overline V_d {\left\langle F_p \right\rangle }$
-stable
![]() $\widetilde {L}_d$
-transversal in
$\widetilde {L}_d$
-transversal in
![]() $\mathrm {Irr}_{cusp}({K_{0,d}})$
from Propositions 4.5 and 4.8. Note that
$\mathrm {Irr}_{cusp}({K_{0,d}})$
from Propositions 4.5 and 4.8. Note that
![]() $K_{0,1}=1$
. The group
$K_{0,1}=1$
. The group
![]() ${K_0}$
is a central product of the groups
${K_0}$
is a central product of the groups
![]() ${K_{0,d}}$
(
${K_{0,d}}$
(
![]() $d\in \mathbb D$
) according to Lemma 3.13. Hence, the irreducible characters of
$d\in \mathbb D$
) according to Lemma 3.13. Hence, the irreducible characters of
![]() $K_0$
are obtained as the products of the irreducible characters of
$K_0$
are obtained as the products of the irreducible characters of
![]() ${K_{0,d}}$
. The central product of the characters in
${K_{0,d}}$
. The central product of the characters in
![]() $\mathbb {T}^{\circ }_d$
form a subset
$\mathbb {T}^{\circ }_d$
form a subset
![]() $\mathbb {K}_0\subseteq \mathrm {Irr}({K_0})$
. We see that
$\mathbb {K}_0\subseteq \mathrm {Irr}({K_0})$
. We see that
![]() $\mathbb {K}_0$
is
$\mathbb {K}_0$
is
![]() $V_{\mathrm {D}} E_L$
-stable since
$V_{\mathrm {D}} E_L$
-stable since
![]() $V_{\mathrm {D}}E_L$
and
$V_{\mathrm {D}}E_L$
and
![]() $\overline V {\left\langle F_p \right\rangle }$
act on each factor
$\overline V {\left\langle F_p \right\rangle }$
act on each factor
![]() ${K_{0,d}}$
as
${K_{0,d}}$
as
![]() $\overline V_d{\left\langle F_p \right\rangle }$
. Let
$\overline V_d{\left\langle F_p \right\rangle }$
. Let
![]() ${\widehat T}:={\mathbf T}\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
. The automorphisms of
${\widehat T}:={\mathbf T}\cap \mathcal L^{-1}({\left\langle h_0\right\rangle })$
. The automorphisms of
![]() $\widetilde {L} $
induced on
$\widetilde {L} $
induced on
![]() ${K_0}$
are induced by
${K_0}$
are induced by
![]() $K_0$
,
$K_0$
,
![]() $\widehat T=\prod _{d\in \mathbb D} \widehat T_d$
and
$\widehat T=\prod _{d\in \mathbb D} \widehat T_d$
and
![]() $t_{{\underline {l}},2}=\prod _{d\in \mathbb D} t_{J_d,2}$
(see Lemma 4.2). According to Lemma 4.3, the element
$t_{{\underline {l}},2}=\prod _{d\in \mathbb D} t_{J_d,2}$
(see Lemma 4.2). According to Lemma 4.3, the element
![]() $t_{J_d,2}$
acts trivially on
$t_{J_d,2}$
acts trivially on
![]() $G_d$
, whenever
$G_d$
, whenever
![]() $d\geq 1$
. Hence,
$d\geq 1$
. Hence,
![]() $\mathbb {K}_0$
is an
$\mathbb {K}_0$
is an
![]() $\widetilde {L}$
-transversal of
$\widetilde {L}$
-transversal of
![]() $\mathrm {Irr}_{cusp}({K_0})$
as well. According to Propositions 4.5 and 4.8, maximal extendibility holds with respect to
$\mathrm {Irr}_{cusp}({K_0})$
as well. According to Propositions 4.5 and 4.8, maximal extendibility holds with respect to
![]() ${K_{0,d}}\lhd \widetilde {L}_d$
. Since
${K_{0,d}}\lhd \widetilde {L}_d$
. Since
![]() $[\widetilde {L}_d,\widetilde {L}_{d'}]=1$
for every
$[\widetilde {L}_d,\widetilde {L}_{d'}]=1$
for every
![]() $d,d'\in \mathbb D$
with
$d,d'\in \mathbb D$
with
![]() $d\neq d'$
, this implies that maximal extendibility holds also with respect to
$d\neq d'$
, this implies that maximal extendibility holds also with respect to
![]() ${K_0} \lhd \widetilde {L}$
as
${K_0} \lhd \widetilde {L}$
as
![]() $\widetilde {L}\leq {\left\langle \left.\widetilde {L}_d\vphantom {d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
. Since
$\widetilde {L}\leq {\left\langle \left.\widetilde {L}_d\vphantom {d\in \mathbb D}\hskip .1em\right.\mid d\in \mathbb D \right\rangle }$
. Since
![]() $\widetilde {L}/ {K_0}$
is abelian by Lemma 3.13,
$\widetilde {L}/ {K_0}$
is abelian by Lemma 3.13,
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\mathbb {T}$
are again
$\mathbb {T}$
are again
![]() $NE_L$
-stable
$NE_L$
-stable
![]() $\widetilde {L}$
-transversals in
$\widetilde {L}$
-transversals in
![]() $\mathrm {Irr}_{cusp}(K)$
and
$\mathrm {Irr}_{cusp}(K)$
and
![]() $\mathrm {Irr}_{cusp}(L)$
, respectively.
$\mathrm {Irr}_{cusp}(L)$
, respectively.
We apply the following statement in order to construct some extension map with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathrm {Irr}_{cusp}(L)$
satisfying Equation (2.2) from Theorem 2.7.
$\mathrm {Irr}_{cusp}(L)$
satisfying Equation (2.2) from Theorem 2.7.
Proposition 4.11. There exists a
![]() $V_{\mathrm {D}}\rtimes E_L$
-equivariant extension map
$V_{\mathrm {D}}\rtimes E_L$
-equivariant extension map
![]() ${\Lambda _0}$
with respect to
${\Lambda _0}$
with respect to
![]() $H\lhd V_{\mathrm {D}}$
.
$H\lhd V_{\mathrm {D}}$
.
This ensures Assumption 3.2(ii.1) with the choice made in Lemma 3.11.
Proof. Recall
![]() $\overline V:=H{\left\langle \overline V_d\mid d\in \mathbb D\right\rangle }$
and
$\overline V:=H{\left\langle \overline V_d\mid d\in \mathbb D\right\rangle }$
and
![]() $V_{\mathrm {D}}:=\overline V\cap {{\mathbf G}}$
(see Theorem 3.22). Let
$V_{\mathrm {D}}:=\overline V\cap {{\mathbf G}}$
(see Theorem 3.22). Let
![]() ${\widetilde H_{\epsilon }}:={\left\langle \widetilde H_d\mid d\in \mathbb D_{\epsilon }\right\rangle }$
. We apply the extension maps from Proposition 4.1, Lemma 4.7, and Proposition 4.8(c) for constructing a
${\widetilde H_{\epsilon }}:={\left\langle \widetilde H_d\mid d\in \mathbb D_{\epsilon }\right\rangle }$
. We apply the extension maps from Proposition 4.1, Lemma 4.7, and Proposition 4.8(c) for constructing a
![]() $\overline V$
-equivariant extension map for
$\overline V$
-equivariant extension map for
![]() $H\lhd V_{\mathrm {D}}$
. Note that by the definition of
$H\lhd V_{\mathrm {D}}$
. Note that by the definition of
![]() $\overline V$
,
$\overline V$
,
![]() $\overline {\mathbf {n}}_1 \in \overline V\setminus V_{\mathrm {D}}$
whenever
$\overline {\mathbf {n}}_1 \in \overline V\setminus V_{\mathrm {D}}$
whenever
![]() $\gamma \in E_L$
, and then
$\gamma \in E_L$
, and then
![]() $\overline {\mathbf {n}}_1$
and
$\overline {\mathbf {n}}_1$
and
![]() $\gamma $
induce the same automorphism on
$\gamma $
induce the same automorphism on
![]() ${{\mathbf G}}$
according to Definition 3.4. By Theorem 3.22,
${{\mathbf G}}$
according to Definition 3.4. By Theorem 3.22,
![]() $[F_p,V_{\mathrm {D}}]=1$
. Altogether, it is sufficient to prove that maximal extendibility holds with respect to
$[F_p,V_{\mathrm {D}}]=1$
. Altogether, it is sufficient to prove that maximal extendibility holds with respect to
![]() $H\lhd \overline V$
.
$H\lhd \overline V$
.
Let
![]() $\lambda \in \mathrm {Irr}(H)$
and
$\lambda \in \mathrm {Irr}(H)$
and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H\mid \lambda )$
. Then
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde H\mid \lambda )$
. Then
![]() $\widetilde {\lambda }=\odot _{d\in \mathbb D}\widetilde {\lambda }_{d}$
for some
$\widetilde {\lambda }=\odot _{d\in \mathbb D}\widetilde {\lambda }_{d}$
for some
![]() $\widetilde {\lambda }_d\in \mathrm {Irr}(\widetilde H_d)$
(
$\widetilde {\lambda }_d\in \mathrm {Irr}(\widetilde H_d)$
(
![]() $d\in \mathbb D$
). Let
$d\in \mathbb D$
). Let
![]() $\psi _d$
be the extension of
$\psi _d$
be the extension of
![]() $\lambda _d:={\left. \lambda \right\rceil _{{H_d}}}$
to
$\lambda _d:={\left. \lambda \right\rceil _{{H_d}}}$
to
![]() $(V_d)_{\lambda _d}$
given by Proposition 4.1, Lemma 4.7, and Proposition 4.8(c).
$(V_d)_{\lambda _d}$
given by Proposition 4.1, Lemma 4.7, and Proposition 4.8(c).
Assume
![]() $\lambda (h_0)=1$
. Let
$\lambda (h_0)=1$
. Let
![]() $\overline \lambda \in \mathrm {Irr}(H/{\left\langle h_0\right\rangle })$
be associated with
$\overline \lambda \in \mathrm {Irr}(H/{\left\langle h_0\right\rangle })$
be associated with
![]() $\lambda $
. It is sufficient to show that
$\lambda $
. It is sufficient to show that
![]() $\overline \lambda $
extends to
$\overline \lambda $
extends to
![]() $\overline V_{\overline \lambda }/{\left\langle h_0\right\rangle }$
. Since
$\overline V_{\overline \lambda }/{\left\langle h_0\right\rangle }$
. Since
![]() $[\overline V_d/{\left\langle h_0\right\rangle },\overline V_{d'}/{\left\langle h_0\right\rangle }]=1$
according to (3.2), the group
$[\overline V_d/{\left\langle h_0\right\rangle },\overline V_{d'}/{\left\langle h_0\right\rangle }]=1$
according to (3.2), the group
![]() $\overline V/{\left\langle h_0\right\rangle }$
is the central product of the groups
$\overline V/{\left\langle h_0\right\rangle }$
is the central product of the groups
![]() $\overline V_d/{\left\langle h_0\right\rangle }$
. The characters
$\overline V_d/{\left\langle h_0\right\rangle }$
. The characters
![]() $\psi _d$
(
$\psi _d$
(
![]() $d\in \mathbb D$
) define extensions
$d\in \mathbb D$
) define extensions
![]() $\overline \psi _d$
of
$\overline \psi _d$
of
![]() $\overline \lambda _d$
to
$\overline \lambda _d$
to
![]() $(\overline V_d)_{\lambda _d}/{\left\langle h_0\right\rangle }$
and
$(\overline V_d)_{\lambda _d}/{\left\langle h_0\right\rangle }$
and
![]() $\overline \psi := \odot _{d\in \mathbb D}\overline {\psi }_{d}$
lifts to a character
$\overline \psi := \odot _{d\in \mathbb D}\overline {\psi }_{d}$
lifts to a character
![]() $\psi ^{\circ }$
of
$\psi ^{\circ }$
of
![]() ${\left\langle \left.(\overline V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }$
. Recall
${\left\langle \left.(\overline V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }$
. Recall
![]() $H\geq {\left\langle H_d\mid d\in \mathbb D\right\rangle }$
. According to [Reference SpäthS3, 4.1(a)] we see that
$H\geq {\left\langle H_d\mid d\in \mathbb D\right\rangle }$
. According to [Reference SpäthS3, 4.1(a)] we see that
![]() $ \lambda $
has an extension
$ \lambda $
has an extension
![]() $\psi $
to
$\psi $
to
![]() $\overline V_{\lambda }$
such that
$\overline V_{\lambda }$
such that
![]() ${\left. \psi \right\rceil _{{{\left\langle \left.(V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }_{\lambda }}}} = {\left. \psi ^{\circ }\right\rceil _{{{\left\langle \left.(V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }_{\lambda }}}}$
. The extension map with respect to
${\left. \psi \right\rceil _{{{\left\langle \left.(V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }_{\lambda }}}} = {\left. \psi ^{\circ }\right\rceil _{{{\left\langle \left.(V_d)_{\lambda _d}\vphantom {{d\in \mathbb D}}\hskip .1em\right.\mid {d\in \mathbb D} \right\rangle }_{\lambda }}}}$
. The extension map with respect to
![]() $H\lhd V_{\mathrm {D}}$
for
$H\lhd V_{\mathrm {D}}$
for
![]() $\mathrm {Irr}(H\mid 1_{{\left\langle h_0\right\rangle } })$
obtained this way is then automatically
$\mathrm {Irr}(H\mid 1_{{\left\langle h_0\right\rangle } })$
obtained this way is then automatically
![]() $\overline V\rtimes {\left\langle F_p \right\rangle }$
-equivariant.
$\overline V\rtimes {\left\langle F_p \right\rangle }$
-equivariant.
Assume otherwise
![]() $\lambda (h_0)=-1$
. As in Lemma 3.10, let
$\lambda (h_0)=-1$
. As in Lemma 3.10, let
![]() ${\mathbb D_{\mathrm {odd}}}:= \{ i\in \mathbb D\mid i \,\,\, {\mathrm {odd}}\}$
and
${\mathbb D_{\mathrm {odd}}}:= \{ i\in \mathbb D\mid i \,\,\, {\mathrm {odd}}\}$
and
![]() ${\mathbb D_{\mathrm {even}}}:= \{ i\in \mathbb D \mid i \,\,\, {\mathrm {even}}\}$
. For
${\mathbb D_{\mathrm {even}}}:= \{ i\in \mathbb D \mid i \,\,\, {\mathrm {even}}\}$
. For
![]() ${\epsilon }\in \{ {\mathrm {odd}},{\mathrm {even}}\}$
, recall
${\epsilon }\in \{ {\mathrm {odd}},{\mathrm {even}}\}$
, recall
and
![]() $H=H_{\mathrm {even}}\times H_{\mathrm {odd}}$
(see Lemma 3.10). Analogously, we define
$H=H_{\mathrm {even}}\times H_{\mathrm {odd}}$
(see Lemma 3.10). Analogously, we define
Notice that by this definition
![]() $V_{\mathrm {even}}\leq V_{\mathrm {D}}$
and hence
$V_{\mathrm {even}}\leq V_{\mathrm {D}}$
and hence
![]() $V_{\mathrm {D}}=H (V_{\mathrm {even}}. (V_{\mathrm {odd}}\cap V_{\mathrm {D}}))$
.
$V_{\mathrm {D}}=H (V_{\mathrm {even}}. (V_{\mathrm {odd}}\cap V_{\mathrm {D}}))$
.
Let
![]() $\widetilde {\lambda }_{{\epsilon }}:={\left. \widetilde {\lambda }\right\rceil _{{\widetilde H_{\epsilon }}}}$
and
$\widetilde {\lambda }_{{\epsilon }}:={\left. \widetilde {\lambda }\right\rceil _{{\widetilde H_{\epsilon }}}}$
and
![]() $\lambda _{{\epsilon }}:={\left. \lambda \right\rceil _{{ H_{\epsilon }}}}$
. Since
$\lambda _{{\epsilon }}:={\left. \lambda \right\rceil _{{ H_{\epsilon }}}}$
. Since
![]() $[\overline V_d,\overline V_{d'}]=1$
for every
$[\overline V_d,\overline V_{d'}]=1$
for every
![]() $d\in \mathbb D_{\mathrm {even}}$
and
$d\in \mathbb D_{\mathrm {even}}$
and
![]() $d'\in \mathbb D$
by (3.2), the extensions
$d'\in \mathbb D$
by (3.2), the extensions
![]() $\psi _d$
(
$\psi _d$
(
![]() $d\in \mathbb D_{\mathrm {even}}$
) allow us to define an extension of
$d\in \mathbb D_{\mathrm {even}}$
) allow us to define an extension of
![]() $\lambda _{\mathrm {even}}$
to
$\lambda _{\mathrm {even}}$
to
![]() $(\overline V_{{\mathrm {even}}})_{\lambda _{\mathrm {even}}}$
.
$(\overline V_{{\mathrm {even}}})_{\lambda _{\mathrm {even}}}$
.
Now,
![]() $H_{\mathrm {even}}$
is the central product of the groups
$H_{\mathrm {even}}$
is the central product of the groups
![]() $H_d$
(
$H_d$
(
![]() $d\in \mathbb D_{\mathrm {even}}$
) and
$d\in \mathbb D_{\mathrm {even}}$
) and
![]() $(V_{\mathrm {even}})_{\lambda _{\mathrm {even}}}$
is analogously the central product of the groups
$(V_{\mathrm {even}})_{\lambda _{\mathrm {even}}}$
is analogously the central product of the groups
![]() $(\overline V_d)_{\lambda _d}$
. Hence, the product of the characters
$(\overline V_d)_{\lambda _d}$
. Hence, the product of the characters
![]() $\psi _d$
(
$\psi _d$
(
![]() $d\in \mathbb D_{{\mathrm {even}}}$
) defines an extension
$d\in \mathbb D_{{\mathrm {even}}}$
) defines an extension
![]() $\widehat {\lambda }_{\mathrm {even}}\in \mathrm {Irr}((V_{\mathrm {even}})_{ \lambda _{\mathrm {even}}})$
of
$\widehat {\lambda }_{\mathrm {even}}\in \mathrm {Irr}((V_{\mathrm {even}})_{ \lambda _{\mathrm {even}}})$
of
![]() $\lambda _{\mathrm {even}}$
.
$\lambda _{\mathrm {even}}$
.
In order to extend
![]() $\lambda _{\mathrm {odd}}$
to
$\lambda _{\mathrm {odd}}$
to
![]() $(V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}$
, we first extend
$(V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}$
, we first extend
![]() $\widetilde {\lambda }_{\mathrm {odd}}:={\left. \widetilde {\lambda }\right\rceil _{{\widetilde H_{\mathrm {odd}}}}}$
. Again,
$\widetilde {\lambda }_{\mathrm {odd}}:={\left. \widetilde {\lambda }\right\rceil _{{\widetilde H_{\mathrm {odd}}}}}$
. Again,
![]() $\widetilde {\lambda }_{\mathrm {odd}}$
is the central product of characters
$\widetilde {\lambda }_{\mathrm {odd}}$
is the central product of characters
![]() $\widetilde {\lambda }_d$
(
$\widetilde {\lambda }_d$
(
![]() $d\in \mathbb D_{\mathrm {odd}}$
). According to Proposition 4.1(b) and Lemma 4.7(b), we have
$d\in \mathbb D_{\mathrm {odd}}$
). According to Proposition 4.1(b) and Lemma 4.7(b), we have
![]() $(\overline V_d)_{\widetilde {\lambda }_d}\leq V_{\mathrm {D}}$
. The same holds also for
$(\overline V_d)_{\widetilde {\lambda }_d}\leq V_{\mathrm {D}}$
. The same holds also for
![]() $d=-1$
by straight-forward calculations.
$d=-1$
by straight-forward calculations.
Let
![]() $\nu \in \mathrm {Irr}(\widetilde H_{\mathrm {odd}})$
with
$\nu \in \mathrm {Irr}(\widetilde H_{\mathrm {odd}})$
with
![]() $\ker (\nu )=H_{\mathrm {odd}}$
. According to Lemma 4.7(b), there exists some element
$\ker (\nu )=H_{\mathrm {odd}}$
. According to Lemma 4.7(b), there exists some element
![]() $c_d\in \overline V_{d}$
such that
$c_d\in \overline V_{d}$
such that
![]() $(\overline V_d)_{\lambda _d}={\left\langle (\overline V_d)_{\widetilde {\lambda }_d}, c_d\right\rangle }$
, which satisfies
$(\overline V_d)_{\lambda _d}={\left\langle (\overline V_d)_{\widetilde {\lambda }_d}, c_d\right\rangle }$
, which satisfies
![]() $\widetilde {\lambda }_d^{c_d}=\widetilde {\lambda }_d {\left. \nu \right\rceil _{{\widetilde H_d}}}$
. The extensions
$\widetilde {\lambda }_d^{c_d}=\widetilde {\lambda }_d {\left. \nu \right\rceil _{{\widetilde H_d}}}$
. The extensions
![]() ${\left. \psi _d\right\rceil _{{(\overline V_d)_{\widetilde {\lambda }_d }}}}$
define easily extensions
${\left. \psi _d\right\rceil _{{(\overline V_d)_{\widetilde {\lambda }_d }}}}$
define easily extensions
![]() $\psi ^{\prime }_d$
of
$\psi ^{\prime }_d$
of
![]() $\widetilde {\lambda }_d$
to
$\widetilde {\lambda }_d$
to
![]() $\widetilde H_d (\overline V_d)_{\widetilde {\lambda }_d }$
. The restriction
$\widetilde H_d (\overline V_d)_{\widetilde {\lambda }_d }$
. The restriction
![]() ${\left. \psi ^{\prime }_d\right\rceil _{{(V_d)_{\widetilde {\lambda }_d}}}}$
is then
${\left. \psi ^{\prime }_d\right\rceil _{{(V_d)_{\widetilde {\lambda }_d}}}}$
is then
![]() $c_d$
-stable. Since
$c_d$
-stable. Since
![]() $(\overline V_d)_{\widetilde {\lambda }_d}$
is contained in
$(\overline V_d)_{\widetilde {\lambda }_d}$
is contained in
![]() $V_{\mathrm {D}}$
, the group
$V_{\mathrm {D}}$
, the group
![]() $(\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}} }$
is the central product of the groups
$(\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}} }$
is the central product of the groups
![]() $\widetilde H_d (\overline V_d)_{\widetilde {\lambda }_d}$
(
$\widetilde H_d (\overline V_d)_{\widetilde {\lambda }_d}$
(
![]() $d\in \mathbb D_{\mathrm {odd}}$
). The product
$d\in \mathbb D_{\mathrm {odd}}$
). The product
![]() $\psi ':=\prod _{d\in \mathbb D_{\mathrm {odd}}}\psi ^{\prime }_d$
determines uniquely an extension
$\psi ':=\prod _{d\in \mathbb D_{\mathrm {odd}}}\psi ^{\prime }_d$
determines uniquely an extension
![]() $\psi "$
of
$\psi "$
of
![]() $\widetilde {\lambda }_{{\mathrm {odd}}}$
to
$\widetilde {\lambda }_{{\mathrm {odd}}}$
to
![]() $\widetilde H_{\mathrm {odd}} (\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}}}$
. Routine calculations show that
$\widetilde H_{\mathrm {odd}} (\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}}}$
. Routine calculations show that
![]() $(\overline V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}=(\overline V_{\mathrm {odd}})_{ \widetilde {\lambda }_{\mathrm {odd}} }{\left\langle c_{\mathrm {odd}}\right\rangle }$
where
$(\overline V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}=(\overline V_{\mathrm {odd}})_{ \widetilde {\lambda }_{\mathrm {odd}} }{\left\langle c_{\mathrm {odd}}\right\rangle }$
where
![]() $c_{\mathrm {odd}}=\prod _{d\in \mathbb D_{\mathrm {odd}}} c_d$
. The character
$c_{\mathrm {odd}}=\prod _{d\in \mathbb D_{\mathrm {odd}}} c_d$
. The character
![]() ${\left. \psi "\right\rceil _{{H_{\mathrm {odd}}(\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}}}}}}$
is then
${\left. \psi "\right\rceil _{{H_{\mathrm {odd}}(\overline V_{\mathrm {odd}})_{\widetilde {\lambda }_{\mathrm {odd}}}}}}$
is then
![]() $c_{\mathrm {odd}}$
-stable and extends to
$c_{\mathrm {odd}}$
-stable and extends to
![]() $(\overline V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}$
. This way we obtain an extension
$(\overline V_{{\mathrm {odd}}})_{\lambda _{\mathrm {odd}}}$
. This way we obtain an extension
![]() $\widehat {\lambda }_{\mathrm {odd}}$
of
$\widehat {\lambda }_{\mathrm {odd}}$
of
![]() $\lambda _{\mathrm {odd}}$
to
$\lambda _{\mathrm {odd}}$
to
![]() $(\overline V_{\mathrm {odd}})_{ \lambda _{\mathrm {odd}}}$
.
$(\overline V_{\mathrm {odd}})_{ \lambda _{\mathrm {odd}}}$
.
Recall
![]() $[\overline V_{\mathrm {odd}}, \overline V_{\mathrm {even}}]=1$
. Hence, the extensions
$[\overline V_{\mathrm {odd}}, \overline V_{\mathrm {even}}]=1$
. Hence, the extensions
![]() $\widehat {\lambda }_{\mathrm {odd}}$
and
$\widehat {\lambda }_{\mathrm {odd}}$
and
![]() $\widehat {\lambda }_{\mathrm {even}}$
determine an extension of
$\widehat {\lambda }_{\mathrm {even}}$
determine an extension of
![]() $\lambda $
to
$\lambda $
to
![]() $\overline V_{\lambda }$
(see [Reference SpäthS1, Lem. 4.2]).
$\overline V_{\lambda }$
(see [Reference SpäthS1, Lem. 4.2]).
In the next step, we show that there exists an extension map with respect to
![]() ${K_0}\lhd {K_0} \rtimes \epsilon (V_{\mathrm {D}})$
for the set
${K_0}\lhd {K_0} \rtimes \epsilon (V_{\mathrm {D}})$
for the set
![]() $\mathbb {K}_0$
from Proposition 4.10 as required in Proposition 3.2.
$\mathbb {K}_0$
from Proposition 4.10 as required in Proposition 3.2.
Proposition 4.12. There exists a
![]() $ V_{\mathrm {D}} E_L$
-equivariant extension map
$ V_{\mathrm {D}} E_L$
-equivariant extension map
![]() ${\Lambda _{\epsilon }}$
with respect to
${\Lambda _{\epsilon }}$
with respect to
![]() ${K_0}\lhd {K_0} \rtimes \epsilon (V_{\mathrm {D}})$
for
${K_0}\lhd {K_0} \rtimes \epsilon (V_{\mathrm {D}})$
for
![]() $\mathbb {K}_0$
, where
$\mathbb {K}_0$
, where
![]() $\epsilon : V_{\mathrm {D}} E_L \rightarrow V_{\mathrm {D}}E_L/H$
is the canonical morphism.
$\epsilon : V_{\mathrm {D}} E_L \rightarrow V_{\mathrm {D}}E_L/H$
is the canonical morphism.
Proof. By Propositions 4.5 and 4.8, there exist
![]() $\overline V_d{\left\langle F_p \right\rangle }$
-equivariant extension maps
$\overline V_d{\left\langle F_p \right\rangle }$
-equivariant extension maps
![]() $\Lambda _{{\epsilon }_d}$
with respect to
$\Lambda _{{\epsilon }_d}$
with respect to
![]() $K_{0,d}\lhd K_{0,d} \rtimes {\epsilon }(\overline V_d)$
for
$K_{0,d}\lhd K_{0,d} \rtimes {\epsilon }(\overline V_d)$
for
![]() $\mathbb {T}_d^{\circ }$
, whenever
$\mathbb {T}_d^{\circ }$
, whenever
![]() $d\in \mathbb D$
with
$d\in \mathbb D$
with
![]() $d\neq 1$
. Note that the case
$d\neq 1$
. Note that the case
![]() $d=1$
is trivial since
$d=1$
is trivial since
![]() $K_{0,1}=1$
. The group
$K_{0,1}=1$
. The group
![]() ${K_0}\rtimes {\epsilon }(\overline V)$
is the direct product of the groups
${K_0}\rtimes {\epsilon }(\overline V)$
is the direct product of the groups
![]() $K_{0,d} \rtimes {\epsilon }_d(\overline V_d)$
. Using the maps
$K_{0,d} \rtimes {\epsilon }_d(\overline V_d)$
. Using the maps
![]() $\Lambda _{{\epsilon }_d}$
(
$\Lambda _{{\epsilon }_d}$
(
![]() $d\in \mathbb D$
), we therefore obtain an extension map
$d\in \mathbb D$
), we therefore obtain an extension map
![]() $\Lambda _{\epsilon }$
as required.
$\Lambda _{\epsilon }$
as required.
This leads to the following statement. We use the set
with
![]() $\mathbb {K}_0$
from Proposition 4.10. For the application of Proposition 3.2, we use the group
$\mathbb {K}_0$
from Proposition 4.10. For the application of Proposition 3.2, we use the group
![]() $M=KV_{\mathrm {D}}$
(see also Corollary 3.23).
$M=KV_{\mathrm {D}}$
(see also Corollary 3.23).
Proposition 4.13. There exists a
![]() $V E_L$
-equivariant extension map
$V E_L$
-equivariant extension map
![]() ${\Lambda _{K\lhd M}}$
with respect to
${\Lambda _{K\lhd M}}$
with respect to
![]() $K\lhd M$
for
$K\lhd M$
for
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
Proof. By the above, all the assumptions of Proposition 3.2 are satisfied. The groups satisfy the required assumptions in Proposition 3.2
(i) according to Corollary 3.23. Using the set
![]() $\mathbb {K}$
, given as
$\mathbb {K}$
, given as
![]() $\mathrm {Irr}(K\mid \mathbb {K}_0)$
from Proposition 4.10, the set
$\mathrm {Irr}(K\mid \mathbb {K}_0)$
from Proposition 4.10, the set
![]() $\mathbb {K}_0$
coincides with
$\mathbb {K}_0$
coincides with
![]() $\bigcup _{\lambda \in \mathbb {K}}\mathrm {Irr}({\left. \lambda \right\rceil _{{{K_0}}}})$
. With the
$\bigcup _{\lambda \in \mathbb {K}}\mathrm {Irr}({\left. \lambda \right\rceil _{{{K_0}}}})$
. With the
![]() $V_{\mathrm {D}} E_L$
-equivariant extension map
$V_{\mathrm {D}} E_L$
-equivariant extension map
![]() $\Lambda _0$
for
$\Lambda _0$
for
![]() $H\lhd V_{\mathrm {D}}$
from Proposition 4.11 and the extension map
$H\lhd V_{\mathrm {D}}$
from Proposition 4.11 and the extension map
![]() $\Lambda _{\epsilon }$
for
$\Lambda _{\epsilon }$
for
![]() ${K_0} \lhd {K_0} \rtimes {\epsilon }(\overline V)$
from Proposition 4.12, Assumption 3.2
(ii) is satisfied. The application of this statement implies the result.
${K_0} \lhd {K_0} \rtimes {\epsilon }(\overline V)$
from Proposition 4.12, Assumption 3.2
(ii) is satisfied. The application of this statement implies the result.
For the set
![]() $\mathbb {T}$
defined as
$\mathbb {T}$
defined as
![]() $\mathrm {Irr}(L\mid \mathbb {K})$
in Proposition 4.10, we verify that there exists an
$\mathrm {Irr}(L\mid \mathbb {K})$
in Proposition 4.10, we verify that there exists an
![]() $NE_L$
-equivariant extension map with respect to
$NE_L$
-equivariant extension map with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Proof of Theorems 3.1(b) and B
For the proof, it is sufficient to construct for every
![]() $\lambda \in \mathbb {T}=\mathrm {Irr}(L\mid \mathbb {K})$
some
$\lambda \in \mathbb {T}=\mathrm {Irr}(L\mid \mathbb {K})$
some
![]() $NE_L$
-stable extension to
$NE_L$
-stable extension to
![]() $N_{\lambda }$
. A character
$N_{\lambda }$
. A character
![]() $\lambda \in \mathbb {T}$
lies above a unique
$\lambda \in \mathbb {T}$
lies above a unique
![]() $\lambda _0\in \mathbb {K}=\mathrm {Irr}(K\mid \mathbb {K}_0)$
. Moreover, some extension
$\lambda _0\in \mathbb {K}=\mathrm {Irr}(K\mid \mathbb {K}_0)$
. Moreover, some extension
![]() $\widetilde {\lambda }_0\in \mathrm {Irr}(L_{\lambda _0})$
to
$\widetilde {\lambda }_0\in \mathrm {Irr}(L_{\lambda _0})$
to
![]() $L_{\lambda _0}$
satisfies
$L_{\lambda _0}$
satisfies
![]() $(\widetilde {\lambda }_0)^L=\lambda $
. By the properties of
$(\widetilde {\lambda }_0)^L=\lambda $
. By the properties of
![]() $\mathbb {K}$
, we see
$\mathbb {K}$
, we see
![]() $N_{\lambda _0}=L_{\lambda _0} M_{\lambda _0}$
, which is normalized by
$N_{\lambda _0}=L_{\lambda _0} M_{\lambda _0}$
, which is normalized by
![]() $(NE_L)_{\widetilde {\lambda }_0}$
-. By Proposition 4.13, the character
$(NE_L)_{\widetilde {\lambda }_0}$
-. By Proposition 4.13, the character
![]() $\lambda _0$
has a
$\lambda _0$
has a
![]() $(\overline V {\left\langle F_p \right\rangle })_{\lambda _0}$
-stable extension to
$(\overline V {\left\langle F_p \right\rangle })_{\lambda _0}$
-stable extension to
![]() $M_{\lambda _0}$
. According to [Reference SpäthS3, 4.1], this defines an extension
$M_{\lambda _0}$
. According to [Reference SpäthS3, 4.1], this defines an extension
![]() $\phi $
of
$\phi $
of
![]() $\widetilde {\lambda }_0$
to
$\widetilde {\lambda }_0$
to
![]() $N_{\widetilde {\lambda }_0}$
since
$N_{\widetilde {\lambda }_0}$
since
![]() $N_{\widetilde {\lambda }_0}\leq L_{\lambda _0}M_{\lambda _0}$
. By the construction, we see that
$N_{\widetilde {\lambda }_0}\leq L_{\lambda _0}M_{\lambda _0}$
. By the construction, we see that
![]() $\phi ^{N_{\lambda }}$
is an extension of
$\phi ^{N_{\lambda }}$
is an extension of
![]() $\lambda $
.
$\lambda $
.
As
![]() $\mathbb {T}$
is an M-stable
$\mathbb {T}$
is an M-stable
![]() $\widetilde {L}$
-transversal,
$\widetilde {L}$
-transversal,
![]() $\widetilde N_{\lambda _0}=\widetilde {L}_{\lambda _0} M_{\lambda _0}$
and
$\widetilde N_{\lambda _0}=\widetilde {L}_{\lambda _0} M_{\lambda _0}$
and
![]() $(\widetilde NE_L)_{\lambda _0}=\widetilde {L}_{\lambda _0} \widehat M_{\lambda _0}$
. Hence, this extension of
$(\widetilde NE_L)_{\lambda _0}=\widetilde {L}_{\lambda _0} \widehat M_{\lambda _0}$
. Hence, this extension of
![]() $\lambda _0$
defines an extension of
$\lambda _0$
defines an extension of
![]() $\lambda $
as required.
$\lambda $
as required.
Later this ensures Assumption 2.12 (ii).
Remark 4.14. While Theorem 3.1(b) assumes q to be odd, the proof would give a similar conclusion in the other case. For even q, every
![]() $\chi \in \mathrm {Irr}(G)$
satisfies
$\chi \in \mathrm {Irr}(G)$
satisfies
![]() $({\widetilde G} E)_{\chi }={\widetilde G}_{\chi } E_{\chi }$
since
$({\widetilde G} E)_{\chi }={\widetilde G}_{\chi } E_{\chi }$
since
![]() ${\widetilde G}=G$
in the notation of 2.2. Nevertheless, the conclusion of Theorem 3.1(b) holds as well. We observe that the arguments from before prove that there exists some
${\widetilde G}=G$
in the notation of 2.2. Nevertheless, the conclusion of Theorem 3.1(b) holds as well. We observe that the arguments from before prove that there exists some
![]() $N E_L$
-equivariant extension map
$N E_L$
-equivariant extension map
![]() ${K_0}\lhd {K_0} V_{\mathrm {D}}$
for
${K_0}\lhd {K_0} V_{\mathrm {D}}$
for
![]() $\mathrm {Irr}_{cusp}(L)$
, where
$\mathrm {Irr}_{cusp}(L)$
, where
![]() $V_{\mathrm {D}}$
is isomorphic to
$V_{\mathrm {D}}$
is isomorphic to
![]() $N/L$
and is defined as before with
$N/L$
and is defined as before with
![]() $1=\pm \varpi $
in the argument of the Chevalley generators.
$1=\pm \varpi $
in the argument of the Chevalley generators.
5 More on cuspidal characters
In order to prove our main theorem, we need more specific results on cuspidal characters, especially with regard to automorphisms. We keep q a power of an odd prime.
Proposition 5.1. Let
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $\chi \in \mathrm {Irr}_{cusp}(\operatorname {GL}_n(q))$
, and
$\chi \in \mathrm {Irr}_{cusp}(\operatorname {GL}_n(q))$
, and
![]() $\gamma \in \mathrm {Aut}(\operatorname {GL}_n(q))$
given by transpose-inverse up to some inner automorphism.
$\gamma \in \mathrm {Aut}(\operatorname {GL}_n(q))$
given by transpose-inverse up to some inner automorphism.
-
(a) If
 $\chi ^{\gamma }=\chi $
, then
$\chi ^{\gamma }=\chi $
, then
 $2\mid n$
and
$2\mid n$
and
 $\operatorname Z(\operatorname {GL}_n(q)) \leq \ker (\chi )$
.
$\operatorname Z(\operatorname {GL}_n(q)) \leq \ker (\chi )$
. -
(b) If
 $\chi ^{\gamma } = \chi \delta $
for
$\chi ^{\gamma } = \chi \delta $
for
 $\delta \in \mathrm {Irr}(\operatorname {GL}_n(q))$
, a linear character of multiplicative order 2, then
$\delta \in \mathrm {Irr}(\operatorname {GL}_n(q))$
, a linear character of multiplicative order 2, then
 $2\mid n$
.
$2\mid n$
.
Proof. Let us recall the form of elements of
![]() $\mathrm {Irr}_{cusp}(\operatorname {GL}_n(q))$
(see also [Reference BonnaféB1, 16.1]). We write
$\mathrm {Irr}_{cusp}(\operatorname {GL}_n(q))$
(see also [Reference BonnaféB1, 16.1]). We write
![]() ${{\mathbf K}}:=\operatorname {GL}_n({\mathbb {F}})$
and
${{\mathbf K}}:=\operatorname {GL}_n({\mathbb {F}})$
and
![]() ${{\mathbf K}}^*:=\operatorname {GL}_n({\mathbb {F}})$
as the dual with
${{\mathbf K}}^*:=\operatorname {GL}_n({\mathbb {F}})$
as the dual with
![]() ${\mathbb {F}}_q$
-structures given by F. Let
${\mathbb {F}}_q$
-structures given by F. Let
![]() $s\in ({{\mathbf K}}^*)^F=\operatorname {GL}_n(q)$
be such that the Lusztig series
$s\in ({{\mathbf K}}^*)^F=\operatorname {GL}_n(q)$
be such that the Lusztig series
![]() $\mathcal E({{\mathbf K}}^F,(s))$
associated with s contains a cuspidal character. Combining [Reference Geck and MalleGM, 3.2.22] and the fact that the group
$\mathcal E({{\mathbf K}}^F,(s))$
associated with s contains a cuspidal character. Combining [Reference Geck and MalleGM, 3.2.22] and the fact that the group
![]() ${\operatorname C}_{{{\mathbf K}}^*}(s)^F$
of type A can have cuspidal unipotent characters only when it is a torus (see, e.g., [Reference Geck and MalleGM, Exam. 2.4.20]), we get that s is regular and
${\operatorname C}_{{{\mathbf K}}^*}(s)^F$
of type A can have cuspidal unipotent characters only when it is a torus (see, e.g., [Reference Geck and MalleGM, Exam. 2.4.20]), we get that s is regular and
![]() ${\mathrm {C}}_{{{\mathbf K}}^*}(s)$
is a Coxeter torus. This can be summed up in the fact that the spectrum of s is a single orbit of length n under F, or equivalently
${\mathrm {C}}_{{{\mathbf K}}^*}(s)$
is a Coxeter torus. This can be summed up in the fact that the spectrum of s is a single orbit of length n under F, or equivalently
![]() ${\mathbb {F}}_{q^{}}{[\zeta ]}={\mathbb {F}}_{q^{n}}$
for any eigenvalue
${\mathbb {F}}_{q^{}}{[\zeta ]}={\mathbb {F}}_{q^{n}}$
for any eigenvalue
![]() $\zeta $
of s. Concerning the action of
$\zeta $
of s. Concerning the action of
![]() $\gamma $
, note that an element of
$\gamma $
, note that an element of
![]() $\mathcal E({{\mathbf K}}^F,(s))$
is sent to an element of
$\mathcal E({{\mathbf K}}^F,(s))$
is sent to an element of
![]() $\mathcal E({{\mathbf K}}^F,(s^{-1}))$
(apply [Reference Cabanes and SpäthCS1, 3.1]).
$\mathcal E({{\mathbf K}}^F,(s^{-1}))$
(apply [Reference Cabanes and SpäthCS1, 3.1]).
For the proof of (a), let
![]() $\chi \in \mathcal E({{\mathbf K}}^F,(s))$
be invariant under
$\chi \in \mathcal E({{\mathbf K}}^F,(s))$
be invariant under
![]() $\gamma $
. Then s and
$\gamma $
. Then s and
![]() $s^{-1}$
have the same spectrum. If
$s^{-1}$
have the same spectrum. If
![]() $1$
or
$1$
or
![]() $-1$
is an eigenvalue of s, then
$-1$
is an eigenvalue of s, then
![]() $s\in \{\operatorname {Id}_n,-\operatorname {Id}_n\}$
and
$s\in \{\operatorname {Id}_n,-\operatorname {Id}_n\}$
and
![]() $n=1$
since the eigenvalues of s form a single F-orbit. This is impossible, so inversion is without fixed point on the spectrum of s. This implies that n is even and that the product of the eigenvalues of s is
$n=1$
since the eigenvalues of s form a single F-orbit. This is impossible, so inversion is without fixed point on the spectrum of s. This implies that n is even and that the product of the eigenvalues of s is
![]() $1$
. So
$1$
. So
![]() $s\in [{{\mathbf K}}^*,{{\mathbf K}}^*]^F$
and this implies that all characters of
$s\in [{{\mathbf K}}^*,{{\mathbf K}}^*]^F$
and this implies that all characters of
![]() $\mathcal E ({{\mathbf K}}^F,(s))$
have
$\mathcal E ({{\mathbf K}}^F,(s))$
have
![]() $\operatorname Z(\operatorname {GL}_n(q))$
in their kernel (see [Reference Cabanes, Schaeffer Fry and SpäthCE, p. 207]).
$\operatorname Z(\operatorname {GL}_n(q))$
in their kernel (see [Reference Cabanes, Schaeffer Fry and SpäthCE, p. 207]).
For the proof of part (b), note that by the assumptions q is odd and
![]() $\operatorname {SL}_n(q)$
is perfect (see [Reference MaslowskiMT, 24.17]). By the correspondence induced by duality between (linear) characters of
$\operatorname {SL}_n(q)$
is perfect (see [Reference MaslowskiMT, 24.17]). By the correspondence induced by duality between (linear) characters of
![]() ${{\mathbf K}}^F/[{{\mathbf K}} ,{{\mathbf K}}]^F$
and elements of
${{\mathbf K}}^F/[{{\mathbf K}} ,{{\mathbf K}}]^F$
and elements of
![]() $\operatorname Z ({{\mathbf K}}^*)^F$
(see, e.g., [Reference Digne and MichelDM, 11.4.12]), we have
$\operatorname Z ({{\mathbf K}}^*)^F$
(see, e.g., [Reference Digne and MichelDM, 11.4.12]), we have
![]() $\delta \mathcal E({{\mathbf K}}^F,(s)) = \mathcal E({{\mathbf K}}^F,(-s))$
. Assuming
$\delta \mathcal E({{\mathbf K}}^F,(s)) = \mathcal E({{\mathbf K}}^F,(-s))$
. Assuming
![]() $\chi ^{\gamma } = \chi \delta $
, the same considerations as above show that s and
$\chi ^{\gamma } = \chi \delta $
, the same considerations as above show that s and
![]() $-s^{-1}$
have the same eigenvalues. The spectrum of s is of the form
$-s^{-1}$
have the same eigenvalues. The spectrum of s is of the form
![]() $\{ F(\zeta ), F^2(\zeta ), \dots ,F^n(\zeta )=\zeta \}$
with
$\{ F(\zeta ), F^2(\zeta ), \dots ,F^n(\zeta )=\zeta \}$
with
![]() ${\mathbb {F}}_{q^{}}[\zeta ]={\mathbb {F}}_{q^{n}}$
. Since s and
${\mathbb {F}}_{q^{}}[\zeta ]={\mathbb {F}}_{q^{n}}$
. Since s and
![]() $-s^{-1}$
have the same eigenvalues, then
$-s^{-1}$
have the same eigenvalues, then
![]() $-\zeta ^{-1} = F^a(\zeta )$
for some
$-\zeta ^{-1} = F^a(\zeta )$
for some
![]() $1\leq a\leq n$
. We have
$1\leq a\leq n$
. We have
![]() $F^{2a}(\zeta )=-F^a(\zeta )^{-1}=\zeta $
and therefore
$F^{2a}(\zeta )=-F^a(\zeta )^{-1}=\zeta $
and therefore
![]() ${\mathbb {F}}_{q^{2a}}\supseteq {\mathbb {F}}_{q^{}}[\zeta ]={\mathbb {F}}_{q^{n}}$
. Then n divides
${\mathbb {F}}_{q^{2a}}\supseteq {\mathbb {F}}_{q^{}}[\zeta ]={\mathbb {F}}_{q^{n}}$
. Then n divides
![]() $2a$
. Assume now that n is odd. This implies that n divides
$2a$
. Assume now that n is odd. This implies that n divides
![]() $a\leq n$
. So
$a\leq n$
. So
![]() $a=n$
and
$a=n$
and
![]() $-\zeta ^{-1} =F^n(\zeta )=\zeta $
. But then,
$-\zeta ^{-1} =F^n(\zeta )=\zeta $
. But then,
![]() $\zeta ^2=-1$
and
$\zeta ^2=-1$
and
![]() ${\mathbb {F}}_{q^{}}[\zeta ]\subseteq {\mathbb {F}}_{q^{2}}$
, which contradicts
${\mathbb {F}}_{q^{}}[\zeta ]\subseteq {\mathbb {F}}_{q^{2}}$
, which contradicts
![]() $n\geq 3$
. So we get our claim that
$n\geq 3$
. So we get our claim that
![]() $2\mid n$
.
$2\mid n$
.
The following statement is used later for computing the relative Weyl groups associated with cuspidal characters of a Levi subgroup of
![]() $\mathrm {D}_{l,\mathrm {sc}}(q)$
.
$\mathrm {D}_{l,\mathrm {sc}}(q)$
.
Proposition 5.2. Let
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $\psi \in \mathrm {Irr}_{cusp}(\operatorname {SL}_n(q))$
, and
$\psi \in \mathrm {Irr}_{cusp}(\operatorname {SL}_n(q))$
, and
![]() $\gamma \in \mathrm {Aut}(\operatorname {GL}_n(q))$
given by transpose-inverse up to some inner automorphism. If
$\gamma \in \mathrm {Aut}(\operatorname {GL}_n(q))$
given by transpose-inverse up to some inner automorphism. If
![]() $ |\operatorname {GL}_n(q):\operatorname {GL}_n(q)_{\psi }|$
is even and
$ |\operatorname {GL}_n(q):\operatorname {GL}_n(q)_{\psi }|$
is even and
![]() $\psi ^{\gamma }=\psi $
, then
$\psi ^{\gamma }=\psi $
, then
![]() $n=2$
and
$n=2$
and
![]() $\psi $
is one of the two characters
$\psi $
is one of the two characters
![]() $\operatorname {R}^{\prime }_{\sigma }(\theta _0)$
(
$\operatorname {R}^{\prime }_{\sigma }(\theta _0)$
(
![]() $\sigma \in \{\pm 1\}$
) of degree
$\sigma \in \{\pm 1\}$
) of degree
![]() $\frac {q-1}{2}$
from [Reference BonnaféB2, Table 5.4].
$\frac {q-1}{2}$
from [Reference BonnaféB2, Table 5.4].
Proof. According to [Reference BonnaféB2, Table 5.4], the two characters
![]() $\operatorname {R}^{\prime }_{\sigma }(\theta _0)$
(
$\operatorname {R}^{\prime }_{\sigma }(\theta _0)$
(
![]() $\sigma \in \{\pm 1\}$
) are the only characters of
$\sigma \in \{\pm 1\}$
) are the only characters of
![]() $\operatorname {SL}_2(q)$
that are cuspidal and not
$\operatorname {SL}_2(q)$
that are cuspidal and not
![]() $\operatorname {GL}_2(q)$
-stable. The characters
$\operatorname {GL}_2(q)$
-stable. The characters
![]() $\operatorname {R}(\theta )$
given there are
$\operatorname {R}(\theta )$
given there are
![]() $\operatorname {GL}_2(q)$
-stable and the other characters
$\operatorname {GL}_2(q)$
-stable and the other characters
![]() $R_{\sigma }(\alpha _0)$
(
$R_{\sigma }(\alpha _0)$
(
![]() $\sigma \in \{\pm 1\}$
) are in the principal Harish-Chandra series. Note that
$\sigma \in \{\pm 1\}$
) are in the principal Harish-Chandra series. Note that
![]() $\gamma $
then restricts to an inner automorphism of
$\gamma $
then restricts to an inner automorphism of
![]() $\operatorname {SL}_2(q)$
.
$\operatorname {SL}_2(q)$
.
Now, consider
![]() $n\geq 3$
. Let
$n\geq 3$
. Let
![]() $\psi $
be as in the proposition, and let
$\psi $
be as in the proposition, and let
![]() $\chi \in \mathrm {Irr}(\operatorname {GL}_n(q)\mid \psi )$
, so that
$\chi \in \mathrm {Irr}(\operatorname {GL}_n(q)\mid \psi )$
, so that
![]() $\chi $
is cuspidal thanks to Lemma 2.5
(c). We keep the notation of the proof of Proposition 5.1 with
$\chi $
is cuspidal thanks to Lemma 2.5
(c). We keep the notation of the proof of Proposition 5.1 with
![]() $\chi \in \mathcal E (\operatorname {GL}_n(q),(s))$
and
$\chi \in \mathcal E (\operatorname {GL}_n(q),(s))$
and
![]() $\zeta $
some eigenvalue of s.
$\zeta $
some eigenvalue of s.
By Clifford theory,
![]() $\chi $
is induced from a character of
$\chi $
is induced from a character of
![]() $\operatorname {GL}_n(q)_{\psi }$
. Then the assumption
$\operatorname {GL}_n(q)_{\psi }$
. Then the assumption
![]() $2\mid |\operatorname {GL}_n(q):\operatorname {GL}_n(q)_{\psi }|$
implies
$2\mid |\operatorname {GL}_n(q):\operatorname {GL}_n(q)_{\psi }|$
implies
![]() $\chi = \nu _1\chi $
for
$\chi = \nu _1\chi $
for
![]() $\nu _1\in \mathrm {Irr}(\operatorname {GL}_n(q))$
the linear character of order
$\nu _1\in \mathrm {Irr}(\operatorname {GL}_n(q))$
the linear character of order
![]() $2$
with kernel containing
$2$
with kernel containing
![]() $\operatorname {SL}_n(q)$
. Hence, s is
$\operatorname {SL}_n(q)$
. Hence, s is
![]() $\operatorname {GL}_n(q)$
-conjugate to
$\operatorname {GL}_n(q)$
-conjugate to
![]() $-s$
. Then
$-s$
. Then
![]() $-\zeta \in \{ F(\zeta ), F^2(\zeta ),\ldots , F^n(\zeta )=\zeta \}$
since this is the spectrum of s.
$-\zeta \in \{ F(\zeta ), F^2(\zeta ),\ldots , F^n(\zeta )=\zeta \}$
since this is the spectrum of s.
Clifford theory also tells us that the assumption
![]() $\psi ^{\gamma }=\psi $
implies
$\psi ^{\gamma }=\psi $
implies
![]() $\chi ^{\gamma }=\nu _2\chi $
for some linear character
$\chi ^{\gamma }=\nu _2\chi $
for some linear character
![]() $\nu _2$
of
$\nu _2$
of
![]() $\operatorname {GL}_n(q)$
with
$\operatorname {GL}_n(q)$
with
![]() $\operatorname {SL}_n(q)$
in its kernel. Then
$\operatorname {SL}_n(q)$
in its kernel. Then
![]() $s^{-1}$
is conjugate to
$s^{-1}$
is conjugate to
![]() $\lambda s$
for some
$\lambda s$
for some
![]() $\lambda \in {\mathbb {F}}_q^{\times }$
. As before, we obtain
$\lambda \in {\mathbb {F}}_q^{\times }$
. As before, we obtain
![]() $\zeta ^{-1}\in \{\lambda F(\zeta ), \lambda F^2(\zeta ), \ldots , \lambda F^n(\zeta )=\lambda \zeta \}$
.
$\zeta ^{-1}\in \{\lambda F(\zeta ), \lambda F^2(\zeta ), \ldots , \lambda F^n(\zeta )=\lambda \zeta \}$
.
We can now write
![]() $-\zeta =F^a(\zeta )$
and
$-\zeta =F^a(\zeta )$
and
![]() $\lambda \zeta ^{-1}=F^b(\zeta )$
for
$\lambda \zeta ^{-1}=F^b(\zeta )$
for
![]() $1\leq a,b\leq n$
. The first equality gives
$1\leq a,b\leq n$
. The first equality gives
![]() $F^{2a}(\zeta )=-F^a(\zeta )=\zeta $
and the second
$F^{2a}(\zeta )=-F^a(\zeta )=\zeta $
and the second
![]() $F^{2b}(\zeta )=\lambda F^b(\zeta )^{-1}=\zeta $
since
$F^{2b}(\zeta )=\lambda F^b(\zeta )^{-1}=\zeta $
since
![]() $\lambda \in {\mathbb {F}}_q$
. So
$\lambda \in {\mathbb {F}}_q$
. So
![]() $\zeta \in {\mathbb {F}}_{q^{2a}}\cap {\mathbb {F}}_{q^{2b}}$
, but since
$\zeta \in {\mathbb {F}}_{q^{2a}}\cap {\mathbb {F}}_{q^{2b}}$
, but since
![]() ${\mathbb {F}}_q[\zeta ]={\mathbb {F}}_{q^{n}}$
, we get that n divides both
${\mathbb {F}}_q[\zeta ]={\mathbb {F}}_{q^{n}}$
, we get that n divides both
![]() $2a$
and
$2a$
and
![]() $2b$
. The latter are at most
$2b$
. The latter are at most
![]() $ 2n$
, so
$ 2n$
, so
![]() $2a,2b\in \{ {n} ,2n\}$
. Having
$2a,2b\in \{ {n} ,2n\}$
. Having
![]() $a=n$
would imply
$a=n$
would imply
![]() $-\zeta =F^n(\zeta )=\zeta $
, which is impossible because q is odd. So n is even and
$-\zeta =F^n(\zeta )=\zeta $
, which is impossible because q is odd. So n is even and
![]() $a={\frac n 2}$
. On the other hand, if
$a={\frac n 2}$
. On the other hand, if
![]() $b=n$
, then
$b=n$
, then
![]() $\zeta =F^n(\zeta )=\lambda \zeta ^{-1}$
and therefore
$\zeta =F^n(\zeta )=\lambda \zeta ^{-1}$
and therefore
![]() $\zeta ^2\in {\mathbb {F}}_q$
. Then
$\zeta ^2\in {\mathbb {F}}_q$
. Then
![]() ${\mathbb {F}}_q[\zeta ]\subseteq {\mathbb {F}}_{q^{2}}$
and this implies
${\mathbb {F}}_q[\zeta ]\subseteq {\mathbb {F}}_{q^{2}}$
and this implies
![]() $n=2$
.
$n=2$
.
There remains the case when
![]() $b={\frac n 2}=a$
. Then
$b={\frac n 2}=a$
. Then
![]() $\lambda \zeta ^{-1}=F^a(\zeta )=-\zeta $
and again
$\lambda \zeta ^{-1}=F^a(\zeta )=-\zeta $
and again
![]() $\zeta ^2\in {\mathbb {F}}_q$
. This yields
$\zeta ^2\in {\mathbb {F}}_q$
. This yields
![]() $n=2$
as seen before.
$n=2$
as seen before.
We complement the above by a result on cuspidal characters of
![]() $\mathrm {D}_{l,\mathrm {sc}}(q)$
, which follows from a combination of results from [Reference Malle and SpäthMal2] and [Reference SpäthS4]. We use
$\mathrm {D}_{l,\mathrm {sc}}(q)$
, which follows from a combination of results from [Reference Malle and SpäthMal2] and [Reference SpäthS4]. We use
![]() ${{\mathbf G}}$
, F,
${{\mathbf G}}$
, F,
![]() $\gamma $
from Notation 3.3 and
$\gamma $
from Notation 3.3 and
![]() $h_0$
from Notation 3.9. Recall the Lang map
$h_0$
from Notation 3.9. Recall the Lang map
![]() $\mathcal L$
defined on
$\mathcal L$
defined on
![]() ${{\mathbf G}}$
by
${{\mathbf G}}$
by
![]() $\mathcal L(g)=g^{-1}F(g)$
. Note that
$\mathcal L(g)=g^{-1}F(g)$
. Note that
![]() $\mathcal L^{-1}({\left\langle h_0\right\rangle })/{\left\langle h_0\right\rangle }=({{\mathbf G}}/{\left\langle h_0\right\rangle })^F=\operatorname {SO}_{2l}({\mathbb {F}}_q)$
.
$\mathcal L^{-1}({\left\langle h_0\right\rangle })/{\left\langle h_0\right\rangle }=({{\mathbf G}}/{\left\langle h_0\right\rangle })^F=\operatorname {SO}_{2l}({\mathbb {F}}_q)$
.
Proposition 5.3. Recall
![]() ${\widetilde G}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))={\operatorname N}_{{{\mathbf G}}}({{{{\mathbf G}}^F}})$
(see Remark 2.16). If
${\widetilde G}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))={\operatorname N}_{{{\mathbf G}}}({{{{\mathbf G}}^F}})$
(see Remark 2.16). If
![]() $\lambda \in \mathrm {Irr}_{cusp}({{{{\mathbf G}}^F}}\mid 1_{{\left\langle h_0\right\rangle }})$
with
$\lambda \in \mathrm {Irr}_{cusp}({{{{\mathbf G}}^F}}\mid 1_{{\left\langle h_0\right\rangle }})$
with
![]() ${\widetilde G}_{\lambda }\leq \mathcal L^{-1}({\left\langle h_0\right\rangle })$
, then
${\widetilde G}_{\lambda }\leq \mathcal L^{-1}({\left\langle h_0\right\rangle })$
, then
![]() $\gamma $
acts trivially on
$\gamma $
acts trivially on
![]() $\lambda $
and
$\lambda $
and
![]() $\mathrm {Irr}(\mathcal L^{-1}({\left\langle h_0\right\rangle }) \mid \lambda )$
.
$\mathrm {Irr}(\mathcal L^{-1}({\left\langle h_0\right\rangle }) \mid \lambda )$
.
Proof. Recall that a character of
![]() $\widetilde {{\mathbf G}}^F$
is called semisimple when it corresponds to a trivial unipotent character through the Jordan decomposition of characters. The components of their restrictions to
$\widetilde {{\mathbf G}}^F$
is called semisimple when it corresponds to a trivial unipotent character through the Jordan decomposition of characters. The components of their restrictions to
![]() ${{\mathbf G}}^F$
are also called the semisimple characters of
${{\mathbf G}}^F$
are also called the semisimple characters of
![]() ${{\mathbf G}}^F$
. In particular, both are of degree prime to p (see [Reference Geck and MalleGM, 2.6.11]).
${{\mathbf G}}^F$
. In particular, both are of degree prime to p (see [Reference Geck and MalleGM, 2.6.11]).
According to [Reference Malle and SpäthMal2, Th. 1], there exists a semisimple character
![]() $\rho \in \mathrm {Irr}({{{{\mathbf G}}^F}})$
with
$\rho \in \mathrm {Irr}({{{{\mathbf G}}^F}})$
with
![]() $({{\widetilde G}} E)_{\rho }=({{\widetilde G}} E)_{\lambda }$
, where
$({{\widetilde G}} E)_{\rho }=({{\widetilde G}} E)_{\lambda }$
, where
![]() $\rho $
and
$\rho $
and
![]() $\lambda $
lie in the same rational Lusztig series. We use now results from [Reference SpäthS4] to investigate
$\lambda $
lie in the same rational Lusztig series. We use now results from [Reference SpäthS4] to investigate
![]() $\rho $
further. In a first step, we prove that
$\rho $
further. In a first step, we prove that
![]() $\gamma $
acts trivially on
$\gamma $
acts trivially on
![]() $\rho $
and
$\rho $
and
![]() $\mathrm {Irr}(\mathcal L^{-1}({\left\langle h_0\right\rangle }) \mid \rho )$
.
$\mathrm {Irr}(\mathcal L^{-1}({\left\langle h_0\right\rangle }) \mid \rho )$
.
We assume that
![]() ${{\mathbf G}}$
,
${{\mathbf G}}$
,
![]() ${\mathbf T}$
, and
${\mathbf T}$
, and
![]() $\Delta $
are as given in Notation 3.3, and let
$\Delta $
are as given in Notation 3.3, and let
![]() ${\mathbf U}:={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Delta \right\rangle }$
and
${\mathbf U}:={\left\langle {\mathbf X}_{\alpha }\mid {\alpha }\in \Delta \right\rangle }$
and
![]() ${\mathbf B}:={\mathbf T}{\mathbf U}$
. As group
${\mathbf B}:={\mathbf T}{\mathbf U}$
. As group
![]() $\widetilde {{\mathbf G}}$
introduced in 2.2, we use the particular choice from [Reference SpäthS4, 3.1]. Then
$\widetilde {{\mathbf G}}$
introduced in 2.2, we use the particular choice from [Reference SpäthS4, 3.1]. Then
![]() ${{{\widetilde {\mathbf G}}^F}}$
and
${{{\widetilde {\mathbf G}}^F}}$
and
![]() ${\widetilde G}$
induce the same automorphisms on
${\widetilde G}$
induce the same automorphisms on
![]() ${{{{\mathbf G}}^F}}$
. Let
${{{{\mathbf G}}^F}}$
. Let
![]() $\widetilde {\mathbf B}:={\mathbf B}\operatorname Z(\widetilde {\mathbf G})$
. Let
$\widetilde {\mathbf B}:={\mathbf B}\operatorname Z(\widetilde {\mathbf G})$
. Let
![]() $\widetilde {\Omega }:\mathrm {Irr}_{p'}({{{\widetilde {\mathbf G}}^F}})\longrightarrow \mathrm {Irr}_{p'}(\widetilde {\mathbf B}^F)$
be the
$\widetilde {\Omega }:\mathrm {Irr}_{p'}({{{\widetilde {\mathbf G}}^F}})\longrightarrow \mathrm {Irr}_{p'}(\widetilde {\mathbf B}^F)$
be the
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})\rtimes E({{{{\mathbf G}}^F}}) $
-equivariant bijection with
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})\rtimes E({{{{\mathbf G}}^F}}) $
-equivariant bijection with
![]() $\mathrm {Irr}({\left. \widetilde {\psi }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})= \mathrm {Irr}({\left. \widetilde {\Omega }(\widetilde {\psi })\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})$
for every
$\mathrm {Irr}({\left. \widetilde {\psi }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})= \mathrm {Irr}({\left. \widetilde {\Omega }(\widetilde {\psi })\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})$
for every
![]() $\psi \in \mathrm {Irr}_{p'}({{{\widetilde {\mathbf G}}^F}})$
from [Reference SpäthS4, 3.3(a)].
$\psi \in \mathrm {Irr}_{p'}({{{\widetilde {\mathbf G}}^F}})$
from [Reference SpäthS4, 3.3(a)].
Let
![]() $\widetilde {\rho }\in \mathrm {Irr}(\widetilde {{\mathbf G}}^F\mid \rho )$
,
$\widetilde {\rho }\in \mathrm {Irr}(\widetilde {{\mathbf G}}^F\mid \rho )$
,
![]() $\widetilde {\phi } := \widetilde {\Omega }(\widetilde {\rho })$
, and
$\widetilde {\phi } := \widetilde {\Omega }(\widetilde {\rho })$
, and
![]() $\phi \in \mathrm {Irr}({\left. \widetilde {\phi }\right\rceil _{{ {\mathbf B}^F}}})$
. Let C be the Cartan matrix associated with
$\phi \in \mathrm {Irr}({\left. \widetilde {\phi }\right\rceil _{{ {\mathbf B}^F}}})$
. Let C be the Cartan matrix associated with
![]() $\Delta $
and
$\Delta $
and
![]() $C^{-1}=(c^{\prime }_{{\alpha } \beta })$
its inverse. Let
$C^{-1}=(c^{\prime }_{{\alpha } \beta })$
its inverse. Let
![]() $\zeta \in {\mathbb {F}}^{\times }$
be a root of unity of order
$\zeta \in {\mathbb {F}}^{\times }$
be a root of unity of order
![]() $\det (C) (q-1)=4(q-1)$
. For
$\det (C) (q-1)=4(q-1)$
. For
![]() ${\alpha }\in \Delta $
, we set
${\alpha }\in \Delta $
, we set
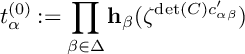 $$ \begin{align*}t^{(0)}_{\alpha}:=\prod_{\beta\in\Delta} {\mathbf h} _{\beta}(\zeta^{\det(C) c^{\prime}_{{\alpha} \beta}})\end{align*} $$
$$ \begin{align*}t^{(0)}_{\alpha}:=\prod_{\beta\in\Delta} {\mathbf h} _{\beta}(\zeta^{\det(C) c^{\prime}_{{\alpha} \beta}})\end{align*} $$
(see also [Reference MalleMas, 8.1]). Then we can choose elements
![]() $t_{\alpha }\in t^{(0)}_{\alpha } \operatorname Z(\widetilde {\mathbf G})\cap \widetilde {\mathbf T}^F$
such that
$t_{\alpha }\in t^{(0)}_{\alpha } \operatorname Z(\widetilde {\mathbf G})\cap \widetilde {\mathbf T}^F$
such that
![]() $\widetilde {\mathbf T}^F=\operatorname Z({{{\widetilde {\mathbf G}}^F}}){\left\langle t_{\alpha }\mid {\alpha } \in \Delta \right\rangle }$
(see [Reference MalleMas, §8]). Assume that
$\widetilde {\mathbf T}^F=\operatorname Z({{{\widetilde {\mathbf G}}^F}}){\left\langle t_{\alpha }\mid {\alpha } \in \Delta \right\rangle }$
(see [Reference MalleMas, §8]). Assume that
![]() $\Delta $
is given as in Notation 3.3, and let
$\Delta $
is given as in Notation 3.3, and let
![]() ${\alpha }\in \{e_2\pm e_1\}$
. The entries of
${\alpha }\in \{e_2\pm e_1\}$
. The entries of
![]() $C^{-1}$
can be found in [Reference Onishchik and VinbergOV, p. 296]. We see
$C^{-1}$
can be found in [Reference Onishchik and VinbergOV, p. 296]. We see
![]() $\mathcal L(t^{(0)}_{\alpha })=(t^{(0)}_{\alpha })^{q-1}\in {\mathbf h} _{\underline {l}}(\varpi ){\left\langle h_0\right\rangle }$
. Hence,
$\mathcal L(t^{(0)}_{\alpha })=(t^{(0)}_{\alpha })^{q-1}\in {\mathbf h} _{\underline {l}}(\varpi ){\left\langle h_0\right\rangle }$
. Hence,
![]() $t_{\alpha }$
induces a diagonal automorphism of
$t_{\alpha }$
induces a diagonal automorphism of
![]() ${{{{\mathbf G}}^F}}$
associated with some element in
${{{{\mathbf G}}^F}}$
associated with some element in
![]() ${\mathbf h} _{\underline {l}}(\varpi ){\left\langle h_0\right\rangle }$
in the notation of Remark 2.16(b).
${\mathbf h} _{\underline {l}}(\varpi ){\left\langle h_0\right\rangle }$
in the notation of Remark 2.16(b).
We abbreviate
![]() ${\widehat G}:=\mathcal L^{-1}({\left\langle h_0\right\rangle })$
. The assumption
${\widehat G}:=\mathcal L^{-1}({\left\langle h_0\right\rangle })$
. The assumption
![]() ${\widetilde G}_{\lambda }\leq \widehat G$
implies
${\widetilde G}_{\lambda }\leq \widehat G$
implies
![]() $\lambda ^{t_{\alpha }}\neq \lambda $
. Via the construction, we have
$\lambda ^{t_{\alpha }}\neq \lambda $
. Via the construction, we have
![]() $(\widetilde GE)_{\rho }=(\widetilde GE)_{\lambda }$
and hence
$(\widetilde GE)_{\rho }=(\widetilde GE)_{\lambda }$
and hence
![]() $ \rho ^{t_{\alpha }}\neq \rho $
. By Clifford theory, the character
$ \rho ^{t_{\alpha }}\neq \rho $
. By Clifford theory, the character
![]() $\widetilde {\rho }$
satisfies
$\widetilde {\rho }$
satisfies
![]() $\widetilde {\rho } (t_{\alpha } {{{{\mathbf G}}^F}})=0$
and is stable under multiplying with linear characters with kernel
$\widetilde {\rho } (t_{\alpha } {{{{\mathbf G}}^F}})=0$
and is stable under multiplying with linear characters with kernel
(see 2.16(b)). As
![]() $\widetilde {\Omega }$
is an
$\widetilde {\Omega }$
is an
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
-equivariant bijection, the character
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
-equivariant bijection, the character
![]() $\widetilde {\phi }$
has to satisfy
$\widetilde {\phi }$
has to satisfy
![]() $\widetilde {\phi }(t_{\alpha })=0$
as well. As in Remark 2.16,
$\widetilde {\phi }(t_{\alpha })=0$
as well. As in Remark 2.16,
![]() $\widetilde {\phi }$
can be extended to some character
$\widetilde {\phi }$
can be extended to some character
![]() $\kappa $
on
$\kappa $
on
![]() $\widetilde {\mathbf B}^F\widetilde Z=\widetilde B_0.\widetilde Z $
, where
$\widetilde {\mathbf B}^F\widetilde Z=\widetilde B_0.\widetilde Z $
, where
![]() $\widetilde {\mathcal {L}}$
is the Lang map on
$\widetilde {\mathcal {L}}$
is the Lang map on
![]() $\widetilde {{\mathbf G}}$
,
$\widetilde {{\mathbf G}}$
,
![]() $\widetilde Z:=\widetilde {\mathcal {L}}^{-1}(\operatorname Z({{\mathbf G}}))\cap \operatorname Z(\widetilde {\mathbf G})$
, and
$\widetilde Z:=\widetilde {\mathcal {L}}^{-1}(\operatorname Z({{\mathbf G}}))\cap \operatorname Z(\widetilde {\mathbf G})$
, and
![]() $\widetilde B_0:= \mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {\mathbf B}$
. Note that
$\widetilde B_0:= \mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {\mathbf B}$
. Note that
![]() ${\widetilde B_0}=\operatorname Z({{{{\mathbf G}}^F}}){\left\langle t_{\beta }^{(0)}\mid \beta \in \Delta \right\rangle } {\mathbf U}^F$
. Then
${\widetilde B_0}=\operatorname Z({{{{\mathbf G}}^F}}){\left\langle t_{\beta }^{(0)}\mid \beta \in \Delta \right\rangle } {\mathbf U}^F$
. Then
![]() $\kappa (t_{\alpha }^{(0)})=0$
. The character
$\kappa (t_{\alpha }^{(0)})=0$
. The character
![]() ${\left. \kappa \right\rceil _{{\widetilde B_0}}}$
is
${\left. \kappa \right\rceil _{{\widetilde B_0}}}$
is
![]() $\gamma $
-stable, since
$\gamma $
-stable, since
![]() $\mathrm {Irr}({\left. \kappa \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}} |)=\mathrm {Irr}({\left. \phi \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}})$
is
$\mathrm {Irr}({\left. \kappa \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}} |)=\mathrm {Irr}({\left. \phi \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}})$
is
![]() $\gamma $
-stable because of
$\gamma $
-stable because of
![]() $h_0\in \ker (\phi )$
and
$h_0\in \ker (\phi )$
and
![]() $t_{\beta }^{(0)}$
is
$t_{\beta }^{(0)}$
is
![]() $\gamma $
-fixed for every
$\gamma $
-fixed for every
![]() $\beta \in \Delta \setminus \{ e_2\pm e_1\}$
according to the explicit value of
$\beta \in \Delta \setminus \{ e_2\pm e_1\}$
according to the explicit value of
![]() $C^{-1}$
.
$C^{-1}$
.
As
![]() $\kappa $
is
$\kappa $
is
![]() $\gamma $
-stable,
$\gamma $
-stable,
![]() $\phi \in \mathrm {Irr}({\left. \kappa \right\rceil _{{{\mathbf B}^F}}}) =\mathrm {Irr}({\left. \widetilde {\phi }\right\rceil _{{{\mathbf B}^F}}})$
can be assumed to be
$\phi \in \mathrm {Irr}({\left. \kappa \right\rceil _{{{\mathbf B}^F}}}) =\mathrm {Irr}({\left. \widetilde {\phi }\right\rceil _{{{\mathbf B}^F}}})$
can be assumed to be
![]() $\gamma $
-stable (see [Reference SpäthS4, 3.6(a)]). By Clifford theory,
$\gamma $
-stable (see [Reference SpäthS4, 3.6(a)]). By Clifford theory,
![]() ${\left. \kappa \right\rceil _{{\widetilde B_0}}}$
is of the form
${\left. \kappa \right\rceil _{{\widetilde B_0}}}$
is of the form
![]() $\widehat {\phi }^{\widetilde B_0}$
for a unique
$\widehat {\phi }^{\widetilde B_0}$
for a unique
![]() $\widehat {\phi }\in \mathrm {Irr}((\widetilde B_0)_{\phi })$
. As
$\widehat {\phi }\in \mathrm {Irr}((\widetilde B_0)_{\phi })$
. As
![]() $\phi $
extends to
$\phi $
extends to
![]() $\widetilde {\mathbf B}^F_{\phi }$
according to [Reference SpäthS4, Th. 3.5(a)], the character
$\widetilde {\mathbf B}^F_{\phi }$
according to [Reference SpäthS4, Th. 3.5(a)], the character
![]() $\widehat {\phi }$
is an extension of
$\widehat {\phi }$
is an extension of
![]() $\phi $
. As
$\phi $
. As
![]() $\kappa $
and
$\kappa $
and
![]() $\phi $
are
$\phi $
are
![]() $\gamma $
-stable,
$\gamma $
-stable,
![]() $\widehat {\phi }$
is
$\widehat {\phi }$
is
![]() $\gamma $
-stable. Note that
$\gamma $
-stable. Note that
![]() $(\widetilde B_0)_{\phi }\leq \widehat B:=\mathcal L^{-1}({\left\langle h_0\right\rangle })\cap {\mathbf B}$
.
$(\widetilde B_0)_{\phi }\leq \widehat B:=\mathcal L^{-1}({\left\langle h_0\right\rangle })\cap {\mathbf B}$
.
Via the statement given in Proposition 2.18, some
![]() ${{\widetilde G}}$
-conjugate
${{\widetilde G}}$
-conjugate
![]() $\rho '$
of
$\rho '$
of
![]() $\rho $
is
$\rho $
is
![]() $\gamma $
-stable and has also a
$\gamma $
-stable and has also a
![]() $\gamma $
-stable extension to
$\gamma $
-stable extension to
![]() $\widehat G$
. If
$\widehat G$
. If
![]() $\rho '\neq \rho $
, we observe that
$\rho '\neq \rho $
, we observe that
![]() $(\widehat G {\left\langle \gamma \right\rangle })^{t'}=\widehat G {\left\langle \gamma \right\rangle }$
for every
$(\widehat G {\left\langle \gamma \right\rangle })^{t'}=\widehat G {\left\langle \gamma \right\rangle }$
for every
![]() $t'\in \mathcal L^{-1}({\mathbf h} _{\underline {l}}(\varpi ))$
. Hence, the character
$t'\in \mathcal L^{-1}({\mathbf h} _{\underline {l}}(\varpi ))$
. Hence, the character
![]() $\rho $
extends to
$\rho $
extends to
![]() $\widehat G {\left\langle \gamma \right\rangle }$
, as well.
$\widehat G {\left\langle \gamma \right\rangle }$
, as well.
We deduce from this result on
![]() $\rho $
the analogous property of
$\rho $
the analogous property of
![]() $ \lambda $
. Recall that
$ \lambda $
. Recall that
![]() $\lambda $
and
$\lambda $
and
![]() $\rho $
are in the same rational Lusztig series and that
$\rho $
are in the same rational Lusztig series and that
![]() $({{{\widetilde {\mathbf G}}^F}} E)_{\rho }=({{{\widetilde {\mathbf G}}^F}} E)_{\lambda }$
, in particular
$({{{\widetilde {\mathbf G}}^F}} E)_{\rho }=({{{\widetilde {\mathbf G}}^F}} E)_{\lambda }$
, in particular
![]() ${{{\widetilde {\mathbf G}}^F}}_{\rho }={{{\widetilde {\mathbf G}}^F}}_{\lambda }$
. Recall that
${{{\widetilde {\mathbf G}}^F}}_{\rho }={{{\widetilde {\mathbf G}}^F}}_{\lambda }$
. Recall that
![]() $\widetilde {\rho }\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}\mid \rho )$
and
$\widetilde {\rho }\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}\mid \rho )$
and
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
acts on
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
acts on
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
by multiplication with linear characters. As
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
by multiplication with linear characters. As
![]() ${{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}}$
is abelian and maximal extendibility holds with respect to
${{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}}$
is abelian and maximal extendibility holds with respect to
![]() ${{{{\mathbf G}}^F}}\lhd {{{\widetilde {\mathbf G}}^F}}$
, we see
${{{{\mathbf G}}^F}}\lhd {{{\widetilde {\mathbf G}}^F}}$
, we see
Let
![]() $\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
be the rational Lusztig series containing
$\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
be the rational Lusztig series containing
![]() $\widetilde {\rho }$
. The character
$\widetilde {\rho }$
. The character
![]() $\widetilde {\rho }$
is semisimple. The series
$\widetilde {\rho }$
is semisimple. The series
![]() $\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
contains exactly one regular character (see [Reference Digne and MichelDM, 12.4.10]). By the definition of semisimple and regular in [Reference Digne and MichelDM, 12.4.1], we see that there exists also a unique regular character in that series. Let
$\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
contains exactly one regular character (see [Reference Digne and MichelDM, 12.4.10]). By the definition of semisimple and regular in [Reference Digne and MichelDM, 12.4.1], we see that there exists also a unique regular character in that series. Let
![]() $\widetilde {\rho }'\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
be the Alvis–Curtis dual of
$\widetilde {\rho }'\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
be the Alvis–Curtis dual of
![]() $\widetilde {\rho }$
up to a sign (see [Reference Digne and MichelDM, 7.2]). Then
$\widetilde {\rho }$
up to a sign (see [Reference Digne and MichelDM, 7.2]). Then
![]() $\{\widetilde {\rho }'\}=\mathrm {Irr}(\Gamma ^{({{{\widetilde {\mathbf G}}^F}})})\cap \mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
, where
$\{\widetilde {\rho }'\}=\mathrm {Irr}(\Gamma ^{({{{\widetilde {\mathbf G}}^F}})})\cap \mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
, where
![]() $\Gamma ^{({{{\widetilde {\mathbf G}}^F}})}$
denotes the Gelfand–Graev character of
$\Gamma ^{({{{\widetilde {\mathbf G}}^F}})}$
denotes the Gelfand–Graev character of
![]() ${{{\widetilde {\mathbf G}}^F}}$
. Since it vanishes outside unipotent elements, the Gelfand–Graev character is stable under
${{{\widetilde {\mathbf G}}^F}}$
. Since it vanishes outside unipotent elements, the Gelfand–Graev character is stable under
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
. Hence,
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
. Hence,
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})_{\widetilde {\rho }'}$
coincides with the stabilizer of
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})_{\widetilde {\rho }'}$
coincides with the stabilizer of
![]() $\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
in
$\mathcal E({{{\widetilde {\mathbf G}}^F}},s)$
in
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
. This group is called
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})$
. This group is called
![]() $B(s)$
in [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.13]. By the construction of Alvis–Curtis duality, this implies
$B(s)$
in [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.13]. By the construction of Alvis–Curtis duality, this implies
![]() $\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})_{\widetilde {\rho }}=B(s)$
. The characters
$\mathrm {Irr}({{{\widetilde {\mathbf G}}^F}}/{{{{\mathbf G}}^F}})_{\widetilde {\rho }}=B(s)$
. The characters
![]() $\widetilde {\rho }^{\gamma }$
and
$\widetilde {\rho }^{\gamma }$
and
![]() $\widetilde {\lambda }^{\gamma }$
belong to
$\widetilde {\lambda }^{\gamma }$
belong to
![]() $\mathcal E({{{\widetilde {\mathbf G}}^F}},\gamma ^{-1}(s))$
. As
$\mathcal E({{{\widetilde {\mathbf G}}^F}},\gamma ^{-1}(s))$
. As
![]() $\lambda $
and
$\lambda $
and
![]() $\rho $
are
$\rho $
are
![]() $\gamma $
-stable,
$\gamma $
-stable,
![]() $\widetilde {\rho }^{\gamma } = \widetilde {\rho } \mu $
and
$\widetilde {\rho }^{\gamma } = \widetilde {\rho } \mu $
and
![]() $\widetilde {\lambda }^{\gamma }=\widetilde {\lambda } \mu '$
for linear characters
$\widetilde {\lambda }^{\gamma }=\widetilde {\lambda } \mu '$
for linear characters
![]() $\mu ,\mu '\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
. Since
$\mu ,\mu '\in \mathrm {Irr}({{{\widetilde {\mathbf G}}^F}})$
. Since
![]() $\widetilde {\rho }^{\gamma }$
and
$\widetilde {\rho }^{\gamma }$
and
![]() $\widetilde {\lambda }^{\gamma }$
are in the same rational series,
$\widetilde {\lambda }^{\gamma }$
are in the same rational series,
![]() $\mu \in \mu 'B(s)$
or equivalently
$\mu \in \mu 'B(s)$
or equivalently
![]() ${\left. \mu \right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\rho }}}} = {\left. \mu '\right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\lambda }}}}$
.
${\left. \mu \right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\rho }}}} = {\left. \mu '\right\rceil _{{{{{\widetilde {\mathbf G}}^F}}_{\lambda }}}}$
.
Because of
![]() $\mathrm {Irr}({\left. \widetilde {\rho }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})=\mathrm {Irr}({\left. \widetilde {\lambda }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})$
, Proposition 2.18 allows to conclude that
$\mathrm {Irr}({\left. \widetilde {\rho }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})=\mathrm {Irr}({\left. \widetilde {\lambda }\right\rceil _{{\operatorname Z({{{\widetilde {\mathbf G}}^F}})}}})$
, Proposition 2.18 allows to conclude that
![]() $\lambda $
has a
$\lambda $
has a
![]() $\gamma $
-stable extension to
$\gamma $
-stable extension to
![]() $\widehat G$
as
$\widehat G$
as
![]() $\rho $
has such an extension.
$\rho $
has such an extension.
6 Character theory for the relative inertia groups
 $W(\lambda )$
$W(\lambda )$
The aim of this section is to ensure Assumption 2.8 (ii), namely to prove (a main step toward) the following statement.
Theorem 6.1. Let
![]() $l\geq 4$
. Let
$l\geq 4$
. Let
![]() ${{\mathbf G}}^F=\mathrm {D}_{l,\mathrm {sc}}(q)$
with odd q, and let
${{\mathbf G}}^F=\mathrm {D}_{l,\mathrm {sc}}(q)$
with odd q, and let
![]() $L={{\mathbf L}}^F$
be a standard Levi subgroup of
$L={{\mathbf L}}^F$
be a standard Levi subgroup of
![]() ${{{{\mathbf G}}^F}}$
(see Notation 3.3). Let N,
${{{{\mathbf G}}^F}}$
(see Notation 3.3). Let N,
![]() $\widetilde N':= \widetilde {T}_0 N$
, and
$\widetilde N':= \widetilde {T}_0 N$
, and
![]() $E_L:=\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}({{\mathbf L}}^F)$
be associated with L as in Lemma 2.8. If Hypothesis 2.14 holds for every
$E_L:=\operatorname {Stab}_{E({{{{\mathbf G}}^F}})}({{\mathbf L}}^F)$
be associated with L as in Lemma 2.8. If Hypothesis 2.14 holds for every
![]() $l'$
with
$l'$
with
![]() $4\leq l'< l$
, then there exists some
$4\leq l'< l$
, then there exists some
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N'$
-transversal in
$\widetilde N'$
-transversal in
![]() $\mathrm {Irr}_{cusp}(N)$
.
$\mathrm {Irr}_{cusp}(N)$
.
Some technicalities (mainly in the case where
![]() ${{\mathbf G}}=\mathrm {D}_{4,sc}({\mathbb {F}})$
) delay the complete proof until §7. We construct the
${{\mathbf G}}=\mathrm {D}_{4,sc}({\mathbb {F}})$
) delay the complete proof until §7. We construct the
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N'$
-transversal as a subset of
$\widetilde N'$
-transversal as a subset of
![]() $\mathrm {Irr}(N\mid \mathbb {T})$
, where
$\mathrm {Irr}(N\mid \mathbb {T})$
, where
![]() $\mathbb {T}$
is the
$\mathbb {T}$
is the
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() ${\widetilde N'}$
-transversal from Theorem 3.1(a). In Lemma 6.3, we find some
${\widetilde N'}$
-transversal from Theorem 3.1(a). In Lemma 6.3, we find some
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N'$
-transversal of
$\widetilde N'$
-transversal of
![]() $\mathrm {Irr}(N\mid \{ \lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}^{\prime }_{\lambda }=L \})$
where
$\mathrm {Irr}(N\mid \{ \lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}^{\prime }_{\lambda }=L \})$
where
![]() $\widetilde {L}'=\widetilde {T}_0 L$
as in Theorem 2.8.
$\widetilde {L}'=\widetilde {T}_0 L$
as in Theorem 2.8.
In order to find the transversal of
![]() $\mathrm {Irr}(N\mid \{ \lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}^{\prime }_{\lambda }\neq L \})$
with the required properties, we apply the strategy mapped out by Proposition 2.12, itself based on the parametrization of Proposition 2.10. Thanks to Theorem 3.1, the two first assumptions of Proposition 2.12 can be assumed, in particular there exist some
$\mathrm {Irr}(N\mid \{ \lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}^{\prime }_{\lambda }\neq L \})$
with the required properties, we apply the strategy mapped out by Proposition 2.12, itself based on the parametrization of Proposition 2.10. Thanks to Theorem 3.1, the two first assumptions of Proposition 2.12 can be assumed, in particular there exist some
![]() $\widehat N$
-equivariant extension map
$\widehat N$
-equivariant extension map
![]() $\Lambda _{L,\mathbb {T}}$
with respect to
$\Lambda _{L,\mathbb {T}}$
with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathbb {T}$
, where
$\mathbb {T}$
, where
![]() $\widehat N=NE_L$
. We have to ensure the remaining Assumption 2.12(iii) and study the characters of the relative Weyl groups and their Clifford theory.
$\widehat N=NE_L$
. We have to ensure the remaining Assumption 2.12(iii) and study the characters of the relative Weyl groups and their Clifford theory.
As already discussed in §2.3, characters in such a transversal have a stabilizer in
![]() $\widetilde N' E_L$
with a specific structure, namely such a
$\widetilde N' E_L$
with a specific structure, namely such a
![]() $\psi \in \mathrm {Irr}(N)$
satisfies
$\psi \in \mathrm {Irr}(N)$
satisfies
(see also Lemma 2.4). For studying a character
![]() $\psi \in \mathrm {Irr}(N\mid \mathbb {T})$
, we apply the parametrization
$\psi \in \mathrm {Irr}(N\mid \mathbb {T})$
, we apply the parametrization
![]() $\Upsilon $
from Proposition 2.10(a) and the extension map
$\Upsilon $
from Proposition 2.10(a) and the extension map
![]() $\Lambda _{L,\mathbb {T}}$
with respect to
$\Lambda _{L,\mathbb {T}}$
with respect to
![]() $L\lhd N$
for
$L\lhd N$
for
![]() $\mathbb {T}$
. Then
$\mathbb {T}$
. Then
![]() $\psi =\Upsilon (\overline {(\lambda ,\eta )})=(\Lambda _{L,\mathbb {T}}(\lambda )\eta )^N$
with
$\psi =\Upsilon (\overline {(\lambda ,\eta )})=(\Lambda _{L,\mathbb {T}}(\lambda )\eta )^N$
with
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
. According to Proposition 2.11, the character
$\eta \in \mathrm {Irr}(W(\lambda ))$
. According to Proposition 2.11, the character
![]() $\psi =\Upsilon (\overline {(\lambda ,\eta )})$
satisfies Equation (6.1) if
$\psi =\Upsilon (\overline {(\lambda ,\eta )})$
satisfies Equation (6.1) if
![]() $\eta $
is
$\eta $
is
![]() $\widehat K(\lambda )_{\eta _0}$
-stable, where
$\widehat K(\lambda )_{\eta _0}$
-stable, where
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
,
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
,
where
![]() $\widehat W=NE_L/L$
and
$\widehat W=NE_L/L$
and
![]() $\widehat K(\lambda )=\widehat W_{\lambda }$
. The aim of this section is Corollary 6.36, namely to prove that for every
$\widehat K(\lambda )=\widehat W_{\lambda }$
. The aim of this section is Corollary 6.36, namely to prove that for every
![]() $\lambda \in \mathbb {T}$
,
$\lambda \in \mathbb {T}$
,
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
, and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}^{\prime }_{\lambda }\mid \lambda )$
, and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
,
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
,
there exists some
![]() $ K(\lambda )_{\eta _0}$
-stable
$ K(\lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
,
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
,
where
![]() $K(\lambda )$
is the group from Notation 6.4. According to Lemma 6.5, such a character
$K(\lambda )$
is the group from Notation 6.4. According to Lemma 6.5, such a character
![]() $\eta $
is also
$\eta $
is also
![]() $\widehat K(\lambda )_{\eta _0}$
-stable, whenever
$\widehat K(\lambda )_{\eta _0}$
-stable, whenever
![]() ${{\mathbf G}}$
is not of type
${{\mathbf G}}$
is not of type
![]() $\mathrm {D}_4$
.
$\mathrm {D}_4$
.
In the proof, some arguments depend on the group
![]() $\widetilde {L}^{\prime }_{\lambda }$
. As in Remark 2.16, we relate the group
$\widetilde {L}^{\prime }_{\lambda }$
. As in Remark 2.16, we relate the group
![]() $\widetilde {L}'$
to subgroups of
$\widetilde {L}'$
to subgroups of
![]() ${{\mathbf G}}$
.
${{\mathbf G}}$
.
Notation 6.2. Recall the definitions
![]() $\widetilde {L}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {{\mathbf L}}$
and
$\widetilde {L}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))\cap {{\mathbf L}}$
and
![]() $\widehat L:=\mathcal L^{-1}({\left\langle h_0\right\rangle })\cap {{\mathbf L}}$
from Lemma 3.13, where
$\widehat L:=\mathcal L^{-1}({\left\langle h_0\right\rangle })\cap {{\mathbf L}}$
from Lemma 3.13, where
![]() $\mathcal L:{{\mathbf G}}\rightarrow {{\mathbf G}}$
is given by
$\mathcal L:{{\mathbf G}}\rightarrow {{\mathbf G}}$
is given by
![]() $x\mapsto x^{-1} F(x)$
. Recall
$x\mapsto x^{-1} F(x)$
. Recall
![]() $\widetilde N':=\widetilde {T}_0 N$
and set analogously
$\widetilde N':=\widetilde {T}_0 N$
and set analogously
![]() ${\widetilde N}:=\widetilde {L} N$
. Then
${\widetilde N}:=\widetilde {L} N$
. Then
![]() $\widetilde {L}'$
and
$\widetilde {L}'$
and
![]() $\widetilde N'$
induce on
$\widetilde N'$
induce on
![]() ${{\mathbf G}}$
the same automorphisms as
${{\mathbf G}}$
the same automorphisms as
![]() $\widetilde {L}$
and
$\widetilde {L}$
and
![]() $\widetilde N$
, respectively.
$\widetilde N$
, respectively.
Note that by an application of Lang’s theorem,
![]() $\mathcal L({{\mathbf L}})={{\mathbf L}}\supseteq \operatorname Z({{\mathbf G}})$
so that
$\mathcal L({{\mathbf L}})={{\mathbf L}}\supseteq \operatorname Z({{\mathbf G}})$
so that
![]() $L\lneq \widehat L\lneq \widetilde {L}$
.
$L\lneq \widehat L\lneq \widetilde {L}$
.
For
![]() $\lambda \in \mathbb {T}$
, the characters of
$\lambda \in \mathbb {T}$
, the characters of
![]() $W(\lambda )$
and
$W(\lambda )$
and
![]() $W(\widetilde {\lambda })$
defined as above will be investigated depending on the value of
$W(\widetilde {\lambda })$
defined as above will be investigated depending on the value of
![]() $\widetilde {L}_{\lambda }$
. The set
$\widetilde {L}_{\lambda }$
. The set
![]() $\mathrm {Irr}_{cusp}(L)$
can be partitioned in the following way:
$\mathrm {Irr}_{cusp}(L)$
can be partitioned in the following way:
where
![]() ${\mathbb {M}^{(X)}}:=\{ \lambda \in \mathrm {Irr}_{cusp} (L)\mid \widetilde {L}_{\lambda }=X\}$
for any subgroup
${\mathbb {M}^{(X)}}:=\{ \lambda \in \mathrm {Irr}_{cusp} (L)\mid \widetilde {L}_{\lambda }=X\}$
for any subgroup
![]() $L\leq X\leq \widetilde {L}$
and
$L\leq X\leq \widetilde {L}$
and
![]() ${\mathbb {M}_0}:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)} \cup \mathbb {M}^{({\widehat L})}\cup \mathbb {M}^{({\widetilde {L}})})$
. (In case of
${\mathbb {M}_0}:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)} \cup \mathbb {M}^{({\widehat L})}\cup \mathbb {M}^{({\widetilde {L}})})$
. (In case of
![]() $|\operatorname Z({{{{\mathbf G}}^F}})|=2$
, one has
$|\operatorname Z({{{{\mathbf G}}^F}})|=2$
, one has
![]() $\mathbb {M}^{(L)}=\emptyset $
.) Note that the sets are by definition
$\mathbb {M}^{(L)}=\emptyset $
.) Note that the sets are by definition
![]() ${\widetilde N} E_L$
-stable as L,
${\widetilde N} E_L$
-stable as L,
![]() ${\widehat L}$
, and
${\widehat L}$
, and
![]() ${\widetilde {L}}$
are
${\widetilde {L}}$
are
![]() $\widetilde N E_L$
-stable. In the following, we construct an
$\widetilde N E_L$
-stable. In the following, we construct an
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N$
-transversal in
$\widetilde N$
-transversal in
![]() $\mathrm {Irr}_{cusp}(N\mid \mathbb {M}')$
for each of those four given
$\mathrm {Irr}_{cusp}(N\mid \mathbb {M}')$
for each of those four given
![]() $NE_L$
-stable subsets
$NE_L$
-stable subsets
![]() $\mathbb {M}'\subseteq \mathrm {Irr}_{cusp}(L)$
.
$\mathbb {M}'\subseteq \mathrm {Irr}_{cusp}(L)$
.
Lemma 6.3. Let
![]() ${\mathbb T^{(L)}}:= \mathbb {T} \cap \mathbb {M}^{(L)}$
. Then
${\mathbb T^{(L)}}:= \mathbb {T} \cap \mathbb {M}^{(L)}$
. Then
![]() $\mathrm {Irr}(N\mid \mathbb {T}^{(L)})$
is an
$\mathrm {Irr}(N\mid \mathbb {T}^{(L)})$
is an
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N'$
-transversal in
$\widetilde N'$
-transversal in
![]() $\mathrm {Irr}(N\mid \mathbb {M}^{(L)})$
.
$\mathrm {Irr}(N\mid \mathbb {M}^{(L)})$
.
Proof. The set
![]() $\mathbb {T}$
is by construction
$\mathbb {T}$
is by construction
![]() $N E_L$
-stable, and no two elements are
$N E_L$
-stable, and no two elements are
![]() $\widetilde {L}$
-conjugate. Hence, for
$\widetilde {L}$
-conjugate. Hence, for
![]() $\lambda \in \mathbb {T}^{(L)}$
, we have
$\lambda \in \mathbb {T}^{(L)}$
, we have
![]() $(NE_L \widetilde {L})_{\lambda }=( NE_L)_{\lambda }$
by Lemma 2.4. By Clifford theory,
$(NE_L \widetilde {L})_{\lambda }=( NE_L)_{\lambda }$
by Lemma 2.4. By Clifford theory,
![]() $\mathrm {Irr}(N\mid \mathbb {T}^{(L)})$
is an
$\mathrm {Irr}(N\mid \mathbb {T}^{(L)})$
is an
![]() $\widetilde N$
-transversal in
$\widetilde N$
-transversal in
![]() $\mathrm {Irr}(L\mid \mathbb {M}^{(L)})$
and is
$\mathrm {Irr}(L\mid \mathbb {M}^{(L)})$
and is
![]() $NE_L$
-stable.
$NE_L$
-stable.
Determining an
![]() $ N E_L$
-stable
$ N E_L$
-stable
![]() $\widetilde {L}$
-transversal in
$\widetilde {L}$
-transversal in
![]() $\mathrm {Irr}(N\mid \mathbb {M}')$
for the other sets
$\mathrm {Irr}(N\mid \mathbb {M}')$
for the other sets
![]() $\mathbb {M}'$
is more involved. We start by some general descriptions of
$\mathbb {M}'$
is more involved. We start by some general descriptions of
![]() $W(\lambda )$
and related groups for
$W(\lambda )$
and related groups for
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
(see Proposition 6.28). Afterward, we collect some particular results on cuspidal characters. In the following two subsections, we verify for characters of
$\lambda \in \mathrm {Irr}_{cusp}(L)$
(see Proposition 6.28). Afterward, we collect some particular results on cuspidal characters. In the following two subsections, we verify for characters of
![]() $W(\lambda )$
the above condition under the assumption that
$W(\lambda )$
the above condition under the assumption that
![]() $\lambda \in \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
or
$\lambda \in \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
or
![]() $\lambda \in \mathbb {M}^{(\widehat L)}$
.
$\lambda \in \mathbb {M}^{(\widehat L)}$
.
In §6.4, we ensure a closely related condition on characters of
![]() $W(\lambda )$
for
$W(\lambda )$
for
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
with
$\lambda \in \mathrm {Irr}_{cusp}(L)$
with
![]() $\widetilde {L}_{\lambda }=\widehat L$
. In §7, we show how these considerations prove Theorem 6.1 and how this implies Theorem A.
$\widetilde {L}_{\lambda }=\widehat L$
. In §7, we show how these considerations prove Theorem 6.1 and how this implies Theorem A.
6.1 Understanding
 $\mathrm {Irr}_{cusp}(N)$
via characters of subgroups of W
$\mathrm {Irr}_{cusp}(N)$
via characters of subgroups of W
We start by recalling some basic notation and introducing subgroups of
![]() ${\widehat W}:=\widehat N/L = NE_L/L$
as in 2.8. Additionally, let
${\widehat W}:=\widehat N/L = NE_L/L$
as in 2.8. Additionally, let
![]() $\overline N:={\mathrm {N}}_{{\overline {\mathbf G}}^F}({{\mathbf L}})$
and
$\overline N:={\mathrm {N}}_{{\overline {\mathbf G}}^F}({{\mathbf L}})$
and
![]() ${\overline W}=\overline N/L$
(see also Proposition 3.16).
${\overline W}=\overline N/L$
(see also Proposition 3.16).
Notation 6.4. Let
![]() ${{\mathbf G}}$
and
${{\mathbf G}}$
and
![]() $F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be as in Notation 3.3 with odd q. Let
$F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be as in Notation 3.3 with odd q. Let
![]() ${{\mathbf L}}$
be the standard Levi subgroup of
${{\mathbf L}}$
be the standard Levi subgroup of
![]() $({{\mathbf G}},F)$
such that
$({{\mathbf G}},F)$
such that
![]() $L={{\mathbf L}}^F$
. For any J with
$L={{\mathbf L}}^F$
. For any J with
![]() $L\leq J\leq \widetilde {L}$
and
$L\leq J\leq \widetilde {L}$
and
![]() $\lambda \in \mathbb {Z}\mathrm {Irr}(J)$
, we set
$\lambda \in \mathbb {Z}\mathrm {Irr}(J)$
, we set
![]() $W(\lambda ):=N_{\lambda }/L$
. If additionally J is
$W(\lambda ):=N_{\lambda }/L$
. If additionally J is
![]() $E_L$
-stable,
$E_L$
-stable,
![]() $\overline W$
acts on
$\overline W$
acts on
![]() $\mathrm {Char}(J)$
; hence, we can define
$\mathrm {Char}(J)$
; hence, we can define
![]() $\overline W(\lambda ):=\overline W_{\lambda }$
and
$\overline W(\lambda ):=\overline W_{\lambda }$
and
![]() $ {K(\lambda )}:=\overline W_{{\left. \lambda ^{J {\left\langle F_p \right\rangle }}\right\rceil _{J}}}$
.
$ {K(\lambda )}:=\overline W_{{\left. \lambda ^{J {\left\langle F_p \right\rangle }}\right\rceil _{J}}}$
.
The groups
![]() $K(\lambda )$
and
$K(\lambda )$
and
![]() $\widehat K(\lambda )$
are strongly related; in particular, by the following result, it is sufficient to consider
$\widehat K(\lambda )$
are strongly related; in particular, by the following result, it is sufficient to consider
![]() $K(\lambda )$
instead of
$K(\lambda )$
instead of
![]() $\widehat K(\lambda )$
if
$\widehat K(\lambda )$
if
![]() ${{\mathbf G}}$
is not of type
${{\mathbf G}}$
is not of type
![]() $\mathrm {D}_4$
. Recall that
$\mathrm {D}_4$
. Recall that
![]() $\gamma $
is the graph automorphism of
$\gamma $
is the graph automorphism of
![]() ${{\mathbf G}}$
of order
${{\mathbf G}}$
of order
![]() $2$
swapping
$2$
swapping
![]() ${\alpha }_1$
and
${\alpha }_1$
and
![]() ${\alpha }_2$
.
${\alpha }_2$
.
Lemma 6.5. Let
![]() $E^{\circ }:={\left\langle F_p,\gamma \right\rangle }$
,
$E^{\circ }:={\left\langle F_p,\gamma \right\rangle }$
,
![]() ${E^{\circ }_L}:=E^{\circ }\cap E_L$
,
${E^{\circ }_L}:=E^{\circ }\cap E_L$
,
![]() $\lambda \in \mathbb {T}$
,
$\lambda \in \mathbb {T}$
,
![]() $\widetilde {\lambda }$
defined as above,
$\widetilde {\lambda }$
defined as above,
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, and
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, and
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
. Then
$\eta \in \mathrm {Irr}(W(\lambda ))$
. Then
![]() $\eta $
is
$\eta $
is
![]() $\widehat K(\lambda )_{\eta _0}\cap (W\rtimes E^{\circ } _L)$
-stable if and only if it is
$\widehat K(\lambda )_{\eta _0}\cap (W\rtimes E^{\circ } _L)$
-stable if and only if it is
![]() $ K(\lambda )_{\eta _0}$
-stable.
$ K(\lambda )_{\eta _0}$
-stable.
Proof. Note that
![]() $F_p\in \operatorname Z(\widehat W)$
; hence,
$F_p\in \operatorname Z(\widehat W)$
; hence,
![]() $\eta $
and
$\eta $
and
![]() $\eta _0$
are
$\eta _0$
are
![]() $F_p$
-stable. Recall that
$F_p$
-stable. Recall that
![]() $\overline W$
can be identified with the quotient
$\overline W$
can be identified with the quotient
![]() $(\widehat W\cap ( W \rtimes E^{\circ }_L ))/{\left\langle F_p \right\rangle }$
. The group
$(\widehat W\cap ( W \rtimes E^{\circ }_L ))/{\left\langle F_p \right\rangle }$
. The group
![]() $\widehat K(\lambda )\cap (W\rtimes E^{\circ }_L)$
then projects to
$\widehat K(\lambda )\cap (W\rtimes E^{\circ }_L)$
then projects to
![]() $K(\lambda )$
, that is, for every
$K(\lambda )$
, that is, for every
![]() $w\in \overline W$
and
$w\in \overline W$
and
![]() $e\in {\left\langle F_p \right\rangle }$
with
$e\in {\left\langle F_p \right\rangle }$
with
![]() $\lambda ^{we}=\lambda $
, we see
$\lambda ^{we}=\lambda $
, we see
![]() $({\left.\lambda ^{LE^{\circ }_L}\right\rceil _{L}})^w=\lambda $
. This implies
$({\left.\lambda ^{LE^{\circ }_L}\right\rceil _{L}})^w=\lambda $
. This implies
![]() $\widehat K(\lambda ){\left\langle F_p \right\rangle } \cap \overline W= K(\lambda )$
and
$\widehat K(\lambda ){\left\langle F_p \right\rangle } \cap \overline W= K(\lambda )$
and
![]() $\widehat K(\lambda )_{\eta _0}{\left\langle F_p \right\rangle } \cap \overline W= K(\lambda )_{\eta _0}$
. As
$\widehat K(\lambda )_{\eta _0}{\left\langle F_p \right\rangle } \cap \overline W= K(\lambda )_{\eta _0}$
. As
![]() $F_p$
stabilizes
$F_p$
stabilizes
![]() $\eta $
, this implies the statement.
$\eta $
, this implies the statement.
For
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, the group
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, the group
![]() $W(\widetilde {\lambda })$
is determined by
$W(\widetilde {\lambda })$
is determined by
![]() ${\left. \widetilde {\lambda }\right\rceil _{L}}$
, as W acts trivially on the characters of
${\left. \widetilde {\lambda }\right\rceil _{L}}$
, as W acts trivially on the characters of
![]() $\widetilde {L}_{\lambda } /L$
. Note that
$\widetilde {L}_{\lambda } /L$
. Note that
![]() $ W(\widetilde {\lambda })\neq W({\left. \widetilde {\lambda }\right\rceil _{L}})$
in general. We can work with the group
$ W(\widetilde {\lambda })\neq W({\left. \widetilde {\lambda }\right\rceil _{L}})$
in general. We can work with the group
![]() $\widetilde {L}$
instead of
$\widetilde {L}$
instead of
![]() $\widetilde {L}'$
because of the following observation.
$\widetilde {L}'$
because of the following observation.
Lemma 6.6. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
,
$\lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L} \mid \widehat {\lambda })$
.
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L} \mid \widehat {\lambda })$
.
-
(a) Then
 $\overline W(\widetilde {\lambda })=\overline W(\widetilde {\lambda }') {\text { and }} W(\widetilde {\lambda })= W(\widetilde {\lambda }')$
for every
$\overline W(\widetilde {\lambda })=\overline W(\widetilde {\lambda }') {\text { and }} W(\widetilde {\lambda })= W(\widetilde {\lambda }')$
for every
 $\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde {L}' \mid \lambda )$
.
$\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde {L}' \mid \lambda )$
. -
(b) Then
 $\overline W(\widetilde {\lambda })\leq \overline W(\widehat {\lambda }) \leq \overline W(\lambda ) {\text { and }} W(\widetilde {\lambda })\leq W(\widehat {\lambda }) \leq W(\lambda )$
.
$\overline W(\widetilde {\lambda })\leq \overline W(\widehat {\lambda }) \leq \overline W(\lambda ) {\text { and }} W(\widetilde {\lambda })\leq W(\widehat {\lambda }) \leq W(\lambda )$
.
Proof. By the construction of
![]() $\mathbb {T}$
, the character
$\mathbb {T}$
, the character
![]() $\lambda \in \mathbb {T}$
satisfies
$\lambda \in \mathbb {T}$
satisfies
![]() $(\widehat N \widetilde {L})_{\lambda }= \widehat N_{\lambda } \widetilde {L}_{\lambda }$
. Because of
$(\widehat N \widetilde {L})_{\lambda }= \widehat N_{\lambda } \widetilde {L}_{\lambda }$
. Because of
![]() $\widetilde {\mathbf G}=\operatorname Z(\widetilde {\mathbf G}){{\mathbf G}}$
, the group
$\widetilde {\mathbf G}=\operatorname Z(\widetilde {\mathbf G}){{\mathbf G}}$
, the group
![]() $\widetilde {L}'$
is a subgroup of
$\widetilde {L}'$
is a subgroup of
![]() $\widetilde {L} \operatorname Z(\widetilde {\mathbf G})$
and
$\widetilde {L} \operatorname Z(\widetilde {\mathbf G})$
and
![]() $\widetilde {L}'={{\mathbf L}}\cap \widetilde {L} \operatorname Z(\widetilde {\mathbf G})$
. This implies
$\widetilde {L}'={{\mathbf L}}\cap \widetilde {L} \operatorname Z(\widetilde {\mathbf G})$
. This implies
![]() $(NE_L)_{\widetilde {\lambda }}=(NE_L)_{\widetilde {\lambda }'}$
and hence part (a) (see Remark 2.16 for a similar argument).
$(NE_L)_{\widetilde {\lambda }}=(NE_L)_{\widetilde {\lambda }'}$
and hence part (a) (see Remark 2.16 for a similar argument).
As
![]() $h_0$
is centralized by
$h_0$
is centralized by
![]() $\widehat N$
, the group
$\widehat N$
, the group
![]() $\widehat L$
is normalized by N and
$\widehat L$
is normalized by N and
![]() $\overline N$
. The containments from part (b) follow from this by straightforward considerations.
$\overline N$
. The containments from part (b) follow from this by straightforward considerations.
For
![]() $\lambda \in \mathbb {T}$
and
$\lambda \in \mathbb {T}$
and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L} \mid \lambda )$
, we compute
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L} \mid \lambda )$
, we compute
![]() $\overline W(\widetilde {\lambda })$
as an approximation of
$\overline W(\widetilde {\lambda })$
as an approximation of
![]() $W(\widetilde {\lambda })$
. For
$W(\widetilde {\lambda })$
. For
![]() $I\in {\mathcal O}$
and
$I\in {\mathcal O}$
and
![]() $d\in \mathbb D$
, we use the groups
$d\in \mathbb D$
, we use the groups
![]() ${{\mathbf G}}_I$
,
${{\mathbf G}}_I$
,
![]() $L_I$
,
$L_I$
,
![]() $\widehat L_I$
, and
$\widehat L_I$
, and
![]() ${{\mathbf L}}_d$
from Notation 3.9 and Lemmas 3.12 and 3.13. In Lemma 3.13, the structure of
${{\mathbf L}}_d$
from Notation 3.9 and Lemmas 3.12 and 3.13. In Lemma 3.13, the structure of
![]() ${{\mathbf L}}$
and some of its subgroups was already studied. Additionally, we use the following properties of
${{\mathbf L}}$
and some of its subgroups was already studied. Additionally, we use the following properties of
![]() $\widehat L$
.
$\widehat L$
.
Proposition 6.7 (The structure of
 $\widehat L$
)
$\widehat L$
)
For
![]() $d\in \mathbb D$
and
$d\in \mathbb D$
and
![]() $I\in {\mathcal O}$
, let
$I\in {\mathcal O}$
, let
![]() ${\widehat L_d}:=\widehat L\cap {{\mathbf L}}_d$
.
${\widehat L_d}:=\widehat L\cap {{\mathbf L}}_d$
.
-
(a)
 $L_1$
is a split torus of rank
$L_1$
is a split torus of rank
 $|J_1|$
.
$|J_1|$
. -
(b)
 $\widehat L$
is the central product of
$\widehat L$
is the central product of
 $\widehat L_d$
(
$\widehat L_d$
(
 $d\in \mathbb D$
) over
$d\in \mathbb D$
) over
 ${\left\langle h_0\right\rangle }$
.
${\left\langle h_0\right\rangle }$
. -
(c)
 $\widehat L_d$
is the central product of
$\widehat L_d$
is the central product of
 $\widehat L_I$
(
$\widehat L_I$
(
 $I\in {\mathcal O}_d$
) over
$I\in {\mathcal O}_d$
) over
 ${\left\langle h_0\right\rangle }$
.
${\left\langle h_0\right\rangle }$
. -
(d)
 $[\widehat L_I,\widehat L_{I'}]=1$
for all
$[\widehat L_I,\widehat L_{I'}]=1$
for all
 $I,I'\in {\mathcal O}$
with
$I,I'\in {\mathcal O}$
with
 $I\neq I'$
.
$I\neq I'$
.
Proof. The first three parts follow from Lemma 3.13(c).
Part (d) is clear if
![]() $I\in {\mathcal O}_1$
or
$I\in {\mathcal O}_1$
or
![]() $I'\in {\mathcal O}_1$
. Note that the groups
$I'\in {\mathcal O}_1$
. Note that the groups
![]() $\widehat L_I$
and
$\widehat L_I$
and
![]() $\widehat L_{I'}$
contain the root subgroups for
$\widehat L_{I'}$
contain the root subgroups for
![]() $\Phi _I$
and
$\Phi _I$
and
![]() $\Phi _{I'}$
, which are orthogonal to each other. At least one of them is of type
$\Phi _{I'}$
, which are orthogonal to each other. At least one of them is of type
![]() $\mathrm A_l$
. Hence, no nontrivial linear combination of roots from
$\mathrm A_l$
. Hence, no nontrivial linear combination of roots from
![]() $\Phi _I$
and
$\Phi _I$
and
![]() $\Phi _{I'}$
is a root itself. Hence, by Chevalley’s commutator formula, we see that the commutator of the groups is trivial.
$\Phi _{I'}$
is a root itself. Hence, by Chevalley’s commutator formula, we see that the commutator of the groups is trivial.
We continue using the groups
![]() $\overline V_d$
from Lemma 3.21 for the description of
$\overline V_d$
from Lemma 3.21 for the description of
![]() $\overline W(\widehat {\lambda })$
. We write
$\overline W(\widehat {\lambda })$
. We write
![]() ${\mathrm {Irr}_{cusp}(\widehat L)}$
for
${\mathrm {Irr}_{cusp}(\widehat L)}$
for
![]() $\mathrm {Irr}(\widehat L\mid \mathrm {Irr}_{cusp}(L))$
.
$\mathrm {Irr}(\widehat L\mid \mathrm {Irr}_{cusp}(L))$
.
Lemma 6.8 (Characters of
 $\widehat L$
)
$\widehat L$
)
Let
![]() $\widehat {\lambda }\in \mathrm {Irr}_{cusp}(\widehat L)$
,
$\widehat {\lambda }\in \mathrm {Irr}_{cusp}(\widehat L)$
,
![]() $\widehat {\lambda }_d\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_d}}})$
for every
$\widehat {\lambda }_d\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_d}}})$
for every
![]() $d\in \mathbb D$
and
$d\in \mathbb D$
and
![]() $\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
for every
$\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
for every
![]() $I \in {\mathcal O}$
. Then:
$I \in {\mathcal O}$
. Then:
-
(a)
 $\widehat {\lambda } = \odot _{d\in \mathbb D}\widehat {\lambda }_{d} $
and
$\widehat {\lambda } = \odot _{d\in \mathbb D}\widehat {\lambda }_{d} $
and
 $\widehat {\lambda }_d=\odot _{I\in {\mathcal O}_d}\widehat {\lambda }_{I}$
for every
$\widehat {\lambda }_d=\odot _{I\in {\mathcal O}_d}\widehat {\lambda }_{I}$
for every
 $d\in \mathbb D$
,
$d\in \mathbb D$
, -
(b)
 $ \widehat {\lambda }_d \in \mathrm {Irr}_{cusp}(\widehat L_d)$
and
$ \widehat {\lambda }_d \in \mathrm {Irr}_{cusp}(\widehat L_d)$
and
 $ \widehat {\lambda }_I \in \mathrm {Irr}_{cusp}(\widehat L_I)$
,
$ \widehat {\lambda }_I \in \mathrm {Irr}_{cusp}(\widehat L_I)$
, -
(c)
 $\overline W(\widehat {\lambda })$
is the direct product of the groups
$\overline W(\widehat {\lambda })$
is the direct product of the groups
 $ {\overline W_{d}(\widehat {\lambda })}:=(\overline V_d)_{\widehat {\lambda }}/H_d $
(
$ {\overline W_{d}(\widehat {\lambda })}:=(\overline V_d)_{\widehat {\lambda }}/H_d $
(
 $d\in \mathbb D$
), and
$d\in \mathbb D$
), and -
(d)
 $(\overline V_d)_{\widehat {\lambda }}/H_d = (\overline V_d)_{\widehat {\lambda }_d}/H_d$
.
$(\overline V_d)_{\widehat {\lambda }}/H_d = (\overline V_d)_{\widehat {\lambda }_d}/H_d$
.
Proof. The description of
![]() $\widehat {\lambda }$
and
$\widehat {\lambda }$
and
![]() $\widehat {\lambda }_d$
in (a) follows from the structure of
$\widehat {\lambda }_d$
in (a) follows from the structure of
![]() $\widehat L$
and
$\widehat L$
and
![]() $\widehat L_d$
given in Proposition 6.7. The characters
$\widehat L_d$
given in Proposition 6.7. The characters
![]() $\widehat {\lambda }_d$
and
$\widehat {\lambda }_d$
and
![]() $\widehat {\lambda }_I$
cover a cuspidal character of
$\widehat {\lambda }_I$
cover a cuspidal character of
![]() $L_d$
and
$L_d$
and
![]() $L_I$
, respectively, by Lemma 2.15, which then also gives (b). Considering the roots underlying
$L_I$
, respectively, by Lemma 2.15, which then also gives (b). Considering the roots underlying
![]() $V_d$
and
$V_d$
and
![]() ${{\mathbf L}}_{d'}$
, we see that the Chevalley relations imply
${{\mathbf L}}_{d'}$
, we see that the Chevalley relations imply
![]() $[V_d,{{\mathbf L}}_{d'}]=1$
for
$[V_d,{{\mathbf L}}_{d'}]=1$
for
![]() $d,d'\in \mathbb D$
with
$d,d'\in \mathbb D$
with
![]() $d\neq d'$
. This implies the parts (c) and (d).
$d\neq d'$
. This implies the parts (c) and (d).
For a more explicit description of the groups
![]() $\overline W(\widehat {\lambda })$
, we introduce some elements of
$\overline W(\widehat {\lambda })$
, we introduce some elements of
![]() $\overline V$
using the maps
$\overline V$
using the maps
![]() $\kappa _d$
(
$\kappa _d$
(
![]() $d\in \mathbb D$
) from Lemma 3.21. For
$d\in \mathbb D$
) from Lemma 3.21. For
![]() $d\in \mathbb D\setminus \{-1\}$
, recall
$d\in \mathbb D\setminus \{-1\}$
, recall
![]() ${\mathcal O}_d=\{I_{d,1},\ldots , I_{d,a_d}\}$
from Notation 3.17.
${\mathcal O}_d=\{I_{d,1},\ldots , I_{d,a_d}\}$
from Notation 3.17.
Notation 6.9. Let
![]() $d\in \mathbb D\setminus \{-1\}$
and
$d\in \mathbb D\setminus \{-1\}$
and
![]() ${c_{I_{d,j}}}:=\kappa _d(\mathbf {n}_{e_j}(\varpi ))\in \overline V_d$
for every
${c_{I_{d,j}}}:=\kappa _d(\mathbf {n}_{e_j}(\varpi ))\in \overline V_d$
for every
![]() $j\in {\underline {a_d}}$
. Note that for every
$j\in {\underline {a_d}}$
. Note that for every
![]() $I\in {\mathcal O}_d$
,
$I\in {\mathcal O}_d$
,
![]() $c_{I}$
is some
$c_{I}$
is some
![]() $\overline V_d$
-conjugate of
$\overline V_d$
-conjugate of
![]() $\overline {\mathbf {n}}_1^{(d)}$
and
$\overline {\mathbf {n}}_1^{(d)}$
and
![]() $\rho _{{\mathbf T}}(c_I)=\prod _{i\in I}(i,-i)$
, where
$\rho _{{\mathbf T}}(c_I)=\prod _{i\in I}(i,-i)$
, where
![]() $\rho _{{\mathbf T}}: \overline N_0\rightarrow {\mathcal {S}}_{\pm {\underline {l}}}$
is the natural epimorphism (see before Proposition 3.16). If
$\rho _{{\mathbf T}}: \overline N_0\rightarrow {\mathcal {S}}_{\pm {\underline {l}}}$
is the natural epimorphism (see before Proposition 3.16). If
![]() $2\nmid |I|$
and
$2\nmid |I|$
and
![]() $I\notin {\mathcal O}_{-1}\cup {\mathcal O}_1$
, then by considerations as in the proof of Lemma 4.4
(b),
$I\notin {\mathcal O}_{-1}\cup {\mathcal O}_1$
, then by considerations as in the proof of Lemma 4.4
(b),
![]() $c_I$
acts as transpose-inverting on
$c_I$
acts as transpose-inverting on
![]() $L_I$
via the identification of
$L_I$
via the identification of
![]() $L_I$
with
$L_I$
with
![]() $\operatorname {GL}_{|I|}(q)$
.
$\operatorname {GL}_{|I|}(q)$
.
We define additionally the subgroups
and
![]() ${V_S}:={\left\langle \left.V_{d,S} \vphantom {d\in \mathbb D\setminus \{-1\}}\hskip .1em\right.\mid d\in \mathbb D\setminus \{-1\} \right\rangle }$
. Then
${V_S}:={\left\langle \left.V_{d,S} \vphantom {d\in \mathbb D\setminus \{-1\}}\hskip .1em\right.\mid d\in \mathbb D\setminus \{-1\} \right\rangle }$
. Then
![]() $\rho _{{\mathbf T}}(V_S(L\cap N_0))/\rho _{\mathbf T}(L\cap N_0)= {\mathcal {S}}_{{\mathcal O}}\leq {\mathcal {S}}_{\pm {\mathcal O}}$
.
$\rho _{{\mathbf T}}(V_S(L\cap N_0))/\rho _{\mathbf T}(L\cap N_0)= {\mathcal {S}}_{{\mathcal O}}\leq {\mathcal {S}}_{\pm {\mathcal O}}$
.
If
![]() $-1\in \mathbb D$
, then we set
$-1\in \mathbb D$
, then we set
![]() $c_{J_{-1}}:={\overline {\mathbf n}}_1$
from 3.19.
$c_{J_{-1}}:={\overline {\mathbf n}}_1$
from 3.19.
Using the notation of permutation groups given in Notation 3.14, we identify the group
![]() $\overline W=\overline N/L$
with
$\overline W=\overline N/L$
with
![]() ${\mathcal {S}}_{\pm {\mathcal O}}$
. Computations in
${\mathcal {S}}_{\pm {\mathcal O}}$
. Computations in
![]() $\overline W$
show that
$\overline W$
show that
![]() $\overline V=H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle } V_S$
.
$\overline V=H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle } V_S$
.
Definition 6.10. Let
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L)$
. We call
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L)$
. We call
![]() $\widehat {\lambda }$
standardized if for every
$\widehat {\lambda }$
standardized if for every
![]() $I,I'\in {\mathcal O}$
the characters
$I,I'\in {\mathcal O}$
the characters
![]() $\widehat {\lambda }_{I}$
and
$\widehat {\lambda }_{I}$
and
![]() $\widehat {\lambda }_{I'}$
are either
$\widehat {\lambda }_{I'}$
are either
![]() $V_S$
-conjugate or not
$V_S$
-conjugate or not
![]() $\overline V$
-conjugate. For such
$\overline V$
-conjugate. For such
![]() $\widehat {\lambda }$
, we call the characters in
$\widehat {\lambda }$
, we call the characters in
![]() $\mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{L}})$
also standardized.
$\mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{L}})$
also standardized.
Computations show that every standardized character
![]() $\widehat {\lambda }$
satisfies
$\widehat {\lambda }$
satisfies
![]() $\overline V_{\widehat {\lambda }}= H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widehat {\lambda }} (V_S)_{ \widehat {\lambda } } $
and every
$\overline V_{\widehat {\lambda }}= H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widehat {\lambda }} (V_S)_{ \widehat {\lambda } } $
and every
![]() $\overline N$
-orbit in
$\overline N$
-orbit in
![]() $\mathrm {Irr}(\widehat L)$
contains a standardized character. For a more explicit description of
$\mathrm {Irr}(\widehat L)$
contains a standardized character. For a more explicit description of
![]() $\overline W_{d}( \widehat {\lambda })$
, we introduce the following notation.
$\overline W_{d}( \widehat {\lambda })$
, we introduce the following notation.
Notation 6.11. Let E be a set, and let M be a subset of
![]() $2^E$
, the set of all subsets of E. For
$2^E$
, the set of all subsets of E. For
![]() $m'\subseteq E$
, we write
$m'\subseteq E$
, we write
![]() ${m'\subset \subset M}$
if
${m'\subset \subset M}$
if
![]() $m'\subseteq m$
for some
$m'\subseteq m$
for some
![]() $m\in M$
.
$m\in M$
.
Using the notation of permutation groups given in Notation 3.14, we identify the group
![]() $\overline W=\overline N/L$
with
$\overline W=\overline N/L$
with
![]() ${\mathcal {S}}_{\pm {\mathcal O}}$
. In the following, we describe
${\mathcal {S}}_{\pm {\mathcal O}}$
. In the following, we describe
![]() $\overline W_d(\widehat {\lambda }_d)$
as a subgroup of
$\overline W_d(\widehat {\lambda }_d)$
as a subgroup of
![]() ${\mathcal {S}}_{\pm {\mathcal O}_d}$
. We use the Young-like subgroups of
${\mathcal {S}}_{\pm {\mathcal O}_d}$
. We use the Young-like subgroups of
![]() ${\mathcal {S}}_{\pm {\mathcal O}_d}$
from Notation 3.14 that are associated with a partition of
${\mathcal {S}}_{\pm {\mathcal O}_d}$
from Notation 3.14 that are associated with a partition of
![]() ${\mathcal O}_d$
.
${\mathcal O}_d$
.
Lemma 6.12. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
be standardized. We set
$\lambda \in \mathrm {Irr}_{cusp}(L)$
be standardized. We set
Let
![]() ${Y(\widehat {\lambda })} \vdash {\mathcal O}_{c}(\widehat {\lambda })$
and
${Y(\widehat {\lambda })} \vdash {\mathcal O}_{c}(\widehat {\lambda })$
and
![]() $ {Y'(\widehat {\lambda })}\vdash ({\mathcal O}(\widehat {\lambda }) \setminus {\mathcal O}_{c}(\widehat {\lambda }))$
be the partitions such that
$ {Y'(\widehat {\lambda })}\vdash ({\mathcal O}(\widehat {\lambda }) \setminus {\mathcal O}_{c}(\widehat {\lambda }))$
be the partitions such that
![]() $\{I,I'\}\subset \subset Y(\widehat {\lambda })$
or
$\{I,I'\}\subset \subset Y(\widehat {\lambda })$
or
![]() $\{I, I'\}\subset \subset Y'(\widehat {\lambda })$
if and only if
$\{I, I'\}\subset \subset Y'(\widehat {\lambda })$
if and only if
![]() $\widehat {\lambda }_{I}$
and
$\widehat {\lambda }_{I}$
and
![]() $\widehat {\lambda }_{I'}$
are
$\widehat {\lambda }_{I'}$
are
![]() $V_{S}$
-conjugate. Then
$V_{S}$
-conjugate. Then
where
![]() ${\mathcal {Y}}_{\pm Y(\widehat {\lambda })}$
and
${\mathcal {Y}}_{\pm Y(\widehat {\lambda })}$
and
![]() ${\mathcal {Y}}_{Y'(\widehat {\lambda })}$
are defined as in Notation 3.14.
${\mathcal {Y}}_{Y'(\widehat {\lambda })}$
are defined as in Notation 3.14.
Proof. Note
![]() $Y'(\widehat {\lambda })\cup Y(\widehat {\lambda }) \vdash {\mathcal O}$
. As
$Y'(\widehat {\lambda })\cup Y(\widehat {\lambda }) \vdash {\mathcal O}$
. As
![]() $\widehat {\lambda }$
is standardized,
$\widehat {\lambda }$
is standardized,
This gives our claim.
Let
![]() $\zeta \in {\mathbb {F}}^{\times }$
with
$\zeta \in {\mathbb {F}}^{\times }$
with
![]() $\varpi =\zeta ^{(q-1)_2}$
and
$\varpi =\zeta ^{(q-1)_2}$
and
![]() ${t_{I,2}}:= {\mathbf h} _{I}(\zeta )$
for every
${t_{I,2}}:= {\mathbf h} _{I}(\zeta )$
for every
![]() $I \subseteq {\underline {l}}$
as in Lemma 3.13. For
$I \subseteq {\underline {l}}$
as in Lemma 3.13. For
![]() $I\in {\mathcal O}\setminus \{J_{-1}\}$
, the element
$I\in {\mathcal O}\setminus \{J_{-1}\}$
, the element
![]() $t_{I,2}$
satisfies
$t_{I,2}$
satisfies
![]() $[{{\mathbf L}}_I,t_{I,2}]=1$
.
$[{{\mathbf L}}_I,t_{I,2}]=1$
.
Lemma 6.13 (Structure of
 $\overline W(\widetilde {\lambda })$
)
$\overline W(\widetilde {\lambda })$
)
Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
,
$\lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
,
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
,
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
![]() $\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
, and
$\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
, and
![]() $\widetilde {\lambda }_I\in \mathrm {Irr}(\widetilde {L}_I\mid \widehat {\lambda }_I)$
(
$\widetilde {\lambda }_I\in \mathrm {Irr}(\widetilde {L}_I\mid \widehat {\lambda }_I)$
(
![]() $I\in {\mathcal O}_c(\widehat {\lambda })$
). Assume that
$I\in {\mathcal O}_c(\widehat {\lambda })$
). Assume that
![]() $\widehat {\lambda }$
is standardized and
$\widehat {\lambda }$
is standardized and
![]() $\widetilde {L}_{\widehat {\lambda }}=\widetilde {L}$
. We set
$\widetilde {L}_{\widehat {\lambda }}=\widetilde {L}$
. We set
-
(a) For
 $I\in {\mathcal O}_c(\widehat {\lambda })\setminus \{J_{-1}\}$
and
$I\in {\mathcal O}_c(\widehat {\lambda })\setminus \{J_{-1}\}$
and
 ${\epsilon }=\pm 1$
, we have
${\epsilon }=\pm 1$
, we have
 $I \in {\mathcal O}_{c,{\epsilon }} (\widehat {\lambda }) \Leftrightarrow \widehat {\lambda }_I(t_{I,2}^2)= \epsilon \widehat {\lambda }_I(1)$
.
$I \in {\mathcal O}_{c,{\epsilon }} (\widehat {\lambda }) \Leftrightarrow \widehat {\lambda }_I(t_{I,2}^2)= \epsilon \widehat {\lambda }_I(1)$
. -
(b)
 $ \overline W(\widetilde {\lambda })\leq {\mathcal {S}}_{\pm {\mathcal O}_{c,1}(\widehat {\lambda })}\times {\mathcal {S}}^{\mathrm {D}}_{\pm {\mathcal O}_{c,-1}(\widehat {\lambda })}$
, more precisely
$ \overline W(\widetilde {\lambda })\leq {\mathcal {S}}_{\pm {\mathcal O}_{c,1}(\widehat {\lambda })}\times {\mathcal {S}}^{\mathrm {D}}_{\pm {\mathcal O}_{c,-1}(\widehat {\lambda })}$
, more precisely  $$\begin{align*}\overline W(\widetilde{\lambda})= \left({\left\langle\left.(I,-I)\vphantom{I\in {\mathcal O}_{c,1}(\widehat{\lambda})}\hskip.1em\right.\mid I\in {\mathcal O}_{c,1}(\widehat{\lambda}) \right\rangle} {\left\langle\left.(I,-I)(I',-I')\vphantom{I,I'\in {\mathcal O}_{c,-1}(\widehat{\lambda})}\hskip.1em\right.\mid I,I'\in {\mathcal O}_{c,-1}(\widehat{\lambda}) \right\rangle}\right) \rtimes {\mathcal{Y}}_{Y(\widehat{\lambda})\cup Y'(\widehat{\lambda})}.\end{align*}$$
$$\begin{align*}\overline W(\widetilde{\lambda})= \left({\left\langle\left.(I,-I)\vphantom{I\in {\mathcal O}_{c,1}(\widehat{\lambda})}\hskip.1em\right.\mid I\in {\mathcal O}_{c,1}(\widehat{\lambda}) \right\rangle} {\left\langle\left.(I,-I)(I',-I')\vphantom{I,I'\in {\mathcal O}_{c,-1}(\widehat{\lambda})}\hskip.1em\right.\mid I,I'\in {\mathcal O}_{c,-1}(\widehat{\lambda}) \right\rangle}\right) \rtimes {\mathcal{Y}}_{Y(\widehat{\lambda})\cup Y'(\widehat{\lambda})}.\end{align*}$$
If the character
![]() $\widehat {\lambda }$
is clear from the context, we write
$\widehat {\lambda }$
is clear from the context, we write
![]() ${{\mathcal O}_{c,\epsilon }}$
instead of
${{\mathcal O}_{c,\epsilon }}$
instead of
![]() ${\mathcal O}_{c,{\epsilon }}(\widehat {\lambda })$
.
${\mathcal O}_{c,{\epsilon }}(\widehat {\lambda })$
.
Proof. Note that the description of
![]() $\widetilde {L}$
given in Lemma 3.13(e) shows that
$\widetilde {L}$
given in Lemma 3.13(e) shows that
![]() $\widehat {\lambda }$
extends to
$\widehat {\lambda }$
extends to
![]() $\widetilde {L}$
if and only if
$\widetilde {L}$
if and only if
![]() $\widehat {\lambda }_I$
extends to
$\widehat {\lambda }_I$
extends to
![]() $\widetilde {L}_I:=\widehat L_I{\left\langle t_{I,2}\right\rangle }$
for every
$\widetilde {L}_I:=\widehat L_I{\left\langle t_{I,2}\right\rangle }$
for every
![]() $I\in {\mathcal O}$
.
$I\in {\mathcal O}$
.
We have
![]() $t_{{\underline {l}},2}:=\prod _{I\in {\mathcal O}} t_{I,2}$
,
$t_{{\underline {l}},2}:=\prod _{I\in {\mathcal O}} t_{I,2}$
,
![]() $\mathcal L(t_{{\underline {l}},2})= {\mathbf h} _{\underline l}(\varpi )$
, and
$\mathcal L(t_{{\underline {l}},2})= {\mathbf h} _{\underline l}(\varpi )$
, and
![]() $\widetilde {L}={\left\langle \widehat L, t_{{\underline {l}},2}\right\rangle }$
(see Lemma 3.13). This implies
$\widetilde {L}={\left\langle \widehat L, t_{{\underline {l}},2}\right\rangle }$
(see Lemma 3.13). This implies
![]() $\widetilde {L}\leq {\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle }$
. By the Chevalley relations, we see
$\widetilde {L}\leq {\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle }$
. By the Chevalley relations, we see
![]() $[V_{S},t_{{\underline {l}},2}]=1$
. Let
$[V_{S},t_{{\underline {l}},2}]=1$
. Let
![]() $I,I'\in {\mathcal O}$
such that
$I,I'\in {\mathcal O}$
such that
![]() $\widehat {\lambda }_I$
and
$\widehat {\lambda }_I$
and
![]() $\widehat {\lambda }_{I'}$
are
$\widehat {\lambda }_{I'}$
are
![]() $V_S$
-conjugate. Then we can choose their extensions
$V_S$
-conjugate. Then we can choose their extensions
![]() $\widetilde {\lambda }_I$
and
$\widetilde {\lambda }_I$
and
![]() $\widetilde {\lambda }_{I'}$
to
$\widetilde {\lambda }_{I'}$
to
![]() $\widetilde {L}_I$
and
$\widetilde {L}_I$
and
![]() $\widetilde {L}_{I'}$
such that they are
$\widetilde {L}_{I'}$
such that they are
![]() $V_S$
-conjugate, as
$V_S$
-conjugate, as
![]() ${\mathrm {N}}_{V_S}(\widehat L_I)= H {\mathrm {C}}_{V_S}(\widehat L_I)$
, and therefore
${\mathrm {N}}_{V_S}(\widehat L_I)= H {\mathrm {C}}_{V_S}(\widehat L_I)$
, and therefore
![]() $\widetilde {\lambda }_{I'}$
is uniquely determined by
$\widetilde {\lambda }_{I'}$
is uniquely determined by
![]() $\widetilde {\lambda }_{I}$
.
$\widetilde {\lambda }_{I}$
.
Let
![]() $\phi \in \mathrm {Irr}({\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle })$
with
$\phi \in \mathrm {Irr}({\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle })$
with
![]() ${\left. \phi \right\rceil _{{\widetilde {L}_I}}} =\widetilde {\lambda }_I$
for every
${\left. \phi \right\rceil _{{\widetilde {L}_I}}} =\widetilde {\lambda }_I$
for every
![]() $I\in {\mathcal O}$
. Without loss of generality, we may assume
$I\in {\mathcal O}$
. Without loss of generality, we may assume
![]() ${\left.\phi \right\rceil _{{\widetilde {L}}}}=\widetilde {\lambda }$
. By the above construction, we have
${\left.\phi \right\rceil _{{\widetilde {L}}}}=\widetilde {\lambda }$
. By the above construction, we have
![]() $(V_S)_{\phi }=(V_S)_{\widehat {\lambda }}$
. Because of
$(V_S)_{\phi }=(V_S)_{\widehat {\lambda }}$
. Because of
![]() $\overline V_{\widehat {\lambda }}=H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widehat {\lambda }} (V_S)_{\widehat {\lambda }}$
, it is sufficient to determine
$\overline V_{\widehat {\lambda }}=H {\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widehat {\lambda }} (V_S)_{\widehat {\lambda }}$
, it is sufficient to determine
![]() ${\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widetilde {\lambda }}$
for computing
${\left\langle c_I\mid I \in {\mathcal O}\right\rangle }_{\widetilde {\lambda }}$
for computing
![]() $\overline V_{\widetilde {\lambda }}$
.
$\overline V_{\widetilde {\lambda }}$
.
Let
![]() $\mu _I\in \mathrm {Irr}(\widetilde {L}_I)$
be the linear character with
$\mu _I\in \mathrm {Irr}(\widetilde {L}_I)$
be the linear character with
![]() $\ker (\mu _I)= \widehat L_I$
. For any
$\ker (\mu _I)= \widehat L_I$
. For any
![]() $Q \subseteq {\mathcal O}$
, let
$Q \subseteq {\mathcal O}$
, let
![]() $\mu _{Q}\in \mathrm {Irr}({\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle })$
be the linear character with
$\mu _{Q}\in \mathrm {Irr}({\left\langle \widetilde {L}_I\mid I \in {\mathcal O}\right\rangle })$
be the linear character with
![]() ${\left\langle L_I\mid I \in {\mathcal O}\right\rangle } \leq \ker (\mu _Q)$
such that for every
${\left\langle L_I\mid I \in {\mathcal O}\right\rangle } \leq \ker (\mu _Q)$
such that for every
![]() $I\in {\mathcal O}$
, the inclusion
$I\in {\mathcal O}$
, the inclusion
![]() $\widetilde {L}_I\leq \ker (\mu _{Q })$
holds if and only if
$\widetilde {L}_I\leq \ker (\mu _{Q })$
holds if and only if
![]() $I \notin Q$
. Note that
$I \notin Q$
. Note that
![]() $\mu _{Q}(t_{{\underline {l}},2})=1$
if and only if
$\mu _{Q}(t_{{\underline {l}},2})=1$
if and only if
![]() $|Q|$
is even.
$|Q|$
is even.
For
![]() $Q \subseteq {\mathcal O}$
, let
$Q \subseteq {\mathcal O}$
, let
![]() $c_{Q }:=\prod _{I\in {Q }} c_I\in \overline V$
. If
$c_{Q }:=\prod _{I\in {Q }} c_I\in \overline V$
. If
![]() $Q'\subseteq {\mathcal O}_c(\widehat {\lambda })$
, then
$Q'\subseteq {\mathcal O}_c(\widehat {\lambda })$
, then
![]() $c_{Q'}\in \overline V_{\widehat {\lambda }}$
and we see that
$c_{Q'}\in \overline V_{\widehat {\lambda }}$
and we see that
![]() $\phi ^{c_{Q'}}= \phi \mu _{Q' \cap {\mathcal O}_{c,-1}}$
. As
$\phi ^{c_{Q'}}= \phi \mu _{Q' \cap {\mathcal O}_{c,-1}}$
. As
![]() $\mu _{{Q'} \cap {\mathcal O}_{c,-1}} ( t_{{\underline {l}},2} )= (-1)^{|{Q' \cap {\mathcal O}_{c,-1}}|}$
, this leads to a proof of part (b), in particular
$\mu _{{Q'} \cap {\mathcal O}_{c,-1}} ( t_{{\underline {l}},2} )= (-1)^{|{Q' \cap {\mathcal O}_{c,-1}}|}$
, this leads to a proof of part (b), in particular
Let
![]() $I\in {\mathcal O}_c(\widehat {\lambda })\setminus \{J_{-1}\}$
. Then
$I\in {\mathcal O}_c(\widehat {\lambda })\setminus \{J_{-1}\}$
. Then
![]() $c_I$
acts by inverting on
$c_I$
acts by inverting on
![]() ${\mathbf T}_I$
, in particular
${\mathbf T}_I$
, in particular
![]() $t_{I,2}^{c_I}=t_{I,2}^{-1}$
and
$t_{I,2}^{c_I}=t_{I,2}^{-1}$
and
![]() $[c_I,t_{I,2}]=t_{I,2}^{-2}$
. Because of
$[c_I,t_{I,2}]=t_{I,2}^{-2}$
. Because of
![]() $t_{I,2}\in \operatorname Z({{\mathbf L}}_I)$
, we see that
$t_{I,2}\in \operatorname Z({{\mathbf L}}_I)$
, we see that
![]() $[t_{\underline {l}},\overline V_d] \subseteq \operatorname Z({{\mathbf L}})$
. Any extension
$[t_{\underline {l}},\overline V_d] \subseteq \operatorname Z({{\mathbf L}})$
. Any extension
![]() $\widetilde {\lambda }_I$
of
$\widetilde {\lambda }_I$
of
![]() $\widehat {\lambda }_I$
to
$\widehat {\lambda }_I$
to
![]() ${\left\langle \widehat L_I,t_{I,2}\right\rangle }$
satisfies
${\left\langle \widehat L_I,t_{I,2}\right\rangle }$
satisfies
![]() $\widetilde {\lambda }_I(t_{I,2})\neq 0$
since
$\widetilde {\lambda }_I(t_{I,2})\neq 0$
since
![]() $t_{I,2} \in \operatorname Z(\widetilde {L}_I)$
.
$t_{I,2} \in \operatorname Z(\widetilde {L}_I)$
.
Note that
![]() $\nu _I\in \mathrm {Irr}({\left.\widetilde {\lambda }\right\rceil _{{\operatorname Z(\widehat L_I)}}})$
is linear. As
$\nu _I\in \mathrm {Irr}({\left.\widetilde {\lambda }\right\rceil _{{\operatorname Z(\widehat L_I)}}})$
is linear. As
![]() $\widehat {\lambda }_I$
is
$\widehat {\lambda }_I$
is
![]() $c_I$
-stable,
$c_I$
-stable,
![]() $\nu _I$
has multiplicative order
$\nu _I$
has multiplicative order
![]() $1$
or
$1$
or
![]() $2$
. We observe that
$2$
. We observe that
![]() $t_{I,2}^{c_I}= t_{I,2}^{-1}\in \operatorname Z(\widetilde {L}_I)$
and hence
$t_{I,2}^{c_I}= t_{I,2}^{-1}\in \operatorname Z(\widetilde {L}_I)$
and hence
Accordingly,
![]() $\widetilde {\lambda }_I$
is
$\widetilde {\lambda }_I$
is
![]() $c_I$
-invariant if and only if
$c_I$
-invariant if and only if
![]() $[c_I,t_{I,2}] \in \ker (\nu _I)= \ker (\widehat {\lambda })\cap \operatorname Z( \widehat L_I )$
. This proves (a).
$[c_I,t_{I,2}] \in \ker (\nu _I)= \ker (\widehat {\lambda })\cap \operatorname Z( \widehat L_I )$
. This proves (a).
The group
![]() $W(\lambda )$
is then generated by
$W(\lambda )$
is then generated by
![]() $W(\widehat {\lambda })$
and an element that is described below.
$W(\widehat {\lambda })$
and an element that is described below.
Lemma 6.14. Let
![]() $\mu \in \mathrm {Irr}(\widehat L)$
with
$\mu \in \mathrm {Irr}(\widehat L)$
with
![]() $\ker (\mu )=L$
and
$\ker (\mu )=L$
and
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L)$
. Additionally, for every
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L)$
. Additionally, for every
![]() $I\in {\mathcal O}$
, let
$I\in {\mathcal O}$
, let
![]() $\mu _I\in \mathrm {Irr}(\widehat L_I)$
with
$\mu _I\in \mathrm {Irr}(\widehat L_I)$
with
![]() $\ker (\mu _I)=L_I$
,
$\ker (\mu _I)=L_I$
,
![]() $\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
and
$\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
and
![]() $\lambda _I\in \mathrm {Irr}({\left.\widehat {\lambda }_I\right\rceil _{{L_I}}})$
.
$\lambda _I\in \mathrm {Irr}({\left.\widehat {\lambda }_I\right\rceil _{{L_I}}})$
.
-
(a) Let
 $x\in \overline W\setminus \overline W(\widehat {\lambda })$
and
$x\in \overline W\setminus \overline W(\widehat {\lambda })$
and
 $\lambda \in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{L}}})$
. Then
$\lambda \in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{L}}})$
. Then
 $x\in \overline W(\lambda )$
if and only if, for every
$x\in \overline W(\lambda )$
if and only if, for every
 $I\in {\mathcal O}$
, the equality
$I\in {\mathcal O}$
, the equality
 $(\widehat {\lambda }_I)^x=\widehat {\lambda }_{I'}\mu _{I'}$
holds, where
$(\widehat {\lambda }_I)^x=\widehat {\lambda }_{I'}\mu _{I'}$
holds, where
 $I'\in {\mathcal O}$
with
$I'\in {\mathcal O}$
with
 $(\widehat L_I)^x=\widehat L_{I'}$
.
$(\widehat L_I)^x=\widehat L_{I'}$
. -
(b) We set
 ${\mathcal O}_{ext}:=\{ I \in {\mathcal O} \mid {\left. \widehat {\lambda }_I\right\rceil _{{L_I}}} = \lambda _I \}$
and
${\mathcal O}_{ext}:=\{ I \in {\mathcal O} \mid {\left. \widehat {\lambda }_I\right\rceil _{{L_I}}} = \lambda _I \}$
and
 ${\mathcal O}_{ind}:= {\mathcal O}\setminus {\mathcal O}_{ext}$
. Then
${\mathcal O}_{ind}:= {\mathcal O}\setminus {\mathcal O}_{ext}$
. Then
 $W(\lambda )$
stabilizes
$W(\lambda )$
stabilizes
 ${\mathcal O}_{ext}$
and
${\mathcal O}_{ext}$
and
 ${\mathcal O}_{ind}$
.
${\mathcal O}_{ind}$
.
Proof. Since
![]() $\widehat L/L$
has order 2, we see that
$\widehat L/L$
has order 2, we see that
![]() $\mu _{{\mathcal O}}$
, the product of the characters
$\mu _{{\mathcal O}}$
, the product of the characters
![]() $\widehat {\mu }_I$
(
$\widehat {\mu }_I$
(
![]() $I\in {\mathcal O}$
) defined as in the proof of Lemma 6.13, is an extension of
$I\in {\mathcal O}$
) defined as in the proof of Lemma 6.13, is an extension of
![]() $\mu $
. This implies part (a).
$\mu $
. This implies part (a).
For part (b), we observe that for
![]() $I\in {\mathcal O}$
,
$I\in {\mathcal O}$
,
![]() $\sigma \in W(\lambda )$
and
$\sigma \in W(\lambda )$
and
![]() $I':=\sigma ^{-1}(I)$
the characters
$I':=\sigma ^{-1}(I)$
the characters
![]() ${\left. \widehat {\lambda }_I\right\rceil _{{L_I}}}$
and
${\left. \widehat {\lambda }_I\right\rceil _{{L_I}}}$
and
![]() ${\left. (\widehat {\lambda }_I)^{\sigma }\right\rceil _{{L_{I'}}}} ={\left. \widehat {\lambda }_{I'}\mu _{I'}\right\rceil _{{L_{I'}}}}$
have the same number of constituents. This proves part (b) since
${\left. (\widehat {\lambda }_I)^{\sigma }\right\rceil _{{L_{I'}}}} ={\left. \widehat {\lambda }_{I'}\mu _{I'}\right\rceil _{{L_{I'}}}}$
have the same number of constituents. This proves part (b) since
![]() $I\in {\mathcal O}_{ind}$
if and only if
$I\in {\mathcal O}_{ind}$
if and only if
![]() ${\left. \widehat {\lambda }_I\right\rceil _{{L_I}}}$
is reducible.
${\left. \widehat {\lambda }_I\right\rceil _{{L_I}}}$
is reducible.
6.2 Cuspidal characters of
 $L_I$
$L_I$
The aim here is to describe the structure of
![]() $\overline W(\widetilde {\lambda })$
by analyzing
$\overline W(\widetilde {\lambda })$
by analyzing
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda }) $
(see Lemma 6.13). We show in this section that for some
${\mathcal O}_{c,-1}(\widehat {\lambda }) $
(see Lemma 6.13). We show in this section that for some
![]() $I\in {\mathcal O}$
there exist no or only few
$I\in {\mathcal O}$
there exist no or only few
![]() $c_I$
-stable cuspidal characters of
$c_I$
-stable cuspidal characters of
![]() $L_I$
and study the kernel of those characters (see Corollary 6.22).
$L_I$
and study the kernel of those characters (see Corollary 6.22).
For
![]() $I\in {\mathcal O}$
, let
$I\in {\mathcal O}$
, let
![]() ${\mathrm {Irr}_{cusp}(\widehat L_I)}:=\mathrm {Irr}(\widehat L_I\mid \mathrm {Irr}_{cusp}(L_I))$
and call those characters cuspidal as well.
${\mathrm {Irr}_{cusp}(\widehat L_I)}:=\mathrm {Irr}(\widehat L_I\mid \mathrm {Irr}_{cusp}(L_I))$
and call those characters cuspidal as well.
Lemma 6.15. Let
![]() $I\in {\mathcal O}_d$
for some
$I\in {\mathcal O}_d$
for some
![]() $d\in \mathbb D_{\mathrm {odd}}\setminus \{\pm 1\}$
. There exists no
$d\in \mathbb D_{\mathrm {odd}}\setminus \{\pm 1\}$
. There exists no
![]() $c_I$
-stable character in
$c_I$
-stable character in
![]() $\mathrm {Irr}_{cusp}(\widehat L_I)$
.
$\mathrm {Irr}_{cusp}(\widehat L_I)$
.
Proof. According to Lemma 4.2(c),
![]() $L_I\cong \operatorname {GL}_d(q)$
and the element
$L_I\cong \operatorname {GL}_d(q)$
and the element
![]() $c_I$
defined in Notation 6.9 induces on
$c_I$
defined in Notation 6.9 induces on
![]() $G_I$
a combination of an inner automorphism and the nontrivial graph automorphism according to Lemma 4.4
(b). The element
$G_I$
a combination of an inner automorphism and the nontrivial graph automorphism according to Lemma 4.4
(b). The element
![]() $c_I$
acts on the torus
$c_I$
acts on the torus
![]() ${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
from Lemma 4.2 by inverting. Hence, via the isomorphism
${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
from Lemma 4.2 by inverting. Hence, via the isomorphism
![]() $L_I \cong \operatorname {GL}_d(q)$
, the element
$L_I \cong \operatorname {GL}_d(q)$
, the element
![]() $c_I$
induces on
$c_I$
induces on
![]() $L_I$
a combination of an inner automorphism and the nontrivial graph automorphism.
$L_I$
a combination of an inner automorphism and the nontrivial graph automorphism.
According to Proposition 5.1(a), there is no cuspidal character of
![]() $\operatorname {GL}_d(q)$
that is invariant under transpose-inverse. So no character in
$\operatorname {GL}_d(q)$
that is invariant under transpose-inverse. So no character in
![]() $\mathrm {Irr}_{cusp}(L_I)$
is
$\mathrm {Irr}_{cusp}(L_I)$
is
![]() $c_I$
-stable. Now, the element
$c_I$
-stable. Now, the element
![]() $t_I$
from Lemma 3.13 can be chosen such that
$t_I$
from Lemma 3.13 can be chosen such that
![]() $[t_I,{{\mathbf L}}_I]=1$
(see Lemma 4.3). This implies that every cuspidal character of
$[t_I,{{\mathbf L}}_I]=1$
(see Lemma 4.3). This implies that every cuspidal character of
![]() $\widehat L_I$
is an extension of a cuspidal character of
$\widehat L_I$
is an extension of a cuspidal character of
![]() $L_I$
. This proves that there is no
$L_I$
. This proves that there is no
![]() $c_I$
-stable character in
$c_I$
-stable character in
![]() $\mathrm {Irr}_{cusp}(\widehat L_I)$
.
$\mathrm {Irr}_{cusp}(\widehat L_I)$
.
With the following statement, the above shows that
![]() ${\mathcal O}_{c,1}(\widehat {\lambda })\cap {\mathcal O}_d=\emptyset $
for every
${\mathcal O}_{c,1}(\widehat {\lambda })\cap {\mathcal O}_d=\emptyset $
for every
![]() $d\in \mathbb D\setminus \{\pm 1\}$
and
$d\in \mathbb D\setminus \{\pm 1\}$
and
![]() $\widehat {\lambda }\in \mathrm {Irr}_{cusp}(\widehat L)$
with
$\widehat {\lambda }\in \mathrm {Irr}_{cusp}(\widehat L)$
with
![]() $h_0\in \ker (\widehat {\lambda })$
.
$h_0\in \ker (\widehat {\lambda })$
.
Proposition 6.16. Let
![]() $I\in {\mathcal O}_d$
for some
$I\in {\mathcal O}_d$
for some
![]() $d\in \mathbb D\setminus \{\pm 1\}$
. Then every
$d\in \mathbb D\setminus \{\pm 1\}$
. Then every
![]() $\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid 1_{{\left\langle h_0\right\rangle }})$
with
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid 1_{{\left\langle h_0\right\rangle }})$
with
![]() $\psi ^{c_I}=\psi $
satisfies
$\psi ^{c_I}=\psi $
satisfies
![]() ${\mathbf Z}_I^F\leq \ker (\psi )$
, where
${\mathbf Z}_I^F\leq \ker (\psi )$
, where
![]() ${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
is as in Lemma 4.2.
${\mathbf Z}_I:={\mathbf h} _I({\mathbb {F}}^{\times })$
is as in Lemma 4.2.
Proof. Under the isomorphism
![]() ${{\mathbf L}}_I/{\left\langle h_0\right\rangle }\cong \operatorname {GL}_d({\mathbb {F}})$
from Lemma 4.2, we obtain
${{\mathbf L}}_I/{\left\langle h_0\right\rangle }\cong \operatorname {GL}_d({\mathbb {F}})$
from Lemma 4.2, we obtain
![]() $\widehat L_I/{\left\langle h_0\right\rangle } \cong \operatorname {GL}_d(q)$
. Via this isomorphism,
$\widehat L_I/{\left\langle h_0\right\rangle } \cong \operatorname {GL}_d(q)$
. Via this isomorphism,
![]() ${\mathbf Z}_I^F$
is mapped to
${\mathbf Z}_I^F$
is mapped to
![]() $\operatorname Z(\operatorname {GL}_d(q))$
. Let
$\operatorname Z(\operatorname {GL}_d(q))$
. Let
![]() $\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid 1_{{\left\langle h_0\right\rangle }})$
. If
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid 1_{{\left\langle h_0\right\rangle }})$
. If
![]() $\psi $
is
$\psi $
is
![]() $c_I$
-invariant, then it corresponds to a cuspidal character of
$c_I$
-invariant, then it corresponds to a cuspidal character of
![]() $\operatorname {GL}_d(q)$
that is invariant under transpose-inverse (see Lemma 4.4
(b)). According to Proposition 5.1(a), such a character is trivial on the center. This implies
$\operatorname {GL}_d(q)$
that is invariant under transpose-inverse (see Lemma 4.4
(b)). According to Proposition 5.1(a), such a character is trivial on the center. This implies
![]() ${\mathbf Z}_I^F\leq \ker (\psi )$
.
${\mathbf Z}_I^F\leq \ker (\psi )$
.
Theorem 6.17. Let
![]() $\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial,
$\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial,
![]() $d\in \mathbb D_{{\mathrm {even}}}$
,
$d\in \mathbb D_{{\mathrm {even}}}$
,
![]() $I\in {\mathcal O}_d$
, and let
$I\in {\mathcal O}_d$
, and let
![]() $t_{I,2}$
be as defined before Lemma 6.13.
$t_{I,2}$
be as defined before Lemma 6.13.
-
(a) If
 $d\geq 4$
, every
$d\geq 4$
, every
 $\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
 $\psi ^{c_I}=\psi $
satisfies
$\psi ^{c_I}=\psi $
satisfies
 $t_{I,2}^2\in \ker (\psi )$
.
$t_{I,2}^2\in \ker (\psi )$
. -
(b) If
 $d=2$
and
$d=2$
and
 $4\mid (q-1)$
, there is a unique
$4\mid (q-1)$
, there is a unique
 $\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
 $\psi ^{c_I}=\psi $
and
$\psi ^{c_I}=\psi $
and
 $t_{I,2}^2\notin \ker (\psi )$
.
$t_{I,2}^2\notin \ker (\psi )$
.
The proof goes through the next three lemmas. We keep
![]() $\nu $
the nontrivial irreducible character of
$\nu $
the nontrivial irreducible character of
![]() ${\left\langle h_0\right\rangle }$
. As a first step toward a proof of the above, we determine the inertia group in
${\left\langle h_0\right\rangle }$
. As a first step toward a proof of the above, we determine the inertia group in
![]() $\widehat L_I$
of cuspidal
$\widehat L_I$
of cuspidal
![]() $c_I$
-stable characters of
$c_I$
-stable characters of
![]() $L_I$
.
$L_I$
.
Lemma 6.18. Let
![]() $d\in \mathbb D_{{\mathrm {even}}}$
,
$d\in \mathbb D_{{\mathrm {even}}}$
,
![]() $I\in {\mathcal O}_d$
,
$I\in {\mathcal O}_d$
,
![]() $\psi \in \mathrm {Irr}_{cusp}(L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}(L_I\mid \nu )$
with
![]() $\psi ^{c_I}=\psi $
, and
$\psi ^{c_I}=\psi $
, and
![]() $t_{I,2}^2\notin \ker (\psi )$
. Then
$t_{I,2}^2\notin \ker (\psi )$
. Then
![]() $(\widehat L_I) _{\psi }=L_I$
.
$(\widehat L_I) _{\psi }=L_I$
.
Proof. For the proof, it is sufficient to show that a character
![]() $\psi $
with the above properties and
$\psi $
with the above properties and
![]() $(\widehat L_I)_{\psi }=\widehat L_{I}$
cannot exist. Recall
$(\widehat L_I)_{\psi }=\widehat L_{I}$
cannot exist. Recall
![]() $t_{I,2}^2={\mathbf h} _I(\zeta ')$
, where
$t_{I,2}^2={\mathbf h} _I(\zeta ')$
, where
![]() $\zeta '\in {\mathbb {F}}^{\times }$
is a root of unity of order
$\zeta '\in {\mathbb {F}}^{\times }$
is a root of unity of order
![]() $2(q-1)_2$
.
$2(q-1)_2$
.
Let
![]() ${{\mathbf G}}':=\mathrm {D}_{2d,sc}({\mathbb {F}})$
with an
${{\mathbf G}}':=\mathrm {D}_{2d,sc}({\mathbb {F}})$
with an
![]() ${\mathbb {F}}_q$
-structure given by a standard Frobenius endomorphism
${\mathbb {F}}_q$
-structure given by a standard Frobenius endomorphism
![]() $F_1: {{\mathbf G}}'\rightarrow {{\mathbf G}}'$
. Let
$F_1: {{\mathbf G}}'\rightarrow {{\mathbf G}}'$
. Let
![]() ${{\mathbf L}}'$
be the Levi subgroup of
${{\mathbf L}}'$
be the Levi subgroup of
![]() ${{\mathbf G}}'$
of type
${{\mathbf G}}'$
of type
![]() $\mathrm A_{d-1}\times \mathrm A_{d-1}$
such that
$\mathrm A_{d-1}\times \mathrm A_{d-1}$
such that
![]() ${\mathcal O}({{\mathbf L}}')={\mathcal O}_d({{\mathbf L}}')= \{I_1,I_2\}$
be defined by
${\mathcal O}({{\mathbf L}}')={\mathcal O}_d({{\mathbf L}}')= \{I_1,I_2\}$
be defined by
![]() ${{\mathbf L}}'$
as in 3.8. Then
${{\mathbf L}}'$
as in 3.8. Then
![]() $\psi $
defines cuspidal characters
$\psi $
defines cuspidal characters
![]() $\lambda _{I_1}\in \mathrm {Irr}_{cusp}(L_{I_1})$
and
$\lambda _{I_1}\in \mathrm {Irr}_{cusp}(L_{I_1})$
and
![]() $\lambda _{I_2}\in \mathrm {Irr}_{cusp}(L_{I_2})$
that have extensions to
$\lambda _{I_2}\in \mathrm {Irr}_{cusp}(L_{I_2})$
that have extensions to
![]() $\widehat L_{I_1}$
and
$\widehat L_{I_1}$
and
![]() $\widehat L_{I_2}$
and are
$\widehat L_{I_2}$
and are
![]() $V_S'$
-stable, where
$V_S'$
-stable, where
![]() $V^{\prime }_S$
is associated with
$V^{\prime }_S$
is associated with
![]() ${{\mathbf G}}'$
and
${{\mathbf G}}'$
and
![]() ${{\mathbf L}}'$
as in Definition 6.10. We can choose
${{\mathbf L}}'$
as in Definition 6.10. We can choose
![]() $\widehat {\lambda }_{I_j}\in \mathrm {Irr}(\widehat L_{I_j}\mid \lambda _{I_j})$
(
$\widehat {\lambda }_{I_j}\in \mathrm {Irr}(\widehat L_{I_j}\mid \lambda _{I_j})$
(
![]() $j=1,2$
) such that they are not
$j=1,2$
) such that they are not
![]() $V^{\prime }_S$
-conjugate. The group
$V^{\prime }_S$
-conjugate. The group
![]() $\widehat L':=\widehat L_{I_1}.\widehat L_{I_2}$
is a central product of the groups
$\widehat L':=\widehat L_{I_1}.\widehat L_{I_2}$
is a central product of the groups
![]() $\widehat L_{I_j}$
(
$\widehat L_{I_j}$
(
![]() $j\in \underline 2$
) over
$j\in \underline 2$
) over
![]() ${\left\langle h_0\right\rangle }$
. Let
${\left\langle h_0\right\rangle }$
. Let
![]() $\widehat {\lambda }':=\widehat {\lambda }_{I_1}\ .\ \widehat {\lambda }_{I_2}\in \mathrm {Irr}(\widehat L')$
,
$\widehat {\lambda }':=\widehat {\lambda }_{I_1}\ .\ \widehat {\lambda }_{I_2}\in \mathrm {Irr}(\widehat L')$
,
![]() $\lambda '={\left. \widehat {\lambda }'\right\rceil _{{L'}}}$
and
$\lambda '={\left. \widehat {\lambda }'\right\rceil _{{L'}}}$
and
![]() $\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde {L}'\mid \widehat {\lambda }')$
where
$\widetilde {\lambda }'\in \mathrm {Irr}(\widetilde {L}'\mid \widehat {\lambda }')$
where
![]() $L':=({{\mathbf L}}')^F$
,
$L':=({{\mathbf L}}')^F$
,
![]() $\widehat L':={\mathcal L'}^{-1}({\left\langle h_0\right\rangle })\cap {{\mathbf L}}'$
and
$\widehat L':={\mathcal L'}^{-1}({\left\langle h_0\right\rangle })\cap {{\mathbf L}}'$
and
![]() $\widetilde {L}':=\mathcal L '{}^{-1}(\operatorname Z({{\mathbf G}}'))\cap {{\mathbf L}}'$
for the Lang map
$\widetilde {L}':=\mathcal L '{}^{-1}(\operatorname Z({{\mathbf G}}'))\cap {{\mathbf L}}'$
for the Lang map
![]() $\mathcal L '\colon x\mapsto x^{-1}F'(x)$
of
$\mathcal L '\colon x\mapsto x^{-1}F'(x)$
of
![]() ${{\mathbf G}} '$
.
${{\mathbf G}} '$
.
Defining W,
![]() $\overline W$
from the above for
$\overline W$
from the above for
![]() ${{\mathbf G}} '$
and
${{\mathbf G}} '$
and
![]() ${{\mathbf L}} '$
, note that
${{\mathbf L}} '$
, note that
![]() $ W(\widehat {\lambda }')=\overline W(\widehat {\lambda }')={\left\langle (I_1,-I_1), (I_2,-I_2)\right\rangle }$
and
$ W(\widehat {\lambda }')=\overline W(\widehat {\lambda }')={\left\langle (I_1,-I_1), (I_2,-I_2)\right\rangle }$
and
![]() $W(\lambda ')=\overline W(\lambda ') ={\mathcal {S}}_{\pm {\mathcal O}({{\mathbf L}}')}$
. Note also that
$W(\lambda ')=\overline W(\lambda ') ={\mathcal {S}}_{\pm {\mathcal O}({{\mathbf L}}')}$
. Note also that
![]() $W(\widetilde {\lambda }') = {\left\langle (I_1,-I_1) (I_2,-I_2)\right\rangle }\leq \operatorname Z(W(\lambda '))= [W(\lambda '), W(\lambda ')]$
.
$W(\widetilde {\lambda }') = {\left\langle (I_1,-I_1) (I_2,-I_2)\right\rangle }\leq \operatorname Z(W(\lambda '))= [W(\lambda '), W(\lambda ')]$
.
Now, observe that the nontrivial character of
![]() $W(\widetilde {\lambda }')$
is
$W(\widetilde {\lambda }')$
is
![]() $W(\lambda ')$
-stable but does not extend to
$W(\lambda ')$
-stable but does not extend to
![]() $W(\lambda ')$
as the kernel of any linear character of
$W(\lambda ')$
as the kernel of any linear character of
![]() $W(\lambda ')$
contains
$W(\lambda ')$
contains
![]() $\operatorname Z(W(\lambda '))= [W(\lambda '), W(\lambda ')]$
. This also implies that for some character
$\operatorname Z(W(\lambda '))= [W(\lambda '), W(\lambda ')]$
. This also implies that for some character
![]() $\eta \in \mathrm {Irr}(W(\lambda '))$
, the constituent
$\eta \in \mathrm {Irr}(W(\lambda '))$
, the constituent
![]() $\eta _0$
of
$\eta _0$
of
![]() ${\left. \eta \right\rceil _{{W(\widetilde {\lambda }')}}}$
has multiplicity
${\left. \eta \right\rceil _{{W(\widetilde {\lambda }')}}}$
has multiplicity
![]() $2$
in
$2$
in
![]() ${\left. \eta \right\rceil _{{W(\widetilde {\lambda }')}}}$
. The character
${\left. \eta \right\rceil _{{W(\widetilde {\lambda }')}}}$
. The character
![]() $\operatorname {R}_{\widetilde {L}'}^{{\widetilde G}'}(\widetilde {\lambda }')_{\eta _0}$
restricts to
$\operatorname {R}_{\widetilde {L}'}^{{\widetilde G}'}(\widetilde {\lambda }')_{\eta _0}$
restricts to
![]() $({{\mathbf G}}')^F$
and has only constituents with multiplicity
$({{\mathbf G}}')^F$
and has only constituents with multiplicity
![]() $1$
according to [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11].
$1$
according to [Reference Cabanes, Schaeffer Fry and SpäthCE, 15.11].
Like in other places, these results are considering first the situation of Harish-Chandra induction for a group
![]() $(\widetilde {{\mathbf G}}')^{F_1}$
that comes from a regular embedding of
$(\widetilde {{\mathbf G}}')^{F_1}$
that comes from a regular embedding of
![]() ${{\mathbf G}}'$
into a group with connected center. These results can then be applied to the groups
${{\mathbf G}}'$
into a group with connected center. These results can then be applied to the groups
![]() ${\widetilde G}':=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}'))$
and the subgroup
${\widetilde G}':=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}'))$
and the subgroup
![]() $\widetilde {L}'$
.
$\widetilde {L}'$
.
On the other hand, according to [Reference BonnaféB1, 13.9(b)], the character
![]() $\operatorname {R}_{L'}^{G'}(\lambda ')_{\eta }$
has multiplicity
$\operatorname {R}_{L'}^{G'}(\lambda ')_{\eta }$
has multiplicity
![]() $2$
in
$2$
in
![]() $\operatorname {R}_{\widetilde {L}'}^{{\widetilde G}'}(\widetilde {\lambda }')_{\eta _0}$
. This is a contradiction. This implies that a character
$\operatorname {R}_{\widetilde {L}'}^{{\widetilde G}'}(\widetilde {\lambda }')_{\eta _0}$
. This is a contradiction. This implies that a character
![]() $\psi $
with the above properties cannot exist and proves the statement.
$\psi $
with the above properties cannot exist and proves the statement.
In the next step, we continue to consider the case where
![]() $I\in {\mathcal O}_d$
with
$I\in {\mathcal O}_d$
with
![]() $2\mid d$
.
$2\mid d$
.
Lemma 6.19. Let
![]() $\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial, and let
$\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial, and let
![]() $I\in {\mathcal O}_d$
for some
$I\in {\mathcal O}_d$
for some
![]() $d\in \mathbb D_{\mathrm {even}}$
with
$d\in \mathbb D_{\mathrm {even}}$
with
![]() $d>2$
. Then every
$d>2$
. Then every
![]() $\psi \in \mathrm {Irr}_{cusp}( L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}( L_I\mid \nu )$
with
![]() $\psi ^{c_I}=\psi $
satisfies
$\psi ^{c_I}=\psi $
satisfies
![]() $t_{I,2}^2\in \ker (\psi )$
.
$t_{I,2}^2\in \ker (\psi )$
.
Proof. Let
![]() $z:=t_{I,2}^2={\mathbf h} _{\underline {l}}(\zeta ')$
for some
$z:=t_{I,2}^2={\mathbf h} _{\underline {l}}(\zeta ')$
for some
![]() $\zeta '\in {\mathbb {F}}^{\times }$
a root of unity of order
$\zeta '\in {\mathbb {F}}^{\times }$
a root of unity of order
![]() $2(q-1)_2$
, and
$2(q-1)_2$
, and
![]() $\psi \in \mathrm {Irr}_{cusp}(L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}(L_I\mid \nu )$
with
![]() $\psi ^{c_I}=\psi $
and
$\psi ^{c_I}=\psi $
and
![]() $z\notin \ker (\psi )$
. According to Lemma 6.18,
$z\notin \ker (\psi )$
. According to Lemma 6.18,
![]() $\psi ^{\widehat L_I}$
is irreducible. Note
$\psi ^{\widehat L_I}$
is irreducible. Note
![]() $z\in \operatorname Z({{\mathbf L}}_I)$
. Since
$z\in \operatorname Z({{\mathbf L}}_I)$
. Since
![]() $d\geq 4$
, it is sufficient to show the statement in the case where
$d\geq 4$
, it is sufficient to show the statement in the case where
![]() $I={\underline {l}}$
and hence
$I={\underline {l}}$
and hence
![]() $L_I=L$
.
$L_I=L$
.
The group
![]() $L_0:=[{{\mathbf L}},{{\mathbf L}}]^F$
satisfies
$L_0:=[{{\mathbf L}},{{\mathbf L}}]^F$
satisfies
![]() $L_0\cong \operatorname {SL}_l(q)$
(see Lemma 4.2). Let
$L_0\cong \operatorname {SL}_l(q)$
(see Lemma 4.2). Let
![]() $\psi _0\in \mathrm {Irr}( {\left.\psi \right\rceil _{{L_0}}})$
. According to Lemma 2.15,
$\psi _0\in \mathrm {Irr}( {\left.\psi \right\rceil _{{L_0}}})$
. According to Lemma 2.15,
![]() $\psi _0$
is cuspidal. Following Lemma 4.3, the automorphisms of
$\psi _0$
is cuspidal. Following Lemma 4.3, the automorphisms of
![]() $L_0$
induced by
$L_0$
induced by
![]() $\widehat L$
are diagonal automorphisms of
$\widehat L$
are diagonal automorphisms of
![]() $L_0$
. Since
$L_0$
. Since
![]() ${\mathrm {C}}_{\widehat L}(L_0)\leq \operatorname Z({{\mathbf L}})$
and
${\mathrm {C}}_{\widehat L}(L_0)\leq \operatorname Z({{\mathbf L}})$
and
![]() $\widehat L/({\mathrm {C}}_{\widehat L}(L_0)L_0)$
is cyclic, we can see that maximal extendibility holds with respect to
$\widehat L/({\mathrm {C}}_{\widehat L}(L_0)L_0)$
is cyclic, we can see that maximal extendibility holds with respect to
![]() $L_0\lhd L$
. As
$L_0\lhd L$
. As
![]() $\psi ^{\widehat L}$
is irreducible,
$\psi ^{\widehat L}$
is irreducible,
![]() $\widehat L_{\psi }=L$
. As
$\widehat L_{\psi }=L$
. As
![]() $\widehat L/L_0$
is abelian, this implies
$\widehat L/L_0$
is abelian, this implies
![]() $\widehat L_{\psi _0}\leq L$
.
$\widehat L_{\psi _0}\leq L$
.
We now use the fact
![]() $L_0\cong \operatorname {SL}_l(q)$
. Let
$L_0\cong \operatorname {SL}_l(q)$
. Let
![]() ${{\mathbf H}}:=\operatorname {GL}_l({\mathbb {F}})$
, and let
${{\mathbf H}}:=\operatorname {GL}_l({\mathbb {F}})$
, and let
![]() $F':{{\mathbf H}}\longrightarrow {{\mathbf H}}$
be a Frobenius endomorphisms giving an
$F':{{\mathbf H}}\longrightarrow {{\mathbf H}}$
be a Frobenius endomorphisms giving an
![]() ${\mathbb {F}}_q$
-structure such that
${\mathbb {F}}_q$
-structure such that
![]() ${{\mathbf H}}^{F'}\cong \operatorname {GL}_l(q)$
. Via
${{\mathbf H}}^{F'}\cong \operatorname {GL}_l(q)$
. Via
![]() $[{{\mathbf H}},{{\mathbf H}}]\cong [{{\mathbf L}},{{\mathbf L}}]$
, we identify
$[{{\mathbf H}},{{\mathbf H}}]\cong [{{\mathbf L}},{{\mathbf L}}]$
, we identify
![]() $[{{\mathbf H}},{{\mathbf H}}]^F$
with
$[{{\mathbf H}},{{\mathbf H}}]^F$
with
![]() $L_0$
. Hence,
$L_0$
. Hence,
![]() $\psi _0$
defines
$\psi _0$
defines
![]() $\psi _0'\in \mathrm {Irr}_{cusp}([{{\mathbf H}},{{\mathbf H}}]^F)$
. By the above, this implies
$\psi _0'\in \mathrm {Irr}_{cusp}([{{\mathbf H}},{{\mathbf H}}]^F)$
. By the above, this implies
The character
![]() $\psi ^{\widehat L}$
is
$\psi ^{\widehat L}$
is
![]() $c_I$
-stable. Hence,
$c_I$
-stable. Hence,
![]() ${\left.\psi \right\rceil _{{L_0}}}$
is
${\left.\psi \right\rceil _{{L_0}}}$
is
![]() $c_I$
-stable. Following Notation 6.9,
$c_I$
-stable. Following Notation 6.9,
![]() $c_I$
acts on
$c_I$
acts on
![]() $L_0$
by a graph automorphism and
$L_0$
by a graph automorphism and
![]() $\widehat L$
acts on
$\widehat L$
acts on
![]() $L_0$
as diagonal automorphisms.
$L_0$
as diagonal automorphisms.
As
![]() ${\left. \psi \right\rceil _{{L_0}}}$
is
${\left. \psi \right\rceil _{{L_0}}}$
is
![]() $c_I$
-stable, we can choose
$c_I$
-stable, we can choose
![]() $\psi '$
to be stable under the graph automorphism of
$\psi '$
to be stable under the graph automorphism of
![]() $\operatorname {SL}_l(q)$
and it is cuspidal according to Lemma 2.15. In this situation,
$\operatorname {SL}_l(q)$
and it is cuspidal according to Lemma 2.15. In this situation,
![]() $\psi _0$
only exists if
$\psi _0$
only exists if
![]() $l=2$
(see Proposition 5.2). By the assumption
$l=2$
(see Proposition 5.2). By the assumption
![]() $d>2$
, so we get a contradiction. This implies our claim that any
$d>2$
, so we get a contradiction. This implies our claim that any
![]() $c_I$
-stable character
$c_I$
-stable character
![]() $\psi $
satisfies
$\psi $
satisfies
![]() $t_{I,2}^2\in \ker (\psi )$
.
$t_{I,2}^2\in \ker (\psi )$
.
Lemma 6.20. Let
![]() $I\in {\mathcal O}_2$
and
$I\in {\mathcal O}_2$
and
![]() $\nu $
as in Lemma 6.19. There are exactly two characters
$\nu $
as in Lemma 6.19. There are exactly two characters
![]() $\psi \in \mathrm {Irr}_{cusp}( L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}( L_I\mid \nu )$
with
![]() $\psi ^{c_I}=\psi $
and
$\psi ^{c_I}=\psi $
and
![]() $t_{I,2}^2\notin \ker (\psi )$
. Those characters are
$t_{I,2}^2\notin \ker (\psi )$
. Those characters are
![]() $\widehat L$
-conjugate.
$\widehat L$
-conjugate.
Proof. From the proof of Lemma 6.19 and Proposition 5.2, we see that there are two
![]() $\operatorname {GL}_2(q)$
-conjugate characters
$\operatorname {GL}_2(q)$
-conjugate characters
![]() $\psi _0\in \mathrm {Irr}({\left. \psi \right\rceil _{{[{{\mathbf L}}_I,{{\mathbf L}}_I]^F}}})$
, that are the only possible constituents of
$\psi _0\in \mathrm {Irr}({\left. \psi \right\rceil _{{[{{\mathbf L}}_I,{{\mathbf L}}_I]^F}}})$
, that are the only possible constituents of
![]() $\psi $
. If
$\psi $
. If
![]() $I=\{i,i'\}$
, then
$I=\{i,i'\}$
, then
![]() $\psi _0({\mathbf h} _{e_i-e_{i'}}(-1))=(-1)^{\frac {q+1}{2}} \psi _0(1)$
according to [Reference BonnaféB
Reference Bonnafé2, Table 5.4]. Then
$\psi _0({\mathbf h} _{e_i-e_{i'}}(-1))=(-1)^{\frac {q+1}{2}} \psi _0(1)$
according to [Reference BonnaféB
Reference Bonnafé2, Table 5.4]. Then
![]() ${{\mathbf L}}^F \cong \operatorname {SL}_2(q)\times {\mathbf Z}_I^F$
by Lemma 4.2, in particular
${{\mathbf L}}^F \cong \operatorname {SL}_2(q)\times {\mathbf Z}_I^F$
by Lemma 4.2, in particular
![]() $h_0={\mathbf h} _{I}(\varpi ) {\mathbf h} _{e_i-e_{i'}}(-1)$
. Because of
$h_0={\mathbf h} _{I}(\varpi ) {\mathbf h} _{e_i-e_{i'}}(-1)$
. Because of
![]() $\psi (h_0)=- \psi (1)$
, this implies
$\psi (h_0)=- \psi (1)$
, this implies
![]() $\psi ({\mathbf h} _{I}(\varpi )) = - (-1)^{\frac {q+1}{2}} \psi (1) =(-1)^{\frac {q-1}{2}} \psi (1) $
.
$\psi ({\mathbf h} _{I}(\varpi )) = - (-1)^{\frac {q+1}{2}} \psi (1) =(-1)^{\frac {q-1}{2}} \psi (1) $
.
Let
![]() $\kappa \in \mathrm {Irr}({\mathbf Z}_I^F)$
such that
$\kappa \in \mathrm {Irr}({\mathbf Z}_I^F)$
such that
![]() $\psi =\psi _0\times \kappa $
. As
$\psi =\psi _0\times \kappa $
. As
![]() $c_I$
acts by inverting on
$c_I$
acts by inverting on
![]() ${\mathbf Z}_I$
,
${\mathbf Z}_I$
,
![]() $\kappa $
has multiplicative order 1 or 2. The assumption
$\kappa $
has multiplicative order 1 or 2. The assumption
![]() $t_{I,2}^2\notin \ker (\psi )$
implies that
$t_{I,2}^2\notin \ker (\psi )$
implies that
![]() $\kappa $
has order
$\kappa $
has order
![]() $2$
. This proves that given
$2$
. This proves that given
![]() $\psi _0$
, the character
$\psi _0$
, the character
![]() $\kappa $
is uniquely determined by the fact that
$\kappa $
is uniquely determined by the fact that
![]() $\psi $
is
$\psi $
is
![]() $c_I$
-stable and
$c_I$
-stable and
![]() $t_{I,2}^2\not \in \ker (\psi )$
. Hence, the only characters with the given properties are
$t_{I,2}^2\not \in \ker (\psi )$
. Hence, the only characters with the given properties are
![]() $\widehat L $
-conjugate.
$\widehat L $
-conjugate.
Thanks to the above three statements, we can now show Theorem 6.17.
Proof of Theorem 6.17
Let
![]() $\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial,
$\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
be nontrivial,
![]() $d\in \mathbb D_{\mathrm {even}}$
,
$d\in \mathbb D_{\mathrm {even}}$
,
![]() $I\in {\mathcal O}_d$
, and
$I\in {\mathcal O}_d$
, and
![]() $\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_I\mid \nu )$
with
![]() $\psi ^{c_I}=\psi $
. If
$\psi ^{c_I}=\psi $
. If
![]() $d> 2$
, then
$d> 2$
, then
![]() $t^2_{I,2}\in \ker (\psi )$
according to Lemma 6.19. This shows part (a).
$t^2_{I,2}\in \ker (\psi )$
according to Lemma 6.19. This shows part (a).
Assume
![]() $d=2$
and
$d=2$
and
![]() $t^2_{I,2}\notin \ker (\psi )$
. The set
$t^2_{I,2}\notin \ker (\psi )$
. The set
![]() $\mathrm {Irr}({\left. \psi \right\rceil _{{L_I}}})$
contains two characters according to Lemma 6.18. Following Lemma 4.4
(b) together with Proposition 2.19(b), the character
$\mathrm {Irr}({\left. \psi \right\rceil _{{L_I}}})$
contains two characters according to Lemma 6.18. Following Lemma 4.4
(b) together with Proposition 2.19(b), the character
![]() $\psi '\in \mathrm {Irr}({\left. \psi \right\rceil _{{L_I}}})$
is cuspidal, and satisfies
$\psi '\in \mathrm {Irr}({\left. \psi \right\rceil _{{L_I}}})$
is cuspidal, and satisfies
![]() $(\psi ')^{c_I}=\psi '$
and
$(\psi ')^{c_I}=\psi '$
and
![]() $t^2_{I,2}\notin \ker (\psi ')$
. Then there are exactly two
$t^2_{I,2}\notin \ker (\psi ')$
. Then there are exactly two
![]() $\widehat L_I$
-conjugate characters in
$\widehat L_I$
-conjugate characters in
![]() $\mathrm {Irr}_{cusp}(L_I\mid \nu )$
with those properties (see Lemma 6.20). Since
$\mathrm {Irr}_{cusp}(L_I\mid \nu )$
with those properties (see Lemma 6.20). Since
![]() $|\widehat L_I:L_I|=2$
, this implies that there is only one character
$|\widehat L_I:L_I|=2$
, this implies that there is only one character
![]() $\psi $
with the given properties. This proves (b).
$\psi $
with the given properties. This proves (b).
Lemma 6.21. If
![]() $\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
is nontrivial, then every
$\nu \in \mathrm {Irr}({\left\langle h_0\right\rangle })$
is nontrivial, then every
![]() $\psi \in \mathrm {Irr}_{cusp}(\widehat L_{J_{-1}}\mid \nu )$
satisfies
$\psi \in \mathrm {Irr}_{cusp}(\widehat L_{J_{-1}}\mid \nu )$
satisfies
![]() $\psi ^{c_{J_{-1}}} \neq \psi $
.
$\psi ^{c_{J_{-1}}} \neq \psi $
.
Proof. Note
![]() ${\mathbf h} _{J_{-1}}(\varpi )\in \operatorname Z({{\mathbf L}}_{-1})$
and
${\mathbf h} _{J_{-1}}(\varpi )\in \operatorname Z({{\mathbf L}}_{-1})$
and
![]() $[c_{J_{-1}},{\mathbf h} _{J_{-1}}(\varpi )]=h_0$
. No extension
$[c_{J_{-1}},{\mathbf h} _{J_{-1}}(\varpi )]=h_0$
. No extension
![]() $\widehat {\nu }\in \mathrm {Irr}(\operatorname Z({{\mathbf L}}_{-1})^F\mid \nu )$
is
$\widehat {\nu }\in \mathrm {Irr}(\operatorname Z({{\mathbf L}}_{-1})^F\mid \nu )$
is
![]() $c_{J_{-1}}$
-stable. This implies that
$c_{J_{-1}}$
-stable. This implies that
![]() $\psi _{-1}$
is not
$\psi _{-1}$
is not
![]() $c_{J_{-1}}$
-stable.
$c_{J_{-1}}$
-stable.
The above leads to the following statement on the sets
![]() ${\mathcal O}_c(\widehat {\lambda })$
,
${\mathcal O}_c(\widehat {\lambda })$
,
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })$
and
${\mathcal O}_{c,-1}(\widehat {\lambda })$
and
![]() $Y(\widehat {\lambda })$
introduced earlier in Lemmas 6.12 and 6.13. We use the notation
$Y(\widehat {\lambda })$
introduced earlier in Lemmas 6.12 and 6.13. We use the notation
![]() ${o(\mu )}$
to denote the multiplicative order of a linear character
${o(\mu )}$
to denote the multiplicative order of a linear character
![]() $\mu $
of a finite group.
$\mu $
of a finite group.
Corollary 6.22. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
,
$\lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\widehat {\lambda }$
and
$\widehat {\lambda }$
and
![]() $\widehat {\lambda }_I$
associated with
$\widehat {\lambda }_I$
associated with
![]() $\lambda $
as in Lemma 6.13. If
$\lambda $
as in Lemma 6.13. If
![]() $\widehat {\lambda }$
is standardized, then:
$\widehat {\lambda }$
is standardized, then:
-
(a)
 ${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}\cup \{1,-1\}} {\mathcal O}_d$
.
${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}\cup \{1,-1\}} {\mathcal O}_d$
. -
(b) If
 $h_0\in \ker (\lambda )$
, then
$h_0\in \ker (\lambda )$
, then
 ${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq \{J_{-1}\}\cup \{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)\mid 2 \}$
.
${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq \{J_{-1}\}\cup \{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)\mid 2 \}$
. -
(c) If
 $h_0\notin \ker (\lambda )$
, then
$h_0\notin \ker (\lambda )$
, then
 ${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
and all
${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
and all
 $\{\widehat {\lambda }_I\mid I \in {\mathcal O}_{c,-1}(\widehat {\lambda })\}$
are
$\{\widehat {\lambda }_I\mid I \in {\mathcal O}_{c,-1}(\widehat {\lambda })\}$
are
 $V_S$
-conjugate, that is,
$V_S$
-conjugate, that is,
 ${\mathcal O}_{c,-1}(\widehat {\lambda })\in Y(\widehat {\lambda })$
.
${\mathcal O}_{c,-1}(\widehat {\lambda })\in Y(\widehat {\lambda })$
.
Proof. Lemma 6.15 implies that
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })\cap {\mathcal O}_d=\emptyset $
for every
${\mathcal O}_{c,-1}(\widehat {\lambda })\cap {\mathcal O}_d=\emptyset $
for every
![]() $d\in \mathbb D_{\mathrm {odd}} \setminus \{\pm 1\}$
. This gives (a).
$d\in \mathbb D_{\mathrm {odd}} \setminus \{\pm 1\}$
. This gives (a).
For the proof of (b), assume
![]() $h_0\in \ker (\lambda )$
. Then Corollary 6.16 implies
$h_0\in \ker (\lambda )$
. Then Corollary 6.16 implies
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_{-1}\cup {\mathcal O}_1$
. For
${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_{-1}\cup {\mathcal O}_1$
. For
![]() $I\in {\mathcal O}_1$
, the character
$I\in {\mathcal O}_1$
, the character
![]() $\widehat {\lambda }_I$
is
$\widehat {\lambda }_I$
is
![]() $c_I$
-stable if and only if
$c_I$
-stable if and only if
![]() $o(\widehat {\lambda }_I)\mid 2$
.
$o(\widehat {\lambda }_I)\mid 2$
.
For the proof of (c), assume
![]() $h_0\notin \ker (\lambda )$
. Then
$h_0\notin \ker (\lambda )$
. Then
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })\cap {\mathcal O}_1=\emptyset $
and
${\mathcal O}_{c,-1}(\widehat {\lambda })\cap {\mathcal O}_1=\emptyset $
and
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
according to Theorem 6.17. Lemma 6.20 proves that
${\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
according to Theorem 6.17. Lemma 6.20 proves that
![]() $\{\widehat {\lambda }_I\mid I \in {\mathcal O}_{c,-1}(\widehat {\lambda })\}$
are
$\{\widehat {\lambda }_I\mid I \in {\mathcal O}_{c,-1}(\widehat {\lambda })\}$
are
![]() $V_S$
-conjugate. Hence, the partition
$V_S$
-conjugate. Hence, the partition
![]() $Y(\widehat {\lambda })$
from Lemma 6.12 contains
$Y(\widehat {\lambda })$
from Lemma 6.12 contains
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })$
.
${\mathcal O}_{c,-1}(\widehat {\lambda })$
.
Recall
![]() $K(\lambda ):=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
. For any
$K(\lambda ):=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
. For any
![]() $\overline W$
-stable
$\overline W$
-stable
![]() $L\leq J\leq \widetilde {L}$
,
$L\leq J\leq \widetilde {L}$
,
![]() $\kappa \in \mathrm {Irr}(J)$
, and
$\kappa \in \mathrm {Irr}(J)$
, and
![]() $Q\subseteq {\mathcal O}$
, let
$Q\subseteq {\mathcal O}$
, let
![]() ${\overline W^Q(\kappa )}:=\overline W(\kappa )\cap {\mathcal {S}}_{\pm Q }$
and
${\overline W^Q(\kappa )}:=\overline W(\kappa )\cap {\mathcal {S}}_{\pm Q }$
and
![]() ${W^Q(\kappa )}:=\overline W^Q(\kappa )\cap W$
.
${W^Q(\kappa )}:=\overline W^Q(\kappa )\cap W$
.
Proposition 6.23. Let
![]() $ \lambda \in \mathbb {T}$
,
$ \lambda \in \mathbb {T}$
,
![]() $\widehat {\lambda } \in \mathrm {Irr}_{cusp}(\widehat L\mid \lambda )$
,
$\widehat {\lambda } \in \mathrm {Irr}_{cusp}(\widehat L\mid \lambda )$
,
![]() $\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
(
$\widehat {\lambda }_I\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L_I}}})$
(
![]() $I\in {\mathcal O}$
), and
$I\in {\mathcal O}$
), and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
. Assume that
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
. Assume that
![]() $\widehat {\lambda }$
is standardized in the sense of 6.10. We set
$\widehat {\lambda }$
is standardized in the sense of 6.10. We set
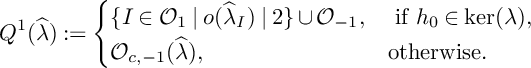 $$ \begin{align*} { Q^1(\widehat{\lambda})}:= \begin{cases} \{ I \in {\mathcal O}_1\mid o(\widehat{\lambda}_I)\mid 2\} \cup {\mathcal O}_{-1}, &\text{ if } h_0\in\ker(\lambda),\\ {\mathcal O}_{c,-1}(\widehat{\lambda}), &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} { Q^1(\widehat{\lambda})}:= \begin{cases} \{ I \in {\mathcal O}_1\mid o(\widehat{\lambda}_I)\mid 2\} \cup {\mathcal O}_{-1}, &\text{ if } h_0\in\ker(\lambda),\\ {\mathcal O}_{c,-1}(\widehat{\lambda}), &\text{otherwise}. \end{cases} \end{align*} $$
Then:
-
(a)
 $Q^1(\widehat {\lambda })$
is
$Q^1(\widehat {\lambda })$
is
 $K(\lambda )$
-stable, and
$K(\lambda )$
-stable, and -
(b)
 $W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
, where
$W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
, where
 ${Q^2(\widehat {\lambda })}:={\mathcal O}\setminus Q^1(\widehat {\lambda })$
, and
${Q^2(\widehat {\lambda })}:={\mathcal O}\setminus Q^1(\widehat {\lambda })$
, and
 ${W^j(\widetilde {\lambda })}:= W^{Q^j(\widehat {\lambda })}(\widetilde {\lambda })$
for
${W^j(\widetilde {\lambda })}:= W^{Q^j(\widehat {\lambda })}(\widetilde {\lambda })$
for
 $j\in \underline 2$
.
$j\in \underline 2$
.
Proof. Let
![]() $e\in {\left\langle F_0\right\rangle }$
such that
$e\in {\left\langle F_0\right\rangle }$
such that
![]() $\lambda $
and
$\lambda $
and
![]() $ \lambda ^e$
are
$ \lambda ^e$
are
![]() $\overline N$
-conjugate. As
$\overline N$
-conjugate. As
![]() $\widehat {\lambda }$
is standardized, then
$\widehat {\lambda }$
is standardized, then
![]() $\widehat {\lambda }^e$
is also standardized. As the orders of
$\widehat {\lambda }^e$
is also standardized. As the orders of
![]() $\widehat {\lambda }_I$
and
$\widehat {\lambda }_I$
and
![]() $(\widehat {\lambda }_I)^e$
coincide for every
$(\widehat {\lambda }_I)^e$
coincide for every
![]() $I\in {\mathcal O}$
, we see that
$I\in {\mathcal O}$
, we see that
![]() $Q^1(\widehat {\lambda })=Q^1(\widehat {\lambda }^e)$
from the definition, whenever
$Q^1(\widehat {\lambda })=Q^1(\widehat {\lambda }^e)$
from the definition, whenever
![]() $h_0\in \ker (\lambda )=\ker (\widehat {\lambda }^e)$
and hence
$h_0\in \ker (\lambda )=\ker (\widehat {\lambda }^e)$
and hence
![]() $h_0\in \ker (\widehat {\lambda }^e)$
.
$h_0\in \ker (\widehat {\lambda }^e)$
.
Assume
![]() $h_0\notin \ker (\lambda )$
. Then
$h_0\notin \ker (\lambda )$
. Then
![]() $h_0\notin \ker (\lambda ^e)$
. Let
$h_0\notin \ker (\lambda ^e)$
. Let
![]() $I\in {\mathcal O}\setminus \{J_{-1}\}$
. Because of
$I\in {\mathcal O}\setminus \{J_{-1}\}$
. Because of
![]() $c_I^e\in c_I{\left\langle h_0\right\rangle }$
, we see
$c_I^e\in c_I{\left\langle h_0\right\rangle }$
, we see
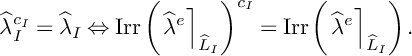 $$ \begin{align*}\widehat{\lambda}_I^{c_I}=\widehat{\lambda}_I \Leftrightarrow \mathrm{Irr}\left({\left. \widehat{\lambda}^e\right\rceil_{{\widehat L_I}}}\right)^{c_I} = \mathrm{Irr}\left({\left. \widehat{\lambda}^e\right\rceil_{{\widehat L_I}}}\right).\end{align*} $$
$$ \begin{align*}\widehat{\lambda}_I^{c_I}=\widehat{\lambda}_I \Leftrightarrow \mathrm{Irr}\left({\left. \widehat{\lambda}^e\right\rceil_{{\widehat L_I}}}\right)^{c_I} = \mathrm{Irr}\left({\left. \widehat{\lambda}^e\right\rceil_{{\widehat L_I}}}\right).\end{align*} $$
In the case of
![]() $\widehat {\lambda }_I^{c_I}=\widehat {\lambda }_I$
, the character
$\widehat {\lambda }_I^{c_I}=\widehat {\lambda }_I$
, the character
![]() $\widehat {\lambda }_I$
has some
$\widehat {\lambda }_I$
has some
![]() $c_I$
-stable extension to
$c_I$
-stable extension to
![]() $\widetilde {L}_I$
if and only if the unique character in
$\widetilde {L}_I$
if and only if the unique character in
![]() $\mathrm {Irr}({\left. \widehat {\lambda }^e\right\rceil _{{\widehat L_I}}})$
has some
$\mathrm {Irr}({\left. \widehat {\lambda }^e\right\rceil _{{\widehat L_I}}})$
has some
![]() $c_I$
-stable extension to
$c_I$
-stable extension to
![]() $\widetilde {L}_I$
. (The set
$\widetilde {L}_I$
. (The set
![]() $\mathrm {Irr}({\left. \phi \right\rceil _{{\widehat L_I}}})$
is a singleton for every
$\mathrm {Irr}({\left. \phi \right\rceil _{{\widehat L_I}}})$
is a singleton for every
![]() $\phi \in \mathrm {Irr}_{cusp}(\widehat L)$
, since
$\phi \in \mathrm {Irr}_{cusp}(\widehat L)$
, since
![]() $\widehat L$
is the central product of the groups
$\widehat L$
is the central product of the groups
![]() $\widehat L_I$
over
$\widehat L_I$
over
![]() ${\left\langle h_0\right\rangle }$
.) This shows
${\left\langle h_0\right\rangle }$
.) This shows
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda })={\mathcal O}_{c,-1}(\widehat {\lambda }^e)$
and
${\mathcal O}_{c,-1}(\widehat {\lambda })={\mathcal O}_{c,-1}(\widehat {\lambda }^e)$
and
![]() $Q^1(\widehat {\lambda })=Q^1(\widehat {\lambda }^e)$
by the definition of those sets. Let
$Q^1(\widehat {\lambda })=Q^1(\widehat {\lambda }^e)$
by the definition of those sets. Let
![]() $w\in \overline W$
and
$w\in \overline W$
and
![]() $e\in {\left\langle F_p \right\rangle }$
with
$e\in {\left\langle F_p \right\rangle }$
with
![]() $we\in \widehat K(\lambda )$
. Then
$we\in \widehat K(\lambda )$
. Then
![]() $\widehat {\lambda }^w$
is standardized and
$\widehat {\lambda }^w$
is standardized and
![]() $Q^1(\widehat {\lambda })^w= Q^1(\widehat {\lambda }^w)$
. Accordingly,
$Q^1(\widehat {\lambda })^w= Q^1(\widehat {\lambda }^w)$
. Accordingly,
![]() $w\in K(\lambda )$
stabilizes
$w\in K(\lambda )$
stabilizes
![]() $Q^1(\widehat {\lambda })$
. This implies part (a).
$Q^1(\widehat {\lambda })$
. This implies part (a).
For part (b), recall the description of
![]() $\overline W(\widetilde {\lambda })$
from Lemma 6.6:
$\overline W(\widetilde {\lambda })$
from Lemma 6.6:
First assume
![]() $h_0\in \ker (\lambda )$
. By construction,
$h_0\in \ker (\lambda )$
. By construction,
![]() ${\mathcal O}_c(\widehat {\lambda })\subseteq Q^1(\widehat {\lambda }) \cup \bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
and hence
${\mathcal O}_c(\widehat {\lambda })\subseteq Q^1(\widehat {\lambda }) \cup \bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
and hence
![]() $\overline W(\widetilde {\lambda })=\overline W^1(\widetilde {\lambda })\times \overline W^2(\widetilde {\lambda })$
. According to Corollary 6.22(a), we observe
$\overline W(\widetilde {\lambda })=\overline W^1(\widetilde {\lambda })\times \overline W^2(\widetilde {\lambda })$
. According to Corollary 6.22(a), we observe
![]() $(I,-I)\in W$
for every
$(I,-I)\in W$
for every
![]() $I\in {\mathcal O}_c(\widehat {\lambda })\setminus Q^1(\widehat {\lambda })$
. This implies
$I\in {\mathcal O}_c(\widehat {\lambda })\setminus Q^1(\widehat {\lambda })$
. This implies
![]() $\overline W^2(\widetilde {\lambda })\leq W$
and
$\overline W^2(\widetilde {\lambda })\leq W$
and
![]() $W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
by the definition of W.
$W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
by the definition of W.
It remains to consider the case where
![]() $h_0\notin \ker (\lambda )$
. Then
$h_0\notin \ker (\lambda )$
. Then
![]() $Q^1(\widehat {\lambda })={\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
by Corollary 6.22(c) and hence
$Q^1(\widehat {\lambda })={\mathcal O}_{c,-1}(\widehat {\lambda })\subseteq {\mathcal O}_2$
by Corollary 6.22(c) and hence
![]() $\overline W^1(\widetilde {\lambda })\leq W$
. By the structure of
$\overline W^1(\widetilde {\lambda })\leq W$
. By the structure of
![]() $\overline W(\widetilde {\lambda })$
described in Lemma 6.6, we see
$\overline W(\widetilde {\lambda })$
described in Lemma 6.6, we see
![]() $W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
.
$W(\widetilde {\lambda })=W^1(\widetilde {\lambda })\times W^2(\widetilde {\lambda })$
.
6.3 Clifford theory for
 $W(\widetilde {\lambda })\lhd W(\lambda )$
in the case of
$W(\widetilde {\lambda })\lhd W(\lambda )$
in the case of
 $\widehat L\widetilde {L}_{\lambda }= \widetilde {L}$
$\widehat L\widetilde {L}_{\lambda }= \widetilde {L}$
In this section, we study the characters of
![]() $W(\widetilde {\lambda })$
, in particular their Clifford theory with respect to
$W(\widetilde {\lambda })$
, in particular their Clifford theory with respect to
![]() $K(\lambda )$
. Assuming
$K(\lambda )$
. Assuming
![]() $\widehat L\widetilde {L}_{\lambda }=\widetilde {L}$
, we prove maximal extendibility with respect to
$\widehat L\widetilde {L}_{\lambda }=\widetilde {L}$
, we prove maximal extendibility with respect to
![]() $ W (\widetilde {\lambda })\lhd K(\lambda )$
. This result is required for a later application of Proposition 2.11. We consider the following situation.
$ W (\widetilde {\lambda })\lhd K(\lambda )$
. This result is required for a later application of Proposition 2.11. We consider the following situation.
Notation 6.24. Let
![]() $ \lambda \in \mathrm {Irr}_{cusp}(L)$
,
$ \lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
such that
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \widehat {\lambda })$
such that
![]() $\widehat {\lambda }$
is standardized and
$\widehat {\lambda }$
is standardized and
![]() $\widehat L \widetilde {L}_{\lambda }=\widetilde {L}$
(or equivalently
$\widehat L \widetilde {L}_{\lambda }=\widetilde {L}$
(or equivalently
![]() ${\left. \widetilde {\lambda }\right\rceil _{{\widehat L}}}=\widehat {\lambda }$
).
${\left. \widetilde {\lambda }\right\rceil _{{\widehat L}}}=\widehat {\lambda }$
).
For further computations, we use the groups
![]() ${K^j(\lambda )}$
associated with the subsets
${K^j(\lambda )}$
associated with the subsets
![]() $Q^j(\lambda )\subseteq {\mathcal O}$
from Proposition 6.23, where
$Q^j(\lambda )\subseteq {\mathcal O}$
from Proposition 6.23, where
![]() $K^j(\lambda ):= (K(\lambda ) {\mathcal {S}}_{ \pm ( {\mathcal O}\setminus Q^j(\lambda ))}) \cap {\mathcal {S}}_{\pm Q^j(\lambda )}$
for
$K^j(\lambda ):= (K(\lambda ) {\mathcal {S}}_{ \pm ( {\mathcal O}\setminus Q^j(\lambda ))}) \cap {\mathcal {S}}_{\pm Q^j(\lambda )}$
for
![]() $j\in \underline 2$
.
$j\in \underline 2$
.
Lemma 6.25. If maximal extendibility holds with respect to
![]() $W^j(\widetilde {\lambda })\lhd K^j(\lambda )$
for every
$W^j(\widetilde {\lambda })\lhd K^j(\lambda )$
for every
![]() $j\in \underline 2$
, then maximal extendibility holds with respect to
$j\in \underline 2$
, then maximal extendibility holds with respect to
![]() $W(\widetilde {\lambda })\lhd K(\lambda )$
, in particular for every
$W(\widetilde {\lambda })\lhd K(\lambda )$
, in particular for every
![]() $\eta _0 \in \mathrm {Irr}(W(\widetilde {\lambda }))$
there exists some
$\eta _0 \in \mathrm {Irr}(W(\widetilde {\lambda }))$
there exists some
![]() $K(\lambda )_{\eta _0}$
-stable
$K(\lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W (\lambda )\mid \eta _0)$
.
$\eta \in \mathrm {Irr}(W (\lambda )\mid \eta _0)$
.
In that situation, the above statement will ensure Assumption 2.12(iii) for
![]() $\overline {(\lambda ,\eta )}\in \mathcal P(L)$
via Lemma 6.5.
$\overline {(\lambda ,\eta )}\in \mathcal P(L)$
via Lemma 6.5.
Proof. Recall
![]() $K( \lambda ):= \overline W_{{\left.\lambda ^{L {\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
by the definition in 6.4. As
$K( \lambda ):= \overline W_{{\left.\lambda ^{L {\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
by the definition in 6.4. As
![]() $K(\lambda )$
stabilizes
$K(\lambda )$
stabilizes
![]() $Q^1(\widehat {\lambda })$
and
$Q^1(\widehat {\lambda })$
and
![]() $Q^2(\widehat {\lambda })$
by Proposition 6.23,
$Q^2(\widehat {\lambda })$
by Proposition 6.23,
![]() $K(\lambda )\leq {\mathcal {S}}_{\pm Q^1(\widehat {\lambda })}\times {\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. This rewrites as
$K(\lambda )\leq {\mathcal {S}}_{\pm Q^1(\widehat {\lambda })}\times {\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. This rewrites as
![]() $K(\lambda )\leq K^1(\lambda )\times K^2(\lambda )$
. Recall that
$K(\lambda )\leq K^1(\lambda )\times K^2(\lambda )$
. Recall that
![]() ${\mathcal O}_{c,-1}(\widehat {\lambda }) \subseteq Q^1(\widehat {\lambda })$
.
${\mathcal O}_{c,-1}(\widehat {\lambda }) \subseteq Q^1(\widehat {\lambda })$
.
Since maximal extendibility holds with respect to
![]() $W^j(\widetilde {\lambda })\lhd K^j(\lambda )$
for
$W^j(\widetilde {\lambda })\lhd K^j(\lambda )$
for
![]() $j \in \underline 2$
by assumption, maximal extendibility holds with respect to
$j \in \underline 2$
by assumption, maximal extendibility holds with respect to
This implies the statement as
![]() $K(\lambda )\leq K^1(\lambda )\times K^2(\lambda )$
.
$K(\lambda )\leq K^1(\lambda )\times K^2(\lambda )$
.
For
![]() $\lambda \in \mathbb {T}$
with
$\lambda \in \mathbb {T}$
with
![]() $\widetilde {L}_{\lambda }=\widetilde {L}$
, we study first the Clifford theory of
$\widetilde {L}_{\lambda }=\widetilde {L}$
, we study first the Clifford theory of
![]() $W^2(\widetilde {\lambda })\lhd K^2(\lambda )$
for the groups from Lemma 6.25.
$W^2(\widetilde {\lambda })\lhd K^2(\lambda )$
for the groups from Lemma 6.25.
Lemma 6.26. Let
![]() $W^1(\widetilde {\lambda })$
,
$W^1(\widetilde {\lambda })$
,
![]() $W^2(\widetilde {\lambda })$
,
$W^2(\widetilde {\lambda })$
,
![]() $K^1(\lambda )$
, and
$K^1(\lambda )$
, and
![]() $K^2(\lambda )$
be the groups from Lemma 6.25. Then:
$K^2(\lambda )$
be the groups from Lemma 6.25. Then:
-
(a) maximal extendibility holds with respect to
 $W^{2}(\widetilde {\lambda })\lhd K^2(\lambda )$
, and
$W^{2}(\widetilde {\lambda })\lhd K^2(\lambda )$
, and -
(b) maximal extendibility holds with respect to
 $W^{1}(\widetilde {\lambda })\lhd K^1(\lambda )$
, if
$W^{1}(\widetilde {\lambda })\lhd K^1(\lambda )$
, if
 $h_0\notin \ker (\lambda )$
.
$h_0\notin \ker (\lambda )$
.
Proof. Let
![]() $Y(\widehat {\lambda })\vdash {\mathcal O}_c(\widehat {\lambda })$
and
$Y(\widehat {\lambda })\vdash {\mathcal O}_c(\widehat {\lambda })$
and
![]() $Y'(\widehat {\lambda })\vdash {\mathcal O}\setminus {\mathcal O}_c(\widehat {\lambda })$
be the partitions from Lemma 6.12. In order to prove part (a), we can assume
$Y'(\widehat {\lambda })\vdash {\mathcal O}\setminus {\mathcal O}_c(\widehat {\lambda })$
be the partitions from Lemma 6.12. In order to prove part (a), we can assume
![]() $Q^2(\widehat {\lambda })={\mathcal O}$
without loss of generality. We have
$Q^2(\widehat {\lambda })={\mathcal O}$
without loss of generality. We have
![]() $\overline W(\widetilde {\lambda }) =\overline W^2(\lambda )={\mathcal {Y}}_{\pm Y(\widehat {\lambda })}\times {\mathcal {Y}}_{Y'(\widehat {\lambda })}$
(see Lemma 6.13).
$\overline W(\widetilde {\lambda }) =\overline W^2(\lambda )={\mathcal {Y}}_{\pm Y(\widehat {\lambda })}\times {\mathcal {Y}}_{Y'(\widehat {\lambda })}$
(see Lemma 6.13).
If
![]() $h_0\in \ker (\lambda )$
, then
$h_0\in \ker (\lambda )$
, then
![]() ${\mathcal O}_c(\widehat {\lambda })\cap ({\mathcal O}_1\cup {\mathcal O}_{-1})=\emptyset $
by the choice of
${\mathcal O}_c(\widehat {\lambda })\cap ({\mathcal O}_1\cup {\mathcal O}_{-1})=\emptyset $
by the choice of
![]() $Q^1(\widehat {\lambda })$
according to Corollary 6.22. If
$Q^1(\widehat {\lambda })$
according to Corollary 6.22. If
![]() $h_0\notin \ker (\lambda )$
, Proposition 6.21 implies
$h_0\notin \ker (\lambda )$
, Proposition 6.21 implies
![]() ${\mathcal O}_c(\widehat {\lambda })\cap {\mathcal O}_{-1}=\emptyset $
and analogously we see
${\mathcal O}_c(\widehat {\lambda })\cap {\mathcal O}_{-1}=\emptyset $
and analogously we see
![]() ${\mathcal O}_c(\widehat {\lambda })\cap {\mathcal O}_{1}=\emptyset $
.
${\mathcal O}_c(\widehat {\lambda })\cap {\mathcal O}_{1}=\emptyset $
.
This implies
![]() ${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}}{\mathcal O}_d$
. Accordingly,
${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}}{\mathcal O}_d$
. Accordingly,
![]() $W(\widetilde {\lambda })$
is the direct product of groups
$W(\widetilde {\lambda })$
is the direct product of groups
![]() $W_d(\widetilde {\lambda })$
for
$W_d(\widetilde {\lambda })$
for
![]() $d\in \mathbb D$
. It suffices to consider the case where
$d\in \mathbb D$
. It suffices to consider the case where
![]() ${\mathcal O}={\mathcal O}_d=Q^2(\widehat {\lambda })$
for some
${\mathcal O}={\mathcal O}_d=Q^2(\widehat {\lambda })$
for some
![]() $d\in \mathbb D$
and
$d\in \mathbb D$
and
![]() ${\mathcal O}_c(\widehat {\lambda })\in \{{\mathcal O},\emptyset \}$
. Additionally, we can assume that
${\mathcal O}_c(\widehat {\lambda })\in \{{\mathcal O},\emptyset \}$
. Additionally, we can assume that
![]() $Y(\widehat {\lambda })$
and
$Y(\widehat {\lambda })$
and
![]() $Y'(\widehat {\lambda })$
are partitions whose elements have all the same cardinality. If
$Y'(\widehat {\lambda })$
are partitions whose elements have all the same cardinality. If
![]() ${\mathcal O}_c(\widehat {\lambda })={\mathcal O}$
, then
${\mathcal O}_c(\widehat {\lambda })={\mathcal O}$
, then
![]() $W^2(\lambda )\cong (\mathrm C_2\wr {\mathcal {S}}_k)^a$
for some positive integers k and a. Then
$W^2(\lambda )\cong (\mathrm C_2\wr {\mathcal {S}}_k)^a$
for some positive integers k and a. Then
![]() $K^2(\lambda )\cong (\mathrm C_2\wr {\mathcal {S}}_k)\wr {\mathcal {S}}_a$
, and hence maximal extendibility holds with respect to
$K^2(\lambda )\cong (\mathrm C_2\wr {\mathcal {S}}_k)\wr {\mathcal {S}}_a$
, and hence maximal extendibility holds with respect to
![]() $W^2(\widetilde {\lambda })\lhd K^2(\lambda )$
.
$W^2(\widetilde {\lambda })\lhd K^2(\lambda )$
.
If
![]() ${\mathcal O}_{c}(\widehat {\lambda })=\emptyset $
, then
${\mathcal O}_{c}(\widehat {\lambda })=\emptyset $
, then
![]() $W^2(\lambda )={\mathcal {Y}}_{Y'}$
and hence it is isomorphic to a direct product of symmetric groups. The group
$W^2(\lambda )={\mathcal {Y}}_{Y'}$
and hence it is isomorphic to a direct product of symmetric groups. The group
![]() $K^2(\lambda )\leq {\mathrm {N}}_{{\mathcal {S}}_{\pm {\mathcal O}_d}}({\mathcal {Y}}_Y)$
is isomorphic to
$K^2(\lambda )\leq {\mathrm {N}}_{{\mathcal {S}}_{\pm {\mathcal O}_d}}({\mathcal {Y}}_Y)$
is isomorphic to
![]() $(C {\mathcal {Y}}_Y)\rtimes {\mathcal {S}}_{Y}$
, where
$(C {\mathcal {Y}}_Y)\rtimes {\mathcal {S}}_{Y}$
, where
![]() $C:= {\left\langle \prod _{k\in y}( k,-k) \mid y\in Y\right\rangle }\leq {\mathcal {S}}_{\pm {\mathcal O}_d}$
. By Lemma 4.6, maximal extendibility holds with respect to
$C:= {\left\langle \prod _{k\in y}( k,-k) \mid y\in Y\right\rangle }\leq {\mathcal {S}}_{\pm {\mathcal O}_d}$
. By Lemma 4.6, maximal extendibility holds with respect to
![]() $W_2(\widetilde {\lambda })\lhd K_2(\lambda )$
. This proves part (a).
$W_2(\widetilde {\lambda })\lhd K_2(\lambda )$
. This proves part (a).
For part (b), we assume
![]() ${\mathcal O}_{c,-1}(\lambda )={\mathcal O}$
,
${\mathcal O}_{c,-1}(\lambda )={\mathcal O}$
,
![]() $h_0\notin \ker (\lambda )$
, and as before
$h_0\notin \ker (\lambda )$
, and as before
![]() $Q^1(\widehat {\lambda })={\mathcal O}$
. By Corollary 6.22(c), we have
$Q^1(\widehat {\lambda })={\mathcal O}$
. By Corollary 6.22(c), we have
![]() $K(\lambda )= W$
and
$K(\lambda )= W$
and
![]() $|W:W(\widetilde {\lambda })|=2$
(see Corollary 6.16(c)). As
$|W:W(\widetilde {\lambda })|=2$
(see Corollary 6.16(c)). As
![]() $W(\lambda )/W(\widetilde {\lambda })$
is cyclic, maximal extendibility holds with respect to
$W(\lambda )/W(\widetilde {\lambda })$
is cyclic, maximal extendibility holds with respect to
![]() $W(\widetilde {\lambda })\lhd K(\lambda )$
.
$W(\widetilde {\lambda })\lhd K(\lambda )$
.
It remains to prove the following.
Proposition 6.27. Maximal extendibility holds with respect to
![]() $W^1(\widetilde {\lambda })\lhd K^1(\lambda )$
, if
$W^1(\widetilde {\lambda })\lhd K^1(\lambda )$
, if
![]() $h_0\in \ker (\lambda )$
.
$h_0\in \ker (\lambda )$
.
Proof. Let
![]() $O_{1,i}=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=i\}$
for
$O_{1,i}=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=i\}$
for
![]() $i\in \underline 4$
and
$i\in \underline 4$
and
![]() $l_i:= |O_{1,i}|$
. By Lemmas 6.12 and 6.13, we have
$l_i:= |O_{1,i}|$
. By Lemmas 6.12 and 6.13, we have
![]() $\overline W_{Q^1(\widehat {\lambda })}(\widetilde {\lambda })\leq C\times {\mathcal {S}}_{\pm O_{1,1}}\times {\mathcal {S}}_{\pm O_{1,2}}$
, where
$\overline W_{Q^1(\widehat {\lambda })}(\widetilde {\lambda })\leq C\times {\mathcal {S}}_{\pm O_{1,1}}\times {\mathcal {S}}_{\pm O_{1,2}}$
, where
![]() $C\leq W_{{\mathcal O}_{-1}}(\widehat {\lambda })$
and C is then either trivial or a cyclic group of order
$C\leq W_{{\mathcal O}_{-1}}(\widehat {\lambda })$
and C is then either trivial or a cyclic group of order
![]() $2$
. The group structures depend on
$2$
. The group structures depend on
![]() $J_{-1}$
and those groups are described in Table 6.1, where
$J_{-1}$
and those groups are described in Table 6.1, where
![]() $W(\mathrm B_j)$
and
$W(\mathrm B_j)$
and
![]() $W(\mathrm {D}_j)$
are Coxeter groups of type
$W(\mathrm {D}_j)$
are Coxeter groups of type
![]() $\mathrm B_j$
and
$\mathrm B_j$
and
![]() $\mathrm {D}_j$
, respectively.
$\mathrm {D}_j$
, respectively.
Table 6.1 Isomorphism types of
![]() $W^1(\widetilde {\lambda })$
and
$W^1(\widetilde {\lambda })$
and
![]() $K^1(\lambda )$
$K^1(\lambda )$

Note that in all cases
![]() $\overline W_{O_{1,1}}(\widetilde {\lambda })$
is a Coxeter group of type
$\overline W_{O_{1,1}}(\widetilde {\lambda })$
is a Coxeter group of type
![]() $\mathrm B_{l_1}$
. Considering the structure, we observe that in all cases the statement holds according to Lemma 4.6.
$\mathrm B_{l_1}$
. Considering the structure, we observe that in all cases the statement holds according to Lemma 4.6.
Recall that
![]() $\mathbb {M}^{(X)}=\{\lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}_{\lambda } = X\}$
and
$\mathbb {M}^{(X)}=\{\lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}_{\lambda } = X\}$
and
![]() $\mathbb {M}_0:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)}\cup \mathbb {M}^{(\widetilde {L})})$
for X with
$\mathbb {M}_0:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)}\cup \mathbb {M}^{(\widetilde {L})})$
for X with
![]() $L\leq X\leq \widetilde {L}$
. For characters in
$L\leq X\leq \widetilde {L}$
. For characters in
![]() $\mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
, the above proves the following:
$\mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
, the above proves the following:
Proposition 6.28. Let
![]() $\lambda \in \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
, that is,
$\lambda \in \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}_0$
, that is,
![]() $\widehat L \widetilde {L}_{\lambda }=\widetilde {L}$
. For every
$\widehat L \widetilde {L}_{\lambda }=\widetilde {L}$
. For every
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \lambda )$
and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}\mid \lambda )$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
![]() $K( \lambda )_{\eta _0}$
-stable
$K( \lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
6.4 Clifford theory for
 $W(\widehat {\lambda })\lhd W(\lambda )$
in the case of
$W(\widehat {\lambda })\lhd W(\lambda )$
in the case of
 $\widetilde {L}_{\lambda }= \widehat L$
$\widetilde {L}_{\lambda }= \widehat L$
We now study
![]() $W(\lambda )$
and
$W(\lambda )$
and
![]() $W(\widehat {\lambda })$
for characters
$W(\widehat {\lambda })$
for characters
![]() $\lambda \in \mathbb {M}^{(\widehat L)}$
, where
$\lambda \in \mathbb {M}^{(\widehat L)}$
, where
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
is standardized. We prove statements on the characters of
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
is standardized. We prove statements on the characters of
![]() $W(\widehat {\lambda })$
and their possible extensions to
$W(\widehat {\lambda })$
and their possible extensions to
![]() $W(\lambda )$
. The results later imply that there exists some
$W(\lambda )$
. The results later imply that there exists some
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N$
-transversal in
$\widetilde N$
-transversal in
![]() $\mathrm {Irr}(N\mid \mathbb {M}^{(\widehat L)})$
.
$\mathrm {Irr}(N\mid \mathbb {M}^{(\widehat L)})$
.
In the following, we study the Clifford theory of
![]() $W(\widehat {\lambda })\lhd K(\lambda )$
for
$W(\widehat {\lambda })\lhd K(\lambda )$
for
![]() $\lambda \in \mathbb {M}^{(\widehat L)}$
, where
$\lambda \in \mathbb {M}^{(\widehat L)}$
, where
![]() $K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
.
$K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
.
Lemma 6.29. Assume
![]() $|\operatorname Z({{{{\mathbf G}}^F}})|=2$
or equivalently
$|\operatorname Z({{{{\mathbf G}}^F}})|=2$
or equivalently
![]() $q\equiv 3 (4)$
and
$q\equiv 3 (4)$
and
![]() $2\nmid l$
. Every
$2\nmid l$
. Every
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
satisfies
$\lambda \in \mathrm {Irr}_{cusp}(L)$
satisfies
![]() $\widehat L\leq \widetilde {L}_{\lambda }$
. Then
$\widehat L\leq \widetilde {L}_{\lambda }$
. Then
![]() $\mathrm {Irr}_{cusp}(N\mid \mathbb {T}\cap \mathbb {M}^{(\widehat L)}) $
is an
$\mathrm {Irr}_{cusp}(N\mid \mathbb {T}\cap \mathbb {M}^{(\widehat L)}) $
is an
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde {L}$
-transversal of
$\widetilde {L}$
-transversal of
![]() $\mathrm {Irr}_{cusp}(N\mid \mathbb {M}^{(\widehat L)})$
.
$\mathrm {Irr}_{cusp}(N\mid \mathbb {M}^{(\widehat L)})$
.
Proof. The arguments given in Lemma 6.3 show the statement.
According to Lemma 6.29, we can now assume
![]() $\operatorname Z({{{{\mathbf G}}^F}})=\operatorname Z({{\mathbf G}})$
. We do that until the end of the section.
$\operatorname Z({{{{\mathbf G}}^F}})=\operatorname Z({{\mathbf G}})$
. We do that until the end of the section.
Lemma 6.30. If
![]() $|\operatorname Z({{{{\mathbf G}}^F}})|=4$
and
$|\operatorname Z({{{{\mathbf G}}^F}})|=4$
and
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
with
$\lambda \in \mathrm {Irr}_{cusp}(L)$
with
![]() $\widetilde {L}_{\lambda }=\widehat L$
, then
$\widetilde {L}_{\lambda }=\widehat L$
, then
![]() $-1\in \mathbb D$
and
$-1\in \mathbb D$
and
![]() $\widehat {\lambda }_{-1}^{t_{{\underline {l}},2}}\neq \widehat {\lambda }_{-1}$
. Moreover,
$\widehat {\lambda }_{-1}^{t_{{\underline {l}},2}}\neq \widehat {\lambda }_{-1}$
. Moreover,
![]() $\widehat {\lambda }_{-1}^{\mathbf {n}_{e_1}(\varpi )}=\widehat {\lambda }_{-1}$
, if
$\widehat {\lambda }_{-1}^{\mathbf {n}_{e_1}(\varpi )}=\widehat {\lambda }_{-1}$
, if
![]() $h_0\in \ker (\lambda )$
or
$h_0\in \ker (\lambda )$
or
![]() ${\mathsf {type}}(\Phi _{-1})$
is not of type
${\mathsf {type}}(\Phi _{-1})$
is not of type
![]() $\mathrm {D}_{|J_{-1}|}$
.
$\mathrm {D}_{|J_{-1}|}$
.
Proof. Recall that maximal extendibility holds with respect to
![]() $L\lhd \widetilde {L}$
(see Theorem 2.17). Accordingly,
$L\lhd \widetilde {L}$
(see Theorem 2.17). Accordingly,
![]() $\widetilde {L}_{\lambda }=\widehat L$
implies that
$\widetilde {L}_{\lambda }=\widehat L$
implies that
![]() $\lambda $
is not
$\lambda $
is not
![]() $t_{{\underline {l}},2}$
-stable for the element
$t_{{\underline {l}},2}$
-stable for the element
![]() $t_{{\underline {l}},2}\in {\mathbf T}$
from Lemma 3.13. If
$t_{{\underline {l}},2}\in {\mathbf T}$
from Lemma 3.13. If
![]() $\zeta \in {\mathbb {F}}^{\times }$
with
$\zeta \in {\mathbb {F}}^{\times }$
with
![]() $\zeta ^{(q-1)_2}=\varpi $
and
$\zeta ^{(q-1)_2}=\varpi $
and
![]() $t_{I,2}:={\mathbf h} _I(\zeta )$
as in Lemma 6.13, then
$t_{I,2}:={\mathbf h} _I(\zeta )$
as in Lemma 6.13, then
![]() $t_{{\underline {l}},2}=\prod _{I\in {\mathcal O}} t_{I,2}$
. Recall that
$t_{{\underline {l}},2}=\prod _{I\in {\mathcal O}} t_{I,2}$
. Recall that
![]() $\widetilde {L}=\widehat L{\left\langle t_{{\underline {l}},2}\right\rangle }$
. The character
$\widetilde {L}=\widehat L{\left\langle t_{{\underline {l}},2}\right\rangle }$
. The character
![]() $\widehat {\lambda }$
is
$\widehat {\lambda }$
is
![]() $t_{{\underline {l}},2}$
-stable, if
$t_{{\underline {l}},2}$
-stable, if
![]() $\widehat {\lambda }_I$
is
$\widehat {\lambda }_I$
is
![]() $t_{I,2}$
-stable for every
$t_{I,2}$
-stable for every
![]() $I\in {\mathcal O}$
. For
$I\in {\mathcal O}$
. For
![]() $I\in {\mathcal O}\setminus \{ J_{-1}\}$
, we see
$I\in {\mathcal O}\setminus \{ J_{-1}\}$
, we see
![]() $t_{I,2}\in {\mathrm {C}}_{{{\mathbf L}}_I}(\widehat L_I)$
and hence
$t_{I,2}\in {\mathrm {C}}_{{{\mathbf L}}_I}(\widehat L_I)$
and hence
![]() $\widehat {\lambda }_I$
is
$\widehat {\lambda }_I$
is
![]() $t_{I,2}$
-stable. As
$t_{I,2}$
-stable. As
![]() $\widehat {\lambda }$
is not
$\widehat {\lambda }$
is not
![]() $t_{{\underline {l}},2}$
-stable,
$t_{{\underline {l}},2}$
-stable,
![]() $-1\in \mathbb D$
and
$-1\in \mathbb D$
and
![]() $\widehat {\lambda }_{-1}$
is not
$\widehat {\lambda }_{-1}$
is not
![]() $t_{{\underline {l}},2}$
-stable.
$t_{{\underline {l}},2}$
-stable.
In the next step, we prove
![]() $\widehat {\lambda }_{-1}^{\mathbf {n}_{e_1}(\varpi )}=\widehat {\lambda }_{-1}$
. Since
$\widehat {\lambda }_{-1}^{\mathbf {n}_{e_1}(\varpi )}=\widehat {\lambda }_{-1}$
. Since
![]() $\lambda _{-1}^{t_{{\underline {l}},2}}\neq \lambda _{-1}$
, Proposition 5.3 implies that
$\lambda _{-1}^{t_{{\underline {l}},2}}\neq \lambda _{-1}$
, Proposition 5.3 implies that
![]() $\widehat {\lambda }_{-1}$
is
$\widehat {\lambda }_{-1}$
is
![]() $\gamma $
-stable, if
$\gamma $
-stable, if
![]() ${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{|J_{-1}|}$
. We consider the other possible values of
${\mathsf {type}}(\Phi _{-1})=\mathrm {D}_{|J_{-1}|}$
. We consider the other possible values of
![]() ${\mathsf {type}}(\Phi _{{-1}})$
. We first assume
${\mathsf {type}}(\Phi _{{-1}})$
. We first assume
![]() ${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_1\times \mathrm A_1$
. Then
${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_1\times \mathrm A_1$
. Then
![]() $L_{-1}=\operatorname {SL}_2(q)\times \operatorname {SL}_2(q)$
. Let
$L_{-1}=\operatorname {SL}_2(q)\times \operatorname {SL}_2(q)$
. Let
![]() $\lambda _{-1,1},\lambda _{-1,2}\in \mathrm {Irr}(\operatorname {SL}_2(q))$
such that
$\lambda _{-1,1},\lambda _{-1,2}\in \mathrm {Irr}(\operatorname {SL}_2(q))$
such that
![]() ${\left. \lambda \right\rceil _{{L_{-1}}}} = \lambda _{-1,1}\times \lambda _{-1,2}$
. By the proof of Proposition 4.8,
${\left. \lambda \right\rceil _{{L_{-1}}}} = \lambda _{-1,1}\times \lambda _{-1,2}$
. By the proof of Proposition 4.8,
![]() $\widetilde {L}_{\lambda }\leq \widehat L$
implies that both characters
$\widetilde {L}_{\lambda }\leq \widehat L$
implies that both characters
![]() $\lambda _{-1,1}$
and
$\lambda _{-1,1}$
and
![]() $\lambda _{-1,2}$
are not
$\lambda _{-1,2}$
are not
![]() $\operatorname {GL}_2(q)$
-stable. Additionally, they are cuspidal. Following [Reference BonnaféB
Reference Bonnafé2, Table 5.4], the characters
$\operatorname {GL}_2(q)$
-stable. Additionally, they are cuspidal. Following [Reference BonnaféB
Reference Bonnafé2, Table 5.4], the characters
![]() $\lambda _{-1,1}$
and
$\lambda _{-1,1}$
and
![]() $\lambda _{-1,2}$
are uniquely determined up to
$\lambda _{-1,2}$
are uniquely determined up to
![]() $\operatorname {GL}_2(q)$
-conjugation. After applying some
$\operatorname {GL}_2(q)$
-conjugation. After applying some
![]() $\widetilde {L}$
-conjugation, we obtain that
$\widetilde {L}$
-conjugation, we obtain that
![]() $\lambda _{-1,1}$
and
$\lambda _{-1,1}$
and
![]() $\lambda _{-1,2}$
are
$\lambda _{-1,2}$
are
![]() $\mathbf {n} _{e_1}(\varpi )$
-conjugate. As
$\mathbf {n} _{e_1}(\varpi )$
-conjugate. As
![]() $\widehat L$
induces on the
$\widehat L$
induces on the
![]() $\operatorname {SL}_2(q)$
-factors of
$\operatorname {SL}_2(q)$
-factors of
![]() $L_{-1}$
simultaneous (non-inner) diagonal automorphisms, the set
$L_{-1}$
simultaneous (non-inner) diagonal automorphisms, the set
![]() $\mathrm {Irr}(\widehat L_{-1}|{\lambda _{-1}})$
contains only one character; hence,
$\mathrm {Irr}(\widehat L_{-1}|{\lambda _{-1}})$
contains only one character; hence,
![]() $\widehat {\lambda }_{-1}$
is again
$\widehat {\lambda }_{-1}$
is again
![]() $\mathbf {n}_{e_1}(\varpi )$
-stable.
$\mathbf {n}_{e_1}(\varpi )$
-stable.
It remains to consider the case where
![]() ${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_3$
. Again, the character
${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_3$
. Again, the character
![]() $\lambda _{-1}$
is not
$\lambda _{-1}$
is not
![]() $\widetilde {L}$
-stable. Via the isomorphism
$\widetilde {L}$
-stable. Via the isomorphism
![]() $L_{-1}\cong \operatorname {SL}_4(q)$
, we see that
$L_{-1}\cong \operatorname {SL}_4(q)$
, we see that
![]() $t_{{\underline {l}},2}$
induces on
$t_{{\underline {l}},2}$
induces on
![]() $\operatorname {SL}_4(q)$
a diagonal automorphism corresponding to a generator of
$\operatorname {SL}_4(q)$
a diagonal automorphism corresponding to a generator of
![]() $\operatorname Z(\operatorname {SL}_4(q))$
in the sense of 2.16
(b) (see also the proof of Proposition 4.8). We take any
$\operatorname Z(\operatorname {SL}_4(q))$
in the sense of 2.16
(b) (see also the proof of Proposition 4.8). We take any
![]() $\chi \in \mathrm {Irr}(\operatorname {GL}_4(q)\mid \lambda _{-1})$
. Then
$\chi \in \mathrm {Irr}(\operatorname {GL}_4(q)\mid \lambda _{-1})$
. Then
![]() $\chi $
is cuspidal (see Lemma 2.15
(c)). Using the description of cuspidal characters of general linear groups recalled in the proof of Proposition 5.1, we let
$\chi $
is cuspidal (see Lemma 2.15
(c)). Using the description of cuspidal characters of general linear groups recalled in the proof of Proposition 5.1, we let
![]() $s\in \operatorname {GL}_4(q)$
and
$s\in \operatorname {GL}_4(q)$
and
![]() $\zeta \in {\mathbb {F}}^{\times }$
such that
$\zeta \in {\mathbb {F}}^{\times }$
such that
![]() $\chi $
belongs to the rational Lusztig series of s and
$\chi $
belongs to the rational Lusztig series of s and
![]() $\zeta \in {\mathbb {F}}_{q^4}\setminus {\mathbb {F}}_{q^2}$
is an eigenvalue of s. Let
$\zeta \in {\mathbb {F}}_{q^4}\setminus {\mathbb {F}}_{q^2}$
is an eigenvalue of s. Let
![]() $\det :\operatorname {GL}_4({\mathbb {F}})\rightarrow {\mathbb {F}}^{\times }$
denote the determinant and
$\det :\operatorname {GL}_4({\mathbb {F}})\rightarrow {\mathbb {F}}^{\times }$
denote the determinant and
![]() $\det ^*$
the associated linear character of
$\det ^*$
the associated linear character of
![]() $\operatorname {GL}_4({\mathbb {F}})$
with kernel
$\operatorname {GL}_4({\mathbb {F}})$
with kernel
![]() $\operatorname {SL}_4({\mathbb {F}})$
. By the assumptions on
$\operatorname {SL}_4({\mathbb {F}})$
. By the assumptions on
![]() $\chi $
, we see that
$\chi $
, we see that
![]() $\chi =\chi (\det ^*)^{\frac {q-1}2}$
and hence s and
$\chi =\chi (\det ^*)^{\frac {q-1}2}$
and hence s and
![]() $-s$
are conjugate. Then
$-s$
are conjugate. Then
![]() $-\zeta \in \{\zeta , \zeta ^q, \zeta ^{q^2},\zeta ^{q^3} \}$
. Hence, using again o to denote multiplicative order,
$-\zeta \in \{\zeta , \zeta ^q, \zeta ^{q^2},\zeta ^{q^3} \}$
. Hence, using again o to denote multiplicative order,
![]() $o(\zeta )_2=2(q^2-1)_2$
, as
$o(\zeta )_2=2(q^2-1)_2$
, as
![]() $-\zeta \in \{\zeta , \zeta ^q, \zeta ^{q^3} \}$
would imply that
$-\zeta \in \{\zeta , \zeta ^q, \zeta ^{q^3} \}$
would imply that
![]() $\zeta \in {\mathbb {F}}_{q^2}$
or
$\zeta \in {\mathbb {F}}_{q^2}$
or
![]() $\zeta \in {\mathbb {F}}_{q^6}$
, contradicting
$\zeta \in {\mathbb {F}}_{q^6}$
, contradicting
![]() $\zeta \in {\mathbb {F}}_{q^4}\setminus {\mathbb {F}}_{q^2}$
. In order to compute
$\zeta \in {\mathbb {F}}_{q^4}\setminus {\mathbb {F}}_{q^2}$
. In order to compute
![]() $\ker ({\left. \chi \right\rceil _{{\operatorname Z(\operatorname {SL}_4(q))}}})$
, we see that
$\ker ({\left. \chi \right\rceil _{{\operatorname Z(\operatorname {SL}_4(q))}}})$
, we see that
![]() $\det s= \zeta ^{\frac {q^4-1}{q-1}}$
is not a square in
$\det s= \zeta ^{\frac {q^4-1}{q-1}}$
is not a square in
![]() ${\mathbb {F}}_q^{\times }$
since
${\mathbb {F}}_q^{\times }$
since
![]() $o(\zeta )_2=2(q^2-1)_2$
. This contradicts
$o(\zeta )_2=2(q^2-1)_2$
. This contradicts
![]() $h_0\in \ker (\lambda )$
, as
$h_0\in \ker (\lambda )$
, as
![]() $h_0$
corresponds to the central involution of
$h_0$
corresponds to the central involution of
![]() $\operatorname {SL}_4(q)$
. Hence, there exists no cuspidal character
$\operatorname {SL}_4(q)$
. Hence, there exists no cuspidal character
![]() $\lambda _{-1}$
of
$\lambda _{-1}$
of
![]() $L_{-1}$
that satisfies
$L_{-1}$
that satisfies
![]() $h_0\in \ker (\lambda )$
and
$h_0\in \ker (\lambda )$
and
![]() $\lambda _{-1}^{t_{{\underline {l}},2}}\neq \lambda _{-1}$
. This shows that
$\lambda _{-1}^{t_{{\underline {l}},2}}\neq \lambda _{-1}$
. This shows that
![]() ${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_3$
is not possible. This finishes our proof.
${\mathsf {type}}(\Phi _{{-1}})=\mathrm A_3$
is not possible. This finishes our proof.
Lemma 6.31. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
and
$\lambda \in \mathrm {Irr}_{cusp}(L)$
and
![]() $\widehat {\lambda } \in \mathrm {Irr}(\widehat L\mid \lambda )$
such that
$\widehat {\lambda } \in \mathrm {Irr}(\widehat L\mid \lambda )$
such that
![]() $h_0\notin \ker (\lambda )$
and
$h_0\notin \ker (\lambda )$
and
![]() $W(\widehat {\lambda })\neq W(\lambda )$
. Then maximal extendibility holds with respect to
$W(\widehat {\lambda })\neq W(\lambda )$
. Then maximal extendibility holds with respect to
![]() $W(\widehat {\lambda })\lhd K(\lambda )$
.
$W(\widehat {\lambda })\lhd K(\lambda )$
.
Proof. We first determine
![]() $W(\widehat {\lambda })$
. Denote
$W(\widehat {\lambda })$
. Denote
![]() $c_{-1}:=c_{J_{-1}}$
. As the character
$c_{-1}:=c_{J_{-1}}$
. As the character
![]() $\mathrm {Irr}({\left. \lambda \right\rceil _{{\operatorname Z(L_{-1})}}})$
is not
$\mathrm {Irr}({\left. \lambda \right\rceil _{{\operatorname Z(L_{-1})}}})$
is not
![]() $c_{-1}$
-stable,
$c_{-1}$
-stable,
![]() $\lambda _{-1}$
is not
$\lambda _{-1}$
is not
![]() $c_{-1}$
-stable. This implies
$c_{-1}$
-stable. This implies
![]() $J_{-1}\notin {\mathcal O}_c(\widehat {\lambda })$
.
$J_{-1}\notin {\mathcal O}_c(\widehat {\lambda })$
.
If
![]() $I\in {\mathcal O}_1$
,
$I\in {\mathcal O}_1$
,
![]() $\widehat {\lambda }_I$
is a linear character. Since
$\widehat {\lambda }_I$
is a linear character. Since
![]() $h_0\notin \ker (\lambda )$
and hence
$h_0\notin \ker (\lambda )$
and hence
![]() $h_0\notin \ker (\widehat {\lambda }_I)$
, the order of
$h_0\notin \ker (\widehat {\lambda }_I)$
, the order of
![]() $\widehat {\lambda }_I$
is divisible by
$\widehat {\lambda }_I$
is divisible by
![]() $2(q-1)_2\geq 4$
. Hence,
$2(q-1)_2\geq 4$
. Hence,
![]() ${\mathcal O}_{c}(\widehat {\lambda })\cap {\mathcal O}_1= \emptyset $
.
${\mathcal O}_{c}(\widehat {\lambda })\cap {\mathcal O}_1= \emptyset $
.
Together with Lemma 6.14 and Corollary 6.22(a), this leads to
![]() ${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{{\mathrm {even}}}}{\mathcal O}_d$
. The structure of
${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{{\mathrm {even}}}}{\mathcal O}_d$
. The structure of
![]() $W(\widehat {\lambda })$
is given by Lemma 6.13, and we observe
$W(\widehat {\lambda })$
is given by Lemma 6.13, and we observe
![]() $\overline W(\widehat {\lambda })=W(\widehat {\lambda })$
. As in the proof of Lemma 6.26, we can apply Lemma 4.6, and we see that maximal extendibility holds with respect to
$\overline W(\widehat {\lambda })=W(\widehat {\lambda })$
. As in the proof of Lemma 6.26, we can apply Lemma 4.6, and we see that maximal extendibility holds with respect to
![]() $W(\widehat {\lambda })\lhd {\mathrm {N}}_{\overline W}(W(\widehat {\lambda }))$
. Because of
$W(\widehat {\lambda })\lhd {\mathrm {N}}_{\overline W}(W(\widehat {\lambda }))$
. Because of
![]() $K(\lambda )\leq {\mathrm {N}}_{\overline W}(W(\widehat {\lambda }))$
, this proves maximal extendibility with respect to
$K(\lambda )\leq {\mathrm {N}}_{\overline W}(W(\widehat {\lambda }))$
, this proves maximal extendibility with respect to
![]() $W(\widehat {\lambda })\lhd K(\lambda )$
.
$W(\widehat {\lambda })\lhd K(\lambda )$
.
As in Lemma 6.25, we associate with
![]() $\lambda $
subsets
$\lambda $
subsets
![]() $Q^1(\widehat {\lambda })$
and
$Q^1(\widehat {\lambda })$
and
![]() $Q^2(\widehat {\lambda })$
of
$Q^2(\widehat {\lambda })$
of
![]() ${\mathcal O}$
. Recall
${\mathcal O}$
. Recall
![]() $ K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{{L}}}}$
, whenever
$ K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{{L}}}}$
, whenever
![]() ${{\mathbf G}}$
is not of type
${{\mathbf G}}$
is not of type
![]() $\mathrm {D}_4$
.
$\mathrm {D}_4$
.
Lemma 6.32. Let
![]() $\lambda \in \mathbb {M}^{(\widehat L)}\cap \mathrm {Irr}(L\mid 1_{{\left\langle h_0\right\rangle }})$
and
$\lambda \in \mathbb {M}^{(\widehat L)}\cap \mathrm {Irr}(L\mid 1_{{\left\langle h_0\right\rangle }})$
and
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
with
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
with
![]() $W(\lambda )\neq W(\widehat {\lambda })$
. Let
$W(\lambda )\neq W(\widehat {\lambda })$
. Let
Let
![]() ${\overline W^j (\widehat {\lambda })}:=\overline W(\widehat {\lambda })\cap {\mathcal {S}}_{\pm Q^j(\widehat {\lambda })} $
,
${\overline W^j (\widehat {\lambda })}:=\overline W(\widehat {\lambda })\cap {\mathcal {S}}_{\pm Q^j(\widehat {\lambda })} $
,
![]() ${W^j(\widehat {\lambda })}:=\overline W^j(\widehat {\lambda })\cap W$
,
${W^j(\widehat {\lambda })}:=\overline W^j(\widehat {\lambda })\cap W$
,
![]() ${\widehat L^{(i)}}:={\left\langle \widehat L_I\mid I \in Q^i(\widehat {\lambda })\right\rangle }$
, and
${\widehat L^{(i)}}:={\left\langle \widehat L_I\mid I \in Q^i(\widehat {\lambda })\right\rangle }$
, and
![]() ${L^{(i)}}:=L\cap \widehat L^{(i)}$
, for
${L^{(i)}}:=L\cap \widehat L^{(i)}$
, for
![]() $i,j\in \underline {2}$
.
$i,j\in \underline {2}$
.
-
(a) Then
 $K(\lambda )$
stabilizes
$K(\lambda )$
stabilizes
 $Q^1(\widehat {\lambda })$
and where
$Q^1(\widehat {\lambda })$
and where $$ \begin{align*}W(\widehat{\lambda})=W^1(\widehat{\lambda}^{(1)})\times W^2(\widehat{\lambda}^{(2)}),\end{align*} $$
$$ \begin{align*}W(\widehat{\lambda})=W^1(\widehat{\lambda}^{(1)})\times W^2(\widehat{\lambda}^{(2)}),\end{align*} $$
 $\widehat {\lambda }^{(i)}\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L^{(i)}}}})$
.
$\widehat {\lambda }^{(i)}\in \mathrm {Irr}({\left. \widehat {\lambda }\right\rceil _{{\widehat L^{(i)}}}})$
.
-
(b) If
 $x\in W(\lambda ) \setminus W(\widehat {\lambda })$
, then
$x\in W(\lambda ) \setminus W(\widehat {\lambda })$
, then
 $x=x_1x_2$
for some
$x=x_1x_2$
for some
 $x_i\in W^i(\lambda ^{(i)})$
(
$x_i\in W^i(\lambda ^{(i)})$
(
 $i\in \underline 2$
), where
$i\in \underline 2$
), where
 $\lambda ^{(i)}\in \mathrm {Irr}({\left. \lambda \right\rceil _{{L^{(i)}}}})$
.
$\lambda ^{(i)}\in \mathrm {Irr}({\left. \lambda \right\rceil _{{L^{(i)}}}})$
. -
(c)
 $|{\mathcal O}_d\cap Q^2(\widehat {\lambda })|$
is even for every
$|{\mathcal O}_d\cap Q^2(\widehat {\lambda })|$
is even for every
 $d\in \mathbb D_{\mathrm {odd}}\setminus \{-1\}$
.
$d\in \mathbb D_{\mathrm {odd}}\setminus \{-1\}$
. -
(d) Let
 $\overline W^i:=\overline W \cap {\mathcal {S}}_{\pm Q^i(\widehat {\lambda })}$
and
$\overline W^i:=\overline W \cap {\mathcal {S}}_{\pm Q^i(\widehat {\lambda })}$
and
 ${K^i( \lambda )}:= (\overline W^i)_{{\left. (\lambda ^{(i)})^{ L^{(i)}{\left\langle F_p \right\rangle }}\right\rceil _{{L^{(i)}}}}}$
for
${K^i( \lambda )}:= (\overline W^i)_{{\left. (\lambda ^{(i)})^{ L^{(i)}{\left\langle F_p \right\rangle }}\right\rceil _{{L^{(i)}}}}}$
for
 $i\in \underline 2$
. If
$i\in \underline 2$
. If
 ${\mathcal O}_1\cap Q^1(\widehat {\lambda })\neq \emptyset $
, then
${\mathcal O}_1\cap Q^1(\widehat {\lambda })\neq \emptyset $
, then
 $K(\lambda ) \leq K^1(\lambda )\times {\mathrm {N}}_{\overline W^2}( W^2(\widehat {\lambda }))$
.
$K(\lambda ) \leq K^1(\lambda )\times {\mathrm {N}}_{\overline W^2}( W^2(\widehat {\lambda }))$
.
Proof. First note that
![]() $\widehat N$
normalizes the groups
$\widehat N$
normalizes the groups
![]() ${{\mathbf L}}_I$
(
${{\mathbf L}}_I$
(
![]() $I\in {\mathcal O}$
) and hence there is a well-defined action of
$I\in {\mathcal O}$
) and hence there is a well-defined action of
![]() $\widehat W$
on
$\widehat W$
on
![]() ${\mathcal O}$
. Now,
${\mathcal O}$
. Now,
![]() $Q^1(\widehat {\lambda })$
is defined using
$Q^1(\widehat {\lambda })$
is defined using
![]() $\widehat {\lambda }$
(and is independent of the choice of
$\widehat {\lambda }$
(and is independent of the choice of
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
). Note that by this definition any element in
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
). Note that by this definition any element in
![]() $\widehat N_{\lambda }$
stabilizes
$\widehat N_{\lambda }$
stabilizes
![]() $Q^1(\widehat {\lambda })$
. Without loss of generality, we can assume that
$Q^1(\widehat {\lambda })$
. Without loss of generality, we can assume that
![]() $\widehat {\lambda }$
is standardized and hence
$\widehat {\lambda }$
is standardized and hence
![]() $\overline W(\lambda )$
is given in Lemma 6.13.
$\overline W(\lambda )$
is given in Lemma 6.13.
Accordingly,
![]() $\overline W(\widehat {\lambda })= \overline W^1(\widehat {\lambda })\times \overline W^2(\widehat {\lambda })$
. As
$\overline W(\widehat {\lambda })= \overline W^1(\widehat {\lambda })\times \overline W^2(\widehat {\lambda })$
. As
![]() $\lambda \in \mathrm {Irr}(L\mid 1_{{\left\langle h_0\right\rangle }})$
, Corollary 6.22 implies
$\lambda \in \mathrm {Irr}(L\mid 1_{{\left\langle h_0\right\rangle }})$
, Corollary 6.22 implies
![]() ${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
. By the definition of
${\mathcal O}_c(\widehat {\lambda })\subseteq \bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
. By the definition of
![]() $Q^2(\widehat {\lambda })$
, we observe
$Q^2(\widehat {\lambda })$
, we observe
![]() $\overline W^2(\widehat {\lambda })=W^2(\widehat {\lambda })$
.
$\overline W^2(\widehat {\lambda })=W^2(\widehat {\lambda })$
.
According to Lemma 6.8(d),
![]() $\overline W(\widehat {\lambda })$
is the direct product of the groups
$\overline W(\widehat {\lambda })$
is the direct product of the groups
![]() $\overline W_d(\widehat {\lambda })$
, where
$\overline W_d(\widehat {\lambda })$
, where
![]() $\overline W_d(\widehat {\lambda }):=(\overline V_d)_{\widehat {\lambda }}/H_d$
. For
$\overline W_d(\widehat {\lambda }):=(\overline V_d)_{\widehat {\lambda }}/H_d$
. For
![]() $\overline W^1(\widehat {\lambda })$
we note that
$\overline W^1(\widehat {\lambda })$
we note that
where
![]() $ {Q^{1,j}(\lambda )}:=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=j\}$
and
$ {Q^{1,j}(\lambda )}:=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=j\}$
and
![]() $\overline W^{1,j}(\widehat {\lambda }):=\overline W^1(\widehat {\lambda })\cap {\mathcal {S}}_{\pm Q^{1,4}(\lambda )}$
. This proves that
$\overline W^{1,j}(\widehat {\lambda }):=\overline W^1(\widehat {\lambda })\cap {\mathcal {S}}_{\pm Q^{1,4}(\lambda )}$
. This proves that
![]() $\overline W(\widehat {\lambda })=\overline W^1(\widehat {\lambda })\times \overline W^2(\widehat {\lambda })$
. By the above
$\overline W(\widehat {\lambda })=\overline W^1(\widehat {\lambda })\times \overline W^2(\widehat {\lambda })$
. By the above
![]() $W^2(\widehat {\lambda })=\overline W^2(\widehat {\lambda })$
and hence
$W^2(\widehat {\lambda })=\overline W^2(\widehat {\lambda })$
and hence
![]() $W(\widehat {\lambda })=\overline W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })= W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })$
. Since
$W(\widehat {\lambda })=\overline W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })= W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })$
. Since
![]() $\widehat {\lambda }=\widehat {\lambda }^{(1)}\times \widehat {\lambda }^{(2)}$
, we note that
$\widehat {\lambda }=\widehat {\lambda }^{(1)}\times \widehat {\lambda }^{(2)}$
, we note that
![]() $W^1(\widehat {\lambda }^{(1)})=W^1(\widehat {\lambda }^{(1)})$
and
$W^1(\widehat {\lambda }^{(1)})=W^1(\widehat {\lambda }^{(1)})$
and
![]() $W^2(\widehat {\lambda })=W^2(\widehat {\lambda }^{(2)})$
, proving (a).
$W^2(\widehat {\lambda })=W^2(\widehat {\lambda }^{(2)})$
, proving (a).
As
![]() $x\in K(\lambda )$
stabilizes
$x\in K(\lambda )$
stabilizes
![]() $Q^1(\widehat {\lambda })$
by (a), it can be written as product
$Q^1(\widehat {\lambda })$
by (a), it can be written as product
![]() $x_1x_2$
where
$x_1x_2$
where
![]() $x_i\in \overline W^i( \lambda ^{(i)})$
. Since
$x_i\in \overline W^i( \lambda ^{(i)})$
. Since
![]() $\widehat {\lambda }^x=\widehat {\lambda } \mu $
for the faithful character
$\widehat {\lambda }^x=\widehat {\lambda } \mu $
for the faithful character
![]() $\mu $
of
$\mu $
of
![]() $\widehat L/L$
, it satisfies
$\widehat L/L$
, it satisfies
![]() $(\widehat {\lambda } ^{(i)})^x= \widehat {\lambda }^{(i)} \mu ^{(i)}$
where
$(\widehat {\lambda } ^{(i)})^x= \widehat {\lambda }^{(i)} \mu ^{(i)}$
where
![]() $\mu ^{(i)}={\left. \mu \right\rceil _{{\widehat L^{(i)}}}}$
with
$\mu ^{(i)}={\left. \mu \right\rceil _{{\widehat L^{(i)}}}}$
with
![]() $\widehat L^{(i)}:={\left\langle \widehat L_I\mid I \in Q^i(\lambda )\right\rangle }$
. Hence,
$\widehat L^{(i)}:={\left\langle \widehat L_I\mid I \in Q^i(\lambda )\right\rangle }$
. Hence,
![]() $(\widehat {\lambda } ^{(i)})^{x_i}= \widehat {\lambda }^{(i)} \mu ^{(i)}$
.
$(\widehat {\lambda } ^{(i)})^{x_i}= \widehat {\lambda }^{(i)} \mu ^{(i)}$
.
In the following, we show that any element
![]() $x_2 \in \overline W^2$
with
$x_2 \in \overline W^2$
with
![]() $(\widehat {\lambda } ^{(2)})^{x_i}= \widehat {\lambda }^{(2)} \mu ^{(i)}$
also satisfies
$(\widehat {\lambda } ^{(2)})^{x_i}= \widehat {\lambda }^{(2)} \mu ^{(i)}$
also satisfies
![]() $x_2\in W$
. This then implies the statement in part (b). Recall that
$x_2\in W$
. This then implies the statement in part (b). Recall that
![]() $\overline W_d\leq W$
for
$\overline W_d\leq W$
for
![]() $d\in \mathbb D_{\mathrm {even}}$
. Hence, without loss of generality, we can assume that
$d\in \mathbb D_{\mathrm {even}}$
. Hence, without loss of generality, we can assume that
![]() $Q^2(\widehat {\lambda })\subseteq {\mathcal O}_d$
for some
$Q^2(\widehat {\lambda })\subseteq {\mathcal O}_d$
for some
![]() $d\in \mathbb D_{\mathrm {odd}} \setminus \{ -1\}$
.
$d\in \mathbb D_{\mathrm {odd}} \setminus \{ -1\}$
.
For
![]() $I_0\in {\mathcal O}$
and
$I_0\in {\mathcal O}$
and
![]() $\kappa \in \mathrm {Irr}_{cusp}(\widetilde {L}_{I_0})$
, we set
$\kappa \in \mathrm {Irr}_{cusp}(\widetilde {L}_{I_0})$
, we set
Let
![]() $\mu _I$
be defined as in Lemma 6.14. Then
$\mu _I$
be defined as in Lemma 6.14. Then
![]() $x_2({\mathcal O}_{\kappa }(\widehat {\lambda }))= {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
(see 6.14(a)). With
$x_2({\mathcal O}_{\kappa }(\widehat {\lambda }))= {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
(see 6.14(a)). With
![]() $ {\overline {\mathcal O}_{\kappa }(\widehat {\lambda })}:={\mathcal O}_{\kappa }(\widehat {\lambda })\cup {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
, the element x can be written as product of
$ {\overline {\mathcal O}_{\kappa }(\widehat {\lambda })}:={\mathcal O}_{\kappa }(\widehat {\lambda })\cup {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
, the element x can be written as product of
![]() $x_{\overline {\mathcal O}_{\kappa }(\lambda )}\in {\mathcal {S}}_{\pm \overline {\mathcal O}_{\kappa }(\lambda )}$
where
$x_{\overline {\mathcal O}_{\kappa }(\lambda )}\in {\mathcal {S}}_{\pm \overline {\mathcal O}_{\kappa }(\lambda )}$
where
![]() $I\in {\mathcal O}$
and
$I\in {\mathcal O}$
and
![]() $\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
runs over the
$\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
runs over the
![]() ${\left\langle \mu _I\right\rangle }\times {\left\langle c_I\right\rangle }$
-orbits in
${\left\langle \mu _I\right\rangle }\times {\left\langle c_I\right\rangle }$
-orbits in
![]() $\mathrm {Irr}_{cusp}(\widehat L_I)$
. To prove
$\mathrm {Irr}_{cusp}(\widehat L_I)$
. To prove
![]() $x_2\in W$
, it is sufficient to prove
$x_2\in W$
, it is sufficient to prove
![]() $x_{\overline {\mathcal O}_{\kappa }(\lambda )}\in W$
. Hence, we assume
$x_{\overline {\mathcal O}_{\kappa }(\lambda )}\in W$
. Hence, we assume
![]() $Q^2(\widehat {\lambda })= {\mathcal O}_{\kappa }(\widehat {\lambda })\cup {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
for some
$Q^2(\widehat {\lambda })= {\mathcal O}_{\kappa }(\widehat {\lambda })\cup {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
for some
![]() $\kappa \in \mathrm {Irr}(\widehat L_{I_0})$
.
$\kappa \in \mathrm {Irr}(\widehat L_{I_0})$
.
If
![]() $I_0\in {\mathcal O}_1$
, we observe that
$I_0\in {\mathcal O}_1$
, we observe that
![]() $o(\kappa )\notin \{1,2,4\}$
by the definition of
$o(\kappa )\notin \{1,2,4\}$
by the definition of
![]() $Q^2(\widehat {\lambda })$
. This implies
$Q^2(\widehat {\lambda })$
. This implies
![]() $\kappa \mu _{I_0} \notin \{\kappa , \kappa ^{c_{I_0}} \}$
and hence
$\kappa \mu _{I_0} \notin \{\kappa , \kappa ^{c_{I_0}} \}$
and hence
![]() ${\mathcal O}_{\kappa }(\widehat {\lambda })\cap {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })=\emptyset $
. Note that
${\mathcal O}_{\kappa }(\widehat {\lambda })\cap {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })=\emptyset $
. Note that
![]() $\overline W^2(\widehat {\lambda })\leq W$
. The element
$\overline W^2(\widehat {\lambda })\leq W$
. The element
![]() $x_2$
satisfies
$x_2$
satisfies
![]() $x_2({\mathcal O}_{\kappa }(\widehat {\lambda })) = {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
as element of
$x_2({\mathcal O}_{\kappa }(\widehat {\lambda })) = {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
as element of
![]() ${\mathcal {S}}_{Q^2(\widehat {\lambda })}$
. Recall
${\mathcal {S}}_{Q^2(\widehat {\lambda })}$
. Recall
![]() $\widehat {\lambda }$
is standardized. Let
$\widehat {\lambda }$
is standardized. Let
![]() $I\in {\mathcal O}_{\kappa }(\widehat {\lambda })$
and
$I\in {\mathcal O}_{\kappa }(\widehat {\lambda })$
and
![]() $I'\in {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
. If
$I'\in {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
. If
![]() $\widehat {\lambda }_I$
and
$\widehat {\lambda }_I$
and
![]() $\widehat {\lambda }_{I'}$
are
$\widehat {\lambda }_{I'}$
are
![]() $V_S$
-conjugate,
$V_S$
-conjugate,
for every
![]() ${\epsilon }\in \{\pm 1\}$
as element of
${\epsilon }\in \{\pm 1\}$
as element of
![]() ${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. Otherwise,
${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. Otherwise,
for every
![]() ${\epsilon }\in \{\pm 1\}$
as element of
${\epsilon }\in \{\pm 1\}$
as element of
![]() ${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. In both cases, we see
${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. In both cases, we see
![]() $x_2\in W$
.
$x_2\in W$
.
Assume
![]() $I_0\in {\mathcal O}_d$
for
$I_0\in {\mathcal O}_d$
for
![]() $d\in \mathbb D_{\mathrm {odd}}\setminus \{\pm 1\}$
. Hence,
$d\in \mathbb D_{\mathrm {odd}}\setminus \{\pm 1\}$
. Hence,
![]() $L_{I_0}\cong \operatorname {GL}_d(q)$
by Lemma 4.2 and
$L_{I_0}\cong \operatorname {GL}_d(q)$
by Lemma 4.2 and
![]() $c_{I_0}$
acts on
$c_{I_0}$
acts on
![]() $L_{I_0}$
as a graph automorphism by Lemma 4.4(c). According to Lemma 6.15, we have
$L_{I_0}$
as a graph automorphism by Lemma 4.4(c). According to Lemma 6.15, we have
![]() $\kappa \neq \kappa ^{c_{I_0}}$
and
$\kappa \neq \kappa ^{c_{I_0}}$
and
![]() $\overline W^2(\widehat {\lambda })\leq W$
. Proposition 5.1(b) leads to
$\overline W^2(\widehat {\lambda })\leq W$
. Proposition 5.1(b) leads to
![]() $\kappa \mu _{I_0} \notin \{\kappa , \kappa ^{c_{I_0}} \}$
. We see again that
$\kappa \mu _{I_0} \notin \{\kappa , \kappa ^{c_{I_0}} \}$
. We see again that
![]() ${\mathcal O}_{\kappa }(\widehat {\lambda })$
and
${\mathcal O}_{\kappa }(\widehat {\lambda })$
and
![]() $ {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
are disjoint. This implies again that there exists some
$ {\mathcal O}_{\kappa \mu _{I_0}}(\widehat {\lambda })$
are disjoint. This implies again that there exists some
![]() ${\epsilon }'\in \{\pm 1\}$
such that
${\epsilon }'\in \{\pm 1\}$
such that
for every
![]() ${\epsilon }\in \{\pm 1\}$
as elements of
${\epsilon }\in \{\pm 1\}$
as elements of
![]() ${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. Again
${\mathcal {S}}_{\pm Q^2(\widehat {\lambda })}$
. Again
![]() $x_2\in W$
. Altogether this proves part (b).
$x_2\in W$
. Altogether this proves part (b).
The considerations above imply
![]() $|{\mathcal O}_{\kappa }(\widehat {\lambda })|=|{\mathcal O}_{\kappa \mu _I}(\widehat {\lambda })|$
for every
$|{\mathcal O}_{\kappa }(\widehat {\lambda })|=|{\mathcal O}_{\kappa \mu _I}(\widehat {\lambda })|$
for every
![]() $I\in {\mathcal O}$
and
$I\in {\mathcal O}$
and
![]() $\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
. If
$\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
. If
![]() ${\mathcal O}_{\kappa }(\widehat {\lambda })\subseteq Q^2(\widehat {\lambda })$
, the sets are disjoint so that
${\mathcal O}_{\kappa }(\widehat {\lambda })\subseteq Q^2(\widehat {\lambda })$
, the sets are disjoint so that
![]() $2\mid |\overline {\mathcal O}_{\kappa }(\widehat {\lambda })|$
. This also applies if
$2\mid |\overline {\mathcal O}_{\kappa }(\widehat {\lambda })|$
. This also applies if
![]() $I\in {\mathcal O}_1$
and
$I\in {\mathcal O}_1$
and
![]() $\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
with
$\kappa \in \mathrm {Irr}_{cusp}(\widehat L_I)$
with
![]() $o(\kappa )\mid 2$
. This gives part (c).
$o(\kappa )\mid 2$
. This gives part (c).
Recall
![]() $K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle } } \right\rceil _{L}}}$
. We see that
$K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle } } \right\rceil _{L}}}$
. We see that
![]() $Q^1(\kappa )=Q^1(\lambda )$
and
$Q^1(\kappa )=Q^1(\lambda )$
and
![]() $Q^2(\kappa )=Q^2(\lambda )$
for every constituent
$Q^2(\kappa )=Q^2(\lambda )$
for every constituent
![]() $\kappa $
of
$\kappa $
of
![]() ${\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{{L}}}$
. Accordingly, we see that
${\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{{L}}}$
. Accordingly, we see that
![]() $K(\lambda )\leq {\mathcal {S}}_{\pm Q^1(\lambda )}\times {\mathcal {S}}_{\pm Q^2(\lambda )} $
.
$K(\lambda )\leq {\mathcal {S}}_{\pm Q^1(\lambda )}\times {\mathcal {S}}_{\pm Q^2(\lambda )} $
.
By definition,
![]() $\lambda ^{(i)}$
is uniquely determined by
$\lambda ^{(i)}$
is uniquely determined by
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $w\in K(\lambda )$
,
$w\in K(\lambda )$
,
![]() $w_1\in {\mathcal {S}}_{\pm Q^1(\lambda )}$
, and
$w_1\in {\mathcal {S}}_{\pm Q^1(\lambda )}$
, and
![]() $w_2\in {\mathcal {S}}_{\pm Q^2(\lambda )}$
with
$w_2\in {\mathcal {S}}_{\pm Q^2(\lambda )}$
with
![]() $w=w_1w_2$
. As
$w=w_1w_2$
. As
![]() $\lambda ^{w_1w_2}$
is some
$\lambda ^{w_1w_2}$
is some
![]() $L{\left\langle F_p \right\rangle }$
conjugate of
$L{\left\langle F_p \right\rangle }$
conjugate of
![]() $\lambda $
, the character
$\lambda $
, the character
![]() $(\lambda ^{(1)})^{w}=(\lambda ^{(1)})^{w_1}$
is an
$(\lambda ^{(1)})^{w}=(\lambda ^{(1)})^{w_1}$
is an
![]() $L^{(1)} {\left\langle {F_p}\right\rangle }$
-conjugate of
$L^{(1)} {\left\langle {F_p}\right\rangle }$
-conjugate of
![]() $\lambda ^{(1)}$
. Hence,
$\lambda ^{(1)}$
. Hence,
![]() $w_1\in K^ 1(\lambda )$
. Analogously, we can argue for
$w_1\in K^ 1(\lambda )$
. Analogously, we can argue for
![]() $w_2$
and get
$w_2$
and get
![]() $w_2\in {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda }))$
, as required in (d).
$w_2\in {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda }))$
, as required in (d).
We study first the Clifford theory for
![]() $W(\widehat {\lambda })\lhd W(\lambda )$
by considering subgroups associated with
$W(\widehat {\lambda })\lhd W(\lambda )$
by considering subgroups associated with
![]() $Q^1(\widehat {\lambda })$
and
$Q^1(\widehat {\lambda })$
and
![]() $Q^2(\widehat {\lambda })$
.
$Q^2(\widehat {\lambda })$
.
Lemma 6.33. In the situation of Lemma 6.32, maximal extendibility holds with respect to
![]() $W^2(\widehat {\lambda }^{(2)})\lhd {\mathrm {N}}_{\overline W^2}(W(\widehat {\lambda }^{(2)}))$
.
$W^2(\widehat {\lambda }^{(2)})\lhd {\mathrm {N}}_{\overline W^2}(W(\widehat {\lambda }^{(2)}))$
.
Proof. Without loss of generality, we can assume that
![]() $\widehat {\lambda }$
is standardized. The structure of
$\widehat {\lambda }$
is standardized. The structure of
![]() $\overline W(\widehat {\lambda })$
is then given by Lemma 6.12. As in the proof of Lemma 6.26(a), the groups
$\overline W(\widehat {\lambda })$
is then given by Lemma 6.12. As in the proof of Lemma 6.26(a), the groups
![]() $W^2( \widehat {\lambda }^{(2)})$
and
$W^2( \widehat {\lambda }^{(2)})$
and
![]() ${\mathrm {N}}_{\overline W^2}(W(\widehat {\lambda }^{(2)}))$
satisfy Lemma 4.6 and accordingly maximal extendibility holds.
${\mathrm {N}}_{\overline W^2}(W(\widehat {\lambda }^{(2)}))$
satisfy Lemma 4.6 and accordingly maximal extendibility holds.
Proposition 6.34. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L\mid 1_{{\left\langle h_0\right\rangle }})$
,
$\lambda \in \mathrm {Irr}_{cusp}(L\mid 1_{{\left\langle h_0\right\rangle }})$
,
![]() $\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
$\widehat {\lambda }\in \mathrm {Irr}(\widehat L\mid \lambda )$
, and
![]() $\eta _0\in \mathrm {Irr}(W(\widehat {\lambda }))$
with
$\eta _0\in \mathrm {Irr}(W(\widehat {\lambda }))$
with
![]() $\widetilde {L}_{\lambda }=\widehat L$
.
$\widetilde {L}_{\lambda }=\widehat L$
.
-
(a) If
 $Q^1(\widehat {\lambda })={\mathcal O}$
, then every
$Q^1(\widehat {\lambda })={\mathcal O}$
, then every
 $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
 $K(\lambda )_{\eta _0}$
-stable.
$K(\lambda )_{\eta _0}$
-stable. -
(b) Maximal extendibility holds with respect to
 $W^1(\widehat {\lambda }^{(1)})\lhd K^1(\lambda ^{(1)})$
.
$W^1(\widehat {\lambda }^{(1)})\lhd K^1(\lambda ^{(1)})$
.
Proof. The statement in (a) is trivial if
![]() $W(\widehat {\lambda })= W(\lambda )$
. Hence, we assume in the following
$W(\widehat {\lambda })= W(\lambda )$
. Hence, we assume in the following
![]() $W(\widehat {\lambda })\neq W(\lambda )$
and
$W(\widehat {\lambda })\neq W(\lambda )$
and
![]() $Q^1(\widehat {\lambda })={\mathcal O}$
. According to Lemma 6.30,
$Q^1(\widehat {\lambda })={\mathcal O}$
. According to Lemma 6.30,
![]() $-1\in \mathbb D$
and
$-1\in \mathbb D$
and
![]() $\widehat {\lambda }_{-1}$
is
$\widehat {\lambda }_{-1}$
is
![]() $c_{J_{-1}}$
-stable, that is,
$c_{J_{-1}}$
-stable, that is,
In order to study those groups, we introduce more notation: For
![]() $j\in \{1,2,4\}$
, let
$j\in \{1,2,4\}$
, let
![]() $Q^{1,j}=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=j\}$
and
$Q^{1,j}=\{I\in {\mathcal O}_1\mid o(\widehat {\lambda }_I)=j\}$
and
![]() $l_j:= |Q^{1,j}|$
. Then
$l_j:= |Q^{1,j}|$
. Then
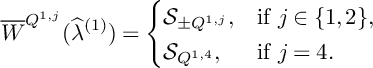 $$ \begin{align*}\overline W^{Q^{1,j}}(\widehat{\lambda}^{(1)}) =\begin{cases} {\mathcal{S}}_{\pm Q^{1,j}}, & \text{if }j\in \{1,2\},\\ {\mathcal{S}}_{ Q^{1,4}}, & \text{if }j=4. \end{cases}\end{align*} $$
$$ \begin{align*}\overline W^{Q^{1,j}}(\widehat{\lambda}^{(1)}) =\begin{cases} {\mathcal{S}}_{\pm Q^{1,j}}, & \text{if }j\in \{1,2\},\\ {\mathcal{S}}_{ Q^{1,4}}, & \text{if }j=4. \end{cases}\end{align*} $$
Accordingly,
![]() $\overline W^{1}(\widehat {\lambda })= \overline W_{-1}(\widehat {\lambda })\times {\mathcal {S}}_{\pm Q^{1,1}}\times {\mathcal {S}}_{\pm Q^{1,2}}\times {\mathcal {S}}_{ Q^{1,4}}$
. Additionally,
$\overline W^{1}(\widehat {\lambda })= \overline W_{-1}(\widehat {\lambda })\times {\mathcal {S}}_{\pm Q^{1,1}}\times {\mathcal {S}}_{\pm Q^{1,2}}\times {\mathcal {S}}_{ Q^{1,4}}$
. Additionally,
![]() $\overline W_{{\left. \widehat {\lambda }^{\widehat L E_L }\right\rceil _{{\widehat L}}}}$
stabilizes the sets
$\overline W_{{\left. \widehat {\lambda }^{\widehat L E_L }\right\rceil _{{\widehat L}}}}$
stabilizes the sets
![]() $J_{-1}$
and
$J_{-1}$
and
![]() $Q^{1,j}$
(
$Q^{1,j}$
(
![]() $j \in \{1,2,4\}$
). If
$j \in \{1,2,4\}$
). If
![]() $W(\lambda )\neq W(\widehat {\lambda })$
, every
$W(\lambda )\neq W(\widehat {\lambda })$
, every
![]() $x\in W(\lambda )\setminus W(\widehat {\lambda })$
satisfies
$x\in W(\lambda )\setminus W(\widehat {\lambda })$
satisfies
![]() $x(Q^{1,1})=Q^{1,2}$
as element of
$x(Q^{1,1})=Q^{1,2}$
as element of
![]() ${\mathcal {S}}_{Q^1(\widehat {\lambda })}$
(see the proof of Lemma 6.32). Hence, in that case
${\mathcal {S}}_{Q^1(\widehat {\lambda })}$
(see the proof of Lemma 6.32). Hence, in that case
![]() $l_1=l_2$
.
$l_1=l_2$
.
Following the arguments given in the proof of Lemma 6.32, the element
![]() $x_1\in W^1(\lambda )\setminus W^1(\widehat {\lambda })$
can be written as
$x_1\in W^1(\lambda )\setminus W^1(\widehat {\lambda })$
can be written as
![]() $x_{-1} x_{\{1,2\}} x_{4}$
, where
$x_{-1} x_{\{1,2\}} x_{4}$
, where
![]() $x_{-1}\in {\left\langle (J_{-1},-J_{-1})\right\rangle }$
,
$x_{-1}\in {\left\langle (J_{-1},-J_{-1})\right\rangle }$
,
![]() $x_{\{1,2\}}\in {\mathcal {S}}_{\pm (Q^{1,1}\cup Q^{1,2})}$
with
$x_{\{1,2\}}\in {\mathcal {S}}_{\pm (Q^{1,1}\cup Q^{1,2})}$
with
![]() $x_{\{1,2\}}(Q^{1,1})=Q^{1,2}$
as element of
$x_{\{1,2\}}(Q^{1,1})=Q^{1,2}$
as element of
![]() ${\mathcal {S}}_{(Q^{1,1}\cup Q^{1,2})}$
and
${\mathcal {S}}_{(Q^{1,1}\cup Q^{1,2})}$
and
![]() $x_{4}\in {\left\langle x_4^{\circ }\right\rangle }$
with
$x_{4}\in {\left\langle x_4^{\circ }\right\rangle }$
with
 $$ \begin{align*}x_{4}^{\circ}:=\prod_{i\in Q^{1,4}} (i,-i)\in {\mathcal{S}}_{\pm Q^{1,4}}.\end{align*} $$
$$ \begin{align*}x_{4}^{\circ}:=\prod_{i\in Q^{1,4}} (i,-i)\in {\mathcal{S}}_{\pm Q^{1,4}}.\end{align*} $$
Note that
![]() $-1\in \mathbb D$
according to Lemma 6.30 and hence
$-1\in \mathbb D$
according to Lemma 6.30 and hence
![]() $\gamma \in E_L$
. In this notation, we have
$\gamma \in E_L$
. In this notation, we have
We see
![]() $W(\widehat {\lambda })\cong {\mathcal {S}}_{\pm Q^{1,1}}\times {\mathcal {S}}_{\pm Q^{1,2}}\times {\mathcal {S}}_{Q^{1,4}}$
. Since
$W(\widehat {\lambda })\cong {\mathcal {S}}_{\pm Q^{1,1}}\times {\mathcal {S}}_{\pm Q^{1,2}}\times {\mathcal {S}}_{Q^{1,4}}$
. Since
![]() $ K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
, we have
$ K(\lambda )=\overline W_{{\left. \lambda ^{L{\left\langle F_p \right\rangle }}\right\rceil _{L}}}$
, we have
for the element x from above and with
![]() $c_{-1}:=\rho _{{\mathbf T}}(c_{J_{-1}})$
. Note
$c_{-1}:=\rho _{{\mathbf T}}(c_{J_{-1}})$
. Note
![]() $W(\widehat {\lambda }){\left\langle x,c_{-1}, x_{4}\right\rangle }\leq K^1=W( \lambda ){\left\langle c_{-1}, x_{4}^{\circ }\right\rangle }$
. We observe
$W(\widehat {\lambda }){\left\langle x,c_{-1}, x_{4}\right\rangle }\leq K^1=W( \lambda ){\left\langle c_{-1}, x_{4}^{\circ }\right\rangle }$
. We observe
![]() $ c_{-1},x_{4}^{\circ }\in \operatorname Z(W(\lambda ){\left\langle c_{-1}, x_{4}^{\circ }\right\rangle })$
. This implies that every character
$ c_{-1},x_{4}^{\circ }\in \operatorname Z(W(\lambda ){\left\langle c_{-1}, x_{4}^{\circ }\right\rangle })$
. This implies that every character
![]() $\eta \in \mathrm {Irr}(W^1(\lambda ))$
is
$\eta \in \mathrm {Irr}(W^1(\lambda ))$
is
![]() $K^1$
-stable. This proves part (a), and even that every character of
$K^1$
-stable. This proves part (a), and even that every character of
![]() $\mathrm {Irr}(W(\lambda ))$
extends to
$\mathrm {Irr}(W(\lambda ))$
extends to
![]() $K^1$
.
$K^1$
.
Now, by the definition of
![]() $W^1(\widehat {\lambda }^{(1)})$
and
$W^1(\widehat {\lambda }^{(1)})$
and
![]() $K^1(\lambda ^{(1)})$
, we see that in the general case the groups obtained as
$K^1(\lambda ^{(1)})$
, we see that in the general case the groups obtained as
![]() $K^1(\lambda )$
coincide with
$K^1(\lambda )$
coincide with
![]() $K(\lambda )$
for a group of smaller rank where for the character
$K(\lambda )$
for a group of smaller rank where for the character
![]() $\widehat {\lambda }^{(1)}$
part (a) can be applied. This then proves part (b).
$\widehat {\lambda }^{(1)}$
part (a) can be applied. This then proves part (b).
We consider the general case.
Proposition 6.35. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
with
$\lambda \in \mathrm {Irr}_{cusp}(L)$
with
![]() $\widetilde {L}_{\lambda }=\widehat L$
and
$\widetilde {L}_{\lambda }=\widehat L$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widehat {\lambda }))$
. Then every character in
$\eta _0\in \mathrm {Irr}(W(\widehat {\lambda }))$
. Then every character in
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
![]() $K(\lambda )_{\eta _0}$
-stable.
$K(\lambda )_{\eta _0}$
-stable.
Proof. Note that because of
![]() $|\widehat L_{\lambda }:L|=2$
it is sufficient to prove that some character in
$|\widehat L_{\lambda }:L|=2$
it is sufficient to prove that some character in
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
![]() $K(\lambda )_{\eta _0}$
-stable. According to Lemmas 6.33 and 6.34, we can assume
$K(\lambda )_{\eta _0}$
-stable. According to Lemmas 6.33 and 6.34, we can assume
![]() $Q^1(\widehat {\lambda })\neq {\mathcal O}\neq Q^2(\widehat {\lambda })$
for the sets
$Q^1(\widehat {\lambda })\neq {\mathcal O}\neq Q^2(\widehat {\lambda })$
for the sets
![]() $Q^1(\widehat {\lambda })$
and
$Q^1(\widehat {\lambda })$
and
![]() $Q^2(\widehat {\lambda })$
from Lemma 6.32.
$Q^2(\widehat {\lambda })$
from Lemma 6.32.
By Lemma 6.31, we can assume
![]() $h_0\in \ker (\lambda ) $
. The groups
$h_0\in \ker (\lambda ) $
. The groups
![]() $W^i(\widehat {\lambda })$
(
$W^i(\widehat {\lambda })$
(
![]() $i\in \underline 2$
) satisfy
$i\in \underline 2$
) satisfy
![]() $W(\widehat {\lambda })=W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })$
(see Lemma 6.32).
$W(\widehat {\lambda })=W^1(\widehat {\lambda })\times W^2(\widehat {\lambda })$
(see Lemma 6.32).
If
![]() ${\mathcal O}_1\cap Q^1(\widehat {\lambda })\neq \emptyset $
, then
${\mathcal O}_1\cap Q^1(\widehat {\lambda })\neq \emptyset $
, then
![]() $K(\lambda )\leq K^1(\lambda )\times {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda } ^{(2)}))$
(see Lemma 6.32(d)). Let
$K(\lambda )\leq K^1(\lambda )\times {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda } ^{(2)}))$
(see Lemma 6.32(d)). Let
![]() $\eta _i\in \mathrm {Irr}(W^i(\widehat {\lambda }))$
such that
$\eta _i\in \mathrm {Irr}(W^i(\widehat {\lambda }))$
such that
![]() $\eta _0=\eta _1\times \eta _2$
. According to Lemma 6.34,
$\eta _0=\eta _1\times \eta _2$
. According to Lemma 6.34,
![]() $\eta _1$
has a
$\eta _1$
has a
![]() $K^1(\lambda )_{\eta _1}$
-stable extension to
$K^1(\lambda )_{\eta _1}$
-stable extension to
![]() $W^1(\lambda )_{\eta _1}$
and maximal extendibility holds with respect to
$W^1(\lambda )_{\eta _1}$
and maximal extendibility holds with respect to
![]() $W^2(\widehat {\lambda })\lhd {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda } ^{(2)}))$
according to Lemma 6.33. This proves the statement in that case.
$W^2(\widehat {\lambda })\lhd {\mathrm {N}}_{\overline W^2}(W^2(\widehat {\lambda } ^{(2)}))$
according to Lemma 6.33. This proves the statement in that case.
If
![]() ${\mathcal O}_1\cap Q^1(\widehat {\lambda })= \emptyset $
, then
${\mathcal O}_1\cap Q^1(\widehat {\lambda })= \emptyset $
, then
![]() $Q^1(\widehat {\lambda })=\{J_{-1}\}$
. Then
$Q^1(\widehat {\lambda })=\{J_{-1}\}$
. Then
![]() $|W^1(\widehat {\lambda })|=1$
and therefore
$|W^1(\widehat {\lambda })|=1$
and therefore
![]() $W(\widehat {\lambda })=W^2(\widehat {\lambda })$
. Then the stability statement follows by applying again Lemma 6.33.
$W(\widehat {\lambda })=W^2(\widehat {\lambda })$
. Then the stability statement follows by applying again Lemma 6.33.
Together with Proposition 6.28, this leads to the following statement.
Corollary 6.36. Let
![]() $\lambda \in \mathbb {T}$
with
$\lambda \in \mathbb {T}$
with
![]() $\widetilde {L}_{\lambda }\neq L$
,
$\widetilde {L}_{\lambda }\neq L$
,
![]() $\widetilde \lambda \in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, and
$\widetilde \lambda \in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
. Then there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
. Then there exists some
![]() $K(\lambda )_{\eta _0}$
-stable
$K(\lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
.
7 Proof of Theorem A
In the following, we explain how Corollary 6.36 about the action of
![]() $K(\lambda )$
on
$K(\lambda )$
on
![]() $\mathrm {Irr}(W(\lambda ))$
proves Theorem 6.1. As already sketched in the beginning of §6 based on Proposition 2.11, knowing the action of
$\mathrm {Irr}(W(\lambda ))$
proves Theorem 6.1. As already sketched in the beginning of §6 based on Proposition 2.11, knowing the action of
![]() $\widehat K(\lambda )$
on
$\widehat K(\lambda )$
on
![]() $\mathrm {Irr}(W(\lambda ))$
is crucial to verify Theorem 6.1. Unless
$\mathrm {Irr}(W(\lambda ))$
is crucial to verify Theorem 6.1. Unless
![]() ${{\mathbf G}}$
is of type
${{\mathbf G}}$
is of type
![]() $\mathrm {D}_4$
, the action
$\mathrm {D}_4$
, the action
![]() $\widehat K(\lambda )$
on
$\widehat K(\lambda )$
on
![]() $\mathrm {Irr}(W(\lambda ))$
is given by the action of
$\mathrm {Irr}(W(\lambda ))$
is given by the action of
![]() $K(\lambda )$
(see Lemma 6.5).
$K(\lambda )$
(see Lemma 6.5).
Via Harish-Chandra induction, we transfer the result of Theorem 6.1 on characters of N to a weak version of Theorem A. Special considerations are needed to determine the stabilizers in
![]() ${{\widetilde G}} E$
of characters
${{\widetilde G}} E$
of characters
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
, whenever L is not
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
, whenever L is not
![]() $E({{{{\mathbf G}}^F}})$
-stable.
$E({{{{\mathbf G}}^F}})$
-stable.
Lemma 7.1. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
,
$\lambda \in \mathrm {Irr}_{cusp}(L)$
,
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, and
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
, and
![]() $\eta _0\in \mathrm {Irr}(W(\lambda ))$
. Then some character in
$\eta _0\in \mathrm {Irr}(W(\lambda ))$
. Then some character in
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
is
![]() $\widehat K(\lambda )_{\eta _0}$
-stable.
$\widehat K(\lambda )_{\eta _0}$
-stable.
Proof. According to Corollary 6.36, there exists some
![]() $K(\lambda )_{\eta _0}$
-stable
$K(\lambda )_{\eta _0}$
-stable
![]() $\eta $
in
$\eta $
in
![]() $\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. According to Lemma 6.5, the character
$\mathrm {Irr}(W(\lambda )\mid \eta _0)$
. According to Lemma 6.5, the character
![]() $\eta $
is
$\eta $
is
![]() $\widehat K(\lambda )_{\eta _0}\cap (W\rtimes E_L^{\circ } )$
-stable, where
$\widehat K(\lambda )_{\eta _0}\cap (W\rtimes E_L^{\circ } )$
-stable, where
![]() $E^{\circ }:={\left\langle F_p,\gamma _0\right\rangle }$
and
$E^{\circ }:={\left\langle F_p,\gamma _0\right\rangle }$
and
![]() $E_L^{\circ }:=E^{\circ }\cap E_L$
. If
$E_L^{\circ }:=E^{\circ }\cap E_L$
. If
![]() ${{\mathbf G}}$
is not of type
${{\mathbf G}}$
is not of type
![]() $\mathrm {D}_4$
or
$\mathrm {D}_4$
or
![]() $E_L\leq {\left\langle F_p,\gamma _0\right\rangle }$
, this is the above statement.
$E_L\leq {\left\langle F_p,\gamma _0\right\rangle }$
, this is the above statement.
Accordingly, we can assume in the following that
![]() ${{\mathbf G}}$
is of type
${{\mathbf G}}$
is of type
![]() $\mathrm {D}_4$
and L is
$\mathrm {D}_4$
and L is
![]() $\gamma _3$
-stable for the graph automorphism
$\gamma _3$
-stable for the graph automorphism
![]() $\gamma _3$
of
$\gamma _3$
of
![]() $\mathrm {D}_4({\mathbb {F}})$
from Notation 3.3. If
$\mathrm {D}_4({\mathbb {F}})$
from Notation 3.3. If
![]() $L=T_0$
, the statement follows from [Reference Malle and TestermanMS, Th. 3.7]. Otherwise, L is one of the other two possible
$L=T_0$
, the statement follows from [Reference Malle and TestermanMS, Th. 3.7]. Otherwise, L is one of the other two possible
![]() $\gamma _3$
-stable Levi subgroups. In both cases, easy calculations show that
$\gamma _3$
-stable Levi subgroups. In both cases, easy calculations show that
![]() $W(L)$
is a
$W(L)$
is a
![]() $2$
-group. According to our considerations above, we know that there is some
$2$
-group. According to our considerations above, we know that there is some
![]() $K(\lambda )_{\eta _0}$
-stable
$K(\lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
. As
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
. As
![]() $[K(\lambda ):W(\lambda )]\in \{1,2\}$
, the character
$[K(\lambda ):W(\lambda )]\in \{1,2\}$
, the character
![]() $\eta _0$
extends to its inertia group
$\eta _0$
extends to its inertia group
![]() $K(\lambda )_{\eta _0}$
. This shows that maximal extendibility holds with respect to
$K(\lambda )_{\eta _0}$
. This shows that maximal extendibility holds with respect to
![]() $W(\widetilde {\lambda })\lhd K(\lambda )$
. Let
$W(\widetilde {\lambda })\lhd K(\lambda )$
. Let
![]() $K'(\lambda )=(\widehat K(\lambda ){\left\langle F_p \right\rangle })\cap (W\rtimes {\left\langle \gamma ,\gamma _3\right\rangle })$
. When we identify
$K'(\lambda )=(\widehat K(\lambda ){\left\langle F_p \right\rangle })\cap (W\rtimes {\left\langle \gamma ,\gamma _3\right\rangle })$
. When we identify
![]() $\overline W$
with
$\overline W$
with
![]() $W\rtimes {\left\langle \gamma \right\rangle }$
, we can see
$W\rtimes {\left\langle \gamma \right\rangle }$
, we can see
![]() $K(\lambda )$
as a subgroup of
$K(\lambda )$
as a subgroup of
![]() $K'(\lambda )$
with index
$K'(\lambda )$
with index
![]() $1$
or
$1$
or
![]() $3$
. Hence,
$3$
. Hence,
![]() $K(\lambda )_{\eta _0}$
has index
$K(\lambda )_{\eta _0}$
has index
![]() $1$
or
$1$
or
![]() $3$
in
$3$
in
![]() $K'(\lambda )_{\eta _0}$
. The character
$K'(\lambda )_{\eta _0}$
. The character
![]() $\eta _0$
extends to
$\eta _0$
extends to
![]() $K(\lambda )_{\eta _0}$
by the above.
$K(\lambda )_{\eta _0}$
by the above.
Assume that
![]() $K(\lambda )_{\eta _0}/ W(\widetilde {\lambda }) $
is a Sylow
$K(\lambda )_{\eta _0}/ W(\widetilde {\lambda }) $
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $K'(\lambda )/W(\widetilde {\lambda })$
. Let
$K'(\lambda )/W(\widetilde {\lambda })$
. Let
![]() $K_3$
be a subgroup of
$K_3$
be a subgroup of
![]() $K'(\lambda )_{\eta _0}$
with
$K'(\lambda )_{\eta _0}$
with
![]() $W(\lambda )_{\eta _0}\leq K_3$
such that
$W(\lambda )_{\eta _0}\leq K_3$
such that
![]() $K_3/W(\lambda )_{\eta _0}$
is a Sylow
$K_3/W(\lambda )_{\eta _0}$
is a Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $K'(\lambda )_{\eta _0}/W(\widetilde {\lambda })$
. The character
$K'(\lambda )_{\eta _0}/W(\widetilde {\lambda })$
. The character
![]() $\eta _0$
extends to
$\eta _0$
extends to
![]() $K_3$
as
$K_3$
as
![]() $|W(\widetilde {\lambda })|$
is coprime to
$|W(\widetilde {\lambda })|$
is coprime to
![]() $3$
according to [Reference IsaacsI, (11.32)]. This implies that
$3$
according to [Reference IsaacsI, (11.32)]. This implies that
![]() $\eta _0$
extends to
$\eta _0$
extends to
![]() $K(\lambda )_{\eta _0}$
. Maximal extendibility holds with respect to
$K(\lambda )_{\eta _0}$
. Maximal extendibility holds with respect to
![]() $W(\widetilde {\lambda })\lhd K'(\lambda )$
as well. (This can be seen via an application of [Reference IsaacsI, (11.31)].)
$W(\widetilde {\lambda })\lhd K'(\lambda )$
as well. (This can be seen via an application of [Reference IsaacsI, (11.31)].)
If
![]() $K(\lambda )_{\eta _0}/ W(\widetilde {\lambda }) $
is not a Sylow
$K(\lambda )_{\eta _0}/ W(\widetilde {\lambda }) $
is not a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $K'(\lambda )_{\eta _0}/W(\widetilde {\lambda })$
, the group
$K'(\lambda )_{\eta _0}/W(\widetilde {\lambda })$
, the group
![]() $K(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}=(K(\lambda )_{\eta _0})^{\gamma _3}$
contains a Sylow
$K(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}=(K(\lambda )_{\eta _0})^{\gamma _3}$
contains a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $K'(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}$
and hence by the above
$K'(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}$
and hence by the above
![]() $(\eta _0)^{\gamma _3}$
extends to
$(\eta _0)^{\gamma _3}$
extends to
![]() $K'(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}$
. Via conjugation, this implies that
$K'(\lambda ^{\gamma _3})_{\eta _0^{\gamma _3}}$
. Via conjugation, this implies that
![]() $\eta _0$
extends to
$\eta _0$
extends to
![]() $K'(\lambda )_{\eta _0}$
.
$K'(\lambda )_{\eta _0}$
.
We can now show Theorem 6.1.
Proof of Theorem 6.1
Recall
![]() $\mathbb {M}^{(X)}:=\{\lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}=X\}$
for the subgroups
$\mathbb {M}^{(X)}:=\{\lambda \in \mathrm {Irr}_{cusp}(L)\mid \widetilde {L}=X\}$
for the subgroups
![]() $L\leq X\leq \widetilde {L}$
and
$L\leq X\leq \widetilde {L}$
and
![]() $\mathbb {M}_0:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)} \cup \mathbb {M}^{(\widehat L)} \cup \mathbb {M}^{(\widetilde {L})} )$
(see before Lemma 6.3). As the sets
$\mathbb {M}_0:=\mathrm {Irr}_{cusp}(L)\setminus (\mathbb {M}^{(L)} \cup \mathbb {M}^{(\widehat L)} \cup \mathbb {M}^{(\widetilde {L})} )$
(see before Lemma 6.3). As the sets
![]() $\mathbb {M}^{(L)}$
,
$\mathbb {M}^{(L)}$
,
![]() $\mathbb {M}^{(\widehat L)}$
,
$\mathbb {M}^{(\widehat L)}$
,
![]() $\mathbb {M}^{(\widetilde {L})}$
, and
$\mathbb {M}^{(\widetilde {L})}$
, and
![]() $\mathbb {M}_0$
are
$\mathbb {M}_0$
are
![]() $E_L$
-stable, it is sufficient to construct an
$E_L$
-stable, it is sufficient to construct an
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() $\widetilde {L}$
-transversal in
$\widetilde {L}$
-transversal in
![]() $\mathrm {Irr}(N\mid \mathbb {M}')$
for
$\mathrm {Irr}(N\mid \mathbb {M}')$
for
![]() $\mathbb {M}'\in \{\mathbb {M}^{(L)}, \mathbb {M}^{(\widehat L)}, \mathbb {M}^{(\widetilde {L})}\}$
. Note that since every character of N is N-stable, one can equivalently also construct
$\mathbb {M}'\in \{\mathbb {M}^{(L)}, \mathbb {M}^{(\widehat L)}, \mathbb {M}^{(\widetilde {L})}\}$
. Note that since every character of N is N-stable, one can equivalently also construct
![]() $E_L$
-stable
$E_L$
-stable
![]() $\widetilde N'$
-transversals. Lemma 6.3 provides an
$\widetilde N'$
-transversals. Lemma 6.3 provides an
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() $\widetilde {L}$
-transversal in
$\widetilde {L}$
-transversal in
![]() $\mathrm {Irr}(N\mid \mathbb {M}^{(L)})$
.
$\mathrm {Irr}(N\mid \mathbb {M}^{(L)})$
.
Lemma 7.1 shows that for every
![]() $\lambda \in \mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)}$
and every character
$\lambda \in \mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)}$
and every character
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there is some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there is some
![]() $K(\widetilde {\lambda })_{\eta _0}$
-stable
$K(\widetilde {\lambda })_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
, where
$\eta \in \mathrm {Irr}(W(\lambda )\mid \eta _0)$
, where
![]() $\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
.
$\widetilde {\lambda }\in \mathrm {Irr}(\widetilde {L}_{\lambda }\mid \lambda )$
.
Assumptions (i) and (ii) of Proposition 2.11 are satisfied with
![]() $\mathbb {T}':=\mathbb {T} \cap (\mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)})$
from Proposition 4.10 and the extension map
$\mathbb {T}':=\mathbb {T} \cap (\mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)})$
from Proposition 4.10 and the extension map
![]() $\Lambda $
from Theorem 3.1. For every
$\Lambda $
from Theorem 3.1. For every
![]() $\lambda \in \mathbb {T}'$
and
$\lambda \in \mathbb {T}'$
and
![]() $\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
$\eta _0\in \mathrm {Irr}(W(\widetilde {\lambda }))$
, there exists some
![]() $K(\lambda )_{\eta _0}$
-stable
$K(\lambda )_{\eta _0}$
-stable
![]() $\eta \in \mathrm {Irr}(W(\lambda ))$
. This allows us to apply Proposition 2.12 and hence some
$\eta \in \mathrm {Irr}(W(\lambda ))$
. This allows us to apply Proposition 2.12 and hence some
![]() $\widehat N$
-stable
$\widehat N$
-stable
![]() $\widetilde N$
-transversal in
$\widetilde N$
-transversal in
![]() $\mathrm {Irr}_{cusp}(N\mid \mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)} )$
exists.
$\mathrm {Irr}_{cusp}(N\mid \mathbb {M}_0\cup \mathbb {M}^{(\widetilde {L})}\cup \mathbb {M}^{(\widehat L)} )$
exists.
Theorem 6.1 implies according to Theorem 2.8 that the equation
![]() $({{\widetilde G}} E_L)_{\chi }={{\widetilde G}}_{\chi }(E_L)_{\chi }$
holds for every character
$({{\widetilde G}} E_L)_{\chi }={{\widetilde G}}_{\chi }(E_L)_{\chi }$
holds for every character
![]() $\chi $
of a
$\chi $
of a
![]() ${\widetilde G}$
-transversal in
${\widetilde G}$
-transversal in
![]() $ \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Accordingly, we have constructed an
$ \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Accordingly, we have constructed an
![]() $E_L$
-stable
$E_L$
-stable
![]() ${{\widetilde G}}$
-transversal of
${{\widetilde G}}$
-transversal of
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
(see Lemma 2.4).
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
(see Lemma 2.4).
Corollary 7.2. Let
![]() ${{\mathbf G}}=\mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
, let
${{\mathbf G}}=\mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
, let
![]() $F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be a standard Frobenius endomorphism, and let E be defined as in Notation 3.3 and
$F:{{\mathbf G}}\rightarrow {{\mathbf G}}$
be a standard Frobenius endomorphism, and let E be defined as in Notation 3.3 and
![]() ${{\widetilde G}}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
for the Lang map
${{\widetilde G}}:=\mathcal L^{-1}(\operatorname Z({{\mathbf G}}))$
for the Lang map
![]() $\mathcal L$
defined by F on
$\mathcal L$
defined by F on
![]() ${{\mathbf G}}$
. Let L be a standard Levi subgroup of
${{\mathbf G}}$
. Let L be a standard Levi subgroup of
![]() ${{{{\mathbf G}}^F}}$
, and let
${{{{\mathbf G}}^F}}$
, and let
![]() $E_L$
be its stabilizer in
$E_L$
be its stabilizer in
![]() $E({{{{\mathbf G}}^F}})$
. If Hypothesis 2.14 holds for every
$E({{{{\mathbf G}}^F}})$
. If Hypothesis 2.14 holds for every
![]() $l'< l$
, then there exists an
$l'< l$
, then there exists an
![]() $E_L$
-stable
$E_L$
-stable
![]() ${{\widetilde G}}$
-transversal in
${{\widetilde G}}$
-transversal in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
.
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
.
Proof. For a given fixed Levi subgroup L, we apply Theorem 2.8 whose assumptions follow from Theorems 3.1 and 6.1.
Condition
![]() $A'(\infty )$
from 2.3 and equivalently Theorem A require to replace in the above statement
$A'(\infty )$
from 2.3 and equivalently Theorem A require to replace in the above statement
![]() $E_L$
by E and study
$E_L$
by E and study
![]() $({\widetilde G} E)_{\chi }$
. Hence, we study the stabilizers of characters in
$({\widetilde G} E)_{\chi }$
. Hence, we study the stabilizers of characters in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
in the case where L is a standard Levi subgroup that is not E-stable.
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
in the case where L is a standard Levi subgroup that is not E-stable.
Proposition 7.3. We keep
![]() ${{\mathbf G}}=\mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
and assume Hypothesis 2.14 holds for every
${{\mathbf G}}=\mathrm {D}_{l,\mathrm {sc}}({\mathbb {F}})$
and assume Hypothesis 2.14 holds for every
![]() $l'< l$
. Let
$l'< l$
. Let
![]() ${\mathbf T}$
and
${\mathbf T}$
and
![]() ${{\mathbf L}}$
as in Notation 2.5. Let
${{\mathbf L}}$
as in Notation 2.5. Let
![]() $E^{\circ }:={\left\langle F_p,\gamma \right\rangle }\leq E$
in the notation of 3.3. Assume that no
$E^{\circ }:={\left\langle F_p,\gamma \right\rangle }\leq E$
in the notation of 3.3. Assume that no
![]() ${\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T})$
-conjugate of
${\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T})$
-conjugate of
![]() ${{\mathbf L}}$
is E-stable. Let
${{\mathbf L}}$
is E-stable. Let
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Then
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
. Then
![]() ${{\widetilde G}}_{\chi }={{\widetilde G}}$
or
${{\widetilde G}}_{\chi }={{\widetilde G}}$
or
![]() $({\widetilde G} E^{\circ })_{\chi }\leq {\widetilde G}_{\chi } (E^{\circ }\cap E_L)$
.
$({\widetilde G} E^{\circ })_{\chi }\leq {\widetilde G}_{\chi } (E^{\circ }\cap E_L)$
.
Proof. Let
![]() $N_0:={\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T})$
. We consider first the possible structure of L, in particular the values of
$N_0:={\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T})$
. We consider first the possible structure of L, in particular the values of
![]() $\mathbb D(L)$
. Then we give the possible values of
$\mathbb D(L)$
. Then we give the possible values of
![]() $\widetilde {L}_{\chi }$
via describing
$\widetilde {L}_{\chi }$
via describing
![]() $W(\lambda )$
.
$W(\lambda )$
.
We see that L is
![]() $F_p$
-stable. If L is
$F_p$
-stable. If L is
![]() $\gamma $
-stable, then
$\gamma $
-stable, then
![]() $E({{{{\mathbf G}}^F}})=E_L$
. By our assumption
$E({{{{\mathbf G}}^F}})=E_L$
. By our assumption
![]() $E_L\neq E$
, we have
$E_L\neq E$
, we have
![]() $\gamma \notin E_L$
. We observe that then
$\gamma \notin E_L$
. We observe that then
![]() $-1\notin \mathbb D(L)$
, as otherwise the system of simple roots
$-1\notin \mathbb D(L)$
, as otherwise the system of simple roots
![]() $\Delta '$
, associated with L as in Notation 3.5 is
$\Delta '$
, associated with L as in Notation 3.5 is
![]() $\gamma $
-stable, which then implies
$\gamma $
-stable, which then implies
![]() $ \gamma \in E_L$
.
$ \gamma \in E_L$
.
If
![]() $1\in \mathbb D(L)$
, then some
$1\in \mathbb D(L)$
, then some
![]() $N_0$
-conjugate of L is
$N_0$
-conjugate of L is
![]() $\gamma $
-stable: the conjugation is given by some element
$\gamma $
-stable: the conjugation is given by some element
![]() $v\in N_0:={\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T}_0)$
that corresponds to some
$v\in N_0:={\mathrm {N}}_{{{{\mathbf G}}^F}}({\mathbf T}_0)$
that corresponds to some
![]() $\sigma \in {\mathcal {S}}_{\pm \underline l} $
with the following properties:
$\sigma \in {\mathcal {S}}_{\pm \underline l} $
with the following properties:
![]() $\sigma ({\underline {l}})={\underline {l}}$
,
$\sigma ({\underline {l}})={\underline {l}}$
,
![]() $1\in \sigma (J_1)$
and
$1\in \sigma (J_1)$
and
![]() $\sigma (\Delta ')\subseteq \Delta $
. The Levi subgroup L satisfies accordingly
$\sigma (\Delta ')\subseteq \Delta $
. The Levi subgroup L satisfies accordingly
![]() $1\notin \mathbb D(L)$
.
$1\notin \mathbb D(L)$
.
Let
![]() $W_0=N_0/{\mathbf T}^F$
. For the proof of the statement, we consider
$W_0=N_0/{\mathbf T}^F$
. For the proof of the statement, we consider
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
with
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
with
![]() $({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E_L$
. Then
$({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E_L$
. Then
![]() $\chi ^{\gamma }$
and
$\chi ^{\gamma }$
and
![]() $\chi $
are
$\chi $
are
![]() ${{\widetilde G}} E_L$
-conjugate. For the statement, we have to show that
${{\widetilde G}} E_L$
-conjugate. For the statement, we have to show that
![]() ${{\widetilde G}}_{\chi }={{\widetilde G}}$
. We assume that
${{\widetilde G}}_{\chi }={{\widetilde G}}$
. We assume that
![]() $\chi ^{\gamma }$
and
$\chi ^{\gamma }$
and
![]() $\chi $
are
$\chi $
are
![]() ${{\widetilde G}} E_L$
-conjugate. Let
${{\widetilde G}} E_L$
-conjugate. Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
with
$\lambda \in \mathrm {Irr}_{cusp}(L)$
with
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
. Then
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
. Then
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(\gamma (L),\lambda ^{\gamma })$
are
$(\gamma (L),\lambda ^{\gamma })$
are
![]() ${{\widetilde G}} E_L$
-conjugate, in particular
${{\widetilde G}} E_L$
-conjugate, in particular
![]() $\gamma (L)$
and L are
$\gamma (L)$
and L are
![]() $N_0$
-conjugate. This shows
$N_0$
-conjugate. This shows
![]() $\overline W(L)\neq W(L)$
, or equivalently
$\overline W(L)\neq W(L)$
, or equivalently
![]() $\mathbb D_{\mathrm {odd}}\neq \emptyset $
. Let
$\mathbb D_{\mathrm {odd}}\neq \emptyset $
. Let
![]() ${{\mathcal O}_{\mathrm {odd}}}=\bigcup _{d\in \mathbb D_{\mathrm {odd}}} {\mathcal O}_d$
,
${{\mathcal O}_{\mathrm {odd}}}=\bigcup _{d\in \mathbb D_{\mathrm {odd}}} {\mathcal O}_d$
,
![]() ${{\mathcal O}_{\mathrm {even}}}=\bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
, and
${{\mathcal O}_{\mathrm {even}}}=\bigcup _{d\in \mathbb D_{\mathrm {even}}} {\mathcal O}_d$
, and
![]() $I_0\in {\mathcal O}_{{\mathrm {odd}}}$
. Without loss of generality, we assume
$I_0\in {\mathcal O}_{{\mathrm {odd}}}$
. Without loss of generality, we assume
![]() $1\in I_0$
. Otherwise, we replace L by some
$1\in I_0$
. Otherwise, we replace L by some
![]() $N_0$
-conjugate. Let
$N_0$
-conjugate. Let
![]() $w_0:=\prod _{i\in I_0} (i,-i)\in W_0$
and
$w_0:=\prod _{i\in I_0} (i,-i)\in W_0$
and
![]() $n_0\in \overline N={\mathrm {N}}_{\overline {{\mathbf G}}^F}({\mathbf T})$
the corresponding element. Hence,
$n_0\in \overline N={\mathrm {N}}_{\overline {{\mathbf G}}^F}({\mathbf T})$
the corresponding element. Hence,
![]() $w_0\in \gamma N_0$
. We note that N induces on L the outer automorphisms W, while any
$w_0\in \gamma N_0$
. We note that N induces on L the outer automorphisms W, while any
![]() $w'\in \overline W\setminus W$
is induced by elements of
$w'\in \overline W\setminus W$
is induced by elements of
![]() ${\mathrm {N}}_{{{{{\mathbf G}}^F}} {\left\langle \gamma \right\rangle }}(L)\setminus N$
. This proves that in this case L and
${\mathrm {N}}_{{{{{\mathbf G}}^F}} {\left\langle \gamma \right\rangle }}(L)\setminus N$
. This proves that in this case L and
![]() $\gamma (L)$
are actually
$\gamma (L)$
are actually
![]() $N_0$
-conjugate. Hence, the Harish-Chandra series satisfy
$N_0$
-conjugate. Hence, the Harish-Chandra series satisfy
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L))=\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (\gamma (L), \mathrm {Irr}_{cusp}(\gamma (L)))$
.
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L))=\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (\gamma (L), \mathrm {Irr}_{cusp}(\gamma (L)))$
.
Let
![]() $\lambda \in \mathrm {Irr}_{cusp}(L)$
. Assume that
$\lambda \in \mathrm {Irr}_{cusp}(L)$
. Assume that
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(L,\lambda )^{e\gamma }$
are
$(L,\lambda )^{e\gamma }$
are
![]() ${{{{\mathbf G}}^F}}$
-conjugate for some
${{{{\mathbf G}}^F}}$
-conjugate for some
![]() $e\in {\left\langle F_p \right\rangle }$
. This implies that
$e\in {\left\langle F_p \right\rangle }$
. This implies that
![]() $(L,\lambda )=(L,\lambda )^{e \overline n}$
for some
$(L,\lambda )=(L,\lambda )^{e \overline n}$
for some
![]() $\overline n\in \overline N\setminus N$
. Note that
$\overline n\in \overline N\setminus N$
. Note that
![]() $W(\lambda )^{\overline n}=W(\lambda )$
. Because of
$W(\lambda )^{\overline n}=W(\lambda )$
. Because of
![]() $-1\notin \mathbb D(L)$
and
$-1\notin \mathbb D(L)$
and
![]() $\mathbb D_{\mathrm {odd}}\neq \emptyset $
, we observe
$\mathbb D_{\mathrm {odd}}\neq \emptyset $
, we observe
![]() $\widetilde {L}_{\lambda }=\widetilde {L}$
, as
$\widetilde {L}_{\lambda }=\widetilde {L}$
, as
![]() ${\left\langle \widehat L_{I_0}, t_{{\underline {l}},2}\right\rangle }\leq {\mathrm {C}}_{{\mathbf G}}(L)L$
.
${\left\langle \widehat L_{I_0}, t_{{\underline {l}},2}\right\rangle }\leq {\mathrm {C}}_{{\mathbf G}}(L)L$
.
Assume
![]() $h_0\in \ker (\lambda )$
and that some
$h_0\in \ker (\lambda )$
and that some
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
satisfies
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
satisfies
![]() ${{\widetilde G}}_{\chi }\neq {{\widetilde G}}$
. According to Corollary 6.22, the equation
${{\widetilde G}}_{\chi }\neq {{\widetilde G}}$
. According to Corollary 6.22, the equation
![]() $W(\widehat {\lambda })=W(\widetilde {\lambda })$
holds, as
$W(\widehat {\lambda })=W(\widetilde {\lambda })$
holds, as
![]() $\{\pm 1\}\cap \mathbb D(L)=\emptyset $
. If
$\{\pm 1\}\cap \mathbb D(L)=\emptyset $
. If
![]() $W(\lambda )= W(\widehat {\lambda })$
, then
$W(\lambda )= W(\widehat {\lambda })$
, then
![]() ${{\widetilde G}}_{\chi }={{\widetilde G}}$
. Hence, we assume
${{\widetilde G}}_{\chi }={{\widetilde G}}$
. Hence, we assume
![]() $W(\lambda )\neq W(\widehat {\lambda })$
in the following. Let
$W(\lambda )\neq W(\widehat {\lambda })$
in the following. Let
![]() $W^{\mathrm {odd}}(\lambda ):= (W(\lambda ) {\mathcal {S}}_{\pm {\mathcal O}_{\mathrm {even}}})\cap {\mathcal {S}}_ {\pm {\mathcal O}_{\mathrm {odd}}}$
. Without loss of generality, we can assume
$W^{\mathrm {odd}}(\lambda ):= (W(\lambda ) {\mathcal {S}}_{\pm {\mathcal O}_{\mathrm {even}}})\cap {\mathcal {S}}_ {\pm {\mathcal O}_{\mathrm {odd}}}$
. Without loss of generality, we can assume
![]() $\lambda $
to be standardized, as in every
$\lambda $
to be standardized, as in every
![]() $\overline N$
-orbit in
$\overline N$
-orbit in
![]() $\mathrm {Irr}_{cusp}(L)$
there is at least one standardized character (see after Definition 6.10). As
$\mathrm {Irr}_{cusp}(L)$
there is at least one standardized character (see after Definition 6.10). As
![]() $W(\lambda )\neq W(\widehat {\lambda })$
and
$W(\lambda )\neq W(\widehat {\lambda })$
and
![]() $\lambda $
is standardized,
$\lambda $
is standardized,
![]() $W^{{\mathrm {odd}}}(\widehat {\lambda }) \leq {\mathcal {S}}_{{\mathcal O}_{\mathrm {odd}}}$
and
$W^{{\mathrm {odd}}}(\widehat {\lambda }) \leq {\mathcal {S}}_{{\mathcal O}_{\mathrm {odd}}}$
and
![]() $x\in W(\lambda )\setminus W(\widehat {\lambda })$
can be chosen as an involution with no fixed point in
$x\in W(\lambda )\setminus W(\widehat {\lambda })$
can be chosen as an involution with no fixed point in
![]() ${\mathcal O}_{\mathrm {odd}}$
. We note that
${\mathcal O}_{\mathrm {odd}}$
. We note that
![]() ${\mathrm {N}}_{{\mathcal {S}}_{\pm {\mathcal O}_{\mathrm {odd}}}}(W^{\mathrm {odd}}(\lambda )) \leq W$
. This implies
${\mathrm {N}}_{{\mathcal {S}}_{\pm {\mathcal O}_{\mathrm {odd}}}}(W^{\mathrm {odd}}(\lambda )) \leq W$
. This implies
![]() ${\mathrm {N}}_{\overline W}(W(\lambda )) \leq W$
and hence
${\mathrm {N}}_{\overline W}(W(\lambda )) \leq W$
and hence
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(L,\lambda )^{e\gamma }$
are not
$(L,\lambda )^{e\gamma }$
are not
![]() ${{{{\mathbf G}}^F}}$
-conjugate for any
${{{{\mathbf G}}^F}}$
-conjugate for any
![]() $e\in {\left\langle F_p \right\rangle }$
. This proves that
$e\in {\left\langle F_p \right\rangle }$
. This proves that
![]() $(L,\lambda )^{\gamma }$
is not
$(L,\lambda )^{\gamma }$
is not
![]() ${{{{\mathbf G}}^F}}$
-conjugate to any element of the
${{{{\mathbf G}}^F}}$
-conjugate to any element of the
![]() $E_L$
-orbit of
$E_L$
-orbit of
![]() $(L,\lambda )$
, when
$(L,\lambda )$
, when
![]() $h_0\in \ker (\lambda )$
.
$h_0\in \ker (\lambda )$
.
Assume
![]() $h_0\notin \ker (\lambda )$
and
$h_0\notin \ker (\lambda )$
and
![]() $\nu \in \mathrm {Irr}({\left. \lambda \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}})$
. In the following, we assume
$\nu \in \mathrm {Irr}({\left. \lambda \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}})$
. In the following, we assume
![]() $|\operatorname Z({{{{\mathbf G}}^F}})|=4$
. Then we observe that
$|\operatorname Z({{{{\mathbf G}}^F}})|=4$
. Then we observe that
![]() $ E^{\circ }_{\nu }= {\left\langle F_p \right\rangle }= {\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))$
and hence
$ E^{\circ }_{\nu }= {\left\langle F_p \right\rangle }= {\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))$
and hence
![]() $({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E^{\circ }_{\nu }$
for every
$({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E^{\circ }_{\nu }$
for every
![]() $\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
. If
$\chi \in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\lambda ))$
. If
![]() ${\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))=E_L$
, this implies
${\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))=E_L$
, this implies
![]() $({{\widetilde G}} E)_{\chi } \leq {{\widetilde G}} E_L$
as required. Note that if
$({{\widetilde G}} E)_{\chi } \leq {{\widetilde G}} E_L$
as required. Note that if
![]() $2\mid l$
, then
$2\mid l$
, then
![]() ${\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))=E_L$
. In the following, we prove
${\mathrm {C}}_{E}(\operatorname Z({{{{\mathbf G}}^F}}))=E_L$
. In the following, we prove
![]() $2\mid |{\mathcal O}_{\mathrm {odd}}|$
as this implies
$2\mid |{\mathcal O}_{\mathrm {odd}}|$
as this implies
![]() $2\mid l$
.
$2\mid l$
.
For
![]() $I\in {\mathcal O}$
, let
$I\in {\mathcal O}$
, let
![]() ${\mathbf Z}_I$
be defined as in Lemma 4.2,
${\mathbf Z}_I$
be defined as in Lemma 4.2,
![]() $Z_{I}:={\mathbf Z}_{I}^F$
, and
$Z_{I}:={\mathbf Z}_{I}^F$
, and
![]() $\delta _I\in \mathrm {Irr}({\left.\lambda \right\rceil _{{Z_I}}})$
. Fix
$\delta _I\in \mathrm {Irr}({\left.\lambda \right\rceil _{{Z_I}}})$
. Fix
![]() $d\in \mathbb D_{\mathrm {odd}}$
and
$d\in \mathbb D_{\mathrm {odd}}$
and
![]() $I_d\in {\mathcal O}_d$
. For
$I_d\in {\mathcal O}_d$
. For
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
, we define
$\kappa \in \mathrm {Irr}(Z_{I_d})$
, we define
Recall
![]() $I_d\in {\mathcal O}_{\mathrm {odd}}$
and
$I_d\in {\mathcal O}_{\mathrm {odd}}$
and
![]() $h_0\notin \ker (\lambda )$
. Hence,
$h_0\notin \ker (\lambda )$
. Hence,
![]() $Z_{I_d}\cong \mathrm C_{q-1}$
and
$Z_{I_d}\cong \mathrm C_{q-1}$
and
![]() $o(\delta _{I_d})_2=(q-1)_2$
. On the other hand, we see that
$o(\delta _{I_d})_2=(q-1)_2$
. On the other hand, we see that
where
![]() $\kappa $
runs over the
$\kappa $
runs over the
![]() ${\left\langle c_{I_d}\right\rangle }$
-orbits in
${\left\langle c_{I_d}\right\rangle }$
-orbits in
![]() $\mathrm {Irr}(Z_{I_d})$
. By the above,
$\mathrm {Irr}(Z_{I_d})$
. By the above,
![]() $a_{\kappa }(\lambda )=0$
for every
$a_{\kappa }(\lambda )=0$
for every
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
with
$\kappa \in \mathrm {Irr}(Z_{I_d})$
with
![]() $o(\kappa )_2\neq (q-1)_2$
. If
$o(\kappa )_2\neq (q-1)_2$
. If
![]() $\lambda '\in \mathrm {Irr}_{cusp}(L)$
is
$\lambda '\in \mathrm {Irr}_{cusp}(L)$
is
![]() $\overline N$
-conjugate to
$\overline N$
-conjugate to
![]() $\lambda $
, then
$\lambda $
, then
![]() $a_{\kappa }(\lambda )=a_{\kappa }(\lambda ')$
for every
$a_{\kappa }(\lambda )=a_{\kappa }(\lambda ')$
for every
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
according to the action of
$\kappa \in \mathrm {Irr}(Z_{I_d})$
according to the action of
![]() $\overline V_d$
on the groups
$\overline V_d$
on the groups
![]() $Z_I$
(
$Z_I$
(
![]() $I\in {\mathcal O}_d$
). Note that
$I\in {\mathcal O}_d$
). Note that
![]() $a_{\kappa }(\lambda )=0$
as
$a_{\kappa }(\lambda )=0$
as
![]() $o(\delta _I)_2=(q-1)_2$
for every
$o(\delta _I)_2=(q-1)_2$
for every
![]() $I\in {\mathcal O}_d$
.
$I\in {\mathcal O}_d$
.
Recall that we assume
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(\gamma (L),\lambda ^{\gamma e})$
are
$(\gamma (L),\lambda ^{\gamma e})$
are
![]() ${{{{\mathbf G}}^F}}$
-conjugate. As the order of
${{{{\mathbf G}}^F}}$
-conjugate. As the order of
![]() $\gamma e$
is even, we can choose some
$\gamma e$
is even, we can choose some
![]() $F_0\in {\left\langle F_p \right\rangle }$
such that
$F_0\in {\left\langle F_p \right\rangle }$
such that
![]() ${\left\langle F_0\right\rangle }$
is a Sylow
${\left\langle F_0\right\rangle }$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() ${\left\langle e\right\rangle }$
. Then the
${\left\langle e\right\rangle }$
. Then the
![]() $\overline N$
-orbit of
$\overline N$
-orbit of
![]() $\lambda $
is
$\lambda $
is
![]() $F_0$
-stable. Then
$F_0$
-stable. Then
![]() $F_0$
acts on the characters of
$F_0$
acts on the characters of
![]() $\mathrm {Irr}(Z_{I_d})$
, inducing an action on the set of
$\mathrm {Irr}(Z_{I_d})$
, inducing an action on the set of
![]() ${\left\langle c_{I_d}\right\rangle }$
-orbits in
${\left\langle c_{I_d}\right\rangle }$
-orbits in
![]() $\mathrm {Irr}(Z_{I_d})$
. We denote this set by
$\mathrm {Irr}(Z_{I_d})$
. We denote this set by
![]() $\mathrm {Irr}(Z_{I_d})/{\left\langle c_{I_d}\right\rangle }$
. If
$\mathrm {Irr}(Z_{I_d})/{\left\langle c_{I_d}\right\rangle }$
. If
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
with
$\kappa \in \mathrm {Irr}(Z_{I_d})$
with
![]() $o(\kappa )_2=(q-1)_2$
, the
$o(\kappa )_2=(q-1)_2$
, the
![]() ${\left\langle c_{I_d}\right\rangle }$
-orbit of
${\left\langle c_{I_d}\right\rangle }$
-orbit of
![]() $\kappa $
is not
$\kappa $
is not
![]() $F_0$
-stable. Hence, the
$F_0$
-stable. Hence, the
![]() $F_0$
-orbit in
$F_0$
-orbit in
![]() $\mathrm {Irr}(Z_{I_d})/{\left\langle c_{I_d}\right\rangle }$
containing
$\mathrm {Irr}(Z_{I_d})/{\left\langle c_{I_d}\right\rangle }$
containing
![]() $\kappa $
has an even length. Since the
$\kappa $
has an even length. Since the
![]() $\overline N$
-orbit of
$\overline N$
-orbit of
![]() $\lambda $
is
$\lambda $
is
![]() $F_0$
-stable, we see that
$F_0$
-stable, we see that
![]() $a_{\kappa }(\lambda ^{F_0})=a_{\kappa ^{F_0}}(\lambda )$
. Accordingly,
$a_{\kappa }(\lambda ^{F_0})=a_{\kappa ^{F_0}}(\lambda )$
. Accordingly,
whenever
![]() $\kappa $
runs over a
$\kappa $
runs over a
![]() ${\left\langle c_{I_d}\right\rangle }$
-transversal in
${\left\langle c_{I_d}\right\rangle }$
-transversal in
![]() $\{\kappa '\in \mathrm {Irr}(Z_{I_d})\mid o(\kappa ')_2=(q-1)_2\}$
. By the above,
$\{\kappa '\in \mathrm {Irr}(Z_{I_d})\mid o(\kappa ')_2=(q-1)_2\}$
. By the above,
![]() $a_{\kappa }(\lambda )=0$
for every
$a_{\kappa }(\lambda )=0$
for every
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
with
$\kappa \in \mathrm {Irr}(Z_{I_d})$
with
![]() $o(\kappa )_2\neq (q-1)_2$
. Altogether, this implies
$o(\kappa )_2\neq (q-1)_2$
. Altogether, this implies
![]() $2\mid \sum _{\kappa } a_{\kappa }(\lambda )= |{\mathcal O}_d|$
, where
$2\mid \sum _{\kappa } a_{\kappa }(\lambda )= |{\mathcal O}_d|$
, where
![]() $\kappa \in \mathrm {Irr}(Z_{I_d})$
runs over a
$\kappa \in \mathrm {Irr}(Z_{I_d})$
runs over a
![]() ${\left\langle c_{I_d}\right\rangle }$
-transversal.
${\left\langle c_{I_d}\right\rangle }$
-transversal.
As
![]() $l=\sum _{d\in \mathbb D} d |{\mathcal O}_d|$
and hence
$l=\sum _{d\in \mathbb D} d |{\mathcal O}_d|$
and hence
![]() $l\equiv |{\mathcal O}_{\mathrm {odd}}| \mod 2$
, the rank l is even and
$l\equiv |{\mathcal O}_{\mathrm {odd}}| \mod 2$
, the rank l is even and
![]() ${\mathrm {C}}_E(\operatorname Z({{{{\mathbf G}}^F}}))= {\left\langle F_p \right\rangle }=E_L$
. As explained above, this leads to
${\mathrm {C}}_E(\operatorname Z({{{{\mathbf G}}^F}}))= {\left\langle F_p \right\rangle }=E_L$
. As explained above, this leads to
![]() $({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E_{{\left.\chi \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}}}={{\widetilde G}} E_L$
and hence a contradiction to the assumption on
$({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E_{{\left.\chi \right\rceil _{{\operatorname Z({{{{\mathbf G}}^F}})}}}}={{\widetilde G}} E_L$
and hence a contradiction to the assumption on
![]() $\chi $
.
$\chi $
.
It remains to study the case of
![]() $|Z({{{{\mathbf G}}^F}})|=2$
. Then
$|Z({{{{\mathbf G}}^F}})|=2$
. Then
![]() $2\nmid l$
and
$2\nmid l$
and
![]() $4\nmid (q-1)$
. Note that
$4\nmid (q-1)$
. Note that
![]() $4\nmid (q-1)$
implies
$4\nmid (q-1)$
implies
![]() $2\nmid |E_L|$
and hence
$2\nmid |E_L|$
and hence
![]() $|E_L|$
and
$|E_L|$
and
![]() $o(\gamma )=2$
are coprime. If
$o(\gamma )=2$
are coprime. If
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(\gamma (L),\lambda ^{\gamma })$
are
$(\gamma (L),\lambda ^{\gamma })$
are
![]() ${\mathbf G}^{F} E_L$
-conjugate, then the pairs are already
${\mathbf G}^{F} E_L$
-conjugate, then the pairs are already
![]() ${{{{\mathbf G}}^F}}$
-conjugate. In the following, we see that the
${{{{\mathbf G}}^F}}$
-conjugate. In the following, we see that the
![]() ${\mathbf G}^{F}$
-orbit of
${\mathbf G}^{F}$
-orbit of
![]() $(L,\lambda )$
cannot be
$(L,\lambda )$
cannot be
![]() $\gamma $
-stable. By the above, we have
$\gamma $
-stable. By the above, we have
![]() $\mathbb D_{\mathrm {odd}}\neq \emptyset $
and
$\mathbb D_{\mathrm {odd}}\neq \emptyset $
and
![]() $-1\notin \mathbb D(L)$
. According to Lemma 4.3,
$-1\notin \mathbb D(L)$
. According to Lemma 4.3,
![]() $\lambda $
is
$\lambda $
is
![]() $\widehat L$
-stable, as each
$\widehat L$
-stable, as each
![]() $\lambda _I$
is
$\lambda _I$
is
![]() $\widehat L_I$
-stable for
$\widehat L_I$
-stable for
![]() $I\in {\mathcal O}_{\mathrm {odd}}$
. Hence,
$I\in {\mathcal O}_{\mathrm {odd}}$
. Hence,
![]() $\lambda $
is
$\lambda $
is
![]() $\widetilde {L}$
-stable (see also Lemma 4.3). According to Lemma 6.14, the assumption
$\widetilde {L}$
-stable (see also Lemma 4.3). According to Lemma 6.14, the assumption
![]() $2\nmid l$
implies
$2\nmid l$
implies
![]() $W(\lambda )=W(\widehat {\lambda })$
, even more
$W(\lambda )=W(\widehat {\lambda })$
, even more
![]() $\overline W(\lambda )=\overline W(\widehat {\lambda })\leq W$
. But this implies that
$\overline W(\lambda )=\overline W(\widehat {\lambda })\leq W$
. But this implies that
![]() $(L,\lambda )$
and
$(L,\lambda )$
and
![]() $(L,\lambda )^{\gamma }$
are not
$(L,\lambda )^{\gamma }$
are not
![]() ${{{{\mathbf G}}^F}}$
-conjugate. Hence,
${{{{\mathbf G}}^F}}$
-conjugate. Hence,
![]() $\gamma \notin ({{\widetilde G}} E)_{\chi }$
and hence
$\gamma \notin ({{\widetilde G}} E)_{\chi }$
and hence
![]() $({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} (E_L)_{\chi }$
.
$({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} (E_L)_{\chi }$
.
A last obstacle is formed by the groups
![]() $\mathrm {D}_{4,sc}(q)$
. We keep the same notation.
$\mathrm {D}_{4,sc}(q)$
. We keep the same notation.
Proposition 7.4. If
![]() ${{{{\mathbf G}}^F}}=\mathrm {D}_{4,sc}(q)$
, every
${{{{\mathbf G}}^F}}=\mathrm {D}_{4,sc}(q)$
, every
![]() ${{\widetilde G}}$
-orbit in
${{\widetilde G}}$
-orbit in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}})$
contains some
$\mathrm {Irr}({{{{\mathbf G}}^F}})$
contains some
![]() $\chi $
with
$\chi $
with
![]() $({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
.
$({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
.
Proof. Let
![]() $\chi _0\in \mathrm {Irr}({{{{\mathbf G}}^F}})$
and
$\chi _0\in \mathrm {Irr}({{{{\mathbf G}}^F}})$
and
![]() $E^{\circ }:={\left\langle \gamma ,F_p\right\rangle }$
. Then some Sylow
$E^{\circ }:={\left\langle \gamma ,F_p\right\rangle }$
. Then some Sylow
![]() $2$
-subgroup of E is contained in
$2$
-subgroup of E is contained in
![]() $E^{\circ }$
. We can assume that
$E^{\circ }$
. We can assume that
![]() ${{\widetilde G}} E^{\circ }/{{{{\mathbf G}}^F}}$
contains a Sylow
${{\widetilde G}} E^{\circ }/{{{{\mathbf G}}^F}}$
contains a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $({{\widetilde G}} E^{\circ })_{\chi }/{{{{\mathbf G}}^F}}$
. (Otherwise we can replace
$({{\widetilde G}} E^{\circ })_{\chi }/{{{{\mathbf G}}^F}}$
. (Otherwise we can replace
![]() $\chi _0$
by one of its E-conjugates.) Some
$\chi _0$
by one of its E-conjugates.) Some
![]() ${{\widetilde G}}$
-conjugate
${{\widetilde G}}$
-conjugate
![]() $\chi $
of
$\chi $
of
![]() $\chi _0$
satisfies
$\chi _0$
satisfies
![]() $({{\widetilde G}} E^{\circ })_{\chi }={{\widetilde G}}_{\chi } E^{\circ }_{\chi }$
according to Proposition 7.3. This proves the statement if
$({{\widetilde G}} E^{\circ })_{\chi }={{\widetilde G}}_{\chi } E^{\circ }_{\chi }$
according to Proposition 7.3. This proves the statement if
![]() $({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E^{\circ }$
. Additionally,
$({{\widetilde G}} E)_{\chi }\leq {{\widetilde G}} E^{\circ }$
. Additionally,
![]() $({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
holds if
$({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
holds if
![]() ${{\widetilde G}}_{\chi }={{\widetilde G}}$
.
${{\widetilde G}}_{\chi }={{\widetilde G}}$
.
Accordingly, there is some
![]() $f\in {\left\langle F_p \right\rangle }$
and
$f\in {\left\langle F_p \right\rangle }$
and
![]() $t\in {{\widetilde G}}$
such that
$t\in {{\widetilde G}}$
such that
![]() $\chi $
is
$\chi $
is
![]() $\gamma _3 ft$
-stable and
$\gamma _3 ft$
-stable and
![]() $\gamma _3 ft$
has
$\gamma _3 ft$
has
![]() $3$
-power order in
$3$
-power order in
![]() ${{\widetilde G}} E/{{{{\mathbf G}}^F}}$
. If
${{\widetilde G}} E/{{{{\mathbf G}}^F}}$
. If
![]() $t\in {{{{\mathbf G}}^F}}$
, the equation
$t\in {{{{\mathbf G}}^F}}$
, the equation
![]() $({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
holds. Clearly,
$({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
holds. Clearly,
![]() ${{\widetilde G}}_{\chi }\lhd ({{\widetilde G}} E)_{\chi }$
. Hence,
${{\widetilde G}}_{\chi }\lhd ({{\widetilde G}} E)_{\chi }$
. Hence,
![]() ${{\widetilde G}}_{\chi }$
is normalized by
${{\widetilde G}}_{\chi }$
is normalized by
![]() $\gamma _3 f t$
. But via the
$\gamma _3 f t$
. But via the
![]() ${\left\langle \gamma _3 ,f\right\rangle }$
-equivariant isomorphism
${\left\langle \gamma _3 ,f\right\rangle }$
-equivariant isomorphism
![]() ${{\widetilde G}}/{{{{\mathbf G}}^F}}\cong \operatorname Z({{{{\mathbf G}}^F}})$
, we see that
${{\widetilde G}}/{{{{\mathbf G}}^F}}\cong \operatorname Z({{{{\mathbf G}}^F}})$
, we see that
![]() ${{\widetilde G}}_{\chi }={{{{\mathbf G}}^F}}$
, as there is no
${{\widetilde G}}_{\chi }={{{{\mathbf G}}^F}}$
, as there is no
![]() $\gamma _3 f$
-stable subgroups of
$\gamma _3 f$
-stable subgroups of
![]() $Z({{{{\mathbf G}}^F}})$
apart from
$Z({{{{\mathbf G}}^F}})$
apart from
![]() $\{1\}$
and
$\{1\}$
and
![]() $\operatorname Z({{{{\mathbf G}}^F}})$
.
$\operatorname Z({{{{\mathbf G}}^F}})$
.
The element
![]() $\gamma _3 f$
acts on
$\gamma _3 f$
acts on
![]() $\operatorname Z({{{{\mathbf G}}^F}})$
such that only the trivial element is fixed by
$\operatorname Z({{{{\mathbf G}}^F}})$
such that only the trivial element is fixed by
![]() $\gamma _3 f$
and
$\gamma _3 f$
and
![]() $[\gamma _3 f,\operatorname Z({{{{\mathbf G}}^F}})]=\operatorname Z({{{{\mathbf G}}^F}})\setminus \{1\}$
.
$[\gamma _3 f,\operatorname Z({{{{\mathbf G}}^F}})]=\operatorname Z({{{{\mathbf G}}^F}})\setminus \{1\}$
.
Hence, some
![]() ${{\widetilde G}}$
-conjugate
${{\widetilde G}}$
-conjugate
![]() $\chi '$
of
$\chi '$
of
![]() $\chi $
satisfies
$\chi $
satisfies
![]() $\gamma _3f \in ({{\widetilde G}} E)_{\chi '} $
. We observe that
$\gamma _3f \in ({{\widetilde G}} E)_{\chi '} $
. We observe that
![]() $\gamma _3 f$
is a
$\gamma _3 f$
is a
![]() $3$
-element and hence
$3$
-element and hence
![]() $o(f)$
is a power of
$o(f)$
is a power of
![]() $3$
. Note that f acts trivially on
$3$
. Note that f acts trivially on
![]() $\operatorname Z({{\mathbf G}})$
. Since
$\operatorname Z({{\mathbf G}})$
. Since
![]() $\chi $
satisfies
$\chi $
satisfies
![]() $({{\widetilde G}} E^{\circ })_{\chi }= {{{{\mathbf G}}^F}} E^{\circ }_{\chi }$
and
$({{\widetilde G}} E^{\circ })_{\chi }= {{{{\mathbf G}}^F}} E^{\circ }_{\chi }$
and
![]() $[\operatorname Z({{{{\mathbf G}}^F}}),F_p]=1$
, this leads to
$[\operatorname Z({{{{\mathbf G}}^F}}),F_p]=1$
, this leads to
![]() $({{\widetilde G}} E^{\circ })_{\chi '}\in \{ G E^{\circ }_{\chi }, \ {{{{\mathbf G}}^F}} {\left\langle F_p, \gamma \widehat t\right\rangle }_{\chi '}\}$
for some
$({{\widetilde G}} E^{\circ })_{\chi '}\in \{ G E^{\circ }_{\chi }, \ {{{{\mathbf G}}^F}} {\left\langle F_p, \gamma \widehat t\right\rangle }_{\chi '}\}$
for some
![]() $\widehat t \in {{\widetilde G}}$
with
$\widehat t \in {{\widetilde G}}$
with
![]() $\mathcal L(\widehat t)=h_0$
. Let
$\mathcal L(\widehat t)=h_0$
. Let
![]() $\widehat G:=\mathcal L^{-1}({\left\langle h_0\right\rangle })$
. In the latter case,
$\widehat G:=\mathcal L^{-1}({\left\langle h_0\right\rangle })$
. In the latter case,
Recalling that the orders of
![]() ${\widetilde G}/(\operatorname Z({\widetilde G}){{{{\mathbf G}}^F}})$
and f are coprime, we get
${\widetilde G}/(\operatorname Z({\widetilde G}){{{{\mathbf G}}^F}})$
and f are coprime, we get
![]() $\widehat t^{-1} \gamma _3(\widehat t)\in {\left\langle \widehat t^{-1} \gamma _3(\widehat t) f^2\right\rangle }$
, but
$\widehat t^{-1} \gamma _3(\widehat t)\in {\left\langle \widehat t^{-1} \gamma _3(\widehat t) f^2\right\rangle }$
, but
![]() $\widehat t^{-1} \gamma _3(\widehat t)\in {{\widetilde G}}_{\chi }$
and
$\widehat t^{-1} \gamma _3(\widehat t)\in {{\widetilde G}}_{\chi }$
and
![]() $\widehat t^{-1} \gamma _3(\widehat t)\notin {{{{\mathbf G}}^F}}$
. This leads to a contradiction, and we see that
$\widehat t^{-1} \gamma _3(\widehat t)\notin {{{{\mathbf G}}^F}}$
. This leads to a contradiction, and we see that
![]() $({{\widetilde G}} E^{\circ })_{\chi '}= {{{{\mathbf G}}^F}} E^{\circ }_{\chi }$
and hence
$({{\widetilde G}} E^{\circ })_{\chi '}= {{{{\mathbf G}}^F}} E^{\circ }_{\chi }$
and hence
![]() $({{\widetilde G}} E)_{\chi '}={{{{\mathbf G}}^F}} {\left\langle E^{\circ }_{\chi '}, \gamma _3f\right\rangle }$
.
$({{\widetilde G}} E)_{\chi '}={{{{\mathbf G}}^F}} {\left\langle E^{\circ }_{\chi '}, \gamma _3f\right\rangle }$
.
We can now deduce Theorem A from Theorem 2.8.
Proof of Theorem A
For a given fixed Levi subgroup L of
![]() ${{{{\mathbf G}}^F}}$
, we apply Theorem 2.8 whose assumptions follow from Theorems 3.1 and 6.1. In this way, we obtain an
${{{{\mathbf G}}^F}}$
, we apply Theorem 2.8 whose assumptions follow from Theorems 3.1 and 6.1. In this way, we obtain an
![]() $E_L$
-stable
$E_L$
-stable
![]() ${\widetilde G}$
-transversal in
${\widetilde G}$
-transversal in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
(see Lemma 7.2). If L is E-stable,
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
(see Lemma 7.2). If L is E-stable,
![]() $E_L=E$
and this gives the required statement. If L has an E-stable
$E_L=E$
and this gives the required statement. If L has an E-stable
![]() ${{{{\mathbf G}}^F}}$
-conjugate
${{{{\mathbf G}}^F}}$
-conjugate
![]() $L'$
, then we observe that
$L'$
, then we observe that
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))=\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L',\mathrm {Irr}_{cusp}(L')))$
and there exists an E-stable
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))=\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L',\mathrm {Irr}_{cusp}(L')))$
and there exists an E-stable
![]() ${{\widetilde G}}$
-transversal in
${{\widetilde G}}$
-transversal in
![]() $\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L',\mathrm {Irr}_{cusp}(L')))$
.
$\mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L',\mathrm {Irr}_{cusp}(L')))$
.
It remains to consider the case where
![]() $E_L\neq E$
and no
$E_L\neq E$
and no
![]() ${{{{\mathbf G}}^F}}$
-conjugate of L is E-stable. Then according to Propositions 7.3 and 7.4, every
${{{{\mathbf G}}^F}}$
-conjugate of L is E-stable. Then according to Propositions 7.3 and 7.4, every
![]() $\chi '\in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
has some
$\chi '\in \mathrm {Irr}({{{{\mathbf G}}^F}}\mid (L,\mathrm {Irr}_{cusp}(L)))$
has some
![]() ${{\widetilde G}}$
-conjugate
${{\widetilde G}}$
-conjugate
![]() $\chi $
with
$\chi $
with
![]() $({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
.
$({{\widetilde G}} E)_{\chi }={{\widetilde G}}_{\chi } E_{\chi }$
.
Acknowledgments
I thank Julian Brough, Lucas Ruhstorfer, Gunter Malle, and the anonymous referee for their remarks on versions of the paper.