Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-13T02:47:13.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure valued solutions of asymptotically homogeneous semilinear hyperbolic systems in one space variable

Published online by Cambridge University Press:  20 January 2009

F. Demengel  and
J. Rauch
F. Demengel
Affiliation:
Département de MathematiquesUniversité de Paris SudOrsay, 91405 Cedex, France
J. Rauch
Affiliation:
Department of MathematicsUniversity of MichiganAnn Arbor, MI 48109, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study systems which in characteristic coordinates have the form

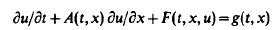
where A is a k × k diagonal matrix with distinct real eigenvalues. The nonlinearity F is assumed to be asymptotically homogeneous in the sense, that it is a sum of two terms, one positively homogeneous of degree one in u and a second which is sublinear in u and vanishes when u = 0. In this case, F(t, x, u(t)) is meaningful provided that u(t) is a Radon measure, and, for Radon measure initial data there is a unique solution (Theorem 2.1).

The main result asserts that if μn is a sequence of initial data such that, in characteristic coordinates, the positive and negative parts of each component, 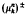, converge weakly to μ±, then the solutions coverge weakly and the limit has an interesting description given by a nonlinear superposition principle.

Simple weak converge of the initial data does not imply weak convergence of the solutions.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , Issue 3 , October 1990 , pp. 443 - 460
Copyright
Copyright © Edinburgh Mathematical Society 1990

References

REFERENCES

1.Bourbaki, N., Integration, chapter 5 (second edition) (Hermann, Paris), 65–67.Google Scholar
2.Demengel, F. and Rauch, J., Continuite faible des fonctions de mesures (non convexes), C.R. Acad. Sci. Paris, Sér. I. Math. 305 (1987), 63–66.Google Scholar
3.Demengel, F. and Rauch, J., Superposition d'ondes singulières, C.R. Acad. Sci. Paris, Sér. I. Math. 304 (1987), 447–449.Google Scholar
4.Demengel, F. and Rauch, J., Weak convergence of asymptotically homogeneous functions of measures, Nonlinear Anal. (1990), to appear.CrossRefGoogle Scholar
5.Oberguggenberger, M., Weak limits of solutions of semilinear hyperbolic systems, Math. Ann. 274 (1986), 599–607.CrossRefGoogle Scholar
6.Rauch, J. and Reed, M., Nonlinear superposition and absorption of delta waves in one space dimension, J. Fund. Anal. 73 (1987), 152–178.CrossRefGoogle Scholar