Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cencelj, Matija
Repovš, Dušan
and
Virk, Žiga
2015.
Multiple perturbations of a singular eigenvalue problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 119,
Issue. ,
p.
37.
Chen, Wei
and
Tang, Chun-Lei
2020.
INFINITELY MANY SOLUTIONS FOR CRITICAL FRACTIONAL EQUATION WITH SIGN-CHANGING WEIGHT FUNCTION.
Journal of Applied Analysis & Computation,
Vol. 10,
Issue. 1,
p.
131.

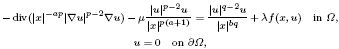
 ≡ ((
≡ ((