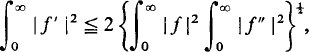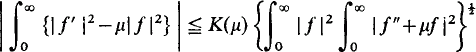Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Copson, E. T.
1977.
On two inequalities of Brodlie and Everitt.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 77,
Issue. 3-4,
p.
329.
1977.
On an integral inequality.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 357,
Issue. 1690,
p.
271.
Russell, A.
1979.
On certain fourth-order integral inequalities.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 83,
Issue. 3-4,
p.
205.
Beesack, P. R.
1979.
A simpler proof of two inequalities of Brodlie and Everitt.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 84,
Issue. 3-4,
p.
259.
Phóng, Vũ Qúôc
1981.
On inequalities for powers of linear operators and for quadratic forms.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 89,
Issue. 1-2,
p.
25.
Everitt, W. N.
and
Sleeman, B. D.
1981.
Ordinary and Partial Differential Equations.
Vol. 846,
Issue. ,
p.
227.
1982.
A return to the Hardy-Littlewood integral inequality.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 380,
Issue. 1779,
p.
447.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
1.
Benammar, M.
Bennewitz, C.
Beynon, M. J.
Brown, B. M.
Dias, N. G. J.
Evans, W. D.
Everitt, W. N.
Kirby, V. G.
and
Littlejohn, L. L.
1998.
Recent Progress in Inequalities.
p.
127.
Brown, B. M.
and
Marletta, M.
1998.
On a conjecture of Bennewitz, and the behaviour of the Titchmarsh–Weyl matrix near a pole.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 454,
Issue. 1973,
p.
1383.
Everitt, W. N.
and
Zettl, Anton
2003.
Gian-Carlo Rota on Analysis and Probability.
p.
227.
Gesztesy, Fritz
Nichols, Roger
and
Stanfill, Jonathan
2021.
A Survey of Some Norm Inequalities.
Complex Analysis and Operator Theory,
Vol. 15,
Issue. 2,