Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-06T14:08:41.867Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugacy classes in finite groups

Published online by Cambridge University Press:  14 November 2011

Antonio Vera López
Antonio Vera López
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad del Pais Vasco, Apartado 644, Bilbao, Spain
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper, the number of conjugacy classes in a finite group G is analysed in terms of the number of ordered pairs that generate it. Using this relation, we give a new elementary proof of one of A. Mann's results for finite groups, namely: |G| ≡ r(G) (mod. d|G|. δ|G|), where 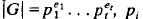, prime and pi ≠ Pj for every i≠j, r(G) denotes the number of conjugacy classes of elements of G, d|G| = g.c.d. (p1 − 1, … pt − 1) and δ|G| = g.c.d. 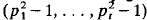. The above congruence is obtained without using character theory. We also obtain new local congruences that slightly improve Mann's congruence.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 259 - 264
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Feit, W.. Characters of Finite Groups (New York: W. A. Benjamin, 1967).Google Scholar
2Hall, P.. The Eulerian functions of a group. Quart. J. Math. Oxford 7 (1936), 134–151.CrossRefGoogle Scholar
3Hirsch, K. A.. On a theorem of Burnside. Quart. J. Math. Oxford Ser. (2) 1 (1950), 97–99.CrossRefGoogle Scholar
4Huppert, B.. Endliche Gruppen, Vol. I (Berlin: Springer, 1967).CrossRefGoogle Scholar
5Mann, A.. Conjugacy classes in finite groups. Israel J. Math. 31 (1978),78–84.CrossRefGoogle Scholar
6Polland, J.. Two problems on finite groups with k conjugate classes. /. Austral.Math. Soc. 8 (1968), 49–55.CrossRefGoogle Scholar
7Waall, R. W. Van der. On a theorem of Burnside. Elem. Math. 25 (1970), 136–137.Google Scholar
8, A. Vera López. Conjugacy classes in finite solvable groups. Israel J. Math. 47 (1984), 241–245.CrossRefGoogle Scholar