Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-04T03:22:42.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant

Part of: Parabolic equations and systems Physiological, cellular and medical topics Partial differential equations Representations of solutions

Published online by Cambridge University Press:  30 April 2024

Minghua Zhang ,
Chunlai Mu  and
Hongying Yang
Minghua Zhang
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P.R. China (mhzhang2209@163.com; clmu2005@163.com)
Chunlai Mu
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P.R. China (mhzhang2209@163.com; clmu2005@163.com)
Hongying Yang
Affiliation:
School of Sciences, Shihezi University, Shihezi 832000, P.R. China (yanghongying1980@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the following quasilinear chemotaxis system with consumption of chemoattractant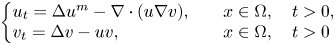

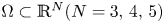\[ \left\{\begin{array}{@{}ll} u_t=\Delta u^{m}-\nabla\cdot(u\nabla v),\quad & x\in \Omega,\quad t>0,\\ v_t=\Delta v-uv,\quad & x\in \Omega,\quad t>0\\ \end{array}\right. \]
in a bounded domain $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ with smooth boundary $\partial \Omega$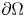. It is shown that if $m>\max \{1,\,\frac {3N-2}{2N+2}\}$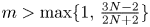, for any reasonably smooth nonnegative initial data, the corresponding no-flux type initial-boundary value problem possesses a globally bounded weak solution. Furthermore, we prove that the solution converges to the spatially homogeneous equilibrium $(\bar {u}_0,\,0)$ 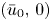in an appropriate sense as $t\rightarrow \infty$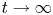, where $\bar {u}_0=\frac {1}{|\Omega |}\int _\Omega u_0$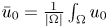. This result not only partly extends the previous global boundedness result in Fan and Jin (J. Math. Phys. 58 (2017), 011503) and Wang and Xiang (Z. Angew. Math. Phys. 66 (2015), 3159–3179) to $m>\frac {3N-2}{2N}$ 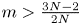in the case $N\geq 3$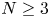, but also partly improves the global existence result in Zheng and Wang (Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 669–686) to $m>\frac {3N}{2N+2}$ 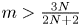when $N\geq 2$.

Keywords

boundednesschemotaxisweak solutionlarge time behaviourquasilinear

MSC classification

Primary: 35B40: Asymptotic behavior of solutions
Secondary: 35D30: Weak solutions 35K51: Initial-boundary value problems for second-order parabolic systems 92C17: Cell movement (chemotaxis, etc.)
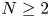Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cao, X.. Global classical solutions in chemotaxis(–Navier)–Stokes system with rotational flux term. J. Differ. Equ. 261 (2016), 6883–6914.CrossRefGoogle Scholar
Cao, X. and Lankeit, J.. Global classical small-data solutions for a three-dimensional chemotaxis Navier–Stokes system involving matrix-valued sensitivities. Calc. Var. Part. Differ. Equ. 55 (2016), 107.CrossRefGoogle Scholar
Di Francesco, M., Lorz, A. and Markowich, P.. Chemotaxis–fluid coupled model for swimming bacteria with nonlinear diffusion: global existence and asymptotic behavior. Discrete Contin. Dyn. Syst. 28 (2010), 1437–1453.CrossRefGoogle Scholar
Evans, L. C., Partial Differential Equations (Providence, RI: American Mathematical Society, 2010).Google Scholar
Fan, L. and Jin, H.. Global existence and asymptotic behavior to a chemotaxis system with consumption of chemoattractant in higher dimensions. J. Math. Phys. 58 (2017), 011503.CrossRefGoogle Scholar
Jin, C., Global bounded solution in three-dimensional chemotaxis–Stokes model with arbitrary porous medium slow diffusion. eprint arXiv:2101.11235.Google Scholar
Horstmann, D. and Winkler, M.. Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215 (2005), 52–107.CrossRefGoogle Scholar
Ladyzhenskaia, O. A., Solonnikov, V. A. and Ural'tseva, N. N.. Linear and quasi-linear equations of parabolic type (Providence: American Mathematical Society, 1968).CrossRefGoogle Scholar
Lions, P.. Résolution de problèmes elliptiques quasilinéaires. Arch. Rational Mech. Anal. 74 (1980), 335–353.CrossRefGoogle Scholar
Lorz, A.. Coupled chemotaxis fluid model. Math. Models Methods Appl. Sci. 20 (2010), 987–1004.CrossRefGoogle Scholar
Nagai, T., Senba, T. and Yoshida, K.. Application of the Trudinger–Moser inequality to a parabolic system of chemotaxis. Funkcial. Ekvac. 40 (1997), 411–433.Google Scholar
Tao, Y.. Boundedness in a chemotaxis model with oxygen consumption by bacteria. J. Math. Anal. Appl. 381 (2011), 521–529.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Boundedness in a quasilinear parabolic–parabolic Keller–Segel system with subcritical sensitivity. J. Differ. Equ. 252 (2012), 692–715.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equ. 252 (2012), 2520–2543.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Global existence and boundedness in a Keller–Segel–Stokes model with arbitrary porous medium diffusion. Discrete Contin. Dyn. Syst. 32 (2012), 1901–1914.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Locally bounded global solutions in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion. Ann. Inst. H. Poincaré C Anal. Non Linéaire 30 (2013), 157–178.CrossRefGoogle Scholar
Tian, Y. and Xiang, Z.. Global boundedness to a 3D chemotaxis–Stokes system with porous medium cell diffusion and general sensitivity. Adv. Nonlinear Anal. 12 (2022), 23–53.CrossRefGoogle Scholar
Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C., Kessler, J. and Goldstein, R.. Bacterial swimming and oxygen transport near contact lines. Proc. Natl. Acad. Sci. USA 102 (2005), 2277–2282.CrossRefGoogle ScholarPubMed
Wang, L., Mu, C., Lin, K. and Zhao, J.. Global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Z. Angew. Math. Phys. 66 (2015), 1633–1648.CrossRefGoogle Scholar
Wang, L., Mu, C. and Zhou, S.. Boundedness in a parabolic–parabolic chemotaxis system with nonlinear diffusion. Z. Angew. Math. Phys. 65 (2014), 1137–1152.CrossRefGoogle Scholar
Wang, W.. Global boundedness of weak solutions for a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 268 (2020), 7047–7091.CrossRefGoogle Scholar
Wang, Y.. Boundedness in a 2D chemotaxis–Stokes system with general sensitivity and nonlinear diffusion. Comput. Math. Appl. 76 (2018), 818–830.CrossRefGoogle Scholar
Wang, Y. and Xie, L.. Boundedness for a 3D chemotaxis–Stokes system with porous medium diffusion and tensor-valued chemotactic sensitivity. Z. Angew. Math. Phys. 68 (2017), 29.CrossRefGoogle Scholar
Wang, Y. and Xiang, Z.. Global existence and boundedness in a higher-dimensional quasilinear chemotaxis system. Z. Angew. Math. Phys. 66 (2015), 3159–3179.CrossRefGoogle Scholar
Winkler, M.. Boundedness in the higher-dimensional parabolic–parabolic chemotaxis system with logistic source. Commun. Partial Differ. Equ. 35 (2010), 1516–1537.CrossRefGoogle Scholar
Winkler, M.. Global large-data solutions in a chemotaxis–(Navier–)Stokes system modeling cellular swimming in fluid drops. Commun. Partial Differ. Equ. 37 (2012), 319–351.CrossRefGoogle Scholar
Winkler, M.. Stabilization in a two-dimensional chemotaxis–Navier–Stokes system. Arch. Ration. Mech. Anal. 211 (2014), 455–487.CrossRefGoogle Scholar
Winkler, M.. Boundedness and large time behavior in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Calc. Var. Part. Differ. Equ. 54 (2015), 3789–3828.CrossRefGoogle Scholar
Winkler, M.. Global weak solutions in a three-dimensional chemotaxis–Navier–Stokes system. Ann. Inst. H. Poincaré C Anal. Non Linéaire 33 (2016), 1329–1352.CrossRefGoogle Scholar
Winkler, M.. How far do chemotaxis-driven forces influence regularity in the Navier–Stokes system?. Trans. Am. Math. Soc. 369 (2017), 3067–3125.CrossRefGoogle Scholar
Winkler, M.. Global existence and stabilization in a degenerate chemotaxis–Stokes system with mildly strong diffusion enhancement. J. Differ. Equ. 264 (2018), 6109–6151.CrossRefGoogle Scholar
Winkler, M.. Global mass-preserving solutions in a two-dimensional chemotaxis–Stokes system with rotational flux components. J. Evol. Equ. 18 (2018), 1267–1289.CrossRefGoogle Scholar
Winkler, M.. Can rotational fluxes impede the tendency toward spatial homogeneity in nutrient Taxis(–Stokes) systems?. Int. Math. Res. Not. IMRN 11 (2021), 8106–8152.CrossRefGoogle Scholar
Winkler, M.. Chemotaxis–Stokes interaction with very weak diffusion enhancement: blow-up exclusion via detection of absorption-induced entropy structures involving multiplicative couplings. Adv. Nonlinear Stud. 22 (2022), 88–117.CrossRefGoogle Scholar
Xiang, T.. How strong a logistic damping can prevent blow-up for the minimal Keller–Segel chemotaxis system?. J. Math. Anal. Appl. 459 (2018), 1172–1200.CrossRefGoogle Scholar
Zhang, Q. and Li, Y.. Global weak solutions for the three-dimensional chemotaxis–Navier–Stokes system with nonlinear diffusion. J. Differ. Equ. 259 (2015), 3730–3754.CrossRefGoogle Scholar
Zheng, J.. Global existence and boundedness in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Ann. Mat. Pura Appl. 201 (2022), 243–288.CrossRefGoogle Scholar
Zheng, J. and Ke, Y.. Global bounded weak solutions for a chemotaxis–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 289 (2021), 182–235.CrossRefGoogle Scholar
Zheng, J. and Ke, Y.. Further study on the global existence and boundedness of the weak solution in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Commun. Nonlinear Sci. Numer. Simul. 115 (2022), 106732.CrossRefGoogle Scholar
Zheng, J. and Qi, D.. Global existence and boundedness in an $N$-dimensional chemotaxis–Navier–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 335 (2022), 347–397.CrossRefGoogle Scholar
Zheng, J. and Wang, Y.. A note on global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 669–686.Google Scholar