In this paper, we study intersection configurations – which describe the behaviour of multiple (finite) intersections of subgroups with respect to finite generability – in the realm of free and free times free-abelian (FTFA) groups. We say that a configuration is realizable in a group $G$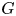 if there exist subgroups $H_1,\ldots, H_k \leqslant G$ 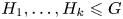realizing it. It is well known that free groups ${\mathbb {F}_{n}}$ 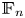satisfy the Howson property: the intersection of any two finitely generated subgroups is again finitely generated. We show that the Howson property is indeed the only obstruction for multiple intersection configurations to be realizable within nonabelian free groups. On the contrary, FTFA groups ${\mathbb {F}_{n}} \times \mathbb {Z}^m$ 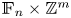are well known to be non-Howson. We also study multiple intersections within FTFA groups, providing an algorithm to decide, given $k\geq 2$ 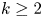finitely generated subgroups, whether their intersection is again finitely generated and, in the affirmative case, compute a ‘basis’ for it. We finally prove that any intersection configuration is realizable in an FTFA group ${\mathbb {F}_{n}} \times \mathbb {Z}^m$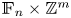, for $n\geq 2$ 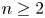and large enough $m$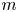. As a consequence, we exhibit finitely presented groups where every intersection configuration is realizable.