Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-05T16:01:43.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Nowhere scattered multiplier algebras

Published online by Cambridge University Press:  05 January 2024

Eduard Vilalta Open the ORCID record for Eduard Vilalta [Opens in a new window]
Eduard Vilalta*
Affiliation:
Fields Institute for Research in Mathematical Sciences, Toronto M5T 3J1, Canada Previous institution: Departament de Matemàtiques, Universitat Autònoma de Barcelona, Bellaterra, Barcelona 08193, Spain (eduardvilaltavila@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study sufficient conditions under which a nowhere scattered $\mathrm {C}^*$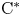-algebra $A$ 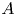has a nowhere scattered multiplier algebra $\mathcal {M}(A)$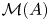, that is, we study when $\mathcal {M}(A)$ 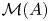has no nonzero, elementary ideal-quotients. In particular, we prove that a $\sigma$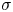-unital $\mathrm {C}^*$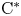-algebra $A$ 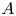of

  1. (i) finite nuclear dimension, or

  2. (ii) real rank zero, or

  3. (iii) stable rank one with $k$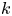-comparison,

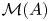is nowhere scattered if and only if $\mathcal {M}(A)$ is.

Keywords

C*-algebramultiplier algebraCuntz semigroup
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 30
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antoine, R., Perera, F., Robert, L. and Thiel, H.. Edwards’ condition for quasitraces on C*-algebras. Proc. Roy. Soc. Edinburgh Sect. A 151 (2021), 525–547.CrossRefGoogle Scholar
Antoine, R., Perera, F., Robert, L. and Thiel, H.. C*-algebras of stable rank one and their Cuntz semigroups. Duke Math. J. 171 (2022), 33–99.CrossRefGoogle Scholar
Antoine, R., Perera, F. and Thiel, H.. Tensor products and regularity properties of Cuntz semigroups. Mem. Amer. Math. Soc. 251 (2018), viii+191.Google Scholar
Antoine, R., Perera, F. and Thiel, H.. Cuntz semigroups of ultraproduct C*-algebras. J. Lond. Math. Soc. (2) 102 (2020), 994–1029.CrossRefGoogle Scholar
Ara, P., Perera, F. and Toms, A. S., $K$-theory for operator algebras. Classification of C*-algebras, in Aspects of operator algebras and applications, Contemp. Math. Vol. 534 (Amer. Math. Soc., Providence, RI, 2011), pp. 1–71.CrossRefGoogle Scholar
Asadi-Vasfi, A., Thiel, H. and Vilalta, E., Ranks of soft operators in nowhere scattered C*-algebras, preprint arXiv:2310.00663 [math.OA], 2023.Google Scholar
Bosa, J.. Stable elements and property (S). J. Math. Anal. Appl. 512 (2022), 126171. 16.CrossRefGoogle Scholar
Brown, L. G. and Pedersen, G. K.. C*-algebras of real rank zero. J. Funct. Anal. 99 (1991), 131–149.CrossRefGoogle Scholar
Brown, L. G. and Pedersen, G. K.. Limits and C*-algebras of low rank or dimension. J. Operator Theory 61 (2009), 381–417.Google Scholar
Brown, N. P. and Ciuperca, A.. Isomorphism of Hilbert modules over stably finite C*-algebras. J. Funct. Anal. 257 (2009), 332–339.CrossRefGoogle Scholar
Chand, A. and Robert, L.. Simplicity bounded normal generation, and automatic continuity of groups of unitaries. Adv. Math. 415 (2023), 108894. 52 p.CrossRefGoogle Scholar
Christensen, M. S., Regularity of C*-algebras and central sequence algebras, 2017, Thesis (Ph.D.). University of Copenhagen (Denmark).Google Scholar
Ciuperca, A., Robert, L. and Santiago, L.. The Cuntz semigroup of ideals and quotients and a generalized Kasparov stabilization theorem. J. Operator Theory 64 (2010), 155–169.Google Scholar
Coward, K. T., Elliott, G. A. and Ivanescu, C.. The Cuntz semigroup as an invariant for C*-algebras. J. Reine Angew. Math. 623 (2008), 161–193.Google Scholar
Cuntz, J.. Dimension functions on simple C*-algebras. Math. Ann. 233 (1978), 145–153.CrossRefGoogle Scholar
Elliott, G. A.. Derivations of matroid $C^{\ast }$-algebras. II. Ann. Math. (2) 100 (1974), 407–422.CrossRefGoogle Scholar
Elliott, G. A., Robert, L. and Santiago, L.. The cone of lower semicontinuous traces on a $\mathrm {C}^*$-algebra. Amer. J. Math. 133 (2011), 969–1005.CrossRefGoogle Scholar
Elliott, G. A. and Rørdam, M., Perturbation of Hausdorff moment sequences, and an application to the theory of C*-algebras of real rank zero, in Operator Algebras: The Abel Symposium 2004, Abel Symp., Vol. 1 (Springer, Berlin, 2006), pp. 97–115.CrossRefGoogle Scholar
Engbers, M., Decomposition of simple Cuntz semigroups, Ph.D. Thesis, WWU Münster, 2014.Google Scholar
Farah, I., Hart, B., Lupini, M., Robert, L., Tikuisis, A., Vignati, A. and Winter, W.. Model theory of C*-algebras. Mem. Amer. Math. Soc. 271 (2021), viii+127.Google Scholar
Gardella, E. and Perera, F., The modern theory of Cuntz semigroups of $\mathrm {C}^*$-algebras, preprint arXiv:2212.02290 [math.OA], 2022.Google Scholar
Kaftal, V., Ng, P. W. and Zhang, S.. Strict comparison of positive elements in multiplier algebras. Canad. J. Math. 69 (2017), 373–407.CrossRefGoogle Scholar
Kaftal, V., Ng, P. W. and Zhang, S.. Purely infinite corona algebras. J. Operator Theory 82 (2019), 307–355.CrossRefGoogle Scholar
Kirchberg, E., Central sequences in C*-algebras and strongly purely infinite algebras, in Operator Algebras: The Abel Symposium 2004, Abel Symp. Vol. 1 (Springer, Berlin, 2006), pp. 175–231.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Infinite non-simple C*-algebras: absorbing the Cuntz algebra $\mathcal {O}_\infty$. Adv. Math. 167 (2002), 195–264.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. When central sequence C*-algebras have characters. Internat. J. Math. 26 (2015), 1550049. 32.CrossRefGoogle Scholar
Kucerovsky, D., Ng, P. W. and Perera, F.. Purely infinite corona algebras of simple $C^\ast$-algebras. Math. Ann. 346 (2010), 23–40.CrossRefGoogle Scholar
Kucerovsky, D. and Perera, F.. Purely infinite corona algebras of simple $C^*$-algebras with real rank zero. J. Operator Theory 65 (2011), 131–144.Google Scholar
Larsen, N. S. and Osaka, H.. Extremal richness of multiplier algebras and corona algebras of simple $C^*$-algebras. J. Operator Theory 38 (1997), 131–149.Google Scholar
Lin, H. X.. Simple $C^*$-algebras with continuous scales and simple corona algebras. Proc. Amer. Math. Soc. 112 (1991), 871–880.Google Scholar
Lin, H.. Exponential rank of C*-algebras with real rank zero and the Brown-Pedersen conjectures. J. Funct. Anal. 114 (1993), 1–11.CrossRefGoogle Scholar
Lin, H.. Simple corona $C^*$-algebras. Proc. Amer. Math. Soc. 132 (2004), 3215–3224.CrossRefGoogle Scholar
Lin, H. and Ng, P. W.. The corona algebra of the stabilized Jiang-Su algebra. J. Funct. Anal. 270 (2016), 1220–1267.CrossRefGoogle Scholar
Ng, P. W. and Winter, W.. Nuclear dimension and the corona factorization property. Int. Math. Res. Not. 2010 (2010), 261–278.CrossRefGoogle Scholar
Pedersen, G. K.. Applications of weak${\ast }$ semicontinuity in $\mathrm {C}^*$-algebra theory. Duke Math. J. 39 (1972), 431–450.CrossRefGoogle Scholar
Perera, F.. Extremal richness of multiplier and corona algebras of simple $C^\ast$-algebras with real rank zero. J. Operator Theory 44 (2000), 413–431.Google Scholar
Perera, F. and Rørdam, M.. AF-embeddings into C*-algebras of real rank zero. J. Funct. Anal. 217 (2004), 142–170.CrossRefGoogle Scholar
Robert, L.. The cone of functionals on the Cuntz semigroup. Math. Scand. 113 (2013), 161–186.CrossRefGoogle Scholar
Robert, L.. On the Lie ideals of $C^*$-algebras. J. Operator Theory 75 (2016), 387–408.CrossRefGoogle Scholar
Robert, L. and Rørdam, M.. Divisibility properties for C*-algebras. Proc. Lond. Math. Soc. (3) 106 (2013), 1330–1370.CrossRefGoogle Scholar
Robert, L. and Tikuisis, A.. Nuclear dimension and $\mathcal {Z}$-stability of non-simple C*-algebras. Trans. Amer. Math. Soc. 369 (2017), 4631–4670.CrossRefGoogle Scholar
Rørdam, M.. Ideals in the multiplier algebra of a stable $\mathrm {C}^*$-algebra. J. Operator Theory 25 (1991), 283–298.Google Scholar
Rørdam, M.. On the structure of simple C*-algebras tensored with a UHF-algebra. II. J. Funct. Anal. 107 (1992), 255–269.CrossRefGoogle Scholar
Rørdam, M. and Winter, W.. The Jiang-Su algebra revisited. J. Reine Angew. Math. 642 (2010), 129–155.Google Scholar
Sakai, S.. Derivations of simple C*-algebras. III. Tohoku Math. J. (2) 23 (1971), 559–564.CrossRefGoogle Scholar
Thiel, H., The Cuntz semigroup, lecture notes available at www.math.uni-muenster.de/u/hannes.thiel/, 2017.Google Scholar
Thiel, H.. Ranks of operators in simple C*-algebras with stable rank one. Comm. Math. Phys. 377 (2020), 37–76.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E.. Covering dimension of Cuntz semigroups II. Internat. J. Math. 32 (2021), 2150100. 27 p.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E., Nowhere scattered C*-algebras, J. Noncommut. Geom. (to appear), preprint arXiv:2112.09877 [math.OA], 2021.Google Scholar
Thiel, H. and Vilalta, E.. Covering dimension of Cuntz semigroups. Adv. Math. 394 (2022), 108016. 44 p.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E.. The Global Glimm Property. Trans. Amer. Math. Soc. 376 (2023), 4713–4744. DOI: 10.1090/tran/8880. 2022.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E., Soft operators in C*-algebras, preprint arXiv:2304.11644 [math.OA], 2023.Google Scholar
Vilalta, E.. A local characterization for the Cuntz semigroup of AI-algebras. J. Math. Anal. Appl. 506 (2022), 125612. 47.CrossRefGoogle Scholar
Winter, W.. Nuclear dimension and $\mathcal {Z}$-stability of pure C*-algebras. Invent. Math. 187 (2012), 259–342.CrossRefGoogle Scholar
Winter, W. and Zacharias, J.. The nuclear dimension of C*-algebras. Adv. Math. 224 (2010), 461–498.CrossRefGoogle Scholar
Zhang, S.. A Riesz decomposition property and ideal structure of multiplier algebras. J. Operator Theory 24 (1990), 209–225.Google Scholar