Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-16T12:29:44.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Some existence, uniqueness and nonuniqueness theorems for solutions of parabolic equations with discontinuous nonlinearities

Published online by Cambridge University Press:  14 November 2011

Eduard Feireisl  and
John Norbury
Eduard Feireisl
Affiliation:
Institute of Mathematics ČSAV, Prague, Czechoslovakia
John Norbury
Affiliation:
Mathematical Institute, St Giles, Oxford, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We consider the problem

where H stands for the maximal monotone graph associated with the Heaviside step function. It is shown that the problem possesses at least one (strong) solution belonging to an appropriate function space. Moreover, we prove:

(i) There is a smooth initial function u0, u0≧1, where the equality holds at exactly one point such that there are at least two different solutions corresponding to the initial data u0.

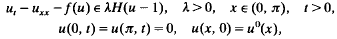
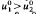(ii) The comparison principle: The relation for any x ≠ 0, implies u1(t)>u2(t), t≧0 for any u1, u2 solving the problem with the initial data 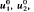, respectively.

(iii) For a “reasonable” set of initial data the solution is uniquely determined. Moreover, the free boundary {(x, t)| u(x, t) = 1} is regular and on its complement the equation holds in a classical sense.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 119 , Issue 1-2 , 1991 , pp. 1 - 17
Copyright
Copyright © Royal Society of Edinburgh 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Douchet, J.. The number of positive solutions of a nonlinear problem with discontinuous nonlinearity. Proc. Roy. Soc. Edinburgh Sect. A 90 (1981), 281–291.CrossRefGoogle Scholar
2Ekeland, I. and Temam, R.. Convex analysis and variational problems (Amsterdam: North-Holland, 1976).Google Scholar
3Friedman, A.. Partial differential equations of parabolic type (New York: Prentice-Hall, 1964).Google Scholar
4Henry, D.. Geometric theory of semilinear parabolic equations, Lecture Notes in Mathematics 840 (Berlin: Springer, 1981).CrossRefGoogle Scholar
5Ishii, H.. Asymptotic stability and blowing up of solutions of some nonlinear equations. J Differential Equations 26 (1977), 291–319.CrossRefGoogle Scholar
6Koi, Y. and Watanabe, J.. On nonlinear evolution equations with a difference term of subdifferentials. Proc. Japan Acad. 52 (8) (1976), 413–416.Google Scholar
7Lacey, A. A.. The spatial dependence of supercritical reacting systems. IMA J. Appl. Math. 27 (1981), 71–84.CrossRefGoogle Scholar
8Nistri, P.. Positive solutions of a nonlinear eigenvalue problem with discontinuous nonlinearity. Proc. Roy. Soc. Edinburgh Sect. A 83 (1979), 133–145.CrossRefGoogle Scholar
9Norbury, J. and Stuart, A. M.. A model for porous medium combustion. Q. J. Mech. Appl. Math. 42 (1) (1989), 159–178.CrossRefGoogle Scholar
10Norbury, J. and Stuart, A. M.. Parabolic problems arising in porous medium combustion. IMA J. Appl Math. 39 (1987), 241–257.CrossRefGoogle Scholar
11Ôtani, M.. On the existence of strong solutions for du/dt(t) + ∂ψ2(u(t)) ∍ f(t). J. Fac. Sci. Univ. Tokyo, Sect. IA Math. 24 (3) (1977), 575–605.Google Scholar
12Ôtani, M.. Nonmonotone perturbations for nonlinear parabolic equations associated with subdifferential operators, Cauchy problem. J. Differential Equations 46 (2) (1982), 268–299.CrossRefGoogle Scholar
13Ôtani, M.. Nonmonotone perturbations for nonlinear parabolic equations associated with subdifferential operators, Periodic problems. J. Differential Equations 54 (2) (1984), 248–273.CrossRefGoogle Scholar
14Ôtani, M.. Existence and asymptotic stability of strong solutions of nonlinear evolution equations with a difference term of subdifferentials. Qualitative theory of Differential Equations, Vol. I, II (Szeqed: North-Holland, 1981).Google Scholar
15Pisani, R.. Boundary value problem for parabolic operators with discontinuous nonlinearities. Rend. 1st. Mat. Univ. Trieste 14 (1982), 85–98.Google Scholar
16Stuart, C. A.. Differential equations with discontinuous nonlinearities. Arch. Rational Mech. Anal. 63 (1976), 59–78.CrossRefGoogle Scholar
17Stuart, C. A.. The number of solutions of boundary value problems with discontinuous nonlinearities. Arch. Rational Mech. Anal. 66 (1977), 225–235.CrossRefGoogle Scholar
18Terman, D.. A free boundary problem arising from a bistable reaction diffusion equation. SIAM J. Math. Anal. 14 (1983), 1107–1129.CrossRefGoogle Scholar
19Terman, D.. A free boundary arising from a model for nerve conduction. J. Differential Equations 58 (3) (1985), 345–363.CrossRefGoogle Scholar