Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-16T22:18:13.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic differential equations driven by fractional Brownian motion with locally Lipschitz drift and their implicit Euler approximation

Part of: Stochastic analysis

Published online by Cambridge University Press:  02 September 2020

Shao-Qin Zhang  and
Chenggui Yuan
Shao-Qin Zhang
Affiliation:
School of Statistics and Mathematics, Central University of Finance and Economics, Beijing100081, China (zhangsq@cufe.edu.cn)
Chenggui Yuan
Affiliation:
Department of Mathematics, Swansea University, Bay CampusSA1 8EN, UK (C.Yuan@swansea.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study a class of one-dimensional stochastic differential equations driven by fractional Brownian motion with Hurst parameter 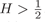$ H \gt \frac{1}{2}$. The drift term of the equation is locally Lipschitz and unbounded in the neighbourhood of the origin. We show the existence, uniqueness and positivity of the solutions. The estimates of moments, including the negative power moments, are given. We also develop the implicit Euler scheme, proved that the scheme is positivity preserving and strong convergent, and obtain rate of convergence. Furthermore, by using Lamperti transformation, we show that our results can be applied to stochastic interest rate models such as mean-reverting stochastic volatility model and strongly nonlinear Aït-Sahalia type model.

Keywords

Locally Lipschitz driftfractional Brownian motionimplicit Euler schemeoptimal strong convergence rateinterest rate models

MSC classification

Primary: 60H35: Computational methods for stochastic equations
Secondary: 60H10: Stochastic ordinary differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 4 , August 2021 , pp. 1278 - 1304
Check for updates
Copyright
Copyright © The Author(s) 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aït-Sahalia, Y.. Testing continuous-time models of the spot interest rate. Rev. Financ. Stud. 9 (1996), 385–426.CrossRefGoogle Scholar
Alòs, A. and Nualart, D.. Stochastic integration with respect to the fractional Brownian motion. Stoch. Stoch. Rep. 75 (2003), 129–152.CrossRefGoogle Scholar
Alòs, E., Mazet, O. and Nualart, D.. Stochastic calculus with respect to Gaussian processes. Ann. Probab. 29 (2001), 766–801.CrossRefGoogle Scholar
Barton, R. J. and Poor, H. V.. Signal detection in fractional gaussian noise. IEEE Trans. Inf. Theory 34 (1988), 943–959.CrossRefGoogle Scholar
Berkaoui, A., Bossy, M. and Diop, A.. Euler scheme for SDEs with non-Lipschitz diffusion coefficient: strong convergence. ESAIM-Probab. Stat. 12 (2008), 1–11.CrossRefGoogle Scholar
Biagini, F., Hu, Y., ∅ksendal, B. and Zhang, T.. Stochastic calculus for fractional Brownian motion and applications (London: Springer, 2008).CrossRefGoogle Scholar
Cox, J. C., Ingersoll, J. E. Jr and Ross, S. A.. A theory of term structure of interest rates. Econometrica 53 (1985), 385–407.CrossRefGoogle Scholar
Decreusefond, L. and Üstünel, A. S.. Stochastic analysis of the fractional Brownian motion. Potential Anal. 10 (1999), 177–214.CrossRefGoogle Scholar
Dereich, S., Neuenkirch, A. and Szpruch, L.. An Euler-type method for the strong approximation of the Cox-Ingersoll-Ross process. Proc. R. Soc. A 468 (2012), 1105–1115.CrossRefGoogle Scholar
Fan, X.-L. and Zhang, S.-Q.. On SDEs driven by fractional Brownian motions with irregular drifts. arXiv:1810.01669v1 (2018).Google Scholar
Gyöngy, I. and Rásonyi, M.. A note on Euler approximations for SDEs with Hölder continuous diffusion coefficients. Stoch. Proc. Appl. 121 (2011), 2189–2200.CrossRefGoogle Scholar
Hong, J., Huang, C., Kamrani, M. and Wang, X.. Optimal strong convergence rate of a Backward Euler type scheme for the Cox-Ingersoll-Ross model driven by fractional Brownian motion. Stoch. Proc. Appl. 130 (2020), 2675–2692.CrossRefGoogle Scholar
Hu, Y., Liu, Y. and Nualart, D.. Crank–Nicolson scheme for stochastic differential equations driven by fractional Brownian motion. arXiv 1709.01614.Google Scholar
Hu, Y., Nualart, D. and Song, X.. A singular stochastic differential equation driven by fractional Brownian motion. Stat. Prab. Letter 78 (2008), 2075–2085.CrossRefGoogle Scholar
Hu, Y., Liu, Y. and Nualart, D.. Rate of convergence and asymptotic error distribution of Euler approximation schemes for fractional diffusions. Ann. Appl. Probab. 26 (2016), 1147–1207.CrossRefGoogle Scholar
Mao, X., Truman, A. and Yuan, C.. Euler-Maruyama approximations in mean-reverting stochastic volatility model under regime-switching. Int. J. Stoch. Anal. (2006), Art. ID 80967, 20pp.Google Scholar
Marcus, M. and Rosen, J.. Markov processes, Gaussian processes and local times (New York: Cambridge University Press, 2006).CrossRefGoogle Scholar
Mishura, Y. and Yurchenko-Tytarenko, A.. Fractional Cox-Ingersoll-Ross process with non-zero. Mod. Stoch. Theory Appl. 5 (2018), 99–111.CrossRefGoogle Scholar
Neuenkirch, A.. Optimal approximation of SDE's with additive fractional noise. J. Complexity 22 (2006), 459–474.CrossRefGoogle Scholar
Nualart, D.. The Malliavin Calculus and related topics, 2nd edn (Berlin Heidelberg: Springer-Verlag, 2006).Google Scholar
Rostek, S. and Schöbel, R.. A note on the use of fractional Brownian motion for financial modeling. Econ. Model. 30 (2013), 30–35.CrossRefGoogle Scholar
Szpruch, L., Mao, X., Higham, D. J. and Pan, J.. Numerical simulation of a strongly nonlinear Ait-Sahalia-type interest rate model. BIT Numer. Math. 51 (2011), 405–425.CrossRefGoogle Scholar
Xiao, Y.. Sample path properties of anisotropic Gaussian random fields. In A minicourse on stochastic partial differential equations. Lecture Notes in Mathematics (1962) pp. 145–212.Google Scholar
Zähle, M.. Integration with respect to fractal functions and stochastic calculus I. Probab. Theory Relat. Fields 111 (1998), 333–374.Google Scholar