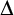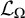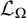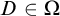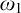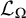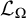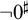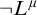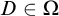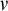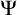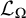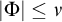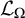1 Introduction
Lindström’s 1969 theorem [Reference Lindström14] (reprinted in [Reference Béziau2, pp. 237–246]; also see [Reference Flum9, theorem 1.1.4]) characterizes first-order logic
![]() ${\mathcal {L}}_{\omega \omega }$
as the maximal compact logic satisfying the downward Löwenheim–Skolem theorem. After this fundamental result a variety of methods were developed for constructing extensions of
${\mathcal {L}}_{\omega \omega }$
as the maximal compact logic satisfying the downward Löwenheim–Skolem theorem. After this fundamental result a variety of methods were developed for constructing extensions of
![]() ${\mathcal {L}}_{\omega \omega }$
. The six Parts A–F of the book [Reference Barwise and Feferman1] may give an idea of the range of techniques available for such extensions, and their applications to algebra, probability, topology, set theory and game theory. In [Reference Barwise and Feferman1] one can also find a comprehensive study of extensions of
${\mathcal {L}}_{\omega \omega }$
. The six Parts A–F of the book [Reference Barwise and Feferman1] may give an idea of the range of techniques available for such extensions, and their applications to algebra, probability, topology, set theory and game theory. In [Reference Barwise and Feferman1] one can also find a comprehensive study of extensions of
![]() ${\mathcal {L}}_{\omega \omega }$
satisfying many forms of interpolation, compactness, and Löwenheim–Skolem properties.
${\mathcal {L}}_{\omega \omega }$
satisfying many forms of interpolation, compactness, and Löwenheim–Skolem properties.
Ultrafilters and ultraproducts have a pervasive role in the literature, both for the characterization of all these properties in extensions of
![]() ${\mathcal {L}}_{\omega \omega }$
and for the construction of such extensions. For instance, in [Reference Makowsky15], [Reference Makowsky and Shelah16, pp. 230–234] and [Reference Makowsky and Shelah17, sec. 3] various compactness properties of a logic
${\mathcal {L}}_{\omega \omega }$
and for the construction of such extensions. For instance, in [Reference Makowsky15], [Reference Makowsky and Shelah16, pp. 230–234] and [Reference Makowsky and Shelah17, sec. 3] various compactness properties of a logic
![]() ${\mathcal {L}}$
are characterized in terms of ultrafilters. As another example, in [Reference Sgro20] one can find a general method to construct logics on classes of models satisfying a maximality condition with respect to a suitable variant of the Łoś ultraproduct theorem. Likewise, the paper [Reference Sgro21] is devoted to the construction of logics via the property of being preserved from the models to their ultraproduct. Specific examples are given involving cardinality quantifiers. From a fragment of second-order logic having this preservation property, in [Reference Sgro21, p. 636] the author constructs a compact
${\mathcal {L}}$
are characterized in terms of ultrafilters. As another example, in [Reference Sgro20] one can find a general method to construct logics on classes of models satisfying a maximality condition with respect to a suitable variant of the Łoś ultraproduct theorem. Likewise, the paper [Reference Sgro21] is devoted to the construction of logics via the property of being preserved from the models to their ultraproduct. Specific examples are given involving cardinality quantifiers. From a fragment of second-order logic having this preservation property, in [Reference Sgro21, p. 636] the author constructs a compact
![]() $\Delta $
-closed logic
$\Delta $
-closed logic
![]() $\mathcal L$
(in the sense of [Reference Ebbinghaus7, p. 18]).
$\mathcal L$
(in the sense of [Reference Ebbinghaus7, p. 18]).
Pursuing this line of research, in the present paper every (nonempty) class
![]() $\Omega $
of uniform ultrafilters is shown to generate a
$\Omega $
of uniform ultrafilters is shown to generate a
![]() $\Delta $
-closed logic
$\Delta $
-closed logic
![]() ${\mathcal {L}}_\Omega $
. Depending on
${\mathcal {L}}_\Omega $
. Depending on
![]() $\Omega $
,
$\Omega $
,
![]() ${\mathcal {L}}_\Omega $
may satisfy various forms of compactness.
${\mathcal {L}}_\Omega $
may satisfy various forms of compactness.
All logics constructed in the present paper naturally arise from classes of ultrafilters and automatically satisfy the basic regularity/closure properties considered in abstract model theory [Reference Ebbinghaus7, definitions 1.2.1–1.2.3].
1.1 Main results
With
![]() $\operatorname {\mathrm {Str}}(\tau )$
denoting the class of all structures of type
$\operatorname {\mathrm {Str}}(\tau )$
denoting the class of all structures of type
![]() $\tau $
, and
$\tau $
, and
![]() $\sigma \subseteq \tau $
, let
$\sigma \subseteq \tau $
, let
![]() $\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma \colon \operatorname {\mathrm {Str}}(\tau )\to \operatorname {\mathrm {Str}}(\sigma )$
denote the reduct operation. For any class
$\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma \colon \operatorname {\mathrm {Str}}(\tau )\to \operatorname {\mathrm {Str}}(\sigma )$
denote the reduct operation. For any class
![]() $\Omega $
of uniform ultrafilters, let
$\Omega $
of uniform ultrafilters, let
![]() $L(\tau )=L(\tau , \Omega )$
be the family of subclasses
$L(\tau )=L(\tau , \Omega )$
be the family of subclasses
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
such that there is a finite type
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
such that there is a finite type
![]() $\sigma \subseteq \tau $
and a class
$\sigma \subseteq \tau $
and a class
![]() $\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
having the following property:
$\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
having the following property:
For every
![]() $D\in \Omega $
, both
$D\in \Omega $
, both
![]() $\chi $
and its complement
$\chi $
and its complement
![]() $\operatorname {\mathrm {Str}}(\sigma )\setminus \chi $
are closed under isomorphisms and ultraproducts modulo D, and
$\operatorname {\mathrm {Str}}(\sigma )\setminus \chi $
are closed under isomorphisms and ultraproducts modulo D, and
![]() $\psi $
is the class of expansions to
$\psi $
is the class of expansions to
![]() $\tau $
of all structures in
$\tau $
of all structures in
![]() $\chi $
.
$\chi $
.
In Sections 3 and 4 the following results are proved:
(i) There is a unique regular logic
![]() ${\mathcal {L}}={\mathcal {L}}_\Omega $
whose elementary classes of any type
${\mathcal {L}}={\mathcal {L}}_\Omega $
whose elementary classes of any type
![]() $\tau $
coincide with the classes in
$\tau $
coincide with the classes in
![]() $L(\tau )$
.
$L(\tau )$
.
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed. If
$\Delta $
-closed. If
![]() $\Omega $
contains a
$\Omega $
contains a
![]() $\kappa $
-descendingly incomplete ultrafilter,Footnote
1
$\kappa $
-descendingly incomplete ultrafilter,Footnote
1
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\kappa $
-relatively compact.Footnote
2
$\kappa $
-relatively compact.Footnote
2
![]() ${\mathcal {L}}$
is compact only if
${\mathcal {L}}$
is compact only if
![]() $\Omega $
is a proper class. See Theorem 3.1(i).
$\Omega $
is a proper class. See Theorem 3.1(i).
(ii) (Assuming
![]() $\neg 0^\sharp $
or
$\neg 0^\sharp $
or
![]() $\neg L^{\mu }$
.Footnote
3
) Let
$\neg L^{\mu }$
.Footnote
3
) Let
![]() $D\in \Omega $
be an ultrafilter over a regular cardinal
$D\in \Omega $
be an ultrafilter over a regular cardinal
![]() $\nu $
. Then for a family
$\nu $
. Then for a family
![]() $\Psi $
of
$\Psi $
of
![]() ${\mathcal {L}}$
-sentences with
${\mathcal {L}}$
-sentences with
![]() $|\Psi |\leq \nu $
to have a model it is sufficient that every finite subfamily of
$|\Psi |\leq \nu $
to have a model it is sufficient that every finite subfamily of
![]() $\Psi $
has a model. In particular, if
$\Psi $
has a model. In particular, if
![]() $\Omega $
is a proper class and each
$\Omega $
is a proper class and each
![]() $D\in \Omega $
is an ultrafilter over a regular cardinal, then
$D\in \Omega $
is an ultrafilter over a regular cardinal, then
![]() ${\mathcal {L}}$
is compact. See Theorem 3.1(ii).
${\mathcal {L}}$
is compact. See Theorem 3.1(ii).
(iii) If
![]() $\Omega $
is a set or
$\Omega $
is a set or
![]() $\Omega $
contains a countably incomplete ultrafilter, then
$\Omega $
contains a countably incomplete ultrafilter, then
![]() ${\mathcal {L}}$
is not generated by Mostowski cardinality quantifiers. See Theorem 4.1.
${\mathcal {L}}$
is not generated by Mostowski cardinality quantifiers. See Theorem 4.1.
(iv) Every ultrafilter
![]() $D\in \Omega $
is
$D\in \Omega $
is
![]() $\omega _1$
-complete iff
$\omega _1$
-complete iff
![]() ${\mathcal {L}}$
contains the quantifier “there are infinitely many” iff
${\mathcal {L}}$
contains the quantifier “there are infinitely many” iff
![]() ${\mathcal {L}}$
contains the quantifier “there are uncountably many” iff
${\mathcal {L}}$
contains the quantifier “there are uncountably many” iff
![]() ${\mathcal {L}}$
contains the well-ordering quantifier iff
${\mathcal {L}}$
contains the well-ordering quantifier iff
![]() ${\mathcal {L}}$
is not
${\mathcal {L}}$
is not
![]() $\omega $
-relatively compact. See Theorem 4.3 and Corollary 4.4.
$\omega $
-relatively compact. See Theorem 4.3 and Corollary 4.4.
(v) If in (ii) we assume, instead of
![]() $\neg L^\mu $
, the existence of a proper class of measurable cardinals, then (ii) no longer holds. See Corollary 4.5.
$\neg L^\mu $
, the existence of a proper class of measurable cardinals, then (ii) no longer holds. See Corollary 4.5.
Using Lindström’s characterization theorem, in Theorem 4.7 and Corollary 4.8, certain specific assumptions on the map
![]() $\Omega \mapsto {\mathcal {L}}$
are shown to be related to the Chang–Keisler conjecture [Reference Chang and Keisler4, p. 599, conjecture 18].
$\Omega \mapsto {\mathcal {L}}$
are shown to be related to the Chang–Keisler conjecture [Reference Chang and Keisler4, p. 599, conjecture 18].
Throughout this paper we will work with classes, typically with subclasses of
![]() $\operatorname {\mathrm {Str}}(\tau )$
, and with families or collections of classes, such as the family of all elementary classes of type
$\operatorname {\mathrm {Str}}(\tau )$
, and with families or collections of classes, such as the family of all elementary classes of type
![]() $\tau $
in a logic
$\tau $
in a logic
![]() ${\mathcal {L}}.$
All these mathematical entities can be handled by adding an extra stage of flexibility to the Gödel–Bernays–von Neumann set theory. For the sake of definiteness, throughout this paper we will adopt the Isbell–Mac Lane–Feferman approach, where our families are called “conglomerates.” See [Reference Herrlich and Strecker10, pp. 329–331] for details. Our syntax-free approach to abstract logics via their elementary classes agrees with Lindström’s approach in his characterization theorem.
${\mathcal {L}}.$
All these mathematical entities can be handled by adding an extra stage of flexibility to the Gödel–Bernays–von Neumann set theory. For the sake of definiteness, throughout this paper we will adopt the Isbell–Mac Lane–Feferman approach, where our families are called “conglomerates.” See [Reference Herrlich and Strecker10, pp. 329–331] for details. Our syntax-free approach to abstract logics via their elementary classes agrees with Lindström’s approach in his characterization theorem.
We will refrain from introducing new logics. By letting
![]() $\Omega $
range over arbitrary classes of uniform ultrafilters, our readers will be able to manufacture the logics that best suit their needs.
$\Omega $
range over arbitrary classes of uniform ultrafilters, our readers will be able to manufacture the logics that best suit their needs.
Standard background references for model theory, abstract model theory and set theory are, respectively, given by [Reference Barwise and Feferman1, Reference Chang and Keisler4, Reference Jech11], where the reader can find the definitions of all unexplained notions occurring in this paper.
2 Basic notation and terminology
Following common usage we let
![]() $\alpha , \beta , \gamma $
denote ordinals and let
$\alpha , \beta , \gamma $
denote ordinals and let
![]() $\kappa , \lambda , \mu ,\nu $
denote cardinals.
$\kappa , \lambda , \mu ,\nu $
denote cardinals.
![]() $\mathsf V$
is the class of all sets. A symbol is a pair
$\mathsf V$
is the class of all sets. A symbol is a pair
![]() $R=\langle \alpha ,a\rangle $
where
$R=\langle \alpha ,a\rangle $
where
![]() $\alpha $
is an ordinal and a is an integer: the absolute value
$\alpha $
is an ordinal and a is an integer: the absolute value
![]() $|a|$
is the arity (= number of places) of R. R is said to be a function, constant, or relation symbol according as
$|a|$
is the arity (= number of places) of R. R is said to be a function, constant, or relation symbol according as
![]() $a<0, \,a=0$
, or
$a<0, \,a=0$
, or
![]() $a>0$
.
$a>0$
.
A type (“language” in [Reference Chang and Keisler4, p. 18], “vocabulary” in [Reference Ebbinghaus7, p. 26]) is a set of symbols. Following [Reference Chang and Keisler4], in this paper we will only consider one-sorted types. We let
![]() $\sigma , \tau $
denote types. We say that
$\sigma , \tau $
denote types. We say that
![]() $\tau $
is relational if it does not contain function or constant symbols. The empty type is known as the pure identity language. Following [Reference Chang and Keisler4, p. 22], identity is understood as a logical symbol, denoted
$\tau $
is relational if it does not contain function or constant symbols. The empty type is known as the pure identity language. Following [Reference Chang and Keisler4, p. 22], identity is understood as a logical symbol, denoted
![]() $=$
.Footnote
4
$=$
.Footnote
4
A structure (“model” in [Reference Chang and Keisler4, p. 20]) of type
![]() $\tau $
is a function
$\tau $
is a function
where
![]() $A={\mathfrak {A}}(\emptyset )$
is a nonempty set, called the universe of
$A={\mathfrak {A}}(\emptyset )$
is a nonempty set, called the universe of
![]() ${\mathfrak {A}}$
, and for each constant symbol
${\mathfrak {A}}$
, and for each constant symbol
![]() $c \in \tau ,$
$c \in \tau ,$
![]() ${\mathfrak {A}}(c)$
is an element of A, and for each
${\mathfrak {A}}(c)$
is an element of A, and for each
![]() $|a|$
-ary relation (resp. function) symbol
$|a|$
-ary relation (resp. function) symbol
![]() $R \in \tau ,$
$R \in \tau ,$
![]() ${\mathfrak {A}}(R)$
is an
${\mathfrak {A}}(R)$
is an
![]() $|a|$
-ary relation (resp. function) over A. We write
$|a|$
-ary relation (resp. function) over A. We write
![]() $c^{\mathfrak {A}}$
and
$c^{\mathfrak {A}}$
and
![]() $R^{\mathfrak {A}}$
instead of
$R^{\mathfrak {A}}$
instead of
![]() ${\mathfrak {A}}(c)$
and
${\mathfrak {A}}(c)$
and
![]() ${\mathfrak {A}}(R)$
.
${\mathfrak {A}}(R)$
.
![]() $\operatorname {\mathrm {Str}}(\tau )$
denotes the class of all structures of type
$\operatorname {\mathrm {Str}}(\tau )$
denotes the class of all structures of type
![]() $\tau .$
R and S will usually denote unary relation symbols, E a binary relation symbol, and c a constant symbol. Further,
$\tau .$
R and S will usually denote unary relation symbols, E a binary relation symbol, and c a constant symbol. Further,
![]() $M,N,A,B$
are the universes of
$M,N,A,B$
are the universes of
![]() ${\mathfrak {M}}, {\mathfrak {N}},{\mathfrak {A}},\mathfrak B.$
Structures will be displayed as in [Reference Chang and Keisler4, p. 20]: thus, e.g., by writing
${\mathfrak {M}}, {\mathfrak {N}},{\mathfrak {A}},\mathfrak B.$
Structures will be displayed as in [Reference Chang and Keisler4, p. 20]: thus, e.g., by writing
![]() ${\mathfrak {A}}=\langle A,E,c,S_\alpha \rangle _{\alpha <\kappa }$
we mean that
${\mathfrak {A}}=\langle A,E,c,S_\alpha \rangle _{\alpha <\kappa }$
we mean that
![]() ${\mathfrak {A}}$
is a structure of type
${\mathfrak {A}}$
is a structure of type
![]() $\{ E,c,S_\alpha \}_{\alpha <\kappa }$
and by a traditional abuse of notation,
$\{ E,c,S_\alpha \}_{\alpha <\kappa }$
and by a traditional abuse of notation,
![]() $E=E^{{\mathfrak {A}}}, c=c^{{\mathfrak {A}}}, S_\alpha =S_\alpha ^{{\mathfrak {A}}}$
for each
$E=E^{{\mathfrak {A}}}, c=c^{{\mathfrak {A}}}, S_\alpha =S_\alpha ^{{\mathfrak {A}}}$
for each
![]() $\alpha <\kappa .$
$\alpha <\kappa .$
If
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
and
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
and
![]() $\sigma \subseteq \tau $
then the reduct of
$\sigma \subseteq \tau $
then the reduct of
![]() ${\mathfrak {M}}$
to
${\mathfrak {M}}$
to
![]() $\sigma $
(in symbols,
$\sigma $
(in symbols,
![]() ${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \sigma $
, or
${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \sigma $
, or
![]() ${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma $
for greater definiteness) is the structure of type
${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma $
for greater definiteness) is the structure of type
![]() $\sigma $
obtained by restricting to
$\sigma $
obtained by restricting to
![]() $\sigma \cup \{\emptyset \}$
the domain
$\sigma \cup \{\emptyset \}$
the domain
![]() $\tau \cup \{\emptyset \}$
of
$\tau \cup \{\emptyset \}$
of
![]() ${\mathfrak {M}}.$
We say that
${\mathfrak {M}}.$
We say that
![]() $\mathfrak B\in \operatorname {\mathrm {Str}}(\tau )$
is an expansion (to
$\mathfrak B\in \operatorname {\mathrm {Str}}(\tau )$
is an expansion (to
![]() $\tau $
) of
$\tau $
) of
![]() ${\mathfrak {A}}\in \operatorname {\mathrm {Str}}(\sigma )$
if
${\mathfrak {A}}\in \operatorname {\mathrm {Str}}(\sigma )$
if
![]() $\tau \supseteq \sigma $
and
$\tau \supseteq \sigma $
and
![]() ${\mathfrak {A}} =\mathfrak B\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \sigma .$
If
${\mathfrak {A}} =\mathfrak B\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \sigma .$
If
![]() $\sigma $
is a relational type,
$\sigma $
is a relational type,
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\sigma )$
and
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\sigma )$
and
![]() $M'$
is a nonempty subset of M, then
$M'$
is a nonempty subset of M, then
For
![]() $\Theta $
a set of first-order sentences, we let
$\Theta $
a set of first-order sentences, we let
![]() ${\mathfrak {A}}\models \Theta $
mean that
${\mathfrak {A}}\models \Theta $
mean that
![]() ${\mathfrak {A}}$
satisfies every
${\mathfrak {A}}$
satisfies every
![]() $\theta \in \Theta $
. For D an ultrafilter over an infinite set I, we let
$\theta \in \Theta $
. For D an ultrafilter over an infinite set I, we let
![]() $\Pi _D{\mathfrak {A}}$
denote the ultrapower of
$\Pi _D{\mathfrak {A}}$
denote the ultrapower of
![]() ${\mathfrak {A}}$
modulo D. As in [Reference Chang and Keisler4, p. 215], for any map
${\mathfrak {A}}$
modulo D. As in [Reference Chang and Keisler4, p. 215], for any map
![]() $g\colon I\to A$
we let
$g\colon I\to A$
we let
![]() $g_D\in \Pi _DA$
denote the
$g_D\in \Pi _DA$
denote the
![]() $=_D$
-equivalence class of g. Given a family
$=_D$
-equivalence class of g. Given a family
![]() $\{{\mathfrak {A}}_i\}_{i\in I}$
of structures of type
$\{{\mathfrak {A}}_i\}_{i\in I}$
of structures of type
![]() $\tau $
, we let
$\tau $
, we let
![]() $\Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle $
denote their ultraproduct modulo D. A class
$\Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle $
denote their ultraproduct modulo D. A class
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is closed under ultraproducts modulo D if
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is closed under ultraproducts modulo D if
![]() $\{{\mathfrak {A}}_i\}_{i\in I} \subseteq \psi $
implies
$\{{\mathfrak {A}}_i\}_{i\in I} \subseteq \psi $
implies
![]() $\Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle \in \psi .$
We say that
$\Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle \in \psi .$
We say that
![]() $\psi $
is closed under isomorphisms if
$\psi $
is closed under isomorphisms if
![]() $\mathfrak B\cong {\mathfrak {A}} \in \psi $
implies
$\mathfrak B\cong {\mathfrak {A}} \in \psi $
implies
![]() $\mathfrak B \in \psi .$
$\mathfrak B \in \psi .$
2.1 Preparatory results
The next four lemmas are routine exercises for readers familiar with Łoś ultraproduct theorem and its consequences ([Reference Keisler12, theorem 3.1], [Reference Chang and Keisler4, sec. 4]). As a warm up we only prove the first one.
Lemma 2.1. Let D be a
![]() $\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter over a set I. Let
$\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter over a set I. Let
![]() ${\mathfrak {A}}=\langle A,E,S_\alpha \rangle _{\alpha <\kappa }$
be a structure of type
${\mathfrak {A}}=\langle A,E,S_\alpha \rangle _{\alpha <\kappa }$
be a structure of type
![]() $\tau =\{E,S_\alpha \}_{\alpha <\kappa }$
, where E is an equivalence relation having exactly
$\tau =\{E,S_\alpha \}_{\alpha <\kappa }$
, where E is an equivalence relation having exactly
![]() $\kappa $
distinct equivalence classes, denoted
$\kappa $
distinct equivalence classes, denoted
![]() $\{A_\beta \mid \beta <\kappa \},$
and
$\{A_\beta \mid \beta <\kappa \},$
and
![]() $S_\alpha =\bigcup _{\beta <\alpha } A_\beta $
for each
$S_\alpha =\bigcup _{\beta <\alpha } A_\beta $
for each
![]() $\alpha <\kappa \,\,\,$
(with
$\alpha <\kappa \,\,\,$
(with
![]() $S_0=\emptyset $
).
$S_0=\emptyset $
).
Then for every expansion
![]() ${\mathfrak {M}}$
of
${\mathfrak {M}}$
of
![]() ${\mathfrak {A}}$
to any type
${\mathfrak {A}}$
to any type
![]() $\tau ^+\supseteq \tau $
and every constant symbol
$\tau ^+\supseteq \tau $
and every constant symbol
![]() $c\notin \tau ^+$
, the ultrapower
$c\notin \tau ^+$
, the ultrapower
![]() $\Pi _D{\mathfrak {M}}$
has an expansion
$\Pi _D{\mathfrak {M}}$
has an expansion
![]() $\mathfrak B$
of type
$\mathfrak B$
of type
![]() $\tau ^+\cup \{c\}$
such that
$\tau ^+\cup \{c\}$
such that
Proof. We first consider the particular case
![]() $\tau ^+=\tau $
, i.e.,
$\tau ^+=\tau $
, i.e.,
![]() ${\mathfrak {M}}= {\mathfrak {A}}.$
Let
${\mathfrak {M}}= {\mathfrak {A}}.$
Let
be a sequence of elements of D with empty intersection. Let the function
![]() $t\colon I\to \kappa $
map each
$t\colon I\to \kappa $
map each
![]() $i\in I$
to
$i\in I$
to
For each
![]() $\alpha <\kappa $
pick an element
$\alpha <\kappa $
pick an element
![]() $x_\alpha \in A_\alpha .$
For each
$x_\alpha \in A_\alpha .$
For each
![]() $i\in I$
let
$i\in I$
let
![]() ${\mathfrak {A}}_i$
be the expansion of
${\mathfrak {A}}_i$
be the expansion of
![]() ${\mathfrak {A}}$
to the type
${\mathfrak {A}}$
to the type
![]() $\tau \cup \{c\}$
such that
$\tau \cup \{c\}$
such that
![]() $c^{{\mathfrak {A}}_i}=x_{t(i)}.$
Let
$c^{{\mathfrak {A}}_i}=x_{t(i)}.$
Let
![]() $\mathfrak B= \Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle \in \operatorname {\mathrm {Str}}(\tau \cup \{c\}).$
By Łoś theorem,
$\mathfrak B= \Pi _D\langle {\mathfrak {A}}_i\mid i\in I\rangle \in \operatorname {\mathrm {Str}}(\tau \cup \{c\}).$
By Łoś theorem,
Thus
![]() $\mathfrak B\models \{\neg S_\alpha c\mid \alpha <\kappa \}$
. By the expansion theorem ([Reference Chang and Keisler4, theorem 4.1.8], [Reference Keisler12, proposition 4.1]),
$\mathfrak B\models \{\neg S_\alpha c\mid \alpha <\kappa \}$
. By the expansion theorem ([Reference Chang and Keisler4, theorem 4.1.8], [Reference Keisler12, proposition 4.1]),
which shows that
![]() $\mathfrak B$
is the desired expansion of
$\mathfrak B$
is the desired expansion of
![]() $\Pi _D{\mathfrak {M}}\,\,\,(=\Pi _D{\mathfrak {A}})$
.
$\Pi _D{\mathfrak {M}}\,\,\,(=\Pi _D{\mathfrak {A}})$
.
In the general case when
![]() ${\mathfrak {M}}$
is an expansion of
${\mathfrak {M}}$
is an expansion of
![]() ${\mathfrak {A}}$
in a type
${\mathfrak {A}}$
in a type
![]() $\tau ^+ $
strictly containing
$\tau ^+ $
strictly containing
![]() $\tau ,$
again from the expansion theorem it follows that
$\tau ,$
again from the expansion theorem it follows that
Arguing as in case
![]() $\tau ^+=\tau $
, it is not hard to see that the universe of the structure
$\tau ^+=\tau $
, it is not hard to see that the universe of the structure
![]() $(\Pi _D{\mathfrak {M}})\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau $
has an element c with
$(\Pi _D{\mathfrak {M}})\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau $
has an element c with
As a consequence,
![]() $\langle \Pi _D{\mathfrak {M}},c\rangle \models \{\neg S_\alpha c\mid \alpha <\kappa \}.$
$\langle \Pi _D{\mathfrak {M}},c\rangle \models \{\neg S_\alpha c\mid \alpha <\kappa \}.$
Lemma 2.2. Let D be an ultrafilter over a set I,
![]() $\tau $
a relational type, and
$\tau $
a relational type, and
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ).$
Assume
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ).$
Assume
![]() $E\in \tau $
and
$E\in \tau $
and
![]() $E^{{\mathfrak {M}}}$
is an equivalence relation. For any map
$E^{{\mathfrak {M}}}$
is an equivalence relation. For any map
![]() $g\colon I\to M$
let
$g\colon I\to M$
let
![]() $g_D\in \Pi _D{\mathfrak {M}}$
denote the
$g_D\in \Pi _D{\mathfrak {M}}$
denote the
![]() $=_D$
-equivalence class of g. Let further
$=_D$
-equivalence class of g. Let further
and for every
![]() $i\in I,$
$i\in I,$
![]() $ Eg(i)=\{x\in M\mid {\mathfrak {M}}\models xEg(i)\}. $
$ Eg(i)=\{x\in M\mid {\mathfrak {M}}\models xEg(i)\}. $
Then, with “
![]() $\mathsf I$
” as defined in (1),
$\mathsf I$
” as defined in (1),
![]() $ (\Pi _D{\mathfrak {M}}) \mathsf I Eg_D \,\,\cong \,\, \Pi _D\langle ({\mathfrak {M}} \mathsf I Eg(i))\mid i\in I\rangle. $
$ (\Pi _D{\mathfrak {M}}) \mathsf I Eg_D \,\,\cong \,\, \Pi _D\langle ({\mathfrak {M}} \mathsf I Eg(i))\mid i\in I\rangle. $
Definition 2.3. For
![]() $\tau $
a relational type, let
$\tau $
a relational type, let
![]() $R,E$
be relation symbols not in
$R,E$
be relation symbols not in
![]() $\tau $
, with R unary and E binary. For each class
$\tau $
, with R unary and E binary. For each class
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
the class
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
the class
![]() $\psi ^{RE}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
is defined by stipulating that for any
$\psi ^{RE}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
is defined by stipulating that for any
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
,
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
,
where
![]() $Ex=\{y\in M\mid {\mathfrak {M}}\models yEx\}.$
$Ex=\{y\in M\mid {\mathfrak {M}}\models yEx\}.$
Intuitively,
![]() $R^{{\mathfrak {M}}}$
is the union of the equivalence classes
$R^{{\mathfrak {M}}}$
is the union of the equivalence classes
![]() $Ex$
such that the substructure of
$Ex$
such that the substructure of
![]() ${\mathfrak {M}}$
with universe
${\mathfrak {M}}$
with universe
![]() $Ex$
satisfies
$Ex$
satisfies
![]() $\psi .$
$\psi .$
Lemma 2.4. Let D be an ultrafilter over I, and
![]() $\tau $
a relational type not containing the relation symbols R (unary) and E (binary). Let us assume that the class
$\tau $
a relational type not containing the relation symbols R (unary) and E (binary). Let us assume that the class
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complementary class
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complementary class
![]() $\operatorname {\mathrm {Str}}(\tau )\setminus \psi $
are both closed under isomorphisms and ultraproducts modulo D.
$\operatorname {\mathrm {Str}}(\tau )\setminus \psi $
are both closed under isomorphisms and ultraproducts modulo D.
Then
![]() $\Pi _D{\mathfrak {M}}$
belongs to
$\Pi _D{\mathfrak {M}}$
belongs to
![]() $ \psi ^{RE}$
for all
$ \psi ^{RE}$
for all
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
such that
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \cup \{R,E\})$
such that
![]() ${\mathfrak {M}}\in \psi ^{RE}$
.
${\mathfrak {M}}\in \psi ^{RE}$
.
Combining [Reference Chang and Keisler4, theorem 4.1.8 and exercise 4.1.11] with [Reference Eklof and Barwise8, theorem 4.2 and p. 114] we obtain:
Lemma 2.5. Let D be an ultrafilter over I, and
![]() $\tau $
a relational type not containing the unary relation symbol R. Assume the class
$\tau $
a relational type not containing the unary relation symbol R. Assume the class
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complementary class
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complementary class
![]() $\operatorname {\mathrm {Str}}(\tau )\setminus \psi $
are both closed under isomorphisms and ultraproducts modulo D. Define
$\operatorname {\mathrm {Str}}(\tau )\setminus \psi $
are both closed under isomorphisms and ultraproducts modulo D. Define
![]() $\psi ^R\subseteq \operatorname {\mathrm {Str}}(\tau \cup \{R\})$
by the following stipulation:
$\psi ^R\subseteq \operatorname {\mathrm {Str}}(\tau \cup \{R\})$
by the following stipulation:
Then both
![]() $\psi ^R$
and its complement are closed under isomorphisms and ultraproducts modulo D.
$\psi ^R$
and its complement are closed under isomorphisms and ultraproducts modulo D.
Following [Reference Vaughan22, p. 251], a topological space X is said to be
![]() $[\nu ,\mu ]$
-compact if every open cover of cardinality
$[\nu ,\mu ]$
-compact if every open cover of cardinality
![]() $\leq \mu $
has a subcover of cardinality
$\leq \mu $
has a subcover of cardinality
![]() $<\nu .$
$<\nu .$
Proposition 2.6. Let D be a
![]() $\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter over a set I. Let
$\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter over a set I. Let
![]() $\tau $
be a relational type, and J be a set having the property that for each
$\tau $
be a relational type, and J be a set having the property that for each
![]() $j\in J$
there is a class
$j\in J$
there is a class
![]() $\psi _j\subseteq \operatorname {\mathrm {Str}}(\tau )$
such that both
$\psi _j\subseteq \operatorname {\mathrm {Str}}(\tau )$
such that both
![]() $\psi _j$
and
$\psi _j$
and
![]() $\neg \psi _j=\operatorname {\mathrm {Str}}(\tau )\setminus \psi _j$
are closed under isomorphisms and ultraproducts modulo D.
$\neg \psi _j=\operatorname {\mathrm {Str}}(\tau )\setminus \psi _j$
are closed under isomorphisms and ultraproducts modulo D.
Then
![]() $\operatorname {\mathrm {Str}} (\tau )$
is
$\operatorname {\mathrm {Str}} (\tau )$
is
![]() $[\kappa ,\kappa ]$
-compact for the topology generated by the subbase
$[\kappa ,\kappa ]$
-compact for the topology generated by the subbase
![]() $\{\neg \psi _j\}_{j\in J}.$
$\{\neg \psi _j\}_{j\in J}.$
Proof. Arguing by way of contradiction, let
![]() $\{F_\alpha \mid \alpha <\kappa \}$
be a family of closed subspaces of
$\{F_\alpha \mid \alpha <\kappa \}$
be a family of closed subspaces of
![]() $\operatorname {\mathrm {Str}}(\tau )$
with empty intersection, such that for no
$\operatorname {\mathrm {Str}}(\tau )$
with empty intersection, such that for no
![]() $W\subseteq \kappa $
with
$W\subseteq \kappa $
with
![]() $|W|<\kappa $
we have
$|W|<\kappa $
we have
![]() $\bigcap _{\alpha \in W} F_\alpha =\emptyset .$
For each
$\bigcap _{\alpha \in W} F_\alpha =\emptyset .$
For each
![]() $\beta <\kappa $
let
$\beta <\kappa $
let
![]() $\hat F_\beta =\bigcap _{\alpha <\beta } F_\alpha $
(with
$\hat F_\beta =\bigcap _{\alpha <\beta } F_\alpha $
(with
![]() $\hat F_0=\operatorname {\mathrm {Str}}(\tau )$
). Then
$\hat F_0=\operatorname {\mathrm {Str}}(\tau )$
). Then
 $$ \begin{align} \hat F_0\supseteq \hat F_1\supseteq\dots\supseteq \hat F_\beta\supseteq \cdots,\, (\beta<\kappa),\,\,\,\,\, \hat F_\beta\not=\emptyset,\,\,\, \,\,\,\,\bigcap_{\beta<\kappa}\hat F_\beta =\emptyset. \end{align} $$
$$ \begin{align} \hat F_0\supseteq \hat F_1\supseteq\dots\supseteq \hat F_\beta\supseteq \cdots,\, (\beta<\kappa),\,\,\,\,\, \hat F_\beta\not=\emptyset,\,\,\, \,\,\,\,\bigcap_{\beta<\kappa}\hat F_\beta =\emptyset. \end{align} $$
We may safely assume that the subbase
![]() $\{\neg \psi _j\}_{j\in J}$
is closed under finite intersections. In this way, every closed set is a (possibly infinite) intersection of closed subsets of
$\{\neg \psi _j\}_{j\in J}$
is closed under finite intersections. In this way, every closed set is a (possibly infinite) intersection of closed subsets of
![]() $\operatorname {\mathrm {Str}}(\tau )$
taken from the family
$\operatorname {\mathrm {Str}}(\tau )$
taken from the family
![]() $\{\psi _j\}_{j\in J}.$
By (2) there is a sequence
$\{\psi _j\}_{j\in J}.$
By (2) there is a sequence
![]() $J_0\subseteq J_1\subseteq \dots \subseteq J_\beta \subseteq \cdots \,\,\,(\beta <\kappa )$
of subsets of J satisfying
$J_0\subseteq J_1\subseteq \dots \subseteq J_\beta \subseteq \cdots \,\,\,(\beta <\kappa )$
of subsets of J satisfying
Since each
![]() $\psi _j$
is closed under isomorphisms, we also have a sequence of structures
$\psi _j$
is closed under isomorphisms, we also have a sequence of structures
![]() ${\mathfrak {A}}_\beta \in \operatorname {\mathrm {Str}}(\tau )$
satisfying
${\mathfrak {A}}_\beta \in \operatorname {\mathrm {Str}}(\tau )$
satisfying
Let
where each
![]() $S_\alpha $
and
$S_\alpha $
and
![]() $R_j$
is a unary relation symbol, and E is binary. Since J is a set,
$R_j$
is a unary relation symbol, and E is binary. Since J is a set,
![]() $\tau ^+$
is a type. Define
$\tau ^+$
is a type. Define
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ^+)$
by the following stipulations:
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ^+)$
by the following stipulations:
-
(i)
 $M=\bigcup _{\alpha <\kappa } A_\alpha ,$
$M=\bigcup _{\alpha <\kappa } A_\alpha ,$
 $(M \mathsf I A_\alpha )\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau ={\mathfrak {A}}_\alpha ,$
and for every
$(M \mathsf I A_\alpha )\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau ={\mathfrak {A}}_\alpha ,$
and for every
 $T\in \tau ,\,\,\, T^{\mathfrak {M}}=\bigcup _{\alpha <\kappa } T^{{\mathfrak {A}}_\alpha }.$
$T\in \tau ,\,\,\, T^{\mathfrak {M}}=\bigcup _{\alpha <\kappa } T^{{\mathfrak {A}}_\alpha }.$
-
(ii)
 $E^{\mathfrak {M}}$
is an equivalence relation with
$E^{\mathfrak {M}}$
is an equivalence relation with
 $\kappa $
components, and for every
$\kappa $
components, and for every
 $x,y\in M,$
$x,y\in M,$
 $xE^{\mathfrak {M}}y$
iff there is
$xE^{\mathfrak {M}}y$
iff there is
 $\alpha <\kappa $
with
$\alpha <\kappa $
with
 $x,y\in A_\alpha $
.
$x,y\in A_\alpha $
. -
(iii)
 $S_0^{\mathfrak {M}} =\emptyset $
,
$S_0^{\mathfrak {M}} =\emptyset $
,
 $S_\alpha ^{\mathfrak {M}} =\bigcup _{\beta <\alpha } A_\beta $
for every
$S_\alpha ^{\mathfrak {M}} =\bigcup _{\beta <\alpha } A_\beta $
for every
 $\alpha <\kappa .$
$\alpha <\kappa .$
-
(iv)
 $R^{\mathfrak {M}}_j=\bigcup \{A_\beta \mid {\mathfrak {A}}_\beta \in \psi _j\}$
for every
$R^{\mathfrak {M}}_j=\bigcup \{A_\beta \mid {\mathfrak {A}}_\beta \in \psi _j\}$
for every
 $j\in J.$
$j\in J.$
The existence of
![]() ${\mathfrak {M}}$
satisfying condition (i) is ensured by our assumption that
${\mathfrak {M}}$
satisfying condition (i) is ensured by our assumption that
![]() $\tau $
is relational and the
$\tau $
is relational and the
![]() $A_\alpha $
’s are pairwise disjoint. With the notation of Definition 2.3, by (i), (ii), and (iv) we can write
$A_\alpha $
’s are pairwise disjoint. With the notation of Definition 2.3, by (i), (ii), and (iv) we can write
i.e.,
If
![]() $x\in M\setminus S^{\mathfrak {M}}_{\alpha +1}$
then by (iii),
$x\in M\setminus S^{\mathfrak {M}}_{\alpha +1}$
then by (iii),
![]() $Ex=A_\beta $
for a unique
$Ex=A_\beta $
for a unique
![]() $\beta $
with
$\beta $
with
![]() $\alpha <\beta < \kappa .$
Then by (2)–(4), conditions (i) and (ii) yield
$\alpha <\beta < \kappa .$
Then by (2)–(4), conditions (i) and (ii) yield
whence, by (iv),
![]() $x\in R_j^{\mathfrak {M}}$
for each
$x\in R_j^{\mathfrak {M}}$
for each
![]() $j\in J_\beta $
. A fortiori,
$j\in J_\beta $
. A fortiori,
![]() $x\in R_j^{\mathfrak {M}}$
for each
$x\in R_j^{\mathfrak {M}}$
for each
![]() $j\in J_\alpha ,$
and we may write
$j\in J_\alpha ,$
and we may write
By Lemma 2.1, the ultrapower
![]() $\Pi _D {\mathfrak {M}}$
has an expansion
$\Pi _D {\mathfrak {M}}$
has an expansion
![]() $\mathfrak B =\langle \Pi _D{\mathfrak {M}},c\rangle $
such that
$\mathfrak B =\langle \Pi _D{\mathfrak {M}},c\rangle $
such that
![]() $\mathfrak B \models \neg \{S_\alpha c\mid \alpha < \kappa \}$
. Combining Łoś theorem with (6) we can write
$\mathfrak B \models \neg \{S_\alpha c\mid \alpha < \kappa \}$
. Combining Łoś theorem with (6) we can write
As a consequence,
For every
![]() $j\in J$
let
$j\in J$
let
From (5) we have
![]() ${\mathfrak {M}}_j \in \psi _j^{R_jE}$
. Lemma 2.4 now yields
${\mathfrak {M}}_j \in \psi _j^{R_jE}$
. Lemma 2.4 now yields
Setting now
![]() ${\mathfrak {N}}=\Pi _D{\mathfrak {M}}$
, by Definition 2.3 we have
${\mathfrak {N}}=\Pi _D{\mathfrak {M}}$
, by Definition 2.3 we have
By (7),
![]() $({\mathfrak {N}} \, \mathsf I \,Ec)\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau \in \psi _j$
for all
$({\mathfrak {N}} \, \mathsf I \,Ec)\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau \in \psi _j$
for all
![]() $j\in \bigcup _{\alpha <\kappa }J_\alpha .$
Finally, by (3),
$j\in \bigcup _{\alpha <\kappa }J_\alpha .$
Finally, by (3),
![]() $({\mathfrak {N}} \, \mathsf I \,Ec)\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau $
belongs to
$({\mathfrak {N}} \, \mathsf I \,Ec)\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau $
belongs to
![]() $\hat F_\beta $
for all
$\hat F_\beta $
for all
![]() $\beta <\kappa $
, in contradiction with (2). The proof is complete.
$\beta <\kappa $
, in contradiction with (2). The proof is complete.
3 From classes of ultrafilters to logics
3.1 Logics, elementary classes,
 $\Delta $
-closure. Statement of the main theorem
$\Delta $
-closure. Statement of the main theorem
Following [Reference Ebbinghaus7, definition 1.1.1], by a logic
![]() ${\mathcal {L}}$
we mean a pair
${\mathcal {L}}$
we mean a pair
![]() $(\operatorname {\mathrm {Stc}}_{{\mathcal {L}}},\models _{{\mathcal {L}}})$
, where
$(\operatorname {\mathrm {Stc}}_{{\mathcal {L}}},\models _{{\mathcal {L}}})$
, where
![]() $\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}$
is a map assigning to every type
$\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}$
is a map assigning to every type
![]() $\tau $
a family
$\tau $
a family
![]() $\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}(\tau )$
, called the family of sentences in
$\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}(\tau )$
, called the family of sentences in
![]() ${\mathcal {L}}$
of type
${\mathcal {L}}$
of type
![]() $\tau $
, and
$\tau $
, and
![]() $\models _{{\mathcal {L}}}$
(called
$\models _{{\mathcal {L}}}$
(called
![]() ${\mathcal {L}}$
-satisfaction) is a relation between structures and sentences satisfying conditions (i)–(v) in [Reference Ebbinghaus7, p. 28]. Via
${\mathcal {L}}$
-satisfaction) is a relation between structures and sentences satisfying conditions (i)–(v) in [Reference Ebbinghaus7, p. 28]. Via
![]() $\models _{{\mathcal {L}}}$
, each sentence
$\models _{{\mathcal {L}}}$
, each sentence
![]() $\psi $
of type
$\psi $
of type
![]() $\tau $
is identified with a class, also denoted
$\tau $
is identified with a class, also denoted
![]() $\psi $
, of structures of type
$\psi $
, of structures of type
![]() $\tau $
. We write
$\tau $
. We write
![]() ${\mathcal {L}}(\tau )$
instead of
${\mathcal {L}}(\tau )$
instead of
![]() $\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}(\tau ).$
Given
$\operatorname {\mathrm {Stc}}_{{\mathcal {L}}}(\tau ).$
Given
![]() $\Phi \subseteq {\mathcal {L}}(\tau )$
we say that
$\Phi \subseteq {\mathcal {L}}(\tau )$
we say that
![]() $\Phi $
has a model if there is
$\Phi $
has a model if there is
![]() ${\mathfrak {N}}\in \operatorname {\mathrm {Str}}(\tau )$
such that
${\mathfrak {N}}\in \operatorname {\mathrm {Str}}(\tau )$
such that
![]() ${\mathfrak {N}}\models _{{\mathcal {L}}}\phi $
for all
${\mathfrak {N}}\models _{{\mathcal {L}}}\phi $
for all
![]() $\phi \in \Phi $
.
$\phi \in \Phi $
.
As already remarked,
![]() $\models $
denotes the satisfaction relation of first-order logic.
$\models $
denotes the satisfaction relation of first-order logic.
Following [Reference Makowsky and Shelah16, p. 230] logic
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\kappa $
-relatively compact (
$\kappa $
-relatively compact (
![]() $\operatorname {\mathrm {\kappa {-r.c.}}}$
) if for any two sets
$\operatorname {\mathrm {\kappa {-r.c.}}}$
) if for any two sets
![]() $\Psi ,\Xi $
of sentences in
$\Psi ,\Xi $
of sentences in
![]() ${\mathcal {L}}$
with
${\mathcal {L}}$
with
![]() $|\Psi |=\kappa $
, if
$|\Psi |=\kappa $
, if
![]() $\Psi _0\cup \Xi $
has a model for every
$\Psi _0\cup \Xi $
has a model for every
![]() $\Psi _0\subseteq \Psi $
with
$\Psi _0\subseteq \Psi $
with
![]() $|\Psi _0|<\kappa $
and arbitrary
$|\Psi _0|<\kappa $
and arbitrary
![]() $\Xi $
, then so does
$\Xi $
, then so does
![]() $\Psi \cup \Xi .$
$\Psi \cup \Xi .$
A class
![]() $\chi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is elementary of type
$\chi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is elementary of type
![]() $\tau $
in
$\tau $
in
![]() ${\mathcal {L}}$
if there is
${\mathcal {L}}$
if there is
![]() $\psi \in {\mathcal {L}}(\tau )$
such that
$\psi \in {\mathcal {L}}(\tau )$
such that
![]() ${\chi =\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ) \mid {\mathfrak {M}}\models _{{\mathcal {L}}}\psi \}}$
.
${\chi =\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ) \mid {\mathfrak {M}}\models _{{\mathcal {L}}}\psi \}}$
.
![]() $EC_{{\mathcal {L}}}^\tau $
denotes the family of all such classes. Two logics are equivalent if they have the same elementary classes. For types
$EC_{{\mathcal {L}}}^\tau $
denotes the family of all such classes. Two logics are equivalent if they have the same elementary classes. For types
![]() $\sigma \subseteq \tau $
and
$\sigma \subseteq \tau $
and
![]() $\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
we let
$\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
we let
where
![]() $\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,_\sigma ^\tau \colon \operatorname {\mathrm {Str}}(\tau )\to \operatorname {\mathrm {Str}}(\sigma )$
is the reduct operation.
$\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,_\sigma ^\tau \colon \operatorname {\mathrm {Str}}(\tau )\to \operatorname {\mathrm {Str}}(\sigma )$
is the reduct operation.
Following [Reference Ebbinghaus7, p. 18] we say that
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed if it has the following property: Let
$\Delta $
-closed if it has the following property: Let
![]() $\tau \subseteq \tau '\cap \tau "$
,
$\tau \subseteq \tau '\cap \tau "$
,
![]() $\psi '\in EC^{\tau '}_{{\mathcal {L}}}$
,
$\psi '\in EC^{\tau '}_{{\mathcal {L}}}$
,
![]() $\psi "\in EC^{\tau "}_{{\mathcal {L}}}$
. Suppose
$\psi "\in EC^{\tau "}_{{\mathcal {L}}}$
. Suppose
![]() $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi '= \operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_\tau )\psi "$
. Then
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi '= \operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_\tau )\psi "$
. Then
![]() $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi ' \in EC^\tau _{{\mathcal {L}}}.$
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi ' \in EC^\tau _{{\mathcal {L}}}.$
The following theorem is our first main result in this paper:
Theorem 3.1. Let
![]() $\Omega $
be a nonempty class of uniform ultrafilters. Let the map
$\Omega $
be a nonempty class of uniform ultrafilters. Let the map
![]() $L=L_\Omega $
assign to every type
$L=L_\Omega $
assign to every type
![]() $\tau $
the family
$\tau $
the family
![]() $L(\tau )$
specified as follows:
$L(\tau )$
specified as follows:
![]() $\psi \in L(\tau )$
iff
$\psi \in L(\tau )$
iff
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and there is a finite type
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and there is a finite type
![]() $\sigma \subseteq \tau $
and a class
$\sigma \subseteq \tau $
and a class
![]() $\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
such that
$\chi \subseteq \operatorname {\mathrm {Str}}(\sigma )$
such that
![]() $\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma )^{-1}\chi $
, with both
$\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma )^{-1}\chi $
, with both
![]() $\chi $
and
$\chi $
and
![]() $\operatorname {\mathrm {Str}}(\sigma )\setminus \chi $
closed under isomorphisms and ultraproducts modulo D for all
$\operatorname {\mathrm {Str}}(\sigma )\setminus \chi $
closed under isomorphisms and ultraproducts modulo D for all
![]() $D\in \Omega $
.
$D\in \Omega $
.
We then have:
-
(i) Up to equivalence, there is a unique regular logic
 ${\mathcal {L}}={\mathcal {L}}_\Omega $
such that for every type
${\mathcal {L}}={\mathcal {L}}_\Omega $
such that for every type
 $\tau $
,
$\tau $
,
 $L(\tau )=EC^\tau _{{\mathcal {L}}}.$
$L(\tau )=EC^\tau _{{\mathcal {L}}}.$
 ${\mathcal {L}}$
is
${\mathcal {L}}$
is
 $\Delta $
-closed. If
$\Delta $
-closed. If
 $\Omega $
contains a
$\Omega $
contains a
 $\kappa $
-descendingly incomplete ultrafilter,
$\kappa $
-descendingly incomplete ultrafilter,
 ${\mathcal {L}}$
is
${\mathcal {L}}$
is
 $\kappa $
-relatively compact.
$\kappa $
-relatively compact.
 ${\mathcal {L}}$
is compact only if
${\mathcal {L}}$
is compact only if
 $\Omega $
is a proper class.
$\Omega $
is a proper class. -
(ii)
 $(\neg 0^\sharp $
or
$(\neg 0^\sharp $
or
 $\neg L^\mu )$
If
$\neg L^\mu )$
If
 $D\in \Omega $
is an ultrafilter over a regular cardinal
$D\in \Omega $
is an ultrafilter over a regular cardinal
 $\nu $
then for a family
$\nu $
then for a family
 $\Psi $
of
$\Psi $
of
 ${\mathcal {L}}$
-sentences with
${\mathcal {L}}$
-sentences with
 $|\Psi |\leq \nu $
to have a model it is sufficient that every finite subfamily of
$|\Psi |\leq \nu $
to have a model it is sufficient that every finite subfamily of
 $\Psi $
has a model. In particular, if
$\Psi $
has a model. In particular, if
 $\Omega $
is a proper class and each
$\Omega $
is a proper class and each
 $D\in \Omega $
is an ultrafilter over a regular cardinal, then
$D\in \Omega $
is an ultrafilter over a regular cardinal, then
 ${\mathcal {L}}$
is compact.
${\mathcal {L}}$
is compact.
3.2 First part of the proof of Theorem 3.1(i): Basic properties of
 $L=L_\Omega $
$L=L_\Omega $
Proposition 3.2. With the above notation and terminology concerning
![]() $\Omega $
and L, we have:
$\Omega $
and L, we have:
-
(1) Both
 $\emptyset $
and
$\emptyset $
and
 $\operatorname {\mathrm {Str}}(\tau )$
belong to
$\operatorname {\mathrm {Str}}(\tau )$
belong to
 $L(\tau ).$
$L(\tau ).$
-
(2) If
 $\psi $
belongs to
$\psi $
belongs to
 $ L(\tau )$
then so does its complement
$ L(\tau )$
then so does its complement
 $\neg \psi =\operatorname {\mathrm {Str}}(\tau )\setminus \psi .$
$\neg \psi =\operatorname {\mathrm {Str}}(\tau )\setminus \psi .$
-
(3) Every
 $\psi \in L(\tau )$
(as well as
$\psi \in L(\tau )$
(as well as
 $\neg \psi $
) is closed under isomorphisms and ultraproducts modulo D for all
$\neg \psi $
) is closed under isomorphisms and ultraproducts modulo D for all
 $D\in \Omega .$
$D\in \Omega .$
-
(4) For every finite type
 $\tau ,$
if both
$\tau ,$
if both
 $\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complement are closed under isomorphisms and ultraproducts modulo D for all
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau )$
and its complement are closed under isomorphisms and ultraproducts modulo D for all
 $D\in \Omega $
, then
$D\in \Omega $
, then
 $\psi $
belongs to
$\psi $
belongs to
 $L(\tau )$
.
$L(\tau )$
. -
(5) If
 $\psi \in L(\tau )$
and
$\psi \in L(\tau )$
and
 $\zeta \supseteq \tau $
then
$\zeta \supseteq \tau $
then
 $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,_\tau ^\zeta )^{-1} \psi \in L(\zeta )$
.
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,_\tau ^\zeta )^{-1} \psi \in L(\zeta )$
. -
(6) Let
 $\rho \colon \tau \to \sigma $
be an arity preserving bijection of
$\rho \colon \tau \to \sigma $
be an arity preserving bijection of
 $\tau $
onto
$\tau $
onto
 $\sigma $
sending relations, constants and functions to relations, constants and functions. (For short,
$\sigma $
sending relations, constants and functions to relations, constants and functions. (For short,
 $\rho $
is a renaming.) For each
$\rho $
is a renaming.) For each
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
let
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
let
 ${\mathfrak {M}}^\rho \in \operatorname {\mathrm {Str}}(\sigma )$
be the structure with the same universe as
${\mathfrak {M}}^\rho \in \operatorname {\mathrm {Str}}(\sigma )$
be the structure with the same universe as
 ${\mathfrak {M}}$
, where each symbol
${\mathfrak {M}}$
, where each symbol
 $S\in \sigma $
is interpreted precisely as the symbol
$S\in \sigma $
is interpreted precisely as the symbol
 $\rho ^{-1}$
is interpreted in
$\rho ^{-1}$
is interpreted in
 ${\mathfrak {M}}.$
Let
${\mathfrak {M}}.$
Let
 $\psi ^\rho =\{{\mathfrak {M}}^\rho \mid {\mathfrak {M}}\in \psi \}.$
Then for all
$\psi ^\rho =\{{\mathfrak {M}}^\rho \mid {\mathfrak {M}}\in \psi \}.$
Then for all
 $\psi \in L(\tau )$
,
$\psi \in L(\tau )$
,
 $\psi ^\rho \in L(\sigma )$
.
$\psi ^\rho \in L(\sigma )$
. -
(7) For every first-order sentence
 $\theta $
of a finite type
$\theta $
of a finite type
 $\tau $
, the class belongs to
$\tau $
, the class belongs to $$ \begin{align*}\psi=\{{\mathfrak{N}}\in \operatorname{\mathrm{Str}}(\tau)\mid {\mathfrak{N}}\models \theta\} \end{align*} $$
$$ \begin{align*}\psi=\{{\mathfrak{N}}\in \operatorname{\mathrm{Str}}(\tau)\mid {\mathfrak{N}}\models \theta\} \end{align*} $$
 $L(\tau )$
.
$L(\tau )$
.
-
(8) If
 $\psi ,\phi \in L(\tau )$
then
$\psi ,\phi \in L(\tau )$
then
 $\psi \cap \phi \in L(\tau ).$
$\psi \cap \phi \in L(\tau ).$
-
(9) For any
 $\psi \in L(\tau )$
and constant symbol c, let the class
$\psi \in L(\tau )$
and constant symbol c, let the class
 $ \exists c\psi \subseteq \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
be defined by If
$ \exists c\psi \subseteq \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
be defined by If $$ \begin{align*}\exists c\psi = \left(\,{\mathbin{\vert\mkern-0.3mu\grave{}}}\,\tau^\tau_{\tau\setminus\{c\}}\right) \,\,\psi. \end{align*} $$
$$ \begin{align*}\exists c\psi = \left(\,{\mathbin{\vert\mkern-0.3mu\grave{}}}\,\tau^\tau_{\tau\setminus\{c\}}\right) \,\,\psi. \end{align*} $$
 $c\notin \tau $
then
$c\notin \tau $
then
 $\exists c \psi =\psi .$
If
$\exists c \psi =\psi .$
If
 $c\in \tau $
then for every
$c\in \tau $
then for every
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
we have:
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
we have:
 ${\mathfrak {M}} \in \exists c\psi $
iff there is
${\mathfrak {M}} \in \exists c\psi $
iff there is
 $m\in M$
such that
$m\in M$
such that
 $\langle {\mathfrak {M}}, c/m\rangle \in \psi $
. Here
$\langle {\mathfrak {M}}, c/m\rangle \in \psi $
. Here
 $\langle {\mathfrak {M}}, c/m\rangle $
denotes the expansion of
$\langle {\mathfrak {M}}, c/m\rangle $
denotes the expansion of
 ${\mathfrak {M}} $
to
${\mathfrak {M}} $
to
 $\tau $
where c is interpreted by m.
$\tau $
where c is interpreted by m.
-
(10) For every
 $\psi \in L(\tau )$
and constant symbol c,
$\psi \in L(\tau )$
and constant symbol c,
 $\exists c\psi $
belongs to
$\exists c\psi $
belongs to
 $L(\tau \setminus \{c\})$
.
$L(\tau \setminus \{c\})$
. -
(11) Let
 $\tau ,\, \tau ', \, \tau "$
be types, with
$\tau ,\, \tau ', \, \tau "$
be types, with
 $\tau $
finite and coinciding with
$\tau $
finite and coinciding with
 $\tau '\cap \tau "$
. Let
$\tau '\cap \tau "$
. Let
 $\psi ' \in L(\tau ')$
and
$\psi ' \in L(\tau ')$
and
 $\psi " \in L(\tau ")$
. Suppose further
$\psi " \in L(\tau ")$
. Suppose further
 $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi ' =\operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_{\tau })\psi ".$
Then
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi ' =\operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_{\tau })\psi ".$
Then
 $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi '$
belongs to
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi '$
belongs to
 $L(\tau ).$
$L(\tau ).$
-
(12) For
 $\mu $
a cardinal and
$\mu $
a cardinal and
 $\tau $
a fixed but otherwise arbitrary type, suppose we are given classes of structures
$\tau $
a fixed but otherwise arbitrary type, suppose we are given classes of structures
 $\{\chi _\alpha \mid \alpha <\mu \} \subseteq L(\tau )$
. Let
$\{\chi _\alpha \mid \alpha <\mu \} \subseteq L(\tau )$
. Let
 $\mathcal T$
be the topology on
$\mathcal T$
be the topology on
 $\operatorname {\mathrm {Str}}(\tau )$
generated by the subbase
$\operatorname {\mathrm {Str}}(\tau )$
generated by the subbase
 $\{\neg \chi _\alpha \mid \alpha <\mu \}$
. Then
$\{\neg \chi _\alpha \mid \alpha <\mu \}$
. Then
 $\mathcal T$
is a
$\mathcal T$
is a
 $[\kappa ,\kappa ]$
-compact topology for each cardinal
$[\kappa ,\kappa ]$
-compact topology for each cardinal
 $\kappa $
such that there is a
$\kappa $
such that there is a
 $\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter
$\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter
 $D\in \Omega $
.
$D\in \Omega $
.
Proof. (1)–(7) are immediate consequences of the definition of
![]() $L(\tau ).$
(8) routinely follows from (2), (3) and (5). (9) is trivial.
$L(\tau ).$
(8) routinely follows from (2), (3) and (5). (9) is trivial.
To prove (10), skipping all trivialities, assume
![]() $c\in \tau .$
For some finite type
$c\in \tau .$
For some finite type
![]() $\sigma _0\subseteq \tau $
and class
$\sigma _0\subseteq \tau $
and class
![]() $\chi _0\subseteq \operatorname {\mathrm {Str}}(\sigma _0)$
we can write
$\chi _0\subseteq \operatorname {\mathrm {Str}}(\sigma _0)$
we can write
![]() $\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _{\sigma _0})^{-1}\chi _0$
. Let
$\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _{\sigma _0})^{-1}\chi _0$
. Let
![]() $\sigma =\sigma _0\cup \{c\}$
and
$\sigma =\sigma _0\cup \{c\}$
and
![]() $\chi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\sigma _{\sigma _0})^{-1}\chi _0.$
By (3) and (5), both
$\chi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\sigma _{\sigma _0})^{-1}\chi _0.$
By (3) and (5), both
![]() $\chi $
and
$\chi $
and
![]() $\neg \chi $
are in
$\neg \chi $
are in
![]() $L(\sigma )$
and are closed under isomorphisms and ultraproducts modulo D for all
$L(\sigma )$
and are closed under isomorphisms and ultraproducts modulo D for all
![]() $D\in \Omega $
. Furthermore,
$D\in \Omega $
. Furthermore,
![]() $\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma )^{-1}\chi $
(and
$\psi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^\tau _\sigma )^{-1}\chi $
(and
![]() $c\in \sigma $
). Let
$c\in \sigma $
). Let
![]() $\sigma '=\sigma \setminus \{c\}$
and
$\sigma '=\sigma \setminus \{c\}$
and
![]() $\tau '=\tau \setminus \{c\}.$
By making repeated use of (9) we get
$\tau '=\tau \setminus \{c\}.$
By making repeated use of (9) we get
![]() $\exists c\psi = (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\sigma '})^{-1}\exists c\chi .$
From the expansion theorem [Reference Chang and Keisler4, Theorem 4.1.8] it follows that for all
$\exists c\psi = (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\sigma '})^{-1}\exists c\chi .$
From the expansion theorem [Reference Chang and Keisler4, Theorem 4.1.8] it follows that for all
![]() $D\in \Omega $
both classes
$D\in \Omega $
both classes
![]() $\exists c\chi $
and
$\exists c\chi $
and
![]() $\neg \exists c \chi $
are closed under ultraproducts modulo D. Both classes are also closed under isomorphisms. Since
$\neg \exists c \chi $
are closed under ultraproducts modulo D. Both classes are also closed under isomorphisms. Since
![]() $\sigma '$
is finite we conclude that
$\sigma '$
is finite we conclude that
![]() $\exists c\psi $
belongs to
$\exists c\psi $
belongs to
![]() $L(\tau ')=L(\tau \setminus \{c\})$
, which settles (10).
$L(\tau ')=L(\tau \setminus \{c\})$
, which settles (10).
Next, (11) is easily proved using the expansion theorem and (3) and (4).
The special case of (12) when
![]() $\tau $
is relational is taken care of by (3) and Proposition 2.6. The general case for an arbitrary type
$\tau $
is relational is taken care of by (3) and Proposition 2.6. The general case for an arbitrary type
![]() $\tau $
is a tedious but routine variant of the special case, again using Proposition 2.6 together with (10).
$\tau $
is a tedious but routine variant of the special case, again using Proposition 2.6 together with (10).
3.3 Second part of the proof of Theorem 3.1(i): The construction of
 ${\mathcal {L}}={\mathcal {L}}_\Omega $
${\mathcal {L}}={\mathcal {L}}_\Omega $
For every structure
![]() ${\mathfrak {M}}$
there is exactly one type
${\mathfrak {M}}$
there is exactly one type
![]() $\tau =\tau _{\mathfrak {M}}$
such that
$\tau =\tau _{\mathfrak {M}}$
such that
![]() ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ).$
For every nonempty class
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ).$
For every nonempty class
![]() $\psi $
of structures of the same type there is exactly one
$\psi $
of structures of the same type there is exactly one
![]() $\tau =\tau _\psi $
such that
$\tau =\tau _\psi $
such that
![]() $\psi \subseteq \operatorname {\mathrm {Str}}(\tau ).$
$\psi \subseteq \operatorname {\mathrm {Str}}(\tau ).$
Definition 3.3. Adopt the above notation and terminology concerning
![]() $\Omega $
and
$\Omega $
and
![]() $L=L_\Omega $
. Given any type
$L=L_\Omega $
. Given any type
![]() $\tau $
, the family
$\tau $
, the family
![]() ${\mathcal {L}}(\tau )$
of sentences of type
${\mathcal {L}}(\tau )$
of sentences of type
![]() $\tau $
in
$\tau $
in
![]() ${\mathcal {L}}={\mathcal {L}}_\Omega $
and its satisfaction relation
${\mathcal {L}}={\mathcal {L}}_\Omega $
and its satisfaction relation
![]() $\models _{{\mathcal {L}}}$
are defined by:
$\models _{{\mathcal {L}}}$
are defined by:
-
(*)
 $\psi \in {\mathcal {L}}(\tau )$
if either
$\psi \in {\mathcal {L}}(\tau )$
if either
 $\psi $
is empty or
$\psi $
is empty or
 $\psi $
is a nonempty class of structures of the same type
$\psi $
is a nonempty class of structures of the same type
 $\tau _\psi $
, with
$\tau _\psi $
, with
 $\tau _\psi $
finite,
$\tau _\psi $
finite,
 $\tau _\psi \subseteq \tau , $
and
$\tau _\psi \subseteq \tau , $
and
 $\psi \in L(\tau _\psi ).$
$\psi \in L(\tau _\psi ).$
-
(**)
 ${\mathfrak {M}}$
satisfies
${\mathfrak {M}}$
satisfies
 $\psi $
in
$\psi $
in
 ${\mathcal {L}}$
, in symbols,
${\mathcal {L}}$
, in symbols,
 ${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
, if
${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
, if
 $\tau _\psi \subseteq \tau _{\mathfrak {M}}$
and
$\tau _\psi \subseteq \tau _{\mathfrak {M}}$
and
 ${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau _\psi \in \psi $
.
${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau _\psi \in \psi $
.
Since
![]() $\psi $
is a sentence of
$\psi $
is a sentence of
![]() ${\mathcal {L}}(\tau )$
for some
${\mathcal {L}}(\tau )$
for some
![]() $\tau $
, the type
$\tau $
, the type
![]() $\tau _\psi $
is well defined in (**). Moreover,
$\tau _\psi $
is well defined in (**). Moreover,
![]() $\tau _\psi $
is finite and
$\tau _\psi $
is finite and
![]() $\psi $
is a member of
$\psi $
is a member of
![]() ${\mathcal {L}}(\tau _\psi ).$
We use the notation
${\mathcal {L}}(\tau _\psi ).$
We use the notation
Recalling the definition at the outset of Section 3, we say that
![]() $\chi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is an elementary class of type
$\chi \subseteq \operatorname {\mathrm {Str}}(\tau )$
is an elementary class of type
![]() $\tau $
in
$\tau $
in
![]() ${\mathcal {L}}$
, in symbols,
${\mathcal {L}}$
, in symbols,
![]() $\chi \in EC^\tau _{{\mathcal {L}}}$
, if
$\chi \in EC^\tau _{{\mathcal {L}}}$
, if
![]() $\chi =\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi $
for some
$\chi =\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi $
for some
![]() $\psi \in {\mathcal {L}}(\tau ).$
$\psi \in {\mathcal {L}}(\tau ).$
The proof of the following proposition is a main prerequisite to prove (in the next subsection) that
![]() ${\mathcal {L}}={\mathcal {L}}_\Omega $
is a regular logic having all the properties stated in Theorem 3.1.
${\mathcal {L}}={\mathcal {L}}_\Omega $
is a regular logic having all the properties stated in Theorem 3.1.
Proposition 3.4. With the above notation we have:
-
(1) For every
 $\tau $
,
$\tau $
,
 $EC^\tau _{{\mathcal {L}}}=L(\tau ).$
$EC^\tau _{{\mathcal {L}}}=L(\tau ).$
-
(2) (Monotonicity) If
 $\sigma \subseteq \tau $
then
$\sigma \subseteq \tau $
then
 ${\mathcal {L}}(\sigma )\subseteq {\mathcal {L}}(\tau ).$
${\mathcal {L}}(\sigma )\subseteq {\mathcal {L}}(\tau ).$
-
(3) (“Type” property) If
 ${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
then
${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
then
 $\psi \in {\mathcal {L}}(\tau _{\mathfrak {M}})$
.
$\psi \in {\mathcal {L}}(\tau _{\mathfrak {M}})$
. -
(4) (Isomorphism) If
 ${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
and
${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
and
 ${\mathfrak {N}}\cong {\mathfrak {M}}$
then
${\mathfrak {N}}\cong {\mathfrak {M}}$
then
 ${\mathfrak {N}}\models _{{\mathcal {L}}}\psi $
.
${\mathfrak {N}}\models _{{\mathcal {L}}}\psi $
. -
(5) (Reduct) Let
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\sigma )$
,
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\sigma )$
,
 $\psi \in {\mathcal {L}}(\tau )$
, and
$\psi \in {\mathcal {L}}(\tau )$
, and
 $\tau \subseteq \sigma $
. Then
$\tau \subseteq \sigma $
. Then
 ${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
iff
${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
iff
 ${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau \models _{{\mathcal {L}}}\psi $
.
${\mathfrak {M}}\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\, \tau \models _{{\mathcal {L}}}\psi $
. -
(6) (Renaming) Let
 $\rho $
be a renaming of
$\rho $
be a renaming of
 $\tau $
onto
$\tau $
onto
 $\sigma .$
(See Proposition 3.2(6).) Then for every
$\sigma .$
(See Proposition 3.2(6).) Then for every
 $\psi \in {\mathcal {L}}(\tau )$
there is
$\psi \in {\mathcal {L}}(\tau )$
there is
 $\chi \in {\mathcal {L}}(\sigma )$
such that for all
$\chi \in {\mathcal {L}}(\sigma )$
such that for all
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
,
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )$
,
 ${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
iff
${\mathfrak {M}}\models _{{\mathcal {L}}}\psi $
iff
 ${\mathfrak {M}}^\rho \models _{{\mathcal {L}}}\chi .$
${\mathfrak {M}}^\rho \models _{{\mathcal {L}}}\chi .$
-
(7) (Atoms) For every
 $\tau $
and atomic first-order sentence
$\tau $
and atomic first-order sentence
 $\xi $
of type
$\xi $
of type
 $\tau $
there is
$\tau $
there is
 $\psi \in {\mathcal {L}}(\tau )$
with
$\psi \in {\mathcal {L}}(\tau )$
with
 $\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi =\{{\mathfrak {N}}\in \operatorname {\mathrm {Str}}(\tau ) \mid {\mathfrak {N}}\models \xi \}.$
$\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi =\{{\mathfrak {N}}\in \operatorname {\mathrm {Str}}(\tau ) \mid {\mathfrak {N}}\models \xi \}.$
-
(8) (Negation) For all
 $\tau $
and
$\tau $
and
 $\psi \in {\mathcal {L}}(\tau )$
there is
$\psi \in {\mathcal {L}}(\tau )$
there is
 $\chi \in {\mathcal {L}}(\tau )$
with
$\chi \in {\mathcal {L}}(\tau )$
with
 $\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\chi =\operatorname {\mathrm {Str}}(\tau )\setminus \operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi .$
$\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\chi =\operatorname {\mathrm {Str}}(\tau )\setminus \operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi .$
-
(9) (Conjunction) For every type
 $\tau $
and classes
$\tau $
and classes
 $\psi ,\phi \in {\mathcal {L}}(\tau )$
there is
$\psi ,\phi \in {\mathcal {L}}(\tau )$
there is
 $\chi \in {\mathcal {L}}(\tau )$
with
$\chi \in {\mathcal {L}}(\tau )$
with
 $\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\chi $
=
$\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\chi $
=
 $\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi \cap \operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\phi $
.
$\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi \cap \operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\phi $
. -
(10) (Quantification) For every
 $\tau $
, constant symbol c, and
$\tau $
, constant symbol c, and
 $\psi \in {\mathcal {L}}(\tau )$
there is
$\psi \in {\mathcal {L}}(\tau )$
there is
 $\chi \in {\mathcal {L}}(\tau \setminus \{c\})$
such that for all
$\chi \in {\mathcal {L}}(\tau \setminus \{c\})$
such that for all
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
, with
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau \setminus \{c\})$
, with $$ \begin{align*}{\mathfrak{M}}\models_{{\mathcal{L}}}\chi\text{ iff }\langle{\mathfrak{M}},c/m\rangle \models_{{\mathcal{L}}}\psi\text{ for some }m\in M, \end{align*} $$
$$ \begin{align*}{\mathfrak{M}}\models_{{\mathcal{L}}}\chi\text{ iff }\langle{\mathfrak{M}},c/m\rangle \models_{{\mathcal{L}}}\psi\text{ for some }m\in M, \end{align*} $$
 $\langle {\mathfrak {M}},c/m\rangle $
as in Proposition 3.2(10).
$\langle {\mathfrak {M}},c/m\rangle $
as in Proposition 3.2(10).
-
(11) (
 $\Delta $
-closure) For all
$\Delta $
-closure) For all
 $\tau \subseteq \tau '\cap \tau "$
,
$\tau \subseteq \tau '\cap \tau "$
,
 $\psi '\in EC^{\tau '}_{{\mathcal {L}}}$
, and
$\psi '\in EC^{\tau '}_{{\mathcal {L}}}$
, and
 $\psi "\in EC^{\tau "}_{{\mathcal {L}}}$
, if
$\psi "\in EC^{\tau "}_{{\mathcal {L}}}$
, if
 $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi '= \operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_\tau )\psi "$
, then
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi '= \operatorname {\mathrm {Str}}(\tau )\setminus (\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau "}_\tau )\psi "$
, then
 $(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi ' \in EC^\tau _{{\mathcal {L}}}.$
$(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_\tau )\psi ' \in EC^\tau _{{\mathcal {L}}}.$
-
(12) If
 $\Omega $
contains a
$\Omega $
contains a
 $\kappa $
-descendingly incomplete ultrafilter,
$\kappa $
-descendingly incomplete ultrafilter,
 ${\mathcal {L}}$
is
${\mathcal {L}}$
is
 $\kappa $
-relatively compact.
$\kappa $
-relatively compact. -
(13) (Finite Occurrence Property) For every sentence
 $\psi \in {\mathcal {L}}$
there is a smallest type
$\psi \in {\mathcal {L}}$
there is a smallest type
 $\tau $
such that
$\tau $
such that
 $\psi \in {\mathcal {L}}(\tau ).$
Furthermore, such
$\psi \in {\mathcal {L}}(\tau ).$
Furthermore, such
 $\tau $
is finite.
$\tau $
is finite. -
(14) Let
 $\tau $
be a finite relational type,
$\tau $
be a finite relational type,
 $R\notin \tau $
a unary relation symbol,
$R\notin \tau $
a unary relation symbol,
 $\phi \in {\mathcal {L}}(\tau )$
and
$\phi \in {\mathcal {L}}(\tau )$
and
 $\tau ^+= \tau \cup \{R\}.$
Then there exists
$\tau ^+= \tau \cup \{R\}.$
Then there exists
 $\psi \in {\mathcal {L}}(\tau ^+)$
such that for all
$\psi \in {\mathcal {L}}(\tau ^+)$
such that for all
 ${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ^+),$
${\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau ^+),$
 $$ \begin{align*}{\mathfrak{M}}\models_{{\mathcal{L}}}\psi\text{ iff }(R^{\mathfrak{M}}\not=\emptyset\text{ and }({\mathfrak{M}}\,{\mathbin{\vert\mkern-0.3mu\grave{}}}\, \tau) \mathsf I R^{\mathfrak{M}}\models_{{\mathcal{L}}}\phi). \end{align*} $$
$$ \begin{align*}{\mathfrak{M}}\models_{{\mathcal{L}}}\psi\text{ iff }(R^{\mathfrak{M}}\not=\emptyset\text{ and }({\mathfrak{M}}\,{\mathbin{\vert\mkern-0.3mu\grave{}}}\, \tau) \mathsf I R^{\mathfrak{M}}\models_{{\mathcal{L}}}\phi). \end{align*} $$
Proof. (1) follows by definition from Proposition 3.2(1)–(5). Properties (2), (3) and (5) are immediate consequences of Definition 3.3. (4) Follows from Proposition 3.2(3). (6) follows from (1) and Proposition 3.2(6). By (1), conditions (7)–(10), respectively, follow from Propositions 3.2(7), 3.2(2), 3.2(8) and 3.2(10) and (11).
To prove (11) we argue as follows: By the renaming property (6) we can safely assume
![]() $\tau =\tau '\cap \tau ".$
By (1),
$\tau =\tau '\cap \tau ".$
By (1),
![]() $\psi '\in L(\tau ')$
and
$\psi '\in L(\tau ')$
and
![]() $\psi "\in L(\tau ")$
. By Proposition 3.2(4), for some finite
$\psi "\in L(\tau ")$
. By Proposition 3.2(4), for some finite
![]() $\sigma '\subseteq \tau '$
and
$\sigma '\subseteq \tau '$
and
![]() $\sigma "\subseteq \tau "$
there are
$\sigma "\subseteq \tau "$
there are
![]() $\chi '\in L(\sigma ')$
and
$\chi '\in L(\sigma ')$
and
![]() $\chi "\in L(\sigma ")$
such that
$\chi "\in L(\sigma ")$
such that
The finite type
![]() $\sigma =\sigma '\cap \sigma "$
is contained in
$\sigma =\sigma '\cap \sigma "$
is contained in
![]() $\tau. $
Let
$\tau. $
Let
Then
A routine application of Proposition 3.2(3), (4), and (12) yields
From Proposition 3.2(2) and (11) we obtain
By (1), we finally obtain
![]() $\phi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi '\in EC^\tau _{{\mathcal {L}}},$
which settles (11).
$\phi =(\,{\mathbin {\vert \mkern -0.3mu\grave {}}}\,^{\tau '}_{\tau })\psi '\in EC^\tau _{{\mathcal {L}}},$
which settles (11).
A proof of (12) can be obtained from (1) in combination with Proposition 3.2(12). (13) is trivial. (14) follows from (1) together with Proposition 3.2(3) and (4), in combination with Lemma 2.5.
3.4 Last part of the proof of Theorem 3.1(i):
 ${\mathcal {L}}$
has the desired properties
${\mathcal {L}}$
has the desired properties
By Proposition 3.4(1),
![]() ${\mathcal {L}}$
is uniquely determined by
${\mathcal {L}}$
is uniquely determined by
![]() $\Omega $
up to equivalence.
$\Omega $
up to equivalence.
We next prove that
![]() ${\mathcal {L}}$
is a regular logic.
${\mathcal {L}}$
is a regular logic.
By Proposition 3.4(2)–(10),
![]() ${\mathcal {L}}$
has the monotony, type, isomorphism, reduct, renaming properties, and is closed under first-order atomic sentences, negation, conjunction and existential quantification. The finite occurrence property holds by Proposition 3.4(13). By Proposition 3.4(11),
${\mathcal {L}}$
has the monotony, type, isomorphism, reduct, renaming properties, and is closed under first-order atomic sentences, negation, conjunction and existential quantification. The finite occurrence property holds by Proposition 3.4(13). By Proposition 3.4(11),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed. These properties, together with the finite occurrence property, imply the substitution property [Reference Ebbinghaus7, definition 1.2.3]. As a consequence,
$\Delta $
-closed. These properties, together with the finite occurrence property, imply the substitution property [Reference Ebbinghaus7, definition 1.2.3]. As a consequence,
![]() ${\mathcal {L}}$
has elimination of function and constant symbols [Reference Ebbinghaus7, definition 1.2.3 and p. 31]. To prove that
${\mathcal {L}}$
has elimination of function and constant symbols [Reference Ebbinghaus7, definition 1.2.3 and p. 31]. To prove that
![]() ${\mathcal {L}}$
has the relativization property [Reference Ebbinghaus7, definition 1.2.2], we argue as follows: Given sentences
${\mathcal {L}}$
has the relativization property [Reference Ebbinghaus7, definition 1.2.2], we argue as follows: Given sentences
![]() $\phi ,\chi $
, a relativization of
$\phi ,\chi $
, a relativization of
![]() $\phi $
to
$\phi $
to
![]() $\{c\mid \chi (c)\}$
is obtained by assuming
$\{c\mid \chi (c)\}$
is obtained by assuming
![]() $\phi \in {\mathcal {L}}(\tau '),\chi \in {\mathcal {L}}(\tau ")$
for finite types
$\phi \in {\mathcal {L}}(\tau '),\chi \in {\mathcal {L}}(\tau ")$
for finite types
![]() $\tau ',\tau "$
, with
$\tau ',\tau "$
, with
![]() $\tau '$
relational. This assumption is made without loss of generality, because
$\tau '$
relational. This assumption is made without loss of generality, because
![]() ${\mathcal {L}}$
has the finite occurrence property and allows elimination of function and constant symbols. We next let
${\mathcal {L}}$
has the finite occurrence property and allows elimination of function and constant symbols. We next let
![]() $R\notin \tau '\cup \tau "$
be a unary relation symbol. Then Proposition 3.4(14) yields a sentence
$R\notin \tau '\cup \tau "$
be a unary relation symbol. Then Proposition 3.4(14) yields a sentence
![]() $\tilde \psi \in {\mathcal {L}}(\tau '\cup \{R\})$
providing the desired relativization. Replacing now
$\tilde \psi \in {\mathcal {L}}(\tau '\cup \{R\})$
providing the desired relativization. Replacing now
![]() $Rc$
in
$Rc$
in
![]() $\tilde \psi $
by
$\tilde \psi $
by
![]() $\chi (c)$
(which is allowed by the substitution property) we finally obtain a sentence
$\chi (c)$
(which is allowed by the substitution property) we finally obtain a sentence
![]() $\psi \in {\mathcal {L}}(\tau '\cup (\tau "\setminus \{c\}))$
yielding a relativization of
$\psi \in {\mathcal {L}}(\tau '\cup (\tau "\setminus \{c\}))$
yielding a relativization of
![]() $\phi $
to
$\phi $
to
![]() $\{c\mid \chi (c)\}. $
Thus
$\{c\mid \chi (c)\}. $
Thus
![]() ${\mathcal {L}}$
is closed under relativization.
${\mathcal {L}}$
is closed under relativization.
The proof that
![]() ${\mathcal {L}}$
is a regular logic is now complete.
${\mathcal {L}}$
is a regular logic is now complete.
By Proposition 3.4(12),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\operatorname {\mathrm {\kappa {-r.c.}}}$
whenever
$\operatorname {\mathrm {\kappa {-r.c.}}}$
whenever
![]() $\Omega $
contains a
$\Omega $
contains a
![]() $\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter.
$\operatorname {\mathrm {\kappa {-d.i.}}}$
ultrafilter.
To conclude the proof of Theorem 3.1(i), assume
![]() $\Omega $
to be a set, with the intent of proving that its associated logic
$\Omega $
to be a set, with the intent of proving that its associated logic
![]() ${\mathcal {L}}={\mathcal {L}}_\Omega $
is not compact. Without loss of generality, each
${\mathcal {L}}={\mathcal {L}}_\Omega $
is not compact. Without loss of generality, each
![]() $D\in \Omega $
is a uniform ultrafilter over some cardinal
$D\in \Omega $
is a uniform ultrafilter over some cardinal
![]() $\mu _D\geq \omega .$
Let
$\mu _D\geq \omega .$
Let
![]() $\{\mu _D\mid D\in \Omega \}$
be the set of cardinals which are the index set of some ultrafilter in
$\{\mu _D\mid D\in \Omega \}$
be the set of cardinals which are the index set of some ultrafilter in
![]() $\Omega .$
Let
$\Omega .$
Let
We then have
As a consequence, each
![]() $\mu _D$
is small for
$\mu _D$
is small for
![]() $\mu ^*$
, in the sense that for any family
$\mu ^*$
, in the sense that for any family
![]() $\langle \kappa _i\mid i\in I\rangle $
, if
$\langle \kappa _i\mid i\in I\rangle $
, if
![]() $|I|\leq \mu _d$
and
$|I|\leq \mu _d$
and
![]() $\kappa _i<\mu ^*$
for all
$\kappa _i<\mu ^*$
for all
![]() $i\in I,$
then the cardinality of the cartesian product
$i\in I,$
then the cardinality of the cartesian product
![]() $\Pi _{i\in I}\kappa _i$
is
$\Pi _{i\in I}\kappa _i$
is
![]() $<\mu ^*.$
Now let
$<\mu ^*.$
Now let
![]() $\psi ^*\subseteq \operatorname {\mathrm {Str}}(\emptyset )$
be defined by
$\psi ^*\subseteq \operatorname {\mathrm {Str}}(\emptyset )$
be defined by
![]() $\psi ^*=\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\emptyset )\mid |M|\geq \mu ^*\}.$
Thus
$\psi ^*=\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\emptyset )\mid |M|\geq \mu ^*\}.$
Thus
![]() $\psi ^*$
is the class of all structures in the pure identity language, whose universe has at least
$\psi ^*$
is the class of all structures in the pure identity language, whose universe has at least
![]() $\mu ^*$
elements. For every ultrafilter
$\mu ^*$
elements. For every ultrafilter
![]() $D\in \Omega $
, say D over
$D\in \Omega $
, say D over
![]() $\mu _D$
, and for every set
$\mu _D$
, and for every set
![]() $\{{\mathfrak {M}}_\alpha \mid \alpha <\mu _D\}\subseteq \neg \psi ^*$
, the ultraproduct
$\{{\mathfrak {M}}_\alpha \mid \alpha <\mu _D\}\subseteq \neg \psi ^*$
, the ultraproduct
![]() $ \Pi _D\langle {\mathfrak {M}}_\alpha \mid \alpha <\mu _D\rangle $
belongs to
$ \Pi _D\langle {\mathfrak {M}}_\alpha \mid \alpha <\mu _D\rangle $
belongs to
![]() $\neg \psi ^*.$
As a matter of fact, since
$\neg \psi ^*.$
As a matter of fact, since
![]() $\mu _D$
is small for
$\mu _D$
is small for
![]() $\mu ^*$
,
$\mu ^*$
,
Likewise, by [Reference Chang and Keisler4, proposition 4.3.6(ii) and (iv)], for every
![]() $\{{\mathfrak {N}}_\alpha \mid \alpha <\mu _D\}\subseteq \psi ^*$
we have
$\{{\mathfrak {N}}_\alpha \mid \alpha <\mu _D\}\subseteq \psi ^*$
we have
![]() $ \Pi _D\langle {\mathfrak {N}}_\alpha \mid \alpha <\mu _D\rangle \in \psi ^*$
.
$ \Pi _D\langle {\mathfrak {N}}_\alpha \mid \alpha <\mu _D\rangle \in \psi ^*$
.
Thus for every
![]() $D\in \Omega $
both classes
$D\in \Omega $
both classes
![]() $\psi ^*$
and
$\psi ^*$
and
![]() $\neg \psi ^*$
are closed under ultraproducts modulo D. Trivially, both classes are also closed under isomorphisms. By Propositions 3.2(4) and 3.4(1),
$\neg \psi ^*$
are closed under ultraproducts modulo D. Trivially, both classes are also closed under isomorphisms. By Propositions 3.2(4) and 3.4(1),
One now routinely checks that
![]() ${\mathcal {L}}$
is not compact. Let
${\mathcal {L}}$
is not compact. Let
![]() $\tau =\{c_\beta \mid \beta <\mu ^*\}$
. Let
$\tau =\{c_\beta \mid \beta <\mu ^*\}$
. Let
![]() $\Upsilon \subseteq {\mathcal {L}}(\tau )$
be defined by
$\Upsilon \subseteq {\mathcal {L}}(\tau )$
be defined by
where
![]() $c_\alpha \not = c_\beta $
is an abbreviation of the class
$c_\alpha \not = c_\beta $
is an abbreviation of the class
![]() $\{{\mathfrak {N}} \in {\operatorname {\mathrm {Str}}}(\tau ) \mid {\mathfrak {N}} \models c_\alpha \not =c_\beta \}$
. By Proposition 3.2(5) and (7),
$\{{\mathfrak {N}} \in {\operatorname {\mathrm {Str}}}(\tau ) \mid {\mathfrak {N}} \models c_\alpha \not =c_\beta \}$
. By Proposition 3.2(5) and (7),
![]() $\Upsilon \subseteq {\mathcal {L}}(\tau ).$
Furthermore, every finite subfamily of
$\Upsilon \subseteq {\mathcal {L}}(\tau ).$
Furthermore, every finite subfamily of
![]() $\Upsilon $
has a model, but
$\Upsilon $
has a model, but
![]() $\Upsilon $
has none. This proves that
$\Upsilon $
has none. This proves that
![]() ${\mathcal {L}}$
is not compact. The proof of Theorem 3.1(i) is now complete.
${\mathcal {L}}$
is not compact. The proof of Theorem 3.1(i) is now complete.
Proof of Theorem 3.1(ii).
We prepare:
Proposition 3.5. Let
![]() $\kappa $
be an infinite cardinal. Then a topological (not necessarily Hausdorff) space is
$\kappa $
be an infinite cardinal. Then a topological (not necessarily Hausdorff) space is
![]() $[\lambda ,\lambda ]$
-compact for all regular
$[\lambda ,\lambda ]$
-compact for all regular
![]() $\lambda $
with
$\lambda $
with
![]() $\omega \leq \lambda \leq \kappa $
iff every open cover of cardinality
$\omega \leq \lambda \leq \kappa $
iff every open cover of cardinality
![]() $\leq \kappa $
has a finite subcover.
$\leq \kappa $
has a finite subcover.
Proof [Reference Vaughan22, theorem 2A].
Proposition 3.6.
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\operatorname {\mathrm {\kappa {-r.c.}}}$
iff it has the following property:
$\operatorname {\mathrm {\kappa {-r.c.}}}$
iff it has the following property:
For every set J, type
![]() $\tau $
and family
$\tau $
and family
![]() $\{\psi _j\mid j\in J\}\subseteq L(\tau )$
closed under complement (i.e., negation), closed under finite intersections, and containing
$\{\psi _j\mid j\in J\}\subseteq L(\tau )$
closed under complement (i.e., negation), closed under finite intersections, and containing
![]() $EC^\tau _{{\mathcal {L}}_{\omega \omega }}$
, the class
$EC^\tau _{{\mathcal {L}}_{\omega \omega }}$
, the class
![]() $\operatorname {\mathrm {Str}}(\tau )$
is
$\operatorname {\mathrm {Str}}(\tau )$
is
![]() $[\kappa ,\kappa ]$
-compact with respect to the topology generated by the subbase
$[\kappa ,\kappa ]$
-compact with respect to the topology generated by the subbase
![]() $\{\neg \psi _j\mid j\in J\}.$
$\{\neg \psi _j\mid j\in J\}.$
Proof. [Reference Mannila18, theorem 1] which uses a different notation.
Let
![]() $D\in \Omega $
be a uniform ultrafilter over a regular (infinite) cardinal
$D\in \Omega $
be a uniform ultrafilter over a regular (infinite) cardinal
![]() $\nu $
. By [Reference Donder, Jensen, Koppelberg, Jensen and Prestel6, theorem 4.3 and remarks on pages 89–91], D is
$\nu $
. By [Reference Donder, Jensen, Koppelberg, Jensen and Prestel6, theorem 4.3 and remarks on pages 89–91], D is
![]() $\operatorname {\mathrm {\lambda {-d.i.}}}$
for all regular
$\operatorname {\mathrm {\lambda {-d.i.}}}$
for all regular
![]() $\lambda $
with
$\lambda $
with
![]() $\omega \leq \lambda \leq \nu .$
(Here the authors of [Reference Donder, Jensen, Koppelberg, Jensen and Prestel6] make use of the hypotheses
$\omega \leq \lambda \leq \nu .$
(Here the authors of [Reference Donder, Jensen, Koppelberg, Jensen and Prestel6] make use of the hypotheses
![]() $\neg L^\mu $
or
$\neg L^\mu $
or
![]() $0^\sharp .$
) By Proposition 3.4(12),
$0^\sharp .$
) By Proposition 3.4(12),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\operatorname {\mathrm {\lambda {-r.c.}}}$
for all regular
$\operatorname {\mathrm {\lambda {-r.c.}}}$
for all regular
![]() $\lambda $
with
$\lambda $
with
![]() $\omega \leq \lambda \leq \nu .$
Let
$\omega \leq \lambda \leq \nu .$
Let
![]() $\Psi $
be a family of sentences of
$\Psi $
be a family of sentences of
![]() ${\mathcal {L}}(\tau )$
with
${\mathcal {L}}(\tau )$
with
![]() $|\Psi |\leq \nu .$
For each
$|\Psi |\leq \nu .$
For each
![]() $\psi \in \Psi $
let
$\psi \in \Psi $
let
![]() $\dot \psi =\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi. $
Next let us equip
$\dot \psi =\operatorname {\mathrm {{Mod}}}^\tau _{{\mathcal {L}}}\psi. $
Next let us equip
![]() $\operatorname {\mathrm {Str}}(\tau )$
with the topology
$\operatorname {\mathrm {Str}}(\tau )$
with the topology
![]() $\mathcal T$
generated by the subbase
$\mathcal T$
generated by the subbase
Without loss of generality this subbase is closed under finite intersections. By Proposition 3.5, every open cover of
![]() $\operatorname {\mathrm {Str}}(\tau )$
of cardinality
$\operatorname {\mathrm {Str}}(\tau )$
of cardinality
![]() $\leq \nu $
has a finite subcover. By Proposition 3.6,
$\leq \nu $
has a finite subcover. By Proposition 3.6,
![]() $\operatorname {\mathrm {Str}}(\tau )$
is
$\operatorname {\mathrm {Str}}(\tau )$
is
![]() $[\lambda ,\lambda ]$
-compact for all regular
$[\lambda ,\lambda ]$
-compact for all regular
![]() $\lambda $
with
$\lambda $
with
![]() $\omega \leq \lambda \leq \nu .$
Thus, if every finite subfamily of
$\omega \leq \lambda \leq \nu .$
Thus, if every finite subfamily of
![]() $\Psi $
has a model,
$\Psi $
has a model,
![]() $\Psi $
has a model. This proves the first statement in Theorem 3.1(ii).
$\Psi $
has a model. This proves the first statement in Theorem 3.1(ii).
To prove the last statement we argue as follows: From the assumption that
![]() $\Omega $
be a proper class with each
$\Omega $
be a proper class with each
![]() $D\in \Omega $
a uniform ultrafilter over a regular cardinal it follows that the class
$D\in \Omega $
a uniform ultrafilter over a regular cardinal it follows that the class
is proper. The same argument in the first part of the proof now shows that every family
![]() $\Psi \subseteq {\mathcal {L}}(\tau )$
with
$\Psi \subseteq {\mathcal {L}}(\tau )$
with
![]() $|\Psi |\leq \nu $
satisfies the compactness theorem. Since
$|\Psi |\leq \nu $
satisfies the compactness theorem. Since
![]() $\nu $
is an arbitrarily large regular cardinal,
$\nu $
is an arbitrarily large regular cardinal,
![]() ${\mathcal {L}}$
is compact.
${\mathcal {L}}$
is compact.
Having thus proved Theorem 3.1(ii), the proof of Theorem 3.1 is complete.
Corollary 3.7. The logic
![]() ${\mathcal {L}}$
generated by the class
${\mathcal {L}}$
generated by the class
![]() $\Omega ^*$
of all uniform ultrafilters over all infinite cardinals is (equivalent to)
$\Omega ^*$
of all uniform ultrafilters over all infinite cardinals is (equivalent to)
![]() ${\mathcal {L}}_{\omega \omega }.$
${\mathcal {L}}_{\omega \omega }.$
Proof. By Theorem 3.1(i),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\kappa $
-r.c for every regular cardinal
$\kappa $
-r.c for every regular cardinal
![]() $\kappa .$
By Propositions 3.5 and 3.6,
$\kappa .$
By Propositions 3.5 and 3.6,
![]() ${\mathcal {L}}$
is compact. By Proposition 3.4(4)–(10), every elementary class of
${\mathcal {L}}$
is compact. By Proposition 3.4(4)–(10), every elementary class of
![]() ${\mathcal {L}}_{\omega \omega }$
is an elementary class of
${\mathcal {L}}_{\omega \omega }$
is an elementary class of
![]() ${\mathcal {L}}$
. Thus
${\mathcal {L}}$
. Thus
![]() ${\mathcal {L}}$
-equivalence
${\mathcal {L}}$
-equivalence
![]() $\equiv _{{\mathcal {L}}}$
is finer than
$\equiv _{{\mathcal {L}}}$
is finer than
![]() ${\mathcal {L}}_{\omega \omega }$
-equivalence
${\mathcal {L}}_{\omega \omega }$
-equivalence
![]() $\equiv $
. Conversely, let us assume
$\equiv $
. Conversely, let us assume
![]() ${\mathfrak {A}}\equiv \mathfrak B$
. The proof of the Keisler–Shelah theorem [Reference Chang and Keisler4, Theorem 6.1.15] yields
${\mathfrak {A}}\equiv \mathfrak B$
. The proof of the Keisler–Shelah theorem [Reference Chang and Keisler4, Theorem 6.1.15] yields
![]() $\lambda \geq \omega $
and a uniform ultrafilter D over
$\lambda \geq \omega $
and a uniform ultrafilter D over
![]() $\lambda $
such that
$\lambda $
such that
![]() $\Pi _D {\mathfrak {A}}\cong \Pi _D\mathfrak B$
. Since
$\Pi _D {\mathfrak {A}}\cong \Pi _D\mathfrak B$
. Since
![]() $D\in \Omega ^*$
and the elementary classes of
$D\in \Omega ^*$
and the elementary classes of
![]() ${\mathcal {L}}$
are closed under ultrapowers and isomorphisms, Propositions 3.2(3) and 3.4(1) yield
${\mathcal {L}}$
are closed under ultrapowers and isomorphisms, Propositions 3.2(3) and 3.4(1) yield
![]() $ {\mathfrak {A}} \equiv _{{\mathcal {L}}} \Pi _D {\mathfrak {A}} \text { and } \mathfrak B \equiv _{{\mathcal {L}}} \Pi _D \mathfrak B, \text { whence } {\mathfrak {A}} \equiv _{{\mathcal {L}}} \mathfrak B. $
Therefore,
$ {\mathfrak {A}} \equiv _{{\mathcal {L}}} \Pi _D {\mathfrak {A}} \text { and } \mathfrak B \equiv _{{\mathcal {L}}} \Pi _D \mathfrak B, \text { whence } {\mathfrak {A}} \equiv _{{\mathcal {L}}} \mathfrak B. $
Therefore,
![]() $\equiv $
is finer than (whence it coincides with)
$\equiv $
is finer than (whence it coincides with)
![]() $\equiv _{{\mathcal {L}}}$
. The compactness of
$\equiv _{{\mathcal {L}}}$
. The compactness of
![]() ${\mathcal {L}}$
and
${\mathcal {L}}$
and
![]() ${\mathcal {L}}_{\omega \omega }$
now routinely yields the desired conclusion.
${\mathcal {L}}_{\omega \omega }$
now routinely yields the desired conclusion.
4 Applications and examples
Q is a cardinality quantifier if for some ordinal
![]() $\alpha $
$\alpha $
We say that
![]() ${\mathcal {L}}$
is generated by cardinality quantifiers if
${\mathcal {L}}$
is generated by cardinality quantifiers if
![]() ${\mathcal {L}}= {\mathcal {L}}(Q_\alpha )_{\alpha \in W}$
for some nonempty class W of ordinals. We also say that
${\mathcal {L}}= {\mathcal {L}}(Q_\alpha )_{\alpha \in W}$
for some nonempty class W of ordinals. We also say that
![]() ${\mathcal {L}}$
contains the quantifier
${\mathcal {L}}$
contains the quantifier
![]() $Q_\alpha $
if
$Q_\alpha $
if
![]() $EC^\tau _{{\mathcal {L}}}\supseteq EC^\tau _{{\mathcal {L}}(Q)}\,$
for all
$EC^\tau _{{\mathcal {L}}}\supseteq EC^\tau _{{\mathcal {L}}(Q)}\,$
for all
![]() $\tau .$
$\tau .$
Theorem 4.1. Let
![]() $\Omega $
be a class of uniform ultrafilters over infinite cardinals. Assume that either
$\Omega $
be a class of uniform ultrafilters over infinite cardinals. Assume that either
![]() $\Omega $
is a set or
$\Omega $
is a set or
![]() $\,\,\Omega $
contains a countably incomplete ultrafilter. Then the logic
$\,\,\Omega $
contains a countably incomplete ultrafilter. Then the logic
![]() ${\mathcal {L}}$
obtained from
${\mathcal {L}}$
obtained from
![]() $\Omega $
via Theorem 3.1(i) is not generated by cardinality quantifiers.
$\Omega $
via Theorem 3.1(i) is not generated by cardinality quantifiers.
Proof.
The case when
![]() $\Omega $
is a set.
$\Omega $
is a set.
The final part of the proof of Theorem 3.1(i) yields a cardinal
![]() $\mu ^*>\omega $
such that the class
$\mu ^*>\omega $
such that the class
![]() $\psi ^*=\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )\mid |M|\geq \mu ^*\}$
belongs to
$\psi ^*=\{{\mathfrak {M}}\in \operatorname {\mathrm {Str}}(\tau )\mid |M|\geq \mu ^*\}$
belongs to
![]() $EC^\emptyset _{{\mathcal {L}}}$
. See (8). Since
$EC^\emptyset _{{\mathcal {L}}}$
. See (8). Since
![]() ${\mathcal {L}}$
is a
${\mathcal {L}}$
is a
![]() $\Delta $
-closed regular logic with the finite occurrence property then, by [Reference Ebbinghaus7, theorem 4.1.3],
$\Delta $
-closed regular logic with the finite occurrence property then, by [Reference Ebbinghaus7, theorem 4.1.3],
![]() ${\mathcal {L}}$
contains the quantifier
${\mathcal {L}}$
contains the quantifier
![]() $Q^*$
“there are at least
$Q^*$
“there are at least
![]() $\mu ^*$
many.”
$\mu ^*$
many.”
By way of contradiction, assume
![]() ${\mathcal {L}}$
is generated by cardinality quantifiers, say,
${\mathcal {L}}$
is generated by cardinality quantifiers, say,
![]() ${\mathcal {L}}={\mathcal {L}}(Q^*,Q_\alpha )_{\alpha \in W}$
for some class W of ordinals. Let
${\mathcal {L}}={\mathcal {L}}(Q^*,Q_\alpha )_{\alpha \in W}$
for some class W of ordinals. Let
![]() $\mathsf {On}$
be the class of all ordinals, and
$\mathsf {On}$
be the class of all ordinals, and
![]() ${\mathcal {L}}^+= {\mathcal {L}}(Q_\alpha )_{\alpha \in \mathsf {On}}.$
For any
${\mathcal {L}}^+= {\mathcal {L}}(Q_\alpha )_{\alpha \in \mathsf {On}}.$
For any
![]() $\kappa ,\lambda \geq \omega $
let
$\kappa ,\lambda \geq \omega $
let
![]() ${\mathfrak {A}}^\kappa _\lambda =\langle A,E\rangle $
, where E is an equivalence relation over A having exactly
${\mathfrak {A}}^\kappa _\lambda =\langle A,E\rangle $
, where E is an equivalence relation over A having exactly
![]() $\lambda $
distinct equivalence classes, each one of cardinality
$\lambda $
distinct equivalence classes, each one of cardinality
![]() $\kappa .$
The back and forth argument of [Reference Caicedo3, proof of theorem 4.4, p. 93], combined the proof of
$\kappa .$
The back and forth argument of [Reference Caicedo3, proof of theorem 4.4, p. 93], combined the proof of
![]() ${\mathfrak {A}}^{\omega _1}_{\omega _1}\equiv _{{\mathcal {L}}(Q_1)} {\mathfrak {A}}^{\omega _1}_{\omega }$
in [Reference Ebbinghaus7, corollary 4.2.8] yields
${\mathfrak {A}}^{\omega _1}_{\omega _1}\equiv _{{\mathcal {L}}(Q_1)} {\mathfrak {A}}^{\omega _1}_{\omega }$
in [Reference Ebbinghaus7, corollary 4.2.8] yields
Let
![]() $\mathfrak B=\langle {\mathfrak {A}}^{\mu ^*}_{\mu ^*},f\rangle $
, with the unary function f picking one element from every equivalence class. Then
$\mathfrak B=\langle {\mathfrak {A}}^{\mu ^*}_{\mu ^*},f\rangle $
, with the unary function f picking one element from every equivalence class. Then
![]() $ {\mathcal {L}}(E,f)$
contains a sentence
$ {\mathcal {L}}(E,f)$
contains a sentence
![]() $\psi $
stating “the range of f has
$\psi $
stating “the range of f has
![]() $\geq \mu ^*$
elements” with
$\geq \mu ^*$
elements” with
![]() $\mathfrak B\models _{{\mathcal {L}}}\psi .$
Similarly, let
$\mathfrak B\models _{{\mathcal {L}}}\psi .$
Similarly, let
![]() $\mathfrak D=\langle {\mathfrak {A}}^{\mu ^*}_{\omega },g\rangle $
, where g chooses a member of every equivalence class. Then some sentence
$\mathfrak D=\langle {\mathfrak {A}}^{\mu ^*}_{\omega },g\rangle $
, where g chooses a member of every equivalence class. Then some sentence
![]() $\chi \in {\mathcal {L}}(E,g)$
stating “the range of g has
$\chi \in {\mathcal {L}}(E,g)$
stating “the range of g has
![]() $<\mu ^* $
elements” is satisfied by
$<\mu ^* $
elements” is satisfied by
![]() $\mathfrak D$
in
$\mathfrak D$
in
![]() ${\mathcal {L}}$
. Since
${\mathcal {L}}$
. Since
![]() ${\mathcal {L}}$
contains all first-order sentences,
${\mathcal {L}}$
contains all first-order sentences,
![]() ${\mathcal {L}}(E)$
contains a sentence stating “E is an equivalence relation.” Therefore we can safely assume that for every structure
${\mathcal {L}}(E)$
contains a sentence stating “E is an equivalence relation.” Therefore we can safely assume that for every structure
![]() ${\mathfrak {M}}$
of type
${\mathfrak {M}}$
of type
![]() $\{E\}$
exactly one of the following alternatives holds:
$\{E\}$
exactly one of the following alternatives holds:
(i) either
![]() ${\mathfrak {M}}$
can be expanded to a model of
${\mathfrak {M}}$
can be expanded to a model of
![]() $\psi $
of type
$\psi $
of type
![]() $\{f,E\}$
,
$\{f,E\}$
,
(ii) or
![]() ${\mathfrak {M}}$
can be expanded to a model of
${\mathfrak {M}}$
can be expanded to a model of
![]() $\chi $
of type
$\chi $
of type
![]() $\{g,E\}$
.
$\{g,E\}$
.
Upon setting
by Proposition 3.4(1) we obtain
Since
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed, Proposition 3.4(1) yields a sentence
$\Delta $
-closed, Proposition 3.4(1) yields a sentence
![]() $\phi \in {\mathcal {L}}(E)$
such that
$\phi \in {\mathcal {L}}(E)$
such that
This contradicts (9), and settles the case when
![]() $\Omega $
is a set.
$\Omega $
is a set.
The case when
![]() $\Omega $
contains a countably incomplete ultrafilter D.
$\Omega $
contains a countably incomplete ultrafilter D.
Proceeding as in the first case, by way of contradiction assume
![]() ${\mathcal {L}}$
is generated by cardinality quantifiers, say,
${\mathcal {L}}$
is generated by cardinality quantifiers, say,
![]() ${\mathcal {L}}={\mathcal {L}}(Q^*,Q_\alpha )_{\alpha \in W}$
for some nonempty class W of ordinals. Assume D is an ultrafilter over
${\mathcal {L}}={\mathcal {L}}(Q^*,Q_\alpha )_{\alpha \in W}$
for some nonempty class W of ordinals. Assume D is an ultrafilter over
![]() $\mu .$
$\mu .$
Claim. The quantifier
![]() $Q_0$
saying “there are infinitely many” is not contained in
$Q_0$
saying “there are infinitely many” is not contained in
![]() ${\mathcal {L}}$
.
${\mathcal {L}}$
.
As a matter of fact, by [Reference Chang and Keisler4, lemma 4.2.3], our standing hypothesis about D amounts to assuming the existence of a partition
![]() $\tilde X$
of
$\tilde X$
of
![]() $\mu $
into
$\mu $
into
![]() ${<}\omega_1$
components, none of which belongs to D. Now
${<}\omega_1$
components, none of which belongs to D. Now
![]() $\tilde X$
has exactly
$\tilde X$
has exactly
![]() $\omega $
many components, say,
$\omega $
many components, say,
For each
![]() $n<\omega $
let
$n<\omega $
let
![]() ${\mathfrak {M}}_n\in \operatorname {\mathrm {Str}}(\emptyset )$
be such that
${\mathfrak {M}}_n\in \operatorname {\mathrm {Str}}(\emptyset )$
be such that
![]() $M_n$
has exactly
$M_n$
has exactly
![]() $n+1$
elements. For each
$n+1$
elements. For each
![]() $\alpha <\mu $
let
$\alpha <\mu $
let
![]() $n(\alpha )$
be the only
$n(\alpha )$
be the only
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $\alpha \in X_n.$
Let
$\alpha \in X_n.$
Let
From Łoś theorem it follows that the universe N of
![]() ${\mathfrak {N}}$
is infinite. Letting now
${\mathfrak {N}}$
is infinite. Letting now
we have proved that
![]() $\neg \psi $
is not closed under ultraproducts modulo D. From Propositions 3.2(3) and 3.4(1) it follows that
$\neg \psi $
is not closed under ultraproducts modulo D. From Propositions 3.2(3) and 3.4(1) it follows that
![]() $\psi \notin EC^{\emptyset }_{{\mathcal {L}}}$
, whence, a fortiori,
$\psi \notin EC^{\emptyset }_{{\mathcal {L}}}$
, whence, a fortiori,
![]() ${\mathcal {L}}$
does not contain the quantifier
${\mathcal {L}}$
does not contain the quantifier
![]() $Q_0.$
Our claim is thus settled.
$Q_0.$
Our claim is thus settled.
Since
![]() $0\notin W\not =\emptyset $
, there exists an ordinal
$0\notin W\not =\emptyset $
, there exists an ordinal
![]() $\beta>0$
such that
$\beta>0$
such that
![]() ${\mathcal {L}}$
contains the quantifier “there are at least
${\mathcal {L}}$
contains the quantifier “there are at least
![]() $\aleph _\beta $
many.” The argument in the proof of Case 1 yields a contradiction also in the present case.
$\aleph _\beta $
many.” The argument in the proof of Case 1 yields a contradiction also in the present case.
Remark 4.2. Theorem 4.1 shows that for any set
![]() $\Omega $
of uniform ultrafilters the expressive power of the logic
$\Omega $
of uniform ultrafilters the expressive power of the logic
![]() ${\mathcal {L}}$
generated by
${\mathcal {L}}$
generated by
![]() $\Omega $
goes beyond the crude cardinality properties of universes of structures. Specifically, the proof of the first case gives examples of quantifiers, such as equivalence quantifiers, contained in
$\Omega $
goes beyond the crude cardinality properties of universes of structures. Specifically, the proof of the first case gives examples of quantifiers, such as equivalence quantifiers, contained in
![]() ${\mathcal {L}}$
, but not contained in any logic generated by cardinality quantifiers. As an application, from the
${\mathcal {L}}$
, but not contained in any logic generated by cardinality quantifiers. As an application, from the
![]() $\Delta $
-closure property of
$\Delta $
-closure property of
![]() ${\mathcal {L}}$
it follows that in the language
${\mathcal {L}}$
it follows that in the language
![]() $\tau =(\cdot ,^{-1},e)$
of groups one can express in
$\tau =(\cdot ,^{-1},e)$
of groups one can express in
![]() ${\mathcal {L}}$
the fact that the center of a group has
${\mathcal {L}}$
the fact that the center of a group has
![]() ${\geq} \mu ^*$
elements, where
${\geq} \mu ^*$
elements, where
![]() $\mu ^*=(2^\mu )^+$
and
$\mu ^*=(2^\mu )^+$
and
![]() $\mu =\mathrm{sup} \{\mu _D\mid D\in \Omega \}$
. As another application,
$\mu =\mathrm{sup} \{\mu _D\mid D\in \Omega \}$
. As another application,
![]() ${\mathcal {L}}$
can express the fact that a boolean algebra has
${\mathcal {L}}$
can express the fact that a boolean algebra has
![]() ${\geq} \mu ^*$
atoms.
${\geq} \mu ^*$
atoms.
The expressibility of properties increasingly outside the scope of cardinality quantifiers is the subject matter of the following result. We refer to [Reference Ebbinghaus7, definition 4.1.2] and [Reference Mundici19, chapters 1.1 and 2.1] for the well ordering quantifier
![]() $Q^{WO}$
, the Chang quantifier
$Q^{WO}$
, the Chang quantifier
![]() $Q^C$
, the cofinality
$Q^C$
, the cofinality
![]() $\omega $
quantifier
$\omega $
quantifier
![]() $Q^{\mathrm {{cf}}\omega }$
, the Härtig quantifier I, and the Henkin quantifier
$Q^{\mathrm {{cf}}\omega }$
, the Härtig quantifier I, and the Henkin quantifier
![]() $Q^H$
.
$Q^H$
.
Theorem 4.3. Let
![]() $\Omega $
be a class of uniform ultrafilters over infinite cardinals. Let
$\Omega $
be a class of uniform ultrafilters over infinite cardinals. Let
![]() ${\mathcal {L}}$
be the logic generated by
${\mathcal {L}}$
be the logic generated by
![]() $\Omega $
via Theorem 3.1(i). We then have:
$\Omega $
via Theorem 3.1(i). We then have:
-
(i) If every
 $D\in \Omega $
is
$D\in \Omega $
is
 $\omega _1$
-completeFootnote
5
then
$\omega _1$
-completeFootnote
5
then
 ${\mathcal {L}}$
contains all quantifiers
${\mathcal {L}}$
contains all quantifiers
 $Q_0, \,Q_1,\, Q^{WO}$
and
$Q_0, \,Q_1,\, Q^{WO}$
and
 $ Q^{\mathrm {{cf}\omega }}$
.
$ Q^{\mathrm {{cf}\omega }}$
. -
(ii) If some
 $D\in \Omega $
is countably incomplete,Footnote
6
then
$D\in \Omega $
is countably incomplete,Footnote
6
then
 ${\mathcal {L}}$
does not contain the following quantifiers:
${\mathcal {L}}$
does not contain the following quantifiers:
 $Q^{WO}, \,I, \,Q^H, \,Q^C$
, and the quantifier “there are at least
$Q^{WO}, \,I, \,Q^H, \,Q^C$
, and the quantifier “there are at least
 $\lambda $
many” for every
$\lambda $
many” for every
 $\lambda $
satisfying
$\lambda $
satisfying
 $\omega \leq \lambda \leq 2^\omega .$
$\omega \leq \lambda \leq 2^\omega .$
Proof. (i) Following [Reference Chang and Keisler4, p. 231], let
![]() ${\mathcal {L}}_{\omega _1}$
be the logic with countable conjunctions and countable iterations of the universal quantifier, as specified in [Reference Chang and Keisler4, definitions 4.1.9 and 4.1.10, p. 230]. By [Reference Chang and Keisler4, theorem 4.2.11], for every
${\mathcal {L}}_{\omega _1}$
be the logic with countable conjunctions and countable iterations of the universal quantifier, as specified in [Reference Chang and Keisler4, definitions 4.1.9 and 4.1.10, p. 230]. By [Reference Chang and Keisler4, theorem 4.2.11], for every
![]() $D\in \Omega $
and sentence
$D\in \Omega $
and sentence
![]() $\psi \in {\mathcal {L}}_{\omega _1} $
the class
$\psi \in {\mathcal {L}}_{\omega _1} $
the class
![]() $\dot \psi $
of models of
$\dot \psi $
of models of
![]() $\psi $
of type
$\psi $
of type
![]() $\tau $
is closed under ultraproducts modulo D, and so is its complementary class
$\tau $
is closed under ultraproducts modulo D, and so is its complementary class
![]() $\neg \dot \psi = \operatorname {\mathrm {Str}}(\tau )\setminus \dot \psi .$
When
$\neg \dot \psi = \operatorname {\mathrm {Str}}(\tau )\setminus \dot \psi .$
When
![]() $\tau $
is finite, by Propositions 3.2(4) and 3.4(1) we may identify
$\tau $
is finite, by Propositions 3.2(4) and 3.4(1) we may identify
![]() $\dot \psi $
with a sentence of
$\dot \psi $
with a sentence of
![]() ${\mathcal {L}}$
of type
${\mathcal {L}}$
of type
![]() $\tau .$
Now,
$\tau .$
Now,
![]() $Q_0, Q_1, Q^{WO}, Q^{\mathrm {{cf}\omega }}$
are quantifiers of finite type and are contained in the logic
$Q_0, Q_1, Q^{WO}, Q^{\mathrm {{cf}\omega }}$
are quantifiers of finite type and are contained in the logic
![]() ${\mathcal {L}}_{\omega _1}$
. Furthermore,
${\mathcal {L}}_{\omega _1}$
. Furthermore,
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed. Then by [Reference Ebbinghaus7, theorem 4.1.3] all these quantifiers are also contained in
$\Delta $
-closed. Then by [Reference Ebbinghaus7, theorem 4.1.3] all these quantifiers are also contained in
![]() ${\mathcal {L}}$
.
${\mathcal {L}}$
.
(ii) We first show that for every
![]() $\omega \leq \lambda \leq 2^\omega $
,
$\omega \leq \lambda \leq 2^\omega $
,
![]() ${\mathcal {L}}$
does not contain the quantifier “there are at least
${\mathcal {L}}$
does not contain the quantifier “there are at least
![]() $\lambda $
many.”
$\lambda $
many.”
The proof of the second case in Theorem 4.1 shows that
![]() ${\mathcal {L}}$
does not contain
${\mathcal {L}}$
does not contain
![]() $Q_0$
. Next let Q be the quantifier “there are at least
$Q_0$
. Next let Q be the quantifier “there are at least
![]() $\xi $
many,” with
$\xi $
many,” with
![]() $\omega _1\leq \xi \leq 2^\omega .$
By [Reference Chang and Keisler4, propositions 4.3.4 and 4.3.9],
$\omega _1\leq \xi \leq 2^\omega .$
By [Reference Chang and Keisler4, propositions 4.3.4 and 4.3.9],
![]() $|\Pi _D\omega |\geq 2^\omega $
whenever D is countably incomplete. Since
$|\Pi _D\omega |\geq 2^\omega $
whenever D is countably incomplete. Since
![]() $\omega <\xi $
and
$\omega <\xi $
and
![]() $|\Pi _D\omega |\geq \xi ,$
letting
$|\Pi _D\omega |\geq \xi ,$
letting
it follows that the class
![]() $\neg \psi $
is not closed under ultraproducts modulo D, whence, by Propositions 3.2(3) and 3.4(1),
$\neg \psi $
is not closed under ultraproducts modulo D, whence, by Propositions 3.2(3) and 3.4(1),
![]() $\psi \notin EC^\emptyset _{{\mathcal {L}}}$
, and Q is not contained in
$\psi \notin EC^\emptyset _{{\mathcal {L}}}$
, and Q is not contained in
![]() ${\mathcal {L}}.$
${\mathcal {L}}.$
It is not hard to see that
![]() ${\mathcal {L}}$
does not contain
${\mathcal {L}}$
does not contain
![]() $Q^{WO}$
. For otherwise (absurdum hypothesis), let
$Q^{WO}$
. For otherwise (absurdum hypothesis), let
![]() ${\mathcal {L}}'=\Delta {\mathcal {L}}(Q^{WO})$
be the smallest
${\mathcal {L}}'=\Delta {\mathcal {L}}(Q^{WO})$
be the smallest
![]() $\Delta $
-closed logic containing
$\Delta $
-closed logic containing
![]() ${\mathcal {L}}(Q^{WO})$
. Then all
${\mathcal {L}}(Q^{WO})$
. Then all
![]() ${\mathcal {L}}'$
-elementary classes are in
${\mathcal {L}}'$
-elementary classes are in
![]() ${\mathcal {L}},$
because also
${\mathcal {L}},$
because also
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\Delta $
-closed. Consequently,
$\Delta $
-closed. Consequently,
![]() ${\mathcal {L}}'$
contains
${\mathcal {L}}'$
contains
![]() $Q_0$
, because a set is finite iff it can be endowed with a well ordering R such that the reverse ordering
$Q_0$
, because a set is finite iff it can be endowed with a well ordering R such that the reverse ordering
![]() $R^{\leftarrow }$
is also a well ordering, and a set is infinite iff it can be equipped with a non-well-ordered linear ordering. It follows that
$R^{\leftarrow }$
is also a well ordering, and a set is infinite iff it can be equipped with a non-well-ordered linear ordering. It follows that
![]() ${\mathcal {L}}$
, too, contains
${\mathcal {L}}$
, too, contains
![]() $Q_0$
, a contradiction.
$Q_0$
, a contradiction.
One similarly shows that
![]() ${\mathcal {L}}$
does not contain
${\mathcal {L}}$
does not contain
![]() $Q^C$
, because
$Q^C$
, because
![]() $\Delta {\mathcal {L}}(Q^C)$
contains
$\Delta {\mathcal {L}}(Q^C)$
contains
![]() $Q_0.$
Finally,
$Q_0.$
Finally,
![]() ${\mathcal {L}}$
does not contain I and
${\mathcal {L}}$
does not contain I and
![]() $Q^H$
because
$Q^H$
because
![]() $\Delta {\mathcal {L}}(I)$
contains
$\Delta {\mathcal {L}}(I)$
contains
![]() $Q^{WO}$
and
$Q^{WO}$
and
![]() $\Delta {\mathcal {L}}(Q^H)$
contains
$\Delta {\mathcal {L}}(Q^H)$
contains
![]() $Q_0$
. (See [Reference Ebbinghaus7, sections 2.3 and 2.5] and [Reference Mundici19].)
$Q_0$
. (See [Reference Ebbinghaus7, sections 2.3 and 2.5] and [Reference Mundici19].)
Corollary 4.4. Let
![]() $\Omega $
be a nonempty class of uniform ultrafilters over infinite cardinals. Let
$\Omega $
be a nonempty class of uniform ultrafilters over infinite cardinals. Let
![]() ${\mathcal {L}}$
be the logic generated by
${\mathcal {L}}$
be the logic generated by
![]() $\Omega $
via Theorem 3.1(i). Then the following conditions are equivalent:
$\Omega $
via Theorem 3.1(i). Then the following conditions are equivalent:
-
(i) Each
 $D\in \Omega $
is
$D\in \Omega $
is
 $\omega _1$
-complete.
$\omega _1$
-complete. -
(ii)
 ${\mathcal {L}}$
contains
${\mathcal {L}}$
contains
 $Q_0.$
$Q_0.$
-
(iii)
 ${\mathcal {L}}$
contains
${\mathcal {L}}$
contains
 $Q_1.$
$Q_1.$
-
(iv)
 ${\mathcal {L}}$
contains
${\mathcal {L}}$
contains
 $Q^{WO}.$
$Q^{WO}.$
-
(v)
 ${\mathcal {L}}$
is not
${\mathcal {L}}$
is not
 $\omega $
-relatively compact.
$\omega $
-relatively compact.
Proof. Theorem 4.3 immediately yields the equivalences
![]() $ \textrm{(i)}\Leftrightarrow \textrm{(ii)}\Leftrightarrow \textrm{(iii)} \Leftrightarrow \textrm{(iv)}.$
One easily proves the implication (ii)
$ \textrm{(i)}\Leftrightarrow \textrm{(ii)}\Leftrightarrow \textrm{(iii)} \Leftrightarrow \textrm{(iv)}.$
One easily proves the implication (ii)
![]() $\Rightarrow $
(v). Finally, to prove (v)
$\Rightarrow $
(v). Finally, to prove (v)
![]() $\Rightarrow $
(i), let us suppose that
$\Rightarrow $
(i), let us suppose that
![]() $D\in \Omega $
is not
$D\in \Omega $
is not
![]() $\omega _1$
-complete. In other words, D is countably incomplete, in the sense that there is a countable set
$\omega _1$
-complete. In other words, D is countably incomplete, in the sense that there is a countable set
![]() $E\subseteq D$
such that
$E\subseteq D$
such that
![]() $\bigcap E\notin D.$
(See [Reference Chang and Keisler4, definition 4.3.1, p. 248].) Equivalently, D is
$\bigcap E\notin D.$
(See [Reference Chang and Keisler4, definition 4.3.1, p. 248].) Equivalently, D is
![]() $\omega $
-d.i. To see this, recall [Reference Kunen and Prikry13, definition 0.1] and [Reference Chang and Keisler4, exercise 4.3.10, p. 258]. By Theorem 3.1(i),
$\omega $
-d.i. To see this, recall [Reference Kunen and Prikry13, definition 0.1] and [Reference Chang and Keisler4, exercise 4.3.10, p. 258]. By Theorem 3.1(i),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\omega $
-r.c., whence (v) fails.
$\omega $
-r.c., whence (v) fails.
The following proposition shows that Theorem 3.1(ii) no longer holds without the special hypotheses
![]() $\neg 0^\sharp $
or
$\neg 0^\sharp $
or
![]() $\neg L^\mu $
. It also shows that, assuming the existence of a proper class of measurable cardinals, not all proper classes of uniform ultrafilters over regular cardinals generate
$\neg L^\mu $
. It also shows that, assuming the existence of a proper class of measurable cardinals, not all proper classes of uniform ultrafilters over regular cardinals generate
![]() ${\mathcal {L}}_{\omega \omega }$
. By Theorem 3.1(i), no non-proper class generates
${\mathcal {L}}_{\omega \omega }$
. By Theorem 3.1(i), no non-proper class generates
![]() ${\mathcal {L}}_{\omega \omega }$
.
${\mathcal {L}}_{\omega \omega }$
.
Corollary 4.5. If there is a proper class of measurable cardinals then some proper class of uniform ultrafilters over regular cardinals generates a noncompact logic.
Proof. Let
![]() $\{\mu _i\mid j\in W\}$
be a proper class of measurable cardinals. Let
$\{\mu _i\mid j\in W\}$
be a proper class of measurable cardinals. Let
![]() $ \Omega =\{D_j\mid j\in W\} $
be a class where each
$ \Omega =\{D_j\mid j\in W\} $
be a class where each
![]() $D_j$
is a
$D_j$
is a
![]() $\mu _j$
-complete nonprincipal ultrafilter over
$\mu _j$
-complete nonprincipal ultrafilter over
![]() $\mu _j$
. By [Reference Chang and Keisler4, theorem 4.2.14(i)], for each
$\mu _j$
. By [Reference Chang and Keisler4, theorem 4.2.14(i)], for each
![]() $j\in W$
the ultrafilter
$j\in W$
the ultrafilter
![]() $D_j$
is uniform and
$D_j$
is uniform and
![]() $\omega _1$
-complete, and
$\omega _1$
-complete, and
![]() $\mu _j$
is regular. By Corollary 4.4(i)
$\mu _j$
is regular. By Corollary 4.4(i)
![]() $\Rightarrow $
(ii), the logic
$\Rightarrow $
(ii), the logic
![]() ${\mathcal {L}}$
generated by
${\mathcal {L}}$
generated by
![]() $\Omega $
is not compact.
$\Omega $
is not compact.
Remark 4.6. By Corollary 3.7,
![]() ${\mathcal {L}}_{\omega \omega }$
is generated (via Theorem 3.1(i)) by some proper class of all uniform ultrafilters over regular cardinals. Let
${\mathcal {L}}_{\omega \omega }$
is generated (via Theorem 3.1(i)) by some proper class of all uniform ultrafilters over regular cardinals. Let
![]() $\mathsf {A}$
be short hand for the following statement:
$\mathsf {A}$
be short hand for the following statement:
Next let
![]() $\mathsf B$
stand for “Every uniform ultrafilter is regular.” The existence of a measurable cardinal entails
$\mathsf B$
stand for “Every uniform ultrafilter is regular.” The existence of a measurable cardinal entails
![]() $\neg \mathsf B.$
Footnote
7
On the other hand, Donder [Reference Donder5] proved that
$\neg \mathsf B.$
Footnote
7
On the other hand, Donder [Reference Donder5] proved that
![]() $\mathsf B$
is consistent relative to ZFC. Finally, let
$\mathsf B$
is consistent relative to ZFC. Finally, let
![]() $\mathsf C$
be an abbreviation of Conjecture 18 in [Reference Chang and Keisler4, p. 599], which reads:
$\mathsf C$
be an abbreviation of Conjecture 18 in [Reference Chang and Keisler4, p. 599], which reads:
“Let
![]() ${\mathfrak {A}},\, \mathfrak B\in \operatorname {\mathrm {Str}}(\tau )$
with
${\mathfrak {A}},\, \mathfrak B\in \operatorname {\mathrm {Str}}(\tau )$
with
![]() ${\mathfrak {A}}\,\equiv \,\mathfrak B$
, and
${\mathfrak {A}}\,\equiv \,\mathfrak B$
, and
![]() $|A|,\,|B|,\,|\tau |,\, \omega \leq \kappa $
.
$|A|,\,|B|,\,|\tau |,\, \omega \leq \kappa $
.
Then
![]() $\Pi _D{\mathfrak {A}}\,\cong \, \Pi _D\mathfrak B,$
for every regular ultrafilter D over
$\Pi _D{\mathfrak {A}}\,\cong \, \Pi _D\mathfrak B,$
for every regular ultrafilter D over
![]() $\kappa .$
”
$\kappa .$
”
Theorem 4.7.
![]() $\mathsf {B} \& \mathsf {C}\Rightarrow \mathsf {A} \Rightarrow $
“there is no proper class of measurable cardinals.”
$\mathsf {B} \& \mathsf {C}\Rightarrow \mathsf {A} \Rightarrow $
“there is no proper class of measurable cardinals.”
Proof. The second implication follows from Corollary 4.5. For the first implication, assume
![]() $ \mathsf {B}$
and
$ \mathsf {B}$
and
![]() $ \mathsf {C}$
to hold. For
$ \mathsf {C}$
to hold. For
![]() $\Omega $
an arbitrary proper class of uniform ultrafilters over regular cardinals, let
$\Omega $
an arbitrary proper class of uniform ultrafilters over regular cardinals, let
![]() ${\mathcal {L}}$
be the logic generated by
${\mathcal {L}}$
be the logic generated by
![]() $\Omega $
via Theorem 3.1(i). Since all elementary classes of
$\Omega $
via Theorem 3.1(i). Since all elementary classes of
![]() ${\mathcal {L}}_{\omega \omega }$
are in
${\mathcal {L}}_{\omega \omega }$
are in
![]() ${\mathcal {L}}$
, then for all structures
${\mathcal {L}}$
, then for all structures
![]() ${\mathfrak {A}}, \mathfrak B$
of type
${\mathfrak {A}}, \mathfrak B$
of type
![]() $\tau $
,
$\tau $
,
Conversely, we claim that
![]() $\equiv $
is finer than
$\equiv $
is finer than
![]() $\equiv _{{\mathcal {L}}}.$
As a matter of fact, assume
$\equiv _{{\mathcal {L}}}.$
As a matter of fact, assume
![]() ${\mathfrak {A}}\equiv \mathfrak B$
. Since
${\mathfrak {A}}\equiv \mathfrak B$
. Since
![]() $\Omega $
is a proper class there is
$\Omega $
is a proper class there is
![]() $D\in \Omega $
and
$D\in \Omega $
and
![]() $\kappa \geq \omega $
such that D is a uniform ultrafilter over
$\kappa \geq \omega $
such that D is a uniform ultrafilter over
![]() $\kappa $
, and
$\kappa $
, and
![]() $|A|, \,|B|, \, |\tau | \leq \kappa .$
Assumption
$|A|, \,|B|, \, |\tau | \leq \kappa .$
Assumption
![]() $\mathsf B$
ensures that D is regular. Assumption
$\mathsf B$
ensures that D is regular. Assumption
![]() $\mathsf C$
yields
$\mathsf C$
yields
![]() $\Pi _D{\mathfrak {A}}\cong \Pi _D\mathfrak B.$
By Propositions 3.2(3) and 3.4(1), every elementary class of
$\Pi _D{\mathfrak {A}}\cong \Pi _D\mathfrak B.$
By Propositions 3.2(3) and 3.4(1), every elementary class of
![]() ${\mathcal {L}}$
is closed under isomorphisms and ultrapowers. Therefore,
${\mathcal {L}}$
is closed under isomorphisms and ultrapowers. Therefore,
whence
![]() $\equiv $
is finer than
$\equiv $
is finer than
![]() $\equiv _{{\mathcal {L}}}$
, as required to settle our claim. Having thus proved
$\equiv _{{\mathcal {L}}}$
, as required to settle our claim. Having thus proved
there remains to prove that
![]() ${\mathcal {L}}$
is equivalent to
${\mathcal {L}}$
is equivalent to
![]() ${\mathcal {L}}_{\omega \omega }.$
Trivially,
${\mathcal {L}}_{\omega \omega }.$
Trivially,
![]() ${\mathcal {L}}$
cannot contain the quantifier
${\mathcal {L}}$
cannot contain the quantifier
![]() $Q_0$
. For otherwise, some sentence in the pure identity language of
$Q_0$
. For otherwise, some sentence in the pure identity language of
![]() ${\mathcal {L}}$
could distinguish between finite and infinite sets, against (10). By Corollary 4.4(v)
${\mathcal {L}}$
could distinguish between finite and infinite sets, against (10). By Corollary 4.4(v)
![]() $\Rightarrow $
(ii),
$\Rightarrow $
(ii),
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $\omega $
-relatively compact. As a consequence, every countable set of sentences of
$\omega $
-relatively compact. As a consequence, every countable set of sentences of
![]() ${\mathcal {L}}$
has the compactness property. In other words,
${\mathcal {L}}$
has the compactness property. In other words,
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() $[\omega , \omega ]$
-compact. From (10) it follows that
$[\omega , \omega ]$
-compact. From (10) it follows that
![]() ${\mathcal {L}}$
has the Löwenheim property [Reference Ebbinghaus7, 1.2.4(vii)], stating that every sentence
${\mathcal {L}}$
has the Löwenheim property [Reference Ebbinghaus7, 1.2.4(vii)], stating that every sentence
![]() $\psi $
of
$\psi $
of
![]() ${\mathcal {L}}$
having an infinite model has a countable model. By Lindström’s characterization theorem ([Reference Lindström14] or [Reference Flum9, theorem 2.1.4]), first-order logic is the only
${\mathcal {L}}$
having an infinite model has a countable model. By Lindström’s characterization theorem ([Reference Lindström14] or [Reference Flum9, theorem 2.1.4]), first-order logic is the only
![]() $[\omega ,\omega ]$
-compact logic having the Löwenheim property, in the sense that every sentence
$[\omega ,\omega ]$
-compact logic having the Löwenheim property, in the sense that every sentence
![]() $\psi $
of
$\psi $
of
![]() ${\mathcal {L}}$
having an infinite model has a countable model. Thus
${\mathcal {L}}$
having an infinite model has a countable model. Thus
![]() ${\mathcal {L}}$
is equivalent to
${\mathcal {L}}$
is equivalent to
![]() ${\mathcal {L}}_{\omega \omega }$
, as desired.
${\mathcal {L}}_{\omega \omega }$
, as desired.
Corollary 4.8. In the core model,
![]() $\mathsf C$
implies
$\mathsf C$
implies
![]() $ \mathsf A.$
$ \mathsf A.$
Proof. In the core model, every uniform ultrafilter is regular [Reference Donder5, sec. 4]. Now apply Theorem 4.7.
Acknowledgements
The author gratefully acknowledges the referee’s careful reading of this paper, and valuable suggestions for improvement.