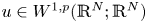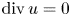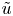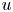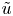1. Introduction
1.1. Lipschitz extensions and truncations
A technique that is important both in functional analytic results and in applications to partial differential equations (PDEs) is Lipschitz extension. More precisely, consider a metric space $(X,\,d)$![]() , a closed subset $Y \subset X$
, a closed subset $Y \subset X$![]() and a function $u \colon Y \to \mathbb {R}^d$
and a function $u \colon Y \to \mathbb {R}^d$![]() that is Lipschitz continuous, i.e. there is $L>0$
that is Lipschitz continuous, i.e. there is $L>0$![]() such that
such that
The aim of Lipschitz extension is to find a function $\tilde {u} \colon X \to \mathbb {R}^d$![]() that coincides with $u$
that coincides with $u$![]() on $Y$
on $Y$![]() and still is Lipschitz continuous on $X$
and still is Lipschitz continuous on $X$![]() with the same Lipschitz constant (or a constant that is only worse by some additional multiplicative constant). Such an extension result has been achieved by McShane and Kirszbraun [Reference Kirszbraun25, Reference McShane27] and, in a slightly different setting, by Whitney [Reference Stein33, Reference Whitney34].
with the same Lipschitz constant (or a constant that is only worse by some additional multiplicative constant). Such an extension result has been achieved by McShane and Kirszbraun [Reference Kirszbraun25, Reference McShane27] and, in a slightly different setting, by Whitney [Reference Stein33, Reference Whitney34].
In contrast, the task for truncation is as follows. Given $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$![]() , $1\leq p <\infty$
, $1\leq p <\infty$![]() and $L>0$
and $L>0$![]() , find $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^d)$
, find $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^d)$![]() , such that
, such that
(T1’) $\Vert D \tilde {u} \Vert _{L^{\infty }} \leq C(d) L$
 for a dimensional constant $C(d)$
for a dimensional constant $C(d)$ .
.(T2’) $u$
 and $\tilde {u}$
and $\tilde {u}$ coincide on a set of large measure.
coincide on a set of large measure.
The most common approach to this truncation is to redefine the function $u$![]() on a rather small set by using aforementioned Lipschitz extension. The basis for this work is the extension due to Whitney [Reference Whitney34], which has been adapted and refined for truncations in [Reference Acerbi and Fusco1, Reference Acerbi and Fusco2, Reference Diening, Málek and Steinhauer15, Reference Zhang35].
on a rather small set by using aforementioned Lipschitz extension. The basis for this work is the extension due to Whitney [Reference Whitney34], which has been adapted and refined for truncations in [Reference Acerbi and Fusco1, Reference Acerbi and Fusco2, Reference Diening, Málek and Steinhauer15, Reference Zhang35].
There are different ways to quantify (T2’). The first option is
(T2a’) $\mathcal {L}^N(\{ u \neq \tilde {u}\}) \leq C(d)L^{-p} \Vert u \Vert _{W^{1,p}}^p$
 ,
,
whereas another option is
(T2b’) $\mathcal {L}^N(\{ u \neq \tilde {u}\}) \leq C(d)L^{-p} \displaystyle\int _{\{\vert u \vert + \vert Du\vert \geq L\}} \vert u \vert ^p + \vert D u \vert ^p \,\mathrm {d} x$
 .
.
We explain the merits of (T2a’) and (T2b’) later (cf. §§ 1.3), but obviously (T2b’) is stronger than (T2a’).
From (T2b’) we may indeed infer a bound of the $W^{1,p}$![]() -distance between $u$
-distance between $u$![]() and $\tilde {u}$
and $\tilde {u}$![]() (e.g. [Reference Zhang35]), namely that
(e.g. [Reference Zhang35]), namely that
for (T2a’) at least the $W^{1,r}$![]() -distance, $r< p$
-distance, $r< p$![]() can be effectively bounded.
can be effectively bounded.
It is worth mentioning, that for sequences of functions $u_n$![]() there is an even stronger statement (both improving (T1’) and (T2b’)) that not only bounds the $L^p$
there is an even stronger statement (both improving (T1’) and (T2b’)) that not only bounds the $L^p$![]() distance, but already the $L^{\infty }$
distance, but already the $L^{\infty }$![]() -distance (cf. [Reference Müller28]), i.e.
-distance (cf. [Reference Müller28]), i.e.
(T2c’) Suppose that $K\subset \mathbb {R}^{N \times d}$
 compact and convex and that $u_n \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$
compact and convex and that $u_n \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$ is such that $\operatorname {dist}(Du_n,\,K) \to 0$
is such that $\operatorname {dist}(Du_n,\,K) \to 0$ in $L^p$
in $L^p$ . Then there is $\tilde {u}_n$
. Then there is $\tilde {u}_n$ , such that $\tilde {u}_n-u_n \to 0$
, such that $\tilde {u}_n-u_n \to 0$ in $W^{1,p}$
in $W^{1,p}$ and $\operatorname {dist}(D\tilde {u}_n,\,K) \to 0$
and $\operatorname {dist}(D\tilde {u}_n,\,K) \to 0$ in $L^{\infty }$
in $L^{\infty }$ .
.
1.2. Solenoidal truncation and the main statement
We might be presented with an additional requirement that $u$![]() is divergence-free, for example if $u$
is divergence-free, for example if $u$![]() is the velocity of an incompressible flow. The truncated version $\tilde {u}$
is the velocity of an incompressible flow. The truncated version $\tilde {u}$![]() then also shall satisfy this differential constraint. In particular, in this work we give a proof to the following theorem that shows that a truncation satisfying (T1’) and (T2b’) is possible in a divergence-free setting.
then also shall satisfy this differential constraint. In particular, in this work we give a proof to the following theorem that shows that a truncation satisfying (T1’) and (T2b’) is possible in a divergence-free setting.
Theorem 1.1 Let $N \geq 2$![]() and suppose that $1 \leq p <\infty$
and suppose that $1 \leq p <\infty$![]() , $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^N)$
, $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^N)$![]() obeys $\operatorname {div} u=0$
obeys $\operatorname {div} u=0$![]() and that $L>0$
and that $L>0$![]() . There is a (dimensional) constant $C>0$
. There is a (dimensional) constant $C>0$![]() and a function $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^N)$
and a function $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^N)$![]() , such that
, such that
(T1) $\Vert \tilde {u} \Vert _{W^{1,\infty }} \leq CL$
 ;
;(T2) $\mathcal {L}^N(\{ u \neq \tilde {u}\}) \leq C(d)L^{-p} \int _{\{ \vert u \vert + \vert Du\vert \geq L\}} \vert u \vert + \vert D u \vert \,\mathrm {d} x$
 ;
;(T3) $\operatorname {div} \tilde {u} =0$
 .
.
It should be mentioned that (although not explicitly stated in this form), theorem 1.1 was already established by Breit, Diening & Fuchs [Reference Breit, Diening and Fuchs7]. We, however, give a different, more geometric construction of the function $\tilde {u}$![]() in theorem 1.1. We further comment about the applications in the following §§ 1.3. First, we give some variants of theorem 1.1.
in theorem 1.1. We further comment about the applications in the following §§ 1.3. First, we give some variants of theorem 1.1.
Remark 1.2
(i) If (T2) is replaced by (T2a’) and $p>1$
 , then [Reference Breit, Diening and Schwarzacher9, Section 4] offers a quite elegant truncation using that $\operatorname {div} u =0$
, then [Reference Breit, Diening and Schwarzacher9, Section 4] offers a quite elegant truncation using that $\operatorname {div} u =0$ is (essentially) equivalent to $u = \operatorname {curl} v$
is (essentially) equivalent to $u = \operatorname {curl} v$ for a suitable $v$
for a suitable $v$ in space dimension three. The approach of [Reference Breit, Diening and Schwarzacher9] is then further adapted to evolutionary problems, where one, in addition, needs to take care of the time derivative. In the present work, we stick to the simpler stationary framework.
in space dimension three. The approach of [Reference Breit, Diening and Schwarzacher9] is then further adapted to evolutionary problems, where one, in addition, needs to take care of the time derivative. In the present work, we stick to the simpler stationary framework.(ii) In principle, the approach pursued here might be applied to solenoidal maps on (orientable) manifolds. As already an unconstrained truncation for maps on manifolds faces some challenges (cf. [Reference Roberts and Schmeding31]), we however only consider $\mathbb {R}^N$
 .
.(iii) One may get the result mentioned in theorem 1.1 not only for $u$
 satisfying $\operatorname {div} u=0$
satisfying $\operatorname {div} u=0$ , but, in more generality, for differential forms $v \colon \mathbb {R}^N \to \Lambda ^r$
, but, in more generality, for differential forms $v \colon \mathbb {R}^N \to \Lambda ^r$ that satisfy $dv=0$
that satisfy $dv=0$ , where $d$
, where $d$ denotes the exterior derivative. We refer to §§ 4.1 and proposition 4.1 for further discussion.
denotes the exterior derivative. We refer to §§ 4.1 and proposition 4.1 for further discussion.(iv) The statement of theorem 1.1 is also relevant for different regularities (e.g. $L^{\infty }$
 - instead of $W^{1,\infty }$
- instead of $W^{1,\infty }$ ), cf. [Reference Behn, Gmeineder and Schiffer5, Reference Schiffer32] for a discussion of (T2b’) and [Reference Gallenmüller21, Reference Gallenmüller and Wiedemann22] for a discussion of (T2c’) in that setting.
), cf. [Reference Behn, Gmeineder and Schiffer5, Reference Schiffer32] for a discussion of (T2b’) and [Reference Gallenmüller21, Reference Gallenmüller and Wiedemann22] for a discussion of (T2c’) in that setting.(v) In principle, it is also imaginable to construct a divergence-free truncation on bounded domains that additionally preserves boundary values (cf. [Reference Friesecke, James and Müller20] in an unconstrained static setting and [Reference Diening, Schwarzacher, Stroffolini and Verde17] for parabolic problems).
We explain the different approaches to proving a statement in the style of theorem 1.1 in § 2. As mentioned in the remark, in [Reference Breit, Diening and Schwarzacher9] the authors use that divergence-free functions $u$![]() may be written as $u =\operatorname {curl} v$
may be written as $u =\operatorname {curl} v$![]() and then perform a higher-order truncation on $v$
and then perform a higher-order truncation on $v$![]() . Our approach is, however, much closer to the treatment by Breit, Diening & Fuchs, [Reference Breit, Diening and Fuchs7]. There, the truncation is defined as a modification of the usual Lipschitz truncation. First, one truncates as if the additional constraint $\operatorname {div} u =0$
. Our approach is, however, much closer to the treatment by Breit, Diening & Fuchs, [Reference Breit, Diening and Fuchs7]. There, the truncation is defined as a modification of the usual Lipschitz truncation. First, one truncates as if the additional constraint $\operatorname {div} u =0$![]() is not present and then adds small modifications/corrections to return to solenoidal functions. In [Reference Breit, Diening and Fuchs7] this is achieved by application of the Bogovskiĭ-operator (cf. [Reference Bogovskiĭ6]). In the present work we propose to use some structure coming from the definition of the truncation and explicitly give a quite elementary definition of a local correction. The connection between both approaches might be seen through a careful definition of the Bogovskiĭ-operator for a special class of functions, also cf. [Reference Costabel and McIntosh12].
is not present and then adds small modifications/corrections to return to solenoidal functions. In [Reference Breit, Diening and Fuchs7] this is achieved by application of the Bogovskiĭ-operator (cf. [Reference Bogovskiĭ6]). In the present work we propose to use some structure coming from the definition of the truncation and explicitly give a quite elementary definition of a local correction. The connection between both approaches might be seen through a careful definition of the Bogovskiĭ-operator for a special class of functions, also cf. [Reference Costabel and McIntosh12].
1.3. Solenoidal truncation and its applications
While seemingly being only a technical lemma, adaptations of theorem 1.1 have a variety of applications in the calculus of variations and partial differential equations. First and foremost, solenoidal Lipschitz truncation and its generalizations to parabolic (i.e. time-dependent) problems are used to get existence results for non-linear problems, in particular for viscous fluid mechanics. e.g. [Reference Breit, Diening and Fuchs7, Reference Breit, Diening and Schwarzacher9, Reference Diening, Málek and Steinhauer15, Reference Diening, Ružička and Wolf16, Reference Frehse, Málek and Steinhauer19] and [Reference Bäumle and Růžička4, Reference Breit, Diening and Schwarzacher9, Reference Bulíček, Burczak and Schwarzacher11, Reference Diening, Kreuzer and Süli14] for further refinements. The strategy roughly is as follows. The non-linear problem is approximated by a sequence of problems solvable with classical methods (e.g. monotonicity method) that have solutions $u_n$![]() . The issue is the incompatibility of the nonlinearity (let us call it $f$
. The issue is the incompatibility of the nonlinearity (let us call it $f$![]() ) with weak convergence, i.e. if $u_n \rightharpoonup u$
) with weak convergence, i.e. if $u_n \rightharpoonup u$![]() , then in general $f(u_n)$
, then in general $f(u_n)$![]() does not converge weakly to $f(u)$
does not converge weakly to $f(u)$![]() . Recall that there are usually effects of concentrations and oscillations present in weakly converging sequences. While oscillations do not fare well with nonlinearities, concentrations do. As a consequence, Lipschitz truncation cuts away concentrations and allows us to focus on oscillation effects (and show that these do not exist). Therefore, one concludes $f(u_n) \rightharpoonup f(u)$
. Recall that there are usually effects of concentrations and oscillations present in weakly converging sequences. While oscillations do not fare well with nonlinearities, concentrations do. As a consequence, Lipschitz truncation cuts away concentrations and allows us to focus on oscillation effects (and show that these do not exist). Therefore, one concludes $f(u_n) \rightharpoonup f(u)$![]() .
.
Consequently, especially for the (non-Newtonian) Navier–Stokes equations (cf. [Reference Breit, Diening and Fuchs7, Reference Breit, Diening and Schwarzacher9, Reference Diening, Ružička and Wolf16]), where one expects concentration effects for a sequence $u_n$![]() (also see the survey [Reference Buckmaster and Vicol10]), it is clear that truncation property (T2a’) is enough. In particular, when considering such a sequence $u_n$
(also see the survey [Reference Buckmaster and Vicol10]), it is clear that truncation property (T2a’) is enough. In particular, when considering such a sequence $u_n$![]() , for fixed $L>0$
, for fixed $L>0$![]() , we do not have
, we do not have
so, in such a context, (T2a’) and (T2b’) do not offer a qualitative difference, and so (T2a’) is sufficient (eg. [Reference Breit, Diening and Schwarzacher9]). That theorem 1.1 is proven in [Reference Breit, Diening and Fuchs7] with (T2b’) instead of (T2a’) is, in that context, only an interesting byproduct.
It should also be mentioned that the time-dependent case (cf. [Reference Breit, Diening and Schwarzacher9]) features an additional challenge compared to the present stationary setting (cf. [Reference Breit, Diening and Fuchs7]): The time derivative $\partial _t u$![]() usually is an element of a space like $L^r((0,\,T);(W^1_r)')$
usually is an element of a space like $L^r((0,\,T);(W^1_r)')$![]() ; i.e. it features a negative Sobolev space. This also motivates the potential truncation (cf. § 2.3.1), as writing $u = \operatorname {curl} v$
; i.e. it features a negative Sobolev space. This also motivates the potential truncation (cf. § 2.3.1), as writing $u = \operatorname {curl} v$![]() means that $\partial _t v \in L^r((0,\,T);L^r)$
means that $\partial _t v \in L^r((0,\,T);L^r)$![]() . While this method is very effective in $L^p$
. While this method is very effective in $L^p$![]() -spaces (cf. [Reference Breit, Diening and Schwarzacher9, Reference Bulíček, Burczak and Schwarzacher11, Reference Diening, Schwarzacher, Stroffolini and Verde17]), it falls short in spaces, in which classical solution theory to the equation $\operatorname {curl} v=u$
-spaces (cf. [Reference Breit, Diening and Schwarzacher9, Reference Bulíček, Burczak and Schwarzacher11, Reference Diening, Schwarzacher, Stroffolini and Verde17]), it falls short in spaces, in which classical solution theory to the equation $\operatorname {curl} v=u$![]() fails, for instance in $L^1$
fails, for instance in $L^1$![]() . It remains to be seen, whether the present ’direct’ approach of constructing the truncation can be translated to a time-dependent setting.
. It remains to be seen, whether the present ’direct’ approach of constructing the truncation can be translated to a time-dependent setting.
In contrast, in problems arising in the broad context of solid mechanics, bound (T2b’) is explicitly required, cf. [Reference Acerbi and Fusco1, Reference Acerbi and Fusco2, Reference Friesecke, James and Müller20, Reference Zhang35] and [Reference Müller29] for an overview. In particular, the goal of ruling out concentrations is different: Oscillations do occur and we can ignore concentrations effects for the sequences (e.g. as they are minimizing sequences to certain functionals). So when truncating, we need to further quantify the difference between the function and its truncation, i.e. (T2b’). We refer to [Reference Behn, Gmeineder and Schiffer5, Reference Müller29, Reference Schiffer32, Reference Zhang35] for more discussions on that matter.
The even stronger bound (T2c’) is for instance relevant for convex integration (e.g. for the (in)compressible Euler equation), cf. [Reference Gallenmüller21, Reference Gallenmüller and Wiedemann22] for more discussions.
Finally, we shall also mentioned, that apart from $W^{1,p}$![]() -$W^{1,\infty }$
-$W^{1,\infty }$![]() and $L^p$
and $L^p$![]() -$L^{\infty }$
-$L^{\infty }$![]() truncation also other regularities of (solenoidal) truncation may be studied, for example in $BV$
truncation also other regularities of (solenoidal) truncation may be studied, for example in $BV$![]() (cf. [Reference Evans and Gariepy18, Ch. 6],[Reference Breit, Diening and Gmeineder8]).
(cf. [Reference Evans and Gariepy18, Ch. 6],[Reference Breit, Diening and Gmeineder8]).
1.4. Structure of the article
The remainder of this article is organized as follows. In § 2 we revisit the classical Whitney's extension/truncation theorem and its modern variant with the additional constraint of solenoidality. In more detail, we recall the construction of a Whitney cover in § 2.1 and recall its application in form of Whitney's extension and truncation result in § 2.2. Furthermore, we shortly outline two previous methods to obtain solenoidal Lipschitz truncations and thus also theorem 1.1 in particular: The potential truncation, following [Reference Breit, Diening and Schwarzacher9] and a truncation via local corrections, following [Reference Breit, Diening and Fuchs7].
In § 3 we present a proof to theorem 1.1. First of all, without the usage of differential forms, we give a formula for the truncation in dimension $N=3$![]() . Higher dimensions require writing divergence-free functions as closed $(N-1)$
. Higher dimensions require writing divergence-free functions as closed $(N-1)$![]() -forms, hence we take a short detour on differential forms and Stokes’ theorem in § 3.2. Then we are ready to define the truncation in § 3.3. Sections 3.4, 3.5 & 3.6 are then devoted to the proof of theorem 1.1.
-forms, hence we take a short detour on differential forms and Stokes’ theorem in § 3.2. Then we are ready to define the truncation in § 3.3. Sections 3.4, 3.5 & 3.6 are then devoted to the proof of theorem 1.1.
Finally, in § 4 we discuss some possible extensions, in particular a parallel result to theorem 1.1 for closed differential forms, and open questions.
2. Whitney's truncation theorem and its application to (solenoidal) Lipschitz truncation
In this section, we revisit approaches to obtain a (solenoidal) Lipschitz truncation based on Whitney's extension. First, we recall Whitney's original approach and its consequences for truncation theorems, cf. [Reference Acerbi and Fusco1, Reference Zhang35]. Then we shortly discuss the modifications to this approach to obtain a solenoidal Lipschitz truncation from [Reference Breit, Diening and Fuchs7] and [Reference Breit, Diening and Schwarzacher9] (in the stationary case) and compare it to the ansatz of the present work.
2.1. Whitney cubes
Our goal is to extend a function from a closed set $X \subset \mathbb {R}^N$![]() to $\mathbb {R}^N$
to $\mathbb {R}^N$![]() . In the context of truncation, we leave the function $u \colon \mathbb {R}^N \to \mathbb {R}^N$
. In the context of truncation, we leave the function $u \colon \mathbb {R}^N \to \mathbb {R}^N$![]() untouched on some set $X$
untouched on some set $X$![]() and modify it on $X^C$
and modify it on $X^C$![]() . We often refer to $X$
. We often refer to $X$![]() as the ‘good set’ and to its complement as the ‘bad set’. Further, we assume that $X$
as the ‘good set’ and to its complement as the ‘bad set’. Further, we assume that $X$![]() is closed and, therefore, $X^C$
is closed and, therefore, $X^C$![]() is open.
is open.
Following Stein's book [Reference Stein33, Chapter VI], we can cover $X^C$![]() by open, dyadic cubes $(Q_i^{\ast })_{i \in \mathbb {N}}$
by open, dyadic cubes $(Q_i^{\ast })_{i \in \mathbb {N}}$![]() with the following properties:
with the following properties:
(i*) $X^C = \bigcup _{i \in \mathbb {N}} \bar {Q}_i^{\ast }$
 ;
;(ii*) $Q_i^{\ast } \cap Q_j^{\ast } = \emptyset$
 if $i \neq j$
if $i \neq j$ ;
;(iii*) ${1}/{4} \operatorname {dist}(Q_i^{\ast },\,X) \leq l(Q_i^{\ast }) \leq 4\operatorname {dist}(Q_i^{\ast },\,X)$
 where $l(Q_i^{\ast })$
where $l(Q_i^{\ast })$ denotes the sidelength of $Q_i^{\ast }$
denotes the sidelength of $Q_i^{\ast }$ ;
;(iv*) if $\bar {Q}_i^{\ast } \cap \bar {Q}_j^{\ast } \neq \emptyset$
 , then ${1}/{4} l(Q_i^{\ast }) \leq l(Q_j^{\ast }) \leq 4 l(Q_i^{\ast })$
, then ${1}/{4} l(Q_i^{\ast }) \leq l(Q_j^{\ast }) \leq 4 l(Q_i^{\ast })$ ;
;(v*) for each $i \in \mathbb {N}$
 , the number of cubes $Q_j^{\ast }$
, the number of cubes $Q_j^{\ast }$ such that $\bar {Q}_i^{\ast } \cap \bar {Q}_j^{\ast } \neq \emptyset$
such that $\bar {Q}_i^{\ast } \cap \bar {Q}_j^{\ast } \neq \emptyset$ is bounded by a dimensional constant $C(N)$
is bounded by a dimensional constant $C(N)$ .
.
Furthermore, for each cube $Q_i^{\ast }$![]() , we denote by $c_i$
, we denote by $c_i$![]() the centre of the cube $Q_i^{\ast }$
the centre of the cube $Q_i^{\ast }$![]() . We may also find a projection point $z_i \in X$
. We may also find a projection point $z_i \in X$![]() , such that $\operatorname {dist}(Q_i^{\ast },\,z_i) \leq 4 \operatorname {dist}(Q_i^{\ast },\,X)$
, such that $\operatorname {dist}(Q_i^{\ast },\,z_i) \leq 4 \operatorname {dist}(Q_i^{\ast },\,X)$![]() . Moreover, we define the measure $\mu _i$
. Moreover, we define the measure $\mu _i$![]() as
as
where ${1}/{2} Q_i^{\ast }$![]() is the open cube with axis parallel faces, centre $c_i$
is the open cube with axis parallel faces, centre $c_i$![]() and sidelength ${1}/{2}l(Q_i^{\ast })$
and sidelength ${1}/{2}l(Q_i^{\ast })$![]() .
.
In addition, we also consider slightly blown-up open cubes $Q_i=(1+\epsilon ) Q_i^{\ast }$![]() with the same centre $c_i$
with the same centre $c_i$![]() but sidelength $(1+\varepsilon )l(Q_i^{\ast })$
but sidelength $(1+\varepsilon )l(Q_i^{\ast })$![]() . If $\epsilon$
. If $\epsilon$![]() is sufficiently small (e.g. $\varepsilon < {1}/{32}$
is sufficiently small (e.g. $\varepsilon < {1}/{32}$![]() ), then these cubes have the following properties:
), then these cubes have the following properties:
(i*) $X^C = \bigcup _{i \in \mathbb {N}} Q_i$
 ;
;(ii*) for all $i \in \mathbb {N}$
 , the number of cubes $Q_j$
, the number of cubes $Q_j$ with $Q_j \cap Q_i \neq \emptyset$
with $Q_j \cap Q_i \neq \emptyset$ is bounded by $C(N)$
is bounded by $C(N)$ ;
;(iii*) ${1}/{5} \operatorname {dist}(Q_i,\,X) \leq l(Q_i) \leq 5\operatorname {dist}(Q_i,\,X)$
 , where $l(Q_i)$
, where $l(Q_i)$ is the sidelength of $Q_i$
is the sidelength of $Q_i$ ($l(Q_i) =(1+\epsilon )l(Q_i^{\ast })$
($l(Q_i) =(1+\epsilon )l(Q_i^{\ast })$ ;
;(iv*) if $Q_i \cap Q_j \neq \emptyset$
 , then ${1}/{4} l(Q_i) \leq l(Q_j) \leq 4 l(Q_i)$
, then ${1}/{4} l(Q_i) \leq l(Q_j) \leq 4 l(Q_i)$ .
.
We now take $\varphi \in C_c^{\infty }((-\varepsilon /2,\,1+\varepsilon /2)^N)$![]() with $\varphi \equiv 1$
with $\varphi \equiv 1$![]() on $[0,\,1]^N$
on $[0,\,1]^N$![]() . By translation and scaling we get $\varphi _j^{\ast } \in C_c^{\infty }(Q_j)$
. By translation and scaling we get $\varphi _j^{\ast } \in C_c^{\infty }(Q_j)$![]() with $\varphi ^{\ast }_j \equiv 1$
with $\varphi ^{\ast }_j \equiv 1$![]() on $Q_j^{\ast }$
on $Q_j^{\ast }$![]() .
.
Using the properties of the cubes $Q_j$![]() we can show (again, cf. [Reference Stein33]), that
we can show (again, cf. [Reference Stein33]), that
defines a partition of unity on $X^C$![]() , i.e.
, i.e.

Moreover, $\varphi _j \in C_c^{\infty }(Q_j)$![]() and they satisfy the bound
and they satisfy the bound
Before we continue with Whitney's extension theorem, we again point out that all the dimensional constants $C(N)$![]() and $C(N,\,k)$
and $C(N,\,k)$![]() in above construction do not depend on the regularity of the set $X$
in above construction do not depend on the regularity of the set $X$![]() ; all we need is the set $X$
; all we need is the set $X$![]() to be closed.
to be closed.
2.2. Whitney extension and the related truncation theorem
Given a closed set $X \subset \mathbb {R}^N$![]() and a Lipschitz continuous function $u \colon X \to \mathbb {R}$
and a Lipschitz continuous function $u \colon X \to \mathbb {R}$![]() with Lipschitz constant $L>0$
with Lipschitz constant $L>0$![]() , we define
, we define

Lemma 2.1 Whitney truncation
If $u \colon X \to \mathbb {R}$![]() is Lipschitz continuous with Lipschitz constant $L$
is Lipschitz continuous with Lipschitz constant $L$![]() , then $\tilde {u} \colon \mathbb {R}^N \to \mathbb {R}$
, then $\tilde {u} \colon \mathbb {R}^N \to \mathbb {R}$![]() is Lipschitz continuous with Lipschitz constant $C_N L$
is Lipschitz continuous with Lipschitz constant $C_N L$![]() for a purely dimensional constant $C_N$
for a purely dimensional constant $C_N$![]() .
.
A detailed proof can be found in [Reference Stein33, Chapter VI]. We give a brief heuristic idea, why lemma 2.1 works, as a similar argument is used in § 3.
Observe that $\tilde {u} \in C^{\infty }(X^C)$![]() and that locally, only finitely many terms are nonzero. Therefore, we can compute its derivative for $y \in X^C$
and that locally, only finitely many terms are nonzero. Therefore, we can compute its derivative for $y \in X^C$![]() :
:
Note that we explicitly used in the second step that $(\varphi _i)_{i \in \mathbb {N}}$![]() and $(\varphi _j)_{j \in \mathbb {N}}$
and $(\varphi _j)_{j \in \mathbb {N}}$![]() are partitions of unity. Applying the bound for the derivative of $\varphi _i$
are partitions of unity. Applying the bound for the derivative of $\varphi _i$![]() and the Lipschitz bound for $u(x_i)-u(x_j)$
and the Lipschitz bound for $u(x_i)-u(x_j)$![]() yields an $L^{\infty }$
yields an $L^{\infty }$![]() -bound for the derivative of $\tilde {u}$
-bound for the derivative of $\tilde {u}$![]() .
.
Together with the observation, that $\tilde {u}$![]() is continuous, this leads to Lipschitz continuity of $\tilde {u}$
is continuous, this leads to Lipschitz continuity of $\tilde {u}$![]() .
.
This approach can then be applied to Lipschitz truncation as follows: First, we find a ‘good set’ $X$![]() , on which $u$
, on which $u$![]() is Lipschitz continuous. For the truncation we then take $\tilde {u} \equiv u$
is Lipschitz continuous. For the truncation we then take $\tilde {u} \equiv u$![]() on the good set and redefine is on the bad set as in (2.3). An important part in showing Lipschitz continuity for $\tilde {u}$
on the good set and redefine is on the bad set as in (2.3). An important part in showing Lipschitz continuity for $\tilde {u}$![]() is therefore the following lemma 2.3 that connects Lipschitz continuity to the (centred) Hardy–Littlewood maximal function $\mathscr {M} u$
is therefore the following lemma 2.3 that connects Lipschitz continuity to the (centred) Hardy–Littlewood maximal function $\mathscr {M} u$![]() that is defined via
that is defined via
where ${\unicode{x2A0F}}$![]() denotes the average integral. The associated operator then has the following properties.
denotes the average integral. The associated operator then has the following properties.
Lemma 2.2 The maximal function
The maximal operator is sublinear, i.e.
for almost every $y\in \mathbb {R}^N$![]() . Moreover, it is bounded as a map from $L^p(\mathbb {R}^N) \to L^p(\mathbb {R}^N)$
. Moreover, it is bounded as a map from $L^p(\mathbb {R}^N) \to L^p(\mathbb {R}^N)$![]() , whenever $1< p\leq \infty$
, whenever $1< p\leq \infty$![]() . For $p=1$
. For $p=1$![]() , $\mathscr {M}$
, $\mathscr {M}$![]() is not bounded from $L^1(\mathbb {R}^N)$
is not bounded from $L^1(\mathbb {R}^N)$![]() to $L^1(\mathbb {R}^N)$
to $L^1(\mathbb {R}^N)$![]() , but from $L^1(\mathbb {R}^N)$
, but from $L^1(\mathbb {R}^N)$![]() to $L^{1,\infty }(\mathbb {R}^N)$
to $L^{1,\infty }(\mathbb {R}^N)$![]() , i.e.
, i.e.
for every $\lambda >0$![]() and $u \in L^1(\mathbb {R}^N)$
and $u \in L^1(\mathbb {R}^N)$![]() .
.
Key to the truncation statement then are the following two observations. The first one, proven in [Reference Acerbi and Fusco1, Reference Liu26] proves that a function $u$![]() is Lipschitz continuous on sublevel sets of its maximal function.
is Lipschitz continuous on sublevel sets of its maximal function.
Lemma 2.3 Let $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$![]() be continuous. There exists a dimensional constant $C$
be continuous. There exists a dimensional constant $C$![]() , such that for all $\lambda >0$
, such that for all $\lambda >0$![]() and all $x,\,y \in X_{\lambda }= \{ \mathscr {M} (Du) \leq \lambda \}$
and all $x,\,y \in X_{\lambda }= \{ \mathscr {M} (Du) \leq \lambda \}$![]() we have
we have
The second ingredient is an estimate on the measure of the ‘bad set’, the complement of $X_{\lambda }$![]() , cf. [Reference Zhang35].
, cf. [Reference Zhang35].
Lemma 2.4 Let $v \in L^p(\mathbb {R}^N;\mathbb {R}^d)$![]() , $1 \leq p< \infty$
, $1 \leq p< \infty$![]() . There is a dimensional constant $C$
. There is a dimensional constant $C$![]() , such that for all $\lambda >0$
, such that for all $\lambda >0$![]() we have
we have
These results are combined to get a Lipschitz truncation in the fashion we already mentioned: We take $u \colon \mathbb {R}^N \to \mathbb {R}^d$![]() , set $\tilde {u}=u$
, set $\tilde {u}=u$![]() on the ‘good set’ $X_{\lambda }$
on the ‘good set’ $X_{\lambda }$![]() and then extend this restriction via Lipschitz extension (2.3) to the full space.
and then extend this restriction via Lipschitz extension (2.3) to the full space.
Defining the extension as in (2.3) only bears the problem that $u(z_i)$![]() might not be well-defined for an arbitrarily chosen $z_i$
might not be well-defined for an arbitrarily chosen $z_i$![]() . There are several workarounds for this problem, e.g. only taking Lebesgue points, considering $u \in C^1(\mathbb {R}^N)$
. There are several workarounds for this problem, e.g. only taking Lebesgue points, considering $u \in C^1(\mathbb {R}^N)$![]() first and then using a density argument or using an averaged value of the function instead.
first and then using a density argument or using an averaged value of the function instead.
In the following, we pursue the third approach. Therefore, we define:
A suitable adaptation of lemma 2.3 and the estimate (2.5) then yield the following:
Lemma 2.5 Lipschitz truncation
Let $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$![]() . Define the set $X_{\lambda } = \{ \mathscr {M} u \leq \lambda \} \cup \{\mathscr {M} (Du) \leq \lambda \}$
. Define the set $X_{\lambda } = \{ \mathscr {M} u \leq \lambda \} \cup \{\mathscr {M} (Du) \leq \lambda \}$![]() . Then, for a dimensional constant $C>0$
. Then, for a dimensional constant $C>0$![]() , the truncation $T_{\operatorname {Lip}} u$
, the truncation $T_{\operatorname {Lip}} u$![]() as in (2.6) has the following properties
as in (2.6) has the following properties
(i) the function $T_{\operatorname {Lip}} u$
 is Lipschitz continuous and $\Vert T_{\operatorname {Lip}} u \Vert _{W^{1,\infty }} \leq C \lambda$
is Lipschitz continuous and $\Vert T_{\operatorname {Lip}} u \Vert _{W^{1,\infty }} \leq C \lambda$ ;
;(ii) the set $X_{\lambda }^C \supset \{ u \neq T_{\operatorname {Lip}} u\}$
 has $\mathcal {L}^N$
has $\mathcal {L}^N$ -measure bounded by
\[ \mathcal{L}^N(X_{\lambda}^C) \leq C \lambda^{{-}p} \int_{\{\vert u \vert \geq \lambda\} \cup \{\vert Du \vert \geq \lambda\}} \vert u \vert^p + \vert D u\vert^p \,{\textrm d}x; \]
-measure bounded by
\[ \mathcal{L}^N(X_{\lambda}^C) \leq C \lambda^{{-}p} \int_{\{\vert u \vert \geq \lambda\} \cup \{\vert Du \vert \geq \lambda\}} \vert u \vert^p + \vert D u\vert^p \,{\textrm d}x; \]
(iii) as a consequence of (ii) we have
\[ \Vert u - T_{\operatorname{Lip}} u \Vert_{W^{1,p}}^p \leq C \int_{\{\vert u \vert \geq \lambda\} \cup \{\vert Du \vert \geq \lambda\}} \vert u \vert^p + \vert D u\vert^p \,{\textrm d}x. \]
2.3. Solenoidal truncation
In this section we shortly describe previous approaches to solenoidal Lipschitz truncation and compare it to the approach in the present work.
2.3.1. Potential truncation.
First of all, in [Reference Breit, Diening and Schwarzacher9, Section 4] (see also [Reference Behn, Gmeineder and Schiffer5, Reference Gallenmüller21] for related discussions), the truncation is obtained by writing a divergence-free function $u \in W^{1,p}(\mathbb {R}^3;\mathbb {R}^3)$![]() as
as
for a function $v \in \dot {W}^{2,p}(\mathbb {R}^3;\mathbb {R}^3)$![]() , truncate $v$
, truncate $v$![]() to obtain some $\tilde {v} \in W^{2,\infty }(\mathbb {R}^3;\mathbb {R}^3)$
to obtain some $\tilde {v} \in W^{2,\infty }(\mathbb {R}^3;\mathbb {R}^3)$![]() and set $\tilde {u}= \operatorname {curl} \tilde v$
and set $\tilde {u}= \operatorname {curl} \tilde v$![]() .
.
This approach is particularly well-suited to evolutionary problems (i.e. $u \colon [0,\,\infty ) \times \mathbb {R}^N \to \mathbb {R}^N)$![]() and can (together with parabolic Lipschitz truncation) also tackle the usually quite low regularity of the time derivative $\partial _t u$
and can (together with parabolic Lipschitz truncation) also tackle the usually quite low regularity of the time derivative $\partial _t u$![]() .
.
Seeking for a sharper result in space and not in space-time (which severely complicates the matter), this form of truncation can, however, only achieve property (T2a’) and not (T2b’). Even if $u \in W^{1,\infty }(\mathbb {R}^3;\mathbb {R}^3)$![]() , its potential $v$
, its potential $v$![]() is not in $W^{2,\infty }(\mathbb {R}^3;\mathbb {R}^3)$
is not in $W^{2,\infty }(\mathbb {R}^3;\mathbb {R}^3)$![]() in general (Ornstein's non-inequality [Reference de Leeuw and Mirkil13, Reference Ornstein30]) and $\tilde {v} \neq v$
in general (Ornstein's non-inequality [Reference de Leeuw and Mirkil13, Reference Ornstein30]) and $\tilde {v} \neq v$![]() regardless of the truncation parameter $L$
regardless of the truncation parameter $L$![]() .
.
Let us further note that in dimension $N=2$![]() , (T2b’) is satisfied; the reason being that the map $u \mapsto v$
, (T2b’) is satisfied; the reason being that the map $u \mapsto v$![]() is bounded from $W^{1,\infty }(\mathbb {R}^2;\mathbb {R}^2)$
is bounded from $W^{1,\infty }(\mathbb {R}^2;\mathbb {R}^2)$![]() to $W^{2,\infty }(\mathbb {R}^2)$
to $W^{2,\infty }(\mathbb {R}^2)$![]() . Hence, the truncation of [Reference Breit, Diening and Schwarzacher9] (together with the correct spaces), actually yields property (T2b’) both in space and space-time. Moreover, the truncation constructed in [Reference Breit, Diening and Schwarzacher9] in the stationary setting coincides with the truncation constructed in this work in space dimension two.
. Hence, the truncation of [Reference Breit, Diening and Schwarzacher9] (together with the correct spaces), actually yields property (T2b’) both in space and space-time. Moreover, the truncation constructed in [Reference Breit, Diening and Schwarzacher9] in the stationary setting coincides with the truncation constructed in this work in space dimension two.
2.3.2. Truncation via local corrections.
In contrast, the work [Reference Breit, Diening and Fuchs7] is directly suited towards stationary problems in more involved spaces, e.g. Orlicz spaces. In particular, the truncation outlined in [Reference Breit, Diening and Fuchs7] is able to obtain (T2b’). Instead of writing $u=\operatorname {curl} v$![]() , we work with $u$
, we work with $u$![]() directly, find $\tilde {u}$
directly, find $\tilde {u}$![]() as in (2.3) and then add corrector terms to restore solenoidality. As the ‘good set’ one takes the set where the maximal function of $u$
as in (2.3) and then add corrector terms to restore solenoidality. As the ‘good set’ one takes the set where the maximal function of $u$![]() and of $Du$
and of $Du$![]() is smallFootnote 1 .
is smallFootnote 1 .
In more detail, we first add a global corrector term $\Pi u$![]() , such $\tilde {u} + \Pi u =: \tilde {T}u$
, such $\tilde {u} + \Pi u =: \tilde {T}u$![]() is still a $W^{1,\infty }$
is still a $W^{1,\infty }$![]() -truncation of $u$
-truncation of $u$![]() . In the second step, one adds local corrector terms $\mathrm {Cor}_i \in W^{1,\infty }_0(Q_i;\mathbb {R}^3)$
. In the second step, one adds local corrector terms $\mathrm {Cor}_i \in W^{1,\infty }_0(Q_i;\mathbb {R}^3)$![]() , that satisfy the divergence-equation
, that satisfy the divergence-equation
Finally, one obtains the divergence-free truncation via
As one only modifies the function on the bad set $\{ \mathscr {M} u > \lambda \} \cup \{\mathscr {M}(Du) >\lambda \}$![]() , one is able to obtain (T2b’). One crucial observation (cf. [Reference Breit, Diening and Fuchs7, Lemma 2.11]) to get $T_{\operatorname {div}} u \in W^{1,\infty }$
, one is able to obtain (T2b’). One crucial observation (cf. [Reference Breit, Diening and Fuchs7, Lemma 2.11]) to get $T_{\operatorname {div}} u \in W^{1,\infty }$![]() is the following:
is the following:
First note that the observation that $\mathrm {Cor}_i$![]() belongs to $W^{1,\infty }$
belongs to $W^{1,\infty }$![]() is not trivial; the divergence equation (2.7) and its solution operator (the Bogovskiĭ operator [Reference Bogovskiĭ6]) is not bounded from $L^{\infty }$
is not trivial; the divergence equation (2.7) and its solution operator (the Bogovskiĭ operator [Reference Bogovskiĭ6]) is not bounded from $L^{\infty }$![]() to $W^{1,\infty }$
to $W^{1,\infty }$![]() . Instead, one uses that $\operatorname {div} (\varphi _i(\tilde {u}+\Pi u))$
. Instead, one uses that $\operatorname {div} (\varphi _i(\tilde {u}+\Pi u))$![]() has a very specific form. It is a much smoother function, hence the solution to the divergence equation is in $W^{1,\infty }$
has a very specific form. It is a much smoother function, hence the solution to the divergence equation is in $W^{1,\infty }$![]() . A uniform $W^{1,\infty }$
. A uniform $W^{1,\infty }$![]() -bound for the solution is achieved via the following argument: The partition of unity is obtained by formula (2.1) for a cover consisting of $Q_i^{\ast }$
-bound for the solution is achieved via the following argument: The partition of unity is obtained by formula (2.1) for a cover consisting of $Q_i^{\ast }$![]() and associated functions $\varphi _i^{\ast }$
and associated functions $\varphi _i^{\ast }$![]() . But actually, as all cubes $Q_i^{\ast }$
. But actually, as all cubes $Q_i^{\ast }$![]() are dyadic, there are only finitely many configurations how the cover can locally look like. In particular, up to scaling and translation, we only need to solve
are dyadic, there are only finitely many configurations how the cover can locally look like. In particular, up to scaling and translation, we only need to solve
a finite amount of times as, up to scaling and translation, there are only finitely many functions the right-hand-side can realize. As we then only argue about finitely many different corrector terms, the uniform $W^{1,\infty }$![]() -bound is an easy consequence.
-bound is an easy consequence.
2.3.3. Truncations via local corrections II.
In this work, we study a modification of the second approach by explicitly constructing the corrector terms using that our truncation has a very particular form. This approach only relies on
(a) some purely geometric estimates;
(b) the existence of a cover with sets $Q_i$
 (that are not necessarily cubes);
(that are not necessarily cubes);(c) a partition of unity $\varphi _i$
 that satisfies estimate (2.2).
that satisfies estimate (2.2).
In particular, the assumptions on the cover over cubes and the partition of unity are less restrictive than in [Reference Breit, Diening and Fuchs7], which, for instance, might be useful for geometries on manifolds.
Comparing the present ansatz to [Reference Breit, Diening and Fuchs7], we also add correctors such that $\tilde {u}$![]() first given by (2.3) is modified to be divergence-free. Instead of solving the divergence-equation via the Bogovskiĭ operator, we give explicit formulas for the corrector terms that rely on certain cancellations and Stokes’ theorem. In space dimension three, those corrections are defined on pairs and tuples of cubes, i.e.
first given by (2.3) is modified to be divergence-free. Instead of solving the divergence-equation via the Bogovskiĭ operator, we give explicit formulas for the corrector terms that rely on certain cancellations and Stokes’ theorem. In space dimension three, those corrections are defined on pairs and tuples of cubes, i.e.
In general dimension, we need more corrector terms, which is connected to the nice algebraic structure provided for the divergence operator.
2.4. Truncation for differential forms
The construction done for the divergence (in three space dimensions) fits into a more general framework for closed differential forms - we introduce the exact notation in § 3. Recall that a divergence-free function $u \colon \mathbb {R}^N \to \mathbb {R}^N$![]() can be identified with a closed differential form (meaning the exterior derivative vanishes) $\hat {u} \colon \mathbb {R}^N \to \Lambda ^{N-1}$
can be identified with a closed differential form (meaning the exterior derivative vanishes) $\hat {u} \colon \mathbb {R}^N \to \Lambda ^{N-1}$![]() ; in particular the divergence operator might be identified with the operator of exterior differentiation.
; in particular the divergence operator might be identified with the operator of exterior differentiation.
The approach of constructing the corrector terms heavily builds on this algebraic structure and, correspondingly, on Stokes’ theorem. This connection becomes easily visible when dealing with $\operatorname {curl}$![]() -free functions, these are $v \colon \mathbb {R}^N \to \mathbb {R}^N$
-free functions, these are $v \colon \mathbb {R}^N \to \mathbb {R}^N$![]() obeys
obeys
These can also be put into the framework of closed forms, i.e. $\hat {v} \colon \mathbb {R}^N \to \Lambda ^1$![]() . The results then reads as follows.
. The results then reads as follows.
Lemma 2.6 Let $N \geq 2$![]() and suppose that $1 \leq p <\infty$
and suppose that $1 \leq p <\infty$![]() , $v \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^N)$
, $v \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^N)$![]() obeys $\operatorname {curl} v=0$
obeys $\operatorname {curl} v=0$![]() and that $L>0$
and that $L>0$![]() . There is a (dimensional) constant $C>0$
. There is a (dimensional) constant $C>0$![]() and a function $\tilde {v} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^N)$
and a function $\tilde {v} \in W^{1,\infty }(\mathbb {R}^N;\mathbb {R}^N)$![]() , such that
, such that
(T1) $\Vert \tilde {v} \Vert _{W^{1,\infty }} \leq CL$
 ;
;(T2) $\mathcal {L}^N(\{ v \neq \tilde {v}\}) \leq C(d)L^{-p} \int _{\{\vert v \vert + \vert Dv\vert \geq L\}} \vert v \vert + \vert D v \vert \,\mathrm {d} x$
 ;
;(T3) $\operatorname {curl} \tilde {v} =0$
 .
.
The proof of this result can be achieved quite directly by writing $v= \nabla V$![]() for some $V \in \dot {W}^{2,p}(\mathbb {R}^N,\,\mathbb {R}^N)$
for some $V \in \dot {W}^{2,p}(\mathbb {R}^N,\,\mathbb {R}^N)$![]() , truncating $V$
, truncating $V$![]() to obtain some $\bar {V}$
to obtain some $\bar {V}$![]() and then considering the derivative of $\bar {V}$
and then considering the derivative of $\bar {V}$![]() . The existence of such a $V$
. The existence of such a $V$![]() is ensured by the differential constraint $\operatorname {curl} v=0$
is ensured by the differential constraint $\operatorname {curl} v=0$![]() .
.
In particular, on the ’bad set’ $X^C$![]() , we have (recall that $z_i$
, we have (recall that $z_i$![]() was a projection point of $Q_i$
was a projection point of $Q_i$![]() onto $X$
onto $X$![]() )
)
Now, one can calculate the derivative of $\bar {V}$![]() and then replace $Du$
and then replace $Du$![]() by $v$
by $v$![]() to obtain
to obtain

if $z_i=z_j$![]() , we define the integral in (2.8) to be zero.
, we define the integral in (2.8) to be zero.
Observe that (2.8) features the previously discussed structure. That is, the first sum in (2.8) coincides with the unconstrained extension and the second is a correction to satisfy the constraint $\operatorname {curl} \bar {v}=0$![]() .
.
The general case of differential forms ($\operatorname {curl}$![]() -free functions are closed $1$
-free functions are closed $1$![]() -forms) requires multiple steps of corrections. This is carried out in § 3. On the other hand, such a construction involving corrections does not seem to be limited to differential forms, but probably can be achieved for a wider class of differential operators (cf. § 4.2).
-forms) requires multiple steps of corrections. This is carried out in § 3. On the other hand, such a construction involving corrections does not seem to be limited to differential forms, but probably can be achieved for a wider class of differential operators (cf. § 4.2).
3. Solenoidal Lipschitz truncation
This section is concerned with the proof of theorem 1.1 and its immediate consequences. The proof in general dimension requires some basic methods of differential geometry; to demonstrate the strategy we shortly outline the strategy in 3D (which corresponds to closed $2$![]() -forms in higher dimensions), as there a coordinate-wise computation is still feasible.
-forms in higher dimensions), as there a coordinate-wise computation is still feasible.
3.1. Definition of the truncation in three space dimensions
We shortly outline the three-dimensional case. To this end, let $X \subset \mathbb {R}^3$![]() be a closed set and $(Q_i)_{i \in \mathbb {N}}$
be a closed set and $(Q_i)_{i \in \mathbb {N}}$![]() be a Whitney cover of $X^C$
be a Whitney cover of $X^C$![]() featuring a partition of unity $\varphi _i$
featuring a partition of unity $\varphi _i$![]() and measures $\mu _i$
and measures $\mu _i$![]() (cf. § 2.1). For simplicity, we write
(cf. § 2.1). For simplicity, we write
For points $x_{i_1},\,\ldots,\,x_{i_k} \in \mathbb {R}^3$![]() denote by
denote by
the convex hull of those points. If $k=2$![]() , we denote this by the direct line $[x_{i_1},\,x_{i_2}]:=\operatorname {Sim}(i_1,\,i_2)$
, we denote this by the direct line $[x_{i_1},\,x_{i_2}]:=\operatorname {Sim}(i_1,\,i_2)$![]() between these points. If $k=2,\,3,\,4$
between these points. If $k=2,\,3,\,4$![]() , we call this object a non-degenerate simplex if its dimension is $(k-1)$
, we call this object a non-degenerate simplex if its dimension is $(k-1)$![]() , i.e. $\mathcal {H}^{k-1}(\operatorname {Sim}(i_1,\,\ldots,\,i_k))>0$
, i.e. $\mathcal {H}^{k-1}(\operatorname {Sim}(i_1,\,\ldots,\,i_k))>0$![]() .
.
Definition 3.1 Given $u \in W^{1,p}(\mathbb {R}^3;\mathbb {R}^3)$![]() , tuples $(a,\,b,\,c) \in \{(1,\,2,\,3),\,(2,\,3,\,1), (3,\,1,\,2)\}$
, tuples $(a,\,b,\,c) \in \{(1,\,2,\,3),\,(2,\,3,\,1), (3,\,1,\,2)\}$![]() and $X \subset \mathbb {R}^3$
and $X \subset \mathbb {R}^3$![]() , we define the truncation operator $T$
, we define the truncation operator $T$![]() as follows:
as follows:

where the correction term $S$![]() is defined as
is defined as

if $i \neq j$![]() and $A_{\alpha \beta }(i,\,i) =0$
and $A_{\alpha \beta }(i,\,i) =0$![]() for all $i \in \mathbb {N}$
for all $i \in \mathbb {N}$![]() .
.
The corrector $R$![]() is defined via
is defined via
if $i$![]() , $j$
, $j$![]() and $k$
and $k$![]() are pairwise disjoint and $B(i,\,i,\,k)=B(i,\,j,\,i)=B(i,\,j,\,j)=0$
are pairwise disjoint and $B(i,\,i,\,k)=B(i,\,j,\,i)=B(i,\,j,\,j)=0$![]() .
.
We may prove the following statement, which is part of the higher dimensional treatment in § 3.3 ff.
Theorem 3.2 If $u \in W^{1,p}(\mathbb {R}^3;\mathbb {R}^3)$![]() with $\operatorname {div} u=0$
with $\operatorname {div} u=0$![]() and $\lambda >0$
and $\lambda >0$![]() , set
, set
Then the truncated $T u$![]() defined in definition 3.1 satisfies all the assertions of theorem 1.1 for a.e. $L>0$
defined in definition 3.1 satisfies all the assertions of theorem 1.1 for a.e. $L>0$![]() with $L={\lambda }/{2}$
with $L={\lambda }/{2}$![]() .
.
This is of course just a special case of the statement for general dimension below, cf. theorem 3.5. In 3D, however, every computation can also be done in the local coordinates. The proof then roughly proceeds as follows:
St.1: Argue that $T_0 u \in W^{1,p}(\mathbb {R}^3;\mathbb {R}^3)$
 and that $Su,\,Ru \in W^{1,p}_0(X^C;\mathbb {R}^3)$
and that $Su,\,Ru \in W^{1,p}_0(X^C;\mathbb {R}^3)$ ;
;St.2: Compute that in $X^C$
 we have $\operatorname {div} Tu=0$
we have $\operatorname {div} Tu=0$ (which we can do via pointwise computation).
(which we can do via pointwise computation).St.3: Show $L^{\infty }$
 -bounds on $D (Tu)$
-bounds on $D (Tu)$ .
.
Furthermore, we mention that the treatment of $\operatorname {curl}$![]() -free functions, i.e. closed $1$
-free functions, i.e. closed $1$![]() -forms (lemma 2.8), is also done in a coordinate-wise fashion, cf. formula (2.8). Extending above to arbitrary space dimension, one may get a truncation result for closed two-forms. The goal of the following subsections is to generalize it to arbitrary dimension.
-forms (lemma 2.8), is also done in a coordinate-wise fashion, cf. formula (2.8). Extending above to arbitrary space dimension, one may get a truncation result for closed two-forms. The goal of the following subsections is to generalize it to arbitrary dimension.
3.2. Intermezzo: differential forms and Stokes’ theorem
We shortly recall some basic notation and properties of differential forms. Taking $\mathbb {R}^N$![]() as the physical space, $(\mathbb {R}^N)^{\ast }$
as the physical space, $(\mathbb {R}^N)^{\ast }$![]() denotes its dual and
denotes its dual and

denotes the $r$![]() -fold wedge product of the dual. Likewise, $V^r$
-fold wedge product of the dual. Likewise, $V^r$![]() denotes the $r$
denotes the $r$![]() -fold wedge product of $\mathbb {R}^N$
-fold wedge product of $\mathbb {R}^N$![]() with itself. Observe that $\Lambda ^0=\mathbb {R}$
with itself. Observe that $\Lambda ^0=\mathbb {R}$![]() , $\Lambda ^1= (\mathbb {R}^N)^{\ast }$
, $\Lambda ^1= (\mathbb {R}^N)^{\ast }$![]() and that $\Lambda ^{N}$
and that $\Lambda ^{N}$![]() is isomorphic to $\mathbb {R}$
is isomorphic to $\mathbb {R}$![]() . Moreover, $\Lambda ^r$
. Moreover, $\Lambda ^r$![]() is the dual of $V^r$
is the dual of $V^r$![]() and we write $\omega [\nu ]$
and we write $\omega [\nu ]$![]() to indicate the dual pairing of $\omega \in \Lambda ^r$
to indicate the dual pairing of $\omega \in \Lambda ^r$![]() with $\nu \in V^r$
with $\nu \in V^r$![]() .
.
We call a (smooth) map $u \colon \mathbb {R}^N \to \Lambda ^r$![]() an $r$
an $r$![]() -form. Moreover, there is the exterior derivative $d$
-form. Moreover, there is the exterior derivative $d$![]() , that maps $r$
, that maps $r$![]() -forms into $(r+1)$
-forms into $(r+1)$![]() -forms with the following properties:
-forms with the following properties:
(i) $d \circ d=0$
 ;
;(ii) If $\alpha \in C^{\infty }(\mathbb {R}^N;\Lambda ^r)$
 and $\beta \in C^{\infty }(\mathbb {R}^N;\Lambda ^s)$
and $\beta \in C^{\infty }(\mathbb {R}^N;\Lambda ^s)$ , then
\[ d (\alpha \wedge \beta) = d \alpha \wedge \beta + ({-}1)^r \alpha \wedge d \beta \]
, then
\[ d (\alpha \wedge \beta) = d \alpha \wedge \beta + ({-}1)^r \alpha \wedge d \beta \]
(iii) $d \colon C^{\infty }(\mathbb {R}^N;\Lambda ^0) \to C^{\infty }(\mathbb {R}^N;\Lambda ^1)$
 is the gradient.
is the gradient.
Usually, one may identify a divergence-free function $u \colon \mathbb {R}^N \to \mathbb {R}^N$![]() with a function $\bar {u} \in \mathbb {R}^N \to \Lambda ^1$
with a function $\bar {u} \in \mathbb {R}^N \to \Lambda ^1$![]() obeying $d^{\ast } u=0$
obeying $d^{\ast } u=0$![]() through seeing the divergence as the adjoint to the gradient. Instead of this, we use a different identification with $(N-1)$
through seeing the divergence as the adjoint to the gradient. Instead of this, we use a different identification with $(N-1)$![]() -forms. In particular, for the standard basis $e_i$
-forms. In particular, for the standard basis $e_i$![]() of $\mathbb {R}^N$
of $\mathbb {R}^N$![]() denote by $dx_i$
denote by $dx_i$![]() the map in $(\mathbb {R}^N)^{\ast }$
the map in $(\mathbb {R}^N)^{\ast }$![]() given by
given by

Then the vectors
form a basis of $\Lambda ^{N-1}$![]() and we may define an isomorphism $\Psi \colon \mathbb {R}^N \to \Lambda ^{N-1}$
and we may define an isomorphism $\Psi \colon \mathbb {R}^N \to \Lambda ^{N-1}$![]() that is defined on the standard basis as $e_i \mapsto \omega _i$
that is defined on the standard basis as $e_i \mapsto \omega _i$![]() . Then we have
. Then we have
and therefore we routinely identify $u$![]() with the $(N-1)$
with the $(N-1)$![]() -form $\Psi (u)$
-form $\Psi (u)$![]() .
.
One then can formulate Stokes’ theorem that, for a $(r+1)$![]() -dimensional manifold $M$
-dimensional manifold $M$![]() links the integral of $d u$
links the integral of $d u$![]() on $M$
on $M$![]() to the boundary integral of $u$
to the boundary integral of $u$![]() . Of special interest in the present setting is the case where $M$
. Of special interest in the present setting is the case where $M$![]() is a simplex; to this end recall that for an index $I=(i_1,\,\ldots,\,i_k)$
is a simplex; to this end recall that for an index $I=(i_1,\,\ldots,\,i_k)$![]() and $x_{i_1},\,\ldots,\,x_{i_k} \in \mathbb {R}^N$
and $x_{i_1},\,\ldots,\,x_{i_k} \in \mathbb {R}^N$![]() we denote by
we denote by
If the dimension of $\operatorname {Sim}(x_I)$![]() is $(k-1)$
is $(k-1)$![]() , we call the simplex non-degenerate. In that case, we define
, we call the simplex non-degenerate. In that case, we define
to be the generalized normal. For any $(k-2)$![]() -dimensional face opposite to $x_{i_l}$
-dimensional face opposite to $x_{i_l}$![]() , i.e. $\operatorname {Sim}^l(x_I) = \operatorname {Sim}(x_{i_1},\,\ldots,\,x_{i_{l-1}},\,x_{i_{l+1}},\,\ldots,\,x_{i_k})$
, i.e. $\operatorname {Sim}^l(x_I) = \operatorname {Sim}(x_{i_1},\,\ldots,\,x_{i_{l-1}},\,x_{i_{l+1}},\,\ldots,\,x_{i_k})$![]() we can accordingly define a normal vector $\nu ^l(x_I)$
we can accordingly define a normal vector $\nu ^l(x_I)$![]() on this face. Further observe that $\vert \nu (x_I) \vert = \mathcal {H}^{k-1}(\operatorname {Sim}(x_I))$
on this face. Further observe that $\vert \nu (x_I) \vert = \mathcal {H}^{k-1}(\operatorname {Sim}(x_I))$![]() .
.
Stokes’ theorem on simplices now reads as follows:

3.3. Definition of the truncation for divergence-free functions
Similarly to definition 3.1, we are now able to define the truncation through one part, that corresponds to $W^{1,\infty }$![]() -truncation, and another part consisting of a bunch of corrector terms.
-truncation, and another part consisting of a bunch of corrector terms.
From now on, instead of working with $u \colon \mathbb {R}^N \to \mathbb {R}^N$![]() , through the identification discussed in the previous subsection we instead consider a non-renamed $(N-1)$
, through the identification discussed in the previous subsection we instead consider a non-renamed $(N-1)$![]() -form $u \colon \mathbb {R}^N \to \Lambda ^{N-1}$
-form $u \colon \mathbb {R}^N \to \Lambda ^{N-1}$![]() . The condition of solenoidality then coincides with closedness of the form, i.e. that the exterior derivative vanishes.
. The condition of solenoidality then coincides with closedness of the form, i.e. that the exterior derivative vanishes.
To define correct analogues of $A_{\alpha \beta }$![]() and $B$
and $B$![]() as in definition 3.1, for $u \colon \mathbb {R}^N \to \Lambda ^{N-1}$
as in definition 3.1, for $u \colon \mathbb {R}^N \to \Lambda ^{N-1}$![]() we define the objects
we define the objects
as follows: We first understand $v=Du$![]() as an element of $\Lambda ^1 \otimes \Lambda ^{N-1}$
as an element of $\Lambda ^1 \otimes \Lambda ^{N-1}$![]() and consider the pairing of the first component of this tensor with some $\nu \in V^r$
and consider the pairing of the first component of this tensor with some $\nu \in V^r$![]() as
as

and then map $V^s \otimes \Lambda ^{N-1}$![]() , $s=r-1,\,r$
, $s=r-1,\,r$![]() to $\Lambda ^{N-1-s}$
to $\Lambda ^{N-1-s}$![]() through a duality pairing, i.e. finally
through a duality pairing, i.e. finally

Corresponding to definition 3.1, let $X \subset \mathbb {R}^N$![]() be a closed set and cover its complement with Whitney cubes $Q_i$
be a closed set and cover its complement with Whitney cubes $Q_i$![]() . Consider a partition of unity $\varphi _i$
. Consider a partition of unity $\varphi _i$![]() on $Q_i$
on $Q_i$![]() , measures $\mu _i$
, measures $\mu _i$![]() and the product measure $\mu _I$
and the product measure $\mu _I$![]() for $I=(i_1,\,\ldots,\,i_r)$
for $I=(i_1,\,\ldots,\,i_r)$![]() and, for simplicity, write
and, for simplicity, write
Definition 3.3 Formula for divergence-free extension
Let $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() , $X \subset \mathbb {R}^N$
, $X \subset \mathbb {R}^N$![]() closed. We define
closed. We define

where
and
We define the integral in (3.11) to be zero if the simplex $\operatorname {Sim}(x_I)$![]() is degenerate.
is degenerate.
Observe that the definition of $A_k(I)$![]() is antisymmetric in the index, i.e. if $\sigma \in S(k+1)$
is antisymmetric in the index, i.e. if $\sigma \in S(k+1)$![]() is a permutation and $\tilde {I}=(i_{\sigma (1)},\,\ldots,\,i_{\sigma (k+1)})$
is a permutation and $\tilde {I}=(i_{\sigma (1)},\,\ldots,\,i_{\sigma (k+1)})$![]() , then
, then
and in particular $A_k(I)=0$![]() if $i_{j_1}=i_{j_2}$
if $i_{j_1}=i_{j_2}$![]() for some $j_1 \neq j_2$
for some $j_1 \neq j_2$![]() . Further, as a minor note, $S_k u$
. Further, as a minor note, $S_k u$![]() maps to $\Lambda ^{N-1}$
maps to $\Lambda ^{N-1}$![]() : The wedge product of all $\varphi$
: The wedge product of all $\varphi$![]() 's is an element of $\Lambda ^k$
's is an element of $\Lambda ^k$![]() and, by definition, $A_k(I) \in \Lambda ^{N-k-1}$
and, by definition, $A_k(I) \in \Lambda ^{N-k-1}$![]() .
.
Remark 3.4 Definition 3.1 vs definition 3.3
For clarity, we shortly argue why definition 3.3 is the generalization of the 3D-case, definition 3.1. As mentioned before, we identify $(\mathbb {R}^3)^{\ast } \wedge (\mathbb {R}^3)^{\ast }$![]() with $\mathbb {R}^3$
with $\mathbb {R}^3$![]() in the following way:
in the following way:
The terms for $S$![]() , $R$
, $R$![]() , $A$
, $A$![]() and $B$
and $B$![]() in definition 3.1 then are nothing else than $S_1$
in definition 3.1 then are nothing else than $S_1$![]() , $S_2$
, $S_2$![]() , $A_1$
, $A_1$![]() and $A_2$
and $A_2$![]() in above definition 3.3 written in a coordinate-wise fashion.
in above definition 3.3 written in a coordinate-wise fashion.
The remainder of this section is devoted to prove the following result.
Theorem 3.5 Let $u \in W^{1,p}(\mathbb {R}^N,\,\Lambda ^{N-1})$![]() with $d u=0$
with $d u=0$![]() and $\lambda >0$
and $\lambda >0$![]() , set
, set
Then the truncated $Tu$![]() defined in definition 3.3 satisfies all the assertions of theorem 1.1 (with the identification of closed $(N-1)$
defined in definition 3.3 satisfies all the assertions of theorem 1.1 (with the identification of closed $(N-1)$![]() -forms to divergence-free functions) for a.e. $L>0$
-forms to divergence-free functions) for a.e. $L>0$![]() with $L=\lambda /2$
with $L=\lambda /2$![]() .
.
3.4. Structure of the proof and auxiliary results
In this section, we outline the different steps of the proof. First of all, we remind the reader of the following unconstrained truncation result.
Lemma 3.6 [Reference Zhang35]
Let $X$![]() be as in theorem 3.5 and $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$
be as in theorem 3.5 and $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() . Then $\tilde {u}$
. Then $\tilde {u}$![]() defined as
defined as

satisfies $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\Lambda ^{N-1})$![]() and $\Vert D \tilde {u} \Vert _{W^{1,\infty }} \leq C \lambda$
and $\Vert D \tilde {u} \Vert _{W^{1,\infty }} \leq C \lambda$![]() .
.
Moreover, recall that due to lemma 2.4 we have the following bound on the measure of $X_{\lambda }$![]() .
.
Lemma 3.7 Let $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() . Then the set $X_{\lambda }$
. Then the set $X_{\lambda }$![]() defined in theorem 3.5 obeys
defined in theorem 3.5 obeys
It remains to show that the corrector terms $S_1,\,\ldots,\,S_k$![]() are well-behaved and achieve their goal, i.e. that those terms are bounded in $W^{1,\infty }(\mathbb {R}^N;\Lambda ^{N-1})$
are well-behaved and achieve their goal, i.e. that those terms are bounded in $W^{1,\infty }(\mathbb {R}^N;\Lambda ^{N-1})$![]() and that together with to $T_0u$
and that together with to $T_0u$![]() they give a solenoidal vector field. We formulate these properties in two separate lemmas.
they give a solenoidal vector field. We formulate these properties in two separate lemmas.
Lemma 3.8 Let $k \in 1,\,\ldots,\,N-1$![]() , $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$
, $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() and $X_{\lambda }$
and $X_{\lambda }$![]() be defined as in theorem 3.5. Then
be defined as in theorem 3.5. Then
(i) $S_k u \in C^{\infty }(X_{\lambda }^C;\Lambda ^{N-1})$
 ;
;(ii) $S_k u \in W^{1,1}_0(X_{\lambda }^C;\Lambda ^{N-1})$
 ;
;(iii) $S_k u \in W^{1,\infty }(\mathbb {R}^N;\Lambda ^{N-1})$
 and $\Vert S_k u \Vert _{W^{1,\infty }} \leq C \lambda$
and $\Vert S_k u \Vert _{W^{1,\infty }} \leq C \lambda$ .
.
The unconstrained truncation $T_0 u$![]() and all $S_k u$
and all $S_k u$![]() are smooth functions in the open set $X_{\lambda }^C$
are smooth functions in the open set $X_{\lambda }^C$![]() . Therefore, to prove that $d T u =0$
. Therefore, to prove that $d T u =0$![]() globally, it suffices to compute the exterior derivative pointwisely.
globally, it suffices to compute the exterior derivative pointwisely.
Lemma 3.9 On the bad set $X_{\lambda }^C$![]() we have $Tu \in C^{\infty }(X^C;\Lambda ^{N-1})$
we have $Tu \in C^{\infty }(X^C;\Lambda ^{N-1})$![]() and, moreover, the strong derivative satisfies
and, moreover, the strong derivative satisfies

This lemma is a quite straightforward calculation and depends on certain cancellations and Stokes’ theorem. Before proving lemmas 3.8 and 3.9, we shortly realize that these lead directly to the proof of theorem 3.5.
Proof Proof of theorem 3.5:
Consider $Tu$![]() as given in (3.8). Lemma 3.6 combined with lemma 3.8 gives that
as given in (3.8). Lemma 3.6 combined with lemma 3.8 gives that

and therefore $Tu \in W^{1,\infty }(\mathbb {R}^N;\Lambda ^{N-1})$![]() . Furthermore, we obtain the bound $\Vert T u \Vert _{W^{1,\infty }} \leq C \lambda$
. Furthermore, we obtain the bound $\Vert T u \Vert _{W^{1,\infty }} \leq C \lambda$![]() .
.
Consequently, to prove that $d (Tu) =0$![]() , it suffices to check that $d (Tu)=0$
, it suffices to check that $d (Tu)=0$![]() pointwise almost everywhere. But we have $d (Tu) (y)=0$
pointwise almost everywhere. But we have $d (Tu) (y)=0$![]() for almost every $y \in X_{\lambda }^{\circ }$
for almost every $y \in X_{\lambda }^{\circ }$![]() , as $Tu =u$
, as $Tu =u$![]() in this (open) set. On the other hand, lemma 3.9 shows that $d (Tu) =0$
in this (open) set. On the other hand, lemma 3.9 shows that $d (Tu) =0$![]() for every $y \in (X_{\lambda }^C)$
for every $y \in (X_{\lambda }^C)$![]() . As for almost every $\lambda >0$
. As for almost every $\lambda >0$![]() we have $\mathcal {L}^N(\partial X_{\lambda }) =0$
we have $\mathcal {L}^N(\partial X_{\lambda }) =0$![]() , we are finished in showing that $d(Tu)=0$
, we are finished in showing that $d(Tu)=0$![]() .
.
It remains to check the bound for the set where $u \neq T u$![]() , i.e. (T2). But $\{ u \neq Tu\} \subset X_{\lambda }^C$
, i.e. (T2). But $\{ u \neq Tu\} \subset X_{\lambda }^C$![]() and the measure of the latter is bounded in lemma 3.7.
and the measure of the latter is bounded in lemma 3.7.
3.5. $L^{\infty }$ -bounds
-bounds
This section is devoted to the proof of lemma 3.8. Before proving the lemma, shortly recall that $Q_i$![]() is a cover of the bad set, every point is only contained in finitely many cubes $Q_i$
is a cover of the bad set, every point is only contained in finitely many cubes $Q_i$![]() and that $\varphi _i \in C^{\infty }(Q_i;[0,\,1])$
and that $\varphi _i \in C^{\infty }(Q_i;[0,\,1])$![]() is a partition of unity.
is a partition of unity.
In order to tackle the terms appearing in the definition of $A_k$![]() in the appropriate fashion, let us formulate the following lemma.
in the appropriate fashion, let us formulate the following lemma.
Lemma 3.10 Let $1\leq k \leq N-1$![]() , $Q_1=[-1/2,\,1/2]^N$
, $Q_1=[-1/2,\,1/2]^N$![]() , $Q_2,\,\ldots Q_{k+1}$
, $Q_2,\,\ldots Q_{k+1}$![]() cubes of sidelength $1/4 \leq l(Q_r) \leq 4$
cubes of sidelength $1/4 \leq l(Q_r) \leq 4$![]() with $Q_r \subset B_{10}(0)$
with $Q_r \subset B_{10}(0)$![]() , $2 \leq r \leq k+1$
, $2 \leq r \leq k+1$![]() . Suppose that $v \in L^1(B_{10}(0))$
. Suppose that $v \in L^1(B_{10}(0))$![]() . Then we can estimate
. Then we can estimate
Observe that this inequality scales as follows: If $Q_1=[-1/2 \rho,\,1/2 \rho ]$![]() and $v \in L^1(B_{10\rho }(0))$
and $v \in L^1(B_{10\rho }(0))$![]() , then the left-hand-side scales with a factor of $\rho ^k$
, then the left-hand-side scales with a factor of $\rho ^k$![]() and the right-hand-side scales with $\rho ^N$
and the right-hand-side scales with $\rho ^N$![]() .
.
It is possible to prove the lemma in various different ways (e.g. by transformation rule or coarea formula), below we use Young's convolution inequality.
Proof Proof of lemma 3.10:
We extend $v$![]() by zero outside of $B_{10}(0)$
by zero outside of $B_{10}(0)$![]() . First of all, we rewrite the integral in the simplex by transformation rule
. First of all, we rewrite the integral in the simplex by transformation rule

where $\mathbb {D}_k= \{t \in [0,\,1]^{k+1} \colon t_1+\ldots t_{k+1}=1\}$![]() . As $\mathcal {H}^k(\operatorname {Sim}(x_1,\,\ldots,\,x_{k+1}))$
. As $\mathcal {H}^k(\operatorname {Sim}(x_1,\,\ldots,\,x_{k+1}))$![]() is uniformly bounded, we can absorb it into a constant. We proceed by estimating the integral over $\mathbb {D}_k^1 = \{t \in \mathbb {D}_k \colon t_1 \geq {1}/({k+1})\}$
is uniformly bounded, we can absorb it into a constant. We proceed by estimating the integral over $\mathbb {D}_k^1 = \{t \in \mathbb {D}_k \colon t_1 \geq {1}/({k+1})\}$![]() instead of $\mathbb {D}_k$
instead of $\mathbb {D}_k$![]() , the estimate over the full integral follows from symmetry arguments. We now use Fubini's theorem and write
, the estimate over the full integral follows from symmetry arguments. We now use Fubini's theorem and write

where in this context (and this context only) $t_iQ_i$![]() is the cube with sidelength $t_il(Q_i)$
is the cube with sidelength $t_il(Q_i)$![]() and centre $t_ic_i$
and centre $t_ic_i$![]() . Applying Young's convolution inequality yields that
. Applying Young's convolution inequality yields that

where in the last inequality we use that $t_1 \geq {1}/{k+1}$![]() in $\mathbb {D}_k^1$
in $\mathbb {D}_k^1$![]() .
.
We are now ready to prove the Lipschitz bounds, i.e. lemma 3.8.
Proof Proof of lemma 3.8:
For (i) observe that all $\varphi _i$![]() 's are smooth and therefore any summand is smooth. Hence, as locally the sum is finite, we conclude $Tu \in C^{\infty }(X_{\lambda }^C;\Lambda ^{N-1})$
's are smooth and therefore any summand is smooth. Hence, as locally the sum is finite, we conclude $Tu \in C^{\infty }(X_{\lambda }^C;\Lambda ^{N-1})$![]() . In particular, only summing over a finite index set (e.g. $I \in \{1,\,\ldots,\,M\}^k$
. In particular, only summing over a finite index set (e.g. $I \in \{1,\,\ldots,\,M\}^k$![]() ), these sums are contained in $C_c^{\infty }(X_{\lambda };\Lambda ^{N-1})$
), these sums are contained in $C_c^{\infty }(X_{\lambda };\Lambda ^{N-1})$![]() .
.
Due to this observation, for (ii), it suffices to prove that the sum converges absolutely in $W^{1,1}(\mathbb {R}^N;\mathbb {R}^N)$![]() . Fix the first index of $I$
. Fix the first index of $I$![]() , i.e. fix $i_1 \in \mathbb {N}$
, i.e. fix $i_1 \in \mathbb {N}$![]() . Then only finitely many terms are nonzero. Moreover, $Q_{i_r} \cap Q_{i_1} \neq \emptyset$
. Then only finitely many terms are nonzero. Moreover, $Q_{i_r} \cap Q_{i_1} \neq \emptyset$![]() and therefore the sidelength of the cubes are comparable. Therefore,
and therefore the sidelength of the cubes are comparable. Therefore,
On the other hand, we apply lemma 3.10 to $v = D u[ \nu ] \cdot (y-z)$![]() . Observe that due to the definition of $Q_i$
. Observe that due to the definition of $Q_i$![]() , $20 Q_i \cap X_{\lambda } \neq \emptyset$
, $20 Q_i \cap X_{\lambda } \neq \emptyset$![]() and therefore, due to the definition of $X_{\lambda }$
and therefore, due to the definition of $X_{\lambda }$![]() as a sublevel set of the maximal function of $Du$
as a sublevel set of the maximal function of $Du$![]() and the estimate $\vert y- z \vert \leq Cl(Q_i)$
and the estimate $\vert y- z \vert \leq Cl(Q_i)$![]() ,
,
Therefore,
which leads to
The same bounds including the derivative lead to
and we conclude
and, as this function is supported on $Q_{i_1}$![]() , we obtain
, we obtain
Again, for only finitely many indices $I$![]() with this fixed $i_1$
with this fixed $i_1$![]() , the summand is nonzero, hence for any $j \in \mathbb {N}$
, the summand is nonzero, hence for any $j \in \mathbb {N}$![]()
Summing over all $j$![]() and realizing that the $Q_j$
and realizing that the $Q_j$![]() 's cover $X_{\lambda }^C$
's cover $X_{\lambda }^C$![]() only a finite number of times, we finally obtain
only a finite number of times, we finally obtain
Therefore, the sum converges absolutely in $W^{1,1}_0(X_\lambda ^C)$![]() , i.e. each $S_k u \in W^{1,1}_0(X_\lambda ^C)$
, i.e. each $S_k u \in W^{1,1}_0(X_\lambda ^C)$![]() .
.
The $W^{1,\infty }$![]() bound (iii) now follows from the previously made estimates.
bound (iii) now follows from the previously made estimates.
3.6. Calculations of the pointwise divergence/exterior derivative
In this section we show that for each $y \in X_{\lambda }^C$![]() we have $d Tu (y) =0$
we have $d Tu (y) =0$![]() . This is pure calculation combined with Stokes’ theorem. We formulate it in the following lemma. For further reference denote by
. This is pure calculation combined with Stokes’ theorem. We formulate it in the following lemma. For further reference denote by

Lemma 3.11 Let $y \in X^C$![]() . Then the following identities hold for the truncation terms as in definition 3.3
. Then the following identities hold for the truncation terms as in definition 3.3
(i) We have
\[ dT_0u ={-}R_1 u. \]
(ii) For $1 \leq k \leq N-2$
 we have
\[ dS_k u = R_{k}u -R_{k+1} u. \]
we have
\[ dS_k u = R_{k}u -R_{k+1} u. \]
(iii) We have
\[ dS_{N-1} u = R_{N-1} u. \]
Observe that lemma 3.9 instantly follows by summing over parts (i)–(ii).
Proof. We start with the exterior derivative of $T_0 u$![]() , i.e. (i). As the only term depending on the variable $y$
, i.e. (i). As the only term depending on the variable $y$![]() is $\varphi _i$
is $\varphi _i$![]() , we obtain for the derivative with respect to $y$
, we obtain for the derivative with respect to $y$![]()
Using that $\varphi _i$![]() is a partition of unity, i.e. $\sum _{j \in \mathbb {N}} \varphi _j=1$
is a partition of unity, i.e. $\sum _{j \in \mathbb {N}} \varphi _j=1$![]() and $\sum _{i \in \mathbb {N}} d \varphi _i =0$
and $\sum _{i \in \mathbb {N}} d \varphi _i =0$![]() in the interior of $X^C$
in the interior of $X^C$![]() , we obtain:
, we obtain:

Application of the fundamental theorem of calculus (i.e. one-dimensional Stokes’ theorem) component-wise yields
A similar trick leads to the second statement, (ii). Observe that, in contrast to statement (i), $A_k(I)$![]() does depend on $y$
does depend on $y$![]() , hence
, hence

Now a computation (it, for instance, suffices to check this coordinate-wise and while assuming that $Du[\nu (x_I)] = dx_1 \wedge \ldots \wedge dx_{N-k}$![]() ) reveals that
) reveals that
Hence, the second sum in (3.19) equals $R_k u$![]() . For the first term, we observe as $\varphi _{i_r}$
. For the first term, we observe as $\varphi _{i_r}$![]() is a partition of unity on $X^C$
is a partition of unity on $X^C$![]()

where $\tilde {I} =(i_1,\,\ldots,\,i_{k+2}) \in \mathbb {N}^{k+2}$![]() and $\tilde {I}_r=(i_1,\,\ldots,\,i_{r-1},\,i_{r+1},\,\ldots,\,i_{k+2})$
and $\tilde {I}_r=(i_1,\,\ldots,\,i_{r-1},\,i_{r+1},\,\ldots,\,i_{k+2})$![]() . Recall that
. Recall that
Thus, the terms in (3.20) form a boundary integral of a $(k+1)$![]() -dimensional simplex. After a suitable identification of spaces (i.e. identifying a wedge product space $\Lambda ^{N-1}$
-dimensional simplex. After a suitable identification of spaces (i.e. identifying a wedge product space $\Lambda ^{N-1}$![]() with suitable (skew-symmetric) elements in $\Lambda ^k \otimes \Lambda ^{N-1-k}$
with suitable (skew-symmetric) elements in $\Lambda ^k \otimes \Lambda ^{N-1-k}$![]() ), we can apply Stokes’ theorem by writing
), we can apply Stokes’ theorem by writing

for suitable $F\colon \mathbb {R}^N \to \Lambda ^k \otimes \Lambda ^{N-k-1}$![]() . Applying Stokes’ theorem componentwise, one obtains
. Applying Stokes’ theorem componentwise, one obtains

Again, a for instance coordinate-wise computation (using that $du=0$![]() ) yields that the latter integral is exactly $-(N-k)B_{k+1}(\tilde {I})$
) yields that the latter integral is exactly $-(N-k)B_{k+1}(\tilde {I})$![]() .
.
For (iii) the calculation is exactly the same. It suffices to see that $R_N u =0$![]() , i.e. that $B_N(I)=0$
, i.e. that $B_N(I)=0$![]() . Note that for any index $I$
. Note that for any index $I$![]()
Considering the definition of $Du[\nu (x_I)]$![]() for $\nu (x_I) \in V^N \simeq \mathbb {R}$
for $\nu (x_I) \in V^N \simeq \mathbb {R}$![]() , we obtain $Du[\nu (x_I)] = du (\nu (x_I))$
, we obtain $Du[\nu (x_I)] = du (\nu (x_I))$![]() . As $u$
. As $u$![]() is solenoidal, $du=0$
is solenoidal, $du=0$![]() and hence $B_N(I)=0$
and hence $B_N(I)=0$![]() . Therefore $R_{N}=0$
. Therefore $R_{N}=0$![]() , finishing the proof.
, finishing the proof.
4. Further remarks
In this closing section we discuss some further applications/variants of the technique that was used in § 3 to obtain the truncation.
4.1. Truncation for closed differential forms
The solenoidal truncation is achieved by identifying functions $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^N)$![]() with a non-renamed closed form $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$
with a non-renamed closed form $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() . Via careful construction of the corrector terms using the structure of differential forms we then obtained a solenoidal trunction. This construction with the same arguments can also be repeated if $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$
. Via careful construction of the corrector terms using the structure of differential forms we then obtained a solenoidal trunction. This construction with the same arguments can also be repeated if $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^{N-1})$![]() is replaced by a lower-order form, i.e. $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^r)$
is replaced by a lower-order form, i.e. $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^r)$![]() . In particular, we get the following result.
. In particular, we get the following result.
Proposition 4.1 Let $N \geq 2$![]() and suppose that $1 \leq p <\infty$
and suppose that $1 \leq p <\infty$![]() , $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^r)$
, $u \in W^{1,p}(\mathbb {R}^N;\Lambda ^r)$![]() obeys $d u=0$
obeys $d u=0$![]() and that $L>0$
and that $L>0$![]() . There is a (dimensional) constant $C>0$
. There is a (dimensional) constant $C>0$![]() and a function $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\Lambda ^r)$
and a function $\tilde {u} \in W^{1,\infty }(\mathbb {R}^N;\Lambda ^r)$![]() , such that
, such that
(T1) $\Vert \tilde {u} \Vert _{W^{1,\infty }} \leq CL$
 ;
;(T2) $\mathcal {L}^N(\{ u \neq \tilde {u}\}) \leq C(d)L^{-p} \int _{\{\vert u \vert + \vert Du\vert \geq L\}} \vert u \vert + \vert D u \vert \,\mathrm {d} x$
 ;
;[(T3) $d \tilde {u} =0$
 .
.
As the proof is very similar to the proof in § 3 we only give a brief sketch. We take the same setup as in § 3.3, i.e. we take the bad set as a sublevel set of the maximal function, cover it with cubes $Q_i$![]() , consider a partition of unity $\varphi _i$
, consider a partition of unity $\varphi _i$![]() and measures $\mu _i$
and measures $\mu _i$![]() .
.
Proof Proof(Sketch):
Parallel to the beginning of § 3.3, for $u \colon \mathbb {R}^N \to \Lambda ^{r}$![]() and a normal $\nu \in V^s$
and a normal $\nu \in V^s$![]() , $1 \leq s \leq r$
, $1 \leq s \leq r$![]() , we may give a meaning to
, we may give a meaning to
by understanding $Du$![]() as an element of $\Lambda ^1 \otimes \Lambda ^{r}$
as an element of $\Lambda ^1 \otimes \Lambda ^{r}$![]() . Then,
. Then,
Now as in definition 3.3, consider

where again $T_0 u$![]() is the usual Lipschitz extension
is the usual Lipschitz extension
and

Define the integral in (4.3) to be zero if the simplex $\operatorname {Sim}(x_I)$![]() is degenerate.
is degenerate.
We claim that with $X=X_{\lambda }= \{ M u \leq \lambda \} \cup \{\mathscr {M} (Du) \leq \lambda \}$![]() and $\lambda =L/2$
and $\lambda =L/2$![]() , $Tu$
, $Tu$![]() obeys the properties of the proposition.
obeys the properties of the proposition.
To show this claim, might argue exactly as in § 3: First of all, parallel to lemma 3.6, $T_0$![]() is a sufficient unconstrained truncation and the measure of the bad set is also already bounded; lemma 3.7 still works as it never really used the structure of the target space $\Lambda ^{N-1}$
is a sufficient unconstrained truncation and the measure of the bad set is also already bounded; lemma 3.7 still works as it never really used the structure of the target space $\Lambda ^{N-1}$![]() .
.
Furthermore, by using the same calculation, we can show the natural counterpart to lemma 3.8 (the Lipschitz bounds). Finally, we may show the analogue of lemma 3.11, i.e. if for $1 \leq k \leq r$![]()

then for any $1 \leq k \leq r-1$![]() we have
we have
As seen in § 3, these statements then complete the proof, as we can show the Lipschitz bound, the bound on the set $\{ u \neq Tu\}$![]() and closedness of the differential form $Tu$
and closedness of the differential form $Tu$![]() .
.
4.2. General differential constraints
Generalizing above question, taking some $u \in W^{1,p}(\mathbb {R}^N;\mathbb {R}^d)$![]() , one may ask to truncate under the first-order differential constraint
, one may ask to truncate under the first-order differential constraint
where

Unconstrained truncation corresponds to $\mathscr {A} =0$![]() and the case of differential forms is represented by $\mathscr {A} = d$
and the case of differential forms is represented by $\mathscr {A} = d$![]() and, in particular, closed $(N-1)$
and, in particular, closed $(N-1)$![]() forms by $\mathscr {A}=\operatorname {div}$
forms by $\mathscr {A}=\operatorname {div}$![]() . While this general case is out of reach with the results of this paper, the technique of constructing corrector terms does not seem to be entirely hopeless. Meanwhile, similar to [Reference Behn, Gmeineder and Schiffer5, Conjecture 6.4], we conjecture that a truncation result á la 1.1 is possible for some $\mathscr {A}$
. While this general case is out of reach with the results of this paper, the technique of constructing corrector terms does not seem to be entirely hopeless. Meanwhile, similar to [Reference Behn, Gmeineder and Schiffer5, Conjecture 6.4], we conjecture that a truncation result á la 1.1 is possible for some $\mathscr {A}$![]() , whenever $\mathscr {A}$
, whenever $\mathscr {A}$![]() satisfies the complex constant rank condition (i.e. the Fourier symbol has constant rank over all complex Fourier modes).
satisfies the complex constant rank condition (i.e. the Fourier symbol has constant rank over all complex Fourier modes).
4.3. Lower regularity
Corresponding to the $W^{1,p}$![]() -case one might ask to truncate divergence-free $L^p$
-case one might ask to truncate divergence-free $L^p$![]() functions to be in $L^{\infty }$
functions to be in $L^{\infty }$![]() (cf. [Reference Schiffer32]). While these questions turn out to be quite different, they both fit in a larger common framework. In our setting of divergence-free $W^{1,p}$
(cf. [Reference Schiffer32]). While these questions turn out to be quite different, they both fit in a larger common framework. In our setting of divergence-free $W^{1,p}$![]() -truncation, consider $w=Du$
-truncation, consider $w=Du$![]() . The solenoidal Lipschitz truncation now corresponds to a $L^{\infty }$
. The solenoidal Lipschitz truncation now corresponds to a $L^{\infty }$![]() -truncation of $w$
-truncation of $w$![]() under the following constraints
under the following constraints
i.e. $\operatorname {curl}$![]() is taken column-wise and $\operatorname {div}$
is taken column-wise and $\operatorname {div}$![]() row-wise. This can be abstractly set as $\mathscr {B} w=0$
row-wise. This can be abstractly set as $\mathscr {B} w=0$![]() . Consequently, Lipschitz truncation of a function $u$
. Consequently, Lipschitz truncation of a function $u$![]() under a constraint $\mathscr {A} u=0$
under a constraint $\mathscr {A} u=0$![]() is closely connected to the $L^{\infty }$
is closely connected to the $L^{\infty }$![]() -truncation of $w$
-truncation of $w$![]() ($=Du$
($=Du$![]() ) under some constraint $\mathscr {B} w=0$
) under some constraint $\mathscr {B} w=0$![]() . As mentioned before, the latter has been examined in [Reference Behn, Gmeineder and Schiffer5, Reference Schiffer32] in greater detail; in particular (as above) the authors in [Reference Behn, Gmeineder and Schiffer5] have conjectured that a low-regularity truncation is possible whenever $\mathscr {B}$
. As mentioned before, the latter has been examined in [Reference Behn, Gmeineder and Schiffer5, Reference Schiffer32] in greater detail; in particular (as above) the authors in [Reference Behn, Gmeineder and Schiffer5] have conjectured that a low-regularity truncation is possible whenever $\mathscr {B}$![]() obeys the complex constant rank condition.
obeys the complex constant rank condition.
4.4. Solenoidal extensions for $W^{1,\infty }$
As alluded to in § 2.2, extensions and truncations are connected from a technical perspective. Indeed, in the unconstrained setting, truncation is derived by extending the function of a cleverly chosen subset to the full space. As it becomes visible through the formula for the truncation (3.8), the same analogy is not true for constrained truncation and extension. In particular, all the approaches to constrained truncation (cf. [Reference Breit, Diening and Fuchs7, Reference Breit, Diening and Schwarzacher9] etc. and (3.8)) use to a certain extent that the function is already defined on the bad set. Therefore, constructing an extension is actually more challenging than constructing a truncation, and while certain key ideas stay the same, there are a lot of challenges coming from the geometric properties of the underlying domain. We refer to the forthcoming article [Reference Gmeineder and Schiffer23] for a thorough investigation of solenoidal extension, especially for the borderline cases $p=1$![]() and $p=\infty$
and $p=\infty$![]() (also cf. [Reference Acosta, Durán and Muschietti3, Reference Kato, Mitrea, Ponce and Taylor24] for $1< p<\infty$
(also cf. [Reference Acosta, Durán and Muschietti3, Reference Kato, Mitrea, Ponce and Taylor24] for $1< p<\infty$![]() ).
).
Acknowledgements
The author would like to thank Franz Gmeineder and the anonymous referee for helpful suggestions. The research conducted in this work was achieved while the author was still supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the graduate school BIGS of the Hausdorff Center for Mathematics (GZ EXC 59 and 2047/1, Projekt-ID 390685813).