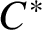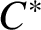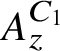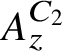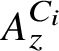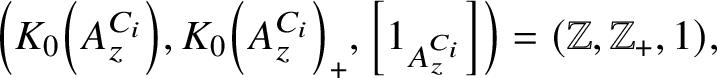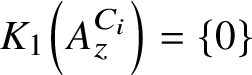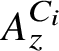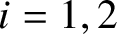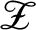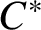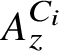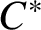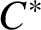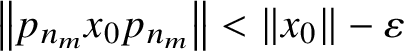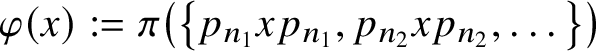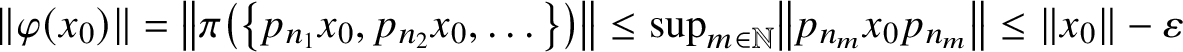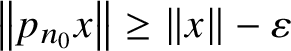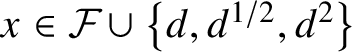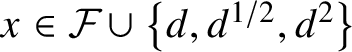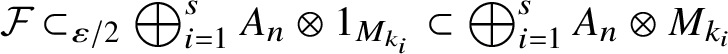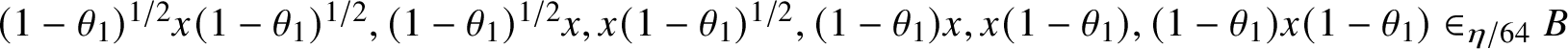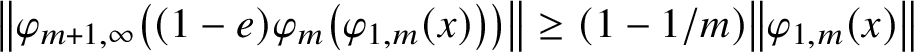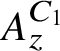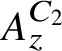1. Introduction
Simple unital projectionless amenable
![]() $C^*$
-algebras were first constructed by Blackadar [Reference Blackadar2]. The
$C^*$
-algebras were first constructed by Blackadar [Reference Blackadar2]. The
![]() $C^*$
-algebra A constructed by Blackadar has the property that
$C^*$
-algebra A constructed by Blackadar has the property that
![]() $K_0(A)=\mathbb {Z}$
with the usual order but with nontrivial
$K_0(A)=\mathbb {Z}$
with the usual order but with nontrivial
![]() $K_1(A)$
. The Jiang–Su algebra
$K_1(A)$
. The Jiang–Su algebra
![]() ${\mathscr Z}$
given by Jiang and Su [Reference Jiang and Su27] is a unital infinite-dimensional separable amenable simple
${\mathscr Z}$
given by Jiang and Su [Reference Jiang and Su27] is a unital infinite-dimensional separable amenable simple
![]() $C^*$
-algebra with Elliott invariant exactly the same as that of the complex field
$C^*$
-algebra with Elliott invariant exactly the same as that of the complex field
![]() $\mathbb {C}$
, Let A be any
$\mathbb {C}$
, Let A be any
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $C^*$
-algebra. Then
$C^*$
-algebra. Then
![]() $K_i(A)=K_i(A\otimes {\mathscr Z})$
(
$K_i(A)=K_i(A\otimes {\mathscr Z})$
(
![]() $i=0,1$
) as abelian groups and
$i=0,1$
) as abelian groups and
![]() $T(A)\cong T(A\otimes {\mathscr Z})$
. If A is a separable simple
$T(A)\cong T(A\otimes {\mathscr Z})$
. If A is a separable simple
![]() $C^*$
-algebra, then
$C^*$
-algebra, then
![]() $A\otimes {\mathscr Z}$
has nice regularity properties. For example,
$A\otimes {\mathscr Z}$
has nice regularity properties. For example,
![]() $A\otimes {\mathscr Z}$
is either purely infinite or stably finite [Reference Rørdam42]. In fact, if
$A\otimes {\mathscr Z}$
is either purely infinite or stably finite [Reference Rørdam42]. In fact, if
![]() $A\otimes {\mathscr Z}$
is not purely infinite, then it has stable rank one when A is not stably projectionless [Reference Rørdam42], or it almost has stable rank one when it is stably projectionless [Reference Robert38]. Also,
$A\otimes {\mathscr Z}$
is not purely infinite, then it has stable rank one when A is not stably projectionless [Reference Rørdam42], or it almost has stable rank one when it is stably projectionless [Reference Robert38]. Also,
![]() $A\otimes {\mathscr Z}$
has weakly unperforated
$A\otimes {\mathscr Z}$
has weakly unperforated
![]() $K_0$
-group [Reference Gong, Jiang and Su23]. Another important regularity property is that
$K_0$
-group [Reference Gong, Jiang and Su23]. Another important regularity property is that
![]() $A\otimes {\mathscr Z}$
has strict comparison [Reference Rørdam42] (see also Definition 2.6). If A has weakly unperforated
$A\otimes {\mathscr Z}$
has strict comparison [Reference Rørdam42] (see also Definition 2.6). If A has weakly unperforated
![]() $K_0(A)$
, then A and
$K_0(A)$
, then A and
![]() $A\otimes {\mathscr Z}$
have the same Elliott invariant. In other words, A and
$A\otimes {\mathscr Z}$
have the same Elliott invariant. In other words, A and
![]() $A\otimes {\mathscr Z}$
are not distinguishable from the Elliott invariant.
$A\otimes {\mathscr Z}$
are not distinguishable from the Elliott invariant.
The Jiang–Su algebra
![]() ${\mathscr Z}$
is an inductive limit of
${\mathscr Z}$
is an inductive limit of
![]() $1$
-dimensional noncommutative CW complexes. In fact,
$1$
-dimensional noncommutative CW complexes. In fact,
![]() ${\mathscr Z}$
is the unique infinite-dimensional separable simple
${\mathscr Z}$
is the unique infinite-dimensional separable simple
![]() $C^*$
-algebra with finite nuclear dimension in the UCT class which has the same Elliott invariant as that of the complex field
$C^*$
-algebra with finite nuclear dimension in the UCT class which has the same Elliott invariant as that of the complex field
![]() $\mathbb {C}$
(see [Reference Elliott and Niu16, Corollary 4.12]). These properties give
$\mathbb {C}$
(see [Reference Elliott and Niu16, Corollary 4.12]). These properties give
![]() ${\mathscr Z}$
a prominent role in the study of structure of
${\mathscr Z}$
a prominent role in the study of structure of
![]() $C^*$
-algebras, in particular in the study of classification of amenable simple
$C^*$
-algebras, in particular in the study of classification of amenable simple
![]() $C^*$
-algebras.
$C^*$
-algebras.
Attempts to construct a nonnuclear Jiang–Su-type
![]() $C^*$
-algebra have been on the horizon for over a decade. In particular, after Dădărlat’s construction of nonamenable models for non–type I separable unital AF-algebras [Reference Dădărlat13], this should be possible. The construction in [Reference Dădărlat13] generalised some earlier constructions of simple
$C^*$
-algebra have been on the horizon for over a decade. In particular, after Dădărlat’s construction of nonamenable models for non–type I separable unital AF-algebras [Reference Dădărlat13], this should be possible. The construction in [Reference Dădărlat13] generalised some earlier constructions of simple
![]() $C^*$
-algebras of real rank zero such as that of Goodearl [Reference Goodearl25]. Jiang and Su’s construction has a quite different feature. To avoid producing any nontrivial projections, unlike Dădărlat’s construction, Jiang and Su did not use any finite-dimensional representations as a direct summand of connecting maps in the inductive systems. The construction used prime-dimension drop algebras, and connecting maps were highly inventive so that the traces eventually collapse to one. In fact, Rørdam and Winter took another approach [Reference Rørdam and Winter43] using a
$C^*$
-algebras of real rank zero such as that of Goodearl [Reference Goodearl25]. Jiang and Su’s construction has a quite different feature. To avoid producing any nontrivial projections, unlike Dădărlat’s construction, Jiang and Su did not use any finite-dimensional representations as a direct summand of connecting maps in the inductive systems. The construction used prime-dimension drop algebras, and connecting maps were highly inventive so that the traces eventually collapse to one. In fact, Rørdam and Winter took another approach [Reference Rørdam and Winter43] using a
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $C\!\left([0,1], M_{\mathfrak {p}}\otimes M_{\mathfrak {q}}\right )$
, where
$C\!\left([0,1], M_{\mathfrak {p}}\otimes M_{\mathfrak {q}}\right )$
, where
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $\mathfrak {q}$
are relatively prime supernatural numbers. One possible attempt to construct a nonamenable Jiang–Su-type
$\mathfrak {q}$
are relatively prime supernatural numbers. One possible attempt to construct a nonamenable Jiang–Su-type
![]() $C^*$
-algebra would use
$C^*$
-algebra would use
![]() $C\!\left([0,1], B_{\mathfrak {p}}\otimes B_{{\mathfrak {q}}}\right )$
, where
$C\!\left([0,1], B_{\mathfrak {p}}\otimes B_{{\mathfrak {q}}}\right )$
, where
![]() $B_{\mathfrak {p}}$
and
$B_{\mathfrak {p}}$
and
![]() $B_{\mathfrak {q}}$
are, respectively, nonamenable models for
$B_{\mathfrak {q}}$
are, respectively, nonamenable models for
![]() $M_{\mathfrak {p}}$
and
$M_{\mathfrak {p}}$
and
![]() $M_{\mathfrak {q}}$
constructed in [Reference Dădărlat13]. However, one usually would avoid computation of the K-theory of tensor products of nonexact simple
$M_{\mathfrak {q}}$
constructed in [Reference Dădărlat13]. However, one usually would avoid computation of the K-theory of tensor products of nonexact simple
![]() $C^*$
-algebras such as
$C^*$
-algebras such as
![]() $B_{\mathfrak {p}}$
and
$B_{\mathfrak {p}}$
and
![]() $B_{\mathfrak {q}}$
. Moreover, Rørdam and Winter’s construction depends on knowing the existence of the Jiang–Su algebra
$B_{\mathfrak {q}}$
. Moreover, Rørdam and Winter’s construction depends on knowing the existence of the Jiang–Su algebra
![]() ${\mathscr Z}$
. On the other hand, if one considers nonexact interval ‘dimension drop algebras’, besides controlling K-theory one has additional issues such as the fact that each fibre of the ‘dimension drop algebra’ is not simple (unlike the usual dimension drop algebras, whose fibres are simple matrix algebras).
${\mathscr Z}$
. On the other hand, if one considers nonexact interval ‘dimension drop algebras’, besides controlling K-theory one has additional issues such as the fact that each fibre of the ‘dimension drop algebra’ is not simple (unlike the usual dimension drop algebras, whose fibres are simple matrix algebras).
We will present some nonexact (or exact but nonnuclear) unital separable simple
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_z^C$
which have the property that their Elliott invariants are the same as that of the Jiang–Su algebra
$A_z^C$
which have the property that their Elliott invariants are the same as that of the Jiang–Su algebra
![]() ${\mathscr Z}$
– namely,
${\mathscr Z}$
– namely,
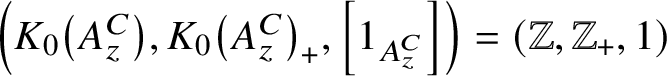 $\left (K_0\left (A_z^C\right ), K_0\left (A_z^C\right )_+, \left [1_{A_z^C}\right ]\right )=(\mathbb {Z}, \mathbb {Z}_+,1)$
,
$\left (K_0\left (A_z^C\right ), K_0\left (A_z^C\right )_+, \left [1_{A_z^C}\right ]\right )=(\mathbb {Z}, \mathbb {Z}_+,1)$
,
![]() $K_1\left (A_z^C\right ) =\{0\}$
and
$K_1\left (A_z^C\right ) =\{0\}$
and
![]() $A_z^C$
has a unique tracial state. Moreover,
$A_z^C$
has a unique tracial state. Moreover,
![]() $A_z^C$
has stable rank one and has strict comparison for positive elements.
$A_z^C$
has stable rank one and has strict comparison for positive elements.
![]() $A_z^C$
has no (nonzero)
$A_z^C$
has no (nonzero)
![]() $2$
-quasitrace other than the unique tracial state. Even though
$2$
-quasitrace other than the unique tracial state. Even though
![]() $A_z^C$
may not be exact, it is essentially tracially approximated by
$A_z^C$
may not be exact, it is essentially tracially approximated by
![]() ${\mathscr Z}$
. In particular, it is essentially tracially approximated by unital simple
${\mathscr Z}$
. In particular, it is essentially tracially approximated by unital simple
![]() $C^*$
-algebras with nuclear dimension
$C^*$
-algebras with nuclear dimension
![]() $1$
.
$1$
.
In this paper, we will also study the tracial approximation. We will make it precise what we mean by saying that
![]() $A_z^C$
is essentially tracially approximated by
$A_z^C$
is essentially tracially approximated by
![]() ${\mathscr Z}$
(Definition 3.1, Lemma 8.1). We expect that regularity properties such as stable rank one, strict comparison for positive elements and almost unperforated Cuntz semigroups, as well as approximate divisibility, are preserved by tracial approximation. In fact, we show that if a unital separable simple
${\mathscr Z}$
(Definition 3.1, Lemma 8.1). We expect that regularity properties such as stable rank one, strict comparison for positive elements and almost unperforated Cuntz semigroups, as well as approximate divisibility, are preserved by tracial approximation. In fact, we show that if a unital separable simple
![]() $C^*$
-algebra A is essentially tracially in
$C^*$
-algebra A is essentially tracially in
![]() ${\cal C}_{\mathscr Z}$
, the class of
${\cal C}_{\mathscr Z}$
, the class of
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras, then – as far as the usual regularity properties are concerned – A behaves just like
$C^*$
-algebras, then – as far as the usual regularity properties are concerned – A behaves just like
![]() $C^*$
-algebras in
$C^*$
-algebras in
![]() ${\cal C}_{\mathscr Z}$
. More precisely, we show that if A is simple and essentially tracially in
${\cal C}_{\mathscr Z}$
. More precisely, we show that if A is simple and essentially tracially in
![]() ${\cal C}_{\mathscr Z}$
, then A is tracially approximately divisible. If A is not purely infinite, then it has stable rank one (or almost has stable rank one, if A is not unital) and has strict comparison, and its Cuntz semigroup is almost unperforated. If A is essentially tracially in the class of exact
${\cal C}_{\mathscr Z}$
, then A is tracially approximately divisible. If A is not purely infinite, then it has stable rank one (or almost has stable rank one, if A is not unital) and has strict comparison, and its Cuntz semigroup is almost unperforated. If A is essentially tracially in the class of exact
![]() $C^*$
-algebras, then every
$C^*$
-algebras, then every
![]() $2$
-quasitrace of
$2$
-quasitrace of
![]() $\overline {aAa}$
, for any a in the Pedersen ideal of A, is in fact a trace.
$\overline {aAa}$
, for any a in the Pedersen ideal of A, is in fact a trace.
Using
![]() $A_z^C$
, we present a large class of nonexact (or exact but nonnuclear) unital separable simple
$A_z^C$
, we present a large class of nonexact (or exact but nonnuclear) unital separable simple
![]() $C^*$
-algebras which exhaust all possible weakly unperforated Elliott invariants. Moreover, every
$C^*$
-algebras which exhaust all possible weakly unperforated Elliott invariants. Moreover, every
![]() $C^*$
-algebra in the class is essentially tracially in the class of unital separable simple
$C^*$
-algebra in the class is essentially tracially in the class of unital separable simple
![]() $C^*$
-algebras which are
$C^*$
-algebras which are
![]() ${\mathscr Z}$
-stable, and has nuclear dimension at most
${\mathscr Z}$
-stable, and has nuclear dimension at most
![]() $1$
.
$1$
.
The paper is organised as follows: Section 2 serves as preliminaries, where some frequently used notations and definitions are listed. Section 3 introduces the notion of essential tracial approximation for simple
![]() $C^*$
-algebras. In Section 4 we present some basic properties of essential tracial approximation. For example, we show that if A is a simple
$C^*$
-algebras. In Section 4 we present some basic properties of essential tracial approximation. For example, we show that if A is a simple
![]() $C^*$
-algebra and is essentially tracially approximated by
$C^*$
-algebra and is essentially tracially approximated by
![]() $C^*$
-algebras whose Cuntz semigroups are almost unperforated, then the Cuntz semigroup of A is almost unperforated (Theorem 4.3). In particular, A has strict comparison for positive elements. In Section 5 we study the separable simple
$C^*$
-algebras whose Cuntz semigroups are almost unperforated, then the Cuntz semigroup of A is almost unperforated (Theorem 4.3). In particular, A has strict comparison for positive elements. In Section 5 we study the separable simple
![]() $C^*$
-algebras which are essentially tracially approximated by
$C^*$
-algebras which are essentially tracially approximated by
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras. We show that such
$C^*$
-algebras. We show that such
![]() $C^*$
-algebras are either purely infinite or almost have stable rank one (or do have stable rank one, if the
$C^*$
-algebras are either purely infinite or almost have stable rank one (or do have stable rank one, if the
![]() $C^*$
-algebras are unital). These simple
$C^*$
-algebras are unital). These simple
![]() $C^*$
-algebras are tracially approximately divisible and have strict comparison for positive elements. In Section 6 we begin the construction of
$C^*$
-algebras are tracially approximately divisible and have strict comparison for positive elements. In Section 6 we begin the construction of
![]() $A_z^C$
. In Section 7 we show that the construction in Section 6 can be made simple, and the Elliott invariant of
$A_z^C$
. In Section 7 we show that the construction in Section 6 can be made simple, and the Elliott invariant of
![]() $A_z^C$
is precisely the same as that of a complex field, just as with the Jiang–Su algebra
$A_z^C$
is precisely the same as that of a complex field, just as with the Jiang–Su algebra
![]() ${\mathscr Z}$
. In Section 8 we show that
${\mathscr Z}$
. In Section 8 we show that
![]() $A_z^C$
has all expected regularity properties. Moreover,
$A_z^C$
has all expected regularity properties. Moreover,
![]() $A_z^C$
is essentially tracially approximated by
$A_z^C$
is essentially tracially approximated by
![]() ${\mathscr Z}$
. Using
${\mathscr Z}$
. Using
![]() $A_z^C$
, we also produce, for each weakly unperforated Elliott invariant, a unital separable simple nonexact (or exact but nonnuclear)
$A_z^C$
, we also produce, for each weakly unperforated Elliott invariant, a unital separable simple nonexact (or exact but nonnuclear)
![]() $C^*$
-algebra B which has the said Elliott invariant, has stable rank one, is essentially tracially approximated by
$C^*$
-algebra B which has the said Elliott invariant, has stable rank one, is essentially tracially approximated by
![]() $C^*$
-algebras with nuclear dimension at most
$C^*$
-algebras with nuclear dimension at most
![]() $1$
, has almost unperforated Cuntz semigroup, has strict comparison for positive elements and has no
$1$
, has almost unperforated Cuntz semigroup, has strict comparison for positive elements and has no
![]() $2$
-quasitraces which are not traces.
$2$
-quasitraces which are not traces.
2. Preliminaries
In this paper, the set of all positive integers is denoted by
![]() $\mathbb {N}$
. If A is unital,
$\mathbb {N}$
. If A is unital,
![]() $U(A)$
is the unitary group of A. A linear map is said to be c.p.c., if it is a completely positive contraction.
$U(A)$
is the unitary group of A. A linear map is said to be c.p.c., if it is a completely positive contraction.
Notation 2.1. Let A be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() ${\cal F}\subset A$
be a subset. Let
${\cal F}\subset A$
be a subset. Let
![]() $\epsilon>0$
. Set
$\epsilon>0$
. Set
![]() $a,b\in A$
and write
$a,b\in A$
and write
![]() $a\approx _{\epsilon }b$
if
$a\approx _{\epsilon }b$
if
![]() $\lVert a-b\rVert < \epsilon $
. We write
$\lVert a-b\rVert < \epsilon $
. We write
![]() $a\in _\varepsilon {\cal F}$
if there is
$a\in _\varepsilon {\cal F}$
if there is
![]() $x\in {\cal F}$
such that
$x\in {\cal F}$
such that
![]() $a\approx _\varepsilon x$
.
$a\approx _\varepsilon x$
.
Notation 2.2. Let A be a
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $S\subset A$
be a subset of A. Denote by
$S\subset A$
be a subset of A. Denote by
![]() $\mathrm {Her}_A(S)$
(or just
$\mathrm {Her}_A(S)$
(or just
![]() $\mathrm {Her}(S)$
, when A is clear) the hereditary
$\mathrm {Her}(S)$
, when A is clear) the hereditary
![]() $C^*$
-subalgebra of A generated by S. Denote by
$C^*$
-subalgebra of A generated by S. Denote by
![]() $A^{\textbf{1}}$
the closed unit ball of A, by
$A^{\textbf{1}}$
the closed unit ball of A, by
![]() $A_+$
the set of all positive elements in A, by
$A_+$
the set of all positive elements in A, by
![]() $A_+^{\textbf{1}}:=A_+\cap A^{\textbf{1}}$
and by
$A_+^{\textbf{1}}:=A_+\cap A^{\textbf{1}}$
and by
![]() $A_{\mathrm {sa}}$
the set of all self-adjoint elements in A. Denote by
$A_{\mathrm {sa}}$
the set of all self-adjoint elements in A. Denote by
![]() $\widetilde A$
(or
$\widetilde A$
(or
![]() $A^{\sim }$
) the minimal unitisation of A. When A is unital, denote by
$A^{\sim }$
) the minimal unitisation of A. When A is unital, denote by
![]() $GL(A)$
the set of invertible elements of A and by
$GL(A)$
the set of invertible elements of A and by
![]() $U(A)$
the unitary group of A.
$U(A)$
the unitary group of A.
Notation 2.3. Let
![]() $\epsilon>0$
. Define a continuous function
$\epsilon>0$
. Define a continuous function
![]() $f_{\epsilon }: {{[0,+\infty )}} \rightarrow [0,1]$
by
$f_{\epsilon }: {{[0,+\infty )}} \rightarrow [0,1]$
by
 $$ \begin{align*} f_{\epsilon}(t) := \begin{cases} 0, &t\in {{[0,\epsilon/2]}},\\ 1, &t\in [\epsilon,\infty),\\ \mathrm{linear}, &{t\in[\epsilon/2, \epsilon].} \end{cases} \end{align*} $$
$$ \begin{align*} f_{\epsilon}(t) := \begin{cases} 0, &t\in {{[0,\epsilon/2]}},\\ 1, &t\in [\epsilon,\infty),\\ \mathrm{linear}, &{t\in[\epsilon/2, \epsilon].} \end{cases} \end{align*} $$
Definition 2.4. Let A be a
![]() $C^*$
-algebra and set
$C^*$
-algebra and set
![]() $M_{\infty }(A)_+:=\bigcup _{n\in \mathbb {N}}M_n(A)_+$
. For
$M_{\infty }(A)_+:=\bigcup _{n\in \mathbb {N}}M_n(A)_+$
. For
![]() $x\in M_n(A)$
, we identify x with
$x\in M_n(A)$
, we identify x with
![]() $\mathrm {diag}(x,0)\in M_{n+m}(A)$
for all
$\mathrm {diag}(x,0)\in M_{n+m}(A)$
for all
![]() $m\in \mathbb {N}$
. Set
$m\in \mathbb {N}$
. Set
![]() $a\in M_n(A)_+$
and
$a\in M_n(A)_+$
and
![]() $b\in M_m(A)_+$
. We may write
$b\in M_m(A)_+$
. We may write
![]() $a\oplus b:=\mathrm {diag}(a,b)\in M_{n+m}(A)_+$
. If
$a\oplus b:=\mathrm {diag}(a,b)\in M_{n+m}(A)_+$
. If
![]() $a, b\in M_n(A)$
, we write
$a, b\in M_n(A)$
, we write
![]() $a \lesssim b$
if there are
$a \lesssim b$
if there are
![]() $x_i\in M_n(A)$
such that
$x_i\in M_n(A)$
such that
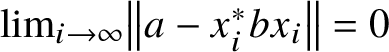 $\lim _{i\rightarrow \infty }\left \lVert a-x_i^*bx_i\right \rVert =0$
. We write
$\lim _{i\rightarrow \infty }\left \lVert a-x_i^*bx_i\right \rVert =0$
. We write
![]() $a \sim b$
if
$a \sim b$
if
![]() $a \lesssim b$
and
$a \lesssim b$
and
![]() $b \lesssim a$
hold. The Cuntz relation
$b \lesssim a$
hold. The Cuntz relation
![]() $\sim $
is an equivalence relation. Set
$\sim $
is an equivalence relation. Set
![]() $W(A):=M_{\infty }(A)_+/\sim $
. Let
$W(A):=M_{\infty }(A)_+/\sim $
. Let
![]() $\langle a\rangle $
denote the equivalence class of a. We write
$\langle a\rangle $
denote the equivalence class of a. We write
![]() $\langle a\rangle \leq \langle b\rangle $
if
$\langle a\rangle \leq \langle b\rangle $
if
![]() $a \lesssim b$
.
$a \lesssim b$
.
![]() $(W(A),\leq )$
is a partially ordered abelian semigroup. Let
$(W(A),\leq )$
is a partially ordered abelian semigroup. Let
![]() $\mathrm {Cu}(A)=W(A\otimes {\cal K})$
.
$\mathrm {Cu}(A)=W(A\otimes {\cal K})$
.
![]() $W(A)$
(resp.,
$W(A)$
(resp.,
![]() $\mathrm {Cu}(A)$
) is called almost unperforated if, for any
$\mathrm {Cu}(A)$
) is called almost unperforated if, for any
![]() $\langle a \rangle , \langle b\rangle \in W(A)$
(resp.,
$\langle a \rangle , \langle b\rangle \in W(A)$
(resp.,
![]() $\mathrm {Cu}(A)$
) and any
$\mathrm {Cu}(A)$
) and any
![]() $k\in \mathbb {N}$
, when
$k\in \mathbb {N}$
, when
![]() $(k+1)\langle a\rangle \leq k\langle b\rangle $
, we have
$(k+1)\langle a\rangle \leq k\langle b\rangle $
, we have
![]() $\langle a \rangle \leq \langle b\rangle $
(see [Reference Rørdam40]).
$\langle a \rangle \leq \langle b\rangle $
(see [Reference Rørdam40]).
Let
![]() $B\subset A$
be a hereditary
$B\subset A$
be a hereditary
![]() $C^*$
-subalgebra, and set
$C^*$
-subalgebra, and set
![]() $a,b\in B_+$
. It is clear that
$a,b\in B_+$
. It is clear that
![]() $a\lesssim _B b$
implies
$a\lesssim _B b$
implies
![]() $a\lesssim _A b$
. Conversely, if
$a\lesssim _A b$
. Conversely, if
![]() $a\lesssim _A b$
, then, for any
$a\lesssim _A b$
, then, for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $x\in A$
such that
$x\in A$
such that
![]() $\left \lVert a-x^*bx\right \rVert <\varepsilon /4$
. Choose
$\left \lVert a-x^*bx\right \rVert <\varepsilon /4$
. Choose
![]() $e\in B_+^{\textbf{1}}$
such that
$e\in B_+^{\textbf{1}}$
such that
![]() $\lVert a-eae\rVert <\varepsilon /4$
. Then
$\lVert a-eae\rVert <\varepsilon /4$
. Then
 $\left \lVert a-ex^*b^{1/4} b^{1/2} b^{1/4} xe\right \rVert <\varepsilon /2$
. It follows that
$\left \lVert a-ex^*b^{1/4} b^{1/2} b^{1/4} xe\right \rVert <\varepsilon /2$
. It follows that
![]() $a\lesssim _B b^{1/2}\sim _B b$
. In other words,
$a\lesssim _B b^{1/2}\sim _B b$
. In other words,
![]() $a\lesssim _A b \Leftrightarrow a\lesssim _B b$
.
$a\lesssim _A b \Leftrightarrow a\lesssim _B b$
.
Remark 2.5. It is known to some experts that the condition that
![]() $W(A)$
be almost unperforated is equivalent to the condition that
$W(A)$
be almost unperforated is equivalent to the condition that
![]() $\mathrm {Cu}(A)$
be almost unperforated. To see this briefly, let us assume that
$\mathrm {Cu}(A)$
be almost unperforated. To see this briefly, let us assume that
![]() $W(A)$
is almost unperforated and set
$W(A)$
is almost unperforated and set
![]() $a, b\in (A\otimes {\cal K})_+$
such that
$a, b\in (A\otimes {\cal K})_+$
such that
![]() $(k+1)\langle a\rangle \le k\langle b\rangle $
. Let
$(k+1)\langle a\rangle \le k\langle b\rangle $
. Let
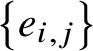 $\left \{e_{i,j}\right \}$
be the system of matrix units for
$\left \{e_{i,j}\right \}$
be the system of matrix units for
![]() ${\cal K}$
and
${\cal K}$
and
![]() $E_n=\sum _{i=1}^n1_{\tilde A}\otimes e_{i,i}$
, and let
$E_n=\sum _{i=1}^n1_{\tilde A}\otimes e_{i,i}$
, and let
![]() $\varepsilon>0$
. Note that
$\varepsilon>0$
. Note that
![]() $E_naE_n\in M_n(A)_+$
for all
$E_naE_n\in M_n(A)_+$
for all
![]() $n\in \mathbb {N}$
. Moreover,
$n\in \mathbb {N}$
. Moreover,
![]() $a\approx _{\varepsilon /8} E_naE_n$
for some large
$a\approx _{\varepsilon /8} E_naE_n$
for some large
![]() $n\in \mathbb {N}$
. It follows from [Reference Rørdam40, Proposition 2.2] that
$n\in \mathbb {N}$
. It follows from [Reference Rørdam40, Proposition 2.2] that
![]() $(a-\varepsilon )_+\lesssim (E_naE_n-\varepsilon /4)_+$
and
$(a-\varepsilon )_+\lesssim (E_naE_n-\varepsilon /4)_+$
and
![]() $(E_naE_n-\varepsilon /4)_+\lesssim (a-\varepsilon /8)_+$
. By [Reference Rørdam40, Proposition 2.4], there exists
$(E_naE_n-\varepsilon /4)_+\lesssim (a-\varepsilon /8)_+$
. By [Reference Rørdam40, Proposition 2.4], there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $(k+1)\langle (a-\varepsilon /8)_+\rangle \le k\langle (b-\delta )_+\rangle $
. Repeating Rørdam’s results [Reference Rørdam40], one obtains that
$(k+1)\langle (a-\varepsilon /8)_+\rangle \le k\langle (b-\delta )_+\rangle $
. Repeating Rørdam’s results [Reference Rørdam40], one obtains that
![]() $\langle (b-\delta )_+\rangle \le {{\langle E_mbE_m\rangle }}$
for some even larger m (
$\langle (b-\delta )_+\rangle \le {{\langle E_mbE_m\rangle }}$
for some even larger m (
![]() $m\ge n$
). Now one has
$m\ge n$
). Now one has
![]() $(k+1)\langle (E_naE_n-\varepsilon /4)_+\rangle \le k\langle E_mbE_m\rangle $
. By the last paragraph of Definition 2.4, this holds in
$(k+1)\langle (E_naE_n-\varepsilon /4)_+\rangle \le k\langle E_mbE_m\rangle $
. By the last paragraph of Definition 2.4, this holds in
![]() $M_m(A)$
. Since
$M_m(A)$
. Since
![]() $W(A)$
is almost unperforated,
$W(A)$
is almost unperforated,
![]() $(a-\varepsilon )_+\lesssim (E_naE_n-\varepsilon /4)_+\lesssim E_mbE_m$
. Then
$(a-\varepsilon )_+\lesssim (E_naE_n-\varepsilon /4)_+\lesssim E_mbE_m$
. Then
![]() $(a-\varepsilon )_+\lesssim E_mbE_m\lesssim b$
. It follows that
$(a-\varepsilon )_+\lesssim E_mbE_m\lesssim b$
. It follows that
![]() $a\lesssim b$
. Therefore
$a\lesssim b$
. Therefore
![]() $W(A)$
being almost unperforated implies that
$W(A)$
being almost unperforated implies that
![]() $\mathrm {Cu}(A)$
is almost unperforated.
$\mathrm {Cu}(A)$
is almost unperforated.
To see the converse, just notice again that A is a hereditary
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $A\otimes {\cal K}$
; then
$A\otimes {\cal K}$
; then
![]() $\langle a\rangle \leq \langle b\rangle $
in
$\langle a\rangle \leq \langle b\rangle $
in
![]() $\mathrm {Cu}(A)=W(A\otimes {\cal K})$
implies
$\mathrm {Cu}(A)=W(A\otimes {\cal K})$
implies
![]() $\langle a\rangle \leq \langle b\rangle $
in
$\langle a\rangle \leq \langle b\rangle $
in
![]() $W(A)$
.
$W(A)$
.
Definition 2.6. Denote by
![]() $QT(A)$
the set of
$QT(A)$
the set of
![]() $2$
-quasitraces of A with
$2$
-quasitraces of A with
![]() $\lVert \tau \rVert =1$
(see [Reference Blackadar and Handelman4, II 1.1, II 2.3]) and by
$\lVert \tau \rVert =1$
(see [Reference Blackadar and Handelman4, II 1.1, II 2.3]) and by
![]() $T(A)$
the set of all tracial states on A. We will also use
$T(A)$
the set of all tracial states on A. We will also use
![]() $T(A)$
as well as
$T(A)$
as well as
![]() $QT(A)$
for the extensions on
$QT(A)$
for the extensions on
![]() $M_k(A)$
for each k. In fact,
$M_k(A)$
for each k. In fact,
![]() $T(A)$
and
$T(A)$
and
![]() $QT(A)$
may be extended to lower semicontinuous traces and lower semicontinuous quasitraces on
$QT(A)$
may be extended to lower semicontinuous traces and lower semicontinuous quasitraces on
![]() $A\otimes {\cal K}$
(see before [Reference Elliott, Robert and Santiago17, Proposition 4.2] and [Reference Blanchard and Kirchberg7, Remark 2.27(viii)]).
$A\otimes {\cal K}$
(see before [Reference Elliott, Robert and Santiago17, Proposition 4.2] and [Reference Blanchard and Kirchberg7, Remark 2.27(viii)]).
Let A be a
![]() $C^*$
-algebra. Denote by
$C^*$
-algebra. Denote by
![]() $\mathrm {Ped}(A)$
the Pedersen ideal of A (see [Reference Pedersen36, 5.6]). Suppose that A is a
$\mathrm {Ped}(A)$
the Pedersen ideal of A (see [Reference Pedersen36, 5.6]). Suppose that A is a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra. Choose
$C^*$
-algebra. Choose
![]() $b\in \mathrm {Ped}(A)_+$
with
$b\in \mathrm {Ped}(A)_+$
with
![]() $\lVert b\rVert =1$
. Put
$\lVert b\rVert =1$
. Put
![]() $B:=\overline {bAb}=\mathrm {Her}(b)$
. Then by [Reference Brown8],
$B:=\overline {bAb}=\mathrm {Her}(b)$
. Then by [Reference Brown8],
![]() $A\otimes {\cal K}\cong B\otimes {\cal K}$
. For each
$A\otimes {\cal K}\cong B\otimes {\cal K}$
. For each
![]() $\tau \in QT(B)$
, define a lower semicontinuous function
$\tau \in QT(B)$
, define a lower semicontinuous function
![]() $d_\tau : A\otimes {\cal K}_+ \rightarrow [0,+\infty ]$
,
$d_\tau : A\otimes {\cal K}_+ \rightarrow [0,+\infty ]$
,
![]() $x\mapsto \lim _{n\rightarrow \infty }\tau \left (f_{1/n}(x)\right )$
. The function
$x\mapsto \lim _{n\rightarrow \infty }\tau \left (f_{1/n}(x)\right )$
. The function
![]() $d_{\tau }$
is called the dimension function induced by
$d_{\tau }$
is called the dimension function induced by
![]() $\tau $
.
$\tau $
.
We say A has strict comparison (for positive elements) if, for any
![]() $a, b\in A\otimes {\cal K}_+$
, the statement
$a, b\in A\otimes {\cal K}_+$
, the statement
![]() $d_\tau (a)<d_\tau (b)$
for all
$d_\tau (a)<d_\tau (b)$
for all
![]() $\tau \in QT(B)$
implies that
$\tau \in QT(B)$
implies that
![]() $a\lesssim b$
.
$a\lesssim b$
.
3. Tracial approximation
Definition 3.1. Let
![]() ${\cal P}$
be a class of
${\cal P}$
be a class of
![]() $C^*$
-algebras that is closed under isomorphisms, and let A be a simple
$C^*$
-algebras that is closed under isomorphisms, and let A be a simple
![]() $C^*$
-algebra. We say A is essentially tracially in
$C^*$
-algebra. We say A is essentially tracially in
![]() ${\cal P}$
(abbreviated as ‘e. tracially in
${\cal P}$
(abbreviated as ‘e. tracially in
![]() ${\cal P}$
’) if, for any finite subset
${\cal P}$
’) if, for any finite subset
![]() ${\cal F}\subset A$
, any
${\cal F}\subset A$
, any
![]() $\varepsilon>0$
and any
$\varepsilon>0$
and any
![]() $s\in A_+\setminus \{0\}$
, there exist an element
$s\in A_+\setminus \{0\}$
, there exist an element
![]() $e\in A_+^{\textbf{1}}$
and a nonzero
$e\in A_+^{\textbf{1}}$
and a nonzero
![]() $C^*$
-subalgebra B of A which is in
$C^*$
-subalgebra B of A which is in
![]() ${\cal P}$
such that the following hold:
${\cal P}$
such that the following hold:
-
(1)
 $\lVert ex-xe\rVert <\varepsilon \text { for all } {{x}} \in {\cal F}$
.
$\lVert ex-xe\rVert <\varepsilon \text { for all } {{x}} \in {\cal F}$
. -
(2)
 $(1-e)x\in _{\varepsilon } B$
and
$(1-e)x\in _{\varepsilon } B$
and
 $\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
$\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
.
$x\in {\cal F}$
. -
(3)
 $e\lesssim s$
.
$e\lesssim s$
.
Proposition 3.2. Let
![]() ${\cal P}$
be a class of
${\cal P}$
be a class of
![]() $C^*$
-algebras and let A be a simple
$C^*$
-algebras and let A be a simple
![]() $C^*$
-algebra. Then A is e. tracially in
$C^*$
-algebra. Then A is e. tracially in
![]() ${\cal P}$
if and only if the following hold: For any
${\cal P}$
if and only if the following hold: For any
![]() $\varepsilon>0$
, any finite subset
$\varepsilon>0$
, any finite subset
![]() ${\cal F}\subset A$
, any
${\cal F}\subset A$
, any
![]() $a \in A_+\setminus \{0\}$
and any finite subset
$a \in A_+\setminus \{0\}$
and any finite subset
![]() ${\cal G}\subset C_0([0,1])$
, there exist an element
${\cal G}\subset C_0([0,1])$
, there exist an element
![]() $e\in A_+^{\textbf{1}}$
and a nonzero
$e\in A_+^{\textbf{1}}$
and a nonzero
![]() $C^*$
-subalgebra B of A such that B in
$C^*$
-subalgebra B of A such that B in
![]() $\mathcal {P}$
, and the following hold:
$\mathcal {P}$
, and the following hold:
-
(1)
 $\lVert ex-xe\rVert <\varepsilon $
for all
$\lVert ex-xe\rVert <\varepsilon $
for all
 $ x\in \cal F$
.
$ x\in \cal F$
. -
(2)
 $g(1-e)x\in _\varepsilon B$
for all
$g(1-e)x\in _\varepsilon B$
for all
 $g\in {\cal G}$
and
$g\in {\cal G}$
and
 $\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
$\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
. and
$x\in {\cal F}$
. and -
(3)
 $e\lesssim a$
.
$e\lesssim a$
.
Proof. The ‘if’ part follows easily by taking
![]() ${\cal G}=\{\iota \}$
, where
${\cal G}=\{\iota \}$
, where
![]() $\iota (t)=t$
for all
$\iota (t)=t$
for all
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
We now show the ‘only if’ part.
Suppose that A is e. tracially in
![]() ${\cal P}$
. Let
${\cal P}$
. Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() ${\cal F}\subset A$
be a finite subset, and without loss of generality we may assume that
${\cal F}\subset A$
be a finite subset, and without loss of generality we may assume that
![]() ${\cal F}\subset A^{\textbf{1}}$
. Moreover, without loss of generality (omitting an error within
${\cal F}\subset A^{\textbf{1}}$
. Moreover, without loss of generality (omitting an error within
![]() $\varepsilon /16$
, say), we may further assume that there is
$\varepsilon /16$
, say), we may further assume that there is
![]() $e_A\in A_+^{\textbf{1}}$
such that
$e_A\in A_+^{\textbf{1}}$
such that
Set
![]() $a\in A_+\setminus \{0\}$
, let
$a\in A_+\setminus \{0\}$
, let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() ${\cal G}=\{g_1,g_2,\dotsc ,g_n\}\subset C_0([0,1])$
be a finite subset.
${\cal G}=\{g_1,g_2,\dotsc ,g_n\}\subset C_0([0,1])$
be a finite subset.
By the Weierstrass theorem, there are
![]() $m\in \mathbb {N}$
and polynomials
$m\in \mathbb {N}$
and polynomials
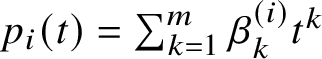 $p_i(t)=\sum _{k=1}^m \beta _k^{\left (i\right )}t^k$
such that
$p_i(t)=\sum _{k=1}^m \beta _k^{\left (i\right )}t^k$
such that
Let
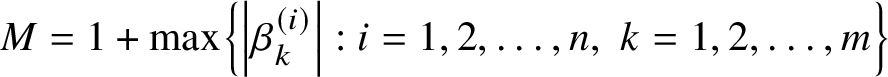 $M=1+\max \left \{\left \lvert \beta _k^{\left (i\right )}\right \rvert :i=1,2,\dotsc ,n, \ k=1,2,\dotsc ,m\right \}$
and
$M=1+\max \left \{\left \lvert \beta _k^{\left (i\right )}\right \rvert :i=1,2,\dotsc ,n, \ k=1,2,\dotsc ,m\right \}$
and
![]() $\delta := \frac {\varepsilon }{32m^3M}$
.
$\delta := \frac {\varepsilon }{32m^3M}$
.
Now, since A is e. tracially in
![]() ${\cal P}$
, there exist an element
${\cal P}$
, there exist an element
![]() $e\in A_+^{\textbf{1}}$
and a nonzero
$e\in A_+^{\textbf{1}}$
and a nonzero
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
such that B in
$B\subset A$
such that B in
![]() $\mathcal {P}$
, and the following hold:
$\mathcal {P}$
, and the following hold:
-
(1)
 $\ \lVert ex-xe\rVert <\delta \text { for all } x\in {\cal F}\cup \{e_A\}$
.
$\ \lVert ex-xe\rVert <\delta \text { for all } x\in {\cal F}\cup \{e_A\}$
. -
(2′)
 $(1-e)x\in _{\delta } B$
and
$(1-e)x\in _{\delta } B$
and
 $\lVert (1-e)x\rVert \ge \lVert x\rVert -\delta $
for all
$\lVert (1-e)x\rVert \ge \lVert x\rVert -\delta $
for all
 $x\in {\cal F}\cup \{e_A\}$
.
$x\in {\cal F}\cup \{e_A\}$
. -
(3)
 $\ e\lesssim a$
.
$\ e\lesssim a$
.
It remains to show that
![]() $g_i(1-e)x\in _{\varepsilon /2} B$
for all
$g_i(1-e)x\in _{\varepsilon /2} B$
for all
![]() $x\in {\cal F}$
,
$x\in {\cal F}$
,
![]() $i=1,2,\dotsc ,n$
.
$i=1,2,\dotsc ,n$
.
Claim: For all
![]() $x\in {\cal F}$
and all
$x\in {\cal F}$
and all
![]() $k\in \{1,2,\dotsc ,m\}$
, we have
$k\in \{1,2,\dotsc ,m\}$
, we have
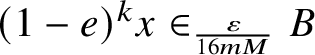 $(1-e)^kx\in _{\frac {\varepsilon }{16mM}} B$
. In fact,
$(1-e)^kx\in _{\frac {\varepsilon }{16mM}} B$
. In fact,
 $$ \begin{align} {{(1-e)^kx\overset{\text{(e3.1)}}{=}(1-e)^ke_A^{k-1}x \overset{(1)}{\approx_{k^2\delta}}\overbrace{(1-e)e_A(1-e)e_A\dotsm (1-e)e_A}^{k-1}(1-e)x \overset{(2')}{\in_{k\delta}} B.}} \end{align} $$
$$ \begin{align} {{(1-e)^kx\overset{\text{(e3.1)}}{=}(1-e)^ke_A^{k-1}x \overset{(1)}{\approx_{k^2\delta}}\overbrace{(1-e)e_A(1-e)e_A\dotsm (1-e)e_A}^{k-1}(1-e)x \overset{(2')}{\in_{k\delta}} B.}} \end{align} $$
Note that
![]() $2k^2\delta \le 2m^2\delta <\varepsilon /16mM$
. The claim follows.
$2k^2\delta \le 2m^2\delta <\varepsilon /16mM$
. The claim follows.
By formula (e3.2) and the claim, for
![]() $x\in {\cal F}$
and
$x\in {\cal F}$
and
![]() $i\in \{1,2,\dotsc ,n\}$
we have
$i\in \{1,2,\dotsc ,n\}$
we have
 $$ \begin{align} g_i(1-e)x\approx_{\varepsilon/4}p_i(1-e)x =\sum_{k=1}^m{\beta}_k^{\left(i\right)} (1-e)^k x\in_{\varepsilon/4} B.\nonumber \\[-26pt] \end{align} $$
$$ \begin{align} g_i(1-e)x\approx_{\varepsilon/4}p_i(1-e)x =\sum_{k=1}^m{\beta}_k^{\left(i\right)} (1-e)^k x\in_{\varepsilon/4} B.\nonumber \\[-26pt] \end{align} $$
Remark 3.3.
-
(1) A similar notion as in Definition 3.1 could also be defined for nonsimple
 $C^*$
-algebras. However, in the present paper we are interested in only the simple case.
$C^*$
-algebras. However, in the present paper we are interested in only the simple case. -
(2) Note that in Proposition 3.2,
 $g(1-e)$
is an element in
$g(1-e)$
is an element in
 ${\widetilde A}$
. But
${\widetilde A}$
. But
 $g(1-e)x\in A$
. In the case that A is unital, the condition
$g(1-e)x\in A$
. In the case that A is unital, the condition
 $\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
$\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
in condition (2) of the definition 3.1 is redundant for most cases (we leave the discussion to [Reference Fu and Lin22]).
$x\in {\cal F}$
in condition (2) of the definition 3.1 is redundant for most cases (we leave the discussion to [Reference Fu and Lin22]). -
(3) The notion of tracial approximation was first introduced in [Reference Lin29] (see also [Reference Lin30]). Let
 ${\cal P}$
be a class of unital
${\cal P}$
be a class of unital
 $C^*$
-algebras – for example, the class of
$C^*$
-algebras – for example, the class of
 $C^*$
-algebras which are isomorphic to
$C^*$
-algebras which are isomorphic to
 $C^*$
-algebras of the form
$C^*$
-algebras of the form
 $C([0,1], F)$
, where F are finite-dimensional
$C([0,1], F)$
, where F are finite-dimensional
 $C^*$
-algebras. If, in Definition 3.1,
$C^*$
-algebras. If, in Definition 3.1,
 $1-e$
can be chosen to be the unit of
$1-e$
can be chosen to be the unit of
 $B (\in {\cal P})$
, then A is TAI or A has tracial rank at most
$B (\in {\cal P})$
, then A is TAI or A has tracial rank at most
 $1$
[Reference Lin30, Reference Lin32]. In general, if A is unital simple and is TA
$1$
[Reference Lin30, Reference Lin32]. In general, if A is unital simple and is TA
 ${\cal P}$
(see [Reference Elliott, Gong, Lin and Niu14, Definition 2.2] and [Reference Fan and Fang18]), then A is e. tracially in
${\cal P}$
(see [Reference Elliott, Gong, Lin and Niu14, Definition 2.2] and [Reference Fan and Fang18]), then A is e. tracially in
 ${\cal P}$
. The difference is that we allow e to be a positive element rather than a projection.
${\cal P}$
. The difference is that we allow e to be a positive element rather than a projection.To see this, let A be a unital simple
 $C^*$
-algebra which is TA
$C^*$
-algebra which is TA
 ${\cal P}$
. Fix a finite subset
${\cal P}$
. Fix a finite subset
 ${\cal F}\subset A$
that contains
${\cal F}\subset A$
that contains
 $1_A$
. Fix
$1_A$
. Fix
 $\varepsilon>0$
and
$\varepsilon>0$
and
 $a\in A_+\backslash \{0\}$
. By a well-known result due to Blackadar (see, for example, [Reference Blackadar3, II.8.5.6]), there is a unital separable simple
$a\in A_+\backslash \{0\}$
. By a well-known result due to Blackadar (see, for example, [Reference Blackadar3, II.8.5.6]), there is a unital separable simple
 $C^*$
-subalgebra
$C^*$
-subalgebra
 $C\subset A$
such that
$C\subset A$
such that
 ${\cal F}\subset C$
. Let
${\cal F}\subset C$
. Let
 $\{{\cal F}_n\}_{n\in \mathbb {N}}$
be an increasing sequence of finite subsets of C whose union is dense in C, and
$\{{\cal F}_n\}_{n\in \mathbb {N}}$
be an increasing sequence of finite subsets of C whose union is dense in C, and
 ${\cal F} \subset {\cal F}_1$
. Since A is TA
${\cal F} \subset {\cal F}_1$
. Since A is TA
 ${\cal P}$
in the sense of [Reference Elliott, Gong, Lin and Niu14, Definition 2.2], there are nonzero projections
${\cal P}$
in the sense of [Reference Elliott, Gong, Lin and Niu14, Definition 2.2], there are nonzero projections
 $p_n\in A$
and
$p_n\in A$
and
 $C^*$
-algebras
$C^*$
-algebras
 $B_n\subset A$
with
$B_n\subset A$
with
 $B_n$
in
$B_n$
in
 ${\cal P}$
, and
${\cal P}$
, and
 $p_n$
is the unit of
$p_n$
is the unit of
 $B_n$
(
$B_n$
(
 $n\in \mathbb {N}$
), which satisfies
$n\in \mathbb {N}$
), which satisfies-
(i)
 $\lVert p_nx-xp_n\rVert <\varepsilon /2n$
for all
$\lVert p_nx-xp_n\rVert <\varepsilon /2n$
for all
 $x\in {\cal F}_n$
,
$x\in {\cal F}_n$
, -
(ii)
 $p_nxp_n\in _{\varepsilon /2n}B_n$
for all
$p_nxp_n\in _{\varepsilon /2n}B_n$
for all
 $x\in {\cal F}_n$
and
$x\in {\cal F}_n$
and -
(iii)
 $1-p_n\lesssim a$
.
$1-p_n\lesssim a$
.
Assume that for each
 $n\in \mathbb {N}$
, there is some
$n\in \mathbb {N}$
, there is some
 $x\in {\cal F}$
such that
$x\in {\cal F}$
such that
 $\lVert p_nxp_n\rVert \le \lVert p_nx\rVert <\lVert x\rVert -\varepsilon $
. Then since
$\lVert p_nxp_n\rVert \le \lVert p_nx\rVert <\lVert x\rVert -\varepsilon $
. Then since
 ${\cal F}$
is a finite set, we can find
${\cal F}$
is a finite set, we can find
 $x_0\in {\cal F}$
and an increasing sequence of natural numbers
$x_0\in {\cal F}$
and an increasing sequence of natural numbers
 $\{n_m\}_{m\in \mathbb {N}}$
such that
$\{n_m\}_{m\in \mathbb {N}}$
such that
 $\left \lVert p_{n_m}x_0p_{n_m}\right \rVert <\lVert x_0\rVert -\varepsilon $
for all
$\left \lVert p_{n_m}x_0p_{n_m}\right \rVert <\lVert x_0\rVert -\varepsilon $
for all
 $m\in \mathbb {N}$
. Define a c.p.c. linear map
$m\in \mathbb {N}$
. Define a c.p.c. linear map
 $\varphi : C\to l^\infty (A)/c_0(A)$
by
$\varphi : C\to l^\infty (A)/c_0(A)$
by
 $\varphi (x):=\pi \left (\left \{p_{n_1}xp_{n_1},p_{n_2}xp_{n_2},\dotsc \right \}\right )$
, where
$\varphi (x):=\pi \left (\left \{p_{n_1}xp_{n_1},p_{n_2}xp_{n_2},\dotsc \right \}\right )$
, where
 $x\in C$
and
$x\in C$
and
 $\pi :l^\infty (A)\to l^\infty (A)/c_0(A)$
is the quotient map. By condition (i) we see that
$\pi :l^\infty (A)\to l^\infty (A)/c_0(A)$
is the quotient map. By condition (i) we see that
 $\varphi $
is a homomorphism. Since
$\varphi $
is a homomorphism. Since
 $\varphi (1_A)= \pi \left (\left \{p_{n_1},p_{n_2},\dotsc \right \}\right )\neq 0$
,
$\varphi (1_A)= \pi \left (\left \{p_{n_1},p_{n_2},\dotsc \right \}\right )\neq 0$
,
 $\varphi $
is nonzero. Since C is simple,
$\varphi $
is nonzero. Since C is simple,
 $\varphi $
is injective and hence isometric. However,
$\varphi $
is injective and hence isometric. However,
 $\lVert \varphi (x_0)\rVert =\left \lVert \pi \left (\left \{p_{n_1}x_0,p_{n_2}x_0,\dotsc \right \}\right )\right \rVert \leq \sup _{m\in \mathbb {N}}\left \lVert p_{n_m}x_0p_{n_m}\right \rVert \leq \lVert x_0\rVert -\varepsilon $
: a contradiction. Therefore, there is
$\lVert \varphi (x_0)\rVert =\left \lVert \pi \left (\left \{p_{n_1}x_0,p_{n_2}x_0,\dotsc \right \}\right )\right \rVert \leq \sup _{m\in \mathbb {N}}\left \lVert p_{n_m}x_0p_{n_m}\right \rVert \leq \lVert x_0\rVert -\varepsilon $
: a contradiction. Therefore, there is
 $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
 $\left \lVert p_{n_0}x\right \rVert \geq \lVert x\rVert -\varepsilon $
for all
$\left \lVert p_{n_0}x\right \rVert \geq \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
. Set
$x\in {\cal F}$
. Set
 $e:=1_A-p_{n_0}$
; then by (i)–(iii) and the choice of
$e:=1_A-p_{n_0}$
; then by (i)–(iii) and the choice of
 $n_0$
, we have
$n_0$
, we have-
(1′)
 $\lVert ex-xe\rVert <\varepsilon $
for all
$\lVert ex-xe\rVert <\varepsilon $
for all
 $x\in {\cal F}$
,
$x\in {\cal F}$
, -
(2′)
 $(1-e)x\in _{\varepsilon }B_{n_0}$
and
$(1-e)x\in _{\varepsilon }B_{n_0}$
and
 $\lVert (1-e)x\rVert \geq \lVert x\rVert -\varepsilon $
for all
$\lVert (1-e)x\rVert \geq \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
and
$x\in {\cal F}$
and -
(3′)
 $e\lesssim a$
.
$e\lesssim a$
.
Hence A is e. tracially in
 ${\cal P}$
.
${\cal P}$
.We note also that in general, a
 $C^*$
-algebra that is essentially tracially in
$C^*$
-algebra that is essentially tracially in
 ${\cal P}$
may not be TA
${\cal P}$
may not be TA
 ${\cal P}$
(see Remark 8.5).
${\cal P}$
(see Remark 8.5). -
-
(4) The current definition is also related to the notion of a ‘centrally large subalgebra’ ([Reference Phillips37, Definition 4.1] and [Reference Archey, Buck and Phillips1, Definition 2.1]) but not the same. The main difference is that the
 $C^*$
-subalgebra B in [Reference Archey, Buck and Phillips1, Definition 2.1] is fixed. In fact, for a simple unital
$C^*$
-subalgebra B in [Reference Archey, Buck and Phillips1, Definition 2.1] is fixed. In fact, for a simple unital
 $C^*$
-algebra A and a class of
$C^*$
-algebra A and a class of
 $C^*$
-algebras
$C^*$
-algebras
 ${\cal P}$
, if A has a centrally large subalgebra B with
${\cal P}$
, if A has a centrally large subalgebra B with
 $B\in {\cal P}$
, then A is essentially tracially in
$B\in {\cal P}$
, then A is essentially tracially in
 ${\cal P}$
. On the other hand, in general, if A is essentially tracially in
${\cal P}$
. On the other hand, in general, if A is essentially tracially in
 ${\cal P}$
, one may not find a centrally large
${\cal P}$
, one may not find a centrally large
 $C^*$
-subalgebra B which is in
$C^*$
-subalgebra B which is in
 ${\cal P}$
(for example, if
${\cal P}$
(for example, if
 ${\cal P}$
is the class of finite-dimensional
${\cal P}$
is the class of finite-dimensional
 $C^*$
-algebras, then every unital infinite-dimensional simple AF-algebra is e. tracially in
$C^*$
-algebras, then every unital infinite-dimensional simple AF-algebra is e. tracially in
 ${\cal P}$
, but may not have centrally large finite-dimensional
${\cal P}$
, but may not have centrally large finite-dimensional
 $C^*$
-subalgebras [Reference Phillips37, Theorem 6.8]).
$C^*$
-subalgebras [Reference Phillips37, Theorem 6.8]). -
(5) In [Reference Fu and Lin21], a notion of asymptotically tracial approximation is introduced, studying tracial approximation of certain properties which are closely related to weakly stable relations. It also mainly studies unital simple
 $C^*$
-algebras with a rich structure of projections. This is different from Definition 3.1. However, if A is a unital (infinite-dimensional) simple
$C^*$
-algebras with a rich structure of projections. This is different from Definition 3.1. However, if A is a unital (infinite-dimensional) simple
 $C^*$
-algebra which is asymptotically tracially in the class
$C^*$
-algebra which is asymptotically tracially in the class
 ${\cal C}$
of
${\cal C}$
of
 $1$
-dimensional noncommutative CW complexes, then one can show that A is also essentially tracially in the same class
$1$
-dimensional noncommutative CW complexes, then one can show that A is also essentially tracially in the same class
 ${\cal C}$
. Moreover, many classes
${\cal C}$
. Moreover, many classes
 ${\cal P}$
of
${\cal P}$
of
 $C^*$
-algebras are preserved by asymptotically tracial approximation [Reference Fu and Lin21, Section 4]. Some more discussion may be found in a forthcoming paper [Reference Fu and Lin22].
$C^*$
-algebras are preserved by asymptotically tracial approximation [Reference Fu and Lin21, Section 4]. Some more discussion may be found in a forthcoming paper [Reference Fu and Lin22].
Definition 3.4. Let
![]() ${\cal P}$
be a class of
${\cal P}$
be a class of
![]() $C^*$
-algebras. The class
$C^*$
-algebras. The class
![]() ${\cal P}$
is said to have property (H) if, for any nonzero A in
${\cal P}$
is said to have property (H) if, for any nonzero A in
![]() ${\cal P}$
and any nonzero hereditary
${\cal P}$
and any nonzero hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
, B is also in
$B\subset A$
, B is also in
![]() ${\cal P}$
.
${\cal P}$
.
Proposition 3.5. Let
![]() ${\cal P}$
be a class of
${\cal P}$
be a class of
![]() $C^*$
-algebras which has property (H). Suppose that A is a simple
$C^*$
-algebras which has property (H). Suppose that A is a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal P}$
. Then every nonzero hereditary
${\cal P}$
. Then every nonzero hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
is also e. tracially in
$B\subset A$
is also e. tracially in
![]() ${\cal P}$
.
${\cal P}$
.
Proof. Assume
![]() ${\cal P}$
has property (H) and A is e. tracially in
${\cal P}$
has property (H) and A is e. tracially in
![]() ${\cal P}$
. Let
${\cal P}$
. Let
![]() $B\subset A$
be a nonzero hereditary
$B\subset A$
be a nonzero hereditary
![]() $C^*$
-subalgebra of A. Set
$C^*$
-subalgebra of A. Set
![]() ${\cal F}\subset B$
and
${\cal F}\subset B$
and
![]() $s\in B_+\setminus \{0\}$
, and
$s\in B_+\setminus \{0\}$
, and
![]() $\varepsilon \in (0,1/4)$
.
$\varepsilon \in (0,1/4)$
.
Without loss of generality, we may assume that
![]() ${\cal F}\subset B_+^{\textbf{1}}$
. Let
${\cal F}\subset B_+^{\textbf{1}}$
. Let
![]() $d\in B_+^{\textbf{1}}$
be such that
$d\in B_+^{\textbf{1}}$
be such that
![]() $dx\approx _{{\varepsilon /32}} x\approx _{{\varepsilon /32}} xd$
and
$dx\approx _{{\varepsilon /32}} x\approx _{{\varepsilon /32}} xd$
and
![]() $x\approx _{{{\varepsilon /32}}}dxd$
for all
$x\approx _{{{\varepsilon /32}}}dxd$
for all
![]() $x\in {\cal F}$
.
$x\in {\cal F}$
.
Put
![]() $\varepsilon _1=\varepsilon /32$
. By [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3], there is
$\varepsilon _1=\varepsilon /32$
. By [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3], there is
![]() $\delta _1\in (0,{{\varepsilon _1}})$
such that for any
$\delta _1\in (0,{{\varepsilon _1}})$
such that for any
![]() $C^*$
-algebra E and any
$C^*$
-algebra E and any
![]() $x,y\in E_+^{\textbf{1}}$
, if
$x,y\in E_+^{\textbf{1}}$
, if
![]() $x\approx _{\delta _1} y$
, then there is an injective homomorphism
$x\approx _{\delta _1} y$
, then there is an injective homomorphism
![]() $\psi : \mathrm {Her}_{E}\left (f_{{{\varepsilon _1}}/2}(x)\right )\to \mathrm {Her}_{E}(y)$
satisfying
$\psi : \mathrm {Her}_{E}\left (f_{{{\varepsilon _1}}/2}(x)\right )\to \mathrm {Her}_{E}(y)$
satisfying
![]() $z\approx _{{\varepsilon _1}} \psi (z)$
for all
$z\approx _{{\varepsilon _1}} \psi (z)$
for all
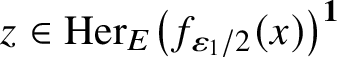 $z\in \mathrm {Her}_{E}\left (f_{{{\varepsilon _1}}/2}(x)\right )^{\textbf{1}}$
.
$z\in \mathrm {Her}_{E}\left (f_{{{\varepsilon _1}}/2}(x)\right )^{\textbf{1}}$
.
Note that there is
![]() $\delta _2\in (0,\delta _1)$
such that for any
$\delta _2\in (0,\delta _1)$
such that for any
![]() $C^*$
-algebra E and any
$C^*$
-algebra E and any
![]() $x,y\in E_+^{\textbf{1}}$
, if
$x,y\in E_+^{\textbf{1}}$
, if
![]() $xy\approx _{\delta _2} yx$
, then
$xy\approx _{\delta _2} yx$
, then
 $x^{1/4}y\approx _{\delta _1/2} yx^{1/4}$
,
$x^{1/4}y\approx _{\delta _1/2} yx^{1/4}$
,
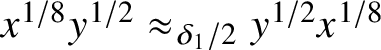 $x^{1/8}y^{1/2}\approx _{\delta _1/2} y^{1/2}x^{1/8}$
and
$x^{1/8}y^{1/2}\approx _{\delta _1/2} y^{1/2}x^{1/8}$
and
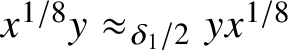 $x^{1/8}y\approx _{\delta _1/2 }yx^{1/8}$
.
$x^{1/8}y\approx _{\delta _1/2 }yx^{1/8}$
.
Let
![]() $\delta =\delta _2/2$
. Let
$\delta =\delta _2/2$
. Let
 ${\cal G}=\left \{t,t^{1/4},t^{1/8}\right \}\subset C_0([0,1])$
. Since A is e. tracially in
${\cal G}=\left \{t,t^{1/4},t^{1/8}\right \}\subset C_0([0,1])$
. Since A is e. tracially in
![]() ${\cal P}$
, by Proposition 3.2 there exist a positive element
${\cal P}$
, by Proposition 3.2 there exist a positive element
![]() $a\in A_+^{\textbf{1}}$
and a nonzero
$a\in A_+^{\textbf{1}}$
and a nonzero
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $C\subset A$
which is in
$C\subset A$
which is in
![]() ${\cal P}$
such that
${\cal P}$
such that
-
(1)
 $\lVert ax-xa\rVert <{\delta }$
for all
$\lVert ax-xa\rVert <{\delta }$
for all
 $x\in {\cal F}\cup \left \{d,d^{1/2},d^2\right \}$
,
$x\in {\cal F}\cup \left \{d,d^{1/2},d^2\right \}$
, -
(2)
 $g(1-a) x\in _{\delta } C$
for all
$g(1-a) x\in _{\delta } C$
for all
 $g\in {\cal G}$
and
$g\in {\cal G}$
and
 $\lVert (1-a)x\rVert \ge \lVert x\rVert -\delta $
for all
$\lVert (1-a)x\rVert \ge \lVert x\rVert -\delta $
for all
 $x\in {\cal F}\cup \left \{d,d^{1/2},d^2\right \}$
and
$x\in {\cal F}\cup \left \{d,d^{1/2},d^2\right \}$
and -
(3)
 $a\lesssim s$
.
$a\lesssim s$
.
By (2), there is
![]() $c\in C$
such that
$c\in C$
such that
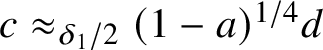 $ c\approx _{\delta _1/2} (1-a)^{1/4}d$
. By (1) and the choice of
$ c\approx _{\delta _1/2} (1-a)^{1/4}d$
. By (1) and the choice of
![]() $\delta _2$
, we have
$\delta _2$
, we have
![]() $c\approx _{\delta _1}d^{1/2}(1-a)^{1/4}d^{1/2}$
. Then by [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] and the choice of
$c\approx _{\delta _1}d^{1/2}(1-a)^{1/4}d^{1/2}$
. Then by [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] and the choice of
![]() $\delta _1$
, there is a monomorphism
$\delta _1$
, there is a monomorphism
 $$ \begin{align*} \varphi: \mathrm{Her}_A\left(f_{{{\varepsilon_1}}/2}(c)\right)\to \mathrm{Her}_A\left(d^{1/2}(1-a)^{1/4}d^{1/2}\right)\subset B \end{align*} $$
$$ \begin{align*} \varphi: \mathrm{Her}_A\left(f_{{{\varepsilon_1}}/2}(c)\right)\to \mathrm{Her}_A\left(d^{1/2}(1-a)^{1/4}d^{1/2}\right)\subset B \end{align*} $$
satisfying
![]() $\lVert \varphi (x)-x\rVert <{{\varepsilon _1}}$
for all
$\lVert \varphi (x)-x\rVert <{{\varepsilon _1}}$
for all
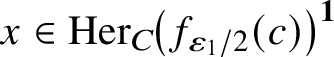 $x\in \mathrm {Her}_C\!\left(f_{{{\varepsilon _1}}/2}(c)\right )^{\textbf{1}}$
. Define
$x\in \mathrm {Her}_C\!\left(f_{{{\varepsilon _1}}/2}(c)\right )^{\textbf{1}}$
. Define
![]() $D:=\varphi \left (\mathrm {Her}_C\!\left(f_{{{\varepsilon _1}}/2}(c)\right )\right )\subset B$
. Since C is in
$D:=\varphi \left (\mathrm {Her}_C\!\left(f_{{{\varepsilon _1}}/2}(c)\right )\right )\subset B$
. Since C is in
![]() ${\cal P}$
and
${\cal P}$
and
![]() ${\cal P}$
has property (H),
${\cal P}$
has property (H),
![]() $D\cong \mathrm {Her}_C\!\left(f_{\varepsilon _1/2}(c)\right )$
is in
$D\cong \mathrm {Her}_C\!\left(f_{\varepsilon _1/2}(c)\right )$
is in
![]() ${\cal P}$
. Set
${\cal P}$
. Set
![]() $b:=dad\in B_+^{\textbf{1}}$
. Then by (1) and the choice of d, we have
$b:=dad\in B_+^{\textbf{1}}$
. Then by (1) and the choice of d, we have
By (2), for any
![]() $x\in {\cal F}$
there is
$x\in {\cal F}$
there is
![]() $\bar x\in C$
such that
$\bar x\in C$
such that
![]() $(1-a)^{1/4}x(1-a)^{1/4}\approx _{2{{\varepsilon _1}}} \bar x$
. Then
$(1-a)^{1/4}x(1-a)^{1/4}\approx _{2{{\varepsilon _1}}} \bar x$
. Then
 $$ \begin{align} \begin{split} (1-b)x &= (1-dad)x \approx_{3{{\varepsilon_1}}} (1-a)dxd\\ &\approx_{4{{\varepsilon_1}}} (1-a)^{1/8}d(1-a)^{1/8} \cdot(1-a)^{1/4}x(1-a)^{1/4}\cdot (1-a)^{1/8}d(1-a)^{1/8}\\ &\approx_{4{{\varepsilon_1}}} c\bar xc \approx_{2{{\varepsilon_1}}} (c-{{\varepsilon_1}})_+\bar x (c-{{\varepsilon_1}})_+\\ &\approx_{{{\varepsilon_1}}} \varphi((c-{{\varepsilon_1}})_+\bar x (c-{{\varepsilon_1}})_+)\in D. \end{split} \end{align} $$
$$ \begin{align} \begin{split} (1-b)x &= (1-dad)x \approx_{3{{\varepsilon_1}}} (1-a)dxd\\ &\approx_{4{{\varepsilon_1}}} (1-a)^{1/8}d(1-a)^{1/8} \cdot(1-a)^{1/4}x(1-a)^{1/4}\cdot (1-a)^{1/8}d(1-a)^{1/8}\\ &\approx_{4{{\varepsilon_1}}} c\bar xc \approx_{2{{\varepsilon_1}}} (c-{{\varepsilon_1}})_+\bar x (c-{{\varepsilon_1}})_+\\ &\approx_{{{\varepsilon_1}}} \varphi((c-{{\varepsilon_1}})_+\bar x (c-{{\varepsilon_1}})_+)\in D. \end{split} \end{align} $$
In other words,
Therefore, for all
![]() $x\in {\cal F}$
,
$x\in {\cal F}$
,
 $$ \begin{align} \begin{split} \lVert(1-b)x\rVert&=\lVert(1-dad)x\rVert \ge \left\lVert\left(1-a d^2\right)x\right\rVert-\delta \\ &\ge \lVert(1-a)x\rVert-3\varepsilon_1 \ge \lVert x\rVert-\delta-3\varepsilon_1\ge \lVert x\rVert-\varepsilon. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \lVert(1-b)x\rVert&=\lVert(1-dad)x\rVert \ge \left\lVert\left(1-a d^2\right)x\right\rVert-\delta \\ &\ge \lVert(1-a)x\rVert-3\varepsilon_1 \ge \lVert x\rVert-\delta-3\varepsilon_1\ge \lVert x\rVert-\varepsilon. \end{split} \end{align} $$
By (3), we have
![]() $b=dad\lesssim _A s$
. Note that
$b=dad\lesssim _A s$
. Note that
![]() $b, s\in B$
. Since B is a hereditary
$b, s\in B$
. Since B is a hereditary
![]() $C^*$
-subalgebra, we have
$C^*$
-subalgebra, we have
![]() $b\lesssim _B s$
. By formulas (e3.5) and (e3.7), we see that B is also e. tracially in
$b\lesssim _B s$
. By formulas (e3.5) and (e3.7), we see that B is also e. tracially in
![]() ${\cal P}$
.
${\cal P}$
.
4. Basic properties
Notation 4.1. Let
![]() ${\cal W}$
be the class of
${\cal W}$
be the class of
![]() $C^*$
-algebras A such that
$C^*$
-algebras A such that
![]() $W(A)$
is almost unperforated.
$W(A)$
is almost unperforated.
Let
![]() ${\mathscr Z}$
be the Jiang–Su algebra [Reference Jiang and Su27]. A
${\mathscr Z}$
be the Jiang–Su algebra [Reference Jiang and Su27]. A
![]() $C^*$
-algebra A is called
$C^*$
-algebra A is called
![]() ${\mathscr Z}$
-stable if
${\mathscr Z}$
-stable if
![]() $A\otimes {\mathscr Z}\cong A$
. Let
$A\otimes {\mathscr Z}\cong A$
. Let
![]() ${\cal C}_{\mathscr Z}$
be the class of separable
${\cal C}_{\mathscr Z}$
be the class of separable
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras.
$C^*$
-algebras.
Lemma 4.2. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal W}$
, and set
${\cal W}$
, and set
![]() $a,b,c\in A_+\backslash \{0\}$
. Suppose that there exists
$a,b,c\in A_+\backslash \{0\}$
. Suppose that there exists
![]() $n\in \mathbb {N}$
satisfying
$n\in \mathbb {N}$
satisfying
![]() $(n+1)\langle a\rangle \leq n\langle b\rangle $
. Then for any
$(n+1)\langle a\rangle \leq n\langle b\rangle $
. Then for any
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $a_1,a_2\in A_+$
such that
$a_1,a_2\in A_+$
such that
-
(1)
 $a\approx _{\epsilon }a_1+a_2$
,
$a\approx _{\epsilon }a_1+a_2$
, -
(2)
 $a_1\lesssim _A b$
and
$a_1\lesssim _A b$
and -
(3)
 $a_2 \lesssim _A c$
.
$a_2 \lesssim _A c$
.
Proof. Without loss of generality, one may assume that
![]() $a,b,c\in A_+^{\textbf{1}}\backslash \{0\}$
and
$a,b,c\in A_+^{\textbf{1}}\backslash \{0\}$
and
![]() $\epsilon <1/2$
. Then
$\epsilon <1/2$
. Then
![]() $(n+1)\langle a\rangle \leq n\langle b\rangle $
implies that there exists
$(n+1)\langle a\rangle \leq n\langle b\rangle $
implies that there exists
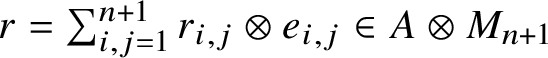 $r=\sum _{i,j=1}^{n+1}r_{i,j}\otimes e_{i,j}\in A\otimes M_{n+1}$
such that
$r=\sum _{i,j=1}^{n+1}r_{i,j}\otimes e_{i,j}\in A\otimes M_{n+1}$
such that
 $$ \begin{align} a\otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\epsilon/128}r^*\left(b \otimes \sum_{i=1}^{{{n}}}e_{i,i}\right)r. \end{align} $$
$$ \begin{align} a\otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\epsilon/128}r^*\left(b \otimes \sum_{i=1}^{{{n}}}e_{i,i}\right)r. \end{align} $$
Set
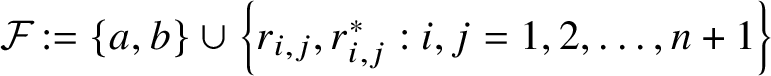 ${\cal F}:=\{a,b\}\cup \left \{r_{i,j},r_{i,j}^*:i,j=1, 2 ,\dotsc , n+1\right \}$
and
${\cal F}:=\{a,b\}\cup \left \{r_{i,j},r_{i,j}^*:i,j=1, 2 ,\dotsc , n+1\right \}$
and
![]() $M:=1+\lVert r\rVert $
. Let
$M:=1+\lVert r\rVert $
. Let
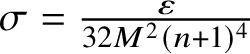 $\sigma =\frac {\varepsilon }{32M^2(n+1)^4}$
. Since A is e. tracially in
$\sigma =\frac {\varepsilon }{32M^2(n+1)^4}$
. Since A is e. tracially in
![]() ${\cal W}$
, by Proposition 3.2, for any
${\cal W}$
, by Proposition 3.2, for any
 $\delta \in \left (0, \frac {\varepsilon }{256M(n+1)^2}\right )$
, there exist
$\delta \in \left (0, \frac {\varepsilon }{256M(n+1)^2}\right )$
, there exist
![]() $f\in A_+^{\textbf{1}}\setminus \{0\}$
and a
$f\in A_+^{\textbf{1}}\setminus \{0\}$
and a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
which has almost unperforated
$B\subset A$
which has almost unperforated
![]() $W(B)$
such that
$W(B)$
such that
-
(1′)
 $\lVert fx-xf \rVert <\delta $
for
$\lVert fx-xf \rVert <\delta $
for
 $x\in {\cal F}$
,
$x\in {\cal F}$
, -
(2′)
 $(1-f)^{ 1/4} x, (1-f)^{ 1/2} a(1-f)^{ 1/2 }, (1-f)^{1/4}x (1-f)^{ 1/4} \in _\delta B$
for all
$(1-f)^{ 1/4} x, (1-f)^{ 1/2} a(1-f)^{ 1/2 }, (1-f)^{1/4}x (1-f)^{ 1/4} \in _\delta B$
for all
 $x\in {\cal F}$
and
$x\in {\cal F}$
and -
(3′)
 $f\lesssim c$
.
$f\lesssim c$
.
Put
![]() $g=1-f$
. Let
$g=1-f$
. Let
 $$ \begin{align*} {\cal G}:=\left\{g^{ {1/4}}x, g^{1/2}xg^{1/2}, g^{1/4}xg^{1/4} : x\in {\cal F}\right\}. \end{align*} $$
$$ \begin{align*} {\cal G}:=\left\{g^{ {1/4}}x, g^{1/2}xg^{1/2}, g^{1/4}xg^{1/4} : x\in {\cal F}\right\}. \end{align*} $$
Set
![]() $x\in {\cal G}\cap A_+$
. By (2
$x\in {\cal G}\cap A_+$
. By (2
![]() $'$
), there is
$'$
), there is
![]() $\bar x\in B$
such that
$\bar x\in B$
such that
![]() $\lVert x-\bar x\rVert <\delta $
. Let
$\lVert x-\bar x\rVert <\delta $
. Let
![]() $x':=\left (\bar x+\bar x^*\right )/2\in B_{\mathrm {sa}}$
. Then
$x':=\left (\bar x+\bar x^*\right )/2\in B_{\mathrm {sa}}$
. Then
![]() $x\approx _\delta x'$
. Then
$x\approx _\delta x'$
. Then
![]() $x'+\delta \geq x\geq 0$
, which implies
$x'+\delta \geq x\geq 0$
, which implies
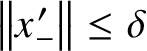 $\left \lVert x^{\prime }_-\right \rVert \leq \delta $
. Then
$\left \lVert x^{\prime }_-\right \rVert \leq \delta $
. Then
![]() $x\approx _\delta x'=x^{\prime }_+-x^{\prime }_-\approx _\delta x^{\prime }_+\in B_+$
. Therefore, there is a map
$x\approx _\delta x'=x^{\prime }_+-x^{\prime }_-\approx _\delta x^{\prime }_+\in B_+$
. Therefore, there is a map
![]() ${\alpha }:{\cal G}\to B$
such that
${\alpha }:{\cal G}\to B$
such that
![]() ${\alpha }({\cal G}\cap A_+)\subset B_+$
, and
${\alpha }({\cal G}\cap A_+)\subset B_+$
, and
From (1
![]() $'$
) and (2
$'$
) and (2
![]() $'$
), one can choose
$'$
), one can choose
![]() $\delta $
sufficiently small such that
$\delta $
sufficiently small such that
 $$ \begin{align} a\approx_{\varepsilon/16} g^{{1/2}}ag^{{1/2}}+ (1-g)^{1/2}a(1-g)^{1/2} \mathrm{\ and\ } \end{align} $$
$$ \begin{align} a\approx_{\varepsilon/16} g^{{1/2}}ag^{{1/2}}+ (1-g)^{1/2}a(1-g)^{1/2} \mathrm{\ and\ } \end{align} $$
 $$ \begin{align} \left(g^{{1/2}}{{a}}g^{{1/2}}-\varepsilon/8\right)_+ \approx_{\varepsilon/16} \left(\alpha\left(g^{{1/2}}{{a}} g^{{1/2}}\right)-\epsilon/8\right)_+. \end{align} $$
$$ \begin{align} \left(g^{{1/2}}{{a}}g^{{1/2}}-\varepsilon/8\right)_+ \approx_{\varepsilon/16} \left(\alpha\left(g^{{1/2}}{{a}} g^{{1/2}}\right)-\epsilon/8\right)_+. \end{align} $$
By (1
![]() $'$
) and formula (e4.1) (with
$'$
) and formula (e4.1) (with
![]() $\delta $
sufficiently small), one can also assume that
$\delta $
sufficiently small), one can also assume that
 $$ \begin{align} g^{{1/2}}ag^{{1/2}}\otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/64} R^* \left(g^{{1/4}} b g^{{1/4}}\otimes \sum_{i=1}^{n}e_{i,i}\right)R, \end{align} $$
$$ \begin{align} g^{{1/2}}ag^{{1/2}}\otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/64} R^* \left(g^{{1/4}} b g^{{1/4}}\otimes \sum_{i=1}^{n}e_{i,i}\right)R, \end{align} $$
where
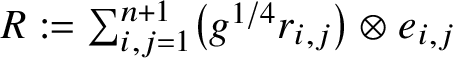 $R:=\sum _{i,j=1}^{n+1}\left ({{g^{1/4}}}{{r_{i,j}}} \right )\otimes e_{i,j}$
. By formulas (e4.5) and (e4.2) and
$R:=\sum _{i,j=1}^{n+1}\left ({{g^{1/4}}}{{r_{i,j}}} \right )\otimes e_{i,j}$
. By formulas (e4.5) and (e4.2) and
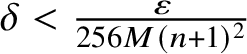 $\delta <\frac {\varepsilon }{256M(n+1)^2}$
, one has
$\delta <\frac {\varepsilon }{256M(n+1)^2}$
, one has
 $$ \begin{align} \alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) \otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/32} {{\bar R^*}} \left( {\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) \otimes \sum_{i=1}^{n}e_{i,i}\right){{\bar R}}, \end{align} $$
$$ \begin{align} \alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) \otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/32} {{\bar R^*}} \left( {\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) \otimes \sum_{i=1}^{n}e_{i,i}\right){{\bar R}}, \end{align} $$
where
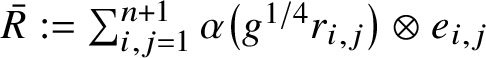 $\bar R:= \sum _{i,j=1}^{n+1}{\alpha }\left (g^{1/4}{{r_{i,j}}} \right )\otimes e_{i,j}$
. Then by the choice of
$\bar R:= \sum _{i,j=1}^{n+1}{\alpha }\left (g^{1/4}{{r_{i,j}}} \right )\otimes e_{i,j}$
. Then by the choice of
![]() $\sigma $
,
$\sigma $
,
 $$ \begin{align} \alpha\left(g^{1/2}{a}g^{1/2}\right) \otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/16} {{\bar R^*}} \left( \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right)-\sigma\right)_+ \otimes \sum_{i=1}^{n}e_{i,i}\right){{\bar R}}. \end{align} $$
$$ \begin{align} \alpha\left(g^{1/2}{a}g^{1/2}\right) \otimes \sum_{i=1}^{n+1}e_{i,i} \approx_{\varepsilon/16} {{\bar R^*}} \left( \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right)-\sigma\right)_+ \otimes \sum_{i=1}^{n}e_{i,i}\right){{\bar R}}. \end{align} $$
By formula (e4.7) and [Reference Rørdam40, Proposition 2.2], one has
 $$ \begin{align} \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+\otimes \sum_{i=1}^{n+1}e_{i,i} \lesssim \left({\alpha}\left(g^{1/4} b g^{1/4}\right) -\sigma\right)_+\otimes \sum_{i=1}^{n}e_{i,i}. \end{align} $$
$$ \begin{align} \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+\otimes \sum_{i=1}^{n+1}e_{i,i} \lesssim \left({\alpha}\left(g^{1/4} b g^{1/4}\right) -\sigma\right)_+\otimes \sum_{i=1}^{n}e_{i,i}. \end{align} $$
Since
![]() $W(B)$
is almost unperforated, one obtains
$W(B)$
is almost unperforated, one obtains
 $$ \begin{align} \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+ \lesssim \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) -\sigma\right)_+. \end{align} $$
$$ \begin{align} \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+ \lesssim \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) -\sigma\right)_+. \end{align} $$
By [Reference Rørdam40, Proposition 2.2] and formulas (e4.4), (e4.9) and (e4.2), it follows that
 $$ \begin{align} \left(g^{{1/2}}{{a}}g^{{1/2}}-\varepsilon/4\right)_+ &\lesssim \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+ \hspace{6pc} \end{align} $$
$$ \begin{align} \left(g^{{1/2}}{{a}}g^{{1/2}}-\varepsilon/4\right)_+ &\lesssim \left(\alpha\left(g^{{1/2}}{{a}}g^{{1/2}}\right) -\epsilon/8\right)_+ \hspace{6pc} \end{align} $$
 $$ \begin{align} & \hspace{6pc} \lesssim \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) -\sigma\right)_+ \lesssim g^{1/4}{{b}}g^{1/4} \lesssim b. \end{align} $$
$$ \begin{align} & \hspace{6pc} \lesssim \left({\alpha}\left(g^{1/4}{{b}}g^{1/4}\right) -\sigma\right)_+ \lesssim g^{1/4}{{b}}g^{1/4} \lesssim b. \end{align} $$
By (1
![]() $'$
) and the choice of
$'$
) and the choice of
![]() $\delta $
,
$\delta $
,
 $$ \begin{align} a\approx_{\varepsilon/16} (1-f)^{1/2}a(1-f)^{1/2}+f^{1/2} a f^{1/2}. \end{align} $$
$$ \begin{align} a\approx_{\varepsilon/16} (1-f)^{1/2}a(1-f)^{1/2}+f^{1/2} a f^{1/2}. \end{align} $$
Choose
 $$ \begin{align} a_1&:=\left(g^{{1/2}}a g^{{1/2}}-\varepsilon/2\right)_+ =\left((1-f)^{1/2}a(1-f)^{1/2}-\varepsilon/2\right)_+ \mathrm{\ and\ } \end{align} $$
$$ \begin{align} a_1&:=\left(g^{{1/2}}a g^{{1/2}}-\varepsilon/2\right)_+ =\left((1-f)^{1/2}a(1-f)^{1/2}-\varepsilon/2\right)_+ \mathrm{\ and\ } \end{align} $$
Then by formula (e4.11), one has
![]() $a_1\lesssim _A b$
. Note that (3
$a_1\lesssim _A b$
. Note that (3
![]() $'$
) implies
$'$
) implies
![]() $a_2 \lesssim _A c$
. Thus
$a_2 \lesssim _A c$
. Thus
![]() $a_1$
and
$a_1$
and
![]() $a_2$
satisfy (2) and (3) of the lemma. By formula (e4.12),
$a_2$
satisfy (2) and (3) of the lemma. By formula (e4.12),
 $$ \begin{align*} a\approx_{\varepsilon/16} (1-f)^{{1/2}}a(1-f)^{{1/2}}+f^{{1/2}}af^{{1/2}} \approx_{\epsilon/2} a_1+a_2. \end{align*} $$
$$ \begin{align*} a\approx_{\varepsilon/16} (1-f)^{{1/2}}a(1-f)^{{1/2}}+f^{{1/2}}af^{{1/2}} \approx_{\epsilon/2} a_1+a_2. \end{align*} $$
So (1) of the lemma also holds, and the lemma follows.
Theorem 4.3. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal W}$
(see Notation 4.1). Then
${\cal W}$
(see Notation 4.1). Then
![]() $A\in {\cal W}$
.
$A\in {\cal W}$
.
Proof. We may assume that A is nonelementary. Set
![]() $a,b\in M_m(A)_+\setminus \{0\}$
with
$a,b\in M_m(A)_+\setminus \{0\}$
with
![]() $\lVert a\rVert =1=\lVert b\rVert $
for some integer
$\lVert a\rVert =1=\lVert b\rVert $
for some integer
![]() $m\ge 1$
. Set
$m\ge 1$
. Set
![]() $n\in \mathbb {N}$
and assume
$n\in \mathbb {N}$
and assume
![]() $(n+1)\langle a\rangle \leq n\langle b\rangle $
. To prove the theorem, it suffices to prove that
$(n+1)\langle a\rangle \leq n\langle b\rangle $
. To prove the theorem, it suffices to prove that
![]() $a\lesssim b$
.
$a\lesssim b$
.
Note that if
![]() $B\in {\cal W}$
, then for each integer m, we have
$B\in {\cal W}$
, then for each integer m, we have
![]() $M_m(B)\in {\cal W}$
. It follows that
$M_m(B)\in {\cal W}$
. It follows that
![]() $M_m(A)$
is e. tracially in
$M_m(A)$
is e. tracially in
![]() ${\cal W}$
. To simplify notation, without loss of generality one may assume
${\cal W}$
. To simplify notation, without loss of generality one may assume
![]() $a, b\in A_+$
.
$a, b\in A_+$
.
By [Reference Fu and Lin21, Lemma 4.3],
![]() $\mathrm {Her}\left (f_{1/4}(b)\right )_+$
contains
$\mathrm {Her}\left (f_{1/4}(b)\right )_+$
contains
![]() $2n+1$
nonzero mutually orthogonal elements
$2n+1$
nonzero mutually orthogonal elements
![]() $b_0, b_1, \dotsc ,b_{2n}$
such that
$b_0, b_1, \dotsc ,b_{2n}$
such that
![]() $\langle b_i\rangle =\langle b_0\rangle $
,
$\langle b_i\rangle =\langle b_0\rangle $
,
![]() $i=1, 2, \dotsc ,2n$
. Without loss of generality, we may assume that
$i=1, 2, \dotsc ,2n$
. Without loss of generality, we may assume that
![]() $\lVert b_0\rVert =1$
. If
$\lVert b_0\rVert =1$
. If
![]() $b_0$
is a projection, choose
$b_0$
is a projection, choose
![]() $e_0=b_0$
. Otherwise, by replacing
$e_0=b_0$
. Otherwise, by replacing
![]() $b_0$
by
$b_0$
by
![]() $g_1(b_0)$
for some continuous function
$g_1(b_0)$
for some continuous function
![]() $g_1\in C_0([0,1])$
, we may assume that there is a nonzero
$g_1\in C_0([0,1])$
, we may assume that there is a nonzero
![]() $e_0\in A_+$
such that
$e_0\in A_+$
such that
![]() $b_0e_0=e_0b_0=e_0$
. Replacing b by
$b_0e_0=e_0b_0=e_0$
. Replacing b by
![]() $g(b)$
for some
$g(b)$
for some
![]() $g\in C_0((0, 1])$
, one may assume that
$g\in C_0((0, 1])$
, one may assume that
![]() $bb_0=b_0b=b_0$
. Put
$bb_0=b_0b=b_0$
. Put
![]() $c=b-b_0$
. Note that
$c=b-b_0$
. Note that
Keep in mind that
![]() $b\ge c + e_0$
,
$b\ge c + e_0$
,
![]() $c \perp e_0$
and
$c \perp e_0$
and
![]() $2n\langle b_0\rangle \le {{\langle c\rangle =\langle b-b_0 \rangle }}$
. One has
$2n\langle b_0\rangle \le {{\langle c\rangle =\langle b-b_0 \rangle }}$
. One has
By Lemma 4.2, for any
![]() $\varepsilon \in (0,1/2)$
there exist
$\varepsilon \in (0,1/2)$
there exist
![]() $a_1,a_2\in A_+$
such that
$a_1,a_2\in A_+$
such that
-
(i)
 $a\approx _{\epsilon /2}a_1+a_2$
,
$a\approx _{\epsilon /2}a_1+a_2$
, -
(ii)
 $a_1\lesssim _A c$
and
$a_1\lesssim _A c$
and -
(iii)
 $a_2\lesssim _A e_0$
.
$a_2\lesssim _A e_0$
.
By (i)–(iii) and applying [Reference Rørdam40, Proposition 2.2] (recall
![]() $be_0=e_0b=e_0$
), one obtains
$be_0=e_0b=e_0$
), one obtains
Since this holds for every
![]() $\varepsilon \in (0,1/2)$
, one concludes that
$\varepsilon \in (0,1/2)$
, one concludes that
![]() $a\lesssim b$
.
$a\lesssim b$
.
Corollary 4.4. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal C}_{\mathscr Z}$
. Then
${\cal C}_{\mathscr Z}$
. Then
![]() $W(A)$
is almost unperforated.
$W(A)$
is almost unperforated.
Proof. It follows from [Reference Rørdam42, Theorem 4.5] and Theorem 4.3.
Definition 4.5. Let A be a
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() ${\cal T}$
denote the class of
${\cal T}$
denote the class of
![]() $C^*$
-algebras A such that for every
$C^*$
-algebras A such that for every
![]() $a\in \mathrm {Ped}(A)_+\setminus \{0\}$
, every
$a\in \mathrm {Ped}(A)_+\setminus \{0\}$
, every
![]() $2$
-quasitrace of
$2$
-quasitrace of
![]() $\overline {aAa}$
is a trace.
$\overline {aAa}$
is a trace.
Set
![]() $A\in {\cal T}$
and let
$A\in {\cal T}$
and let
![]() $B\subset A$
be a hereditary
$B\subset A$
be a hereditary
![]() $C^*$
-subalgebra. If
$C^*$
-subalgebra. If
![]() $b\in \mathrm {Ped}(B)_+\setminus \{0\}$
, then
$b\in \mathrm {Ped}(B)_+\setminus \{0\}$
, then
![]() $b\in \mathrm {Ped}(A)_+$
and
$b\in \mathrm {Ped}(A)_+$
and
![]() $\overline {bBb}=\overline {bAb}$
. It follows that every
$\overline {bBb}=\overline {bAb}$
. It follows that every
![]() $2$
-quasitrace of
$2$
-quasitrace of
![]() $\overline {bBb}$
is a trace. Hence
$\overline {bBb}$
is a trace. Hence
![]() ${\cal T}$
has property (H).
${\cal T}$
has property (H).
Proposition 4.6. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal T}$
. Then A is in
${\cal T}$
. Then A is in
![]() ${\cal T}$
.
${\cal T}$
.
Proof. Fix
![]() $a\in \mathrm {Ped} (A)_+^{\textbf{1}}$
and let
$a\in \mathrm {Ped} (A)_+^{\textbf{1}}$
and let
![]() $C=\mathrm {Her}(a)$
. We will show that every
$C=\mathrm {Her}(a)$
. We will show that every
![]() $2$
-quasitrace of C is a trace. We may assume that C is nonelementary. Set
$2$
-quasitrace of C is a trace. We may assume that C is nonelementary. Set
![]() $\tau \in QT(C)$
. Fix
$\tau \in QT(C)$
. Fix
![]() $x, y\in C_{\mathrm {sa}}$
with
$x, y\in C_{\mathrm {sa}}$
with
![]() $\lVert x\rVert ,\lVert y\rVert \leq 1/2$
. Set
$\lVert x\rVert ,\lVert y\rVert \leq 1/2$
. Set
![]() $\varepsilon \in (0,1/2)$
. Let
$\varepsilon \in (0,1/2)$
. Let
![]() ${\cal F}:=\{x,y,x+y\}$
. Let
${\cal F}:=\{x,y,x+y\}$
. Let
![]() $n\in \mathbb {N}$
be such that
$n\in \mathbb {N}$
be such that
![]() $\varepsilon>1/n$
. By [Reference Fu and Lin21, Lemma 4.3], there exist mutually orthogonal norm
$\varepsilon>1/n$
. By [Reference Fu and Lin21, Lemma 4.3], there exist mutually orthogonal norm
![]() $1$
positive elements
$1$
positive elements
![]() $c_1,c_2,\dotsc , c_n\in A_+\backslash \{0\}$
such that
$c_1,c_2,\dotsc , c_n\in A_+\backslash \{0\}$
such that
![]() $c_1\sim c_2\sim \dotsb \sim c_n$
. Then
$c_1\sim c_2\sim \dotsb \sim c_n$
. Then
![]() $d_{\tau } ( c_1 )\leq 1/n<\varepsilon $
.
$d_{\tau } ( c_1 )\leq 1/n<\varepsilon $
.
Let
![]() $\delta \in (0,\varepsilon )$
be such that for any
$\delta \in (0,\varepsilon )$
be such that for any
![]() $d\in C_+^{\textbf{1}}$
and
$d\in C_+^{\textbf{1}}$
and
![]() $z\in C_{\mathrm {sa}}^{\textbf{1}}$
, if
$z\in C_{\mathrm {sa}}^{\textbf{1}}$
, if
![]() $\lVert [d,z]\rVert <\delta $
, then
$\lVert [d,z]\rVert <\delta $
, then
and
 $$ \begin{align} \tau(z)\approx_\varepsilon \tau\left((1-d)^{1/2}z(1-d)^{1/2}\right)+\tau\left(d^{1/2}zd^{1/2}\right). \end{align} $$
$$ \begin{align} \tau(z)\approx_\varepsilon \tau\left((1-d)^{1/2}z(1-d)^{1/2}\right)+\tau\left(d^{1/2}zd^{1/2}\right). \end{align} $$
(Note [Reference Blackadar and Handelman4, II.2.6] that
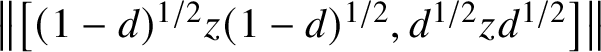 $\left \lVert \left [(1-d)^{1/2}z(1-d)^{1/2},d^{1/2}zd^{1/2}\right ]\right \rVert $
can be sufficiently small depending on
$\left \lVert \left [(1-d)^{1/2}z(1-d)^{1/2},d^{1/2}zd^{1/2}\right ]\right \rVert $
can be sufficiently small depending on
![]() $\delta $
.) Note that
$\delta $
.) Note that
![]() ${\cal T}$
has property (H). Since A is simple and e. tracially in
${\cal T}$
has property (H). Since A is simple and e. tracially in
![]() ${\cal T}$
, by Proposition 3.5 C is also e. tracially in
${\cal T}$
, by Proposition 3.5 C is also e. tracially in
![]() ${\cal T}$
. There exist an element
${\cal T}$
. There exist an element
![]() $e\in C_+^{\textbf{1}}$
and a nonzero
$e\in C_+^{\textbf{1}}$
and a nonzero
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset C$
such that B is in
$B\subset C$
such that B is in
![]() $\mathcal {T}$
, and the following are true:
$\mathcal {T}$
, and the following are true:
-
(1)
 $\lVert ez-ze\rVert <\delta $
for all
$\lVert ez-ze\rVert <\delta $
for all
 $z\in \cal F$
.
$z\in \cal F$
. -
(2)
 $(1-e)^{1/2}z(1-e)^{1/2}\in _{\delta /2} B$
for all
$(1-e)^{1/2}z(1-e)^{1/2}\in _{\delta /2} B$
for all
 $z\in {\cal F}$
.
$z\in {\cal F}$
. -
(3)
 $e\lesssim c_1$
.
$e\lesssim c_1$
.
We may choose
![]() $e_B\in \mathrm {Ped}(B)_+^{\textbf{1}}$
such that
$e_B\in \mathrm {Ped}(B)_+^{\textbf{1}}$
such that
-
(2′)
 $(1-e)^{1/2}z(1-e)^{1/2}\in _{\delta } B_1:=\overline {e_BBe_B}$
for all
$(1-e)^{1/2}z(1-e)^{1/2}\in _{\delta } B_1:=\overline {e_BBe_B}$
for all
 $z\in {\cal F}$
.
$z\in {\cal F}$
.
Note that for
![]() $z\in {\cal F}$
,
$z\in {\cal F}$
,
![]() $e^{1/2}ze^{1/2}$
is self-adjoint. One has
$e^{1/2}ze^{1/2}$
is self-adjoint. One has
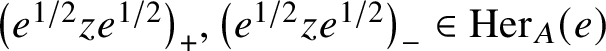 $\left (e^{1/2}ze^{1/2}\right )_+,\left (e^{1/2}ze^{1/2}\right )_-\in \mathrm {Her}_A(e)$
. Then
$\left (e^{1/2}ze^{1/2}\right )_+,\left (e^{1/2}ze^{1/2}\right )_-\in \mathrm {Her}_A(e)$
. Then
 $$ \begin{align} \left\lvert\tau\left(e^{1/2}ze^{1/2}\right)\right\rvert &= \left\lvert\tau\left(\left(e^{1/2}ze^{1/2}\right)_+\right)-\tau\left(\left(e^{1/2}ze^{1/2}\right)_-\right)\right\rvert \hspace{6pc} \end{align} $$
$$ \begin{align} \left\lvert\tau\left(e^{1/2}ze^{1/2}\right)\right\rvert &= \left\lvert\tau\left(\left(e^{1/2}ze^{1/2}\right)_+\right)-\tau\left(\left(e^{1/2}ze^{1/2}\right)_-\right)\right\rvert \hspace{6pc} \end{align} $$
 $$ \begin{align} & \hspace{7pc} \leq d_\tau\left(\left(e^{1/2}ze^{1/2}\right)_+\right)+d_\tau\left(\left(e^{1/2}ze^{1/2}\right)_-\right) \leq 2d_\tau(e)\leq 2\varepsilon. \end{align} $$
$$ \begin{align} & \hspace{7pc} \leq d_\tau\left(\left(e^{1/2}ze^{1/2}\right)_+\right)+d_\tau\left(\left(e^{1/2}ze^{1/2}\right)_-\right) \leq 2d_\tau(e)\leq 2\varepsilon. \end{align} $$
Then by (1), the choice of
![]() $\delta $
and formulas (e4.18) and (e4.19), for
$\delta $
and formulas (e4.18) and (e4.19), for
![]() $z\in {\cal F}$
,
$z\in {\cal F}$
,
 $$ \begin{align} \hspace{3pc} \tau(z) &\approx_{2\varepsilon} \tau\left((1-e)^{1/2}z(1-e)^{1/2}\right)+\tau\left(e^{1/2}ze^{1/2}\right) \end{align} $$
$$ \begin{align} \hspace{3pc} \tau(z) &\approx_{2\varepsilon} \tau\left((1-e)^{1/2}z(1-e)^{1/2}\right)+\tau\left(e^{1/2}ze^{1/2}\right) \end{align} $$
 $$ \begin{align} \text{(by formula (e4.21))}&\approx_{2\varepsilon} \tau\left((1-e)^{1/2}z(1-e)^{1/2}\right). \hspace{7pc} \end{align} $$
$$ \begin{align} \text{(by formula (e4.21))}&\approx_{2\varepsilon} \tau\left((1-e)^{1/2}z(1-e)^{1/2}\right). \hspace{7pc} \end{align} $$
By (2
![]() $'$
), there are
$'$
), there are
![]() $\bar x, \bar y\in (B_1)_{\mathrm {sa}}$
such that
$\bar x, \bar y\in (B_1)_{\mathrm {sa}}$
such that
Then
 $$ \begin{align*} \tau(x+y) &\overset{\text{formula (e 4.23)}}{\approx_{{{4\varepsilon}}}} \tau\left((1-e)^{1/2}(x+y)(1-e)^{1/2}\right) \\ &\overset{\text{formula (e 4.24)}}{\approx_{{4\delta}}} \tau\left(\bar x+\bar y\right) \\ \text{(}\tau\ \text{is a trace on}\ B_1\text{)}&\overset{\phantom{\text{formula (e 4.24)}}}{=} \tau(\bar x)+\tau(\bar y) \\ &\overset{\text{formula (e 4.24)}}{\approx_{{4\delta}}} \tau\left((1-e)^{1/2}x(1-e)^{1/2}\right)+ \tau\left((1-e)^{1/2}y(1-e)^{1/2}\right) \\ &\overset{\text{formula (e 4.23)}}{\approx_{{4\varepsilon}}} \tau(x)+ \tau(y). \end{align*} $$
$$ \begin{align*} \tau(x+y) &\overset{\text{formula (e 4.23)}}{\approx_{{{4\varepsilon}}}} \tau\left((1-e)^{1/2}(x+y)(1-e)^{1/2}\right) \\ &\overset{\text{formula (e 4.24)}}{\approx_{{4\delta}}} \tau\left(\bar x+\bar y\right) \\ \text{(}\tau\ \text{is a trace on}\ B_1\text{)}&\overset{\phantom{\text{formula (e 4.24)}}}{=} \tau(\bar x)+\tau(\bar y) \\ &\overset{\text{formula (e 4.24)}}{\approx_{{4\delta}}} \tau\left((1-e)^{1/2}x(1-e)^{1/2}\right)+ \tau\left((1-e)^{1/2}y(1-e)^{1/2}\right) \\ &\overset{\text{formula (e 4.23)}}{\approx_{{4\varepsilon}}} \tau(x)+ \tau(y). \end{align*} $$
Since
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\delta $
are arbitrary small, we have
$\delta $
are arbitrary small, we have
![]() $\tau (x+y)=\tau (x)+\tau (y)$
, and therefore
$\tau (x+y)=\tau (x)+\tau (y)$
, and therefore
![]() $\tau $
is a trace on C.
$\tau $
is a trace on C.
Definition 4.7. Let A be a
![]() $C^*$
-algebra. Recall that an element
$C^*$
-algebra. Recall that an element
![]() $a\in \mathrm {Ped}(A)_+$
is said to be infinite if there are nonzero elements
$a\in \mathrm {Ped}(A)_+$
is said to be infinite if there are nonzero elements
![]() $b, c\in \mathrm {Ped}(A)_+$
such that
$b, c\in \mathrm {Ped}(A)_+$
such that
![]() $bc=cb=0$
,
$bc=cb=0$
,
![]() $b+c\lesssim c$
and
$b+c\lesssim c$
and
![]() $c\lesssim a$
. A is said to be finite if every element
$c\lesssim a$
. A is said to be finite if every element
![]() $a\in \mathrm {Ped}(A)_+$
is not infinite (see, for example, [Reference Lin and Zhang33, Definition 1.1]). A is stably finite if
$a\in \mathrm {Ped}(A)_+$
is not infinite (see, for example, [Reference Lin and Zhang33, Definition 1.1]). A is stably finite if
![]() $M_n(A)$
is finite for every integer
$M_n(A)$
is finite for every integer
![]() $n\ge 1$
.
$n\ge 1$
.
Recall that a simple
![]() $C^*$
-algebra A is purely infinite if and only if every nonzero element in
$C^*$
-algebra A is purely infinite if and only if every nonzero element in
![]() $\mathrm {Ped}(A)_+$
is infinite (see [Reference Lin and Zhang33, Condition (vii), Theorem 2.2]). Let
$\mathrm {Ped}(A)_+$
is infinite (see [Reference Lin and Zhang33, Condition (vii), Theorem 2.2]). Let
![]() ${\cal PI}$
be the class of
${\cal PI}$
be the class of
![]() $C^*$
-algebras such that every nonzero positive element in the Pedersen ideal is infinite.
$C^*$
-algebras such that every nonzero positive element in the Pedersen ideal is infinite.
Theorem 4.8. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal PI}$
. Then A is purely infinite.
${\cal PI}$
. Then A is purely infinite.
Proof. Note that A has infinite dimension. Set
![]() $a\in \mathrm {Ped}(A)_+\setminus \{0\}$
with
$a\in \mathrm {Ped}(A)_+\setminus \{0\}$
with
![]() $\lVert a\rVert =1$
.
$\lVert a\rVert =1$
.
Since
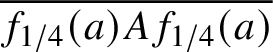 $\overline {f_{1/4}(a)Af_{1/4}(a)}$
is an infinite-dimensional simple
$\overline {f_{1/4}(a)Af_{1/4}(a)}$
is an infinite-dimensional simple
![]() $C^*$
-algebra, one may choose
$C^*$
-algebra, one may choose
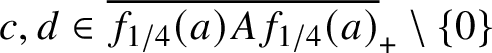 $c, d\in \overline {f_{1/4}(a)Af_{1/4}(a)}_+\setminus \{0\}$
such that
$c, d\in \overline {f_{1/4}(a)Af_{1/4}(a)}_+\setminus \{0\}$
such that
![]() $cd=dc=0$
.
$cd=dc=0$
.
Since A is e. tracially in
![]() ${\cal PI}$
, there exist a sequence of positive elements
${\cal PI}$
, there exist a sequence of positive elements
![]() $e_n\in A_+$
with
$e_n\in A_+$
with
![]() $\lVert e_n\rVert \le 1$
and a sequence of
$\lVert e_n\rVert \le 1$
and a sequence of
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B_n\subset A$
such that
$B_n\subset A$
such that
![]() $B_n$
in
$B_n$
in
![]() ${\cal PI}$
, and the following are true:
${\cal PI}$
, and the following are true:
-
(1)
 $a\approx _{1/2^n} e_n^{1/2}ae_n^{1/2}+(1-e_n)^{1/2}a(1-e_n)^{1/2}$
.
$a\approx _{1/2^n} e_n^{1/2}ae_n^{1/2}+(1-e_n)^{1/2}a(1-e_n)^{1/2}$
. -
(2)
 $(1-e_n)^{1/2}a(1-e_n)^{1/2}\in _{1/2^n} B_n$
and
$(1-e_n)^{1/2}a(1-e_n)^{1/2}\in _{1/2^n} B_n$
and
 $\left \lVert (1-e_n)^{1/2}a(1-e_n)^{1/2}\right \rVert \ge \lVert a\rVert -{1/2^n}$
.
$\left \lVert (1-e_n)^{1/2}a(1-e_n)^{1/2}\right \rVert \ge \lVert a\rVert -{1/2^n}$
. -
(3)
 $e_n\lesssim c$
.
$e_n\lesssim c$
.
By (2), there is
![]() $b_n\in {B_n}_+$
such that
$b_n\in {B_n}_+$
such that
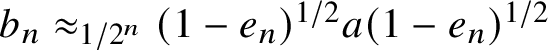 $b_n\approx _{1/2^n} (1-e_n)^{1/2}a(1-e_n)^{1/2}$
. Then by (1),
$b_n\approx _{1/2^n} (1-e_n)^{1/2}a(1-e_n)^{1/2}$
. Then by (1),
 $$ \begin{align} a\approx_{2/2^n} b_n+e_n^{1/2}ae_n^{1/2}. \end{align} $$
$$ \begin{align} a\approx_{2/2^n} b_n+e_n^{1/2}ae_n^{1/2}. \end{align} $$
Note that
![]() $\inf _n\{\lVert b_n\rVert \}\ge \lVert a\rVert /2>0$
. Choose
$\inf _n\{\lVert b_n\rVert \}\ge \lVert a\rVert /2>0$
. Choose
![]() $0<\varepsilon <\lVert a\rVert /16$
.
$0<\varepsilon <\lVert a\rVert /16$
.
By [Reference Phillips37, Lemma 1.7], for all sufficiently large n we have
 $$ \begin{align} {{0\neq(b_{n}-2\varepsilon)_+\lesssim \left(b_{n}+e_{n}^{1/2}ae_{n}^{1/2}-2\varepsilon\right)_+\lesssim a.}} \end{align} $$
$$ \begin{align} {{0\neq(b_{n}-2\varepsilon)_+\lesssim \left(b_{n}+e_{n}^{1/2}ae_{n}^{1/2}-2\varepsilon\right)_+\lesssim a.}} \end{align} $$
Note that
![]() $(b_{n}-2\varepsilon )_+\in \mathrm {Ped}(B_n)_+\setminus \{0\}$
. Then there are
$(b_{n}-2\varepsilon )_+\in \mathrm {Ped}(B_n)_+\setminus \{0\}$
. Then there are
![]() $d_1, d_2\in \mathrm {Ped}(B_n)_+\setminus \{0\}$
such that
$d_1, d_2\in \mathrm {Ped}(B_n)_+\setminus \{0\}$
such that
![]() $d_1\perp d_2$
,
$d_1\perp d_2$
,
![]() $d_1+d_2\lesssim d_2\lesssim (b_{n}-2\varepsilon )_+$
and
$d_1+d_2\lesssim d_2\lesssim (b_{n}-2\varepsilon )_+$
and
It follows that a is infinite, and therefore A is purely infinite.
Proposition 4.9 [Reference Rørdam42, Corollary 5.1]
Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebrasuch that
$C^*$
-algebrasuch that
![]() $W(A)$
is almost unperforated. If A is not purely infinite, then
$W(A)$
is almost unperforated. If A is not purely infinite, then
![]() $\overline {aAa}$
has a nonzero
$\overline {aAa}$
has a nonzero
![]() $2$
-quasitrace for every
$2$
-quasitrace for every
![]() $a\in \mathrm {Ped}(A)_+\setminus \{0\}$
. Consequently, A is stably finite.
$a\in \mathrm {Ped}(A)_+\setminus \{0\}$
. Consequently, A is stably finite.
Proof. This is a theorem of Rørdam [Reference Rørdam42, Corollary 5.1]. Since we do not assume that A is exact and will use only
![]() $2$
-quasitraces, some more explanation is in order. The explanation, of course, follows exactly the same lines as the proof of [Reference Rørdam42, Corollary 5.1].
$2$
-quasitraces, some more explanation is in order. The explanation, of course, follows exactly the same lines as the proof of [Reference Rørdam42, Corollary 5.1].
Set
![]() $a\in \mathrm {Ped}(A)_+^{\textbf{1}}$
and
$a\in \mathrm {Ped}(A)_+^{\textbf{1}}$
and
![]() $B:=\overline {aAa}$
. Then B is algebraically simple (see, for example, [Reference Blackadar3, II.5.4.2]). Assume that B has no nonzero
$B:=\overline {aAa}$
. Then B is algebraically simple (see, for example, [Reference Blackadar3, II.5.4.2]). Assume that B has no nonzero
![]() $2$
-quasitraces.
$2$
-quasitraces.
Consider
![]() $W(B)$
. Note that
$W(B)$
. Note that
![]() $W(B)\subset W(A)$
, and
$W(B)\subset W(A)$
, and
![]() $W(B)$
has the property that if
$W(B)$
has the property that if
![]() $x\in W(B)$
and
$x\in W(B)$
and
![]() $y\in W(A)$
such that
$y\in W(A)$
such that
![]() $y\le x$
, then
$y\le x$
, then
![]() $y\in W(B)$
. It follows that
$y\in W(B)$
. It follows that
![]() $W(B)$
is almost unperforated. Since B is algebraically simple, every element in
$W(B)$
is almost unperforated. Since B is algebraically simple, every element in
![]() $W(B)$
is a strong order unit.
$W(B)$
is a strong order unit.
Set
![]() $t, t'\in W(B)$
(with t a strong order unit). The statement (and the proof) of [Reference Rørdam40, Proposition 3.1] imply that if there is no state on
$t, t'\in W(B)$
(with t a strong order unit). The statement (and the proof) of [Reference Rørdam40, Proposition 3.1] imply that if there is no state on
![]() $W(B)$
(with the strong order unit t), then there must be some integer
$W(B)$
(with the strong order unit t), then there must be some integer
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $u\in W(B)$
such that
$u\in W(B)$
such that
Then by [Reference Rørdam40, Proposition 3.2] (see the proof also), as
![]() $W(B)$
is almost unperforated,
$W(B)$
is almost unperforated,
On the other hand, by [Reference Blackadar and Handelman4, II.2.2], every lower semicontinuous dimension function on
![]() $W(B)$
is induced by a
$W(B)$
is induced by a
![]() $2$
-quasitrace on B. Since B is assumed to have no nonzero
$2$
-quasitrace on B. Since B is assumed to have no nonzero
![]() $2$
-quasitraces, combining with [Reference Rørdam40, Proposition 4.1] (as well as the paragraph before it) shows that there is no state on
$2$
-quasitraces, combining with [Reference Rørdam40, Proposition 4.1] (as well as the paragraph before it) shows that there is no state on
![]() $W(B)$
. Therefore formula (e4.29) implies that for any
$W(B)$
. Therefore formula (e4.29) implies that for any
![]() $b, c\in B_+\setminus \{0\}$
, we have
$b, c\in B_+\setminus \{0\}$
, we have
![]() $b\lesssim c$
. It follows that B is purely infinite and so is A.
$b\lesssim c$
. It follows that B is purely infinite and so is A.
To see the last part of the statement, suppose that there are
![]() $b, c\in \mathrm {Ped}(A)_+^{\textbf{1}}\setminus \{0\}$
such that
$b, c\in \mathrm {Ped}(A)_+^{\textbf{1}}\setminus \{0\}$
such that
![]() $bc=cb=0$
and
$bc=cb=0$
and
![]() $b+c\lesssim c$
. Let
$b+c\lesssim c$
. Let
![]() $a=b+c$
and
$a=b+c$
and
![]() $B=\overline {aAa}$
. Note that
$B=\overline {aAa}$
. Note that
![]() $a\in \mathrm {Ped}(A)_+$
. Then B has nonzero
$a\in \mathrm {Ped}(A)_+$
. Then B has nonzero
![]() $2$
-quasitraces.
$2$
-quasitraces.
Therefore
On the other hand, for any
![]() $\tau \in QT(B)$
and any
$\tau \in QT(B)$
and any
![]() $1>\varepsilon >0$
,
$1>\varepsilon >0$
,
Fix
![]() $1>\varepsilon _0>0$
such that
$1>\varepsilon _0>0$
such that
![]() $f_{\varepsilon _0}(b)\not =0$
. Since B is algebraically simple,
$f_{\varepsilon _0}(b)\not =0$
. Since B is algebraically simple,
![]() $\tau \left (f_{\varepsilon _0}(b)\right )>0$
for all
$\tau \left (f_{\varepsilon _0}(b)\right )>0$
for all
![]() $2$
-quasitraces
$2$
-quasitraces
![]() $\tau $
. Fix
$\tau $
. Fix
![]() $\tau \in QT(B)$
. Then, by equation (e4.31),
$\tau \in QT(B)$
. Then, by equation (e4.31),
This contradicts formula (e4.30). It follows that no such pairs b and c exist. Thus A is finite.
Since
![]() $M_n(A)$
has the same relevant property as A, we conclude that A is stably finite.
$M_n(A)$
has the same relevant property as A, we conclude that A is stably finite.
Corollary 4.10. Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebrasuch that A is e. tracially in
$C^*$
-algebrasuch that A is e. tracially in
![]() ${\cal W}$
. Then A has strict comparison.
${\cal W}$
. Then A has strict comparison.
Proof. By Theorem 4.3,
![]() $W(A)$
is almost unperforated. It follows from Remark 2.5 that
$W(A)$
is almost unperforated. It follows from Remark 2.5 that
![]() $\mathrm {Cu}(A)$
is almost unperforated. Fix
$\mathrm {Cu}(A)$
is almost unperforated. Fix
![]() $e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and let
$e\in \mathrm {Ped}(A)_+\setminus \{0\}$
and let
![]() $B:=\mathrm {Her}(e)$
. As in the proof of Proposition 4.9, every lower semicontinuous dimension function on
$B:=\mathrm {Her}(e)$
. As in the proof of Proposition 4.9, every lower semicontinuous dimension function on
![]() $W(B)$
is induced by a
$W(B)$
is induced by a
![]() $2$
-quasitrace of B. Set
$2$
-quasitrace of B. Set
![]() $a, b\in (A\otimes {\cal K})_+$
such that
$a, b\in (A\otimes {\cal K})_+$
such that
![]() $d_\tau (a)<d_\tau (b)$
for all
$d_\tau (a)<d_\tau (b)$
for all
![]() $\tau \in QT(B)$
. By [Reference Elliott, Robert and Santiago17, Propositions 4.2, 4.6],
$\tau \in QT(B)$
. By [Reference Elliott, Robert and Santiago17, Propositions 4.2, 4.6],
![]() $a\lesssim b$
.
$a\lesssim b$
.
5. Essentially tracially
 ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
 $C^*$
-algebras
$C^*$
-algebras
Recall from Notation 4.1 that
![]() ${\cal C}_{\mathscr Z}$
is the class of separable
${\cal C}_{\mathscr Z}$
is the class of separable
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras.
$C^*$
-algebras.
Theorem 5.1. Let A be a
![]() $\sigma $
-unital simple
$\sigma $
-unital simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal C}_{\mathscr Z}$
. Then A is either purely infinite or stably finite. Moreover, if A is not purely infinite, then it has strict comparison for positive elements.
${\cal C}_{\mathscr Z}$
. Then A is either purely infinite or stably finite. Moreover, if A is not purely infinite, then it has strict comparison for positive elements.
Proof. It follows from [Reference Rørdam42, Theorem 4.5] that every
![]() $C^*$
-algebra B in
$C^*$
-algebra B in
![]() ${\cal C}_{\mathscr Z}$
has almost unperforated
${\cal C}_{\mathscr Z}$
has almost unperforated
![]() $W(B)$
. It follows from Theorem 4.3 and Remark 2.5 that
$W(B)$
. It follows from Theorem 4.3 and Remark 2.5 that
![]() $\mathrm {Cu}(A)$
is almost unperforated. By Proposition 4.9, if A is not purely infinite, then it is stably finite, and by the proof of Corollary 4.10, A has strict comparison for positive elements.
$\mathrm {Cu}(A)$
is almost unperforated. By Proposition 4.9, if A is not purely infinite, then it is stably finite, and by the proof of Corollary 4.10, A has strict comparison for positive elements.
Definition 5.2. Let A be a simple
![]() $C^*$
-algebra. A is said to be tracially approximately divisible if for any
$C^*$
-algebra. A is said to be tracially approximately divisible if for any
![]() $\varepsilon>0$
, any
$\varepsilon>0$
, any
![]() ${\cal F}=\{x_1,x_2,\dotsc ,x_m\}\subset A$
, any element
${\cal F}=\{x_1,x_2,\dotsc ,x_m\}\subset A$
, any element
![]() $e_F\in A_+^{\textbf{1}}$
with
$e_F\in A_+^{\textbf{1}}$
with
![]() $e_Fy_i=y_i=y_ie_F$
for some
$e_Fy_i=y_i=y_ie_F$
for some
![]() $y_i\approx _{\varepsilon /4} x_i$
,
$y_i\approx _{\varepsilon /4} x_i$
,
![]() $1\le i\le m$
, any
$1\le i\le m$
, any
![]() $s\in A_+\setminus \{0\}$
, and any integer
$s\in A_+\setminus \{0\}$
, and any integer
![]() $n\ge 1$
, there are
$n\ge 1$
, there are
![]() $\theta \in A_+^{\textbf{1}}$
, a
$\theta \in A_+^{\textbf{1}}$
, a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $D\otimes M_n\subset A$
and a c.p.c. map
$D\otimes M_n\subset A$
and a c.p.c. map
![]() ${\beta }: A\to A$
such that the following are true:
${\beta }: A\to A$
such that the following are true:
-
(1)
 $x\approx _\varepsilon x'+{\beta }(x)$
for all
$x\approx _\varepsilon x'+{\beta }(x)$
for all
 $x\in {\cal F}$
, where
$x\in {\cal F}$
, where
 $\lVert x'\rVert \le \lVert x\rVert $
,
$\lVert x'\rVert \le \lVert x\rVert $
,
 $x'\in \mathrm {Her}(\theta )$
.
$x'\in \mathrm {Her}(\theta )$
. -
(2)
 ${\beta }(x)\in _\varepsilon D\otimes 1_n$
and
${\beta }(x)\in _\varepsilon D\otimes 1_n$
and
 $e_F{\beta }(x)\approx _{\varepsilon } {\beta }(x)\approx _\varepsilon {\beta }(x)e_F$
for all
$e_F{\beta }(x)\approx _{\varepsilon } {\beta }(x)\approx _\varepsilon {\beta }(x)e_F$
for all
 $x\in {\cal F}$
.
$x\in {\cal F}$
. -
(3)
 $\theta \lesssim s. $
$\theta \lesssim s. $
The notion of approximate divisibility for
![]() $C^*$
-algebras was introduced in [Reference Blackadar and Kirchberg6]. The term ‘tracially approximate divisibility’ appeared in [Reference Lin32] (for special cases, see [Reference Lin32, Definition 5.3, proof of Theorem 5.4], [Reference Lin29, Lemma 6.10], [Reference Elliott, Gong, Lin and Niu15, Definition 10.1]).
$C^*$
-algebras was introduced in [Reference Blackadar and Kirchberg6]. The term ‘tracially approximate divisibility’ appeared in [Reference Lin32] (for special cases, see [Reference Lin32, Definition 5.3, proof of Theorem 5.4], [Reference Lin29, Lemma 6.10], [Reference Elliott, Gong, Lin and Niu15, Definition 10.1]).
-
(1) If A is a unital separable simple
 $C^*$
-algebra which is approximately divisible, then it is tracially approximately divisible. To see this, recall that by [Reference Blackadar and Kirchberg6, Theorem 1.4(d)], A has strict comparison. Let
$C^*$
-algebra which is approximately divisible, then it is tracially approximately divisible. To see this, recall that by [Reference Blackadar and Kirchberg6, Theorem 1.4(d)], A has strict comparison. Let
 $\varepsilon>0$
, a finite subset
$\varepsilon>0$
, a finite subset
 ${\cal F}\subset A$
,
${\cal F}\subset A$
,
 $a\in A_+\setminus \{0\}$
and
$a\in A_+\setminus \{0\}$
and
 $n\in \mathbb {N}$
be given. We assume that
$n\in \mathbb {N}$
be given. We assume that
 $1\in {\cal F}$
. Choose an integer m such that
$1\in {\cal F}$
. Choose an integer m such that
 $d_\tau (a)\ge 1/m$
for all
$d_\tau (a)\ge 1/m$
for all
 $\tau \in QT(A)$
(recall that A is a unital separable simple
$\tau \in QT(A)$
(recall that A is a unital separable simple
 $C^*$
-algebra and
$C^*$
-algebra and
 $QT(A)$
is a simplex, by [Reference Blackadar, Kumjian and Rørdam5, II.4.4]). Choose an integer
$QT(A)$
is a simplex, by [Reference Blackadar, Kumjian and Rørdam5, II.4.4]). Choose an integer
 $k>mn$
. It follows from [Reference Blackadar and Kirchberg6, Corollary 2.10] that we may assume that
$k>mn$
. It follows from [Reference Blackadar and Kirchberg6, Corollary 2.10] that we may assume that
 ${\cal F}\subset _{\varepsilon /2} \bigoplus _{i=1}^s A_n\otimes 1_{M_{k_i}}\subset \bigoplus _{i=1}^s A_n\otimes M_{k_i}$
, where
${\cal F}\subset _{\varepsilon /2} \bigoplus _{i=1}^s A_n\otimes 1_{M_{k_i}}\subset \bigoplus _{i=1}^s A_n\otimes M_{k_i}$
, where
 $A_n$
is a
$A_n$
is a
 $C^*$
-subalgebra of A and
$C^*$
-subalgebra of A and
 $k_i\ge k$
. Write
$k_i\ge k$
. Write
 $k_i=l_imn+r_i$
, where
$k_i=l_imn+r_i$
, where
 $l_i, r_i\in \mathbb {N}$
and
$l_i, r_i\in \mathbb {N}$
and
 $0\le r_i < mn$
,
$0\le r_i < mn$
,
 $i=1,2,\dotsc ,s$
. Note that
$i=1,2,\dotsc ,s$
. Note that
 $1\in \bigoplus _{i=1}^s A_n\otimes M_{k_i}$
. So each
$1\in \bigoplus _{i=1}^s A_n\otimes M_{k_i}$
. So each
 $A_n$
is unital. In each
$A_n$
is unital. In each
 $M_{k_i}$
, find a projection
$M_{k_i}$
, find a projection
 $e_i$
with rank
$e_i$
with rank
 $l_imn$
,
$l_imn$
,
 $i=1,2,\dotsc ,s$
. Put
$i=1,2,\dotsc ,s$
. Put
 $e=\oplus _{i=1}^s 1_{A_n}\otimes e_i$
and
$e=\oplus _{i=1}^s 1_{A_n}\otimes e_i$
and
 $\theta =1-e$
. We will identify
$\theta =1-e$
. We will identify
 $M_{l_imn}$
with
$M_{l_imn}$
with
 $M_{l_im}\otimes M_n$
. Then we have
$M_{l_im}\otimes M_n$
. Then we have-
(i)
 $\theta x\approx _{\varepsilon } x\theta $
for all
$\theta x\approx _{\varepsilon } x\theta $
for all
 $x\in {\cal F}$
,
$x\in {\cal F}$
, -
(ii)
 $(1-\theta )x(1-\theta )=exe\in _{\varepsilon } \bigoplus _{i=1}^s A_n\otimes e_i\subset \bigoplus _{i=1}^s \left (A_n\otimes M_{l_im}\right )\otimes 1_n$
and
$(1-\theta )x(1-\theta )=exe\in _{\varepsilon } \bigoplus _{i=1}^s A_n\otimes e_i\subset \bigoplus _{i=1}^s \left (A_n\otimes M_{l_im}\right )\otimes 1_n$
and -
(iii)
 $\theta \lesssim a$
, as
$\theta \lesssim a$
, as
 $d_\tau (1-e)<1/mn<d_\tau (a)$
for all
$d_\tau (1-e)<1/mn<d_\tau (a)$
for all
 $\tau \in QT(A)$
.
$\tau \in QT(A)$
.
From this we conclude that A is tracially approximately divisible (see also Proposition 5.3).
-
-
(2) Note that the Jiang–Su algebra
 ${\mathscr Z}$
is not approximately divisible, as it has no nontrivial projections. However, by Theorem 5.9, it is tracially approximately divisible.
${\mathscr Z}$
is not approximately divisible, as it has no nontrivial projections. However, by Theorem 5.9, it is tracially approximately divisible. -
(3) In a subsequent paper [Reference Fu, Li and Lin20, Theorem 4.11], at least in the separable case, we show that the converse of Proposition 5.3 also holds. In fact, in [Reference Fu, Li and Lin20, Lemma 4.9] we show that a weaker version of Definition 5.2, without mentioning
 $e_F$
, implies the conditions stated in Proposition 5.3. In other words, in Definition 5.2, any reference to
$e_F$
, implies the conditions stated in Proposition 5.3. In other words, in Definition 5.2, any reference to
 $e_F$
could be omitted. However, the proof is somewhat more involved; we refer the reader to [Reference Fu, Li and Lin20] for further discussion.
$e_F$
could be omitted. However, the proof is somewhat more involved; we refer the reader to [Reference Fu, Li and Lin20] for further discussion. -
(4) There is also a notion called ‘tracially almost divisibility’ (see [Reference Winter48, Definition 3.5]). That definition uses quasitraces, whereas Definition 5.2 does not mention quasitraces. They are quite different. However, it is not hard to show that tracially approximate divisibility implies tracially almost divisibility. In [Reference Fu, Li and Lin20], we show a separable simple
 $C^*$
-algebra A which is tracially approximately divisible, has strict comparison and stable rank one and has a nice description of its Cuntz semigroup. These imply, in particular, that A has the tracially almost divisible property defined in [Reference Winter48, Definition 3.5]. The converse, in general, does not hold even with strict comparison – for example,
$C^*$
-algebra A which is tracially approximately divisible, has strict comparison and stable rank one and has a nice description of its Cuntz semigroup. These imply, in particular, that A has the tracially almost divisible property defined in [Reference Winter48, Definition 3.5]. The converse, in general, does not hold even with strict comparison – for example,
 $A=C^*_{\mathrm {red}}(F_\infty )$
(see [Reference Fu, Li and Lin20, 7.3]).
$A=C^*_{\mathrm {red}}(F_\infty )$
(see [Reference Fu, Li and Lin20, 7.3]).
Proposition 5.3 compare [Reference Lin32, 5.3]
Suppose that A is a simple
![]() $C^*$
-algebra which satisfies the following conditions: For any
$C^*$
-algebra which satisfies the following conditions: For any
![]() $\varepsilon>0$
, any finite subset
$\varepsilon>0$
, any finite subset
![]() ${\cal F}\subset A$
, any
${\cal F}\subset A$
, any
![]() $s\in A_+\setminus \{0\}$
and any integer
$s\in A_+\setminus \{0\}$
and any integer
![]() $n\ge 1$
, there are
$n\ge 1$
, there are
![]() $\theta \in A_+^{\textbf{1}}$
and a
$\theta \in A_+^{\textbf{1}}$
and a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $D\otimes M_n\subset A$
such that
$D\otimes M_n\subset A$
such that
-
(i)
 $\theta x\approx _{\varepsilon } x\theta $
for all
$\theta x\approx _{\varepsilon } x\theta $
for all
 $x\in {\cal F}$
,
$x\in {\cal F}$
, -
(ii)
 ${{(1-\theta )}}x\in _{\varepsilon } D\otimes 1_n$
for all
${{(1-\theta )}}x\in _{\varepsilon } D\otimes 1_n$
for all
 $x\in {\cal F}$
and
$x\in {\cal F}$
and -
(iii)
 $\theta \lesssim s$
.
$\theta \lesssim s$
.
Then A is tracially approximately divisible.
Proof. Let
![]() ${\cal F}\subset A$
a finite subset,
${\cal F}\subset A$
a finite subset,
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $s\in A_+\setminus \{0\}$
and an integer n be given. Suppose that there are a finite subset
$s\in A_+\setminus \{0\}$
and an integer n be given. Suppose that there are a finite subset
![]() ${\cal F}'$
and an element
${\cal F}'$
and an element
![]() $e_F\in A_+^{\textbf{1}}$
such that
$e_F\in A_+^{\textbf{1}}$
such that
![]() $e_Fy=y=ye_F$
for all
$e_Fy=y=ye_F$
for all
![]() $y\in {\cal F}'$
, and if
$y\in {\cal F}'$
, and if
![]() $x\in {\cal F}$
, there is
$x\in {\cal F}$
, there is
![]() $y\in {\cal F}'$
such that
$y\in {\cal F}'$
such that
![]() $\lVert y-x\rVert <\varepsilon /4$
. Without loss of generality, we may assume that
$\lVert y-x\rVert <\varepsilon /4$
. Without loss of generality, we may assume that
![]() ${\cal F}\subset A^{\textbf{1}}$
. We may further assume that
${\cal F}\subset A^{\textbf{1}}$
. We may further assume that
![]() ${\cal F}'\subset A^{\textbf{1}}$
.
${\cal F}'\subset A^{\textbf{1}}$
.
Let
![]() $\delta \in (0,\varepsilon /8)$
be a positive number such that for any elements
$\delta \in (0,\varepsilon /8)$
be a positive number such that for any elements
![]() $z\in A^{\textbf{1}}$
and
$z\in A^{\textbf{1}}$
and
![]() ${{w}}\in A_+^{\textbf{1}}$
,
${{w}}\in A_+^{\textbf{1}}$
,
![]() $\lVert zw-wz\rVert <\delta $
implies that
$\lVert zw-wz\rVert <\delta $
implies that
 $$ \begin{align} {{\left\lVert(1-w)^{1/2}z-z(1-w)^{1/2}\right\rVert<\varepsilon/8.}} \end{align} $$
$$ \begin{align} {{\left\lVert(1-w)^{1/2}z-z(1-w)^{1/2}\right\rVert<\varepsilon/8.}} \end{align} $$
Put
![]() ${\cal F}_1={\cal F}\cup \{e_F\}\cup {\cal F}'$
. Suppose that there are
${\cal F}_1={\cal F}\cup \{e_F\}\cup {\cal F}'$
. Suppose that there are
![]() $\theta \in A_+^{\textbf{1}}$
and D as in the statement of the proposition, such that (i), (ii) and (iii) hold for
$\theta \in A_+^{\textbf{1}}$
and D as in the statement of the proposition, such that (i), (ii) and (iii) hold for
![]() $\delta $
(in place of
$\delta $
(in place of
![]() $\varepsilon $
) and
$\varepsilon $
) and
![]() ${\cal F}_1$
(in place of
${\cal F}_1$
(in place of
![]() ${\cal F}$
).
${\cal F}$
).
Then in Definition 5.2(3) holds.
Define
![]() ${\beta }: A\to A$
by
${\beta }: A\to A$
by
![]() ${\beta }(a):= (1-\theta )^{1/2}a(1-\theta )^{1/2}$
for all
${\beta }(a):= (1-\theta )^{1/2}a(1-\theta )^{1/2}$
for all
![]() $a\in A$
. It is a c.p.c. map. For each
$a\in A$
. It is a c.p.c. map. For each
![]() $x\in {\cal F}_1$
, define
$x\in {\cal F}_1$
, define
![]() $x_1:=\theta ^{1/2} x\theta ^{1/2} \,\in \mathrm {Her}(\theta )$
. Then
$x_1:=\theta ^{1/2} x\theta ^{1/2} \,\in \mathrm {Her}(\theta )$
. Then
![]() $\lVert x_1\rVert \le \lVert x\rVert $
. Note that by the choice of
$\lVert x_1\rVert \le \lVert x\rVert $
. Note that by the choice of
![]() $\delta $
, for all
$\delta $
, for all
![]() $x\in {\cal F}\cup {\cal F}'$
,
$x\in {\cal F}\cup {\cal F}'$
,
 $$ \begin{align} e_F{\beta}(x)=e_F(1-\theta)^{1/2}x(1-\theta)^{1/2}\approx_{\varepsilon/8}(1-\theta)^{1/2}e_Fx(1-\theta)^{1/2}\approx_{\varepsilon/8} {\beta}(x) \approx_{\varepsilon/4} {\beta}(x)e_F. \end{align} $$
$$ \begin{align} e_F{\beta}(x)=e_F(1-\theta)^{1/2}x(1-\theta)^{1/2}\approx_{\varepsilon/8}(1-\theta)^{1/2}e_Fx(1-\theta)^{1/2}\approx_{\varepsilon/8} {\beta}(x) \approx_{\varepsilon/4} {\beta}(x)e_F. \end{align} $$
Moreover, for all
![]() $x\in {\cal F}_1$
,
$x\in {\cal F}_1$
,
 $$ \begin{align} {\beta}(x)=(1-\theta)^{1/2}x(1-\theta)^{1/2} {{ \approx_{\varepsilon/8} (1-\theta)}}x\in_{\delta} D\otimes 1_n. \end{align} $$
$$ \begin{align} {\beta}(x)=(1-\theta)^{1/2}x(1-\theta)^{1/2} {{ \approx_{\varepsilon/8} (1-\theta)}}x\in_{\delta} D\otimes 1_n. \end{align} $$
So Definition 5.2(2) holds. Also by the choice of
![]() $\delta $
, for all
$\delta $
, for all
![]() $x\in {\cal F}_1$
,
$x\in {\cal F}_1$
,
 $$ \begin{align} x=\theta x+(1-\theta)x\approx_{\varepsilon/4} \theta^{1/2}x\theta^{1/2}+(1-\theta)^{1/2}x(1-\theta)^{1/2}=x_1+{\beta}(x). \end{align} $$
$$ \begin{align} x=\theta x+(1-\theta)x\approx_{\varepsilon/4} \theta^{1/2}x\theta^{1/2}+(1-\theta)^{1/2}x(1-\theta)^{1/2}=x_1+{\beta}(x). \end{align} $$
Hence Definition 5.2(1) holds. Thus A is tracially approximately divisible.
The following lemma is convenient folklore:
Lemma 5.4. Let
![]() $\delta>0$
. There is an integer
$\delta>0$
. There is an integer
![]() $N(\delta )\ge 1$
such that for any
$N(\delta )\ge 1$
such that for any
![]() $C^*$
-algebra A, any
$C^*$
-algebra A, any
![]() $e\in A_+^{\textbf{1}}$
and any
$e\in A_+^{\textbf{1}}$
and any
![]() $x\in A$
, if
$x\in A$
, if
![]() $x^*x\le e$
and
$x^*x\le e$
and
![]() $xx^*\le e$
, then
$xx^*\le e$
, then
Proof. Let
![]() $\delta>0$
be given. Choose
$\delta>0$
be given. Choose
![]() ${{N(\delta )}}\ge 1$
such that
${{N(\delta )}}\ge 1$
such that
 $$ \begin{align} \max\left\{\left\lvert{{\left(1-t^{1/n}\right)^2t}}\right\rvert: t\in [0,1]\right\}<\delta^2 \mathrm{\ for\ all\ } n\ge {{N(\delta)}}. \end{align} $$
$$ \begin{align} \max\left\{\left\lvert{{\left(1-t^{1/n}\right)^2t}}\right\rvert: t\in [0,1]\right\}<\delta^2 \mathrm{\ for\ all\ } n\ge {{N(\delta)}}. \end{align} $$
Then for any
![]() $C^*$
-algebra A, any
$C^*$
-algebra A, any
![]() $e\in A_+^{\textbf{1}}$
and any
$e\in A_+^{\textbf{1}}$
and any
![]() $x\in A$
satisfying
$x\in A$
satisfying
![]() $x^*x\le e$
and
$x^*x\le e$
and
![]() $xx^*\le e$
,
$xx^*\le e$
,
 $$ \begin{align} \left\lVert\left(1-e^{1/n}\right)x\right\rVert = \left\lVert\left(1-e^{1/n}\right)xx^*\left(1-e^{1/n}\right)\right\rVert^{1/2} \leq \left\lVert\left(1-e^{1/n}\right)e\left(1-e^{1/n}\right)\right\rVert^{1/2} <\delta \end{align} $$
$$ \begin{align} \left\lVert\left(1-e^{1/n}\right)x\right\rVert = \left\lVert\left(1-e^{1/n}\right)xx^*\left(1-e^{1/n}\right)\right\rVert^{1/2} \leq \left\lVert\left(1-e^{1/n}\right)e\left(1-e^{1/n}\right)\right\rVert^{1/2} <\delta \end{align} $$
for all
![]() $n\geq N(\delta )$
. Similarly, we also have
$n\geq N(\delta )$
. Similarly, we also have
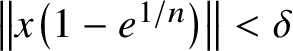 $\left \lVert x\left (1-e^{1/n}\right )\right \rVert <\delta $
for all
$\left \lVert x\left (1-e^{1/n}\right )\right \rVert <\delta $
for all
![]() $n\geq N(\delta )$
. The lemma follows.
$n\geq N(\delta )$
. The lemma follows.
Theorem 5.5. If A is a simple
![]() $C^*$
-algebra which is tracially approximately divisible, then every hereditary
$C^*$
-algebra which is tracially approximately divisible, then every hereditary
![]() $C^*$
-subalgebra of A is also tracially approximately divisible.
$C^*$
-subalgebra of A is also tracially approximately divisible.
Proof. Let B be a hereditary
![]() $C^*$
-subalgebra of A,
$C^*$
-subalgebra of A,
![]() ${\cal F}\subset B^{\textbf{1}}$
be a finite subset,
${\cal F}\subset B^{\textbf{1}}$
be a finite subset,
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $s\in B_+\setminus \{0\}$
be a positive element and
$s\in B_+\setminus \{0\}$
be a positive element and
![]() $n\ge 1$
be an integer. Suppose also that there exists a finite subset
$n\ge 1$
be an integer. Suppose also that there exists a finite subset
![]() ${\cal F}'\subset B^{\textbf{1}}$
such that
${\cal F}'\subset B^{\textbf{1}}$
such that
![]() $y\in _{\varepsilon /4}{\cal F}'$
for all
$y\in _{\varepsilon /4}{\cal F}'$
for all
![]() $y\in {\cal F}$
, and there exists an element
$y\in {\cal F}$
, and there exists an element
![]() $e_F\in B_+^{\textbf{1}}$
such that
$e_F\in B_+^{\textbf{1}}$
such that
![]() $e_Fx=x=xe_F$
for all
$e_Fx=x=xe_F$
for all
![]() $x\in {\cal F}'$
. Let
$x\in {\cal F}'$
. Let
![]() $g_0, g_1\in C_0([0,1])$
be such that
$g_0, g_1\in C_0([0,1])$
be such that
![]() $0\le g_0, g_1\le 1$
,
$0\le g_0, g_1\le 1$
,
![]() $g_0(0)=0$
,
$g_0(0)=0$
,
![]() $g_0(t)=1$
for
$g_0(t)=1$
for
![]() $t\in [1-\varepsilon /64,1]$
and
$t\in [1-\varepsilon /64,1]$
and
![]() $g_0$
is linear on
$g_0$
is linear on
![]() $[0, 1-\varepsilon /64];$
and
$[0, 1-\varepsilon /64];$
and
![]() $g_1(t)=0$
if
$g_1(t)=0$
if
![]() $t\in [0,1-\varepsilon /64]$
,
$t\in [0,1-\varepsilon /64]$
,
![]() $g_1(1)=1$
and
$g_1(1)=1$
and
![]() $g_1$
is linear on
$g_1$
is linear on
![]() $[1-\varepsilon /64, 1]$
. Put
$[1-\varepsilon /64, 1]$
. Put
![]() $b_0:=g_0(e_F)$
and
$b_0:=g_0(e_F)$
and
![]() $b_1:=g_1(e_F)$
. Then
$b_1:=g_1(e_F)$
. Then
Since for all
![]() $x\in {\cal F'}$
we have
$x\in {\cal F'}$
we have
![]() $e_Fxx^*=xx^*=xx^*e_F$
and
$e_Fxx^*=xx^*=xx^*e_F$
and
![]() $e_Fx^*x=x^*x=x^*xe_F$
, by the spectral theory, we have
$e_Fx^*x=x^*x=x^*xe_F$
, by the spectral theory, we have
![]() $b_ixx^*=xx^*=xx^*b_i$
and
$b_ixx^*=xx^*=xx^*b_i$
and
![]() $b_ix^*x=x^*x=x^*xb_i$
,
$b_ix^*x=x^*x=x^*xb_i$
,
![]() $i=0,1$
. It follows that
$i=0,1$
. It follows that
Let
![]() ${\cal F}_1= \{b_1\}\cup {\cal F}'$
. Choose
${\cal F}_1= \{b_1\}\cup {\cal F}'$
. Choose
![]() $\delta>0$
in [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] associated with
$\delta>0$
in [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] associated with
![]() $\varepsilon /64$
(in place of
$\varepsilon /64$
(in place of
![]() $\varepsilon $
) and
$\varepsilon $
) and
![]() $\sigma =\varepsilon /64$
. Set
$\sigma =\varepsilon /64$
. Set
![]() $\eta =\min \{\delta /4, \varepsilon /256\}$
.
$\eta =\min \{\delta /4, \varepsilon /256\}$
.
We choose
![]() $N:= N(\eta )\ge 1$
as in Lemma 5.4.
$N:= N(\eta )\ge 1$
as in Lemma 5.4.
Let
![]() $0<\delta _1<\eta /2$
. Moreover, we choose
$0<\delta _1<\eta /2$
. Moreover, we choose
![]() $\delta _1$
sufficiently small that if
$\delta _1$
sufficiently small that if
![]() $C_1\subset C_2$
is any pair of
$C_1\subset C_2$
is any pair of
![]() $C^*$
-algebras and
$C^*$
-algebras and
![]() $c\in C_2$
with
$c\in C_2$
with
![]() $0\le c\le 1$
and
$0\le c\le 1$
and
![]() $c\in _{\delta _1} C_1$
, and if
$c\in _{\delta _1} C_1$
, and if
![]() $0\le c_1, c_2\le 1$
and
$0\le c_1, c_2\le 1$
and
![]() $c_1c_2\approx _{\delta _1} c_2\approx _{\delta _1}c_2c_1$
, then
$c_1c_2\approx _{\delta _1} c_2\approx _{\delta _1}c_2c_1$
, then
 $$ \begin{align} c^{1/N}\in_{\eta} (C_1)_+^{\textbf{1}}\qquad \text{and} \qquad c_1c_2^{1/N}c_1\approx_\eta c_2^{1/N}. \end{align} $$
$$ \begin{align} c^{1/N}\in_{\eta} (C_1)_+^{\textbf{1}}\qquad \text{and} \qquad c_1c_2^{1/N}c_1\approx_\eta c_2^{1/N}. \end{align} $$
Since A is tracially approximately divisible, there are
![]() $\theta _a\in A_+^{\textbf{1}}$
, a
$\theta _a\in A_+^{\textbf{1}}$
, a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $D_a\otimes M_n\subset A$
and a c.p.c. map
$D_a\otimes M_n\subset A$
and a c.p.c. map
![]() ${\beta }: A\to A$
such that
${\beta }: A\to A$
such that
-
(1)
 $x\approx _{\delta _1/2} x_1+ {\beta }(x) $
such that
$x\approx _{\delta _1/2} x_1+ {\beta }(x) $
such that
 $\lVert x_1\rVert \le 1$
and
$\lVert x_1\rVert \le 1$
and
 $x_1\in \mathrm {Her}(\theta _a)$
for all
$x_1\in \mathrm {Her}(\theta _a)$
for all
 $x\in {\cal F}_1$
,
$x\in {\cal F}_1$
, -
(2)
 ${\beta }(x)\in _{\delta _1/2} D_a\otimes 1_n$
and
${\beta }(x)\in _{\delta _1/2} D_a\otimes 1_n$
and
 $ b_0{\beta }(x)\approx _{\delta _1/2} {\beta }(x)\approx _{\delta _1/2} {\beta }(x)b_0 \text { for all } x\in {\cal F}_1$
and
$ b_0{\beta }(x)\approx _{\delta _1/2} {\beta }(x)\approx _{\delta _1/2} {\beta }(x)b_0 \text { for all } x\in {\cal F}_1$
and -
(3)
 $\theta _a\lesssim s$
.
$\theta _a\lesssim s$
.
Choose
![]() $d(x)\in (D_a\otimes 1_n)^{\textbf{1}}$
such that
$d(x)\in (D_a\otimes 1_n)^{\textbf{1}}$
such that
Let
![]() $b_2={\beta }(b_1)^{1/N}$
. By equation (e5.9),
$b_2={\beta }(b_1)^{1/N}$
. By equation (e5.9),
![]() ${\beta }(b_1)\ge {{{\beta }(x)^*{\beta }(x)}}$
and
${\beta }(b_1)\ge {{{\beta }(x)^*{\beta }(x)}}$
and
![]() ${\beta }(b_1)\ge {\beta }(x){\beta }(x)^*$
for all
${\beta }(b_1)\ge {\beta }(x){\beta }(x)^*$
for all
![]() $x\in {\cal F}'$
(see, for example, [Reference Blackadar, Kumjian and Rørdam5, Corollary 4.1.3]). By condition (2) here, the choice of N and application of Lemma 5.4,
$x\in {\cal F}'$
(see, for example, [Reference Blackadar, Kumjian and Rørdam5, Corollary 4.1.3]). By condition (2) here, the choice of N and application of Lemma 5.4,
 $$ \begin{align} b_2{\beta}(x)={\beta}(b_1)^{1/N}{\beta}(x) \approx_\eta {\beta}(x)\qquad \mathrm{\ for\ all\ } x\in {\cal F}'. \end{align} $$
$$ \begin{align} b_2{\beta}(x)={\beta}(b_1)^{1/N}{\beta}(x) \approx_\eta {\beta}(x)\qquad \mathrm{\ for\ all\ } x\in {\cal F}'. \end{align} $$
Recall that
![]() ${\beta }(b_1)\in _{\delta _1} D_a\otimes 1_n$
. By the choice of
${\beta }(b_1)\in _{\delta _1} D_a\otimes 1_n$
. By the choice of
![]() $\delta _1$
, we may choose
$\delta _1$
, we may choose
![]() $d\in (D_a\otimes 1_n)_+$
such that
$d\in (D_a\otimes 1_n)_+$
such that
Then, with
![]() $b:=b_0b_2b_0$
, by the second part of formula (e5.10),
$b:=b_0b_2b_0$
, by the second part of formula (e5.10),
By the choice of
![]() $\eta $
, applying [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] yields an isomorphism
$\eta $
, applying [Reference Elliott, Gong, Lin and Niu15, Lemma 3.3] yields an isomorphism
 $$ \begin{align*} \varphi: \overline{f_{\varepsilon/64}(d)(D_a\otimes M_n)f_{\varepsilon/64}(d)}\to \overline{bAb} \subset B \end{align*} $$
$$ \begin{align*} \varphi: \overline{f_{\varepsilon/64}(d)(D_a\otimes M_n)f_{\varepsilon/64}(d)}\to \overline{bAb} \subset B \end{align*} $$
such that
 $$ \begin{align} \lVert \varphi(y)-y\rVert<\varepsilon/64\lVert y\rVert\mathrm{\ for\ all\ } y\in \overline{f_{\varepsilon/64}(d)(D\otimes 1_n)f_{\varepsilon/64}(d)}. \end{align} $$
$$ \begin{align} \lVert \varphi(y)-y\rVert<\varepsilon/64\lVert y\rVert\mathrm{\ for\ all\ } y\in \overline{f_{\varepsilon/64}(d)(D\otimes 1_n)f_{\varepsilon/64}(d)}. \end{align} $$
Note that
 $\overline {f_{\varepsilon /64}(d)(D_a\otimes M_n)f_{\varepsilon /64}(d)}\cong D_1\otimes M_n$
and
$\overline {f_{\varepsilon /64}(d)(D_a\otimes M_n)f_{\varepsilon /64}(d)}\cong D_1\otimes M_n$
and
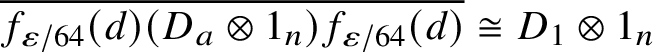 $\overline {f_{\varepsilon /64}(d)(D_a\otimes 1_n)f_{\varepsilon /64}(d)}\cong D_1\otimes 1_n$
for some
$\overline {f_{\varepsilon /64}(d)(D_a\otimes 1_n)f_{\varepsilon /64}(d)}\cong D_1\otimes 1_n$
for some
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $D_1\subset D_a$
. Let
$D_1\subset D_a$
. Let
![]() $D_b=\varphi (D_1)$
. Define a c.p.c. map
$D_b=\varphi (D_1)$
. Define a c.p.c. map
![]() ${\alpha }: B\to {{B}}$
by
${\alpha }: B\to {{B}}$
by
Then, for all
![]() $x\in {\cal F}_1$
, by formulas (e5.14) and (e5.11),
$x\in {\cal F}_1$
, by formulas (e5.14) and (e5.11),
 $$ \begin{align} \hspace{3pc} &\approx_{\delta_1} f_{\varepsilon/64}(d)d d(x) df_{\varepsilon/64}(d)\in_{\varepsilon/64} D_b\otimes 1_n\subset \overline{bAb}\subset B. \end{align} $$
$$ \begin{align} \hspace{3pc} &\approx_{\delta_1} f_{\varepsilon/64}(d)d d(x) df_{\varepsilon/64}(d)\in_{\varepsilon/64} D_b\otimes 1_n\subset \overline{bAb}\subset B. \end{align} $$
If
![]() $y\in {\cal F}$
, choose
$y\in {\cal F}$
, choose
![]() $x\in {\cal F}'$
such that
$x\in {\cal F}'$
such that
![]() $\lVert y-x\rVert <\varepsilon /4$
. Then
$\lVert y-x\rVert <\varepsilon /4$
. Then
![]() ${\alpha }(y)\approx _{\varepsilon /4} {\alpha }(x)\in _{\varepsilon /4} D_b\otimes 1_n$
. Define
${\alpha }(y)\approx _{\varepsilon /4} {\alpha }(x)\in _{\varepsilon /4} D_b\otimes 1_n$
. Define
![]() $y_1=b_0x_1b_0$
. Then, by conditions (1) and (2) and equation (e5.12),
$y_1=b_0x_1b_0$
. Then, by conditions (1) and (2) and equation (e5.12),
Note that
![]() $\delta _1/2+\varepsilon /4+2\eta +2\delta _1+\varepsilon /4<\varepsilon $
. Put
$\delta _1/2+\varepsilon /4+2\eta +2\delta _1+\varepsilon /4<\varepsilon $
. Put
![]() $\delta _2:=3\delta _1/2+2\eta $
. Then
$\delta _2:=3\delta _1/2+2\eta $
. Then
![]() $0<\delta _2<5\varepsilon /256$
. Also for all
$0<\delta _2<5\varepsilon /256$
. Also for all
![]() $y\in {\cal F}$
,
$y\in {\cal F}$
,
(recall
![]() $\lVert b_0-e_F\rVert <\varepsilon /64$
). Put
$\lVert b_0-e_F\rVert <\varepsilon /64$
). Put
![]() $\theta _b=b_0\theta _a b_0$
. Then
$\theta _b=b_0\theta _a b_0$
. Then
![]() $y_1\in \overline {\theta _bB\theta _b}$
. Moreover,
$y_1\in \overline {\theta _bB\theta _b}$
. Moreover,
From formulas (e5.22), (e5.18), (e5.24) and (e5.25), the theorem follows.
Lemma 5.6. Let A be a
![]() $C^*$
-algebra and set
$C^*$
-algebra and set
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $e_1,\dotsc ,e_n\in A_+$
be mutually orthogonal nonzero positive elements. Assume
$e_1,\dotsc ,e_n\in A_+$
be mutually orthogonal nonzero positive elements. Assume
![]() $d_1,\dotsc , d_n\in A_+$
such that
$d_1,\dotsc , d_n\in A_+$
such that
![]() $d_i\lesssim e_i$
(
$d_i\lesssim e_i$
(
![]() $i=1,\dotsc ,n$
), and
$i=1,\dotsc ,n$
), and
![]() $e_i d_j=0$
whenever
$e_i d_j=0$
whenever
![]() $i\le j$
and
$i\le j$
and
![]() $i,j=1,\dotsc ,n$
. Then for any
$i,j=1,\dotsc ,n$
. Then for any
![]() $a\in {{\overline {d_1Ad_1+\dotsb + d_nAd_n}}}$
and any
$a\in {{\overline {d_1Ad_1+\dotsb + d_nAd_n}}}$
and any
![]() $\varepsilon>0$
, there are nilpotent elements
$\varepsilon>0$
, there are nilpotent elements
![]() $x,y\in A$
such that
$x,y\in A$
such that
![]() $\lVert a-yx\rVert <\varepsilon $
.
$\lVert a-yx\rVert <\varepsilon $
.
Proof. Set
![]() $a\in {{\overline {d_1Ad_1+\dotsb +d_nAd_n}}}$
and fix
$a\in {{\overline {d_1Ad_1+\dotsb +d_nAd_n}}}$
and fix
![]() $\varepsilon>0$
. Then there exist
$\varepsilon>0$
. Then there exist
![]() $a_1,\dotsc ,a_n\in A$
and
$a_1,\dotsc ,a_n\in A$
and
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $a\approx _{\varepsilon } f_\delta (d_1)a_1f_\delta (d_1)+\dotsb +f_{\delta }(d_n)a_nf_\delta (d_n)$
. Set
$a\approx _{\varepsilon } f_\delta (d_1)a_1f_\delta (d_1)+\dotsb +f_{\delta }(d_n)a_nf_\delta (d_n)$
. Set
![]() $x_1,\dotsc ,x_n\in A$
such that
$x_1,\dotsc ,x_n\in A$
such that
![]() $x_i^*x_i=f_\delta (d_i)$
and
$x_i^*x_i=f_\delta (d_i)$
and
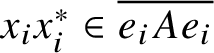 $x_ix_i^*\in \overline {e_iAe_i}$
,
$x_ix_i^*\in \overline {e_iAe_i}$
,
![]() $i=1,\dotsc ,n$
(see [Reference Rørdam40, Proposition 2.4]). For
$i=1,\dotsc ,n$
(see [Reference Rørdam40, Proposition 2.4]). For
![]() $i,j\in \{1,\dotsc ,n\}$
and
$i,j\in \{1,\dotsc ,n\}$
and
![]() $i\leq j$
,
$i\leq j$
,
![]() $e_id_j=0$
implies
$e_id_j=0$
implies
 $x_j^*x_jx_ix_i^*=0$
, thus
$x_j^*x_jx_ix_i^*=0$
, thus
Claim 1:
![]() ${{(x_1+x_2+\dotsb +x_n)^{n+1}=0}}$
.
${{(x_1+x_2+\dotsb +x_n)^{n+1}=0}}$
.
Proof of Claim 1: Note that
![]() $(x_1+x_2+\dotsb +x_n)^{n+1}$
is a sum of
$(x_1+x_2+\dotsb +x_n)^{n+1}$
is a sum of
![]() $n^{n+1}$
terms with the form
$n^{n+1}$
terms with the form
![]() $x_{k_1}x_{k_2}\dotsm x_{k_{n+1}} (k_1,\dotsc ,k_{n+1}\in \{1,\dotsc ,n\})$
. Assume
$x_{k_1}x_{k_2}\dotsm x_{k_{n+1}} (k_1,\dotsc ,k_{n+1}\in \{1,\dotsc ,n\})$
. Assume
![]() $x_{k_1}x_{k_2}\dotsm x_{k_n+1}\neq 0$
; then
$x_{k_1}x_{k_2}\dotsm x_{k_n+1}\neq 0$
; then
![]() $x_{k_i}x_{k_{i+1}}\neq 0$
(
$x_{k_i}x_{k_{i+1}}\neq 0$
(
![]() $i=1,\dotsc ,n$
). By equation (e5.26), it follows that
$i=1,\dotsc ,n$
). By equation (e5.26), it follows that
![]() $k_{i+1}\leq k_i-1$
(
$k_{i+1}\leq k_i-1$
(
![]() $i=1,\dotsc ,n$
). In particular,
$i=1,\dotsc ,n$
). In particular,
![]() $k_{n+1}\le k_n-1$
. Then
$k_{n+1}\le k_n-1$
. Then
![]() $k_{n+1}\le k_n-1\le k_{n-1}-2$
. An induction implies that
$k_{n+1}\le k_n-1\le k_{n-1}-2$
. An induction implies that
![]() $k_{n+1}\leq k_1-n\leq 0$
, which gives a contradiction. Thus all
$k_{n+1}\leq k_1-n\leq 0$
, which gives a contradiction. Thus all
![]() $n^{n+1}$
terms of the form
$n^{n+1}$
terms of the form
![]() $x_{k_1}x_{k_2}\dotsm x_{n+1}$
are zero. It follows that
$x_{k_1}x_{k_2}\dotsm x_{n+1}$
are zero. It follows that
![]() $(x_1+x_2+\dotsb +x_n)^{n+1}=0$
.
$(x_1+x_2+\dotsb +x_n)^{n+1}=0$
.
Claim 2:
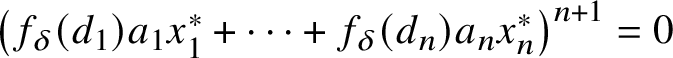 $\left (f_\delta (d_1)a_1x_1^*+\dotsb +f_{\delta }(d_n)a_nx_n^*\right )^{n+1}=0$
.
$\left (f_\delta (d_1)a_1x_1^*+\dotsb +f_{\delta }(d_n)a_nx_n^*\right )^{n+1}=0$
.
Proof of Claim 2: Let
![]() $y_i=f_\delta (d_i)a_ix_i^*$
(
$y_i=f_\delta (d_i)a_ix_i^*$
(
![]() $i=1,\dotsc ,n$
). For
$i=1,\dotsc ,n$
). For
![]() $i\leq j$
, using equation (e5.26), we have
$i\leq j$
, using equation (e5.26), we have
 $$ \begin{align} y_iy_j = f_\delta(d_i)a_ix_i^*f_\delta\left(d_j\right)a_jx_j^* = f_\delta(d_i)a_ix_i^*\left(x_j^*x_j\right)a_jx_j^*=f_\delta(d_i)a_i\left(x_jx_i\right)^*x_ja_jx_j^* =0. \end{align} $$
$$ \begin{align} y_iy_j = f_\delta(d_i)a_ix_i^*f_\delta\left(d_j\right)a_jx_j^* = f_\delta(d_i)a_ix_i^*\left(x_j^*x_j\right)a_jx_j^*=f_\delta(d_i)a_i\left(x_jx_i\right)^*x_ja_jx_j^* =0. \end{align} $$
Then, as in the proof of Claim 1, we have
![]() $(y_1+\dotsb +y_n)^{n+1} =0$
. Claim 2 follows.
$(y_1+\dotsb +y_n)^{n+1} =0$
. Claim 2 follows.
Let
![]() $x=x_1+\dotsb +x_n$
and let
$x=x_1+\dotsb +x_n$
and let
![]() $y=y_1+\dotsb +y_n=f_\delta (d_1)a_1x_1^*+\dotsb +f_{\delta }(d_n)a_nx_n^*$
. Then by Claims 1 and 2, both x and y are nilpotent elements. For
$y=y_1+\dotsb +y_n=f_\delta (d_1)a_1x_1^*+\dotsb +f_{\delta }(d_n)a_nx_n^*$
. Then by Claims 1 and 2, both x and y are nilpotent elements. For
![]() $i,j\in \{1,\dotsc ,n\}$
and
$i,j\in \{1,\dotsc ,n\}$
and
![]() $i\neq j$
,
$i\neq j$
,
![]() $e_ie_j=0$
implies
$e_ie_j=0$
implies
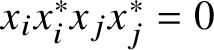 $x_ix_i^*x_jx_j^*=0$
, thus
$x_ix_i^*x_jx_j^*=0$
, thus
![]() $ x_i^*x_j=0. $
Then
$ x_i^*x_j=0. $
Then
![]() $yx=f_\delta (d_1)a_1f_\delta (d_1)+\dotsb +f_{\delta }(d_n)a_nf_\delta (d_n)\approx _\varepsilon a$
.
$yx=f_\delta (d_1)a_1f_\delta (d_1)+\dotsb +f_{\delta }(d_n)a_nf_\delta (d_n)\approx _\varepsilon a$
.
Recall that a non-unital
![]() $C^*$
-algebra is said to almost have stable rank one if for every hereditary
$C^*$
-algebra is said to almost have stable rank one if for every hereditary
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
, B lies in the closure of invertible elements of
$B\subset A$
, B lies in the closure of invertible elements of
![]() $\widetilde B$
[Reference Robert38, Definition 3.1].
$\widetilde B$
[Reference Robert38, Definition 3.1].
Theorem 5.7. Let A be a simple
![]() $C^*$
-algebra which is tracially approximately divisible. Suppose that A is stably finite and
$C^*$
-algebra which is tracially approximately divisible. Suppose that A is stably finite and
![]() $W(A)$
is almost unperforated. Then A has stable rank one if it is unital, or almost has stable rank one if it is not unital.
$W(A)$
is almost unperforated. Then A has stable rank one if it is unital, or almost has stable rank one if it is not unital.
Proof. We assume that A is infinite-dimensional. Fix an element
![]() $x\in A$
and fix
$x\in A$
and fix
![]() $\varepsilon>0$
. We may assume that x is not invertible. Since A is finite, x is not one-sided invertible. To show that x is a norm limit of invertible elements, it suffices to show that
$\varepsilon>0$
. We may assume that x is not invertible. Since A is finite, x is not one-sided invertible. To show that x is a norm limit of invertible elements, it suffices to show that
![]() $ux$
is a norm limit of invertible elements for some unitary
$ux$
is a norm limit of invertible elements for some unitary
![]() $u\in {\widetilde A}$
. Note that since A is simple,
$u\in {\widetilde A}$
. Note that since A is simple,
![]() ${\widetilde A}$
is prime. Thus, by [Reference Rørdam39, Proposition 3.2, Lemma 3.5], we may assume that there is
${\widetilde A}$
is prime. Thus, by [Reference Rørdam39, Proposition 3.2, Lemma 3.5], we may assume that there is
![]() $a'\in \widetilde A_+\backslash \{0\}$
and
$a'\in \widetilde A_+\backslash \{0\}$
and
![]() $a'x=xa'=0$
. There is
$a'x=xa'=0$
. There is
![]() $e\in A_+$
such that
$e\in A_+$
such that
![]() $a'ea'\not =0$
. Put
$a'ea'\not =0$
. Put
![]() $a=a'ea'$
.
$a=a'ea'$
.
Let
![]() $B_0=\{z\in A: az=za=0\}$
. Then
$B_0=\{z\in A: az=za=0\}$
. Then
![]() $x\in B_0$
, and
$x\in B_0$
, and
![]() $B_0$
is a hereditary
$B_0$
is a hereditary
![]() $C^*$
-subalgebra of A. There is
$C^*$
-subalgebra of A. There is
![]() $e_b'\in {B_0}_+$
with
$e_b'\in {B_0}_+$
with
![]() $\lVert e_b\rVert =1$
such that
$\lVert e_b\rVert =1$
such that
![]() $e_b'xe_b'\approx _{\varepsilon /64}x$
. So
$e_b'xe_b'\approx _{\varepsilon /64}x$
. So
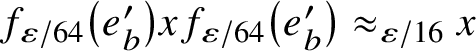 $f_{\varepsilon /64}\left (e_b'\right )xf_{\varepsilon /64}\left (e_b'\right )\approx _{\varepsilon /16}x$
. Put
$f_{\varepsilon /64}\left (e_b'\right )xf_{\varepsilon /64}\left (e_b'\right )\approx _{\varepsilon /16}x$
. Put
 $e_b=f_{\varepsilon /64}\left (e_b'\right )$
and
$e_b=f_{\varepsilon /64}\left (e_b'\right )$
and
![]() $B=\mathrm {Her}(e_b)$
. Without loss of generality, we may further assume that
$B=\mathrm {Her}(e_b)$
. Without loss of generality, we may further assume that
![]() $x\in B$
.
$x\in B$
.
Since we assume that A is infinite-dimensional,
![]() $\overline {aAa}$
contains nonzero positive elements
$\overline {aAa}$
contains nonzero positive elements
![]() $a_0,a_1$
such that
$a_0,a_1$
such that
![]() $a_0a_1=0$
.
$a_0a_1=0$
.
Since A is simple, there is
![]() $c\in A$
such that
$c\in A$
such that
![]() $e_bc(a_1)^{1/2}\not =0$
(see the proof of [Reference Cuntz12, 1.8]).
$e_bc(a_1)^{1/2}\not =0$
(see the proof of [Reference Cuntz12, 1.8]).
Note that since
![]() $e_b\in \mathrm {Ped}(B)$
, we have
$e_b\in \mathrm {Ped}(B)$
, we have
![]() $\mathrm {Ped}(B)=B$
(see, for example, [Reference Blackadar3, II.5.4.2]). It follows that there are
$\mathrm {Ped}(B)=B$
(see, for example, [Reference Blackadar3, II.5.4.2]). It follows that there are
![]() $y_1,y_2,\dotsc ,y_m\in B$
such that
$y_1,y_2,\dotsc ,y_m\in B$
such that
 $$ \begin{align} \sum_{i=1}^m y_i^*e_bca_1c^*e_by_i=e_b. \end{align} $$
$$ \begin{align} \sum_{i=1}^m y_i^*e_bca_1c^*e_by_i=e_b. \end{align} $$
It then follows that
![]() $\langle e_b\rangle \le m\langle a_1\rangle $
. Put
$\langle e_b\rangle \le m\langle a_1\rangle $
. Put
![]() $n=2m$
.
$n=2m$
.
For any
![]() $z_1,z_2,\dotsc ,z_n\in B_+$
which are n mutually orthogonal and mutually equivalent positive elements,
$z_1,z_2,\dotsc ,z_n\in B_+$
which are n mutually orthogonal and mutually equivalent positive elements,
Since
![]() $W(A)$
is almost unperforated,
$W(A)$
is almost unperforated,
Since B is a hereditary
![]() $C^*$
-subalgebra of A, by Theorem 5.5, B is also tracially approximately divisible. There are
$C^*$
-subalgebra of A, by Theorem 5.5, B is also tracially approximately divisible. There are
![]() $b\in B_+^{\textbf{1}}$
, a
$b\in B_+^{\textbf{1}}$
, a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $D\otimes M_n\subset B$
and a c.p.c. map
$D\otimes M_n\subset B$
and a c.p.c. map
![]() ${\beta }: A\to A$
such that
${\beta }: A\to A$
such that
-
(1)
 $x\approx _{\varepsilon /8} x_0+{\beta }(x)$
, where
$x\approx _{\varepsilon /8} x_0+{\beta }(x)$
, where
 $x_0\in \overline {bAb}$
,
$x_0\in \overline {bAb}$
, -
(2)
 ${\beta }(x)\in _{\varepsilon /8} D\otimes 1_n$
and
${\beta }(x)\in _{\varepsilon /8} D\otimes 1_n$
and -
(3)
 $b\lesssim a_0$
.
$b\lesssim a_0$
.
Thus, there is
![]() $x_1\in D\setminus \{0\}$
such that
$x_1\in D\setminus \{0\}$
such that
Choose a positive element
![]() $d\in D$
such that
$d\in D$
such that
By the choice of n, we have
![]() $d\otimes e_{1,1}\lesssim a_1$
, where
$d\otimes e_{1,1}\lesssim a_1$
, where
 $\left \{e_{i,j}\right \}$
forms a system of matrix units for
$\left \{e_{i,j}\right \}$
forms a system of matrix units for
![]() $M_n$
.
$M_n$
.
Define
![]() $g_1:= a_0$
,
$g_1:= a_0$
,
![]() $g_2 := a_1$
,
$g_2 := a_1$
,
![]() $g_{2+i}:= d\otimes e_{i,i}$
(
$g_{2+i}:= d\otimes e_{i,i}$
(
![]() $i=1,\dotsc ,n-1$
).
$i=1,\dotsc ,n-1$
).
Define
![]() $h_1:= b$
,
$h_1:= b$
,
![]() $h_{1+i}:= d\otimes e_{i,i}$
(
$h_{1+i}:= d\otimes e_{i,i}$
(
![]() $i=1,\dotsc ,n$
).
$i=1,\dotsc ,n$
).
Note that
![]() $h_i\lesssim g_i$
(
$h_i\lesssim g_i$
(
![]() $i=1,\dotsc ,n+1$
) and
$i=1,\dotsc ,n+1$
) and
![]() $g_ih_j=0$
, if
$g_ih_j=0$
, if
![]() $i\le j$
and
$i\le j$
and
![]() $i,j=1,\dotsc ,n+1$
. Note that
$i,j=1,\dotsc ,n+1$
. Note that
![]() $x_0+dx_1d\otimes 1_n\in \overline {h_1Ah_1}+\overline {h_2Ah_2}+\dotsb +\overline {h_{n+1}Ah_{n+1}}$
. Then by Lemma 5.6, there are nilpotent elements
$x_0+dx_1d\otimes 1_n\in \overline {h_1Ah_1}+\overline {h_2Ah_2}+\dotsb +\overline {h_{n+1}Ah_{n+1}}$
. Then by Lemma 5.6, there are nilpotent elements
![]() $v,w\in A$
such that
$v,w\in A$
such that
![]() $x_0+dx_1d\otimes 1_n\approx _{\varepsilon /4}vw$
. Choose
$x_0+dx_1d\otimes 1_n\approx _{\varepsilon /4}vw$
. Choose
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $vw\approx _{\varepsilon /4}(v+\delta )(w+\delta )$
. Since
$vw\approx _{\varepsilon /4}(v+\delta )(w+\delta )$
. Since
![]() $v,w$
are nilpotent elements,
$v,w$
are nilpotent elements,
![]() $v+\delta $
and
$v+\delta $
and
![]() $w+\delta $
are invertible. Then, combining formulas (e5.30) and (e5.31),
$w+\delta $
are invertible. Then, combining formulas (e5.30) and (e5.31),
 $$ \begin{align} x\approx_{\varepsilon/4} x_0+x_1\otimes 1_n \approx_{\varepsilon/4} x_0+dx_1d\otimes 1_n\approx_{\varepsilon/2} (v+\delta)(w+\delta) \in GL\left(\widetilde A\right). \end{align} $$
$$ \begin{align} x\approx_{\varepsilon/4} x_0+x_1\otimes 1_n \approx_{\varepsilon/4} x_0+dx_1d\otimes 1_n\approx_{\varepsilon/2} (v+\delta)(w+\delta) \in GL\left(\widetilde A\right). \end{align} $$
Therefore we have shown that
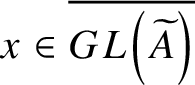 $x\in \overline {GL\left (\widetilde A\right )}$
. Thus, in the case that A is unital, A has stable rank one. Since, by Theorem 5.5, this works for every hereditary
$x\in \overline {GL\left (\widetilde A\right )}$
. Thus, in the case that A is unital, A has stable rank one. Since, by Theorem 5.5, this works for every hereditary
![]() $C^*$
-subalgebra of A, A almost has stable rank one in the case that A is not unital.
$C^*$
-subalgebra of A, A almost has stable rank one in the case that A is not unital.
Remark 5.8. Under the assumption of Theorem 5.7, if
![]() $x\in A$
is not invertible, then there is a unitary
$x\in A$
is not invertible, then there is a unitary
![]() $u\in \tilde A$
such that
$u\in \tilde A$
such that
![]() $(ux)e=e(ux)=0$
for some
$(ux)e=e(ux)=0$
for some
![]() $e\in A_+\setminus \{0\}$
. The proof shows that
$e\in A_+\setminus \{0\}$
. The proof shows that
![]() $ux$
can be approximated by products of two nilpotents in A. The idea of the proof is taken from the proof of [Reference Elliott, Gong, Lin and Niu15, Lemma 11.1], which originates from that of [Reference Robert38, Lemma 2.1] and [Reference Rørdam39].
$ux$
can be approximated by products of two nilpotents in A. The idea of the proof is taken from the proof of [Reference Elliott, Gong, Lin and Niu15, Lemma 11.1], which originates from that of [Reference Robert38, Lemma 2.1] and [Reference Rørdam39].
In a subsequent paper [Reference Fu, Li and Lin20], we will show that a separable simple
![]() $C^*$
-algebra which is tracially approximately divisible has strict comparison for positive elements. So there is a redundancy in the assumption of Theorem 5.7.
$C^*$
-algebra which is tracially approximately divisible has strict comparison for positive elements. So there is a redundancy in the assumption of Theorem 5.7.
Theorem 5.9. Let A be a simple
![]() $C^*$
-algebra. If A is essentially tracially in
$C^*$
-algebra. If A is essentially tracially in
![]() ${\cal C}_{\mathscr Z}$
, then it is tracially approximately divisible.
${\cal C}_{\mathscr Z}$
, then it is tracially approximately divisible.
Proof. We assume that A is infinite-dimensional. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal C}_{\mathscr Z}$
. By [Reference Rørdam42, Theorem 4.5], every
${\cal C}_{\mathscr Z}$
. By [Reference Rørdam42, Theorem 4.5], every
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebra B has almost unperforated
$C^*$
-algebra B has almost unperforated
![]() $W(B)$
(see Remark 2.5). Then, by Theorem 4.3,
$W(B)$
(see Remark 2.5). Then, by Theorem 4.3,
![]() $W(A)$
is almost unperforated. Let
$W(A)$
is almost unperforated. Let
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() ${\cal F}\subset A^{\textbf{1}}$
a finite subset,
${\cal F}\subset A^{\textbf{1}}$
a finite subset,
![]() $a\in A_+\setminus \{0\}$
and
$a\in A_+\setminus \{0\}$
and
![]() $n\ge 1$
an integer be given. Since A is infinite dimensional, choose
$n\ge 1$
an integer be given. Since A is infinite dimensional, choose
![]() $a_1, a_2\in \mathrm {Her}(a)_+\setminus \{0\}$
such that
$a_1, a_2\in \mathrm {Her}(a)_+\setminus \{0\}$
such that
![]() $a_1a_2=a_2a_1=0$
.
$a_1a_2=a_2a_1=0$
.
There are
![]() $e_A\in A_+^{\textbf{1}}$
and
$e_A\in A_+^{\textbf{1}}$
and
![]() $\delta>0$
such that
$\delta>0$
such that
Note that by Theorem 5.5,
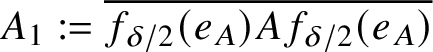 $A_1:=\overline {f_{\delta /2}(e_A)Af_{\delta /2}(e_A)}$
is also a (
$A_1:=\overline {f_{\delta /2}(e_A)Af_{\delta /2}(e_A)}$
is also a (
![]() $\sigma $
-unital) simple
$\sigma $
-unital) simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal C}_{\mathscr Z}$
(as
${\cal C}_{\mathscr Z}$
(as
![]() ${\cal C}_{\mathscr Z}$
has property (H); see [Reference Toms and Winter46, Corollary 3.1]).
${\cal C}_{\mathscr Z}$
has property (H); see [Reference Toms and Winter46, Corollary 3.1]).
Note also that
![]() $f_{\delta /2}(e_A)af_{\delta /2}(e_A)\lesssim a$
. To simplify notation, by replacing x by
$f_{\delta /2}(e_A)af_{\delta /2}(e_A)\lesssim a$
. To simplify notation, by replacing x by
![]() $f_\delta (e_A)xf_\delta (e_A)$
for all
$f_\delta (e_A)xf_\delta (e_A)$
for all
![]() $x\in {\cal F}$
, a by
$x\in {\cal F}$
, a by
![]() $f_{\delta /2}(e_A)af_{\delta /2}(e_A)$
and
$f_{\delta /2}(e_A)af_{\delta /2}(e_A)$
and
![]() $a_i$
by
$a_i$
by
![]() $f_{\delta /2}(e_A)a_if_{\delta /2}(e_A)$
(
$f_{\delta /2}(e_A)a_if_{\delta /2}(e_A)$
(
![]() $i=1,2$
), without loss of generality we may assume that
$i=1,2$
), without loss of generality we may assume that
![]() $x, a, a_1, a_2\in A_1$
. We may also assume, without loss of generality,
$x, a, a_1, a_2\in A_1$
. We may also assume, without loss of generality,
for some strictly positive element
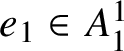 $e_1\in A_1^{1} $
. Note that
$e_1\in A_1^{1} $
. Note that
![]() $f_{\delta /2}(e_A)\in \mathrm {Ped}(A)$
. Therefore
$f_{\delta /2}(e_A)\in \mathrm {Ped}(A)$
. Therefore
![]() $A_1$
is algebraically simple and
$A_1$
is algebraically simple and
![]() $f_{\delta /2}(e_A)$
is a strictly positive element of
$f_{\delta /2}(e_A)$
is a strictly positive element of
![]() $A_1$
. There are an integer
$A_1$
. There are an integer
![]() $l\ge 1$
and
$l\ge 1$
and
![]() $x_i\in A_1$
,
$x_i\in A_1$
,
![]() $i=1,2,\dotsc ,l$
, such that
$i=1,2,\dotsc ,l$
, such that
 $$ \begin{align} \sum_{i=1}^l x_i^*a_1x_i=e_1. \end{align} $$
$$ \begin{align} \sum_{i=1}^l x_i^*a_1x_i=e_1. \end{align} $$
Set
![]() ${\cal F}_1={\cal F}\cup \{e_1\}$
. Choose
${\cal F}_1={\cal F}\cup \{e_1\}$
. Choose
![]() $0<\eta <\varepsilon /2$
such that if
$0<\eta <\varepsilon /2$
such that if
![]() $\theta '\in A_+^{\textbf{1}}$
with
$\theta '\in A_+^{\textbf{1}}$
with
![]() $\lVert \theta 'x-x\theta '\rVert <\eta $
, then
$\lVert \theta 'x-x\theta '\rVert <\eta $
, then
 $$ \begin{align} (\theta')^{1/2}x\approx_{\varepsilon/2} x(\theta')^{1/2}\mathrm{\ for\ all\ } x\in {\cal F}_1. \end{align} $$
$$ \begin{align} (\theta')^{1/2}x\approx_{\varepsilon/2} x(\theta')^{1/2}\mathrm{\ for\ all\ } x\in {\cal F}_1. \end{align} $$
There exist
![]() $\theta _1\in A_+^{\textbf{1}}$
and a
$\theta _1\in A_+^{\textbf{1}}$
and a
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-subalgebra B of
$C^*$
-subalgebra B of
![]() $A_1$
such that
$A_1$
such that
-
(i)
 $\lVert \theta _1x-x\theta _1\rVert <\eta /64$
and
$\lVert \theta _1x-x\theta _1\rVert <\eta /64$
and
 $\left \lVert (1-\theta _1)^{1/2}x-x(1-\theta _1)^{1/2}\right \rVert <\eta /64$
for all
$\left \lVert (1-\theta _1)^{1/2}x-x(1-\theta _1)^{1/2}\right \rVert <\eta /64$
for all
 $x\in {\cal F}_1$
,
$x\in {\cal F}_1$
, -
(ii)
 $(1-\theta _1)^{1/2}x(1-\theta _1)^{1/2}, (1-\theta _1)^{1/2}x, x(1-\theta _1)^{1/2}, (1-\theta _1)x, x(1-\theta _1), (1-\theta _1)x(1-\theta _1)\in _{\eta /64} B$
for all
$(1-\theta _1)^{1/2}x(1-\theta _1)^{1/2}, (1-\theta _1)^{1/2}x, x(1-\theta _1)^{1/2}, (1-\theta _1)x, x(1-\theta _1), (1-\theta _1)x(1-\theta _1)\in _{\eta /64} B$
for all
 $x\in {\cal F}_1$
and
$x\in {\cal F}_1$
and -
(iii)
 $\theta _1\lesssim a_2$
.
$\theta _1\lesssim a_2$
.
Let
 $$ \begin{align*} {\cal F}_2&=\left\{(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}, (1-\theta_1)^{1/2}x, x(1-\theta_1)^{1/2}, (1-\theta)x, x(1-\theta_1), (1-\theta_1)x(1-\theta_1): \right. \nonumber \\ &\left. \quad x\in {\cal F}\right\}. \end{align*} $$
$$ \begin{align*} {\cal F}_2&=\left\{(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}, (1-\theta_1)^{1/2}x, x(1-\theta_1)^{1/2}, (1-\theta)x, x(1-\theta_1), (1-\theta_1)x(1-\theta_1): \right. \nonumber \\ &\left. \quad x\in {\cal F}\right\}. \end{align*} $$
For each
![]() $f\in {\cal F}_2$
, fix
$f\in {\cal F}_2$
, fix
![]() $b(f)\in B$
such that
$b(f)\in B$
such that
![]() $\lVert b(f)\rVert \le 1$
and
$\lVert b(f)\rVert \le 1$
and
Let
![]() ${\cal G}=\{b(f): f\in {\cal F}_2\}$
. We write
${\cal G}=\{b(f): f\in {\cal F}_2\}$
. We write
![]() $B=C\otimes {\mathscr Z}$
. Since
$B=C\otimes {\mathscr Z}$
. Since
![]() ${\mathscr Z}$
is strongly self-absorbing, without loss of generality we may assume that there is a finite subset
${\mathscr Z}$
is strongly self-absorbing, without loss of generality we may assume that there is a finite subset
![]() ${\cal G}_1\subset C$
such that
${\cal G}_1\subset C$
such that
![]() ${\cal G}=\{y\otimes 1_{\mathscr Z}: y\in {\cal G}_1\}\subset C\otimes 1_{\mathscr Z}$
. To further simplify notation, without loss of generality we may assume that there exists a strictly positive element
${\cal G}=\{y\otimes 1_{\mathscr Z}: y\in {\cal G}_1\}\subset C\otimes 1_{\mathscr Z}$
. To further simplify notation, without loss of generality we may assume that there exists a strictly positive element
![]() $e_C\in C$
such that
$e_C\in C$
such that
where
![]() $e_b=e_C\otimes 1_{\mathscr Z}$
.
$e_b=e_C\otimes 1_{\mathscr Z}$
.
For any integer n, choose m such that
![]() $m> l$
and n divides m. Let
$m> l$
and n divides m. Let
![]() $\psi : M_m\to {\mathscr Z}$
be an order
$\psi : M_m\to {\mathscr Z}$
be an order
![]() $0$
c.p.c. map such that
$0$
c.p.c. map such that
(see [Reference Rørdam and Winter43, Proposition 5.1(iv) implying (ii)]). Define
![]() $\varphi : M_m\to B$
by
$\varphi : M_m\to B$
by
![]() $\varphi (c):= e_C\otimes \psi (c)$
for all
$\varphi (c):= e_C\otimes \psi (c)$
for all
![]() $c\in M_m$
. Set
$c\in M_m$
. Set
Note that
It follows from formulas (e5.37) and (e5.41) that for any
![]() $y\in {\cal F}_2$
,
$y\in {\cal F}_2$
,
Define
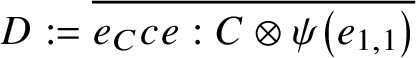 $D:= \overline {e_Cce:C\otimes \psi \left (e_{1,1}\right )}$
and
$D:= \overline {e_Cce:C\otimes \psi \left (e_{1,1}\right )}$
and
![]() $D'$
the
$D'$
the
![]() $C^*$
-subalgebra generated by
$C^*$
-subalgebra generated by
Recall that
![]() $\psi $
gives a homomorphism
$\psi $
gives a homomorphism
![]() $H: C^*(\psi (1_m))\otimes M_m \to {\mathscr Z}$
such that
$H: C^*(\psi (1_m))\otimes M_m \to {\mathscr Z}$
such that
![]() $H(\iota \otimes g)=\psi (g)$
for all
$H(\iota \otimes g)=\psi (g)$
for all
![]() $g\in M_m $
, where
$g\in M_m $
, where
![]() $\iota (t)=t$
for
$\iota (t)=t$
for
![]() $t\in \mathrm {sp}(\psi (1_m))$
(see [Reference Winter and Zacharias49, Corollary 4.1]). It follows that
$t\in \mathrm {sp}(\psi (1_m))$
(see [Reference Winter and Zacharias49, Corollary 4.1]). It follows that
![]() $D'\cong D\otimes M_m$
. Define
$D'\cong D\otimes M_m$
. Define
![]() ${\beta }_1: A\to A$
by
${\beta }_1: A\to A$
by
 $$ \begin{align} {\beta}_1(y):= \left(1_{\widetilde{A}}-\theta_2\right)^{1/2}y\left(1_{\widetilde{A}}-\theta_2\right)^{1/2}\mathrm{\ for\ all\ } y\in A \end{align} $$
$$ \begin{align} {\beta}_1(y):= \left(1_{\widetilde{A}}-\theta_2\right)^{1/2}y\left(1_{\widetilde{A}}-\theta_2\right)^{1/2}\mathrm{\ for\ all\ } y\in A \end{align} $$
(where
![]() $1_{\widetilde {A}}$
denotes the identity of
$1_{\widetilde {A}}$
denotes the identity of
![]() $\widetilde {A}$
when A is not unital and is the identity of A if A has one). Note also that
$\widetilde {A}$
when A is not unital and is the identity of A if A has one). Note also that
![]() $(1-\theta )^{1/2}$
is an element which has the form
$(1-\theta )^{1/2}$
is an element which has the form
![]() $1+f_1(\theta )$
for
$1+f_1(\theta )$
for
![]() $f_1(t)=(1-t)^{1/2}-1\in C_0([0,1])^{\textbf{1}}$
. If
$f_1(t)=(1-t)^{1/2}-1\in C_0([0,1])^{\textbf{1}}$
. If
![]() $g=y\otimes 1_{\mathscr Z}\in {\cal G}$
, then (noting that
$g=y\otimes 1_{\mathscr Z}\in {\cal G}$
, then (noting that
![]() $y\in {\cal G}_1\subset C$
, and seeing equation (e5.38)),
$y\in {\cal G}_1\subset C$
, and seeing equation (e5.38)),
 $$ \begin{align} &=(e_C\otimes \psi(1_m)) (y\otimes 1_{\mathscr Z})=\left(e_C^{1/2}ye_C^{1/2}\right)\otimes \psi(1_m)\in D\otimes 1_m. \end{align} $$
$$ \begin{align} &=(e_C\otimes \psi(1_m)) (y\otimes 1_{\mathscr Z})=\left(e_C^{1/2}ye_C^{1/2}\right)\otimes \psi(1_m)\in D\otimes 1_m. \end{align} $$
Define a c.p.c. map
![]() ${\beta }: A\to A$
by
${\beta }: A\to A$
by
 $$ \begin{align} {\beta}(x):= {\beta}_1\left((1-\theta_1)^{1/2}x (1-\theta_1)^{1/2}\right)\mathrm{\ for\ all\ } x\in A. \end{align} $$
$$ \begin{align} {\beta}(x):= {\beta}_1\left((1-\theta_1)^{1/2}x (1-\theta_1)^{1/2}\right)\mathrm{\ for\ all\ } x\in A. \end{align} $$
For
![]() $x\in {\cal F}$
, let
$x\in {\cal F}$
, let
![]() $f=(1-\theta _1)^{1/2}x(1-\theta _1)^{1/2}$
. Then, by formula (e5.37),
$f=(1-\theta _1)^{1/2}x(1-\theta _1)^{1/2}$
. Then, by formula (e5.37),
 $$ \begin{align} {\beta}(x)={\beta}_1\left((1-\theta_1)^{1/2}x (1-\theta_1)^{1/2}\right)\approx_{\eta/32} {\beta}_1(b(f))\in D\otimes 1_m. \end{align} $$
$$ \begin{align} {\beta}(x)={\beta}_1\left((1-\theta_1)^{1/2}x (1-\theta_1)^{1/2}\right)\approx_{\eta/32} {\beta}_1(b(f))\in D\otimes 1_m. \end{align} $$
Put
![]() $\theta =\theta _1+(1-\theta _1)^{1/2}\theta _2(1-\theta _1)^{1/2}$
. We have
$\theta =\theta _1+(1-\theta _1)^{1/2}\theta _2(1-\theta _1)^{1/2}$
. We have
For
![]() $x\in {\cal F}$
, let
$x\in {\cal F}$
, let
![]() $f'=(1-\theta _1)x$
. Recall that we assume that
$f'=(1-\theta _1)x$
. Recall that we assume that
![]() $b(f')=y'\otimes 1_{\mathscr Z}$
for some
$b(f')=y'\otimes 1_{\mathscr Z}$
for some
![]() $y'\in C^{\textbf{1}}$
. Then for
$y'\in C^{\textbf{1}}$
. Then for
![]() $x\in {\cal F}$
, applying formulas (e5.37) and (e5.41) repeatedly, we have
$x\in {\cal F}$
, applying formulas (e5.37) and (e5.41) repeatedly, we have
 $$ \begin{align} &\approx_{\eta/32} b(f')(1-\theta_2)=(1-\theta_2)^{1/2} b(f')(1-\theta_2)^{1/2} \end{align} $$
$$ \begin{align} &\approx_{\eta/32} b(f')(1-\theta_2)=(1-\theta_2)^{1/2} b(f')(1-\theta_2)^{1/2} \end{align} $$
 $$ \begin{align} \hspace{2pc} &={\beta}_1(b(f'))\approx_{\eta/32} {\beta}_1\left((1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}\right)={\beta}(x). \end{align} $$
$$ \begin{align} \hspace{2pc} &={\beta}_1(b(f'))\approx_{\eta/32} {\beta}_1\left((1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}\right)={\beta}(x). \end{align} $$
From equations (e5.49) and (e5.54), we have
Recall that
![]() $(1-\theta _1)^{1/2}x, x(1-\theta _1)^{1/2}, (1-\theta _1)^{1/2}x(1-\theta _1)^{1/2} \in {\cal F}_2$
. Hence, for
$(1-\theta _1)^{1/2}x, x(1-\theta _1)^{1/2}, (1-\theta _1)^{1/2}x(1-\theta _1)^{1/2} \in {\cal F}_2$
. Hence, for
![]() $x\in {\cal F}$
, by (i) above and formula (e5.42),
$x\in {\cal F}$
, by (i) above and formula (e5.42),
 $$ \begin{align} \hspace{-0.5pc} \theta x &=\left(\theta_1+(1-\theta_1)^{1/2}\theta_2(1-\theta_1)^{1/2}\right) x\approx_{2\eta/64} x\theta_1+(1-\theta_1)^{1/2} \theta_2 x(1- \theta_1)^{1/2} \end{align} $$
$$ \begin{align} \hspace{-0.5pc} \theta x &=\left(\theta_1+(1-\theta_1)^{1/2}\theta_2(1-\theta_1)^{1/2}\right) x\approx_{2\eta/64} x\theta_1+(1-\theta_1)^{1/2} \theta_2 x(1- \theta_1)^{1/2} \end{align} $$
 $$ \begin{align} & \hspace{1pc} \approx_{\eta/32} x\theta_1+(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}\theta_2 \approx_{\eta/32} x \theta_1+\theta_2(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2} \end{align} $$
$$ \begin{align} & \hspace{1pc} \approx_{\eta/32} x\theta_1+(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2}\theta_2 \approx_{\eta/32} x \theta_1+\theta_2(1-\theta_1)^{1/2}x(1-\theta_1)^{1/2} \end{align} $$
 $$ \begin{align} &\approx_{\eta/32} x\theta_1+(1-\theta_1)^{1/2} x\theta_2(1-\theta_1)^{1/2} \hspace{12pc} \end{align} $$
$$ \begin{align} &\approx_{\eta/32} x\theta_1+(1-\theta_1)^{1/2} x\theta_2(1-\theta_1)^{1/2} \hspace{12pc} \end{align} $$
 $$ \begin{align} &\approx_{\eta/64} x\theta_1+ x(1-\theta_1)^{1/2}\theta_2(1-\theta_1)^{1/2}=\theta x. \hspace{10pc} \end{align} $$
$$ \begin{align} &\approx_{\eta/64} x\theta_1+ x(1-\theta_1)^{1/2}\theta_2(1-\theta_1)^{1/2}=\theta x. \hspace{10pc} \end{align} $$
Note that by formulas (e5.40) and (e5.35), in
![]() $W(A)$
we have
$W(A)$
we have
 $$ \begin{align} & \hspace{2pc} \le m\left\langle e_C\otimes \psi\left(e_{1,1}\right)\right\rangle \le \langle e_C\otimes \psi(1_m)\rangle\le \langle e_C\otimes 1_{\mathscr Z}\rangle\le l \langle a_1 \rangle. \end{align} $$
$$ \begin{align} & \hspace{2pc} \le m\left\langle e_C\otimes \psi\left(e_{1,1}\right)\right\rangle \le \langle e_C\otimes \psi(1_m)\rangle\le \langle e_C\otimes 1_{\mathscr Z}\rangle\le l \langle a_1 \rangle. \end{align} $$
Therefore (recall that
![]() $W(A)$
is almost unperforated), since
$W(A)$
is almost unperforated), since
![]() $l<m$
,
$l<m$
,
It follows (noting that
![]() $a_1a_2=a_2a_1=0$
) that
$a_1a_2=a_2a_1=0$
) that
Finally, the theorem follows from formulas (e5.59), (e5.55) and (e5.63), the fact that
![]() $D\otimes 1_n$
is embedded into
$D\otimes 1_n$
is embedded into
![]() $D\otimes 1_m$
unitally (as n divides m) and Proposition 5.3.
$D\otimes 1_m$
unitally (as n divides m) and Proposition 5.3.
Corollary 5.10. Let A be a simple
![]() $C^*$
-algebra which is e. tracially in
$C^*$
-algebra which is e. tracially in
![]() ${\cal C}_{\mathscr Z}$
. If A is not purely infinite, then it has stable rank one if it is unital and almost has stable rank one if it is not unital.
${\cal C}_{\mathscr Z}$
. If A is not purely infinite, then it has stable rank one if it is unital and almost has stable rank one if it is not unital.
Proof. By Theorem 5.9, A is tracially approximately divisible. By Theorem 5.1, if A is not purely infinite, then it has strict comparison for positive elements. It follows then from Theorem 5.7 that A has stable rank one if it is unital and almost has stable rank one if it is not unital.
Remark 5.11. For the rest of this paper, we will present nonamenable examples of
![]() $C^*$
-algebras which are possibly stably projectionless and are essentially tracially in the class
$C^*$
-algebras which are possibly stably projectionless and are essentially tracially in the class
![]() ${\cal C}_{\mathscr Z}$
, the class of
${\cal C}_{\mathscr Z}$
, the class of
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras.
$C^*$
-algebras.
6. Construction of
 $A_z^C$
$A_z^C$
In this section we first fix a separable residually finite-dimensional (RFD)
![]() $C^*$
-algebra C, which may not be exact.
$C^*$
-algebra C, which may not be exact.
Let B be the unitisation of
![]() $C_0((0,1], C)$
. Since
$C_0((0,1], C)$
. Since
![]() $C_0((0,1], C)$
is contractible,
$C_0((0,1], C)$
is contractible,
![]() $V(B)=\mathbb {N}\cup \{0\}$
,
$V(B)=\mathbb {N}\cup \{0\}$
,
![]() $K_0(B)=\mathbb {Z}$
and
$K_0(B)=\mathbb {Z}$
and
![]() $K_1(B)=\{0\}$
.
$K_1(B)=\{0\}$
.
Let us make the convention that B includes the case that
![]() $C=\{0\}$
– that is,
$C=\{0\}$
– that is,
![]() $B=\mathbb {C}$
.
$B=\mathbb {C}$
.
Let
![]() $\mathfrak {p}=p_1^{r_1}\cdot p_2^{r_2}\cdot \dotsb $
be a supernatural number, where
$\mathfrak {p}=p_1^{r_1}\cdot p_2^{r_2}\cdot \dotsb $
be a supernatural number, where
![]() $p_1, p_2,\dotsc $
is a sequence (possibly finite) of distinct prime numbers and
$p_1, p_2,\dotsc $
is a sequence (possibly finite) of distinct prime numbers and
![]() $r_i\in \mathbb {N}\cup \{\infty \}$
. Denote by
$r_i\in \mathbb {N}\cup \{\infty \}$
. Denote by
![]() $\mathbb D_{\mathfrak {p}}$
the subgroup of
$\mathbb D_{\mathfrak {p}}$
the subgroup of
![]() $\mathbb {Q}$
generated by finite sums of rational numbers of the form
$\mathbb {Q}$
generated by finite sums of rational numbers of the form
![]() ${\frac {m}{p_j^i}}$
, where
${\frac {m}{p_j^i}}$
, where
![]() $m\in \mathbb {Z}$
and
$m\in \mathbb {Z}$
and
 $i\in \mathbb {N}\cap \left [1, r_j\right ]$
.
$i\in \mathbb {N}\cap \left [1, r_j\right ]$
.
Denote by
![]() $M_{\mathfrak {p}}$
the UHF-algebra associated with the supernatural number
$M_{\mathfrak {p}}$
the UHF-algebra associated with the supernatural number
![]() $\mathfrak {p}$
.
$\mathfrak {p}$
.
The following is a result of Dădărlat [Reference Dădărlat13]:
Theorem 6.1. Fix a supernatural number
![]() $\mathfrak {d}$
. There is a unital simple
$\mathfrak {d}$
. There is a unital simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_{\mathfrak {d}}$
which is an inductive limit of
$A_{\mathfrak {d}}$
which is an inductive limit of
![]() $M_{m(n)}(B)$
with injective and unital connecting maps such that
$M_{m(n)}(B)$
with injective and unital connecting maps such that
 $$ \begin{align*} \left(K_0(A_{\mathfrak{d}}), K_0(A_{\mathfrak{d}})_+, \left[1_{{A_{\mathfrak{d}}}} \right]\right)=(\mathbb D_{\mathfrak{d}}, {\mathbb D_{\mathfrak{d}}}_+,1), \end{align*} $$
$$ \begin{align*} \left(K_0(A_{\mathfrak{d}}), K_0(A_{\mathfrak{d}})_+, \left[1_{{A_{\mathfrak{d}}}} \right]\right)=(\mathbb D_{\mathfrak{d}}, {\mathbb D_{\mathfrak{d}}}_+,1), \end{align*} $$
![]() $K_1(A_{\mathfrak {d}})=\{0\}$
, and
$K_1(A_{\mathfrak {d}})=\{0\}$
, and
![]() $A_{\mathfrak {d}}$
has a unique tracial state and tracial rank zero.
$A_{\mathfrak {d}}$
has a unique tracial state and tracial rank zero.
Proof. This is taken from [Reference Dădărlat13]; we retain the notation used there. For the supernatural number
![]() $\mathfrak {d}$
, there is a standard Bratteli system
$\mathfrak {d}$
, there is a standard Bratteli system
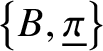 $\left \{B, \underline {\pi }\right \}$
given by Glimm. We use Dădărlat’s restricted system as defined in [Reference Dădărlat13, Definition 3]. Let
$\left \{B, \underline {\pi }\right \}$
given by Glimm. We use Dădărlat’s restricted system as defined in [Reference Dădărlat13, Definition 3]. Let
![]() $D=AF\left (\underline {\pi }\right )$
. Then D is the UHF-algebra with
$D=AF\left (\underline {\pi }\right )$
. Then D is the UHF-algebra with
![]() $(K_0(D), K_0(D)_+, [1_D])=(\mathbb D_{\mathfrak {d}}, {\mathbb D_{\mathfrak {d}}}_+,1)$
. Set
$(K_0(D), K_0(D)_+, [1_D])=(\mathbb D_{\mathfrak {d}}, {\mathbb D_{\mathfrak {d}}}_+,1)$
. Set
![]() $A_{\mathfrak {d}}:=B\left (\underline {\pi }\right )$
as in [Reference Dădărlat13, Proposition 8]. Note that [Reference Dădărlat13, Definition 3(ii)] implies that the connecting maps in the restricted system are injective (see also [Reference Dădărlat13, proof of Proposition 8]). The proof of [Reference Dădărlat13, Proposition 9] shows that
$A_{\mathfrak {d}}:=B\left (\underline {\pi }\right )$
as in [Reference Dădărlat13, Proposition 8]. Note that [Reference Dădărlat13, Definition 3(ii)] implies that the connecting maps in the restricted system are injective (see also [Reference Dădărlat13, proof of Proposition 8]). The proof of [Reference Dădărlat13, Proposition 9] shows that
![]() $B\left (\underline {\pi }\right )$
is a unital simple
$B\left (\underline {\pi }\right )$
is a unital simple
![]() $C^*$
-algebra of real rank zero and stable rank one,
$C^*$
-algebra of real rank zero and stable rank one,
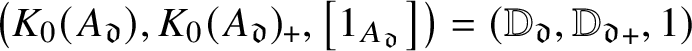 $\left (K_0(A_{\mathfrak {d}}), K_0(A_{\mathfrak {d}})_+, \left [1_{{A_{\mathfrak {d}}}} \right ]\right )=(\mathbb D_{\mathfrak {d}}, {\mathbb D_{\mathfrak {d}}}_+,1)$
, and has a unique tracial state. Note also that since
$\left (K_0(A_{\mathfrak {d}}), K_0(A_{\mathfrak {d}})_+, \left [1_{{A_{\mathfrak {d}}}} \right ]\right )=(\mathbb D_{\mathfrak {d}}, {\mathbb D_{\mathfrak {d}}}_+,1)$
, and has a unique tracial state. Note also that since
![]() $K_1(B)=0$
,
$K_1(B)=0$
,
![]() $K_1\left (B\left (\underline {\pi }\right )\right )=0$
. So
$K_1\left (B\left (\underline {\pi }\right )\right )=0$
. So
![]() $K_1(A_{\mathfrak {d}})=0$
. The fact that
$K_1(A_{\mathfrak {d}})=0$
. The fact that
![]() $A_{\mathfrak {d}}$
has tracial rank zero is also known and, for example, follows from [Reference Lin28, Theorem 3.7.9].
$A_{\mathfrak {d}}$
has tracial rank zero is also known and, for example, follows from [Reference Lin28, Theorem 3.7.9].
We will review the construction of
![]() $A_{\mathfrak {d}}$
and introduce some notation for our construction.
$A_{\mathfrak {d}}$
and introduce some notation for our construction.
Definition 6.2. Fix a supernatural number
![]() $\mathfrak {d}$
. Choose a Bratteli system
$\mathfrak {d}$
. Choose a Bratteli system
![]() $AF\left (\underline {\pi }\right )$
(see [Reference Dădărlat13, Definition 2]) for
$AF\left (\underline {\pi }\right )$
(see [Reference Dădărlat13, Definition 2]) for
![]() $M_{\mathfrak {d}}$
given by Glimm. Recall that
$M_{\mathfrak {d}}$
given by Glimm. Recall that
![]() $B= C_0((0,1], C)^{\sim }$
. Following Dădărlat’s construction (see [Reference Dădărlat13, Definition 3, proof of Proposition 8]), one may write
$B= C_0((0,1], C)^{\sim }$
. Following Dădărlat’s construction (see [Reference Dădărlat13, Definition 3, proof of Proposition 8]), one may write
![]() $A_{\mathfrak {d}}=\lim _{n\to \infty }\left (M_{d_n'}(B), \delta _n'\right )$
,
$A_{\mathfrak {d}}=\lim _{n\to \infty }\left (M_{d_n'}(B), \delta _n'\right )$
,
![]() $d_{n+1}'=d_n\cdot d_n'$
, where
$d_{n+1}'=d_n\cdot d_n'$
, where
![]() $d_n, d_{n}'>1$
are integers,
$d_n, d_{n}'>1$
are integers,
![]() $\delta _n': M_{d_n'}(B)\to M_{d_{n+1}'}(B)$
is defined by
$\delta _n': M_{d_n'}(B)\to M_{d_{n+1}'}(B)$
is defined by
 $$ \begin{align} \delta_n'(f):= \begin{pmatrix} f & 0\\ 0 & \gamma_n(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_n'}(B) \end{align} $$
$$ \begin{align} \delta_n'(f):= \begin{pmatrix} f & 0\\ 0 & \gamma_n(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_n'}(B) \end{align} $$
and
![]() $\gamma _n: B\to M_{d_{n}-1}$
is a unital homomorphism, a
$\gamma _n: B\to M_{d_{n}-1}$
is a unital homomorphism, a
![]() $d_{n}-1$
-dimensional representation (we then use
$d_{n}-1$
-dimensional representation (we then use
![]() $\gamma _n$
for the extension
$\gamma _n$
for the extension
![]() $\gamma _n\otimes \operatorname {id}_{d_n'}: M_{d_n'}(B)\to M_{\left (d_{n}-1\right )d_n'}$
) which also has the form described in the proof of [Reference Dădărlat13, Proposition 8]. By that proof, this can always be done.
$\gamma _n\otimes \operatorname {id}_{d_n'}: M_{d_n'}(B)\to M_{\left (d_{n}-1\right )d_n'}$
) which also has the form described in the proof of [Reference Dădărlat13, Proposition 8]. By that proof, this can always be done.
In the Bratteli system
![]() $AF\left (\underline {\pi }\right )$
, we may also assume, by passing to a subsequence, that
$AF\left (\underline {\pi }\right )$
, we may also assume, by passing to a subsequence, that
 $$ \begin{align} \lim_{n\to\infty}d_{n}=\infty. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}d_{n}=\infty. \end{align} $$
Also, we assume for any n that
![]() $\{\gamma _m: m\ge n\}$
is a separating sequence of finite-dimensional representations. For a more specific construction of
$\{\gamma _m: m\ge n\}$
is a separating sequence of finite-dimensional representations. For a more specific construction of
![]() $A_{\mathfrak {d}}$
, readers are referred to [Reference Dădărlat13, Definition 3, Proposition 8, Section 3].
$A_{\mathfrak {d}}$
, readers are referred to [Reference Dădărlat13, Definition 3, Proposition 8, Section 3].
It is important that for any
![]() $\tau \in T(B)$
,
$\tau \in T(B)$
,
 $$ \begin{align} \lim_{n\to\infty}\left\lvert\tau\circ \delta_n'(a)-\tau(\gamma_n(a))\right\rvert=0\mathrm{\ for\ all\ } a\in M_{d_n'}(B). \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left\lvert\tau\circ \delta_n'(a)-\tau(\gamma_n(a))\right\rvert=0\mathrm{\ for\ all\ } a\in M_{d_n'}(B). \end{align} $$
(Note that by
![]() $\tau $
we mean
$\tau $
we mean
![]() $\tau \otimes \mathrm {tr}_{d^{\prime }_{n}}$
, where
$\tau \otimes \mathrm {tr}_{d^{\prime }_{n}}$
, where
![]() $\mathrm {tr}_{d_{n}'}$
is the tracial state of
$\mathrm {tr}_{d_{n}'}$
is the tracial state of
![]() $M_{d_{n}'}$
.)
$M_{d_{n}'}$
.)
Consider
![]() $\delta _{m,n}':={\delta }_{n-1}'\circ \delta _{n-2}'\circ \dotsb \circ \delta _m': M_{d_m'}(B)\to M_{d_n'}(B)$
. Then we may write
$\delta _{m,n}':={\delta }_{n-1}'\circ \delta _{n-2}'\circ \dotsb \circ \delta _m': M_{d_m'}(B)\to M_{d_n'}(B)$
. Then we may write
 $$ \begin{align} \delta_{m,n}'(f)=\begin{pmatrix} f & 0\\ 0 & \gamma_{m,n}(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_m'}(B), \end{align} $$
$$ \begin{align} \delta_{m,n}'(f)=\begin{pmatrix} f & 0\\ 0 & \gamma_{m,n}(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_m'}(B), \end{align} $$
where
![]() $\gamma _{m,n}: B\to M_{d_n'/d^{\prime }_m-1} $
is a finite-dimensional representation. (In the rest of the paper, we also use
$\gamma _{m,n}: B\to M_{d_n'/d^{\prime }_m-1} $
is a finite-dimensional representation. (In the rest of the paper, we also use
![]() $\gamma _{m,n}:= \gamma _{m,n}\otimes \operatorname {id}_N : M_{N}(B)\to M_{\left (d_n'/d^{\prime }_m -1\right )N}$
for all integers
$\gamma _{m,n}:= \gamma _{m,n}\otimes \operatorname {id}_N : M_{N}(B)\to M_{\left (d_n'/d^{\prime }_m -1\right )N}$
for all integers
![]() $N\ge 1$
.) Therefore, if we fix a finite subset
$N\ge 1$
.) Therefore, if we fix a finite subset
![]() ${\cal F}_m\subset M_{d_m'}(B)$
, we may assume that for any
${\cal F}_m\subset M_{d_m'}(B)$
, we may assume that for any
![]() $a\in {\cal F}_m\setminus \{0\}$
, we have
$a\in {\cal F}_m\setminus \{0\}$
, we have
![]() $\gamma _{m,n}(a)\not =0$
for some large
$\gamma _{m,n}(a)\not =0$
for some large
![]() $n\ge m$
. Choose a function
$n\ge m$
. Choose a function
![]() $g\in C([0, \lVert a\rVert )_+$
such that
$g\in C([0, \lVert a\rVert )_+$
such that
![]() $0\le g(t)\le 1$
for all
$0\le g(t)\le 1$
for all
![]() $t\in [0, \infty )$
,
$t\in [0, \infty )$
,
![]() $g(t)=1$
if
$g(t)=1$
if
![]() $t \in [\lVert a\rVert -\lVert a\rVert /2m, \lVert a\rVert )$
and
$t \in [\lVert a\rVert -\lVert a\rVert /2m, \lVert a\rVert )$
and
![]() $g(t)=0$
if
$g(t)=0$
if
![]() $t\in [0,\lVert a\rVert -\lVert a\rVert /m]$
. We may assume that
$t\in [0,\lVert a\rVert -\lVert a\rVert /m]$
. We may assume that
![]() $\gamma _{m,n}(g(\lvert a\rvert ))\not =0$
for all
$\gamma _{m,n}(g(\lvert a\rvert ))\not =0$
for all
![]() $a\in {\cal F}_m\setminus \{0\}$
. It follows that
$a\in {\cal F}_m\setminus \{0\}$
. It follows that
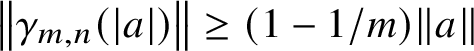 $\left \lVert \gamma _{m,n}(\lvert a\rvert )\right \rVert \ge (1-1/m)\lVert a\rVert $
for all
$\left \lVert \gamma _{m,n}(\lvert a\rvert )\right \rVert \ge (1-1/m)\lVert a\rVert $
for all
![]() $a\in {\cal F}_m\setminus \{0\}$
. Thus we may assume that for any
$a\in {\cal F}_m\setminus \{0\}$
. Thus we may assume that for any
![]() $a\in {\cal F}_m$
and all
$a\in {\cal F}_m$
and all
![]() $n> m$
,
$n> m$
,
 $$ \begin{align} \left\lVert{\gamma}_{m,n}(a)\right\rVert\ge (1-1/m)\lVert a\rVert. \end{align} $$
$$ \begin{align} \left\lVert{\gamma}_{m,n}(a)\right\rVert\ge (1-1/m)\lVert a\rVert. \end{align} $$
In what follows,
![]() $A_{\mathfrak {d}}=\lim _{n\to \infty }\left (M_{d_n'}(B), \delta _n'\right )$
is the
$A_{\mathfrak {d}}=\lim _{n\to \infty }\left (M_{d_n'}(B), \delta _n'\right )$
is the
![]() $C^*$
-algebra in Theorem 6.1 and
$C^*$
-algebra in Theorem 6.1 and
![]() $\delta _n'$
is as described in formula (e6.1) such that formula (e6.5) holds for
$\delta _n'$
is as described in formula (e6.1) such that formula (e6.5) holds for
![]() $n\ge m+1$
.
$n\ge m+1$
.
We wish to construct a unital simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_z^C$
with a unique tracial state such that
$A_z^C$
with a unique tracial state such that
![]() $K_0\left (A_z^C\right )=\mathbb {Z}$
and
$K_0\left (A_z^C\right )=\mathbb {Z}$
and
![]() $K_1\left (A_z^C\right )=\{0\}$
.
$K_1\left (A_z^C\right )=\{0\}$
.
The strategy is to have a Jiang–Su-style inductive limit of some
![]() $C^*$
-subalgebras of
$C^*$
-subalgebras of
![]() $C\!\left([0,1], M_p(B)\otimes M_q(B)\right )$
for some nonnuclear RFD algebra B, or perhaps some
$C\!\left([0,1], M_p(B)\otimes M_q(B)\right )$
for some nonnuclear RFD algebra B, or perhaps some
![]() $C^*$
-subalgebra of
$C^*$
-subalgebra of
![]() $C\!\left([0,1], M_{pq}(B)\right )$
. However, there are several difficulties to be resolved. One should avoid using
$C\!\left([0,1], M_{pq}(B)\right )$
. However, there are several difficulties to be resolved. One should avoid using
![]() $M_p(B)\otimes M_q(B)$
as building blocks, since there are different
$M_p(B)\otimes M_q(B)$
as building blocks, since there are different
![]() $C^*$
-tensor products and potential difficulties in computing the K-theory. Other issues include the fact that each fibre
$C^*$
-tensor products and potential difficulties in computing the K-theory. Other issues include the fact that each fibre
![]() $M_m(B)$
is not simple.
$M_m(B)$
is not simple.
We begin with the following building blocks:
Definition 6.3. For a pair of integers
![]() $m,k\ge 1$
, define
$m,k\ge 1$
, define
Note that here one views
![]() $M_m(B)\otimes 1_k, 1_m\otimes M_k \subset M_m(B)\otimes M_k = M_{mk}(B)$
as unital
$M_m(B)\otimes 1_k, 1_m\otimes M_k \subset M_m(B)\otimes M_k = M_{mk}(B)$
as unital
![]() $C^*$
-subalgebras.
$C^*$
-subalgebras.
Fix integers
![]() $m,n\ge 1$
. Let
$m,n\ge 1$
. Let
![]() $D(m,k)=M_m(B)\oplus M_k$
. Define
$D(m,k)=M_m(B)\oplus M_k$
. Define
![]() $\varphi _0: D(m,k)\to M_m(B)\otimes 1_k$
by
$\varphi _0: D(m,k)\to M_m(B)\otimes 1_k$
by
![]() $\varphi _0((a,b)):= a\otimes 1_k$
for all
$\varphi _0((a,b)):= a\otimes 1_k$
for all
![]() $(a,b)\in D(m,k)$
and
$(a,b)\in D(m,k)$
and
![]() $\varphi _1: D(m,k)\to M_k$
by
$\varphi _1: D(m,k)\to M_k$
by
![]() $\varphi _1((a,b))=1_m\otimes b$
.
$\varphi _1((a,b))=1_m\otimes b$
.
Then
Denote by
![]() $\pi _e: E_{m,k} \to D(m,k)$
the quotient map which maps
$\pi _e: E_{m,k} \to D(m,k)$
the quotient map which maps
![]() $(f,g)$
to g. Denote by
$(f,g)$
to g. Denote by
![]() $\pi _0: E_{m,k}\to M_m(B)\otimes 1_k$
the homomorphism defined by
$\pi _0: E_{m,k}\to M_m(B)\otimes 1_k$
the homomorphism defined by
![]() $\pi _0((f,g)):= \varphi _0(g)=f(0)$
and by
$\pi _0((f,g)):= \varphi _0(g)=f(0)$
and by
![]() $\pi _1: E_{m,k}\to 1_m\otimes M_k$
the homomorphism defined by
$\pi _1: E_{m,k}\to 1_m\otimes M_k$
the homomorphism defined by
![]() $\pi _1((f,g)):= \varphi _1(g)=f(1)$
.
$\pi _1((f,g)):= \varphi _1(g)=f(1)$
.
Lemma 6.4. If m and k are relatively prime, then
![]() $E_{m,k} $
has no proper projections.
$E_{m,k} $
has no proper projections.
Proof. Recall that
![]() $B=C_0 ((0,1], C)^{\sim }$
, the unitisation of
$B=C_0 ((0,1], C)^{\sim }$
, the unitisation of
![]() $C_0((0,1], C)$
. Let
$C_0((0,1], C)$
. Let
![]() $\tau _B$
be the tracial state on
$\tau _B$
be the tracial state on
![]() $M_m(B)$
induced by the quotient map
$M_m(B)$
induced by the quotient map
![]() $B\to B/C_0((0,1],C)\cong \mathbb {C}$
, and let
$B\to B/C_0((0,1],C)\cong \mathbb {C}$
, and let
![]() $\mathrm {tr}_k$
be the tracial state of
$\mathrm {tr}_k$
be the tracial state of
![]() $M_k$
. Let
$M_k$
. Let
![]() $\tau =\tau _B\otimes \mathrm {tr}_k$
.
$\tau =\tau _B\otimes \mathrm {tr}_k$
.
Let
![]() $e\in E_{m,k} $
be a nonzero projection. Note that
$e\in E_{m,k} $
be a nonzero projection. Note that
![]() $E_{m,k} \subset C([0,1], M_{mk}(B))$
. Note also that
$E_{m,k} \subset C([0,1], M_{mk}(B))$
. Note also that
![]() $K_0(B)=\mathbb {Z}$
and
$K_0(B)=\mathbb {Z}$
and
![]() $1_B$
is the only nonzero projection of B. Then for each
$1_B$
is the only nonzero projection of B. Then for each
![]() $x\in [0,1]$
,
$x\in [0,1]$
,
![]() $e(x)$
is a nonzero projection in
$e(x)$
is a nonzero projection in
![]() $M_{mk}(B)$
. One easily shows that
$M_{mk}(B)$
. One easily shows that
![]() $\tau (e(x))$
is a constant function on
$\tau (e(x))$
is a constant function on
![]() $[0,1]$
. Let
$[0,1]$
. Let
![]() $\tau (e(x))=r\in (0,1]$
. But
$\tau (e(x))=r\in (0,1]$
. But
![]() $\tau (e(0))\in \{i/m: i=0,1,\dotsc ,m\}$
and
$\tau (e(0))\in \{i/m: i=0,1,\dotsc ,m\}$
and
![]() $\tau (e(1))\in \{j/k,i=0,1,\dotsc ,k\}$
. Since m and k are relatively prime,
$\tau (e(1))\in \{j/k,i=0,1,\dotsc ,k\}$
. Since m and k are relatively prime,
![]() $\tau (e(0))=\tau (e(1))=1$
. Hence
$\tau (e(0))=\tau (e(1))=1$
. Hence
![]() $\tau (e(x))=1$
for all
$\tau (e(x))=1$
for all
![]() $x\in [0,1]$
. This is possible only when
$x\in [0,1]$
. This is possible only when
![]() $e=1_m\otimes 1_k$
.
$e=1_m\otimes 1_k$
.
Lemma 6.5. Suppose that m and k are relatively prime. Then
 $$ \begin{align*} \left(K_0\left(E_{m,k}\right), K_0\left(E_{m,k}\right)_+, \left[1_{E_{m,k}}\right]\right)=(\mathbb{Z}, \mathbb{N}\cup \{0\}, 1)\qquad \text{and} \qquad K_1\left(E_{m,k}\right)=\{0\}. \end{align*} $$
$$ \begin{align*} \left(K_0\left(E_{m,k}\right), K_0\left(E_{m,k}\right)_+, \left[1_{E_{m,k}}\right]\right)=(\mathbb{Z}, \mathbb{N}\cup \{0\}, 1)\qquad \text{and} \qquad K_1\left(E_{m,k}\right)=\{0\}. \end{align*} $$
Proof. Let
 $$ \begin{align*} I=\left\{f\in E_{m,k}: f(0)=f(1)=0\right\}. \end{align*} $$
$$ \begin{align*} I=\left\{f\in E_{m,k}: f(0)=f(1)=0\right\}. \end{align*} $$
Then
![]() $I\cong C_0((0,1))\otimes M_{mk}(B) =S(M_{mk}(B))$
. It follows that
$I\cong C_0((0,1))\otimes M_{mk}(B) =S(M_{mk}(B))$
. It follows that
Consider the short exact sequence
 $$ \begin{align} 0\to I\stackrel{\iota_I}{\longrightarrow} E_{m,k}\stackrel{\pi_e}{\longrightarrow} D(m,k)\to 0, \end{align} $$
$$ \begin{align} 0\to I\stackrel{\iota_I}{\longrightarrow} E_{m,k}\stackrel{\pi_e}{\longrightarrow} D(m,k)\to 0, \end{align} $$
where
![]() $\iota _I: I\to E_{m,k}$
is the embedding and
$\iota _I: I\to E_{m,k}$
is the embedding and
![]() $\pi _e: E_{m,k}\to D(m,k)$
is the quotient map. One obtains the following six-term exact sequence:
$\pi _e: E_{m,k}\to D(m,k)$
is the quotient map. One obtains the following six-term exact sequence:
 $$ \begin{align} \begin{array}{ccccc} K_0(I) & \stackrel{{\iota_I}_{*0}}\longrightarrow & K_0\left(E_{m,k}\right) & \stackrel{{\pi_e}_{*0}}{\longrightarrow} & K_0(D(m,k))\\ \uparrow_{\delta_1} & & & & \downarrow_{\delta_0}\\ K_1(D(m,k)) & \stackrel{{\pi_e}_{*1}}{\longleftarrow} & K_1\left(E_{m,k}\right) & \stackrel{{\iota_I}_{*1}}{\longleftarrow} & K_1(I), \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccccc} K_0(I) & \stackrel{{\iota_I}_{*0}}\longrightarrow & K_0\left(E_{m,k}\right) & \stackrel{{\pi_e}_{*0}}{\longrightarrow} & K_0(D(m,k))\\ \uparrow_{\delta_1} & & & & \downarrow_{\delta_0}\\ K_1(D(m,k)) & \stackrel{{\pi_e}_{*1}}{\longleftarrow} & K_1\left(E_{m,k}\right) & \stackrel{{\iota_I}_{*1}}{\longleftarrow} & K_1(I), \end{array} \end{align} $$
which becomes
 $$ \begin{align} \begin{array}{ccccc} 0 & \stackrel{{\iota_I}_{*0}}\longrightarrow & K_0\left(E_{m,k}\right) & \stackrel{{\pi_e}_{*0}}{\longrightarrow} & \mathbb{Z}\oplus \mathbb{Z}\\ \uparrow_{\delta_1} & & & & \downarrow_{\delta_0}\\ 0 & \stackrel{{\pi_e}_{*1}}{\longleftarrow} & K_1\left(E_{m,k}\right) & \stackrel{{\iota_I}_{*1}}{\longleftarrow} & \mathbb{Z}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccccc} 0 & \stackrel{{\iota_I}_{*0}}\longrightarrow & K_0\left(E_{m,k}\right) & \stackrel{{\pi_e}_{*0}}{\longrightarrow} & \mathbb{Z}\oplus \mathbb{Z}\\ \uparrow_{\delta_1} & & & & \downarrow_{\delta_0}\\ 0 & \stackrel{{\pi_e}_{*1}}{\longleftarrow} & K_1\left(E_{m,k}\right) & \stackrel{{\iota_I}_{*1}}{\longleftarrow} & \mathbb{Z}. \end{array} \end{align} $$
Note that
 $$ \begin{align*} \mathrm{im}\left({\pi_e}_{*0}\right)=\left\{(x, y)\in K_0(D(m,k)): {\varphi_0}_{*0}(x)={\varphi_1}_{*0}(y)\right\}. \end{align*} $$
$$ \begin{align*} \mathrm{im}\left({\pi_e}_{*0}\right)=\left\{(x, y)\in K_0(D(m,k)): {\varphi_0}_{*0}(x)={\varphi_1}_{*0}(y)\right\}. \end{align*} $$
The lemma follows from a straightforward computation.
Set
![]() $\tau \in T(C([0,1], M_{mk}(B)))$
. By, for example, [Reference Ivanescu and Kučerovský26, Theorem 2.1] and the Choquet and Fubini theorems,
$\tau \in T(C([0,1], M_{mk}(B)))$
. By, for example, [Reference Ivanescu and Kučerovský26, Theorem 2.1] and the Choquet and Fubini theorems,
 $$ \begin{align*} \tau(f)=\int_{\partial_e T\left(C\left(\left[0,1\right]\right)\right)\times \partial_eT\left(M_{mk}(B)\right)} f d(\mu\times\mu_B) \end{align*} $$
$$ \begin{align*} \tau(f)=\int_{\partial_e T\left(C\left(\left[0,1\right]\right)\right)\times \partial_eT\left(M_{mk}(B)\right)} f d(\mu\times\mu_B) \end{align*} $$
for all
![]() $f\in \operatorname {Aff}(T(C([0,1], M_{mk}(B))))_{\mathrm {sa}}$
, where
$f\in \operatorname {Aff}(T(C([0,1], M_{mk}(B))))_{\mathrm {sa}}$
, where
![]() $\mu $
is a probability Borel measure on
$\mu $
is a probability Borel measure on
![]() $[0,1]$
and
$[0,1]$
and
![]() $\mu _B$
is a probability Borel measure on
$\mu _B$
is a probability Borel measure on
![]() $\partial _eT(M_{mk}(B))$
. By the Fubini theorem again, we may write
$\partial _eT(M_{mk}(B))$
. By the Fubini theorem again, we may write
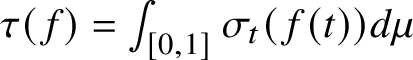 $\tau (f)=\int _{\left [0,1\right ]} \sigma _t(f(t))d\mu $
, where
$\tau (f)=\int _{\left [0,1\right ]} \sigma _t(f(t))d\mu $
, where
![]() $\sigma _t$
is a tracial state of
$\sigma _t$
is a tracial state of
![]() $M_{mk}(B)$
. Let I be the ideal in the proof of Lemma 6.5. Then
$M_{mk}(B)$
. Let I be the ideal in the proof of Lemma 6.5. Then
![]() $I\cong C_0((0,1))\otimes M_{mk}(B)$
. Now set
$I\cong C_0((0,1))\otimes M_{mk}(B)$
. Now set
![]() $\tau \in T\left (E_{m,k}\right )$
such that
$\tau \in T\left (E_{m,k}\right )$
such that
![]() $\lVert \tau \rvert _I\rVert \not =0$
. Since
$\lVert \tau \rvert _I\rVert \not =0$
. Since
![]() $(1/\lVert \tau _I\rVert )\tau \rvert _I$
can be extended to a tracial state of
$(1/\lVert \tau _I\rVert )\tau \rvert _I$
can be extended to a tracial state of
![]() $C([0,1], M_{mk}(B))$
, we may write
$C([0,1], M_{mk}(B))$
, we may write
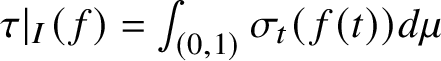 $\tau \rvert _{I}(f)=\int _{\left (0,1\right )} \sigma _t(f(t))d\mu $
for all
$\tau \rvert _{I}(f)=\int _{\left (0,1\right )} \sigma _t(f(t))d\mu $
for all
![]() $f\in C_0((0,1))\otimes M_{mk}(B)$
, where
$f\in C_0((0,1))\otimes M_{mk}(B)$
, where
![]() $\sigma _t$
is a tracial state of
$\sigma _t$
is a tracial state of
![]() $M_{mk}(B)$
and
$M_{mk}(B)$
and
![]() $\mu $
is a Borel measure on
$\mu $
is a Borel measure on
![]() $(0,1)$
(with
$(0,1)$
(with
![]() $\lVert \mu \rVert =\lVert \tau \rvert _I\rVert \le 1$
). Since
$\lVert \mu \rVert =\lVert \tau \rvert _I\rVert \le 1$
). Since
![]() $E_{m,k}/I=M_m(B)\oplus M_k$
, as in [Reference Lin31, 2.5], one may write
$E_{m,k}/I=M_m(B)\oplus M_k$
, as in [Reference Lin31, 2.5], one may write
 $$ \begin{align} \tau(f)=\int_0^1 \sigma_t(f(t))d\nu\mathrm{\ for\ all\ } f\in E_{m,k}, \end{align} $$
$$ \begin{align} \tau(f)=\int_0^1 \sigma_t(f(t))d\nu\mathrm{\ for\ all\ } f\in E_{m,k}, \end{align} $$
where
![]() $\sigma _0$
is a tracial state on
$\sigma _0$
is a tracial state on
![]() $M_m(B)$
,
$M_m(B)$
,
![]() $\sigma _1$
is a tracial state on
$\sigma _1$
is a tracial state on
![]() $M_k$
,
$M_k$
,
![]() $\nu $
is a probability Borel measure on
$\nu $
is a probability Borel measure on
![]() $[0,1]$
,
$[0,1]$
,
![]() $\nu \rvert _{\left (0,1\right )}=\mu \rvert _{\left (0,1\right )}$
, and if
$\nu \rvert _{\left (0,1\right )}=\mu \rvert _{\left (0,1\right )}$
, and if
![]() $\lVert \tau \rvert _I\rVert =0$
, then
$\lVert \tau \rvert _I\rVert =0$
, then
![]() $\nu \rvert _{\left (0,1\right )}=0$
.
$\nu \rvert _{\left (0,1\right )}=0$
.
Notation 6.6. Let
![]() $\gamma : B\to M_r$
be a finite-dimensional representation with rank r – that is,
$\gamma : B\to M_r$
be a finite-dimensional representation with rank r – that is,
![]() $\gamma $
is a finite direct sum of irreducible representations
$\gamma $
is a finite direct sum of irreducible representations
![]() $\gamma _j: j=1,2,\dotsc ,l$
, each of which has rank
$\gamma _j: j=1,2,\dotsc ,l$
, each of which has rank
![]() $r_j$
(
$r_j$
(
![]() $1\le j\le l$
), such that
$1\le j\le l$
), such that
 $r=\sum _{j=1}^l r_j$
. We will also use
$r=\sum _{j=1}^l r_j$
. We will also use
![]() $\gamma $
for
$\gamma $
for
![]() $\gamma \otimes \operatorname {id}_m:M_m(B)\to M_{rm}$
for all integers
$\gamma \otimes \operatorname {id}_m:M_m(B)\to M_{rm}$
for all integers
![]() $m\ge 1$
. In what follows we may also write
$m\ge 1$
. In what follows we may also write
![]() $M_L$
for
$M_L$
for
![]() $M_L(\mathbb {C}\cdot 1_B)$
for all integers
$M_L(\mathbb {C}\cdot 1_B)$
for all integers
![]() $L\ge 1$
. In this way,
$L\ge 1$
. In this way,
![]() $\gamma $
(or
$\gamma $
(or
![]() $\gamma \otimes \operatorname {id}_m$
) is a homomorphism from
$\gamma \otimes \operatorname {id}_m$
) is a homomorphism from
![]() $M_m(B)$
into
$M_m(B)$
into
![]() $M_{rm}\subset M_{rm}(B)$
.
$M_{rm}\subset M_{rm}(B)$
.
Let
![]() $\xi _0, \xi _1,\xi _2,\dotsc ,\xi _{{k-1}}: [0,1]\to [0,1]$
be continuous paths. Define a homomorphism
$\xi _0, \xi _1,\xi _2,\dotsc ,\xi _{{k-1}}: [0,1]\to [0,1]$
be continuous paths. Define a homomorphism
by
 $$ \begin{align*} H(f)(t):= \begin{pmatrix} f\circ \xi_0(t) & 0 &\dotsb & 0\\ 0 & \gamma(f\circ \xi_1 (t) ) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma (f\circ \xi_{k-1}(t) )\end{pmatrix} \mathrm{\ for\ all\ } f\in C([0,1], M_{mn}(B)) \end{align*} $$
$$ \begin{align*} H(f)(t):= \begin{pmatrix} f\circ \xi_0(t) & 0 &\dotsb & 0\\ 0 & \gamma(f\circ \xi_1 (t) ) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma (f\circ \xi_{k-1}(t) )\end{pmatrix} \mathrm{\ for\ all\ } f\in C([0,1], M_{mn}(B)) \end{align*} $$
and
![]() $t\in [0,1]$
. Note that H can be also defined on
$t\in [0,1]$
. Note that H can be also defined on
![]() $E_{m,n}\subset C([0,1], M_{mn}(B))$
. But in general, H does not map
$E_{m,n}\subset C([0,1], M_{mn}(B))$
. But in general, H does not map
![]() $E_{m,n}$
into
$E_{m,n}$
into
![]() $E_{m,n}$
. However, with some restrictions on the boundary (restriction on
$E_{m,n}$
. However, with some restrictions on the boundary (restriction on
![]() $\xi _i$
s), it is possible that H maps
$\xi _i$
s), it is possible that H maps
![]() $E_{m,n}$
into
$E_{m,n}$
into
![]() $E_{m,n}$
.
$E_{m,n}$
.
For the convenience of the construction, let us add some notation and terminology.
Set
![]() $f, g\in M_n(B)$
. We write
$f, g\in M_n(B)$
. We write
![]() $f=^s g$
if there is a scalar unitary
$f=^s g$
if there is a scalar unitary
![]() $w\in M_n$
such that
$w\in M_n$
such that
![]() $w^*fw=g$
. Also, if
$w^*fw=g$
. Also, if
![]() $f, g\in C([0,1], M_n(B))$
, we write
$f, g\in C([0,1], M_n(B))$
, we write
![]() $f=^s g$
if there is a unitary
$f=^s g$
if there is a unitary
![]() $w\in C([0,1], M_n)$
such that
$w\in C([0,1], M_n)$
such that
![]() $w^*fw=g$
.
$w^*fw=g$
.
6.7. We will construct
![]() $A=\lim _{n\to \infty }(A_n, \varphi _m)$
. The construction will be by induction. Fix B as in Notation 6.6. Set
$A=\lim _{n\to \infty }(A_n, \varphi _m)$
. The construction will be by induction. Fix B as in Notation 6.6. Set
![]() $A_1=E_{3, 5}$
.
$A_1=E_{3, 5}$
.
Denote by
![]() ${\bar {\mathfrak {3}}}$
the supernatural number
${\bar {\mathfrak {3}}}$
the supernatural number
![]() $3^\infty $
. Write
$3^\infty $
. Write
![]() $A_{{\bar {\mathfrak {3}}}}=\lim _{n\to \infty } \left (M_{d_n'}(B), \delta _n'\right )$
(see Theorem 6.1), where
$A_{{\bar {\mathfrak {3}}}}=\lim _{n\to \infty } \left (M_{d_n'}(B), \delta _n'\right )$
(see Theorem 6.1), where
 $$ \begin{align} \delta_n'(f)=\begin{pmatrix} f & 0\\ 0 & \gamma_n(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_n'}(B), \end{align} $$
$$ \begin{align} \delta_n'(f)=\begin{pmatrix} f & 0\\ 0 & \gamma_n(f)\end{pmatrix} \mathrm{\ for\ all\ } f\in M_{d_n'}(B), \end{align} $$
as in formula (e6.1), which also has the properties in equations (e6.2) and (e6.3) (with
![]() $d_n=3^l$
for some integer
$d_n=3^l$
for some integer
![]() $l\ge 1$
). Hence, without loss of generality, by passing to a subsequence we may assume, for all n,
$l\ge 1$
). Hence, without loss of generality, by passing to a subsequence we may assume, for all n,
 $$ \begin{align} \frac{1}{d_n-1} <1/3^n. \end{align} $$
$$ \begin{align} \frac{1}{d_n-1} <1/3^n. \end{align} $$
Recall that
![]() $B=C_0((0,1], C)^{\sim }$
. For each
$B=C_0((0,1], C)^{\sim }$
. For each
![]() $t\in [0,1]$
, denote by
$t\in [0,1]$
, denote by
![]() $\theta _t: B\to B$
the homomorphism defined, for all
$\theta _t: B\to B$
the homomorphism defined, for all
![]() $f\in B$
, by
$f\in B$
, by
Note also that for any integer
![]() $l\ge 1$
, we will use
$l\ge 1$
, we will use
![]() $\theta _t$
for
$\theta _t$
for
![]() $\theta _t\otimes \operatorname {id}_{l}: M_{l}(B)\to M_{l}(B)$
. Thus, if
$\theta _t\otimes \operatorname {id}_{l}: M_{l}(B)\to M_{l}(B)$
. Thus, if
![]() $f\in M_l(B)$
,
$f\in M_l(B)$
,
It should be noted that
![]() $\theta _0=\operatorname {id}_{M_l(B)}$
.
$\theta _0=\operatorname {id}_{M_l(B)}$
.
We state the inductive step as the following lemma:
Lemma 6.8. For
![]() $A_m=E_{p_m, q_m}$
with
$A_m=E_{p_m, q_m}$
with
![]() $(p_m, q_m)=1$
, we have
$(p_m, q_m)=1$
, we have
![]() $(5, p_m)=1$
and
$(5, p_m)=1$
and
![]() $(3, q_m)=1$
. There exist
$(3, q_m)=1$
. There exist
![]() $A_{m+1}=E_{p_{m+1}, q_{m+1}}$
, where
$A_{m+1}=E_{p_{m+1}, q_{m+1}}$
, where
![]() $(p_{m+1}, q_{m+1})=1$
,
$(p_{m+1}, q_{m+1})=1$
,
![]() $(5, p_{m+1})=1$
and
$(5, p_{m+1})=1$
and
![]() $(3, q_{m+1})=1$
, and a unital injective homomorphism
$(3, q_{m+1})=1$
, and a unital injective homomorphism
![]() $\varphi _m: A_m\to A_{m+1}$
of the form
$\varphi _m: A_m\to A_{m+1}$
of the form
 $$ \begin{align} \varphi_{m}(f) (t) =u^*\begin{pmatrix} \Theta_{m}(f)(t) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(f\circ \xi_1(t))\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(f\circ \xi_k(t))\otimes 1_5 \end{pmatrix} u \end{align} $$
$$ \begin{align} \varphi_{m}(f) (t) =u^*\begin{pmatrix} \Theta_{m}(f)(t) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(f\circ \xi_1(t))\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(f\circ \xi_k(t))\otimes 1_5 \end{pmatrix} u \end{align} $$
for all
![]() $f\in A_m$
, where
$f\in A_m$
, where
![]() $u\in U\left (C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )\right )$
,
$u\in U\left (C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )\right )$
,
![]() $\Theta _{m}: A_m\to C\!\left([0,1], M_{5kp_mq_m}(B)\right )$
is a homomorphism,
$\Theta _{m}: A_m\to C\!\left([0,1], M_{5kp_mq_m}(B)\right )$
is a homomorphism,
![]() $k\ge 1$
is an integer,
$k\ge 1$
is an integer,
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $\gamma _m: M_{p_mq_m}(B)\to M_{R(m)p_mq_m}$
is a finite-dimensional representation, where
$\gamma _m: M_{p_mq_m}(B)\to M_{R(m)p_mq_m}$
is a finite-dimensional representation, where
![]() $R(m)\ge 1$
is an integer. Moreover, the following are true:
$R(m)\ge 1$
is an integer. Moreover, the following are true:
-
(1) Each
 $\xi _i: [0,1]\to [0,1]$
is a continuous map which has one of the following three forms: (e6.17)
$\xi _i: [0,1]\to [0,1]$
is a continuous map which has one of the following three forms: (e6.17) $$ \begin{align} \xi_i(t)&=\begin{cases} (2/3)t & \text{if } t\in [0,3/4],\\ 1/2 & \text{if } t\in (3/4,1],\end{cases} \hspace{2pc} \end{align} $$
(e6.18)
$$ \begin{align} \xi_i(t)&=\begin{cases} (2/3)t & \text{if } t\in [0,3/4],\\ 1/2 & \text{if } t\in (3/4,1],\end{cases} \hspace{2pc} \end{align} $$
(e6.18) $$ \begin{align} \xi_i(t)&=1/2\mathrm{\ for\ all\ } t\in [0,1], \hspace{3.5pc} \end{align} $$
(e6.19)and each type of
$$ \begin{align} \xi_i(t)&=1/2\mathrm{\ for\ all\ } t\in [0,1], \hspace{3.5pc} \end{align} $$
(e6.19)and each type of $$ \begin{align} \xi_i(t)&=\begin{cases} 1/2+(2/3)t & \text{if } t\in [0,3/4],\\ 1 & \text{if } t\in (3/4,1], \end{cases} \end{align} $$
$$ \begin{align} \xi_i(t)&=\begin{cases} 1/2+(2/3)t & \text{if } t\in [0,3/4],\\ 1 & \text{if } t\in (3/4,1], \end{cases} \end{align} $$
 $\xi _i$
appears in equation (e6.16) at least once.
$\xi _i$
appears in equation (e6.16) at least once.
-
(2)
 $5k/5kR(m)= 1/R(m) <1/3^{m}$
.
$5k/5kR(m)= 1/R(m) <1/3^{m}$
. -
(3) For a fixed finite subset
 ${\cal F}_m\subset A_m\setminus \{0\}\subset C\!\left([0,1], M_{p_mq_m}(B)\right )$
,
${\cal F}_m\subset A_m\setminus \{0\}\subset C\!\left([0,1], M_{p_mq_m}(B)\right )$
,  $$ \begin{align*} \lVert\gamma_m(f(t))\rVert> (1-1/2m)\lVert f\rVert \not=0\mathrm{\ for\ some\ }t \in [0,1]. \end{align*} $$
$$ \begin{align*} \lVert\gamma_m(f(t))\rVert> (1-1/2m)\lVert f\rVert \not=0\mathrm{\ for\ some\ }t \in [0,1]. \end{align*} $$
-
(4) We have
(e6.20)where $$ \begin{align} \Theta_m(f)=\mathrm{diag}\left(\theta^{(1)}(f) ,\dotsc, \theta^{(k)}(f)\right), \end{align} $$
$$ \begin{align} \Theta_m(f)=\mathrm{diag}\left(\theta^{(1)}(f) ,\dotsc, \theta^{(k)}(f)\right), \end{align} $$
 $\theta ^{(i)}: E_{p_m, q_m}\to C\!\left([0,1], M_{5p_mq_m}(B)\right )$
is defined – if
$\theta ^{(i)}: E_{p_m, q_m}\to C\!\left([0,1], M_{5p_mq_m}(B)\right )$
is defined – if
 $\xi _i(3/4)=1/2$
– for each
$\xi _i(3/4)=1/2$
– for each
 $f\in E_{p_m, q_m}$
by and where
$f\in E_{p_m, q_m}$
by and where $$ \begin{align*} \theta^{(i)}(f)(t):= \begin{cases} f(\xi_i(t)) & \text{if }t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & \text{if }t\in (3/4,1], \end{cases} \end{align*} $$
$$ \begin{align*} \theta^{(i)}(f)(t):= \begin{cases} f(\xi_i(t)) & \text{if }t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & \text{if }t\in (3/4,1], \end{cases} \end{align*} $$
 $\theta _t: M_{p_mq_m}(B)\to M_{p_mq_m}(B)$
(recall that
$\theta _t: M_{p_mq_m}(B)\to M_{p_mq_m}(B)$
(recall that
 $B= C_0((0,1], C)^{\sim } $
) is a unital homomorphism defined by (e6.21)and, if
$B= C_0((0,1], C)^{\sim } $
) is a unital homomorphism defined by (e6.21)and, if $$ \begin{align} \theta_t(f)(x):= f((1-t)x)\mathrm{\ for\ all\ } x\in (0,1] {\mathrm{\ and\ all\ }} t\in [0,1] \end{align} $$
$$ \begin{align} \theta_t(f)(x):= f((1-t)x)\mathrm{\ for\ all\ } x\in (0,1] {\mathrm{\ and\ all\ }} t\in [0,1] \end{align} $$
 $\xi _i(3/4)=1$
, for each
$\xi _i(3/4)=1$
, for each
 $f\in E_{p_m,q_m}$
,
$f\in E_{p_m,q_m}$
,  $$ \begin{align*} \theta^{(i)}(f)(t)=f(\xi_i(t)),\quad{{t\in [0,1].}} \end{align*} $$
$$ \begin{align*} \theta^{(i)}(f)(t)=f(\xi_i(t)),\quad{{t\in [0,1].}} \end{align*} $$
Proof. To avoid the potential complication of computing relative primality of integers, we will have a three-stage construction.
Stage 1: Write
![]() $A_m=E_{p_m, q_m}$
, where
$A_m=E_{p_m, q_m}$
, where
![]() $(p_m, q_m)=1$
. Also
$(p_m, q_m)=1$
. Also
![]() $(5, p_m)=1$
and
$(5, p_m)=1$
and
![]() $(3, q_m)=1$
.
$(3, q_m)=1$
.
Fix any finite subset
![]() ${\cal F}_m\subset E_{p_m,q_m}\setminus \{0\}$
. One can choose a finite subset
${\cal F}_m\subset E_{p_m,q_m}\setminus \{0\}$
. One can choose a finite subset
![]() $S\subset [0,1]$
such that, for any
$S\subset [0,1]$
such that, for any
![]() $f\in {\cal F}_m$
, there is
$f\in {\cal F}_m$
, there is
![]() $s\in S$
,
$s\in S$
,
![]() $ \lVert f(s)\rVert> (1-1/2m)\lVert f\rVert \not =0. $
Note that
$ \lVert f(s)\rVert> (1-1/2m)\lVert f\rVert \not =0. $
Note that
![]() ${\cal F}'=\{f(s): f\in {\cal F}_m\text { and } s\in S\}\setminus \{0\}$
is a finite subset of
${\cal F}'=\{f(s): f\in {\cal F}_m\text { and } s\in S\}\setminus \{0\}$
is a finite subset of
![]() $M_{p_mq_m}(B)$
. By passing to a subsequence, we may assume (replacing
$M_{p_mq_m}(B)$
. By passing to a subsequence, we may assume (replacing
![]() $\gamma _m$
by
$\gamma _m$
by
![]() ${\gamma }_{m,n}$
as mentioned in formula (e6.5)) that
${\gamma }_{m,n}$
as mentioned in formula (e6.5)) that
It follows that for any
![]() $f\in {\cal F}_m$
,
$f\in {\cal F}_m$
,
Define
![]() $\psi _m': M_{p_m}(B)\otimes M_{q_m}\to M_{d_mp_m}(B)\otimes M_{5q_m}$
by
$\psi _m': M_{p_m}(B)\otimes M_{q_m}\to M_{d_mp_m}(B)\otimes M_{5q_m}$
by
![]() $ \psi _m':= \delta _m\otimes s$
, where
$ \psi _m':= \delta _m\otimes s$
, where
 $$ \begin{align} \delta_{m}(a)=\begin{pmatrix} a & 0\\ 0 & \gamma_m(a)\end{pmatrix}\mathrm{\ for\ all\ } a\in M_{p_m}(B),\mathrm{\ and\ } s(c)=c\otimes 1_5\mathrm{\ for\ all\ } c\in M_{q_m}. \end{align} $$
$$ \begin{align} \delta_{m}(a)=\begin{pmatrix} a & 0\\ 0 & \gamma_m(a)\end{pmatrix}\mathrm{\ for\ all\ } a\in M_{p_m}(B),\mathrm{\ and\ } s(c)=c\otimes 1_5\mathrm{\ for\ all\ } c\in M_{q_m}. \end{align} $$
Define
![]() $\psi _m: E_{p_m, q_m}\to E_{d_{m} p_m, 5q_m}$
by
$\psi _m: E_{p_m, q_m}\to E_{d_{m} p_m, 5q_m}$
by
Set
![]() $f\in E_{p_m, q_m}$
. Then
$f\in E_{p_m, q_m}$
. Then
![]() $f(0)=b\otimes 1_{q_m}$
, where
$f(0)=b\otimes 1_{q_m}$
, where
![]() $b\in M_{p_m}(B)$
. Thus,
$b\in M_{p_m}(B)$
. Thus,
On the other hand,
![]() $f(1)=1_{p_m}\otimes c$
, where
$f(1)=1_{p_m}\otimes c$
, where
![]() $c\in M_{q_m}$
. Thus
$c\in M_{q_m}$
. Thus
So indeed,
![]() $\psi _m$
maps
$\psi _m$
maps
![]() $E_{p_m, q_m}$
into
$E_{p_m, q_m}$
into
![]() $E_{d_mp_m, 5q_m}$
.
$E_{d_mp_m, 5q_m}$
.
Note that for
![]() $t\in [0,1]$
, we have for all
$t\in [0,1]$
, we have for all
![]() $f\in E_{p_m,q_m}$
(writing
$f\in E_{p_m,q_m}$
(writing
![]() $\gamma _m$
for
$\gamma _m$
for
![]() $\gamma _m\otimes \operatorname {id}_{M_{q_{_m}}}$
)
$\gamma _m\otimes \operatorname {id}_{M_{q_{_m}}}$
)
 $$ \begin{align} \psi_m(f)(t)=\psi_m'(f(t))=\begin{pmatrix} f(t) & 0\\ 0 & \gamma_m(f(t))\end{pmatrix} \otimes 1_5. \end{align} $$
$$ \begin{align} \psi_m(f)(t)=\psi_m'(f(t))=\begin{pmatrix} f(t) & 0\\ 0 & \gamma_m(f(t))\end{pmatrix} \otimes 1_5. \end{align} $$
Recall that
![]() $\gamma _m: M_{p_mq_m}(B)\to M_{R(m)p_mq_m}$
is a unital homomorphism with
$\gamma _m: M_{p_mq_m}(B)\to M_{R(m)p_mq_m}$
is a unital homomorphism with
![]() $R(m)=d_m-1$
. Note that by formula (e6.13), we may assume that
$R(m)=d_m-1$
. Note that by formula (e6.13), we may assume that
![]() $R(m)>3^m$
.
$R(m)>3^m$
.
Stage 2: We will use a modified construction of Jiang and Su and define
![]() $\varphi _m$
on
$\varphi _m$
on
![]() $[0,3/4]$
.
$[0,3/4]$
.
Choose a (first) pair of different prime numbers
![]() $k_0$
and
$k_0$
and
![]() $k_1$
such that
$k_1$
such that
In particular,
![]() $k_0, k_1\not =3, 5$
.
$k_0, k_1\not =3, 5$
.
Recall that
![]() $(3,q_m)=1$
,
$(3,q_m)=1$
,
![]() $(5,p_m)=1$
and
$(5,p_m)=1$
and
![]() $d_m=3^{l_m}$
for some
$d_m=3^{l_m}$
for some
![]() $l_m\ge 1$
. Therefore,
$l_m\ge 1$
. Therefore,
![]() $(k_0d_mp_m, k_15q_m)=1$
. Let
$(k_0d_mp_m, k_15q_m)=1$
. Let
![]() $p_{m+1}=k_0d_mp_m$
,
$p_{m+1}=k_0d_mp_m$
,
![]() $q_{m+1}=k_15q_m$
and
$q_{m+1}=k_15q_m$
and
![]() $k=k_0k_1$
. Then
$k=k_0k_1$
. Then
![]() $(p_{m+1}, q_{m+1})=1$
,
$(p_{m+1}, q_{m+1})=1$
,
![]() $(5, p_{m+1})=1$
and
$(5, p_{m+1})=1$
and
![]() $(3, q_{m+1})=1$
. Write
$(3, q_{m+1})=1$
. Write
where
![]() $m(0), r_0, m(1), r_1\ge 1$
are integers and
$m(0), r_0, m(1), r_1\ge 1$
are integers and
Moreover, by formula (e6.29),
 $$ \begin{align}\nonumber k-r_1-r_0&>k-q_{m+1}-p_{m+1}=k-k_15q_m-k_0d_mp_m\\\nonumber &= k_1\left(k_0-5q_m\right)-k_0d_mp_m \\ &>k_1\left(10q_m\right)-k_0d_mp_m> 0. \end{align} $$
$$ \begin{align}\nonumber k-r_1-r_0&>k-q_{m+1}-p_{m+1}=k-k_15q_m-k_0d_mp_m\\\nonumber &= k_1\left(k_0-5q_m\right)-k_0d_mp_m \\ &>k_1\left(10q_m\right)-k_0d_mp_m> 0. \end{align} $$
We will construct paths
![]() $\xi _i$
. At
$\xi _i$
. At
![]() $t=0$
, define
$t=0$
, define
 $$ \begin{align} \xi_i(0):= \begin{cases} 0 & {\text{if }}1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k. \end{cases} \end{align} $$
$$ \begin{align} \xi_i(0):= \begin{cases} 0 & {\text{if }}1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k. \end{cases} \end{align} $$
Note that since
![]() $r_05q_m=t_0q_{m+1}$
for some integer
$r_05q_m=t_0q_{m+1}$
for some integer
![]() $t_0\ge 1$
. Note also that if
$t_0\ge 1$
. Note also that if
![]() $f\in E_{d_mp_m, 5q_m}$
, then
$f\in E_{d_mp_m, 5q_m}$
, then
![]() $f(0)=b\otimes 1_{5q_m}$
for some
$f(0)=b\otimes 1_{5q_m}$
for some
![]() $b\in M_{d_mp_m}(B)$
. Hence
$b\in M_{d_mp_m}(B)$
. Hence
![]() $f(0)\otimes 1_{r_0}=b\otimes 1_{r_05q_m}=\left (b\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
for any
$f(0)\otimes 1_{r_0}=b\otimes 1_{r_05q_m}=\left (b\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
for any
![]() $f\in E_{d_mp_m, 5q_m}$
. On the other hand, for any
$f\in E_{d_mp_m, 5q_m}$
. On the other hand, for any
![]() $f\in E_{d_mp_m,5q_m} $
,
$f\in E_{d_mp_m,5q_m} $
,
In fact, there is a scalar unitary
![]() $s_0\in M_{m(0)q_{m+1}d_mp_m5q_m}$
such that
$s_0\in M_{m(0)q_{m+1}d_mp_m5q_m}$
such that
 $$ \begin{align*} s_0^*\mathrm{diag}(\overbrace{b,b,\dotsc,b}^{k-r_0})s_0=b\otimes 1_{m(0)q_{m+1}}\mathrm{\ for\ all\ } b\in M_{d_mp_m5q_{m}}(B) \end{align*} $$
$$ \begin{align*} s_0^*\mathrm{diag}(\overbrace{b,b,\dotsc,b}^{k-r_0})s_0=b\otimes 1_{m(0)q_{m+1}}\mathrm{\ for\ all\ } b\in M_{d_mp_m5q_{m}}(B) \end{align*} $$
(recall that
![]() $f(1/2)\in M_{d_mp_m5q_{m}}(B)$
). Therefore, there exists a unitary
$f(1/2)\in M_{d_mp_m5q_{m}}(B)$
). Therefore, there exists a unitary
![]() $v_0\in U\left (M_{p_{m+1}q_{m+1}}\right )$
such that for all
$v_0\in U\left (M_{p_{m+1}q_{m+1}}\right )$
such that for all
![]() $f\in E_{d_mp_m,5q_m}$
,
$f\in E_{d_mp_m,5q_m}$
,
 $$ \begin{align} \rho_0(f):=v_0^*\begin{pmatrix} f(\xi_1(0)) & 0 &\dotsb & 0\\ 0 & f(\xi_2(0)) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & f( \xi_{k}(0))\end{pmatrix}v_0 \end{align} $$
$$ \begin{align} \rho_0(f):=v_0^*\begin{pmatrix} f(\xi_1(0)) & 0 &\dotsb & 0\\ 0 & f(\xi_2(0)) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & f( \xi_{k}(0))\end{pmatrix}v_0 \end{align} $$
is in
![]() $M_{p_{m+1}}(B)\otimes 1_{q_{m+1}}$
. So
$M_{p_{m+1}}(B)\otimes 1_{q_{m+1}}$
. So
![]() $\rho _0$
defines a homomorphism from
$\rho _0$
defines a homomorphism from
![]() $E_{d_mp_m, 5q_m}$
into
$E_{d_mp_m, 5q_m}$
into
![]() $M_{p_{m+1}}(B)\otimes 1_{q_{m+1}}$
.
$M_{p_{m+1}}(B)\otimes 1_{q_{m+1}}$
.
At
![]() $t=3/4$
, define
$t=3/4$
, define
 $$ \begin{align} \xi_i(3/4):= \begin{cases} 1/2 & \text{if } 1\le i\le k-r_1,\\ 1 & \text{if }k-r_1<i\le k. \end{cases} \end{align} $$
$$ \begin{align} \xi_i(3/4):= \begin{cases} 1/2 & \text{if } 1\le i\le k-r_1,\\ 1 & \text{if }k-r_1<i\le k. \end{cases} \end{align} $$
As in the case at
![]() $0$
, by formula (e6.32),
$0$
, by formula (e6.32),
So one may write
![]() $r_1d_mp_m=t_1p_{m+1}$
for some integer
$r_1d_mp_m=t_1p_{m+1}$
for some integer
![]() $t_1\ge 1$
. Set
$t_1\ge 1$
. Set
![]() $f\in E_{d_mp_m, 5q_m}$
. Then
$f\in E_{d_mp_m, 5q_m}$
. Then
![]() $f(1)=1_{d_mp_m}\otimes c$
for some
$f(1)=1_{d_mp_m}\otimes c$
for some
![]() $c\in M_{5q_m}$
. It follows that
$c\in M_{5q_m}$
. It follows that
![]() $1_{r_1}\otimes f(1)=1_{p_{m+1}}\otimes \left (1_{t_1}\otimes c\right )$
. Also,
$1_{r_1}\otimes f(1)=1_{p_{m+1}}\otimes \left (1_{t_1}\otimes c\right )$
. Also,
In fact, there is a scalar unitary
![]() $s_1\in M_{m(1)p_{m+1}d_mp_m5q_m}$
such that
$s_1\in M_{m(1)p_{m+1}d_mp_m5q_m}$
such that
 $$ \begin{align*} s_1^*\mathrm{diag}(\overbrace{b, b,\dotsc,b}^{k-r_1})s_1=1_{m(1)p_{m+1}}\otimes b\mathrm{\ for\ all\ } b\in M_{d_mp_m5q_m}(B). \end{align*} $$
$$ \begin{align*} s_1^*\mathrm{diag}(\overbrace{b, b,\dotsc,b}^{k-r_1})s_1=1_{m(1)p_{m+1}}\otimes b\mathrm{\ for\ all\ } b\in M_{d_mp_m5q_m}(B). \end{align*} $$
Thus there is a unitary
![]() $v_{3/4}\in U\left (M_{p_{m+1}q_{m+1}}\right )$
such that for
$v_{3/4}\in U\left (M_{p_{m+1}q_{m+1}}\right )$
such that for
![]() $f\in E_{d_mp_m, 5q_m}$
,
$f\in E_{d_mp_m, 5q_m}$
,
 $$ \begin{align} \rho_{3/4}(f) :=v_{3/4}^*\begin{pmatrix} f(\xi_1(3/4)) & 0 &\dotsb & 0\\ 0 & f(\xi_2(3/4)) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & f(\xi_{k}(3/4))\end{pmatrix}v_{3/4} \end{align} $$
$$ \begin{align} \rho_{3/4}(f) :=v_{3/4}^*\begin{pmatrix} f(\xi_1(3/4)) & 0 &\dotsb & 0\\ 0 & f(\xi_2(3/4)) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & f(\xi_{k}(3/4))\end{pmatrix}v_{3/4} \end{align} $$
defines a homomorphism from
![]() $E_{d_mp_m, 5q_m}$
to
$E_{d_mp_m, 5q_m}$
to
![]() $1_{p_{m+1}}\otimes M_{q_{m+1}}(B)$
.
$1_{p_{m+1}}\otimes M_{q_{m+1}}(B)$
.
To connect
![]() $\xi _i(0)$
and
$\xi _i(0)$
and
![]() $\xi _i(3/4)$
continuously, on
$\xi _i(3/4)$
continuously, on
![]() $[0,3/4]$
, let us define (see formula (e6.33))
$[0,3/4]$
, let us define (see formula (e6.33))
 $$ \begin{align} \xi_i(t):= \begin{cases} 2t/3 & \text{if } 1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k-r_1,\\ 1/2+2t/3 &\text{if } k-r_1<i\le k.\end{cases} \end{align} $$
$$ \begin{align} \xi_i(t):= \begin{cases} 2t/3 & \text{if } 1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k-r_1,\\ 1/2+2t/3 &\text{if } k-r_1<i\le k.\end{cases} \end{align} $$
Let
![]() $v\in C\!\left([0, 3/4], M_{p_{m+1}q_{m+1}}\right )$
be a unitary such that
$v\in C\!\left([0, 3/4], M_{p_{m+1}q_{m+1}}\right )$
be a unitary such that
![]() $v(0)=v_0$
and
$v(0)=v_0$
and
![]() $v(3/4)=v_{3/4}$
. Now, on
$v(3/4)=v_{3/4}$
. Now, on
![]() $[0,3/4]$
, define, for all
$[0,3/4]$
, define, for all
![]() $f\in E_{p_m, q_m}$
,
$f\in E_{p_m, q_m}$
,
 $$ \begin{align} \varphi_m(f)(t):= v(t)^*\begin{pmatrix} \psi_m(f)\circ\xi_1(t) & 0 &\dotsb & 0\\ 0 & \psi_m(f)\circ \xi_2(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \psi_m(f)\circ \xi_{k}(t)\end{pmatrix}v(t). \end{align} $$
$$ \begin{align} \varphi_m(f)(t):= v(t)^*\begin{pmatrix} \psi_m(f)\circ\xi_1(t) & 0 &\dotsb & 0\\ 0 & \psi_m(f)\circ \xi_2(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \psi_m(f)\circ \xi_{k}(t)\end{pmatrix}v(t). \end{align} $$
Stage 3: We connect
![]() $3/4$
to
$3/4$
to
![]() $1$
, recalling that
$1$
, recalling that
![]() $\pi _1\left (E_{p_{m+1}, q_{m+1}}\right )=1_{p_{m+1}}\otimes M_{q_{m+1}}$
.
$\pi _1\left (E_{p_{m+1}, q_{m+1}}\right )=1_{p_{m+1}}\otimes M_{q_{m+1}}$
.
We first extend
![]() $\xi _i$
by defining
$\xi _i$
by defining
Recall equation (e6.28); at
![]() $t=3/4$
, for each i and for
$t=3/4$
, for each i and for
![]() $f\in E_{p_m,q_m}$
,
$f\in E_{p_m,q_m}$
,
 $$ \begin{align} \psi_m(f)(\xi_i(3/4))=\begin{pmatrix} f(\xi_i(3/4)) & 0\\ 0 & \gamma_m(f(\xi_i(3/4)))\end{pmatrix} \otimes 1_5. \end{align} $$
$$ \begin{align} \psi_m(f)(\xi_i(3/4))=\begin{pmatrix} f(\xi_i(3/4)) & 0\\ 0 & \gamma_m(f(\xi_i(3/4)))\end{pmatrix} \otimes 1_5. \end{align} $$
For
![]() $k-r_1< i\le k$
, define, for
$k-r_1< i\le k$
, define, for
![]() $t\in ( 3/4, 1]$
and
$t\in ( 3/4, 1]$
and
![]() $f\in E_{p_m,q_m}$
,
$f\in E_{p_m,q_m}$
,
 $$ \begin{align} \hspace{-0.2in} {\tilde \psi}_{m,i}(f)(t) := \begin{pmatrix} f(\xi_i(3/4)) & 0\\ 0& \gamma_m(f(\xi_i(3/4))) \end{pmatrix}\otimes 1_5 = \begin{pmatrix} f(1) & 0\\ 0& \gamma_m(f(1))\end{pmatrix}\otimes 1_5. \end{align} $$
$$ \begin{align} \hspace{-0.2in} {\tilde \psi}_{m,i}(f)(t) := \begin{pmatrix} f(\xi_i(3/4)) & 0\\ 0& \gamma_m(f(\xi_i(3/4))) \end{pmatrix}\otimes 1_5 = \begin{pmatrix} f(1) & 0\\ 0& \gamma_m(f(1))\end{pmatrix}\otimes 1_5. \end{align} $$
Recall that
![]() $\gamma _m(f(1))=f(1)\otimes 1_{d_m-1}$
. Therefore there exists a scalar unitary
$\gamma _m(f(1))=f(1)\otimes 1_{d_m-1}$
. Therefore there exists a scalar unitary
![]() $s_3\in M_{p_mq_m5d_m}$
such that
$s_3\in M_{p_mq_m5d_m}$
such that
Note that
![]() $f(1)$
has the form
$f(1)$
has the form
![]() $1_{p_m}\otimes c$
for some
$1_{p_m}\otimes c$
for some
![]() $c\in M_{q_m}$
. So there is a scalar unitary
$c\in M_{q_m}$
. So there is a scalar unitary
![]() $s_4\in M_{t_1p_{m+1}q_m 5}$
such that
$s_4\in M_{t_1p_{m+1}q_m 5}$
such that
Now recall formula (e6.14) for the definition of
![]() $\theta _t$
. For
$\theta _t$
. For
![]() $1\le i\le k-r_1$
, define, for
$1\le i\le k-r_1$
, define, for
![]() $t\in (3/4, 1]$
,
$t\in (3/4, 1]$
,
 $$ \begin{align} {\tilde \psi}_{m,i}(f)(t):= \begin{pmatrix}\theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & 0\\ 0& \gamma_m(f(\xi_i(t)))\end{pmatrix}\otimes 1_5\mathrm{\ for\ all\ } f\in E_{p_m, q_m}. \end{align} $$
$$ \begin{align} {\tilde \psi}_{m,i}(f)(t):= \begin{pmatrix}\theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & 0\\ 0& \gamma_m(f(\xi_i(t)))\end{pmatrix}\otimes 1_5\mathrm{\ for\ all\ } f\in E_{p_m, q_m}. \end{align} $$
Note that
![]() $\theta _1(f(\xi _i(3/4)))=\theta _1(f(1/2))\in M_{p_mq_m}$
(see formulas (e6.38) and (e6.15)). Recall that
$\theta _1(f(\xi _i(3/4)))=\theta _1(f(1/2))\in M_{p_mq_m}$
(see formulas (e6.38) and (e6.15)). Recall that
![]() $\varphi _m(f)(3/4)\in 1_{p_{m+1}}\otimes M_{q_{m+1}}(B)$
. Note that for
$\varphi _m(f)(3/4)\in 1_{p_{m+1}}\otimes M_{q_{m+1}}(B)$
. Note that for
![]() $1\le i\le k-r_1$
,
$1\le i\le k-r_1$
,
 $$ \begin{align*} {\tilde \psi}_{m,i}(f)(1)=\begin{pmatrix}\theta_1(f(1/2)) & 0\\ 0& \gamma_m(f(1/2))\end{pmatrix}\otimes 1_5\mathrm{\ for\ all\ } f\in E_{p_m, q_m}. \end{align*} $$
$$ \begin{align*} {\tilde \psi}_{m,i}(f)(1)=\begin{pmatrix}\theta_1(f(1/2)) & 0\\ 0& \gamma_m(f(1/2))\end{pmatrix}\otimes 1_5\mathrm{\ for\ all\ } f\in E_{p_m, q_m}. \end{align*} $$
Moreover (see also equation (e6.30)), there is a scalar unitary
![]() $s_5\in M_{m(1)p_{m+1}d_mp_mq_m 5}$
such that
$s_5\in M_{m(1)p_{m+1}d_mp_mq_m 5}$
such that
 $$ \begin{align*} s_5^*\mathrm{diag}\left({\tilde \psi}_{m,1} (f)(1), \dotsc, {\tilde \psi}_{m, k-r_1} (f)(1)\right)s_5=1_{m(1)p_{m+1}}\otimes \begin{pmatrix} \theta_1(f(1/2)) & 0\\ 0& \gamma_m(f(1/2))\end{pmatrix}\otimes 1_5. \end{align*} $$
$$ \begin{align*} s_5^*\mathrm{diag}\left({\tilde \psi}_{m,1} (f)(1), \dotsc, {\tilde \psi}_{m, k-r_1} (f)(1)\right)s_5=1_{m(1)p_{m+1}}\otimes \begin{pmatrix} \theta_1(f(1/2)) & 0\\ 0& \gamma_m(f(1/2))\end{pmatrix}\otimes 1_5. \end{align*} $$
Thus, for
![]() $t=1$
, there is a unitary
$t=1$
, there is a unitary
![]() $v_1\in 1_{p_{m+1}}\otimes M_{q_{m+1}}$
such that
$v_1\in 1_{p_{m+1}}\otimes M_{q_{m+1}}$
such that
 $$ \begin{align} \rho_1(f):= v_1^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(1) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(1) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(1)\end{pmatrix}v_1 \end{align} $$
$$ \begin{align} \rho_1(f):= v_1^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(1) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(1) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(1)\end{pmatrix}v_1 \end{align} $$
defines a homomorphism from
![]() $E_{p_m, q_m}$
to
$E_{p_m, q_m}$
to
![]() $1_{p_{m+1}}\otimes M_{q_{m+1}}$
. There is a continuous path of unitaries
$1_{p_{m+1}}\otimes M_{q_{m+1}}$
. There is a continuous path of unitaries
![]() $\{v(t): t\in [3/4, 1]\}\subset M_{p_{m+1}q_{m+1}}$
such that
$\{v(t): t\in [3/4, 1]\}\subset M_{p_{m+1}q_{m+1}}$
such that
![]() $v(3/4)$
is as defined and
$v(3/4)$
is as defined and
![]() $v(1)=v_1$
– so now
$v(1)=v_1$
– so now
![]() $v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
with
$v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
with
![]() $v(0)=v_0$
and
$v(0)=v_0$
and
![]() $v(1)=v_1$
, and
$v(1)=v_1$
, and
![]() $v(3/4)$
is consistent with the previous definition. Now define, for
$v(3/4)$
is consistent with the previous definition. Now define, for
![]() $t\in (3/4, 1]$
,
$t\in (3/4, 1]$
,
 $$ \begin{align} \varphi_m(f)(t):= v(t)^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(t) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(t)\end{pmatrix}v(t) \end{align} $$
$$ \begin{align} \varphi_m(f)(t):= v(t)^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(t) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(t)\end{pmatrix}v(t) \end{align} $$
for all
![]() $f\in E_{p_m, q_m}$
. Note that by formulas (e6.43), (e6.46), (e6.47) and (e6.39),
$f\in E_{p_m, q_m}$
. Note that by formulas (e6.43), (e6.46), (e6.47) and (e6.39),
Hence
![]() $\varphi _m$
is a unital injective homomorphism from
$\varphi _m$
is a unital injective homomorphism from
![]() $E_{p_m, q_m}$
to
$E_{p_m, q_m}$
to
![]() $E_{p_{m+1}, q_{m+1}}$
. (Note that injectivity follows from the fact that
$E_{p_{m+1}, q_{m+1}}$
. (Note that injectivity follows from the fact that
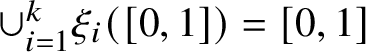 $\cup _{i=1}^k \xi _i([0,1])=[0,1]$
, as
$\cup _{i=1}^k \xi _i([0,1])=[0,1]$
, as
![]() $r_0\ge 1$
and
$r_0\ge 1$
and
![]() $k-r_1>0$
.)
$k-r_1>0$
.)
For convenience of notation and for later use, let us define
![]() $\tilde \psi _{m,i}: E_{p_m, q_m} \to C\!\left([0,1], M_{d_mp_m5q_m}(B)\right )$
by
$\tilde \psi _{m,i}: E_{p_m, q_m} \to C\!\left([0,1], M_{d_mp_m5q_m}(B)\right )$
by
 $$ \begin{align} \tilde \psi_{m,i}(f)(t):= \begin{cases} \psi_m(f\circ \xi_i(t)) &\text{if } t\in [0,3/4],\\ \tilde \psi_{m,i}(f)(t) &\text{if } t\in (3/4,1], \end{cases} \end{align} $$
$$ \begin{align} \tilde \psi_{m,i}(f)(t):= \begin{cases} \psi_m(f\circ \xi_i(t)) &\text{if } t\in [0,3/4],\\ \tilde \psi_{m,i}(f)(t) &\text{if } t\in (3/4,1], \end{cases} \end{align} $$
for all
![]() $f\in E_{p_m,q_m}$
. Then we may write, for all
$f\in E_{p_m,q_m}$
. Then we may write, for all
![]() $t\in [0,1]$
and all
$t\in [0,1]$
and all
![]() $f\in E_{p_m, q_m}$
,
$f\in E_{p_m, q_m}$
,
 $$ \begin{align} \varphi_m(f)(t)=v(t)^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(t) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(t)\end{pmatrix}v(t). \end{align} $$
$$ \begin{align} \varphi_m(f)(t)=v(t)^*\begin{pmatrix} {\tilde \psi}_{m,1}(f)(t) & 0 &\dotsb & 0\\ 0 & {\tilde \psi}_{m,2}(f)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & {\tilde \psi}_{m,k}(f)(t)\end{pmatrix}v(t). \end{align} $$
Define
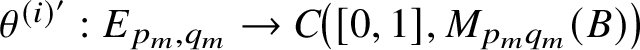 $\theta ^{(i)'}: E_{p_m, q_m}\to C\!\left([0,1], M_{p_mq_m}(B)\right )$
, for each
$\theta ^{(i)'}: E_{p_m, q_m}\to C\!\left([0,1], M_{p_mq_m}(B)\right )$
, for each
![]() $f\in E_{p_m, q_m}$
, by
$f\in E_{p_m, q_m}$
, by
 $$ \begin{align} \theta^{(i)'}(f)(t):= \begin{cases} f(\xi_i(t)) & \text{if }t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & \text{if }t\in (3/4,1],\end{cases} \end{align} $$
$$ \begin{align} \theta^{(i)'}(f)(t):= \begin{cases} f(\xi_i(t)) & \text{if }t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}(f(\xi_i(t))) & \text{if }t\in (3/4,1],\end{cases} \end{align} $$
if
![]() $\xi _i(3/4)=1/2;$
and if
$\xi _i(3/4)=1/2;$
and if
![]() $\xi _i(3/4)=1$
, define
$\xi _i(3/4)=1$
, define
Define
![]() $\theta ^{(i)}(f):=\theta ^{(i)'}(f)\otimes 1_5$
for
$\theta ^{(i)}(f):=\theta ^{(i)'}(f)\otimes 1_5$
for
![]() $f\in E_{p_m,q_m}$
and
$f\in E_{p_m,q_m}$
and
![]() $\Theta _m: E_{p_m, q_m}\to C\!\left([0,1], M_{5kp_{m}q_{m}}(B)\right )$
, for each
$\Theta _m: E_{p_m, q_m}\to C\!\left([0,1], M_{5kp_{m}q_{m}}(B)\right )$
, for each
![]() $f\in E_{p_m, q_m}$
, by
$f\in E_{p_m, q_m}$
, by
 $$ \begin{align} \Theta_m(f):= \mathrm{diag}\left(\theta^{(1)}(f) ,\dotsc, \theta^{(k)}(f)\right)\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
$$ \begin{align} \Theta_m(f):= \mathrm{diag}\left(\theta^{(1)}(f) ,\dotsc, \theta^{(k)}(f)\right)\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
By formulas (e6.48), (e6.28) and (e6.46), as well as the definition of
![]() $\Theta _m$
, and by conjugating another unitary in
$\Theta _m$
, and by conjugating another unitary in
![]() $C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
, we may write
$C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
, we may write
 $$ \begin{align} \varphi_{m}(f)=u^*\begin{pmatrix} \Theta_{m}(f) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(f\circ \xi_1) \otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(f\circ \xi_k)\otimes 1_5 \end{pmatrix} u \mathrm{\ for\ all\ } f\in A_m. \end{align} $$
$$ \begin{align} \varphi_{m}(f)=u^*\begin{pmatrix} \Theta_{m}(f) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(f\circ \xi_1) \otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(f\circ \xi_k)\otimes 1_5 \end{pmatrix} u \mathrm{\ for\ all\ } f\in A_m. \end{align} $$
So
![]() $\varphi _m$
does have the form of formula (e6.16). Condition (1) of the lemma follows from the definition of
$\varphi _m$
does have the form of formula (e6.16). Condition (1) of the lemma follows from the definition of
![]() $\xi _i$
and formulas (e6.40), (e6.42) and (e6.33). Condition (2) follows from formulas (e6.13) and (e6.28) (and two lines after it). Condition (3) follows from formula (e6.23). Finally, condition (4) follows from the definition of
$\xi _i$
and formulas (e6.40), (e6.42) and (e6.33). Condition (2) follows from formulas (e6.13) and (e6.28) (and two lines after it). Condition (3) follows from formula (e6.23). Finally, condition (4) follows from the definition of
![]() $\Theta _m$
.
$\Theta _m$
.
Definition 6.9. From 6.7 and Lemma 6.8, inductively, we define
![]() $A_1=E_{3,5}$
,
$A_1=E_{3,5}$
,
![]() $A_m=E_{p_m, q_m}$
and homomorphism s
$A_m=E_{p_m, q_m}$
and homomorphism s
![]() $\varphi _m: A_m\to A_{m+1}=A_{p_{m+1}, q_{m+1}}$
as described in Lemma 6.8. Then we define
$\varphi _m: A_m\to A_{m+1}=A_{p_{m+1}, q_{m+1}}$
as described in Lemma 6.8. Then we define
![]() $A=\lim _{n\to \infty }(A_m, \varphi _m)$
.
$A=\lim _{n\to \infty }(A_m, \varphi _m)$
.
Remark 6.10. It should be noted that if
![]() $f(0), f(1)\in M_{p_mq_m}$
, then
$f(0), f(1)\in M_{p_mq_m}$
, then
![]() $\Theta _m(f(0))$
and
$\Theta _m(f(0))$
and
![]() $\Theta _m(f(1))$
are also scalar matrices.
$\Theta _m(f(1))$
are also scalar matrices.
7. Conclusion of the construction
Definition 7.1. Let
![]() $\{\xi _i: 1\le i\le m\}$
be a collection of maps described in Lemma 6.8(1). Note that each of the three types occurs at least once. Such a collection is said to be full. Let
$\{\xi _i: 1\le i\le m\}$
be a collection of maps described in Lemma 6.8(1). Note that each of the three types occurs at least once. Such a collection is said to be full. Let
 $C_2:=\left \{\xi _i^{(1)}\circ \xi _j^{(2)}: 1\le i\le m_1, 1\le j\le m_2\right \}$
be a collection of compositions of two maps in Lemma 6.8(1). This collection is called full if
$C_2:=\left \{\xi _i^{(1)}\circ \xi _j^{(2)}: 1\le i\le m_1, 1\le j\le m_2\right \}$
be a collection of compositions of two maps in Lemma 6.8(1). This collection is called full if
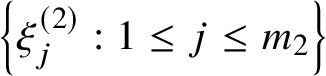 $\left \{\xi _{j}^{(2)}: 1\le j\le m_2\right \}$
is a full collection, and for each fixed
$\left \{\xi _{j}^{(2)}: 1\le j\le m_2\right \}$
is a full collection, and for each fixed
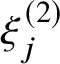 $\xi _j^{(2)}$
,
$\xi _j^{(2)}$
,
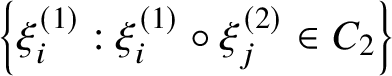 $\left \{\xi _i^{(1)}: \xi _i^{(1)}\circ \xi _j^{(2)}\in C_2\right \}$
is also a full collection. Inductively, a collection of n compositions of maps in Lemma 6.8(1),
$\left \{\xi _i^{(1)}: \xi _i^{(1)}\circ \xi _j^{(2)}\in C_2\right \}$
is also a full collection. Inductively, a collection of n compositions of maps in Lemma 6.8(1),
 $$ \begin{align*} C_n=\left\{\xi_{j(1)}^{(1)}\circ \xi_{j(2)}^{(2)}\circ \dotsb \circ \xi_{j(n)}^{(n)}: 1\le j(i)\le m_i: i=1,2,\dotsc,n\right\} \end{align*} $$
$$ \begin{align*} C_n=\left\{\xi_{j(1)}^{(1)}\circ \xi_{j(2)}^{(2)}\circ \dotsb \circ \xi_{j(n)}^{(n)}: 1\le j(i)\le m_i: i=1,2,\dotsc,n\right\} \end{align*} $$
is called full if
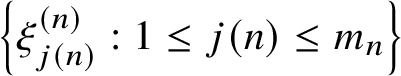 $\left \{\xi _{j(n)}^{(n)}: 1\le j(n)\le m_n\right \}$
is a full collection, and for each fixed
$\left \{\xi _{j(n)}^{(n)}: 1\le j(n)\le m_n\right \}$
is a full collection, and for each fixed
 $\xi _{j(n)}^{(n)}$
, the collection
$\xi _{j(n)}^{(n)}$
, the collection
 $$ \begin{align*} \left\{\xi_{j(1)}^{(1)}\circ \xi_{j(2)}^{(2)}\circ\dotsb \circ \xi_{j(n-1)}^{(n-1)}: \xi_{j(1)}\circ \xi_{j(2)}\circ\dotsb \circ \xi_{j(n-1)}\circ \xi_{j(n)}\in C_n\right\} \end{align*} $$
$$ \begin{align*} \left\{\xi_{j(1)}^{(1)}\circ \xi_{j(2)}^{(2)}\circ\dotsb \circ \xi_{j(n-1)}^{(n-1)}: \xi_{j(1)}\circ \xi_{j(2)}\circ\dotsb \circ \xi_{j(n-1)}\circ \xi_{j(n)}\in C_n\right\} \end{align*} $$
is full.
Lemma 7.2. Let
![]() $\Xi =\xi _{j(1)}\circ \xi _{j(2)}\circ \dotsb \circ \xi _{j(n)}: [0,1]\to [0,1]$
be a composition of n maps, where each
$\Xi =\xi _{j(1)}\circ \xi _{j(2)}\circ \dotsb \circ \xi _{j(n)}: [0,1]\to [0,1]$
be a composition of n maps, where each
![]() $\xi _{j(k)}: [0,1]\to [0,1]$
(
$\xi _{j(k)}: [0,1]\to [0,1]$
(
![]() $1\le k\le n$
) is one of the three types of continuous maps given in Lemma 6.8(1). Then for any
$1\le k\le n$
) is one of the three types of continuous maps given in Lemma 6.8(1). Then for any
![]() $x, y\in [0,1]$
,
$x, y\in [0,1]$
,
Moreover, if
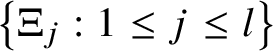 $\left \{\Xi _j: 1\le j\le l\right \}$
is a full collection of compositions of n maps as before, then
$\left \{\Xi _j: 1\le j\le l\right \}$
is a full collection of compositions of n maps as before, then
 $$ \begin{align} \cup^l_{j=1} \Xi_j([0,1])=[0,1], \end{align} $$
$$ \begin{align} \cup^l_{j=1} \Xi_j([0,1])=[0,1], \end{align} $$
and for each
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
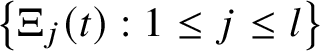 $ \left \{\Xi _j(t): 1\le j\le l\right \} $
is
$ \left \{\Xi _j(t): 1\le j\le l\right \} $
is
![]() $(2/3)^n$
-dense in
$(2/3)^n$
-dense in
![]() $[0,1]$
.
$[0,1]$
.
Proof. Note that for each i and for any
![]() $x,y\in [0,1]$
, we have
$x,y\in [0,1]$
, we have
![]() $\lvert \xi _i(x)-\xi _i(y)\rvert \leq (2/3)\lvert x-y\rvert $
. Then, by induction, for all
$\lvert \xi _i(x)-\xi _i(y)\rvert \leq (2/3)\lvert x-y\rvert $
. Then, by induction, for all
![]() $x, y\in [0,1]$
,
$x, y\in [0,1]$
,
 $$ \begin{align} \lvert\Xi(x)-\Xi(y)\rvert &= \left\lvert\xi_{j(1)}\circ \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(x)- \xi_{j(1)}\circ \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(y)\right\rvert \end{align} $$
$$ \begin{align} \lvert\Xi(x)-\Xi(y)\rvert &= \left\lvert\xi_{j(1)}\circ \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(x)- \xi_{j(1)}\circ \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(y)\right\rvert \end{align} $$
 $$ \begin{align} &\le (2/3)\left\lvert\xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(x)- \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(y)\right\rvert \hspace{3.5pc} \end{align} $$
$$ \begin{align} &\le (2/3)\left\lvert\xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(x)- \xi_{j(2)}\circ \dotsb \circ \xi_{j(n)}(y)\right\rvert \hspace{3.5pc} \end{align} $$
One already observes that
![]() $\cup _{j\in S}\xi _j([0,1])=[0,1]$
if
$\cup _{j\in S}\xi _j([0,1])=[0,1]$
if
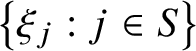 $\left \{\xi _j: j\in S\right \}$
is a full collection. An induction shows that if
$\left \{\xi _j: j\in S\right \}$
is a full collection. An induction shows that if
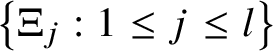 $\left \{\Xi _j: 1\le j\le l\right \}$
is a full collection, then
$\left \{\Xi _j: 1\le j\le l\right \}$
is a full collection, then
 $$ \begin{align*} \cup_{j=1}^l \Xi_j([0,1])=[0,1]. \end{align*} $$
$$ \begin{align*} \cup_{j=1}^l \Xi_j([0,1])=[0,1]. \end{align*} $$
To show the last statement, fix
![]() $t\in [0,1]$
. Set
$t\in [0,1]$
. Set
![]() $x\in [0,1]$
. Then for some
$x\in [0,1]$
. Then for some
![]() $y\in [0,1]$
and
$y\in [0,1]$
and
![]() $j\in \{1,2,\dotsc ,l\}$
,
$j\in \{1,2,\dotsc ,l\}$
,
Now, by the first part of the statement, for any
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
 $$ \begin{align*} \left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert \le (2/3)^n. \end{align*} $$
$$ \begin{align*} \left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert \le (2/3)^n. \end{align*} $$
It follows that
 $$ \begin{align*} \left\lvert\Xi_j(t)-x\right\rvert=\left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert \le (2/3)^n. \\[-38pt] \end{align*} $$
$$ \begin{align*} \left\lvert\Xi_j(t)-x\right\rvert=\left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert \le (2/3)^n. \\[-38pt] \end{align*} $$
Theorem 7.3. The inductive limit A defined in Definition 6.9 can be made into a unital simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_z^C$
such that
$A_z^C$
such that
 $$ \begin{align} \left(K_0(A_z), K_0(A_z)_+, \left[1_{A_z}\right], K_1(A_z)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
$$ \begin{align} \left(K_0(A_z), K_0(A_z)_+, \left[1_{A_z}\right], K_1(A_z)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
If C is not exact, then
![]() $A_z^C$
is not exact.
$A_z^C$
is not exact.
Proof. For convenience, one makes an additional requirement in the construction. Let
![]() ${\cal F}_{m,1}\subset {\cal F}_{m,2},\dotsc ,{\cal F}_{m,n},\dotsc $
be an increasing sequence of finite subsets of
${\cal F}_{m,1}\subset {\cal F}_{m,2},\dotsc ,{\cal F}_{m,n},\dotsc $
be an increasing sequence of finite subsets of
![]() $A_m$
such that
$A_m$
such that
![]() $\cup _n {\cal F}_{m,n}$
is dense in
$\cup _n {\cal F}_{m,n}$
is dense in
![]() $A_m$
.
$A_m$
.
One requires
![]() $\varphi _m\left ({\cal F}_{m,m+1} \right )\subset {\cal F}_{m+1,1}$
and
$\varphi _m\left ({\cal F}_{m,m+1} \right )\subset {\cal F}_{m+1,1}$
and
![]() $\varphi _m\left ({\cal F}_{m, m+n}\right )\subset {\cal F}_{m+1,n}$
,
$\varphi _m\left ({\cal F}_{m, m+n}\right )\subset {\cal F}_{m+1,n}$
,
![]() $m, n=1,2,\dotsc $
.
$m, n=1,2,\dotsc $
.
This is done inductively as follows: Choose any increasing sequence of finite subsets
![]() ${\cal F}_{1,1}\subset {\cal F}_{1,2},\dotsc , \subset A_1$
such that
${\cal F}_{1,1}\subset {\cal F}_{1,2},\dotsc , \subset A_1$
such that
![]() $\cup _n {\cal F}_{1,n}$
is dense in
$\cup _n {\cal F}_{1,n}$
is dense in
![]() $A_1$
. Specify
$A_1$
. Specify
![]() ${\cal F}_1={\cal F}_{1,1}\setminus \{0\}$
. Choose
${\cal F}_1={\cal F}_{1,1}\setminus \{0\}$
. Choose
![]() $A_2$
and define
$A_2$
and define
![]() $\varphi _1: A_1\to A_2$
as in the construction of Lemma 6.8.
$\varphi _1: A_1\to A_2$
as in the construction of Lemma 6.8.
Choose an increasing sequence of finite subsets
![]() ${\cal F}_{2,1}, {\cal F}_{2,2},\dotsc $
of
${\cal F}_{2,1}, {\cal F}_{2,2},\dotsc $
of
![]() $A_2$
such that
$A_2$
such that
![]() $\varphi _1\left ({\cal F}_{1,n}\right )\subset {\cal F}_{2,n}$
(
$\varphi _1\left ({\cal F}_{1,n}\right )\subset {\cal F}_{2,n}$
(
![]() $n=1,2,\dotsc $
) such that
$n=1,2,\dotsc $
) such that
![]() $\cup _n{\cal F}_{2,n}$
is dense in
$\cup _n{\cal F}_{2,n}$
is dense in
![]() $A_2$
. Specify
$A_2$
. Specify
![]() ${\cal F}_2={\cal F}_{2,1}\setminus \{0\}$
.
${\cal F}_2={\cal F}_{2,1}\setminus \{0\}$
.
Once
![]() ${\cal F}_{m,1},{\cal F}_{m,2},\dotsc $
are determined, specify
${\cal F}_{m,1},{\cal F}_{m,2},\dotsc $
are determined, specify
![]() ${\cal F}_m={\cal F}_{m,1}\setminus \{0\}$
. Then construct
${\cal F}_m={\cal F}_{m,1}\setminus \{0\}$
. Then construct
![]() $A_{m+1}$
and
$A_{m+1}$
and
![]() $\varphi _m: A_m\to A_{m+1}$
as in Lemma 6.8. Choose
$\varphi _m: A_m\to A_{m+1}$
as in Lemma 6.8. Choose
![]() ${\cal F}_{m+1,1}, {\cal F}_{m+1,2},\dotsc $
so that
${\cal F}_{m+1,1}, {\cal F}_{m+1,2},\dotsc $
so that
![]() $\varphi _m\left ({\cal F}_{m,m+1}\right )\subset {\cal F}_{m+1,1}$
and
$\varphi _m\left ({\cal F}_{m,m+1}\right )\subset {\cal F}_{m+1,1}$
and
![]() $\varphi _m\left ({\cal F}_{m,m+n}\right )\subset {\cal F}_{m+1,n}$
, as well as
$\varphi _m\left ({\cal F}_{m,m+n}\right )\subset {\cal F}_{m+1,n}$
, as well as
![]() ${\cal F}_{m+1,n}\subset {\cal F}_{m+1,n+1}$
. Moreover,
${\cal F}_{m+1,n}\subset {\cal F}_{m+1,n+1}$
. Moreover,
![]() $\cup _n {\cal F}_{m+1,n}$
is dense in
$\cup _n {\cal F}_{m+1,n}$
is dense in
![]() $A_{m+1}$
. Choose
$A_{m+1}$
. Choose
![]() ${\cal F}_{m+1}={\cal F}_{m+1,1}\setminus \{0\}$
. Thus the requirement can be made.
${\cal F}_{m+1}={\cal F}_{m+1,1}\setminus \{0\}$
. Thus the requirement can be made.
Let us now prove that A is simple. For this, we will prove the following claim:
Claim: For any fixed i, and
![]() $g\in A_i\backslash \{0\}$
, there exists
$g\in A_i\backslash \{0\}$
, there exists
![]() $n>i$
such that
$n>i$
such that
![]() $\varphi _{i,n}(g)$
is full in
$\varphi _{i,n}(g)$
is full in
![]() $A_n$
. Without loss of generality, we may assume that
$A_n$
. Without loss of generality, we may assume that
![]() $\lVert g\rVert =1$
. There are j and
$\lVert g\rVert =1$
. There are j and
![]() $f\in {\cal F}_{i,j}$
such that
$f\in {\cal F}_{i,j}$
such that
![]() $\lVert f-g\rVert <1/64$
.
$\lVert f-g\rVert <1/64$
.
To simplify notation, without loss of generality we may write
![]() $i=1$
. Set
$i=1$
. Set
![]() $\varphi _{j,j'}=\varphi _{j'-1}\circ \dotsb \circ \varphi _j$
for
$\varphi _{j,j'}=\varphi _{j'-1}\circ \dotsb \circ \varphi _j$
for
![]() $j'>j$
. Then
$j'>j$
. Then
![]() $\varphi _{1, j'}(f) \in \varphi _{j'}\left ({\cal F}_{j'-1, j'}\right )\subset {\cal F}_{j', 1}$
. Recall also that each
$\varphi _{1, j'}(f) \in \varphi _{j'}\left ({\cal F}_{j'-1, j'}\right )\subset {\cal F}_{j', 1}$
. Recall also that each
![]() $\varphi _j$
is unital and injective. To further simplify the notation, without loss of generality we may write
$\varphi _j$
is unital and injective. To further simplify the notation, without loss of generality we may write
![]() ${\cal F}_{i,j}\setminus \{0\}={\cal F}_m={\cal F}_{m,1}\setminus \{0\}$
. We assume that
${\cal F}_{i,j}\setminus \{0\}={\cal F}_m={\cal F}_{m,1}\setminus \{0\}$
. We assume that
![]() $m>128$
. By construction, for some
$m>128$
. By construction, for some
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
By continuity, there is
![]() $n(m)\ge 1$
such that for any
$n(m)\ge 1$
such that for any
![]() $(2/3)^{n(m)-1}$
-dense set S of
$(2/3)^{n(m)-1}$
-dense set S of
![]() $[0,1]$
,
$[0,1]$
,
For any
![]() $f\in C\!\left([0,1], M_{p_mq_m}(B)\right )$
and i, denote
$f\in C\!\left([0,1], M_{p_mq_m}(B)\right )$
and i, denote
![]() $h(t)=\gamma _m(f\circ \xi _i(t)){\otimes 1_5}$
(for
$h(t)=\gamma _m(f\circ \xi _i(t)){\otimes 1_5}$
(for
![]() $t\in [0,1]$
). Then, for any
$t\in [0,1]$
). Then, for any
![]() $k>m$
and j (
$k>m$
and j (
![]() $t\in [0,1]$
),
$t\in [0,1]$
),
where
![]() $R(k)$
is the rank of
$R(k)$
is the rank of
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\xi _i$
and
$\xi _i$
and
![]() $\xi _j$
are as defined in Lemma 6.8(1). Denote
$\xi _j$
are as defined in Lemma 6.8(1). Denote
Therefore, from Lemma 6.8 and formula (e6.16) (also keep in mind Remark 6.10), we may write, for each
![]() $f\in A_m=E_{p_m,q_m}$
,
$f\in A_m=E_{p_m,q_m}$
,
 $$ \begin{align} \varphi_{m, m+2}(f) =w_1^*\begin{pmatrix} H_0(f) &&& 0\\ &\bar\gamma_m\left(f\circ \xi^{(2)}_1\right)\otimes 1_{R(m+1)}&&\\ &&\ddots &\\ 0&&& \bar\gamma_m\left(f\circ \xi^{(2)}_{l(m+1)}\right)\otimes 1_{R(m+1)}\end{pmatrix} w_1, \end{align} $$
$$ \begin{align} \varphi_{m, m+2}(f) =w_1^*\begin{pmatrix} H_0(f) &&& 0\\ &\bar\gamma_m\left(f\circ \xi^{(2)}_1\right)\otimes 1_{R(m+1)}&&\\ &&\ddots &\\ 0&&& \bar\gamma_m\left(f\circ \xi^{(2)}_{l(m+1)}\right)\otimes 1_{R(m+1)}\end{pmatrix} w_1, \end{align} $$
where
![]() $H_0: A_m\to C\!\left([0,1], M_{L_0p_mq_m}\right )$
is a homomorphism (for some integer
$H_0: A_m\to C\!\left([0,1], M_{L_0p_mq_m}\right )$
is a homomorphism (for some integer
![]() $L_0\geq 1$
),
$L_0\geq 1$
),
![]() $w_1\in C\!\left([0,1], M_{p_{m+2}q_{m+2}}\right )$
is a unitary,
$w_1\in C\!\left([0,1], M_{p_{m+2}q_{m+2}}\right )$
is a unitary,
![]() $R(m+1)$
is the rank of
$R(m+1)$
is the rank of
![]() $\bar \gamma _{m+1}$
and
$\bar \gamma _{m+1}$
and
 $\left \{\xi ^{(2)}_j: 1\le j\le l(m+1)\right \}$
is a full collection of compositions of two
$\left \{\xi ^{(2)}_j: 1\le j\le l(m+1)\right \}$
is a full collection of compositions of two
![]() $\xi _i$
s (maps in Lemma 6.8(1)).
$\xi _i$
s (maps in Lemma 6.8(1)).
Therefore, by induction, for any
![]() $n>n(m)+m$
one may write, from the construction of Lemma 6.8 (see equation (e6.16)), for all
$n>n(m)+m$
one may write, from the construction of Lemma 6.8 (see equation (e6.16)), for all
![]() $f\in A_m=E_{p_m,q_m}$
,
$f\in A_m=E_{p_m,q_m}$
,
 $$ \begin{align} \varphi_{m,n}(f)= w^*\begin{pmatrix} H(f) &&&0 \\ & \bar\gamma_m(f\circ \Xi_1)\otimes 1_{R\left(n,1\right)} &&\\ &&\ddots &\\ 0&&& \bar\gamma_m(f\circ \Xi_l)\otimes 1_{R\left(n,l\right)}\end{pmatrix} w, \end{align} $$
$$ \begin{align} \varphi_{m,n}(f)= w^*\begin{pmatrix} H(f) &&&0 \\ & \bar\gamma_m(f\circ \Xi_1)\otimes 1_{R\left(n,1\right)} &&\\ &&\ddots &\\ 0&&& \bar\gamma_m(f\circ \Xi_l)\otimes 1_{R\left(n,l\right)}\end{pmatrix} w, \end{align} $$
where
![]() $H: A_m\to C\!\left([0,1], M_{Lp_mq_m}(B)\right )$
is a homomorphism (for some integer
$H: A_m\to C\!\left([0,1], M_{Lp_mq_m}(B)\right )$
is a homomorphism (for some integer
![]() $L\ge 1$
),
$L\ge 1$
),
![]() $\Xi _j$
is a composition of
$\Xi _j$
is a composition of
![]() $n-m$
maps in Lemma 6.8(1) such that the collection
$n-m$
maps in Lemma 6.8(1) such that the collection
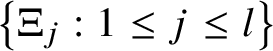 $\left \{\Xi _j: 1\le j\le l\right \}$
is full,
$\left \{\Xi _j: 1\le j\le l\right \}$
is full,
![]() $R(n,j)\ge 1$
is an integer,
$R(n,j)\ge 1$
is an integer,
![]() $j=1,2,\dotsc ,l$
, and
$j=1,2,\dotsc ,l$
, and
![]() $w\in C\!\left([0,1], M_{p_nq_n}\right )$
is a unitary.
$w\in C\!\left([0,1], M_{p_nq_n}\right )$
is a unitary.
It follows from Lemma 7.2 that
 $$ \begin{align} \lvert\Xi_i(x)-\Xi_i(y)\rvert<(2/3)^{m-n}\mathrm{\ for\ all\ } x, y\in [0,1],\quad 1\le i\le l,\qquad\text{and}\qquad \cup_i^l \Xi_i([0,1])=[0,1]. \end{align} $$
$$ \begin{align} \lvert\Xi_i(x)-\Xi_i(y)\rvert<(2/3)^{m-n}\mathrm{\ for\ all\ } x, y\in [0,1],\quad 1\le i\le l,\qquad\text{and}\qquad \cup_i^l \Xi_i([0,1])=[0,1]. \end{align} $$
Fix any
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $x\in [0,1]$
; by Lemma 7.2, there are
$x\in [0,1]$
; by Lemma 7.2, there are
![]() $y\in [0,1]$
and
$y\in [0,1]$
and
![]() $j\in \{1,2,\dotsc ,l\}$
such that
$j\in \{1,2,\dotsc ,l\}$
such that
![]() $\Xi _j(y)=x$
. Then
$\Xi _j(y)=x$
. Then
 $$ \begin{align} \left\lvert\Xi_j(t)-x\right\rvert=\left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert<(2/3)^{n-m}<(2/3)^{n(m)}. \end{align} $$
$$ \begin{align} \left\lvert\Xi_j(t)-x\right\rvert=\left\lvert\Xi_j(t)-\Xi_j(y)\right\rvert<(2/3)^{n-m}<(2/3)^{n(m)}. \end{align} $$
It follows from the choice of
![]() $n(m)$
and formula (e7.8) that, for
$n(m)$
and formula (e7.8) that, for
![]() $f\in {\cal F}_m$
,
$f\in {\cal F}_m$
,
 $$ \begin{align} \left\lVert\gamma_m\left(f\circ \Xi_j(t)\right)\right\rVert\ge (1-1/m)\lVert f\rVert\ge \left(\frac{63}{64}\right)^2 \mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
$$ \begin{align} \left\lVert\gamma_m\left(f\circ \Xi_j(t)\right)\right\rVert\ge (1-1/m)\lVert f\rVert\ge \left(\frac{63}{64}\right)^2 \mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
Since
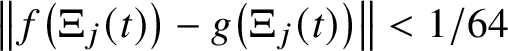 $\left \lVert f\left (\Xi _j(t)\right )-g\left (\Xi _j(t)\right )\right \rVert <1/64$
, this implies that
$\left \lVert f\left (\Xi _j(t)\right )-g\left (\Xi _j(t)\right )\right \rVert <1/64$
, this implies that
 $$ \begin{align} \left\lVert\gamma_m\left(g\left(\Xi_j(t)\right)\right)\right\rVert\ge \frac{63^2-64}{64^2}\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
$$ \begin{align} \left\lVert\gamma_m\left(g\left(\Xi_j(t)\right)\right)\right\rVert\ge \frac{63^2-64}{64^2}\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
Since for each
![]() $t\in [0,1]$
, we have
$t\in [0,1]$
, we have
![]() $\gamma _m(g\circ \Xi _i(t))\in M_{p_mq_m}$
,
$\gamma _m(g\circ \Xi _i(t))\in M_{p_mq_m}$
,
![]() $i=1,2,\dotsc ,l$
, we know that
$i=1,2,\dotsc ,l$
, we know that
![]() $ \varphi _{m,n}(g)(t) $
is not in any closed ideal of
$ \varphi _{m,n}(g)(t) $
is not in any closed ideal of
![]() $M_{p_nq_n}(B)$
for each
$M_{p_nq_n}(B)$
for each
![]() $t\in [0,1]$
. Therefore
$t\in [0,1]$
. Therefore
![]() $\varphi _{m,n}(g)$
is full in
$\varphi _{m,n}(g)$
is full in
![]() $E_{p_n,q_n}=A_n$
. This proves the claim.
$E_{p_n,q_n}=A_n$
. This proves the claim.
It follows from the claim that
![]() $A_z^C$
is simple. To see this, let
$A_z^C$
is simple. To see this, let
![]() $I\subset A_z^C$
be an ideal such that
$I\subset A_z^C$
be an ideal such that
![]() $I\not =A_z^C$
and put
$I\not =A_z^C$
and put
![]() $C_n=\varphi _{n, \infty }(A_n)$
. Then
$C_n=\varphi _{n, \infty }(A_n)$
. Then
![]() $C_n\subset C_{n+1}$
for all n. Set
$C_n\subset C_{n+1}$
for all n. Set
![]() $a\in C_m\setminus \{0\}$
. By the claim, there is
$a\in C_m\setminus \{0\}$
. By the claim, there is
![]() $n'>m$
such that a is full in
$n'>m$
such that a is full in
![]() $C_{n'}$
, and therefore a is full in every
$C_{n'}$
, and therefore a is full in every
![]() $C_n$
for
$C_n$
for
![]() $n\ge n'$
. In other words,
$n\ge n'$
. In other words,
![]() $a\not \in C_n\cap I$
for all n. It follows that
$a\not \in C_n\cap I$
for all n. It follows that
![]() $C_m\cap I=\{0\}$
, as
$C_m\cap I=\{0\}$
, as
![]() $C_m\subset C_n$
for all
$C_m\subset C_n$
for all
![]() $n\ge m$
. It is then standard to show that
$n\ge m$
. It is then standard to show that
![]() $I=\{0\}$
. Thus
$I=\{0\}$
. Thus
![]() $A_z^C$
is simple.
$A_z^C$
is simple.
Since, by Lemma 6.5, we have for each m that
 $$ \begin{align*} \left(K_0(A_m), K_0(A_m)_+, \left[1_{A_m}\right], K_1(A_m)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}), \end{align*} $$
$$ \begin{align*} \left(K_0(A_m), K_0(A_m)_+, \left[1_{A_m}\right], K_1(A_m)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}), \end{align*} $$
one concludes (as each
![]() $\varphi _n$
is unital) that
$\varphi _n$
is unital) that
 $$ \begin{align} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
$$ \begin{align} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
Finally, if C is not exact, then B is not exact, since B has quotients of the form
![]() $\mathbb {C}\oplus C$
, which is not exact.
$\mathbb {C}\oplus C$
, which is not exact.
Define
![]() $\Phi : B\to C([0,1], M_{15}(B))$
by
$\Phi : B\to C([0,1], M_{15}(B))$
by
where
![]() $\theta _t: B\to B$
is defined in formula (e6.14). Note that for
$\theta _t: B\to B$
is defined in formula (e6.14). Note that for
![]() $f\in B$
,
$f\in B$
,
One then obtains a unitary
![]() $u\in C([0,1], M_{15})$
such that
$u\in C([0,1], M_{15})$
such that
Define
![]() $\Psi (f):= u^*\Phi (f)u$
for all
$\Psi (f):= u^*\Phi (f)u$
for all
![]() $f\in B$
. Then
$f\in B$
. Then
![]() $\Psi $
is a unital injective homomorphism. In other words, B is embedded unitally into
$\Psi $
is a unital injective homomorphism. In other words, B is embedded unitally into
![]() $A_1=E_{3,5}$
. Since each
$A_1=E_{3,5}$
. Since each
![]() $\varphi _m: A_m\to A_{m+1}$
is unital and injective, B is embedded into
$\varphi _m: A_m\to A_{m+1}$
is unital and injective, B is embedded into
![]() $A_z^C$
. Since B is not exact, neither is
$A_z^C$
. Since B is not exact, neither is
![]() $A_z^C$
(see, for example, [Reference Wassermann47, Proposition 2.6]).
$A_z^C$
(see, for example, [Reference Wassermann47, Proposition 2.6]).
Proposition 7.4. If C is exact but not nuclear, then
![]() $A_z^C$
is exact and not nuclear.
$A_z^C$
is exact and not nuclear.
Proof. Note that since C is nonnuclear and exact, so is B. Note also that
![]() $A_n=E_{p_n,q_n}$
is a
$A_n=E_{p_n,q_n}$
is a
![]() $C^*$
-subalgebra of the exact
$C^*$
-subalgebra of the exact
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C\!\left([0,1], M_{p_nq_n}(B)\right )$
. So each
$C\!\left([0,1], M_{p_nq_n}(B)\right )$
. So each
![]() $A_n$
is exact. By [Reference Wassermann47, 2.5.5],
$A_n$
is exact. By [Reference Wassermann47, 2.5.5],
![]() $A_z^C$
is exact.
$A_z^C$
is exact.
Let
![]() $\Phi : B\to A_1=E_{3,5}$
be as in the end of the proof of Theorem 7.3. Let
$\Phi : B\to A_1=E_{3,5}$
be as in the end of the proof of Theorem 7.3. Let
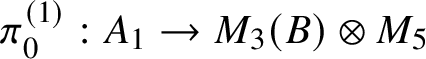 $\pi _0^{(1)}: A_1\to M_3(B)\otimes M_5$
be the evaluation at
$\pi _0^{(1)}: A_1\to M_3(B)\otimes M_5$
be the evaluation at
![]() $0$
, namely
$0$
, namely
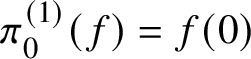 $\pi _0^{(1)}(f)=f(0)$
for all
$\pi _0^{(1)}(f)=f(0)$
for all
![]() $f\in A_1$
. Let
$f\in A_1$
. Let
![]() $\eta _1: M_3(B)\otimes \mathrm {1}_5\to B$
be given by defining
$\eta _1: M_3(B)\otimes \mathrm {1}_5\to B$
be given by defining
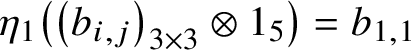 $\eta _1\left (\left (b_{i,j}\right )_{ 3\times 3}\otimes 1_5 \right )=b_{1,1}$
, where
$\eta _1\left (\left (b_{i,j}\right )_{ 3\times 3}\otimes 1_5 \right )=b_{1,1}$
, where
![]() $b_{i,j}\in B$
,
$b_{i,j}\in B$
,
![]() $1\le i,j\le 3$
. Then
$1\le i,j\le 3$
. Then
![]() $\eta _1$
is a norm
$\eta _1$
is a norm
![]() $1$
c.p.c. map. Define
$1$
c.p.c. map. Define
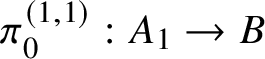 $\pi _0^{\left (1,1\right )}: A_1\to B$
by
$\pi _0^{\left (1,1\right )}: A_1\to B$
by
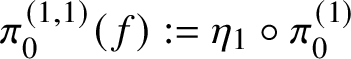 $\pi _0^{\left (1,1\right )}(f):= \eta _1\circ \pi _0^{(1)}$
. Note that
$\pi _0^{\left (1,1\right )}(f):= \eta _1\circ \pi _0^{(1)}$
. Note that
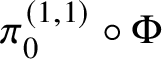 $\pi _0^{\left (1,1\right )}\circ \Phi $
is an isomorphism. In fact,
$\pi _0^{\left (1,1\right )}\circ \Phi $
is an isomorphism. In fact,
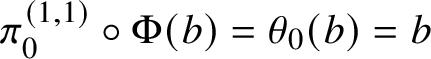 $\pi _0^{\left (1,1\right )}\circ \Phi (b)=\theta _0(b)=b$
(see equation (e7.19)) for all
$\pi _0^{\left (1,1\right )}\circ \Phi (b)=\theta _0(b)=b$
(see equation (e7.19)) for all
![]() $b\in B$
.
$b\in B$
.
The foregoing is illustrated in the following diagram:

We will use the same diagram in the n-stage.
In Lemma 6.8(4), let us denote
![]() $\xi _1$
such that
$\xi _1$
such that
![]() $\xi _1(t)=2t/3$
for
$\xi _1(t)=2t/3$
for
![]() $t\in [0,3/4]$
and
$t\in [0,3/4]$
and
![]() $\theta ^{(1)}(f(0))=f(0)$
for all
$\theta ^{(1)}(f(0))=f(0)$
for all
![]() $f\in E_{3,5}$
(note that we do not change the connecting map, but only for convenience in equation (e7.22)). So by formulas (e6.16), (e6.20), (e6.52) and (e6.53), we may write
$f\in E_{3,5}$
(note that we do not change the connecting map, but only for convenience in equation (e7.22)). So by formulas (e6.16), (e6.20), (e6.52) and (e6.53), we may write
 $$ \begin{align} \varphi_1(f) \left(=\varphi_{1,2}(f)\right) =u_1^* \mathrm{diag}\left(\theta^{\left(1,2\right)}(f), H_1'(f)\right)u_1\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
$$ \begin{align} \varphi_1(f) \left(=\varphi_{1,2}(f)\right) =u_1^* \mathrm{diag}\left(\theta^{\left(1,2\right)}(f), H_1'(f)\right)u_1\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
where
![]() $\theta ^{\left (1,2\right )}:=\theta ^{(1)'}: A_1\to C([0,1], M_{15}(B))$
and
$\theta ^{\left (1,2\right )}:=\theta ^{(1)'}: A_1\to C([0,1], M_{15}(B))$
and
![]() $\theta ^{\left (1,2\right )}(f)(0)=f(0)$
for
$\theta ^{\left (1,2\right )}(f)(0)=f(0)$
for
![]() $f\in A_1$
, and
$f\in A_1$
, and
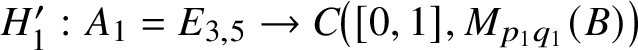 $H_1': A_1=E_{3,5}\to C\!\left([0,1], M_{p_1q_1}(B)\right )$
is a homomorphism. Note that the image of
$H_1': A_1=E_{3,5}\to C\!\left([0,1], M_{p_1q_1}(B)\right )$
is a homomorphism. Note that the image of
![]() $H_1'$
is in a corner of
$H_1'$
is in a corner of
![]() $C\!\left([0,1], M_{p_1q_1}(B)\right )$
, and
$C\!\left([0,1], M_{p_1q_1}(B)\right )$
, and
![]() $u_1\in U\left (C\!\left([0,1], M_{p_2q_2}\right )\right )$
. Similarly, again by formulas (e6.16), (e6.20), (e6.52) and (e6.53), we may also write
$u_1\in U\left (C\!\left([0,1], M_{p_2q_2}\right )\right )$
. Similarly, again by formulas (e6.16), (e6.20), (e6.52) and (e6.53), we may also write
 $$ \begin{align} \varphi_{1,3} (f)=u_2^*\mathrm{diag}\left(\theta^{\left(1,3 \right)}(f), H_2'(f)\right)u_2\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
$$ \begin{align} \varphi_{1,3} (f)=u_2^*\mathrm{diag}\left(\theta^{\left(1,3 \right)}(f), H_2'(f)\right)u_2\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
where
![]() $\theta ^{\left (1,3 \right )}(f)(0)=f(0)$
for
$\theta ^{\left (1,3 \right )}(f)(0)=f(0)$
for
![]() $f\in A_1$
,
$f\in A_1$
,
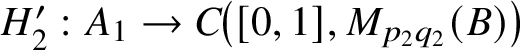 $H_2': A_1\to C\!\left([0,1], M_{p_2q_2}(B)\right )$
is a homomorphism and
$H_2': A_1\to C\!\left([0,1], M_{p_2q_2}(B)\right )$
is a homomorphism and
![]() $u_2\in U\left (C\!\left([0,1], M_{p_3q_3}\right )\right )$
. By induction, for any
$u_2\in U\left (C\!\left([0,1], M_{p_3q_3}\right )\right )$
. By induction, for any
![]() $n>1$
we may write
$n>1$
we may write
 $$ \begin{align} \varphi_{1,n}(f)=u_n^*\mathrm{diag}\left(\theta^{\left(1,n\right)}(f), H^{\prime}_n(f)\right)u_n\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
$$ \begin{align} \varphi_{1,n}(f)=u_n^*\mathrm{diag}\left(\theta^{\left(1,n\right)}(f), H^{\prime}_n(f)\right)u_n\mathrm{\ for\ all\ } f\in A_1, \end{align} $$
where
![]() $\theta ^{\left (1,n\right )}(f)(0)=f(0)$
,
$\theta ^{\left (1,n\right )}(f)(0)=f(0)$
,
![]() $H^{\prime }_n: A_1\to C\!\left([0,1], M_{p_nq_n}(B)\right )$
is a homomorphism and
$H^{\prime }_n: A_1\to C\!\left([0,1], M_{p_nq_n}(B)\right )$
is a homomorphism and
![]() $u_n\in C\!\left([0,1], M_{p_{n+1}q_{n+1}}\right )$
. (One should be warned that
$u_n\in C\!\left([0,1], M_{p_{n+1}q_{n+1}}\right )$
. (One should be warned that
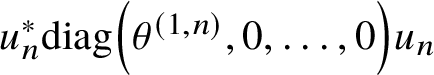 $u_n^*\mathrm {diag}\left (\theta ^{\left (1,n\right )},0,\dotsc ,0\right )u_n$
is not in
$u_n^*\mathrm {diag}\left (\theta ^{\left (1,n\right )},0,\dotsc ,0\right )u_n$
is not in
![]() $A_n$
.)
$A_n$
.)
Now we prove that
![]() $A_z^C$
is not nuclear. We follow the proof of [Reference Dădărlat13, Proposition 6]. Assume otherwise: For any finite subset
$A_z^C$
is not nuclear. We follow the proof of [Reference Dădărlat13, Proposition 6]. Assume otherwise: For any finite subset
![]() ${\cal F}\subset B$
and
${\cal F}\subset B$
and
![]() $\varepsilon>0$
, if
$\varepsilon>0$
, if
![]() $A_z^C$
were nuclear, then
$A_z^C$
were nuclear, then
![]() $\varphi _{1, \infty }\circ \Phi $
would be nuclear. Therefore there would be a finite-dimensional
$\varphi _{1, \infty }\circ \Phi $
would be nuclear. Therefore there would be a finite-dimensional
![]() $C^*$
-algebra D and c.p.c. maps
$C^*$
-algebra D and c.p.c. maps
![]() ${\alpha }: B\to D$
and
${\alpha }: B\to D$
and
![]() ${\beta }: D\to A_z^C$
such that
${\beta }: D\to A_z^C$
such that
 $$ \begin{align} \left\lVert\varphi_{1,\infty}\circ \Phi(b)-{\beta}\circ {\alpha}(b)\right\rVert<\varepsilon/2\mathrm{\ for\ all\ } b\in {\cal F}. \end{align} $$
$$ \begin{align} \left\lVert\varphi_{1,\infty}\circ \Phi(b)-{\beta}\circ {\alpha}(b)\right\rVert<\varepsilon/2\mathrm{\ for\ all\ } b\in {\cal F}. \end{align} $$
Since
![]() $A_z^C$
is assumed to be nuclear, by the Effros–Choi lifting theorem [Reference Choi and Effros11], there exist an integer
$A_z^C$
is assumed to be nuclear, by the Effros–Choi lifting theorem [Reference Choi and Effros11], there exist an integer
![]() $n\ge 1$
and a unital c.p.c. map
$n\ge 1$
and a unital c.p.c. map
![]() ${\beta }_n: D\to A_n$
such that
${\beta }_n: D\to A_n$
such that
 $$ \begin{align} \left\lVert{\beta}(x)-\varphi_{n, \infty}\circ {\beta}_n(x)\right\rVert<\varepsilon/2\mathrm{\ for\ all\ } x\in {\alpha}({\cal F}). \end{align} $$
$$ \begin{align} \left\lVert{\beta}(x)-\varphi_{n, \infty}\circ {\beta}_n(x)\right\rVert<\varepsilon/2\mathrm{\ for\ all\ } x\in {\alpha}({\cal F}). \end{align} $$
Thus
 $$ \begin{align} \left\lVert\varphi_{n, \infty}\left(\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right)\right\rVert<\varepsilon. \end{align} $$
$$ \begin{align} \left\lVert\varphi_{n, \infty}\left(\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right)\right\rVert<\varepsilon. \end{align} $$
As
![]() $\varphi _{n,\infty }$
is an isometry, this implies that
$\varphi _{n,\infty }$
is an isometry, this implies that
 $$ \begin{align} \left\lVert\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right\rVert<\varepsilon\mathrm{\ for\ all\ } b\in B. \end{align} $$
$$ \begin{align} \left\lVert\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right\rVert<\varepsilon\mathrm{\ for\ all\ } b\in B. \end{align} $$
Let
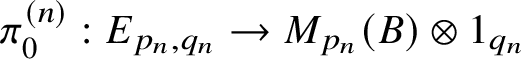 $\pi _0^{(n)}: E_{p_n,q_n}\to M_{p_n}(B)\otimes 1_{q_n}$
be the evaluation at
$\pi _0^{(n)}: E_{p_n,q_n}\to M_{p_n}(B)\otimes 1_{q_n}$
be the evaluation at
![]() $0$
defined by
$0$
defined by
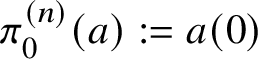 $\pi _0^{(n)}(a):= a(0)$
. We have, by equation (e7.24),
$\pi _0^{(n)}(a):= a(0)$
. We have, by equation (e7.24),
 $$ \begin{align} \pi_0^{(n)}\left(\varphi_{1,n}\circ \Phi(b)\right)=\mathrm{diag}\left(\theta_0(b) \otimes 1_{15}, H_n'(\Phi(f))(0)\right)\mathrm{\ for\ all\ } b\in B. \end{align} $$
$$ \begin{align} \pi_0^{(n)}\left(\varphi_{1,n}\circ \Phi(b)\right)=\mathrm{diag}\left(\theta_0(b) \otimes 1_{15}, H_n'(\Phi(f))(0)\right)\mathrm{\ for\ all\ } b\in B. \end{align} $$
Recall that
![]() $\theta _0(b)=b$
. Now a rank one projection p corresponding the first
$\theta _0(b)=b$
. Now a rank one projection p corresponding the first
![]() $(1,1)$
corner is in
$(1,1)$
corner is in
![]() $M_{p_n}(B)\otimes 1_{q_n}$
. Put
$M_{p_n}(B)\otimes 1_{q_n}$
. Put
![]() $q=u_n(0)^*pu_n(0)$
. We now use the n-stage diagram (e7.21). Let
$q=u_n(0)^*pu_n(0)$
. We now use the n-stage diagram (e7.21). Let
![]() $\eta _n: M_{p_n}(B)\otimes 1_{q_n}\to B$
be defined by
$\eta _n: M_{p_n}(B)\otimes 1_{q_n}\to B$
be defined by
![]() $\eta _n(x):= u_n(0)qxqu_n(0)^*$
for all
$\eta _n(x):= u_n(0)qxqu_n(0)^*$
for all
![]() $x\in M_{p_n}(B)\otimes 1_{q_n}$
which is a unital c.p.c. map
$x\in M_{p_n}(B)\otimes 1_{q_n}$
which is a unital c.p.c. map
 $\eta _n\left (u_n(0)^*\left (\left (b_{i,j}\right )_{p_n\times p_n}\otimes 1_{q_n}\right )u_n(0)\right )=b_{1,1}$
. Note that
$\eta _n\left (u_n(0)^*\left (\left (b_{i,j}\right )_{p_n\times p_n}\otimes 1_{q_n}\right )u_n(0)\right )=b_{1,1}$
. Note that
 $\eta _n\circ \pi _0^{(n)}\circ \varphi _{1,n}\circ \Phi =\mathrm {id}_B$
. By formula (e7.28),
$\eta _n\circ \pi _0^{(n)}\circ \varphi _{1,n}\circ \Phi =\mathrm {id}_B$
. By formula (e7.28),
 $$ \begin{align} \left\lVert b-\eta_n\circ \pi_0^{(n)}\circ {\beta}_n\circ {\alpha}(b)\right\rVert=\left\lVert\eta_n\circ \pi_0^{(n)}\left(\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right)\right\rVert<\varepsilon\mathrm{\ for\ all\ } b\in B. \end{align} $$
$$ \begin{align} \left\lVert b-\eta_n\circ \pi_0^{(n)}\circ {\beta}_n\circ {\alpha}(b)\right\rVert=\left\lVert\eta_n\circ \pi_0^{(n)}\left(\varphi_{1,n}\circ \Phi(b)-{\beta}_n\circ {\alpha}(b)\right)\right\rVert<\varepsilon\mathrm{\ for\ all\ } b\in B. \end{align} $$
This would imply that B is nuclear. Therefore
![]() $A_z^C$
is not nuclear. The foregoing could be illustrated by the following diagram, which is only approximately commutative below the top triangle:
$A_z^C$
is not nuclear. The foregoing could be illustrated by the following diagram, which is only approximately commutative below the top triangle:

Theorem 7.5. The inductive limit
![]() $A_z^C$
in Theorem 7.3 has a unique tracial state.
$A_z^C$
in Theorem 7.3 has a unique tracial state.
Proof. First we note each unital
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_m=E_{p_m, q_m}$
has at least one tracial state, say
$A_m=E_{p_m, q_m}$
has at least one tracial state, say
![]() $\tau _m$
. Note that
$\tau _m$
. Note that
![]() $\varphi _{m, \infty }$
is an injective homomorphism. So we may view
$\varphi _{m, \infty }$
is an injective homomorphism. So we may view
![]() $\tau _m$
as a tracial state of
$\tau _m$
as a tracial state of
![]() $\varphi _{m, \infty }(A_m)$
. Extend
$\varphi _{m, \infty }(A_m)$
. Extend
![]() $\tau _m$
to a state
$\tau _m$
to a state
![]() $t_m$
on
$t_m$
on
![]() $A_z^C$
. Choose a weak*-limit of
$A_z^C$
. Choose a weak*-limit of
![]() $\{t_m\}$
, say t. Then t is a state of the unital
$\{t_m\}$
, say t. Then t is a state of the unital
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_z^C$
. Note that
$A_z^C$
. Note that
![]() $\varphi _{m, \infty }(A_m)\subset \varphi _{n, \infty }(A_n)$
if
$\varphi _{m, \infty }(A_m)\subset \varphi _{n, \infty }(A_n)$
if
![]() $n>m$
. Then for each pair
$n>m$
. Then for each pair
![]() $x, y\in \varphi _{m,\infty }(A_m)$
, and for any
$x, y\in \varphi _{m,\infty }(A_m)$
, and for any
![]() $n>m$
,
$n>m$
,
![]() $t_n(xy)=t_n(yx)$
. It follows that t is a tracial state of
$t_n(xy)=t_n(yx)$
. It follows that t is a tracial state of
![]() $A_z^C$
. In other words,
$A_z^C$
. In other words,
![]() $A_z^C$
has at least one tracial state.
$A_z^C$
has at least one tracial state.
Claim: For each k, each
![]() $a\in A_k$
with
$a\in A_k$
with
![]() $\lVert a\rVert \le 1$
and each
$\lVert a\rVert \le 1$
and each
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $N>k$
such that, for all
$N>k$
such that, for all
![]() $n\ge N$
,
$n\ge N$
,
 $$ \begin{align} \left\lvert\tau_1\left(\varphi_{k, n}(a)\right)-\tau_2\left(\varphi_{k,n}(a)\right)\right\rvert<\varepsilon\mathrm{\ for\ all\ } \tau_1, \tau_2\in T(A_n). \end{align} $$
$$ \begin{align} \left\lvert\tau_1\left(\varphi_{k, n}(a)\right)-\tau_2\left(\varphi_{k,n}(a)\right)\right\rvert<\varepsilon\mathrm{\ for\ all\ } \tau_1, \tau_2\in T(A_n). \end{align} $$
Fix
![]() $a\in A_k$
. To simplify the notation, without loss of generality we may assume that
$a\in A_k$
. To simplify the notation, without loss of generality we may assume that
![]() $k=1$
.
$k=1$
.
Choose
![]() $m>1$
such that
$m>1$
such that
Put
![]() $g=\varphi _{1,m}(a)$
. There is
$g=\varphi _{1,m}(a)$
. There is
![]() $\delta>0$
such that
$\delta>0$
such that
Recall that here we view
![]() $\gamma _m$
as a map from
$\gamma _m$
as a map from
![]() $M_{p_mq_m}(B)$
to
$M_{p_mq_m}(B)$
to
![]() $M_{R(m)p_mq_m}$
. Note that for each
$M_{R(m)p_mq_m}$
. Note that for each
![]() $f\in A_m$
, since
$f\in A_m$
, since
![]() $\gamma _m(f(t))$
is a scalar matrix for all
$\gamma _m(f(t))$
is a scalar matrix for all
![]() $t\in [0,1]$
, we have that
$t\in [0,1]$
, we have that
![]() $\gamma _m(f(t))(x)$
, as an element in
$\gamma _m(f(t))(x)$
, as an element in
![]() $M_{R(m)p_mq_m}(B)$
, is a constant matrix (for
$M_{R(m)p_mq_m}(B)$
, is a constant matrix (for
![]() $x\in (0,1]$
) in
$x\in (0,1]$
) in
![]() $M_{R(m)p_mq_m}( C_0( (0,1], C)^{\sim })$
. Hence (see equation (e7.10) for
$M_{R(m)p_mq_m}( C_0( (0,1], C)^{\sim })$
. Hence (see equation (e7.10) for
![]() $\bar \gamma _m$
), for
$\bar \gamma _m$
), for
![]() $t\in [3/4,1]$
– recalling that
$t\in [3/4,1]$
– recalling that
![]() $\xi _i(t)=\xi _i(3/4)$
for all t in
$\xi _i(t)=\xi _i(3/4)$
for all t in
![]() $[3/4,1]$
–
$[3/4,1]$
–
(Recall the definition of
![]() $\theta _t$
in formula (e6.21)). Therefore (see the definition of
$\theta _t$
in formula (e6.21)). Therefore (see the definition of
![]() $\theta ^{(i)}$
in formula (e6.52)), for any i with
$\theta ^{(i)}$
in formula (e6.52)), for any i with
![]() $\xi _i(3/4)\not =1$
,
$\xi _i(3/4)\not =1$
,
 $$ \begin{align} \theta^{(i)}\left(\bar\gamma_m\left(f\circ\Xi_j\right)\right)(t)&= \begin{cases} \bar\gamma_m\left(f\circ \Xi_j\circ \xi_i\right)(t) &\text{if } t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}\left(\bar\gamma_m\left(f\circ\Xi_j\circ \xi_i\right)(3/4)\right) &\text{if } t\in (3/4,1] \end{cases} \end{align} $$
$$ \begin{align} \theta^{(i)}\left(\bar\gamma_m\left(f\circ\Xi_j\right)\right)(t)&= \begin{cases} \bar\gamma_m\left(f\circ \Xi_j\circ \xi_i\right)(t) &\text{if } t\in [0,3/4],\\ \theta_{4\left(t-3/4\right)}\left(\bar\gamma_m\left(f\circ\Xi_j\circ \xi_i\right)(3/4)\right) &\text{if } t\in (3/4,1] \end{cases} \end{align} $$
For those i such that
![]() $\xi _i(3/4)=1$
, one also has
$\xi _i(3/4)=1$
, one also has
 $$ \begin{align} \theta^{(i)}\left(\bar\gamma_m\left(f\circ \Xi_j\right)\right)=\bar\gamma_m\left(f\circ\Xi_j\circ \xi_i\right). \end{align} $$
$$ \begin{align} \theta^{(i)}\left(\bar\gamma_m\left(f\circ \Xi_j\right)\right)=\bar\gamma_m\left(f\circ\Xi_j\circ \xi_i\right). \end{align} $$
It follows (recall Lemma 6.8(4) for the definition of
![]() $\Theta _{m+1}$
, and also keep Remark 6.10 in mind) that
$\Theta _{m+1}$
, and also keep Remark 6.10 in mind) that
 $$ \begin{align} \Theta_{m+1}(\varphi_m(f))=u^*\begin{pmatrix} \Theta_{m+1}'(f) & 0 &\dotsb & 0\\ 0 & \bar\gamma_{m}\left(f\circ \xi^{(2)}_1\right) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \bar\gamma_m\left(f\circ \xi^{(2)}_{k'}\right) \end{pmatrix} u \mathrm{\ for\ all\ } f\in A_m, \end{align} $$
$$ \begin{align} \Theta_{m+1}(\varphi_m(f))=u^*\begin{pmatrix} \Theta_{m+1}'(f) & 0 &\dotsb & 0\\ 0 & \bar\gamma_{m}\left(f\circ \xi^{(2)}_1\right) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \bar\gamma_m\left(f\circ \xi^{(2)}_{k'}\right) \end{pmatrix} u \mathrm{\ for\ all\ } f\in A_m, \end{align} $$
where
![]() $u\in C\!\left([0,1], M_{5k_2p_{m+1}q_{m+1}}\right )$
is a unitary (the integer
$u\in C\!\left([0,1], M_{5k_2p_{m+1}q_{m+1}}\right )$
is a unitary (the integer
![]() $k_2$
is the integer k in Lemma 6.8 for
$k_2$
is the integer k in Lemma 6.8 for
![]() $\varphi _{m+1}$
),
$\varphi _{m+1}$
),
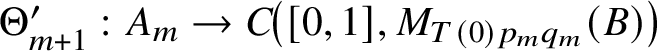 $\Theta _{m+1}': A_m\to C\!\left([0,1], M_{T(0)p_mq_m}(B)\right )$
is a homomorphism for some integer
$\Theta _{m+1}': A_m\to C\!\left([0,1], M_{T(0)p_mq_m}(B)\right )$
is a homomorphism for some integer
![]() $T(0)\ge 1$
and
$T(0)\ge 1$
and
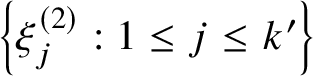 $\left \{\xi ^{(2)}_j: 1\le j\le k'\right \}$
is a full collection of compositions of two maps in Lemma 6.8(1). Moreover, by Lemma 6.8(2),
$\left \{\xi ^{(2)}_j: 1\le j\le k'\right \}$
is a full collection of compositions of two maps in Lemma 6.8(1). Moreover, by Lemma 6.8(2),
Then, combining with equation (e7.9), we may write
![]() $\varphi _{m,m+2}: A_m\to A_{m+2}$
as
$\varphi _{m,m+2}: A_m\to A_{m+2}$
as
 $$ \begin{align} \varphi_{m,m+2}(f)=u_1^*\begin{pmatrix} H_{m+1}(f) & 0 &\dotsb & 0\\ 0 & \bar\gamma_{m}\left(f\circ \xi^{(2)}_1\right) \otimes 1_{r(1)} &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \bar\gamma_m\left(f\circ \xi^{(2)}_{l(m)}\right)\otimes 1_{r(l(m))} \end{pmatrix} u_1 \end{align} $$
$$ \begin{align} \varphi_{m,m+2}(f)=u_1^*\begin{pmatrix} H_{m+1}(f) & 0 &\dotsb & 0\\ 0 & \bar\gamma_{m}\left(f\circ \xi^{(2)}_1\right) \otimes 1_{r(1)} &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \bar\gamma_m\left(f\circ \xi^{(2)}_{l(m)}\right)\otimes 1_{r(l(m))} \end{pmatrix} u_1 \end{align} $$
for all
![]() $f\in A_m$
, where
$f\in A_m$
, where
![]() $u_1\in C\!\left([0,1], M_{p_{m+2}q_{m+2}}\right )$
is a unitary,
$u_1\in C\!\left([0,1], M_{p_{m+2}q_{m+2}}\right )$
is a unitary,
![]() $H_{m+1}: A_m\to C\!\left([0,1], M_{T(1)p_mq_m}(B)\right )$
is a homomorphism for some integer
$H_{m+1}: A_m\to C\!\left([0,1], M_{T(1)p_mq_m}(B)\right )$
is a homomorphism for some integer
![]() $T(1)\ge 1$
,
$T(1)\ge 1$
,
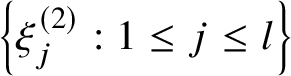 $\left \{\xi ^{(2)}_j: 1\le j\le l\right \}$
is a full collection of compositions of two maps in Lemma 6.8(1) and
$\left \{\xi ^{(2)}_j: 1\le j\le l\right \}$
is a full collection of compositions of two maps in Lemma 6.8(1) and
![]() $r(l(j))\ge 1$
is an integer,
$r(l(j))\ge 1$
is an integer,
![]() $j=1,2,\dotsc ,l(m)$
. Moreover,
$j=1,2,\dotsc ,l(m)$
. Moreover,
 $$ \begin{align} T(1)/5R(m)\left(\sum_{j=1}^{l(m)} r(l(j))\right)<1/3^m. \end{align} $$
$$ \begin{align} T(1)/5R(m)\left(\sum_{j=1}^{l(m)} r(l(j))\right)<1/3^m. \end{align} $$
Therefore, by Lemma 6.8 – noting equations (e6.16), (e6.20) and (e7.36) – and the proof of Theorem 7.3 (see equation (e7.9)), as well as equation (e7.38) repeatedly, one may write, for each
![]() $n>m$
and all
$n>m$
and all
![]() $f\in A_m$
,
$f\in A_m$
,
 $$ \begin{align} \varphi_{m,n}(f)= w^*\begin{pmatrix} H_{m,n}(f) &&&0 \\ & \bar\gamma_m(f\circ \Xi_1) &&\\ &&\ddots &\\ 0&&& \bar\gamma_m(f\circ \Xi_L)\end{pmatrix} w, \end{align} $$
$$ \begin{align} \varphi_{m,n}(f)= w^*\begin{pmatrix} H_{m,n}(f) &&&0 \\ & \bar\gamma_m(f\circ \Xi_1) &&\\ &&\ddots &\\ 0&&& \bar\gamma_m(f\circ \Xi_L)\end{pmatrix} w, \end{align} $$
where
![]() $w\in C\!\left([0,1], M_{p_nq_n}\right )$
is a unitary,
$w\in C\!\left([0,1], M_{p_nq_n}\right )$
is a unitary,
![]() $H_{m,n}: A_m\to C\!\left([0,1], M_{L(0)p_mq_m}(B)\right )$
is a homomorphism for some integer
$H_{m,n}: A_m\to C\!\left([0,1], M_{L(0)p_mq_m}(B)\right )$
is a homomorphism for some integer
![]() $L(0)\ge 1$
,
$L(0)\ge 1$
,
![]() $\Xi _j:[0,1]\to [0,1]$
is a composition of
$\Xi _j:[0,1]\to [0,1]$
is a composition of
![]() $n-m$
many
$n-m$
many
![]() $\xi _i$
s and
$\xi _i$
s and
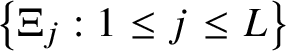 $\left \{\Xi _j:1\le j\le L\right \}$
is a full collection. Moreover,
$\left \{\Xi _j:1\le j\le L\right \}$
is a full collection. Moreover,
We choose N such that
![]() $(2/3)^{N-m}<\delta $
and choose any
$(2/3)^{N-m}<\delta $
and choose any
![]() $n\ge N$
.
$n\ge N$
.
Set
![]() $\tau _i\in T(A_n)$
(
$\tau _i\in T(A_n)$
(
![]() $i=1,2$
). Then, for any
$i=1,2$
). Then, for any
![]() $f\in A_n$
,
$f\in A_n$
,
 $$ \begin{align} \tau_i(f)=\int_0^1 \sigma_i(t) (f(t))d\mu_i,\quad i=1,2, \end{align} $$
$$ \begin{align} \tau_i(f)=\int_0^1 \sigma_i(t) (f(t))d\mu_i,\quad i=1,2, \end{align} $$
where
![]() $\sigma _i(t)$
is a tracial state of
$\sigma _i(t)$
is a tracial state of
![]() $M_{p_nq_n}(B)$
for all
$M_{p_nq_n}(B)$
for all
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
![]() $\sigma _i(0)$
is a tracial state of
$\sigma _i(0)$
is a tracial state of
![]() $M_{p_n}(B)\otimes 1_{q_n}$
,
$M_{p_n}(B)\otimes 1_{q_n}$
,
![]() $\sigma _i(1)$
is a tracial state of
$\sigma _i(1)$
is a tracial state of
![]() $1_{p_n}\otimes M_{q_n}$
and
$1_{p_n}\otimes M_{q_n}$
and
![]() $\mu _i$
is a probability Borel measure on
$\mu _i$
is a probability Borel measure on
![]() $[0,1]$
,
$[0,1]$
,
![]() $i=1,2$
. For each
$i=1,2$
. For each
![]() $t\in [0,1]$
and for
$t\in [0,1]$
and for
![]() $f(t)\in M_{p_nq_n}\subset M_{p_nq_n}(B)$
,
$f(t)\in M_{p_nq_n}\subset M_{p_nq_n}(B)$
,
where
![]() $\mathrm {tr}$
is the normalised trace on
$\mathrm {tr}$
is the normalised trace on
![]() $M_{p_nq_n}$
(see equation (e6.11)). For each
$M_{p_nq_n}$
(see equation (e6.11)). For each
![]() $j\in \{1,2,\dotsc ,L\}$
, by Lemma 7.2,
$j\in \{1,2,\dotsc ,L\}$
, by Lemma 7.2,
 $$ \begin{align} \left\lvert\Xi_j(x)-\Xi_j(y)\right\rvert<(2/3)^{n-m}<\delta\mathrm{\ for\ all\ } x, y\in [0,1]. \end{align} $$
$$ \begin{align} \left\lvert\Xi_j(x)-\Xi_j(y)\right\rvert<(2/3)^{n-m}<\delta\mathrm{\ for\ all\ } x, y\in [0,1]. \end{align} $$
By the choice of
![]() $\delta $
,
$\delta $
,
 $$ \begin{align} \left\lVert g\circ \Xi_j(x) -g\circ \Xi_j(y)\right\rVert<\varepsilon/4\mathrm{\ for\ all\ } x, y\in [0,1]. \end{align} $$
$$ \begin{align} \left\lVert g\circ \Xi_j(x) -g\circ \Xi_j(y)\right\rVert<\varepsilon/4\mathrm{\ for\ all\ } x, y\in [0,1]. \end{align} $$
For each
![]() $f\in A_m$
, write
$f\in A_m$
, write
 $$ \begin{align} H'(f)(t)=\begin{pmatrix} H_{m+1}(f)(t) & 0\\ 0 & 0\end{pmatrix}\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
$$ \begin{align} H'(f)(t)=\begin{pmatrix} H_{m+1}(f)(t) & 0\\ 0 & 0\end{pmatrix}\mathrm{\ for\ all\ } t\in [0,1]. \end{align} $$
Then one has, for each
![]() $f\in A_m$
and
$f\in A_m$
and
![]() $i=1,2$
,
$i=1,2$
,
 $$ \begin{align} \tau_i\left(\varphi_{m,n}(f)\right)&=\int_0^1 \sigma_i(t)\left(\varphi_{m,n}(f)\right) d\mu_i \hspace{12pc} \end{align} $$
$$ \begin{align} \tau_i\left(\varphi_{m,n}(f)\right)&=\int_0^1 \sigma_i(t)\left(\varphi_{m,n}(f)\right) d\mu_i \hspace{12pc} \end{align} $$
 $$ \begin{align} & \hspace{0.5pc} =\int_0^1\sigma_i(t)(H'(f)(t))d\mu_i +\int_0^1 \mathrm{tr}\left(\bigoplus_{j=1}^L\left(f\circ \Xi_j(t)\right)\right)d\mu_i. \end{align} $$
$$ \begin{align} & \hspace{0.5pc} =\int_0^1\sigma_i(t)(H'(f)(t))d\mu_i +\int_0^1 \mathrm{tr}\left(\bigoplus_{j=1}^L\left(f\circ \Xi_j(t)\right)\right)d\mu_i. \end{align} $$
By formula (e7.47), recalling that
![]() $\lVert g\rVert \le 1$
,
$\lVert g\rVert \le 1$
,
 $$ \begin{align} \int_0^1\left\lvert\mathrm{tr}\left(\bigoplus_{j=1}^L(g\circ \Xi_j(1/2)\right)-\bigoplus_{j=1}^L \left(g\circ \Xi_j(t)\right)\right\rvert d\mu_i <(\varepsilon/4)\int_0^1d\mu_i =\varepsilon/4. \end{align} $$
$$ \begin{align} \int_0^1\left\lvert\mathrm{tr}\left(\bigoplus_{j=1}^L(g\circ \Xi_j(1/2)\right)-\bigoplus_{j=1}^L \left(g\circ \Xi_j(t)\right)\right\rvert d\mu_i <(\varepsilon/4)\int_0^1d\mu_i =\varepsilon/4. \end{align} $$
By formula (e7.43),
 $$ \begin{align} \int_0^1\lvert\sigma_i(t)(H'(g)(t))\rvert d\mu_i <(1/3)^m<\varepsilon/4. \end{align} $$
$$ \begin{align} \int_0^1\lvert\sigma_i(t)(H'(g)(t))\rvert d\mu_i <(1/3)^m<\varepsilon/4. \end{align} $$
Recall that
![]() $\varphi _{1,n}(a)=\varphi _{m, n}(g)$
. Thus, by formulas (e7.49), (e7.50), (e7.51) and (e7.52),
$\varphi _{1,n}(a)=\varphi _{m, n}(g)$
. Thus, by formulas (e7.49), (e7.50), (e7.51) and (e7.52),
 $$ \begin{align} \left\lvert\tau_i\left(\varphi_{1,n}(a)\right)-\sum_{j=1}^L\mathrm{tr}\left(g\left(\Xi_j(1/2)\right)\right)\right\rvert<\varepsilon/2,\quad i=1,2. \end{align} $$
$$ \begin{align} \left\lvert\tau_i\left(\varphi_{1,n}(a)\right)-\sum_{j=1}^L\mathrm{tr}\left(g\left(\Xi_j(1/2)\right)\right)\right\rvert<\varepsilon/2,\quad i=1,2. \end{align} $$
Therefore,
 $$ \begin{align} \left\lvert\tau_1\left(\varphi_{1,n}(a)\right)-\tau_2\left(\varphi_{1,n}(a)\right)\right\rvert<\varepsilon. \end{align} $$
$$ \begin{align} \left\lvert\tau_1\left(\varphi_{1,n}(a)\right)-\tau_2\left(\varphi_{1,n}(a)\right)\right\rvert<\varepsilon. \end{align} $$
This proves the claim.
To complete the proof, set
![]() $s_1, s_2\in T\left (A_z^C\right )$
. Set
$s_1, s_2\in T\left (A_z^C\right )$
. Set
![]() $a\in A_z^C$
and
$a\in A_z^C$
and
![]() $\varepsilon>0$
. Then there is
$\varepsilon>0$
. Then there is
![]() $f\in A_k$
for some
$f\in A_k$
for some
![]() $k\ge 1$
such that
$k\ge 1$
such that
 $$ \begin{align} \left\lVert a-\varphi_{k,\infty}(f)\right\rVert<\varepsilon/3. \end{align} $$
$$ \begin{align} \left\lVert a-\varphi_{k,\infty}(f)\right\rVert<\varepsilon/3. \end{align} $$
Let
![]() $\tau _{i,n}=s_i\circ \varphi _{n,\infty }$
. Then, by the claim, there exists
$\tau _{i,n}=s_i\circ \varphi _{n,\infty }$
. Then, by the claim, there exists
![]() $N\ge k$
such that for all
$N\ge k$
such that for all
![]() $n>N$
,
$n>N$
,
 $$ \begin{align} \left\lvert\tau_{1,n}\left(\varphi_{k,n}(f)\right)-\tau_{2 ,n}\left(\varphi_{k,n}(f)\right)\right\rvert<\varepsilon/3. \end{align} $$
$$ \begin{align} \left\lvert\tau_{1,n}\left(\varphi_{k,n}(f)\right)-\tau_{2 ,n}\left(\varphi_{k,n}(f)\right)\right\rvert<\varepsilon/3. \end{align} $$
It follows that
 $$ \begin{align} \left\lvert s_1\left(\varphi_{k,\infty}(f)\right)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert\le \varepsilon/3. \end{align} $$
$$ \begin{align} \left\lvert s_1\left(\varphi_{k,\infty}(f)\right)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert\le \varepsilon/3. \end{align} $$
Therefore,
 $$ \begin{align*} \lvert s_1(a)-s_2(a)\rvert &\le \left\lvert s_1(a)-s_1\left(\varphi_{k,\infty}(f)\right)\right\rvert\\ &\quad +\left\lvert s_1\left(\varphi_{k,\infty}(f)\right)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert+\left\lvert s_2(a)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert <\varepsilon. \end{align*} $$
$$ \begin{align*} \lvert s_1(a)-s_2(a)\rvert &\le \left\lvert s_1(a)-s_1\left(\varphi_{k,\infty}(f)\right)\right\rvert\\ &\quad +\left\lvert s_1\left(\varphi_{k,\infty}(f)\right)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert+\left\lvert s_2(a)-s_2\left(\varphi_{k,\infty}(f)\right)\right\rvert <\varepsilon. \end{align*} $$
It follows that
![]() $s_1(a)=s_2(a)$
. Thus
$s_1(a)=s_2(a)$
. Thus
![]() $A_z^C$
has a unique tracial state.
$A_z^C$
has a unique tracial state.
Remark 7.6. Recall that the construction allows
![]() $B=\mathbb {C}$
(with
$B=\mathbb {C}$
(with
![]() $C=\{0\}$
). In that case, of course,
$C=\{0\}$
). In that case, of course,
![]() $A_z^C={\mathscr Z}$
. Note that when
$A_z^C={\mathscr Z}$
. Note that when
![]() $B=\mathbb {C}$
, we have
$B=\mathbb {C}$
, we have
![]() $\theta _t(b)=b$
for all
$\theta _t(b)=b$
for all
![]() $b\in M_{p_mq_m}$
. In other words,
$b\in M_{p_mq_m}$
. In other words,
![]() $\theta _t=\operatorname {id}_B$
.
$\theta _t=\operatorname {id}_B$
.
Let
 $$ \begin{align} Z_{p_m,q_m}=\left\{f\in C\left([0,1], M_{p_mq_m}\right): f(0)\in M_{p_m}\otimes 1_{q_m}\mathrm{\ and\ } f(1)\in 1_{p_m}\otimes M_{q_m}\right\}. \end{align} $$
$$ \begin{align} Z_{p_m,q_m}=\left\{f\in C\left([0,1], M_{p_mq_m}\right): f(0)\in M_{p_m}\otimes 1_{q_m}\mathrm{\ and\ } f(1)\in 1_{p_m}\otimes M_{q_m}\right\}. \end{align} $$
In general (when
![]() $C\not =\{0\}$
), one has
$C\not =\{0\}$
), one has
![]() $Z_{p_m,q_m}\subset E_{p_m,q_m}$
, as we view
$Z_{p_m,q_m}\subset E_{p_m,q_m}$
, as we view
![]() $\mathbb {C}\subset B$
and
$\mathbb {C}\subset B$
and
![]() $M_{p_mq_m}\subset M_{p_mq_m}(B)$
. Let
$M_{p_mq_m}\subset M_{p_mq_m}(B)$
. Let
![]() $\varphi _m^z={\varphi _m}\rvert _{Z_{p_m,q_m}}$
. Then, since
$\varphi _m^z={\varphi _m}\rvert _{Z_{p_m,q_m}}$
. Then, since
![]() $v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
(see the line before formula (e6.48)),
$v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
(see the line before formula (e6.48)),
![]() $\varphi _m^z\left (Z_{p_m,q_m}\right )\subset Z_{p_{m+1}, q_{m+1}}$
. Thus, one obtains a unital
$\varphi _m^z\left (Z_{p_m,q_m}\right )\subset Z_{p_{m+1}, q_{m+1}}$
. Thus, one obtains a unital
![]() $C^*$
-subalgebra (of
$C^*$
-subalgebra (of
![]() $A_z^C$
)
$A_z^C$
)
 $$ \begin{align} B_z=\lim_{n\to\infty}\left(Z_{p_m, q_m}, \varphi_m^z\right). \end{align} $$
$$ \begin{align} B_z=\lim_{n\to\infty}\left(Z_{p_m, q_m}, \varphi_m^z\right). \end{align} $$
Then
![]() $B_z\cong {\mathscr Z}$
[Reference Jiang and Su27].
$B_z\cong {\mathscr Z}$
[Reference Jiang and Su27].
8. Regularity properties of
 $A_z^C$
$A_z^C$
In this section, let
![]() $A_z^C$
be the
$A_z^C$
be the
![]() $C^*$
-algebra in Theorem 7.3.
$C^*$
-algebra in Theorem 7.3.
Lemma 8.1. The inductive system can be arranged so that
![]() $A_z^C$
has the following properties:
$A_z^C$
has the following properties:
-
(1)
 $A_z^C$
has a unital
$A_z^C$
has a unital
 $C^*$
-subalgebra
$C^*$
-subalgebra
 $B_z\cong {\mathscr Z}$
.
$B_z\cong {\mathscr Z}$
. -
(2) For any finite subset
 ${\cal F}\subset A_m$
and
${\cal F}\subset A_m$
and
 $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
 $e\in (A_{m+1})_+^{\textbf{1}}\setminus \{0\}$
such that the following hold:
$e\in (A_{m+1})_+^{\textbf{1}}\setminus \{0\}$
such that the following hold:-
(i)
 $e(t)\in M_{p_{m+1}q_{m+1}}$
for all
$e(t)\in M_{p_{m+1}q_{m+1}}$
for all
 $t\in [0,1]$
and
$t\in [0,1]$
and
 $e(1)=0$
.
$e(1)=0$
. -
(ii)
 $\lVert ex-xe\rVert <\varepsilon \text { for all } x\in \varphi _m({\cal F})$
.
$\lVert ex-xe\rVert <\varepsilon \text { for all } x\in \varphi _m({\cal F})$
. -
(iii)
 $\varphi _{m+1, \infty }\left ((1-e)^{\beta }\varphi _m(f)\right )\in _{\varepsilon } B_z$
for all
$\varphi _{m+1, \infty }\left ((1-e)^{\beta }\varphi _m(f)\right )\in _{\varepsilon } B_z$
for all
 $f\in {\cal F}$
, and for any
$f\in {\cal F}$
, and for any
 ${\beta } \in (0, \infty )$
, (e8.1)
${\beta } \in (0, \infty )$
, (e8.1) $$ \begin{align} \left\lVert\varphi_{m+1, \infty}\left((1-e)^{{\beta}}\varphi_m(y)\right)\right\rVert\ge (1-\varepsilon)\lVert\varphi_m(y)\rVert \mathrm{\ for\ all\ } y\in {\cal F}_m. \end{align} $$
$$ \begin{align} \left\lVert\varphi_{m+1, \infty}\left((1-e)^{{\beta}}\varphi_m(y)\right)\right\rVert\ge (1-\varepsilon)\lVert\varphi_m(y)\rVert \mathrm{\ for\ all\ } y\in {\cal F}_m. \end{align} $$
-
(iv)
 $d_\tau (e)<1/3^m$
for all
$d_\tau (e)<1/3^m$
for all
 $\tau \in T(A_{m+1})$
.
$\tau \in T(A_{m+1})$
.
-
(Recall that
![]() ${\cal F}_m$
was constructed in the proof of Theorem 7.3.)
${\cal F}_m$
was constructed in the proof of Theorem 7.3.)
Proof. We will keep the notation used in the proof of Lemma 6.8.
For (i), we note that the
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
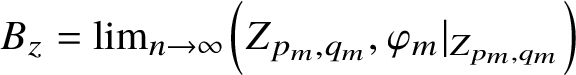 $B_z=\lim _{n\to \infty }\left (Z_{p_m,q_m}, {\varphi _m}\rvert _{Z_{p_m,q_m}}\right )$
has been identified in Remark 7.6, where
$B_z=\lim _{n\to \infty }\left (Z_{p_m,q_m}, {\varphi _m}\rvert _{Z_{p_m,q_m}}\right )$
has been identified in Remark 7.6, where
 $$ \begin{align} Z_{p_m,q_m}=\left\{f\in C\left([0,1], M_{p_mq_m}\right): f(0)\in M_{p_m}\otimes 1_{q_m}\mathrm{\ and\ } f(1)\in 1_{p_m}\otimes M_{q_m}\right\}. \end{align} $$
$$ \begin{align} Z_{p_m,q_m}=\left\{f\in C\left([0,1], M_{p_mq_m}\right): f(0)\in M_{p_m}\otimes 1_{q_m}\mathrm{\ and\ } f(1)\in 1_{p_m}\otimes M_{q_m}\right\}. \end{align} $$
There is
![]() $\delta \in (0,\varepsilon /2) $
such that if
$\delta \in (0,\varepsilon /2) $
such that if
![]() $\lvert t-t'\rvert <2\delta $
,
$\lvert t-t'\rvert <2\delta $
,
In particular, there is
![]() $t_1\in (0,1)$
(
$t_1\in (0,1)$
(
![]() $1-t_1<\delta $
) such that
$1-t_1<\delta $
) such that
Choose a continuous function
![]() $g\in C([0,1])$
such that
$g\in C([0,1])$
such that
![]() $0\le g\le 1$
,
$0\le g\le 1$
,
![]() $g(t)=1$
for all
$g(t)=1$
for all
![]() $t\in [0,t_1]$
and
$t\in [0,t_1]$
and
![]() $g(t)=(1-t)/(1-t_1)$
for
$g(t)=(1-t)/(1-t_1)$
for
![]() $t\in (t_1,1]$
. Let
$t\in (t_1,1]$
. Let
![]() $e_0(t)=g(t)\cdot 1_{A_m}$
for all
$e_0(t)=g(t)\cdot 1_{A_m}$
for all
![]() $t\in [0,1]$
. Note that
$t\in [0,1]$
. Note that
![]() $e_0(0)=1_{p_mq_m}\in M_{p_m}(B)\otimes 1_{q_m}$
and
$e_0(0)=1_{p_mq_m}\in M_{p_m}(B)\otimes 1_{q_m}$
and
![]() $e_0(1)=0\in 1_{p_m}\otimes M_{q_m}$
. So
$e_0(1)=0\in 1_{p_m}\otimes M_{q_m}$
. So
![]() $e_0\in A_m$
. Moreover,
$e_0\in A_m$
. Moreover,
![]() $e_0$
is in the center of
$e_0$
is in the center of
![]() $A_m$
. Define
$A_m$
. Define
![]() $\sigma _0: M_{p_m}(B)\otimes M_{q_m}\to M_{d_mp_m}(B)\otimes M_{5q_m}$
by
$\sigma _0: M_{p_m}(B)\otimes M_{q_m}\to M_{d_mp_m}(B)\otimes M_{5q_m}$
by
![]() $\sigma _0'\otimes s$
, where
$\sigma _0'\otimes s$
, where
 $$ \begin{align} \sigma_0'(a)=\begin{pmatrix}\theta_1(a) &0\\ 0 & 0\end{pmatrix}\mathrm{\ for\ all\ } a\in M_{p_m}(B)\mathrm{\ and\ } s(c)=c\otimes 1_5 \mathrm{\ for\ all\ } c\in M_{q_m}, \end{align} $$
$$ \begin{align} \sigma_0'(a)=\begin{pmatrix}\theta_1(a) &0\\ 0 & 0\end{pmatrix}\mathrm{\ for\ all\ } a\in M_{p_m}(B)\mathrm{\ and\ } s(c)=c\otimes 1_5 \mathrm{\ for\ all\ } c\in M_{q_m}, \end{align} $$
where
![]() $\theta _1: M_{p_m}(B)\to M_{p_m}\subset M_{p_m}(B)$
is defined by
$\theta _1: M_{p_m}(B)\to M_{p_m}\subset M_{p_m}(B)$
is defined by
![]() $\theta _1(c)(x) := c(0)$
for
$\theta _1(c)(x) := c(0)$
for
![]() $c\in M_{p_m}(B)=\, M_{p_m}( C_0( (0,1], C)^{\sim })$
and for all
$c\in M_{p_m}(B)=\, M_{p_m}( C_0( (0,1], C)^{\sim })$
and for all
![]() $x\in [0,1]$
, and the “
$x\in [0,1]$
, and the “
![]() $0$
” in the lower corner of the matrix has the size of
$0$
” in the lower corner of the matrix has the size of
![]() $(d_m-1)p_m\times (d_m-1)p_m$
. Then define
$(d_m-1)p_m\times (d_m-1)p_m$
. Then define
![]() $\sigma _1: A_m\to C\!\left([0,1], M_{d_mp_m5q_m}(B)\right )$
by
$\sigma _1: A_m\to C\!\left([0,1], M_{d_mp_m5q_m}(B)\right )$
by
It follows that for all fixed
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
 $$ \begin{align} & \hspace{3pc} =\begin{pmatrix} \left(\theta_1(g(t)\cdot 1_{p_m}\right)&0\\ 0 & 0\end{pmatrix}\otimes 1_{5q_m} =\begin{pmatrix} g(t)\cdot 1_{p_m}&0\\ 0 & 0\end{pmatrix}\otimes 1_{5q_m}=\begin{pmatrix} g(t)\cdot 1_{p_mq_m} &0\\ 0 & 0\end{pmatrix}\otimes 1_{5}, \end{align} $$
$$ \begin{align} & \hspace{3pc} =\begin{pmatrix} \left(\theta_1(g(t)\cdot 1_{p_m}\right)&0\\ 0 & 0\end{pmatrix}\otimes 1_{5q_m} =\begin{pmatrix} g(t)\cdot 1_{p_m}&0\\ 0 & 0\end{pmatrix}\otimes 1_{5q_m}=\begin{pmatrix} g(t)\cdot 1_{p_mq_m} &0\\ 0 & 0\end{pmatrix}\otimes 1_{5}, \end{align} $$
where the last “0” in the last matrix has the size
![]() $(d_m-1)p_mq_m\times (d_m-1)p_mq_m$
. Thus
$(d_m-1)p_mq_m\times (d_m-1)p_mq_m$
. Thus
where
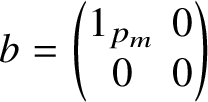 $ b=\begin {pmatrix} 1_{p_m} &0\\ 0 & 0\end {pmatrix}$
. It follows that
$ b=\begin {pmatrix} 1_{p_m} &0\\ 0 & 0\end {pmatrix}$
. It follows that
![]() $\sigma _1(e_0)\in E_{d_mp_m, 5q_m}$
. Note that for each
$\sigma _1(e_0)\in E_{d_mp_m, 5q_m}$
. Note that for each
![]() $\tau \in T(A_m)$
, by formula (e 6.13).
$\tau \in T(A_m)$
, by formula (e 6.13).
Let us recall the definition of
![]() $\tilde \psi _{m,i}$
in the proof of Lemma 6.8,
$\tilde \psi _{m,i}$
in the proof of Lemma 6.8,
![]() $1\le i\le k$
(see formula (e6.50)). Then for all
$1\le i\le k$
(see formula (e6.50)). Then for all
![]() $f\in A_m$
, by formulas (e6.50), (e6.44), (e6.46) and (e6.52), for each
$f\in A_m$
, by formulas (e6.50), (e6.44), (e6.46) and (e6.52), for each
![]() $t\in [0,1]$
we have
$t\in [0,1]$
we have
 $$ \begin{align} \tilde\psi_{m,i}(f)(t)\sigma_1(e_0)(t) &=\begin{pmatrix} \theta^{(i)}(f)(t) & 0\\ 0 & \gamma_m(f(t))\end{pmatrix} \otimes 1_5 \cdot \begin{pmatrix} g(t)\cdot 1_{p_mq_m} &0\\ 0 & 0\end{pmatrix}\otimes 1_{5} \end{align} $$
$$ \begin{align} \tilde\psi_{m,i}(f)(t)\sigma_1(e_0)(t) &=\begin{pmatrix} \theta^{(i)}(f)(t) & 0\\ 0 & \gamma_m(f(t))\end{pmatrix} \otimes 1_5 \cdot \begin{pmatrix} g(t)\cdot 1_{p_mq_m} &0\\ 0 & 0\end{pmatrix}\otimes 1_{5} \end{align} $$
 $$ \begin{align} &=\begin{pmatrix} \theta^{(i)}(f)(t)\cdot g(t)\cdot 1_{p_mq_m}& 0\\ 0 & 0\end{pmatrix}\otimes 1_5 \hspace{1.5pc} \end{align} $$
$$ \begin{align} &=\begin{pmatrix} \theta^{(i)}(f)(t)\cdot g(t)\cdot 1_{p_mq_m}& 0\\ 0 & 0\end{pmatrix}\otimes 1_5 \hspace{1.5pc} \end{align} $$
 $$ \begin{align} & \hspace{4.5pc} =\begin{pmatrix} g(t)\cdot 1_{p_mq_m} & 0\\ 0 & 0\end{pmatrix} \otimes 1_5 \cdot \begin{pmatrix} \theta^{(i)}(f)(t) &0\\ 0 & \gamma_m(f(t))\end{pmatrix}\otimes 1_{5} \end{align} $$
$$ \begin{align} & \hspace{4.5pc} =\begin{pmatrix} g(t)\cdot 1_{p_mq_m} & 0\\ 0 & 0\end{pmatrix} \otimes 1_5 \cdot \begin{pmatrix} \theta^{(i)}(f)(t) &0\\ 0 & \gamma_m(f(t))\end{pmatrix}\otimes 1_{5} \end{align} $$
In other words, for all
![]() $f\in E_{p_m,q_m}$
,
$f\in E_{p_m,q_m}$
,
Define
![]() ${\alpha }: [0,1]\to [0,1]$
by
${\alpha }: [0,1]\to [0,1]$
by
 $$ \begin{align} {\alpha}(t):= \begin{cases} {\frac{t}{t_1}}& \text{if } t\in [0,t_1],\\ 1& \text{if } t\in (t_1,1]. \end{cases} \end{align} $$
$$ \begin{align} {\alpha}(t):= \begin{cases} {\frac{t}{t_1}}& \text{if } t\in [0,t_1],\\ 1& \text{if } t\in (t_1,1]. \end{cases} \end{align} $$
Then for all j,
![]() $f\circ {\alpha }\in E_{p_j,q_j}$
if
$f\circ {\alpha }\in E_{p_j,q_j}$
if
![]() $f\in E_{p_j,q_j}$
. Moreover, by formula (e8.3),
$f\in E_{p_j,q_j}$
. Moreover, by formula (e8.3),
Therefore, for each
![]() $f\in A_m$
, each
$f\in A_m$
, each
![]() $t\in [0,1]$
and each
$t\in [0,1]$
and each
![]() ${\beta }\in (0,\infty )$
, with
${\beta }\in (0,\infty )$
, with
![]() $l=d_mp_m5q_m$
,
$l=d_mp_m5q_m$
,
 $$ \begin{align} (1_l-\sigma_1(e_0))^{\beta}{\tilde\psi_{m,i}}(f)\circ {\alpha} (t)=\begin{pmatrix} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)\circ {\alpha}(t) & 0\\ 0& \gamma_m(f(t))\end{pmatrix} \otimes 1_5, \end{align} $$
$$ \begin{align} (1_l-\sigma_1(e_0))^{\beta}{\tilde\psi_{m,i}}(f)\circ {\alpha} (t)=\begin{pmatrix} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)\circ {\alpha}(t) & 0\\ 0& \gamma_m(f(t))\end{pmatrix} \otimes 1_5, \end{align} $$
for
![]() $i=1,2,\dotsc ,k$
. For
$i=1,2,\dotsc ,k$
. For
![]() $t\in [0,t_1]$
, by the definition of g,
$t\in [0,t_1]$
, by the definition of g,
 $$ \begin{align} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)(t)=0. \end{align} $$
$$ \begin{align} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)(t)=0. \end{align} $$
For
![]() $t\in (t_1,1]$
,
$t\in (t_1,1]$
,
 $$ \begin{align} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)\circ {\alpha} (t)=(1-g(t))^{\beta}\cdot \theta^{(i)}(f)(1)\in M_{p_mq_m}. \end{align} $$
$$ \begin{align} (1-g(t))^{\beta}\cdot 1_{p_mq_m}\cdot \theta^{(i)}(f)\circ {\alpha} (t)=(1-g(t))^{\beta}\cdot \theta^{(i)}(f)(1)\in M_{p_mq_m}. \end{align} $$
Hence
 $$ \begin{align} (1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,i}(f\circ {\alpha}) \in C\left([0,1], M_{d_mp_m5q_m}\right). \end{align} $$
$$ \begin{align} (1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,i}(f\circ {\alpha}) \in C\left([0,1], M_{d_mp_m5q_m}\right). \end{align} $$
Moreover, by formula (e7.8), for
![]() $f\in {\cal F}_m$
we have
$f\in {\cal F}_m$
we have
 $$ \begin{align} \left\lVert(1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,i}(f)\circ {\alpha} \right\rVert\ge (1-1/m)\lVert f\rVert. \end{align} $$
$$ \begin{align} \left\lVert(1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,i}(f)\circ {\alpha} \right\rVert\ge (1-1/m)\lVert f\rVert. \end{align} $$
Using the same v as in formula (e6.48), with
![]() $\sigma _1(e_0)(t)$
repeating k times, define
$\sigma _1(e_0)(t)$
repeating k times, define
 $$ \begin{align} e:=v(t)^*\begin{pmatrix} \sigma_1(e_0)(t) & 0 &\dotsb & 0\\ 0 & \sigma_1(e_0)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \sigma_1(e_0)(t)\end{pmatrix}v(t). \end{align} $$
$$ \begin{align} e:=v(t)^*\begin{pmatrix} \sigma_1(e_0)(t) & 0 &\dotsb & 0\\ 0 & \sigma_1(e_0)(t) &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \sigma_1(e_0)(t)\end{pmatrix}v(t). \end{align} $$
With b as in the line after equation (e8.9),
![]() $b\otimes 1_{5q_m}\otimes 1_{r_0}=b\otimes 1_{r_05q_m}=\left (b\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
(see formula (e6.35)). Since
$b\otimes 1_{5q_m}\otimes 1_{r_0}=b\otimes 1_{r_05q_m}=\left (b\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
(see formula (e6.35)). Since
![]() $\sigma _1(e_0)\in E_{d_mp_m,5q_m}$
, as in equation (e8.9),
$\sigma _1(e_0)\in E_{d_mp_m,5q_m}$
, as in equation (e8.9),
 $$ \begin{align} e(0)=v_0^*\begin{pmatrix} b\otimes 1_{5q_m} & 0 &\dotsb & 0\\ 0 & b\otimes 1_{5q_m} &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & b\otimes 1_{5q_m}\end{pmatrix}v_0\in M_{p_{m+1}}\otimes 1_{q_{m+1}} \end{align} $$
$$ \begin{align} e(0)=v_0^*\begin{pmatrix} b\otimes 1_{5q_m} & 0 &\dotsb & 0\\ 0 & b\otimes 1_{5q_m} &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & b\otimes 1_{5q_m}\end{pmatrix}v_0\in M_{p_{m+1}}\otimes 1_{q_{m+1}} \end{align} $$
(see formula (e6.37)). Combining with the fact that
![]() $e(1)=0$
, one concludes that
$e(1)=0$
, one concludes that
![]() $e\in E_{p_{m+1},q_{m+1}}=A_{m+1}$
. Moreover, by equation (e8.7) and the fact that
$e\in E_{p_{m+1},q_{m+1}}=A_{m+1}$
. Moreover, by equation (e8.7) and the fact that
![]() $v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
(see discussion before formula (e6.48)),
$v\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
(see discussion before formula (e6.48)),
![]() $e(t)\in M_{p_{m+1}q_{m+1}}$
for each
$e(t)\in M_{p_{m+1}q_{m+1}}$
for each
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $e(1)=0$
. So part (2)(i) of the statement of the lemma holds.
$e(1)=0$
. So part (2)(i) of the statement of the lemma holds.
By equation (e8.15) and (e6.51), one computes that for all
![]() $f\in A_m$
,
$f\in A_m$
,
 $$ \begin{align} e\varphi_m(f)&=v^*\begin{pmatrix} \sigma_1(e_0)\tilde\psi_{m,1}(f) & &&0 \\ & & \ddots& \\ 0&& & \sigma_1(e_0)\tilde\psi_{m,k}(f)\end{pmatrix}v \hspace{5.5pc} \end{align} $$
$$ \begin{align} e\varphi_m(f)&=v^*\begin{pmatrix} \sigma_1(e_0)\tilde\psi_{m,1}(f) & &&0 \\ & & \ddots& \\ 0&& & \sigma_1(e_0)\tilde\psi_{m,k}(f)\end{pmatrix}v \hspace{5.5pc} \end{align} $$
 $$ \begin{align} & \hspace{1pc} =v^*\begin{pmatrix} \tilde\psi_{m,1}(f)\sigma_1(e_0) & &&0 \\ & & \ddots& \\ 0&& & \tilde\psi_{m,k}(f)\sigma_1(e_0)\end{pmatrix}v =\varphi_m(f) e. \end{align} $$
$$ \begin{align} & \hspace{1pc} =v^*\begin{pmatrix} \tilde\psi_{m,1}(f)\sigma_1(e_0) & &&0 \\ & & \ddots& \\ 0&& & \tilde\psi_{m,k}(f)\sigma_1(e_0)\end{pmatrix}v =\varphi_m(f) e. \end{align} $$
In other words, part (2)(ii) in the statement of the lemma holds. Now
 $$ \begin{align*} (1-e)^{\beta}\varphi_m(f\circ {\alpha}) =v^*\begin{pmatrix} (1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,1}(f)\circ {\alpha} & &&0 \\ & & \ddots& \\ 0&& & (1_l-\sigma_1(e_0))^{\beta} \tilde\psi_{m,k}(f)\circ {\alpha} \end{pmatrix}v \end{align*} $$
$$ \begin{align*} (1-e)^{\beta}\varphi_m(f\circ {\alpha}) =v^*\begin{pmatrix} (1_l-\sigma_1(e_0))^{\beta}\tilde\psi_{m,1}(f)\circ {\alpha} & &&0 \\ & & \ddots& \\ 0&& & (1_l-\sigma_1(e_0))^{\beta} \tilde\psi_{m,k}(f)\circ {\alpha} \end{pmatrix}v \end{align*} $$
for all
![]() $f\in A_m$
, where
$f\in A_m$
, where
![]() $l=d_mp_m5q_m$
. Note that
$l=d_mp_m5q_m$
. Note that
![]() $(1-e)^{\beta }\varphi _m(f)\circ {\alpha } \in E_{p_{m+1}, q_{m+1}}$
. It follows from formula (e8.21) that
$(1-e)^{\beta }\varphi _m(f)\circ {\alpha } \in E_{p_{m+1}, q_{m+1}}$
. It follows from formula (e8.21) that
 $$ \begin{align} (1-e)^{\beta}\varphi_m(f)\circ {\alpha} \in Z_{p_{m+1}, q_{m+1}}\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
$$ \begin{align} (1-e)^{\beta}\varphi_m(f)\circ {\alpha} \in Z_{p_{m+1}, q_{m+1}}\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
Then, by formula (e8.17),
 $$ \begin{align} (1-e)^{\beta}\varphi_m(f)\in_{\varepsilon/4} Z_{p_{m+1}, q_{m+1}}\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
$$ \begin{align} (1-e)^{\beta}\varphi_m(f)\in_{\varepsilon/4} Z_{p_{m+1}, q_{m+1}}\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
It follows that
 $$ \begin{align} \varphi_{m, \infty}\left((1-e)^{\beta} f\right)\in_{\varepsilon} B_z\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
$$ \begin{align} \varphi_{m, \infty}\left((1-e)^{\beta} f\right)\in_{\varepsilon} B_z\mathrm{\ for\ all\ } f\in {\cal F}. \end{align} $$
Moreover, by formula (e8.22), formula (e8.1) also holds, so part (2)(iii) of the statement of the lemma holds. It follows from formula (e8.10) that part (2)(iv) also holds.
Lemma 8.2. Let
 $$ \begin{align} E_{p,q}=\left\{(f,c): C\left([0,1], M_{pq}(B)\right)\oplus \left(M_p(B)\oplus M_q\right): \pi_0(c)=f(0)\mathrm{\ and\ } \pi_1(c)=f(1)\right\}, \end{align} $$
$$ \begin{align} E_{p,q}=\left\{(f,c): C\left([0,1], M_{pq}(B)\right)\oplus \left(M_p(B)\oplus M_q\right): \pi_0(c)=f(0)\mathrm{\ and\ } \pi_1(c)=f(1)\right\}, \end{align} $$
where
![]() $\pi _0: M_p(B)\oplus M_q \to M_p(B)\otimes 1_q\subset M_{pq}(B)$
defined by
$\pi _0: M_p(B)\oplus M_q \to M_p(B)\otimes 1_q\subset M_{pq}(B)$
defined by
![]() $\pi _0(c_1\oplus c_2):= c_1\otimes 1_q$
for all
$\pi _0(c_1\oplus c_2):= c_1\otimes 1_q$
for all
![]() $c_1\in M_p(B)$
and
$c_1\in M_p(B)$
and
![]() $c_2\in M_q$
, and
$c_2\in M_q$
, and
![]() $\pi _1: M_p(B)\oplus M_q \to 1_p\otimes M_q\subset M_{pq}(B)$
defined by
$\pi _1: M_p(B)\oplus M_q \to 1_p\otimes M_q\subset M_{pq}(B)$
defined by
![]() $\pi _1((c_1\oplus c_2)):= 1_p\otimes c_2$
for all
$\pi _1((c_1\oplus c_2)):= 1_p\otimes c_2$
for all
![]() $c_1\in M_p(B)$
and
$c_1\in M_p(B)$
and
![]() $c_2\in M_q$
(see formula (e6.6)). Let
$c_2\in M_q$
(see formula (e6.6)). Let
 $$ \begin{align} L_{p,q}=\left\{(f,c): C\left([0,1], M_{pq}\right)\oplus M_p: \pi_0\rvert_{M_p}(c)=f(0)\right\}, \end{align} $$
$$ \begin{align} L_{p,q}=\left\{(f,c): C\left([0,1], M_{pq}\right)\oplus M_p: \pi_0\rvert_{M_p}(c)=f(0)\right\}, \end{align} $$
where
![]() $\pi _0\rvert _{M_p}(c) =c\otimes 1_q$
for all
$\pi _0\rvert _{M_p}(c) =c\otimes 1_q$
for all
![]() $c\in M_p$
.
$c\in M_p$
.
Suppose that
![]() $a, b\in {E_{p,q}}_+$
are such that
$a, b\in {E_{p,q}}_+$
are such that
-
(1)
 $a(t)\in C\!\left([0,1], M_{pq}\right )$
and
$a(t)\in C\!\left([0,1], M_{pq}\right )$
and
 $a(1)=0$
and
$a(1)=0$
and -
(2) there is
 $b_0\in C\!\left([0,1], M_{pq}\right )_+$
such that
$b_0\in C\!\left([0,1], M_{pq}\right )_+$
such that
 $b_0(t)\le b(t)$
for all
$b_0(t)\le b(t)$
for all
 $t\in [0,1]$
and (e8.32)(i.e., there exists a sequence
$t\in [0,1]$
and (e8.32)(i.e., there exists a sequence $$ \begin{align} a\lesssim b_0\mathrm{\ in\ } L_{p,q} \end{align} $$
$$ \begin{align} a\lesssim b_0\mathrm{\ in\ } L_{p,q} \end{align} $$
 $x_n\in L_{p,q}$
such that
$x_n\in L_{p,q}$
such that
 $x_n^*b_0x_n\to a$
).
$x_n^*b_0x_n\to a$
).
Then
Proof. Let
![]() $1>\varepsilon >0$
. Consider a continuous function
$1>\varepsilon >0$
. Consider a continuous function
![]() $h_\delta \in E_{p,q}$
:
$h_\delta \in E_{p,q}$
:
 $$ \begin{align} h_\delta(t)=\begin{cases} 1_{M_{pq}(B)} &\text{if } t\in [0,1-\delta],\\ 0&\text{if } t\in (1-\delta/2,1],\\ \text{linear} & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} h_\delta(t)=\begin{cases} 1_{M_{pq}(B)} &\text{if } t\in [0,1-\delta],\\ 0&\text{if } t\in (1-\delta/2,1],\\ \text{linear} & \text{otherwise.} \end{cases} \end{align} $$
Since
![]() $a(1)=0$
, there exists
$a(1)=0$
, there exists
![]() $\delta _0>0$
such that
$\delta _0>0$
such that
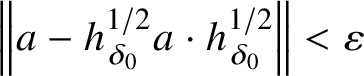 $\left \lVert a-h_{\delta _0}^{1/2}a\cdot h_{\delta _0}^{1/2}\right \rVert <\varepsilon $
.
$\left \lVert a-h_{\delta _0}^{1/2}a\cdot h_{\delta _0}^{1/2}\right \rVert <\varepsilon $
.
Note that
![]() $h_{\delta _0}$
lies in the center of
$h_{\delta _0}$
lies in the center of
![]() $C\!\left([0,1], M_{pq}(B)\right )$
, and for any
$C\!\left([0,1], M_{pq}(B)\right )$
, and for any
![]() $f\in L_{p,q}$
and any
$f\in L_{p,q}$
and any
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
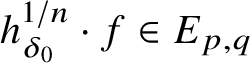 $h^{1/n}_{\delta _0}\cdot f\in E_{p,q}$
. Then since
$h^{1/n}_{\delta _0}\cdot f\in E_{p,q}$
. Then since
![]() $a\lesssim b_0$
in
$a\lesssim b_0$
in
![]() $L_{p,q}$
, one checks
$L_{p,q}$
, one checks
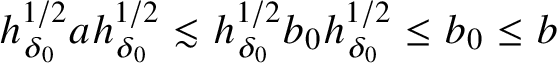 $h_{\delta _0}^{1/2}a h_{\delta _0}^{1/2}\lesssim h_{\delta _0}^{1/2}b_0 h_{\delta _0}^{1/2}\le b_0\le b$
in
$h_{\delta _0}^{1/2}a h_{\delta _0}^{1/2}\lesssim h_{\delta _0}^{1/2}b_0 h_{\delta _0}^{1/2}\le b_0\le b$
in
![]() $E_{p,q}$
. This implies that
$E_{p,q}$
. This implies that
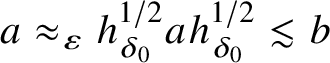 $a\approx _{\varepsilon } h_{\delta _0}^{1/2}a h_{\delta _0}^{1/2}\lesssim b$
in
$a\approx _{\varepsilon } h_{\delta _0}^{1/2}a h_{\delta _0}^{1/2}\lesssim b$
in
![]() $E_{p,q}$
. Since this holds for any
$E_{p,q}$
. Since this holds for any
![]() $1>\varepsilon >0$
, one concludes that
$1>\varepsilon >0$
, one concludes that
![]() $a\lesssim b$
in
$a\lesssim b$
in
![]() $E_{p,q}$
.
$E_{p,q}$
.
Definition 8.3 compare [Reference Fu19, 2.1.1.]
In the spirit of Definition 3.1, a simple
![]() $C^*$
-algebra A is said to have essential tracial nuclear dimension at most n if A is essentially tracially in
$C^*$
-algebra A is said to have essential tracial nuclear dimension at most n if A is essentially tracially in
![]() ${\cal N}_n$
, the class of
${\cal N}_n$
, the class of
![]() $C^*$
-algebras with nuclear dimension at most n – that is, if for any
$C^*$
-algebras with nuclear dimension at most n – that is, if for any
![]() $\varepsilon>0$
and any finite subsets
$\varepsilon>0$
and any finite subsets
![]() ${\cal F}\subset A$
and
${\cal F}\subset A$
and
![]() $a\in A_+\setminus \{0\}$
, there exist an element
$a\in A_+\setminus \{0\}$
, there exist an element
![]() $e\in A_+^{\textbf{1}}$
and a
$e\in A_+^{\textbf{1}}$
and a
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $B\subset A$
which has nuclear dimension at most n such that
$B\subset A$
which has nuclear dimension at most n such that
-
(1)
 $\lVert ex-xe\rVert <\varepsilon $
for all
$\lVert ex-xe\rVert <\varepsilon $
for all
 $x\in {\cal F}$
,
$x\in {\cal F}$
, -
(2)
 $(1-e)x\in _{\varepsilon } B$
and
$(1-e)x\in _{\varepsilon } B$
and
 $\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
$\lVert (1-e)x\rVert \ge \lVert x\rVert -\varepsilon $
for all
 $x\in {\cal F}$
and
$x\in {\cal F}$
and -
(3)
 $e\lesssim a$
.
$e\lesssim a$
.
Let us denote by
![]() ${\cal N}_{{\mathscr Z},s,s}$
the class of separable nuclear simple
${\cal N}_{{\mathscr Z},s,s}$
the class of separable nuclear simple
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebras.
$C^*$
-algebras.
Theorem 8.4. The unital simple
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_z^C$
is essentially tracially in
$A_z^C$
is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
and has essential tracial nuclear dimension at most
${\cal N}_{{\mathscr Z},s,s}$
and has essential tracial nuclear dimension at most
![]() $1$
, stable rank one and strict comparison for positive elements. Moreover,
$1$
, stable rank one and strict comparison for positive elements. Moreover,
![]() $A_z^C$
has a unique tracial state and has no
$A_z^C$
has a unique tracial state and has no
![]() $2$
-quasitraces other than the unique tracial state, and
$2$
-quasitraces other than the unique tracial state, and
 $$ \begin{align} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
$$ \begin{align} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, \{0\}). \end{align} $$
Recall that if C is exact and not nuclear, then
![]() $A_z^C$
is exact and not nuclear (Theorem 7.3), and if
$A_z^C$
is exact and not nuclear (Theorem 7.3), and if
![]() $C$
is not exact, then
$C$
is not exact, then
![]() $A_z^C$
is not exact (Proposition 7.4).
$A_z^C$
is not exact (Proposition 7.4).
Proof. We will first show that
![]() $A_z^C$
is essentially tracially in
$A_z^C$
is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
. We will retain the notation from the construction of
${\cal N}_{{\mathscr Z},s,s}$
. We will retain the notation from the construction of
![]() $A_z^C$
.
$A_z^C$
.
Fix a finite subset
![]() ${\cal F}$
and an element
${\cal F}$
and an element
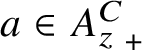 $a\in {A_z^C}_+$
with
$a\in {A_z^C}_+$
with
![]() $\lVert a\rVert =1$
. To verify that
$\lVert a\rVert =1$
. To verify that
![]() $A_z^C$
has the specified property, without loss of generality we may assume that there is a finite subset
$A_z^C$
has the specified property, without loss of generality we may assume that there is a finite subset
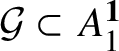 ${\cal G}\subset A_1^{\textbf{1}}$
such that
${\cal G}\subset A_1^{\textbf{1}}$
such that
![]() $\varphi _{1, \infty }({\cal G})={\cal F}$
. Since
$\varphi _{1, \infty }({\cal G})={\cal F}$
. Since
![]() $\cup _{n=1} {\cal F}_{1,n}$
is dense in
$\cup _{n=1} {\cal F}_{1,n}$
is dense in
![]() $A_1$
(see the proof of Theorem 7.3), we may assume that
$A_1$
(see the proof of Theorem 7.3), we may assume that
![]() ${\cal G}\subset {\cal F}_{1,m}$
for some
${\cal G}\subset {\cal F}_{1,m}$
for some
![]() $m\ge 1$
. By the first few lines of the proof of Theorem 7.3, we may assume that
$m\ge 1$
. By the first few lines of the proof of Theorem 7.3, we may assume that
![]() $\varphi _{1,m}({\cal G})\subset \varphi _{1, m}\left ({\cal F}_{1,m}\right )\subset {\cal F}_{m+1,1}$
. Starting from
$\varphi _{1,m}({\cal G})\subset \varphi _{1, m}\left ({\cal F}_{1,m}\right )\subset {\cal F}_{m+1,1}$
. Starting from
![]() $m+1$
instead of
$m+1$
instead of
![]() $1$
, to further simplify notation, without loss of generality we may assume that
$1$
, to further simplify notation, without loss of generality we may assume that
![]() ${\cal G}\subset {\cal F}_{1,1}={\cal F}_1\cup \{0\}$
. Without loss of generality, we may assume that there is
${\cal G}\subset {\cal F}_{1,1}={\cal F}_1\cup \{0\}$
. Without loss of generality, we may assume that there is
![]() $a'\in (A_1)_+^{\textbf{1}}$
with
$a'\in (A_1)_+^{\textbf{1}}$
with
![]() $\lVert a'\rVert =1$
such that
$\lVert a'\rVert =1$
such that
It follows from [Reference Rørdam40, Proposition 2.2] that
Put
![]() $a_0'=f_{1/4}(a')\ (\neq 0)$
. Since
$a_0'=f_{1/4}(a')\ (\neq 0)$
. Since
![]() $A_z^C$
is simple, there are
$A_z^C$
is simple, there are
![]() $x_1,x_2,\dotsc ,x_k\in A_z^C$
such that
$x_1,x_2,\dotsc ,x_k\in A_z^C$
such that
 $$ \begin{align} \sum_{i=1}^k x_i^* \varphi_{1, \infty}\left(a_0'\right)x_i=1. \end{align} $$
$$ \begin{align} \sum_{i=1}^k x_i^* \varphi_{1, \infty}\left(a_0'\right)x_i=1. \end{align} $$
It follows that for some large
![]() $n_0$
, there are
$n_0$
, there are
![]() $y_1,y_2,\dotsc ,y_k\in A_{n_0}$
and
$y_1,y_2,\dotsc ,y_k\in A_{n_0}$
and
![]() $n_1\ge n_0$
such that
$n_1\ge n_0$
such that
 $$ \begin{align} \left\lVert\sum_{i=1}^k \varphi_{n_0, n_1}\left(y_i^*\right) \varphi_{1, n_1}(a_0')\varphi_{n_0, n_1}(y_i)-1_{A_{n_1}}\right\rVert<1/4. \end{align} $$
$$ \begin{align} \left\lVert\sum_{i=1}^k \varphi_{n_0, n_1}\left(y_i^*\right) \varphi_{1, n_1}(a_0')\varphi_{n_0, n_1}(y_i)-1_{A_{n_1}}\right\rVert<1/4. \end{align} $$
It follows that
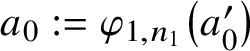 $a_0:=\varphi _{1, n_1}\left (a_0'\right )$
is a full element in
$a_0:=\varphi _{1, n_1}\left (a_0'\right )$
is a full element in
![]() $A_{n_1}$
.
$A_{n_1}$
.
Set
 $$ \begin{align} d=\inf\left\{d_\tau(a_0): \tau\in T\left(A_{n_1}\right)\right\}. \end{align} $$
$$ \begin{align} d=\inf\left\{d_\tau(a_0): \tau\in T\left(A_{n_1}\right)\right\}. \end{align} $$
Since
![]() $a_0$
is full in
$a_0$
is full in
![]() $A_{n_1}$
and
$A_{n_1}$
and
![]() $a_0\in \left (A_{n_1}\right )_+$
, we have
$a_0\in \left (A_{n_1}\right )_+$
, we have
![]() $d>0$
. Choose
$d>0$
. Choose
![]() $m>n_1$
such that
$m>n_1$
such that
By applying Lemma 8.1, we obtain
![]() $e\in (A_{m+1})_+^{\textbf{1}}\setminus \{0\}$
such that
$e\in (A_{m+1})_+^{\textbf{1}}\setminus \{0\}$
such that
-
(i)
 $e(t)\in M_{p_{m+1}q_{m+1}}$
for all
$e(t)\in M_{p_{m+1}q_{m+1}}$
for all
 $t\in [0,1]$
and
$t\in [0,1]$
and
 $e(1)=0$
,
$e(1)=0$
, -
(ii)
 $\lVert ex-xe\rVert <\varepsilon \text { for all } x\in \varphi _m\left (\varphi _{1, m}({\cal G})\right )$
,
$\lVert ex-xe\rVert <\varepsilon \text { for all } x\in \varphi _m\left (\varphi _{1, m}({\cal G})\right )$
, -
(iii)
 $\varphi _{m+1, \infty }\left ((1-e)\varphi _m\left (\varphi _{1, m}(x)\right )\right )\in _{\varepsilon } B_z$
, and for all
$\varphi _{m+1, \infty }\left ((1-e)\varphi _m\left (\varphi _{1, m}(x)\right )\right )\in _{\varepsilon } B_z$
, and for all $$ \begin{align*} \left\lVert\varphi_{m+1, \infty}\left((1-e)\varphi_m\left(\varphi_{1, m}(x)\right)\right)\right\rVert\ge (1-1/m)\left\lVert\varphi_{1,m}(x)\right\rVert \end{align*} $$
$$ \begin{align*} \left\lVert\varphi_{m+1, \infty}\left((1-e)\varphi_m\left(\varphi_{1, m}(x)\right)\right)\right\rVert\ge (1-1/m)\left\lVert\varphi_{1,m}(x)\right\rVert \end{align*} $$
 $x\in {\cal F}_{1,1}$
, and
$x\in {\cal F}_{1,1}$
, and
-
(iv)
 $d_\tau (e)<1/3^m$
for all
$d_\tau (e)<1/3^m$
for all
 $\tau \in T(A_{m+1})$
.
$\tau \in T(A_{m+1})$
.
Denote
![]() $a_1=\varphi _{n_1,m}(a_0)$
. It is full in
$a_1=\varphi _{n_1,m}(a_0)$
. It is full in
![]() $A_m$
. Write, as in Theorem 6.8 and equation (e6.16),
$A_m$
. Write, as in Theorem 6.8 and equation (e6.16),
 $$ \begin{align} \varphi_{m}(a_1)=u^*\begin{pmatrix} \Theta_{m}(a_1) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(a_1\circ \xi_1)\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(a_1\circ \xi_k)\otimes 1_5 \end{pmatrix} u, \end{align} $$
$$ \begin{align} \varphi_{m}(a_1)=u^*\begin{pmatrix} \Theta_{m}(a_1) & 0 &\dotsb & 0\\ 0 & \gamma_{m}(a_1\circ \xi_1)\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(a_1\circ \xi_k)\otimes 1_5 \end{pmatrix} u, \end{align} $$
where
![]() $u\in U\left (C\!\left([0,1], M_{p_{m+1}q_{m+1}}(B)\right )\right )$
,
$u\in U\left (C\!\left([0,1], M_{p_{m+1}q_{m+1}}(B)\right )\right )$
,
![]() $\Theta _{m}: A_m\to C\!\left([0,1], M_{kp_mq_m}(B)\right )$
is a homomorphism,
$\Theta _{m}: A_m\to C\!\left([0,1], M_{kp_mq_m}(B)\right )$
is a homomorphism,
![]() $k\ge 1$
is an integer and
$k\ge 1$
is an integer and
![]() $\gamma _m: B\to M_{R(m)}$
is a finite-dimensional representation. Moreover,
$\gamma _m: B\to M_{R(m)}$
is a finite-dimensional representation. Moreover,
Let
 $$ \begin{align} b_0=u^*\begin{pmatrix} 0 & 0 &\dotsb & 0\\ 0 & \gamma_{m}(a_1\circ \xi_1)\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(a_1\circ \xi_k)\otimes 1_5 \end{pmatrix} u. \end{align} $$
$$ \begin{align} b_0=u^*\begin{pmatrix} 0 & 0 &\dotsb & 0\\ 0 & \gamma_{m}(a_1\circ \xi_1)\otimes 1_5 &\dotsb &0\\ \vdots & \vdots & & \vdots\\ 0 & 0 & \dotsb & \gamma_m(a_1\circ \xi_k)\otimes 1_5 \end{pmatrix} u. \end{align} $$
Note that
![]() $b_0\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
. Moreover, since
$b_0\in C\!\left([0,1], M_{p_{m+1}q_{m+1}}\right )$
. Moreover, since
![]() $a_1\in E_{p_m,q_m}$
, we have
$a_1\in E_{p_m,q_m}$
, we have
![]() $a_1(0)=a_1'\otimes 1_{q_m}$
for some
$a_1(0)=a_1'\otimes 1_{q_m}$
for some
![]() $a_1'\in M_{p_m}(B)$
. Therefore,
$a_1'\in M_{p_m}(B)$
. Therefore,
Put
 $$ \begin{align} c_0'&=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m\left(a_1'\right)\end{pmatrix} \end{align} $$
$$ \begin{align} c_0'&=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m\left(a_1'\right)\end{pmatrix} \end{align} $$
and
 $$ \begin{align} c_0&=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1(0))\end{pmatrix}\otimes 1_5=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m\left(a_1'\right)\end{pmatrix}\otimes 1_{5q_m}=c_0'\otimes 1_{5q_m}. \end{align} $$
$$ \begin{align} c_0&=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1(0))\end{pmatrix}\otimes 1_5=\begin{pmatrix} 0 & 0\\ 0 &\gamma_m\left(a_1'\right)\end{pmatrix}\otimes 1_{5q_m}=c_0'\otimes 1_{5q_m}. \end{align} $$
Note that
![]() $c_0'\in M_{d_mp_m}$
. Put
$c_0'\in M_{d_mp_m}$
. Put
 $$ \begin{align} c_i(t)&=&\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1\circ \xi_i(t))\end{pmatrix}\otimes 1_5, \quad i=r_0+1,r_0+2,\dotsc,k. \end{align} $$
$$ \begin{align} c_i(t)&=&\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1\circ \xi_i(t))\end{pmatrix}\otimes 1_5, \quad i=r_0+1,r_0+2,\dotsc,k. \end{align} $$
Recall (see formula (e6.34)) that at
![]() $t=0$
,
$t=0$
,
 $$ \begin{align} \xi_i(0)=\begin{cases} 0 & {\text{if }} 1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k. \end{cases} \end{align} $$
$$ \begin{align} \xi_i(0)=\begin{cases} 0 & {\text{if }} 1\le i\le r_0,\\ 1/2 & \text{if } r_0<i\le k. \end{cases} \end{align} $$
Recall also (see the line after equation (e6.35)) that
![]() $ r_05q_m=t_0q_{m+1}$
for some integer
$ r_05q_m=t_0q_{m+1}$
for some integer
![]() $t_0\ge 1$
. Hence
$t_0\ge 1$
. Hence
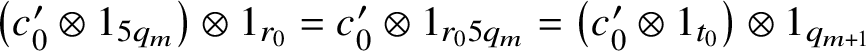 $\left (c_0'\otimes 1_{5q_m}\right )\otimes 1_{r_0}=c_0'\otimes 1_{r_05q_m}=\left (c_0'\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
. On the other hand, since
$\left (c_0'\otimes 1_{5q_m}\right )\otimes 1_{r_0}=c_0'\otimes 1_{r_05q_m}=\left (c_0'\otimes 1_{t_0}\right )\otimes 1_{q_{m+1}}$
. On the other hand, since
![]() $k=r_0+m(0)q_{m+1}$
(see equation (e6.30)), we have
$k=r_0+m(0)q_{m+1}$
(see equation (e6.30)), we have
 $$ \begin{align} \mathrm{diag}\left(c_{r_0+1}(0), \dotsc, c_k(0)\right) =^s\left(\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1(1/2))\end{pmatrix}\otimes 1_5\right)\otimes 1_{m(0)q_{m+1}}. \end{align} $$
$$ \begin{align} \mathrm{diag}\left(c_{r_0+1}(0), \dotsc, c_k(0)\right) =^s\left(\begin{pmatrix} 0 & 0\\ 0 &\gamma_m(a_1(1/2))\end{pmatrix}\otimes 1_5\right)\otimes 1_{m(0)q_{m+1}}. \end{align} $$
Note that
![]() $=^s$
is implemented by the same scalar unitary as in equation (e6.36) (see also the end of Notation 6.6 for the notation
$=^s$
is implemented by the same scalar unitary as in equation (e6.36) (see also the end of Notation 6.6 for the notation
![]() $=^s$
). As in formula (e6.37) (and the line after it), since
$=^s$
). As in formula (e6.37) (and the line after it), since
![]() $b_0\in C\!\left([0,1],M_{p_{m+1}q_{m+1}}\right )$
(mentioned earlier), this implies that
$b_0\in C\!\left([0,1],M_{p_{m+1}q_{m+1}}\right )$
(mentioned earlier), this implies that
![]() $b_0\in L_{p_{m+1}, q_{m+1}}$
(see equation (e8.31)).
$b_0\in L_{p_{m+1}, q_{m+1}}$
(see equation (e8.31)).
Since
![]() $a_1\ge 0$
,
$a_1\ge 0$
,
![]() $b_0(t)\le a_1(t)$
for all
$b_0(t)\le a_1(t)$
for all
![]() $t\in [0,1]$
(see equation (e8.44)). Since
$t\in [0,1]$
(see equation (e8.44)). Since
![]() $\varphi _k$
is an injective unital homomorphism for all k, by equation (e8.40), we also have
$\varphi _k$
is an injective unital homomorphism for all k, by equation (e8.40), we also have
 $$ \begin{align} \inf\{d_\tau(\varphi_m(a_1)): \tau\in T(A_{m+1})\}=\inf\left\{d_\tau\left(\varphi_{n_1, m+1}(a_0)\right): \tau\in T(A_m)\right\}\ge d. \end{align} $$
$$ \begin{align} \inf\{d_\tau(\varphi_m(a_1)): \tau\in T(A_{m+1})\}=\inf\left\{d_\tau\left(\varphi_{n_1, m+1}(a_0)\right): \tau\in T(A_m)\right\}\ge d. \end{align} $$
By formulas (e8.42), (e8.44), (e8.43) and (e8.41), we conclude that for each
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
where
![]() $\sigma $
is the unique tracial state of
$\sigma $
is the unique tracial state of
![]() $M_{p_{m+1}q_{m+1}}$
,
$M_{p_{m+1}q_{m+1}}$
,
![]() $\tau _0$
is the unique tracial state of
$\tau _0$
is the unique tracial state of
![]() $M_{p_{m+1}}\otimes 1_{q_{m+1}}$
and
$M_{p_{m+1}}\otimes 1_{q_{m+1}}$
and
![]() $\tau _1$
is the unique tracial state of
$\tau _1$
is the unique tracial state of
![]() $1_{q_{m+1}}\otimes M_{q_{m+1}}$
. Note that
$1_{q_{m+1}}\otimes M_{q_{m+1}}$
. Note that
![]() $e(1)=0$
. It follows that for all
$e(1)=0$
. It follows that for all
![]() $\tau \in T\left (L_{p_{m+1}, q_{m+1}}\right )$
,
$\tau \in T\left (L_{p_{m+1}, q_{m+1}}\right )$
,
By, for example, [Reference Gong, Lin and Niu24, Theorem 3.18],
By Lemma 8.2,
It follows that
Combining this with (ii) and (iii) here, we conclude that
![]() $A_z^C$
is essentially tracially in
$A_z^C$
is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
. Since
${\cal N}_{{\mathscr Z},s,s}$
. Since
![]() $B_z\cong {\mathscr Z}$
, which has nuclear dimension
$B_z\cong {\mathscr Z}$
, which has nuclear dimension
![]() $1$
[Reference Sato and White44, Theorem 6.4],
$1$
[Reference Sato and White44, Theorem 6.4],
![]() $A_z^C$
has essential tracial nuclear dimension at most
$A_z^C$
has essential tracial nuclear dimension at most
![]() $1$
. Since
$1$
. Since
![]() ${\mathscr Z}$
is in
${\mathscr Z}$
is in
![]() ${\cal T}$
,
${\cal T}$
,
![]() $A_z^C$
is e. tracially in
$A_z^C$
is e. tracially in
![]() ${\cal T}$
. By Proposition 4.6, every
${\cal T}$
. By Proposition 4.6, every
![]() $2$
-quasitrace of
$2$
-quasitrace of
![]() $A_z^C$
is a tracial state. By Corollary 5.10, A has stable rank one.
$A_z^C$
is a tracial state. By Corollary 5.10, A has stable rank one.
Remark 8.5. Note that the proof of Theorem 8.4 actually shows that
![]() $A_z^C$
is essentially tracially approximated by
$A_z^C$
is essentially tracially approximated by
![]() ${\mathscr Z}$
itself, as
${\mathscr Z}$
itself, as
![]() $B_z\cong {\mathscr Z}$
. Let
$B_z\cong {\mathscr Z}$
. Let
![]() ${\cal P}$
be the class of separable nuclear
${\cal P}$
be the class of separable nuclear
![]() $C^*$
-algebras. Then
$C^*$
-algebras. Then
![]() $A_z^C$
is essentially tracially in
$A_z^C$
is essentially tracially in
![]() ${\cal P}$
, since
${\cal P}$
, since
![]() ${\mathscr Z}\in {\cal P}$
. By Proposition 7.4 and Theorem 7.3,
${\mathscr Z}\in {\cal P}$
. By Proposition 7.4 and Theorem 7.3,
![]() $A_z^C$
is not nuclear if C is not nuclear. Since
$A_z^C$
is not nuclear if C is not nuclear. Since
![]() $A_z^C$
has no nonzero projection other than the identity, for nonnuclear C it cannot be TA
$A_z^C$
has no nonzero projection other than the identity, for nonnuclear C it cannot be TA
![]() ${\cal P}$
.
${\cal P}$
.
Theorem 8.6. Let
![]() $(G, G_+, g)$
be a countable weakly unperforated simple ordered group, F be a countable abelian group,
$(G, G_+, g)$
be a countable weakly unperforated simple ordered group, F be a countable abelian group,
![]() $\Delta $
be a metrisable Choquet simplex and
$\Delta $
be a metrisable Choquet simplex and
![]() $\lambda : G\to \operatorname {Aff}_+(\Delta )$
be a homomorphism.
$\lambda : G\to \operatorname {Aff}_+(\Delta )$
be a homomorphism.
Then there is a unital simple nonexact (or exact but nonnuclear)
![]() $C^*$
-algebra A which is e. tracially in
$C^*$
-algebra A which is e. tracially in
![]() ${\cal N}_{{\mathscr Z}, s,s}$
and has essential tracial nuclear dimension at most
${\cal N}_{{\mathscr Z}, s,s}$
and has essential tracial nuclear dimension at most
![]() $1$
, stable rank one and strict comparison for positive elements, such that
$1$
, stable rank one and strict comparison for positive elements, such that
Proof. It follows from [Reference Gong, Lin and Niu24, Theorem 13.50] that there is a unital simple
![]() $A_0$
with finite nuclear dimension which satisfies the UCT such that
$A_0$
with finite nuclear dimension which satisfies the UCT such that
 $$ \begin{align} \left(K_0(A_0), K_0(A_0)_+, \left[1_{A_0}\right], K_1(A_0), T(A_0), \rho_{A_0}\right)=(G, G_+, g, F, \Delta, \lambda). \end{align} $$
$$ \begin{align} \left(K_0(A_0), K_0(A_0)_+, \left[1_{A_0}\right], K_1(A_0), T(A_0), \rho_{A_0}\right)=(G, G_+, g, F, \Delta, \lambda). \end{align} $$
Let
![]() $A_z^C$
be the
$A_z^C$
be the
![]() $C^*$
-algebra in Theorem 7.3 with
$C^*$
-algebra in Theorem 7.3 with
![]() $A_z^C$
nonexact (or exact but nonnuclear). Then define
$A_z^C$
nonexact (or exact but nonnuclear). Then define
![]() $A:= A_0\otimes A_z^C$
. Note that since
$A:= A_0\otimes A_z^C$
. Note that since
![]() $A_0$
is a separable amenable
$A_0$
is a separable amenable
![]() $C^*$
-algebrasatisfying the UCT, by [Reference Schochet45, Theorem 2.14], the Künneth formula holds for the tensor product
$C^*$
-algebrasatisfying the UCT, by [Reference Schochet45, Theorem 2.14], the Künneth formula holds for the tensor product
![]() $A=A_0\otimes A_z^C$
. Since the only normalised
$A=A_0\otimes A_z^C$
. Since the only normalised
![]() $2$
-quasitrace of
$2$
-quasitrace of
![]() $A_z^C$
is the unique tracial state, and
$A_z^C$
is the unique tracial state, and
 $$ \begin{align*} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, 0), \end{align*} $$
$$ \begin{align*} \left(K_0\left(A_z^C\right), K_0\left(A_z^C\right)_+, \left[1_{A_z^C}\right], K_1\left(A_z^C\right)\right)=(\mathbb{Z}, \mathbb{Z}_+, 1, 0), \end{align*} $$
one computes (applying the Künneth formula) that
We will show that A is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
and has e. tracial nuclear dimension at most
${\cal N}_{{\mathscr Z},s,s}$
and has e. tracial nuclear dimension at most
![]() $1$
. Once this is done, by Definition 8.3 A has essentially tracial nuclear dimension at most
$1$
. Once this is done, by Definition 8.3 A has essentially tracial nuclear dimension at most
![]() $1$
and by Corollary 5.10 has stable rank one and strict comparison for positive elements.
$1$
and by Corollary 5.10 has stable rank one and strict comparison for positive elements.
To see that A is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
, set
${\cal N}_{{\mathscr Z},s,s}$
, set
![]() ${{1>\varepsilon }}>0$
, let
${{1>\varepsilon }}>0$
, let
![]() ${\cal F}\subset A^{\textbf{1}}\setminus \{0\}$
be a finite subset and set
${\cal F}\subset A^{\textbf{1}}\setminus \{0\}$
be a finite subset and set
![]() $d\in A_+\setminus \{0\}$
. Without loss of generality, we may assume that
$d\in A_+\setminus \{0\}$
. Without loss of generality, we may assume that
![]() $\lVert x\rVert \ge \varepsilon $
for all
$\lVert x\rVert \ge \varepsilon $
for all
![]() $x\in {\cal F}$
. For each
$x\in {\cal F}$
. For each
![]() $x\in {\cal F}$
, put
$x\in {\cal F}$
, put
![]() $a(x)=g_ {{\varepsilon ^2/32}} (xx^*)$
and
$a(x)=g_ {{\varepsilon ^2/32}} (xx^*)$
and
![]() $b(x)=g_{{\varepsilon ^2/16}} (xx^*)$
, where
$b(x)=g_{{\varepsilon ^2/16}} (xx^*)$
, where
![]() $g_r(t)\in C_0([0,1])$
such that
$g_r(t)\in C_0([0,1])$
such that
![]() $g_r(t)=0$
for
$g_r(t)=0$
for
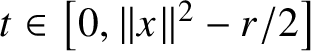 $t\in \left [0, \lVert x\rVert ^{{2}}-r/2\right ]$
,
$t\in \left [0, \lVert x\rVert ^{{2}}-r/2\right ]$
,
![]() $g_r(t)=1$
for
$g_r(t)=1$
for
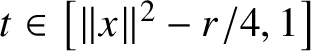 $t\in \left [\lVert x\rVert ^{{2}}-r/4, 1\right ]$
and
$t\in \left [\lVert x\rVert ^{{2}}-r/4, 1\right ]$
and
![]() $g_r$
is linear in
$g_r$
is linear in
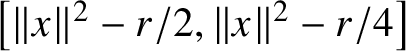 $\left [\lVert x\rVert ^{{2}}-r/2, \lVert x\rVert ^{{2}}-r/4\right ]$
. Note that
$\left [\lVert x\rVert ^{{2}}-r/2, \lVert x\rVert ^{{2}}-r/4\right ]$
. Note that
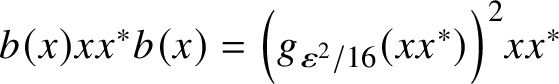 $b(x)xx^*b(x)=\left (g_{{\varepsilon ^2/16}} ( xx^*)\right )^2xx^*$
. Therefore,
$b(x)xx^*b(x)=\left (g_{{\varepsilon ^2/16}} ( xx^*)\right )^2xx^*$
. Therefore,
 $$ \begin{align} b(x)xx^*b(x)\ge \left(\lVert xx^*\rVert-(\varepsilon/4)^2\right)b(x)^2. \end{align} $$
$$ \begin{align} b(x)xx^*b(x)\ge \left(\lVert xx^*\rVert-(\varepsilon/4)^2\right)b(x)^2. \end{align} $$
By Kirchberg’s slice lemma (see, for example, [Reference Rørdam41, Lemma 4.1.9]), for each
![]() $x\in {\cal F}$
there are
$x\in {\cal F}$
there are
![]() $c(x)\in (A_0)_+\setminus \{0\}$
,
$c(x)\in (A_0)_+\setminus \{0\}$
,
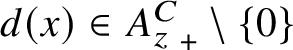 $d(x)\in {A_z^C}_+\setminus \{0\}$
and
$d(x)\in {A_z^C}_+\setminus \{0\}$
and
![]() $z(x)\in A_0\otimes A_z^C$
such that
$z(x)\in A_0\otimes A_z^C$
such that
![]() $z(x)^*z(x)=c(x)\otimes d(x)$
and
$z(x)^*z(x)=c(x)\otimes d(x)$
and
![]() $z(x)z(x)^*\in \mathrm {Her}(a(x))$
. We may assume that
$z(x)z(x)^*\in \mathrm {Her}(a(x))$
. We may assume that
![]() $\lVert c(x)\rVert =\lVert d(x)\rVert =1$
. This also implies that
$\lVert c(x)\rVert =\lVert d(x)\rVert =1$
. This also implies that
![]() $\lVert z(x)z(x)^*\rVert =1$
. Put
$\lVert z(x)z(x)^*\rVert =1$
. Put
 $$ \begin{align*} {\cal F}':={\cal F}\cup\left\{x^*x, xx^*, a(x), b(x), c(x), d(x), d(x)^{1/2}, z(x), z^*(x), z(x)^*z(x), z(x)z(x)^*: x\in {\cal F}\right\}. \end{align*} $$
$$ \begin{align*} {\cal F}':={\cal F}\cup\left\{x^*x, xx^*, a(x), b(x), c(x), d(x), d(x)^{1/2}, z(x), z^*(x), z(x)^*z(x), z(x)z(x)^*: x\in {\cal F}\right\}. \end{align*} $$
Without loss of generality, we may assume that there are
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $M\ge 1$
and finite subsets
$M\ge 1$
and finite subsets
![]() ${\cal F}_0\subset A$
and
${\cal F}_0\subset A$
and
![]() ${\cal F}_1\subset A_z^C$
such that for all
${\cal F}_1\subset A_z^C$
such that for all
![]() $y\in {\cal F}'$
,
$y\in {\cal F}'$
,
 $$ \begin{align} y\in_{\varepsilon^2/64} {\cal F}'':= \left\{\sum_{i=1}^na_i\otimes b_i, a_i\in {\cal F}_0, b_i\in {\cal F}_1\right\}, \end{align} $$
$$ \begin{align} y\in_{\varepsilon^2/64} {\cal F}'':= \left\{\sum_{i=1}^na_i\otimes b_i, a_i\in {\cal F}_0, b_i\in {\cal F}_1\right\}, \end{align} $$
By Kirchberg’s slice lemma, there are
![]() $a_0\in (A_0)_+\setminus \{0\}$
and
$a_0\in (A_0)_+\setminus \{0\}$
and
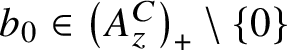 $b_0\in \left (A_z^C\right )_+\setminus \{0\}$
such that
$b_0\in \left (A_z^C\right )_+\setminus \{0\}$
such that
![]() $a_0\otimes b_0\lesssim d$
.
$a_0\otimes b_0\lesssim d$
.
Let us identify
![]() $A_0$
with
$A_0$
with
![]() $A_0\otimes {\mathscr Z}$
(see [Reference Winter48, Corollary 7.3]). In
$A_0\otimes {\mathscr Z}$
(see [Reference Winter48, Corollary 7.3]). In
![]() $A_0\otimes {\mathscr Z}$
, choose
$A_0\otimes {\mathscr Z}$
, choose
![]() $1_{A_0}\otimes a_z$
with
$1_{A_0}\otimes a_z$
with
![]() $a_z\in {\mathscr Z}_+\setminus \{0\}$
such that
$a_z\in {\mathscr Z}_+\setminus \{0\}$
such that
![]() $1_{A_0}\otimes a_z\lesssim _{A_0} a_0$
. Choose
$1_{A_0}\otimes a_z\lesssim _{A_0} a_0$
. Choose
![]() $b_z\in (B_z)_+\setminus \{0\}\subset A_z^C$
such that
$b_z\in (B_z)_+\setminus \{0\}\subset A_z^C$
such that
![]() $b_z\lesssim _{A_z^C} b_0$
.
$b_z\lesssim _{A_z^C} b_0$
.
Note that
![]() $B_z\cong {\mathscr Z}_b\otimes B_z$
, where
$B_z\cong {\mathscr Z}_b\otimes B_z$
, where
![]() ${\mathscr Z}_b\cong {\mathscr Z}$
. Put
${\mathscr Z}_b\cong {\mathscr Z}$
. Put
![]() $c_0:=\sigma (a_z)\otimes b_z\in B_z$
, where
$c_0:=\sigma (a_z)\otimes b_z\in B_z$
, where
![]() $\sigma : 1_{A_0}\otimes {\mathscr Z}(\subset A_0)\to {\mathscr Z}_b\otimes 1_{B_z}$
is an isomorphism. Consider
$\sigma : 1_{A_0}\otimes {\mathscr Z}(\subset A_0)\to {\mathscr Z}_b\otimes 1_{B_z}$
is an isomorphism. Consider
![]() $D_0:=A_0\otimes \sigma \left (1_{A_0}\otimes {\mathscr Z}\right )\otimes 1_{B_z}\subset A_0\otimes B_z$
. We may also write
$D_0:=A_0\otimes \sigma \left (1_{A_0}\otimes {\mathscr Z}\right )\otimes 1_{B_z}\subset A_0\otimes B_z$
. We may also write
![]() $D_0=(A_0\otimes {\mathscr Z})\otimes \sigma \left (1_{A_0}\otimes {\mathscr Z}\right )\otimes 1_{B_z}$
. There is a sequence of unitaries
$D_0=(A_0\otimes {\mathscr Z})\otimes \sigma \left (1_{A_0}\otimes {\mathscr Z}\right )\otimes 1_{B_z}$
. There is a sequence of unitaries
![]() $v_n\in D_0$
such that
$v_n\in D_0$
such that
 $$ \begin{align} \lim_{n\to\infty}v_n^*\left(1_{A_0}\otimes \sigma(a_z)\otimes 1_{B_z}\right)v_n=1_{A_0}\otimes a_z\otimes 1_{B_z}. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}v_n^*\left(1_{A_0}\otimes \sigma(a_z)\otimes 1_{B_z}\right)v_n=1_{A_0}\otimes a_z\otimes 1_{B_z}. \end{align} $$
It follows that
By Remark 8.5, there exists
![]() $e_1\in A_z^C$
with
$e_1\in A_z^C$
with
![]() $0\le e_1\le 1$
such that for all
$0\le e_1\le 1$
such that for all
![]() $f\in {\cal F}_1$
,
$f\in {\cal F}_1$
,
 $$ \begin{align} \lVert e_1f-fe_1\rVert&<\varepsilon^2/ {{64}} {{(nM)}}, \qquad\left(1_{A_z^C}-e_1\right)f\in_{\varepsilon^2/ {{64}} {{(nM)}}} B_z, \end{align} $$
$$ \begin{align} \lVert e_1f-fe_1\rVert&<\varepsilon^2/ {{64}} {{(nM)}}, \qquad\left(1_{A_z^C}-e_1\right)f\in_{\varepsilon^2/ {{64}} {{(nM)}}} B_z, \end{align} $$
 $$ \begin{align} \left\lVert\left(1_{A_z^C}-e_1\right)f\right\rVert&\ge \left(1-\varepsilon^2/{{ {{64}} (nM)}}\right)\lVert f\rVert \mathrm{\ and\ } e_1\lesssim c_0. \end{align} $$
$$ \begin{align} \left\lVert\left(1_{A_z^C}-e_1\right)f\right\rVert&\ge \left(1-\varepsilon^2/{{ {{64}} (nM)}}\right)\lVert f\rVert \mathrm{\ and\ } e_1\lesssim c_0. \end{align} $$
Put
![]() $B=A_0\otimes B_z$
. Then by [Reference Castillejos, Evington, Tikuisis, White and Winter10, Theorem B], B is a separable simple
$B=A_0\otimes B_z$
. Then by [Reference Castillejos, Evington, Tikuisis, White and Winter10, Theorem B], B is a separable simple
![]() ${\mathscr Z}$
-stable
${\mathscr Z}$
-stable
![]() $C^*$
-algebra and has nuclear dimension at most
$C^*$
-algebra and has nuclear dimension at most
![]() $1$
.
$1$
.
Put
![]() $e=1_{A_0}\otimes e_1$
. Then
$e=1_{A_0}\otimes e_1$
. Then
![]() $0\le e\le 1$
. For any
$0\le e\le 1$
. For any
![]() $f''\in {\cal F}''$
, we have that
$f''\in {\cal F}''$
, we have that
![]() $f''=\sum _{i=1}^n a_i\otimes b_i$
for some
$f''=\sum _{i=1}^n a_i\otimes b_i$
for some
![]() $a_i\in {\cal F}_0$
and
$a_i\in {\cal F}_0$
and
![]() $b_i\in {\cal F}_1$
. It follows from formula (e8.66) that
$b_i\in {\cal F}_1$
. It follows from formula (e8.66) that
 $$ \begin{align} \lVert ef''-f''e\rVert=\left\lVert e\left(\sum_{i=1}^n a_i\otimes b_i\right)-\left(\sum_{i=1}^n a_i\otimes b_i\right)e\right\rVert =\left\lVert\sum_{i=1}^n a_i\otimes (e_1b_i-b_ie_1)\right\rVert<\varepsilon^2/ {{64}}. \end{align} $$
$$ \begin{align} \lVert ef''-f''e\rVert=\left\lVert e\left(\sum_{i=1}^n a_i\otimes b_i\right)-\left(\sum_{i=1}^n a_i\otimes b_i\right)e\right\rVert =\left\lVert\sum_{i=1}^n a_i\otimes (e_1b_i-b_ie_1)\right\rVert<\varepsilon^2/ {{64}}. \end{align} $$
Also by formula (e8.66), for
![]() $f''\in {\cal F}''$
,
$f''\in {\cal F}''$
,
 $$ \begin{align} &&\hspace{-0.2in}(1-e)f''=\left(1-1_{A_0}\otimes e_1\right)\left(\sum_{i=1}^n a_i\otimes b_i\right)=\sum_{i=1}^na_i\otimes \left(1_{A_z^C}-e_1\right)b_i\in_{\varepsilon^2/ {{64}} } A_0\otimes B_z. \end{align} $$
$$ \begin{align} &&\hspace{-0.2in}(1-e)f''=\left(1-1_{A_0}\otimes e_1\right)\left(\sum_{i=1}^n a_i\otimes b_i\right)=\sum_{i=1}^na_i\otimes \left(1_{A_z^C}-e_1\right)b_i\in_{\varepsilon^2/ {{64}} } A_0\otimes B_z. \end{align} $$
It follows (recall formula (e8.61)) that for all
![]() $f\in {\cal F}$
,
$f\in {\cal F}$
,
 $$ \begin{align} \lVert ef-fe\rVert<{{\varepsilon^2}}/16\qquad\text{and}\qquad (1-e)f\in_{{{\varepsilon^2/16}}}A_0\otimes B_z=B. \end{align} $$
$$ \begin{align} \lVert ef-fe\rVert<{{\varepsilon^2}}/16\qquad\text{and}\qquad (1-e)f\in_{{{\varepsilon^2/16}}}A_0\otimes B_z=B. \end{align} $$
Moreover, by formulas (e8.65) and (e8.67),
To estimate
![]() $\lVert (1-e)x\rVert $
for
$\lVert (1-e)x\rVert $
for
![]() $x\in {\cal F}$
, we note that by formula (e8.67) (recall that
$x\in {\cal F}$
, we note that by formula (e8.67) (recall that
![]() $\lVert c(x)\rVert =\lVert d(x)\rVert =1$
), for
$\lVert c(x)\rVert =\lVert d(x)\rVert =1$
), for
![]() $x\in {\cal F}$
we have
$x\in {\cal F}$
we have
 $$ \begin{align} \left\lVert(1-e)(c(x)\otimes d(x))^{1/2}\right\rVert &= \left\lVert c(x)^{1/2}\otimes \left(1_{A_z^C}-e_1\right)d(x)^{1/2}\right\rVert \hspace{4pc} \end{align} $$
$$ \begin{align} \left\lVert(1-e)(c(x)\otimes d(x))^{1/2}\right\rVert &= \left\lVert c(x)^{1/2}\otimes \left(1_{A_z^C}-e_1\right)d(x)^{1/2}\right\rVert \hspace{4pc} \end{align} $$
 $$ \begin{align} & \hspace{11pc} \ge \left(1-\varepsilon^2/{{64}}\right)\lVert c(x)\rVert\lVert d(x)\rVert=\left(1-\varepsilon^2/{{64}}\right). \end{align} $$
$$ \begin{align} & \hspace{11pc} \ge \left(1-\varepsilon^2/{{64}}\right)\lVert c(x)\rVert\lVert d(x)\rVert=\left(1-\varepsilon^2/{{64}}\right). \end{align} $$
Then by formulas (e8.70) and (e8.73),
 $$ \begin{align} \nonumber \left\lVert(1-e)z(x)z(x)^*(1-e)\right\rVert&=\left\lVert z(x)^*(1-e)^2z(x)\right\rVert\\[2pt] &\ge \left\lVert(1-e)z(x)^*z(x)(1-e)\right\rVert-\varepsilon^2/{{8}}\\[2pt]\nonumber &=\left\lVert(1-e)(c(x)\otimes d(x))^{1/2}\right\rVert^2-\varepsilon^2/{{8}} \end{align} $$
$$ \begin{align} \nonumber \left\lVert(1-e)z(x)z(x)^*(1-e)\right\rVert&=\left\lVert z(x)^*(1-e)^2z(x)\right\rVert\\[2pt] &\ge \left\lVert(1-e)z(x)^*z(x)(1-e)\right\rVert-\varepsilon^2/{{8}}\\[2pt]\nonumber &=\left\lVert(1-e)(c(x)\otimes d(x))^{1/2}\right\rVert^2-\varepsilon^2/{{8}} \end{align} $$
 $$ \begin{align} & \hspace{9.5pc} \ge\left(1-\varepsilon^2/{{64}}\right)^2-\varepsilon^2/{{8}}>{{1-5\varepsilon^2/32}}. \end{align} $$
$$ \begin{align} & \hspace{9.5pc} \ge\left(1-\varepsilon^2/{{64}}\right)^2-\varepsilon^2/{{8}}>{{1-5\varepsilon^2/32}}. \end{align} $$
Since
![]() $b(x)z(x)z(x)^*=z(x)z(x)^*b(x)=z(x)z(x)^*$
, we compute by formulas (e8.60) and (e8.75)) that for all
$b(x)z(x)z(x)^*=z(x)z(x)^*b(x)=z(x)z(x)^*$
, we compute by formulas (e8.60) and (e8.75)) that for all
![]() $x\in {\cal F}$
,
$x\in {\cal F}$
,
 $$ \begin{align} \left\lVert(1-e)xx^*(1-e)\right\rVert&\ge \left\lVert(1-e)b(x)^{1/2}xx^*b(x)^{1/2}(1-e)\right\rVert \hspace{7pc} \end{align} $$
$$ \begin{align} \left\lVert(1-e)xx^*(1-e)\right\rVert&\ge \left\lVert(1-e)b(x)^{1/2}xx^*b(x)^{1/2}(1-e)\right\rVert \hspace{7pc} \end{align} $$
 $$ \begin{align} &\ge {{\left(\lVert x\rVert^2-\varepsilon^2/16\right)}} \lVert(1-e)b(x)(1-e)\rVert \hspace{1.8pc} \end{align} $$
$$ \begin{align} &\ge {{\left(\lVert x\rVert^2-\varepsilon^2/16\right)}} \lVert(1-e)b(x)(1-e)\rVert \hspace{1.8pc} \end{align} $$
 $$ \begin{align} &\ge {{\left(\lVert x\rVert^2-\varepsilon^2/16\right)}}\left\lVert(1-e)z(x)z(x)^*(1-e)\right\rVert \end{align} $$
$$ \begin{align} &\ge {{\left(\lVert x\rVert^2-\varepsilon^2/16\right)}}\left\lVert(1-e)z(x)z(x)^*(1-e)\right\rVert \end{align} $$
 $$ \begin{align} & \hspace{1.7pc} \ge \left(\lVert x\rVert^2-\varepsilon^2/16\right)\left(1-{{5\varepsilon^2/32}}\right)\ge \lVert x\rVert^2-{{7\varepsilon^2/32}} \end{align} $$
$$ \begin{align} & \hspace{1.7pc} \ge \left(\lVert x\rVert^2-\varepsilon^2/16\right)\left(1-{{5\varepsilon^2/32}}\right)\ge \lVert x\rVert^2-{{7\varepsilon^2/32}} \end{align} $$
(Recall for the last inequality that
![]() $\lVert x\rVert \ge \varepsilon $
.) It follows that for all
$\lVert x\rVert \ge \varepsilon $
.) It follows that for all
![]() $x\in {\cal F}$
,
$x\in {\cal F}$
,
This, together with formula (e8.70), implies that
![]() $A_0\otimes A_z^C$
is essentially tracially in
$A_0\otimes A_z^C$
is essentially tracially in
![]() ${\cal N}_{{\mathscr Z},s,s}$
, since B is
${\cal N}_{{\mathscr Z},s,s}$
, since B is
![]() ${\mathscr Z}$
-stable and has nuclear dimension no more than
${\mathscr Z}$
-stable and has nuclear dimension no more than
![]() $1$
(see [Reference Castillejos, Evington, Tikuisis, White and Winter10, Theorem B]).
$1$
(see [Reference Castillejos, Evington, Tikuisis, White and Winter10, Theorem B]).
Now suppose that we choose
![]() $A_z^C$
not exact. Since
$A_z^C$
not exact. Since
![]() $A_z^C$
embeds into
$A_z^C$
embeds into
![]() $A_0\otimes A_z^C$
and
$A_0\otimes A_z^C$
and
![]() $A_z^C$
is not exact,
$A_z^C$
is not exact,
![]() $A_0\otimes A_z^C$
is also not exact (see, for example, [Reference Wassermann47, Proposition 2.6]). If
$A_0\otimes A_z^C$
is also not exact (see, for example, [Reference Wassermann47, Proposition 2.6]). If
![]() $A_z^C$
is exact but not nuclear, then
$A_z^C$
is exact but not nuclear, then
![]() $A_0\otimes A_z^C$
is exact but not nuclear (by [Reference Brown and Ozawa9, Propositions 10.2.7, 10.1.7]).
$A_0\otimes A_z^C$
is exact but not nuclear (by [Reference Brown and Ozawa9, Propositions 10.2.7, 10.1.7]).
Remark 8.7.
-
(1) Let
 $A_0$
be a unital separable nuclear purely infinite simple
$A_0$
be a unital separable nuclear purely infinite simple
 $C^*$
-algebra in the UCT class. Then the proof of Theorem 8.6 also shows that
$C^*$
-algebra in the UCT class. Then the proof of Theorem 8.6 also shows that
 $A:=A_0\otimes A_z^C$
is a nonexact purely infinite simple
$A:=A_0\otimes A_z^C$
is a nonexact purely infinite simple
 $C^*$
-algebra (if C is nonexact) which has essential tracial nuclear dimension
$C^*$
-algebra (if C is nonexact) which has essential tracial nuclear dimension
 $1$
and
$1$
and
 $\mathrm {Ell}(A)=\mathrm {Ell}(A_0)$
.
$\mathrm {Ell}(A)=\mathrm {Ell}(A_0)$
. -
(2) If the RFD
 $C^*$
-algebra C at the beginning of Section 6 is amenable, then
$C^*$
-algebra C at the beginning of Section 6 is amenable, then
 $C_0((0,1], C)$
is a nuclear contractible
$C_0((0,1], C)$
is a nuclear contractible
 $C^*$
-algebra which satisfies the UCT. It follows that the unitisation B of
$C^*$
-algebra which satisfies the UCT. It follows that the unitisation B of
 $C_0((0,1], C)$
also satisfies the UCT. Therefore
$C_0((0,1], C)$
also satisfies the UCT. Therefore
 $D(m,k)$
and
$D(m,k)$
and
 $I=C_0((0,1), M_{mk}(B))$
in formula (e6.8) satisfy the UCT. Thus
$I=C_0((0,1), M_{mk}(B))$
in formula (e6.8) satisfy the UCT. Thus
 $E_{m,k}$
is nuclear and satisfies the UCT. It follows that
$E_{m,k}$
is nuclear and satisfies the UCT. It follows that
 $A_z^C$
is a unital amenable separable simple stable rank one
$A_z^C$
is a unital amenable separable simple stable rank one
 $C^*$
-algebra with a unique tracial state which also has strict comparison for positive elements and satisfies the UCT. By [Reference Matui34, Theorem 1.1],
$C^*$
-algebra with a unique tracial state which also has strict comparison for positive elements and satisfies the UCT. By [Reference Matui34, Theorem 1.1],
 $A_z^C$
is
$A_z^C$
is
 ${\mathscr Z}$
-stable. By [Reference Matui and Sato35, Theorem 1.1],
${\mathscr Z}$
-stable. By [Reference Matui and Sato35, Theorem 1.1],
 $A_z^C$
has finite nuclear dimension. Then by [Reference Elliott and Niu16, Corollary 4.11],
$A_z^C$
has finite nuclear dimension. Then by [Reference Elliott and Niu16, Corollary 4.11],
 $A_z^C$
is classifiable by the Elliott invariant (see also [Reference Elliott and Niu16, Remark 4.6]). Since
$A_z^C$
is classifiable by the Elliott invariant (see also [Reference Elliott and Niu16, Remark 4.6]). Since
 $A_z^C$
has the same Elliott invariant of
$A_z^C$
has the same Elliott invariant of
 ${\mathscr Z}$
, it follows that
${\mathscr Z}$
, it follows that
 $A_z^C\cong {\mathscr Z}$
.
$A_z^C\cong {\mathscr Z}$
. -
(3) On the other hand, we make no attempt at this time to classify
 $C^*$
-algebras
$C^*$
-algebras
 $A_z^C$
constructed in Section 6 in the nonnuclear cases. We do not know whether
$A_z^C$
constructed in Section 6 in the nonnuclear cases. We do not know whether
 $A_z^{C_1}$
is isomorphic to
$A_z^{C_1}$
is isomorphic to
 $A_z^{C_2}$
if
$A_z^{C_2}$
if
 $C_1$
and
$C_1$
and
 $C_2$
are nonisomorphic, nonnuclear
$C_2$
are nonisomorphic, nonnuclear
 $C^*$
-subalgebras. In fact, as it stands,
$C^*$
-subalgebras. In fact, as it stands,
 $A_z^C$
may depend on the connecting maps used in the construction.
$A_z^C$
may depend on the connecting maps used in the construction.
Conflict of interest
None.
Financial support
The first author was supported by the China Postdoctoral Science Foundation (grant KLH1414009) and partially supported by an NSFC grant (NSFC 11420101001) and a Discovery Grant of the NSERC of Canada. The second author was partially supported by an NSF grant (DMS-1954600). Both authors would like to acknowledge the support during their visits to the Research Center of Operator Algebras at East China Normal University, which is partially supported by the Shanghai Key Laboratory of PMMP, Science and Technology Commission of Shanghai Municipality (STCSM), grant 13dz2260400 and an NNSF grant (11531003).