Introduction

A glacier’s volume is its most fundamental geometric property, and knowledge of changes in the total volume of all the world’s glaciers and ice caps (GIC) is essential in making accurate estimates of near-term sea-level rise (Reference MeierMeier and others, 2007; Reference Bahr, Dyurgerov and MeierBahr and others, 2009; Reference PfefferPfeffer, 2011; Reference HockRadić and Hock, 2011; Reference Mernild, Lipscomb, Bahr and ZempMernild and others, 2013). Unfortunately, among the hundreds of thousands of glaciers and ice caps around the world, direct volume observations exist for only a scant few. In almost all cases, a glacier’s volume (as well as subsurface geometry, internal velocities, sliding rates and other internal parameters) is inferred from surface parameters (e.g. surface mass balance, surface velocity and surface geometry). In particular, estimates of GIC volume have been extrapolated from surface area using volume/area scaling (Reference Chen and OhmuraChen and Ohmura, 1990; Reference BahrBahr and others, 1997; Reference HockRadić and Hock, 2010) and have, more recently, been extrapolated by numerical inversions of emergence velocities and the surface geometry (e.g. Reference Huss and FarinottiHuss and Farinotti, 2012; Clarke and others, 2013).

Both volume/area scaling and numerical inversions take information about the surface boundary of a glacier and extrapolate that information to the bottom boundary. For example, a typical scaling analysis uses the surface area to estimate the volume; or more explicitly, scaling is used to estimate the mean glacier thickness, from which volume (thickness × area) is estimated. Similarly, numerical inversions for volume also give estimates of the position of the bottom boundary, because no matter how it is calculated, a glacier’s estimated volume together with easily observed area gives us information about the average thickness of the ice. Although volume/area scaling is not often called an inversion, it is in essence an inversion: surface data are being used to infer unseen parameters within the glacier, such as thickness (e.g. Lliboutry, 1987, p. 177; Reference ZhdanovZhdanov, 2002, p. 4).

Inversions of this type over-specify data on one boundary (the glacier surface) and under-specify the conditions on another boundary (the glacier bed). An unbalanced placement of boundary conditions is a notorious way to create unstable solutions (e.g. Reference Courant, Hilbert and CuffeyCourant and Hilbert, 1966, p. 227–230), and for the system of equations that describe a glacier (continuity, force balance and constitutive), placing all of the boundary conditions at the surface can create both a calculation instability and an ‘ill-posed boundary-value problem’ (e.g. Lliboutry, 1987, p. 11, 178). The term ‘ill-posed’ does not indicate that the boundary conditions are incorrect or improperly specified. Instead, as originally defined by Hadamard, a problem is ill-posed (1) if the solution is not unique or (2) if the solution is not stable (not continuously dependent on the data) or (3) if the solution does not exist (Reference ZhdanovZhdanov, 2002). Importantly, we do not have to show that each of (1), (2) and (3) are true to establish the ill-posed problem; we only need to show that any one (or more) of (1), (2) and (3) are true. Generally geophysicists assume the existence of a solution (it is rarely proved a priori) and instead focus on stability, but for our arguments we will focus on both stability and uniqueness. Intuitively, both an instability and/or non-uniqueness imply that there are a cloud of other possible or likely solutions.

In the case of glaciers, the ill-posed problem is purely a consequence of how boundary conditions are applied; it has nothing to do with the type of numerical solution, and will exist whether or not the glacier volume is derived from a finite-element analysis, finite-difference analysis, volume/area scaling analysis or by any other approach. The ill-posed nature of the problem is inevitable, and, as long as the boundary conditions are over-specified on the surface and under-specified at the bed, it cannot be improved with better models, different models, new models or analytical or numerical models. The solution is intrinsically unstable (or non-unique) because of the manner in which the boundary-value problem has been set up. Until there are additional data specified at points other than at the surface of the glacier, the volume solution will remain ill-posed (e.g. Reference Courant, Hilbert and CuffeyCourant and Hilbert, 1966; Reference ZhdanovZhdanov, 2002).

Ill-posed boundary-value problems are well studied in engineering, applied mathematics, geophysics and their associated disciplines. For many ill-posed geophysical problems, approximate rather than exact solutions are possible, though ‘inverse source problems’ of the type discussed here will have an infinite number of possible approximations (Reference ZhdanovZhdanov, 2002, p. 4 and 18). Within glaciology, the theoretical and practical implications of ill-posed inversions have been evaluated by a number of authors, including Reference Hantz and LliboutryHantz and Lliboutry (1981), Reference Balise and RaymondBalise and Raymond (1985), Lliboutry (1987, p. 177), MacAyeal (1993), Reference Bahr, Pfeffer and MeierBahr and others (1994), Reference Joughin, Ayeal and TulaczykJoughin and others (2004), Reference TrufferTruffer (2004), Reference Chandler, Hubbard, Hubbard and NienowChandler and others (2006), Reference Gudmundsson and RaymondGudmundsson and Raymond (2008), Reference Maxwell, Truffer, Avdonin, Stuefer and NabbMaxwell and others (2008) and Reference Raymond and GudmundssonRaymond and Gudmundsson (2009), among many others. The theoretical implications are that information is lost exponentially as a calculation progresses deeper into a glacier and becomes increasingly unstable (Reference Bahr, Pfeffer and MeierBahr and others, 1994; Reference ZhdanovZhdanov, 2002, p. 26). Therefore, appropriate control of the calculation can dampen (though not eliminate) the instability and can lead to reasonable and approximate (though non-unique and less precise) solutions.

For example, reasonable solutions have been approximated by many numerical approaches, (e.g. Reference Huss and FarinottiHuss and Farinotti, 2012; Clarke and others, 2013). In these models, a numerical inversion uses surface topography to extract the basal shear stress. In turn, this allows an iterative (or other) solution for the glacier thickness. When the thickness is calculated at many locations, the glacier volume can be estimated, but it is dependent entirely on an ill-posed boundary-value problem, where estimations of the basal shear stress have been derived from surface parameters. This is by no means an indictment of the models or of numerical inversions in general, and it is only an acknowledgement that the calculation must be non-unique, even when the solution is entirely reasonable and stable.

Similarly, scaling techniques (e.g. Reference BahrBahr and others, 1997) use the surface area (one boundary) to infer the average thickness (bottom boundary) via a volume/area power-law relationship, V = cS^γ , where V is volume, S is area and c and γ are scaling parameters. At first glance, the solution appears stable and therefore well-posed. However, note that c, while often described as a constant, is in fact a random variable. The parameter c has a distribution of possible values (Reference BahrBahr, 1997a), and therefore the calculated volume also has a distribution of values. Thus, the scaled-volume solution is not unique, and the problem is ill-posed. Of course, the placement of all the boundary conditions on the surface of the glacier makes that nearly inevitable; and if a problem is ill-posed, an analytical scaling solution cannot make it well-posed. Only with the application of special filtering, a Bayesian analysis or other regularization techniques (e.g. Reference Bahr, Pfeffer and MeierBahr and others, 1994; Reference ZhdanovZhdanov, 2002; Reference TrufferTruffer, 2004; Reference Raymond and GudmundssonRaymond and Gudmundsson, 2009) will the analytical solution or model give a reasonable (though still non-unique) approximation to the exact solution. In the case of volume/area scaling, the distribution of c is routinely replaced by its mean value (or a value estimated from a regression), and the resulting volume solution becomes stable and reasonable, but most certainly not unique.

While the ill-posed nature of the problem might appear to be an annoying burden, it does have some advantages.

Consider all of the world’s glaciers that have a specified area within plus or minus some arbitrarily small tolerance. With great certainty, we know that these glaciers will not all have the same volume, because they are each on different basal topography in different local climates, etc. For the specified glacier area (plus or minus the tolerance), there will be a distribution of associated glacier volumes. The distribution may be small and have a well-defined mean; but the volume cannot, and intuitively should not, be uniquely determined from the area. In this respect, the ill-posed volume/area scaling problem reassuringly agrees with our understanding of actual glaciers.

Similarly, we know that a glacier’s surface does not reflect every small bump and divot in the basal topography. The flowing ice ‘averages away’ many of these small-scale basal features, and a variety of different basal conditions can be accommodated by essentially identical surface topographies. Conversely, this means that each observed surface must correspond to a variety of possible basal topographies, and a small change at the surface could be due to substantially different conditions on the bed. This instability is encompassed nicely by the ill-posed nature of the inversion problem. The fact that numerical models reproduce this intuitive instability is reassuring.

Identifying Reasonable (Regularized) Solutions

The problem of deriving a glacier’s volume from surface data will always be ill-posed, but there are three important mitigating factors that make both scaling and numerical inversions useful and practical tools. First, ill-posed does not mean unsolvable. A great deal of progress has been made by turning ill-posed problems in seismology, geodesy, geomagnetism and other geophysical disciplines into a set of equivalent well-posed problems, typically through a process called regularization, which places reasonable bounds on the solution (Reference ZhdanovZhdanov, 2002). In essence, part of the solution (or part of the form of the solution) is guessed or assumed, and the inversion is therefore constrained and no longer ill-posed. Similar progress has been made with regularization of glacier inversions (e.g. Reference TrufferTruffer, 2004; Reference Maxwell, Truffer, Avdonin, Stuefer and NabbMaxwell and others, 2008; Reference Raymond and GudmundssonRaymond and Gudmundsson, 2009; Reference Habermann, Maxwell and TrufferHabermann and others, 2012), and even though these and future improvements will always be an approximation, ill-posed inversions are best treated with careful calculation and interpretation rather than assumed intractability.

As a second mitigating factor, the random errors in volume will differ for each glacier, and by the law of large numbers, the sum of many glaciers’ volumes will give a good estimate of their total volume. Thus, while ill-posed estimates of single glacier values are invariably highly uncertain, the average or aggregate value of a sufficiently large sample of glaciers will be more robust. As shown in the following sections, the variance in glacier volume estimates depends strongly on the sample size, and for small samples (or individual glaciers) can grow exponentially large, making the total volume estimate much less reliable. Furthermore, each method for estimating glacier volume will have additional sources of error that are separate from the ill-posed calculation (e.g. errors in data, errors from numerical instabilities and errors in specified parameters (such as the scaling constant, or flow law creep parameter A or sliding law)). The impact of these additional errors on the variance of the total volume must be evaluated separately from the ill-posed boundary-value problem. However, unless special precautions are taken (as described in the following section), it is the exponentially large variance from the ill-posed calculation that has the greatest potential to overwhelm an estimate of total GIC volume. This is one of the primary points of this paper: extra care must be taken to ensure that the ill-posed calculation is carefully controlled or the associated errors may become the dominant (though all too often ignored) source of volume error and variance.

As a third mitigating factor, the ill-posed instability is dependent on the spatial wavelength or resolution of the solution (e.g. Reference Bahr, Pfeffer and MeierBahr and others, 1994; Reference ZhdanovZhdanov, 2002, p. 30–31; Reference TrufferTruffer, 2004; Reference Chandler, Hubbard, Hubbard and NienowChandler and others, 2006; Reference Habermann, Maxwell and TrufferHabermann and others, 2012). In this context we are defining the spatial wavelength (and related spatial frequency) as the length scale of variation of whatever surface properties are being projected downwards in the inversion for distributions at the bed. For example, if velocity data obtained at the surface are used to infer velocity at the bed, we might ask what a change in along-flow speed over half the ice thickness in the along-flow direction tells us about variations in the along-flow speed at the bed; in this example, the wavelength, λ, would be H/ 2, where H is the ice thickness. More formally, the wavelength, λ, is the spatial wavelength of a Fourier decomposition of the solution and of the surface observations (which are a part of the solution).

In particular, high-resolution model results will be less accurate than low-resolution results (where the highest possible resolution is the discretization or sampling interval, and the smallest resolvable spatial wavelength is twice the resolution). For example, a model with 100 m gridcells will have smaller errors than a model interpreted at 10 m intervals. Although perhaps counterintuitive, errors from neighboring gridcells do not cancel. Instead, the errors only grow increasingly unstable with finer grids and with calculations that go further from the surface data towards the bed. Bahr and others (1994, p. 513–514) use a perturbation solution to show that the errors grow chaotically (in the mathematical sense) and exponentially large no matter what type of inversion is used. However, the rate of exponential growth is smaller for longer wavelengths. Therefore, at suitably long spatial wavelengths a stable solution at the bed of the glacier is still possible when inverting from surface data. The trick is to eliminate the unstable short frequencies that generate most of the errors. Eliminating or smoothing high frequencies has been the strategy of many glacier inversions, and it is another example of regularization (which assumes something about the structure of the solution at the bed) (e.g. Reference TrufferTruffer, 2004; Reference Habermann, Maxwell and TrufferHabermann and others, 2012).

In practice, short spatial wavelengths in the thickness solution can be removed with a low-pass frequency-domain filter (apply a Fourier transform to the solution and then truncate high frequencies in the frequency domain). If we assume smooth basal topography, for example, then the resulting low-resolution, long-wavelength solution will be very accurate. In reality, such an assumption of smooth basal topography may not be realistic for an arbitrary glacier. Many glaciers have icefalls, overdeepened valleys, barely submerged nunataks and other high spatial frequency features which can be buried under ice and cannot be known a priori. If glacier volume is estimated from the sum of the calculated thickness distribution, then the law of large numbers ensures that random errors will cancel in the summation. In other words, the volume and the mean glacier thickness will be well represented. However, if short spatial wavelengths are represented in the solution in an attempt to include high spatial frequency features in the basal topography (icefalls, etc.), then the errors in the calculated thickness will grow exponentially larger and the variance in their sum will become exponentially large (cf. central limit theorem). If the variance gets too large (as it will with short wavelengths; see Eqn (1)), then the estimate of the volume is effectively meaningless.

To avoid filtering explicitly, other numerical techniques employ differing strategies for regularizing and removing the unphysical short-wavelength oscillations. For example, an inversion with Bayesian inference assigns probabilities to each solution, so the short-wavelength errors become a possible but improbable solution (Reference Raymond and GudmundssonRaymond and Gudmundsson, 2009). Regardless of the particular technique (filtering, Bayesian or other), the improbable high-amplitude short-wavelength errors must be identified, minimized and/or removed.

Most published inversions already acknowledge the need for averaging, filters or error suppression of some kind (e.g. Reference Huss and FarinottiHuss and Farinotti, 2012; McNabb and others, 2012; Clarke and others, 2013), and we expect that these models will provide reasonable volume estimates with minimal errors from the ill-posed instabilities. However, the potential for large ill-posed errors is so significant, we argue that careful analysis and exposition about ill-posed errors is essential for accurate GIC volume estimates. For example, errors in scaled volume grow only linearly with errors in the scaling parameter, c; but as the next section shows, this is trivial compared with the huge exponential growth rates of errors in an ill-posed inversion calculation. (For a discussion and comparison of growth rates, see Reference ShafferShaffer, 2010, ch. 3.) Every numerical volume estimate should discuss the ill-posed errors explicitly and should explain precisely how these potentially huge errors have been controlled or eliminated.

When evaluating the ill-posed errors in a numerical solution of glacier volume, it is natural to ask whether a volume/area scaling solution provides any significant benefit (such as stability), or if the greater resolution of a numerical inversion makes the numerical volume solution preferable and more accurate. To address this, we do not develop a new technique for inversions, nor do we derive a new technique for error suppression or removing short-wavelength errors. Instead, we assume and use existing theory in the form of Eqn (1) to discuss glacier volume estimations as an ill-posed inversion. As the following analysis shows, volume/area scaling inherently averages over long wavelengths and does not over-interpret the ill-posed results at shorter wavelengths. In contrast, numerical inversions with fixed grid spacing can over-interpret the volume estimation by including excessively short wavelengths, especially on large glaciers. Nevertheless, both methods of volume estimation are useful in different contexts; therefore the following section also details the appropriate wavelengths for filtering numerical inversions. After filtering, numerical inversions and volume/area scaling have notable trade-offs between resolution and errors, but both give roughly equivalent measures of the glacier volume.

Error Analysis For The Ill-Posed Volume Problem

Although the mathematical details of the following analysis are extensive, the basic approach is intuitive and simple. Any errors in a specified (or calculated) stress at the surface of a glacier will grow exponentially larger when the resulting stress is estimated at the bed of a glacier (Reference Bahr, Pfeffer and MeierBahr and others, 1994). Using scaling relationships all other glaciological parameters can be related to the stress (Reference BahrBahr, 1997a). Therefore, small errors in the stress at the surface will translate to exponentially large errors for any and all parameters estimated at the bed of a glacier. In particular, the thickness estimate (equivalently, the estimated position of the bottom boundary) will have exponentially large errors. Volume is calculated as an integral or summation over the thickness, and the summation may cancel the errors (mean value theorem), but this summation will still leave an exponentially large variance. The variance can be so large that the volume calculation is effectively meaningless. The mathematical details show that the calculation errors are larger at high spatial frequencies and are larger when the glacier is thicker. Therefore, models that use finely spaced grids on large glaciers will have tremendous errors (and an enormous variance in the estimated volume) unless high-frequency components of the solution are eliminated. In contrast, volume/area scaling automatically eliminates these unstable high frequencies, because the inherent wavelengths of the scaling solution are very long and on the order of twice the glacier’s length.

Our analysis starts with the previously published conclusions of Reference Bahr, Pfeffer and MeierBahr and others (1994), which showed that deviatoric stress errors from the ill-posed calculation grow exponentially as

(1)

where || … || is an appropriate norm (e.g. the sup norm), z _s is the surface elevation, z _b is the elevation of the bed, H = z _s – z _b is the thickness of the ice and k is spatial frequency in the along-glacier direction, x. The Δ indicate a measurement or calculation error, so is the measurement error of a stress at the surface of the glacier, and is the resulting inversion calculation error at the bed. The hat notation, ^, indicates that the function has been Fourier transformed in the along-glacier direction, x (but not transformed in the vertical direction, z); in other words, along-glacier spatial variations in x have been transformed to the spatial frequency domain, k. Spatial frequency is related to spatial wavelength by k = 2π/ λ, so Eqn (1) indicates that the low-frequency (and long-wavelength) components of the solution have relatively small errors while the high-frequency (and short-wavelength) components of the solution have exponentially larger errors.

The value of r (n) is a constant that depends on Glen’s constitutive law parameter, n, as

(2)

where Re[…] gives the real component of a complex number (Reference Bahr, Pfeffer and MeierBahr and others, 1994). For the typical value of n = 3, the function gives r (n) ≈ 0: 6, but regardless of the exact value, the growth rate is always exponential. Even at spatial wavelengths of half an ice thickness, the errors at the bed will be huge with when n = 3; in other words, for λ ˜ H/ 2 (or equivalently k ˜ 4π/H), basal errors will exceed surface errors by a factor of ˜ 2000, i.e. by over three orders of magnitude. For reasonable errors that grow by no more than an order of magnitude, one ice thickness is the shortest practical horizontal wavelength at the bed, in which case

The exponential form of Eqn (1) follows from the stress equilibrium and strain-rate compatibility equations (Reference Bahr, Pfeffer and MeierBahr and others, 1994), and can be derived exactly and without simplifications or assumptions when n = 1. It is also trivially derived for the case of perfect plasticity as n → ∞. For more general n, Eqn (1) has also been derived with a perturbation analysis under plane-strain and any one of the following assumptions: (1) highly compressive and tensile flows or (2) small surface slopes or (3) glaciers that are decoupled from the bed with high basal sliding rates and low basal shear (Reference Bahr, Pfeffer and MeierBahr and others, 1994). Any one of these assumptions is limiting, but they each lead to the same conclusion, suggesting that Eqn (1) is a generally applicable result. In fact, Eqn (1) is consistent with virtually all other geophysical inverse problems that have similar exponential growth rates for errors and have the same inverse dependence on the spatial wavelength (Reference ZhdanovZhdanov, 2002). Therefore, we assume the exponential growth of errors in Eqn (1) as a reasonable departure point for our analysis.

In an interesting Monte Carlo inversion, Reference Chandler, Hubbard, Hubbard and NienowChandler and others (2006) have suggested that Eqn (1) should have a power-law rather than an exponential form. If this is the case, then the derivations that follow in this paper will be conservative, and practical solutions at the bed of a glacier could include some shorter spatial wavelengths than indicated here. However, although postulated, no analytical power-law formulation for error growth has been derived, so we will use the exponential form, which is guaranteed to give a reasonable and conservative lower bound for the limiting short wavelengths.

To avoid exponentially large errors from the ill-posed calculation, the spatial wavelength, λ = 2π/ k, must be selected so that the right-hand side of Eqn (1) grows as either a constant or as an even slower function of the glacier size. Practically this means keeping the exponent’s value ≪ 1:

(3)

(For n = 3, the constant terms become 2πr(n) = 3: 77, and the shortest acceptable wavelength will be approximately four times the glacier thickness.

For simplicity in some later calculations, we define a normalized wavelength, ?, that allows us to discuss the spatial wavelength in multiples of the glacier thickness.

(4)

This is a fundamental measure of length in the ill-posed calculation. For example, if a model estimates the stress at the bed as a function of position, then Eqn (3) implies the computed basal stress should be filtered so that Λ ≫ 1. If an order of magnitude is considered sufficiently larger, then this suggests filtering all Λ < 10. Certainly, filtering all Λ < 1 is a minimal requirement.

For Λ ≫ 1, the exponential in Eqn (1) can be approximated by its McLaurin series and

(5)

Therefore

(6)

is the fractional (or percentage) increase in the errors between the surface and the bed. For example, Λ = 10 will generate errors at the bed that are 10% larger than at the surface.

We can compare the fractional increase, δ for two different inversions by taking their ratio. This gives a relative increase, or relative error,

(7)

For example, ε = 10 would imply that the first inversion technique has an order-of-magnitude greater percentage increase in errors than the second technique. In the following sections we specifically focus on values of and appropriate to (1) volume/area scaling and (2) numerical models with a resolution constrained by a fixed grid spacing. The two techniques can then be quantitatively compared with ε.

Thickness errors

Stresses (as in Eqn (1)) are difficult to measure directly and are generally inferred from velocities using Glen’s flow law. Intuitively, we know that an error in the measured surface velocity must translate to some magnitude of error in the calculated thickness and that this, in turn, can affect volume calculations. For example, if the measured surface velocity is too large compared with the actual velocity, then the glacier will appear to be too thick, because there would need to be more ice to deform and produce the excess velocity. Likewise, if the measured surface velocity is too small, then the calculated thickness would appear to be too thin. To help motivate our more detailed calculations, we note that the relationships between velocity (and stress) and thickness are nicely illustrated with the well-known ‘slab on a slope’ (or ‘laminar flow’) solution, which relates thickness to velocity for an ice slab of uniform thickness:

(8)

or, equivalently,

(9)

(Paterson, 1994, p. 251). If there is an error in the measured surface velocity, u(x, z_s ), then Eqn (9) shows that there will be a related error in the thickness, H. Moreover, if the basal velocity has an exponentially large calculation error (Reference Bahr, Pfeffer and MeierBahr and others, 1994), then Eqn (9) shows that the thickness will also have an exponentially large error. The exponent, 1/(1 + n), reduces the magnitude of this error, but does not change the exponential form.

Similarly, for shear stress in the ‘slab on a slope’ solution,

(10)

where ρ is ice density, g is gravity and is the surface slope of the glacier. In this case, an exponentially large error in the calculated basal shear, σ^′ _xz (x, z_s), is translated linearly to an exponentially large error in the calculated thickness, H. More precisely, for an error or perturbation, Δ, in the basal shear,

(11)

where ΔH is the error or perturbation in the thickness. Subtracting Eqn (10) from Eqn (11) and rearranging,

(12)

Fourier-transforming to the spatial frequency domain and substituting Eqn (1),

(13)

In other words, if the basal shear has been calculated from the surface shear, then the error in the basal shear will be exponentially large; for a ‘slab on a slope’, this means that the calculated thickness will also have an exponentially large error.

To generalize these results, the above relationship between shear stress and thickness can be made mathematically precise without reference to the assumptions used in a ‘slab on a slope’ solution. In particular, a dimensional analysis (e.g. Reference Welty, Wicks and WilsonWelty and others, 1984; Reference Schmidt and HousenSchmidt and Housen, 1995) shows that the fundamental relationship between glacier stress and thickness is linear and monotonically increasing. In particular, for all coordinate directions, i and j, and for the component of gravity, g_j , in the j th coordinate direction,

(14)

for some dimensionless constant, Π _ij , which is a glacio-logical equivalent of other well-known dimensionless parameters in fluid mechanics (e.g. Reynolds or Froude numbers). Equation (14) is exact, it is an inevitable consequence of a dimensional analysis and it is independent of any assumptions. The constant ? _ij , will vary with the choice of i and j, will vary with the axes orientations (to include an angle, as in Eqn (10)) and will vary from glacier to glacier; but in all cases the linear relationship between stress and thickness is inviolable. Stretching transformations (e.g. Reference LoganLogan, 1987) of the fully three-dimensional (3-D) stress equilibrium, constitutive and force-balance equations also give the same result (e.g. Reference Bahr and RundleBahr and Rundle, 1995, p. 638). Note that in the context of Eqn (14), σ_ij refers to a full nondeviatoric stress, and that all stress components are, to first order, small deviations from the overburden, ρg_jH. This first-order relationship to the overburden is most obvious when partitioning stresses into lithostatic and non-lithostatic components (e.g. Reference Van der Veen and WhillansVan der Veen and Whillans, 1989; Cuffey and Paterson, 2010, p. 321). The vertically integrated force-balance equations also show the primarily linear relationship between thickness and stress. (See, e.g., eqns (8.56) and (8.59) of Cuffey and Paterson, 2010, p. 325.)

In the dimensional context of Eqn (14), σ_ij and H refer to characteristic values. The choice of a characteristic value is determined by the particular problem being solved, though for any choice of characteristic values, the dimensionless parameters, Π _ij , can vary (in the same way that the dimensionless Reynolds number can vary in fluid mechanics). For example, the characteristic thickness could be the average thickness over the entire glacier, the average thickness along the center line, the average along the equilibrium line, or it could be a single value at a particular location (e.g. the thickness at the intersection of the equilibrium line and center line). There is no single correct answer, but clearly the average thickness over the entire glacier is an appropriate characteristic thickness for a glacier volume calculation. Importantly, by the mean value theorem of calculus, the average thickness will always be equal to the thickness at a particular location. Therefore, without loss of generality, the following analysis assumes that the characteristic thickness is always given by the value of the thickness at a single location within the glacier. Likewise, a reasonable characteristic value for stress will be the average over the bed of the glacier, but this can always be replaced by the value of the stress at a single location. Further details of choosing appropriate characteristic values can be found in many engineering references (e.g. Reference Welty, Wicks and WilsonWelty and others, 1984).

Deviatoric shear stresses are identical to non-deviatoric shear stresses, and from Eqn (14) with I ≠ j,

(15)

where σ^′ _ij is the same characteristic value as σ_ij. For normal stresses,

(16)

Substituting Eqn (14) repeatedly,

(17)

(18)

Recall that the Π _ij are dimensionless parameters and are constants determined by the particular problem being solved. Therefore, in general and without assumptions, deviatoric stresses are linearly related to thickness by

(19)

where П'_ij = ρg _jП_ij when i≠j, and П'_ij = ρg _j[П_ii − ⅓(П_xx + П_yy + П_zz)] when i=j.

If the characteristic thickness and stress are selected as values at a particular point on the bed (e.g. at the intersection of the equilibrium line and the center line), then the form of this general equation is identical to the ‘slab on a slope’ solution in Eqn (10), and by the same logic, substituting Eqns (1) and (5) gives

(20)

Therefore, at the most fundamental level, any errors in the specified surface stress will be transferred to the calculated thickness, and the errors in the calculated thickness will be exponentially larger for bigger glaciers (larger H in the exponent).

The volume, V, of a glacier is the integral of thickness over the glacier’s surface area, S. Therefore, by the mean value theorem, the integral can be replaced by the value of the thickness, H, below some particular point, (x, y), on the surface

(21)

By definition, H is also the average thickness of the glacier and is the characteristic value. Substituting Eqn (19),

(22)

In other words, errors in any of the surface area (Eqns (21) or (22)) or thickness (Eqn (21)) or the stress (Eqn (22)) will introduce errors in the volume. From Eqns (1) and (20), the stress and thickness errors can be exponentially large, and therefore we fully expect that the volume errors in Eqns (21) and (22) will also be large. After introducing scaling arguments, a detailed Fourier transform of Eqn (21) will follow further below, but the motivations behind the calculation of volume errors are now clear. Using the above, we can turn to detailed analyses of volume/area scaling and numerical inversions.

Ill-posed errors from volume/area scaling

Consider the special case where a glacier’s volume is estimated by scaling with the surface area:

(23)

where γ = 1: 375 for glaciers and 1.25 for ice caps, and c is a scaling parameter with mean value 0.034 (Reference BahrBahr, 1997a; Reference Bahr, Meier and PeckhamBahr and others, 1997). The volume solution cannot be unique because c has a distribution of values. Therefore, viewed as an inversion, volume/area scaling is ill-posed. Nonetheless, it seems obvious that the solution is stable. Small changes in the surface area will lead to small changes in the volume. For example, with small surface errors where ΔS ≪ S, higher-order terms of ΔS vanish and

(24)

In other words, for a fixed surface area, S, the volume error, ΔV, scales linearly with the surface error, ΔS, and the error is stable. It is not immediately obvious, however, why the scaling solution should be stable when most other inversions are unstable. This section shows that volume/area scaling happens to use sufficiently long wavelengths that the ill-posed inversion errors are vanishingly small. The ill-posed errors exist in a scaling solution, but they become irrelevant.

Volume/area scaling is only one of a large suite of scaling relationships that follow from a dimensional analysis of the relevant continuum mechanical variables. Two other examples are the well-known response time relationships, t αz/u_z and t α x/u_x . Another example is the fundamental dimensional relationship between the velocity and the length scale u _x α Aρ ⁿ g_x ⁿ z ⁿ⁺¹ (cf. ‘slab on a slope’, Eqn (8)). Other dimensional relationships exist for all the fundamental continuum parameters (stress, velocity, thickness, length, time, etc.). These dimensional relationships can be generalized as power laws (Reference Schmidt and HousenSchmidt and Housen, 1995), and in particular, Bahr (1997a) has shown that the surface area, S, can be related to any other glaciological continuum parameter, P, by a power-law scaling relationship of the form

(25)

for some scaling parameter C_p and exponent γ _p . Because all of these scaling relationships are derived from a dimensional analysis (and equivalently from stretching transformations of the continuum equations), the suite of scaling relationships is valid as a complete set. In other words, we cannot accept some of the scaling relationships and reject others. Some of these relationships may be very difficult to verify with data (e.g. those that involve a difficult-to-measure stress), and

others may be somewhat easier to verify with data (e.g. volume/area scaling, for which limited measurements are available). However, because the scaling relationships exist as a set, the verification of one relationship implies the existence of all the others.

This is particularly relevant when estimating volume from area, because we can convert volume/area scaling (verified with data) to an equivalent volume/stress relationship. In essence, if volume scales with area (Eqn (23)), and area scales with stress (Eqn (25)), then volume must scale with stress. In particular, from Eqn (25)

(26)

where substitutions of Eqns (19) and (23) show γ_σ = 1/(γ – 1)(and c_σ = (c/Π′_ij)γ_σ Combining with volume/area scaling (Eqn (23))

(27)

where c _v = c c_σ ^γ and γ_v = γ_v = γ γ_σ = γ/( γ – 1) note that the characteristic value of the stress in Eqn (27) must be positive to avoid non-physical complex-valued volumes. It follows that errors in stress will generate errors in the calculated volume

(28)

For small errors (which might still be growing exponentially), Δ σ ′ _ij≪ σ ′_ij and higher-order terms of γ σ ′ _ij ⁰ _ij become negligibly small, so that

(29)

Similarly,

(30)

From Eqns (1) and (20), we know that the magnitude of the errors in the stress will depend on the wavelengths under consideration. Each of Eqns (24–30) are scaling relationships that use characteristic quantities, so the applicable wavelength is the characteristic length. Because all of the power-law scaling relationships exist as a set, the characteristic value used in one scaling relationship must be the same characteristic value used in all of the other scaling relationships. For example, when estimating a glacier’s volume, the same characteristic length that applies to volume/area scaling must also apply to area/stress scaling, as well as to volume/stress scaling. Any differences would lead to contradictions in Eqn (25) (such as different values of the glacier surface area, S, when calculated from different parameters, P).

The necessity of a common length scale is particularly apparent when considering small perturbations in P. From Eqn (25) with γP ≪ P_,

(31)

Multiplying both sides by P and rearranging

(32)

Repeatedly selecting P as the length, L, volume, V, and stress, σ′_ij (as well as any other continuum parameter),

(33)

In other words, each parameter and its error is related to the same length scale, L, by Eqn (33).

It is possible to have multiple length scales in the same analysis (e.g. a glacier width, W, and a glacier thickness, H), but it is not possible to have the same (single) length scale, L, with two different values in the same problem. For example, we cannot assign 1 km to the glacier’s total length in the direction of flow and then in a different equation in the same analysis assign 10 km to the length in the direction of flow. Instead, the length scale, L, must be consistent across all equations. For practical examples, see the treatment of fluid mechanical problems that use both Reynolds and Froude numbers (or other dimensionless numbers) in the same problem (e.g. Reference Welty, Wicks and WilsonWelty and others, 1984).

Intuitively, in a glacier volume calculation, the appropriate characteristic length scale is the glacier length in the direction of flow. Rigorously, the characteristic length, L, for volume/area and volume/stress scaling can be derived from the empirically validated area/length relationship

(34)

where b ≈ 1 is a scaling constant and q = 0: 6 for glaciers and q = 1 for ice caps (Reference BahrBahr, 1997b) (cf. Eqn (25)). Solving for L gives the characteristic glacier length associated with area/length scaling, and therefore, as discussed above, this is the length scale associated with volume/area and volume/stress scaling. Given the length scale, L, the associated wavelength is λ = 2L (the theoretically minimum resolvable wavelength is given by twice the shortest distance that is assigned a value by a model, and the volume scaling solution does not assign or evaluate distances smaller than L). From Eqn (34),

(35)

We can now calculate the ill-posed inversion stress errors at the particular wavelength used by volume/area scaling. Substituting Eqn (35) into Eqn (1) and using k = 2π/λ,

(36)

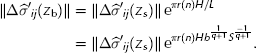
We can further reduce this equation by replacing the thickness, H, with a combination of Eqns (21) and (23):

(37)

(called thickness/area scaling; cf. Eqn (25)). Substituting gives

(38)

where

(39)

for both glaciers and ice caps (the values for γ and q are given after Eqns (23) and (34)), and

(40)

for n = 3, r (3) = 0: 6, c = 0: 034 and b = 1. From Eqn (5), the fundamental (normalized) wavelength associated with scaling is

(41)

and from Eqn (6), the fractional (or percentage) error associated with scaling is

(42)

The parameters b and c have a distribution of values (Reference BahrBahr, 1997a) and can vary significantly from glacier to glacier. However, even with order-of-magnitude estimates of b and c, the parameter m remains small. Furthermore, the term S^{- 0: 25} rapidly approaches zero for glaciers larger than 1 km². Therefore, for any value of S > 1, the wavelength Λ_s ≫ 1 and

(43)

In other words, for all but the smallest glaciers, there is no significant dependence on glacier size, and

(44)

At the wavelengths relevant to scaling, stress errors do not increase significantly during an inversion calculation and δ _s → 0. Nevertheless, while close to zero, δ _s is not exactly zero, as shown in Eqn (42). This will be relevant below, when we use ∊ to compare the scaling solution with the numerical inversion (Eqn (7)).

By restricting our attention to small perturbations, we can show explicitly the relationship between stress errors in Eqn (38) and volume/area scaling errors in Eqn (24). Combine Eqn (38) with the Fourier-transformed errors calculated from volume/stress scaling in Eqn (29):

(45)

Combine Eqn (45) with Fourier-transformed errors estimated from area/stress scaling in Eqn (30).

(46)

Remove the stresses with one more application of volume/stress and area/stress scaling.

(47)

Substituting Eqn (37),

(48)

Where γ = γ_v/γ_σ, as noted after Eqn (27). Again, for glaciers larger than 1 km², the exponential in Eqn (48) rapidly approaches 1, and

(49)

Remarkably, this is a Fourier-transformed restatement of the errors in volume/area scaling (Eqn (24)). In other words, the general stress error relationship in Eqn (1) reduces to the errors we expect from volume/area scaling (Eqn (49)). At wavelengths relevant to scaling, the stress errors do not increase significantly with the calculation depth, and the volume errors do not increase exponentially with the thickness of the glacier. At the long wavelengths inherently used by volume/area and volume/stress scaling, there is no exponential growth of the errors between the surface and the bed of the glacier. The short and problematic wavelengths have been automatically excluded by volume/area scaling.

In some respects, this conclusion is obvious. Volume/area scaling applies to the longest possible wavelengths that could be assigned to a glacier: those wavelengths that are defined by distances encompassing the entire surface. If any volume calculation should be stable, it should be the longest-wavelength solution. However, the rigorous derivations above illustrate that scaling is not special or exempt from the ill-posed errors that apply to all inversions. Instead, those errors are just vanishingly small for glaciers larger than 1 km², and no additional averaging or filtering is necessary to control the ill-posed instability when using volume/area scaling.

Ill-posed errors from numerical inversions

Every model is different, and it is difficult to generalize how ill-posed errors will propagate in an arbitrary and unspecified numerical inversion. Nevertheless, certain features are common to most or all models. For example, volumes are inferred as a summation of the glacier’s thickness at many locations. In turn, the thickness is established by calculating stress (and velocity) fields within the glacier. The models may use measurements of the velocities and stresses at the surface, or the models may calculate the velocities and stresses at the surface. Either way, errors in the measured or calculated surface stresses will lead to errors in the thickness and volume, as described above. If the short-wavelength components of the solution are not suppressed, then the resulting thickness and volume errors could be exponentially huge.

Consider for example, a hypothetical numerical model with a grid spacing of dx along the surface of a glacier. The wavelength is λ = 2dx, and from Eqn (1)

(50)

If dx is fixed, then the errors in Eqn (50) will grow exponentially with glacier thickness, H.

The appropriate horizontal grid spacing, dx, will depend on the size of the glacier. The exponent in Eqn (50) must be kept small, and the exponent depends on the thickness of the glacier:

(51)

For a very small glacier of 1 km², the average thickness will be 34 m (Eqn (37)), and the grid spacing should be dx ≫ 64 m. For an exceptionally large glacier of 10 000 km², the average thickness will be 1075 m, and the grid spacing should be dx ≫ 2026 m.

The actual choice of grid spacing, dx, will depend on the acceptable level of errors, but ‘much greater than’ is typically taken to be an order of magnitude. Therefore,

(52)

where Λ_m = 10 is selected for the typical order-of-magnitude estimate (see discussion below Eqn (4)). Therefore, the appropriate horizontal grid spacing, dx, should be ˜20 times the ice thickness. That value is consistent with the findings of Reference Kamb, Echelmeyer and LliboutryKamb and Echelmeyer (1986), who note that basal shear should be averaged over 10–20 times the local ice thickness.

The implications are staggering when placed in the context of a glacier’s expected length. For a very small glacier of 1 km², the approximate glacier length (from area/length scaling in Eqn (34)) will be 1000 m, and the horizontal grid spacing should be dx ≈ 640 m. That is a grid spacing of more than half the expected length of the glacier. For an exceptionally large glacier of 10 000 km², the approximate glacier length will be 316 km, and the grid spacing should be dx ≈ 15: 6 km. That is ˜5% of the total length. In other words, a numerical inversion will barely resolve the world’s smallest glaciers, and it can only fit 10–20 gridpoints inside the world’s largest glaciers. Table 1 gives the number of modeling gridpoints for various glacier sizes.

Table 1.

The maximum number of horizontal gridpoints that can be placed within a glacier with the specified surface area (for Λ_m = 10). Any additional gridpoints would include unstable high frequencies from ill-posed errors. The number of gridpoints is rounded down to the nearest integer and roughly doubles for each order-of-magnitude increase in glacier area. Small glaciers are barely resolved by the necessary grid spacing (only one gridpoint within the glacier), while even the world’s largest glaciers have very few gridpoints. The length, L = S ^0.625, and thickness, H = 0: 034S ^0.375, are estimated from scaling arguments (Eqns (34) and (37)). The grid spacing, dx = 1: 88?H = 18: 8H, is estimated from Eqn (52). The number of gridpoints is [L= dx]

Grid sizes that are too small could lead to significant volume errors. To better understand the potential volume errors in a numerical inversion, we make several reasonable approximations and assumptions in the following derivations. First, we assume small errors, with ΔS ≪ S and ΔH ≪ H these errors could still be growing exponentially.

Second, we reasonably assume that the surface area, S, is roughly constant but the error, ΔS, is a variable. Third, we assume that Π _ij is order unity; this non-dimensional parameter comes from the thickness/stress relationship (Eqn (14)), and as discussed elsewhere, non-dimensional numbers are expected to have order unity (e.g. Reference Schmidt and HousenSchmidt and Housen, 1995). From the ‘slab on a slope’ solution (Eqn (10)), it is reasonable that Π _ij ≈ sin ?, where ? is the slope of a glacier, and Π _ij will therefore fall between 0 and 1. The relationship between Π _ij and Π′ _ij implies that ?′ _ij will have order ρg sinθ. Fourth, we assume that the stress errors, , at the surface are roughly the same for all glaciers. In other words, whatever measurement or calculation precision is appropriate for one glacier will also apply to all other glaciers.

Now recall that V = SH, where H is the characteristic thickness (Eqn (21)). Therefore,

(53)

The last term is negligible for small errors (see assumptions), so

(54)

where the last term of each line follows from an application of volume/area scaling errors (Eqn (24)) and thickness/area scaling (Eqn (37)). Solving for ΔV,

(55)

Where γ_v = γ/( γ – 1) is the volume/stress scaling exponent

(Eqn (27)). Fourier-transforming the errors while holding the surface area constant,

(56)

The errors in the thickness are already known from Eqn (20), so substituting gives

(57)

Note that S/ Π ′ _ij = c_vσ ′_ij ^γ-1, so this is a restatement of the volume errors derived from our scaling analysis in Eqn (45); but in this case, the Fourier-transformed volume errors have been derived from V = SH, rather than from volume/stress scaling. The consistency bolsters our arguments.

We can now compare the relative volume errors for two different glaciers with the ratio . The surface stress errors, , are unknown, but we assume that they are similar for all glaciers (as discussed above). Therefore, from Eqns (50) and (57), and for a glacier with surface area S ₁ and slope θ ₁, the volume error will be

(58)

where thickness is approximated by Eqn (37). Note that the parameter Π′ _ij1 is different for every glacier, but is expected to have order ρgsinθ₁ (see discussion of assumptions above).

With a second glacier of area S ₂ and slope θ ₂, we can calculate the relative volume errors as

(59)

where

(60)

We assume that the both glaciers have similar dimensionless parameters, Π’ _ij , so that Π’ _{ij 2}/Π’ _ij1 ≈ θ ₂ = θ ₁ ≈ 1. This is particularly likely if the glaciers have similar slopes (see discussion of assumptions above), but small differences in typical slopes (1–4°) will have little effect on the order-of-magnitude results discussed below. Therefore,

(61)

As a case example, let S ₁ ≈ 1000 km² and S ₂ ≈ 1 km². For S ₁ ≫ S ₂, the ratio (S ₂ /S ₁)^γ-1 approaches zero, and

(62)

Now consider several different grid spacings. (1) For a horizontal grid spacing dx = 1000 m, the relative volume errors will be . In other words, we expect that the largest glaciers will have volume errors on the order of 1000 times greater than the errors for a small glacier.(2) For a finer grid spacing of dx = 100 m, we find . Volume errors for the large glacier will be on the order of a million times greater than the small glacier. (3) If we were tempted to use an even finer-resolution model with dx = 10 m, then the relative error becomes a ludicrously large, . It is clear that at all but the largest grid sizes, the ill-posed volume errors will completely swamp any volume calculation.

As another illustration, suppose that for any selected grid spacing the numerical inversion correctly calculates the volume of a very small, 1 km², glacier to within 10%. The volume of this small glacier is V ₂ = c S ₂ ^γ = 0: 034 km³, and ΔV ₂ in Eqn (61) is ˜ 0.0034 km³. In this scenario, we can estimate the volume errors for the larger, 1000 km², glacier for any particular grid size. (1) If dx = 1000 m, the volume errors for the larger glacier will be ˜ 8 km³. That is ˜ 2% of the expected glacier volume of 453 km³. (2) If dx = 100 m, the volume errors will be ˜17 219 km³. That is ˜38 times larger than the expected glacier volume. Such a calculation would be useless. (3) If we naively select dx = 10 m, then the volume errors will be on the order of an absurdly large 1 × 10³⁷ km³. No reasonable volume estimate can ever be made with 100 m or finer horizontal grid resolution, unless the high-frequency components of the solution are filtered.

Several assumptions have gone into this rough approximation of the volume errors, but clearly the inversion errors will be very significant (and even outrageous) if they are not carefully controlled, particularly for large glaciers modeled with fine grids that contain short wavelengths. However, in defense of all numerical inversions, we do not expect most models to generate ill-posed errors nearly so large. Most models use averaging schemes to eliminate potential instabilities. For example, Reference Huss and FarinottiHuss and Farinotti (2012) average stresses over 10–20 ice thicknesses during each iteration, and they indicate that the final ice-thickness distribution is smoothed by an unspecified amount. Averaging and smoothing will act as low-pass filters, and their length scale of 10H –20H is consistent with both our findings and those of Reference Kamb, Echelmeyer and LliboutryKamb and Echelmeyer (1986). However, the precise effect of averaging and smoothing is difficult to quantify, while low-pass filtering or Bayesian statistics (Reference Raymond and GudmundssonRaymond and Gudmundsson, 2009) or other well-reasoned error suppression (e.g. Reference ZhdanovZhdanov, 2002; Reference Maxwell, Truffer, Avdonin, Stuefer and NabbMaxwell and others, 2008) should give more defensible and precise results. At the least, the effects of averaging should be explored and explained in detail for the relevant parameters, such as thickness and volume. This is unlikely to change any model’s results, but it will help assure that the potentially large and dominant errors from the ill-posed calculation have been properly controlled.

Regardless of the technique used to control the ill-posed errors, modelers should carefully question the seemingly reasonable (and intuitive) belief that a finer-resolution model will always give more information about a glacier’s basal conditions. For an ill-posed inversion with no data about basal or englacial conditions, that simply is not the case. The ill-posed errors will overwhelm any calculation.

A Comparison of Numerical Inversions and Scaling

For the moment, consider only ill-posed errors, and assume that all other sources of error are negligible (errors from data, unknown parameters, numerical schemes, etc.). With these assumptions in mind, numerical models will have a higher resolution than scaling. The wavelength of a scaling calculation increases with the area of a glacier as λ_s = 2S ^0.625 (Eqn (35)), while the wavelength of a numerical calculation increases as λ _m = Λ_m 2πr(n)c S^0.375 with Λ_m ≈ 10 (Eqns (37) and (52)). Therefore, for all glaciers >1 km², the shortest appropriate wavelength of a numerical model will be smaller than the wavelength of a scaling solution. In other words, a numerical model can produce a higher-resolution image of the bed, even after short-wavelength components of the solution have been eliminated to minimize the ill-posed errors.

In particular, by combining the above relationships (Eqns (35), (37) and (52)), the modeling and scaling wavelengths can be compared explicitly:

(63)

where Λ_m ? 10 (see discussion below Eqn (52)). For parameters appropriate to a glacier λ _m α λ_s ^0.6 and for parameters appropriate to an ice cap λ _m α λ_s ^0.5. Therefore, roughly speaking, the scaling wavelengths will be quadratically larger than the modeling wavelengths. For all but the very smallest glaciers (λ _s < 1 km), the numerical modeling solution will have a greater resolution than the scaling solution because λ _m < λ _s. For most glaciers, the numerical modeling wavelengths will be one to two orders of magnitude smaller than the scaling wavelengths.

However, greater model resolution (when compared with scaling) does not translate to greater accuracy and precision. The shortest wavelength of a numerical model, λ _m, has been selected to minimize the magnitude of the ill-posed errors (see previous section and the selection of Λ_m), but it does not actually eliminate the ill-posed errors, that will still grow as the exponential, e^2πr(n)H/λ_{m =} e1/Λ_m ≈ 1 + 1/Λ_m = 1 + δ_m. In other words, for Λ_m = 10, the ill-posed errors at the bed of a glacier will be δ _m ? 10% larger than the measurement errors at the surface.

For many modeling applications δ _m = 10% will be adequate. However, the exponential errors in a scaling calculation grow as δ _s = 0: 064 S ^0:25 (Eqn (42)). For a 1000 km² glacier, the scaling solution has errors that (to an order of magnitude) are only δ _s = 1%. Therefore, the relative error is ∊? = δ _m/δ _s = 10 (Eqn (7)), and scaling is an order of magnitude more accurate than modeling. Even if the modeling errors are small, for some applications the order of magnitude improvement with scaling could be significant.

We could instead choose to filter the numerical model solutions at even longer spatial wavelengths. This will further reduce the model’s ill-posed errors. For example, increasing λ _m by another order of magnitude (by choosing Λ_m = 100 rather than Λ_m = 10) will make the model’s resolution comparable to the scaling resolution (similar wavelengths). As reasonably expected, when the scaling and model resolutions are comparable, then the ill-posed errors are also comparable (and δ _m ˜ δ_s). However, choosing Λ_m = 100 increases the grid spacing by a factor of 10 in Table 1, and even the world’s largest glaciers would be barely resolved by the numerical model.

There will always be a trade-off between resolution and errors. For a 1000 km² glacier, when Λ_m = 10, then ∊ =δ _m/δ_s = 10. If Λ_m = 100, then ∊ = 1. If ?_m = 1000, then ∊ = 0.1. In other words, Λ_m and ∊ have an inverse relationship. If the resolution of the model increases (i.e. the grid becomes finer) by an order of magnitude, then the relative accuracy of the modeling decreases by an order of magnitude (in comparison with scaling). Neither the scaling nor the numerical inversion have an inherent advantage, and the choice of a scaling solution or a numerical modeling solution will depend on the application. Figure 1 shows the trade-off between numerical errors and resolution when compared with scaling.

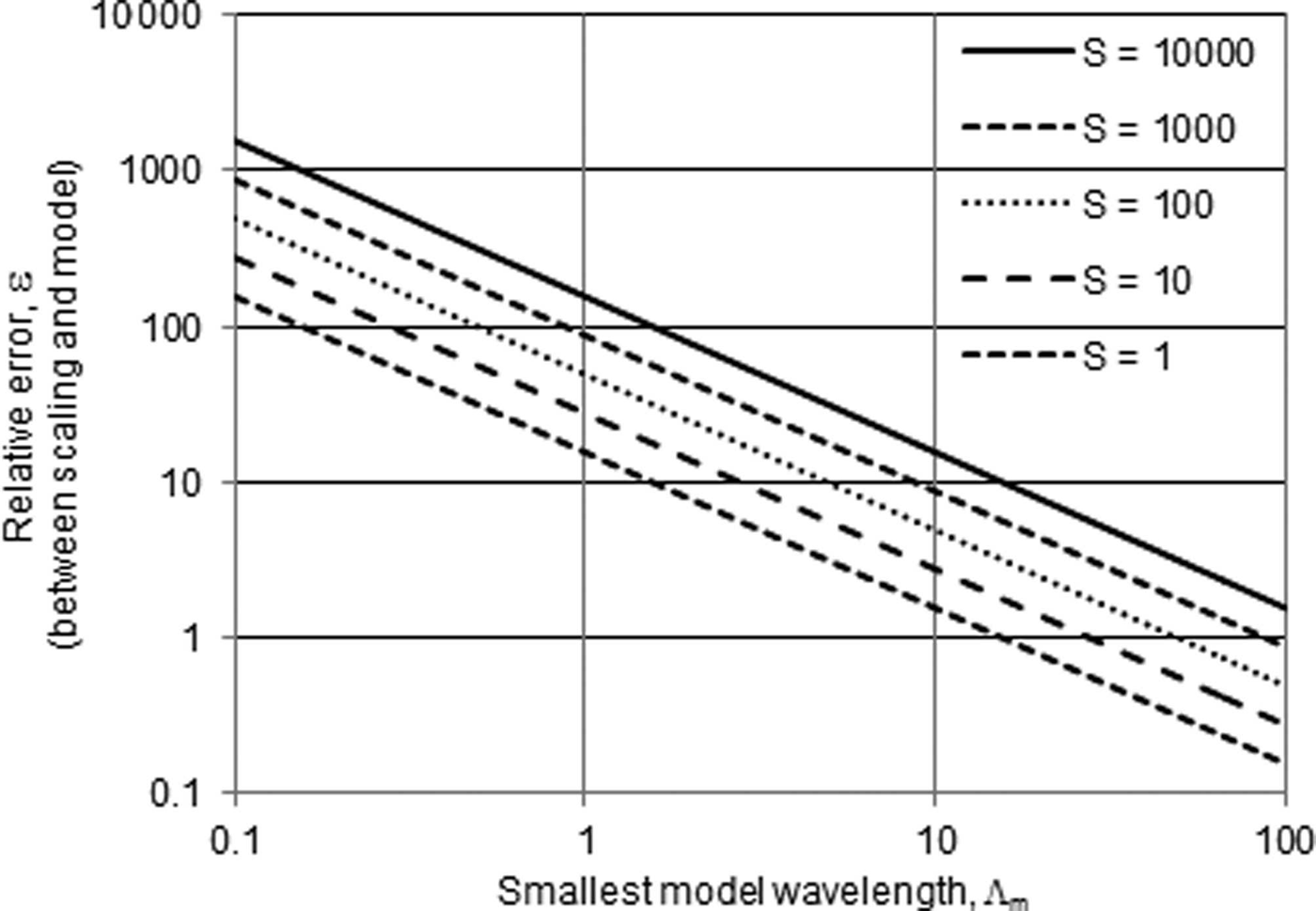
Fig. 1.

Wavelength versus relative error. Λ_m is the smallest wavelength used by a numerical model, and ∊ is the relative error between scaling and the model for glaciers of various sizes (km²). Higher values of ∊ indicate greater modeling errors relative to scaling errors. For example, Λ_m = 10 is a typical value that keeps ill-posed errors small and is equivalent to filtering all wavelengths <40 times the thickness (Eqn (4)). In that case, for a 1000 km² glacier, ∊ ≈ 10, implying that scaling errors, δ_s, are an order of magnitude smaller than the modeling errors, δ_m (see Eqn (7)). Note that values of Λ_m ≫ 10 are unlikely, because this will lead to excessively large model grid spaces (Table 1). At Λ_m = 100, for example, the model will not be able to resolve any glaciers except for a few of the world’s largest (in Table 1 multiply the grid spacing by a factor of 10). Therefore, the plot indicates that scaling has smaller ill-posed errors than numerical modeling (∊ > 1) for most plausible scenarios.

While the purpose of this paper is an analysis of ill-posed errors, it is worth emphasizing that other sources of error could have a significant impact on both the scaling estimate of a glacier’s volume and the numerical estimate of a glacier’s volume. Numerical inversion models can have errors due to the surface data (area, slope, etc.), errors due to uncertain parameters (e.g. Glen’s flow law parameter, sliding law parameters, shape factors), errors due to the numerical scheme (round-off precision, stability, etc.) and errors due to any simplifications of the continuum physics. Scaling is derived from the full 3-D continuum mechanics and has only three sources of error, the parameter, c, the exponent, γ, and the area data, S, (technically, γ is fixed by the physics and should not be considered a significant source of error; Reference Bahr, Meier and PeckhamBahr and others, 1997). Without a detailed analysis of a particular numerical model, it is difficult to quantitatively compare the impact of these other sources of errors. However, it is clear that scaling will have fewer potential sources of error than modeling; this will make an assessment of the volume/area scaling errors significantly simpler. However, while numerical modeling has many more potential sources of error, a numerical model also retains significantly greater flexibility, such as the ability (with ?) to fine-tune the resolution versus the magnitude of the errors.

Aggregate Errors

Conclusions

Errors from the ill-posed boundary-value calculation are by far the most significant source of error in glacier volume estimates derived from surface observations. Other significant sources of error exist, but unless proper spatial filtering, or another equivalent error suppression technique, is applied, the ill-posed calculation errors can grow exponentially and quickly swamp all other sources of error. Before considering any other source of error (from data, from model parameters or from numerical instabilities), the ill-posed errors must be controlled by filtering all short wavelengths. We recommend removing all horizontal wavelengths less than ˜40 times a glacier’s thickness, or equivalently specifying a horizontal grid spacing greater than or equal to ˜20 times the thickness (cf. Reference Kamb, Echelmeyer and LliboutryKamb and Echelmeyer, 1986). Although many published volume calculations discuss sources of errors due to data and model parameters, the ill-posed errors are rarely, if ever, acknowledged beyond

a cursory nod to numerical averaging over long spatial wavelengths. Instead, a detailed analysis of potential ill-posed errors should be the first and primary consideration in any glacier volume estimate.

Volume/area scaling intrinsically eliminates ill-posed errors by automatically filtering all wavelengths smaller than twice the glacier length. This is the longest wavelength solution that can still resolve a glacier, and as discussed, the longest possible wavelength solution will be the most stable. Numerical inversions can also filter appropriate wavelengths (or employ an equivalent technique that eliminates non-physical short-wavelength components of the solution) and are an important alternative to power-law scaling methods. Both approaches have advantages. Scaling typically has smaller ill-posed errors, but a numerical inversion will typically have greater resolution. Power-law scaling has fewer free parameters, but numerical inversions can give both the volume and additional information, such as velocities and stresses inside a glacier.

This paper makes no analysis of errors caused by the choice of numerical schemes, by the choice of numerical model parameters or by the choice of power-law scaling parameters. These errors must be evaluated separately for each model and scaling application. However, if all other sources of error are equal, then neither volume/area scaling nor numerical modeling has an inherent advantage in resolution, accuracy or precision when estimating a single glacier’s volume or the world’s total GIC volume. The accuracy, precision and resolution of any technique is limited by the ill-posed inversion.