1. Introduction
Glacial valleys are generally described as U-shaped in cross-section (e.g. Reference StrahlerStrahler, 1960, p. 392). The U-shape is commonly cited as evidence for prior glaciation in an area and is thus useful for reconstructing paleoenvironments. A number of studies of the cross-sectional morphology of glacial valleys have been conducted in recent years. Various analytical models, including the power model (y = ax b) (Reference SvenssonSvensson, 1959; Reference GrafGraf, 1970; Reference Doornkamp and KingDoornkamp and King, 1971; Reference KeqinJiao, 1981; Reference GengnianLiu, 1989; Reference Li, Gengnian and ZhijiuLi and others, 1999) and the quadratic model (y = a + bx + cx 2) (Reference WheelerWheeler, 1984; Reference AugustinusAugustinus, 1992; Reference JamesJames, 1996), have been used to describe valley cross-sections and their evolution. In addition, considerable progress has been made in analyzing the influence of glaciological (Reference HarborHarbor, 1992) and bedrock (Reference AugustinusAugustinus, 1992, Reference Augustinus1995; Reference HarborHarbor, 1995) boundary conditions on the development of valley cross-profiles, in theoretical studies of the development of valley cross-profile morphology (Reference Hirano and AniyaHirano and Aniya, 1988, Reference Hirano and Aniya1989, Reference Hirano and Aniya1990; Reference HarborHarbor, 1990) and in numerical simulation of valley evolution (Reference HarborHarbor, 1992, Reference Harbor1995).
Despite the frequent description of glacial valleys as U-shaped, there are many non-U-shaped glacial valleys (Reference Doornkamp and KingDoornkamp and King, 1971; Reference WheelerWheeler, 1984). For example, the interaction of glacial processes and patterns of rock resistance to erosion can lead to non-U-shaped glaciated valleys (Reference HarborHarbor, 1995). At the same time, some U-shaped valleys owe their shape to structural characteristics of the bedrock (Reference AugustinusAugustinus, 1992, Reference Augustinus1995). These complications result in disputes about whether areas have been glaciated, especially at low altitudes (Reference Yafeng, Zhijiu and LiShi and others, 1989). In order to resolve these disputes, it can be helpful to study the longitudinal variation of cross-profile morphology along valleys rather than simply exploring morphological characteristics in a single cross-section. Studies of this longitudinal variation are also helpful for exploring spatial erosion patterns of alpine glaciers.
Previous work in this field has focused on longitudinal profiles of glacial valleys (Reference LewisLewis, 1947; Reference NyeNye, 1952; Reference HookeHooke, 1991), but, except for some qualitative observations in a few areas (Reference ZhijiuCui, 1981a; Reference KeqinJiao, 1981; Reference GengnianLiu, 1989), longitudinal variations in cross-profile morphology have not received appropriate attention. In this paper, measurements of cross-sections of glacial valleys in the middle Tien Shan mountains, China, are used as a basis for discussing systematic longitudinal variations in cross-profile morphology.
2. Study Areas
The glacial valleys we studied were selected from the Bingdaban area of the Tien Shan, an area where there are U-in-U troughs (Reference ZhijiuCui, 1981a). The outer or higher troughs are believed to have formed during the Early Wangfeng Ice Age (probably oxygen isotope stage 8 (Reference JingtaiWang, 1981a)), while the inner ones, cut into the floors of the outer troughs, formed in the Middle and Late Wangfeng Ice Ages (stages 6 and 2). The inner troughs remain relatively unmodified by subsequent processes, as landforms are modified only slowly in these high-altitude areas. Owing to their better preservation, the inner troughs are ideal for studying the morphology of glacial valley cross-sections.
The bedrock in this area is composed mainly of metamorphic rocks such as gneiss and quartz-schist, and secondarily of granitic rocks. Based on previous work (Reference ZhijiuCui, 1981a; Reference HeigangXiong, 1991; Reference Zhijiu, Heigang and GengnianCui and others, 1998) and our field investigations, the influence of lithology is reflected mainly in the development of micro-landforms in glacial valleys such as striae and roches moutonnees. The effect of lithology on cross-section shape is apparent only locally (Reference ZhijiuCui, 1981a). Furthermore, while the distribution and orientations of glacial valleys are controlled by the dominant structures in the area (Reference ZhijiuCui, 1981a; Reference JingtaiWang, 1981b), these structures do not have a major influence on the shapes of valley cross-sections. In short, the dominant factor influencing cross-section shape is the capacity for glacial erosion as defined by the glacier thickness and ice flux (Reference JingtaiWang, 1981b).
Deposits of slope debris and moraine in these glacial valleys are normally only 10–20 m thick, but locally, as in the vicinity of Wangfeng road maintenance station (Wangfeng station), they can be up to 40–60 m (Reference ZhijiuCui, 1981b; Reference Zhijiu, Heigang and GengnianCui and others, 1998). Postglacial rivers do not cut into the bedrock in most of these glacial valleys; near Wangfeng station, however, they have cut to a depth of 2–3 m.
Fifty-six cross-sections of inner troughs were sampled from 1 : 50 000 Chinese Survey topographic maps with 20 m contour intervals (Fig. 1). Most of the cross-sections were located in such a way as to analyze systematic longitudinal variations in cross-profile morphology along the Glacier No. 8, Qongsaersayi, Qindawangsayi and Yawuertuaiken valleys. Ten to fifteen data points were obtained on each cross-section. Some representative cross-sections of U-shaped valleys that are approximately symmetrical are shown in Figure 2.

Fig. 1. Locations of cross-profiles of glacial valleys in the Bingdaban area.

Fig. 2. Some typical cross-sections in the Bingdaban area.
3. Analytical Models of Glacial Valley Cross-Sections
Two principal models have been widely used to describe the morphology of glacial valley cross-sections. The most common is the power model, first used by Reference SvenssonSvensson (1959) to describe glacial valleys in the Lapporten area, Sweden. In this model the shape of a valley is represented by
where x and y are the horizontal and vertical distances from the lowest point of the cross-section, and a and b are constants which can be determined by either visual or least-squares fits on double logarithmic plots (Reference SvenssonSvensson, 1959; Reference GrafGraf, 1970; Reference Doornkamp and KingDoornkamp and King, 1971; Reference KeqinJiao, 1981; Reference WheelerWheeler, 1984; Reference Hirano and AniyaHirano and Aniya, 1988; Reference GengnianLiu, 1989; Reference AugustinusAugustinus, 1992; Reference JamesJames, 1996; Reference Li, Gengnian and ZhijiuLi and others, 1999). Some of these studies have suggested that the valley morphology progressively approaches a true parabolic form with increasing glacial erosion, and that the stage of valley evolution can thus be gauged by the proximity of b to 2.0 (Reference SvenssonSvensson, 1959; Reference GrafGraf, 1970; Reference KeqinJiao, 1981; Reference Hirano and AniyaHirano and Aniya, 1988; Reference GengnianLiu, 1989). Other studies show that boundary conditions such as bedrock erodibility and slope stability, rock mass strength and rock structure also influence b (Reference AugustinusAugustinus, 1992). Reference GrafGraf (1970) noted that the power model needs an additional parameter, a form ratio (depth/width) in order to describe valley morphology completely.
There are several fundamental limitations of using the power model to describe overall valley morphology. First, least-squares fits to logarithmic data are strongly influenced by local valley-bottom morphology and the selection of the origin (x, y = 0, 0) (Reference WheelerWheeler, 1984; Reference Harbor and WheelerHarbor and Wheeler, 1992; Reference JamesJames, 1996). Second, the need to locate the coordinate system precisely at the center of the valley bottom poses a problem in many valleys (Reference JamesJames, 1996). Third, power models are sensitive to the sampling method employed; quite different results may be obtained by fitting functions to different subsets of the valley profile data (Reference JamesJames, 1996). Fourth, power models are not appropriate for comparing cross-section morphology longitudinally along asymmetrical glacial valleys, for two reasons: (1) each cross-section must be divided into two parts with different values of a and b, and (2) averaging the values from the two sides does not provide a mathematically consistent way of describing the overall cross-section morphology where the degree of asymmetry varies along the valley.
The second model commonly used to describe the morphology of glacial valley cross-sections is the quadratic model:
(Reference WheelerWheeler, 1984; Reference AugustinusAugustinus, 1992; Reference JamesJames, 1996). Such a quadratic equation can fit a symmetrical valley cross-section completely, without the need to treat opposing valley sides separately (Reference JamesJames, 1996). However, as with the power model, it is, for the same reasons, not appropriate for systematic comparison of cross-sections longitudinally along asymmetrical valleys.
Because neither the power nor the quadratic model is adequate for systematic theoretical analysis of longitudinal variations in asymmetric glacial valley cross-sections, a new model is needed.
4. A New Model of Glacial Valley Cross-section Morphology
4.1. General description
In this paper, we use a modification of the power model, which we call the variable width/depth ratio (VWDR) model, to describe the overall morphology of glacial valley cross-sections. In this model we define G(y) by (Fig. 3):
where (y − y 0) is the height above the valley bottom, taken to be at y = y 0, w is the width of the valley at height y, and G(y) is the VWDR at elevation y. (When y is the altitude of the trimline, G(y) is equal to 1/FR, where FR is the form ratio defined by Reference GrafGraf (1970).)

Fig. 3. Definition of parameters in the VWDR.
In order to avoid the influence of postglacial cut or fill, the valley cross-section is smoothed before calculations are undertaken (Fig. 4). Specifically: (1) the altitude of the valley bottom is adjusted if the floor is incised by fluvial or other processes; and (2) valley-side morphology is interpolated where talus or till are present.

Fig. 4. Method of smoothing of valley cross-sections before calculating VWDR values: (1) interpolate across the valley bottom if the valley has been incised by fluvial or other processes in postglacial time; (2) interpolate beneath talus or moraines on valley sides.
The adjustments are rather simple in this area because deposits on the valley floor and sides are generally < 10–20 m thick. Even in the vicinity of Wangfeng station, which has the thickest deposits (40–60 m), in a dataset compiled from maps with 20 m contour intervals only one or two points need to be adjusted. Thus, we can easily adjust these points by interpolating, by eye, using neighboring points to define the curvature of the valley side. More commonly, the problem points were removed. This did not affect the calculations noticeably. Furthermore, postglacial rivers do not cut into the bedrock in most parts of these glacial valleys. Where rivers do cut into the bedrock, near Wangfeng station (Fig. 1), the depth of incision is only 2–3 m, which also is not enough to affect the calculations.
As with the power model, double-log plots of G(y) against (y − y 0) typically result in straight lines (Fig. 5), which thus may be described by:

Fig. 5. Relationship between G and valley depth (d). Points A and B are discussed in text.
where d is the depth (y − y 0), and m and n are constants. The 56 valley cross-sections shown in Figure 1 have been fit with this model, and values of m, n and the explained variance, R 2, calculated by least-squares techniques (Table 1). While this model, unlike the power model, incorporates data from both sides of the valley and thus can be used to describe asymmetrical valley cross-sections, it does not describe a cross-section uniquely because the horizontal (or x) coordinates of the valley sides do not appear in the equations.
To provide a physical interpretation of m and n, replace G with w/d in Equation (4), thus:
Table 1. Statistical data on cross-sections of glacial valleys in the Tien Shan mountains
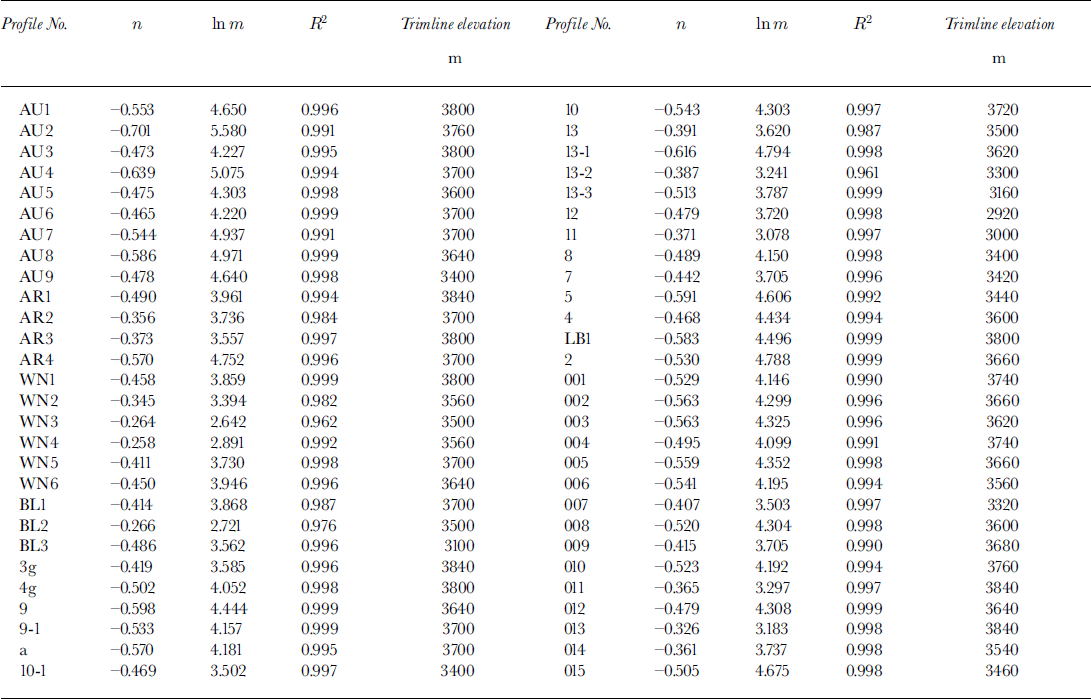
From this it is clear that m is the width of the valley when d = 1, so m is a measure of the width of the valley bottom. It is also clear that −1 < n <0. n = −1 describes a rectangular valley of constant width, m, with vertical sides. Values of n < −1 would describe a valley that narrows upward, which occasionally occurs but would be unrealistic in the present circumstances. n = 0 represents the limiting case of a V-shaped valley. Higher values of n correspond to valleys with convex upward sides. Thus, as n varies from −1 to 0 for a given value of m, valley-side slopes become progressively gentler and approach linear. Now consider the situation in which the valley cross-section is symmetrical so w = 2x. Then,
or
Comparison of this with Equation (1) will demonstrate that n = −0.5 corresponds to the parabolic case (b = 2).
4.2. Advantages and disadvantages of the VWDR model
The VWDR model can describe the integrated morphological characteristics of entire valley cross-sections, regard less of whether the valley is symmetrical or asymmetrical. Power functions cannot do this. Furthermore, because the w/d ratio is used, the data are less sensitive to lateral positioning than is the case with power models.
The VWDR model is directly linked to the form ratio, FR, because, by definition, G = 1/FR at the trimline altitude. The VWDR model can also be used to estimate the location of trimlines and the value of FR even where, owing to map errors or modification by postglacial processes, the trimline is not evident on maps or in the field. To do this, we plot ln G vs ln d and seek breaks in slope. For example, in Figure 5, the points to the left of A and B are for the inner valley, and A and B represent positions of the trimline. Where the valley walls rise above the trimline, the slope of the ln G vs ln d relation decreases (n becomes less negative), and the valley begins to widen out more rapidly with increasing elevation. This is inferred to represent valley sides formed by different processes or by an earlier glaciation. At the break in slope, G = 1/FR.
On the other hand, the VWDR model does not resolve all problems with traditional models. It, too, is sensitive to the determination of the valley-floor altitude in situations in which incision has occurred. Thus, although it can reduce problems associated with positioning in the x direction, the problems in the y direction still exist. Furthermore, although the VWDR model can describe the overall morphology of a valley cross-section, it loses the information on variability from the two sides, and cannot be used to generate a valley cross-section plot.
Although the VWDR model has some limitations, where valley-floor elevations are well known from previous fieldwork it can be used to compare different valley cross-sections and to study longitudinal variations in cross-section morphology along a glacial valley.
5. Longitudinal variations in Cross-Section Shape along Glacial valleys
5.1. Classification of glacial valleys
To facilitate discussion, we classify glacial valleys into two basic types based on differences in map or plan form (Fig. 6):

Fig. 6. Classification of glacial valleys. A, B, simple valleys; C, compound valley. (1) upper simple-valley section; (2) confluent section; (3) lower simple section.
-
(1) Simple valleys: A simple valley is one that has a single glacially scoured channel over most of its length. It may have more than one cirque at its head, but otherwise has no major tributaries.
-
(2) Compound valleys: Compound valleys are valleys with one or more major tributaries. In general, the respective channels of a compound valley may be considered to be simple valleys. Compound valleys commonly can be subdivided into three sections: (i) an upper simple-valley section, (ii) a confluent section and (iii) a lower simple section.
5.2. Longitudinal variation in cross-section morphology along glacial valleys
Longitudinal variations in m, n and the trimline altitude along the valleys from which most of the cross-sections discussed herein were obtained are given in Figures 7 and 8. These parameters vary systematically downstream from the valley head in both simple and compound valleys.

Fig. 7. Longitudinal variation of trimline altitude, In m and n along some simple valleys: (a) Glacial valley No. 8; (b) Qongsaersayi valley; (c) Qindawangsayi valley; (d) Yawuertuaiken valley.

Fig. 8. Longitudinal variation of trimline altitude, In m and n along some compound valleys. The short vertical arrows in each panel show the locations of confluences, (a) Daxigou valley; (b) Glacier No. 8–Daxigou valley; (c) Akesudangha–Ayoutuai-ken valley; (d) Tawuertuaiken–Ayoutuaiken valley.
In simple valleys, m initially increases (the valley floor becomes wider) from the head of the valley, and then decreases to the valley end. Correspondingly, n decreases, or becomes more negative, initially (valley sides become steeper) and then increases. In compound valleys, the same pattern is observed except that m and n oscillate in confluent valley sections. As expected, the trimline altitude decreases with increasing distance down-valley, in both simple and compound valleys.
5.3. Discussion
Basal temperatures in alpine glaciers are likely to be at the pressure-melting point except, in some situations, for a region in the lower part of the ablation area where the glacier may be frozen to its bed (Reference Hooke, Gould and BrzozowskiHooke and others, 1983; Reference Xiangsong, Guocai, Songlin, Jiyang and YingZhang and others, 1985; Reference Baolin, Maohuan and ZichuCai and others, 1987). Such temperate or polythermal alpine glaciers are therefore highly erosive. Glacial valleys are one of the most important landforms produced by such glaciers. The morphological characteristics of these valleys reflect both glacial dynamics and boundary conditions such as bedrock lithology and structure (Reference Embleton and ThornesEmbleton and Thornes, 1979; Reference AugustinusAugustinus, 1992, Reference Augustinus1995; Reference HarborHarbor, 1995). As noted earlier, bedrock lithology and structure affect micro-landforms in the glacial valleys studied herein, but not their overall cross-sectional shape. Thus, we hypothesize that the observed longitudinal variations in these glacial valleys are largely a consequence of differences in glacial dynamics, and hence erosion potential. Specifically, the wider valley floors and steeper valley walls (U-shapes) indicated by higher values of m and lower values of n imply more glacial erosion.
The erosive potential of a temperate glacier is determined by the ice-volume flux and by the frequency and magnitude of fluctuations in basal water pressure (Reference Embleton and ThornesEmbleton and Thornes, 1979; Reference JingtaiWang, 1981b; Reference Iverson and MenziesIverson, 1995). Frequent large water-pressure fluctuations are likely to be particularly significant where convexities in the bed cause crevassing at the surface (Reference HookeHooke, 1991), but otherwise may occur anywhere along a glacial valley. Thus, they should not be expected to produce systematic down-valley changes in cross-sectional shape. The ice flux, however, reaches a maximum in the vicinity of the equilibrium line of glaciers in simple valleys. Thus, erosion is likely to be most vigorous there, resulting in broader valley bottoms and steeper valley sides.
Reference ZhenshuanZhang (1981) has studied variations in equilibrium-line altitude (ELA) at the head of Ürümqi River, a north-flowing river in the Bingdaban area, using several methods. He concluded that the ELA in this area was at 3630 ± 40 m during the Middle and Late Wangfeng Ice Ages, when the valleys under discussion were last modified by glacial erosion. Reference HeigangXiong (1991) pointed out that the ELA in the areas of southward flow is 100–150 m higher than in areas of northward flow in the Bingdaban area. The trimlines in Figure 7 are at or close to these elevations at cross-sections 9 (3640 m), 005 (3660 m), 13-1 (3620 m) and AU4 (3700 m) in Glacial valley No. 8 and in Qongsaersayi, Qindawangsayi and Yawuertuaiken valleys, respectively. This is consistent with the higher values of m and lower values of n at these cross-sections. We can also divide the cross-sections of simple valleys into three groups, namely those above, at and below the ELA, and average the values of m and n in each group (Tables 2 and 3). The average values of m are larger and of n are more negative for the middle group.
Table 2. Average values and standard deviation of m and n for simple valleys in the Tien Shan mountains

Table 3. ANOVA1 analysis of statistical significance of m and n for differences between groups for simple valleys

Most of the characteristics of glaciers in compound valleys are similar to those of glaciers in simple valleys, but in compound valleys there are important interactions at glacial confluences. This is because ice flux increases more at confluences than in other areas, so the potential for erosion is larger here.
In Figure 8, locations of confluences are indicated by short vertical arrows. It will be noted that m increases and n becomes more negative from the upper simple-valley section to the confluent section in each of these compound valleys, reflecting the expected increase in erosion at confluences. Although the confluences are, in some cases, near the ELA (e.g. 2 and 4 in Fig. 8a), the implied increases in erosion are inferred to result primarily from increases in ice flux from the tributary valleys. Supporting this interpretation is the observation that the valleys widen appreciably below confluences, whereas simple valleys do not widen as dramatically at the ELA. The values of m and n appear to oscillate within the confluent section, reflecting the impact of successive confluences, while undergoing an overall decline. From the confluent section to the lower simple section, as ice flux diminishes, m decreases and n becomes less negative. Again, if we sort the cross-sections of compound valleys into three groups, those in upper simple-valley sections, those near confluences in confluent sections, and those further from confluences in confluent sections, it will be seen that the average value of m is larger and of n is more negative near confluences (Tables 4 and 5).
6. Conclusions
Longitudinal variations in cross-section morphology along glacial valleys can reflect variations in the erosive potential of the glaciers if the influence of boundary conditions such as the bedrock lithology and structure can be eliminated. These variations can be studied quantitatively by comparing successive cross-sections with the use of the VWDR model. In this model, which has some advantages over the other two commonly used ones, the power and quadratic models, the parameter G(y) = w/(y − y 0) is plotted as a function of d = (y − y 0). Statistical analysis reveals a power relation between G and d characterized by two parameters, m and n; m is a measure of the breadth of the valley bottom and n is a measure of the steepness of the valley sides.
With this model, we studied longitudinal variations in cross-section morphology along glacial valleys in the Bingdaban area using data from 56 cross-sections. In simple valleys, m increases and n becomes more negative from the head of the valley to the equilibrium line, as the valley bottom becomes broader and the sides steeper. Conversely, m decreases and n becomes less negative from the equilibrium line to the end of the valley, as the valley bottom narrows and the sides become gentler. In compound valleys, m and n follow the same pattern, except that they may oscillate through the confluent section. These variations are believed to result from longitudinal changes in glacier erosion potential along the valleys.
These conclusions are based on a field study in the middle Tien Shan mountains of China. Whether or not they are generally applicable needs further study in other areas.
Acknowledgements
We thank R. LeB. Hooke for undertaking editorial revision and text improvement, and all the members of Tien Shan Glacier Station for their help with the fieldwork. We are also deeply indebted to J. Harbor, A. James and P. Augustinus for reviewing and providing numerous constructive criticisms and suggestions. The research was supported by the National Natural Science Foundation of China (project No. 49671075).















