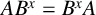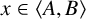1 Introduction
All groups considered in the paper are finite.
Recall that a group G is said to be a minimal nonnilpotent group or Schmidt group if G is not nilpotent and every proper subgroup of G is nilpotent. It is clear that every nonnilpotent group contains Schmidt subgroups, and their embedding has a strong structural impact (see, for example, [Reference Ballester-Bolinches, Kamornikov, Tyutyanov and Pérez-Calabuig2, Reference Ballester-Bolinches, Kamornikov and Yi3, Reference Vedernikov10]).
However, the following extensions of permutability turn out to be important in the structural study of groups and were introduced by Guo et al. in [Reference Guo, Shum and Skiba6].
Definition 1.1. Let A and B be subgroups of a group G.
-
(1) A is said to be G-permutable with B if there exists some
$g \in G$
such that
$AB^g = B^gA$
. -
(2) A is said to be hereditarily G-permutable with B (or G-h-permutable with B, for short) if there exists some
$g \in \langle A,B\rangle $
such that
$AB^g = B^gA$
. -
(3) A is said to be G-permutable in G if A is G-permutable with all subgroups of G.
-
(4) A is said to be hereditarily G-permutable (or G-h-permutable, for short) in G if A is hereditarily G-permutable with all subgroups of G.
It is clear that permutability implies G-permutability but the converse does not hold in general as the Sylow
$2$
-subgroups of the symmetric group of degree
$3$
show.
Our main goal here is to complete the structural study of groups in which every Schmidt subgroup of a group G is G-h-permutable. This study was started in [Reference Ballester-Bolinches, Kamornikov, Tyutyanov and Pérez-Calabuig2] where we prove the following important fact.
Theorem 1.2 [Reference Ballester-Bolinches, Kamornikov, Tyutyanov and Pérez-Calabuig2, Theorem B].
If every Schmidt subgroup of a group G is G-h-permutable in G, then G is soluble.
Observe that the alternating group of degree
$4$
is a nonsupersoluble Schmidt group.
Let
$p_1> p_2 > \cdots > p_r$
be the primes dividing
$|G|$
and let
$P_i$
be a Sylow
$p_i$
-subgroup of G, for each
$i = 1, 2, \ldots , r$
. Then we say that G is a Sylow tower group of supersoluble type if all subgroups
$P_1, P_1P_2, \ldots , P_1P_2\cdots P_{r-1}$
are normal in G. The class of all Sylow tower groups of supersoluble type is denoted by
$\mathfrak {D}$
.
Recall that if
$\mathfrak {F}$
is a nonempty class of groups and
$\pi $
is a set of primes, then
$\mathfrak {F}_\pi $
is the class of all
$\pi $
-groups in
$\mathfrak {F}$
. In particular, if p is a prime, then
$\mathfrak {N}_p$
is the class of all p-groups and
$\mathfrak {D}_{\pi (p-1)}$
is the class of all Sylow tower groups G of supersoluble type such that every prime dividing
$|G|$
also divides
$p-1$
.
If G is a group, then
$\operatorname {\mathrm {Soc}}(G)$
is the product of all minimal normal subgroups of G and
$\Phi (G)$
is the Frattini subgroup of G, that is, the intersection of all maximal subgroups of G.
Our main goal here is to describe completely the groups G with trivial Frattini subgroup which have their Schmidt subgroups G-h-permutable.
Theorem 1.3. Let G be a group with
$\Phi (G) = 1$
. Assume that
$\mathfrak {F} = LF (F)$
is the saturated formation locally defined by the canonical local definition F such that
$F(p) = \mathfrak {N}_p \mathfrak {D}_{\pi (p-1)}$
for every prime p. If every Schmidt subgroup of G is G-h-permutable in G, then the following statements hold:
-
(1)
$G = [\operatorname {\mathrm {Soc}}(G)]M$
is the semidirect product of
$\operatorname {\mathrm {Soc}}(G)$
with an
$\mathfrak {F}$
-group M; -
(2) if
$\Phi (M) = 1$
, then M is supersoluble.
We shall adhere to the notation and terminology of [Reference Ballester-Bolinches and Ezquerro1, Reference Doerk and Hawkes4].
2 Definitions and preliminary results
Our first lemma collects some basic properties of G-h-permutable subgroups which are very useful in induction arguments. Its proof is straightforward.
Lemma 2.1. Let A, B and K be subgroups of G with K normal in G. Then, the following statements hold.
-
(1) If A is G-h-permutable with B, then
$AK/K$
is
$G/K$
-h-permutable with
$BK/K$
in
$G/K$
. -
(2) If
$K \subseteq A$
, then
$A/K$
is
$G/K$
-h-permutable with
$BK/K$
in
$G/K$
if and only if A is G-h-permutable with B in G. -
(3) If A is G-h-permutable in G, then
$AK/K$
is
$G/K$
-h-permutable in
$G/K$
. -
(4) If
$A \subseteq B$
and A is G-h-permutable in G, then A is B-h-permutable in B.
The following result describes the structure of Schmidt groups.
Lemma 2.2 [Reference Gol’fand5, Reference Schmidt8].
Let S be a Schmidt group. Then S satisfies the following properties:
-
(1) the order of S is divisible by exactly two prime numbers p and q;
-
(2) S is a semidirect product
$S = [P]\langle a\rangle $
, where P is a normal Sylow p-subgroup of S and
$\langle a\rangle $
is a nonnormal Sylow q-subgroup of S and
$\langle a^q\rangle \in \operatorname {\mathrm {Z}}(S)$
; -
(3) P is the nilpotent residual of S, that is, the smallest normal subgroup of S with nilpotent quotient;
-
(4)
$P/ \Phi (P)$
is a noncentral chief factor of S and
$\Phi (P) = P{'} \subseteq \operatorname {\mathrm {Z}}(S)$
; -
(5)
$\Phi (S) = \operatorname {\mathrm {Z}}(S) = P{'} \times \langle a^q \rangle $
; -
(6)
$\Phi (P)$
is the centraliser
$C_P(a)$
of a in P; -
(7) if
$\operatorname {\mathrm {Z}}(S) = 1$
, then
$|S| = p^mq$
, where m is the order of p modulo q.
In what follows,
$\operatorname {\mathrm {Sch}}(G)$
denotes the set of all Schmidt subgroups of a group G. Following [Reference Ballester-Bolinches, Kamornikov and Yi3], a Schmidt group with a normal Sylow p-subgroup will be called an
$S_{\langle p,q \rangle }$
-group.
The proof of Theorem 1.3 follows after a series of lemmas. They give us an interesting picture of the groups with supersoluble Schmidt subgroups.
Lemma 2.3. Let
$\mathfrak {F} = \{H \mid \operatorname {\mathrm {Sch}}(H) \subseteq \mathfrak {U} \}$
, where
$\mathfrak {U}$
is the class of all supersoluble groups. Then,
$\mathfrak {F}$
satisfies the following properties:
-
(1) if
$G \in \mathfrak {F}$
, then G is a Sylow tower group of supersoluble type; in particular, G is a soluble group; -
(2)
$\mathfrak {F}$
is a subgroup-closed saturated Fitting formation; -
(3)
$\mathfrak {U} \subseteq \mathfrak {F}$
; -
(4)
$\mathfrak {F} = LF(F)$
, where F is the canonical local definition such that
$F(p) = \mathfrak {N}_p \mathfrak {D}_{\pi (p-1)}$
for every prime p.
Proof. Statements (1), (2) and (3) follow from [Reference Monakhov7, Lemma 4 and Theorem 2].
Let
$\mathfrak {H} = LF (F)$
be a local formation defined by the formation function F with
$F(p) = \mathfrak {N}_p \mathfrak {D}_{\pi (p-1)}$
for every prime p. Assume that
$\mathfrak {F} \nsubseteq \mathfrak {H}$
. Let G be a group in
$\mathfrak {F} \setminus \mathfrak {H}$
of minimal order. Since
$\mathfrak {F}$
is a saturated formation, it follows that G is a primitive soluble group. Let
$N = \operatorname {\mathrm {Soc}}(G)$
be the unique minimal normal subgroup of G. Then
$G/N \in \mathfrak {H}$
. Since G is a Sylow tower group of supersoluble type and
$\operatorname {\mathrm {C}}_G(N) = N$
, we see that N is a Sylow p-subgroup of G, where p is the largest prime dividing
$|G|$
.
Let
$q \in \pi (G)$
with
$q \neq p$
and let Q be a Sylow q-subgroup of G. Since
$N = \operatorname {\mathrm {C}}_G(N)$
, it follows that
$PQ$
is not nilpotent. Hence, G has an
$S_{\langle p,q\rangle }$
-subgroup S, which is supersoluble p-closed because
$G \in \mathfrak {F}$
. Then, by statements (4) and (5) of Lemma 2.2,
$|S/\operatorname {\mathrm {Z}}(S)| = pq$
and therefore, by statement (7) of Lemma 2.2, q divides
$p-1$
. Since G is a Sylow tower group of supersoluble type, it follows that
$$ \begin{align*} G/N = G/\operatorname{\mathrm{C}}_G(N) \in \mathfrak{D}_{\pi(p-1)},\end{align*} $$
and thus
$G \in \mathfrak {H}$
, which is a contradiction. Hence,
$\mathfrak {F} \subseteq \mathfrak {H}$
.
Assume that
$\mathfrak {F} \neq \mathfrak {H}$
, and let G be a group in
$\mathfrak {H} \setminus \mathfrak {F}$
of minimal order. Since
$\mathfrak {H}$
is a saturated formation and
$F(p)$
is a formation of soluble groups for all primes p, it follows that G is a primitive soluble group. Let N be a unique minimal normal subgroup of G. The choice of G yields
$G \in \mathfrak {H}$
and
$G/N \in \mathfrak {F}$
. Since G is soluble, N is a p-group for some prime p, and from
$G \in \mathfrak {H}$
, it follows that
$$ \begin{align*}G/N = G/\operatorname{\mathrm{C}}_G(N) \in \mathfrak{N}_p \mathfrak{D}_{\pi(p-1)}.\end{align*} $$
We conclude that
$G/N \in \mathfrak {D}_{\pi (p-1)}$
because
$\operatorname {\mathrm {O}}_p(G/N) = 1$
by [Reference Doerk and Hawkes4, Lemma A.13.6].
Let S be an
$S_{\langle r,q\rangle }$
-subgroup of G. If
$r \neq p$
, then S is contained in some Hall
$p'$
-subgroup H of G. Since
$H \cong G/N \in \mathfrak {F}$
, we see that
$S \in \mathfrak {U}$
. If
$r = p$
, then from
$G/N \in \mathfrak {D}_{\pi (p-1)}$
, it follows that q divides
$p-1$
. Thus, by Lemma 2.2,
$S \in \mathfrak {U}$
. Consequently, every Schmidt subgroup of G is supersoluble, which is a contradiction. Hence,
$\mathfrak {F} = \mathfrak {H}$
.
The following examples show that groups in Lemma 2.3 may not be supersoluble.
Example 2.4. Let
$$ \begin{align*}Q = \langle a,b \mid a^4 = b^4 = 1,\, a^2 = b^2,\, b^{-1}ab = a^{-1} \rangle \end{align*} $$
be the quaternion group of order
$8$
. Then G has a faithful and irreducible module A over the field of
$5$
elements of dimension
$2$
. Let
$G = [A]Q$
be the corresponding semidirect product. Then G is not supersoluble and
$C = [A]\langle a\rangle $
and
$D = [A]\langle b\rangle $
are supersoluble and normal subgroups of
$G = CD$
. By Lemma 2.3,
$G \in \mathfrak {F} = \{H\, |\, \operatorname {\mathrm {Sch}}(H) \subseteq \mathfrak {U}\}$
.
Example 2.5. Assume that M is a nonabelian group of order
$21$
. Then M has a faithful and irreducible module N over
$\text {GF}(43)$
, the field of
$43$
elements (see, for example, [Reference Doerk and Hawkes4, Corollary B.11.8]). Consider the semidirect product
$G = [N]M$
. It is obvious that G is not supersoluble. By Lemma 2.3,
$G \in \mathfrak {F} = \{H\,|\, \operatorname {\mathrm {Sch}}(H) \subseteq \mathfrak {U}\}$
.
The following result is of interest although it is not needed for the proof of Theorem 1.3.
Proposition 2.6. Let
$\mathfrak {F} = \{H \mid \operatorname {\mathrm {Sch}}(H) \subseteq \mathfrak {U}\}$
. Then, for every
$n\in \mathbb {N}$
, there exists a group
$G \in \mathfrak {F}$
of nilpotent length n.
Proof. Let
$n \geq 2$
and let
$p_1, p_2, \ldots , p_n$
be primes such that
$p_1 < p_2 < \cdots < p_n$
and
$p_i$
divides
$p_j-1$
for all
$i < j$
, where
$i = 1,2, \ldots , n-1$
,
$j = 2, \ldots , n$
. By Dirichlet’s theorem, there exists an infinite set of primes of the form
$$ \begin{align*} p_1p_2\cdots p_{n_0} + 1, \end{align*} $$
where
$n_0 \in \mathbb {N}$
. Assume that
$p_{n+1}$
is one of them. It is obvious that
$p_i$
divides
$p_{n+1} - 1$
for any
$i = 1,2, \ldots , n$
.
Assume that
$G_1$
is a cyclic group of order
$p_1$
. Assume that
$i \geq 2$
and
$G_{i -1}$
is in
$\mathfrak F$
and of nilpotent length
$i-1$
. By [Reference Doerk and Hawkes4, Corollary B.11.8],
$G_{i -1}$
has a faithful and irreducible module
$V_{p_i}$
over the field of
$p_i$
elements. Let
$G_i = [V_{p_i}]G_{i-1}$
be the corresponding semidirect product. Then
$\operatorname {\mathrm {F}}(G_i) = V_{p_i}$
and hence the nilpotent length of
$G_i$
is equal to i. Furthermore, by Lemma 2.3,
$G_i \in \mathfrak {F}$
. In particular,
$G_n$
is an
$\mathfrak {F}$
-group of nilpotent length n.
The following subgroup embedding property was introduced by Vasil’ev, Vasil’eva and Tyutyanov in [Reference Vasil’ev, Vasil’eva and Tyutyanov9].
Definition 2.7. A subgroup H of a group G is said to be
$\mathbb {P}$
-subnormal in G if there exists a chain of subgroups
$$ \begin{align*} H = H_0 \subseteq H_1 \subseteq \cdots \subseteq H_{n-1} \subseteq H_n = G \end{align*} $$
such that for every
$i = 1, 2, \ldots , n$
, either
$|H_i : H_{i-1}| \in \mathbb {P}$
or
$H_{i-1}$
is normal in
$H_i$
.
Note that
$\mathbb {P}$
-subnormality coincides with K-
$\mathfrak {U}$
-subnormality (see [Reference Ballester-Bolinches and Ezquerro1, Ch. 6]) in the soluble universe.
Lemma 2.8. Let A be a G-h-permutable subgroup of a soluble group G. Then, A is
$\mathbb {P}$
-subnormal in G. In particular, the supersoluble residual
$A^{\mathfrak {U}}$
of A is subnormal in G.
Proof. Let G be a group of smallest order for which the lemma is not true, and let L be a minimal normal subgroup of G. Since G is soluble,
$|L| = p^n$
for some prime
$p \in \pi (G)$
and
$n \geq 1$
. Suppose that
$G = AL$
. Then A is a maximal subgroup of G and
$A \cap L = 1$
. Let
$L_1$
be a subgroup of prime order of L. Then,
$AL_1^x = L_1^xA$
for some
$x \in G$
. Consequently,
$AL_1^x$
is a subgroup of G. Since A is maximal in G and
$A \neq AL_1^x$
, we see that
$AL_1^x = G$
. Because
$$ \begin{align*}|G:A| = |AL_1^x|/|A| =|L_1^x|/|A \cap L_1^x| = |L_1^x|,\end{align*} $$
we conclude that
$|G:A| = p$
and then A is
$\mathbb {P}$
-subnormal in G, which is a contradiction. Hence,
$G \neq AL$
. Since
$|AL| < |G|$
, by Lemma 2.1, it follows that A is
$\mathbb {P}$
-subnormal in
$AL$
. By Lemma 2.1,
$AL/L$
is
$(G/L)$
-h-permutable in
$G/L$
, and from
$|G/L| < |G|$
, it follows that
$AL/L$
is
$\mathbb {P}$
-subnormal in
$G/L$
. In particular,
$AL$
is
$\mathbb {P}$
-subnormal in G by [Reference Ballester-Bolinches and Ezquerro1, Lemma 6.1.6]. However, then A is a
$\mathbb {P}$
-subnormal subgroup of G by [Reference Ballester-Bolinches and Ezquerro1, Lemma 6.1.7], which is a contradiction. Consequently, A is
$\mathbb {P}$
-subnormal in G. Applying [Reference Ballester-Bolinches and Ezquerro1, Lemma 6.1.9], we conclude that
$A^{\mathfrak {U}}$
is subnormal in G.
Example 2.9. Let G be a group isomorphic to the alternating group of degree
$6$
. Since G does not have maximal subgroups of prime index, the identity subgroup
$1$
of G is G-h-permutable but not
$\mathbb {P}$
-subnormal in G. Thus, the solubility of the group G in Lemma 2.8 is essential.
Lemma 2.10. Let
$G \in \mathfrak {F} = \{H\,|\, \operatorname {\mathrm {Sch}}(H) \subseteq \mathfrak {U} \}$
. If
$\Phi (G) = 1$
and every Schmidt subgroup of G is G-h-permutable in G, then G is supersoluble.
Proof. We argue by induction on
$|G|$
. Let N be a minimal normal subgroup of G. Since G is soluble by Lemma 2.3, it follows that N is p-elementary abelian for some prime p. Since
$\Phi (G) = 1$
, it follows that
$G = NM$
for some maximal subgroup M of G and
$N \cap M = 1$
.
Suppose that
$NM_{p'}$
is p-nilpotent. Then
$NM_{p'} \subseteq \operatorname {\mathrm {C}}_G(N)$
. Then
$G/\operatorname {\mathrm {C}}_G(N)$
is a p-group. Since
$\operatorname {\mathrm {O}}_p(G/\operatorname {\mathrm {C}}_G(N)) = 1$
by [Reference Doerk and Hawkes4, Lemma A.13.6], we have
$N \subseteq \operatorname {\mathrm {Z}}(G)$
. Then
$G = N \times M$
. Now, M belongs to
$\mathfrak {F}$
and
$\Phi (M) \subseteq \Phi (G) = 1$
by [Reference Doerk and Hawkes4, Theorem A.9.2]. By induction, M is supersoluble. Hence, G is supersoluble.
Assume that
$NM_{p'}$
is not p-nilpotent. Consequently,
$NM_{p'}$
contains a minimal non-p-nilpotent group X. By [Reference Ballester-Bolinches and Ezquerro1, Corollary 6.4.5], X is an
$S_{\langle p,q \rangle }$
-subgroup
$X = [P]Q$
and
$P \subseteq N$
. We can assume without loss of generality that
$Q \subseteq M_{p'}$
. Since the subgroup
$[P]Q$
is G-h-permutable, we may assume that
$([P]Q)M = PM$
is a subgroup of G. Consequently,
$P = N$
and
$NQ$
is an
$S_{\langle p,q\rangle }$
-subgroup G. By hypothesis,
$NQ$
is supersoluble. Hence, in view of Lemma 2.2,
$|N/\Phi (N)| = p$
by Lemma 2.2. Since
$\Phi (N) = 1$
, it follows that
$|N| = p$
.
Consequently, we may assume that every minimal normal subgroup of G is cyclic. Then, by [Reference Doerk and Hawkes4, Theorem A.10.6],
$\operatorname {\mathrm {F}}(G)$
is a direct product of normal subgroups of G of prime order and so
$G/\operatorname {\mathrm {C}}_G(\operatorname {\mathrm {F}}(G))$
is abelian. Since
$\operatorname {\mathrm {C}}_G(\operatorname {\mathrm {F}}(G)) \subseteq \operatorname {\mathrm {F}}(G)$
by [Reference Doerk and Hawkes4, Theorem A.10.6], it follows that
$G/\operatorname {\mathrm {F}}(G)$
is abelian. In particular, G is supersoluble.
3 Proof of Theorem 1.3
Since G is soluble and
$\Phi (G) = 1$
, we conclude that
$\operatorname {\mathrm {F}}(G) = \operatorname {\mathrm {Soc}}(G)$
and
$G = [\operatorname {\mathrm {Soc}}(G)]M$
for some subgroup M of G, that is,
$\operatorname {\mathrm {Soc}}(G) \cap M = 1$
by [Reference Doerk and Hawkes4, Theorem A.10.6].
Let S be a Schmidt subgroup of M. Suppose that S is an
$S_{\langle p,q \rangle }$
-subgroup. Then, by hypothesis, S is G-h-permutable in G. Consequently, by Lemma 2.8, S is
$\mathbb {P}$
-subnormal in G and
$S^{\mathfrak {U}}$
is subnormal in G. In view of Lemma 2.2, we see that either
$S^{\mathfrak {U}} \neq 1$
is a p-subgroup of S or
$S^{\mathfrak {U}} = 1$
. Assume that
$S^{\mathfrak {U}} \neq 1$
. Then,
$$ \begin{align*} S^{\mathfrak{U}} \subseteq F(G) \cap M = 1, \end{align*} $$
which is a contradiction. Therefore, every Schmidt subgroup of M is supersoluble.
By Lemma 2.3, it follows that
$M \in \mathfrak {F} = LF (F)$
, where F is the formation function given by
$F(r) = \mathfrak {N}_r \mathfrak {D}_{\pi (r-1)}$
for any prime r.
By Lemma 2.10, M is supersoluble provided that
$\Phi (M) = 1$
.
Open access
