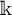1 Introduction
1.1 Background
This paper introduces certain diagrammatic supercategories via generators and relations. These supercategories provide a combinatorial model of certain monoidal supercategories of representations for the type P Lie superalgebra
![]() ${\mathfrak {p}} (n)$
. The prefix “super” means there is a
${\mathfrak {p}} (n)$
. The prefix “super” means there is a
![]() ${\mathbb {Z}}/2{\mathbb {Z}}$
-grading and definitions include signs according to the grading. For example, a supercategory is a category enriched in the category of
${\mathbb {Z}}/2{\mathbb {Z}}$
-grading and definitions include signs according to the grading. For example, a supercategory is a category enriched in the category of
![]() ${\mathbb {Z}}_2$
-graded vector spaces, while a monoidal supercategory is additionally equipped with a monoidal structure satisfying a graded analogue of the interchange law. Recall that the type P Lie superalgebra is one of the so-called strange families which appears in Kac’s classification of the simple complex Lie superalgebras [Reference Kac18]. It has no direct analogue in the classical world, and its representation theory is still relatively mysterious. One reason for this is that many classical techniques used to study Lie algebras cannot be directly adapted to the study of
${\mathbb {Z}}_2$
-graded vector spaces, while a monoidal supercategory is additionally equipped with a monoidal structure satisfying a graded analogue of the interchange law. Recall that the type P Lie superalgebra is one of the so-called strange families which appears in Kac’s classification of the simple complex Lie superalgebras [Reference Kac18]. It has no direct analogue in the classical world, and its representation theory is still relatively mysterious. One reason for this is that many classical techniques used to study Lie algebras cannot be directly adapted to the study of
![]() ${\mathfrak {p}}(n)$
, e.g., its enveloping superalgebra has trivial center, so the tools of central characters cannot be used.
${\mathfrak {p}}(n)$
, e.g., its enveloping superalgebra has trivial center, so the tools of central characters cannot be used.
In [Reference Moon22], Moon gave a generators and relations presentation for the endomorphism algebras of the tensor powers of the natural supermodule for
![]() ${\mathfrak {p}} (n)$
. Due to their similarity to Brauer’s algebras for the orthogonal and symplectic Lie algebras, they are variously called X Brauer algebras where
${\mathfrak {p}} (n)$
. Due to their similarity to Brauer’s algebras for the orthogonal and symplectic Lie algebras, they are variously called X Brauer algebras where
![]() $X \in \left\{\text {marked}, \text {odd}, \text {periplectic} \right\}$
. Building on Moon’s work, the second author and Tharp introduced a diagrammatic supercategory that describes the full sub-supercategory of
$X \in \left\{\text {marked}, \text {odd}, \text {periplectic} \right\}$
. Building on Moon’s work, the second author and Tharp introduced a diagrammatic supercategory that describes the full sub-supercategory of
![]() ${\mathfrak {p}} (n)$
-supermodules which are tensor products of the natural supermodule [Reference Kujawa and Tharp20] (see also [Reference Serganova26]). The objects of this supercategory are nonnegative integers, and the morphisms are
${\mathfrak {p}} (n)$
-supermodules which are tensor products of the natural supermodule [Reference Kujawa and Tharp20] (see also [Reference Serganova26]). The objects of this supercategory are nonnegative integers, and the morphisms are
![]() ${\mathbb {k}}$
-linear combinations of Brauer diagrams that are subject to signed versions of Brauer’s original relations. The endomorphism algebras in this supercategory give a diagrammatic realization of Moon’s algebra. Since then, there has been substantial work applying diagrammatic, combinatorial, and categorical techniques to the study of
${\mathbb {k}}$
-linear combinations of Brauer diagrams that are subject to signed versions of Brauer’s original relations. The endomorphism algebras in this supercategory give a diagrammatic realization of Moon’s algebra. Since then, there has been substantial work applying diagrammatic, combinatorial, and categorical techniques to the study of
![]() ${\mathfrak {p}}(n)$
and Moon’s algebra (see [Reference Balagovic, Daugherty, Entova-Aizenbud, Halacheva, Hennig, Im, Letzter, Norton, Serganova and Stroppel2–Reference Boe and Kujawa4, Reference Chen and Peng8–Reference Coulembier and Ehrig12] and the references therein). The present paper further develops this approach to the representation theory of
${\mathfrak {p}}(n)$
and Moon’s algebra (see [Reference Balagovic, Daugherty, Entova-Aizenbud, Halacheva, Hennig, Im, Letzter, Norton, Serganova and Stroppel2–Reference Boe and Kujawa4, Reference Chen and Peng8–Reference Coulembier and Ehrig12] and the references therein). The present paper further develops this approach to the representation theory of
![]() ${\mathfrak {p}} (n)$
.
${\mathfrak {p}} (n)$
.
Because we allow all (not just grading-preserving) homomorphisms, the category of finite-dimensional
![]() ${\mathfrak {p}} (n)$
-supermodules is a supercategory. As this supercategory is closed under taking tensor products and duals, this structure makes the supercategory of finite-dimensional
${\mathfrak {p}} (n)$
-supermodules is a supercategory. As this supercategory is closed under taking tensor products and duals, this structure makes the supercategory of finite-dimensional
![]() ${\mathfrak {p}} (n)$
-supermodules into a rigid monoidal supercategory in the sense of [Reference Brundan and Ellis5]. In this paper, we introduce and study diagrammatic supercategories which completely describe certain natural monoidal sub-supercategories of
${\mathfrak {p}} (n)$
-supermodules into a rigid monoidal supercategory in the sense of [Reference Brundan and Ellis5]. In this paper, we introduce and study diagrammatic supercategories which completely describe certain natural monoidal sub-supercategories of
![]() ${\mathfrak {p}} (n)$
-supermodules.
${\mathfrak {p}} (n)$
-supermodules.
1.2 Main results on webs
For the discussion in this subsection, we assume that
![]() ${\mathbb {k}}$
is an integral domain where two is invertible. In Section 3, we use generators and relations to define a
${\mathbb {k}}$
is an integral domain where two is invertible. In Section 3, we use generators and relations to define a
![]() ${\mathbb {k}}$
-linear monoidal supercategory called
${\mathbb {k}}$
-linear monoidal supercategory called
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. The objects of this supercategory are finite tuples of nonnegative integers. Morphisms in this supercategory are
${\mathfrak {p}\text {-}\mathbf {Web}}$
. The objects of this supercategory are finite tuples of nonnegative integers. Morphisms in this supercategory are
![]() ${\mathbb {k}}$
-linear combinations of webs, which are diagrams obtained by vertically and horizontally concatenating the generating diagrams (explained below in Definition 3.1.1). In this paper, we use the convention that diagrams are read from bottom to top. For example, given any integer
${\mathbb {k}}$
-linear combinations of webs, which are diagrams obtained by vertically and horizontally concatenating the generating diagrams (explained below in Definition 3.1.1). In this paper, we use the convention that diagrams are read from bottom to top. For example, given any integer
![]() $a> 1$
, the following sum of webs is a morphism in
$a> 1$
, the following sum of webs is a morphism in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
from
${\mathfrak {p}\text {-}\mathbf {Web}}$
from
![]() $(1,a,1)$
to
$(1,a,1)$
to
![]() $(a)$
:
$(a)$
:

Compared to webs that have previously appeared in the literature, experienced readers will notice that our webs contain (unoriented) cups and caps on strings of thickness one which are decorated by beads. These are odd morphisms in the category, and correspond to the fact that the object 1 is self-dual. The bead is used to distinguish these unoriented morphisms from the oriented cups and caps drawn in the oriented version of the web category (see below). The one-valent vertex, called an antenna, is a shorthand used to represent the composition of a beaded cap with the split. See (3.1).
In Section 4, we introduce an oriented version of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
which we call
${\mathfrak {p}\text {-}\mathbf {Web}}$
which we call
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. Again, this is a monoidal supercategory defined by generators and relations. The objects of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. Again, this is a monoidal supercategory defined by generators and relations. The objects of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are finite words in the symbols
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are finite words in the symbols
As before, morphisms are
![]() ${\mathbb {k}}$
-linear combinations of diagrams obtained by vertical and horizontal concatenations of generating diagrams. Any such diagram is called an oriented web. For example, given any integer
${\mathbb {k}}$
-linear combinations of diagrams obtained by vertical and horizontal concatenations of generating diagrams. Any such diagram is called an oriented web. For example, given any integer
![]() $a \geq 1$
, the following sum of oriented webs is a morphism in
$a \geq 1$
, the following sum of oriented webs is a morphism in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
from
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
from
![]() $\uparrow _1 \, \uparrow _a \, \downarrow _1 $
to
$\uparrow _1 \, \uparrow _a \, \downarrow _1 $
to
![]() $\uparrow _1 \, \uparrow _{a-1}$
:
$\uparrow _1 \, \uparrow _{a-1}$
:

Experienced webslingers will also note that these webs are decorated with yellow and blue dots, which reverse the orientation of the strand. These represent odd morphisms in this category. The yellow dot encodes an isomorphism
![]() $\uparrow _1{\rightarrow }\downarrow _1$
, while the blue dot encodes its inverse.
$\uparrow _1{\rightarrow }\downarrow _1$
, while the blue dot encodes its inverse.
Our first set of results concern the structure of these categories. In Corollaries 3.3.2 and 4.3.2, we prove that both
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are symmetric braided categories and that
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are symmetric braided categories and that
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is rigid. This is perhaps not surprising since these categories are constructed to provide diagrammatic models of categories of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is rigid. This is perhaps not surprising since these categories are constructed to provide diagrammatic models of categories of
![]() ${\mathfrak {p}}(n)$
-supermodules which have these properties. In Corollary 6.3.2, we give a
${\mathfrak {p}}(n)$
-supermodules which have these properties. In Corollary 6.3.2, we give a
![]() ${\mathbb {k}}$
-linear “stable basis” for the morphism spaces in
${\mathbb {k}}$
-linear “stable basis” for the morphism spaces in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
in terms of web diagrams (see Sections 3.5 and 6.7 for details). By applying standard techniques (Section 4.4), we extend our arguments to prove a basis theorem for the morphisms in
${\mathfrak {p}\text {-}\mathbf {Web}}$
in terms of web diagrams (see Sections 3.5 and 6.7 for details). By applying standard techniques (Section 4.4), we extend our arguments to prove a basis theorem for the morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
We also describe relationships among these categories that could be predicted by readers familiar with webs in other settings. Let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
denote the full subcategory of
${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
denote the full subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
consisting of all objects which are sequences of ones, and let
${\mathfrak {p}\text {-}\mathbf {Web}}$
consisting of all objects which are sequences of ones, and let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
denote the full subcategory of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
denote the full subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
consisting of all objects which are finite sequences of upward oriented arrows labeled by nonnegative integers. In Theorem 6.4.4, we demonstrate
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
consisting of all objects which are finite sequences of upward oriented arrows labeled by nonnegative integers. In Theorem 6.4.4, we demonstrate
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
is isomorphic to the marked Brauer supercategory introduced in [Reference Kujawa and Tharp20]. In Theorem 6.8.3, we prove that
${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
is isomorphic to the marked Brauer supercategory introduced in [Reference Kujawa and Tharp20]. In Theorem 6.8.3, we prove that
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
are isomorphic monoidal supercategories.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
are isomorphic monoidal supercategories.
1.3 Main results on representations of
 ${\mathfrak {p}} (n)$
${\mathfrak {p}} (n)$
Our second set of results require that the ground ring
![]() ${\mathbb {k}}$
is an algebraically closed field of characteristic zero. The results explain how the categories
${\mathbb {k}}$
is an algebraically closed field of characteristic zero. The results explain how the categories
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are combinatorial models for certain natural subcategories of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are combinatorial models for certain natural subcategories of
![]() ${\mathfrak {p}} (n)$
-supermodules.
${\mathfrak {p}} (n)$
-supermodules.
Let
![]() $V_{n}$
denote the natural
$V_{n}$
denote the natural
![]() ${\mathfrak {p}} (n)$
-supermodule coming from its usual matrix representation, and for
${\mathfrak {p}} (n)$
-supermodule coming from its usual matrix representation, and for
![]() $a \geq 0$
, let
$a \geq 0$
, let
![]() $S^a(V_n)$
and
$S^a(V_n)$
and
![]() $\bigwedge ^a(V_n)$
denote its ath symmetric and exterior powers. Write
$\bigwedge ^a(V_n)$
denote its ath symmetric and exterior powers. Write
![]() ${\mathfrak {p}} (n)\text{-}\mathrm{mod}_{V}$
for the full subcategory of
${\mathfrak {p}} (n)\text{-}\mathrm{mod}_{V}$
for the full subcategory of
![]() ${\mathfrak {p}} (n)$
-modules consisting of all finite tensor powers of
${\mathfrak {p}} (n)$
-modules consisting of all finite tensor powers of
![]() $V_n$
, and let
$V_n$
, and let
![]() ${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
and
${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
and
![]() ${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}$
denote the full subcategory consisting of tensor products of
${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}$
denote the full subcategory consisting of tensor products of
![]() $S^{a}(V_{n})$
for various
$S^{a}(V_{n})$
for various
![]() $a \geq 0$
, and tensor products of
$a \geq 0$
, and tensor products of
![]() $S^{a}(V_{n})$
and its dual
$S^{a}(V_{n})$
and its dual
![]() $S^{a}(V_{n})^{*}$
for various
$S^{a}(V_{n})^{*}$
for various
![]() $a \geq 0$
, respectively. We remark that since
$a \geq 0$
, respectively. We remark that since
![]() $S^{a}(V_{n})^{*} \cong \bigwedge ^{a}(V_{n})$
for all
$S^{a}(V_{n})^{*} \cong \bigwedge ^{a}(V_{n})$
for all
![]() $a \geq 1$
, the category
$a \geq 1$
, the category
![]() ${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}$
also, up to isomorphism, includes exterior powers.
${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}$
also, up to isomorphism, includes exterior powers.
We can now describe the main results of the paper. For each
![]() $n \geq 1$
, we demonstrate that certain categories of
$n \geq 1$
, we demonstrate that certain categories of
![]() ${\mathfrak {p}}(n)$
-modules are equivalent to a quotient of the aforementioned web categories obtained by imposing one additional relation (which depends on n). That is, the single diagrammatic category
${\mathfrak {p}}(n)$
-modules are equivalent to a quotient of the aforementioned web categories obtained by imposing one additional relation (which depends on n). That is, the single diagrammatic category
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
can be used to describe the category
${\mathfrak {p}\text {-}\mathbf {Web}}$
can be used to describe the category
![]() ${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
for all
${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
for all
![]() $n \geq 1$
. Similarly,
$n \geq 1$
. Similarly,
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
describes
${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
describes
![]() ${\mathfrak {p}} (n)\text{-}\mathrm{mod}_{V}$
and
${\mathfrak {p}} (n)\text{-}\mathrm{mod}_{V}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
describes
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
describes
![]() ${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}.$
${\mathfrak {p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}.$
To be precise, for every
![]() $n \geq 1$
, we show in Theorems 6.1.1, 6.4.2, and 6.5.1 that there are essentially surjective functors of
$n \geq 1$
, we show in Theorems 6.1.1, 6.4.2, and 6.5.1 that there are essentially surjective functors of
![]() ${\mathbb {k}}$
-linear, monoidal supercategories:
${\mathbb {k}}$
-linear, monoidal supercategories:
 $$ \begin{align*} F &: {\mathfrak{p}\text{-}\mathbf{Web}}_{1} {\rightarrow} {\mathfrak{p}} (n)\text{-}\mathrm{mod}_{V}, \\ G &: {\mathfrak{p}\text{-}\mathbf{Web}} {\rightarrow} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow\downarrow} &: {\mathfrak{p}\text{-}\mathbf{Web}}_{\uparrow\downarrow} {\rightarrow} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}. \end{align*} $$
$$ \begin{align*} F &: {\mathfrak{p}\text{-}\mathbf{Web}}_{1} {\rightarrow} {\mathfrak{p}} (n)\text{-}\mathrm{mod}_{V}, \\ G &: {\mathfrak{p}\text{-}\mathbf{Web}} {\rightarrow} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow\downarrow} &: {\mathfrak{p}\text{-}\mathbf{Web}}_{\uparrow\downarrow} {\rightarrow} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}. \end{align*} $$
In Theorems 6.4.2, 6.7.2, and 6.8.2, we show that these functors are full. It is worth noting that fullness can fail in positive characteristic. See Remark 6.7.3 for an example.
Next, using results of [Reference Coulembier10], we define a certain morphism
where
![]() $\ell = (n+1)(n+2)/2$
, and
$\ell = (n+1)(n+2)/2$
, and
![]() $1^{\ell }$
and
$1^{\ell }$
and
![]() $\uparrow _{1}^{\ell }$
denote an
$\uparrow _{1}^{\ell }$
denote an
![]() $\ell $
-tuple of ones and
$\ell $
-tuple of ones and
![]() $\uparrow _{1}$
’s, respectively. The definition of this morphism is subtle, and it does not seem to admit a nice diagrammatic description. We define
$\uparrow _{1}$
’s, respectively. The definition of this morphism is subtle, and it does not seem to admit a nice diagrammatic description. We define
![]() ${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}$
to be the monoidal supercategory given by the same generators and relations as
${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}$
to be the monoidal supercategory given by the same generators and relations as
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, along with the single additional relation
${\mathfrak {p}\text {-}\mathbf {Web}}$
, along with the single additional relation
The monoidal supercategories
![]() ${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}_{1}$
and
${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}_{1}$
and
![]() ${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are defined similarly.
${{\mathfrak {p}} (n)\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are defined similarly.
In Theorem 7.2.1, it is shown that the functors F, G, and
![]() $G_{\uparrow \downarrow }$
induce equivalences of monoidal supercategories:
$G_{\uparrow \downarrow }$
induce equivalences of monoidal supercategories:
 $$ \begin{align*} F &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{1} \xrightarrow{\cong} {\mathfrak{p}} (n)\text{-}\mathrm{mod}_{V}, \\ G &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}} \xrightarrow{\cong} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow\downarrow} &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{\uparrow\downarrow} \xrightarrow{\cong} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}. \end{align*} $$
$$ \begin{align*} F &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{1} \xrightarrow{\cong} {\mathfrak{p}} (n)\text{-}\mathrm{mod}_{V}, \\ G &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}} \xrightarrow{\cong} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow\downarrow} &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{\uparrow\downarrow} \xrightarrow{\cong} {\mathfrak{p}(n)\text{-}\mathrm{mod}_{\mathcal{S},\mathcal{S}^{*}}}. \end{align*} $$
It is worth noting that these categories of
![]() ${\mathfrak {p}} (n)$
-supermodules are not semisimple, unlike some of the more familiar contexts where web categories are used.
${\mathfrak {p}} (n)$
-supermodules are not semisimple, unlike some of the more familiar contexts where web categories are used.
1.4 Future work
Cautis, Kamnitzer, and Morrison [Reference Cautis, Kamnitzer and Morrison7] illustrated that Howe-type dualities give rise to web-like categories, but it is also sometimes the case that a Howe duality can be deduced from the existence of web-like categories (see [Reference Queffelec and Sartori23, Reference Sartori and Tubbenhauer25]). In a sequel to this paper, we use the results herein to construct a Howe duality between
![]() ${\mathfrak {p}} (m)$
and
${\mathfrak {p}} (m)$
and
![]() ${\mathfrak {p}} (n)$
[Reference Davidson, Kujawa and Muth13].
${\mathfrak {p}} (n)$
[Reference Davidson, Kujawa and Muth13].
In [Reference Balagović, Daugherty, Entova-Aizenbud, Halacheva, Hennig, Im, Letzter, Norton, Serganova and Stroppel3], the authors introduce the affine VW-supercategory. This can be regarded as an extension of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
given by including an additional even morphism
${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
given by including an additional even morphism
![]() $1 {\rightarrow } 1$
which defines a subalgebra of
$1 {\rightarrow } 1$
which defines a subalgebra of
![]() $\operatorname {End}_{{\mathfrak {p}\text {-}\mathbf {Web}}_1}(1^d)$
isomorphic to a polynomial ring in d variables. This diagrammatic supercategory admits a functor to the category of endofunctors of
$\operatorname {End}_{{\mathfrak {p}\text {-}\mathbf {Web}}_1}(1^d)$
isomorphic to a polynomial ring in d variables. This diagrammatic supercategory admits a functor to the category of endofunctors of
![]() ${\mathfrak {p}}(n)\text{-}\mathrm{mod}$
of the form
${\mathfrak {p}}(n)\text{-}\mathrm{mod}$
of the form
![]() $V^{\otimes d} \otimes -$
where the additional generator acts via a Casimir-like element. It would be interesting to define and study affine versions of
$V^{\otimes d} \otimes -$
where the additional generator acts via a Casimir-like element. It would be interesting to define and study affine versions of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, as well.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, as well.
In [Reference Ahmed, Grantcharov and Guay1], Ahmed, Grantcharov, and Guay introduced a quantum superalgebra of type P via the FRT formalism. As an outcome of the construction, they obtain a Hopf superalgebra with a quantum analogue of the natural representation and an action of the braid group on its tensor powers. We expect one can also define quantum analogues of Moon’s algebra and the supercategories
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
,
${\mathfrak {p}\text {-}\mathbf {Web}}_{1}$
,
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, and
${\mathfrak {p}\text {-}\mathbf {Web}}$
, and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
1.5 Conventions
Throughout the paper, we will write
![]() ${\mathbb {k}}$
for our ground ring. Our requirements for
${\mathbb {k}}$
for our ground ring. Our requirements for
![]() ${\mathbb {k}}$
will vary, so we will endeavor to make clear what is assumed in each section. At a minimum,
${\mathbb {k}}$
will vary, so we will endeavor to make clear what is assumed in each section. At a minimum,
![]() ${\mathbb {k}}$
will always be a commutative ring with identity.
${\mathbb {k}}$
will always be a commutative ring with identity.
We assume the reader is familiar with monoidal categories, defining them by generators and relations, and in using diagrammatics to represent morphisms in such categories. See Section 2.1 for a brief discussion and [Reference Kassel19, Reference Turaev29] for further background. To set our conventions, we read diagrams bottom to top with vertical concatenation corresponding to composition of morphisms. Horizontal concatenation corresponds to the monoidal (or tensor) product of morphisms.
This paper investigates mathematical objects in the “super” (i.e.,
![]() ${\mathbb {Z}}_{2}={\mathbb {Z}}/2{\mathbb {Z}}$
-graded) setting. To establish nomenclature, we say an element has parity r if it is homogenous and of degree
${\mathbb {Z}}_{2}={\mathbb {Z}}/2{\mathbb {Z}}$
-graded) setting. To establish nomenclature, we say an element has parity r if it is homogenous and of degree
![]() $r \in {\mathbb {Z}}_{2}$
. We write
$r \in {\mathbb {Z}}_{2}$
. We write
![]() $|{w}|$
for the parity of a homogeneous element, and we say that w is even (resp. odd) if
$|{w}|$
for the parity of a homogeneous element, and we say that w is even (resp. odd) if
![]() $|{w}| = \bar {0}$
(resp.
$|{w}| = \bar {0}$
(resp.
![]() $|{w}| = \bar {1}$
). We view
$|{w}| = \bar {1}$
). We view
![]() ${\mathbb {k}}$
as a superalgebra concentrated in parity
${\mathbb {k}}$
as a superalgebra concentrated in parity
![]() $\bar {0}$
.
$\bar {0}$
.
In particular, the context of this work is
![]() ${\mathbb {k}}$
-linear monoidal supercategories. As with
${\mathbb {k}}$
-linear monoidal supercategories. As with
![]() ${\mathbb {k}} $
-linear monoidal categories, they can be studied using a graphical calculus. One difference is that there is now a graded version of the interchange law. Diagrammatically, this so-called super-interchange law introduces a sign whenever two odd morphisms are isotopied past each other in the vertical direction:
${\mathbb {k}} $
-linear monoidal categories, they can be studied using a graphical calculus. One difference is that there is now a graded version of the interchange law. Diagrammatically, this so-called super-interchange law introduces a sign whenever two odd morphisms are isotopied past each other in the vertical direction:

Because of this, whenever two diagrams are horizontally concatenated, the left diagram should be understood to be drawn above the right diagram:

See [Reference Brundan and Ellis5, Section 1] for details.
In what follows, we assume all modules, categories, and functors are
![]() ${\mathbb {k}}$
-linear. We also assume that everything is
${\mathbb {k}}$
-linear. We also assume that everything is
![]() ${\mathbb {Z}}_{2}$
-graded and so will sometimes omit the prefix “super.”
${\mathbb {Z}}_{2}$
-graded and so will sometimes omit the prefix “super.”
1.6 ArXiv version
We chose to relegate a number of the more lengthy but straightforward calculations to the arXiv version of the paper. The reader interested in seeing these additional details can download the \LaTeX source file from the arXiv and find a toggle near the beginning of the file which allows one to compile the paper with these calculations included.
2 The
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
category
${\mathfrak {gl}\text {-}\mathbf {Web}}$
category
2.1 Definition of
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
${\mathfrak {gl}\text {-}\mathbf {Web}}$
Let
![]() ${\mathbb {k}}$
be a commutative ring with identity. The definitions and results in this section are generally well known, and we record them for convenience.
${\mathbb {k}}$
be a commutative ring with identity. The definitions and results in this section are generally well known, and we record them for convenience.
Here and below, we will define combinatorial
![]() ${\mathbb {k}}$
-linear strict monoidal (super)categories by generators and relations. This method of construction is well known, and we only briefly describe how this works in our setting. See, for example, [Reference Kassel19, Section XII.1] or [Reference Turaev29, Section I.3] for a careful treatment in the classical case. The objects will be words from some set (e.g.,
${\mathbb {k}}$
-linear strict monoidal (super)categories by generators and relations. This method of construction is well known, and we only briefly describe how this works in our setting. See, for example, [Reference Kassel19, Section XII.1] or [Reference Turaev29, Section I.3] for a careful treatment in the classical case. The objects will be words from some set (e.g.,
![]() ${\mathbb {Z}}_{\geq 1}$
or
${\mathbb {Z}}_{\geq 1}$
or
![]() $\left\{\uparrow _{a}, \downarrow _{a} \mid a \in {\mathbb {Z}}_{\geq 1} \right\}$
) with the monodial product given by concatenation of words. This set of objects will evidently generate the set of all objects under the monoidal product, and the empty word will be the monoidal unit object.
$\left\{\uparrow _{a}, \downarrow _{a} \mid a \in {\mathbb {Z}}_{\geq 1} \right\}$
) with the monodial product given by concatenation of words. This set of objects will evidently generate the set of all objects under the monoidal product, and the empty word will be the monoidal unit object.
Morphisms will be given by providing a set of generating morphisms. A general morphism will be constructed from these generators (and identity morphisms) by a finite sequence of compositions, monoidal products, and
![]() ${\mathbb {k}}$
-linear combinations. Since composition is given by vertical concatenation and the monoidal product is given by horizontal concatenation, a general morphism will be a
${\mathbb {k}}$
-linear combinations. Since composition is given by vertical concatenation and the monoidal product is given by horizontal concatenation, a general morphism will be a
![]() ${\mathbb {k}}$
-linear combination of diagrams with the same objects along the top and bottom, and where each diagram was obtained by a finite sequence of vertical and horizontal concatenations of generating morphisms and identities. To define the category, we impose relations on the morphisms. These relations are local in the sense that if two morphisms are identical other than in some small region where they differ by an imposed relation, then the morphisms are equal in the category. Finally, in the cases when we have a supercategory, the generating morphisms and defining relations will be homogenous in the
${\mathbb {k}}$
-linear combination of diagrams with the same objects along the top and bottom, and where each diagram was obtained by a finite sequence of vertical and horizontal concatenations of generating morphisms and identities. To define the category, we impose relations on the morphisms. These relations are local in the sense that if two morphisms are identical other than in some small region where they differ by an imposed relation, then the morphisms are equal in the category. Finally, in the cases when we have a supercategory, the generating morphisms and defining relations will be homogenous in the
![]() ${\mathbb {Z}}_{2}$
-grading and this will provide the grading on the morphism spaces.
${\mathbb {Z}}_{2}$
-grading and this will provide the grading on the morphism spaces.
Definition 2.1.1 Let
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
denote the strict monoidal
${\mathfrak {gl}\text {-}\mathbf {Web}}$
denote the strict monoidal
![]() ${\mathbb {k}}$
-linear category given by generators and relations as follows. The objects are sequences of nonnegative integers. The morphisms are generated by the diagrams:
${\mathbb {k}}$
-linear category given by generators and relations as follows. The objects are sequences of nonnegative integers. The morphisms are generated by the diagrams:

where
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms split and merge, respectively. The identity morphism of the object
$a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms split and merge, respectively. The identity morphism of the object
![]() $(a_{1}, \dotsc , a_{k})$
will be depicted by k vertical strands labeled in order by
$(a_{1}, \dotsc , a_{k})$
will be depicted by k vertical strands labeled in order by
![]() $a_{1}, \dotsc , a_{k}$
.
$a_{1}, \dotsc , a_{k}$
.
On the morphisms in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
, we impose the following relations for all
${\mathfrak {gl}\text {-}\mathbf {Web}}$
, we impose the following relations for all
![]() $a,b,c \in {\mathbb {Z}}_{\geq 0}$
:
$a,b,c \in {\mathbb {Z}}_{\geq 0}$
:
Web-associativity:

Rung swap:

Going forward, and in the relations defined above, we use the following conventions:
-
• Strands labeled by “0” are to be deleted.
-
• Diagrams containing a negatively labeled strand are to be read as zero.
-
• We will sometimes choose to omit labels on strands when the label is clear from context.
For brevity, we also adopt the convention in calculations that when an equality follows from a previous result, this fact is indicated by placing the relevant equation number over the equals sign in question. We also adopt the convention that we sometimes write
![]() $0$
for the monoidal unit object.
$0$
for the monoidal unit object.
Remark 2.1.2 When
![]() ${\mathbb {k}}$
is a field,
${\mathbb {k}}$
is a field,
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
can be viewed as a non-quantum version of categories which appear in [Reference Queffelec and Sartori23, Reference Sartori and Tubbenhauer25, Reference Tubbenhauer, Vaz and Wedrich28]. It can also be seen to be isomorphic to the Schur category defined in [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6], which appeared as this paper was being prepared. As explained therein, the Schur category is related to the category introduced in [Reference Cautis, Kamnitzer and Morrison7].
${\mathfrak {gl}\text {-}\mathbf {Web}}$
can be viewed as a non-quantum version of categories which appear in [Reference Queffelec and Sartori23, Reference Sartori and Tubbenhauer25, Reference Tubbenhauer, Vaz and Wedrich28]. It can also be seen to be isomorphic to the Schur category defined in [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6], which appeared as this paper was being prepared. As explained therein, the Schur category is related to the category introduced in [Reference Cautis, Kamnitzer and Morrison7].
2.2 Implied relations for
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
${\mathfrak {gl}\text {-}\mathbf {Web}}$
We first record a few relations which are implied by the defining relations of
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
. Many of the relations established in the remainder of Section 2 can be inferred from [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Reference Cautis, Kamnitzer and Morrison7] by using [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Remark 4.8 and Theorem 4.10], or may be viewed as analogues of those shown in [Reference Sartori and Tubbenhauer25, Section 2] in the case
${\mathfrak {gl}\text {-}\mathbf {Web}}$
. Many of the relations established in the remainder of Section 2 can be inferred from [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Reference Cautis, Kamnitzer and Morrison7] by using [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Remark 4.8 and Theorem 4.10], or may be viewed as analogues of those shown in [Reference Sartori and Tubbenhauer25, Section 2] in the case
![]() $q=1$
. Complete proofs of Lemmas 2.2.1, 2.2.2, 2.3.1, and 2.3.2 and Theorem 2.3.3 are also available in [Reference Davidson, Kujawa and Muth14].
$q=1$
. Complete proofs of Lemmas 2.2.1, 2.2.2, 2.3.1, and 2.3.2 and Theorem 2.3.3 are also available in [Reference Davidson, Kujawa and Muth14].
Lemma 2.2.1 For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we have

Lemma 2.2.2 The following equalities hold in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
:
${\mathfrak {gl}\text {-}\mathbf {Web}}$
:

for all admissible
![]() $a,b,c,r,r',r",s,s',s" \in {\mathbb {Z}}_{\geq 0}$
.
$a,b,c,r,r',r",s,s',s" \in {\mathbb {Z}}_{\geq 0}$
.
2.3 Braiding for
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
${\mathfrak {gl}\text {-}\mathbf {Web}}$
We next establish the category
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
admits a symmetric braiding.
${\mathfrak {gl}\text {-}\mathbf {Web}}$
admits a symmetric braiding.
For any
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we define the crossing morphism:
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we define the crossing morphism:

Lemma 2.3.1 For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we have

Using the crossing, we record an identity in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
which will be useful in later calculations. This may be viewed as a special case of the Schur product rule (see [Reference Green17, equation (2.3b)], [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Theorem 4.10]).
${\mathfrak {gl}\text {-}\mathbf {Web}}$
which will be useful in later calculations. This may be viewed as a special case of the Schur product rule (see [Reference Green17, equation (2.3b)], [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Theorem 4.10]).
Lemma 2.3.2 For all
![]() $a,b,c,d \in {\mathbb {Z}}_{\geq 0}$
such that
$a,b,c,d \in {\mathbb {Z}}_{\geq 0}$
such that
![]() $a+b = c+d$
, we have
$a+b = c+d$
, we have

The following theorem describes the basic relations involving the crossing morphism.
Theorem 2.3.3 For all
![]() $a,b,c \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b,c \in {\mathbb {Z}}_{\geq 0}$
, we have



We define a crossing morphism
![]() $\boldsymbol {a} \otimes \boldsymbol {b}~{\rightarrow }~\boldsymbol {b} \otimes \boldsymbol {a}$
for objects
$\boldsymbol {a} \otimes \boldsymbol {b}~{\rightarrow }~\boldsymbol {b} \otimes \boldsymbol {a}$
for objects
![]() $\boldsymbol {a}$
and
$\boldsymbol {a}$
and
![]() $\boldsymbol {b}$
by the following diagram:
$\boldsymbol {b}$
by the following diagram:

The following follows from Theorem 2.3.3.
Corollary 2.3.4 The crossing morphisms defined in (2.7) define a symmetric braiding on
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
.
${\mathfrak {gl}\text {-}\mathbf {Web}}$
.
3 The
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
category
${\mathfrak {p}\text {-}\mathbf {Web}}$
category
3.1 Definition of
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
From now on, we assume
![]() ${\mathbb {k}}$
is an integral domain where
${\mathbb {k}}$
is an integral domain where
![]() $2$
is invertible. For example,
$2$
is invertible. For example,
![]() ${\mathbb {k}}$
could be
${\mathbb {k}}$
could be
![]() ${\mathbb {Z}}[\frac {1}{2}]$
. We again define a diagrammatic
${\mathbb {Z}}[\frac {1}{2}]$
. We again define a diagrammatic
![]() ${\mathbb {k}}$
-linear monoidal supercategories by generators and relations as discussed in Section 2.1.
${\mathbb {k}}$
-linear monoidal supercategories by generators and relations as discussed in Section 2.1.
Definition 3.1.1 Let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
be the strict
${\mathfrak {p}\text {-}\mathbf {Web}}$
be the strict
![]() ${\mathbb {k}}$
-linear monoidal supercategory given by generators and relations as follows. The objects are all sequences of non-negative integers.
${\mathbb {k}}$
-linear monoidal supercategory given by generators and relations as follows. The objects are all sequences of non-negative integers.
The generating morphisms:

for
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms split, merge, cap, and cup, respectively. The
$a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms split, merge, cap, and cup, respectively. The
![]() ${\mathbb {Z}}_2$
-grading is given by declaring splits and merges to have parity
${\mathbb {Z}}_2$
-grading is given by declaring splits and merges to have parity
![]() $\bar 0$
, and caps and cups to have parity
$\bar 0$
, and caps and cups to have parity
![]() $\bar 1$
. The identity morphism of the object
$\bar 1$
. The identity morphism of the object
![]() $(a_{1}, \dotsc , a_{k})$
will be depicted by k vertical strands labeled in order by
$(a_{1}, \dotsc , a_{k})$
will be depicted by k vertical strands labeled in order by
![]() $a_{1}, \dotsc , a_{k}$
.
$a_{1}, \dotsc , a_{k}$
.
To describe the imposed relations, it will be convenient to first define an additional odd morphism,

which we call the antenna. Here and below, when we scale a diagram by an element of
![]() ${\mathbb {k}}$
, we often write the scalar in parentheses to make clear it is not an edge label.
${\mathbb {k}}$
, we often write the scalar in parentheses to make clear it is not an edge label.
The defining relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
are (2.1) and (2.2) along with the following relations for all
${\mathfrak {p}\text {-}\mathbf {Web}}$
are (2.1) and (2.2) along with the following relations for all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
:
$a,b \in {\mathbb {Z}}_{\geq 0}$
:
Straightening:

Antenna retraction:

Cap/rung swap:


Cup/rung swap:


Remark 3.1.2 The diamonds which decorate the odd cup and cap morphisms in the definition of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
are used to distinguish them from the even cup and cap morphisms used in the definition of the oriented web category
${\mathfrak {p}\text {-}\mathbf {Web}}$
are used to distinguish them from the even cup and cap morphisms used in the definition of the oriented web category
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
in Section 4.1.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
in Section 4.1.
Remark 3.1.3 We introduced the antenna in (3.1) because this morphism appears frequently when studying applications for
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. It has the disadvantage of requiring
${\mathfrak {p}\text {-}\mathbf {Web}}$
. It has the disadvantage of requiring
![]() $2$
to be invertible in
$2$
to be invertible in
![]() ${\mathbb {k}}$
. One could define
${\mathbb {k}}$
. One could define
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
over
${\mathfrak {p}\text {-}\mathbf {Web}}$
over
![]() ${\mathbb {Z}}$
by including the antenna as a generating morphism and instead imposing the relation obtained by scaling (3.1) by
${\mathbb {Z}}$
by including the antenna as a generating morphism and instead imposing the relation obtained by scaling (3.1) by
![]() $2$
, along with relations for moving an antenna past other the generating morphisms. This diagrammatic category would be related to the representation theory of the Kostant
$2$
, along with relations for moving an antenna past other the generating morphisms. This diagrammatic category would be related to the representation theory of the Kostant
![]() ${\mathbb {Z}}$
-form
${\mathbb {Z}}$
-form
![]() $U({\mathfrak {p}} )_{{\mathbb {Z}}}$
introduced in [Reference Davidson, Kujawa and Muth13]. We opted not to do this as it would add complexity and was not needed for the applications considered here.
$U({\mathfrak {p}} )_{{\mathbb {Z}}}$
introduced in [Reference Davidson, Kujawa and Muth13]. We opted not to do this as it would add complexity and was not needed for the applications considered here.
3.2 Implied relations for
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
We first record a few additional relations which are implied by the defining relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
Lemma 3.2.1 For all
![]() $a \in {\mathbb {Z}}_{\geq 2}$
, we have
$a \in {\mathbb {Z}}_{\geq 2}$
, we have

Proof We have

as desired.
Lemma 3.2.2 For all
![]() $a \in {\mathbb {Z}}_{\geq 2}$
, we have
$a \in {\mathbb {Z}}_{\geq 2}$
, we have

3.3 Braiding for
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
For
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we define the crossing morphism
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we define the crossing morphism
![]() $(a,b) {\rightarrow } (b,a)$
in
$(a,b) {\rightarrow } (b,a)$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
as in (2.3). The goal of this section is to prove that the crossing morphism can be used to define a symmetric braiding on
${\mathfrak {p}\text {-}\mathbf {Web}}$
as in (2.3). The goal of this section is to prove that the crossing morphism can be used to define a symmetric braiding on
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
Theorem 3.3.1 For all
![]() $a \in {\mathbb {Z}}_{\geq 0} $
, we have
$a \in {\mathbb {Z}}_{\geq 0} $
, we have

Proof We have

and

By Lemma 3.2.2 and (2.1), we have

which implies that

proving the first equality in (3.9). Now, using this equality, we may precompose with two cup morphisms to arrive at the equality

Applying the straightening relation (3.2) to both sides of this equation gives the second equality in (3.9).
Theorem 3.3.1 demonstrates that cups and caps are natural with respect to the crossing. Because the relations in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
also hold in
${\mathfrak {gl}\text {-}\mathbf {Web}}$
also hold in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, the following is an immediate consequence of the above and Theorem 2.3.3.
${\mathfrak {p}\text {-}\mathbf {Web}}$
, the following is an immediate consequence of the above and Theorem 2.3.3.
Corollary 3.3.2 The crossing morphisms defined in (2.7) define a symmetric braiding on
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
3.4 Additional relations in
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
The crossing morphisms allow for the following additional relations on
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
Lemma 3.4.1 For every
![]() $a \in {\mathbb {Z}}_{\geq 0}$
, we have
$a \in {\mathbb {Z}}_{\geq 0}$
, we have

Lemma 3.4.2 We have

Proof The first two relations are easily seen to hold by direct computation and applications of (3.4) to (3.7). The third is obtained by combining the first two:

where the first equality is deduced by putting a cap on top of the first relation, and the second equality is deduced by putting a cup under the second relation. Because
![]() $2$
is invertible in the ground ring
$2$
is invertible in the ground ring
![]() ${\mathbb {k}}$
, the third relation follows.
${\mathbb {k}}$
, the third relation follows.
Lemma 3.4.3 For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we have

Proof First, note that

and similarly,

Therefore, we have

as desired.
Lemma 3.4.4 For all
![]() $a,b,c \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b,c \in {\mathbb {Z}}_{\geq 0}$
, we have

Proof For the first equality, we have

as desired. The second equality is proved in a similar fashion.
Lemma 3.4.5 The following relation holds in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
:
${\mathfrak {p}\text {-}\mathbf {Web}}$
:

Proof We have

proving the first claim. The second claim is similar. For the third, we have

completing the proof.
3.5 A basis for morphism spaces in
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
In this section, we construct
![]() ${\mathbb {k}}$
-spanning sets for the morphism spaces in
${\mathbb {k}}$
-spanning sets for the morphism spaces in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. In Section 6.3, we will show that these are in fact bases. The bases themselves are diagrammatically analogous to bases defined in a different setting in [Reference Stroppel and Webster27, Section 5].
${\mathfrak {p}\text {-}\mathbf {Web}}$
. In Section 6.3, we will show that these are in fact bases. The bases themselves are diagrammatically analogous to bases defined in a different setting in [Reference Stroppel and Webster27, Section 5].
We will write multiple splits and merges in the form

where the diagram should be interpreted as n vertically composed splits, or merges, respectively. By (2.1), the resulting morphism is independent of the split (or merge) order. It will also be convenient to define

Given a matrix A, let us write
![]() $A^{T}$
for the transpose. For any
$A^{T}$
for the transpose. For any
![]() $\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^t$
,
$\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^t$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^u$
, let
$\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^u$
, let
![]() $\chi (\boldsymbol {a}, \boldsymbol {b})$
be the set of tuples
$\chi (\boldsymbol {a}, \boldsymbol {b})$
be the set of tuples
![]() $(A,B,C,D)$
, such that
$(A,B,C,D)$
, such that
 $$ \begin{align*} 2D_{i} + \sum_{j=1}^tA_{ij} + \sum_{j=1}^u C_{ij} = a_i \qquad \text{for all } i =1, \ldots, t, \end{align*} $$
$$ \begin{align*} 2D_{i} + \sum_{j=1}^tA_{ij} + \sum_{j=1}^u C_{ij} = a_i \qquad \text{for all } i =1, \ldots, t, \end{align*} $$
 $$ \begin{align*} \sum_{i=1}^uB_{ij} + \sum_{i=1}^t C_{ij} = b_j \qquad \text{for all } j =1, \ldots, u. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^uB_{ij} + \sum_{i=1}^t C_{ij} = b_j \qquad \text{for all } j =1, \ldots, u. \end{align*} $$
For any
![]() $(A,B,C,D) \in \chi (\boldsymbol {a}, \boldsymbol {b})$
, we define an associated element
$(A,B,C,D) \in \chi (\boldsymbol {a}, \boldsymbol {b})$
, we define an associated element
![]() $\xi ^{(A,B,C,D)} \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a}, \boldsymbol {b})$
via
$\xi ^{(A,B,C,D)} \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a}, \boldsymbol {b})$
via

where X is any diagram composed only of crossings, cups, and caps, where no cup occurs below any cap, and in which:
-
• the strands labeled by
 $A_{ij}$
and
$A_{ij}$
and
 $A_{ji}$
meet in a cap in X;
$A_{ji}$
meet in a cap in X; -
• the strands labeled by
 $B_{ij}$
and
$B_{ij}$
and
 $B_{ji}$
meet in a cup in X; and
$B_{ji}$
meet in a cup in X; and -
• the strand labeled by
 $C_{ij}$
at the bottom of X meets the strand labeled by
$C_{ij}$
at the bottom of X meets the strand labeled by
 $C_{ij}$
at the top of X.
$C_{ij}$
at the top of X.
All such choices for X are equivalent up to sign because of Theorem 2.3.3.
It should be noted that the method of using splits and merges to “explode” or “collapse” the bottom and top of morphisms as done here can be found elsewhere in the literature (see, e.g., [Reference Rose and Tubbenhauer24]).
Example 3.5.1 Let
![]() $\boldsymbol {a} = (9,4,8)$
,
$\boldsymbol {a} = (9,4,8)$
,
![]() $\boldsymbol {b} = (9,6)$
, and set
$\boldsymbol {b} = (9,6)$
, and set
 $$ \begin{align*} A= \begin{bmatrix} 0 & 0 & 1\\ 0 & 0 & 1\\ 1 & 1 & 0 \end{bmatrix} \qquad B= \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \qquad C= \begin{bmatrix} 2& 4 \\ 3 & 0 \\ 3 & 1 \end{bmatrix} \qquad D= \begin{bmatrix} 1 & 0 & 1 \end{bmatrix}. \end{align*} $$
$$ \begin{align*} A= \begin{bmatrix} 0 & 0 & 1\\ 0 & 0 & 1\\ 1 & 1 & 0 \end{bmatrix} \qquad B= \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \qquad C= \begin{bmatrix} 2& 4 \\ 3 & 0 \\ 3 & 1 \end{bmatrix} \qquad D= \begin{bmatrix} 1 & 0 & 1 \end{bmatrix}. \end{align*} $$
Then
![]() $(A,B,C,D) \in \chi (\boldsymbol {a}, \boldsymbol {b})$
, and
$(A,B,C,D) \in \chi (\boldsymbol {a}, \boldsymbol {b})$
, and

Proposition 3.5.2 The set
is a
![]() ${\mathbb {k}}$
-spanning set for
${\mathbb {k}}$
-spanning set for
![]() ${\mathrm { Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
${\mathrm { Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
The set
is a
![]() ${\mathbb {k}}$
-spanning set for
${\mathbb {k}}$
-spanning set for
![]() ${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
Proof We will focus primarily on the statement for the spanning set of morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. The statement for
${\mathfrak {p}\text {-}\mathbf {Web}}$
. The statement for
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
is simpler due to the lack of cups and caps, and should be considered known (see, e.g., [Reference Stroppel and Webster27, Theorem 3.11] or [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Lemma 4.9]).
${\mathfrak {gl}\text {-}\mathbf {Web}}$
is simpler due to the lack of cups and caps, and should be considered known (see, e.g., [Reference Stroppel and Webster27, Theorem 3.11] or [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6, Lemma 4.9]).
Let f be a diagram in
![]() ${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
. By inducting on the number of “out of place” parts, we may apply the defining relations (2.1) and (3.7) of
${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
. By inducting on the number of “out of place” parts, we may apply the defining relations (2.1) and (3.7) of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, Theorem 2.3.3, and Lemma 2.3.2, to rewrite f as a linear combination of diagrams consisting of splits, merges, cups, caps, antennas, and crossings, where:
${\mathfrak {p}\text {-}\mathbf {Web}}$
, Theorem 2.3.3, and Lemma 2.3.2, to rewrite f as a linear combination of diagrams consisting of splits, merges, cups, caps, antennas, and crossings, where:
-
• no merge occurs below any split;
-
• no cup occurs below any cap;
-
• no crossing occurs above any merge or below any split;
-
• no antenna occurs above any merge, cup, cap, or crossing.
Any diagram that satisfies all of the above is equivalent to a constant multiple of some diagram with the following form:

for some labels
![]() $d_i, x_j^{(i)}, y_j^{(i)} \in {\mathbb {Z}}_{\geq 0}$
, and X is a diagram composed only of crossings, cups, and caps, where no cup occurs below any cap.
$d_i, x_j^{(i)}, y_j^{(i)} \in {\mathbb {Z}}_{\geq 0}$
, and X is a diagram composed only of crossings, cups, and caps, where no cup occurs below any cap.
Now, we consider (3.13). Note the following:
-
(1) If two strands which split from
 $a_i$
meet in a cap in X, then by (3.4), the diagram can be rewritten by adding one to
$a_i$
meet in a cap in X, then by (3.4), the diagram can be rewritten by adding one to
 $d_i$
, deleting the strand, and multiplying by 2.
$d_i$
, deleting the strand, and multiplying by 2. -
(2) If two strands which merge in
 $b_i$
meet in a cup in X, then by (3.7), the diagram is zero.
$b_i$
meet in a cup in X, then by (3.7), the diagram is zero. -
(3) If for some
 $i \neq j$
, there is more than one instance of a strand which splits from
$i \neq j$
, there is more than one instance of a strand which splits from
 $a_i$
and a strand which splits from
$a_i$
and a strand which splits from
 $a_j$
meeting in a cap in X, then the diagram is zero by Lemma 3.4.5.
$a_j$
meeting in a cap in X, then the diagram is zero by Lemma 3.4.5. -
(4) If for some
 $i \neq j$
, there is more than one instance of a strand which merges into
$i \neq j$
, there is more than one instance of a strand which merges into
 $b_i$
and a strand which merges into
$b_i$
and a strand which merges into
 $b_j$
meeting in a cup in X, then the diagram is zero by Lemma 3.4.5.
$b_j$
meeting in a cup in X, then the diagram is zero by Lemma 3.4.5. -
(5) If
 $d_i>1$
, then the diagram is zero by Lemma 3.4.5.
$d_i>1$
, then the diagram is zero by Lemma 3.4.5. -
(6) If there is more than one strand in X which splits from
 $a_i$
and merges into
$a_i$
and merges into
 $b_j$
, then by (2.2), the diagram can be written with a single strand which splits from
$b_j$
, then by (2.2), the diagram can be written with a single strand which splits from
 $a_i$
and merges into
$a_i$
and merges into
 $b_j$
, multiplied by some constant.
$b_j$
, multiplied by some constant.
After rewriting as above, we have via Lemma 2.3.1 that (3.13) is equivalent to a constant multiple of some diagram of the form
![]() $\xi ^{(A,B,C,D)}$
, completing the proof for
$\xi ^{(A,B,C,D)}$
, completing the proof for
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
An entirely analogous argument applies for
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
. Since there are no cups, caps, or antennas, it is easier and we leave it to the reader.
${\mathfrak {gl}\text {-}\mathbf {Web}}$
. Since there are no cups, caps, or antennas, it is easier and we leave it to the reader.
3.6 Generating sets for the morphism spaces of
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
In this section, we describe generating sets for the morphism spaces of
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
using only the operations of composition and
${\mathfrak {p}\text {-}\mathbf {Web}}$
using only the operations of composition and
![]() ${\mathbb {k}}$
-linear combinations, and not the monoidal product. These generators (and the relations among them, given in Lemma 3.7.1) are used to establish a Howe duality in [Reference Davidson, Kujawa and Muth13].
${\mathbb {k}}$
-linear combinations, and not the monoidal product. These generators (and the relations among them, given in Lemma 3.7.1) are used to establish a Howe duality in [Reference Davidson, Kujawa and Muth13].
Let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
be the full subcategory of
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
be the full subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
consisting of objects
${\mathfrak {p}\text {-}\mathbf {Web}}$
consisting of objects
![]() ${\textbf {a}} \in {\mathbb {Z}}^m_{\geq 0}$
. We emphasize that the monoidal product in
${\textbf {a}} \in {\mathbb {Z}}^m_{\geq 0}$
. We emphasize that the monoidal product in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
does not preserve the subcategory
${\mathfrak {p}\text {-}\mathbf {Web}}$
does not preserve the subcategory
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
. Hence,
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
. Hence,
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{m}$
is a supercategory and does not inherit a monoidal structure. For
${\mathfrak {p}\text {-}\mathbf {Web}}_{m}$
is a supercategory and does not inherit a monoidal structure. For
![]() $t \in {\mathbb {Z}}_{\geq 0}$
,
$t \in {\mathbb {Z}}_{\geq 0}$
,
![]() ${\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
,
${\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
,
![]() $1 \leq r < s \leq m$
, we define the following morphisms in
$1 \leq r < s \leq m$
, we define the following morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
:
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
:

For
![]() $1 \leq u \leq m$
, we define the additional morphism
$1 \leq u \leq m$
, we define the additional morphism

where again the dot denotes a combination of a split and antenna, as in (3.12).
To remove some of the clutter in the calculations which follow, we will sometimes write products for compositions (e.g.,
![]() $fg = f \circ g$
) and will occasionally omit the label
$fg = f \circ g$
) and will occasionally omit the label
![]() ${\textbf {a}}$
when the domain is clear from context (e.g., writing
${\textbf {a}}$
when the domain is clear from context (e.g., writing
![]() $e_{[r,s]}^{(t)}$
instead of
$e_{[r,s]}^{(t)}$
instead of
![]() $e_{[r,s],{\textbf {a}}}^{(t)}$
). Let us write
$e_{[r,s],{\textbf {a}}}^{(t)}$
). Let us write
![]() $1_{{\textbf {a}}}$
for the identity morphism of
$1_{{\textbf {a}}}$
for the identity morphism of
![]() ${\textbf {a}}$
. Pre- or post-composing by these gives a convenient alternate method for specifying the domain or range of a morphism. For example,
${\textbf {a}}$
. Pre- or post-composing by these gives a convenient alternate method for specifying the domain or range of a morphism. For example,
![]() $e_{[r,s],{\textbf {a}}}^{(t)}=e_{[r,s]}^{(t)} 1_{{\textbf {a}}}$
.
$e_{[r,s],{\textbf {a}}}^{(t)}=e_{[r,s]}^{(t)} 1_{{\textbf {a}}}$
.
In order to establish a generating set for the morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, we need the following technical lemma. Because we are no longer in a monoidal supercategory, we only use composition and
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, we need the following technical lemma. Because we are no longer in a monoidal supercategory, we only use composition and
![]() ${\mathbb {k}}$
-linear combinations when generating morphisms in this category.
${\mathbb {k}}$
-linear combinations when generating morphisms in this category.
Lemma 3.6.1 Label the set of morphisms:
Let
![]() $S_{\{e,f\}}(m)$
represent the
$S_{\{e,f\}}(m)$
represent the
![]() ${\mathbb {k}}$
-linear subcategory of
${\mathbb {k}}$
-linear subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
consisting of all objects in
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
consisting of all objects in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, with morphisms generated by
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, with morphisms generated by
![]() $Y_{\{e,f\}}(m)$
. Then, for all
$Y_{\{e,f\}}(m)$
. Then, for all
![]() ${\textbf {a}}, {\textbf {b}} \in {\mathbb {Z}}_{\geq 0}^m$
,
${\textbf {a}}, {\textbf {b}} \in {\mathbb {Z}}_{\geq 0}^m$
,
![]() $k \in {\mathbb {Z}}_{\geq 0}$
, and
$k \in {\mathbb {Z}}_{\geq 0}$
, and
![]() $i,j \in [1,m]$
, and morphisms
$i,j \in [1,m]$
, and morphisms
![]() $y \in S_{\{e,f\}}(m)$
, the morphism
$y \in S_{\{e,f\}}(m)$
, the morphism

is also in
![]() $S_{\{e,f\}}(m)$
.
$S_{\{e,f\}}(m)$
.
Proof We may assume that y is itself a composition of u many morphisms in
![]() $Y_{\{e,f\}}(m)$
. Our argument will go by nested induction on k and u. First, note that if
$Y_{\{e,f\}}(m)$
. Our argument will go by nested induction on k and u. First, note that if
![]() $k=0$
, the claim holds trivially, so we now fix
$k=0$
, the claim holds trivially, so we now fix
![]() $k>0$
and assume that the claim holds for all y and
$k>0$
and assume that the claim holds for all y and
![]() $k'<k$
.
$k'<k$
.
Assume
![]() $u=0$
. If
$u=0$
. If
![]() $i=j$
, then M is some multiple of the identity morphism by (2.2). If
$i=j$
, then M is some multiple of the identity morphism by (2.2). If
![]() $i>j$
, then
$i>j$
, then
![]() $M=e_{j,i}^{(k)}$
, and if
$M=e_{j,i}^{(k)}$
, and if
![]() $i<j$
, then
$i<j$
, then
![]() $M=f_{i,j}^{(k)}$
. This proves the claim when
$M=f_{i,j}^{(k)}$
. This proves the claim when
![]() $u=0$
. We now assume that
$u=0$
. We now assume that
![]() $u>0$
and that the claim holds for all
$u>0$
and that the claim holds for all
![]() $u'<u$
.
$u'<u$
.
As
![]() $u>0$
, we may write
$u>0$
, we may write
![]() $y=y'e_{[r,s]}^{(t)}$
or
$y=y'e_{[r,s]}^{(t)}$
or
![]() $y=y'f_{[r,s]}^{(t)}$
for some
$y=y'f_{[r,s]}^{(t)}$
for some
![]() $r,s,t$
. We will assume the former, as the latter case is similar. If
$r,s,t$
. We will assume the former, as the latter case is similar. If
![]() $r \neq i$
, then
$r \neq i$
, then
![]() $e_{[r,s]}^{(t)}$
moves freely below past the split on the ith strand in M. Then the induction assumption on u may be used to complete the proof of the claim.
$e_{[r,s]}^{(t)}$
moves freely below past the split on the ith strand in M. Then the induction assumption on u may be used to complete the proof of the claim.
So we now assume that
![]() $y=y'e_{[i,s]}^{(t)}$
, so that M may be written:
$y=y'e_{[i,s]}^{(t)}$
, so that M may be written:

Note that for clarity here we are omitting strands between the ith and sth strands. Using Corollary 3.3.2, any morphisms on strands between the ith and sth strands may be pulled all the way to the right side of the morphism M by introducing crossings. For this reason, any morphisms between the ith and sth strands will not affect our calculations and can be safely ignored.
Using (2.3), M may be rewritten as a linear combination of diagrams of the form

Using (2.1) and (2.2), any diagram as in (3.15) can be written as a linear combination of diagrams of the form

An application of (2.2) allows us to write any diagram as in (3.16) as a linear combination of diagrams of the form

where
![]() $k'+k"=k$
. If
$k'+k"=k$
. If
![]() $k' = 0$
or
$k' = 0$
or
![]() $k"=0$
, then the claim follows by the induction assumption on u. If
$k"=0$
, then the claim follows by the induction assumption on u. If
![]() $k',k">0$
, then applying the induction assumption on k to the
$k',k">0$
, then applying the induction assumption on k to the
![]() $k'$
strand, and subsequently to the
$k'$
strand, and subsequently to the
![]() $k"$
strand proves the claim, and completes the proof.
$k"$
strand proves the claim, and completes the proof.
Given
![]() $\boldsymbol {a} = (a_{1}, \dotsc , a_{r}) \in {\mathbb {Z}}^{r}$
, we write
$\boldsymbol {a} = (a_{1}, \dotsc , a_{r}) \in {\mathbb {Z}}^{r}$
, we write
![]() $|\boldsymbol {a} | = \sum _{i=1}^{r} |a_{i}|$
.
$|\boldsymbol {a} | = \sum _{i=1}^{r} |a_{i}|$
.
Lemma 3.6.2 Morphisms in
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}_m$
are generated under composition by
${\mathfrak {gl}\text {-}\mathbf {Web}}_m$
are generated under composition by
![]() $Y_{\{e,f\}}(m)$
.
$Y_{\{e,f\}}(m)$
.
Proof Let
![]() ${\textbf {a}},{\textbf {b}} \in {\mathbb {Z}}^m_{\geq 0}$
, and let
${\textbf {a}},{\textbf {b}} \in {\mathbb {Z}}^m_{\geq 0}$
, and let
![]() $\xi :=\xi ^{(0,0,C,0)} \in \mathscr {B}$
be an element in
$\xi :=\xi ^{(0,0,C,0)} \in \mathscr {B}$
be an element in
![]() ${\mathrm {Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
as in Proposition 3.5.2. We show by inducting on
${\mathrm {Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
as in Proposition 3.5.2. We show by inducting on
![]() $n=|{\textbf {a}}|+|{\textbf {b}}|$
that
$n=|{\textbf {a}}|+|{\textbf {b}}|$
that
![]() $\xi $
belongs to the set
$\xi $
belongs to the set
![]() $S_{\{e,f\}}(m)$
from Lemma 3.6.1. Since by Proposition 3.5.2 such elements
$S_{\{e,f\}}(m)$
from Lemma 3.6.1. Since by Proposition 3.5.2 such elements
![]() $\xi $
span
$\xi $
span
![]() ${\mathrm {Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
, this will prove the lemma.
${\mathrm {Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
, this will prove the lemma.
If
![]() $n=0$
, then
$n=0$
, then
![]() $\xi $
is the identity morphism. Thus, we may assume that
$\xi $
is the identity morphism. Thus, we may assume that
![]() $n>0$
, and that the claim holds for all
$n>0$
, and that the claim holds for all
![]() $n'<n$
. If
$n'<n$
. If
![]() $C=0$
, then
$C=0$
, then
![]() $\xi $
is the identity morphism, so assume
$\xi $
is the identity morphism, so assume
![]() $C_{ij}>0$
for some
$C_{ij}>0$
for some
![]() $i,j$
. Then, using (2.1), we may write
$i,j$
. Then, using (2.1), we may write

for some basis element
![]() $\xi ' \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}',{\textbf {b}}')$
, where
$\xi ' \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}',{\textbf {b}}')$
, where
![]() $|{\textbf {a}}'|<|{\textbf {a}}|$
and
$|{\textbf {a}}'|<|{\textbf {a}}|$
and
![]() $|{\textbf {b}}'|<|{\textbf {b}}|$
. Applying the induction assumption on n, we have that
$|{\textbf {b}}'|<|{\textbf {b}}|$
. Applying the induction assumption on n, we have that
![]() $\xi ' \in S_{\{e,f\}}(m)$
. Then, applying Lemma 3.6.1, it follows that
$\xi ' \in S_{\{e,f\}}(m)$
. Then, applying Lemma 3.6.1, it follows that
![]() $\xi \in S_{\{e,f\}}(m)$
, as desired.
$\xi \in S_{\{e,f\}}(m)$
, as desired.
Theorem 3.6.3 Morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by the set
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by the set
![]() $\{b_{[1],a} \mid a \in {\mathbb {Z}}_{\geq 0}\}$
when
$\{b_{[1],a} \mid a \in {\mathbb {Z}}_{\geq 0}\}$
when
![]() $m =1$
, and by
$m =1$
, and by
when
![]() $m\geq 2$
.
$m\geq 2$
.
Proof The statement for
![]() $m=1$
follows directly from Proposition 3.5.2, so assume
$m=1$
follows directly from Proposition 3.5.2, so assume
![]() $m \geq 2$
. First, let
$m \geq 2$
. First, let
We first prove a preliminary claim that morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by
![]() $Y'(m)$
. Write
$Y'(m)$
. Write
![]() $S_m$
(resp.
$S_m$
(resp.
![]() $S^{\prime }_m$
) for the subcategory of
$S^{\prime }_m$
) for the subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
generated by morphisms in
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
generated by morphisms in
![]() $Y(m)$
(resp.
$Y(m)$
(resp.
![]() $Y'(m)$
). Let
$Y'(m)$
). Let
![]() ${\textbf {a}},{\textbf {b}} \in {\mathbb {Z}}^m_{\geq 0}$
. By Proposition 3.5.2,
${\textbf {a}},{\textbf {b}} \in {\mathbb {Z}}^m_{\geq 0}$
. By Proposition 3.5.2,
![]() ${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
is spanned by elements of the form
${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}},{\textbf {b}})$
is spanned by elements of the form
![]() $\xi :=\xi ^{(A,B,C,D)} \in \mathscr {B}$
. We show by induction on
$\xi :=\xi ^{(A,B,C,D)} \in \mathscr {B}$
. We show by induction on
![]() $n=|{\textbf {a}}|+|{\textbf {b}}|$
that
$n=|{\textbf {a}}|+|{\textbf {b}}|$
that
![]() $\xi \in S^{\prime }_m$
.
$\xi \in S^{\prime }_m$
.
If
![]() $n=0$
, then
$n=0$
, then
![]() $\xi $
is the identity morphism. Thus, we may assume
$\xi $
is the identity morphism. Thus, we may assume
![]() $n>0$
, and that the claim holds for all
$n>0$
, and that the claim holds for all
![]() $n'<n$
. Note the following:
$n'<n$
. Note the following:
-
• If
 $A_{ij}>0$
for any
$A_{ij}>0$
for any
 $i<j$
, then by (2.1),
$i<j$
, then by (2.1),
 $\xi = \xi 'b_{[i,j],{\textbf {a}}}$
for some basis element
$\xi = \xi 'b_{[i,j],{\textbf {a}}}$
for some basis element
 ${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}', {\textbf {b}})}$
, where
${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}', {\textbf {b}})}$
, where
 $|{\textbf {a}}'|<|{\textbf {a}}|$
.
$|{\textbf {a}}'|<|{\textbf {a}}|$
. -
• If
 $B_{ij}>0$
for any
$B_{ij}>0$
for any
 $i<j$
, then by (2.1),
$i<j$
, then by (2.1),
 $\xi = c_{[i,j],{\textbf {b}}'}\xi '$
for some basis element
$\xi = c_{[i,j],{\textbf {b}}'}\xi '$
for some basis element
 ${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}, {\textbf {b}}')}$
, where
${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}, {\textbf {b}}')}$
, where
 $|{\textbf {b}}'|<|{\textbf {b}}|$
.
$|{\textbf {b}}'|<|{\textbf {b}}|$
. -
• If
 $D_{i}>0$
for any i, then by (2.1),
$D_{i}>0$
for any i, then by (2.1),
 $\xi = \xi 'b_{[i],{\textbf {a}}}$
for some basis element
$\xi = \xi 'b_{[i],{\textbf {a}}}$
for some basis element
 ${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}', {\textbf {b}})}$
, where
${\xi ' \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}({\textbf {a}}', {\textbf {b}})}$
, where
 $|{\textbf {a}}'|<|{\textbf {a}}|$
.
$|{\textbf {a}}'|<|{\textbf {a}}|$
.
In any of these cases, applying the induction assumption on n to
![]() $\xi '$
completes the proof. Therefore, we may assume
$\xi '$
completes the proof. Therefore, we may assume
![]() $A=B=D=0$
. Then the preliminary claim follows by Lemma 3.6.2, so morphisms in
$A=B=D=0$
. Then the preliminary claim follows by Lemma 3.6.2, so morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by
![]() $Y'(m)$
.
$Y'(m)$
.
Since
![]() $S_m$
contains
$S_m$
contains
![]() $e_{[i,i+1],{\textbf {a}}}^{(t)}$
and
$e_{[i,i+1],{\textbf {a}}}^{(t)}$
and
![]() $f_{[i,i+1],{\textbf {a}}}^{(t)}$
for all
$f_{[i,i+1],{\textbf {a}}}^{(t)}$
for all
![]() $1 \leq i < m, {\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
, it follows by (2.3) that
$1 \leq i < m, {\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
, it follows by (2.3) that
![]() $S_m$
contains all crossing morphisms which transpose neighboring strands. Then we have that
$S_m$
contains all crossing morphisms which transpose neighboring strands. Then we have that
![]() $e_{[r,s],{\textbf {a}}}^{(t)}$
,
$e_{[r,s],{\textbf {a}}}^{(t)}$
,
![]() $f_{[r,s],{\textbf {a}}}^{(t)}$
,
$f_{[r,s],{\textbf {a}}}^{(t)}$
,
![]() $b_{[r,s],{\textbf {a}}}$
,
$b_{[r,s],{\textbf {a}}}$
,
![]() $c_{[r,s],{\textbf {a}}}$
belong to
$c_{[r,s],{\textbf {a}}}$
belong to
![]() $S_m$
for all
$S_m$
for all
![]() $1 \leq r < s \leq m$
,
$1 \leq r < s \leq m$
,
![]() ${\textbf {a}} \in {\mathbb {Z}}^m_{\geq 0}$
, as one may generate these elements by pre- and post-composing the morphisms
${\textbf {a}} \in {\mathbb {Z}}^m_{\geq 0}$
, as one may generate these elements by pre- and post-composing the morphisms
![]() $e_{[1,2],{\textbf {a}}}^{(t)}, f_{[1,2],{\textbf {a}}}^{(t)}, b_{[1,2],{\textbf {a}}}, c_{[1,2],{\textbf {a}}}$
with sequences of crossing morphisms. Finally, we have that
$e_{[1,2],{\textbf {a}}}^{(t)}, f_{[1,2],{\textbf {a}}}^{(t)}, b_{[1,2],{\textbf {a}}}, c_{[1,2],{\textbf {a}}}$
with sequences of crossing morphisms. Finally, we have that
![]() $b_{[u],{\textbf {a}}} = (1/2) [ b_{[u,u+1]}, e_{[u,u+1]}^{(1)}]1_{{\textbf {a}}}$
for
$b_{[u],{\textbf {a}}} = (1/2) [ b_{[u,u+1]}, e_{[u,u+1]}^{(1)}]1_{{\textbf {a}}}$
for
![]() $1 \leq u < m$
and
$1 \leq u < m$
and
![]() $b_{[m],{\textbf {a}}} = (1/2) [ b_{[m-1,m]}, f_{[m-1,m]}^{(1)}]1_{{\textbf {a}}}$
by (3.4) and (3.5), so it follows that
$b_{[m],{\textbf {a}}} = (1/2) [ b_{[m-1,m]}, f_{[m-1,m]}^{(1)}]1_{{\textbf {a}}}$
by (3.4) and (3.5), so it follows that
![]() $S_m' \subseteq S_m$
, completing the proof.
$S_m' \subseteq S_m$
, completing the proof.
Corollary 3.6.4 If
![]() ${\mathbb {k}}$
is a field of characteristic zero, then morphisms in
${\mathbb {k}}$
is a field of characteristic zero, then morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by the set
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
are generated under composition by the set
![]() $\{b_{[1],a} \mid a \in {\mathbb {Z}}_{\geq 0}\}$
when
$\{b_{[1],a} \mid a \in {\mathbb {Z}}_{\geq 0}\}$
when
![]() $m =1$
, and by
$m =1$
, and by
when
![]() $m \geq 2$
.
$m \geq 2$
.
Proof It can be deduced from (2.1) and Lemma 2.2.1 (or alternatively, using (2.9) in [Reference Cautis, Kamnitzer and Morrison7] at
![]() $q = 1$
) that
$q = 1$
) that
![]() $(e_{[i,i+1]}^{(1)})^t1_{\textbf {a}}$
and
$(e_{[i,i+1]}^{(1)})^t1_{\textbf {a}}$
and
![]() $(f_{[i,i+1]}^{(1)})^t1_{\textbf {a}}$
are nonzero multiples of
$(f_{[i,i+1]}^{(1)})^t1_{\textbf {a}}$
are nonzero multiples of
![]() $e_{[i,i+1],{\textbf {a}}}^{(t)}$
and
$e_{[i,i+1],{\textbf {a}}}^{(t)}$
and
![]() $f_{[i,i+1],{\textbf {a}}}^{(t)}$
, respectively. Thus, the result follows from Theorem 3.6.3.
$f_{[i,i+1],{\textbf {a}}}^{(t)}$
, respectively. Thus, the result follows from Theorem 3.6.3.
3.7 Relations for morphisms in
 ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
We now establish a number of relations which hold among the generators in
![]() $Y(m)$
. While not utilized in this paper, these relations will be key in establishing the Howe duality result in [Reference Davidson, Kujawa and Muth13].
$Y(m)$
. While not utilized in this paper, these relations will be key in establishing the Howe duality result in [Reference Davidson, Kujawa and Muth13].
Lemma 3.7.1 The following relations hold in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, for all valid
${\mathfrak {p}\text {-}\mathbf {Web}}_m$
, for all valid
![]() $1 \leq i, j \leq m$
, and
$1 \leq i, j \leq m$
, and
![]() ${\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
.
${\textbf {a}} \in {\mathbb {Z}}_{\geq 0}^m$
.
 $$ \begin{align} &[b_{[i,i+1]},c_{[j,j+1]}]1_{\textbf{a}} = \begin{cases} (a_i - a_{i+1})1_{\textbf{a}}, & \text{if } j=i;\\ [e_{[i-1,i]},e_{[i,i+1]}]1_{\textbf{a}}, & \text{if } j=i-1;\\ [f_{[i,i+1]},f_{[i+1,i+2]}]1_{\textbf{a}}, &\text{if } j=i+1;\\ 0, &\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} &[b_{[i,i+1]},c_{[j,j+1]}]1_{\textbf{a}} = \begin{cases} (a_i - a_{i+1})1_{\textbf{a}}, & \text{if } j=i;\\ [e_{[i-1,i]},e_{[i,i+1]}]1_{\textbf{a}}, & \text{if } j=i-1;\\ [f_{[i,i+1]},f_{[i+1,i+2]}]1_{\textbf{a}}, &\text{if } j=i+1;\\ 0, &\text{otherwise}; \end{cases} \end{align} $$
 $$ \begin{align} &[[b_{[i,i+1]},e_{[i,i+1]}^{(1)}],e_{[j,j+1]}^{(1)}]1_{\textbf{a}} = \begin{cases} 2b_{[i+1,i+2]} 1_{\textbf{a}}, & \text{if }j=i+1;\\ 0,&\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} &[[b_{[i,i+1]},e_{[i,i+1]}^{(1)}],e_{[j,j+1]}^{(1)}]1_{\textbf{a}} = \begin{cases} 2b_{[i+1,i+2]} 1_{\textbf{a}}, & \text{if }j=i+1;\\ 0,&\text{otherwise}; \end{cases} \end{align} $$
 $$ \begin{align} &[[c_{[i+1,i]},e_{[i,i+1]}^{(1)}],e_{[j,j+1]}^{(1)}] 1_{\textbf{a}} = \begin{cases} c_{[i,i+1]}1_{\textbf{a}}, & \text{if }j=i+1;\\ 0, & \text{if }j \neq i+1,i-1. \end{cases} \end{align} $$
$$ \begin{align} &[[c_{[i+1,i]},e_{[i,i+1]}^{(1)}],e_{[j,j+1]}^{(1)}] 1_{\textbf{a}} = \begin{cases} c_{[i,i+1]}1_{\textbf{a}}, & \text{if }j=i+1;\\ 0, & \text{if }j \neq i+1,i-1. \end{cases} \end{align} $$
4 The
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
category
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
category
4.1 Definition of
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
We now introduce an oriented version of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. In this section, we continue to assume
${\mathfrak {p}\text {-}\mathbf {Web}}$
. In this section, we continue to assume
![]() ${\mathbb {k}}$
is an integral domain in which
${\mathbb {k}}$
is an integral domain in which
![]() $2$
is invertible. It will again be a diagrammatic supercategory given by generators and relations as outlined in Section 2.1. Because many of the constructions and arguments in this section are similar to those given in the previous section, so we will sometimes be brief in explanations.
$2$
is invertible. It will again be a diagrammatic supercategory given by generators and relations as outlined in Section 2.1. Because many of the constructions and arguments in this section are similar to those given in the previous section, so we will sometimes be brief in explanations.
Definition 4.1.1 The category
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is the
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is the
![]() ${\mathbb {k}}$
-linear strict monoidal supercategory defined as follows. Objects are words (including the empty word) from the set
${\mathbb {k}}$
-linear strict monoidal supercategory defined as follows. Objects are words (including the empty word) from the set
The morphisms are generated as a
![]() ${\mathbb {k}}$
-linear monoidal supercategory by the diagrams:
${\mathbb {k}}$
-linear monoidal supercategory by the diagrams:

for all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms upward split, upward merge, leftward cap, leftward cup, tag-in, tag-out, and rightward crossing, respectively. The parity is given by declaring the tag-in and tag-out morphisms to be odd and the rest of the generating morphisms to be even.
$a,b \in {\mathbb {Z}}_{\geq 0}$
. We call these morphisms upward split, upward merge, leftward cap, leftward cup, tag-in, tag-out, and rightward crossing, respectively. The parity is given by declaring the tag-in and tag-out morphisms to be odd and the rest of the generating morphisms to be even.
To describe the defining relations, it will be convenient to first set a diagrammatic shorthand for certain additional morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. We define morphisms:
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. We define morphisms:

which we call upward cap, upward cup, and upward antenna, respectively. We also define, for all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, rightward cap and rightward cup morphisms:
$a,b \in {\mathbb {Z}}_{\geq 0}$
, rightward cap and rightward cup morphisms:

For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, define the upward crossing
$a,b \in {\mathbb {Z}}_{\geq 0}$
, define the upward crossing

as in (2.3), with all strands oriented upward. We then define the leftward crossing by composing this with the leftward cap and cup morphisms:

With this notation established, we can now give the defining relations for
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. The defining relations of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. The defining relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are:
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are:
Up-arrow relations. Relations (2.1) and (3.7) hold in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, where we interpret the diagrams as having all strands oriented upward.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, where we interpret the diagrams as having all strands oriented upward.
Leftward straightening. For all
![]() $a \in {\mathbb {Z}}_{\geq 0}$
we have
$a \in {\mathbb {Z}}_{\geq 0}$
we have

Left/right crossing inversion. For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we have

Bubble annihilation. For all
![]() $a \in {\mathbb {Z}}_{>0}$
we have
$a \in {\mathbb {Z}}_{>0}$
we have

We remark that including the rightward crossing generator along with the left/right crossing inversion relation is equivalent to imposing the relation that the leftward crossing is invertible. While this latter approach is sometimes used in the literature, we chose to make the inverse morphism explicitly part of the definition.
Going forward, it will be convenient to sometimes write
![]() $\uparrow _{0}$
or
$\uparrow _{0}$
or
![]() $\downarrow _{0}$
for the empty word (i.e., the monoidal unit object).
$\downarrow _{0}$
for the empty word (i.e., the monoidal unit object).
4.2 Additional morphisms
We define downward splits and downward merges by

We define downward crossings like so:

4.3 Implied relations for
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
The following theorem establishes a number of additional relations which follow from the defining relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. In particular, they show that diagrams that are the same as oriented graphs (which may have edges with tag-in and tag-out diagrams) are equal, up to a sign. In particular, up to a sign, tag-in and tag-out morphisms move freely through crossings and along strands.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. In particular, they show that diagrams that are the same as oriented graphs (which may have edges with tag-in and tag-out diagrams) are equal, up to a sign. In particular, up to a sign, tag-in and tag-out morphisms move freely through crossings and along strands.
Theorem 4.3.1 The following equalities hold in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
for all
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
for all
![]() $a,b,c \in \mathbb {Z}_{\geq 0}$
and all admissible strand orientations:
$a,b,c \in \mathbb {Z}_{\geq 0}$
and all admissible strand orientations:














Proof Relations (4.4)–(4.7) hold when all strands are oriented upward, as shown in Theorem 2.3.3. Using this fact, together with (4.1)–(4.3), it is a routine exercise then to prove that the equalities (4.4)–(4.12) hold for all admissible orientations. The equalities (4.13)–(4.17) can be seen to hold thanks to (4.4)–(4.12), Lemma 4.5.1, and Theorem 2.3.3, after noting that

which completes the proof.
For a nonnegative integer a, it will be convenient to adopt the notation
![]() $|_{a}:= \uparrow _{a}$
and
$|_{a}:= \uparrow _{a}$
and
![]() $|_{-a}:= \downarrow _{a}$
. More generally, for
$|_{-a}:= \downarrow _{a}$
. More generally, for
![]() $r \in {\mathbb {Z}}_{\geq 0}$
and
$r \in {\mathbb {Z}}_{\geq 0}$
and
![]() $\boldsymbol {a} =(a_1, \ldots , a_{r}) \in {\mathbb {Z}}^{r}$
, we will write
$\boldsymbol {a} =(a_1, \ldots , a_{r}) \in {\mathbb {Z}}^{r}$
, we will write
as a shorthand for the latter as an object of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. For example,
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. For example,
![]() $|_{(6,2,-9)} = \uparrow _{6}\uparrow _{2}\downarrow _{9}$
.
$|_{(6,2,-9)} = \uparrow _{6}\uparrow _{2}\downarrow _{9}$
.
The up, down, left, and right crossings can be used to define crossing morphisms,
for arbitrary
![]() $a,b \in {\mathbb {Z}}$
. Just as with
$a,b \in {\mathbb {Z}}$
. Just as with
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, we can use these morphisms to make oriented versions of (2.7) and to verify these make
${\mathfrak {p}\text {-}\mathbf {Web}}$
, we can use these morphisms to make oriented versions of (2.7) and to verify these make
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
into a symmetric braided monoidal supercategory.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
into a symmetric braided monoidal supercategory.
The relations (4.1), (4.10) show that
![]() $\uparrow _{a}$
and
$\uparrow _{a}$
and
![]() $\downarrow _{a}$
are left and right duals to each other with the cups and caps as the evaluation and coevaluation morphisms. More generally, using “rainbows” constructed from leftward and rightward caps and cups, we can also construct evaluation and coevaluation morphisms for general objects in
$\downarrow _{a}$
are left and right duals to each other with the cups and caps as the evaluation and coevaluation morphisms. More generally, using “rainbows” constructed from leftward and rightward caps and cups, we can also construct evaluation and coevaluation morphisms for general objects in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. For example, the evaluation and coevaluation morphisms for
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
. For example, the evaluation and coevaluation morphisms for
![]() $\downarrow _{a}\uparrow _{b}\downarrow _{c}$
are
$\downarrow _{a}\uparrow _{b}\downarrow _{c}$
are

Using these, we see that
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is in fact a rigid category. Altogether, we have the following result.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is in fact a rigid category. Altogether, we have the following result.
Corollary 4.3.2 The oriented crossing morphisms endow
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
with the structure of a symmetric braided monoidal supercategory and the evaluation and coevaluation morphisms endow
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
with the structure of a symmetric braided monoidal supercategory and the evaluation and coevaluation morphisms endow
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
with the structure of a rigid supercategory.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
with the structure of a rigid supercategory.
4.4 Isomorphic morphism spaces in
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
We next remind the reader of well-known arguments (e.g., [Reference Etingof, Gelaki, Nikshych and Ostrik16, Proposition 2.10.8]) which use the existence of the braiding morphisms in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
to define isomorphisms between various morphism spaces. Entirely analogous results obviously hold by the same arguments for
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
to define isomorphisms between various morphism spaces. Entirely analogous results obviously hold by the same arguments for
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
The symmetric group
![]() $\mathfrak {S}_r$
acts on
$\mathfrak {S}_r$
acts on
![]() ${\mathbb {Z}}^r$
by place permutation:
${\mathbb {Z}}^r$
by place permutation:
The braiding morphism defines an associated invertible morphism
where
![]() $\beta ^{-1}_{\sigma , |_{\textbf {a}}} = \beta _{\sigma ^{-1}, |_{\sigma \cdot {\textbf {a}}}} $
. More generally, for
$\beta ^{-1}_{\sigma , |_{\textbf {a}}} = \beta _{\sigma ^{-1}, |_{\sigma \cdot {\textbf {a}}}} $
. More generally, for
![]() $r_1,r_2 \in {\mathbb {Z}}_{\geq 0}$
,
$r_1,r_2 \in {\mathbb {Z}}_{\geq 0}$
,
![]() $\boldsymbol {a} \in {\mathbb {Z}}^{r_1}$
,
$\boldsymbol {a} \in {\mathbb {Z}}^{r_1}$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}^{r_2}$
,
$\boldsymbol {b} \in {\mathbb {Z}}^{r_2}$
,
![]() $\sigma \in \mathfrak {S}_{r_1}$
, and
$\sigma \in \mathfrak {S}_{r_1}$
, and
![]() $\omega \in \mathfrak {S}_{r_2}$
, we have an isomorphism of morphism spaces:
$\omega \in \mathfrak {S}_{r_2}$
, we have an isomorphism of morphism spaces:
given by
Let
![]() $\omega _0 \in \mathfrak {S}_r$
be the longest element, so that
$\omega _0 \in \mathfrak {S}_r$
be the longest element, so that
![]() $\omega _{0}\cdot (a_1, \ldots ,a_r) = (a_r, \ldots , a_1)$
. Then, for
$\omega _{0}\cdot (a_1, \ldots ,a_r) = (a_r, \ldots , a_1)$
. Then, for
![]() $\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^{r_1}$
,
$\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^{r_1}$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^{r_2}$
,
$\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^{r_2}$
,
![]() $\boldsymbol {c} \in {\mathbb {Z}}_{\geq 0}^{r_3}$
, and
$\boldsymbol {c} \in {\mathbb {Z}}_{\geq 0}^{r_3}$
, and
![]() $\boldsymbol {d} \in {\mathbb {Z}}_{\geq 0}^{r_4}$
, we have an isomorphism of Hom spaces:
$\boldsymbol {d} \in {\mathbb {Z}}_{\geq 0}^{r_4}$
, we have an isomorphism of Hom spaces:
given by

with inverse given by an entirely similar map, thanks to (4.1).
Let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
(resp.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
(resp.
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\downarrow }$
) be the full subcategory of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\downarrow }$
) be the full subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
consisting of objects of the form
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
consisting of objects of the form
![]() $\uparrow _{\boldsymbol {a}}:=\uparrow _{a_1} \cdots \uparrow _{a_r}$
(resp.
$\uparrow _{\boldsymbol {a}}:=\uparrow _{a_1} \cdots \uparrow _{a_r}$
(resp.
![]() $\downarrow _{\boldsymbol {a}}:= \downarrow _{a_1} \cdots \downarrow _{a_r}$
) for all
$\downarrow _{\boldsymbol {a}}:= \downarrow _{a_1} \cdots \downarrow _{a_r}$
) for all
![]() $r \in {\mathbb {Z}}_{\geq 0}$
and
$r \in {\mathbb {Z}}_{\geq 0}$
and
![]() $\boldsymbol {a} =(a_1, \ldots , a_r) \in {\mathbb {Z}}_{\geq 0}^r$
. Combining (4.19) and (4.20) yields the following lemma.
$\boldsymbol {a} =(a_1, \ldots , a_r) \in {\mathbb {Z}}_{\geq 0}^r$
. Combining (4.19) and (4.20) yields the following lemma.
Lemma 4.4.1 Let
![]() $\boldsymbol {a} \in {\mathbb {Z}}^{r_1}$
and
$\boldsymbol {a} \in {\mathbb {Z}}^{r_1}$
and
![]() $\boldsymbol {b} \in {\mathbb {Z}}^{r_2}$
. Then there exists
$\boldsymbol {b} \in {\mathbb {Z}}^{r_2}$
. Then there exists
![]() $\boldsymbol {c} \in {\mathbb {Z}}_{\geq 0}^{r_3}$
,
$\boldsymbol {c} \in {\mathbb {Z}}_{\geq 0}^{r_3}$
,
![]() $\boldsymbol {d} \in {\mathbb {Z}}_{\geq 0}^{r_4}$
such that
$\boldsymbol {d} \in {\mathbb {Z}}_{\geq 0}^{r_4}$
such that
![]() $|\boldsymbol {c}| + |\boldsymbol {d}| = |\boldsymbol {a}| + |\boldsymbol {b}|$
and there is a parity preserving isomorphism of morphism spaces
$|\boldsymbol {c}| + |\boldsymbol {d}| = |\boldsymbol {a}| + |\boldsymbol {b}|$
and there is a parity preserving isomorphism of morphism spaces
given by
for some invertible morphisms
Given a supercategory
![]() $\mathcal{B}$
, let
$\mathcal{B}$
, let
![]() $\mathcal{B}^{\text {sop}}$
be the category with the same objects and morphisms as
$\mathcal{B}^{\text {sop}}$
be the category with the same objects and morphisms as
![]() $\mathcal{B}$
but with composition given by
$\mathcal{B}$
but with composition given by
![]() $\alpha \bullet \beta := (-1)^{{\mathfrak {p}}{\alpha }{\mathfrak {p}}{\beta }}\beta \circ \alpha $
for all homogeneous morphisms
$\alpha \bullet \beta := (-1)^{{\mathfrak {p}}{\alpha }{\mathfrak {p}}{\beta }}\beta \circ \alpha $
for all homogeneous morphisms
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in
$\beta $
in
![]() $\mathcal{B}$
. Let
$\mathcal{B}$
. Let
![]() $\text {refl}:{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
be the involutive contravariant superfunctor (in the sense of [Reference Brundan and Ellis5, Reference Lepine21]) given by
$\text {refl}:{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
be the involutive contravariant superfunctor (in the sense of [Reference Brundan and Ellis5, Reference Lepine21]) given by
![]() $D \mapsto (-1)^{k(k-1)/2}D'$
on diagrams, where
$D \mapsto (-1)^{k(k-1)/2}D'$
on diagrams, where
![]() $D'$
is the reflection of D along a horizontal axis, and k is the number of tag-in and tag-out generators in D. It is easily checked that this is well defined using Theorem 4.3.1. The following lemma is immediate.
$D'$
is the reflection of D along a horizontal axis, and k is the number of tag-in and tag-out generators in D. It is easily checked that this is well defined using Theorem 4.3.1. The following lemma is immediate.
Lemma 4.4.2 The contravariant superfunctor
![]() $\text {refl}$
is an equivalence of supercategories
$\text {refl}$
is an equivalence of supercategories
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }^{\text {sop}}$
and restricts to an equivalence
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }^{\text {sop}}$
and restricts to an equivalence
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\downarrow }^{\text {sop}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow } {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_{\downarrow }^{\text {sop}}$
.
4.5 Connecting
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
to
${\mathfrak {p}\text {-}\mathbf {Web}}$
to
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
Lemma 4.5.1 There is a well-defined functor of monoidal supercategories
given on objects by
![]() $\iota _\uparrow (k) = \uparrow _k$
and on morphisms by
$\iota _\uparrow (k) = \uparrow _k$
and on morphisms by

Proof The theorem follows immediately from the defining relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
.
Theorem 4.5.2 The functor
![]() $\iota _\uparrow :{\mathfrak {p}\text {-}\mathbf {Web}} {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow $
is full.
$\iota _\uparrow :{\mathfrak {p}\text {-}\mathbf {Web}} {\rightarrow } {\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow $
is full.
Proof We begin by proving a claim.
Claim: Let
![]() $\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^{r}$
,
$\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^{r}$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^s$
, with
$\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^s$
, with
![]() $a_1 = b_1=k$
. If
$a_1 = b_1=k$
. If
![]() $f \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow }(\uparrow _{\boldsymbol {a}}, \uparrow _{\boldsymbol {b}})$
is in the image of
$f \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow }(\uparrow _{\boldsymbol {a}}, \uparrow _{\boldsymbol {b}})$
is in the image of
![]() $\iota _\uparrow $
, then the morphism
$\iota _\uparrow $
, then the morphism

is also in the image of
![]() $\iota _\uparrow $
.
$\iota _\uparrow $
.
We prove the Claim by induction on k, with the base case
![]() $k=0$
being trivial. Let
$k=0$
being trivial. Let
![]() $k>0$
and assume that the claim holds for all
$k>0$
and assume that the claim holds for all
![]() $m<k$
. By Corollary 6.3.2, we may assume that f is of the form
$m<k$
. By Corollary 6.3.2, we may assume that f is of the form
![]() $\iota _\uparrow (\xi )$
for some
$\iota _\uparrow (\xi )$
for some
![]() $\xi \in \mathscr {B}$
. After an isotopy of the strands in
$\xi \in \mathscr {B}$
. After an isotopy of the strands in
![]() $\iota _\uparrow (\xi )$
, we may write
$\iota _\uparrow (\xi )$
, we may write

for some morphisms
![]() $f_1,f_2, f_3$
in the image of
$f_1,f_2, f_3$
in the image of
![]() $\iota _\uparrow $
, and some
$\iota _\uparrow $
, and some
![]() $k' \leq k$
. If
$k' \leq k$
. If
![]() $k'=k$
, then the diagram has a bubble, and is thus zero by (4.3). If
$k'=k$
, then the diagram has a bubble, and is thus zero by (4.3). If
![]() $k'=0$
, then the loop can be untwisted, using Theorem 4.3.1. So we assume now that
$k'=0$
, then the loop can be untwisted, using Theorem 4.3.1. So we assume now that
![]() $0<k'<k$
. Using (4.11) and (4.12), we may rewrite (4.21) as
$0<k'<k$
. Using (4.11) and (4.12), we may rewrite (4.21) as

where g is a morphism in the image of
![]() $\iota _\uparrow $
. Now, applying the inductive assumption for
$\iota _\uparrow $
. Now, applying the inductive assumption for
![]() $k'$
, and then for
$k'$
, and then for
![]() $k-k'$
gives the result, proving the Claim.
$k-k'$
gives the result, proving the Claim.
Now, we prove the lemma. Let f be a diagram in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
. Using (4.18), we may assume that f is composed only of upward splits, upward merges, leftward/rightward/upward cups, leftward/rightward/upward caps, and crossings of all orientations. Let c be the number of leftward/rightward cups in f. We prove by induction on c that f is in the image of
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow }$
. Using (4.18), we may assume that f is composed only of upward splits, upward merges, leftward/rightward/upward cups, leftward/rightward/upward caps, and crossings of all orientations. Let c be the number of leftward/rightward cups in f. We prove by induction on c that f is in the image of
![]() $\iota _\uparrow $
.
$\iota _\uparrow $
.
If
![]() $c=0$
, then since the domain and the codomain are composed only of up-arrows, it must be that there are no downward strands in f, so f is composed only of upward splits, upward merges, upward cups, upward caps, and upward crossings, and hence f is in the image of
$c=0$
, then since the domain and the codomain are composed only of up-arrows, it must be that there are no downward strands in f, so f is composed only of upward splits, upward merges, upward cups, upward caps, and upward crossings, and hence f is in the image of
![]() $\iota _\uparrow $
.
$\iota _\uparrow $
.
Now, for the induction step, assume
![]() $c>0$
. Select any leftward/rightward cup in f. Again, since the domain and the codomain are composed only of up-arrows, it must be that the downward strand leaving from the cup must lead into a leftward/rightward cap in f. Then, using Theorem 4.3.1, we may pull the downward strand to the left side of the diagram, giving a diagram of the form
$c>0$
. Select any leftward/rightward cup in f. Again, since the domain and the codomain are composed only of up-arrows, it must be that the downward strand leaving from the cup must lead into a leftward/rightward cap in f. Then, using Theorem 4.3.1, we may pull the downward strand to the left side of the diagram, giving a diagram of the form

where g is a diagram in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow $
with
${\mathfrak {p}\text {-}\mathbf {Web}}_\uparrow $
with
![]() $c-1$
leftward/rightward cups. By the induction assumption, g is in the image of
$c-1$
leftward/rightward cups. By the induction assumption, g is in the image of
![]() $\iota _\uparrow $
. Thus, by the Claim, f itself is in the image of
$\iota _\uparrow $
. Thus, by the Claim, f itself is in the image of
![]() $\iota _\uparrow $
, completing the proof.
$\iota _\uparrow $
, completing the proof.
We will show in Theorem 6.8.3 that
![]() $\iota _{\uparrow }$
is also faithful.
$\iota _{\uparrow }$
is also faithful.
5 The Lie superalgebra of type P
5.1 The Lie superalgebra of type P
In this section, let
![]() ${\mathbb {k}}$
be a field of characteristic different from two. Let
${\mathbb {k}}$
be a field of characteristic different from two. Let
![]() $I=I_{n|n}$
be the index set
$I=I_{n|n}$
be the index set
![]() $\left\{1, \dotsc ,n, -1, \dotsc , -n \right\}$
with fixed order
$\left\{1, \dotsc ,n, -1, \dotsc , -n \right\}$
with fixed order
![]() $1 < \dotsb < n < -1 < \dotsb < -n$
. Let
$1 < \dotsb < n < -1 < \dotsb < -n$
. Let
![]() $|{~\cdot ~}|: I {\rightarrow } {\mathbb {Z}}_{2}$
be the function defined by
$|{~\cdot ~}|: I {\rightarrow } {\mathbb {Z}}_{2}$
be the function defined by
![]() $|{i}| = \bar {0}$
if
$|{i}| = \bar {0}$
if
![]() $i>0$
and
$i>0$
and
![]() $|{i}|=\bar {1}$
if
$|{i}|=\bar {1}$
if
![]() $i <0$
. Let
$i <0$
. Let
![]() $V=V_{n}$
be the vector space with distinguished basis
$V=V_{n}$
be the vector space with distinguished basis
![]() $\left\{v_{i} \mid i \in I \right\}$
. We define a
$\left\{v_{i} \mid i \in I \right\}$
. We define a
![]() ${\mathbb {Z}}_{2}$
-grading on V by declaring
${\mathbb {Z}}_{2}$
-grading on V by declaring
![]() $|{v_{i}}|=|{i}|$
for all
$|{v_{i}}|=|{i}|$
for all
![]() $i \in I$
. Let
$i \in I$
. Let
![]() ${\mathfrak {gl}} (V) = {\mathfrak {gl}}(n|n)$
denote the superspace of all linear endomorphisms of V. Then
${\mathfrak {gl}} (V) = {\mathfrak {gl}}(n|n)$
denote the superspace of all linear endomorphisms of V. Then
![]() ${\mathfrak {gl}} (V)$
is a Lie superalgebra via the graded version of the commutator bracket:
${\mathfrak {gl}} (V)$
is a Lie superalgebra via the graded version of the commutator bracket:
for all homogeneous
![]() $f,g \in {\mathfrak {gl}} (V)$
. As done here, we frequently only give a formula for homogeneous elements and leave it understood that the general case is obtained via linearity.
$f,g \in {\mathfrak {gl}} (V)$
. As done here, we frequently only give a formula for homogeneous elements and leave it understood that the general case is obtained via linearity.
Define an odd supersymmetric nondegenerate bilinear form on V by declaring
for
![]() $i,j \in I$
. Here, odd means that the associated linear map
$i,j \in I$
. Here, odd means that the associated linear map
![]() $V \otimes V {\rightarrow } {\mathbb {k}}$
is an odd map of superspaces, while supersymmetric means that
$V \otimes V {\rightarrow } {\mathbb {k}}$
is an odd map of superspaces, while supersymmetric means that
![]() $(v,w) = (-1)^{|{v}| |{w}|} (w,v)$
for all homogeneous
$(v,w) = (-1)^{|{v}| |{w}|} (w,v)$
for all homogeneous
![]() $v,w \in V$
.
$v,w \in V$
.
Define a Lie superalgebra
![]() ${\mathfrak {g}} = {\mathfrak {p}} (n) \subseteq {\mathfrak {gl}} (V)$
consisting of all linear maps which preserve the bilinear form given in (5.1). That is, for all homogeneous
${\mathfrak {g}} = {\mathfrak {p}} (n) \subseteq {\mathfrak {gl}} (V)$
consisting of all linear maps which preserve the bilinear form given in (5.1). That is, for all homogeneous
![]() $v,w \in V$
,
$v,w \in V$
,
The supercommutator restricts to define a Lie superalgebra structure on
![]() ${\mathfrak {p}} (n)$
.
${\mathfrak {p}} (n)$
.
With respect to our choice of basis, we can describe
![]() ${\mathfrak {p}}(n)$
as the
${\mathfrak {p}}(n)$
as the
![]() $2n \times 2n$
matrices defined over
$2n \times 2n$
matrices defined over
![]() ${\mathbb {k}}$
of the form
${\mathbb {k}}$
of the form
 $$ \begin{align} {\mathfrak{p}} (n) = \left\{\left(\begin{matrix} A & B \\ C & -A^{t} \end{matrix} \right) \right\}, \end{align} $$
$$ \begin{align} {\mathfrak{p}} (n) = \left\{\left(\begin{matrix} A & B \\ C & -A^{t} \end{matrix} \right) \right\}, \end{align} $$
where
![]() $A,B,C$
are
$A,B,C$
are
![]() $n \times n$
matrices with entries from
$n \times n$
matrices with entries from
![]() ${\mathbb {k}}$
with B symmetric, C skew-symmetric, and where
${\mathbb {k}}$
with B symmetric, C skew-symmetric, and where
![]() $A^{t}$
denotes the transpose of A. In terms of (5.2), the
$A^{t}$
denotes the transpose of A. In terms of (5.2), the
![]() ${\mathbb {Z}}_{2}$
-grading is given by declaring
${\mathbb {Z}}_{2}$
-grading is given by declaring
![]() ${\mathfrak {g}}_{\bar {0}}$
as the subspace of all such matrices where
${\mathfrak {g}}_{\bar {0}}$
as the subspace of all such matrices where
![]() $B=C=0$
and
$B=C=0$
and
![]() ${\mathfrak {g}}_{\bar {1} }$
as the subspace of all such matrices where
${\mathfrak {g}}_{\bar {1} }$
as the subspace of all such matrices where
![]() $A=0$
.
$A=0$
.
A (left)
![]() ${\mathfrak {p}} (n)$
-supermodule is a
${\mathfrak {p}} (n)$
-supermodule is a
![]() ${\mathbb {Z}}_{2}$
-graded
${\mathbb {Z}}_{2}$
-graded
![]() ${\mathbb {k}}$
-vector space with a left
${\mathbb {k}}$
-vector space with a left
![]() ${\mathbb {k}}$
-linear action of
${\mathbb {k}}$
-linear action of
![]() ${\mathfrak {p}} (n)$
which respects the
${\mathfrak {p}} (n)$
which respects the
![]() ${\mathbb {Z}}_{2}$
-grading and which satisfies graded versions of the usual axioms required of a module for a Lie algebra. For example, the natural supermodule is
${\mathbb {Z}}_{2}$
-grading and which satisfies graded versions of the usual axioms required of a module for a Lie algebra. For example, the natural supermodule is
![]() $V_{n}$
with
$V_{n}$
with
![]() ${\mathfrak {p}}(n)$
-supermodule structure given by matrix multiplication. Since we will only consider supermodules we usually leave the prefix “super” implicit going forward.
${\mathfrak {p}}(n)$
-supermodule structure given by matrix multiplication. Since we will only consider supermodules we usually leave the prefix “super” implicit going forward.
We allow for all (not just parity preserving)
![]() ${\mathfrak {p}}(n)$
-module homomorphisms. Consequently, the set of all
${\mathfrak {p}}(n)$
-module homomorphisms. Consequently, the set of all
![]() ${\mathfrak {p}}(n)$
-homomorphisms between two modules is naturally a
${\mathfrak {p}}(n)$
-homomorphisms between two modules is naturally a
![]() ${\mathbb {Z}}_{2}$
-graded vector space. Explicitly,
${\mathbb {Z}}_{2}$
-graded vector space. Explicitly,
![]() $f: M {\rightarrow } N$
is a homogeneous
$f: M {\rightarrow } N$
is a homogeneous
![]() ${\mathfrak {p}} (n)$
-module homomorphism if f is a linear map which satisfies
${\mathfrak {p}} (n)$
-module homomorphism if f is a linear map which satisfies
![]() $f(M_{s}) \subseteq N_{s+|{f}|}$
for
$f(M_{s}) \subseteq N_{s+|{f}|}$
for
![]() $s\in {\mathbb {Z}}_{2}$
and
$s\in {\mathbb {Z}}_{2}$
and
![]() $f(x.m) = (-1)^{|{x}||{f}|}x.f(m)$
for all homogeneous
$f(x.m) = (-1)^{|{x}||{f}|}x.f(m)$
for all homogeneous
![]() $x \in {\mathfrak {p}} (n)$
and
$x \in {\mathfrak {p}} (n)$
and
![]() $m\in M$
.
$m\in M$
.
Since the enveloping superalgebra
![]() $U({\mathfrak {p}} (n))$
is a Hopf superalgebra, the category of
$U({\mathfrak {p}} (n))$
is a Hopf superalgebra, the category of
![]() ${\mathfrak {p}} (n)$
-modules is a monoidal supercategory in the sense of [Reference Brundan and Ellis5]. In what follows, we study particular monoidal sub-supercategories of this category. For every
${\mathfrak {p}} (n)$
-modules is a monoidal supercategory in the sense of [Reference Brundan and Ellis5]. In what follows, we study particular monoidal sub-supercategories of this category. For every
![]() $k \geq 0$
, let
$k \geq 0$
, let
![]() $S^{k}(V_{n})$
denote the kth symmetric power of the natural module
$S^{k}(V_{n})$
denote the kth symmetric power of the natural module
![]() $V_{n}$
(by convention,
$V_{n}$
(by convention,
![]() $S^{0}(V_{n}) = {\mathbb {k}}$
, the trivial module). Let
$S^{0}(V_{n}) = {\mathbb {k}}$
, the trivial module). Let
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}} $
denote the full monoidal sub-supercategory of
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}} $
denote the full monoidal sub-supercategory of
![]() ${\mathfrak {p}}(n)$
-modules generated by
${\mathfrak {p}}(n)$
-modules generated by
![]() $\left\{S^{k}(V_{n}) \mid k \geq 0 \right\}$
, and let
$\left\{S^{k}(V_{n}) \mid k \geq 0 \right\}$
, and let
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
denote the full monoidal sub-supercategory of
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
denote the full monoidal sub-supercategory of
![]() ${\mathfrak {p}}(n)$
-modules generated by
${\mathfrak {p}}(n)$
-modules generated by
![]() $\left\{S^{k}(V_{n}), S^{k}(V_{n})^{*} \mid k \geq 0 \right\}$
. That is,
$\left\{S^{k}(V_{n}), S^{k}(V_{n})^{*} \mid k \geq 0 \right\}$
. That is,
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
is the full subcategory of
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
is the full subcategory of
![]() ${\mathfrak {p}} (n)$
-modules consisting of objects of the form
${\mathfrak {p}} (n)$
-modules consisting of objects of the form
ranging over all
![]() $k \in {\mathbb {Z}}_{\geq 0}$
and
$k \in {\mathbb {Z}}_{\geq 0}$
and
![]() $\boldsymbol {a} = (a_1, \ldots , a_k) \in {\mathbb {Z}}_{\geq 0}^k$
. The objects of
$\boldsymbol {a} = (a_1, \ldots , a_k) \in {\mathbb {Z}}_{\geq 0}^k$
. The objects of
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
are similar except some symmetric powers are replaced by their duals.
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
are similar except some symmetric powers are replaced by their duals.
5.2 Basic
 ${\mathfrak {p}}(n)$
-module maps
${\mathfrak {p}}(n)$
-module maps
To connect our diagrammatic categories to the representation theory of
![]() ${\mathfrak {p}} (n)$
, we introduce certain explicit
${\mathfrak {p}} (n)$
, we introduce certain explicit
![]() ${\mathfrak {p}}(n)$
-module homomorphisms in the categories
${\mathfrak {p}}(n)$
-module homomorphisms in the categories
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
and
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
and
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
.
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
.
We can view the symmetric bisuperalgebra
as the enveloping superalgebra for the abelian Lie superalgebra
![]() $V_{n}$
. This endows
$V_{n}$
. This endows
![]() $S(V_{n})$
with the structure of a
$S(V_{n})$
with the structure of a
![]() ${\mathbb {Z}}$
-graded Hopf superalgebra. In particular, it admits an associative product
${\mathbb {Z}}$
-graded Hopf superalgebra. In particular, it admits an associative product
![]() $m: S(V_n) \otimes S(V_n) {\rightarrow } S(V_n)$
and coassociative coproduct
$m: S(V_n) \otimes S(V_n) {\rightarrow } S(V_n)$
and coassociative coproduct
![]() $\Delta : S(V_n) {\rightarrow } S(V_n) \otimes S(V_n)$
. The product is the usual concatenation product and the coproduct is given on generators
$\Delta : S(V_n) {\rightarrow } S(V_n) \otimes S(V_n)$
. The product is the usual concatenation product and the coproduct is given on generators
![]() $v \in V_{n}$
by
$v \in V_{n}$
by
![]() $\Delta (v) = v \otimes 1 + 1 \otimes v$
. We stress that the multiplication in
$\Delta (v) = v \otimes 1 + 1 \otimes v$
. We stress that the multiplication in
![]() $S(V_n)$
is supercommutative, meaning that
$S(V_n)$
is supercommutative, meaning that
![]() $v w = (-1)^{|{v}||{w}|} w v$
for all homogeneous
$v w = (-1)^{|{v}||{w}|} w v$
for all homogeneous
![]() $v,w \in V_n$
. Corresponding to the direct sum decomposition (5.3), there are also projections
$v,w \in V_n$
. Corresponding to the direct sum decomposition (5.3), there are also projections
![]() $p_k:S(V_n) {\rightarrow } S^k(V_n)$
and inclusions
$p_k:S(V_n) {\rightarrow } S^k(V_n)$
and inclusions
![]() $\iota _k: S^k(V_n) {\rightarrow } S(V_n)$
for all
$\iota _k: S^k(V_n) {\rightarrow } S(V_n)$
for all
![]() $k \in {\mathbb {Z}}_{\geq 0}$
. Each of the maps
$k \in {\mathbb {Z}}_{\geq 0}$
. Each of the maps
![]() $\Delta , m, p_k, \iota _k$
is a
$\Delta , m, p_k, \iota _k$
is a
![]() $U({\mathfrak {p}}(n))$
-module homomorphism, and we use them to construct several module homomorphisms which will be used in the sequel.
$U({\mathfrak {p}}(n))$
-module homomorphism, and we use them to construct several module homomorphisms which will be used in the sequel.
We define the split
![]() $U({\mathfrak {p}}(n))$
-module morphism
$U({\mathfrak {p}}(n))$
-module morphism
via
![]() $\text {spl}^{a,b}_{a+b}:= (p_a \otimes p_b) \circ \Delta \circ \iota _{a+b}$
. Explicitly, we have
$\text {spl}^{a,b}_{a+b}:= (p_a \otimes p_b) \circ \Delta \circ \iota _{a+b}$
. Explicitly, we have
 $$ \begin{align*} \text{spl}^{a,b}_{a+b}(x_1 \cdots x_{a+b})= \sum_{\substack{T = \{t_1< \cdots< t_a\} \\ U = \{u_1< \cdots<u_b\} \\ T \cup U = \{1,\ldots, a+b\} }} (-1)^{\varepsilon(T,U)}x_{t_1} \cdots x_{t_a} \otimes x_{u_1} \cdots x_{u_b}, \end{align*} $$
$$ \begin{align*} \text{spl}^{a,b}_{a+b}(x_1 \cdots x_{a+b})= \sum_{\substack{T = \{t_1< \cdots< t_a\} \\ U = \{u_1< \cdots<u_b\} \\ T \cup U = \{1,\ldots, a+b\} }} (-1)^{\varepsilon(T,U)}x_{t_1} \cdots x_{t_a} \otimes x_{u_1} \cdots x_{u_b}, \end{align*} $$
for all homogeneous
![]() $x_1, \ldots , x_{a+b} \in V_n$
, where
$x_1, \ldots , x_{a+b} \in V_n$
, where
![]() $\varepsilon (T,U) \in {\mathbb {Z}}_2$
is defined by
$\varepsilon (T,U) \in {\mathbb {Z}}_2$
is defined by
Similarly, define the merge
![]() $U({\mathfrak {p}}(n))$
-module morphism
$U({\mathfrak {p}}(n))$
-module morphism
via
![]() $\text {mer}_{a,b}^{a+b}:= p_{a+b} \circ m \circ (\iota _a \otimes \iota _b)$
, or, explicitly,
$\text {mer}_{a,b}^{a+b}:= p_{a+b} \circ m \circ (\iota _a \otimes \iota _b)$
, or, explicitly,
for all
![]() $x_1, \ldots , x_a, y_1, \ldots , y_b \in V_n$
. Both the split and merge maps are even (i.e., parity preserving).
$x_1, \ldots , x_a, y_1, \ldots , y_b \in V_n$
. Both the split and merge maps are even (i.e., parity preserving).
As the odd bilinear form used to define
![]() ${\mathfrak {p}} (n)$
is supersymmetric, it factors through to define the odd antenna
${\mathfrak {p}} (n)$
is supersymmetric, it factors through to define the odd antenna
![]() $U({\mathfrak {p}}(n))$
-module homomorphism
$U({\mathfrak {p}}(n))$
-module homomorphism
![]() $\text {ant}{}:S^2(V_n) {\rightarrow } {\mathbb {k}}$
given by
$\text {ant}{}:S^2(V_n) {\rightarrow } {\mathbb {k}}$
given by
for all
![]() $x_1, x_2 \in V_n$
.
$x_1, x_2 \in V_n$
.
For any
![]() $k \in {\mathbb {Z}}_{\geq 0}$
, we have the evaluation
$k \in {\mathbb {Z}}_{\geq 0}$
, we have the evaluation
![]() $U({\mathfrak {p}}(n))$
-module homomorphism
$U({\mathfrak {p}}(n))$
-module homomorphism
 $$ \begin{gather*} \operatorname{eval}_k: S^k(V_n)^{*} \otimes S^k(V_n) {\rightarrow} {\mathbb{k}}\\ f \otimes x \mapsto f(x). \end{gather*} $$
$$ \begin{gather*} \operatorname{eval}_k: S^k(V_n)^{*} \otimes S^k(V_n) {\rightarrow} {\mathbb{k}}\\ f \otimes x \mapsto f(x). \end{gather*} $$
Dualizing the evaluation map yields the coevaluation
![]() $U({\mathfrak {p}}(n))$
-module homomorphism
$U({\mathfrak {p}}(n))$
-module homomorphism
In particular, we have
 $$ \begin{gather*} \operatorname{coeval}_1: {\mathbb{k}} {\rightarrow} V_n \otimes V_n^{*}, \\ 1 \mapsto \sum_{i \in I_m} v_i \otimes v_i^{*}, \end{gather*} $$
$$ \begin{gather*} \operatorname{coeval}_1: {\mathbb{k}} {\rightarrow} V_n \otimes V_n^{*}, \\ 1 \mapsto \sum_{i \in I_m} v_i \otimes v_i^{*}, \end{gather*} $$
where
![]() $\{v_i^{*} \mid i \in I\}$
is the dual basis for
$\{v_i^{*} \mid i \in I\}$
is the dual basis for
![]() $V_n^{*}$
defined by
$V_n^{*}$
defined by
![]() $v_{i}^{*}(v_{j})=\delta _{i,j}$
.
$v_{i}^{*}(v_{j})=\delta _{i,j}$
.
The odd nondegenerate bilinear form
![]() $(\cdot , \cdot )$
induces an odd
$(\cdot , \cdot )$
induces an odd
![]() $U({\mathfrak {p}}(n))$
-module isomorphism
$U({\mathfrak {p}}(n))$
-module isomorphism
 $$ \begin{gather*} D:V_n {\rightarrow} V_{n}^{*}, \\ v_i \mapsto (v_{i}, -)= v_{-i}^{*}. \end{gather*} $$
$$ \begin{gather*} D:V_n {\rightarrow} V_{n}^{*}, \\ v_i \mapsto (v_{i}, -)= v_{-i}^{*}. \end{gather*} $$
Using this isomorphism, we define the odd cap and cup
![]() $U({\mathfrak {p}}(n))$
-module homomorphisms by
$U({\mathfrak {p}}(n))$
-module homomorphisms by
 $$ \begin{align*} \cap:= & \operatorname{eval}_1 \circ (D \otimes \operatorname{id}) : V_n^{\otimes 2} {\rightarrow} {\mathbb{k}},\\ \cup:= & (\operatorname{id} \otimes D^{-1})\circ \operatorname{coeval}_1 : {\mathbb{k}} {\rightarrow} V_n^{\otimes 2}. \end{align*} $$
$$ \begin{align*} \cap:= & \operatorname{eval}_1 \circ (D \otimes \operatorname{id}) : V_n^{\otimes 2} {\rightarrow} {\mathbb{k}},\\ \cup:= & (\operatorname{id} \otimes D^{-1})\circ \operatorname{coeval}_1 : {\mathbb{k}} {\rightarrow} V_n^{\otimes 2}. \end{align*} $$
On our basis for
![]() $V_{n}$
, these maps are given by
$V_{n}$
, these maps are given by
Finally, for any two
![]() ${\mathfrak {p}} (n)$
-modules M and N, we have the even “tensor swap” homomorphism
${\mathfrak {p}} (n)$
-modules M and N, we have the even “tensor swap” homomorphism
 $$ \begin{gather*} \tau_{M,N}: M \otimes N {\rightarrow} N \otimes M, \\ m \otimes n \mapsto (-1)^{{\mathfrak{p}}{m} {\mathfrak{p}} {n}}n \otimes m, \end{gather*} $$
$$ \begin{gather*} \tau_{M,N}: M \otimes N {\rightarrow} N \otimes M, \\ m \otimes n \mapsto (-1)^{{\mathfrak{p}}{m} {\mathfrak{p}} {n}}n \otimes m, \end{gather*} $$
for all homogeneous
![]() $m\in M$
and
$m\in M$
and
![]() $n\in N$
. Note that
$n\in N$
. Note that
Compare with (2.3) when
![]() $a=b=1$
.
$a=b=1$
.
Note that
![]() $\operatorname {spl}^{a,b}_{a+b}$
,
$\operatorname {spl}^{a,b}_{a+b}$
,
![]() $\operatorname {mer}^{a+b}_{a,b}$
,
$\operatorname {mer}^{a+b}_{a,b}$
,
![]() ${\mathrm {ev}}_{k}$
,
${\mathrm {ev}}_{k}$
,
![]() ${\mathrm {coev}}_{k}$
, and the tensor swap are in fact
${\mathrm {coev}}_{k}$
, and the tensor swap are in fact
![]() ${\mathfrak {gl}} (V)$
-equivariant. On the other hand,
${\mathfrak {gl}} (V)$
-equivariant. On the other hand,
![]() $\text {ant}$
, the odd cup, and the odd cap are only
$\text {ant}$
, the odd cup, and the odd cap are only
![]() ${\mathfrak {p}} (n)$
-equivariant.
${\mathfrak {p}} (n)$
-equivariant.
6 From webs to
 ${\mathfrak {p}}(n)$
-modules
${\mathfrak {p}}(n)$
-modules
6.1 The functor
 $G: {\mathfrak {p}\text {-}\mathbf {Web}} {\rightarrow } {\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}$
$G: {\mathfrak {p}\text {-}\mathbf {Web}} {\rightarrow } {\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}$
Unless otherwise stated, in this section,
![]() ${\mathbb {k}}$
is a field of characteristic not two. Recall
${\mathbb {k}}$
is a field of characteristic not two. Recall
![]() ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
denotes the monoidal supercategory of
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
denotes the monoidal supercategory of
![]() ${\mathfrak {p}} (n)$
-modules generated by symmetric powers of the natural module
${\mathfrak {p}} (n)$
-modules generated by symmetric powers of the natural module
![]() $V_n$
.
$V_n$
.
Theorem 6.1.1 There is a well-defined functor
given on objects by
![]() $G(k) = S^k(V_n)$
and on morphisms by
$G(k) = S^k(V_n)$
and on morphisms by

6.2 The crossing morphism in
 ${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
${{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}$
For short, let
be the tensor swap map introduced in Section 5.2.
Lemma 6.2.1 For all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, we have
$a,b \in {\mathbb {Z}}_{\geq 0}$
, we have

Proof This is well-known
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
(see, e.g., [Reference Tubbenhauer, Vaz and Wedrich28] where it is done for quantum
${\mathfrak {gl}\text {-}\mathbf {Web}}$
(see, e.g., [Reference Tubbenhauer, Vaz and Wedrich28] where it is done for quantum
![]() ${\mathfrak {gl}} (V)$
). It is also routine to check directly. Details are included in the arXiv version.
${\mathfrak {gl}} (V)$
). It is also routine to check directly. Details are included in the arXiv version.
6.3 Basis theorems for
 ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
${\mathfrak {p}\text {-}\mathbf {Web}}$
We now prove that the sets introduced in Section 3.5 form
![]() ${\mathbb {k}}$
-bases for the morphism spaces of
${\mathbb {k}}$
-bases for the morphism spaces of
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
${\mathfrak {gl}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
.
${\mathfrak {p}\text {-}\mathbf {Web}}$
.
Theorem 6.3.1 Assume
![]() $|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
. Then
$|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
. Then
is a family of linearly independent morphisms in
![]() ${\mathrm { Hom}}_{{\mathfrak {p}}(n)}(S^{\boldsymbol {a}}(V_n),S^{\boldsymbol {b}}(V_n))$
.
${\mathrm { Hom}}_{{\mathfrak {p}}(n)}(S^{\boldsymbol {a}}(V_n),S^{\boldsymbol {b}}(V_n))$
.
Proof Let
![]() $(A,B,C,D) \in \chi (\boldsymbol {a},\boldsymbol {b})$
. For all
$(A,B,C,D) \in \chi (\boldsymbol {a},\boldsymbol {b})$
. For all
![]() $i=1, \ldots , t$
and
$i=1, \ldots , t$
and
![]() $j=1,\ldots ,u$
, define
$j=1,\ldots ,u$
, define
 $$ \begin{align*} \texttt{r}_i = \sum_{\ell =1}^u C_{i\ell}, \qquad \qquad |C| = \sum_{k =1}^t \texttt{r}_k, \qquad \text{ and } \qquad P_{ij} = \sum_{k=1}^{i-1} \texttt{r}_k + \sum_{\ell =1 }^{j-1} C_{i \ell}. \end{align*} $$
$$ \begin{align*} \texttt{r}_i = \sum_{\ell =1}^u C_{i\ell}, \qquad \qquad |C| = \sum_{k =1}^t \texttt{r}_k, \qquad \text{ and } \qquad P_{ij} = \sum_{k=1}^{i-1} \texttt{r}_k + \sum_{\ell =1 }^{j-1} C_{i \ell}. \end{align*} $$
For
![]() $X \in \left\{A, B \right\}$
, let
$X \in \left\{A, B \right\}$
, let
be an irredundant list of all pairs of indices
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $i<j$
and
$i<j$
and
![]() $X_{ij} = 1$
. Let
$X_{ij} = 1$
. Let
be an irredundant list of all indices i such that
![]() $D_i = 1$
. It follows from the fact that
$D_i = 1$
. It follows from the fact that
![]() $|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
and the definition of the set
$|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
and the definition of the set
![]() $\chi (\boldsymbol {a},\boldsymbol {b})$
that
$\chi (\boldsymbol {a},\boldsymbol {b})$
that
![]() $|C|+\alpha + \beta + \delta \leq n$
.
$|C|+\alpha + \beta + \delta \leq n$
.
We define the following elements of
![]() $S(V_n)^{\otimes t}$
:
$S(V_n)^{\otimes t}$
:
 $$ \begin{align*} v^{(A,B,C,D),1}&:= v_1 \cdots v_{\texttt{r}_1} \otimes v_{\texttt{r}_1 +1} \cdots v_{\texttt{r}_1 + \texttt{r}_2} \otimes \cdots \otimes v_{\texttt{r}_1 + \cdots + \texttt{r}_{t-1}+1} \cdots v_{|C|} \\ v^{(A,B,C,D),2}&:= \prod_{k=1}^\alpha 1 \otimes \cdots \otimes 1 \otimes v_{|C|+ k} \otimes 1 \otimes \cdots \otimes 1 \otimes v_{-|C|-k} \otimes 1 \otimes \cdots \otimes 1, \\ v^{(A,B,C,D),3}&:= \prod_{k=1}^\delta 1 \otimes \cdots \otimes 1 \otimes v_{|C| + \alpha + k} v_{-|C| - \alpha - k} \otimes 1 \otimes \cdots \otimes 1, \end{align*} $$
$$ \begin{align*} v^{(A,B,C,D),1}&:= v_1 \cdots v_{\texttt{r}_1} \otimes v_{\texttt{r}_1 +1} \cdots v_{\texttt{r}_1 + \texttt{r}_2} \otimes \cdots \otimes v_{\texttt{r}_1 + \cdots + \texttt{r}_{t-1}+1} \cdots v_{|C|} \\ v^{(A,B,C,D),2}&:= \prod_{k=1}^\alpha 1 \otimes \cdots \otimes 1 \otimes v_{|C|+ k} \otimes 1 \otimes \cdots \otimes 1 \otimes v_{-|C|-k} \otimes 1 \otimes \cdots \otimes 1, \\ v^{(A,B,C,D),3}&:= \prod_{k=1}^\delta 1 \otimes \cdots \otimes 1 \otimes v_{|C| + \alpha + k} v_{-|C| - \alpha - k} \otimes 1 \otimes \cdots \otimes 1, \end{align*} $$
where the vectors
![]() $v_{|C|+ k}$
and
$v_{|C|+ k}$
and
![]() $ v_{-|C|-k}$
appear in the
$ v_{-|C|-k}$
appear in the
![]() $i_k^A$
-th and
$i_k^A$
-th and
![]() $j_k^A$
-th slots, respectively, and the term
$j_k^A$
-th slots, respectively, and the term
![]() $v_{|C| + \alpha + k} v_{-|C| - \alpha - k}$
appears in the
$v_{|C| + \alpha + k} v_{-|C| - \alpha - k}$
appears in the
![]() $i_k^D$
-th slot.
$i_k^D$
-th slot.
We also define the following elements of
![]() $S(V_n)^{\otimes u}$
:
$S(V_n)^{\otimes u}$
:
 $$ \begin{align*} w^{(A,B,C,D),1} &:= \prod_{i=1}^t \prod_{j=1}^u 1 \otimes \cdots 1 \otimes v_{P_{ij}+1} \cdots v_{P_{ij}+C_{ij}} \otimes 1 \otimes \cdots \otimes 1, \\ w^{(A,B,C,D),2} &:= \prod_{k=1}^\beta 1 \otimes \cdots \otimes 1 \otimes v_{|C|+ k} \otimes 1 \otimes \cdots \otimes 1 \otimes v_{-|C|-k} \otimes 1 \otimes \cdots \otimes 1, \end{align*} $$
$$ \begin{align*} w^{(A,B,C,D),1} &:= \prod_{i=1}^t \prod_{j=1}^u 1 \otimes \cdots 1 \otimes v_{P_{ij}+1} \cdots v_{P_{ij}+C_{ij}} \otimes 1 \otimes \cdots \otimes 1, \\ w^{(A,B,C,D),2} &:= \prod_{k=1}^\beta 1 \otimes \cdots \otimes 1 \otimes v_{|C|+ k} \otimes 1 \otimes \cdots \otimes 1 \otimes v_{-|C|-k} \otimes 1 \otimes \cdots \otimes 1, \end{align*} $$
where the term
![]() $v_{P_{ij}+1} \cdots v_{P_{ij}+C_{ij}}$
appears in the jth slot, and the vectors
$v_{P_{ij}+1} \cdots v_{P_{ij}+C_{ij}}$
appears in the jth slot, and the vectors
![]() $v_{|C|+ k}$
and
$v_{|C|+ k}$
and
![]() $ v_{-|C|-k}$
appear in the
$ v_{-|C|-k}$
appear in the
![]() $i_k^B$
-th and
$i_k^B$
-th and
![]() $j_k^B$
-th slots, respectively.
$j_k^B$
-th slots, respectively.
Considering
![]() $S(V_n)^{\otimes t}$
and
$S(V_n)^{\otimes t}$
and
![]() $S(V_n)^{\otimes u}$
as associative algebras, we define
$S(V_n)^{\otimes u}$
as associative algebras, we define
 $$ \begin{align*} v^{(A,B,C,D)}&:=v^{(A,B,C,D),1 }\cdot v^{(A,B,C,D),2}\cdot v^{(A,B,C,D),3} \in S^{\boldsymbol{a}}(V_n),\\ w^{(A,B,C,D)}&:=w^{(A,B,C,D),1 }\cdot w^{(A,B,C,D),2} \in S^{\boldsymbol{b}}(V_n). \end{align*} $$
$$ \begin{align*} v^{(A,B,C,D)}&:=v^{(A,B,C,D),1 }\cdot v^{(A,B,C,D),2}\cdot v^{(A,B,C,D),3} \in S^{\boldsymbol{a}}(V_n),\\ w^{(A,B,C,D)}&:=w^{(A,B,C,D),1 }\cdot w^{(A,B,C,D),2} \in S^{\boldsymbol{b}}(V_n). \end{align*} $$
Since
![]() $S^{\boldsymbol {b}}(V_n)$
has a
$S^{\boldsymbol {b}}(V_n)$
has a
![]() ${\mathbb {k}}$
-basis of tensor products of monomials in
${\mathbb {k}}$
-basis of tensor products of monomials in
![]() $\{v_i \mid i \in I_n\}$
, we may define a linear projection map
$\{v_i \mid i \in I_n\}$
, we may define a linear projection map
We define a partial order
![]() $\succeq $
on
$\succeq $
on
![]() $\chi (\boldsymbol {a},\boldsymbol {b})$
by setting
$\chi (\boldsymbol {a},\boldsymbol {b})$
by setting
if and only if
It is straightforward to check, with the aid of Lemma 6.2.1, that
 $$ \begin{align} p_{(A,B,C,D)} \circ G(\xi^{(A',B',C',D')})(v^{(A,B,C,D)}) = \begin{cases} \pm w^{(A,B,C,D)}, & \text{if } (A',B',C',D') = (A,B,C,D),\\ 0, & \text{if } (A',B',C',D') \not \succeq (A,B,C,D). \end{cases} \end{align} $$
$$ \begin{align} p_{(A,B,C,D)} \circ G(\xi^{(A',B',C',D')})(v^{(A,B,C,D)}) = \begin{cases} \pm w^{(A,B,C,D)}, & \text{if } (A',B',C',D') = (A,B,C,D),\\ 0, & \text{if } (A',B',C',D') \not \succeq (A,B,C,D). \end{cases} \end{align} $$
Now, assume that there exist nontrivial scalars
![]() $c_{(A',B',C',D')} \in {\mathbb {k}}$
such that
$c_{(A',B',C',D')} \in {\mathbb {k}}$
such that
Let
![]() $(A,B,C,D) \in \chi (\boldsymbol {a},\boldsymbol {b})$
be maximal in the
$(A,B,C,D) \in \chi (\boldsymbol {a},\boldsymbol {b})$
be maximal in the
![]() $\succeq $
order such that
$\succeq $
order such that
![]() $c_{(A,B,C,D)} \neq 0$
. Then we have by (6.1) that
$c_{(A,B,C,D)} \neq 0$
. Then we have by (6.1) that
 $$ \begin{align*} 0&=\sum_{(A',B',C',D') \in \chi(\boldsymbol{a},\boldsymbol{b})} c_{(A',B',C',D')} p_{(A,B,C,D)} \circ G(\xi^{(A',B',C',D')})(v^{(A,B,C,D)})\\& = \pm c_{(A,B,C,D)}w^{(A,B,C,D)}, \end{align*} $$
$$ \begin{align*} 0&=\sum_{(A',B',C',D') \in \chi(\boldsymbol{a},\boldsymbol{b})} c_{(A',B',C',D')} p_{(A,B,C,D)} \circ G(\xi^{(A',B',C',D')})(v^{(A,B,C,D)})\\& = \pm c_{(A,B,C,D)}w^{(A,B,C,D)}, \end{align*} $$
a contradiction.
Corollary 6.3.2 The set
is a
![]() ${\mathbb {k}}$
-basis for
${\mathbb {k}}$
-basis for
![]() ${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
The previous corollary along with the results of Section 4.4 and Theorem 6.8.3 provide a basis theorem for
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, as well. The following result is also immediate.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, as well. The following result is also immediate.
Corollary 6.3.3 The set
is a
![]() ${\mathbb {k}}$
-basis for
${\mathbb {k}}$
-basis for
![]() ${\mathrm { Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
${\mathrm { Hom}}_{{\mathfrak {gl}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
.
These morphism spaces have been studied in, e.g., [Reference Rose and Tubbenhauer24, Reference Tubbenhauer, Vaz and Wedrich28]. Also, this basis should be compared with the basis of “reduced chicken foot diagrams” given in [Reference Brundan, Entova-Aizenbud, Etingof and Ostrik6].
Remark 6.3.4 The assumption that
![]() ${\mathbb {k}}$
is a field is for convenience and is not required for the basis theorems stated above. Let
${\mathbb {k}}$
is a field is for convenience and is not required for the basis theorems stated above. Let
![]() ${\mathbb {k}}$
be an integral domain in which
${\mathbb {k}}$
be an integral domain in which
![]() $2$
is invertible, and let
$2$
is invertible, and let
![]() $V_{n}$
be the free
$V_{n}$
be the free
![]() ${\mathbb {k}}$
-supermodule of rank
${\mathbb {k}}$
-supermodule of rank
![]() $2n$
with homogenous basis as in Section 5.1. A standard argument using Bergman’s Diamond Lemma shows that
$2n$
with homogenous basis as in Section 5.1. A standard argument using Bergman’s Diamond Lemma shows that
![]() $S^{k}(V_{n})$
is a free
$S^{k}(V_{n})$
is a free
![]() ${\mathbb {k}}$
-supermodule with the obvious basis. Using this basis, one can verify that the maps given in Section 5.2 and the functor G are still defined, and that the above arguments go through without change.
${\mathbb {k}}$
-supermodule with the obvious basis. Using this basis, one can verify that the maps given in Section 5.2 and the functor G are still defined, and that the above arguments go through without change.
6.4
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
and the marked Brauer category
${\mathfrak {p}\text {-}\mathbf {Web}}$
and the marked Brauer category
We now explain how the marked Brauer category introduced in [Reference Kujawa and Tharp20] can be viewed as a subcategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. It should be noted that in [Reference Kujawa and Tharp20] diagrams were read top-to-bottom, contrary to the convention here. However, using the functor
${\mathfrak {p}\text {-}\mathbf {Web}}$
. It should be noted that in [Reference Kujawa and Tharp20] diagrams were read top-to-bottom, contrary to the convention here. However, using the functor
![]() $\text {refl}$
described in Section 4.4, one can easily translate between the two conventions. In this section, we assume that
$\text {refl}$
described in Section 4.4, one can easily translate between the two conventions. In this section, we assume that
![]() ${\mathbb {k}}$
is a field of characteristic different from two.
${\mathbb {k}}$
is a field of characteristic different from two.
Definition 6.4.1 The marked Brauer category
![]() $\mathcal{B}$
is the
$\mathcal{B}$
is the
![]() ${\mathbb {k}}$
-linear strict monoidal supercategory generated by a single object
${\mathbb {k}}$
-linear strict monoidal supercategory generated by a single object
![]() $\bullet $
. For
$\bullet $
. For
![]() $k \in {\mathbb {Z}}_{\geq 0}$
, we will use the notation
$k \in {\mathbb {Z}}_{\geq 0}$
, we will use the notation
![]() $[k]$
to designate the object
$[k]$
to designate the object
![]() $\bullet ^{\otimes k}$
. The category
$\bullet ^{\otimes k}$
. The category
![]() $\mathcal{B}$
has generating morphisms:
$\mathcal{B}$
has generating morphisms:

We call these morphisms twist, cap, and cup, respectively. The
![]() ${\mathbb {Z}}_2$
-grading is given by declaring twists to have parity
${\mathbb {Z}}_2$
-grading is given by declaring twists to have parity
![]() $\bar 0$
, and caps and cups to have parity
$\bar 0$
, and caps and cups to have parity
![]() $\bar 1$
. The defining relations of
$\bar 1$
. The defining relations of
![]() $\mathcal{B}$
are:
$\mathcal{B}$
are:





Let
![]() ${\mathfrak {p}}(n)\text{-}\mathrm{Mod}_{V}$
denote the monoidal supercategory of
${\mathfrak {p}}(n)\text{-}\mathrm{Mod}_{V}$
denote the monoidal supercategory of
![]() ${\mathfrak {p}}(n)$
-modules generated by the natural module
${\mathfrak {p}}(n)$
-modules generated by the natural module
![]() $V_n$
. That is,
$V_n$
. That is,
![]() ${\mathfrak {p}}(n)\text{-}\mathrm{mod}_{V}$
is the full subcategory of
${\mathfrak {p}}(n)\text{-}\mathrm{mod}_{V}$
is the full subcategory of
![]() ${\mathfrak {p}}(n)\text{-}\mathrm{mod}$
consisting of objects of the form
${\mathfrak {p}}(n)\text{-}\mathrm{mod}$
consisting of objects of the form
![]() $\left\{ V_{n}^{\otimes k} \mid k \in {\mathbb {Z}}_{\geq 0}\right\}$
.
$\left\{ V_{n}^{\otimes k} \mid k \in {\mathbb {Z}}_{\geq 0}\right\}$
.
Theorem 6.4.2 [Reference Kujawa and Tharp20, Theorem 5.2.1]
There is a well-defined functor of monoidal supercategories
given by
![]() $F(\bullet ) = V_{n}$
and on morphisms by
$F(\bullet ) = V_{n}$
and on morphisms by

Theorem 6.4.3 If
![]() ${\mathbb {k}}$
is a field of characteristic zero, then the functor F is full. That is, for all
${\mathbb {k}}$
is a field of characteristic zero, then the functor F is full. That is, for all
![]() $a,b \in {\mathbb {Z}}_{\geq 0}$
, the induced map of superspaces,
$a,b \in {\mathbb {Z}}_{\geq 0}$
, the induced map of superspaces,
is surjective.
Proof When
![]() ${\mathbb {k}}={\mathbb {C}}$
, the statement follows from [Reference Deligne, Lehrer and Zhang15, Section 4.9] (see the proof of [Reference Coulembier and Ehrig12, Theorem 5.2.1] for details). The basis theorem for
${\mathbb {k}}={\mathbb {C}}$
, the statement follows from [Reference Deligne, Lehrer and Zhang15, Section 4.9] (see the proof of [Reference Coulembier and Ehrig12, Theorem 5.2.1] for details). The basis theorem for
![]() $\mathcal{B}$
given in [Reference Kujawa and Tharp20, Theorem 2.3.1] and straightforward base change arguments show that the functor is full for an arbitrary characteristic zero field.
$\mathcal{B}$
given in [Reference Kujawa and Tharp20, Theorem 2.3.1] and straightforward base change arguments show that the functor is full for an arbitrary characteristic zero field.
Let
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_1$
be the full monoidal sub-supercategory of
${\mathfrak {p}\text {-}\mathbf {Web}}_1$
be the full monoidal sub-supercategory of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
whose objects are tuples consisting of only ones, including the empty tuple.
${\mathfrak {p}\text {-}\mathbf {Web}}$
whose objects are tuples consisting of only ones, including the empty tuple.
Theorem 6.4.4 There is an isomorphism of monoidal supercategories
given on objects by
![]() $\bullet \mapsto 1$
and on morphisms by
$\bullet \mapsto 1$
and on morphisms by

Proof We first check that relations (6.2)–(6.6) are satisfied in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. Relation (6.2) holds by (3.2). The relations (6.3) and (6.4) hold by Theorem 2.3.3. The relations (6.5) and (6.6) hold by Lemma 3.4.2.
${\mathfrak {p}\text {-}\mathbf {Web}}$
. Relation (6.2) holds by (3.2). The relations (6.3) and (6.4) hold by Theorem 2.3.3. The relations (6.5) and (6.6) hold by Lemma 3.4.2.
The functor
![]() $F'$
restricts to an isomorphism on Hom spaces, as
$F'$
restricts to an isomorphism on Hom spaces, as
![]() $F'$
sends the basis morphisms described in [Reference Kujawa and Tharp20, Theorem 2.3.1] to the basis morphisms of Corollary 6.3.2.
$F'$
sends the basis morphisms described in [Reference Kujawa and Tharp20, Theorem 2.3.1] to the basis morphisms of Corollary 6.3.2.
6.5 The functor
 $G_{\uparrow \downarrow }: {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
$G_{\uparrow \downarrow }: {\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow } {\rightarrow } {{\mathfrak {p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}$
Theorem 6.5.1 There is a well-defined functor of monoidal supercategories
given on objects by
![]() $G_{\uparrow \downarrow }(\uparrow _a) = S^a(V_n)$
and
$G_{\uparrow \downarrow }(\uparrow _a) = S^a(V_n)$
and
![]() $G_{\uparrow \downarrow }(\downarrow _a)=S^a(V_n)^{*}$
. The functor is given on morphisms by
$G_{\uparrow \downarrow }(\downarrow _a)=S^a(V_n)^{*}$
. The functor is given on morphisms by

Proof Note that upward caps, upward cups, and upward antennas are sent to
![]() $\cup $
,
$\cup $
,
![]() $\cap $
, and
$\cap $
, and
![]() $\text {ant}$
, respectively, so the defining up-arrow relations of
$\text {ant}$
, respectively, so the defining up-arrow relations of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are preserved by
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
are preserved by
![]() $G_{\uparrow \downarrow }$
thanks to Theorem 6.1.1. We now check (4.1)–(4.3).
$G_{\uparrow \downarrow }$
thanks to Theorem 6.1.1. We now check (4.1)–(4.3).
Let
![]() $B_a$
be a homogeneous
$B_a$
be a homogeneous
![]() ${\mathbb {k}}$
-basis for
${\mathbb {k}}$
-basis for
![]() $S^a(V_n)$
, with dual basis
$S^a(V_n)$
, with dual basis
![]() $\{x^{*} \mid x \in B_a\}$
for
$\{x^{*} \mid x \in B_a\}$
for
![]() $S^a(V_n)^{*}$
. Then, for
$S^a(V_n)^{*}$
. Then, for
![]() $x,y \in B_a$
, we have
$x,y \in B_a$
, we have
So, for all
![]() $x \in B_a$
, we have
$x \in B_a$
, we have
and
proving (4.1).
By Lemma 6.2.1, we have

From this, it is immediate that for all
![]() $x \in B_a$
,
$x \in B_a$
,
![]() $y \in B_b$
, the image of the leftward crossing under
$y \in B_b$
, the image of the leftward crossing under
![]() $G_{\uparrow \downarrow }$
is
$G_{\uparrow \downarrow }$
is
![]() $\tau _{S^a(V_n)^{*}, S^b(V_n)}$
, and thus we have that relation (4.2) is preserved.
$\tau _{S^a(V_n)^{*}, S^b(V_n)}$
, and thus we have that relation (4.2) is preserved.
Finally, to check relation (4.3), we note that
 $$ \begin{align*} \text{eval}_a \circ \tau_{S^a(V_n)^{*}, S^a(V_n)} \circ \text{coeval}_{a}(1) &= \sum_{x \in B_a} \text{eval}_a \circ \tau_{S^a(V_n)^{*}, S^a(V_n)}(x \otimes x^{*} )\\ &= \sum_{x \in B_a} (-1)^{|x|} \text{eval}_a (x^{*} \otimes x) = \sum_{x \in B_a} (-1)^{|x|} = 0, \end{align*} $$
$$ \begin{align*} \text{eval}_a \circ \tau_{S^a(V_n)^{*}, S^a(V_n)} \circ \text{coeval}_{a}(1) &= \sum_{x \in B_a} \text{eval}_a \circ \tau_{S^a(V_n)^{*}, S^a(V_n)}(x \otimes x^{*} )\\ &= \sum_{x \in B_a} (-1)^{|x|} \text{eval}_a (x^{*} \otimes x) = \sum_{x \in B_a} (-1)^{|x|} = 0, \end{align*} $$
completing the proof.
6.6 Explosion and contraction
In this section,
![]() ${\mathbb {k}}$
can be an integral domain. For short, given
${\mathbb {k}}$
can be an integral domain. For short, given
![]() $k \geq 1 $
, we write
$k \geq 1 $
, we write
![]() $y_k \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(k,1^k)$
and
$y_k \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(k,1^k)$
and
![]() $z_k \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(1^k,k)$
for the morphisms defined by (3.11).
$z_k \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(1^k,k)$
for the morphisms defined by (3.11).
Lemma 6.6.1 For all
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
![]() $z_k \circ y_k = k! \cdot \text {id}_k$
.
$z_k \circ y_k = k! \cdot \text {id}_k$
.
Proof Follows from repeated application of (2.2).
Let
![]() $k \in {\mathbb {Z}}_{\geq 0}$
and
$k \in {\mathbb {Z}}_{\geq 0}$
and
![]() $\boldsymbol {a} = (a_1, \ldots , a_k) \in {\mathbb {Z}}_{\geq 0}^k$
. We identify
$\boldsymbol {a} = (a_1, \ldots , a_k) \in {\mathbb {Z}}_{\geq 0}^k$
. We identify
![]() $\boldsymbol {a}$
with the object
$\boldsymbol {a}$
with the object
![]() $(a_1, \dotsc , a_{k})$
of
$(a_1, \dotsc , a_{k})$
of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
. We will also use the following associated notation:
${\mathfrak {p}\text {-}\mathbf {Web}}$
. We will also use the following associated notation:
For any objects
![]() $\boldsymbol {a}, \boldsymbol {b}$
in
$\boldsymbol {a}, \boldsymbol {b}$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, we have linear maps:
${\mathfrak {p}\text {-}\mathbf {Web}}$
, we have linear maps:
and
We refer to these maps as explosion and contraction, respectively. See the proof of [Reference Rose and Tubbenhauer24, Theorem 1.10] for a picture showing them in use.
Lemma 6.6.2 For every
![]() $f \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a}, \boldsymbol {b})$
, we have
$f \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a}, \boldsymbol {b})$
, we have
![]() $\left(\mathrm{con}_{\boldsymbol {a},\boldsymbol {b}} \circ \mathrm{exp}_{\boldsymbol {a}, \boldsymbol {b}} \right) (f) = \boldsymbol {a}!\boldsymbol {b}! \, f$
.
$\left(\mathrm{con}_{\boldsymbol {a},\boldsymbol {b}} \circ \mathrm{exp}_{\boldsymbol {a}, \boldsymbol {b}} \right) (f) = \boldsymbol {a}!\boldsymbol {b}! \, f$
.
Proof Follows from Lemma 6.6.1.
It should be noted that the explosion and contraction morphisms only involve
![]() ${\mathfrak {gl}\text {-}\mathbf {Web}}$
morphisms and calculations. They first appear in [Reference Rose and Tubbenhauer24] and are now a standard tool in this area.
${\mathfrak {gl}\text {-}\mathbf {Web}}$
morphisms and calculations. They first appear in [Reference Rose and Tubbenhauer24] and are now a standard tool in this area.
6.7 Putting things together,
 ${\mathfrak {p}\text {-}\mathbf {Web}}$
edition
${\mathfrak {p}\text {-}\mathbf {Web}}$
edition
Let
![]() $r,s \in {\mathbb {Z}}_{\geq 0}$
,
$r,s \in {\mathbb {Z}}_{\geq 0}$
,
![]() $\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^r$
,
$\boldsymbol {a} \in {\mathbb {Z}}_{\geq 0}^r$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^s$
. By Theorem 6.1.1, we may define linear maps:
$\boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^s$
. By Theorem 6.1.1, we may define linear maps:
 $$ \begin{gather*} \widetilde{\mathrm{exp}}_{\boldsymbol{a},\boldsymbol{b}}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( V_{n}^{|\boldsymbol{a}|}, V_{n}^{|\boldsymbol{b}|}\right),\\ f \mapsto G\left( y_{\boldsymbol{b}}\right) \circ f \circ G\left(z_{\boldsymbol{a}}\right), \end{gather*} $$
$$ \begin{gather*} \widetilde{\mathrm{exp}}_{\boldsymbol{a},\boldsymbol{b}}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( V_{n}^{|\boldsymbol{a}|}, V_{n}^{|\boldsymbol{b}|}\right),\\ f \mapsto G\left( y_{\boldsymbol{b}}\right) \circ f \circ G\left(z_{\boldsymbol{a}}\right), \end{gather*} $$
and
 $$ \begin{gather*} \widetilde{\mathrm{con}}_{\boldsymbol{a}, \boldsymbol{b}}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(V_{n}^{|\boldsymbol{a}|}, V_{n}^{|\boldsymbol{b}|}\right) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right),\\ g \mapsto G\left(z_{\boldsymbol{b}}\right) \circ g \circ G\left(y_{\boldsymbol{a}}\right). \end{gather*} $$
$$ \begin{gather*} \widetilde{\mathrm{con}}_{\boldsymbol{a}, \boldsymbol{b}}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(V_{n}^{|\boldsymbol{a}|}, V_{n}^{|\boldsymbol{b}|}\right) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right),\\ g \mapsto G\left(z_{\boldsymbol{b}}\right) \circ g \circ G\left(y_{\boldsymbol{a}}\right). \end{gather*} $$
Lemma 6.7.1 For all objects
![]() $\boldsymbol {a}$
and
$\boldsymbol {a}$
and
![]() $\boldsymbol {b}$
in
$\boldsymbol {b}$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, the following diagram commutes:
${\mathfrak {p}\text {-}\mathbf {Web}}$
, the following diagram commutes:

Proof The top and bottom triangles and the middle rectangle commute by Lemma 6.6.2 and Theorem 6.1.1. The triangle on the right can be seen to commute by checking the definitions of
![]() $F, F', G$
on generating morphisms, together with (5.4).
$F, F', G$
on generating morphisms, together with (5.4).
Theorem 6.7.2 If
![]() $\boldsymbol {a},\boldsymbol {b}$
are such that
$\boldsymbol {a},\boldsymbol {b}$
are such that
![]() $|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
, then the map
$|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
, then the map
is injective. If
![]() ${\mathbb {k}}$
is a field of characteristic zero, then the functor G is full.
${\mathbb {k}}$
is a field of characteristic zero, then the functor G is full.
Proof The injectivity statement follows from Theorem 6.3.1 and Corollary 6.3.2.
Now, assume that
![]() ${\mathbb {k}}$
has characteristic zero and consider the diagram in Lemma 6.7.1. Since
${\mathbb {k}}$
has characteristic zero and consider the diagram in Lemma 6.7.1. Since
![]() $F'$
is an isomorphism by Theorem 6.4.4 and F is surjective by Theorem 6.4.3, the map G on the right is surjective. To see surjectivity of G along the left side, let
$F'$
is an isomorphism by Theorem 6.4.4 and F is surjective by Theorem 6.4.3, the map G on the right is surjective. To see surjectivity of G along the left side, let
![]() $\varphi \in {\mathrm { Hom}}_{{\mathfrak {p}}(n)}(S^{\boldsymbol {a}}(V_{n}), S^{\boldsymbol {b}}(V_{n}))$
. Then, by surjectivity of the G on the right, there exists
$\varphi \in {\mathrm { Hom}}_{{\mathfrak {p}}(n)}(S^{\boldsymbol {a}}(V_{n}), S^{\boldsymbol {b}}(V_{n}))$
. Then, by surjectivity of the G on the right, there exists
![]() $\theta \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_1^+}(1^{|\boldsymbol {a}|}, 1^{|\boldsymbol {b}|})$
such that
$\theta \in {\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_1^+}(1^{|\boldsymbol {a}|}, 1^{|\boldsymbol {b}|})$
such that
Then we compute
 $$ \begin{align*} G\left(\frac{\text{con}_{\boldsymbol{a},\boldsymbol{b}}(\theta)}{\boldsymbol{a}!\boldsymbol{b}!}\right) &= \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G(z_{\boldsymbol{b}} \circ \theta \circ y_{\boldsymbol{a}}) = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} Gz_{\boldsymbol{b}} \circ G\theta \circ Gy_{\boldsymbol{a}} = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} Gz_{\boldsymbol{b}} \circ Gy_{\boldsymbol{b}} \circ \varphi \circ Gz_{\boldsymbol{a}}. \circ Gy_{\boldsymbol{a}}\\[4pt] &=\frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G(z_{\boldsymbol{b}} \circ y_{\boldsymbol{b}}) \circ \varphi \circ G(z_{\boldsymbol{a}} \circ y_{\boldsymbol{a}}) = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G\left( \boldsymbol{b}! \cdot \text{id}_{\boldsymbol{b}}\right) \circ \varphi \circ G\left( \boldsymbol{a}!\cdot \text{id}_{\boldsymbol{a}}\right) = \varphi, \end{align*} $$
$$ \begin{align*} G\left(\frac{\text{con}_{\boldsymbol{a},\boldsymbol{b}}(\theta)}{\boldsymbol{a}!\boldsymbol{b}!}\right) &= \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G(z_{\boldsymbol{b}} \circ \theta \circ y_{\boldsymbol{a}}) = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} Gz_{\boldsymbol{b}} \circ G\theta \circ Gy_{\boldsymbol{a}} = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} Gz_{\boldsymbol{b}} \circ Gy_{\boldsymbol{b}} \circ \varphi \circ Gz_{\boldsymbol{a}}. \circ Gy_{\boldsymbol{a}}\\[4pt] &=\frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G(z_{\boldsymbol{b}} \circ y_{\boldsymbol{b}}) \circ \varphi \circ G(z_{\boldsymbol{a}} \circ y_{\boldsymbol{a}}) = \frac{1}{\boldsymbol{a}!\boldsymbol{b}!} G\left( \boldsymbol{b}! \cdot \text{id}_{\boldsymbol{b}}\right) \circ \varphi \circ G\left( \boldsymbol{a}!\cdot \text{id}_{\boldsymbol{a}}\right) = \varphi, \end{align*} $$
as desired. That is, G along the left side of the diagram is surjective, completing the proof.
Via the functor G, Theorem 6.7.2 shows that the basis for
![]() ${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
given in Corollary 6.3.2 could be considered a “stable basis,” or a “basis at infinity” for
${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a},\boldsymbol {b})$
given in Corollary 6.3.2 could be considered a “stable basis,” or a “basis at infinity” for
![]() ${\mathrm { Hom}}_{{\mathfrak {p}}(n)}\left(S^{\boldsymbol {a}}(V_{n}), S^{\boldsymbol {b}}(V_{n})\right)$
in characteristic zero, since G defines an isomorphism whenever
${\mathrm { Hom}}_{{\mathfrak {p}}(n)}\left(S^{\boldsymbol {a}}(V_{n}), S^{\boldsymbol {b}}(V_{n})\right)$
in characteristic zero, since G defines an isomorphism whenever
![]() $n \gg 0$
.
$n \gg 0$
.
Remark 6.7.3 The functor G need not be full over a field
![]() ${\mathbb {k}}$
of positive characteristic. For example, if
${\mathbb {k}}$
of positive characteristic. For example, if
![]() $\text {char}({\mathbb {k}}) = 3$
and v is a nonzero even vector in
$\text {char}({\mathbb {k}}) = 3$
and v is a nonzero even vector in
![]() $V_n$
, then there is a nonzero
$V_n$
, then there is a nonzero
![]() ${\mathfrak {p}}(n)$
-module homomorphism
${\mathfrak {p}}(n)$
-module homomorphism
![]() ${\mathbb {k}} {\rightarrow } S^3(V_n)$
given by
${\mathbb {k}} {\rightarrow } S^3(V_n)$
given by
![]() $1 \mapsto v^3$
, but the image of G in
$1 \mapsto v^3$
, but the image of G in
![]() ${\mathrm {Hom}}_{{\mathfrak {p}}(n)}({\mathbb {k}}, S^3(V_n))$
is zero.
${\mathrm {Hom}}_{{\mathfrak {p}}(n)}({\mathbb {k}}, S^3(V_n))$
is zero.
6.8 Putting things together,
 ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
edition
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
edition
Let
![]() $r,s \in {\mathbb {Z}}_{\geq 0}$
and
$r,s \in {\mathbb {Z}}_{\geq 0}$
and
![]() $\boldsymbol {a} \in {\mathbb {Z}}^r$
,
$\boldsymbol {a} \in {\mathbb {Z}}^r$
,
![]() $\boldsymbol {b} \in {\mathbb {Z}}^s$
. Given a nonnegative integer a, it will be convenient to adopt the notation
$\boldsymbol {b} \in {\mathbb {Z}}^s$
. Given a nonnegative integer a, it will be convenient to adopt the notation
![]() $S^{a}(V_{n}):= S^a(V_{n})$
,
$S^{a}(V_{n}):= S^a(V_{n})$
,
![]() $S^{-a}(V_{n}):= S^a(V_{n})^{*}$
, and, more generally,
$S^{-a}(V_{n}):= S^a(V_{n})^{*}$
, and, more generally,
Let
![]() $\boldsymbol {c}, \boldsymbol {d}, \varphi _1, \varphi _2$
be as in Lemma 4.4.1. By Theorem 6.5.1, we have an invertible linear map:
$\boldsymbol {c}, \boldsymbol {d}, \varphi _1, \varphi _2$
be as in Lemma 4.4.1. By Theorem 6.5.1, we have an invertible linear map:
 $$ \begin{gather*} \tilde{\Phi}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right) \xrightarrow{\sim} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(S^{\boldsymbol{c}}(V_{n}), S^{\boldsymbol{d}}(V_{n})\right)\\[4pt] f \mapsto G_{\uparrow \downarrow}\left(\varphi_2 \right)\circ f \circ G_{\uparrow \downarrow}\left(\varphi_1 \right). \end{gather*} $$
$$ \begin{gather*} \tilde{\Phi}:{\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left( S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})\right) \xrightarrow{\sim} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}\left(S^{\boldsymbol{c}}(V_{n}), S^{\boldsymbol{d}}(V_{n})\right)\\[4pt] f \mapsto G_{\uparrow \downarrow}\left(\varphi_2 \right)\circ f \circ G_{\uparrow \downarrow}\left(\varphi_1 \right). \end{gather*} $$
Lemma 6.8.1 For any
![]() $\boldsymbol {a} \in {\mathbb {Z}}^{r}$
and
$\boldsymbol {a} \in {\mathbb {Z}}^{r}$
and
![]() $\boldsymbol {b} \in {\mathbb {Z}}^{s}$
, let
$\boldsymbol {b} \in {\mathbb {Z}}^{s}$
, let
![]() $\boldsymbol {c}$
and
$\boldsymbol {c}$
and
![]() $\boldsymbol {d}$
be as above. Then the following diagram commutes:
$\boldsymbol {d}$
be as above. Then the following diagram commutes:

Proof The left rectangle commutes by Theorem 6.5.1. The triangle on the right can be seen to commute by checking the definitions of
![]() $\iota _\uparrow , G, G_{\uparrow \downarrow }$
on generating morphisms.
$\iota _\uparrow , G, G_{\uparrow \downarrow }$
on generating morphisms.
Theorem 6.8.2 If
![]() $\boldsymbol {a} \in {\mathbb {Z}}^{r}$
and
$\boldsymbol {a} \in {\mathbb {Z}}^{r}$
and
![]() $\boldsymbol {b} \in {\mathbb {Z}}^{s}$
are such that
$\boldsymbol {b} \in {\mathbb {Z}}^{s}$
are such that
![]() $|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
, then the map
$|\boldsymbol {a}| + |\boldsymbol {b}| \leq 2n$
, then the map
is injective. If
![]() ${\mathbb {k}}$
is a field of characteristic zero, then the functor
${\mathbb {k}}$
is a field of characteristic zero, then the functor
![]() $G_{\uparrow \downarrow }$
is full.
$G_{\uparrow \downarrow }$
is full.
Proof Consider the diagram in Lemma 6.8.1, with
![]() $\boldsymbol {c}, \boldsymbol {d}$
as in Lemma 4.4.1. We have
$\boldsymbol {c}, \boldsymbol {d}$
as in Lemma 4.4.1. We have
![]() $|\boldsymbol {c}| + |\boldsymbol {d}| \leq 2n$
, so the map G is injective by Theorem 6.7.2. Therefore, the map
$|\boldsymbol {c}| + |\boldsymbol {d}| \leq 2n$
, so the map G is injective by Theorem 6.7.2. Therefore, the map
![]() $\iota _\uparrow $
is injective, and is surjective by Theorem 4.5.2, so the map
$\iota _\uparrow $
is injective, and is surjective by Theorem 4.5.2, so the map
![]() $G_{\uparrow \downarrow }$
on the right must be injective. As
$G_{\uparrow \downarrow }$
on the right must be injective. As
![]() $\Phi $
and
$\Phi $
and
![]() $\tilde {\Phi }$
are isomorphisms, we have that the map
$\tilde {\Phi }$
are isomorphisms, we have that the map
![]() $G_{\uparrow \downarrow }$
is injective as well.
$G_{\uparrow \downarrow }$
is injective as well.
Moreover, if
![]() ${\mathbb {k}}$
is a field of characteristic zero, then by Theorem 6.7.2, the map G is surjective, which, in turn, forces all maps in the diagram to be surjective and so
${\mathbb {k}}$
is a field of characteristic zero, then by Theorem 6.7.2, the map G is surjective, which, in turn, forces all maps in the diagram to be surjective and so
![]() $G_{\uparrow \downarrow }$
is full, as claimed.
$G_{\uparrow \downarrow }$
is full, as claimed.
Theorem 6.8.3 The functor
is an isomorphism of categories.
Proof The functor is bijective on objects, and full by Theorem 4.5.2. For any fixed pair of objects
![]() $\boldsymbol {c}$
and
$\boldsymbol {c}$
and
![]() $\boldsymbol {d}$
in
$\boldsymbol {d}$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, we may choose n such that
${\mathfrak {p}\text {-}\mathbf {Web}}$
, we may choose n such that
![]() $2n\geq |\boldsymbol {c}| +|\boldsymbol {d}|$
and consider the diagram in Lemma 6.8.1. Then the map G is injective by Theorem 6.7.2, forcing
$2n\geq |\boldsymbol {c}| +|\boldsymbol {d}|$
and consider the diagram in Lemma 6.8.1. Then the map G is injective by Theorem 6.7.2, forcing
as required.
Conjecture 6.8.4 It is interesting to consider the precise conditions which imply the injectivity and fullness statements of Theorems 6.7.2 and 6.8.2. We conjecture that the fullness statement holds whenever
![]() ${\mathbb {k}}$
is a field with characteristic greater than
${\mathbb {k}}$
is a field with characteristic greater than
![]() $|\boldsymbol {a}| + |\boldsymbol {b}|$
.
$|\boldsymbol {a}| + |\boldsymbol {b}|$
.
6.9 A particular spanning set
In the follow-up paper [Reference Davidson, Kujawa and Muth13], it will be useful to work with a particular spanning set for
![]() ${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
. As the relevant diagrammatics are already defined herein, we request the reader’s indulgence in including the necessary result here. In light of the results of Section 6.4, readers familiar with explosion/contraction arguments will note that the spanning set is a contraction of the Brauer diagram basis for
${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
. As the relevant diagrammatics are already defined herein, we request the reader’s indulgence in including the necessary result here. In light of the results of Section 6.4, readers familiar with explosion/contraction arguments will note that the spanning set is a contraction of the Brauer diagram basis for
![]() ${\mathrm {Hom}}_{\mathcal{B}}\left(\emptyset , |\boldsymbol {a}| + |\boldsymbol {b}| \right)$
given in [Reference Kujawa and Tharp20].
${\mathrm {Hom}}_{\mathcal{B}}\left(\emptyset , |\boldsymbol {a}| + |\boldsymbol {b}| \right)$
given in [Reference Kujawa and Tharp20].
Lemma 6.9.1 Assume that
![]() ${\mathbb {k}}$
is a field of characteristic zero, and
${\mathbb {k}}$
is a field of characteristic zero, and
![]() $\boldsymbol {a}, \boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^{m}$
. Then
$\boldsymbol {a}, \boldsymbol {b} \in {\mathbb {Z}}_{\geq 0}^{m}$
. Then
![]() ${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
is spanned by diagrams of the form
${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
is spanned by diagrams of the form

where all strands except those at the very top of the diagram are thin, the diagram has
![]() $0 \leq j \leq |\boldsymbol {a}|/2$
upward-oriented cups,
$0 \leq j \leq |\boldsymbol {a}|/2$
upward-oriented cups,
![]() $|\boldsymbol {b}|/2 - |\boldsymbol {a}|/2 + j$
downward-oriented cups,
$|\boldsymbol {b}|/2 - |\boldsymbol {a}|/2 + j$
downward-oriented cups,
![]() $|\boldsymbol {a}| - 2j$
leftward-oriented cups,
$|\boldsymbol {a}| - 2j$
leftward-oriented cups,
![]() $\sigma $
consists only of upward-oriented crossings, and
$\sigma $
consists only of upward-oriented crossings, and
![]() $\tau $
consists only of downward-oriented crossings.
$\tau $
consists only of downward-oriented crossings.
Proof Let
![]() $\boldsymbol {b}' = (b_m, \ldots , b_1)$
. We first consider
$\boldsymbol {b}' = (b_m, \ldots , b_1)$
. We first consider
![]() ${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\uparrow ^{\boldsymbol {b}' }, \uparrow ^{\boldsymbol {a}} \right)$
. It follows from Theorem 6.4.4 and Lemma 6.7.1 that this morphism space is spanned by diagrams of the form
${\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\uparrow ^{\boldsymbol {b}' }, \uparrow ^{\boldsymbol {a}} \right)$
. It follows from Theorem 6.4.4 and Lemma 6.7.1 that this morphism space is spanned by diagrams of the form

where D is a marked Brauer diagram as defined in [Reference Kujawa and Tharp20, Section 2.2]. Using the relations discussed in loc. cit., one can replace D with
![]() $\sigma \circ E \circ \tau '$
, where
$\sigma \circ E \circ \tau '$
, where
![]() $\sigma $
and
$\sigma $
and
![]() $\tau '$
consist of only upward-oriented crossings, and where E is a diagram of the form
$\tau '$
consist of only upward-oriented crossings, and where E is a diagram of the form

By Lemma 4.4.1, there is an isomorphism of superspaces
given by

Applying this map to the elements of our spanning set and using the relations in Theorem 4.3.1 to pull
![]() $\tau '$
and the upward-oriented caps to the right side of the diagram, it follows that
$\tau '$
and the upward-oriented caps to the right side of the diagram, it follows that
![]() ${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
is spanned by diagrams of the form (6.7).
${\mathrm { Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }}\left(\emptyset , \uparrow ^{\boldsymbol {a}}\downarrow ^{\boldsymbol {b}} \right)$
is spanned by diagrams of the form (6.7).
7 Category equivalences
7.1 Faithfulness
Throughout this section,
![]() ${\mathbb {k}}$
is an algebraically closed field of characteristic zero. The assumption that
${\mathbb {k}}$
is an algebraically closed field of characteristic zero. The assumption that
![]() ${\mathbb {k}}$
is algebraically closed allows us to cite the results from [Reference Coulembier10] used below. We expect that it is not necessary. We also remark that Coulembier describes how to construct the morphism
${\mathbb {k}}$
is algebraically closed allows us to cite the results from [Reference Coulembier10] used below. We expect that it is not necessary. We also remark that Coulembier describes how to construct the morphism
![]() $f_{n+1}$
. It would be interesting to describe it explicitly in terms of diagrams.
$f_{n+1}$
. It would be interesting to describe it explicitly in terms of diagrams.
Let
![]() $\mathcal{I}_{n}$
denote the kernel of the functor
$\mathcal{I}_{n}$
denote the kernel of the functor
That is,
![]() $\mathcal{I}_{n}$
is the tensor ideal given by
$\mathcal{I}_{n}$
is the tensor ideal given by
for all objects
![]() $[a]$
and
$[a]$
and
![]() $[b]$
in
$[b]$
in
![]() $\mathcal{B}$
. The following is a reformulation of [Reference Coulembier10, Theorem 8.3.1] so that it applies to the category
$\mathcal{B}$
. The following is a reformulation of [Reference Coulembier10, Theorem 8.3.1] so that it applies to the category
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Theorem 7.1.1 Let
![]() $n \geq 1$
and set
$n \geq 1$
and set
![]() $\ell = (n+1)(n+2)/2$
. Then,
$\ell = (n+1)(n+2)/2$
. Then,
![]() $\mathcal{I}_{n}$
is generated as a tensor ideal by a single morphism which lies in
$\mathcal{I}_{n}$
is generated as a tensor ideal by a single morphism which lies in
![]() $\operatorname {End}_{\mathcal{B}}\left( [\ell ]\right)$
.
$\operatorname {End}_{\mathcal{B}}\left( [\ell ]\right)$
.
Proof By [Reference Coulembier10, Theorem 8.3.1], there is a morphism
![]() $f_{n+1} \in \operatorname {End}_{\mathcal{B}}\left( [\ell ] \right)$
which is in the kernel of the functor F. Since F is a functor of
$f_{n+1} \in \operatorname {End}_{\mathcal{B}}\left( [\ell ] \right)$
which is in the kernel of the functor F. Since F is a functor of
![]() ${\mathbb {k}}$
-linear monoidal categories, the tensor ideal generated by
${\mathbb {k}}$
-linear monoidal categories, the tensor ideal generated by
![]() $f_{n+1}$
is also contained in the kernel of F.
$f_{n+1}$
is also contained in the kernel of F.
On the other hand, let
![]() $g \in {\mathrm {Hom}}_{\mathcal{B}}\left( [a], [b] \right)$
be a nonzero element in the kernel of F. By pre- and post-composing with cup and cap diagrams much as in Section 4.4, one can define an isomorphism of superspaces
$g \in {\mathrm {Hom}}_{\mathcal{B}}\left( [a], [b] \right)$
be a nonzero element in the kernel of F. By pre- and post-composing with cup and cap diagrams much as in Section 4.4, one can define an isomorphism of superspaces
where
![]() $r=(a+b)/2$
. Let
$r=(a+b)/2$
. Let
![]() $g' \in {\mathrm {Hom}}_{\mathcal{B}}\left( \left[r \right], \left[r \right] \right)$
be the image of g under this isomorphism. Since F is a monoidal functor,
$g' \in {\mathrm {Hom}}_{\mathcal{B}}\left( \left[r \right], \left[r \right] \right)$
be the image of g under this isomorphism. Since F is a monoidal functor,
![]() $g'$
is in the kernel of the map
$g'$
is in the kernel of the map
![]() $F:\operatorname {End}_{\mathcal{B}}\left( \left[r \right] \right) {\rightarrow } {\mathrm {Hom}}_{{\mathfrak {p}} (n)}\left(V^{\otimes r} \right)$
. By [Reference Coulembier10, Theorem 8.3.1],
$F:\operatorname {End}_{\mathcal{B}}\left( \left[r \right] \right) {\rightarrow } {\mathrm {Hom}}_{{\mathfrak {p}} (n)}\left(V^{\otimes r} \right)$
. By [Reference Coulembier10, Theorem 8.3.1],
![]() $r \geq \ell $
and the kernel of this superalgebra homomorphism is generated as an ideal by
$r \geq \ell $
and the kernel of this superalgebra homomorphism is generated as an ideal by
![]() $f_{n+1} \otimes \operatorname {Id}_{\bullet }^{\otimes \left(r-\ell \right)}$
. Thus,
$f_{n+1} \otimes \operatorname {Id}_{\bullet }^{\otimes \left(r-\ell \right)}$
. Thus,
![]() $g' = \sum _{i} a_{i}\left(f_{n+1} \otimes \operatorname {Id}_{\bullet }^{\otimes \left(r-\ell \right)} \right)b_{i}$
for some
$g' = \sum _{i} a_{i}\left(f_{n+1} \otimes \operatorname {Id}_{\bullet }^{\otimes \left(r-\ell \right)} \right)b_{i}$
for some
![]() $a_{i},b_{i} \in \operatorname {End}_{\mathcal{B}}\left( \left[r \right] \right)$
. Applying the inverse of (7.1) to this expression shows that g lies in the tensor ideal generated by
$a_{i},b_{i} \in \operatorname {End}_{\mathcal{B}}\left( \left[r \right] \right)$
. Applying the inverse of (7.1) to this expression shows that g lies in the tensor ideal generated by
![]() $f_{n+1}$
, proving the claim.
$f_{n+1}$
, proving the claim.
We abuse notation and write
![]() $f_{n+1}$
for the morphism
$f_{n+1}$
for the morphism
![]() $F'(f_{n+1})$
and
$F'(f_{n+1})$
and
![]() $\iota _{\uparrow }(F'(f_{n+1}))$
in
$\iota _{\uparrow }(F'(f_{n+1}))$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, respectively.
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, respectively.
Theorem 7.1.2 For any
![]() $n \geq 1$
, the tensor ideal generated by the morphism
$n \geq 1$
, the tensor ideal generated by the morphism
![]() $f_{n+1}$
in
$f_{n+1}$
in
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and
${\mathfrak {p}\text {-}\mathbf {Web}}$
and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is the kernel of the functors G and
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
is the kernel of the functors G and
![]() $G_{\uparrow \downarrow }$
, respectively.
$G_{\uparrow \downarrow }$
, respectively.
Proof This follow directly from the previous result and standard explosion/contraction arguments. To explain, consider
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and the commutative diagram from Lemma 6.7.1. A simple diagram chase along with the fact that
${\mathfrak {p}\text {-}\mathbf {Web}}$
and the commutative diagram from Lemma 6.7.1. A simple diagram chase along with the fact that
![]() $F'$
is an isomorphism and
$F'$
is an isomorphism and
![]() $f_{n+1}$
is in the kernel of F shows this morphism and, hence, the tensor ideal it generates, lies in the kernel of G.
$f_{n+1}$
is in the kernel of F shows this morphism and, hence, the tensor ideal it generates, lies in the kernel of G.
On the other hand, let
![]() $\boldsymbol {a}$
and
$\boldsymbol {a}$
and
![]() $\boldsymbol {b}$
be objects of
$\boldsymbol {b}$
be objects of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
and let
${\mathfrak {p}\text {-}\mathbf {Web}}$
and let
![]() $f \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a} ,\boldsymbol {b})$
satisfy
$f \in {\mathrm {Hom}}_{{\mathfrak {p}\text {-}\mathbf {Web}}}(\boldsymbol {a} ,\boldsymbol {b})$
satisfy
![]() $G(f)=0$
. Then
$G(f)=0$
. Then
![]() $G(\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b}}(f))=0$
. Since
$G(\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b}}(f))=0$
. Since
![]() $F'$
is an isomorphism, there is a
$F'$
is an isomorphism, there is a
![]() $g \in {\mathrm {Hom}}_{\mathcal{B}}([|\boldsymbol {a} |], [|\boldsymbol {b} |])$
such that
$g \in {\mathrm {Hom}}_{\mathcal{B}}([|\boldsymbol {a} |], [|\boldsymbol {b} |])$
such that
![]() $F'(g) = \mathrm{exp}_{\boldsymbol {a} ,\boldsymbol {b}}(f)$
. By the commutativity of the right-hand triangle,
$F'(g) = \mathrm{exp}_{\boldsymbol {a} ,\boldsymbol {b}}(f)$
. By the commutativity of the right-hand triangle,
![]() $F(g)=0$
and hence, by Theorem 7.1.1, g lies in the tensor ideal of
$F(g)=0$
and hence, by Theorem 7.1.1, g lies in the tensor ideal of
![]() $\mathcal{B}$
generated by
$\mathcal{B}$
generated by
![]() $f_{n+1}$
. Applying the isomorphism
$f_{n+1}$
. Applying the isomorphism
![]() $F'$
, this implies that
$F'$
, this implies that
![]() $\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b} }(f)$
lies in the tensor ideal of
$\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b} }(f)$
lies in the tensor ideal of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
generated by
${\mathfrak {p}\text {-}\mathbf {Web}}$
generated by
![]() $f_{n+1}$
. Since the map
$f_{n+1}$
. Since the map
![]() $\mathrm{con}_{\textsf {a,b}}$
is given by pre- and post-composing with morphisms, tensor ideals are preserved. Therefore,
$\mathrm{con}_{\textsf {a,b}}$
is given by pre- and post-composing with morphisms, tensor ideals are preserved. Therefore,
![]() $\mathrm{con}_{\boldsymbol {a} , \boldsymbol {b} }(\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b} }(f)) = \boldsymbol {a} !\boldsymbol {b} !f$
lies in the tensor ideal of
$\mathrm{con}_{\boldsymbol {a} , \boldsymbol {b} }(\mathrm{exp}_{\boldsymbol {a} , \boldsymbol {b} }(f)) = \boldsymbol {a} !\boldsymbol {b} !f$
lies in the tensor ideal of
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
generated by
${\mathfrak {p}\text {-}\mathbf {Web}}$
generated by
![]() $f_{n+1}$
. Hence, so does f. This proves the claim regarding the functor G.
$f_{n+1}$
. Hence, so does f. This proves the claim regarding the functor G.
Diagram chase arguments using the commutative diagram in Lemma 6.8.1 along with the fact that relevant the maps are given by pre- and post- composing with morphisms (and, hence, preserve tensor ideals) proves the statement for
![]() $G_{\uparrow \downarrow }$
.
$G_{\uparrow \downarrow }$
.
We end this section by pointing out that under the assumptions of the present section, the injectivity statements of Theorems 6.7.2 and 6.8.2 can be made sharp.
Proposition 7.1.3 Let
![]() $n \geq 1$
and set
$n \geq 1$
and set
![]() $\ell = (n+1)(n+2)/2$
. Then, the maps
$\ell = (n+1)(n+2)/2$
. Then, the maps
 $$ \begin{align*} G &:{\mathrm{Hom}}_{{\mathfrak{p}\text{-}\mathbf{Web}}}(\boldsymbol{a},\boldsymbol{b}) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})),\\ G_{\uparrow \downarrow} &:{\mathrm{Hom}}_{{\mathfrak{p}\text{-}\mathbf{Web}}_{\uparrow \downarrow}}(|_{\boldsymbol{a}},|_{\boldsymbol{b}}) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})) \end{align*} $$
$$ \begin{align*} G &:{\mathrm{Hom}}_{{\mathfrak{p}\text{-}\mathbf{Web}}}(\boldsymbol{a},\boldsymbol{b}) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})),\\ G_{\uparrow \downarrow} &:{\mathrm{Hom}}_{{\mathfrak{p}\text{-}\mathbf{Web}}_{\uparrow \downarrow}}(|_{\boldsymbol{a}},|_{\boldsymbol{b}}) {\rightarrow} {\mathrm{Hom}}_{{\mathfrak{p}}(n)}(S^{\boldsymbol{a}}(V_{n}), S^{\boldsymbol{b}}(V_{n})) \end{align*} $$
are injective if and only if
![]() $ |\boldsymbol {a} | + |\boldsymbol {b} | < (n+1)(n+2)$
.
$ |\boldsymbol {a} | + |\boldsymbol {b} | < (n+1)(n+2)$
.
Proof Doing a diagram chase using Lemmas 6.7.1 and 6.8.1, one can show that the injectivity of these maps is equivalent to the injectivity of the map
where
![]() $r = \left(|\boldsymbol {a} | + |\boldsymbol {b} | \right)/2$
. However, by [Reference Coulembier10, Theorem 8.3.1], this map is injective if and only if
$r = \left(|\boldsymbol {a} | + |\boldsymbol {b} | \right)/2$
. However, by [Reference Coulembier10, Theorem 8.3.1], this map is injective if and only if
![]() $r < \ell $
. This proves the claim.
$r < \ell $
. This proves the claim.
7.2 Category equivalences
Let
be the quotient of
![]() $\mathcal{B}$
,
$\mathcal{B}$
,
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}$
, and
${\mathfrak {p}\text {-}\mathbf {Web}}$
, and
![]() ${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, respectively, by the tensor ideal generated by
${\mathfrak {p}\text {-}\mathbf {Web}}_{\uparrow \downarrow }$
, respectively, by the tensor ideal generated by
![]() $f_{n+1}$
, where
$f_{n+1}$
, where
![]() $f_{n+1}$
is the morphism given in Section 7.1.
$f_{n+1}$
is the morphism given in Section 7.1.
As
![]() $f_{n+1}$
is in the kernel of the functors F, G, and
$f_{n+1}$
is in the kernel of the functors F, G, and
![]() $G_{\uparrow \downarrow }$
, they induce well-defined functors which we call by the same name:
$G_{\uparrow \downarrow }$
, they induce well-defined functors which we call by the same name:
 $$ \begin{align} \begin{aligned} F &: \mathcal{B}(n) {\rightarrow} {\mathfrak{p}}(n)\text{-}\mathrm{Mod}_{V}, \\ G&: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}} {\rightarrow} {{\mathfrak{p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow \downarrow} &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{\uparrow \downarrow} {\rightarrow} {{\mathfrak{p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} F &: \mathcal{B}(n) {\rightarrow} {\mathfrak{p}}(n)\text{-}\mathrm{Mod}_{V}, \\ G&: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}} {\rightarrow} {{\mathfrak{p}}(n)\text{-}\mathrm{mod}_{\mathcal{S}}}, \\ G_{\uparrow \downarrow} &: {{\mathfrak{p}} (n)\text{-}\mathbf{Web}}_{\uparrow \downarrow} {\rightarrow} {{\mathfrak{p}}(n)\text{-}\mathrm{mod}_{\mathcal{S, S^{*}}}}. \end{aligned} \end{align} $$
Theorem 7.2.1 The functors given in (7.2) are equivalences of monoidal supercategories.
Proof Taken collectively, the previous theorems show that the functors F, G, and
![]() $G_{\uparrow \downarrow }$
are essentially surjective, full, and faithful, proving the claim.
$G_{\uparrow \downarrow }$
are essentially surjective, full, and faithful, proving the claim.
Acknowledgment
The authors thank the anonymous referee for their detailed and helpful comments.