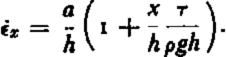Introduction
In a recent paper NyeReference Nye 1 has calculated the equilibrium profile of an ice sheet under the assumption that almost all of the relative motion of ice is concentrated at, or very near to, the bottom of the ice mass. This calculation represents a considerable improvement over his older analysisReference Nye 2 , Reference Nye 3 based on a theory of perfect plasticity. The new equation which he has obtained for the surface profile of a two-dimensional ice sheet lying on a horizontal bed is
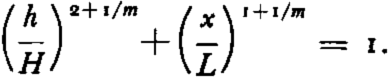
Here h is the height of the upper surface at a distance x from the center, H is the height at the center, and L is the distance from the center of the ice sheet to its edge. The constant m in this equation has a value between 2 and 2.5. (Equation (1) applies in particular to the case where the accumulation of ice and snow is a constant over the ice sheet. If the accumulation rate is not constant with x, a slightly different equation would be obtained.) Besides being based on a better plastic flow relationship, Nye’s present theory predicts the the slope of the upper surface at the center of an ice sheet is zero, whereas the previous theory (which can be obtained when m is set equal to infinity) led to a finite slope.
This paper presents a refinement on Nye’s calculation of the profile of the upper surface, with special reference to the central region of an ice cap, where equation (1) is not free from objection even through it does predict the correct slope at x = 0. Nye assumed in his analysis that the longitudinal stresses are relatively unimportant and that the shear stress parallel to the bed of an ice cap is the dominant stress. This shear stress τ is determined by ice thickness and slope of the upper surface, and is given to a very good approximation by
where ρ is the average density of the ice and g is the gravitational acceleration. Near the center of an ice cap, the slope approaches zero and hence the shear stress at bedrock also must approach zero. One would anticipate, therefore, that the longitudinal stresses are important in this region. Our refinement of the surface profile problem attempts to bring the longitudinal stresses into the analysis. The correction obtained to the profile found by Nye is important only near the center of an ice cap.
Another difficulty in the treatment of the flow of ice in the central region of an ice cap cannot be handled by a simplified analysis. The same type of difficulty has caused the breakdown of all theories in the vicinity of the edge of a glacier or ice sheet. Up to now, it has been assumed in all theories that the stresses and rate of flow are slowly varying functions of the distance x. Since the stresses depend on the thickness of the ice and on the surface slope, this implies that the change in h, and also in dh/dx, must be small over a distance in the x direction of the order of the thickness of the ice. The condition that h be a slowly varying function of distance means that
and the condition that the slope also be a slowly varying function of distance implies that
It is well known that solutions of the profile such as that given by equation (1) lead to an infinite slope at the edge of the ice mass, and thus violate inequality (3). Hence, the edge region must be excluded from consideration. Similarly, equations of type (1) are not applicable in the central region since inequality (4) no longer is valid. The region from the center to a distance of the thickness of the ice must be excluded from the analysis. This is true of both Nye’s analysis and also the refinement of it that we consider here. It would appear that the flow of ice at the very edge and very center of an ice cap can be solved only with an exact and rather difficult treatment of the problem. It is fortunate that these regions are so small, and that approximate analyses satisfactorily deal with the major part of the ice in glaciers and ice sheets.
The principal new feature in the modification of Nye’s theory developed in the following section is the introduction of a more general law for the sliding of ice over the bedrock surface at the bottom of an ice cap or glacier. With this more general sliding law, longitudinal stresses and creep rates can be taken into account without an undue complication in Nye’s analysis. It is found that for large ice sheets no modification really is needed for Nye’s equation for the profile. For small ice caps, a correction over an appreciable fraction of the ice is required.
Throughout this paper it is assumed that the creep properties of ice are isotropic and that the conditions, such as roughness at the bottom of an ice mass, are the same everywhere.
Theory
Effective sliding velocity. In his analysis, Nye considered that most of the differential motion occurred at, or near to, the bottom ice surface. This differential motion gives the overlying ice some average velocity u (an “effective” sliding velocity). On the basis of theoretical expressions for both the differential motion within the bulk of the ice mass and the velocity of sliding of a glacier over the bedrock,Reference Nye 1 , Reference Weertman 4 it is reasonable to use, as Nye does, the equation
where τ is the shear stress at the bottom, B is a constant, and m has a value between 2 and 2.5. Using equation (2) to determine τ, the profile of the ice mass can be calculated from

where a is the rate of accumulation of snow or ice (measured in equivalent of high-density ice) at the distance x from the center of a two-dimensional glacier or ice cap. When a is a constant, Nye’s equation (1) is obtained.
Nye’s treatment has the great advantage that the variation of ice velocity with vertical distance y has been eliminated from the analysis without any great loss in accuracy, since Nye’s arguments indicate that most of the variation of velocity with vertical distance occurs in a narrow region near the bottom of the ice, and can therefore be ignored. The average velocity u depends only on h and dh/dx, and an equation can be obtained relating h with the distance x.
It is possible to introduce longitudinal stress and still retain the advantages of Nye’s theory by modifying equation (5). That this equation must be modified when other stresses are present is to be expected. Suppose there exists an effective longitudinal stressFootnote * σ in addition to the shear stress τ. By Nye’s generalizationReference Nye 5 of the creep equation in uniaxial stress to that in multiaxial stress, the shear creep rate dϵ/dt is no longer given by the equation
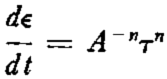
(where A is a temperature-dependent but stress-independent term, and n is a constant whose value is about 3 to 4), but is generalized to
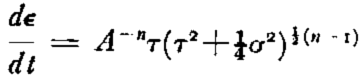
The creep in shear therefore is influenced by the longitudinal stress, very strongly if this stress is large. The effective sliding velocity given by equation (5) is a combination of the actual sliding of ice over bedrock and differential motion within the ice mass. Both of these mechanismsReference Nye 1 , Reference Weertman 4 involve the creep of ice and lead to an equation of the type given by equation (5) when the longitudinal stress is small or zero. If the longitudinal stress σ is not negligible, one might expect from equation (8) that the effective sliding equation (5) will be modified to
(Hereafter σ b is the value of σ at the bottom surface, and τ is the shear stress only at the very bottom of an ice mass.) From the theory of sliding that we have proposed,Reference Nye 2 one would expect such an equation, since the longitudinal stress will speed up the creep flow of ice around irregularities in the bedrock. An equation of the form of equation (9) should also give an estimate of the contribution of a longitudinal stress to the “effective sliding” of the differential motion within the ice mass.
In the following, equation (9) is used to determine the average velocity of ice through any cross-section of a two-dimensional glacier or ice cap. It is, admittedly, not the exact equation for this velocity, but it contains the features to be expected when the longitudinal stress is introduced. The average effective sliding velocity is increased when σ b , the value of σ at the bottom of the ice mass, is increased, and the equation reduces to equation (5), the previously known relation, as σ b approaches zero. Equation (9) does not necessarily require exact solution of the differential motion of ice in both the x and y directions, as would be required by the introduction of a longitudinal stress if equation (5) were used as the boundary condition for the bottom ice surface. However, equation (5) is not expected to give the correct estimate for the velocity of sliding when a longitudinal stress is present (i.e. the longitudinal stress, itself, will change the boundary condition at the bottom surface) and so would have to be abandoned in any event.
Estimate of stresses. Equation (9) requires an estimate of the shear and longitudinal stresses in a glacier. The shear stress σ xy is given by
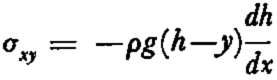
where y = 0 is taken to be at bedrock. Hence, the shear stress τ = σ xy , (y = 0) at the bottom surface is
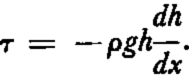
Nye found that the longitudinal creep rate,
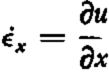
The value of σ at y = 0 can be found by substituting equation (10b) into equation (11a). The longitudinal strain rate can be obtained from equation (6) and is
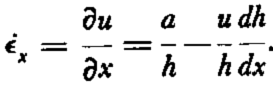
We will be concerned primarily with the case where a/h is the predominant term on the right side of the equation and the other term can be discarded,Footnote * thus
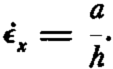
At the bottom surface the approximate equations are:
when σ b is larger than τ,
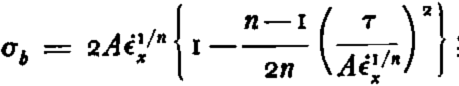
when τ is larger than σ b ,
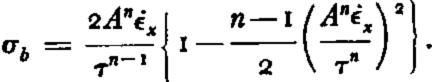
An expression can be obtained for the differential motion of ice by making use of the stresses given by equations (10a) and (11a). The shear creep rate
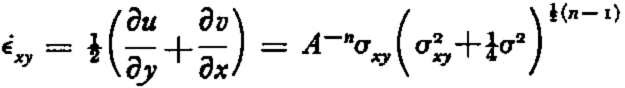
where v is the velocity in the y direction. NyeReference Nye 6 has shown that v does not depend on x, and hence its derivative with respect to x is zero. If the ∂u/∂x is dropped out of equation (13),
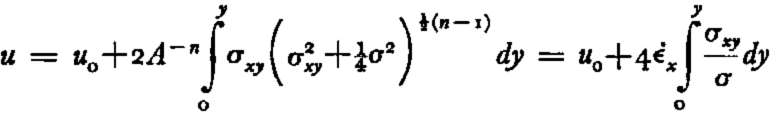
where u 0 is the actual velocity of sliding over bedrock at y = 0. The major contribution to the integral in this last equation comes near the bottom surface, since σ xy has its largest and σ its smallest value there. Because of this behavior the differential motion within the ice again can be considered to occur mainly near the bedrock and as making a contribution to the “effective sliding velocity.”Footnote *
Although it is laborious to work out an exact solution for the integral given in equation (14), it is simple to set limits to its value. With the use of equation (10a) one easily obtains
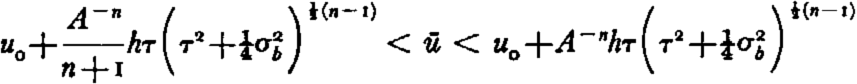
where ū is the average velocity,
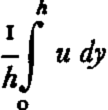
Surface profile calculations. Nye used equation (6) to determine the surface profile. We shall consider how to find the profile for the case of a constant accumulation rate a. The two stresses τ and σ b can be obtained from equations (10b), (11a), and (11c). Substituting these into equation (9) gives the average velocity u of the ice, which is needed in equation (6). As the resultant equation is very clumsy, it is difficult to find a solution for the ice thickness h as a function of the distance x. We can obtain more manageable equations by considering the two limiting regions of the stresses τ and σ b . Near the center of an ice cap, σ b is much larger than τ; away from the center, τ is larger than σ b . We can solve equation (6) for either of the two cases, and then obtain a more general solution by combining these special solutions.
When σ b is much larger than τ, equations (6) and (9), with the help of equation (12a), reduce to
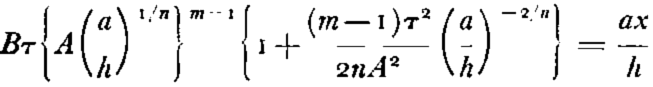
which can be reduced further to
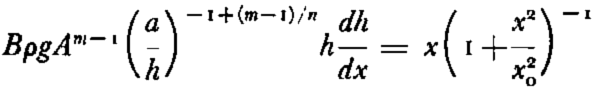
where
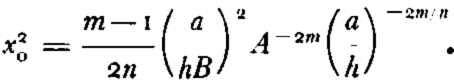
Since this equation will be applied only in the center of an ice cap where the thickness of the ice is not changing very rapidly, a further approximation can be made by substituting H, (the height of the ice at the center of the ice cap) for h in the terms x 0. Equation (17) becomes invalid when
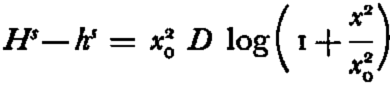
where
and

When the shear stress τ is the dominant stress, equations (6) and (9) become
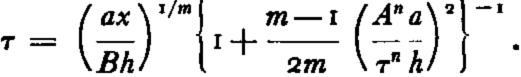
This equation reduces to the relation found by Nye when the stress τ is large, so that the second term on the right-hand side can be neglected. Since the second term on the right-hand side will be appreciable only near the center of an ice cap, we can approximate equation (19) by the following:
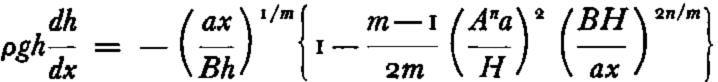
which, when integrated, gives
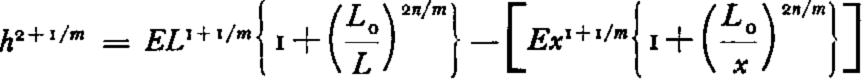
where
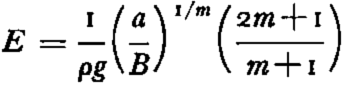
and
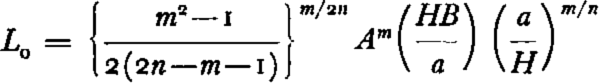
and L, as before, is the distance from the center to the edge of an ice cap. Equation (21) gives the profile in the central region, but is not valid elsewhere. In these equations there is one constant which still has to be determined. It is the thickness H at the center of an ice cap. Once it is known, equations (18) and (21) will give the profile of an ice cap since all other terms appearing in these equations are known. As a first approximation, H is the height which was determined by Nye. The profile he obtained is valid up to a region close to the center of an ice cap and the slope is approximately zero near the center. A better approximation or H can be found from the following argument. Equation (18) breaks down at a distance of approximately x 0 and equation (21) at a distance x approximately equal to L 0. From equations (18) and (21), it can be seen that x 0 and L 0 are approximately of the same magnitude, x 0 being somewhat greater. The average of these two distances c is:
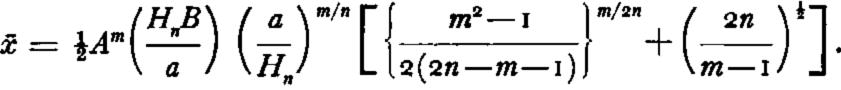
We have substituted for H in this equation the value H n from Nye’s theory, which is given by
Since c is larger than L 0 and smaller than x 0, equations (18) and (21) can both be applied to this value of x. The distance c is thus a reasonable value of x at which to join equations (18) and (21). The value of H then will be fixed automatically. It is found to be approximately
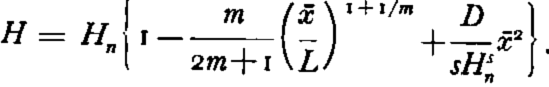
In this approximation for H we have used some of the sample calculations given later in order to drop a number of terms which are smaller than those retained above.
In joining equations (18) and (21) together at x= c , we obtain a profile which has no discontinuities in h but does have, in general, a discontinuity in the slope at the point c . Obviously, the exact profile passes smoothly through this point. It is a simple matter, however, to construct a solution which joins equations (18) and (21) smoothly. The following construction would be reasonable:
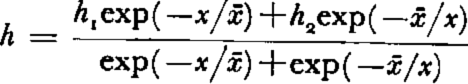
where h 1 is the value of h as determined by equation (18) and h2, the value of h as determined by equation (21). The use of the exponential function insures that, when x is much different from c either h 1 or h 2 determines the value of h, and when c , then h 1 = h 2 = h. However, equations (18) and (21) are very easily joined together graphically as is shown in Figure 3.
Effect of the weight of ice on the bedrock base. Hitherto we have considered the problem of an ice cap resting on a flat, rigid base. Actually, the weight of the ice may cause the bedrock platform to subside. If isostatic conditions prevail, a thickness h of ice will cause the bedrock to sink below its original level by an amount equal to h(ρ i /ρ r ) where ρ i and ρ r refer to the average density of ice and rock respectively. The ratio of these densities is about
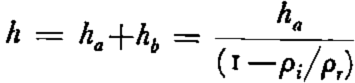
where h a is the thickness above the original position of the bedrock and h b is the thickness below it. The shear stress acting at the base of an ice mass depends almost solely upon the slope of the upper surface and is little influenced by the slope of the bedrock surface (Nye).Reference Nye 7 Hence the shear stress will be given by
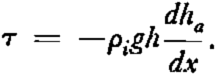
The analysis for the profile of an ice cap resting on a flat base is easily modified to take into account the subsidence of the bedrock and the effect of equation (27). It is easiest to rework the equation in terms of the height h a above the original bedrock surface. Equation (27) can be satisfied if, in the old analysis, the average density ρ is replaced by
h (regardless of whether or not it is being differentiated with respect to x) is replaced by
and H is replaced by a term H a (1−ρ i /ρ r )−1. The above substitutions are made in equations (18), (21), (22), (23), (24), and (25). The height of ice below the original bedrock surface h b is given by

The profile and height above the original bedrock surface of the upper ice surface is, surprisingly, essentially the same as it was for the case where the base platform was perfectly rigid. The profile of the lower ice surface is just the mirror of the upper surface, except that the depth of ice below the original bedrock surface is scaled down by the factor
Sample Calculations
To make sample calculations of the profiles of two-dimensional ice caps, we have to know the values of the various terms which appear in the equations of the previous section.
The value of n has been measured in numerous creep experiments. Results range from about 2.5 to 4.2. We shall use the value 3, which is close to that found by GlenReference Glen 8 for his minimum creep rates, and is the result obtained recently by Butkovich and LandauerReference Butkovich and Landauer 9 from a very extensive series of tests.
The value of A likewise can be determined from experiment. The Butkovich–Landauer set of experiments indicates that its value is about
The value of m never has been measured directly. TheoreticallyReference Weertman 4 it is equal to
The value of B is the most difficult to estimate. It has not been determined either experimentally or from field observations. Unfortunately a value derived from theoryReference Weertman 4 is extremely sensitive to the value taken for the “roughness” of the bedrock. Thus, B cannot be calculated reliably. We can obtain B, however, by using equation (23), which gives the approximate thickness of an ice cap. Rewriting this equation and making the substitutions given by equations (28) and (29) to account for the subsidence of the bedrock surface gives

and, assuming
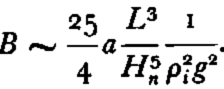
In the dry-snow regions on the plateau of the north Greenland Ice Sheet (at about lat. 79°N.), LangwayFootnote † has determined an accumulation rate of about 15 cm. of water equivalent (about 16 cm. of high-density ice). BullReference Bull 11 has measured the thickness of ice in northern Greenland and obtained a value of 2,680 m. The width of the ice sheet in northern Greenland is about 900 km. (L = 450 km.). The term ρ i g is equal to 9 × 10−2 bar/m. On the basis of these data, one finds that B is 81.2 m./yr.−bar2. This is a reasonable value from what little is known of glacier sliding velocities.
In Figure 1, we have calculated the upper and lower profiles of a two-dimensional ice cap by using the following values
-
n = 3
-
n = 2
-
A =
.
-
a = 0.16 m.yr.
-
L = 450 km.
-
B = 81.2 m.yr.−bar2
-
ρ i g = 0.09 bar/m.
-
ρ i /ρ r =
.
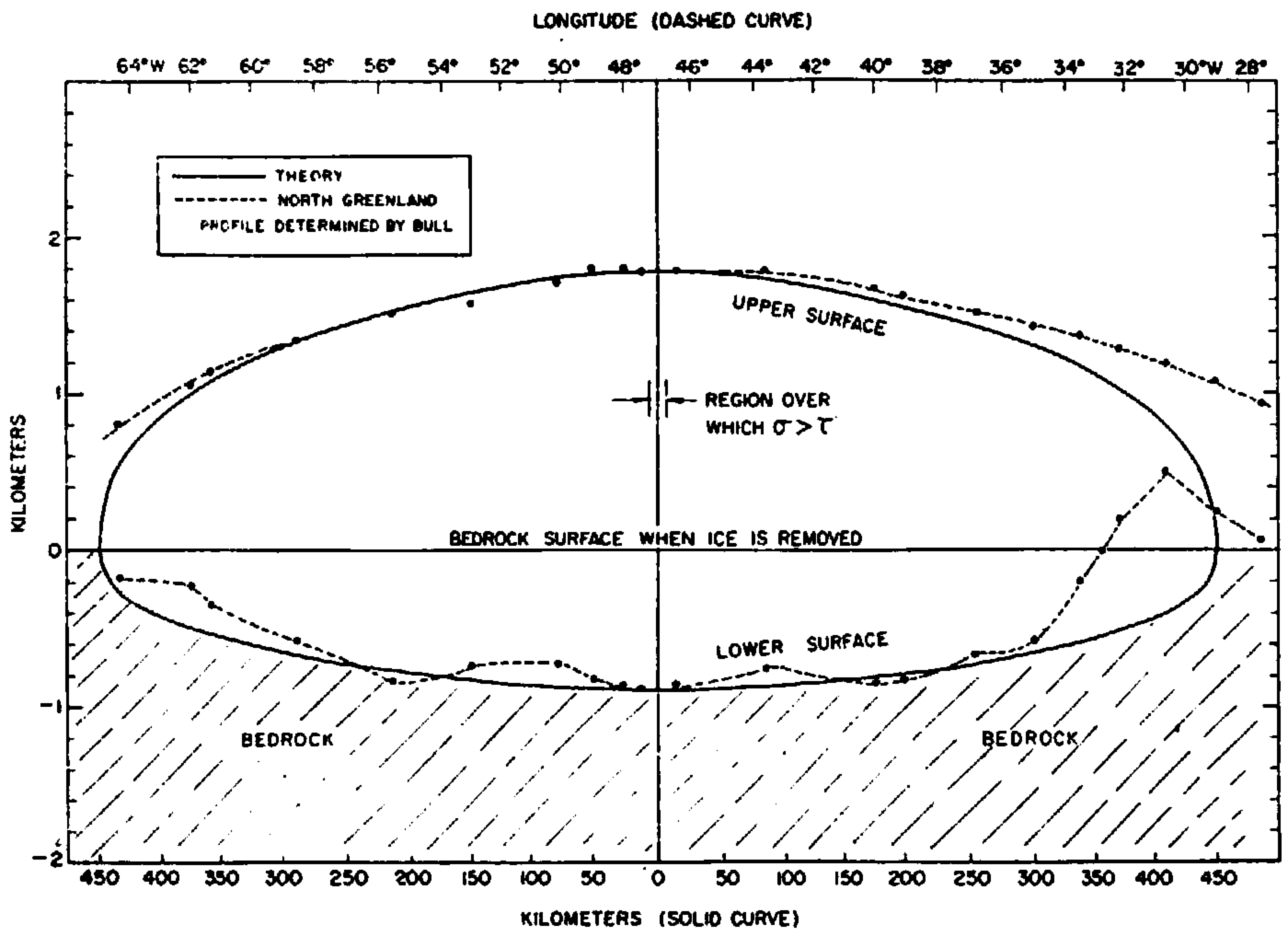
Fig. 1 Profile of a large ice sheet. Solid curve: Theoretical profile of a large ice sheet for which the bedrock is in isostatic equilibrium. If the ice were removed, the bedrock surface would be fiat. Dashed curve: Profile of the north Greenland Ice Sheet at about lat. 78° N. as determined by Bull.Reference Bull 11 (Elevation scale has an arbitrary origin. Altitude above sea-level of the center of the ice sheet is 2,527 m. at the top surface and − 153 m. at the bottom surface)
Also shown in this figure is the east-west profile of the ice sheet measured by BullReference Bull 11 in northern Greenland. (The agreement at the center is, of course, due to the fact that we have determined B from the observed thickness.) Since the major axis of the Greenland Ice Sheet is much longer than its minor axis, cutting the long axis produces a profile of an essentially two-dimensional ice sheet.
It would appear that once B is chosen from the thickness at the center of the ice cap, the remainder of the profile is reasonably well accounted for. Since the lower surface profile also approximates the theoretical curve (except for a buried mountain in the east) the bedrock would be a flat plane if the ice were removed. It was reasonable, therefore, to extend the analysis of the surface profile to include the lower surface profile. The region where our modification of Nye’s theory is applicable is very small in the case of the Greenland Ice Sheet, only a distance of about 6 km. on either side of the center (see Fig. 1). Nye’s theory therefore can be applied essentially over the whole ice sheet. This result will usually be true for any large ice sheet of the proportions of the Greenland or Antarctic Ice Sheets, if B is of the order of the value we used and if the accumulation rate does not fall below about 1 cm./yr.
The situation is different for small ice caps. In Figure 2 we have plotted a profile for an ice cap of the dimensions of the Barnes Ice Cap on Baffin Island. A profile measured by OrvigReference Orvig 12 is also shown. The value of B determined from the Greenland Ice Sheet thickness was used for the theoretical curve. The distance L was taken to be 16.5 km. The accumulation on the Barnes Ice Cap (BairdReference Baird 13 ) varies from 0 to 20 cm./yr. in the accumulation area. We have assumed, for the purpose of calculation, an average value for a of 10 cm./yr. for the whole ice cap. The bottom surface is essentially flat and it is not necessary to make the correction for isostatic sinking of the bedrock. It can be seen from this figure that Nye’s theory is inapplicable over an appreciable fraction of the total width of the ice cap, about 7 km. out of a total width of 33 km.
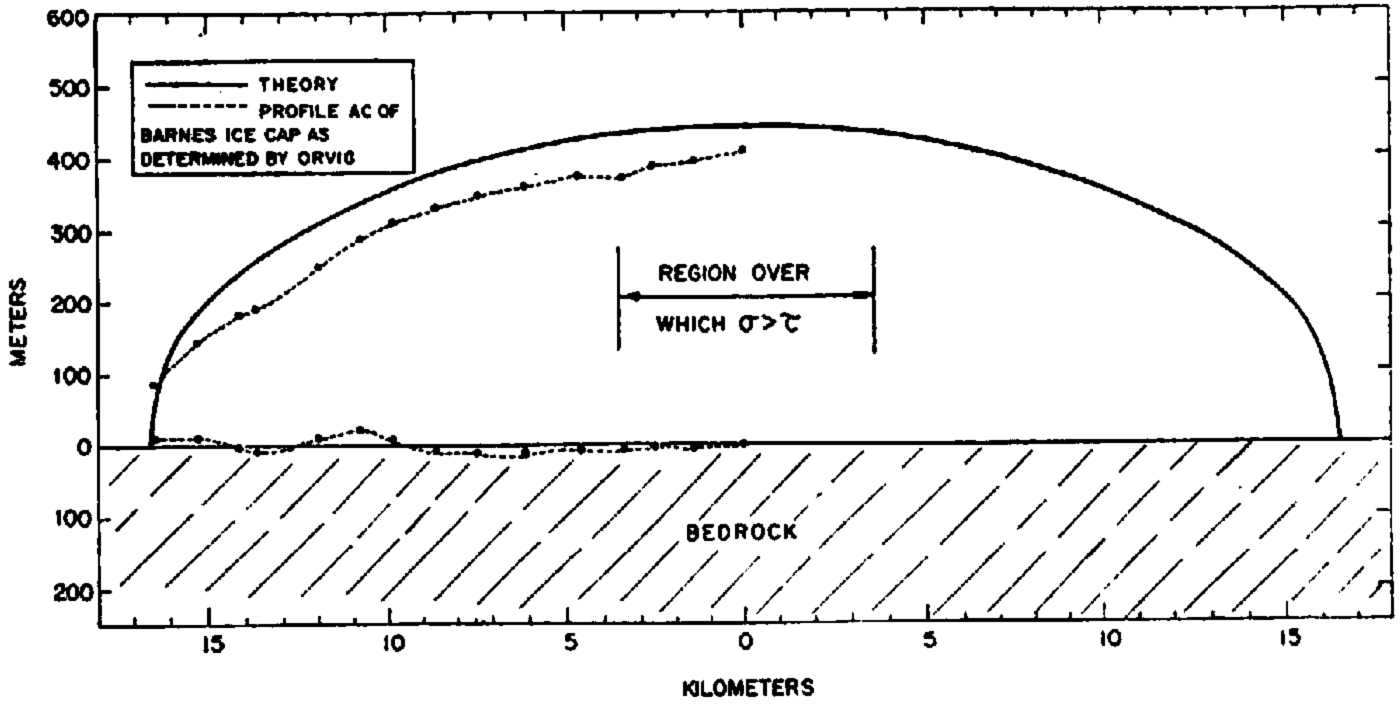
Fig. 2 Profile of a small ice cap. Solid curve: Theoretical profile of a small ice cap with a flat bedrock surface. Dashed curve: Profile of one section of the Barnes Ice Cap as determined by Orvig.Reference Orvig 12 (Elevation scale has an arbitrary origin. Altitude above sea-level at position 0 km. is 866 m. for the surface and 409 m. for the lower surface)
The differences are better illustrated by magnifying the vertical scale. Figure 3 shows the profile in the central region of Figure 2. The dashed curves give Nye’s profileFootnote * and the one calculated by equation (18). The solid line is the smoothed combination of these curves. The difference in thickness at the center of the profile between these curves is only about 13 meters, which is approximately 3 per cent of the total thickness. Our solution does, however, give a “flatter” profile in the central region of an ice cap, as can be seen in Figure 3.
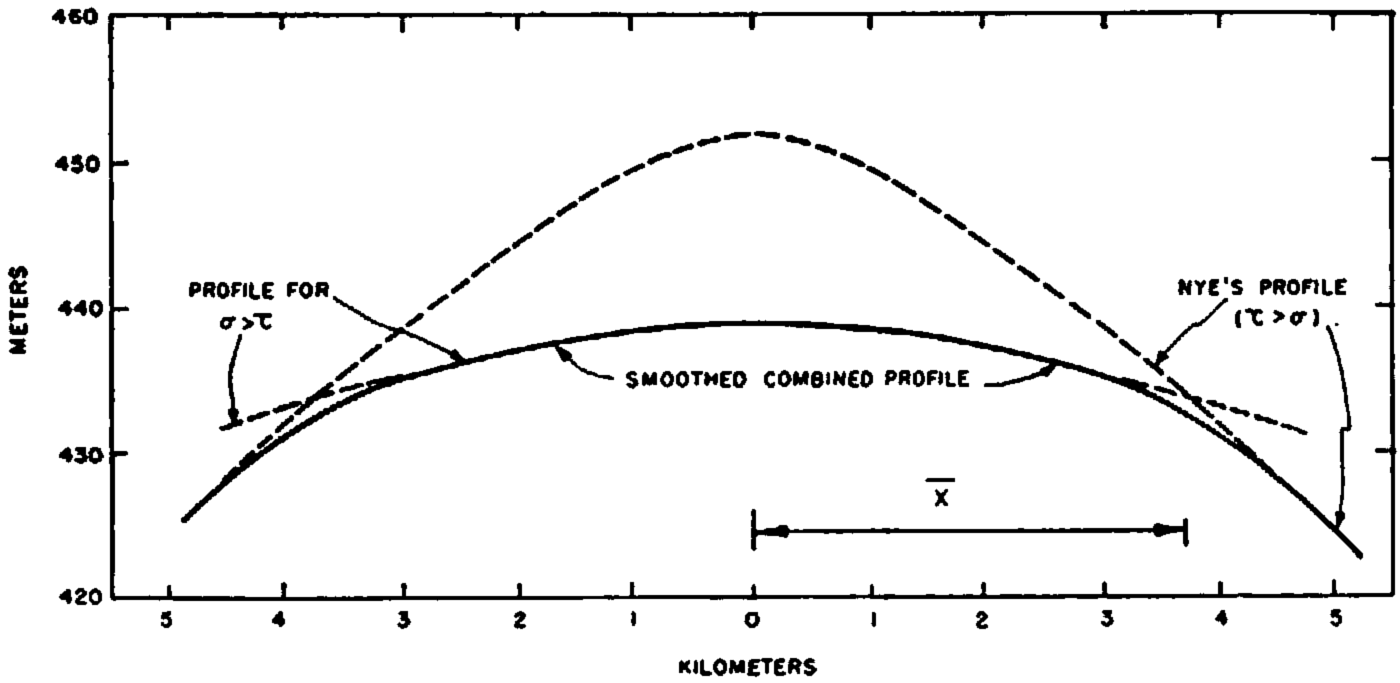
Fig. 3 Comparison of theoretical profiles (central part of Fig. 2) determined by equation (21) (modified to give Nye’s profile) and by equation (18) (dashed lines)
The fact that the theoretical profile is slightly higher than the observed profile may be due to the fact that the ice cap approximates a three-dimensional more closely than a two-dimensional ice cap. Nye has concluded that the thickness of a three-dimensional ice cap is about 11 per cent smaller than that of a two-dimensional cap with the same accumulation rate.
Summary
The law of sliding of ice over bedrock is generalized to include the effect of the presence of a longitudinal stress. The sliding velocity thus depends on both the shear stress acting at the bottom of an ice mass and the longitudinal stress. With this generalized law, it is still possible to make a one-dimensional analysis of the problem of calculating the profile of an ice cap or glacier, such as was carried out by Nye, and yet introduce the effect of large longitudinal stresses.
As a result a profile can be calculated with two equations. One equation is applicable to the central region of an ice cap and the other equation (which was found by Nye) is valid elsewhere. By an appropriate joining of the profiles derived from these two equations, the complete profile of an ice cap can be obtained. From two sample calculations it is shown that, for a large ice sheet, Nye’s theory is valid practically everywhere, and there is no real need to bring in the modification. For a small ice cap, the modification to the profile is valid over an appreciable fraction of the total width of the ice cap.
A very simple extension of the analysis of the ice cap profile allows for the effect of isostatic sinking of the bedrock surface under a large ice sheet. (An initially fiat bedrock surface was assumed. The analysis can be extended to allow for an arbitrarily shaped initial bedrock surface.)
Acknowledgements
I wish to thank Mr. Chester Langway for very informative discussions on the accumulation conditions in northern Greenland. I appreciate the encouragement given to me on this problem by Mr. James Bender.