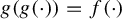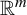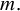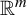1 Introduction
Given a map
$f: X \to X$
on a non-empty set X and a positive integer n, an iterative root of order n (or simply
$n{\mathrm{th}}$
root) of f is a map
$g: X\to X$
such that
$$ \begin{align} g^{n}(x)=f(x) \quad \text{for all } x\in X, \end{align} $$
where for each non-negative integer k,
$g^{k}$
denote the
$k{\mathrm{th}}$
order iterate of g defined recursively by
$g^{0}=\text {id}$
, the identity map on X, and
$g^{k}=g\circ g^{k-1}$
. For
$n=2$
, a solution of equation (1.1) is called an iterative square root (or simply a square root) of f. The iterative root problem (1.1), which is closely related to the embedding flow problem [Reference Fort13, Reference Kuczma22, Reference Zdun53], the invariant curve problem [Reference Kuczma, Choczewski and Ger24], and linearization [Reference Bogatyi9], is of particular interest [Reference Baron and Jarczyk4, Reference Bödewadt8, Reference Kuczma22, Reference Targonski47, Reference Targonski48, Reference Zdun and Solarz54] both in the theory of the functional equations and in that of dynamical systems, and has applications in statistics, signal processing, computer graphics, and information techniques [Reference Iannella and Kindermann16, Reference Kindermann, Omori and Usui19, Reference Martin38]. Since the initial works of Babbage [Reference Babbage3], Abel [Reference Abel1], and Königs [Reference Königs20], various researchers have paid increasing attention to the iterative root problem, and many advances have been made on its solutions for various classes of maps, e.g. continuous maps on intervals and in particular those which are piecewise monotone [Reference Blokh, Coven, Misiurewicz and Nitecki6, Reference Kuczma21, Reference Li, Yang and Zhang28, Reference Li and Zhang30–Reference Liu, Li and Zhang34, Reference Liu and Zhang36, Reference Liu and Zhang37, Reference Zhang and Zhang57, Reference Zhang59], continuous complex maps [Reference Rice, Schweizer and Sklar40, Reference Solarz45, Reference Solarz46, Reference Zdun52], series and transseries [Reference Edgar12], continuous maps on planes and
$\mathbb {R}^{m}$
[Reference Leśniak25, Reference Leśniak26, Reference Narayaninsamy39, Reference Yu, Li and Liu51], and set-valued maps [Reference Jarczyk and Zhang18, Reference Li, Jarczyk, Jarczyk and Zhang27, Reference Li and Zhang29, Reference Liu, Li and Zhang35]. In particular, various properties of the iterative roots have also been studied, see for instance, approximation [Reference Zhang and Zhang60], stability [Reference Xu and Zhang50, Reference Zhang, Zeng, Jarczyk and Zhang58], differentiability [Reference Kuczma23, Reference Zdun and Zhang55, Reference Zhang56], and category and measure [Reference Blokh7, Reference Simon41].
Given a topological space X, let
$\mathcal {C}(X)$
denote the set of all continuous self-maps of X. For each positive integer n, let
$\mathcal {W}(n;X):=\{f^{n}: f\in \mathcal {C}(X)\}$
, the set of
$n{\mathrm{th}}$
iterates of all the maps in
$\mathcal {C}(X)$
, and
$\mathcal {W}(X):=\bigcup _{n=2}^{\infty } \mathcal {W}(n;X)$
. Then it is interesting to ask how big these spaces are inside
$\mathcal {C}(X).$
We need a metric or topology on
${\mathcal C}(X)$
to make this question more precise.
Let X be a compact metric space with metric d. Then it is natural to have the supremum metric (or uniform metric)
$$ \begin{align*}\rho (f,g)=\sup \{ d(f(x), g(x)): x\in X\}\end{align*} $$
on
$C(X)$
, and this is our convention unless mentioned otherwise. Humke and Laczkovich considered the above question when
$X=[0,1]$
with the usual metric
$d(x,y)=|x-y|.$
This paper is heavily motivated by their results. They proved in [Reference Humke and Laczkovich14, Reference Humke and Laczkovich15] that
$\mathcal {W}(2;[0,1])$
is not dense in
$\mathcal {C}([0,1])$
,
$\mathcal {W}(2;[0,1])$
contains no balls of
$\mathcal {C}([0,1])$
(that is, its complement
$(\mathcal {W}(2;[0,1]))^{c}$
is dense in
$\mathcal {C}([0,1])$
), and
$\mathcal {W}(n;[0,1])$
is an analytic non-Borel subset of
$\mathcal {C}([0,1])$
for
$n\ge 2$
. Simon proved in [Reference Simon42–Reference Simon44] that
$\mathcal {W}(2;[0,1])$
is nowhere dense in
$\mathcal {C}([0,1])$
and
$\mathcal {W}([0,1])$
is not dense in
$\mathcal {C}([0,1])$
. Subsequently, nowhere denseness of
$\mathcal {W}([0,1])$
in
${\mathcal C}([0,1])$
was proved by Blokh [Reference Blokh7] using a method different from that of Humke-Laczkovich and Simon.
It is seen that the majority of papers on iterative roots of functions are restricted to continuous self-maps on intervals of the real line. This is not surprising because the setup is simpler to deal with. It has several advantages, including the intermediate value theorem, monotonicity of bijections, and so on. Extending these results to higher dimensions or more generic topological spaces is generally complex. We develop a new approach (see Theorem 2.4) to determine the non-existence of square roots of self-maps on arbitrary sets in §2. This approach can be used effectively to construct continuous self-maps on a wide range of topological spaces, which do not even have discontinuous square roots. We demonstrate the procedure in §3 by showing that the continuous self-maps without square roots are dense in the space of all continuous self-maps of the unit cube in
${\mathbb R}^{m}$
for the supremum metric
$\rho $
(see Theorem 3.8). This is a significant generalization of a similar result in [Reference Humke and Laczkovich15] (Corollary 5, p. 362) for intervals of the real line. We believe that the most significant contribution of this article is the method itself. The scheme can be used in various other settings. We demonstrate this claim in §4 by proving that the continuous self-maps without square roots are dense in the space of all continuous self-maps of
${\mathbb R}^{m}$
for the compact-open topology (see Theorem 4.3).
The outline of the paper is as follows. In §2, we study iterates and orbits of self-maps on arbitrary sets (without any topology). Isaacs conducted a detailed investigation on the fractional iterates of such functions in [Reference Isaacs17]. Here we discuss some of the basic aspects of such an approach. The main new result is Theorem 2.4, which presents a variety of cases in which we can be certain that the given function does not admit any iterative square root. This will be our principal tool in §§3 and 4. Section 2 also contains some background material and new results on fractional iterates of continuous self-maps on general topological spaces. In particular, Theorem 2.6 shows that in some cases, the problem of the non-existence of iterative roots of continuous maps can be reduced to elementary combinatorics.
In §3, we study iterative square roots of continuous self-maps on the unit cube
$I^{m}$
in
${\mathbb R}^{m}.$
We find it convenient to triangulate
$I^{m}$
and sew together affine linear maps piece by piece. For this purpose, we use some fundamental notions and notation from the theory of simplicial complexes. Given any continuous self-map on
$I^{m}$
, we approximate it with a piecewise affine linear map, and in turn close to any such map, we find another piecewise affine linear map with no square roots (see Theorem 3.8). This is the main result of this section. In contrast, we also show that any continuous self-map on
$I^{m}$
with a fixed point on the boundary can be approximated by iterative squares of continuous self-maps (see Theorem 3.9). A simple example shows that fixed points on the boundary are not required for such approximations.
In §4, we analyze continuous self-maps on
${\mathbb R}^{m}$
. As in §3, we prove that the continuous self-maps with no square roots are dense in the space of all continuous self-maps in a suitable topology, namely the compact-open topology (see Theorem 4.3). Finally, in §5, we prove that the squares of continuous self-maps are
$L^{p}$
dense in the space of all continuous self-maps on
$I^{m}$
, generalizing a result of [Reference Humke and Laczkovich15] to higher dimensions.
2 Functions on arbitrary sets and general topological spaces
In this section, we study iterative roots of self-maps on arbitrary sets and continuous self-maps on general topological spaces. First, we consider X to be a non-empty set with no predefined topology, and prove some new results on the existence and non-existence of iterative square roots of maps in
$\mathcal {F}(X)$
, the set of all self-maps on X. Surprisingly, some of these results are useful even when X has a topology and we seek for roots inside
${\mathcal C}(X)$
, the space of all continuous self-maps on X.
Henceforth, let
${\mathbb Z}_{+}$
denote the set
$\{0,1,2,\ldots \}$
of non-negative integers, and for each
$f\in \mathcal {F}(X)$
and
$A\subseteq X$
, let
$R(f)$
denote the range of f and
$f|_{A}$
the restriction of f to A. Given an
$f\in \mathcal {F}(X)$
, we define its graph as the directed graph
$G= (X, E)$
, whose vertex set is X and the edge set is
$E=\{(x, f(x)): x\in X \}$
. In other words, we are looking at the same mathematical structure from a different viewpoint. This allows us to borrow some notions from graph theory. To begin, consider the connected components of G in the context of graph theory. We call C a connected component of X if it is the vertex set of some connected component of the graph of f. Observe that a pair of vertices x and y are in the same connected component
$C\subseteq X$
if and only if there exist
$m,n \in {\mathbb Z}_{+}$
such that
$f^{m}(x)=f^{n}(y).$
The connected component of X containing x is called the orbit of x under f, and is denoted by
$O_{f}(x)$
. An extensive analysis of iterative square roots of functions in
$\mathcal {F}(X)$
can be found in [Reference Isaacs17]. In what follows, we analyze them in some special cases and present all the results needed for our further discussions.
Let
$f\in \mathcal {F}(X)$
, and
$G_{1}$
and
$G_{2}$
be two connected components of the graph G of f. An isomorphism of
$G_{1}$
and
$G_{2}$
is a bijective function
$\phi :C_{1} \to C_{2}$
between the vertex sets of
$G_{1}$
and
$G_{2}$
such that any two vertices x and y are adjacent in
$G_{1}$
if and only if
$\phi (x)$
and
$\phi (y)$
are adjacent in
$G_{2}$
. By the definition of graphs, this means that
$y=f(x)$
if and only if
$\phi (y)= f(\phi (x)).$
In other words,
$G_{2}$
is isomorphic to
$G_{1}$
if and only if there exists a bijective function
$\phi :C_{1}\to C_{2}$
such that
$\phi \circ f= f\circ \phi .$
Proposition 2.1. Let
$f\in \mathcal {F}(X)$
be such that the graph of f has exactly two isomorphic connected components. Then f has an iterative square root in
$\mathcal {F}(X)$
.
Proof. Let
$C_{1}$
and
$C_{2}$
be the two isomorphic connected components of X corresponding to those of the graph of f. Then
$X=C_{1}\cup C_{2}, C_{1}\cap C_{2}=\emptyset $
, and as indicated above, there exists a bijective function
$\phi :C_{1}\to C_{2}$
such that
$\phi \circ f= f\circ \phi $
. Define a map
$g:X\to X$
by
$$ \begin{align*} g(x) = \begin{cases} \phi(x)& \mbox{if}~x\in C_{1},\\ f\circ \phi^{-1}(x)& \mbox{if}~x\in C_{2}.\end{cases} \end{align*} $$
Now, we have
$g(x)=\phi (x)\in C_{2}$
for each
$x\in C_{1}$
, implying that
$g^{2}(x)= f\circ \phi ^{-1}\circ \phi (x)= f(x)$
. Similarly, we have
$g(x)=f\circ \phi ^{-1}(x) \in C_{1}$
for each
$x\in C_{2}$
, and so
$g^{2}(x)= \phi \circ f\circ \phi ^{-1}(x)= f(x)$
. Therefore, g is an iterative square root of f on X.
The above proposition leads to the following result, where a fixed point x of f is said to be isolated if there is no
$y\ne x$
in X such that
$f(y)=x$
. By convention, the empty set and all infinite sets are assumed to have an even number of elements here and elsewhere.
Theorem 2.2. Let
$f\in \mathcal {F}(X)$
be such that excluding isolated fixed points of f, the number of isomorphic copies is even for each connected component of the graph of f. Then f has an iterative square root in
$\mathcal {F}(X)$
.
Proof. Let
$g:X\to X$
be a map defined as
$g(x)=x$
for isolated fixed points
$x\in X$
of f and g as in the previous proposition on the union of pairs of connected components of X corresponding to pairs of isomorphic copies of those of the graph of f. Since there are an even number of connected components, we can pair them, and the result follows from the previous proposition.
The above results are given for general
$f\in \mathcal {F}(X)$
. If we restrict ourselves to injective maps, we can describe the functions with square roots transparently, as seen below. To make our thoughts more concrete, we borrow some ideas and terminologies from [Reference Bhat, De and Rakshit5]. Note that given an injective map
$f\in \mathcal {F}(X)$
, any two points
$x, y \in X$
are in the same orbit under f if and only if there exists an
$n\in {\mathbb Z}_{+}$
such that either
$y=f^{n}(x)$
or
$x=f^{n}(y).$
Indeed, an orbit under f has one of the following forms for some
$x\in X$
:
-
(i)
$\{x, f(x), f^{2}(x), \ldots ,f^{d-1}(x)\}$
for some
$d\in \mathbb {N}$
with
$f^{d}(x)=x$
; -
(ii)
$\{x, f(x), f^{2}(x), \ldots \}$
with
$x\notin R(f)$
; -
(iii)
$\{\ldots ,f^{-2}(x), f^{-1}(x), x, f(x), f^{2}(x), \ldots \}$
.
Therefore, it follows that an injective map
$f\in \mathcal {F}(X)$
with exactly one orbit
$O_{f}(x)$
for some
$x\in X$
is in bijective correspondence with precisely one of the following maps (see [Reference Bhat, De and Rakshit5]).
-
(a) Cyclic permutations: For
$d\in {\mathbb N}$
, consider
${\mathbb Z}_{d} =\{0, 1, 2, \ldots , d-1\}$
with addition modulo
$d.$
Define
$s_{d}: {\mathbb Z}_{d}\to {\mathbb Z}_{d}$
by
$s_{d}(k)=k+1~(\mbox {mod}~d)$
. Note that
${\mathbb Z}_{1}=\{0\}$
and
$s_{1}(0)=0$
. Then
$s_{d}$
is bijective and has exactly one orbit. -
(b) Unilateral translation/shift: Define
$s_{+}: {\mathbb Z}_{+}\to {\mathbb Z}_{+}$
by
$s_{+}(k)=k+1.$
Then
$s_{+}$
is a shift with a single orbit. -
(c) Bilateral translation: Define
$s: {\mathbb Z}\to {\mathbb Z}$
by
$s(k)=k+1$
. Then s is bijective and has exactly one orbit.
More precisely, if
$f\in \mathcal {F}(X)$
has exactly one orbit
$O_{f}(x)$
, then there exists a bijective function
$\phi : O_{f}(x)\to Z$
defined by
$\phi (f^{k}(x))=k$
, where Z is
$\mathbb {Z}_{d}$
(for some
$d\in \mathbb {N}$
),
$\mathbb {Z}_{+}$
or
$\mathbb {Z}$
according as
$O_{f}(x)$
has the form (i), (ii) or (iii), respectively. Consider any arbitrary non-empty sets
$M_{d}$
,
$M_{+}$
and
$M.$
We define
$1_{M_{d}}\times s_{d}: M_{d}\times {\mathbb Z}_{d}\to M_{d}\times {\mathbb Z}_{d}$
by
$$ \begin{align*} (1_{M_{d}}\times s_{d})(l,k)= (l, k+1(\textrm{mod}~d)), \end{align*} $$
called the d-cyclic permutation with multiplicity
$M_{d}$
for each
$d\in \mathbb {N}$
. Similarly, we define
$1_{M_{+}}\times s_{+}:M_{+}\times \mathbb {Z}_{+}\to M_{+}\times \mathbb {Z}_{+}$
and
$1_{M}\times s:M\times \mathbb {Z}\to M\times \mathbb {Z}$
by
$$ \begin{align*} (1_{M_{+}}\times s_{+})(l,k)= (l, k+1)\quad \text{and}\quad (1_{M}\times s)(l,k)= (l, k+1), \end{align*} $$
called the unilateral shift with multiplicity
$M_{+}$
and the bilateral translation with multiplicity M, respectively. Then, given any injective map
$f\in \mathcal {F}(X)$
, decomposing
$X=\bigsqcup _{x\in X} O_{f}(x)$
into orbits under f, we see that
$(X,f)$
is in bijective correspondence with
$(Y,\tilde {f})$
, where
$Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
for some suitable multiplicity spaces
$M_{d}$
,
$M_{+}$
and M (some of these sets may be absent in the union), and
$\tilde {f}$
is
$1_{M_{d}}\times s_{d}$
,
$1_{M_{+}}\times s_{+}$
and
$1_{M}\times s$
on
$M_{d}\times {\mathbb Z}_{d}$
,
$M_{+}\times {\mathbb Z}_{+}$
and
$M\times {\mathbb Z}$
, respectively. Furthermore, the cardinalities of these multiplicity spaces are uniquely determined. We call
$(m_{1}, m_{2}, \ldots , m_{+},m)$
as the multiplicity sequence of f, where
$m_{d}$
,
$m_{+}$
and m are the cardinalities of
$M_{d}$
(for
$d\in {\mathbb N}$
),
$M_{+}$
and M, respectively.
Theorem 2.3. Let
$f\in \mathcal {F}(X)$
be an injective map. Then f has an iterative square root in
$\mathcal {F}(X)$
if and only if the multiplicity sequence
$(m_{1}, m_{2}, \ldots , m_{+},m)$
of f satisfies that
$m_{d}$
with d even,
$m_{+}$
and m are even (
$0$
and infinity allowed).
Proof. Let
$f\in \mathcal {F}(X)$
be an injective map and
$(m_{1}, m_{2}, \ldots , m_{+},m)$
be the multiplicity sequence of f. Suppose that
$f=g^{2}$
for some
$g\in \mathcal {F}(X)$
. Then, clearly g is an injective map on X, and therefore we can associate a multiplicity sequence
$(m_{1}^{\prime }, m_{2}^{\prime }, \ldots , m_{+}^{\prime },m^{\prime })$
for g. Further, it is easily seen that an orbit under g corresponding to a cyclic permutation on
${\mathbb Z}_{d}$
gives rise to two orbits (respectively a unique orbit) under
$g^{2}$
corresponding to cyclic permutation on
${\mathbb Z}_{ {d}/{2}}$
(respectively on
$\mathbb {Z}_{d}$
) whenever d is even (respectively odd). Similarly, an orbit under g corresponding to the unilateral shift on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
$\mathbb {Z}$
) gives rise to two orbits under
$g^{2}$
corresponding to the unilateral shift on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
$\mathbb {Z}$
). Therefore, the multiplicity sequence of
$g^{2}$
is
$(m_{1}^{\prime }+2m_{2}^{\prime }, 2m_{4}^{\prime }, m_{3}^{\prime }+2m_{6}^{\prime }, 2m_{8}^{\prime }, m_{5}^{\prime }+2m_{10}^{\prime }, 2m_{12}^{\prime }, \ldots , 2m_{+}^{\prime }, 2m^{\prime })$
. Consequently, we must have
$m_{+}=2m_{+}^{\prime }$
,
$m=2m^{\prime }$
, and
$$ \begin{align*} m_{d} = \begin{cases} m_{d}^{\prime}+2m_{2d}^{\prime}&\mbox{if }d\text{ is odd},\\ 2m_{2d}^{\prime}& \mbox{if } d \text{ is even},\end{cases} \end{align*} $$
and hence
$m_{d}$
for d even,
$m_{+}$
and m are even.
Conversely, suppose that the multiplicity sequence
$(m_{1}, m_{2}, \ldots , m_{+}, m)$
of f satisfies that
$m_{d}$
for d even,
$m_{+}$
and m are even. Then X can be decomposed into orbits under f as
$X=\bigsqcup _{x\in X} O_{f}(x)$
and
$(X,f)$
is in bijective correspondence with
$(Y,\tilde {f})$
, where
$Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
such that:
-
• each orbit
$O_{f}(x)$
in X under f has one of the above-mentioned forms (i), (ii) or (iii); -
• the cardinalities of multiplicity spaces
$M_{d}$
(for all
$d\in \mathbb {N}$
),
$M_{+}$
and M are
$m_{d}$
,
$m_{+}$
and m, respectively; and -
•
$\tilde {f}$
is
$1_{M_{d}}\times s_{d}$
,
$1_{M_{+}}\times s_{+}$
and
$1_{M}\times s$
on
$M_{d}\times {\mathbb Z}_{d}$
,
$M_{+}\times {\mathbb Z}_{+}$
and
$M\times {\mathbb Z}$
, respectively.
Now, define a map
$g:X\to X$
as follows. If
$d\in \mathbb {N}$
is odd, then for each of the orbits
$O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
corresponding to the cyclic permutation on
${\mathbb Z}_{d}$
, define
$$ \begin{align*}g(f^{l}(x))=f^{(l+({d+1})/{2})(\text{mod}~d)}(x)\end{align*} $$
for all
$0\le l\le d-1$
. Then,
$$ \begin{align*}g^{2}(f^{l}(x))=g(f^{(l+({d+1})/{2})(\text{mod}~d)}(x))=f^{l+d+1(\text{mod}~d)}(x)=f^{l+1}=f(f^{l}(x))\end{align*} $$
for all
$0\le l\le d-1$
, implying that
$g^{2}=f$
on
$O_{f}(x)$
. If
$d\in \mathbb {N}$
is even, then as
$m_{d}$
is even, by pairing any two distinct orbits
$O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
and
$O_{f}(y)=\{y,f(y),f^{2}(y),\ldots , f^{d-1}(y)\}$
corresponding to the cyclic permutation on
${\mathbb Z}_{d}$
, define g on
$O_{f}(x)\cup O_{f}(y)$
by
$$ \begin{align*} g(z) = \begin{cases} \phi(z)& \mbox{if}~z\in O_{f}(x),\\ f\circ \phi^{-1}(z)& \mbox{if}~z\in O_{f}(y),\end{cases} \end{align*} $$
where
$\phi :O_{f}(x)\to O_{f}(y)$
is a bijective function such that
$\phi \circ f= f\circ \phi $
. Then, by a similar argument as in Proposition 2.1, it follows that
$g^{2}=f$
on
$O_{f}(x)\cup O_{f}(y)$
. Since
$m_{+}$
(respectively m) is even, g can be defined similarly on the union
$O_{f}(x)\cup O_{f}(y)$
of each pair of distinct orbits
$O_{f}(x)$
and
$O_{f}(y)$
corresponding to the unilateral shift on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
$\mathbb {Z}$
) such that
$g^{2}=f$
on
$O_{f}(x)\cup O_{f}(y)$
. Therefore, f has a square root in
$\mathcal {F}(X)$
.
For each
$f\in \mathcal {F}(X)$
and
$x\in X$
, let
$f^{-1}(x)$
and
$f^{-2}(x)$
denote the usual inverse images defined by
$f^{-1}(x)=\{y\in X: f(y)=x\}$
and
$f^{-2}(x)=\{y\in X: f^{2}(y)=x\}$
. Further, for each set A, let
$\# A$
denote the number of elements or the cardinality of A. So far, we have studied various conditions under which maps in
$\mathcal {F}(X)$
have square roots. We now have some instances in which they have no square roots. The following result is very useful for constructing functions without square roots in the next two sections.
Theorem 2.4. Let
$f\in \mathcal {F}(X)$
be such that
$f(x_{0})\ne x_{0}$
for some
$x_{0}\in X$
. Then f has no iterative square roots in
$\mathcal {F}(X)$
in the following cases:
Case (i):
$\# f^{-2}(x_{0})>1$
, and
$\# f^{-1}(x)\leq 1$
for all
$x\neq x_{0}$
;
Case (ii):
$ f^{-2}(x_{0})$
is infinite, and
$ f^{-1}(x)$
is finite for all
$x\ne x_{0}$
;
Case (iii):
$f^{-2}(x_{0})$
is uncountable, and
$f^{-1}(x)$
is countable for all
$x\ne x_{0}$
.
Proof. Suppose that
$f=g^{2}$
for some
$g\in \mathcal {F}(X)$
. Consider the action of g on various subsets of X around
$x_{0}$
:
$$ \begin{align*} A_{-2} \xrightarrow{g} B_{-2}\xrightarrow{g} A_{-1} \xrightarrow{g}B_{-1} \xrightarrow{g} \{x_{0}\} \xrightarrow{g} \{y_{0}\}, \end{align*} $$
where
$y_{0}=g(x_{0})$
,
$A_{-1} =f^{-1}(x_{0})$
,
$A_{-2} =f^{-2}(x_{0})$
,
$B_{-1}=g(A_{-1})$
and
$B_{-2}=g(A_{-2})$
. Let
$\tilde {A}_{-1}=f(A_{-2})$
and
$\tilde {B}_{-1}=g(\tilde {A}_{-1})$
. Then
$\tilde {A}_{-1}\subseteq A_{-1}$
,
$\tilde {B}_{-1}\subseteq B_{-1}\subseteq g^{-1}(x_{0})$
and
$B_{-2}\subseteq g^{-1}(A_{-1})$
. Also, since
$f(x_{0})\ne x_{0}$
, we have
$y_{0}\neq x_{0}$
,
$x_{0} \notin A_{-1}$
and
$x_{0}\notin B_{-1}$
.
Case (i): Since
$x_{0}\notin A_{-1}$
and
$\tilde {A}_{-1}\subseteq A_{-1}$
, we have
$\#f^{-1}(x)\leq 1$
for all
$x\in \tilde {A}_{-1}$
. Therefore, as
$A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
$\#A_{-2}>1$
, it follows that
$\#\tilde {A}_{-1}>1$
.
However, since
$y_{0}\ne x_{0}$
, we have
$\#f^{-1}(y_{0})\le 1$
. This implies that
$\#\tilde {B}_{-1}=1$
, because
$\tilde {B}_{-1}\ne \emptyset $
and
$\tilde {B}_{-1}\subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Therefore, as
$x_{0}\notin \tilde {B}_{-1}$
, we get that
$\#f^{-1}(\tilde {B}_{-1})=1$
. Consequently,
$\#B_{-2}=1$
, implying that
$\#\tilde {A}_{-1}=\#f(A_{-2})= \#g(B_{-2})=1$
. This contradicts an earlier conclusion. Hence, f has no square roots in
$\mathcal {F}(X)$
.
Case (ii): Since
$x_{0}\notin A_{-1}$
and
$\tilde {A}_{-1}\subseteq A_{-1}$
, we see that
$f^{-1}(x)$
is finite for all
$x\in \tilde {A}_{-1}$
. Therefore, as
$A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
$A_{-2}$
is infinite, it follows that
$\tilde {A}_{-1}$
is infinite.
However, since
$y_{0}\ne x_{0}$
, we have that
$f^{-1}(y_{0})$
is finite. This implies that
$\tilde {B}_{-1}$
is finite, because
$\tilde {B}_{-1} \subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Also, as
$x_{0}\notin B_{-1}$
and
$\tilde {B}_{-1} \subseteq B_{-1}$
, we see that
$f^{-1}(x)$
is finite for all
$x\in \tilde {B}_{-1}$
. Then it follows that
$f^{-1}(\tilde {B}_{-1})$
is finite. Consequently,
$B_{-2}$
is finite, implying that
$\tilde {A}_{-1}=f(A_{-2})= g(B_{-2})$
is finite. This contradicts the conclusion of the previous paragraph. Hence, f has no square roots in
$\mathcal {F}(X)$
.
Case (iii): The proof of Case (ii) repeatedly uses the fact that a finite union of finite sets is finite. The proof for this case is similar, using the result that a countable union of countable sets is countable.
It is worth noting that
$f^{-2}$
in the previous theorem cannot be replaced by
$f^{-1}$
, as seen from the following.
Example 2.5. Consider the continuous map
$f:[0,1]\to [0,1]$
defined by
$$ \begin{align*} f(x)= \begin{cases} \dfrac{3}{4}& \text{if } 0\leq x\leq \dfrac{1}{2},\\[6pt] \dfrac{5}{8}+\dfrac{x}{4}& \text{if } \dfrac{1}{2}< x\leq 1.\end{cases} \end{align*} $$
Then
$f(\tfrac 34)\neq \tfrac 34$
,
$f^{-1}(\tfrac 34)$
is uncountable and
$f^{-1}(x)$
is finite for all
$x\neq \tfrac 34.$
However, f has a square root
$$ \begin{align*} g(x)= \begin{cases} 1& \text{if } 0\leq x\leq \dfrac{1}{2},\\ \dfrac{5}{4}-\dfrac{x}{2}&\text{if } \dfrac{1}{2}< x\leq 1,\end{cases} \end{align*} $$
on
$[0,1]$
that is even continuous.
The above results are given for an arbitrary set X. In the rest of the section and those that follow, we consider X to be a topological space or a specific metric space and study continuous roots of continuous self-maps on X. It is useful to have some notation in this context. Recall that for a topological space X, the space of all continuous self-maps of X is denoted by
$\mathcal {C}(X)$
. For each
$A\subseteq X$
, let
$A^{0}$
denote the interior of A,
$\overline {A}$
the closure of A and
$\partial A$
the boundary of A. In particular, if X is a metric space equipped with metric d, then for each
$x\in X$
and
$\epsilon>0$
, let
$B_{\epsilon }(x):=\{y\in X: d(x,y)<\epsilon \}$
, the open ball in X around x of radius
$\epsilon $
. For any index set
$\Lambda $
, let
$S_{\Lambda }$
denote the group of all permutations (bijections) on
$\Lambda $
, and for convenience, we denote
$S_{\Lambda }$
by
$S_{k}$
when
$\Lambda =\{1,2,\ldots , k\}$
.
We motivate the next theorem through two examples. The map
$f_{1}(x)=1-x$
on the unit interval
$[0,1]$
as an element of
${\mathcal C}([0,1])$
, with
$[0,1]$
in the usual metric induced by
$|\cdot |$
, has no continuous square roots on
$[0,1]$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426]). However, the map
$f_{2}(x,y) = (1-x, 1-y)$
on
$[0,1]\times [0,1]$
as an element of
${\mathcal C}([0,1]\times [0,1])$
, where
$[0,1]\times [0,1]$
has the metric induced by the norm
$\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, has a continuous square root
$g(x,y)= (y,1-x)$
on
$[0,1]\times [0,1]$
. The reason for these contrasting conclusions can be detected by observing the fixed points of these maps.
Let f be a continuous self-map on a topological space X and Y a non-empty subset of X invariant under f, that is,
$f(Y)\subseteq Y$
. Then it is clear that if x and
$x^{\prime }$
are path-connected in Y, then so are
$f(x)$
and
$f(x^{\prime })$
. Therefore, if
$Y=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
is the decomposition of Y into its path components for some index set
$\Lambda $
, then there exists a unique map
$\sigma _{f,Y}: \Lambda \to \Lambda $
such that
$f(x)\in Y_{\beta }$
whenever
$x\in Y_{\alpha }$
and
$\sigma _{f,Y}(\alpha )=\beta $
(note that y and
$y^{\prime }$
are path-connected in Y if and only if there exists an
$\alpha \in \Lambda $
such that
$y,y^{\prime }\in Y_{\alpha }$
). We call
$\sigma _{f,Y}$
as the map induced by the map f and the invariant set Y. Let
$F(f):=\{x\in X: f(x)=x\}$
, the set of all fixed points of f in X, and
$E(f):= R(f)\setminus F(f)$
, the complement of
$F(f)$
in
$R(f)$
.
Theorem 2.6. Let
$n\in \mathbb {N}$
and
$f\in {\mathcal C}(X)$
be such that
$E(f)$
is invariant under f. If
$f=g^{n}$
for some
$g\in {\mathcal C}(X)$
, then
$E(f)$
is invariant under g and the induced maps satisfy that
$\sigma _{f,E(f)} = \sigma _{g, E(f)}^{n}$
. In other words, if
$\sigma _{f, E(f)}$
has no
$n{\mathrm{th}}$
roots, then f also has no continuous
$n{\mathrm{th}}$
roots on X.
Proof. Let
$E(f)=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
be the decomposition of
$E(f)$
into its path components for some index set
$\Lambda $
. The case
$n=1$
is trivial. So, let
$n>1$
, and consider an arbitrary
$x\in E(f)$
. Then
$x=f(x^{\prime })$
for some
$x^{\prime }\in X$
. Clearly,
$g(x)\in R(f)$
, because
$g(x)= g(f(x^{\prime }))= g(g^{n}(x^{\prime }))=g^{n}(g(x^{\prime }))= f(g(x^{\prime }))$
. Also, if
$g(x)\in F(f)$
, then
$g(x)=f(g(x))= g^{n}(g(x))=g(f(x))$
, implying that
$f(x)=g^{n}(x)=g^{n}(f(x))=f^{2}(x)$
, that is,
$f(x)$
is a fixed point of f. This contradicts the hypothesis that
$E(f)$
is invariant under f. Therefore,
$g(x)\in E(f)$
.
The equality
$\sigma _{f,E(f)}= \sigma _{g, E(f)}^{n}$
follows from the definitions of
$\sigma _{f,E(f)}$
and
$\sigma _{g,E(f)}$
, and the relation
$f=g^{n}.$
In the remainder of this section, we illustrate Theorem 2.6 through some simple examples. Remark that
$\sigma \in S_{k}$
, the group of permutation of k elements, has a square root if and only if the number of even cycles of
$\sigma $
is even. More generally,
$\sigma \in S_{k}$
has an
$n{\mathrm{th}}$
root if and only if for every
$m = 1,2, \ldots,$
it is true that the number of m-cycles that
$\sigma $
has is a multiple of
$((m,n))$
, where
$((m,n)):=\prod _{p|m}^{}p^{e(p,n)}$
,
$e(p,n)$
being the highest power of p dividing n (see [Reference Wilf49, pp. 155–158]).
Corollary 2.7. Let
$a<b$
be real numbers and
$f\in \mathcal {C}([a,b])$
be such that
$f|_{R(f)}$
is a non-constant strictly decreasing map. Then f has no iterative roots of even orders in
$\mathcal {C}([a,b])$
.
Proof. Since
$f:[a,b]\to [a,b]$
is a non-constant strictly decreasing continuous map, we see that
$R(f)$
is a compact interval
$[c,d]$
in
$\mathbb {R}$
for some
$c<d$
in
$[a,b]$
and f has a unique fixed point
$x_0$
in
$(c, d)$
. Also,
$E(f)=[c,x_0)\cup (x_0, d]$
is the decomposition of
$E(f)$
into path components and
$\sigma :=\sigma _{f, E(f)}$
is the transposition of the two-point set
$S_{2}$
. Since
$\sigma $
has no iterative roots of even orders in
$S_{2}$
, it follows from Theorem 2.6 that f has no iterative roots of even orders in
$\mathcal {C}([a,b])$
.
Example 2.8. Consider
$[0,1]\times [0,1]$
in the topology induced by the norm
$\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, and let
$f_{1}, f_{2}$
be the continuous maps on
$[0,1]\times [0,1]$
defined by
$f_{1}(x,y)=(1-x, 0)$
and
$f_{2}(x,y)=(y,x)$
. Then Theorem 2.6 is applicable to
$f_{1}$
and
$f_{2}$
with
$$ \begin{align*}E(f_{1})&= \big\{(x,0): 0\le x<\tfrac{1}{2}\big\}\cup \big\{(x,0):\tfrac{1}{2}<x\le 1\big\};\\ E(f_{2})&= \{ (x,y): 0\leq x<y\leq 1\}\cup \{(x,y): 0\leq y<x\leq 1\}.\end{align*} $$
It follows that both
$f_{1}$
and
$f_{2}$
have no iterative roots of even orders in
$\mathcal {C}([0,1]\times [0,1])$
.
3 Continuous functions on the unit cube in
${\mathbb R}^{m}$
As seen in §1, much literature is available on iterative square roots of functions on compact real intervals. In this section, we extend some of the results in [Reference Humke and Laczkovich15] to the unit cube
$$ \begin{align*} I^{m} :=\{ (x_{1}, x_{2}, \ldots , x_{m})\in {\mathbb R}^{m}: x_{i}\in I~\text{for}~ 1\leq i\leq m\} \end{align*} $$
considered in the metric induced by the norm
$$ \begin{align} \|(x_{1}, x_{2},\ldots,x_{m})\|_{\infty}=\max\{|x_{i}|: 1\le i\le m\}, \end{align} $$
where
$I:=[0,1]$
. In studying iterative roots of continuous maps on intervals, one observes that it becomes essential to look at piecewise linear maps. Here we study their analogs in higher dimensions. It is convenient to have the following elementary notions and notation from the theory of simplicial complexes to present our proofs.
As defined in [Reference Deo10], a set
$S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
in
$\mathbb {R}^{m}$
, where
$k\ge 1$
, is said to be geometrically independent if the set
$\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{k}-x_{0}\}$
is linearly independent in
$\mathbb {R}^{m}$
. Equivalently, S is geometrically independent if and only if for arbitrary reals
$\alpha _{i}$
, the equalities
$\sum _{i=0}^{k}\alpha _{i}x_{i}=0$
and
$\sum _{i=0}^{k}\alpha _{i}=0$
imply that
$\alpha _{i}=0$
for all
$0\le i\le k$
. A set having only one point is assumed to be geometrically independent. If S is geometrically independent, then there exists a unique k-dimensional hyperplane which passes through all the points of S and each point x on this hyperplane can be expressed uniquely as
$x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
such that
$\sum _{i=0}^{k}\alpha _{i}=1$
. The real numbers
$\alpha _{0}, \alpha _{1}, \ldots , \alpha _{k}$
, which are uniquely determined by S, are called the barycentric coordinates of the point x with respect to the set S.
Let
$S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
be a geometrically independent set in
$\mathbb {R}^{m}$
, where
$0\leq k\leq m$
. Then the k-dimensional geometric simplex or k-simplex spanned by S, denoted by
$\sigma $
, is defined as the set of all points
$x\in \mathbb {R}^{m}$
such that
$x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
, where
$\sum _{i=0}^{k}\alpha _{i}=1$
and
$\alpha _{i}\ge 0$
for all
$0\le i \le k$
. Equivalently,
$\sigma $
is the convex hull of S. The points
$x_{0}, x_{1}, \ldots , x_{k}$
are called the vertices of
$\sigma $
, and we usually write
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
to indicate that
$\sigma $
is the k-simplex with vertices
$x_{0}, x_{1}, \ldots , x_{k}$
. If
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex, then the set of those points of
$\sigma $
for which all barycentric coordinates are strictly positive, is called the open k-simplex
$\sigma $
(or the interior of
$\sigma $
), and is denoted by
$\sigma ^{0}$
. If
$\sigma $
is a p-simplex and
$\tau $
is a q-simplex in
$\mathbb {R}^{m}$
such that
$0\le p\le q \le m$
, then we say that
$\sigma $
is a p-dimensional face (or simply a p-simplex) of
$\tau $
if each vertex of
$\sigma $
is also a vertex of
$\tau $
. If
$\sigma $
is a face of
$\tau $
with
$p<q$
, then
$\sigma $
is called a proper face of
$\tau $
. Any zero-dimensional face of a simplex is simply a vertex of the simplex and a one-dimensional face of a simplex is usually called an edge of that simplex.
A finite (respectively countable) simplicial complex
$\mathcal {K}$
is a finite (respectively countable) collection of simplices of
$\mathbb {R}^{m}$
satisfying the following conditions: (i) If
$\sigma \in \mathcal {K}$
, then all the faces of
$\sigma $
are in
$\mathcal {K}$
; (ii) If
$\sigma , \tau \in \mathcal {K}$
, then either
$\sigma \cap \tau =\emptyset $
or
$\sigma \cap \tau $
is a common face of both
$\sigma $
and
$\tau $
. Let
$\mathcal {K}$
be a finite simplicial complex and
$|\mathcal {K}|=\bigcup _{\sigma \in \mathcal {K}}\sigma $
be the union of all simplices of
$\mathcal {K}$
. Then
$|\mathcal {K}|$
is a topological space with the topology inherited from
$\mathbb {R}^{m}$
. The space
$|\mathcal {K}|$
is called the geometric carrier of
$\mathcal {K}$
. A topological subspace of
$\mathbb {R}^{m}$
, which is the geometric carrier of some finite simplicial complex, is called a rectilinear polyhedron. A topological space X is said to be a polyhedron if there exists a finite simplicial complex
$\mathcal {K}$
such that
$|\mathcal {K}|$
is homeomorphic to X. In this case, the space X is said to be triangulable and
$\mathcal {K}$
is called a triangulation of X. A space X is said to be countably triangulable if there exists a countable triangulation of X, that is, there exists a countable simplicial complex
$\mathcal {K}$
of simplices of
$\mathbb {R}^{m}$
such that its geometric carrier
$|\mathcal {K}|$
is homeomorphic to X. Further, we do not distinguish between X and its geometric carrier
$|\mathcal {K}|$
whenever
$X=|\mathcal {K}|$
for some (finite or countable) triangulation
$\mathcal {K}$
of X, because in that case, we always consider the identity map id to be the homeomorphism between
$|\mathcal {K}|$
and X.
If
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex in
$\mathbb {R}^{m}$
, then the point
$\sum _{i=0}^{k}({1}/({k+1}))x_{i}$
is called the barycenter of
$\sigma $
and is denoted by
$\dot {\sigma }$
. In other words, barycenter of
$\sigma $
is that point of
$\sigma $
whose barycentric coordinates, with respect to each of the vertices of
$\sigma $
, are equal. Given a simplicial complex
$\mathcal {K}$
, let
$\mathcal {K}^{(1)}$
be a simplicial complex whose vertices are barycenters of all simplices of
$\mathcal {K}$
, and for any distinct simplices
$\sigma _{1}, \sigma _{2}, \ldots , \sigma _{k}$
of
$\mathcal {K}$
,
$\langle \dot {\sigma _{1}}, \dot {\sigma _{2}}, \ldots , \dot {\sigma _{k}}\rangle $
is a simplex of
$\mathcal {K}^{(1)}$
if and only if
$\sigma _{i}$
is a face of
$\sigma _{i+1}$
for
$i=0, 1,\ldots , k-1$
. Then
$\mathcal {K}^{(1)}$
is a simplicial complex and is called the first barycentric subdivision of
$\mathcal {K}$
. By induction, we define the
$l{\mathrm{th}}$
barycentric subdivision
$\mathcal {K}^{(l)}$
of
$\mathcal {K}$
to be the first barycentric subdivision of
$\mathcal {K}^{(l-1)}$
for each
$l>1$
. We also put
$\mathcal {K}^{(0)}=\mathcal {K}$
for convenience. For a simplicial complex
$\mathcal {K}$
, we define the mesh of
$\mathcal {K}$
, denoted by
$\mbox {mesh}(\mathcal {K})$
, as
$$ \begin{align*} \mbox{mesh}(\mathcal{K})=\max\{\mbox{diam}(\sigma): \sigma ~\text{is a simplex of}~\mathcal{K}\kern2pt\}, \end{align*} $$
where
$\mbox {diam}(\sigma )$
denote the diameter of
$\sigma $
. Then
$\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{(l)})=0$
for every non-empty simplicial complex
$\mathcal {K}$
.
An
$f\in \mathcal {F}(\mathbb {R}^{m})$
is said to be affine linear if
$f(\cdot )=T(\cdot )+z$
for some linear map
$T\in \mathcal {F}(\mathbb {R}^{m})$
and
$z\in \mathbb {R}^{m}$
. Clearly, each affine linear map on
$\mathbb {R}^{m}$
is continuous. An affine linear map f is said to be of full rank if the associated linear map T is invertible. Note that full rank affine linear maps are open maps, that is, they map open sets to open sets. They also map geometrically independent sets to geometrically independent sets. We sew affine linear maps on simplices piece by piece to get many continuous maps on
$\mathbb {R}^{m}$
.
An
${\mathbb R}^{m}$
-valued function f on a subset X of
${\mathbb R}^{m}$
is said to be piecewise affine linear (respectively countably piecewise affine linear) if
$X=|\mathcal {K}\kern2pt|$
for some finite (respectively countable) simplicial complex
$\mathcal {K}$
of simplices of
$\mathbb {R}^{m}$
and
$f|_{\sigma }$
is the restriction of some affine linear map
$\phi _{\sigma }$
on
$\mathbb {R}^{m}$
to
$\sigma $
for every
$\sigma \in \mathcal {K}$
. In this case, we say that f is supported by the simplicial complex
${\mathcal K}.$
Here is a basic construction of piecewise affine linear maps that we use repetitively. Let
$\mathcal {K}$
be a simplicial complex in
$\mathbb {R}^{m}$
and
$U=\{x_{0}, x_{1}, \ldots \}$
be its set of vertices ordered in some arbitrary way. Let
$V=\{y_{0}, y_{1}, \ldots \}$
be an ordered set of points in
${\mathbb R}^{m}$
. Then we can define a
${\mathbb R}^{m}$
-valued function
$f_{U,V}$
on
$|\mathcal {K}|$
satisfying
$f_{U,V}(x_{j})=y_{j}$
for all
$j\in \mathbb {Z}_{+}$
as follows: If
$x\in |\mathcal {K}|$
, then x is in the interior of a unique k-simplex
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
$\mathcal {K}$
for some
$0\le k\le m$
. We write
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
and define
$$ \begin{align} f_{U,V}(x)=\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}. \end{align} $$
Clearly,
$f_{U,V}$
is a continuous piecewise affine linear map on
$|\mathcal {K}|$
satisfying that
$f_{U,V}(x_{j})=y_{j}$
for every
$j\in \mathbb {Z}_{+}$
. Furthermore, if
$|{\mathcal K}|$
is convex and
$y_{j}\in |\mathcal {K}|$
for every j, then
$f_{U,V}$
is a self-map of
$|{\mathcal K}|.$
Lemma 3.1. Let
${\mathcal K}$
and
$f_{U,V}$
be as described above.
-
(i) If
$\sigma =\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
is a k-simplex in
$\mathcal {K}$
and
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{k}}\}$
is geometrically independent in
${\mathbb R}^{m}$
, then
$f_{U,V}|_{\sigma }$
is injective and
$f_{U,V}(\sigma )^{0}=f_{U,V}(\sigma ^{0})$
. -
(ii) If
$V=\{y_{0}, y_{1}, \ldots \}$
and
$W=\{z_{0}, z_{1}, \ldots \}$
are ordered sets in
$|\mathcal {K}|$
such that
$\|y_{j}-z_{j}\|_{\infty }\le \eta $
for all
$j\in \mathbb {Z}_{+}$
, where
$\eta>0$
, then
$\|f_{U,V}(x)-f_{U,W}(x)\|_{\infty }\le \eta $
for all
$x\in |\mathcal {K}|$
.
Proof. The result (i) is trivial. For each
$x\in |\mathcal {K}|$
, by equation (3.2) we have
$$ \begin{align*} \|f_{U,V}(x)-f_{U,W}(x)\|_{\infty}\le \sum_{j=0}^{k}\alpha_{i_{j}}\|y_{i_{j}}-z_{i_{j}}\|_{\infty}\le \eta, \end{align*} $$
proving result (ii).
Lemma 3.2. If
$f\in \mathcal {F}(\mathbb {R}^{m})$
is an affine linear map such that
$f|_{S}=0$
for a geometrically independent set
$S=\{x_{0}, x_{1}, \ldots , x_{m}\}$
of
$\mathbb {R}^{m}$
, then
$f=0$
on
$\mathbb {R}^{m}$
.
Proof. Let
$f(\cdot )=T(\cdot ) +z$
for some
$z\in \mathbb {R}^{m}$
and a linear map
$T\in \mathcal {F}(\mathbb {R}^{m})$
. Since S is geometrically independent, we have
$B=\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{m}-x_{0}\}$
is linearly independent, and therefore it is a Hamel basis for
$\mathbb {R}^{m}$
. To prove
$f= 0$
, consider an arbitrary
$x\in \mathbb {R}^{m}$
. Then
$x=\sum _{j=1}^{m}\alpha _{j}(x_{j}-x_{0})$
for some
$\alpha _{1}, \alpha _{2}, \ldots , \alpha _{m}\in \mathbb {R}$
, implying that
$$ \begin{align*} f(x)&=T\bigg(\sum_{j=1}^{m}\alpha_{j}(x_{j}-x_{0})\bigg)+z\\ &=\sum_{j=1}^{m}\alpha_{j}T(x_{j})-\sum_{j=1}^{m}\alpha_{j}T(x_{0})+z\\ &=\sum_{j=1}^{m}\alpha_{j}(-z)-\sum_{j=1}^{m}\alpha_{j}(-z)+z=z. \end{align*} $$
In particular,
$f(x_{0})=z$
, and therefore we get that
$z=0$
. Hence,
$f=0$
on
$\mathbb {R}^{m}$
.
Using the above lemma, we can deduce the following result on the uniqueness of affine linear maps.
Corollary 3.3. If
$f_{1}, f_{2} \in \mathcal {F}(\mathbb {R}^{m})$
are affine linear maps such that
$f_{1}|_{\sigma }= f_{2}|_{\sigma }$
for some m-simplex
$\sigma \in \mathcal {K}$
, then
$f_{1}=f_{2}$
on
$\mathbb {R}^{m}$
. Consequently, if
$f_{1}|_{U}=f_{2}|_{U}$
for some open subset U of
$\mathbb {R}^{m}$
, then
$f_{1}=f_{2}$
on
$\mathbb {R}^{m}.$
Proof. Follows from the above lemma, because
$f_{1}-f_{2}$
is an affine linear map on
$\mathbb {R}^{m}$
that vanishes on the geometrically independent set of all vertices of
$\sigma $
.
Corollary 3.4. Let
$f \in \mathcal {F}(\mathbb {R}^{m})$
be an affine linear map and
$\sigma $
be an m-simplex in
$\mathbb {R}^{m}$
with vertices
$x_{0}, x_{1}, \ldots , x_{m}$
such that
$y_{0}, y_{1}, \ldots , y_{m}$
are geometrically independent in
$\mathbb {R}^{m}$
, where
$y_{j}=f(x_{j})$
for all
$0\leq j\leq m$
. Then the following statements are true.
-
(i)
$f(U)$
is open for every open set U in the interior of
$\sigma $
. -
(ii) f maps geometrically independent subsets of
${\mathbb R}^{m}$
to geometrically independent subsets. -
(iii) If
$y_{j}\neq x_{j}$
for some
$0\le j\le m$
and
$\{v_{0}, v_{1}, \ldots , v_{m}\}$
is a geometrically independent subset of
$\sigma $
, then there exists at least one j such that
$f(v_{j})\neq v_{j}$
.
Proof. Results (i) and (ii) are trivially true, because geometric independence of
$\{y_{0}, y_{1}, \ldots , y_{m}\}$
implies that f is of full rank. If
$f(v_{j})=v_{j}$
for all
$0\le j\le m$
, then
$f=\text {id}$
on
$\mathbb {R}^{m}$
, implying that
$y_j=f(x_j)=x_j$
for all
$0\le j\le m$
. Therefore, (iii) follows.
For each subset S of
$\mathbb {R}^{m}$
, let
$$ \begin{align*} \textrm{Aff}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=1\bigg\} \end{align*} $$
and
$$ \begin{align*} \textrm{Aff}_{0}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=0\bigg\}. \end{align*} $$
Then
$\text {Aff}_{0}(S)$
is a vector subspace of
$\mathbb {R}^{m}$
and
$\text {Aff}(S)=\text {Aff}_{0}(S)+x$
for some
$x\in S$
, where
$\text { Aff}_{0}(S)+x:=\{y+x:y\in \text {Aff}_{0}(S)\}$
. We say that
$\text {Aff}(S)$
has dimension k, written as
$dim(\text {Aff}(S))=k$
, if
$\text {Aff}_{0}(S)$
is a k-dimensional vector subspace of
$\mathbb {R}^{m}$
. A point
$z\in \mathbb {R}^{m}$
is said to be geometrically independent of S if
$z\notin \text {Aff}(S)$
. Then it is clear that z is geometrically independent of S if and only if
$0$
is geometrically independent of
$S-z$
.
Lemma 3.5. Let S be a countable subset of
$\mathbb {R}^{m}$
. Then for each
$z\in \mathbb {R}^{m}$
and
$\zeta>0$
, there exists a
$y\in B_{\zeta }(z)$
such that y is geometrically independent of Z for all subsets Z of S such that
$\#Z\le m$
.
Proof. Since
$dim(\text {Aff}(Z))\le m-1$
, clearly
$\text {Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}$
is a nowhere dense subset of the complete metric space
$\overline{B_{\zeta/2}(z)}$
for each subset Z of S such that
$\#Z\le m$
. Therefore, by the Baire category theorem, we have
$$ \begin{align*} \overline{B_{\zeta/2}(z)}\ne \bigcup\bigg(\textrm{Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}\bigg), \end{align*} $$
where the union is taken over all subsets Z of S such that
$\#Z\le m$
. Hence, there exists a
$y\in \overline{B_{\zeta/2}(z)}$
such that y is geometrically independent of Z for all subsets Z of S such that
$\#Z\le m$
. Since
$\overline{B_{\zeta/2}(z)}\subseteq B_{\zeta }(z)$
, the result follows.
Lemma 3.6. Let
$z_{1}, z_{2}, \ldots $
be a sequence of points in
$\mathbb {R}^{m}$
and
$\zeta _{1}, \zeta _{2}, \ldots $
be a sequence of positive reals. Then there exists a sequence
$y_{1}, y_{2}, \ldots $
in
$\mathbb {R}^{m}$
such that
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
$j\in \mathbb {N}$
and every subset Z of
$S=\{y_{1}, y_{2}, \ldots \}$
where
$\#Z\le m+1$
is geometrically independent.
Proof. Given
$z_{1}\in \mathbb {R}^{m}$
and
$\zeta _{1}>0$
, consider any
$y_{1}\in B_{\zeta _{1}}(z_{1})$
such that
$y_{1}\ne z_{1}$
. Then clearly any subset Z of
$S_{1}=\{y_{1}\}$
with
$\#Z\le m+1$
is geometrically independent. Next, by induction, suppose that
$k>1$
, and there exist
$y_{1}, y_{2}, \ldots , y_{k} \in \mathbb {R}^{m}$
with
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for
$1\le j\le k$
such that Z is geometrically independent for all subsets Z of
$S_{k}=\{y_{1}, y_{2}, \ldots , y_{k}\}$
with
$\#Z\le m+1$
. Then by Lemma 3.5, there exists
$y_{k+1}\in B_{\zeta _{k+1}}(z_{k+1})$
such that
$y_{k+1}$
is geometrically independent of Z for all subsets Z of
$S_{k}$
such that
$\#Z\le m$
. This implies that Z is geometrically independent for all subsets Z of
$S_{k+1}=\{y_1, y_2, \ldots, y_{k+1}\}$
such that
$\#Z\le m+1$
, proving the result for
$k+1$
. Thus, continuing the above process, we get a sequence
$y_{1}, y_{2}, \ldots $
in
$\mathbb {R}^{m}$
such that
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
$j\in \mathbb {N}$
satisfying the desired property.
In addition to the above notions and results on simplicial complexes, we need the following lemma to prove our results.
Lemma 3.7. Let X be a metric space with metric d and
$f\in \mathcal {C}(X)$
. If
$x\in X$
is not a fixed point of f, then there exists an open set V in X containing x such that
$f^{-1}(V)\cap V=\emptyset $
and
$f(V)\cap V=\emptyset $
.
Proof. Let
$\epsilon =d(x,f(x))$
. Since
$f(x)\ne x$
, clearly
$\epsilon>0$
. Since f is continuous at x, there exists a
$\delta>0$
with
$\delta <{\epsilon }/{4}$
such that
$$ \begin{align} d(f(x), f(y)) <\frac{\epsilon}{4}\quad\text{whenever } y\in X \text{ with }d(x,y)<\delta. \end{align} $$
Let
$V:=B_{{\delta }/{2}}(x)$
.
Claim.
$f^{-1}(V)\cap V=\emptyset $
and
$f(V)\cap V=\emptyset $
.
Suppose that
$y\in f^{-1}(V)\cap V$
. Then
$f(y)\in V$
, implying that
$d(y, f(y))\le d(y,x)+d(x,f(y))<\delta $
. Also, by equation (3.3), we have
$d(f(x), f(y))<{\epsilon }/{4}$
. Therefore,
$\epsilon =d(x, f(x))\le d(x, y)+d(y, f(y))+d(f(y), f(x))<{3\epsilon }/{4}$
is a contradiction. Next, suppose that
$y\in f(V)\cap V$
. Then
$y=f(z)$
for some
$z\in V$
. Therefore, by equation (3.3), we have
$d(f(x), y)<{\epsilon }/{4}$
, implying that
$\epsilon =d(x, f(x))\le d(x, y)+d(y, f(x))<{\epsilon }/{2}$
, which is a contradiction. Thus the claim holds, and the result follows.
Having the above machinery, we are ready to prove our desired results.
Theorem 3.8. If
$h\in \mathcal {C}(I^{m})$
, then for each
$\epsilon>0$
the ball
$B_{\epsilon }(h)$
of radius
$\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
$I^{m}$
. In particular,
$\mathcal {W}(2;I^{m})$
does not contain any ball of
$\mathcal {C}(I^{m})$
.
Proof. Let
$h\in \mathcal {C}(I^{m})$
and
$\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
$f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps.
Step 1: Construct a piecewise affine linear map
$f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
$\mathcal {K}$
of
$I^{m}$
. Since h is uniformly continuous on
$I^{m}$
, there exists a
$\delta>0$
such that
$$ \begin{align} \|h(x)-h(y)\|_{\infty} <\frac{\epsilon }{10} \quad\text{whenever } x, y\in I^{m} \text{with } \|x-y\|_{\infty}<\delta. \end{align} $$
Being a polyhedron,
$I^{m}$
is triangulable. Consider a triangulation
$\mathcal {K}$
of
$I^{m}$
with vertices
$x_{0}, x_{1}, x_{2}, \ldots , x_{r}$
such that
$\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
$2$
-simplex
$\langle x_{i_{0}},x_{i_{1}}\rangle $
of
$\sigma $
and for all m-simplex
$\sigma \in \mathcal {K}$
. Choose
$y_{0}, y_{1}, y_{2},\ldots , y_{r} \in I^{m}$
inductively such that
$y_{j}\ne x_{j}$
and
$$ \begin{align} \|h(x_{j})-y_{j}\|_{\infty} <\frac{\epsilon }{20}\quad\text{for all } 0\le j\le r, \end{align} $$
and
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
$\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K}$
for
$0\le i_{0}, i_{1}, \ldots , i_{m}\le r$
. This is possible by Lemma 3.6. Here, while choosing points
$y_{j}$
with
$y_{j}\in B_{ {\epsilon }/{20} }(h(x_{j}))$
for
$0\le j\le r$
satisfying the geometric independence condition, we have some additional restrictions to fulfill, viz.
$y_{j}\neq x_{j}$
and
$y_{j}\in I^{m}$
for all
$0\le j\le r$
. However, the Baire category theorem provides this flexibility as there are plenty of vectors to choose from. Then,
$$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon}{20}+\frac{\epsilon }{10}+\frac{\epsilon }{20}=\frac{\epsilon }{5} \end{align} $$
whenever
$\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
$2$
-simplex of
$\sigma $
for all m-simplex
$\sigma \in \mathcal {K}$
. Let
$f_{0}:|\mathcal {K}|=I^{m} \to I^{m}$
be the map
$f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
$\{x_{0}, x_{1}, \ldots , x_{r}\}$
and
$\{y_{0}, y_{1}, \ldots , y_{r}\}$
, respectively. Then
$f_{0}$
is a continuous piecewise affine linear self-map of
$I^{m}$
satisfying that
$f_{0}(x_{j})=y_{j}$
for all
$0\le j\le r$
. Also, by using result (i) of Lemma 3.1, we have
$R(f_{0})^{0}\ne \emptyset $
and
$f_{0}|_{\sigma }$
is injective for all
$\sigma \in \mathcal {K}$
. Further, from equation (3.6) we have
$$ \begin{align} \mbox{diam}(f_{0}(\sigma ))<\frac{\epsilon }{5}\quad\text{for all } \sigma \in \mathcal{K}. \end{align} $$
Claim.
$\rho (f_{0},h)<{\epsilon }/{6}$
.
Consider an arbitrary
$x\in I^{m}$
. Then x is in the interior of some unique k-simplex
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
$\mathcal {K}$
for some
$0\le k\le m$
. Let
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (3.4) and (3.5), we have
$$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon }{20}+\frac{\epsilon }{10}\nonumber\\ &<\frac{\epsilon}{6}, \end{align} $$
since
$\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<{\delta }/{4}$
for
$0\le j\le k$
. This proves the claim and Step 1 follows.
Step 2: Obtain an m-simplex
$\Delta \in \mathcal {K} $
containing a non-empty open set
$Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
$f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
$\Delta _{1}$
in
${\mathcal K}.$
Consider any m-simplex
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
$\mathcal {K}$
. Since
$\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
$f_{0}(Z)$
is open in
$I^{m}$
for each open set Z in
$\sigma ^{0}$
. Choose a non-empty open subset
$Y_{0}$
of
$f_0(\sigma )^{0}$
so small that
$Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
$\Delta \in \mathcal {K}$
. Then
$f_{0}(Y_{0})$
has non-empty interior. Again, choose a sufficiently small non-empty open subset Y of
$Y_{0}$
such that
$f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
$\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
Step 3: Show that there exists a barycentric subdivision
$\mathcal {K}^{(s)}$
of
$\mathcal {K}$
for some
$s \in \mathbb {N}$
with an m-simplex
$\sigma _{0}\in \mathcal {K}^{(s)}$
such that
$\sigma _{0}\subseteq Y$
, and
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
$f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
$\sigma \in \mathcal {K}^{(s)}$
with
$\sigma \cap \sigma _{0}\ne \emptyset $
. Since
$y_{j}\neq x_{j}$
for all
$0\le j\le r$
, by Corollary 3.4, we have
$f_{0}(z_{0})\ne z_{0}$
for some
$z_{0}\in Y$
. Choose an open set
$W_0$
in
$I^{m}$
such that
$z_{0}\in W_0\subseteq Y$
and
$f_{0}(x)\ne x$
for all
$x\in W_0$
. Then using Lemma 3.7, we get an open set W in
$I^{m}$
with
$z_{0}\in W\subseteq W_0$
such that
$f_{0}^{-1}(W)\cap W=\emptyset $
and
$f_{0}(W)\cap W=\emptyset $
. Perform a barycentric subdivision of
$\mathcal {K}$
of order s so large that W contains an m-simplex
$\sigma _{0}\in \mathcal {K}^{(s)}$
and all m-simplices
$\sigma \in \mathcal {K}^{(s)}$
adjacent to it, that is,
$\sigma \subseteq W$
for all m-simplices
$\sigma \in \mathcal {K}^{(s)}$
such that
$\sigma \cap \sigma _{0}\ne \emptyset $
. Since
$\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{\kern2pt(l)})=0$
, it is possible to obtain such a subdivision of
$\mathcal {K}$
. This completes the proof of Step 3.
Step 4: Modify
$f_{0}$
slightly to get a new piecewise affine linear map
$f\in B_{\epsilon } (h)$
that is constant on
$\sigma {}_{0}.$
To retain continuity, when we modify
$f_{0}$
on
$\sigma _{0}$
, we must also modify it on all m-simplices in
$\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
$A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
$\sigma _{j}$
is precisely an m-simplex in
$\mathcal {K}^{\kern2pt(s)}$
such that
$\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
$0\le j\le p$
. Then, it is clear that
$A\subseteq W\subseteq \Delta {}^{0}$
.
Let the vertices of
$\sigma _{0}$
be
$u_{0},\ldots , u_{m-1}$
and
$u_{m}$
, and let
$v_{j}:=f_{0}(u_{j})$
for all
$0\le j \le m$
. Then
$v_{j}\ne u_{j}$
for all
$0\le j\le m$
, because
$u_{j}\in W$
for all
$0\le j\le m$
and
$f_{0}(W)\cap W=\emptyset $
. Also, since
$u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors in
$\Delta $
, by result (ii) of Corollary 3.4, we see that
$v_0, v_1,\ldots,v_m$
are geometrically independent. Further, they are all contained in the interior of a single simplex
$\Delta _{1}$
of
$\mathcal {K}$
by Step 2. Hence, by result (iii) of Corollary 3.4, it follows that
$f_{0}(v_{j})\neq v_{j}$
for some
$0\le j\le m$
. Without loss of generality, we assume that
$f_{0}(v_{0})\neq v_{0}.$
Extend
$\{u_{0}, \ldots , u_{m}\}$
to
$\{u_{0}, \ldots , u_{k_0}\}$
with
$k_0 > m$
to include the vertices of all the simplices of
${\mathcal K}^{(s)}$
, and let
$v_{j}:= f_{0}(u_{j})$
for all
$0\leq j\leq k_0$
. Now, define f by
$$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } m<j\leq k_0,\end{cases} \end{align*} $$
and extend it piecewise affine linearly to the whole of
$|{\mathcal K}^{(s)}|= I^{m}$
. Then
$f_{0}$
is modified only on A and
$f(x)=v_{0}$
for all
$x\in \sigma _{0}$
.
Consider an arbitrary
$x\in A$
. Then
$x\in \sigma _{j}$
for some
$0\le j\le p$
. Let
$\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
$x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
$\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (3.7), we have
$$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{5}, \end{align*} $$
implying by equation (3.8) that
$$ \begin{align*} \|f(x)-h(x)\|_{\infty}\le \|f(x)-f_{0}(x)\|_{\infty}+\|f_{0}(x)-h(x)\|_{\infty} < \frac{\epsilon}{5}+\frac{\epsilon}{6}<\frac{\epsilon}{2}. \end{align*} $$
Therefore,
$f\in B_{\epsilon }(h)$
and the proof of Step 4 is completed.
Step 5. Prove that f has no square roots in
$\mathcal {C}(I^{m})$
. Since
$A\subseteq W$
,
$f=f_{0}$
on
$A^{c}$
, and
$f_{0}(W)\cap W=\emptyset $
, we see that
$f(v_{0})\neq v_{0}$
. Also, by Step 3, we have
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
$\sigma \in {\mathcal K}^{(s)}$
with
$\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
$f=f_{0}$
on
$f_{0}^{-1}(\sigma _{0})$
. Further,
$f_{0}^{-1}(\sigma _{0})$
is infinite, since
$\sigma _{0}$
is infinite and
$\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
$f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma {}_{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
$f^{-2}(v_{0})$
is infinite. Moreover,
$f|_{\sigma }$
is injective for every
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
$f^{-1}(x)$
is finite for all
$x\ne v_{0}$
in
$I^{m}$
. Thus, f satisfies the conditions of Case (ii) of Theorem 2.4, proving that it has no square roots in
$\mathcal {C}(I^{m})$
.
Theorem 3.9. Let
$h\in \mathcal {C}(I^{m})$
be such that
$h(x_{0})=x_{0}$
for some
$x_{0} \in \partial I^{m}$
. Then for each
$\epsilon>0$
, the ball
$B_{\epsilon }(h)$
of radius
$\epsilon $
around h contains a map f having a continuous iterative square root on
$I^{m}$
. In other words, the closure of
$\mathcal {W}(2;I^{m})$
contains all maps in
$\mathcal {C}(I^{m})$
that have a fixed point on the boundary of
$I^{m}$
.
Proof. Let
$h\in \mathcal {C}(I^{m})$
be such that
$h(x_{0})=x_{0}$
for some
$x_{0}\in \partial I^{m}$
. In view of Step 1 of Theorem 3.8, without loss of generality, we assume that h is piecewise affine linear on
$I^{m}$
. Since h is uniformly continuous on
$I^{m}$
, there is a
$\delta $
with
$0<\delta <{\epsilon }/{4}$
such that
$$ \begin{align} \|h(x)-h(y)\|_{\infty} <\frac{\epsilon }{4} \quad\text{whenever } x, y\in I^{m} \text{ with } \|x-y\|_{\infty}<\delta. \end{align} $$
Consider a triangulation
$\mathcal {K}$
of
$I^{m}$
with vertices
$x_{0}, x_{1}, x_{2},\ldots , x_{r}$
such that
$\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
$2$
-simplices
$\langle x_{i_{0}},x_{i_{1}}\rangle $
of
$\sigma $
and for all m-simplex
$\sigma \in \mathcal {K}$
. Let
$y_{j}:=h(x_{j})$
for all
$0\le j \le r$
and
$\sigma _{0}=\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex in
$\mathcal {K}$
having
$x_{0}$
as a vertex. Let
$\phi :I^{m} \to I^{m}$
be a homeomorphism such that
$\phi (\sigma _{0})=\overline {I^{m}\setminus \sigma _{0}}$
,
$\phi (\overline {I^{m}\setminus \sigma _{0}})= \sigma _{0}$
,
$\phi =\text {id}$
on
$\partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, and
$\phi ^{2}=\text {id}$
on
$I^{m}$
. This is where we use the assumption that
$x_{0}$
is on the boundary of
$I^{m}.$
Indeed, a little thought shows that there exists a piecewise affine linear map
$\phi $
that satisfies these conditions. Define a function
$f_{1}$
by
$$ \begin{align*} f_{1}(x_{j}) = \begin{cases} x_{j}&\text{if } x_{j}\in \sigma_{0},\\ x_{1}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\in \sigma_{0}^{0},\\ y_{j}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\notin \sigma_{0}^{0}, \end{cases} \end{align*} $$
and extend it piecewise affine linearly to the whole of
$|{\mathcal K}|= I^{m}$
. Then
$f_{1}\in \mathcal {C}(I^{m})$
such that
$f_{1}|_{\sigma _{0}}=\text {id}$
and
$f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
.
Claim.
$\rho (f_{1},h)<\epsilon $
.
Let
$x\in I^{m}$
be arbitrary. If
$x\in \sigma _{0}$
, then there exist non-negative reals
$\alpha _{0}, \alpha _{1}, \ldots , \alpha _{m}$
with
$\sum _{j=0}^{m}\alpha _{j}=1$
such that
$x=\sum _{j=0}^{m}\alpha _{j}x_{j}$
, implying by equation (3.9) that
$$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{j}f_{1}(x_{j})-\sum_{j=0}^{m}\alpha_{j}h(x_{j})\bigg\|_{\infty} \\ &\le \sum_{j=0}^{m}\alpha_{j}\{\|x_{j}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{j})\|_{\infty}\}\\ &< \frac{\epsilon }{4}+\frac{\epsilon }{4}=\frac{\epsilon}{2}, \end{align*} $$
since
$\|x_{j}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$0\le j\le m$
. If
$x\notin \sigma _{0}$
, then there exists a
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K} \text{ with } \sigma \ne \sigma_0$
such that
$x\in \sigma $
. Let
$x=\sum _{j=0}^{m}\alpha _{i_{j}}x_{i_{j}}$
, where
$\alpha _{i_{0}}, \alpha _{i_{1}}, \ldots , \alpha _{i_{m}}$
are non-negative and
$\sum _{j=0}^{m}\alpha _{i_{j}}=1$
. Then by using equation (3.9), we have
$$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{i_{j}}f_{1}(x_{i_{j}})-\sum_{j=0}^{m}\alpha_{i_{j}}h(x_{i_{j}})\bigg\|_{\infty} \le \sum_{j=0}^{m}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\&=\sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|x_{i_{j}}-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|y_{i_{j}}-y_{i_{j}}\|_{\infty} \\&\le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\{\|x_{i_{j}}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{i_{j}})\|_{\infty}\}\\& \quad + \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty} < \frac{\epsilon}{4}+\frac{\epsilon}{4}+\frac{\epsilon}{4}=\frac{3\epsilon}{4}, \end{align*} $$
since
$\|x_{i_{j}}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$0\le j\le m$
such that
$x_{i_{j}}\in \sigma _{0}$
, and
$\|x_{1}-y_{i_{j}}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$0\le j\le m$
such that
$x_{i_{j}}\notin \sigma _{0}$
and
$y_{i_{j}}\in \sigma _{0}^{0}$
. This proves the claim.
Now, define a map
$f:I^{m}\to I^{m}$
by
$$ \begin{align*} f(x) = \begin{cases} f_{1}\circ \phi(x)&\text{if } x\in \sigma_{0},\\ \phi(x)&\text{if } x\notin \sigma_{0}. \end{cases} \end{align*} $$
Since
$f_{1} \circ \phi (x)=x=\phi (x)$
for all
$x\in \partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, clearly f is continuous on
$I^{m}$
. We prove that
$\rho (f^{2},h)<\epsilon $
. Consider an arbitrary
$x\in I^{m}$
. If
$x\in \sigma _{0}$
, then
$f(x)\in \overline {I^{m}\setminus \sigma _{0}}$
, because
$\phi (x)\in \overline {I^{m}\setminus \sigma _{0}}$
and
$f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
. Therefore,
$f^{2}(x)\in \sigma _{0}$
, implying by equation (3.9) that
$$ \begin{align*} \|f^{2}(x)-h(x)\|_{\infty} \le \|f^{2}(x)-x_{0}\|_{\infty}+\|h(x_{0})-h(x)\|_{\infty} <\frac{\epsilon}{4}+\frac{\epsilon}{4}=\frac{\epsilon}{2}, \end{align*} $$
since
$\|f^{2}(x)-x_{0}\|_{\infty }\le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
. If
$x\notin \sigma _{0}$
, then
$f^{2}(x)=f_{1}(x)$
, and therefore
$\|f^{2}(x)-h(x)\|_{\infty } = \|f_{1}(x)-h(x)\|_{\infty }<{3\epsilon }/{4}$
. This completes the proof.
Now it is a natural question to ask what happens if all the fixed points of the map are in the interior of
$I^{m}$
. Theorem 10 of [Reference Humke and Laczkovich15, p. 364] shows that the map
$f(x)=1-x$
on the unit interval
$[0,1]$
, with only
$x=\tfrac 12$
as the fixed point, cannot be approximated by squares of continuous maps. In contrast, we have the following.
Example 3.10. In this example we show that, despite having no continuous square roots, the map
$f:I^{2}\to I^{2}$
defined by
$$ \begin{align*} f(x,y) = \big(1-x, \tfrac{1}{2}\big) \quad \text{for all } (x, y) \in I^{2} \end{align*} $$
having an interior point
$(x,y)=(\tfrac 12,\tfrac 12)$
as the unique fixed point can be approximated by squares of continuous maps on
$I^{2}$
. To prove that f has no continuous square roots, on the contrary, assume that
$f=g^{2}$
for some
$g\in \mathcal {C}(I^{2})$
. Since
$(1-x, \tfrac 12) \in R(g)$
, there exists
$(f_{1}(x), f_{2}(x)) \in I^{2}$
such that
$g(f_{1}(x), f_{2}(x))=(1-x, \tfrac 12)$
for each
$x\in I$
. Then
$$ \begin{align*} g\big(1-x, \tfrac{1}{2}\big)=g^{2}(f_{1}(x), f_{2}(x))=f(f_{1}(x), f_{2}(x))=\big(1-f_{1}(x), \tfrac{1}{2}\big) \quad \text{for all } x\in I, \end{align*} $$
implying that
$$ \begin{align} g\big(x, \tfrac{1}{2}\big)=\big(f_{1}(x), \tfrac{1}{2}\big) \quad \text{for all } x\in I. \end{align} $$
Therefore,
$$ \begin{align*} \big(1-x, \tfrac{1}{2}\big)=f\big(x, \tfrac{1}{2}\big)= g^{2}\big(x, \tfrac{1}{2}\big)=g\big(f_{1}(x), \tfrac{1}{2}\big)=\big(f_{1}^{2}(x), \tfrac{1}{2}\big) \quad \text{for all } x\in I, \end{align*} $$
and hence
$f_{1}^{2}(x)=1-x$
for all
$x\in I$
. Also, from equation (3.10), it follows that
$f_{1}$
is continuous on I. Thus, the map
$x\mapsto 1-x$
has a continuous square root on I, a contradiction to Corollary 2.7. Hence, f has no continuous square roots on
$I^{2}$
.
Now, to prove that f can be approximated by squares of continuous maps, consider an arbitrary
$\epsilon>0$
. Without loss of generality, we assume that
$\epsilon <\tfrac 12.$
The idea is to compress
$I^{2}$
to the small strip
$I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and then rotate this strip ninety degrees clockwise with a suitable scaling to stay within the strip. More explicitly, let
$g:I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
be defined by
$g=g_{1}\circ g_{2}$
, where
$g_{1}:I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}] \to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and
$g_{2}: I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
are given by
$$ \begin{align*} g_{1}(x,y) = \bigg(\dfrac{\epsilon-1}{2\epsilon}, \dfrac{\epsilon+1}{2}\bigg)+(x,y)\left(\begin{array}{cc} 0&-\epsilon \\ \dfrac{1}{\epsilon} &0 \end{array}\right)=\bigg(\dfrac{1}{2}+\dfrac{2y-1}{2\epsilon}, \dfrac{1}{2}- \dfrac{\epsilon(2x-1)}{2}\bigg) \end{align*} $$
and
$$ \begin{align*} g_{2}(x,y) = \begin{cases} \bigg(x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (x, y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg]. \end{cases} \end{align*} $$
Then g is continuous on
$I^{2}$
such that
$$ \begin{align*} g^{2}(x,y) = \begin{cases} \bigg(1-x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (1-x, 1-y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(1-x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg], \end{cases} \end{align*} $$
and it can be easily verified that
$\rho (f,g^{2})<\epsilon $
.
4 Continuous functions on
$\mathbb {R}^{m}$
Consider
$\mathbb {R}^{m}$
in the metric induced by the norm
$\|\cdot \|_{\infty }$
defined as in equation (3.1). Since it is a locally compact separable metric space, by Corollary 7.1 of [Reference Arens2], the compact-open topology on
$\mathcal {C}(\mathbb {R}^{m})$
is metrizable with the metric D given by
$$ \begin{align*} D(f,g)=\sum_{j=1}^{\infty}\mu_{j}(f,g) \end{align*} $$
such that
$$ \begin{align*} \mu_{j}(f,g)&=\min\bigg\{\frac{1}{2^{j}}, \rho_{j}(f,g)\bigg\}\quad \text{for all } j\in \mathbb{N},\\[6pt] \rho_{j}(f,g)&=\sup \{\|f(x)-g(x)\|_{\infty}: x\in M_{j}\}\quad \text{for all } j\in \mathbb{N}, \end{align*} $$
where
$(M_{j})_{j\in \mathbb {N}}$
is a sequence of compact sets in
$\mathbb {R}^{m}$
satisfying that
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
, and if M is any compact subset of
$\mathbb {R}^{m}$
, then
$M\subseteq \bigcup _{i=1}^{k}M_{m_{i}}$
for some finitely many
$M_{m_{1}}, M_{m_{2}}, \ldots , M_{m_{k}}$
. For convenience, we assume that
$M_{j}$
is an m-simplex of
${\mathbb R}^{m}$
for each
$j\in \mathbb {N}$
, and either
$M_{i}\cap M_{j}=\emptyset $
or
$M_{i}\cap M_{j}$
is a common face of both
$M_{i}$
and
$M_{j}$
for all
$i,j\in \mathbb {N}$
. Considering all the faces
$M_{j}$
for all
$j\in \mathbb {N}$
, we get a countable triangulation of
${\mathbb R}^{m}.$
Throughout this section, we fix one such triangulation of
${\mathbb R}^{m}.$
Lemma 4.1. Let
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex of
$\mathbb {R}^{m}$
and
$z\in \sigma $
be such that
$z\ne x_{j}$
for all
$0\le j\le m$
. Then there exists a simplicial complex
$\mathcal {L}_{\sigma }$
with the set of vertices
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
such that
$| \mathcal {L}_{\sigma }| =\sigma $
. In other words, every m-simplex of
$\mathbb {R}^{m}$
can be triangulated to have a desired point as an extra vertex.
Proof. Without loss of generality, we assume that
$z\in \langle x_{0}, x_{1}, \ldots , x_{k}\rangle ^{0}$
for some
$1\le k \le m$
, say
$z=\sum _{j=0}^{k}\alpha _{j}x_{j}$
for some strictly positive real numbers
$\alpha _{j}$
such that
$\sum _{j=0}^{k}\alpha _{j}=1$
. Then
$V_{i}:=\{x_{0}, x_{1},\ldots , x_{i-1}, z, x_{i+1},\ldots , x_{m}\}$
is geometrically independent for all
$0\le i\le k$
. In fact, for a fixed
$0\le i\le k$
, if the real numbers
$\beta _{j}$
are arbitrary such that
$\sum _{j=0}^{m}\beta _{j}=0$
and
$$ \begin{align*}\sum\limits_{\substack{0\le j \le m\\ j\ne i}}^{}\beta_{j}x_{j}+\beta_{i}z=0,\end{align*} $$
then
$$ \begin{align*} \sum_{\substack{0\le j \le k\\ j\ne i}}^{}(\beta_{j}+\beta_{i}\alpha_{j})x_{j}+\beta_{i}\alpha_{i}x_{i}+\sum_{k< j \le m}^{}\beta_{j}x_{j}=0, \end{align*} $$
and therefore by geometric independence of
$\{x_{0}, x_{1}, \ldots , x_{m}\}$
, we have
$\beta _{j}+\beta _{i}\alpha _{j}=\beta _{i}\alpha _{i}=0$
for all
$0\le j\le k$
with
$j\ne i$
, and
$\beta _{j}=0$
for all
$k<j\le m$
. This implies that
$\beta _{j}=0$
for all
$0\le j\le m$
, since
$\alpha _{i}>0$
.
Now, let
$\sigma _{i}:= \langle x_{0}, x_{1}, \ldots , x_{i-1}, z, x_{i+1}, \ldots x_{m}\rangle $
and
${\mathcal L}_{i}$
be the simplicial complex of all faces of
$\sigma _{i}$
for all
$0\le i\le k$
.
Claim.
${\mathcal L}_{\sigma }= \bigcup {}_{i=0}^{k}{\mathcal L}_{i}$
is a triangulation of
$\sigma $
with the set of vertices
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
.
Clearly,
$\mathcal {L}_{\sigma }$
is a collection of simplices of
$\mathbb {R}^{m}$
with
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
as its set of vertices. To show that it is a simplicial complex, consider an arbitrary
$\unicode{x3bb} \in \mathcal {L}_{\sigma }$
. Then
$\unicode{x3bb} \in \mathcal {L}_{i}$
for some
$0\le i\le k$
, implying that
$\kappa \in \mathcal {L}_{i}\subseteq \mathcal {L}_{\sigma }$
whenever
$\kappa $
is a face of
$\unicode{x3bb} $
, because
$\mathcal {L}_{i}$
is a simplicial complex. Next, consider any two simplices
$\unicode{x3bb} , \eta \in \mathcal {L}_{\sigma }$
. If
$\unicode{x3bb} , \eta \in \mathcal {L}_{i}$
for the same
$i\in \{0,1,\ldots ,k\}$
, then clearly
$\unicode{x3bb} \cap \eta $
is either empty or a common face of both
$\unicode{x3bb} $
and
$\eta $
, because
$\mathcal {L}_{i}$
is a simplicial complex. So, let
$\unicode{x3bb} \cap \eta \ne \emptyset $
, and suppose that
$\unicode{x3bb} \in \mathcal {L}_{i}$
and
$\eta \in \mathcal {L}_{j}$
for some
$i\ne j$
, where
$0\le i, j\le k$
. Further, assume that
$\unicode{x3bb} $
and
$\eta $
are s and t dimensional, respectively, for some
$0\le s,t\le m$
. Then it is easily seen
$\unicode{x3bb} \cap \eta $
is the l-simplex with vertex set
$V_{i}\cap V_{j}$
, where
$l=\#(V_{i}\cap V_{j})-1$
. This implies that
$\unicode{x3bb} \cap \eta \in \mathcal {L}_{i}\cap \mathcal {L}_{j}$
, and therefore it is a common face of both
$\unicode{x3bb} $
and
$\eta $
. Hence,
$\mathcal {L}_{\sigma }$
is a simplicial complex.
Now, to prove that
$\mathcal {L}_{\sigma }$
is a triangulation of
$\sigma $
, consider an arbitrary
$x\in \sigma $
. Then
$x\in \unicode{x3bb} :=\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\rangle $
for some s-dimensional face
$\unicode{x3bb} $
of
$\sigma $
, where
$0\le s\le m$
. If
$\unicode{x3bb} \in \mathcal {L}_{i}$
for some
$0\le i\le k$
, then clearly
$x\in |\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
. If
$\unicode{x3bb} \notin \mathcal {L}_{i}$
for all
$0\le i\le k$
, then there exist at least two
$i\in \{0, 1, \ldots , k\}$
such that
$(V_{\unicode{x3bb} }\!\setminus \! \{z\})\cap (V_{i}\!\setminus \!\{z\})\ne \emptyset $
, where
$V_{\unicode{x3bb} }=\{x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\}$
. This implies that
$x\in \unicode{x3bb} \subseteq \bigcup _{i\in \Gamma }|\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
, where
$\Gamma :=\{i: 0\le i\le k~\text {and}~(V_{\unicode{x3bb} }\!\setminus \!\{z\})\cap (V_{i}\setminus \{z\})\ne \emptyset \}$
. Thus the claim holds and result follows.
Lemma 4.2. Let
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
be the decomposition of
$\mathbb {R}^{m}$
fixed above, and let
$\delta _{1}, \delta _{2}, \ldots $
be a sequence of positive real numbers. Then there exists a countable triangulation
$\mathcal {K}= \bigcup _{j=1}^{\infty }{\mathcal K}_{j}$
of
$\mathbb {R}^{m}$
such that
${\mathcal K}_{j}$
is a triangulation of
$M_{j}$
and
$\mbox {diam}(\sigma )<\delta _{j}$
for all
$\sigma \in {\mathcal {K}_{j}}$
and
$j\in \mathbb {N}$
.
Proof. Perform a barycentric subdivision of the m-simplex
$M_{j}$
of sufficient order to get a simplicial complex
$\mathcal {L}_{j}$
such that
$\mbox {diam}(\sigma )<\delta _{j}$
for all
$\sigma \in \mathcal {L}_{j}$
and
$j\in \mathbb {N}$
. Then
$\mathcal {L}:=\bigcup _{j=1}^{\infty }\mathcal {L}_{j}$
is not necessarily a simplicial complex, and therefore need not be a countable triangulation of
$\mathbb {R}^{m}$
, as neighboring m-simplices
$M_{j}$
might have undergone barycentric subdivisions of different orders. Let
$\{\sigma _{1}, \sigma _{2}, \ldots \}$
be the collection of all m-simplices in
$\mathcal {L}$
and V be the set of vertices of all simplices in
$\mathcal {L}$
. Observe that V may contain some points of
$\sigma _{i}$
that are not its vertices for each
$i\in \mathbb {N}$
due to the barycentric subdivision of its neighboring m-simplices. However, there are at most finitely many such points of each
$\sigma _{i}$
, since every compact subset of
${\mathbb R}^{m}$
is contained in a finite union of m-simplices
$M_{j}$
. Now, using Lemma 4.1, we refine
$\sigma _{1}$
inductively so that we have a triangulation of
$\sigma _{1}$
, which includes all these points as vertices. Next, we consider
$\sigma _{2}$
and repeat the same procedure. Note that these refinements add new simplices but do not increase the number of vertices. So, the refinement of
$\sigma _{2}$
does not disturb that of
$\sigma _{1}$
done before. Continuing in this way, we obtain a triangulation
$\mathcal {K}_{j}$
of
$M_{j}$
for each
$j\in \mathbb {N}$
so that
$\mathcal {K}=\bigcup _{j=1}^{\infty }\mathcal {K}_{j}$
is a countable triangulation of
${\mathbb R}^{m}$
with the set of vertices
$V$
. This completes the proof.
Having the above lemmas, we are ready to prove our desired result.
Theorem 4.3. If
$h\in \mathcal {C}(\mathbb {R}^{m})$
, then for each
$\epsilon>0$
, the ball
$B_{\epsilon }(h)$
of radius
$\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
$\mathbb {R}^{m}$
. In particular,
$\mathcal {W}(2;\mathbb {R}^{m})$
does not contain any ball of
$\mathcal {C}(\mathbb {R}^{m})$
.
Proof. Let
$h\in \mathcal {C}(\mathbb {R}^{m})$
and
$\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
$f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps as done in Theorem 3.8.
Step 1: Construct a piecewise affine linear map
$f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
$\mathcal {K}$
of
$\mathbb {R}^{m}$
. Consider the decomposition
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
of
$\mathbb {R}^{m}$
fixed above. Since
$h|_{M_{j}}$
is uniformly continuous, there exists a
$\delta _{j}>0$
such that
$$ \begin{align} \|h(x)-h(y)\|_{\infty} <\frac{1}{2^{j+5}}\quad\text{whenever } x, y\in M_{j} \text{ with } \|x-y\|_{\infty}<\delta_{j} \end{align} $$
for each
$j\in \mathbb {N}$
. Also, by Lemma 4.2, there exists a triangulation
${\mathcal {K}}$
of
$\mathbb {R}^{m}$
such that
$\mbox {diam}(\sigma )<{\delta _{j}}/{4}$
for all m-simplex
$\sigma \in {\mathcal {K}}$
contained in
$M_{j}$
and for all
$j\in \mathbb {N}$
.
Let
$x_{0}, x_{1}, \ldots $
be the vertices of
${\mathcal K} .$
Choose
$y_0,y_1,\ldots$
in
$\mathbb {R}^{m}$
inductively such that
$y_{j}\ne x_{j}$
and
$$ \begin{align} \|h(x_{j})-y_{j}\|_{\infty} <\frac{\epsilon }{2^{j+6}}\quad\text{for all }j\in \mathbb{Z}_{+}, \end{align} $$
and
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
$\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in {\mathcal {K}}$
for
$i_{0}, i_{1}, \ldots , i_{m}\in \mathbb {Z}_{+}$
. This is possible by Lemma 3.6. Here, while choosing points
$y_{j}$
using Baire Category theorem with
$y_{j}\in B_{ {\epsilon }/{2^{j+6}} }(h(x_{j}))$
for all
$j\in \mathbb {Z}_{+}$
, satisfying the geometric independence condition, it is also possible to ensure that
$y_{j}\neq x_{j}$
for all
$j\in \mathbb {Z}_{+}$
. Then, for each
$j\in \mathbb {N}$
, we have
$$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon }{2^{j+5}}+2\frac{\epsilon }{2^{j+6}}=\frac{\epsilon }{2^{j+4}}, \end{align} $$
whenever
$\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
$2$
-simplex of
$\sigma $
for all m-simplex
$\sigma \in {\mathcal {K}}$
contained in
$M_{j}$
. Let
$f_{0}:|{\mathcal {K}}|=\mathbb {R}^{m} \to \mathbb {R}^{m}$
be the map
$f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
$\{x_{0}, x_{1}, \ldots \}$
and
$\{y_{0}, y_{1}, \ldots \}$
, respectively. Then
$f_{0}$
is a continuous piecewise affine linear self-map of
$\mathbb {R}^{m}$
satisfying that
$f_{0}(x_{j})=y_{j}$
for all
$j\in \mathbb {Z}_{+}$
. Also, by using result (i) of Lemma 3.1, we have
$R(f_{0})^{0}\ne \emptyset $
, and
$f_{0}|_{\sigma }$
is injective for all
$\sigma \in {\mathcal {K}}$
contained in
$M_{j}$
for all
$j\in \mathbb {N}$
. Further, from equation (4.3) we have
$$ \begin{align} \mbox{diam}(f_{0}(\sigma ))<\frac{\epsilon }{2^{j+4}}\quad\text{for all } \sigma \in {\mathcal{K}}~\text{contained in}~M_{j}~\text{and for all}~j\in \mathbb{N}. \end{align} $$
Claim.
$D(f_{0},h)<{\epsilon }/{4}$
.
Consider arbitrary
$j\in \mathbb {N}$
and
$x\in M_{j}$
. Then x is in the interior of a unique k-simplex
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
${\mathcal {K}}$
contained in
$M_j$
for some
$0\le k\le m$
. Let
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (4.1) and (4.2), we have
$$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon}{2^{j+6}}+\frac{\epsilon}{2^{j+5}}\nonumber \\ &< \frac{\epsilon}{2^{j+4}}, \end{align} $$
since
$\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<\delta _{j}$
for all
$0\le j\le k$
. Therefore,
$\rho _{j}(f_{0}, h) \le {\epsilon }/{2^{j+4}}<{\epsilon }/{2^{j+2}}$
for all
$j\in \mathbb {N}$
, implying that
$D(f_{0}, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
.
Step 2: Obtain an m-simplex
$\Delta \in {\mathcal {K}}$
contained in
$M_{r}$
for some
$r\in \mathbb {N}$
containing a non-empty open set
$Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
$f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
$\Delta _{1}$
in
${\mathcal K}$
. Consider any m-simplex
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
$\mathcal {K}$
. Since
$\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
$f_{0}(Z)$
is open in
$\mathbb {R}^{m}$
for each open subset Z of
$\sigma ^{0}$
. Choose a sufficiently small non-empty open subset
$Y_{0}$
of
$f_0(\sigma )^{0}$
such that
$Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
$\Delta \in \mathcal {K}$
contained in
$M_r$
for some
$r \in \mathbb{N}$
. Then
$f_{0}(Y_{0})$
has non-empty interior. Again, choose a non-empty open subset Y of
$Y_{0}$
so small that
$f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
$\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
Step 3: Show that there exists a barycentric subdivision
$\mathcal {K}^{\kern2pt(s)}$
of
${\mathcal {K}}$
for some
$s \in \mathbb {N}$
with an m-simplex
$\sigma _{0}\in \mathcal {K}^{\kern2pt(s)}$
such that
$\sigma _{0}\subseteq Y$
, and
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
$f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \cap \sigma _{0}\ne \emptyset $
. The proof is similar to that of Step 3 of Theorem 3.8.
Step 4: Modify
$f_{0}$
slightly to get a new piecewise affine linear map
$f\in B_{\epsilon } (h)$
that is constant on
$\sigma {}_{0}.$
The proof is similar to that of Step 4 of Theorem 3.8; however, we give the details here for clarity. To retain continuity, when we modify
$f_{0}$
on
$\sigma _{0}$
, we must also modify it on all m-simplices in
$\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
$A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
$\sigma _{j}$
is precisely an m-simplex in
$\mathcal {K}^{\kern2pt(s)}$
such that
$\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
$0\le j\le p$
. Then, clearly
$A\subseteq W\subseteq \Delta^{0}$
, where W is as chosen in Step 3.
Let the vertices of
$\sigma _{0}$
be
$u_{0},\ldots , u_{m-1}$
and
$u_{m}$
, and let
$v_{j}:=f_{0}(u_{j})$
for all
$0\le j \le ~m$
. Then
$v_{j}\ne u_{j}$
for all
$0\le j\le m$
, because
$u_{j}\in W$
for all
$0\le j\le m$
and
$f_{0}(W)\cap W=\emptyset $
. Also, as
$u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors contained in
$\Delta $
, by result (ii) of Corollary 3.4, we see that
$v_0, v_1,\ldots,v_m$
are geometrically independent. Further, by Step 2, they are all contained in the interior of a single simplex
$\Delta {}_{1}$
of
${\mathcal {K}}$
. Hence, by result (iii) of Corollary 3.4, we have
$f_{0}(v_{j})\neq v_{j}$
for some
$0\le j\le m$
. Without loss of generality, we assume that
$f_{0}(v_{0})\neq v_{0}.$
Extend
$\{u_{0}, \ldots , u_{m}\}$
to
$\{u_{0}, u_{1}, \ldots \}$
to include the vertices of all the simplices of
${\mathcal K}^{(s)}$
and let
$v_{j}:= f_{0}(u_{j})$
for all
$j \in \mathbb {Z}_{+}$
. Now, define f by
$$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } j>m,\end{cases} \end{align*} $$
and extend it countably piecewise affine linearly to the whole of
$|{\mathcal K}^{(s)}|= \mathbb {R}^{m}$
. Then
$f_{0}$
is modified only on A and
$f(x)=v_{0}$
for all
$x\in \sigma _{0}$
.
Consider an arbitrary
$x\in A$
. Then
$x\in \sigma _{j}$
for some
$0\le j\le p$
. Let
$\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
$x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
$\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (4.4), we have
$$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{2^{r+4}}, \end{align*} $$
implying by equation (4.5) that
$$ \begin{align*} \|f(x)-h(x)\|_{\infty}\le \|f(x)-f_{0}(x)\|_{\infty}+\|f_{0}(x)-h(x)\|_{\infty} < \frac{\epsilon}{2^{r+4}}+\frac{\epsilon}{2^{r+4}}<\frac{\epsilon}{2^{r+3}}. \end{align*} $$
Therefore,
$\rho _{r}(f, h)< {\epsilon }/{2^{r+2}}$
. Also, we have
$\rho _{j}(f, h)=\rho _{j}(f_{0},h)<{\epsilon }/{2^{j+2}}$
for
$j\ne r$
. Hence,
$D(f, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
, proving that
$f\in B_{\epsilon }(h)$
.
Step 5. Prove that f has no square roots in
$\mathcal {C}(\mathbb {R}^{m})$
. It is clear that
$f(v_{0})\neq v_{0}$
, because
$A\subseteq W$
,
$f=f_{0}$
on
$A^{c}$
and
$f_{0}(W)\cap W=\emptyset $
. Also, by Step 3, we have
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
$\sigma \in {\mathcal K}^{(s)}$
with
$\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
$f=f_{0}$
on
$f_{0}^{-1}(\sigma _{0})$
. Further,
$f_{0}^{-1}(\sigma _{0})$
is uncountable, since
$\sigma _{0}$
is uncountable and
$\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
$f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma _{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
$f^{-2}(v_{0})$
is uncountable. Moreover,
$f|_{\sigma }$
is injective for every
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
$f^{-1}(x)$
is countable for all
$x\ne v_{0}$
in
$\mathbb {R}^{m}$
. Thus, f satisfies the hypothesis of Case (iii) of Theorem 2.4, proving that f has no square roots in
$\mathcal {C}(\mathbb {R}^{m})$
.
We have seen in Theorem 3.8 (respectively Theorem 4.3) that each open neighborhood of each map in
$\mathcal {C}(I^{m})$
(respectively in
$\mathcal {C}(\mathbb {R}^{m})$
) has a continuous map which does not have even discontinuous square roots. Additionally, if X and Y are locally compact Hausdorff spaces, and
$\phi :X\to Y$
is a homeomorphism, then the map
$f\mapsto \phi \circ f\circ \phi ^{-1}$
is a homeomorphism of
$\mathcal {C}(X)$
onto
$\mathcal {C}(Y)$
, where both
$\mathcal {C}(X)$
and
$\mathcal {C}(Y)$
have the compact-open topology, and moreover
$f=g^{2}$
on X if and only if
$\phi \circ f\circ \phi ^{-1} = (\phi \circ g\circ \phi ^{-1})^{2}$
on Y. Hence, it follows that Theorem 3.8 (respectively Theorem 4.3) is true if
$I^{m}$
(respectively
$\mathbb {R}^{m}$
) is replaced by any topological space homeomorphic to it. For the same reason, Theorem 3.9 is also true if
$I^{m}$
is replaced by any topological space homeomorphic to it.
5
$L^{p}$
denseness of iterative squares in
$\mathcal {C}(I^{m})$
In this section, we prove that the iterative squares of continuous self-maps on
$I^{m}$
are
$L^{p}$
dense in
$\mathcal {C}(I^{m})$
. Given any nontrivial compact subintervals
$I_{1}, I_{2}, \ldots , I_{m}$
of I, let
$I_{1}\times I_{2}\times \cdots \times I_{m}$
denote the closed rectangular region in
$I^{m}$
defined by
$$ \begin{align*}I_{1}\times I_{2}\times \cdots \times I_{m}=\{(x_{1},x_{2}, \ldots, x_{m}): x_{i}\in I_{i} ~\text{for}~1\le i \le m\}.\end{align*} $$
Consider
$\mathcal {C}(I^{m})$
in the
$L^{p}$
norm defined by
$$ \begin{align*} \|f\|_{p}=\bigg(\int_{I^{m}}^{} \|f(x)\|_{\infty}^{p}\,d\mu(x) \bigg)^{{1}/{p}}, \end{align*} $$
where
$\mu $
is the Lebesgue measure on
${\mathbb R}^{m}$
. First, we prove a result which gives a sufficient condition for extending a given function to a square.
Theorem 5.1. Let K be a proper closed subset of
$I^{m}$
and
$f:K\to I^{m}$
be continuous. Then there exists a
$g\in \mathcal {C}(I^{m})$
such that
$f=g^{2}|_{K}$
.
Proof. Let
$I_{1}\times I_{2}\times \cdots \times I_{m}$
be a closed rectangular region in
$I^{m}\setminus K$
and
$\tilde {g}$
be a homeomorphism of K into
$I_{1}\times I_{2}\times \cdots \times I_{m}$
. Extend
$\tilde {g}$
to
$K\cup R(\tilde {g})$
by setting
$g(x)=f(\tilde {g}^{-1}(x))$
for
$x\in R(\tilde {g})$
. Then g is continuous on the closed set
$K\cup R(\tilde {g})$
, and therefore, by an extension of Tietze’s extension theorem by Dugundji (see Theorem 4.1 and Corollary 4.2 of [Reference Dugundji11, pp. 357–358]), it has an extension to a continuous self-map of
$I^{m}$
, which also we denote by g. Further, for each
$x\in K$
, we have
$$ \begin{align*} g^{2}(x)&=g(g(x))\\[3pt] &=g(\tilde{g}(x))\\[3pt] &=f(\tilde{g}^{-1}(\tilde{g}(x)))~~(\text{since}~\tilde{g}(x)\in R(\tilde{g}))\\[3pt] &=f(x), \end{align*} $$
implying that
$f=g^{2}|_{K}$
.
It is worth noting that the assumption in the above theorem that K is a proper subset of
$I^{m}$
cannot be dropped. Indeed, if
$K=I$
, then the continuous map
$f(x)=1-x$
on K has no square roots in
$\mathcal {C}(I)$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426] or Corollary 2.7). Such maps can be constructed on
$K=I^{m}$
for general m using Theorem 2.6. We now prove our desired result.
Theorem 5.2.
$\mathcal {W}(2;I^{m})$
is
$L^{p}$
dense in
$\mathcal {C}(I^{m})$
.
Proof. Consider an arbitrary
$f\in \mathcal {C}(I^{m})$
. Then, by Theorem 5.1, for each
$\epsilon>0$
, there exists a map
$g_{\epsilon } \in \mathcal {C}(I^{m})$
such that
$f|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}=g_{\epsilon }^{2}|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}$
, where
$I_{\epsilon }=[\epsilon , 1]$
. Now,
$$ \begin{align*} \|g_{\epsilon}^{2}-f\|_{p}^{p}&=\int_{I^{m}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty }^{p}\,d\mu(x)\\[3pt] &=\int_{({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty}^{p}\,d\mu(x)\\[3pt] &\le \mu(({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c})\\[3pt] &=1-(1-\epsilon)^{m}, \end{align*} $$
implying that
$\|g_{\epsilon }^{2}-f\|_{p} \to 0$
as
$\epsilon \to 0$
. Hence,
$\lim \nolimits _{\epsilon \to 0}g_{\epsilon }^{2}=f$
in
$L^{p}$
, and the result follows.
Acknowledgements
The authors are grateful to the referee for his/her many helpful comments. B.V.R.B. is supported by J C Bose Fellowship of the Science and Engineering Board, India. C.G. is supported by the Indian Statistical Institute, Bangalore through J C Bose Fellowship of B.V.R.B., and by the National Board for Higher Mathematics, India through No: 0204/3/2021/R&D-II/7389.
Open access
