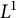1 Introduction
One of the fundamental results to estimate asymptotic entropy in different contexts is the Shannon–McMillan–Breiman theorem [Reference BreimanBre, Reference McMillanMcM53, Reference ShannonSha48]. The analog of the Shannon–McMillan–Breiman theorem for stationary processes on uncountable spaces was developed over 20 years. It started in 60s by Moy [Reference MoyMoy], Perez [Reference PerezPer64], and Kieffer [Reference Kaimanovich and VershikKie], and completed in mid-80s by Barron [Reference BarronBar] and Algoet-Cover [Reference Algoet and CoverAC]. In the context of random walks on countable groups, Derriennic [Reference DerriennicDer80] and Kaimanovich and Vershik [Reference KiefferKV] proved the Shannon–McMillan–Breiman theorem. Their proofs heavily use Kingman’s subadditive ergodic theorem, which fails for random walks on noncountable locally compact groups. Derriennic [Reference DerriennicDer80] asked if one can establish similar results in the context of random walks on noncountable locally compact groups. Although the analog of the Shannon–McMillan–Breiman theorem for stationary processes on continuous spaces was completed in 80s, its analog for random walks on noncountable locally compact groups remained unsolved in the last 40 years, until, in a recent result [Reference Forghani and TiozzoFT22], Forghani and Tiozzo provided a weak version of the Shannon–McMillan–Breiman theorem for random walks on locally compact groups.
One of the questions remaining unsolved to complete the entropy theory of random walks on locally compact groups is proving (or disproving) strong versions of the Shannon–McMillan–Breiman theorem such as almost sure and
$L^1$
convergences. The goal of this short note is to provide an upper bound for the exponential growth of convolutions of a probability density function along almost every sample path for a vast class of random walks on compactly generated groups, Theorem 1.2. As a consequence of this result, we prove strong versions of the Shannon–McMillan–Breiman theorem for groups with subexponential growth, Theorem 1.3.
Let G be a locally compact group (that includes being second countable and Hausdorff) with the unique (up to a positive multiplicative constant) left Haar measure m. Let
$\mu $
be a Borel probability measure on G. We say that
$\mu $
is absolutely continuous if
$\mu $
is absolutely continuous with respect to the left Haar measure m. We denote by
$\frac {d\mu }{dm}$
the Radon–Nikodym derivative of
$\mu $
with respect to m, and by
$\mu ^{*n}$
the n-fold convolution of
$\mu $
. Note that when
$\mu $
is absolutely continuous,
$\mu ^{*n}$
is also absolutely continuous. The n-fold convolution of
$\mu $
is related to the random walk generated by
$\mu $
on G. Let
$(g_i)_{i \geq 1}$
be a sequence of independent identically
$\mu $
-distributed random variables. The position of the random walk
$(G,\mu )$
at time n is
$$ \begin{align*}x_n = g_1g_2 \cdots g_n. \end{align*} $$
By the definition of the n-fold convolution, the distribution of the random variable
$x_n$
is
$\mu ^{*n}$
. A sequence of
${\boldsymbol {x}}=(x_n)_{n\geq 1} $
is called a sample path of the random walk
$(G,\mu )$
. Let
$(\Omega , {\mathbb {P}})$
be the space of sample paths of the random walk
$(G,\mu )$
. The differential entropy of
$\mu ^{*n}$
with respect to m is
$$ \begin{align*}H_n=- \int_G \log {\frac{d\mu^{*n}}{dm}}(g) d\mu^{*n}(g). \end{align*} $$
Note that if G is not a countable group, then
$H_n$
could be negative. For example, let
$G=\Bbb R$
and
$\mu $
be uniformly distributed on the interval
$[-1/4,1/4]$
, then
$H_1<0$
.
Conjecture 1.1 (Strong the Shannon–McMillan–Breiman)
Let G be a locally compact group. Let
$\mu $
be an absolutely continuous probability measure on G with bounded density. If
$H_n< \infty $
for all n, then for
${\mathbb {P}}$
-almost every sample path
$(x_n)$
, and
$$ \begin{align*}-\frac{1}{n} \log \frac{d\mu^{*n}}{dm}(x_n) \to h(\mu) \end{align*} $$
in
$L^1(\Omega , {\mathbb {P}})$
, where
$h(\mu ) = \lim _{n\to \infty }\frac {H_n}{n}$
.
Note that under the assumptions in Conjecture 1.1,
$h(\mu )$
exists and is finite. The invariant quantity
$h(\mu )$
is called the asymptotic entropy of
$\mu $
and plays a crucial role in understanding bounded harmonic functions and the Poisson boundary of a random walk. For instance, when the asymptotic entropy is finite,
$h(\mu )=0$
if and only if all bounded harmonic functions are constant (equivalently, the Poisson boundary is trivial; see [Reference DerriennicDer80, Reference KiefferKV]. A version of the Shannon–McMillan–Breiman theorem is used to prove ray and strip approximations, fundamental criteria to identify the Poisson boundary and bounded harmonic functions of a random walk (see [Reference Forghani and TiozzoFT22, Reference KaimanovichKai00] for more details).
Conjecture 1.1 has been solved when G is a countable group by Kaimanovich and Vershik [Reference KiefferKV] and Derriennic [Reference DerriennicDer80] by using the subadditive ergodic theorem. In the recent development, Forghani and Tiozzo [Reference Forghani and TiozzoFT22] established a weak version of Conjecture 1.1 for random walks on locally compact groups, that is, for
${\mathbb {P}}$
-almost every sample path
$(x_n)$
,
$$ \begin{align} \liminf_{n\to\infty} -\frac{1}{n} \log \frac{d\mu^{*n}}{dm}(x_n) = h(\mu). \end{align} $$
This paper is devoted to investigating Conjecture 1.1. Let K be a symmetric compact subset of G that generates G, that is,
$G=<K>$
. Hence,
$\cup _{n=0}^{\infty } K^n = G$
. The growth of K is
$$ \begin{align*}v(K)= \limsup_{n\to\infty} \frac{\log m(K^n)}{n}. \end{align*} $$
Note that
$v(K)$
is finite (see, for instance, [Reference Forghani and TiozzoFT22]). We say G has a subexponential growth if
$v(K)=0$
for one (equivalently, for every) compact symmetric generator K. For a probability measure
$\mu $
with the compact support K, we define
$v_{\mu }$
to be the growth of its support, that is,
$v_{\mu }= v(K)$
.
Theorem 1.2 Let G be a compactly generated locally compact group. Let
$\mu $
be an absolutely continuous probability measure on G with an almost everywhere bounded density function. If the support of
$\mu $
is compact, then for almost every sample path
${\boldsymbol {x}}=(x_n)$
, we have
$$ \begin{align} h(\mu) \leq \limsup_{n\to\infty}-\frac1n\log \frac{d\mu^{*n}}{dm}(x_n) \leq v_{\mu}. \end{align} $$
Note that the first inequality in (2) follows from (1). The inequality
$h(\mu ) \leq v_{\mu }$
is a consequence of properties of differential entropy (see [Reference DerriennicDer80]). Our contribution is to show that the second inequality in (2) also holds. We prove this theorem in the next section. Even the fact that the limsup should be bounded is not straightforward. The proof is inspired by techniques in [Reference Forghani and TiozzoFT22]. As an application of Theorem 1.2, we affirmatively answer Conjecture 1.1 when G has a subexponential growth.
Theorem 1.3 Let G be a compactly generated locally compact group of subexponential growth. Let
$\mu $
be an absolutely continuous probability measure on G with an almost everywhere bounded density function. If the support of
$\mu $
is compact, then for almost every sample path
${\boldsymbol {x}}=(x_n)$
, and
$$ \begin{align*}\lim_{n\to\infty}\frac1n\log \frac{d\mu^{*n}}{dm}(x_n) = 0 \end{align*} $$
in
$L^1(\Omega , {\mathbb {P}})$
.
Remark 1.4 A compactly generated group has polynomial growth if there exists
$d>0$
such that
$m(K^n) =O(n^d)$
for some compact symmetric generator K. The class of subexponential groups includes groups with polynomial growth. By Gromov’s result, a finitely generated group has polynomial growth if and only if it is virtually nilpotent. More generally, for compactly generated locally compact groups, Losert [Reference LosertLos01] proved that polynomial growth is equivalent to an existence of a normal series of normal closed subgroups
$\{e\} \subset \cdots G_1 \subset G_n=G$
such that
$G_i/G_{i+1}$
is an
$\overline {\mbox {FC}}$
-group for
$i=0,\ldots , n$
.
Remark 1.5 Note that Erschler [Reference ErschlerErs04] provided examples of countable groups with subexponential growth which admit symmetric probability measures with finite entropy such that the asymptotic entropy is positive. Indeed, those probability measures are infinitely supported (hence not compactly supported) and do not contradict Theorem 1.3.
2 Proof of theorems
Proof of Theorem 1.2
The proof relies on the Borel–Cantelli lemma. Let K be the support of the probability measure
$\mu $
. The support of
$\mu ^{*n}$
is
$K^n$
. For almost every sample path
${\boldsymbol {x}}=(x_n)$
, define
$$ \begin{align*}F_n({\boldsymbol{x}}) = \begin{cases} \Big({\frac{d\mu^{*n}}{dm}} { (x_n)}\Big)^{-1}, & x_n \in K^n,\\ 0, & \mbox{otherwise.}\\ \end{cases} \end{align*} $$
Note that
${\frac {d\mu ^{*n}}{dm}}$
is a density function, so
${\frac {d\mu ^{*n}}{dm}}(x)>0$
for
$\mu ^{*n}$
-almost every x in G. Hence,
$F_n({\boldsymbol {x}})$
is well defined. Let
$$ \begin{align*}\limsup_{n\to\infty}\frac{1}{n} \log m(K^n)=v_{\mu}=v. \end{align*} $$
For
$\epsilon>0$
, define
$$ \begin{align*}B_n(\epsilon)=B_n=\Big\{ {\boldsymbol{x}} \in \Omega \ :\ 1 \leq e^{-n(\epsilon+v)} F_n({\boldsymbol{x}}) \Big\}. \end{align*} $$
The definition of the measurable set
$B_n$
implies that
$$ \begin{align} {\mathbb{P}}(B_n) = \int_{B_n} d{\mathbb{P}} \leq e^{-n(\epsilon+v)} \int_{\Omega} F_n({\boldsymbol{x}}) d{\mathbb{P}}({\boldsymbol{x}}). \end{align} $$
Because
$F_n({\boldsymbol {x}})$
only depends on the nth position of the sample path
${\boldsymbol {x}}$
, the Markovian property of the random walk implies that
$$ \begin{align} \int_{\Omega} F_n({\boldsymbol{x}}) d{\mathbb{P}}({\boldsymbol{x}}) = \int_{\{{\boldsymbol{x}}:\ x_n=g \}} F_n({\boldsymbol{x}}) d\mu^{*n}(g). \end{align} $$
Using the definition of
$F_n$
in the above equation yields
$$ \begin{align} \int_{\Omega} F_n({\boldsymbol{x}}) d{\mathbb{P}}({\boldsymbol{x}}) =\int_{K^n} \Big({\frac{d\mu^{*n}}{dm}}(g) \Big)^{-1} d\mu^{*n}(g)= \int_{K^n} 1 d m(g)= m(K^n). \end{align} $$
By combining (3) and (5), we obtain
$$ \begin{align*}{\mathbb{P}}(B_n) \leq e^{-n(\epsilon+v)} m(K^n). \end{align*} $$
Because
$\epsilon +v>0$
, we deduce that
$\sum _n {\mathbb {P}}(B_n)<\infty , $
and applying the Borel–Cantelli lemma implies that
$$ \begin{align*}{\mathbb{P}}(\limsup_{n\to\infty} B_n) =0. \end{align*} $$
Therefore, the complement of
$B_n$
occurs for n sufficiently large. We conclude that for
$\epsilon>0$
, for n sufficiently large, and for almost every
${\boldsymbol {x}}$
in
$\Omega $
,
$$ \begin{align*}e^{n(\epsilon+v)} \geq F_n({\boldsymbol{x}}) \implies n (\epsilon+v) \geq \log F_n({\boldsymbol{x}}); \end{align*} $$
therefore,
$\limsup _{n\to \infty } \frac 1n \log F_n({\boldsymbol {x}}) \leq (\epsilon +v)$
for every
$\epsilon> 0$
, which implies the desired result after letting
$\epsilon $
decrease to
$0$
.
Proof of Theorem 1.3: almost sure convergence
Note that for every g in G and for every natural number n, we can write
$$ \begin{align*}{\frac{d\mu}{dm}}^{*(n+1)}(g) = \int_G {\frac{d\mu}{dm}}(x^{-1} g) d\mu^{*n}(x) \leq \left\| {\frac{d\mu}{dm}}\right\|_{\infty} \int _G d\mu^{*n}(x)= \left\| {\frac{d\mu}{dm}}\right\|_{\infty}. \end{align*} $$
For every sample path
${\boldsymbol {x}} =(x_n)$
,
$$ \begin{align} \limsup_{n\to \infty} \frac1n\log {\frac{d\mu^{*n}}{dm}}(x_n) \leq \limsup_{n\to \infty} \frac1n \log \left\|{\frac{d\mu}{dm}}\right\|_{\infty} = 0. \end{align} $$
Since G has subexponential growth, hence
$v=0$
. Applying Theorem 1.2, we obtain for
${\mathbb {P}}$
-almost every sample path
${\boldsymbol {x}}$
in
$\Omega $
$$ \begin{align} \limsup_{n\to\infty} - \frac1n \log {\frac{d\mu^{*n}}{dm}}(x_n) \leq 0. \end{align} $$
Because
$\limsup _{n\to \infty } - \frac 1n \log {\frac {d\mu ^{*n}}{dm}}(x_n) = -\liminf _{n\to \infty } \frac 1n \log {\frac {d\mu ^{*n}}{dm}}(x_n)$
, combining with (6) yields
$$ \begin{align*}\limsup_{n\to\infty}\frac1n \log {\frac{d\mu^{*n}}{dm}}(x_n) \leq 0 \leq \liminf_{n\to\infty} \frac1n \log {\frac{d\mu^{*n}}{dm}}(x_n), \end{align*} $$
and hence
$\frac 1n \log {\frac {d\mu ^{*n}}{dm}}(x_n) \to 0$
as
$n \to \infty $
for almost every sample path
${\boldsymbol {x}}=(x_n)$
.
Proof of Theorem 1.3:
$L^1$
convergence
The proof follows from Scheffé’s lemma (see, for example, [Reference WilliamsWil91, 5.10]). We have
$\frac 1n\log {\frac {d\mu ^{*n}}{dm}}(x_n) \to 0$
for almost every sample path
${\boldsymbol {x}}=(x_n)$
. Define
$$ \begin{align*}b_n = \frac1n \log\left\| {\frac{d\mu}{dm}}\right\|_{\infty} - \frac1n \log {\frac{d\mu^{*n}}{dm}}(x_n). \end{align*} $$
We have
$b_n \geq 0$
and
$$ \begin{align*}\int_{\Omega} b_n d {\mathbb{P}} = \frac1n \log\left\| {\frac{d\mu}{dm}}\right\|_{\infty}+ \frac1n H_n \to 0. \end{align*} $$
Thus,
$b_n \to 0$
in
$L^1(\Omega , {\mathbb {P}})$
. Also,
$\frac 1n \log \left\| {\frac {d\mu }{dm}}\right\|_{\infty } \to 0$
in
$L^1(\Omega , {\mathbb {P}})$
. Therefore,
$\frac 1n\log {\frac {d\mu ^{*n}}{dm}}(x_n) \to 0$
in
$L^1(\Omega , {\mathbb {P}})$
.
Open access
