Ontologies play a key role in the advent of the Semantic Web. An important problem when dealing with ontologies is the modification of an existing ontology in response to a certain need for change. This problem is a complex and multifaceted one, because it can take several different forms and includes several related subproblems, like heterogeneity resolution or keeping track of ontology versions. As a result, it is being addressed by several different, but closely related and often overlapping research disciplines. Unfortunately, the boundaries of each such discipline are not clear, as the same term is often used with different meanings in the relevant literature, creating a certain amount of confusion. The purpose of this paper is to identify the exact relationships between these research areas and to determine the boundaries of each field, by performing a broad review of the relevant literature.

Computational social choice is a new discipline currently emerging at the interface of social choice theory and computer science. It is concerned with the application of computational techniques to the study of social choice mechanisms, and with the integration of social choice paradigms into computing. The first international workshop specifically dedicated to this topic took place in December 2006 in Amsterdam, attracting a mix of computer scientists, people working in artificial intelligence and multiagent systems, economists, game and social choice theorists, logicians, mathematicians, philosophers, and psychologists as participants.

In this paper we introduce the concept of Kleisli strength for monads in an arbitrary symmetric monoidal category. This generalises the notion of commutative monad and gives us new examples, even in the cartesian-closed category of sets. We exploit the presence of Kleisli strength to derive methods for generating distributive laws. We also introduce linear equations to extend the results to certain quotient monads. Mechanisms are described for finding strengths that produce a large collection of new distributive laws, and consequently monad compositions, including the composition of monadic data types such as lists, trees, exceptions and state.

Pure Pattern Type Systems (P2TS) combine the frameworks and capabilities of rewriting and λ-calculus within a unified setting. Their type systems, which are adapted from Barendregt's λ-cube, are especially interesting from a logical point of view. Until now, strong normalisation, which is an essential property for logical soundness, has only been conjectured: in this paper, we give a positive answer for the simply-typed system and the dependently-typed system.

The proof is based on a translation of terms and types from P2TS into the λ-calculus. First, we deal with untyped terms, ensuring that reductions are faithfully mimicked in the λ-calculus. For this, we rely on an original encoding of the pattern matching capability of P2TS into the System Fω.

Then we show how to translate types: the expressive power of System Fω is needed in order to fully reproduce the original typing judgments of P2TS. We prove that the encoding is correct with respect to reductions and typing, and we conclude with the strong normalisation of simply-typed P2TS terms. The strong normalisation with dependent types is in turn obtained by an intermediate translation into simply-typed terms.

The two expressions ‘The cumulative hierarchy’ and ‘The iterative conception of sets’ are usually taken to be synonymous. However, the second is more general than the first, in that there are recursive procedures that generate some ill-founded sets in addition to well-founded sets. The interesting question is whether or not the arguments in favour of the more restrictive version – the cumulative hierarchy – were all along arguments for the more general version.

Semantic technologies promise to solve many challenging problems of the present Web applications. As they achieve a feasible level of maturity, they become increasingly accepted in various business settings at enterprise level. By contrast, their usability in open environments such as the Web—with respect to issues such as scalability, dynamism and openness—still requires additional investigation. In particular, Semantic Web services have inherited the Web service communication model, which is primarily based on synchronous message exchange technology such as remote procedure call (RPC), thus being incompatible with the REST (REpresentational State Transfer) architectural model of the Web. Recent advances in the field of middleware propose ‘semantic tuplespace computing’ as an instrument for coping with this situation. Arguing that truly Web-compliant Web service communication should be based, analogously to the conventional Web, on shared access to persistently published data instead of message passing, space-based middleware introduces a coordination infrastructure by means of which services can exchange information in a time- and reference-decoupled manner. In this article, we introduce the most important approaches in this newly emerging field. Our objective is to analyze and compare the solutions proposed so far, thus giving an account of the current state-of-the-art, and identifying new directions of research and development.

This paper traces the evolution of thinking on how mathematics relates to the world—from the ancients, through the beginnings of mathematized science in Galileo and Newton, to the rise of pure mathematics in the nineteenth century. The goal is to better understand the role of mathematics in contemporary science.

One interpretation of the conditional If P then Q is as saying that the probability of Q given P is high. This is an interpretation suggested by Adams (1966) and pursued more recently by Edgington (1995). Of course, this probabilistic conditional is nonmonotonic, that is, if the probability of Q given P is high, and R implies P, it need not follow that the probability of Q given R is high. If we were confident of concluding Q from the fact that we knew P, and we have stronger information R, we can no longer be confident of Q. We show nonetheless that usually we would still be justified in concluding Q from R. In other words, probabilistic conditionals are mostly monotonic.

Multi-agent systems are complex systems in which multiple autonomous entities, called agents, cooperate in order to achieve a common or personal goal. These entities may be computer software, robots, and also humans. In fact, many multi-agent systems are intended to operate in cooperation with or as a service for humans. Typically, multi-agent systems are designed assuming perfectly rational, self-interested agents, according to the principles of classical game theory. Recently, such strong assumptions have been relaxed in various ways. One such way is explicitly including principles derived from human behavior. For instance, research in the field of behavioral economics shows that humans are not purely self-interested. In addition, they strongly care about fairness. Therefore, multi-agent systems that fail to take fairness into account, may not be sufficiently aligned with human expectations and may not reach intended goals. In this paper, we present an overview of work in the area of fairness in multi-agent systems. More precisely, we first look at the classical agent model, that is, rational decision making. We then provide an outline of descriptive models of fairness, that is, models that explain how and why humans reach fair decisions. Then, we look at prescriptive, computational models for achieving fairness in adaptive multi-agent systems. We show that results obtained by these models are compatible with experimental and analytical results obtained in the field of behavioral economics.

The integration of first-order and higher-order paradigms has been one of the main challenges in the design of both declarative programming languages and proof environments. It has led to the development of new computation models and new logical frameworks, which have been obtained by enriching first-order rewriting with higher-order capabilities or by adding algebraic features to the λ-calculus.

Several philosophers have argued that the logic of set theory should be intuitionistic on the grounds that the open-endedness of the set concept demands the adoption of a nonclassical semantics. This paper examines to what extent adopting such a semantics has revisionary consequences for the logic of our set-theoretic reasoning. It is shown that in the context of the axioms of standard set theory, an intuitionistic semantics sanctions a classical logic. A Kripke semantics in the context of a weaker axiomatization is then considered. It is argued that this semantics vindicates an intuitionistic logic only insofar as certain constraints are put on its interpretation. Wider morals are drawn about the restrictions that this places on the shape of arguments for an intuitionistic revision of the logic of set theory.

We show that the set of ultimately true sentences in Hartry Field's Revenge-immune solution model to the semantic paradoxes is recursively isomorphic to the set of stably true sentences obtained in Hans Herzberger's revision sequence starting from the null hypothesis. 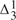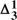We further remark that this shows that a substantial subsystem of second-order number theory is needed to establish the semantic values of sentences in Field's relative consistency proof of his theory over the ground model of the standard natural numbers: -CA0 (second-order number theory with a -comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.

A decision procedure (PrSAT) for classical (Kolmogorov) probability calculus is presented. This decision procedure is based on an existing decision procedure for the theory of real closed fields, which has recently been implemented in Mathematica. A Mathematica implementation of PrSAT is also described, along with several applications to various non-trivial problems in the probability calculus.

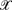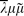is an untyped continuation-style formal language with a typed subset that provides a Curry–Howard isomorphism for a sequent calculus for implicative classical logic. can also be viewed as a language for describing nets by composition of basic components connected by wires. These features make an expressive platform on which many different (applicative) programming paradigms can be mapped. In this paper we will present the syntax and reduction rules for ; in order to demonstrate its expressive power, we will show how elaborate calculi can be embedded, such as the λ-calculus, Bloo and Rose's calculus of explicit substitutions λx, Parigot's λμ and Curien and Herbelin's .

was first presented in Lengrand (2003), where it was called the λξ-calculus. It can be seen as the pure untyped computational content of the reduction system for the implicative classical sequent calculus of Urban (2000).

In this paper, we present a simple sequent calculus for the modal propositional logic S5. We prove that this sequent calculus is theoremwise equivalent to the Hilbert-style system S5, that it is contraction-free and cut-free, and finally that it is decidable. All results are proved in a purely syntactic way.

We propose an imperative version of the Rewriting Calculus, a calculus based on pattern matching, pattern abstraction and side effects, which we call iRho.

We formulate both a static and big-step call-by-value operational semantics of iRho. The operational semantics is deterministic, and immediately suggests how an interpreter for the calculus may be built. The static semantics is given using a first-order type system based on a form of product types, which can be assigned to term-like structures (that is, records).

The calculus is à la Church, that is, pattern abstractions are decorated with the types of the free variables of the pattern.

iRho is a good candidate for the core of a pattern-matching imperative language, where a (monomorphic) typed store can be safely manipulated and where fixed points are built into the language itself.

Properties such as determinism of the interpreter and subject-reduction have been completely checked using a machine-assisted approach with the Coq proof assistant. Progress and decidability of type checking are proved using pen and paper.

It is shown that the standard definitions of truth-functionality, though useful for their purposes, ignore some aspects of the usual informal characterisations of truth-functionality. An alternative definition is given that results in a stronger notion that pays attention to those aspects.

The class of strong random reals can be defined via a natural conception of effective null set. We show that the same class is also characterized by a learning-theoretic criterion of ‘recognizability’.