Refine search
Actions for selected content:
106095 results in Materials Science
High lithium conductivity in Li1-2xCaxSi2N3
-
- Journal:
- Journal of Materials Research / Volume 26 / Issue 9 / 14 May 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1133-1142
- Print publication:
- 14 May 2011
-
- Article
- Export citation
Structural and multiband photoluminescent properties of a hierarchical ZnO/Si nanoheterostructure
-
- Journal:
- Journal of Materials Research / Volume 26 / Issue 9 / 14 May 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1174-1178
- Print publication:
- 14 May 2011
-
- Article
- Export citation
Ion repelling effect of nanopores in a hydrophobic zeolite
-
- Journal:
- Journal of Materials Research / Volume 26 / Issue 9 / 14 May 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1164-1167
- Print publication:
- 14 May 2011
-
- Article
- Export citation
Nonisothermal cold crystallization of poly(ethylene terephthalate)
-
- Journal:
- Journal of Materials Research / Volume 26 / Issue 9 / 14 May 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1107-1115
- Print publication:
- 14 May 2011
-
- Article
- Export citation
Solvothermal synthesis and luminescence of nearly monodisperse LnVO4 nanoparticles
-
- Journal:
- Journal of Materials Research / Volume 26 / Issue 9 / 14 May 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1168-1173
- Print publication:
- 14 May 2011
-
- Article
- Export citation
6 - Transformation of optical fields by structured surfaces
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 185-231
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 427-436
-
- Chapter
- Export citation
2 - Resonant optical properties of nanoporous metal surfaces
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 28-57
-
- Chapter
- Export citation
11 - Linear and nonlinear phenomena with resonating surface polariton waves and their applications
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 386-426
-
- Chapter
- Export citation
List of contributors
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp xiii-xvi
-
- Chapter
- Export citation
9 - Anomalous transmission in waveguides with correlated disorder in surface profiles
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 287-315
-
- Chapter
- Export citation
10 - Cloaking
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 316-385
-
- Chapter
- Export citation
1 - Physics of extraordinary transmission through subwavelength hole arrays
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 1-27
-
- Chapter
- Export citation
4 - Chirality and anisotropy of planar metamaterials
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 94-157
-
- Chapter
- Export citation
8 - Negative refraction using plasmonic structures that are atomically flat
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 269-286
-
- Chapter
- Export citation
5 - Novel optical devices using negative refraction of light by periodically corrugated surfaces
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 158-184
-
- Chapter
- Export citation
7 - Surface electromagnetic waves on structured perfectly conducting surfaces
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 232-268
-
- Chapter
- Export citation
3 - Optical wave interaction with two-dimensional arrays of plasmonic nanoparticles
-
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp 58-93
-
- Chapter
- Export citation
Plate section
-
- Book:
- Structured Surfaces as Optical Metamaterials
- Published online:
- 01 June 2011
- Print publication:
- 21 April 2011, pp -
-
- Chapter
- Export citation




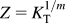 increased exponentially with temperature; activation energies were estimated using Arrhenius plots for the two PET crystallization regimes.
increased exponentially with temperature; activation energies were estimated using Arrhenius plots for the two PET crystallization regimes.
