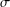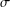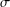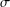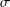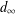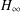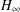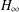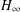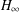Refine search
Actions for selected content:
8124 results in Fluid dynamics and solid mechanics
APPROXIMATE CONTROLLABILITY OF POPULATION DYNAMICS WITH SIZE DEPENDENCE AND SPATIAL DISTRIBUTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 16 May 2017, pp. 474-481
-
- Article
-
- You have access
- Export citation
A NOTE ON MARKOVIAN QUANTUM DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 436-445
-
- Article
-
- You have access
- Export citation
COMPETITIVE ANALYSIS OF INTERRELATED PRICE ONLINE INVENTORY PROBLEMS WITH DEMANDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 368-378
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF THE BOREL
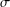 $\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
$\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 265-275
-
- Article
-
- You have access
- Export citation
DELAYED STATE FEEDBACK
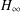 $H_{\infty }$ CONTROL FOR PERIODIC-REVIEW INVENTORY SYSTEMS
$H_{\infty }$ CONTROL FOR PERIODIC-REVIEW INVENTORY SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 397-405
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOUR OF A CLASS OF RESOURCE COMPETITION BIOLOGY SPECIES SYSTEM BY THE FRACTIONAL BROWNIAN MOTION
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 491-499
-
- Article
-
- You have access
- Export citation
Index
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 325-328
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp i-iv
-
- Chapter
- Export citation
5 - Linear Systems and Qualitative Analysis
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 134-179
-
- Chapter
- Export citation
Figures
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp xiii-xiv
-
- Chapter
- Export citation
Acknowledgement
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp xix-xx
-
- Chapter
- Export citation
9 - Two Point Boundary Value Problems
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 267-285
-
- Chapter
- Export citation
Appendix A - Poincarè–Bendixon and Leinard's Theorems
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 307-320
-
- Chapter
- Export citation
8 - Qualitative Theory
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 223-266
-
- Chapter
- Export citation
7 - Regular Sturm–Liouville Theory
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 201-222
-
- Chapter
- Export citation
6 - Series Solutions: Frobenius Theory
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 180-200
-
- Chapter
- Export citation
1 - Introduction and Examples: Physical Models
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 1-21
-
- Chapter
- Export citation
4 - General Theory of Initial Value Problems
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp 99-133
-
- Chapter
- Export citation
Contents
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp vii-xii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Ordinary Differential Equations
- Published online:
- 14 December 2017
- Print publication:
- 11 May 2017, pp v-vi
-
- Chapter
- Export citation