Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-19T05:01:19.978Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LAGUERRE–SOBOLEV TYPE ORTHOGONAL POLYNOMIALS: ZEROS AND ELECTROSTATIC INTERPRETATION

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  08 October 2013

LUIS ALEJANDRO MOLANO MOLANO
LUIS ALEJANDRO MOLANO MOLANO*
Affiliation:
School of Mathematics and Statistics, Universidad Pedagógica y Tecnológica de Colombia, Road North Central, Tunja, Colombia
*
luis.molano01@uptc.edu.co
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the sequence of monic polynomials orthogonal with respect to inner product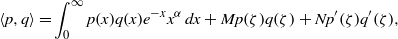

$$\begin{eqnarray*}\langle p, q\rangle = \int \nolimits \nolimits_{0}^{\infty } p(x)q(x){e}^{- x} {x}^{\alpha } \hspace{0.167em} dx+ Mp(\zeta )q(\zeta )+ N{p}^{\prime } (\zeta ){q}^{\prime } (\zeta ),\end{eqnarray*}$$
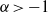where $\alpha \gt - 1$, 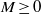$M\geq 0$, $N\geq 0$, 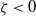$\zeta \lt 0$, and 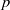$p$ and 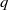$q$ are polynomials with real coefficients. We deduce some interlacing properties of their zeros and, by using standard methods, we find a second-order linear differential equation satisfied by the polynomials and discuss an electrostatic model of their zeros.

Keywords

orthogonal polynomialsLaguerre polynomialsSobolev-type inner productszeroselectrostatic interpretation

MSC classification

Secondary: 42C05: Orthogonal functions and polynomials, general theory
Type
Research Article
Information
The ANZIAM Journal , Volume 55 , Issue 1 , July 2013 , pp. 39 - 54
Copyright
Copyright ©2013 Australian Mathematical Society 

References

Andrews, G. E., Askey, R. and Roy, R., Special functions, Volume 71 of Encyclopedia of Mathematics and its Applications (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Alfaro, M., López, G. and Rezola, M. L., “Some properties of zeros of Sobolev-type orthogonal polynomials”, J. Comput. Appl. Math. 69 (1996) 171–179; doi:10.1016/0377-0427(95)00034-8.CrossRefGoogle Scholar
Alfaro, M., Marcellán, F., Rezola, M. L. and Rounveaux, A., “On orthogonal polynomials of Sobolev type: algebraic properties and zeros”, SIAM J. Math. Anal. 23 (1992) 737–757; doi:10.1137/0523038.CrossRefGoogle Scholar
Chihara, T. S., An introduction to orthogonal polynomials (Gordon and Breach, New York, 1978).Google Scholar
Dueñas, H., Huertas, E. J. and Marcellán, F., “Analytic properties of Laguerre-type orthogonal polynomials”, Integ. Transf. Spec. Funct. 22 (2011) 107–122; doi:10.1080/10652469.2010.499737.CrossRefGoogle Scholar
Dueñas, H., Huertas, E. J. and Marcellán, F., “Asymptotic properties of Laguerre–Sobolev type orthogonal polynomials”, Numer. Algorithms 60 (2012) 51–73; doi:10.1007/s11075-011-9511-4.CrossRefGoogle Scholar
Dueñas, H. and Marcellán, F., “The Laguerre–Sobolev-type orthogonal polynomials. Holonomic equation and electrostatic interpretation”, Rocky Mountain J. Math. 41 (2011) 95–131; doi:10.1216/RMJ-2011-41-1-95.CrossRefGoogle Scholar
Dueñas, H. and Marcellán, F., “The Laguerre–Sobolev-type orthogonal polynomials”, J. Approx. Theory 162 (2010) 421–440; doi:10.1016/j.jat.2009.07.006.CrossRefGoogle Scholar
Fejzullahu, B. Xh. and Zejnullahu, R. Xh., “Orthogonal polynomials with respect to the Laguerre measure perturbed by the canonical transformations”, Integ. Transf. Spec. Funct. 21 (2010) 569–580; doi:10.1080/10652460903442032.CrossRefGoogle Scholar
Heine, E., C. R. Math. Acad. Sci. Berlin, 1864.Google Scholar
Huertas, E. J., Marcellán, F. and Rafaeli, F. R., “Zeros of orthogonal polynomials generated by canonical perturbations on measures”, Appl. Math. Comput. 218 (2012) 7109–7127; doi:10.1016/j.amc.2011.12.073.Google Scholar
Ismail, M. E. H., “An electrostatic model for zeros of general orthogonal polynomials”, Pacific J. Math. 193 (2000) 355–369; doi:10.2140/pjm.2000.193.355.CrossRefGoogle Scholar
Ismail, M. E. H., “More on electrostatic models for zeros of orthogonal polynomials”, Numer. Funct. Anal. Optim. 21 (2000) 191–204; doi:10.1080/01630560008816948.CrossRefGoogle Scholar
Ismail, M. E. H., Classical and quantum orthogonal polynomials in one variable, Volume 98 of Encyclopedia of Mathematics and its Applications (Cambridge University Press, Cambridge, 2005).CrossRefGoogle Scholar
Koekoek, R., Generalizations of the classical Laguerre polynomials and some $q$-analogues, Ph. D. Thesis, Delft University of Technology, 1990.Google Scholar
Koekoek, R. and Meijer, H. G, “A generalization of the Laguerre polynomials”, SIAM J. Math. Anal. 24 (1993) 768–782; doi:10.1137/0524047.CrossRefGoogle Scholar
Molano Molano, L. A., “On asymptotic properties of Laguerre–Sobolev type orthogonal polynomials”, Arab J. Math. Sci. 19 (2013) 173–186; doi:10.1016/j.ajmsc.2013.01.001.CrossRefGoogle Scholar
Lebedev, N. N., Special functions and their applications (Dover Publications, New York, 1972).Google Scholar
Marcellán, F., Zejnullahu, R. Xh., Fejnullahu, B. Xh. and Huertas, E. J., “On orthogonal polynomials with respect to certain discrete Sobolev inner product”, Pacific J. Math. 257 (2012) 167–188; doi:10.2140/pjm.2012.257.167.CrossRefGoogle Scholar
Meijer, H. G., “Laguerre polynomials generalized to a certain discrete Sobolev inner product space”, J. Approx. Theory 73 (1993) 1–16; doi:10.1006/jath.1993.1029.CrossRefGoogle Scholar
Stieltjes, T. J., “Sur certain polynômes que vérifient une équation différentielle linéaire du second ordre et sur la théorie des fonctions de Lamé”, Acta Math. 6 (1885) 321–326; doi:10.1007/BF02400421.CrossRefGoogle Scholar
Szegö, G., Orthogonal polynomials, Volume 23 of American Mathematical Society Colloquium Publication Series (American Mathematical Society, Providence, RI, 1975).Google Scholar