No CrossRef data available.
Article contents
Existence and Uniqueness of Solutions to Singular p-Laplace Equations of Kirchhoff Type
Published online by Cambridge University Press: 16 December 2019
Abstract
In this paper, we study both the existence and uniqueness of nonnegative solutions for the nonlocal 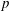 $p$-Laplace equation with singular term
$p$-Laplace equation with singular term 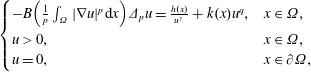 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}-B\Bigl(\frac{1}{p}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D6FB}u|^{p}\text{d}x\Bigr)\unicode[STIX]{x1D6E5}_{p}u=\frac{h(x)}{u^{\unicode[STIX]{x1D6FE}}}+k(x)u^{q},\quad & x\in \unicode[STIX]{x1D6FA},\\ u>0,\quad & x\in \unicode[STIX]{x1D6FA},\\ u=0,\quad & x\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}-B\Bigl(\frac{1}{p}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D6FB}u|^{p}\text{d}x\Bigr)\unicode[STIX]{x1D6E5}_{p}u=\frac{h(x)}{u^{\unicode[STIX]{x1D6FE}}}+k(x)u^{q},\quad & x\in \unicode[STIX]{x1D6FA},\\ u>0,\quad & x\in \unicode[STIX]{x1D6FA},\\ u=0,\quad & x\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{array}\right.\end{eqnarray}$$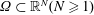 $\unicode[STIX]{x1D6FA}\subset \mathbb{R}^{N}(N\geqslant 1)$ is a bounded domain with smooth boundary
$\unicode[STIX]{x1D6FA}\subset \mathbb{R}^{N}(N\geqslant 1)$ is a bounded domain with smooth boundary 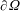 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$, 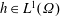 $h\in L^{1}(\unicode[STIX]{x1D6FA})$,
$h\in L^{1}(\unicode[STIX]{x1D6FA})$, 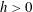 $h>0$ almost everywhere in
$h>0$ almost everywhere in 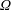 $\unicode[STIX]{x1D6FA}$,
$\unicode[STIX]{x1D6FA}$, 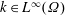 $k\in L^{\infty }(\unicode[STIX]{x1D6FA})$ is a non-negative function,
$k\in L^{\infty }(\unicode[STIX]{x1D6FA})$ is a non-negative function, 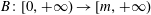 $B:[0,+\infty )\rightarrow [m,+\infty )$ is continuous for some positive constant
$B:[0,+\infty )\rightarrow [m,+\infty )$ is continuous for some positive constant  $m$,
$m$, 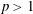 $p>1$,
$p>1$, 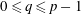 $0\leqslant q\leqslant p-1$, and
$0\leqslant q\leqslant p-1$, and 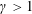 $\unicode[STIX]{x1D6FE}>1$. A “compatibility condition” on the couple
$\unicode[STIX]{x1D6FE}>1$. A “compatibility condition” on the couple 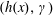 $(h(x),\unicode[STIX]{x1D6FE})$ will be given for the problem to admit at least one solution. To be a little more precise, it is shown that the problem admits at least one solution if and only if there exists a
$(h(x),\unicode[STIX]{x1D6FE})$ will be given for the problem to admit at least one solution. To be a little more precise, it is shown that the problem admits at least one solution if and only if there exists a 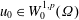 $u_{0}\in W_{0}^{1,p}(\unicode[STIX]{x1D6FA})$ such that
$u_{0}\in W_{0}^{1,p}(\unicode[STIX]{x1D6FA})$ such that 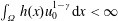 $\int _{\unicode[STIX]{x1D6FA}}h(x)u_{0}^{1-\unicode[STIX]{x1D6FE}}\text{d}x<\infty$. When
$\int _{\unicode[STIX]{x1D6FA}}h(x)u_{0}^{1-\unicode[STIX]{x1D6FE}}\text{d}x<\infty$. When 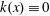 $k(x)\equiv 0$, the weak solution is unique.
$k(x)\equiv 0$, the weak solution is unique.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The work is supported by NSFC (11801052), Fundamental Research Funds for the Central Universities (3132019178).





