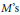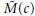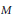Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adachi, Toshiaki
and
Maeda, Sadahiro
2005.
Characterization of totally umbilic hypersurfaces in a space form by circles.
Czechoslovak Mathematical Journal,
Vol. 55,
Issue. 1,
p.
203.
Kim, Young Ho
and
Maeda, Sadahiro
2006.
A Practical Criterion For Some Submanifolds To Be Totally Geodesic.
Monatshefte für Mathematik,
Vol. 149,
Issue. 3,
p.
233.
Cecil, Thomas E.
and
Ryan, Patrick J.
2015.
Geometry of Hypersurfaces.
p.
421.