Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-23T10:06:11.665Z Has data issue: false hasContentIssue false
  • English
  • Français

VALID EDGEWORTH EXPANSIONS FOR THE WHITTLE MAXIMUM LIKELIHOOD ESTIMATOR FOR STATIONARY LONG-MEMORY GAUSSIAN TIME SERIES

Published online by Cambridge University Press:  19 July 2005

Donald W.K. Andrews  and
Offer Lieberman
Donald W.K. Andrews
Affiliation:
Cowles Foundation for Research in Economics, Yale University
Offer Lieberman
Affiliation:
Technion—Israel institute of Technology and Cowles Foundation for Research in Economics, Yale University
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the validity of an Edgeworth expansion to the distribution of the Whittle maximum likelihood estimator for stationary long-memory Gaussian models with unknown parameter 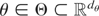. The error of the (s − 2)-order expansion is shown to be o(n−(s−2)/2)—the usual independent and identically distributed rate—for a wide range of models, including the popular ARFIMA(p,d,q) models. The expansion is valid under mild assumptions on the behavior of the spectral density and its derivatives in the neighborhood of the origin. As a by-product, we generalize a theorem by Fox and Taqqu (1987, Probability Theory and Related Fields 74, 213–240) concerning the asymptotic behavior of Toeplitz matrices.

Lieberman, Rousseau, and Zucker (2003, Annals of Statistics 31, 586–612) establish a valid Edgeworth expansion for the maximum likelihood estimator for stationary long-memory Gaussian models. For a significant class of models, their expansion is shown to have an error of o(n−1). The results given here improve upon those of Lieberman et al. in that the results provide an Edgeworth expansion for an asymptotically efficient estimator, as Lieberman et al. do, but the error of the expansion is shown to be o(n−(s−2)/2), not o(n−1), for a broad range of models.

Type
Research Article
Information
Econometric Theory , Volume 21 , Issue 4 , August 2005 , pp. 710 - 734
Copyright
© 2005 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, D.W.K., O. Lieberman, & V. Marmer (2005) Higher-order improvements of the parametric bootstrap for long-memory Gaussian processes. Journal of Econometrics, forthcoming. Cowles Foundation Discussion paper 1378, Yale University. Available at http://cowles.econ.yale.edu.Google Scholar
Beran, J. (1994) Statistics for Long-Memory Processes. Chapman and Hall.
Bhattacharya, R.N. & J.K. Ghosh (1978) On the validity of the formal Edgeworth expansion. Annals of Statistics 6, 434–451.Google Scholar
Dahlhaus, R. (1989) Efficient parameter estimation for self-similar processes. Annals of Statistics 17, 1749–1766.Google Scholar
Durbin, J. (1980) Approximations for densities of sufficient statistics. Biometrika 67, 311–333.Google Scholar
Fox, R. & M.S. Taqqu (1986) Large sample properties of parameter estimates for strongly dependent stationary Gaussian time series. Annals of Statistics 14, 517–532.Google Scholar
Fox, R. & M.S. Taqqu (1987) Central limit theorems for quadratic forms in random variables having long-range dependence. Probability Theory and Related Fields 74, 213–240.Google Scholar
Götze, F. & C. Hipp (1983) Asymptotic expansions for sums of weakly dependent random vectors. Zeitschrift für Wahrscheinlichskeitstheorie und Verwandte Gebiete 64, 211–239.Google Scholar
Götze, F. & C. Hipp (1994) Asymptotic distribution of statistics in time series. Annals of Statistics 22, 2062–2088.Google Scholar
Granger, C.W.J. & R. Joyeux (1980) An introduction to long-memory time series and fractional differencing. Journal of Time Series Analysis 1, 15–30.Google Scholar
Grenander, U. & G. Szegö (1956) Toeplitz Forms and Their Applications. University of California Press. 2nd ed., 1984, Chelsea.
Hosking, J.R.M. (1981) Fractional differencing. Biometrika 68, 165–176.Google Scholar
Hurst, H.E. (1951) Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116, 770–808.Google Scholar
Lahiri, S.N. (1993) Refinements in asymptotic expansions for sums of weakly dependent random vectors. Annals of Probability 21, 791–799.Google Scholar
Lieberman, O. & P.C.B. Phillips (2004) Second Order Expansions for the Distribution of the Maximum Likelihood Estimator of the Fractional Difference Parameter. Econometric Theory 20, 464–484.Google Scholar
Lieberman, O., J. Rousseau, & D.M. Zucker (2003) Valid asymptotic expansions for the maximum likelihood estimator of the parameter of a stationary, Gaussian, strongly dependent process. Annals of Statistics 31, 586–612.Google Scholar
Mandelbrot, B.B. & J.W. Van Ness (1968) Fractional Brownian motions, fractional noises and applications. SIAM Review 10, 422–437.Google Scholar
Robinson, P.M. (1995) Log periodogram regression of time series with long range dependence. Annals of Statistics 23, 1048–1072.Google Scholar
Searle, S.R. (1971) Linear Models. Wiley.
Skovgaard, I.M. (1986) On multivariate Edgeworth expansions. International Statistical Review 54, 169–186.Google Scholar
Taniguchi, M. (1984) Validity of Edgeworth expansions for statistics of time series. Journal of Time Series Analysis 5, 37–51.Google Scholar
Taniguchi, M. (1986) Third order asymptotic properties of maximum likelihood estimators for Gaussian ARMA processes. Journal of Multivariate Analysis 18, 1–31.Google Scholar
Taniguchi, M. (1988) Asymptotic expansions of the distributions of some test statistics for Gaussian ARMA processes. Journal of Multivariate Analysis 27, 494–511.Google Scholar
Taniguchi, M. (1990) Higher Order Asymptotic Theory for Time Series Analysis. Springer Lecture Notes in Statistics, J. Berger, S. Fienberg, J. Gani, K. Krickeberg, I. Olkin, & B. Singer (eds.), vol. 68. Springer.
Taniguchi, M. & Y. Kakizawa (2000) Asymptotic Theory of Statistical Inference for Time Series. Springer.