1. Introduction
Over the past 30 years, aquaculture fish production has increased sharply and has continued to expand around the world due to the dwindling catches of capture fisheries, coupled with increased appetite for fish protein (FAO 2008). Except for salmon farming in Norway, aquaculture production has stagnated over the past three decades in the developed world (FAO 2016). As a result, developing countries (especially China) have been responsible for over 90 per cent of the growth in global farmed fish production. It has been noted that aquaculture, through supplying fish and other aquatic products that are rich in protein, essential fatty acids, vitamins and minerals, can make a significant contribution to eliminating hunger and malnutrition (FAO 2010). In addition, the sector could provide employment opportunities and contribute meaningfully to improving incomes and economic development of the developing world (FAO 2006).
Despite having elevated levels of malnutrition, sub-Saharan Africa (SSA) has not made a meaningful contribution to the growth in aquaculture over the last three decades. Its contribution to world aquaculture production is estimated at less than 1 per cent, and per capita fish consumption within the region is the lowest (barely 9.1 kg per capita in 2009) (Hecht Reference Hecht2006; FAO 2016). The factors contributing to the low output include inadequate domestic and foreign investment in the sector (Leung et al. Reference Leung, Lee and O'Bryen2007).Footnote 1 Fish, however, remains extremely important in the African diet, making up 17.4 per cent of the protein intake (Brummett et al. Reference Brummett, Lazard and Moehl2008). For the region to meet its growing demand for fish protein, it has been estimated that aquaculture must grow at an annual average rate of at least 8.3 per cent, a figure which is significantly higher than the current levels (Muir et al. Reference Muir, Gitonga, Omar, Pouomogne and Radwan2005).
Between the period of 1998 and 2008, statistics available from FAO show aquaculture production increased five-fold due to a number of critical regional projects within SSA and initiatives which increased private investment in the sector (FAO 2010). Between 2000 and 2014, the rise in freshwater fish production resulted in an increase in Africa's contribution to global aquaculture production from 1.23 to 2.32 per cent (FAO 2016).Footnote 2 With regard to employment, the number of people engaged in the industry in Africa has been increasing by 6.2 per cent annually, which is the highest among all other regions (FAO 2016). It is estimated that about 43 per cent of the continent has the potential for farming tilapia (Hishamunda Reference Hishamunda, Leung, Lee and O'Bryen2007).
Notwithstanding the benefits from aquaculture (especially freshwater fish production) in African countries, its expansion could generate some negative externalities. First, nitrogen released from feeds and fish wastes could lead to nutrient over-enrichment and eutrophication in the entire management area if the aquaculture involves water-based systems (i.e., pen or cage culture) (see e.g., EJF 2003; FAO 2008; Wiber et al. Reference Wiber, Young and Wilson2012; Krause et al. Reference Krause, Brugere, Diedrich, Ebeling, Ferse, Mikkelsen, Agúndez, Stead, Stybel and Troell2015). Second, it is possible for diseases to spread from cultured fish to the wild stock and thereby reduce population of the wild stocks. Third, the biological fitness of the wild stock could alter if genetically different species escape from pens and cages. Furthermore, large pens and cages could occupy artisanal fishing grounds. Finally, for small economies like countries in SSA, the demand function for fish is downwards sloping, indicating that harvest from aquaculture could impact revenue and profitability of wild fish catches.Footnote 3
A number of attempts have been made in the literature at modeling aquaculture – capture fisheries interactions (see e.g., Anderson Reference Anderson1985; Anderson and Wilen Reference Anderson and Wilen1986; Ye and Beddington Reference Ye and Beddington1996; Mikkelsen Reference Mikkelsen2007). These studies have considered issues such as the impact of aquaculture on habitat and genetics of wild stocks; the impact of fishery management regimes (say open-access) on aquaculture and wild fish production, fish production technologies, as well as market interactions of capture and farmed fish. To the best of our knowledge none of the studies has modeled foreign capital in aquaculture fish production or explicitly derived the Pigouvian tax (corrective tax) that could internalize the environmental opportunity cost, competition for lake space and the imperfect competition in the fish market. These extensions are considered in our study. The closest to our study is that of Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003), which modelled the ocean space allocation problem for aquaculture fish production when fish markets interact and found that – depending on the nature of the interaction of the two activities, the spatial distribution of the stocks, and the technology employed in fish farming – it may be optimal to allocate the entire ocean space to aquaculture fish production.
It is noteworthy that pens and cages are normally located offshore in natural bodies of water and require sizeable investment which is not affordable to most farmers in SSA. In addition, although fish farming can be done at small to large scale levels, small scale aquaculture fish production is rarely profitable (Brummett et al. Reference Brummett, Lazard and Moehl2008). According to (FAO 2006), for the coming years and decades, Africa (especially SSA) should be a high priority region for aquaculture development and fish production must become an important part of the overall development process for the continent. To realize this objective, more emphasis is put on foreign direct investment (FDI) in aquaculture within the region. As noted by Hishamunda (Reference Hishamunda, Leung, Lee and O'Bryen2007), aquaculture in Africa can only be developed if commercial aquaculture is promoted. As a result, a number of countries in Africa, including Ghana, are making efforts at attracting FDI to the sector from countries like Brazil, China, Chile, France, and the United Kingdom (Hishamunda Reference Hishamunda, Leung, Lee and O'Bryen2007). To the best of our knowledge, no research exists to determine the optimum ad valorem tax to be imposed on foreign investment in aquaculture, hence this study fills this gap as well. The results from our model are empirically illustrated.
The results indicate that both biological and economic parameters determine the Pigouvian tax (optimum ad valorem tax) that corrects the externalities (competition for space, market interaction, and pollution). Since a tax that accounts for competition for space and fish market interactions decreases aquaculture fish production, wild fish catch increases at the optimum. Furthermore, if the capital for the aquaculture comes from FDI, the expression for the Pigouvian tax is the ratio of net to total benefit from aquaculture. The simulated results show that, for capture fisheries, irrespective of the source of the capital for aquaculture, the Pigouvian tax should be decreasing in intrinsic growth rate, pollution from aquaculture and the cost of farming fish. On the other hand, for aquaculture operators, regardless of the source of capital, the tax should increase in intrinsic growth rate of the capture fish stock and pollution but decrease in the cost of farming fish.
The remainder of the paper is organized as follows. Section 2 contains the theoretical model of aquaculture externalities and derives expression for the Pigouvian tax. Section 3 presents an extended model that accounts for foreign investment in aquaculture. The final section, section 4, presents the conclusions of the study.
2. The analytical framework of aquaculture externalities
As noted earlier, we build on the work of Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003). Akin to their formulation, we model lake space allocation between aquaculture and capture fishery. Our model extends their work by explicitly modelling aquaculture pollution and obtains an expression for a Pigouvian tax that internalizes the competition for lake space and pollution externalities. In addition, unlike Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003), our model accounts for foreign capital in aquaculture fish production, which is common in many countries in SSA. We begin by presenting a simple bioeconomic open-loop game theoretic model of the capture fisher's problem and the fish farmer's problem, respectively.Footnote 4 This is followed by a combined model for the social planner, to investigate the competition for lake space, imperfect competition in the fish market, and pollution externalities.
2.1 The capture fisheries manager's problem
Assume the capture (inland) fishery, which is artisanal, is managed separately from aquaculture by a planner. Also, suppose the manager of the inland fishery decides on catch biomass (h), which is traded in an imperfectly competitive market with a downward sloping demand curve.Footnote 5 Following Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003), we assume that buyers cannot distinguish between a species (say tilapia) that is farmed or caught in the wild. Let the price per unit (e.g., kg) of the catch depend on the sum of the wild catch, h, and harvest from aquaculture (z) – i.e., p(h, z). In addition, assume the cost per unit harvest is of a Schaefer type, i.e., c(x), where c x (x)<0, c xx (x) > 0, and x is the capture fish stock in biomass. If future costs and benefits are discounted at the positive rate δ, then the present value of discounted stream of surpluses (i.e., the sum of consumer and producer surpluses) from the capture fishery is:
Let the growth function of the wild stock be g(x, k), where g(x, k) > 0, for x < k,gk
(x,k) > 0,gxx
(x,k) ≤ 0,gkx
(x,k) ≥ 0,gxk
(x,k) ≥ 0 and k is the environmental carrying capacity. Cage culture takes away potential fishing area (decreases wild fish stock) and thereby increases the cost per unit harvest of capture fish. Following the formulation in Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003), let the remainder of the carrying capacity – if cage culture takes away part of the carrying capacity – be k = k(m) = k
0 – ωm, where k
0 is the initial carrying capacity, m is the lake area devoted to aquaculture, and ω is a constant conversion factor of cage area to carrying capacity. The time derivative of the total biomass (i.e.,
![]() $\dot{x})$
increases in the growth of the stock but decreases in human predation (catch). Thus, the stock dynamic equation is:
$\dot{x})$
increases in the growth of the stock but decreases in human predation (catch). Thus, the stock dynamic equation is:
The representative fisher's objective is to maximize equation (1) with respect to catch, subject to the stock evolution (i.e., equation (2)).
The corresponding current value Hamiltonian can be specified as:
where λ is the scarcity value of the capture fish stock or the marginal value assigned by the planner to the marginal reductions in the fish stock, and z(m) is the aquaculture production function that depends on the size of the cage area. Applying the maximum principle to derive the first-order condition with respect to the flow variable h and assuming steady-state conditions (see appendix 1), we obtained the following equation:
Equation (4), which is a reaction function, could potentially be solved for the equilibrium values of the capture fish stock (x) as a function of the size of the area devoted to aquaculture (i.e., x* = x(m)) if the specific forms of the relevant functions are known. Next, we present the aquaculture manager's problem, followed by that of the social planner.
2.2 The aquaculture manager's problem
As indicated earlier, in recent times, policy makers in several African countries have been making conscious efforts at encouraging investment in aquaculture to ease the pressure on capture fish stocks, which are already overcapitalized and overexploited. So far, the response has been encouraging. Suppose that the recurrent operation cost function of an aquaculture with cage area of size m (in 100 square kilometers) that produces z(m) units of farmed fish is ς (m).Footnote 6 And assume that the cost of acquiring (or investing in) v extra units of the lake area is given by the function τ (v), with τ v (v) > 0 (see, e.g., Parks and Bonifaz Reference Parks and Bonifaz1994; Hoagland et al. Reference Hoagland, Jin and Kite-Powell2003). The corresponding present value of the net benefit from the aquaculture is:
Following Parks and Bonifaz (Reference Parks and Bonifaz1994) and Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003), let the equation of motion, which defines the change of the cage area over time, be:
The current value Hamiltonian corresponding to equations (5) and (6) is:
where μ is the shadow value of the cage area. The maximum principle generates the first-order condition, with respect to the flow variable ν, given by equation (29) in appendix 2. Assuming a steady state, we obtain the following equation:
Again, equation (8), which is a reaction function, could be solved for the equilibrium level of m as a function of the wild fish stock (i.e., m* = m(x)). The two reaction functions (i.e., equations (4) and (8)) could be solved simultaneously to obtain the pair of open-loop equilibrium values of m* and x*. It is important to note that these values are suboptimal since they do not account for the competition for lake space, imperfectly competitive market for fish, and pollution externalities.
2.3 Functional forms for numerical simulations
In order to obtain numerical solutions and perform comparative static analysis, we assume the following specific functional forms: a logistic growth function for the capture stock, g(x,k(m)) = rx(1-(x/k 0 – ω m)), where r is the intrinsic growth rate; a Schaefer cost function, c(x) = (c/σ x), where c is cost per unit effort and σ is catchability coefficient; a downward sloping linear demand function, p(h,z) = a – b(h + z), where a, b > 0; a non-linear aquaculture production function of the form z(m) = θ m ε, following; a linear cost function for acquiring v extra units of the management or lake area τ (v) = τ v, assumed for tractability (see, e.g., Hoagland et al. Reference Hoagland, Jin and Kite-Powell2003); and a linear operation cost function, ς (m) = ς m, also assumed for computational convenience, but without loss of generality, following Hoagland et al. (Reference Hoagland, Jin and Kite-Powell2003).
Furthermore, to derive the numerical results, some values were assumed. Since the dominant species is tilapia, the study used an intrinsic growth rate of 1.358 (Romana-Eguia et al. Reference Romana-Eguia, Ikeda, Basiao and Taniguchi2010). Lake Volta has the second largest tilapia farm in Africa, with a carrying capacity of 80,000 metric tons (Vanderpuye Reference Vanderpuye, Kapetsky and Petr1984). As a result, we assume that this figure constitutes the initial carrying capacity of the lake. Following, a social discount rate of 5 per cent was employed. The remainder of the parameter values used in our numerical analysis are chosen for tractability. These values are included in table 1 and tables A1 and A2 in appendix 5. It is noteworthy that since some of the numerical values are chosen arbitrarily, we place emphasis on the direction rather than the magnitude of change in the endogenous variables. As a result, some of the tables for the numerical results corresponding to the directions of change are placed in appendix 5.
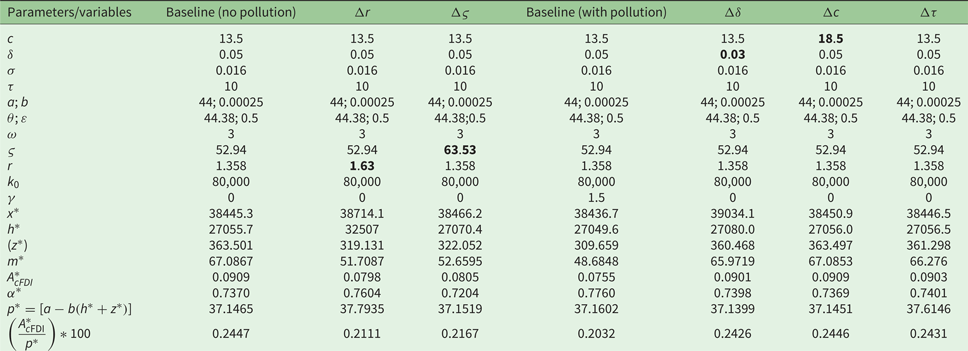
Table 1. Equilibrium wild fish catch and stock, aquaculture fish production, and cage area under non-cooperative management system
Notes: c, cost per unit effort; δ, social discount rate; σ, catchability coefficient; τ, price per unit of additional cage area; a and b, demand function parameters; θ and ε, aquaculture production parameters; r, intrinsic growth rate; k
0, environmental carrying capacity; ω, marginal reduction in environmental carrying capacity due to expansion of aquaculture; γ, marginal reduction in environmental carrying capacity due to pollution; ς, marginal cost of farming fish; x*, capture fish stock; h*, wild fish catch; z*, aquaculture harvest; m*, cage size/area; α, ad valorem tax;
![]() $A_{a}^{\ast} $
, aquaculture tax;
$A_{a}^{\ast} $
, aquaculture tax;
![]() $A_{p}^{\ast} $
, pollution/externality tax;
$A_{p}^{\ast} $
, pollution/externality tax;
![]() $A_{c}^{\ast} $
, capture fisher tax; p*, price of fish.
$A_{c}^{\ast} $
, capture fisher tax; p*, price of fish.
2.4 Numerical results: non-cooperative solutions and sensitivity analysis
From table 1, a higher intrinsic growth rate of capture fish stock, which could depend on, say, species composition, increases both the equilibrium capture fish stock and catch while dampening aquaculture production. Furthermore, aquaculture production declines but the optimal wild catch increases if the cost of farming fish increases. The results are intuitive as increased cost of aquaculture production is expected to decrease its production but increase capture fisheries catch to make up for the shortfall. It is worth noting, however, that these equilibrium values for catch, stock levels, and aquaculture production are suboptimal since competition for lake space, an imperfectly competitive market for fish, and pollution externalities are not accounted for.
2.5 The overall social planner's problem: the cooperative solution
Now suppose an overall social planner exists, and his/her objective is to maximize total surplus from both fisheries (i.e., the cooperative outcome). In addition to taking away fishing area, cage culture imposes a negative externality on the environmental carrying capacity of the remaining capture fisheries area because of chemicals used in farming fish. We call this pollution externality. Assume the pollution from the cage culture depends on the size of the cage area and is given by γ m, where γ is a constant. Thus, the instantaneous carrying capacity becomes k = k 0 – (ω + γ)m. The objective of the planner is to maximize the net benefit from aquaculture and capture fisheries with respect to catch and the increment in the size of the aquaculture, as follows:
The constraints to the objective function are the dynamic equations (i.e., equations (2) and (6)) as well as the carrying capacity constraint. The corresponding current value Hamiltonian is
The first-order condition with respect to the flow variables h and v generates equations (33) and (34) in appendix 3. The corresponding steady-state equations that relate the optimum stock to the optimum size of the cage area are:
 $$\eqalign{ \delta \tau_v &= [p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))]z_m (m) \cr &\quad -\left({c_x (x)g(\cdot ) \over \delta -g_x (\cdot )}\right)g_k (\cdot)k_m (\cdot )-\varsigma_m (m).}$$
$$\eqalign{ \delta \tau_v &= [p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))]z_m (m) \cr &\quad -\left({c_x (x)g(\cdot ) \over \delta -g_x (\cdot )}\right)g_k (\cdot)k_m (\cdot )-\varsigma_m (m).}$$
Equations (11) and (12) could be solved simultaneously for the socially-optimum capture fishery stock and harvest, cage area, and aquaculture production.
2.5.1 Taxing competition for lake space, fish market imperfection and pollution externalities
The first-order conditions and the co-state equations of the social planner are different from those of the capture fisher and the fish farmer, due to: competition for lake space, an imperfectly competitive market for fish, and pollution externalities. Comparing equations (25) and (33) in appendices 1 and 3, respectively, we obtain the tax expressionFootnote 7 :
Equation (13) indicates that the tax (A c ) on the capture fishery should correct for the externality due to the imperfect competition in the fish market, − ph (ċ)z(m). Also, comparing equations (30) and (36), in appendices 2 and 3 respectively, the following expression is obtained for the tax for the fish farmer:
 $$\eqalign{ A_a z_m (m) &= -p_z (\cdot)z_m (m)g(\cdot)-\lambda_s g_k (\cdot)k_m (m) \cr &\quad \Rightarrow A_a = {-p_z (\cdot)z_m (m)g(\cdot)+g_k (\cdot)k_m (m)(c_x (x)g(\cdot)/\delta -g_x (\cdot)) \over z_m (m)} }$$
$$\eqalign{ A_a z_m (m) &= -p_z (\cdot)z_m (m)g(\cdot)-\lambda_s g_k (\cdot)k_m (m) \cr &\quad \Rightarrow A_a = {-p_z (\cdot)z_m (m)g(\cdot)+g_k (\cdot)k_m (m)(c_x (x)g(\cdot)/\delta -g_x (\cdot)) \over z_m (m)} }$$
where k m = − ω since k = k 0 – ω m (no pollution externality). Again, from equation (14), the tax must correct for the strategic pricing effect (–pz (ċ)h) and some capture fish biomass growth effect of increased cage size (–λ s gk (ċ)km (m)(zm (m))−1). Furthermore, if we have pollution externality due to aquaculture so that the carrying capacity is explicitly defined as k = k 0 – (ω + γ )m, the pollution tax can be specified as:
Equation (15) indicates that the pollution tax is the ratio of value of the marginal damage to the carrying capacity – due to the pollution (i.e., –γ (cx (x)g(ċ)/δ –gx (ċ))gk (ċ)) – to the marginal gain resulting from the expansion of the cage area (i.e., z m (m)).
2.6 Numerical results: social optimum outcomes and sensitivity analysis
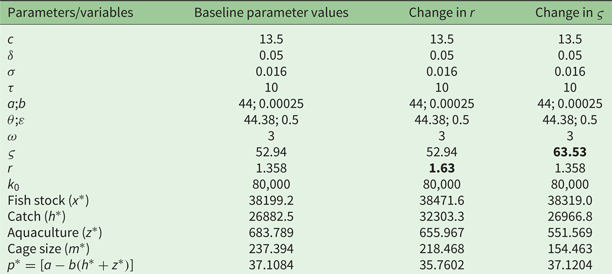
Using the specific functions and the numerical values, the optimal values reported in table A1 in appendix 5 are obtained, and the direction of change of the values is reported in table 2. The results clearly show that the optimum wild catch is higher but aquaculture production is lower, compared to their corresponding non-cooperative values (reported in table 1). The lower aquaculture production is due to internalization of the carrying capacity effect. Interestingly, although the capture fisheries are taxed to address the strategic pricing effect, its optimum catch increased due to increased carrying capacity as less area is made available for aquaculture. The overall net effect is lower aggregate catch, which leads to an increase in the price of fish.
Table 2. Comparative statics (direction of change) of key parameters, optimum wild fish catch, aquaculture harvest, and tax if local capital finances aquaculture and externalities are internalized

Notes: c, cost per unit effort; δ, social discount rate; σ, catchability coefficient; τ, price per unit of additional cage area; a and b, demand function parameters; θ and ε, aquaculture production parameters; r, intrinsic growth rate; k
0, environmental carrying capacity; ω, marginal reduction in environmental carrying capacity due to expansion of aquaculture; γ, marginal reduction in environmental carrying capacity due to pollution; ς, marginal cost of farming fish; x*, capture fish stock; h*, wild fish catch; z*, aquaculture harvest; m*, cage size/area; α*, ad valorem tax;
![]() $(A_{a}^{\ast})$
, aquaculture tax;
$(A_{a}^{\ast})$
, aquaculture tax;
![]() $(A_{p}^{\ast})$
, pollution/externality tax;
$(A_{p}^{\ast})$
, pollution/externality tax;
![]() $(A_{c}^{\ast})$
, capture fisher tax; p*, price of fish.
$(A_{c}^{\ast})$
, capture fisher tax; p*, price of fish.
The advent of pollution from aquaculture lowers the optimum wild catch and aquaculture fish production. For the capture fishery, the reduction in yield is due to the pollution effect, while the production of fish from aquaculture decreases due to the Pigouvian tax. In addition, the pollution imposes an additional tax on the fish farmers, whereas it reduces the tax (due to the lake space competition and imperfect market competition) on the capture fisher. Thus, in addition to incurring a tax for polluting, the fish farmers’ corrective tax for competition for lake space and imperfect competition in the fish market should be adjusted upwards because of the undue advantage they gain by inducing a lower capture fish production.
Regarding the sensitivity analysis of the tax reported in table 2, it was found that in the absence of pollution, the tax on aquaculture is increasing in intrinsic growth rate of the capture fish stock but decreasing if the marginal operating cost of the aquaculture or the marginal cost of acquiring an extra unit of the lake space or social discount rate increases. The intuition is that if the fish in the wild are growing faster, then aquaculture should be discouraged (i.e., taxed more). On the other hand, aquaculture should be encouraged if, all else being equal, its operating cost rises or the society becomes increasingly impatient.
Concerning the tax on capture fishery, it must decrease if intrinsic growth rate or the marginal operating cost of the aquaculture or the cost of acquiring an extra unit of cage area increases. Thus, harvest of capture fishery should be encouraged if the stock is growing faster or the cost of farming fish is rising.
3. Modeling foreign capital in aquaculture
Aquaculture investments in many developing countries are predominantly financed by FDI. Suppose the capital for setting up the aquaculture comes solely from FDI. A feasible policy option will be to impose an ad valorem tax that maximizes economic surplus from both fisheries. Let the tax be α. The social planner's problem is to maximize the following function:
The constraints are the two equations of motion (i.e., equations (2) and (6)) and an additional constraint of an isoperimetric form (see Akpalu and Parks, Reference Akpalu and Parks2007), i.e.,
Equation (17) stipulates that the stream of net benefits that accrues to the provider of the FDI must be non-negative. The corresponding Lagrangian function is:
where ψ is a Lagrange multiplier, and
Again, in the steady state, we get the following equations:
In addition to the first-order conditions, we have the following transversality condition:
Since ψ = 1 (see equation (43) in appendix 4), it follows that ∂L/∂ψ = 0. Thus the tax expression α is:
Equation (22) stipulates that, in the steady state, the ad valorem tax on aquaculture must be the ratio of the net revenue to total revenue from the aquaculture. Equations (19), (20) and (22) may be solved simultaneously for the optimum values x*, m*, and α*.
To obtain the expression for the price-based externality tax (to be paid by the capture fisher), if aquaculture is financed by foreign capital, we compare equations (25) and (44) in appendices 1 and 4, respectively, which gives us:
Equation (23) shows that the capture fishers’ tax for the externality generated, when aquaculture is financed by FDI, is similar to the case where fish farming is locally funded. Similarly, using the specific functional forms and the numerical values, the optimum values of the state and control variables as well as the tax are reported in table A2 in appendix 5.
3.1 Numerical results for FDI: the social optimum outcomes and sensitivity analysis
The results from table A2 in appendix 5 (and the direction of the changes which is reported in table 3) indicate that the ad valorem tax on aquaculture should increase if pollution from farming fish intensifies or the intrinsic growth rate of the capture fish stock increases. Thus, higher intrinsic growth rate implies that capture fisheries should be favored over aquaculture, hence the higher tax rate. On the other hand, the optimum tax rate should be set lower if the cost of farming fish increases. Particularly, there is no difference between the characters of the capture fishery and aquaculture taxes in a situation where capital for aquaculture comes from the domestic economy compared to the case where FDI finances aquaculture. In both cases, the optimum tax rates are reduced if the cost of farming fish increases. This is true despite domestic capital having an opportunity cost within the economy.
Table 3. Comparative statics (direction of change) of key parameters, and optimum wild fish catch, aquaculture harvest, and tax if foreign capital finances aquaculture and externalities are internalized
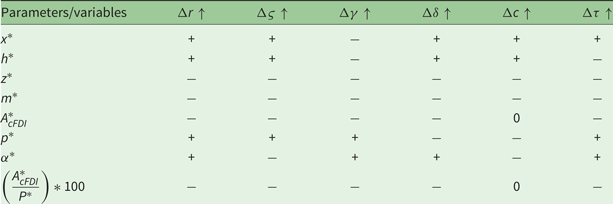
Notes: c, cost per unit effort; δ, social discount rate; σ, catchability coefficient; τ, price per unit of additional cage area; a and b, demand function parameters; θ and ε, aquaculture production parameters; r, intrinsic growth rate; k
0, environmental carrying capacity; ω, marginal reduction in environmental carrying capacity due to expansion of aquaculture; γ, marginal reduction in environmental carrying capacity due to pollution; ς, marginal cost of farming fish; x*, capture fish stock; h*, wild fish catch; z*, aquaculture harvest; m*, cage size/area; α*, ad valorem tax;
![]() $A_{a}^{\ast} $
, aquaculture tax;
$A_{a}^{\ast} $
, aquaculture tax;
![]() $A_{p}^{\ast} $
, pollution/externality tax;
$A_{p}^{\ast} $
, pollution/externality tax;
![]() $A_{cFDI}^{\ast}$
, capture fisher tax; p*, price of fish.
$A_{cFDI}^{\ast}$
, capture fisher tax; p*, price of fish.
4. Conclusion
Due to the increasing over-exploitation of capture fish stocks, developing countries have embarked on policies to promote aquaculture to meet their minimum fish protein requirements. Typically, cage culture interacts with capture fisheries in a number of ways. These include the pollution of capture fisheries by cage culture, the interaction of markets for wild catch and harvest from aquaculture, and competition for space between the two fisheries. In addition, capital for aquaculture in developing countries mostly comes from FDI. The goal of public policy, therefore, is to design instruments capable of internalizing these externalities, as well as ensuring that the resource-rich country obtains a fair share of the return from cage culture from foreign investors. The simple bioeconomic model employed in this paper suggests pathways to achieving these objectives.
The results from the optimization programs indicate that the intertemporal extraction level is higher for the fish farmer but lower for the capture fisher than optimally desired. The reason is that taxes on aquaculture result in a reduction in cage area, which then leads to an increase in wild fish catch in spite of the tax for the market interaction effect (imperfect competition in the fish market). Thus, a tax on both fishers aimed at internalizing the strategic pricing effect, which leads to over-harvesting, only results in a reduction in aquaculture production levels. In addition, the fish farmer must be taxed for the impact of the increased cage size on capture fish biomass growth, as well as the negative externality resulting from chemical usage. The proposed tax is an ad valorem tax, which is easier to implement in developing countries.
The optimum tax rate has been found to be responsive to changes in intrinsic growth rate of the capture fish stock, the cost of farming the fish, and the initial carrying capacity of the wild fish stock. Furthermore, if aquaculture is financed by FDI, the optimum price-based tax on the fish farmer is simply the share of profit in total revenue. It was found that an increase in the cost of farming fish must be accompanied by a reduction in the tax rate, irrespective of where the capital for the farming fish is coming from.
Acknowledgements
The authors wish to express their profound gratitude to the Associate Editor of the journal and two anonymous reviewers for invaluable comments.
Appendix 1
The current value Hamiltonian corresponding to the capture fish problem can be specified as:
where λ is the scarcity value of the capture fish stock or the marginal value assigned by the planner to the marginal reductions in the fish stock. The maximum principle provides the following first-order condition with respect to the flow variable, catch (h):
From equation (25), to maximize intertemporal benefits from the fishery, the net marginal benefit, (ph (h,z)h + p(h + z) – c(x)), must be equal to the scarcity value of the stock (λ). Clearly the net marginal surplus depends on catch, capture fish stock, and biomass production from the aquaculture. The co-state equation corresponding to equation (24) is:
Equation (26) stipulates that in dynamic equilibrium, returns on investing the proceeds from harvesting a kilogram of fish (δ λ) must be equal to the opportunity cost of catching the fish, which includes capital gain (
![]() $\dot{\lambda}$
) and some stock effect (λ gx
– cx
(x)h). In the steady state, there is no gain in fish stock and the shadow price (i.e.,
$\dot{\lambda}$
) and some stock effect (λ gx
– cx
(x)h). In the steady state, there is no gain in fish stock and the shadow price (i.e.,
![]() $\dot{x}=\dot{\lambda}=0)$
, hence the dynamic equation
$\dot{x}=\dot{\lambda}=0)$
, hence the dynamic equation
![]() $\dot{x}=g(x,k(m))-h$
and equation (26) give us g(x, k) = h and λ = – cx
(x)h/δ – gx
(ċ), respectively. Assume that the aquaculture production depends on the cage size, so that the production function is z = z(m). Using this expression and substituting the above values for h and λ in equation (25), we have:
$\dot{x}=g(x,k(m))-h$
and equation (26) give us g(x, k) = h and λ = – cx
(x)h/δ – gx
(ċ), respectively. Assume that the aquaculture production depends on the cage size, so that the production function is z = z(m). Using this expression and substituting the above values for h and λ in equation (25), we have:
 $$\eqalign{ & p_h (g(x,k(m),z(m))g(x,k(m))+p(g(x,k(m)),z(m))-c(x) \cr &\quad ={-c_x (x)g(x,k(m)) \over \delta -g_x (x,k(m))}. }$$
$$\eqalign{ & p_h (g(x,k(m),z(m))g(x,k(m))+p(g(x,k(m)),z(m))-c(x) \cr &\quad ={-c_x (x)g(x,k(m)) \over \delta -g_x (x,k(m))}. }$$
Appendix 2
The current value Hamiltonian corresponding to the farmer's problem is:
where μ is the shadow value of the cage area. The maximum principle generates the following first-order condition with respect to the flow variable v:
In intertemporal equilibrium, the farmer will expand the cage marginally if the marginal benefit of the expansion (i.e., measured by the shadow value of the total cage area, μ) is at least equal to the marginal cost of the expansion (i.e., τ v ). The co-state equation defining the dynamic equilibrium is:
Similarly, from equation (30), in a dynamic equilibrium the capital gain from investing in an extra unit of the cage area (
![]() $\dot{\mu}$
) plus the marginal benefit from fish harvest attributable to the marginal increment in the cage area (i.e., (pz
(h,z(m))z(m) + p(h,z(m)))zm
(m) – ς
m
(m)) should balance the marginal opportunity of interest earnable on μ (i.e., δ μ). In the steady state, we have
$\dot{\mu}$
) plus the marginal benefit from fish harvest attributable to the marginal increment in the cage area (i.e., (pz
(h,z(m))z(m) + p(h,z(m)))zm
(m) – ς
m
(m)) should balance the marginal opportunity of interest earnable on μ (i.e., δ μ). In the steady state, we have
![]() $\dot{\mu} =\dot{m}=v=0$
. Combining equations (29) and (30), and using h = g(x, k(x)), we obtain the following:
$\dot{\mu} =\dot{m}=v=0$
. Combining equations (29) and (30), and using h = g(x, k(x)), we obtain the following:
Appendix 3
The current value Hamiltonian corresponding to the social planner's problem is
The maximum principle generates the following first-order conditions:
Equation (33) differs from (25) by ph (h,z(m))z(m) < 0, indicating that, in intertemporal equilibrium, the socially-optimum catch level is lower than the ‘private’ equilibrium catch level of the capture fisheries’ manager. Consequently, decentralizing the two subsectors could result in over-harvesting of the capture fish stock due to imperfect competition in the market for fish. The corresponding co-state equations (for the co-state variables x and m, respectively) are:
While equations (26) and (35) are the same, (30) and (36) are obviously different. Since pz (h,z(m))zm (m)h < 0 and λ s gk (ċ)km (ċ) = – ω λ s gk (ċ) – γ λ s gk (ċ) < 0, in dynamic equilibrium the net benefit from marginally expanding the cage is overstated, which favors increment in the cage size in equation (30). Thus, properly accounting for the resource use externality (pollution) discourages expansion of aquaculture.
In the steady state,
![]() $\dot{m}=\dot{x} =\dot{\lambda}_{s}=\dot{\mu}_{s}=v=0$
, and h = g(x,k
0 – m(ω + γ )), hence the tax expression becomes:
$\dot{m}=\dot{x} =\dot{\lambda}_{s}=\dot{\mu}_{s}=v=0$
, and h = g(x,k
0 – m(ω + γ )), hence the tax expression becomes:
Also we have the following expressions for the shadow values:
 $$\eqalign{ \mu_s &= {\big[p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))\big]z_m (m) \over \delta } \cr &\quad -{(c_x (x)g(\cdot )/\delta -g_x (\cdot))g_k (\cdot)k_m (\cdot)-\varsigma_m (m) \over \delta }. }$$
$$\eqalign{ \mu_s &= {\big[p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))\big]z_m (m) \over \delta } \cr &\quad -{(c_x (x)g(\cdot )/\delta -g_x (\cdot))g_k (\cdot)k_m (\cdot)-\varsigma_m (m) \over \delta }. }$$
Substituting these values in equations (35) and (36), the equations that relate the optimum stock and cage size become:
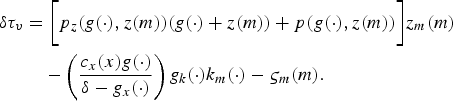 $$\eqalign{ \delta \tau_v &= \bigg[p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))\bigg]z_m (m) \cr &\quad -\left({c_x (x)g(\cdot ) \over \delta -g_x (\cdot )}\right)g_k (\cdot)k_m (\cdot )-\varsigma_m (m). }$$
$$\eqalign{ \delta \tau_v &= \bigg[p_z (g(\cdot ),z(m))(g(\cdot )+z(m))+p(g(\cdot ),z(m))\bigg]z_m (m) \cr &\quad -\left({c_x (x)g(\cdot ) \over \delta -g_x (\cdot )}\right)g_k (\cdot)k_m (\cdot )-\varsigma_m (m). }$$
Appendix 4
The Lagrangian function corresponding to the FDI problem is:
where ψ is a Lagrange multiplier, and
The first-order conditions with respect to the flow variables, following the maximum principle, are:
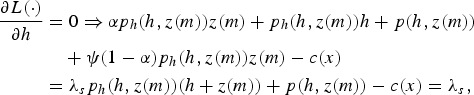 $$\eqalign{ {\partial L(\cdot) \over \partial h}&= 0\Rightarrow \alpha p_h (h,z(m))z(m)+p_h (h,z(m))h+p(h,z(m)) \cr &\quad +\psi (1-\alpha )p_h (h,z(m))z(m)-c(x) \cr &= \lambda_s p_h (h,z(m))(h+z(m))+p(h,z(m))-c(x)=\lambda_s , }$$
$$\eqalign{ {\partial L(\cdot) \over \partial h}&= 0\Rightarrow \alpha p_h (h,z(m))z(m)+p_h (h,z(m))h+p(h,z(m)) \cr &\quad +\psi (1-\alpha )p_h (h,z(m))z(m)-c(x) \cr &= \lambda_s p_h (h,z(m))(h+z(m))+p(h,z(m))-c(x)=\lambda_s , }$$
The co-state equations are
Again, in the steady state,
![]() $\dot{m}=\dot{x}=\dot{\lambda}_{s} = \dot{\mu}_{s}=v=0$
, implies:
$\dot{m}=\dot{x}=\dot{\lambda}_{s} = \dot{\mu}_{s}=v=0$
, implies:
In addition to the first-order conditions, we have the following transversality condition:
Since ψ = 1, it follows that ∂ L/∂ ψ = 0, and the tax expression is:
Appendix 5
Table A1. Optimum wild fish catch, aquaculture harvest, and tax if local capital finances aquaculture and externalities are internalized
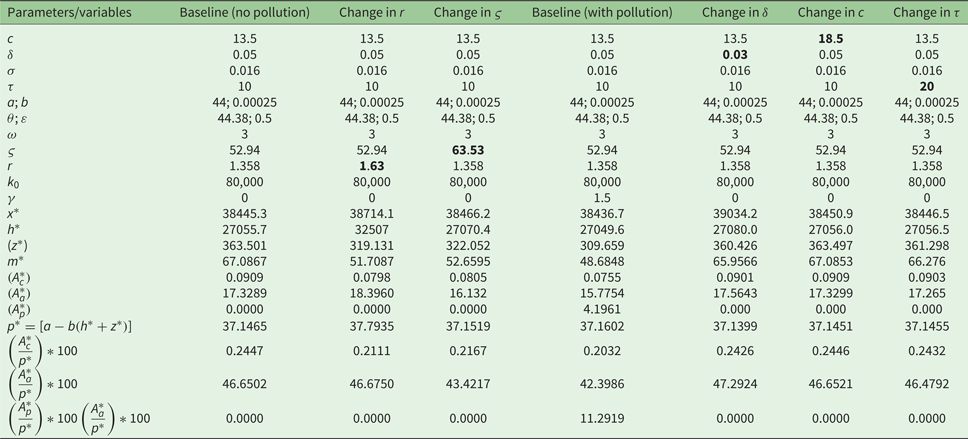
Table A2. Optimum wild fish catch, aquaculture harvest, and tax if foreign capital finances aquaculture and externalities are internalized