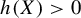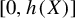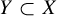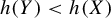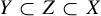1 Introduction
Let G be a countable group and let
$\mathcal A$
be a finite alphabet of symbols. In symbolic dynamics, the central objects of study are the subsystems of the so-called full shift, the dynamical system
$(\mathcal A^G, \sigma )$
, where
$\sigma $
denotes the action of G on
$\mathcal A^G$
by translations (Definition 2.5). Shifts of finite type (Definition 2.12) and sofic shifts (Definition 2.13) are the most widely studied and well understood examples of symbolic dynamical systems. In each of these cases, the system of interest is completely specified by a finite amount of information. This allows for combinatorial, finitary arguments to be applied to the analysis of the dynamics of such systems.
Entropy is one of the most fundamental invariants of a topological dynamical system. Many fundamental results from classical entropy theory (that is, in the case where
$G = \mathbb Z$
) only generalize if G is an amenable group (Definition 2.2). Amenability allows one to ‘approximate’ the group by a sequence of finite subsets in a way that is useful for studying dynamics. See Definition 2.14 for the definition of the entropy of a symbolic dynamical system on an amenable group.
In general, one would like to understand the structure of the collection of subsystems of a given subshift. In this paper, we study the entropies of the SFT subsystems of a given SFT, as well as the entropies of the sofic subsystems of sofic shifts. There are many existing results in the literature in the case where
$G = \mathbb Z$
. For example, the Krieger embedding theorem [Reference Krieger12] characterizes the irreducible SFT subsystems of a given irreducible
$\mathbb Z$
-SFT. Additionally, Lind [Reference Lind13] has provided an algebraic characterization of the real numbers that are realized as the entropy of a
$\mathbb Z$
-SFT.
However, the situation is very different in cases where
$G \neq \mathbb Z$
. Even in the case where
$G = \mathbb Z^d$
for
$d> 1$
, the classes of SFTs and sofic shifts behave quite differently. For example, Boyle, Pavlov, and Schraudner [Reference Boyle, Pavlov and Schraudner5] have shown by example that the subsystems of
$\mathbb Z^d$
sofic shifts can be badly behaved for
$d> 1$
(in contrast to the case where
$d = 1$
). Moreover, Hochman and Meyerovitch [Reference Hochman and Meyerovitch9] have characterized the real numbers that are realized as entropy of a
$\mathbb Z^d$
-SFT (with
$d>1$
), but in contrast to the result of Lind mentioned above, the characterization is in algorithmic terms and unavoidably involves concepts from computability and recursion theory. Nonetheless, Desai [Reference Desai6] has shown that a
$\mathbb Z^d$
-SFT with positive entropy has a wealth of SFT subsystems (sharpening an earlier result of Quas and Trow [Reference Quas and Trow16]).
Theorem 1.1. [Reference Desai6]
Let
$G = \mathbb Z^d$
for some
$d \in \mathbb N$
and let X be a G-SFT such that
$h(X)> 0$
. Then
$$ \begin{align*} \{h(Y) : Y \subset X \text{ and}\ Y\ \text{is an SFT}\kern1pt\} \end{align*} $$
is dense in
$[0,h(X)]$
.
In recent years, several results of the
$G= \mathbb Z$
and
$G = \mathbb Z^d$
cases have seen extensions to larger classes of groups, especially amenable groups. To name a few: Barbieri [Reference Barbieri2] has classified the real numbers that are realized as the entropy of a G-SFT for many types of amenable G (extending the result of Hochman and Meyerovitch mentioned above); Frisch and Tamuz [Reference Frisch and Tamuz8] have investigated the (topologically) generic properties of G-subshifts for arbitrary amenable G; Barbieri and Sablik [Reference Barbieri and Sablik3] have shown how an arbitrary effective G-subshift, where G is finitely generated, may be simulated by a
$G'$
-SFT, where
$G'$
is the semidirect product
$G' = \mathbb Z^2 \rtimes G$
; and Huczek and Kopacz [Reference Huczek and Kopacz10] have (very recently) obtained a partial generalization of Boyle’s lower entropy factor theorem [Reference Boyle4] to countable amenable groups with the comparison property. In this vein, we prove the following generalization of Theorem 1.1 to arbitrary countable amenable groups.
Theorem 4.2. Let G be a countable amenable group, let X be a G-SFT, and let
$Y \subset X$
be any subsystem such that
$h(Y) < h(X)$
. Then
$$ \begin{align*} \{h(Z) : Y \subset Z \subset X \text{ and}\ Z\ \text{is an SFT}\kern1pt\} \end{align*} $$
is dense in
$[h(Y), h(X)]$
.
Choosing
$G = \mathbb Z^d$
and
$Y = \varnothing $
in the above theorem recovers the result of Desai (Theorem 1.1 above). Note that a shift space
$X \subset \mathcal {A}^G$
has at most countably many SFT subsystems, and therefore the set of entropies of SFT subsystems is at most countable. In this sense, Theorem 4.2 is ‘the most one could hope for.’
Remark 1.2. After a preprint of this work was made public, the authors of [Reference Frisch and Tamuz8] made us aware that a short alternate proof of Theorem 4.2 can be derived from their main results. Specifically, they prove there that for any countable amenable group G and any real
${c \geq 0}$
, the set of G-subshifts with entropy c is dense (in fact residual) within the space of G-subshifts with entropy at least c with respect to the Hausdorff topology. This result immediately implies that for any G-SFT X, there exist G-subshifts contained in X that achieve all possible entropies in
$[0, h(X)]$
; then, some simple approximations with G-SFTs (in the sense of our Theorem 2.12) can be used to obtain a proof of Theorem 4.2.
For sofic shifts, we obtain the following result.
Theorem 5.2. Let G be a countable amenable group, let W be a sofic G-shift, and let
$V \subset W$
be any subsystem such that
$h(V) < h(W)$
. Then
$$ \begin{align*} \{h(U) : V \subset U \subset W \text { and}\ U\ \text{is sofic} \} \end{align*} $$
is dense in
$[h(V), h(W)]$
.
From this result, we can quickly derive the fact (Corollary 5.3) that if X is a sofic G-shift, then each real number in
$[0,h(X)]$
can be realized as the entropy of some (not necessarily sofic) subsystem of X. (Recall that the alternate proof of Theorem 4.2 described in Remark 1.2 above relies on a version of this result requiring X to be an SFT.) The tool for proving Theorem 5.2 (from Theorem 4.2) is provided by the following theorem, which may be of independent interest. We note that this result generalizes another theorem of Desai [Reference Desai6, Proposition 4.3], which addressed the case
$G = \mathbb {Z}^d$
.
Theorem 5.1. Let G be a countable amenable group and let W be a sofic G-shift. For every
$\varepsilon> 0$
, there exists an SFT
$\tilde X$
and a one-block code
$\tilde \phi : \tilde X \to W$
such that the maximal entropy gap of
$\tilde \phi $
satisfies
$\mathcal H(\tilde \phi ) < \varepsilon $
.
The maximal entropy gap
$\mathcal H(\tilde \phi )$
is defined in §2 (Definition 2.16). In particular, this result implies that if Y is sofic and
$\varepsilon> 0$
, then there is an SFT X that factors onto Y and satisfies
$h(X) < h(Y) + \varepsilon $
.
Our proofs of Theorems 4.2, 5.1, and 5.2 take the same general approach as the arguments given by Desai for the
$G = \mathbb {Z}^d$
case. However, the extension to the general amenable setting requires substantial new techniques. Indeed, our proofs are made possible by the existence of exact tilings (Definition 3.1) of the group G that possess nice dynamical properties. Such exact tilings are trivial to find for
$\mathbb Z^d$
(by tiling the group using large hypercubes), but were only recently constructed for arbitrary amenable groups by Downarowicz, Huczek, and Zhang [Reference Downarowicz, Huczek and Zhang7]; their construction is the main technical tool employed in this paper.
As mentioned in Remark 1.2 above, Theorem 4.2 can be alternately derived from results in [Reference Frisch and Tamuz8]. We present a self-contained proof here for two reasons. First, we would like to present a direct adaptation of the techniques from [Reference Desai6], since it demonstrates the power of the improved tiling results of [Reference Downarowicz, Huczek and Zhang7]. Second, this presentation provides a unified approach to all of our proofs, since our proofs in the sofic setting (where we are not aware of alternative proofs) also rely on tiling-based constructions that are similar to those in our proof of Theorem 4.2.
The paper is organized as follows. In §2, we discuss basic notions and elementary theorems of symbolic dynamics, set in terms appropriate for countable amenable groups. In §3, we define and explore the concept of tilings and exact tilings of amenable groups, appealing to Downarowicz, Huczek, and Zhang for the existence of certain desirable tilings. In §4, we prove our main results for G-SFTs, and in §5, we prove our main results for sofic G-shifts. Finally, in §6, we provide an example of a
$\mathbb {Z}^2$
sofic shift whose only SFT subsystem is a fixed point.
2 Basics of symbolic dynamics
2.1 Amenable groups
We begin with a brief overview of amenable groups.
Definition 2.1. (Group theory notation)
Let G be a group and let K,
$F \subset G$
be subsets. We employ the following notation:
-
(i) the group identity is denoted by the symbol
$e \in G$
; -
(ii)
$KF = \{ kf : k \in K \text { and } f\in F\}$
; -
(iii)
$K^{-1} = \{k^{-1} : k \in K\}$
; -
(iv)
$Kg = \{kg : k \in K\}$
for each
$g \in G$
; -
(v)
$K \sqcup F$
expresses that K and F are disjoint, and is their (disjoint) union; -
(vi)
$K \triangle F = (K \setminus F) \sqcup (F \setminus K)$
is the symmetric difference of K and F; and -
(vii)
$|K|$
is the cardinality of the (finite) set K.
Definition 2.2. (Følner condition for amenability)
Let G be a countable group. A Følner sequence is a sequence
$(F_n)_{n}$
of finite subsets
$F_n \subset G$
which exhausts G (in the sense that for each
$g \in G$
, we have
$g \in F_n$
for all sufficiently large n) and for which it holds that
$$ \begin{align*} \lim_{n\to\infty} \frac{|KF_n \triangle F_n|}{|F_n|} = 0 \end{align*} $$
for every finite subset
$K \subset G$
. If such a sequence exists, then G is said to be an amenable group.
Throughout this paper, G denotes a fixed countably infinite amenable group and
$(F_n)_{n}$
is a fixed Følner sequence for G.
Definition 2.3. (Invariance)
Let K,
$F \subset G$
be finite subsets, and let
$\varepsilon> 0$
. We say F is
$(K,\varepsilon )$
-invariant if
$$ \begin{align*} \frac{|KF\triangle F|}{|F|} < \varepsilon. \end{align*} $$
If
$e \in K$
and F is
$(K,\varepsilon )$
-invariant, then F is also
$(K',\varepsilon ')$
-invariant for any
$\varepsilon '> \varepsilon $
and any
$K' \subset K$
such that
$e\in K'$
. If F is
$(K,\varepsilon )$
-invariant, then so is the translate
$Fg$
for each fixed
$g \in G$
. Invariance is the primary way by which we say a large finite subset
$F \subset G$
is a ‘good finite approximation’ of G, according to the finitary quantifiers K and
$\varepsilon $
. The amenability of G provides a wealth of nearly invariant sets, which enables such approximation for the purpose of studying the dynamics of G-actions.
Next we develop concepts related to the geometry of finite subsets of G.
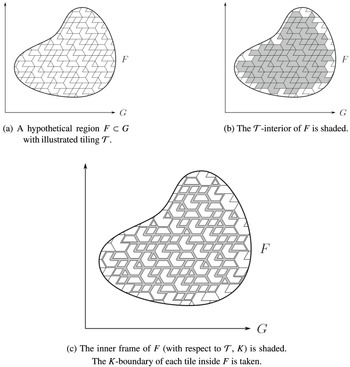
Definition 2.4. (Boundary and interior)
Let K,
$F \subset G$
be finite subsets. The K-boundary of F is the set
$$ \begin{align*} \partial_K F = \{f \in F : Kf \not\subset F\}, \end{align*} $$
and the K-interior of F is the set
$$ \begin{align*} \operatorname{\mathrm{int}}_K F = \{f \in F : Kf \subset F\}. \end{align*} $$
Observe that
$F = (\partial _K F) \sqcup (\operatorname {\mathrm {int}}_K F)$
.
If F is sufficiently invariant with respect to K, then the K-boundary of F is a small subset of F (proportionally), by the following lemma.
Lemma 2.1. Suppose K,
$F \subset G$
are non-empty finite subsets and
$e \in K$
. Then
$$ \begin{align*} \frac{1}{|K|} |KF\triangle F| \leq |\partial_K F| \leq |K||KF \triangle F|. \end{align*} $$
In particular, if F is
$(K,\varepsilon )$
-invariant then
$|\partial _K F| < \varepsilon |K||F|$
.
Proof. If
$e\in K$
, then
$KF \triangle F = KF \setminus F$
. If
$g \in KF \setminus F$
, then
$g = kf$
for some
$k \in K$
and
$f \in \partial _K F$
, by Definition 2.4. Therefore,
$KF \setminus F \subset K \partial _K F$
, in which case
$|KF\setminus F| \leq |K||\partial _K F|$
.
For the second inequality, note that
$f \in \partial _K F$
implies
$\text { there exists } k \in K$
such that
$kf \not \in F$
; therefore,
$g = kf \in KF \setminus F$
is a point such that
$f\in K^{-1}g \subset K^{-1}(KF\setminus F)$
. Consequently
$\partial _K F \subset K^{-1}(KF\setminus F)$
, in which case
$|\partial _K F| \leq |K||KF \setminus F|$
.
Finally, if F is
$(K,\varepsilon )$
-invariant, then
$|\partial _KF| \leq |K||KF \setminus F| < \varepsilon |K||F|$
.
Given finite subsets K,
$F \subset G$
, in this paper, we focus on the
$KK^{-1}$
-boundary and
$KK^{-1}$
-interior of F (rather than the K-boundary and K-interior), and we make use of the following lemma.
Lemma 2.2. Let K,
$F \subset G$
. For any translate
$Kg$
of K (for any
$g \in G$
), either
$Kg \subset F$
or
$Kg \subset (\operatorname {\mathrm {int}}_{KK^{-1}} F)^c$
(or both are true).
Proof. Suppose
$Kg \not \subset (\operatorname {\mathrm {int}}_{KK^{-1}} F)^c$
. Then
$\text { there exists } f \in \operatorname {\mathrm {int}}_{KK^{-1}} F$
such that
${f \in Kg}$
, which implies
$g \in K^{-1} f$
and hence
$Kg \subset KK^{-1}f \subset F$
.
2.2 Shift spaces
Here we present necessary definitions from symbolic dynamics. See Lind and Marcus [Reference Lind and Marcus14] for an introductory treatment of these concepts.
Definition 2.5. (Shifts and subshifts)
Let
$\mathcal A$
be a finite set of symbols equipped with the discrete topology. A function
$x : G \to \mathcal A$
is called an
$\mathcal A$
-labeling of G. By convention, we write
$x_g$
for the symbol
$x(g) \in \mathcal A$
which is placed by x at
$g \in G$
. The set of all
$\mathcal A$
-labelings of G is denoted
$\mathcal A^G$
, which we equip with the product topology. For each
$g \in G$
, let
$\sigma ^g : \mathcal A^G \to \mathcal A^G$
denote the map given by
$$ \begin{align*} (\sigma^g x)_h = x_{hg} \quad \text{for all } h \in G \end{align*} $$
for each
$x\in \mathcal A^G$
. The collection
$\sigma = (\sigma ^g)_{g\in G}$
is an action of G on
$\mathcal A^G$
by homeomorphisms. The pair
$(\mathcal A^G, \sigma )$
is a dynamical system called the full shift over the alphabet
$\mathcal A$
. A subset
$X \subset \mathcal A^G$
is called shift-invariant if
$\sigma ^g x \in X$
for each
$x \in X$
and
$g \in G$
. A closed, shift-invariant subset
$X \subset \mathcal A^G$
is called a subshift or a shift space. For a given
$x \in \mathcal A^G$
, the orbit of x is the subset
$\mathcal O(x) = \{\sigma ^g x : g \in G\} \subset \mathcal A^G$
. The subshift generated by x is the topological closure of
$\mathcal O(x)$
as a subset of
$\mathcal A^G$
, and is denoted
$\overline {\mathcal O}(x) \subset \mathcal A^G$
.
Definition 2.6. (Codes and factors)
Let
$\mathcal A_X$
,
$\mathcal A_W$
be finite alphabets and let
$X \subset \mathcal A_X^G$
and
$W \subset \mathcal A_W^G$
be subshifts. A map
$\phi : X \to W$
is shift-commuting if
$\phi \circ \sigma ^g = \sigma ^g \circ \phi $
for each
$g \in G$
; the map
$\phi $
is said to be a sliding block code if it is continuous and shift-commuting; and
$\phi $
is said to be a factor map if it is a surjective sliding block code. If a factor map exists from X to W, then W is said to be a factor of X and X is said to factor onto W. If a sliding block code
$\phi : X \to W$
is invertible and bi-continuous, then
$\phi $
is said to be a topological conjugacy, in which case X and W are said to be topologically conjugate.
Definition 2.7. (Products of shifts)
If
$\mathcal A$
and
$\Sigma $
are finite alphabets, then
$\mathcal A \times \Sigma $
is also a finite alphabet (of ordered pairs). If
$X \subset \mathcal A^G$
and
$T \subset \Sigma ^G$
are subshifts, then we view the dynamical direct product
$X \times T$
as a subshift of
$(\mathcal A \times \Sigma )^G$
, defined by
$(x,t) \in X \times T$
if and only if
$x \in X$
and
$t \in T$
. The shift space
$X \times T$
factors onto both X and T via the projection maps
$\pi _X$
and
$\pi _T$
, given by
$\pi _X(x,t) = x$
and
$\pi _T(x,t) = t$
for each
$(x,t) \in X\times T$
.
Remark 2.3. Definition 2.7 above introduces an abuse of notation, as technically we have
$(x,t) \in \mathcal A^G \times \Sigma ^G \neq (\mathcal A \times \Sigma )^G$
. However, if equipped with the G-action
$\varsigma $
given by
$\varsigma ^g(x,t) = (\sigma ^g x,\, \sigma ^g t)$
, then
$\mathcal A^G \times \Sigma ^G$
becomes a dynamical system that is topologically conjugate to
$(\mathcal A \times \Sigma )^G$
.
2.3 Patterns
In this section, we describe patterns and their related combinatorics.
Definition 2.8. (Patterns)
Let
$\mathcal A$
be a finite alphabet and let
$F \subset G$
be a finite set. A function
$p : F \to \mathcal A$
is called a pattern, said to be of shape F. The set of all patterns of shape F is denoted
$\mathcal A^F$
. The set of all patterns of any finite shape is denoted
$\mathcal A^* = \bigcup _F \mathcal A^F$
, where the union is taken over all finite subsets
$F \subset G$
.
Remark 2.4. Given a point
$x \in \mathcal A^G$
and a finite subset
$F \subset G$
, we take
$x(F)$
to mean the restriction of x to F, which is itself a pattern of shape F. Usually this is denoted
$x|_F \in \mathcal A^F$
, but we raise F from the subscript for readability.
Definition 2.9. (One-block code)
Let
$\mathcal A_X$
and
$\mathcal A_W$
be finite alphabets and let
$X \subset \mathcal A_X^G$
and
$W \subset \mathcal A_W^G$
be subshifts. A factor map
$\phi : X \to W$
is said to be a one-block code if there exists a function
$\Phi : \mathcal A_X \to \mathcal A_W$
with the property that
$$ \begin{align*} \phi(x)_g = \Phi(x_g) \quad \text{for all } g\in G \end{align*} $$
for each
$x \in X$
.
Definition 2.10. (Occurrence)
Let
$\mathcal A$
be a finite alphabet and let
$F \subset G$
be a finite set. A pattern
$p \in \mathcal A^F$
is said to occur in a point
$x \in \mathcal A^G$
if there exists an element
$g \in G$
such that
$(\sigma ^g x)(F) = p$
. If
$X \subset \mathcal A^G$
is a subshift, then the collection of all patterns of shape F occurring in any point of X is denoted by
$$ \begin{align*} \mathcal P(F,X) = \{(\sigma^g x)(F) \in \mathcal A^F \,{:}\, x\in X \text{ and } g\in G\}. \end{align*} $$
If
$X\subset \mathcal A^G$
is a subshift and
$F \subset G$
is a finite subset, then
$|\mathcal P(F,X)| \leq |\mathcal A|^{|F|}$
. If
$F' \subset G$
is another finite subset, then
$|\mathcal P(F\cup F', X)| \leq |\mathcal P(F,X)| \cdot |\mathcal P(F', X)|$
. If
$F' \subset F$
and
$X' \subset X$
, then
$|\mathcal P(F',X')| \leq |\mathcal P(F,X)|$
.
Definition 2.11. (Forbidden patterns)
Let
$\mathcal A$
be a finite alphabet, let
$F \subset G$
be a finite set, and let
$X \subset \mathcal A^G$
be a subshift. A pattern
$p \in \mathcal A^F$
is said to be allowed in X if
$p \in \mathcal P(F,X)$
(if p occurs in at least one point of X).
Given a (finite or infinite) collection of patterns
$\mathcal F \subset \mathcal A^*$
, a new subshift
$X' \subset X$
may be constructed by expressly forbidding the patterns in
$\mathcal F$
from occurring in points of X. We denote this by
$$ \begin{align*} X' = \mathcal R(X,\mathcal F) = \{x \in X \,{:}\, \text{for all } p \in \mathcal F, p\ \text{does not occur in}\ x\}. \end{align*} $$
For a single pattern p, we abbreviate
$\mathcal R(X, \{p\})$
as
$X \setminus p$
. The shift X is said to be specified by the collection
$\mathcal F$
if
$X = \mathcal R(\mathcal A^G, \mathcal F)$
.
2.4 Shifts of finite type
In this section, we define shifts of finite type and sofic shifts over G. We also discuss many related elementary facts.
Definition 2.12. (SFTs)
A subshift
$X \subset \mathcal A^G$
is a shift of finite type (SFT) if there is a finite collection
$\mathcal F \subset \mathcal A^*$
such that
$X = \mathcal R(\mathcal A^G, \mathcal F)$
. For an SFT, it is always possible to take
$\mathcal F$
in the form
$\mathcal F = \mathcal A^K \setminus \mathcal P(K,X)$
for some large finite subset
$K \subset G$
. In this case, we say X is specified by (patterns of shape) K.
If
$X \subset \mathcal A^G$
is an SFT specified by a finite subset
$K \subset G$
, then it holds that
$$ \begin{align*} x \in X \!\iff\!\text{ for all }g\in G\ ( (\sigma^g x)(K) \in \mathcal P(K,X) ) \end{align*} $$
for each
$x \in \mathcal A^G$
. If K specifies X, then so does
$K'$
for any (finite) subset
$K' \supset K$
. If X and T are SFTs, then so is the dynamical direct product
$X \times T$
.
Definition 2.13. (Sofic shifts)
A subshift W is sofic if there exists an SFT X which factors onto W.
The following elementary facts are needed; we abbreviate the proofs as they are similar to the well-known proofs in the case where
$G = \mathbb Z$
(see [Reference Lind and Marcus14]).
Proposition 2.5. Let X be an SFT, let W be a sofic shift, and let
$\phi : X \to W$
be a factor map. Then there exists an SFT
$\tilde X$
and a topological conjugacy
$\tilde \phi : \tilde X \to X$
such that the composition
$\phi \circ \tilde \phi : \tilde X \to W$
is a one-block code.
Proof. Because
$\phi $
is continuous and shift-commuting, there exists a large finite subset
$K \subset G$
such that for each x,
$x'\in X$
, and each
$g \in G$
, it holds that
$$ \begin{align*} (\sigma^g x)(K) = (\sigma^g x')(K) \!\implies\! \phi(x)_g = \phi(x')_g. \end{align*} $$
Suppose that
$e\in K$
and that
$\mathcal P(K,X)$
specifies X as an SFT. Let
$\tilde {\mathcal A} = \mathcal P(K,X)$
be a new finite alphabet, and let
$\tilde X \subset \tilde {\mathcal A}^G$
be the set of all points
$\tilde x \in \tilde {\mathcal A}^G$
such that
$$ \begin{align*} \text{ there exists } x\in X \quad \text{for all }g\in G, \quad \tilde x_g = (\sigma^g x)(K). \end{align*} $$
Then
$\tilde X$
is an SFT specified by patterns of shape
$K^{-1}K$
. The map
$\tilde \phi : \tilde X \to X$
desired for the theorem is given by
$$ \begin{align*} \tilde \phi(\tilde x)_g = (\tilde x_g)_e \in \mathcal A \quad \text{for all } g\in G \quad\text{for all } \tilde x \in \tilde X.\\[-33pt] \end{align*} $$
Proposition 2.6. For any subshift
$X \subset \mathcal A^G$
, there is a descending family of SFTs
$(X_n)_n$
such that
$X = \bigcap _n X_n$
.
Proof. Let
$(p_n)_n$
enumerate
$\{p\in \mathcal A^* : p\ \text {does not occur in}\ X\}$
, and for each n, let
$$ \begin{align*} X_n = \mathcal R(\mathcal A^G, \{p_1, p_2, \ldots, p_n\}). \end{align*} $$
Then
$(X_n)_n$
witnesses the result.
Proposition 2.7. Let
$X \subset \mathcal A^G$
be a subshift and let
$X_0 \subset \mathcal A^G$
be an SFT such that
${X \subset X_0}$
. If
$(X_n)_n$
is any descending family of subshifts such that
$X = \bigcap _n X_n$
, then
$X_n \subset X_0$
for all sufficiently large n.
Proof. Take
$K\subset G$
to specify
$X_0$
as an SFT. Note
$(\mathcal P(K,X_n))_n$
is a descending family of finite sets, and it is therefore eventually constant. In particular, we have
$$ \begin{align*} \mathcal P(K,X_n) = \mathcal P(K,X) \subset \mathcal P(K,X_0) \end{align*} $$
for all sufficiently large n.
When
$G = \mathbb Z^d$
, SFTs are often reduced via conjugacy to so-called 1-step SFTs, in which the allowed patterns are specified by allowed adjacent pairs of symbols. Such SFTs are often desired because they allow for a kind of ‘surgery’ of patterns. If two patterns occur in two different labelings from a 1-step SFT, and yet they agree on their 1-boundaries, then the first may be excised and replaced by the second. This yields a new labeling which also belongs to the 1-step SFT. Although there is no obvious notion of 1-step SFTs when
$G \neq \mathbb Z^d$
, we do have the following result which allows for this sort of excision and replacement of patterns.
Lemma 2.8. Let
$X \subset \mathcal A^G$
be an SFT specified by
$K \subset G$
, let
$F \subset G$
be a finite subset, and let x,
$y \in X$
be two points such that x and y agree on
$\partial _{KK^{-1}} F$
. Then the point z, defined by
$z_g = y_g$
if
$g \in F$
and
$z_g = x_g$
if
$g \notin F$
, also belongs to X.
Proof. Let
$g\in G$
. By Lemma 2.2, either
$Kg \subset F$
or
$Kg \subset (\operatorname {\mathrm {int}}_{KK^{-1}} F)^c$
. In the first case, we have
$(\sigma ^g z)(K) = (\sigma ^g y)(K)$
which is an allowed pattern in X. In the second case, we have
$Kg \subset (F^c) \sqcup (\partial _{KK^{-1}}F)$
. Since x and y agree on
$\partial _{KK^{-1}} F$
, we have
$(\sigma ^g z)(K) = (\sigma ^g x)(K)$
which is again an allowed pattern in X. In either case,
$(\sigma ^g z)(K)$
is allowed in X for every g, and hence
$z \in X$
.
2.5 Entropy
Let
$X \subset \mathcal A^G$
be a non-empty subshift. Recall that for a given large finite set
$F \subset G$
, the number of patterns of shape F that occur in any point of X is
$|\mathcal P(F,X)|$
, which is at most
$|\mathcal A|^{|F|}$
. As this grows exponentially (with respect to
$|F|$
), we are interested in the exponential growth rate of
$|\mathcal P(F,X)|$
as F becomes very large and approaches the whole group G. For non-empty finite sets
$F \subset G$
, we let
$$ \begin{align*} h(F,X) = \frac1{|F|}\log|\mathcal P(F,X)|. \end{align*} $$
If F,
$F' \subset G$
are disjoint finite subsets, then
$h(F \sqcup F', X) \leq h(F,X) + h(F', X)$
. This is because
$|\mathcal P(F\sqcup F',X)| \leq |\mathcal P(F,X)| \cdot |\mathcal P(F',X)|$
and
$$ \begin{align*} \frac1{|F\sqcup F'|} = \frac1{|F|+|F'|} \leq \min \bigg( \frac1{|F|},\, \frac1{|F'|} \bigg). \end{align*} $$
Definition 2.14. (Entropy)
Let X be a non-empty subshift. The (topological) entropy of X is the non-negative real number
$h(X)$
given by the limit
$$ \begin{align*} h(X) = \lim_{n\to\infty} h(F_n, X), \end{align*} $$
where
$(F_n)_n$
is again the Følner sequence of G. For the empty subshift, we adopt the convention that
$h(\varnothing ) = 0$
.
It is well known that the limit above exists, does not depend on the choice of Følner sequence for G, and is an invariant of topological conjugacy (see [Reference Kerr and Li11]).
For any subshift
$X \subset \mathcal A^G$
and any finite subset
$F\subset G$
, it holds that
$h(F,X) \leq \log |\mathcal A|$
and consequently
$h(X) \leq \log |\mathcal A|$
. More generally, if X and
$X'$
are subshifts such that
$X \subset X'$
, then
$h(F,X) \leq h(F,X')$
for every finite subset
$F \subset G$
and consequently
$h(X) \leq h(X')$
. If X and
$X'$
are subshifts over
$\mathcal A$
, then so is
$X \cup X'$
and
$h(X \cup X') = \max (h(X), h(X'))$
.
The following proposition is a classical fact; a proof is given in [Reference Kerr and Li11].
Proposition 2.9. Let G be a countable amenable group. If a G-shift W is a factor of a G-shift X, then
$h(W) \leq h(X)$
.
Frequently in this paper, we refer to ‘measuring’ or approximating the entropy of a subshift via a large set F. We give a precise definition as follows.
Definition 2.15. (Entropy approximation)
Let
$X \subset \mathcal A^G$
be a subshift and let
$\delta> 0$
. A finite subset
$F \subset G$
is said to
$\delta $
-approximate the entropy of X if
$$ \begin{align*} h(X) - \delta < h(F,X) < h(X) + \delta. \end{align*} $$
We shall more commonly write
$h(X) < h(F,X) + \delta < h(X) + 2\delta $
.
Infinitely many such sets exist for any
$\delta $
, as provided by the Følner sequence and the definition of
$h(X)$
. We introduce this notion so that we may layer invariance conditions and entropy-approximating conditions as needed.
Proposition 2.10. For finitely many choices of i, let
$K_i \subset G$
be any finite subsets and let
$\varepsilon _i> 0$
be any positive constants. For finitely many choices of j, let
$X_j \subset \mathcal A_j^G$
be any subshifts over any finite alphabets and let
$\delta _j> 0$
be any positive constants. There exists a finite subset
$F \subset G$
which is
$(K_i,\varepsilon _i)$
-invariant for every i and which
$\delta _j$
-approximates the entropy of
$X_j$
for every j.
Proof. Choose
$F = F_n$
for sufficiently large n.
The following theorem is an elementary generalization of a classical statement (see [Reference Lind and Marcus14] for a proof in the case where
$G = \mathbb Z$
). We omit the proof here for brevity.
Proposition 2.11. Let
$(X_n)_{n}$
be a descending family of subshifts and let
$X = \bigcap _n X_n$
. Then
$$ \begin{align*} h(X) = \lim_{n\to\infty} h(X_n). \end{align*} $$
It is desirable to work with SFTs as much as possible while preserving (or, in our case, approximating) relevant dynamical quantities. We shall make frequent use of the next theorem, which we justify with several of the above results.
Theorem 2.12. Let
$X \subset \mathcal A^G$
be a subshift and suppose that
$X_0 \subset \mathcal A^G$
is an SFT such that
$X \subset X_0$
. For any
$\varepsilon> 0$
, there exists an SFT
$Z \subset \mathcal A^G$
such that
$X \subset Z \subset X_0$
and
$h(X) \leq h(Z) < h(X) + \varepsilon $
.
Proof. By Proposition 2.6, there is a descending family of SFTs
$(X_n)_n$
such that
$X = \bigcap _n X_n$
. By Proposition 2.7, we have
$X_n \subset X_0$
for all sufficiently large n. By Proposition 2.11, we have
$h(X) \leq h(X_n) < h(X) + \varepsilon $
for all sufficiently large n. Choose
$Z = X_n$
for n large enough to meet both conditions.
If
$\phi : X \to W$
is a factor map of subshifts, then we have already seen that
$h(W) \leq h(X)$
. The ‘entropy drop’ or entropy gap between X and W is the quantity
$h(X) - h(W)$
. A subsystem
$X' \subset X$
induces a corresponding subsystem
$\phi (X') = W' \subset W$
and, later in this paper, we will want a uniform bound for the entropy gap between every
$X'$
and
$W'$
pair. We make this idea precise in the following definition.
Definition 2.16. (Maximal entropy gap)
Suppose
$\phi : X \to W$
is a factor map. The maximal entropy gap of
$\phi $
is the quantity
$$ \begin{align*} \mathcal H(\phi) = \sup_{X'} (h(X') - h(\phi(X'))), \end{align*} $$
where the supremum is taken over all subshifts
$X' \subset X$
. In particular, it holds that
$$ \begin{align*} h(W) \leq h(X) \leq h(W) + \mathcal H(\phi). \end{align*} $$
Recall that if X and T are subshifts, then the dynamical direct product
$X \times T$
factors onto both X and T via the projection map(s)
$\pi _X(x,t) = x$
and
$\pi _T(x,t) = t$
.
Proposition 2.13. Let X and T be shift spaces. The maximal entropy gap of the projection map
$\pi _X : X \times T \to X$
is
$$ \begin{align*} \mathcal H(\pi_X) = h(T). \end{align*} $$
Proof. It is classically known that
$h(X \times T) = h(X) + h(T)$
, in which case
$h(T) = h (X \times T) - h(X) \leq \mathcal H(\pi _X)$
. For the converse inequality, suppose
$Z \subset X \times T$
is any subshift. Note by Definition 2.7 that
$z \in Z$
implies
$z = (z^X, z^T)$
, where
$z^X = \pi _X(z) \in \pi _X(Z) \subset X$
and
$z^T \in T$
. Therefore,
$Z \subset \pi _X(Z) \times T$
, in which case it follows that
$h(Z) \leq h(\pi _X(Z)) + h(T)$
. Since Z was arbitrary, we have
$$ \begin{align*} h(T) \leq \mathcal H(\pi_X) = \sup_Z ( h(Z) - h(\pi_X(Z))) \leq h(T), \end{align*} $$
where the supremum is taken over all subshifts
$Z \subset X \times T$
.
A quick corollary is that when
$h(T) = 0$
, we have
$h(Z) = h(\pi _X(Z))$
for any subsystem
$Z\subset X\times T$
.
3 Tilings of amenable groups
3.1 Definition and encoding
In this section, we consider the notion of tilings of G. The existence of tilings of G with certain properties is essential in our constructions in subsequent sections.
Definition 3.1. (Quasi-tilings and exact tilings)
A quasi-tiling of G is a pair
$(\mathcal S, C)$
, where
$\mathcal S$
is a finite collection of finite subsets of G (called the shapes of the tiling) and C is a function that assigns each shape
$S \in \mathcal S$
to a subset
$C(S) \subset G$
, called the set of centers or center-set attributed to S. We require that e is in S for each
$S \in \mathcal S$
. The following properties are also required.
-
(i) For distinct shapes S,
$S' \in \mathcal S$
, the subsets
$C(S)$
and
$C(S')$
are disjoint. -
(ii) The shapes in
$\mathcal S$
are ‘translate-unique,’ in the sense that for each S,
$$ \begin{align*} S \neq S' \!\implies\! Sg \neq S' \quad \text{for all } g \in G, \end{align*} $$
$S' \in \mathcal S$
.
-
(iii) The map
$(S,c) \mapsto Sc \subset G$
defined on the domain
$\{(S,c) : S \in \mathcal S \text { and } c \in C(S)\}$
is injective.
We may refer to both the pair
$(\mathcal S,C)$
and the collection
$$ \begin{align*} \mathcal T = \mathcal T(\mathcal S,C) = \{Sc \subset G : S \in \mathcal S \text{ and } c \in C(S)\} \end{align*} $$
as ‘the quasi-tiling.’ Each subset
$\tau = Sc \in \mathcal T$
is called a tile. For a quasi-tiling
$\mathcal T$
, we denote the union of all the tiles by
$\bigcup \mathcal T$
. A quasi-tiling
$\mathcal T$
may not necessarily cover G in the sense that
$\bigcup \mathcal T = G$
; nor is it necessary for any two distinct tiles
$\tau $
,
$\tau ' \in \mathcal T$
to be disjoint. However, if both of these conditions are met (that is, if
$\mathcal T$
is a partition of G), then
$\mathcal T$
is called an exact tiling of G.
Ornstein and Weiss [Reference Ornstein and Weiss15] previously constructed quasi-tilings of G with good dynamical properties, and this construction has become a fundamental tool for analyzing the dynamics of G-actions. Downarowicz, Huczek, and Zhang [Reference Downarowicz, Huczek and Zhang7] sharpened this construction, showing that a countable amenable group exhibits many exact tilings with good dynamical properties, as we describe below (see Theorem 3.3).
A quasi-tiling
$\mathcal T$
of G may be encoded in symbolic form, allowing for dynamical properties to be attributed to and studied for quasi-tilings. The encoding method presented here differs from the one presented in [Reference Downarowicz, Huczek and Zhang7], as we will only require exact tilings in this paper. See Remark 3.2 below for further discussion of the relation between our encoding and the encoding given in [Reference Downarowicz, Huczek and Zhang7].
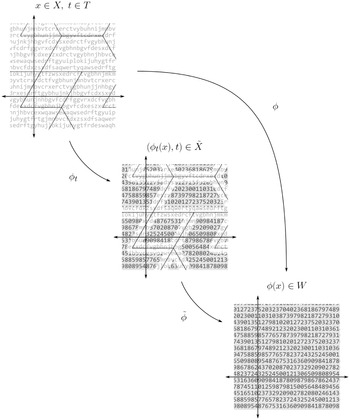
Definition 3.2. (Encoding)
Let
$\mathcal S$
be a finite collection of finite shapes and let
$$ \begin{align*} \Sigma(\mathcal S) = \{(S,s) : s \in S \in \mathcal S\}, \end{align*} $$
which we view as a finite alphabet. If
$\mathcal T$
is an exact tiling of G over
$\mathcal S$
, then it corresponds to a unique point
$t\in \Sigma (\mathcal S)^G$
as follows. For each
$g \in G$
, there is a unique tile
$Sc \in \mathcal T$
containing g; let
$s = gc^{-1} \in S$
and set
$t_g = (S,s)$
.
In the above definition, note that s is the ‘relative position’ of g in the translate
$Sc$
of S. In other words, t labels each element g of G with both the type of shape of the tile containing g and the relative position of g within that tile. In particular,
$g \in C(S) \!\iff t_g = (S,e)$
.
Note that the correspondence
$\mathcal T \mapsto t \in \Sigma (\mathcal S)^G$
, when regarded as a map on the set of all exact tilings of G over
$\mathcal S$
, is injective. However, the correspondence is not surjective in general. Let
$\Sigma _E(\mathcal S) \subset \Sigma (\mathcal S)^G$
be the set of all encodings of exact tilings of G over
$\mathcal S$
. It may be the case that no exact tiling of G over
$\mathcal S$
exists, in which case
$\Sigma _E(\mathcal S) = \varnothing $
. In general, we have the following useful theorem.
Proposition 3.1. Let
$\mathcal S$
be a finite collection of finite shapes drawn from G. Then
$\Sigma _E(\mathcal S) \subset \Sigma (\mathcal S)^G$
is an SFT.
Proof. Let
$\Sigma _1(\mathcal S)$
be the set of all points
$t \in \Sigma (\mathcal S)^G$
that satisfy the following local rule: for each
$g \in G$
, if
$t_g = (S_0, s_0) \in \Sigma (\mathcal S)$
, then
$$ \begin{align} t_{sc} = (S_0, s) \quad \text{for all } s \in S_0, \end{align} $$
where
$c = s_0^{-1}g$
. It is easy to see that
$\Sigma _1(\mathcal S)$
is an SFT and from Definition 3.2, it is immediate that
$\Sigma _E(\mathcal S) \subset \Sigma _1(\mathcal S)$
.
For the reverse inclusion, let
$t \in \Sigma _1(\mathcal S)$
be an arbitrary point satisfying the local rule (R1) everywhere. For each
$S \in \mathcal S$
, let
$C(S) = \{g\in G : t_g = (S,e)\}$
. Then
$\mathcal T = \mathcal T(\mathcal S, C)$
is a quasi-tiling. To complete the proof, it suffices to show that
$\mathcal T$
is exact and encoded by t, since that would give
$t \in \Sigma _E(\mathcal S)$
and then
$\Sigma _E(\mathcal S) = \Sigma _1(\mathcal S)$
.
Let
$g \in G$
, suppose
$t_g = (S,s)$
, and let
$c = s^{-1}g$
. By rule (R1) and the fact that
$e\in S$
, we have
$t_c = t_{ec} = (S,e)$
and therefore
$c \in C(S)$
. Hence,
$g = sc \in Sc \in \mathcal T$
. This demonstrates that
$\bigcup \mathcal T = G$
. Next, suppose
$Sc$
,
$S'c' \in \mathcal T$
are not disjoint and let
$g \in Sc \cap S'c'$
. Then
$g = sc = s'c'$
for some
$s \in S$
and
$s' \in S'$
. From
$c \in C(S)$
, we have
$t_c = (S,e)$
and by the rule (R1), we have
$$ \begin{align*} t_g = t_{sc} = (S,s). \end{align*} $$
By identical proof, we have
$t_g = (S', s')$
, from which it follows that
$S = S'$
and
$s = s'$
. The latter implies that
$$ \begin{align*} c = s^{-1}g = s^{\prime-1}g = c', \end{align*} $$
and hence
$Sc$
and
$S'c'$
are the same tile. This demonstrates that
$\mathcal T$
is a partition of G and therefore
$\mathcal T$
is an exact tiling of G over S. Finally, we note that it is straightforward to check that
$\mathcal T$
is encoded by t, which completes the proof.
Remark 3.2. Before we move on, we note here that the encoding method presented above (Definition 3.2) differs from the one presented in [Reference Downarowicz, Huczek and Zhang7]. The encoding method in that work gives symbolic encodings for all quasi-tilings, which is not necessary for our present purposes. Indeed, the encoding in [Reference Downarowicz, Huczek and Zhang7] uses the alphabet
$\Lambda (\mathcal S) = \mathcal S \cup \{0\}$
, and a point
$\unicode{x3bb} \in \Lambda (\mathcal S)^G$
encodes a quasi-tiling
$(\mathcal S,C)$
when
$\unicode{x3bb} _g = S \!\iff g \in C(S)$
and
$\unicode{x3bb} _g = 0$
otherwise. This is a prudent encoding method for the study of general quasi-tilings, as any quasi-tiling may be encoded in this manner. Our encoding method works only for exact tilings, but is well suited to our purposes. In fact, if one is only interested in exact tilings, then the two encodings are equivalent. Indeed, if
$\Lambda _E(\mathcal S) \subset \Lambda (\mathcal S)^G$
is the collection of all encodings of exact tilings of G over
$\mathcal S$
, then there is a topological conjugacy
$\phi : \Sigma _E(\mathcal S) \to \Lambda _E(\mathcal S)$
given by
$\phi (t)_g = S \!\iff t_g = (S,e)$
and
$\phi (t)_g = 0$
otherwise.
Next we turn our attention to the dynamical properties of tilings, as derived from their encodings.
Definition 3.3. (Dynamical tiling system)
Let
$\mathcal S$
be a finite collection of finite shapes, let
$\mathcal T$
be an exact tiling of G over
$\mathcal S$
, and let
$\mathcal T$
be encoded by the point
$t \in \Sigma _{E}(\mathcal S)$
. The dynamical tiling system generated by
$\mathcal T$
is the subshift generated by t in
$\Sigma (\mathcal S)^G$
, denoted
$\Sigma _{\mathcal T} = \overline {\mathcal O}(t) \subset \Sigma _{E}(\mathcal S)$
.
This allows for the dynamical properties (e.g., entropy) of
$\Sigma _{\mathcal T}$
as a subshift of
$\Sigma (\mathcal S)^G$
to be ascribed to
$\mathcal T$
. The tiling entropy of
$\mathcal T$
is
$h(\mathcal T) = h(\Sigma _{\mathcal T})$
, where the entropy of
$\Sigma _{\mathcal T}$
is a subshift of
$\Sigma (\mathcal S)^G$
.
The tiling entropy of
$\mathcal T$
is a measure of the ‘complexity’ of tile patterns that occur in large regions of G. In particular, when
$\mathcal T$
has entropy zero, the number of ways to cover a large region
$F \subset G$
by tiles in
$\mathcal T$
grows subexponentially (with respect to
$|F|$
).
The following theorem is quickly deduced from the main result of Downarowicz, Huczek, and Zhang [Reference Downarowicz, Huczek and Zhang7], which we state in this form for convenience. It is this result that allows us to use exact tilings of G in this paper.
Theorem 3.3. [Reference Downarowicz, Huczek and Zhang7]
Let
$K \subset G$
be a finite subset and let
$\varepsilon> 0$
. Then there exists a finite collection of finite shapes
$\mathcal S$
with the following properties.
-
(i) Each shape
$S \in \mathcal S$
is
$(K,\varepsilon )$
-invariant. -
(ii)
$K \subset S$
and
$|S|> \varepsilon ^{-1}$
for each shape
$S \in \mathcal S$
. -
(iii) There exists a point
$t_0 \in \Sigma _E(\mathcal S)$
such that
$h(\overline {\mathcal {O}}(t_0)) = 0$
.
The point
$t_0$
encodes an exact tiling
$\mathcal T_0$
of G over
$\mathcal S$
with tiling entropy
$h(\mathcal T_0) = 0$
.
3.2 Approximating sets with tiles
Entropy and other dynamical properties of G-shifts are well measured by sets with strong invariance properties (the Følner sequence
$F_n$
provides a wealth of such sets). However, we would instead like to use an (appropriately selected) exact tiling
$\mathcal T$
for this purpose. In this section, we build good tile approximations of sets: finite collections of tiles
$\mathcal T^* \subset \mathcal T$
attributed to large, suitably invariant subsets
$F \subset G$
that are good in the sense that the symmetric difference
$F \triangle \bigcup \mathcal T^*$
is small (as a proportion of
$|F|$
).
Definition 3.4. (Tile approximation)
Let
$F \subset G$
be a finite subset. An exact tiling
$\mathcal T$
of G induces two finite collections of tiles: the outer approximation of F by
$\mathcal T$
, denoted
$$ \begin{align*} \mathcal T^\times(F) = \{\tau \in \mathcal T : \tau \cap F \neq \varnothing \}, \end{align*} $$
and the inner approximation of F by
$\mathcal T$
, denoted
$$ \begin{align*} \mathcal T^\circ(F) = \{\tau \in \mathcal T : \tau \subset F\}. \end{align*} $$
Denote
$F^\times (\mathcal T) = \bigcup \mathcal T^\times (F)$
and
$F^\circ (\mathcal T) = \bigcup \mathcal T^\circ (F)$
. Observe that
${F^\circ (\mathcal T) \kern1.5pt{\subset}\kern1.5pt F \kern1.5pt{\subset}\kern1.5pt F^\times (\mathcal T)}$
.
Lemma 3.4. Let
$\mathcal S$
be a finite collection of shapes from G and let
$U = \bigcup \mathcal S$
. Let
$\varepsilon> 0$
and choose
$\delta> 0$
such that
$\delta |U||UU^{-1}| < \varepsilon $
. Let
$F \subset G$
be a finite subset that is
$(UU^{-1},\delta )$
-invariant. For any exact tiling
$\mathcal T$
of G over
$\mathcal S$
, the following statements hold:
-
(i)
$|F^\times (\mathcal T) \setminus F^\circ (\mathcal T)| < \varepsilon |F|$
; -
(ii)
$(1-\varepsilon )|F| < |F^\circ (\mathcal T)| \leq |F|$
; and -
(iii)
$|F| \leq |F^\times (\mathcal T)| < (1+\varepsilon )|F|$
.
Proof. First, we observe that each tile
$\tau \in \mathcal T$
is contained in a translate
$Ug$
for some
$g\in G$
; indeed, we have
$\tau = Sc$
for some
$S \in \mathcal S$
and
$c \in C(S) \subset G$
, then
$S \subset U$
implies
$\tau \subset Uc$
. This fact also gives that
$|\tau | \leq |U|$
for every tile
$\tau \in \mathcal T$
.
We claim that every tile
$\tau \in \mathcal T^\times (F) \setminus \mathcal T^\circ (F)$
intersects
$\partial _{UU^{-1}}F$
. To establish the claim, we first note that for each such tile
$\tau $
, it holds that
$\tau \cap F \neq \varnothing $
and
$\tau \not \subset F$
. So let
$f \in \tau \cap F$
and note that
$f\in \tau \subset Ug$
for some
$g\in G$
. From
$\tau \not \subset F$
, we also have
$Ug \not \subset F$
. By Lemma 2.2, we have
$f\in Ug \subset (\operatorname {\mathrm {int}}_{UU^{-1}} F)^c$
, and hence
$f \in F \setminus (\operatorname {\mathrm {int}}_{UU^{-1}} F) = \partial _{UU^{-1}} F$
, which establishes our claim.
By the claim in the previous paragraph, there is a map
$\gamma : \mathcal T^\times (F) \setminus \mathcal T^\circ (F) \to \partial _{UU^{-1}} F$
with the property that
$\gamma (\tau ) \in \tau $
for each
$\tau $
. Observe that
$\gamma $
is injective, as distinct tiles are disjoint, and therefore
$|\mathcal T^\times (F) \setminus \mathcal T^\circ (F)| \leq |\partial _{UU^{-1}} F|$
. We also have that
$$ \begin{align*} |\partial_{UU^{-1}}F| < \delta|UU^{-1}||F|, \end{align*} $$
by the invariance hypothesis on F and Lemma 2.1. Then
$$ \begin{align*} |F^\times(\mathcal T) \setminus F^\circ(\mathcal T)| &= \sum_{\tau \in \mathcal T^\times(F) \setminus \mathcal T^\circ(F)} |\tau|\\ &\leq |\mathcal T^\times(F) \setminus \mathcal T^\circ(F)||U|\\ &\leq |\partial_{UU^{-1}} F||U|\\ &< \delta|U||UU^{-1}||F|\\ &< \varepsilon|F|. \end{align*} $$
This establishes statement (i). The remaining two statements are easy to check using the fact that
$F^\circ (\mathcal T) \subset F \subset F^\times (\mathcal T)$
and statement (i).
One more notion is necessary to develop before moving on from tilings: the frame of a given subset with respect to a given tiling.
Definition 3.5. (Frame of a tiling)
Let F,
$K \subset G$
, and let
$\mathcal T$
be an exact tiling of G. The inner
$(\mathcal T,K)$
-frame of F is the subset
$$ \begin{align*} \operatorname{fr}_{\mathcal T,K}(F) = \bigcup_{\tau} \partial_K(\tau), \end{align*} $$
where the union ranges over all
$\tau \in \mathcal T^\circ (F)$
. See Figure 1 for an illustration.
Figure 1 A sketch of the construction of
$\operatorname {fr}_{\mathcal T,K}(F)$
.
4 Results for SFTs
Having discussed everything about tilings relevant for our purposes, we are now ready to begin discussing our main results. In this section, we present our results for SFTs and in the following section, we turn our attention to sofic shifts.
Theorem 4.1. Let G be a countable amenable group and let X be a G-SFT such that
$h(X)> 0$
. Then
$$ \begin{align*} \{ h(Y) : Y \subset X \text{ and}\ Y\ \text{is an SFT}\kern1pt\} \end{align*} $$
is dense in
$[0, h(X)]$
.
Before we begin the proof, let us give a short outline of the main ideas. The broad strokes of this proof come from Desai [Reference Desai6], whose argument in the case where
$G = \mathbb Z^d$
we are able to extend to the case where G is an arbitrary countable amenable group. This is possible by using the exact tilings of G constructed by Downarowicz, Huczek, and Zhang [Reference Downarowicz, Huczek and Zhang7].
Given an arbitrary
$\varepsilon> 0$
, we produce a family of SFT subshifts of X whose entropies are
$2\varepsilon $
-dense in
$[0,h(X)]$
. We accomplish this by first selecting an exact, zero entropy tiling
$\mathcal T_0$
of G with suitably large, invariant tiles. Then we build subshifts with strongly controlled entropies inside the product system
$Z_0 = X \times \Sigma _0$
, where
$\Sigma _0$
is the dynamical tiling system generated by
$\mathcal T_0$
.
To construct these subshifts from
$Z_0$
, we control which patterns in the X layer can appear in the ‘interior’ of the tiles in the
$\Sigma _0$
layer. We are able to finely comb away entropy from
$Z_0$
by forbidding these patterns one at a time. This process generates a descending family of subsystems for which the entropy drop between consecutive subshifts is less than
$\varepsilon $
. After enough such patterns have been forbidden, the overall entropy is less than
$\varepsilon $
. This collection of subshifts therefore has entropies that are
$\varepsilon $
-dense in
$[0, h(Z_0)]$
. Then we project the subshifts into X and use Theorem 2.12 to produce SFT subsystems of X with entropies that are
$2\varepsilon $
-dense in
$[0,h(X)]$
.
Proof. Let
$X\subset \mathcal A^G$
be an SFT such that
$h(X)>0$
, let
$K \subset G$
be a large finite subset such that
$\mathcal P(K,X)$
specifies X as an SFT, and let
$\varepsilon $
be any constant such that
$0 < \varepsilon < h(X)$
. Choose
$\delta> 0$
such that
$$ \begin{align*} 2\delta + \delta \log 2 + 2 \delta \log |\mathcal A| < \varepsilon. \end{align*} $$
By Theorem 3.3, there exists a finite collection
$\mathcal S$
of finite subsets of G with the following properties.
-
(i) Each shape
$S\in \mathcal S$
is
$(KK^{-1}, \eta )$
-invariant, where
$\eta> 0$
is a constant such that
$\eta |KK^{-1}| < \delta $
. By Lemma 2.1, this implies that
$|\partial _{KK^{-1}} S| < \delta |S|$
for each shape
$S \in \mathcal S$
. -
(ii)
$KK^{-1} \subset S$
and
$|S|> \delta ^{-1}$
for each
$S \in \mathcal S$
. -
(iii) There is a point
$t_0 \in \Sigma _E(\mathcal S)$
such that
$h(\overline {\mathcal {O}}(t_0)) = 0$
. Consequently,
$t_0$
encodes an exact tiling
$\mathcal T_0$
of G over
$\mathcal S$
with tiling entropy zero.
For the remainder of this proof, these are all fixed. We shall abbreviate
$\partial F = \partial _{KK^{-1}}F$
for any finite subset
$F \subset G$
. For a pattern p on F, we take
$\partial p$
to mean
$p(\partial F)$
and call this the border of p (with respect to
$KK^{-1}$
).
Let
$\Sigma _0 = \overline {\mathcal O}(t_0) \subset \Sigma _E(\mathcal S)$
be the dynamical tiling system generated by the tiling
$\mathcal T_0$
, which has entropy zero. Of central importance to this proof is the product system
$X \times \Sigma _0$
, which factors onto X via the projection map
$\pi : X \times \Sigma _0 \to X$
given by
$\pi (x,t) = x$
for each
$(x,t) \in X \times \Sigma _0$
. Let us establish some terminology for certain patterns of interest which occur in this system.
Given a shape
$S \in \mathcal S$
, we shall refer to a pattern
$b = (b^X, b^{\mathcal T}) \in \mathcal P(S, X \times \Sigma _0)$
as a block (to distinguish from patterns of any general shape). If a block
$b \in (\mathcal A \times \Sigma (\mathcal S))^S$
satisfies
$b^{\mathcal T}_s = (S,s)$
for every
$s \in S$
, then we shall say b is aligned. See Figure 2 for an illustration of the aligned property.
Figure 2 A hypothetical collection of shapes
$\mathcal S$
, the appropriate alphabet
$\Sigma (\mathcal S)$
, and (the
$\mathcal T$
-layer of) two aligned blocks are pictured. Each point of each block is labeled with the correct shape type and relative displacement within that shape.
For a subshift
$Z \subset X \times \Sigma _0$
, we denote the subcollection of aligned blocks of shape S that occur in Z by
$$ \begin{align*} \mathcal P^a(S,Z) \subset \mathcal P(S,Z) \subset (\mathcal A \times \Sigma(\mathcal S))^S, \end{align*} $$
where the superscript a identifies the subcollection. Given a shape
$S \in \mathcal S$
and an aligned block b of shape S, consider the border
$\partial b \in (\mathcal A \times \Sigma (\mathcal S))^{\partial S}$
. We are interested in the number of ways that the border
$\partial b$
may be extended to all of S—that is, the number of allowed (and in particular, aligned) interiors for S which agree with
$\partial b$
on the boundary
$\partial S$
. For a subshift
$Z \subset X \times \Sigma _0$
, we denote this collection by
$$ \begin{align*} \operatorname{\mathrm{ints}}^a(\partial b, Z) = \{b' \in \mathcal P^a(S, Z) : \partial b' = \partial b\}. \end{align*} $$
We shall extend all the same terminology described above (blocks, aligned blocks, borders, interiors) to tiles
$\tau = Sc \in \mathcal T_0$
, as there is a bijection between
$\mathcal P(S,Z)$
and
$\mathcal P(\tau , Z) = \mathcal P(Sc, Z)$
. For a given tile
$\tau \in \mathcal T_0$
, a block
$b \in (\mathcal A \times \Sigma (\mathcal S))^\tau $
is aligned if
$b^{\mathcal T}_{sc} = (S,s)$
for each
$sc \in Sc = \tau $
. The subcollection of aligned blocks of shape
$\tau $
occurring in a shift
$Z \subset X \times \Sigma _0$
is denoted
$\mathcal P^a(\tau , Z)$
. Given a border
$\partial b \in (\mathcal A \times \Sigma (\mathcal S))^{\partial \tau }$
, the collection of aligned blocks of shape
$\tau $
occurring in Z agreeing with
$\partial b$
on
$\partial \tau $
is also denoted
$\operatorname {\mathrm {ints}}^a(\partial b, Z) \subset \mathcal P^a(\tau , Z)$
.
For the theorem, we shall inductively construct a descending family of subshifts
$(Z_n)_{n}$
of
$X \times \Sigma _0$
as follows. Begin with
$Z_0 = X \times \Sigma _0$
, then assume
$Z_n$
has been constructed for
$n \geq 0$
. If there exists a shape
$S_n \in \mathcal S$
and an aligned block
$\beta _n \in \mathcal P^a(S_n, Z_n)$
such that
$$ \begin{align*} |{\kern-2pt}\operatorname{\mathrm{ints}}^a(\partial \beta_n, Z_n)|> 1, \end{align*} $$
then let
$Z_{n+1} = Z_n \setminus \beta _n$
. If no such block exists on any shape
$S\in \mathcal S$
, then
$Z_n$
is the final subshift in the chain and the chain is finite in length.
Let us first argue that in fact, the chain must be finite in length. For each
$n \geq 0$
, we have
$Z_{n+1} \subset Z_n$
, in which case
$\mathcal P^a(S,Z_{n+1}) \subset \mathcal P^a(S,Z_n)$
for every shape
$S \in \mathcal S$
. Moreover, for the distinguished shape
$S_n$
(the shape of the forbidden block
$\beta _n$
), it holds that
$\mathcal P^a(S_n, Z_{n+1}) \sqcup \{\beta _n\} \subset \mathcal P^a(S_n, Z_n)$
. This implies that
$$ \begin{align*} \sum_{S \in \mathcal S} |\mathcal P^a(S, Z_n)| \end{align*} $$
strictly decreases with n. There is no infinite strictly decreasing sequence of positive integers, and hence the descending chain must be finite in length. Let
$N \geq 0$
be the index of the terminal subshift, and note by construction that the shift
$Z_N$
satisfies
$$ \begin{align*} |{\kern-2pt}\operatorname{\mathrm{ints}}^a(\partial b, Z_N)| = 1 \end{align*} $$
for every aligned block
$b \in \mathcal P^a(S, Z_N)$
on any shape
$S \in \mathcal S$
.
Most of the rest of the proof aims to establish the following two statements:
$$ \begin{align} h(Z_{n+1}) \leq h(Z_n) < h(Z_{n+1}) + \varepsilon \quad \text{for each } n < N; \text{ and} \end{align} $$
$$ \begin{align} h(Z_N) < \varepsilon. \end{align} $$
To begin, let
$F \subset G$
be a finite subset satisfying the following two conditions:
-
(F1) F is
$(UU^{-1},\vartheta )$
-invariant, where
$U = \bigcup \mathcal S$
and
$\vartheta $
is a positive constant such that
$\vartheta |U||UU^{-1}| < \delta $
. Note this implies that F may be well approximated by tiles from any exact tiling of G over
$\mathcal S$
, in the sense of Lemma 3.4. -
(F2) F is large enough to
$\delta $
-approximate (Definition 2.15) the entropy of
$\Sigma _0$
and
$Z_n$
for every
$n\leq N$
. This implies in particular that
$h(F,\Sigma _0) < \delta $
.
Such a set exists by Proposition 2.10. We fix F for the remainder of this proof.
Now for each
$n \leq N$
, we claim that
$$ \begin{align} |\mathcal P(F,Z_n)| \geq \sum_t \sum_f \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)|, \quad \text{and} \end{align} $$
$$ \begin{align} |\mathcal P(F,Z_n)| \leq |\mathcal A|^{\delta|F|} \cdot \sum_t \sum_f \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)|, \end{align} $$
where the indices t, f, and
$\tau $
are as follows. The variable t ranges over
$\mathcal P(F,\Sigma _0)$
, and therefore t is the restriction to F of an encoding of an exact, zero entropy tiling
$\mathcal T_t$
of G over
$\mathcal S$
. The variable f ranges over all
$(\mathcal A\times \Sigma (\mathcal S))$
-labelings of the
$(\mathcal T_t,\, KK^{-1})$
-frame of F (Definition 3.5) that are allowed in
$Z_0$
and for which
$f^{\mathcal T}$
agrees with t. Lastly, the variable
$\tau $
ranges over the tiles in
$\mathcal T^\circ _t(F)$
.
To begin the argument toward the claims (E1) and (E2), let
$n \leq N$
be arbitrary. To count patterns
$p \in \mathcal P(F,Z_n)$
, write
$p = (p^X, p^{\mathcal T})$
and sum over all possible labelings in the tiling component. We have
$$ \begin{align} |\mathcal P(F, Z_n)| = \sum_t |\{p \in \mathcal P(F,Z_n) : p^{\mathcal T} = t\}|, \end{align} $$
where the sum ranges over all
$t \in \mathcal P(F,\Sigma _0)$
. This is valid because
$Z_n \subset Z_0 = X \times \Sigma _0$
, and hence any
$z = (z^X, z^{\mathcal T}) \in Z_n$
must have
$z^{\mathcal T} \in \Sigma _0$
.
Next, let
$t \in \mathcal P(F,\Sigma _0)$
be fixed. The pattern t extends to/encodes an exact, zero entropy tiling
$\mathcal T_t$
of G over
$\mathcal S$
(possibly distinct from the original selected tiling
$\mathcal T_0$
, but as
$\Sigma _0$
is generated by
$\mathcal T_0$
, one may take
$\mathcal T_t$
to be a translation of
$\mathcal T_0$
that agrees with t on F).
Recall that
$F^\circ (\mathcal T_t) = \bigcup \mathcal T_t^\circ (F) \subset F$
is the inner tile approximation of F by the tiling
$\mathcal T_t$
(Definition 3.4), which we shall abbreviate here as
$F_t^\circ $
. Recall also that the
$(\mathcal T_t,\, KK^{-1})$
-frame of F is the subset
$\bigcup _\tau \partial \tau $
, where the union is taken over all
$\tau \in \mathcal T_t^\circ (F)$
(Definition 3.5). Since K is fixed for this proof, we shall abbreviate the frame as
$\operatorname {fr}_t(F)$
. From equation (4.1), we now split over all allowed labelings of
$\operatorname {fr}_t(F)$
. We have
$$ \begin{align} |\mathcal P(F,Z_n)| = \sum_t \sum_f |\{ p \in \mathcal P(F,Z_n) : p^{\mathcal T} = t \text{ and } p(\operatorname{fr}_t(F)) = f\}|, \end{align} $$
where the first sum is taken over all
$t \in \mathcal P(F, \Sigma _0)$
and the second sum is taken over all
$f \in \mathcal P(\operatorname {fr}_t(F), Z_0)$
for which
$f^{\mathcal T}$
agrees with t.
We have the pattern
$t \in \mathcal P(F,\Sigma _0)$
fixed from before; next we fix a frame pattern
$f \in \mathcal P (\operatorname {fr}_t(F), Z_0)$
such that
$f^{\mathcal T}$
agrees with t. We wish to count the number of patterns
$p \in \mathcal P (F,Z_n)$
such that
$p^{\mathcal T} = t$
and
$p(\operatorname {fr}_t(F)) = f$
. Let this collection be denoted by
$D_n = D (t,f;\, Z_n) \subset \mathcal P(F,Z_n)$
. Observe that each
$D_n$
is finite and
$D_{n+1} \subset D_n$
for each
${n < N}$
. Consider the map
$\gamma : D_0 \to \prod _\tau \mathcal P(\tau , Z_0)$
given by
$\gamma (p) = (p(\tau ))_{\tau }$
, which sends a pattern
$p \in D_0$
to a vector of blocks indexed by
$\mathcal T_t^\circ (F)$
. We claim the map
$\gamma $
is at most
$|\mathcal A|^{\delta |F|}$
-to-1 and for each
$n \leq N$
, we have
$$ \begin{align} \gamma(D_n) = \prod_\tau \operatorname{\mathrm{ints}}^a(f(\partial\tau), Z_n). \end{align} $$
Together, these claims will provide a bound for
$|D_n|$
from above and below, which combine with equation (4.2) to yield the claims (E1) and (E2).
First we argue that
$\gamma $
is at most
$|\mathcal A|^{\delta |F|}$
-to-1. This is where we first invoke the invariance of F. Suppose
$(b_\tau )_\tau \in \prod _\tau \mathcal P(\tau , Z_0)$
is a fixed vector of blocks. If
$p \in D_0$
is a pattern such that
$\gamma (p) = (b_\tau )_\tau $
, then
$p^{\mathcal T}$
is determined by t and
$p(\tau ) = b_\tau $
for each tile
$\tau \in \mathcal T_t^\circ (F)$
. Therefore, p is uniquely determined by
$p^X(F\setminus F_t^\circ )$
, and hence
$|\gamma ^{-1}(b_\tau )_\tau | \leq |\mathcal A|^{|F\setminus F_t^\circ |}$
. By property (F1) of the set F and by Lemma 3.4, we have
$|F\setminus F_t^\circ | < \delta |F|$
and thus the map
$\gamma $
is at most
$|\mathcal A|^{\delta |F|}$
-to-1.
Next, we shall prove the set equality in claim (4.3). Let
$n \leq N$
and let
$p \in D_n$
. For each tile
$\tau \in \mathcal T_t^\circ (F)$
, the block
$p(\tau ) \in \mathcal P(\tau , Z_n) \subset (\mathcal A \times \Sigma (\mathcal S))^\tau $
is aligned; this is because
$p^{\mathcal T} = t$
and t encodes the tiling
$\mathcal T_t$
itself. Moreover, p agrees with f on
$\operatorname {fr}_t(F)$
by assumption that
$p \in D_n = D(t,f;Z_n)$
, in which case
$p(\partial \tau ) = f(\partial \tau )$
for each tile
$\tau \in \mathcal T_t^\circ (F)$
. This demonstrates that
$$ \begin{align*} \gamma(D_n) \subset \prod_\tau \operatorname{\mathrm{ints}}^a(f(\partial\tau), Z_n). \end{align*} $$
We shall prove the reverse inclusion by induction on n. For the
$n = 0$
case, let
$(b_\tau )_{\tau }$
be a vector of blocks such that
$b_\tau \in \mathcal P^a(\tau , Z_0)$
and
$\partial b_\tau = f(\partial \tau )$
for each
$\tau \in \mathcal T_t^\circ (F)$
. To construct a
$\gamma $
-preimage of
$(b_\tau )_\tau $
in
$D_0$
, begin with a point
$x \in X$
such that
$x(\operatorname {fr}_t(F)) = f^X$
. Such a point exists because f occurs in some point of
$Z_0 = X \times \Sigma _0$
. Note that
$$ \begin{align*} x(\partial\tau) = f^X(\partial\tau) = \partial b_\tau^X \end{align*} $$
for each
$\tau \in \mathcal T_t^\circ (F)$
, because
$\partial \tau \subset \operatorname {fr}_t(F)$
for each
$\tau $
. Moreover, for each
$\tau $
, it holds that the block
$b_\tau ^X$
occurs in a point of X, as each block
$b_\tau = (b_\tau ^X, b_\tau ^{\mathcal T})$
occurs in a point of
$Z_0 = X \times \Sigma _0$
. Because X is an SFT specified by patterns of shape K, we may repeatedly apply Lemma 2.8 to excise the block
$x(\tau )$
and replace it with
$b_\tau ^X$
for every
$\tau \in \mathcal T_t^\circ (F)$
. Every tile is disjoint, so the order in which the blocks are replaced does not matter. After at most finitely many steps, we obtain a new point
$x' \in X$
such that
$x'(\operatorname {fr}_t(F)) = f^X$
and
$x'(\tau ) = b_\tau ^X$
for each
$\tau \in \mathcal T_t^\circ (F)$
.
Recall that the point
$t \in \Sigma _0$
is fixed from before. The point
$(x', t) \in X \times \Sigma _0$
is therefore allowed in
$Z_0 = X \times \Sigma _0$
. Let
$p = (x',t)(F) \in \mathcal P(F,Z_0)$
. We have that
$p^{\mathcal T} = t$
and
$p(\operatorname {fr}_t(F)) = f$
by the selection of
$x'$
. This implies that
$p \in D_0$
. It also holds that
$p(\tau ) = b_\tau $
for each
$\tau \in \mathcal T_t^\circ (F)$
, as t itself encodes the tiling
$\mathcal T_t$
from which the tiles
$\tau \in \mathcal T_t^\circ (F)$
are drawn (and each block
$b_\tau $
is aligned, by assumption). We then finally have
$\gamma (p) = (b_\tau )_\tau $
, which settles the case
$n = 0$
.
Now suppose the set equality in claim (4.3) holds for some fixed
$n < N$
, and let
$(b_\tau )_\tau \in \prod _\tau \operatorname {\mathrm {ints}}^a(f(\partial \tau ), Z_{n+1})$
. From the inclusion
$Z_{n+1} \subset Z_n$
and the inductive hypothesis, it follows there is a pattern
$p \in D_n$
such that
$\gamma (p) = (b_\tau )_\tau $
. Suppose
$p = (x,t)(F)$
for some
$(x,t) \in Z_n$
(by induction, t is the point fixed from before). We need to modify p only slightly to find a
$\gamma $
-preimage of
$(b_\tau )_\tau $
which occurs in
$Z_{n+1}$
(and hence belongs to
$D_{n+1}$
).
Consider the block
$\beta _n$
determined at the beginning of this proof, which is forbidden in the subshift
$Z_{n+1}$
. If
$\beta _n$
occurs anywhere in the point
$(x, t)$
, then (by the assumption that
$\beta _n$
is aligned) it must occur on a tile
$\tau \in \mathcal T_t$
. It does not occur on any of the tiles from
$\mathcal T_t^\circ (F)$
, because for each tile
$\tau \in \mathcal T_t^\circ (F)$
, we have
$(x,t)(\tau ) = b_\tau $
which is allowed in
$Z_{n+1}$
by assumption.
Yet,
$\beta _n$
may occur in
$(x, t)$
outside of
$F_t^\circ $
. By the construction of
$Z_{n+1}$
, we have
$$ \begin{align*} |{\kern-2pt}\operatorname{\mathrm{ints}}^a(\partial\beta_n, Z_n)|> 1, \end{align*} $$
and therefore there is an aligned block
$\tilde b$
which occurs in
$Z_n$
such that
$\tilde b \neq \beta _n$
and
$\partial \tilde b = \partial \beta _n$
. Apply Lemma 2.8 at most countably many times to excise
$\beta _n^X$
wherever it may occur in x, replacing it with
$\tilde b^X$
. This yields a new point
$x' \in X$
.
Then
$(x', t)\in Z_0$
also belongs to
$Z_{n+1}$
. It was already the case that none of the blocks
$\beta _0, \ldots , \beta _{n-1}$
could occur anywhere in
$(x,t)$
by the assumption
$(x,t) \in Z_n$
, and now neither does
$\beta _n$
occur anywhere in
$(x',t)$
. The pattern
$p' = (x', t)(F)$
may be distinct from
$p = (x, t)(F)$
(the labeling may change on
$F \setminus F_t^\circ $
), but we did not replace any of the blocks within
$F_t^\circ $
. We still have
$p'(\tau ) = b_\tau $
for each tile
$\tau \in \mathcal T_t^\circ (F)$
, and hence
$p' \in D_{n+1}$
and
$\gamma (p') = (b_\tau )_\tau $
.
This completes the induction, and we conclude that the set equality in claim (4.3) holds for each
$n \leq N$
. From this equality and the fact that
$\gamma $
is at most
$|\mathcal A|^{\delta |F}$
-to-1, we obtain
$$ \begin{align*} \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)| \leq |D(t,f\, ;Z_n)| \leq |\mathcal A|^{\delta|F|} \cdot \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)|. \end{align*} $$
Notice that the above inequalities hold for each fixed
$t \in \mathcal P(F,\Sigma _0)$
, each fixed
$f \in \mathcal P(\operatorname {fr}_t(F), X \times \Sigma _0)$
such that
$f^{\mathcal T} = t(\operatorname {fr}_t(F))$
, and each
$n \leq N$
. From these inequalities and equation (4.2), we conclude that claims (E1) and (E2) hold, that is,
$$ \begin{align} |\mathcal P(F,Z_n)| \geq \sum_t \sum_f \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)|, \quad \text{and} \end{align} $$
$$ \begin{align} |\mathcal P(F,Z_n)| \leq |\mathcal A|^{\delta|F|} \cdot \sum_t \sum_f \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau),Z_n)|, \end{align} $$
where the first sum is taken over all
$t \in \mathcal P(F,\Sigma _0)$
, the second sum over all
$f \in \mathcal P(\operatorname {fr}_t(F), Z_0)$
for which
$f^{\mathcal T}$
agrees with t, and the product over all
$\tau \in \mathcal T_t^\circ (F)$
.
Property (F2) of the set F implies that
$h(F,\Sigma _0) < \delta $
, in which case
$|\mathcal P(F,Z_0)| < e^{\delta |F|}$
. Consequently, the variable t in claims (E1) and (E2) ranges over fewer than
$e^{\delta |F|}$
terms. Moreover, by the selection of
$\mathcal S$
, we have
$|\partial \tau | < \delta |\tau |$
for each
$\tau \in \mathcal T_t^\circ (F)$
, in which case it follows that
$$ \begin{align*} |{\kern-2pt}\operatorname{fr}_t(F)| = \bigg|\bigcup_\tau \partial\tau \bigg| = \sum_\tau |\partial\tau| < \sum_\tau \delta|\tau| = \delta \bigg|\bigcup_\tau \tau \bigg| = \delta |F^\circ_t| \leq \delta|F|. \end{align*} $$
Here we have used that distinct tiles from
$\mathcal T_t$
are disjoint. From this estimate, we deduce that there are fewer than
$|\mathcal A|^{\delta |F|}$
labelings of the frame of F that agree with a fixed t on the
$\mathcal T$
-layer. Consequently, the variable f in claims (E1) and (E2) ranges over fewer than
$|\mathcal A|^{\delta |F|}$
terms. Observe also that the size of
$\mathcal T_t^\circ (F)$
as a collection is small compared to F. Indeed,
$|S|> \delta ^{-1}$
for each shape
$S \in \mathcal S$
, in which case
$$ \begin{align*} |F| \geq |F^\circ_t| = \sum_\tau |\tau| \geq |\mathcal T_t^\circ(F)| \cdot ( \min_{S\in \mathcal S} |S| )> |\mathcal T_t^\circ(F)| \delta^{-1}, \end{align*} $$
and therefore
$|\mathcal T_t^\circ (F)| < \delta |F|$
. Consequently, the variable
$\tau $
in claims (E1) and (E2) ranges over fewer than
$\delta |F|$
terms.
Before returning to claims (U1) and (U2), one more estimate is necessary. For each
$n < N$
, each shape
$S\in \mathcal S$
, and each aligned block
$b \in \mathcal P^a(S, Z_n)$
, we claim that
$$ \begin{align} |{\kern-2pt}\operatorname{\mathrm{ints}}^a(\partial b, Z_n)| \leq 2\, |{\kern-2pt}\operatorname{\mathrm{ints}}^a(\partial b, Z_{n+1})|. \end{align} $$
Let
$S \in \mathcal S$
and let
$b \in \mathcal P^a(S, Z_n)$
be an aligned block occurring in
$Z_n$
, distinct from the forbidden block
$\beta _n$
. Say
$b = (x,t)(S)$
for some
$(x,t) \in Z_n$
. We claim that b occurs in a point of
$Z_{n+1}$
. Note that t extends to/encodes an exact, zero entropy tiling
$\mathcal T_t$
of G over
$\mathcal S$
, and note that S is a tile of
$\mathcal T_t$
. This is because b is aligned by assumption, in which case
$t_e = b^{\mathcal T}_e = (S,e)$
, and therefore
$e \in C_t(S)$
.
Suppose the forbidden block
$\beta _n$
occurs anywhere in
$(x,t)$
. Because
$\beta _n$
is aligned, it must occur on a tile
$\tau \in \mathcal T_t$
. It does not occur on S, because
$b \neq \beta _n$
. By the assumption that
$|{\kern-2pt}\operatorname {\mathrm {ints}}^a(\partial \beta _n, Z_n)|> 1$
, we know there is an aligned block
$\tilde b_n \neq \beta _n$
that occurs in
$Z_n$
such that
$\partial \tilde b_n = \partial \beta _n$
.
Recall X is an SFT specified by patterns of shape K, and
$\tilde b_n^X$
is allowed in X. Again we may apply Lemma 2.8 at most countably many times, excising
$\beta _n^X$
wherever it may occur in x and replacing it with
$\tilde b_n^X$
. At the end, we receive a new point
$x' \in X$
, within which
$\beta _n^X$
does not occur. Then
$(x',t)$
is allowed in
$Z_{n+1}$
and
$(x',t)(S) = b$
, and hence
$b \in \mathcal P^a(S,Z_{n+1})$
.
The conclusion is that
$\beta _n$
is the only aligned block lost from
$Z_n$
to
$Z_{n+1}$
. For each
$b \in \mathcal P^a(S,Z_n)$
, we have either
$\operatorname {\mathrm {ints}}^a(\partial b, Z_n) = \operatorname {\mathrm {ints}}^a(\partial b, Z_{n+1})$
or
$\operatorname {\mathrm {ints}}^a(\partial b, Z_n) = \operatorname {\mathrm {ints}}^a(\partial b, Z_{n+1})\sqcup \{\beta _n\}$
. If two positive integers differ by at most 1, then their ratio is at most 2, and hence the inequality in claim (4.4) follows.
Finally, we shall use the estimates in claims (E1) and (E2) to argue for the ultimate claims (U1) and (U2) made before. For the first, consider a fixed
$n < N$
. It is clear that
$h(Z_{n+1}) \leq h(Z_n)$
by inclusion. For the second inequality in claim (U1), we have
$$ \begin{align*} |\mathcal P(F, Z_n)| &\leq |\mathcal A|^{\delta|F|} \cdot \sum_t\sum_f \prod_\tau |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau), Z_n)| \\ &\leq |\mathcal A|^{\delta|F|} \cdot \sum_t\sum_f \prod_\tau 2\, |{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau), Z_{n+1})|\\ &< |\mathcal A|^{\delta|F|} \cdot 2^{\delta|F|}\cdot\sum_t\sum_f \prod_\tau|{\kern-2pt}\operatorname{\mathrm{ints}}^a(f(\partial\tau), Z_{n+1})|\\ &\leq |\mathcal A|^{\delta|F|} \cdot 2^{\delta|F|}\cdot |\mathcal P(F, Z_{n+1})|, \end{align*} $$
where the inequalities are justified by claim (E2), claim (4.4), the fact that
$|\mathcal T_t^\circ (F)| < \delta |F|$
, and claim (E1), respectively. Taking logs and dividing through by
$|F|$
, we obtain
$$ \begin{align*} h(Z_n) &< h(F,Z_n) + \delta\\ &< ( \delta \log |\mathcal A| + \delta \log 2 + h(F,Z_{n+1})) + \delta\\ &< \delta \log |\mathcal A| + \delta \log 2 + (h(Z_{n+1})+\delta) +\delta \\ &= h(Z_{n+1}) + 2\delta + \delta \log 2 + \delta \log |\mathcal A| \\ &< h(Z_{n+1}) + \varepsilon, \end{align*} $$
where we have used the property (F2) of F, the previous display, the property (F2) again, and our choice of
$\delta $
. This inequality establishes claim (U1). For claim (U2), recall that the terminal shift
$Z_N$
has the property that any aligned border
$\partial b \in \mathcal P^a(\partial S,Z_N)$
on any shape
$S \in \mathcal S$
has exactly
$1$
allowed aligned interior. Hence, we see that
$$ \begin{align*} |\mathcal P(F, Z_N)| &\leq |\mathcal A|^{\delta|F|} \cdot \sum_t\sum_{f} \prod_\tau |{\kern-2pt}\operatorname{ints}^a(f(\partial\tau), Z_N)|\\ &= |\mathcal A|^{\delta|F|} \cdot\sum_t\sum_{f} \prod_\tau 1\\ &< |\mathcal A|^{\delta|F|} \cdot e^{\delta|F|} \cdot |\mathcal A|^{\delta|F|} \cdot 1, \end{align*} $$
where the first inequality is justified by claim (E2) and the last inequality is justified by our bounds on the number of terms in the sums (established previously). Taking logs and dividing through by
$|F|$
, we finally have
$$ \begin{align*} h(Z_N) &< h(F,Z_N) + \delta\\ &< (\delta + 2\delta \log |\mathcal A|) + \delta\\ &= 2\delta + 2 \delta \log |\mathcal A|\\ &< \varepsilon, \end{align*} $$
where we have used the property (F2) of the set F, the previous display, and our choice of
$\delta $
. We have now established claim (U2).
With claims (U1) and (U2) in hand, the rest of the proof is easy. By claims (U1) and (U2), we have that
$(Z_n)_{n\leq N}$
is a family of subshifts of
$X \times \Sigma _0$
such that
$(h(Z_n))_{n\leq N}$
is
$\varepsilon $
-dense in
$[0, h(X\times \Sigma _0)]$
.
For each
$n \leq N$
, let
$X_n = \pi (Z_n) \subset X$
, where
$\pi $
is the projection map
$\pi (x,t) = x$
. From Proposition 2.13,
$\mathcal H(\pi ) = h(\Sigma _0) = 0$
, and hence
$h(X_n) = h(Z_n)$
for every
$n \leq N$
.
Then
$(X_n)_{n\leq N}$
is a descending family of subshifts of X such that
$(h(X_n))_{n\leq N}$
is
$\varepsilon $
-dense in
$[0, h(X)]$
. Though each
$X_n$
may not be an SFT, we do know that X is an SFT. One may therefore apply Theorem 2.12 to construct a family of SFTs
$(Y_n)_{n\leq N}$
such that for each
$n \leq N$
, we have
$X_n \subset Y_n \subset X$
and
$h(X_n) \leq h(Y_n) < h(X_n) + \varepsilon $
. Hence,
$(h(Y_n))_{n\leq N}$
is
$2\varepsilon $
-dense in
$[0, h(X)]$
. As
$\varepsilon $
was arbitrary, we conclude that the entropies of the SFT subsystems of X are dense in
$[0,h(X)]$
.
The following ‘relative’ version of Theorem 4.1 is stronger and easily obtained as a consequence of Theorem 4.1.
Theorem 4.2. Let G be a countable amenable group, let X be a G-SFT, and let
$Y \subset X$
be any subsystem such that
$h(Y) < h(X)$
. Then
$$ \begin{align*} \{h(Z) : Y \subset Z \subset X \text{ and}\ Z\ \text{is an SFT}\kern1pt\} \end{align*} $$
is dense in
$[h(Y), h(X)]$
.
Proof. We prove the density directly. Suppose
$(a,b) \subset [h(Y), h(X)]$
for positive reals
$a < b$
, and let
$\varepsilon < (b - a)/2$
. By Theorem 4.1, there exists an SFT
$Z_0 \subset X$
such that
$a < h(Z_0) < a + \varepsilon $
. Note that these inequalities give
$h(Y) < h(Z_0)$
. Consider the subshift
$Y\cup Z_0 \subset X$
, which has entropy
$$ \begin{align*} h(Y \cup Z_0) = \max(h(Y), h(Z_0)) = h(Z_0) \in (a,a+\varepsilon). \end{align*} $$
Because X is an SFT and
$Y \cup Z_0 \subset X$
, by Theorem 2.12, there is an SFT Z such that
$Y \cup Z_0 \subset Z \subset X$
and
$h(Y \cup Z_0) \leq h(Z) < h(Y\cup Z_0) + \varepsilon $
. Thus we have
$$ \begin{align*} a < h(Y\cup Z_0) \leq h(Z) < h(Y\cup Z_0) + \varepsilon < a + 2\varepsilon < b. \end{align*} $$
Since
$(a,b)$
was arbitrary, the proof is complete.
5 Sofic shifts
5.1 An extension result for sofic shifts
To address the case of sofic shifts, we seek to leverage our results on SFTs. In particular, given a sofic shift W, we would like an SFT X such that W is a factor of X and such that the maximal entropy drop across the factor map is very small. The following theorem guarantees the existence of such SFTs.
Theorem 5.1. Let
$W \subset \mathcal A_W^G$
be a sofic shift. For every
$\varepsilon> 0$
, there exists an SFT
$\tilde X$
and a one-block code
$\tilde \phi : \tilde X \to W$
such that the maximal entropy gap of
$\tilde \phi $
satisfies
$\mathcal H(\tilde \phi ) < \varepsilon $
.
Proof. Since W is sofic, there exists an SFT
$X\subset \mathcal A_X^G$
and a factor map
$\phi : X \to W$
. Without loss of generality, we assume that:
-
(i)
$\phi $
is a one-block code, witnessed by the function
$\Phi : \mathcal A_X \to \mathcal A_W$
; and -
(ii)
$\mathcal A_X$
and
$\mathcal A_W$
are disjoint.
We abbreviate
$\mathcal A_{XW} = \mathcal A_X \sqcup \mathcal A_W$
. Let
$\varepsilon> 0$
and select
$\delta> 0$
such that
$$ \begin{align*} 4\delta + \delta(1+\delta) \log |\mathcal A_X| < \varepsilon/2. \end{align*} $$
Let
$K \subset G$
be a large finite subset that specifies X as an SFT. The set K is fixed for the remainder of this proof, and thus we shall denote
$\partial _{KK^{-1}}F$
by
$ \partial F$
and
$\operatorname {\mathrm {int}}_{KK^{-1}} F$
by
$\operatorname {\mathrm {int}} F$
for any finite set
$F \subset G$
. By Theorem 3.3, there exists a finite set of finite shapes
$\mathcal S$
such that the following conditions are met.
-
(i) Each shape
$S \in \mathcal S$
is
$(KK^{-1},\eta )$
-invariant, where
$\eta> 0$
is a constant such that
$\eta |KK^{-1}| < \delta $
. By Lemma 2.1, this implies
$|\partial S| < \delta |S|$
for each
$S \in \mathcal S$
. -
(ii)
$KK^{-1} \subset S$
and
$|S|> \delta ^{-1}$
for each
$S \in \mathcal S$
. -
(iii) There is a point
$t_0 \in \Sigma _E(\mathcal S)$
such that
$h(\overline {\mathcal O}(t_0)) = 0$
.
Recall by Proposition 3.1 that
$\Sigma _E(\mathcal S)$
is an SFT. By Theorem 2.12, there is an SFT T such that
$\overline {\mathcal O}(t_0) \subset T \subset \Sigma _E(\mathcal S)$
and
$h(T) < h(\overline {\mathcal O}(t_0)) + \delta $
. Consequently, each point
$t\in T$
is an encoding of an exact tiling
$\mathcal T_t$
of G over
$\mathcal S$
(possibly distinct from the original tiling
$\mathcal T_0$
), with tiling system entropy
$$ \begin{align*} h(\mathcal T_t) = h(\overline{\mathcal O}(t)) \leq h(T) < h(\overline{\mathcal O}(t_0)) + \delta = 0 + \delta. \end{align*} $$
Because X and T are SFTs, we have that
$X \times T \subset (\mathcal A_X \times \Sigma (\mathcal S))^G$
is also an SFT.
Let
$t \in T$
be arbitrary and recall that
$\mathcal T_t$
is a partition of G. Thus, for each
$g\in G$
, there is a unique tile
$\tau \in \mathcal T_t$
such that
$g \in \tau $
. We define the notation
$\mathcal T_t(g)$
by setting
$\mathcal T_t(g) = \tau $
. Next we define a map
$\phi _t : X \to \mathcal A_{XW}^G$
by the following rule: for each
$g\in G$
and
$x \in X$
,
$$ \begin{align*} \phi_t(x)_g = \begin{cases} x_g & \text{if } g \in \partial \mathcal T_t(g),\\ \Phi(x_g) & \text{if } g \in \operatorname{\mathrm{int}}\mathcal T_t(g). \end{cases} \end{align*} $$
This map is well defined, as
$\tau = \partial \tau \sqcup \operatorname {\mathrm {int}} \tau $
. The map
$\phi _t$
applies the one-block code
$\phi $
to ‘most’ of a point x, by relabeling the interiors of each tile
$\tau \in \mathcal T_t$
.
We now define a sliding block code
$\varphi : X \times T \to (\mathcal A_{XW} \times \Sigma (\mathcal S))^G$
by applying the map(s)
$\phi _t$
fiber-wise: for each point
$(x,t) \in X \times T$
, let
$$ \begin{align*} \varphi(x,t) = (\phi_t(x),t). \end{align*} $$
It is straightforward to check that
$\varphi $
is indeed a sliding block code (Definition 2.6). For the theorem, the desired shift
$\tilde X$
is identified with the range of this map. Let
$$ \begin{align*} \tilde X = \varphi(X\times T) \subset (\mathcal A_{XW}\times \Sigma(\mathcal S))^G. \end{align*} $$
See Figure 3 for an illustration of the construction. It remains to show that there is a one-block code
$\tilde \phi : \tilde X \to W$
, that the shift
$\tilde X$
is an SFT, and that
$\mathcal H(\tilde \phi ) < \varepsilon $
.
Figure 3 A hypothetical point
$x \in X$
with a tiling
$t \in T$
overlayed; the partially transformed point
$\phi _t(x)$
is pictured, which is labeled with symbols from both X and W; finally, the wholly transformed image point
${\phi (x) \in W}$
is reached.
First, let us show that
$\tilde X$
factors onto W. The factor map is induced by the function
$\tilde \Phi : \mathcal A_{XW} \to \mathcal A_W$
, which is an extension of
$\Phi $
, defined by the following rule:
$\tilde \Phi (\alpha ) = \alpha $
if
$\alpha \in \mathcal A_W$
and
$\tilde \Phi (\alpha ) = \Phi (\alpha )$
if
$\alpha \in \mathcal A_X$
. Let
$\tilde \phi : \tilde X \to \mathcal A_W^G$
be given by
$$ \begin{align*} \tilde\phi(\tilde x, t)_g = \tilde\Phi(\tilde x_g) \quad\text{for all } g\in G \text{ and } \text{for all } (\tilde x, t) \in \tilde X. \end{align*} $$
It is clear that
$\tilde \phi $
is a one-block code. Let us now show that
$\tilde \phi ( \tilde X) = W$
. Let
$x \in X$
and
$t \in T$
, in which case
$(\phi _t(x),t) \in \tilde X$
is an arbitrary point. The effect of applying the map
$\phi _t$
to x is to apply the one-block code
$\phi $
to ‘most’ of x. The map
$\tilde \phi $
then ‘completes’ the relabeling, via the extended function
$\tilde \Phi $
. In fact, we have that
$\tilde \phi (\phi _t(x),t) = \phi (x) \in W$
, and hence
$\tilde \phi (\tilde X) \subset W$
. For the reverse inclusion, let
$w \in W$
. Since
$\phi : X \to W$
is onto, there exists a point
$x \in X$
such that
$\phi (x) = w$
. Choose
$t \in T$
arbitrarily; then
$(\phi _t(x),t) \in \tilde X$
and
$\tilde \phi ( \phi _t(x), t) = \phi (x) = w$
. We conclude that
$\tilde \phi : \tilde X \to W$
is a genuine factor map (and a one-block code).
Let us now show that
$\tilde X$
is an SFT. We repeat that the shift
$\tilde X$
can be written in the following instructive form:
$$ \begin{align*} \tilde X = \{ (\phi_t(x), t) : x \in X \text{ and } t \in T \} \subset (\mathcal A_{XW} \times \Sigma(\mathcal S))^G. \end{align*} $$
To show that
$\tilde X$
is an SFT, we will construct an SFT
$\tilde X_1 \subset (\mathcal A_{XW} \times \Sigma (\mathcal S))^G$
and then prove that
$\tilde X = \tilde X_1$
. Recall that
$K \subset G$
specifies X as an SFT. Let
$K_T \subset G$
be a finite subset such that
$\mathcal P(K_T, T)$
specifies T. We define
$\tilde X_1$
to be the set of points
$(\tilde x,t) \in (\mathcal A_{XW}\times \Sigma (\mathcal S))^G$
that satisfy the following local rules.
-
(R1) Any pattern of shape
$K_T$
that occurs in t must belong to
$\mathcal P(K_T,T)$
, and any pattern of shape K that occurs in
$\tilde x$
and belongs to
$\mathcal A_X^K$
must also belong to
$\mathcal P(K,X)$
(recall
$\mathcal P(K,\tilde X) \subset \mathcal A_{XW}^K = (\mathcal A_X \sqcup \mathcal A_W)^K$
in general). Note by Definition 2.10 that this condition is shift-invariant. -
(R1) For any shape
$S \in \mathcal {S}$
and any
$c \in G$
, if t satisfies
$(\sigma ^c t)_s = (S,s)$
for each
$s \in S$
, then
$\text { there exists } b \in \mathcal P(S,X)$
such that
$(\sigma ^c \tilde x)_s = b_s \in \mathcal A_X$
for all
$s \in \partial S$
and
$(\sigma ^c \tilde x)_s = \Phi (b_s) \in \mathcal A_W$
for all
$s \in \operatorname {\mathrm {int}} S$
.
As these are local rules, they define an SFT; call it
$\tilde X_1 \subset (\mathcal A_{XW} \times \Sigma (\mathcal S))^G$
. Moreover, it is easily checked that any point
$(\phi _t(x),t) \in \tilde X$
satisfies these rules everywhere (by construction of
$\tilde X$
), and so we have
$\tilde X \subset \tilde X_1$
.
For the reverse inclusion, consider a point
$(\tilde x,t) \in \tilde X_1$
. From (R1), it follows that
$t \in T$
, as T is an SFT specified by
$K_T$
. Therefore, t encodes an exact tiling
$\mathcal T_t$
of G over
$\mathcal S$
with
$h(\mathcal T_t) < \delta $
. Let
$(\tau _n)_n$
enumerate the tiles of
$\mathcal T_t$
, and for each n let
$\tau _n = S_nc_n$
for some
$S_n \in \mathcal S$
and
$c_n \in G$
. Recall
$\{\tau _n : n\in \mathbb N\}$
is a partition of G.
Let
$n \in \mathbb N$
, and consider
$c = c_n$
and
$S = S_n$
. Observe that because t encodes the tiling
$\mathcal T_t$
, we have
$(\sigma ^c t)_s = (S,s)$
for each
$s \in S$
. Then by (R2), there exists a block
$b = b_n \in \mathcal P(S,X)$
such that
$(\sigma ^c \tilde x)_s = b_s$
for all
$s \in \partial S$
and
$(\sigma ^c \tilde x)_s =\Phi (b_s)$
for all
$s \in \operatorname {\mathrm {int}} S$
.
Define a point
$x\in \mathcal A_X^G$
by setting
$x(\tau _n) = b_n$
for each
$n \in \mathbb N$
. We claim that x is an allowed point of X and that
$\phi _t(x) = \tilde x$
. Toward this, let
$g \in G$
be arbitrary and consider the translate
$Kg$
(recall that K specifies X as an SFT).
If
$Kg$
intersects the interior of any tile
$\tau _n = S_n c_n$
, then
$Kg \subset \tau _n$
by Lemma 2.2. In this case, the pattern
$(\sigma ^g x)(K)$
is a subpattern of
$b_n$
and must therefore be allowed in X as
$b_n \in \mathcal P(S_n,X)$
. The alternative is that
$Kg$
is disjoint from the interior of every tile, in which case
$Kg \subset \bigcup _n \partial \tau _n$
. By (R2), we also have
$\tilde x_g \in \mathcal A_X$
for every
$g \in \bigcup _n\operatorname {\mathrm {int}}\tau _n$
. In this case, we have
$(\sigma ^g x)(K) = (\sigma ^g \tilde x)(K)$
, which is again allowed in X by (R1).
In either case, we have that
$(\sigma ^g x)(K)$
is allowed in X for any
$g \in G$
and hence
$x \in X$
. Then by the definition of
$\phi _t$
, we see that
$\phi _t(x) = \tilde x$
. Thus, we have found a point
$(x, t) \in X\times T$
such that
$\varphi (x, t) = (\phi _t(x), t) = (\tilde x, t)$
and hence
$(\tilde x,t) \in \tilde X$
. We conclude that
$\tilde X = \tilde X_1$
and therefore
$\tilde X$
is an SFT.
Finally, let us show that
$\mathcal H(\tilde \phi ) < \varepsilon $
. Toward this end, let
$\tilde X' \subset \tilde X$
be any subsystem of
$\tilde X$
and let
$W' = \tilde \phi (\tilde X') \subset W$
. We will show that
$h(\tilde X') - h(W') < \varepsilon /2$
.
Let
$F \subset G$
be a finite subset such that the following conditions are met.
-
(F1) F is
$(UU^{-1},\vartheta )$
-invariant, where
$U = \bigcup \mathcal S$
and
$\vartheta>0$
is a constant such that
$\vartheta |U||UU^{-1}| < \delta $
(recall
$\delta $
was selected at the beginning of this proof). Note this implies that F may be well approximated by tiles from any exact tiling of G over
$\mathcal S$
, in the sense of Lemma 3.4. -
(F2) F is large enough to
$\delta $
-approximate (Definition 2.15) the entropy of the shifts
$X'$
,
$W'$
, and T (recall that
$h(T) < \delta $
, in which case
$h(F,T) < 2\delta $
).
Such a set exists by Proposition 2.10. This set is fixed for the remainder of this proof. Recall that
$\tilde \phi $
is a one-block code, and therefore there is a well-defined map
$\tilde \Phi _F : \mathcal P(F,\tilde X') \to \mathcal P(F,W')$
which takes a pattern
$p \in \mathcal P(F,\tilde X')$
and applies the one-block code to p (at each element of F).
Recall also that a pattern
$p \in \mathcal P(F,\tilde X')$
is of the form
$p = (\phi _t(x),t)(F)$
for some points
$x\in X$
and
$t \in T$
. The point t encodes an exact tiling
$\mathcal T_t$
of G over
$\mathcal S$
. For each tile
$\tau \in \mathcal T_t$
, the definition of
$\phi _t$
implies that
$$ \begin{align} \phi_t(x)(\operatorname{\mathrm{int}} \tau) \in \mathcal A_W^* \quad\text{and}\quad \phi_t(x)(\partial\tau) \in \mathcal A_X^*. \end{align} $$
Let
$q = \tilde \Phi _F(p) \in \mathcal P(F,W')$
. Recall that every element
$g \in F$
belongs to a unique tile
$\tau = \mathcal T_t(g) \in \mathcal T_t^\times (F)$
, where
$\mathcal T_t^\times (F) \subset \mathcal T_t$
is the outer approximation of F by the tiling
$\mathcal T_t$
(Definition 3.4). By equation (5.1), we have that
$$ \begin{align*} q_g = \tilde\Phi_F(p)_g = \tilde\Phi(p^{\tilde X}_g) = \bigg\{\!\! \begin{array}{ll} \Phi(p^{\tilde X}_g) & \text{if } g\in\partial\mathcal T_t(g), \\ p^{\tilde X}_g & \text{if } g \in \operatorname{\mathrm{int}} \mathcal T_t(g). \end{array} \end{align*} $$
In particular, we have
$q_g = p^{\tilde X}_g$
whenever g belongs to the set
$$ \begin{align*} F \cap \bigg( \bigcup_\tau \operatorname{\mathrm{int}} \tau \bigg), \end{align*} $$
where the union is taken over all
$\tau \in \mathcal T_t^\times (F)$
.
In light of these observations, we are ready to estimate
$|\mathcal P(F,\tilde X')|$
in terms of
$|\mathcal P(F,W')|$
. We first use
$\tilde \Phi _F$
to split over
$\mathcal P(F,W')$
and then we split again over all possible T-layers. Indeed, we have
$$ \begin{align} |\mathcal P(F,\tilde X')| = \sum_q \sum_t |\{p \in \tilde{\Phi}_F^{-1}(q) : p^T = t\}|, \end{align} $$
where the sums are taken over all patterns
$q\in \mathcal P(F,W')$
and
$t \in \mathcal P(F,T)$
. Choose and fix patterns q and t. If
$p \in \mathcal P(F,\tilde X')$
is a pattern such that
$\tilde \Phi _F(p) = q$
and
$p^T = t$
, then the observations above imply that p is uniquely determined by
$$ \begin{align*} p^{\tilde X}\bigg(F \cap \bigg( \bigcup_\tau \partial \tau \bigg) \bigg) \in \mathcal A_X^*, \end{align*} $$
where the union is taken over all tiles
$\tau \in \mathcal T_t^\times (F)$
. Moreover, our choice of
$\mathcal S$
and the property (F1) of F together yield that
$$ \begin{align*} \bigg| \bigcup_\tau \partial \tau \bigg| < \delta \bigg| \bigcup_\tau \tau \bigg| = \delta|F_t^\times| < \delta(1+\delta)|F|. \end{align*} $$
Therefore, there are at most
$|\mathcal A_X|^{\delta (1+\delta )|F|}$
patterns p such that
$\tilde \Phi _F(p) = q$
and
$p^T = t$
. From this and equation (5.2), we have
$$ \begin{align*} |\mathcal P(F,\tilde X')| \leq |\mathcal P(F,W')| \cdot |\mathcal P(F,T)| \cdot |\mathcal A_X|^{\delta(1+\delta)|F|}. \end{align*} $$
By taking logs and dividing through by
$|F|$
, we obtain the following:
$$ \begin{align*} h(\tilde X') &< h(F,\tilde X') + \delta\\ &\leq (h(F,W') + h(F,T) + \delta(1+\delta) \log |\mathcal A_X|) + \delta\\ &< (h(W') + \delta) + (2\delta) + \delta(1+\delta) \log |\mathcal A_X| + \delta\\ &= h(W') + 4\delta + \delta(1+\delta) \log |\mathcal A_X|\\ &< h(W') + \varepsilon/2, \end{align*} $$
where we have used property (F2) of the set F, the above inequality, property (F2) again, and our choice of
$\delta $
. Since
$\tilde X' \subset \tilde X$
was arbitrary, we have that
$$ \begin{align*} \mathcal H(\tilde\phi) = \sup_{\tilde X'\subset \tilde X} ( h(\tilde X') - h(\tilde\phi(\tilde X'))) \leq \varepsilon/2 < \varepsilon, \end{align*} $$
which completes the proof.
5.2 Subsystem entropies for sofic shifts
Here we present our main result concerning subsystem entropies for sofic shifts. The proof follows easily by combining our extension result (Theorem 5.1) with our result for SFTs (Theorem 4.2).
Theorem 5.2. Let G be a countable amenable group, let W be a sofic G-shift, and let
$V \subset W$
be any subsystem such that
$h(V) < h(W)$
. Then
$$ \begin{align*} \{h(U) : V \subset U \subset W \text { and}\ U\ \text{is sofic}\} \end{align*} $$
is dense in
$[h(V), h(W)]$
.
Proof. We prove the density directly. Let
$(a,b) \subset [h(V), h(W)]$
for some real numbers
$a < b$
. Let
$\varepsilon < (b - a)/2 < h(W) - h(V)$
. By Theorem 5.1, there exists an SFT X and a factor map
$\phi : X \to W$
such that
$\mathcal H(\phi ) < \varepsilon $
.
Consider the preimage
$Y = \phi ^{-1}(V) \subset X$
, which is a subshift. Note that
$\phi (Y) = V$
because
$\phi $
is surjective, and hence
$\phi |_Y : Y \to V$
is a factor map. We then have that
$$ \begin{align*} h(Y) \leq h(V) + \mathcal H(\phi) < h(V) + \varepsilon < h(W) \leq h(X). \end{align*} $$
Note also that
$b \leq h(W) \leq h(X)$
and that
$a \geq h(V)> h(Y) - \varepsilon $
, which together yield that
$(a+\varepsilon ,b) \subset [h(Y), h(X)]$
. By Theorem 4.2, there exists an SFT Z such that
$Y \subset Z \subset X$
and
$h(Z) \in (a+\varepsilon ,a+2\varepsilon ) \subset (a,b)$
. It follows that
$U = \phi (Z)$
is a sofic shift for which
$V \subset U \subset W$
and
$h(U) \leq h(Z) < h(U) + \varepsilon $
. Then we have
$$ \begin{gather*} a < h(Z) - \varepsilon < h(U) \leq h(Z) < a + 2\varepsilon < b. \end{gather*} $$
Thus
$h(U) \in (a,b)$
, which completes the proof.
If one selects
$V = \varnothing $
for the above theorem, then one recovers the statement that the entropies of the sofic subsystems of W are dense in
$[0,h(W)]$
. Next, we present our result concerning the entropies of arbitrary subsystems of sofic shifts.
Corollary 5.3. Let W be a sofic shift. For every non-negative real
$r \leq h(W)$
, there exists a subsystem
$R \subset W$
for which
$h(R) = r$
.
Proof. If
$h(W) = 0$
, then
$r = 0$
, in which case one may simply select
$R = W$
. If
${h(W)> 0}$
, then let
$W_0 = W$
and let
$(\varepsilon _n)_n$
be a sequence of positive real numbers converging to zero. We have that
$W_0$
is sofic and
$r \leq h(W_0)$
, and without loss of generality, we assume that
$h(W_0) < r + \varepsilon _0$
.
Inductively construct a descending sequence of sofic shifts as follows. If
$W_n \subset W$
is a sofic shift such that
$r \leq h(W_n) < r + \varepsilon _n$
, then by Theorem 5.2, there exists a sofic shift
$W_{n+1} \subset W_n$
for which
$r \leq h(W_{n+1}) < r + \varepsilon _{n+1}$
.
Then
$R = \bigcap _n W_n \subset W$
is a subshift such that
$h(R) = \lim _n h(W_n) = r$
by Pro- position 2.11.
6 A counterexample
Theorem 5.2 implies that the entropies of the sofic subsystems of a sofic shift space W are dense in
$[0,h(W)]$
. One may wonder if this can be somehow ‘sharpened’; that is, one may wonder whether
$$ \begin{align*}\{h(W') : W'\subset W \text{ and}\ W'\ \text{is an {SFT}} \}\end{align*} $$
is dense in
$[0, h(W)]$
. However, this statement is nowhere close to true in general, as we illustrate in this section by counterexample. This example is an adaptation of a construction of Boyle, Pavlov, and Schraudner [Reference Boyle, Pavlov and Schraudner5].
Proposition 6.1. There exists a sofic
$\mathbb Z^2$
-shift with positive entropy whose only SFT subsystem is a singleton.
Proof. We first construct a certain point in
$\{0,1\}^{\mathbb Z}$
as the limit of a sequence of finite words, then consider the subshift it generates. Let
$\delta = 0.1$
and let
$(T_n)_n$
be the sequence of natural numbers given by
$$ \begin{align*} T_n = 2n\cdot2^n\cdot\delta^{-1} + 1 \end{align*} $$
for each n. Let
$w^1 = 010 \in \{0,1\}^3$
and for each n, define the word
$$ \begin{align} w^{n+1} = w^n w^n \ldots w^n {w^n}\, 0^n10^n, \end{align} $$
where the
$w^n$
term is repeated exactly
$T_n$
times. The limit word
$w^\infty \in \{0,1\}^{\mathbb N_0}$
is an infinite one-sided sequence. Define a two-sided sequence
$x^* \in \{0,1\}^{\mathbb Z}$
by
$x^*_i = w^\infty _{|i|}$
for each
$i \in \mathbb Z$
. Let
$X = \overline {\mathcal O}(x^*) \subset \{0,1\}^{\mathbb Z}$
be the subshift generated by
$x^*$
. We claim that X exhibits the following three properties.
-
(P1) X is effective, meaning that there exists a finite algorithm which enumerates a set of words
$\mathcal F \subset \{0,1\}^*$
such that
$X = \mathcal R(\{0,1\}^{\mathbb Z},\, \mathcal F)$
. -
(P2) There exists a point
$x \in X$
such that
$$ \begin{align*} \limsup_{n\to\infty} \frac{|\{k \in [-n,n] : x_k = 1\}|}{2n+1}> 0.1. \end{align*} $$
-
(P3) For each
$x \in X$
, either
$x = 0^{\mathbb Z}$
or x contains the word
$0^n10^n$
for every n.
For (P1), let N be arbitrary. Note that because
$X = \overline {\mathcal O}(x^*)$
, any word of length N occurring in any point
$x \in X$
is also a word occurring in
$x^*$
. By the recursive definition in equation (6.1) and the fact that the sequence
$\{T_n\}_{n=1}^{\infty }$
is recursive, there is an algorithm which, upon input N, prints all the words of length N that do not appear as subwords of
$x^*$
. The shift X is therefore effective.
For (P2), we argue that
$x^*$
satisfies the condition. For each n, let
$L_n$
be the length of the word
$w^n$
. Note that by the recurrence in equation (6.1), we have
$$ \begin{align*} L_{n+1} = T_n L_n + 2n+1 \quad \text{for all } n. \end{align*} $$
For each n, let
$f_n$
be the frequency of 1s in
$w^n$
, given by
$$ \begin{align*} f_n = \frac{|\{ i : w^n_i = 1 \}|}{L_n}. \end{align*} $$
Observe that
$f_n \leq 1$
for each n and
$f_1 = \tfrac 13$
. It follows from the recurrence in equation (6.1) that
$$ \begin{align*} f_{n+1} = \frac{f_n T_n L_n + 1}{T_nL_n + 2n+1} \end{align*} $$
for each n. This implies that
$$ \begin{align*} f_n - f_{n+1} &= \frac{f_nT_nL_n + f_n(2n+1) - f_nT_nL_n - 1}{T_nL_n + 2n+1}\\ &\leq \frac{1(2_n+1)-1}{T_n} \end{align*} $$
in which case
$f_n - f_{n+1} \leq {2n}/{T_n} < {\delta }/{2^n}$
for each n. Hence, we have that
$$ \begin{align*} f_1 - f_n &= (f_1 - f_2) + (f_2 - f_3) + \cdots + (f_{n-1} - f_n)\\ &< \frac\delta 2 + \frac\delta 4 + \cdots + \frac\delta{2^{n-1}}\\[0.3em] &< \delta \end{align*} $$
in which case
$\tfrac 13 - \delta < f_n$
for each n. By the recurrence in equation (6.1), we therefore have that
$$ \begin{align*} \limsup_{n\to\infty} \frac{|\{ k \in [-n,n] : x^*_k = 1 \}|}{2n+1} \geq \frac13 - \delta> 0.1 \end{align*} $$
and the subsequence along
$(L_n)_n$
is a witness.
For (P3), let n be fixed. First, observe that the infinite sequence
$w^\infty $
may be decomposed as a concatenation of blocks, where each block is either the word
$w^n$
or
$0^m10^m$
for some
$m \geq n$
. Moreover, each
$w^n$
begins with
$0$
and ends with
$0^n$
. This implies that
$1$
s belonging to distinct blocks (of the form
$w^n$
or
$0^m10^m$
for
$m \geq n$
) in the decomposition of
$w^\infty $
mentioned above are separated by at least
$n+1$
appearances of the symbol
$0$
. Therefore, if for any
$k \leq n$
we have that
$10^k1$
appears anywhere in
$w^\infty $
, then it must appear as a subword of a single block (rather than overlapping two distinct blocks), and that block must be
$w^n$
.
Next, let
$x \in X$
be arbitrary. If the symbol
$1$
appears in x at most one time, then (P3) trivially holds. Otherwise, assume that
$10^k1$
appears somewhere in x for some
$k \geq 1$
. Without loss of generality, suppose
$x_0 = x_{k+1} = 1$
and
$x_i = 0$
for
$i \in [1,k]$
. Now consider the subword
$\omega = x([-L_n, L_n])$
for any n such that
$k < L_n$
. Because
$X = \overline {\mathcal O}(x^*)$
, the word
$\omega $
must be a subword of
$x^*$
. Then, either
$\omega $
is a subword of
$x^*([-2L_n, 2L_n])$
, or
$\omega $
is a subword of
$w^\infty $
or a mirror reflection of one. In the first case, the definitions of
$x^*$
and
$w^\infty $
imply that
$\omega $
contains the word
$w^n$
or its mirror. In the latter two cases, the observation of the previous paragraph implies that
$\omega $
must contain
$w^n$
or its mirror. In any case,
$0^n10^n$
is a subword of x. As n can be made arbitrarily large, this proves (P3).
We now use the shift X to construct the
$\mathbb Z^2$
-shift which is desired for the theorem. For each point
$x \in X$
, let
$x^{\mathbb Z} \in \{0,1\}^{\mathbb Z^2}$
denote the
$\mathbb Z^2$
-labeling given by
$$ \begin{align*} (x^{\mathbb Z})_{(i,j)} = x_i \end{align*} $$
for each
$(i,j) \in \mathbb Z^2$
. That is,
$x^{\mathbb Z}$
is a
$\mathbb Z^2$
-labeling such that the symbols along each column are constant, and each row is equal to x itself. We shall also denote
$$ \begin{align*} X^{\mathbb Z} = \{x^{\mathbb Z} : x \in X\} \subset \{0,1\}^{\mathbb Z^2}. \end{align*} $$
It is a theorem of Aubrun and Sablik [Reference Aubrun and Sablik1] that if X is effective, then
$X^{\mathbb Z}$
is sofic.
Next, consider the alphabet
$\{0,1,1'\}$
, where we have artificially created two independent
$1$
symbols. Let
$\pi : \{0,1,1'\}^{\mathbb Z^2} \to \{0,1\}^{\mathbb Z^2}$
be the one-block code which collapses 1 and
$1'$
. Let
$Y = \pi ^{-1}(X^{\mathbb Z}) \subset \{0,1,1'\}^{\mathbb Z^2}$
. The shift Y is a copy of the shift
$X^{\mathbb Z}$
, in which the 1 symbols of every point have been replaced either by
$1$
or
$1'$
in every possible combination.
We claim that the shift Y is the desired subshift for the theorem. Specifically, we claim that Y is sofic, that Y has positive entropy, and that the only non-empty SFT subsystem of Y is the singleton
$\{0^{\mathbb Z^2}\}$
.
To prove that Y is sofic, we construct an SFT
$S'$
and a factor map
$\phi ' : S' \to Y$
to witness the soficity of Y. Since
$X^{\mathbb Z}$
is sofic, there is an SFT
$S \subset \mathcal A^{\mathbb Z^2}$
and a factor map
$\phi : S \to X^{\mathbb Z}$
. Without loss of generality, assume that
$\phi $
is a one-block code induced by the function
$\Phi : \mathcal A \to \{0,1\}$
.
Define a new finite alphabet
$\mathcal A \times \{1,1'\}$
and a one-block code
$\phi '$
induced by the function
$\Phi ' : \mathcal A \times \{1,1'\} \to \{0,1,1'\}$
which is given by
$$ \begin{align*} \Phi'(a,b) = \begin{cases} 0 &\mbox{if } \Phi(a) = 0,\\ b &\mbox{if } \Phi(a) = 1, \end{cases} \end{align*} $$
for each
$(a,b) \in \mathcal A \times \{1,1'\}$
.
Let
$S' = S \times \{1,1'\}^{\mathbb Z^2}$
, which we regard as a subshift of
$(\mathcal A\times \{1,1'\})^{\mathbb Z^2}$
. Note that
$S'$
is an SFT, because both S and
$\{1,1'\}^{\mathbb Z^2}$
(the full
$\mathbb Z^2$
-shift on two symbols) are SFTs. A point
$s' \in S'$
is of the form
$s' = (s,\iota )$
, where s is a point of S and
$\iota \in \{1,1'\}^{\mathbb Z^2}$
is an arbitrary
$2$
-coloring of
$\mathbb Z^2$
. The reader may easily check that
$(\pi \circ \phi ')(s,\iota ) = \phi (s) \in X^{\mathbb Z}$
, from which it follows that
$\phi '(S') = \pi ^{-1}(X^{\mathbb Z}) = Y$
. Then
$\phi ' : S' \to Y$
is a factor map. Since
$S'$
is an SFT, we conclude that Y is sofic.
Next, we will show that
$h(Y)> 0$
. From property (P2), the point
$x^* \in X$
exhibits
$1$
s in more than
$10\%$
of the positions in each of infinitely many symmetric intervals, say of the form
$[-\ell _n, \ell _n]$
for an increasing sequence of natural numbers
$(\ell _n)_n$
. Therefore, the point
$(x^*)^{\mathbb Z}$
exhibits
$1$
s in more than
$10\%$
of the positions in each square
$F_n = [-\ell _n,\ell _n]^2$
. Each
$1$
in the pattern
$(x^*)^{\mathbb Z}(F_n)$
may be replaced by
$1$
or
$1'$
independently to yield an allowed pattern of Y, which implies that
$$ \begin{align*} |\mathcal P(F_n, Y)| \geq 2^{0.1|F_n|} \quad \text{for all } n. \end{align*} $$
As
$(F_n)_n$
is a Følner sequence for
$\mathbb Z^2$
, we then have
$h(Y) \geq 0.1 \log 2> 0$
.
It remains to show that the only non-empty SFT subsystem of Y is the singleton
$\{0^{\mathbb Z^2}\}$
. Suppose to the contrary that
$Z \subset Y$
is an SFT subsystem of Y which contains a non-zero point. Since Z is an SFT, we may find a constant
$k \in \mathbb N$
such that the allowed patterns of Z are specified by the shape
$K = [0,k)^2 \subset \mathbb Z^2$
.
Let
$z\in Z$
be a point different from
$0^{\mathbb Z^2}$
and note
$\pi (z) = x^{\mathbb Z} \in X^{\mathbb Z}$
for some
$x \in X$
with
$x \neq 0^{\mathbb Z}$
. By property (P1), the string
$0^n10^n$
appears in x for every n. Let
$n> k$
be fixed. Suppose without loss of generality that
$0^n10^n$
appears centered at the origin of x (with
$x_0 = 1$
and
$x_i = 0$
for
$0 < |i| \leq n$
). Thus we have
$z_{(0,0)} = 1$
or
$1'$
. In fact, by the definition of Y, we have
$z_{(0,j)} \in \{1,1'\}$
for every
$j \in \mathbb Z$
.
Consider the
$i = 0$
column of the point z. Starting with each index
$\ell \in \mathbb Z$
and looking up, there is a corresponding vertically oriented word
$\omega ^\ell \in \{1,1'\}^n$
given by
$\omega ^\ell _j = z_{(0,\ell +j)}$
for each
$j \in [0,n)$
. By the pigeonhole principle, there must exist a word
$\varsigma \in \{1,1'\}^n$
such that
$\varsigma = \omega ^\ell $
for infinitely many choices of
$\ell $
. That is, for infinitely many choices of
$\ell $
, we have
$z_{(0,\ell +j)} = \varsigma _j$
for each
$j \in [0,n)$
.
Let
$\ell _1 < \ell _2$
be two such indices where a repetition occurs, with
$\ell _2 - \ell _1> n$
. That is, we have
$z_{(0,\ell _1 + j)} = z_{(0,\ell _2 +j)} = \varsigma _j$
for every
$j \in [0,n)$
. Now consider the rectangle
$r = z([-n,n] \times [\ell _1,\ell _2))$
. Tile
$\mathbb Z^2$
with infinitely many translated copies of r to obtain a new point
$z' \in \{0,1,1'\}^{\mathbb Z^2}$
. Figure 4 illustrates the construction.
Figure 4 An illustration of the construction of the contradictory point
$z'$
in a hypothetical case where
$n = 3$
and
$k = 2$
.
Every pattern of shape
$K = [0,k)^2$
which occurs in
$z'$
is a pattern which occurs in z (including the pattern of all zeroes), and hence they are all allowed in Z. Because Z is an SFT specified by K, it then follows that
$z' \in Z$
. Because
$Z \subset Y = \pi ^{-1}(X^{\mathbb Z})$
, there must exist a point
$x' \in X$
such that
$\pi (z') = (x')^{\mathbb Z}$
. We obtain a contradiction, as the point
$x'$
cannot satisfy the property (P3) of X. For instance, the word
$0^{3n}10^{3n}$
cannot appear in
$x'$
(as each row of
$z'$
is periodic in the horizontal direction with period
$2n+1 < 3n$
). This demonstrates that if Z is an SFT, then it contains no non-zero point. Therefore, the only non-empty SFT subsystem of Y is
$\{0^{\mathbb Z^2}\}$
.
Acknowledgements
R.B. and K.M. both gratefully acknowledge funding from the National Science Foundation grant DMS-1847144. R.P. gratefully acknowledges the support of a Simons Foundation Collaboration Grant. The authors would also like to express thanks to the anonymous referee for comments and suggestions that significantly improved the paper.
Open access
