Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-18T10:04:19.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Suspension Taylor–Couette flow: co-existence of stationary and travelling waves, and the characteristics of Taylor vortices and spirals

Published online by Cambridge University Press:  15 May 2019

Prashanth Ramesh ,
S. Bharadwaj  and
Meheboob Alam Open the ORCID record for Meheboob Alam [Opens in a new window]
Prashanth Ramesh
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
S. Bharadwaj
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Meheboob Alam*
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: meheboob@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Flow visualization and particle image velocimetry (PIV) measurements are used to unravel the pattern transition and velocity field in the Taylor–Couette flow (TCF) of neutrally buoyant non-Brownian spheres immersed in a Newtonian fluid. With increasing Reynolds number (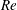$Re$) or the rotation rate of the inner cylinder, the bifurcation sequence in suspension TCF remains same as in its Newtonian counterpart (i.e. from the circular Couette flow (CCF) to stationary Taylor vortex flow (TVF) and then to travelling wavy Taylor vortices (WTV) with increasing 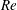$Re$) for small particle volume fractions (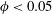$\unicode[STIX]{x1D719}<0.05$). However, at 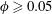$\unicode[STIX]{x1D719}\geqslant 0.05$, non-axisymmetric patterns such as (i) the spiral vortex flow (SVF) and (ii) two mixed or co-existing states of stationary (TVF, axisymmetric) and travelling (WTV or SVF, non-axisymmetric) waves, namely (iia) the ‘TVF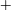$+$WTV’ and (iib) the ‘TVF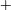$+$SVF’ states, are found, with the former as a primary bifurcation from CCF. While the SVF state appears both in the ramp-up and ramp-down experiments as in the work of Majji et al. (J. Fluid Mech., vol. 835, 2018, pp. 936–969), new co-existing patterns are found only during the ramp-up protocol. The secondary bifurcation TVF 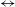$\leftrightarrow$ WTV is found to be hysteretic or sub-critical for 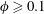$\unicode[STIX]{x1D719}\geqslant 0.1$. In general, there is a reduction in the value of the critical Reynolds number, i.e. $Re_{c}(\unicode[STIX]{x1D719}\neq 0)<Re_{c}(\unicode[STIX]{x1D719}=0)$, for both primary and secondary transitions. The wave speeds of both travelling waves (WTV and SVF) are approximately half of the rotational velocity of the inner cylinder, with negligible dependence on 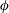$\unicode[STIX]{x1D719}$. The analysis of the radial–axial velocity field reveals that the Taylor vortices in a suspension are asymmetric and become increasingly anharmonic, with enhanced radial transport, with increasing particle loading. Instantaneous streamline patterns on the axial–radial plane confirm that the stationary Taylor vortices can indeed co-exist either with axially propagating spiral vortices or azimuthally propagating wavy Taylor vortices – their long-time stability is demonstrated. It is shown that the azimuthal velocity is considerably altered for $\unicode[STIX]{x1D719}\geqslant 0.05$, resembling shear-band type profiles, even in the CCF regime (i.e. at sub-critical Reynolds numbers) of suspension TCF; its possible role on the genesis of observed patterns as well as on the torque scaling is discussed.

JFM classification

Nonlinear Dynamical Systems: Pattern formation Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 901 - 940
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abcha, N., Crumeyrolle, O., Ezersky, A. B. & Mutabazi, I. 2013 Velocity field of the spiral vortex flow in the Couette–Taylor system. Eur. Phys. J. E 35, 20.Google Scholar
Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Ahrens, J., Geveci, B. & Law, C. 2005 Paraview: an end-user tool for large data visualization. In The Visualization Handbook (ed. Hansen, C. D. & Johnson, C. R.), pp. 717–731. Elsevier.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Bailey, B. C. & Yoda, M. 2003 An aqueous low-viscosity density-and refractive index-matched suspension system. Exp. Fluids 35 (1), 1–3.Google Scholar
Benjamin, T. B. 1978a Bifurcation phenomena in steady flows of a viscous fluid. I. Theory. Proc. R. Soc. Lond. A 359, 1–26.Google Scholar
Benjamin, T. B. 1978b Bifurcation phenomena in steady flows of a viscous fluid. II. Experiments. Proc. R. Soc. Lond. A 359, 27–43.Google Scholar
Benjamin, T. B. & Mullin, T. 1981 Anomalous modes in the Taylor experiment. Proc. R. Soc. Lond. A 377, 221–249.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011 Local transient rheological behavior of concentrated suspensions. J. Rheol. 55, 835–854.Google Scholar
Chandrasekhar, S. 1960 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chossat, P. & Iooss, G. 1994 The Couette–Taylor Problem. Springer.Google Scholar
Cliffe, K. A. & Mullin, T. 1985 A numerical and experimental study of anomalous modes in the Taylor experiment. J. Fluid Mech. 153, 243–258.Google Scholar
Cliffe, K. A., Mullin, T. & Schaeffer, D. G. 2012 The onset of steady vortices in Taylor–Couette flow: the role of approximate symmetry. Phys. Fluids 24, 064102.Google Scholar
Cole, J. A. 1976 Taylor-vortex instability and annulus-length effects. J. Fluid Mech. 75 (1), 1–15.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.Google Scholar
Di Prima, R. C. & Swinney, H. L. 1981 Instabilities and Transition in flow between concentric rotating cylinders. In Hydrodynamic Instabilities and the Transition to Turbulence (ed. Swinney, H. L. & Gollub, J. P.). Springer.Google Scholar
Divoux, T., Fardin, M. A., Manneville, S. & Lerouge, S. 2016 Shear banding of complex fluids. Annu. Rev. Fluid Mech. 48, 539–575.Google Scholar
Donnelly, R. J. & Fultz, D. 1960 Experiments on the stability of viscous flow between rotating cylinders. II. Visual observations. Proc. R. Soc. Lond. A 258, 101–123.Google Scholar
Dutcher, C. S. & Muller, S. J. 2009 Spatio-temporal mode dynamics and higher order transitions in high aspect ratio Newtonian Taylor–Couette flows. J. Fluid Mech. 641, 85–113.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Fardin, M.-A., Lasne, B., Cardoso, O., Grégoire, G., Argentina, M., Decruppe, J.-P. & Lerouge, S. 2009 Taylor-like vortices in shear-banding flow of giant micelles. Phys. Rev. Lett. 103, 028302.Google Scholar
Groisman, A. & Steinberg, V. 1997 Solitary vortex pairs in viscoelastic Couette flow. Phys. Rev. Lett. 78 (8), 1460–1463.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High–Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.Google Scholar
Guazzelli, E. & Pouliquen, O. 2018 Rheology of dense granular suspensions. J. Fluid Mech. 852, P1.Google Scholar
Halow, J. S. & Wills, G. B. 1970 Experimental observations of sphere migration in Couette systems. Ind. Engng Chem. Fundam. 9 (4), 603–607.Google Scholar
Hoffmann, C., Lücke, M. & Pinter, A. 2004 Spiral vortices and Taylor vortices in the annulus between rotating cylinders and the effect of an axial flow. Phys. Rev. E 69, 056309.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65 (2), 365–400.Google Scholar
Jones, C. A. 1985 Transition to wavy Taylor vortices. J. Fluid Mech. 157, 135–162.Google Scholar
King, G. P., Li, Y., Lee, W., Swinney, H. L. & Marcus, P. S. 1984 Wave speeds in wavy Taylor-vortex flow. J. Fluid Mech. 141, 365–390.Google Scholar
Larson, R. G., Shaqfeh, E. S. G. & Muller, S. J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 218, 573–600.Google Scholar
Majji, M. V., Banerjee, S. & Morris, J. F. 2018 Inertial flow transitions of a suspension in Taylor–Couette geometry. J. Fluid Mech. 835, 936–969.Google Scholar
Majji, M. V. & Morris, J. F. 2018 Inertial migration of particles in Taylor–Couette flows. Phys. Fluids 30, 033303.Google Scholar
Martínez-Arias, B., Peixinho, J., Crumeyrolle, O. & Mutabazi, I. 2014 Effect of the number of vortices on the torque scaling in Taylor–Couette flow. J. Fluid Mech. 748, 756–767.Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90, 014501.Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.Google Scholar
Mullin, T. 1982 Mutations of steady cellular flows in the Taylor experiment. J. Fluid Mech. 121, 207–218.Google Scholar
Mullin, T. 1985 Onset of time dependence in Taylor–Couette flow. Phys. Rev. A 31, 1216–1218.Google Scholar
Mullin, T. & Benjamin, T. B. 1980 Transition to oscillatory motion in the Taylor experiment. Nature 288, 567–569.Google Scholar
Mullin, T., Heise, M. & Pfister, G. 2017 Onset of cellular motion in the Taylor–Couette flow. Phys. Rev. Fluids 2, 081901.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.Google Scholar
Park, K. 1984 Universal transition sequence in Taylor wavy-vortex flow. Phys. Rev. A 29, 3458–3460.Google Scholar
Rayleigh, Lord 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–153.Google Scholar
Saha, S. & Alam, M. 2017 Revisiting ignited-quenched transition and the non-Newtonian rheology of a sheared dilute gas–solid suspension. J. Fluid Mech. 833, 206–246.Google Scholar
Segre, G. & Silberberg, A. J. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14 (1), 136–157.Google Scholar
Synge, J. L. 1933 The stability of heterogeneous fluids. Trans. R. Soc. Can. 27 (3), 1–18.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Taylor, G. I. 1936a Fluid friction between rotating cylinders. I. Torque measurements. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Taylor, G. I. 1936b Fluid friction between rotating cylinders. II. Distribution of velocity between concentric cylinders when outer one is rotating and inner one is at rest. Proc. R. Soc. Lond. A 157, 565–578.Google Scholar
Tokgoz, S., Elsinga, G. E., Delfos, R. & Westerweel, J. 2012 Spatial resolution and dissipation rate estimation in Taylor–Couette flow for tomographic PIV. Exp. Fluids 53 (3), 561–583.Google Scholar
Vasseur, P. & Cox, R. G. 1976 The lateral migration of a spherical particle in two-dimensional shear flows. J. Fluid Mech. 78 (2), 385–413.Google Scholar
Wereley, S. T. & Lueptow, R. M. 1998 Spatio-temporal character of non-wavy and wavy Taylor–Couette flow. J. Fluid Mech. 364, 59–80.Google Scholar