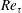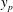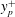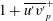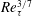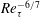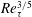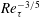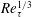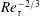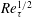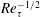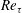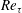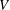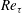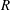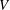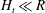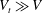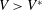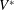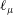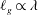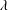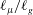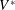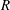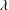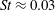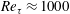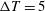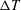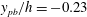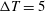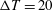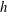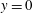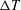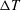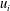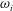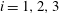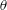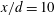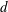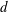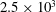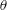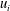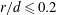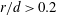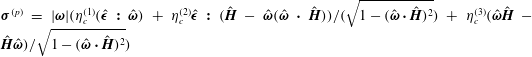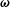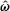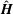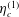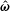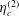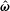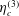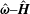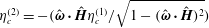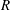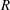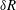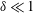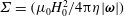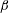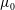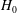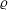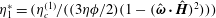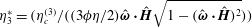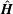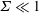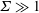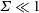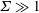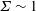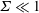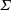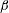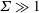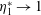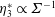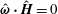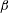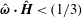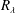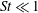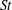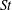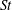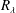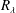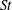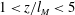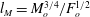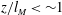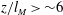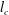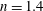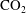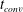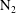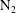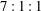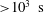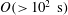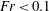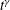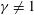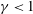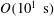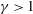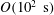JFM Rapids
On the departure of near-wall turbulence from the quasi-steady state
- Lionel Agostini, Michael Leschziner
-
- Published online by Cambridge University Press:
- 20 May 2019, R1
-
- Article
- Export citation
-
An examination is undertaken of the validity and limitations of the quasi-steady hypothesis of near-wall turbulence. This hypothesis is based on the supposition that the statistics of the turbulent fluctuations are universal if scaled by the local, instantaneous, wall shear when its variations are determined from footprints of large-scale, energetic, structures that reside in the outer part of the logarithmic layer. The examination is performed with the aid of direct numerical simulation data for a single Reynolds number, which are processed in a manner that brings out the variability of locally scaled statistics when conditioned on the local value of the wall friction. The key question is to what extent this variability is insignificant, thus reflecting universality. It is shown that the validity of the quasi-steady hypothesis is confined, at best, to a thin layer above the viscous sublayer. Beyond this layer, substantial variations in the conditioned shear-induced production rate of large-scale turbulence cause substantial departures from the hypothesis. Even within the wall-proximate layer, moderate departures are provoked by large-scale distortions in the conditioned strain rate that result in variations in small-scale production of turbulence down to the viscous sublayer.
Non-universal scaling transition of momentum cascade in wall turbulence
- Xi Chen, Fazle Hussain, Zhen-Su She
-
- Published online by Cambridge University Press:
- 24 May 2019, R2
-
- Article
- Export citation
-
As a counterpart of energy cascade, turbulent momentum cascade (TMC) in the wall-normal direction is important for understanding wall turbulence. Here, we report an analytic prediction of non-universal Reynolds number (
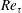 $Re_{\unicode[STIX]{x1D70F}}$) scaling transition of the maximum TMC located at
$Re_{\unicode[STIX]{x1D70F}}$) scaling transition of the maximum TMC located at 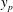 $y_{p}$. We show that in viscous units,
$y_{p}$. We show that in viscous units, 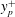 $y_{p}^{+}$ (and
$y_{p}^{+}$ (and 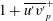 $1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$) displays a scaling transition from
$1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$) displays a scaling transition from 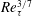 $Re_{\unicode[STIX]{x1D70F}}^{3/7}$ (
$Re_{\unicode[STIX]{x1D70F}}^{3/7}$ (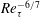 $Re_{\unicode[STIX]{x1D70F}}^{-6/7}$) to
$Re_{\unicode[STIX]{x1D70F}}^{-6/7}$) to 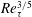 $Re_{\unicode[STIX]{x1D70F}}^{3/5}$ (
$Re_{\unicode[STIX]{x1D70F}}^{3/5}$ (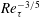 $Re_{\unicode[STIX]{x1D70F}}^{-3/5}$) in turbulent boundary layer, in sharp contrast to that from
$Re_{\unicode[STIX]{x1D70F}}^{-3/5}$) in turbulent boundary layer, in sharp contrast to that from 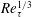 $Re_{\unicode[STIX]{x1D70F}}^{1/3}$ (
$Re_{\unicode[STIX]{x1D70F}}^{1/3}$ (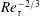 $Re_{\unicode[STIX]{x1D70F}}^{-2/3}$) to
$Re_{\unicode[STIX]{x1D70F}}^{-2/3}$) to 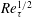 $Re_{\unicode[STIX]{x1D70F}}^{1/2}$ (
$Re_{\unicode[STIX]{x1D70F}}^{1/2}$ (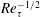 $Re_{\unicode[STIX]{x1D70F}}^{-1/2}$) in a channel/pipe, countering the prevailing view of a single universal near-wall scaling. This scaling transition reflects different near-wall motions in the buffer layer for small
$Re_{\unicode[STIX]{x1D70F}}^{-1/2}$) in a channel/pipe, countering the prevailing view of a single universal near-wall scaling. This scaling transition reflects different near-wall motions in the buffer layer for small 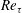 $Re_{\unicode[STIX]{x1D70F}}$ and log layer for large
$Re_{\unicode[STIX]{x1D70F}}$ and log layer for large 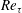 $Re_{\unicode[STIX]{x1D70F}}$, with the non-universality being ascribed to the presence/absence of mean wall-normal velocity
$Re_{\unicode[STIX]{x1D70F}}$, with the non-universality being ascribed to the presence/absence of mean wall-normal velocity 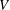 $V$. Our predictions are validated by a large set of data, and a probable flow state with a full coupling between momentum and energy cascades beyond a critical
$V$. Our predictions are validated by a large set of data, and a probable flow state with a full coupling between momentum and energy cascades beyond a critical 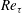 $Re_{\unicode[STIX]{x1D70F}}$ is envisaged.
$Re_{\unicode[STIX]{x1D70F}}$ is envisaged.
A note on the aerodynamic splashing of droplets
- José Manuel Gordillo, Guillaume Riboux
-
- Published online by Cambridge University Press:
- 24 May 2019, R3
-
- Article
- Export citation
-
When a drop of a low-viscosity liquid of radius
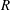 $R$ impacts against an inclined smooth solid substrate at a velocity
$R$ impacts against an inclined smooth solid substrate at a velocity 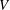 $V$, a liquid sheet of thickness
$V$, a liquid sheet of thickness 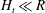 $H_{t}\ll R$ is expelled at a velocity
$H_{t}\ll R$ is expelled at a velocity 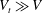 $V_{t}\gg V$. If the impact velocity is such that
$V_{t}\gg V$. If the impact velocity is such that 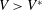 $V>V^{\ast }$, with
$V>V^{\ast }$, with 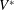 $V^{\ast }$ the critical velocity for splashing, the edge of the expanding liquid sheet lifts off from the wall as a consequence of the gas lubrication force at the wedge region created between the advancing liquid front and the substrate. Here we show that the magnitude of the gas lubrication force is limited by the values of the slip length
$V^{\ast }$ the critical velocity for splashing, the edge of the expanding liquid sheet lifts off from the wall as a consequence of the gas lubrication force at the wedge region created between the advancing liquid front and the substrate. Here we show that the magnitude of the gas lubrication force is limited by the values of the slip length 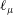 $\ell _{\unicode[STIX]{x1D707}}$ at the gas–liquid interface and of the slip length
$\ell _{\unicode[STIX]{x1D707}}$ at the gas–liquid interface and of the slip length 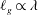 $\ell _{g}\propto \unicode[STIX]{x1D706}$ at the solid, with
$\ell _{g}\propto \unicode[STIX]{x1D706}$ at the solid, with 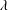 $\unicode[STIX]{x1D706}$ the mean free path of gas molecules. We demonstrate that the splashing regime changes depending on the value of the ratio
$\unicode[STIX]{x1D706}$ the mean free path of gas molecules. We demonstrate that the splashing regime changes depending on the value of the ratio 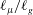 $\ell _{\unicode[STIX]{x1D707}}/\ell _{g}$ – a fact explaining the spreading–splashing–spreading–splashing transition for a fixed (low) value of the gas pressure as the drop impact velocity increases (Xu et al., Phys. Rev. Lett., vol. 94, 2005, 184505; Hao et al., Phys. Rev. Lett., vol. 122, 2019, 054501). We also provide an expression for
$\ell _{\unicode[STIX]{x1D707}}/\ell _{g}$ – a fact explaining the spreading–splashing–spreading–splashing transition for a fixed (low) value of the gas pressure as the drop impact velocity increases (Xu et al., Phys. Rev. Lett., vol. 94, 2005, 184505; Hao et al., Phys. Rev. Lett., vol. 122, 2019, 054501). We also provide an expression for 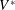 $V^{\ast }$ as a function of the inclination angle of the substrate, the drop radius
$V^{\ast }$ as a function of the inclination angle of the substrate, the drop radius 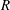 $R$, the material properties of the liquid and the gas, and the mean free path
$R$, the material properties of the liquid and the gas, and the mean free path 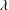 $\unicode[STIX]{x1D706}$, in very good agreement with experiments.
$\unicode[STIX]{x1D706}$, in very good agreement with experiments.
Two-dimensional unsteadiness map of oblique shock wave/boundary layer interaction with sidewalls
- P. K. Rabey, S. P. Jammy, P. J. K. Bruce, N. D. Sandham
-
- Published online by Cambridge University Press:
- 24 May 2019, R4
-
- Article
- Export citation
-
The low-frequency unsteadiness of oblique shock wave/boundary layer interactions (SBLIs) has been investigated using large-eddy simulation (LES) and high-frequency pressure measurements from experiments. Particular attention has been paid to off-centreline behaviour: the LES dataset was generated including sidewalls, and experimental pressure measurements were acquired across the entire span of the reflected shock foot. The datasets constitute the first maps of low-frequency unsteadiness in both streamwise and spanwise directions. The results reveal that significant low-frequency shock motion (with
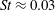 $St\approx 0.03$) occurs away from the centreline, along most of the central separation shock and in the corner regions. The most powerful low-frequency unsteadiness occurs off-centre, likely due to the separation shock being strengthened by shocks arising from the swept interactions on the sidewalls. Both simulation and experimental results exhibit asymmetry about the spanwise centre. In simulations, this may be attributed to a lack of statistical convergence; however, the fact that this is also seen in experiments is indicative that some SBLIs may exhibit some inherent asymmetry across the two spanwise halves of the separation bubble. There is also significant low-frequency power in the corner separations. The relation of the unsteadiness in the corner regions to that in the centre is investigated by means of two-point correlations: a key observation is that significant correlation does not extend across the attached flow channel between the central and corner separations.
$St\approx 0.03$) occurs away from the centreline, along most of the central separation shock and in the corner regions. The most powerful low-frequency unsteadiness occurs off-centre, likely due to the separation shock being strengthened by shocks arising from the swept interactions on the sidewalls. Both simulation and experimental results exhibit asymmetry about the spanwise centre. In simulations, this may be attributed to a lack of statistical convergence; however, the fact that this is also seen in experiments is indicative that some SBLIs may exhibit some inherent asymmetry across the two spanwise halves of the separation bubble. There is also significant low-frequency power in the corner separations. The relation of the unsteadiness in the corner regions to that in the centre is investigated by means of two-point correlations: a key observation is that significant correlation does not extend across the attached flow channel between the central and corner separations.
JFM Papers
Towards the distributed burning regime in turbulent premixed flames
- A. J. Aspden, M. S. Day, J. B. Bell
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 1-21
-
- Article
- Export citation
-
Three-dimensional numerical simulations of canonical statistically steady, statistically planar turbulent flames have been used in an attempt to produce distributed burning in lean methane and hydrogen flames. Dilatation across the flame means that extremely large Karlovitz numbers are required; even at the extreme levels of turbulence studied (up to a Karlovitz number of 8767) distributed burning was only achieved in the hydrogen case. In this case, turbulence was found to broaden the reaction zone visually by around an order of magnitude, and thermodiffusive effects (typically present for lean hydrogen flames) were not observed. In the preheat zone, the species compositions differ considerably from those of one-dimensional flames based a number of different transport models (mixture averaged, unity Lewis number and a turbulent eddy viscosity model). The behaviour is a characteristic of turbulence dominating non-unity Lewis number species transport, and the distinct limit is again attributed to dilatation and its effect on the turbulence. Peak local reaction rates are found to be lower in the distributed case than in the lower Karlovitz cases but higher than in the laminar flame, which is attributed to effects that arise from the modified fuel-temperature distribution that results from turbulent mixing dominating low Lewis number thermodiffusive effects. Finally, approaches to achieve distributed burning at realisable conditions are discussed; factors that increase the likelihood of realising distributed burning are higher pressure, lower equivalence ratio, higher Lewis number and lower reactant temperature.
The connection between the spectrum of turbulent scales and the skin-friction statistics in channel flow at
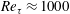 $Re_{\unicode[STIX]{x1D70F}}\approx 1000$
$Re_{\unicode[STIX]{x1D70F}}\approx 1000$
- Lionel Agostini, Michael Leschziner
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 22-51
-
- Article
- Export citation
-
Data from a direct numerical simulation for channel flow at a friction Reynolds number of 1000 are analysed to derive statistical properties that offer insight into the mechanisms by which large-scale structures in the log-law region affect the small-scale turbulence field close to the wall and the statistical skin-friction properties. The data comprise full-volume velocity fields at 150 time levels separated by 50 wall-scaled viscous time units. The scales are separated into wavelength bands by means of the ‘empirical mode decomposition’, of which the two lowest modes are considered to represent the small scales and three upper modes to represent the large scales. Joint and conditional probability density functions are then derived for various scale-specific statistics, with particular emphasis placed on the streamwise and shear stresses conditional on the large-scale fluctuations of the skin friction, generally referred to as ‘footprinting’. Statistics for the small-scale stresses, conditional on the footprints, allow the amplification and attenuation of the small-scale skin friction, generally referred to as ‘modulation’, to be quantified in dependence on the footprints. The analysis leads to the conclusion that modulation does not reflect a direct interaction between small scales and large scales, but arises from variations in shear-induced production that arise from corresponding changes in the conditional velocity profile. This causal relationship also explains the wall-normal change in sign in the correlation between large scales and small scales at a wall-scaled wall distance of approximately 100. The effects of different scales on the skin friction are investigated by means of two identities that describe the relationship between the shear-stress components and the skin friction, one identity based on integral momentum and the other on energy production/dissipation. The two identities yield significant differences in the balance of scale-specific contributions, and the origins of these differences are discussed.
Pseudophase change effects in turbulent channel flow under transcritical temperature conditions
- Kukjin Kim, Jean-Pierre Hickey, Carlo Scalo
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 52-91
-
- Article
- Export citation
-
We have performed direct numerical simulations of compressible turbulent channel flow using R-134a as a working fluid in transcritical temperature ranges (
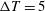 $\unicode[STIX]{x0394}T=5$, 10 and 20 K, where
$\unicode[STIX]{x0394}T=5$, 10 and 20 K, where 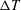 $\unicode[STIX]{x0394}T$ is top-to-bottom temperature difference) at supercritical pressure. At these conditions, a pseudophase change occurs at various wall-normal locations within the turbulent channel from
$\unicode[STIX]{x0394}T$ is top-to-bottom temperature difference) at supercritical pressure. At these conditions, a pseudophase change occurs at various wall-normal locations within the turbulent channel from 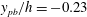 $y_{pb}/h=-0.23$ (
$y_{pb}/h=-0.23$ (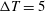 $\unicode[STIX]{x0394}T=5$ K) to 0.89 (
$\unicode[STIX]{x0394}T=5$ K) to 0.89 (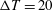 $\unicode[STIX]{x0394}T=20$ K), where
$\unicode[STIX]{x0394}T=20$ K), where 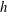 $h$ is the channel half-height and
$h$ is the channel half-height and 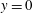 $y=0$ the centreplane position. Increase in
$y=0$ the centreplane position. Increase in 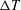 $\unicode[STIX]{x0394}T$ also results in increasing wall-normal gradients in the semi-local friction Reynolds number. Classical, compressible scaling laws of the mean velocity profile are unable to fully collapse real fluid effects in this flow. The proximity to the pseudotransitioning layer inhibits turbulent velocity fluctuations, while locally enhancing the temperature and density fluctuation intensities. Probability distribution analysis reveals that the sheet of fluid undergoing pseudophase change is characterized by a dramatic reduction in the kurtosis of density fluctuations, hence becoming thinner as
$\unicode[STIX]{x0394}T$ also results in increasing wall-normal gradients in the semi-local friction Reynolds number. Classical, compressible scaling laws of the mean velocity profile are unable to fully collapse real fluid effects in this flow. The proximity to the pseudotransitioning layer inhibits turbulent velocity fluctuations, while locally enhancing the temperature and density fluctuation intensities. Probability distribution analysis reveals that the sheet of fluid undergoing pseudophase change is characterized by a dramatic reduction in the kurtosis of density fluctuations, hence becoming thinner as 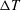 $\unicode[STIX]{x0394}T$ is increased. Instantaneous visualizations show dense fluid ejections from the pseudoliquid viscous sublayer, some reaching the channel core, causing positive values of density skewness in the respective buffer layer region (vice versa for the top wall) and an impoverishment of the turbulent flow structure population near pseudotransitioning conditions.
$\unicode[STIX]{x0394}T$ is increased. Instantaneous visualizations show dense fluid ejections from the pseudoliquid viscous sublayer, some reaching the channel core, causing positive values of density skewness in the respective buffer layer region (vice versa for the top wall) and an impoverishment of the turbulent flow structure population near pseudotransitioning conditions.
The turbulent Kármán vortex
- J. G. Chen, Y. Zhou, R. A. Antonia, T. M. Zhou
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 92-112
-
- Article
- Export citation
-
This work focuses on the temperature (passive scalar) and velocity characteristics within a turbulent Kármán vortex using a phase-averaging technique. The vortices are generated by a circular cylinder, and the three components of the fluctuating velocity and vorticity vectors,
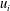 $u_{i}$ and
$u_{i}$ and 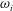 $\unicode[STIX]{x1D714}_{i}$ (
$\unicode[STIX]{x1D714}_{i}$ (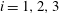 $i=1,2,3$), are simultaneously measured, along with the fluctuating temperature
$i=1,2,3$), are simultaneously measured, along with the fluctuating temperature 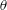 $\unicode[STIX]{x1D703}$ and the temperature gradient vector, at nominally the same spatial point in the plane of mean shear at
$\unicode[STIX]{x1D703}$ and the temperature gradient vector, at nominally the same spatial point in the plane of mean shear at 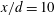 $x/d=10$, where
$x/d=10$, where  $x$ is the streamwise distance from the cylinder axis and
$x$ is the streamwise distance from the cylinder axis and 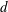 $d$ is the cylinder diameter. We believe this is the first time the properties of fluctuating velocity, temperature, vorticity and temperature gradient vectors have been explored simultaneously within the Kármán vortex in detail. The Reynolds number based on
$d$ is the cylinder diameter. We believe this is the first time the properties of fluctuating velocity, temperature, vorticity and temperature gradient vectors have been explored simultaneously within the Kármán vortex in detail. The Reynolds number based on 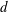 $d$ and the free-stream velocity is
$d$ and the free-stream velocity is 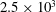 $2.5\times 10^{3}$. The phase-averaged distributions of
$2.5\times 10^{3}$. The phase-averaged distributions of 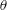 $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and 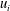 $u_{i}$ follow closely the Gaussian distribution for
$u_{i}$ follow closely the Gaussian distribution for 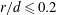 $r/d\leqslant 0.2$ (
$r/d\leqslant 0.2$ ( $r$ is the distance from the vortex centre), but not for
$r$ is the distance from the vortex centre), but not for 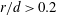 $r/d>0.2$. The collapse of the distributions of the mean-square streamwise derivative of the velocity fluctuations within the Kármán vortex implies that the velocity field within the vortex tends to be more locally isotropic than the flow field outside the vortex. A possible physical explanation is that the large and small scales of velocity and temperature fields are statistically independent of each other near the Kármán vortex centre, but interact vigorously outside the vortex, especially in the saddle region, due to the action of coherent strain rate.
$r/d>0.2$. The collapse of the distributions of the mean-square streamwise derivative of the velocity fluctuations within the Kármán vortex implies that the velocity field within the vortex tends to be more locally isotropic than the flow field outside the vortex. A possible physical explanation is that the large and small scales of velocity and temperature fields are statistically independent of each other near the Kármán vortex centre, but interact vigorously outside the vortex, especially in the saddle region, due to the action of coherent strain rate.
Adjoint-based shape optimization of the microchannels in an inkjet printhead
- Petr V. Kungurtsev, Matthew P. Juniper
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 113-138
-
- Article
- Export citation
-
In drop-on-demand inkjet printheads, ink is pumped steadily through small channels, each of which contains an actuator and a nozzle. When an actuator pulses, a droplet is forced through the nozzle, after which acoustic oscillations reverberate within the channel. Manufacturers would like to damp the residual reverberations, without increasing the pressure drop required to drive the steady flow. In this paper we use gradient-based optimization to show that this can be achieved by constricting the channel where the acoustic velocity is largest and enlarging the channel where the acoustic velocity is smallest. This increases the viscothermal dissipation of the acoustics without changing the viscous dissipation of the steady flow. We separate the compressible Navier–Stokes equations into equations for a steady flow with no oscillations and equations for oscillations with no steady flow. We define two objective functions: the viscous dissipation of the steady flow and the dissipation of the oscillations. We then derive the adjoints for both sets of equations, and obtain expressions for the gradient of each objective function with respect to boundary deformations in Hadamard form. We combine these with a gradient-based optimization algorithm, incorporating constraints such as the shapes of the actuator and nozzle. This algorithm quickly converges to a design that has the same viscous dissipation for the steady flow but a 50 % larger decay rate for the oscillating flow. We show that this design is nearly optimal. It is a shape that inkjet manufacturers, using physical insight and trial and error, have probably not yet considered. We also show how the adjoint fields provide physical insight into the mechanisms affecting each objective function. The main requirements of this method are that the steady flow Mach number and oscillating flow Mach number are small, and that dissipation is dominated by thermoviscous mechanisms. These requirements are often satisfied in microfluidics, so the method in this paper could be applied to many other applications.
Rheology of a suspension of conducting particles in a magnetic field
- V. Kumaran
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 139-185
-
- Article
- Export citation
-
When a suspension of conducting particles is sheared in a magnetic field, the fluid vorticity causes particle rotation. Eddy currents are induced in a conductor rotating in a magnetic field, resulting in magnetic moment, and a magnetic torque due to the external field. In the absence of inertia, the angular velocity of a particle is determined from the condition that the sum of the hydrodynamic and magnetic torques is zero. When the particle angular velocity is different from the fluid rotation rate, the torque exerted by the particles on the fluid results in an antisymmetric particle stress. The stress is of the form
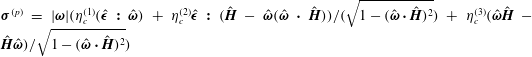 $\unicode[STIX]{x1D748}^{(p)}=|\unicode[STIX]{x1D74E}|(\unicode[STIX]{x1D702}_{c}^{(1)}(\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }\hat{\unicode[STIX]{x1D74E}})+\unicode[STIX]{x1D702}_{c}^{(2)}\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }(\hat{\boldsymbol{H}}-\hat{\unicode[STIX]{x1D74E}}(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}))/(\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})+\unicode[STIX]{x1D702}_{c}^{(3)}(\hat{\unicode[STIX]{x1D74E}}\hat{\boldsymbol{H}}-\hat{\boldsymbol{H}}\hat{\unicode[STIX]{x1D74E}})/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$, where
$\unicode[STIX]{x1D748}^{(p)}=|\unicode[STIX]{x1D74E}|(\unicode[STIX]{x1D702}_{c}^{(1)}(\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }\hat{\unicode[STIX]{x1D74E}})+\unicode[STIX]{x1D702}_{c}^{(2)}\hat{\unicode[STIX]{x1D750}}\boldsymbol{ : }(\hat{\boldsymbol{H}}-\hat{\unicode[STIX]{x1D74E}}(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}))/(\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})+\unicode[STIX]{x1D702}_{c}^{(3)}(\hat{\unicode[STIX]{x1D74E}}\hat{\boldsymbol{H}}-\hat{\boldsymbol{H}}\hat{\unicode[STIX]{x1D74E}})/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$, where 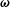 $\unicode[STIX]{x1D74E}$ is the fluid vorticity at the centre of the particle,
$\unicode[STIX]{x1D74E}$ is the fluid vorticity at the centre of the particle, 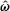 $\hat{\unicode[STIX]{x1D74E}}$ and
$\hat{\unicode[STIX]{x1D74E}}$ and 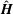 $\hat{\boldsymbol{H}}$ are the unit vectors in the direction of the fluid vorticity and the magnetic field,
$\hat{\boldsymbol{H}}$ are the unit vectors in the direction of the fluid vorticity and the magnetic field, 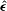 $\hat{\unicode[STIX]{x1D750}}$ is the third order Levi-Civita antisymmetric tensor and
$\hat{\unicode[STIX]{x1D750}}$ is the third order Levi-Civita antisymmetric tensor and 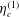 $\unicode[STIX]{x1D702}_{c}^{(1)}$,
$\unicode[STIX]{x1D702}_{c}^{(1)}$, 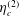 $\unicode[STIX]{x1D702}_{c}^{(2)}$ and
$\unicode[STIX]{x1D702}_{c}^{(2)}$ and 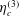 $\unicode[STIX]{x1D702}_{c}^{(3)}$ are called the first, second and third couple stress coefficients. The stress proportional to
$\unicode[STIX]{x1D702}_{c}^{(3)}$ are called the first, second and third couple stress coefficients. The stress proportional to 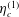 $\unicode[STIX]{x1D702}_{c}^{(1)}$ is in the plane perpendicular to
$\unicode[STIX]{x1D702}_{c}^{(1)}$ is in the plane perpendicular to 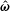 $\hat{\unicode[STIX]{x1D74E}}$, that proportional to
$\hat{\unicode[STIX]{x1D74E}}$, that proportional to 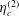 $\unicode[STIX]{x1D702}_{c}^{(2)}$ is in the plane perpendicular to the unit normal to
$\unicode[STIX]{x1D702}_{c}^{(2)}$ is in the plane perpendicular to the unit normal to 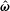 $\hat{\unicode[STIX]{x1D74E}}$ in the
$\hat{\unicode[STIX]{x1D74E}}$ in the 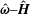 $\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane, and that proportional to
$\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane, and that proportional to 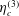 $\unicode[STIX]{x1D702}_{c}^{(3)}$ is in the
$\unicode[STIX]{x1D702}_{c}^{(3)}$ is in the 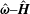 $\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane. A relation
$\hat{\unicode[STIX]{x1D74E}}{-}\hat{\boldsymbol{H}}$ plane. A relation 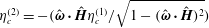 $\unicode[STIX]{x1D702}_{c}^{(2)}=-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\unicode[STIX]{x1D702}_{c}^{(1)}/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$ results from the condition that the component of the eddy current torque along the magnetic field is zero. The couple stress coefficients are obtained for two geometries, a uniform spherical particle of radius
$\unicode[STIX]{x1D702}_{c}^{(2)}=-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\unicode[STIX]{x1D702}_{c}^{(1)}/\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}})$ results from the condition that the component of the eddy current torque along the magnetic field is zero. The couple stress coefficients are obtained for two geometries, a uniform spherical particle of radius 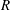 $R$ and a thin spherical shell of radius
$R$ and a thin spherical shell of radius 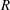 $R$ and thickness
$R$ and thickness 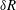 $\unicode[STIX]{x1D6FF}R$ with
$\unicode[STIX]{x1D6FF}R$ with 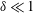 $\unicode[STIX]{x1D6FF}\ll 1$, in the dilute (non-interacting) limit in the absence of fluid inertia. These couple stress coefficients are functions of two dimensionless parameters,
$\unicode[STIX]{x1D6FF}\ll 1$, in the dilute (non-interacting) limit in the absence of fluid inertia. These couple stress coefficients are functions of two dimensionless parameters, 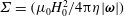 $\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D707}_{0}H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}|\unicode[STIX]{x1D74E}|)$, the ratio of the characteristic magnetic and hydrodynamic torques, and
$\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D707}_{0}H_{0}^{2}/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}|\unicode[STIX]{x1D74E}|)$, the ratio of the characteristic magnetic and hydrodynamic torques, and 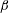 $\unicode[STIX]{x1D6FD}$, the product of the vorticity and current relaxation time. Here
$\unicode[STIX]{x1D6FD}$, the product of the vorticity and current relaxation time. Here 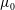 $\unicode[STIX]{x1D707}_{0}$ is the magnetic permeability,
$\unicode[STIX]{x1D707}_{0}$ is the magnetic permeability, 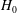 $H_{0}$ is the magnetic field and
$H_{0}$ is the magnetic field and 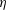 $\unicode[STIX]{x1D702}$ is the fluid viscosity. The parameter
$\unicode[STIX]{x1D702}$ is the fluid viscosity. The parameter 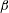 $\unicode[STIX]{x1D6FD}$ has the form
$\unicode[STIX]{x1D6FD}$ has the form 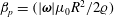 $\unicode[STIX]{x1D6FD}_{p}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}/2\unicode[STIX]{x1D71A})$ for a uniform particle and
$\unicode[STIX]{x1D6FD}_{p}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}/2\unicode[STIX]{x1D71A})$ for a uniform particle and 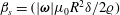 $\unicode[STIX]{x1D6FD}_{s}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}\unicode[STIX]{x1D6FF}/2\unicode[STIX]{x1D71A})$ for a thin shell, where
$\unicode[STIX]{x1D6FD}_{s}=(|\unicode[STIX]{x1D74E}|\unicode[STIX]{x1D707}_{0}R^{2}\unicode[STIX]{x1D6FF}/2\unicode[STIX]{x1D71A})$ for a thin shell, where 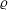 $\unicode[STIX]{x1D71A}$ is the electrical resistivity. Scaled couple stress coefficients are defined,
$\unicode[STIX]{x1D71A}$ is the electrical resistivity. Scaled couple stress coefficients are defined, 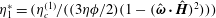 $\unicode[STIX]{x1D702}_{1}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(1)}/((3\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}/2)(1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2})))$ and
$\unicode[STIX]{x1D702}_{1}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(1)}/((3\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}/2)(1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2})))$ and 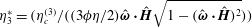 $\unicode[STIX]{x1D702}_{3}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(3)}/((3\unicode[STIX]{x1D719}\unicode[STIX]{x1D702}/2)\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}}))$, which are independent of the fluid viscosity and the particle volume fraction, and which do not depend on
$\unicode[STIX]{x1D702}_{3}^{\ast }=(\unicode[STIX]{x1D702}_{c}^{(3)}/((3\unicode[STIX]{x1D719}\unicode[STIX]{x1D702}/2)\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}\sqrt{1-(\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}})^{2}}))$, which are independent of the fluid viscosity and the particle volume fraction, and which do not depend on 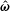 $\hat{\unicode[STIX]{x1D74E}}$ and
$\hat{\unicode[STIX]{x1D74E}}$ and 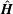 $\hat{\boldsymbol{H}}$ in the limits
$\hat{\boldsymbol{H}}$ in the limits 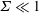 $\unicode[STIX]{x1D6F4}\ll 1$ and
$\unicode[STIX]{x1D6F4}\ll 1$ and 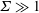 $\unicode[STIX]{x1D6F4}\gg 1$. Here,
$\unicode[STIX]{x1D6F4}\gg 1$. Here, 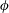 $\unicode[STIX]{x1D719}$ is the volume fraction of the particles. Asymptotic analysis is used to determine the couple stress coefficients in the limits
$\unicode[STIX]{x1D719}$ is the volume fraction of the particles. Asymptotic analysis is used to determine the couple stress coefficients in the limits 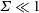 $\unicode[STIX]{x1D6F4}\ll 1$ and
$\unicode[STIX]{x1D6F4}\ll 1$ and 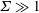 $\unicode[STIX]{x1D6F4}\gg 1$, and a numerical solution procedure is formulated for
$\unicode[STIX]{x1D6F4}\gg 1$, and a numerical solution procedure is formulated for 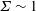 $\unicode[STIX]{x1D6F4}\sim 1$. For
$\unicode[STIX]{x1D6F4}\sim 1$. For 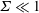 $\unicode[STIX]{x1D6F4}\ll 1$, the particle angular velocity is aligned close to the fluid vorticity, and the scaled couple stress coefficients are
$\unicode[STIX]{x1D6F4}\ll 1$, the particle angular velocity is aligned close to the fluid vorticity, and the scaled couple stress coefficients are 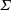 $\unicode[STIX]{x1D6F4}$ times a function of
$\unicode[STIX]{x1D6F4}$ times a function of 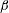 $\unicode[STIX]{x1D6FD}$. For
$\unicode[STIX]{x1D6FD}$. For 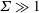 $\unicode[STIX]{x1D6F4}\gg 1$, the particle angular velocity is aligned close to the magnetic field,
$\unicode[STIX]{x1D6F4}\gg 1$, the particle angular velocity is aligned close to the magnetic field, 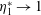 $\unicode[STIX]{x1D702}_{1}^{\ast }\rightarrow 1$ and
$\unicode[STIX]{x1D702}_{1}^{\ast }\rightarrow 1$ and 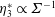 $\unicode[STIX]{x1D702}_{3}^{\ast }\propto \unicode[STIX]{x1D6F4}^{-1}$. When the magnetic field is perpendicular to the fluid vorticity,
$\unicode[STIX]{x1D702}_{3}^{\ast }\propto \unicode[STIX]{x1D6F4}^{-1}$. When the magnetic field is perpendicular to the fluid vorticity, 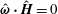 $\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}=0$, the particle angular velocity is aligned along the vorticity, and only the first couple stress coefficient is non-zero. For high
$\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}=0$, the particle angular velocity is aligned along the vorticity, and only the first couple stress coefficient is non-zero. For high 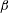 $\unicode[STIX]{x1D6FD}$, there are multiple solutions for the couple stress coefficient. Multiple steady states are also observed for a near perpendicular magnetic field,
$\unicode[STIX]{x1D6FD}$, there are multiple solutions for the couple stress coefficient. Multiple steady states are also observed for a near perpendicular magnetic field, 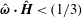 $\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}<(1/3)$, for a reason different from that for a perpendicular magnetic field. Asymptotic analysis is used to explain the existence of multiple steady states in both cases.
$\hat{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\hat{\boldsymbol{H}}<(1/3)$, for a reason different from that for a perpendicular magnetic field. Asymptotic analysis is used to explain the existence of multiple steady states in both cases.
On the universal trends in the noise reduction due to wavy leading edges in aerofoil–vortex interaction
- Jacob M. Turner, Jae Wook Kim
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 186-211
-
- Article
- Export citation
-
Existing studies suggest that wavy leading edges (WLEs) offer substantial reduction of broadband noise generated by an aerofoil undergoing upstream vortical disturbances. In this context, there are two universal trends in the frequency spectra of the noise reduction which have been observed and reported to date: (i) no significant reduction at low frequencies followed by (ii) a rapid growth of the noise reduction that persists in the medium-to-high frequency range. These trends are known to be insensitive to the aerofoil type and flow condition used. This paper aims to provide comprehensive understandings as to how these universal trends are formed and what the major drivers are. The current work is based on very-high-resolution numerical simulations of a semi-infinite flat-plate aerofoil impinged by a prescribed divergence-free vortex in an inviscid base flow at zero incidence angle, continued from recent work by the authors (Turner & Kim, J. Fluid Mech., vol. 811, 2017, pp. 582–611). One of the most significant findings in the current work is that the noise source distribution on the aerofoil surface becomes entirely two-dimensional (highly non-uniform in the spanwise direction as well as streamwise) at high frequencies when the WLE is involved. Also, the sources downstream of the LE make crucial contributions to creating the universal trends across all frequencies. These findings contradict the conventional LE-focused one-dimensional source analysis that has widely been accepted for all frequencies. The current study suggests that the universal trends in the noise-reduction spectra can be properly understood by taking the downstream source contributions into account, in terms of both magnitude and phase variations. After including the downstream sources, it is shown in this paper that the first universal trend is due to the conservation of total (surface integrated) source energy at low frequencies. The surface-integrated source magnitude that decreases faster with the WLE correlates very well with the noise-reduction spectrum at medium frequencies. In the meantime, the high-frequency noise reduction is driven almost entirely by destructive phase interference that increases rapidly and consistently with frequency, explaining the second universal trend.
Bouncing phase variations in pilot-wave hydrodynamics and the stability of droplet pairs
- Miles M. P. Couchman, Sam E. Turton, John W. M. Bush
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 212-243
-
- Article
- Export citation
-
We present the results of an integrated experimental and theoretical investigation of the vertical motion of millimetric droplets bouncing on a vibrating fluid bath. We characterize experimentally the dependence of the phase of impact and contact force between a drop and the bath on the drop’s size and the bath’s vibrational acceleration. This characterization guides the development of a new theoretical model for the coupling between a drop’s vertical and horizontal motion. Our model allows us to relax the assumption of constant impact phase made in models based on the time-averaged trajectory equation of Moláček and Bush (J. Fluid Mech., vol. 727, 2013b, pp. 612–647) and obtain a robust horizontal trajectory equation for a bouncing drop that accounts for modulations in the drop’s vertical dynamics as may arise when it interacts with boundaries or other drops. We demonstrate that such modulations have a critical influence on the stability and dynamics of interacting droplet pairs. As the bath’s vibrational acceleration is increased progressively, initially stationary pairs destabilize into a variety of dynamical states including rectilinear oscillations, circular orbits and side-by-side promenading motion. The theoretical predictions of our variable-impact-phase model rationalize our observations and underscore the critical importance of accounting for variability in the vertical motion when modelling droplet–droplet interactions.
Multiscale preferential sweeping of particles settling in turbulence
- Josin Tom, Andrew D. Bragg
-
- Published online by Cambridge University Press:
- 20 May 2019, pp. 244-270
-
- Article
- Export citation
-
In a seminal article, Maxey (J. Fluid Mech., vol. 174, 1987, pp. 441–465) presented a theoretical analysis showing that enhanced particle settling speeds in turbulence occur through the preferential sweeping mechanism, which depends on the preferential sampling of the fluid velocity gradient field by the inertial particles. However, recent direct numerical simulation (DNS) results in Ireland et al. (J. Fluid Mech., vol. 796, 2016b, pp. 659–711) show that even in a portion of the parameter space where this preferential sampling is absent, the particles nevertheless exhibit enhanced settling velocities. Further, there are several outstanding questions concerning the role of different turbulent flow scales on the enhanced settling, and the role of the Taylor Reynolds number
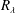 $R_{\unicode[STIX]{x1D706}}$. The analysis of Maxey does not explain these issues, partly since it was restricted to particle Stokes numbers
$R_{\unicode[STIX]{x1D706}}$. The analysis of Maxey does not explain these issues, partly since it was restricted to particle Stokes numbers 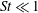 $St\ll 1$. To address these issues, we have developed a new theoretical result, valid for arbitrary
$St\ll 1$. To address these issues, we have developed a new theoretical result, valid for arbitrary 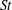 $St$, that reveals the multiscale nature of the mechanism generating the enhanced settling speeds. In particular, it shows how the range of scales at which the preferential sweeping mechanism operates depends on
$St$, that reveals the multiscale nature of the mechanism generating the enhanced settling speeds. In particular, it shows how the range of scales at which the preferential sweeping mechanism operates depends on 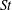 $St$. This analysis is complemented by results from DNS where we examine the role of different flow scales on the particle settling speeds by coarse graining the underlying flow. The results show how the flow scales that contribute to the enhanced settling depend on
$St$. This analysis is complemented by results from DNS where we examine the role of different flow scales on the particle settling speeds by coarse graining the underlying flow. The results show how the flow scales that contribute to the enhanced settling depend on 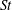 $St$, and that contrary to previous claims, there can be no single turbulent velocity scale that characterizes the enhanced settling speed. The results explain the dependence of the particle settling speeds on
$St$, and that contrary to previous claims, there can be no single turbulent velocity scale that characterizes the enhanced settling speed. The results explain the dependence of the particle settling speeds on 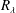 $R_{\unicode[STIX]{x1D706}}$, and show how the saturation of this dependence at sufficiently large
$R_{\unicode[STIX]{x1D706}}$, and show how the saturation of this dependence at sufficiently large 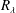 $R_{\unicode[STIX]{x1D706}}$ depends upon
$R_{\unicode[STIX]{x1D706}}$ depends upon 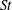 $St$. The results also show that as the Stokes settling velocity of the particles is increased, the flow scales of the turbulence responsible for enhancing the particle settling speed become larger. Finally, we explored the multiscale nature of the preferential sweeping mechanism by considering how particles preferentially sample the fluid velocity gradients coarse grained at various scales. The results show that while rapidly settling particles do not preferentially sample the fluid velocity gradients, they do preferentially sample the fluid velocity gradients coarse grained at scales outside of the dissipation range. This explains the findings of Ireland et al., and further illustrates the truly multiscale nature of the mechanism generating enhanced particle settling speeds in turbulence.
$St$. The results also show that as the Stokes settling velocity of the particles is increased, the flow scales of the turbulence responsible for enhancing the particle settling speed become larger. Finally, we explored the multiscale nature of the preferential sweeping mechanism by considering how particles preferentially sample the fluid velocity gradients coarse grained at various scales. The results show that while rapidly settling particles do not preferentially sample the fluid velocity gradients, they do preferentially sample the fluid velocity gradients coarse grained at scales outside of the dissipation range. This explains the findings of Ireland et al., and further illustrates the truly multiscale nature of the mechanism generating enhanced particle settling speeds in turbulence.
A second-order integral model for buoyant jets with background homogeneous and isotropic turbulence
- Adrian C. H. Lai, Adrian Wing-Keung Law, E. Eric Adams
-
- Published online by Cambridge University Press:
- 20 May 2019, pp. 271-304
-
- Article
- Export citation
-
Buoyant jets or forced plumes are discharged into a turbulent ambient in many natural and engineering applications. The background turbulence generally affects the mixing characteristics of the buoyant jet, and the extent of the influence depends on the characteristics of both the jet discharge and ambient. Previous studies focused on the experimental investigation of the problem (for pure jets or plumes), but the findings were difficult to generalize because suitable scales for normalization of results were not known. A model to predict the buoyant jet mixing in the presence of background turbulence, which is essential in many applications, is also hitherto not available even for a background of homogeneous and isotropic turbulence (HIT). We carried out experimental and theoretical investigations of a buoyant jet discharging into background HIT. Buoyant jets were designed to be in the range of
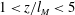 $1<z/l_{M}<5$, where
$1<z/l_{M}<5$, where 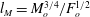 $l_{M}=M_{o}^{3/4}/F_{o}^{1/2}$ is the momentum length scale, with
$l_{M}=M_{o}^{3/4}/F_{o}^{1/2}$ is the momentum length scale, with 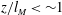 $z/l_{M}<\sim 1$ and
$z/l_{M}<\sim 1$ and 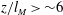 $z/l_{M}>\sim 6$ representing the asymptotic cases of pure jets and plumes, respectively. The background turbulence was generated using a random synthetic jet array, which produced a region of approximately isotropic and homogeneous field of turbulence to be used in the experiments. The velocity scale of the jet was initially much higher, and the length scale smaller, than that of the background turbulence, which is typical in most applications. Comprehensive measurements of the buoyant jet mixing characteristics were performed up to the distance where jet breakup occurred. Based on the experimental findings, a critical length scale
$z/l_{M}>\sim 6$ representing the asymptotic cases of pure jets and plumes, respectively. The background turbulence was generated using a random synthetic jet array, which produced a region of approximately isotropic and homogeneous field of turbulence to be used in the experiments. The velocity scale of the jet was initially much higher, and the length scale smaller, than that of the background turbulence, which is typical in most applications. Comprehensive measurements of the buoyant jet mixing characteristics were performed up to the distance where jet breakup occurred. Based on the experimental findings, a critical length scale 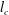 $l_{c}$ was identified to be an appropriate normalizing scale. The momentum flux of the buoyant jet in background HIT was found to be conserved only if the second-order turbulence statistics of the jet were accounted for. A general integral jet model including the background HIT was then proposed based on the conservation of mass (using the entrainment assumption), total momentum and buoyancy fluxes, and the decay function of the jet mean momentum downstream. Predictions of jet mixing characteristics from the new model were compared with experimental observation, and found to be generally in agreement with each other.
$l_{c}$ was identified to be an appropriate normalizing scale. The momentum flux of the buoyant jet in background HIT was found to be conserved only if the second-order turbulence statistics of the jet were accounted for. A general integral jet model including the background HIT was then proposed based on the conservation of mass (using the entrainment assumption), total momentum and buoyancy fluxes, and the decay function of the jet mean momentum downstream. Predictions of jet mixing characteristics from the new model were compared with experimental observation, and found to be generally in agreement with each other.
The evolution of the initial flow structures of a highly under-expanded circular jet
- Huan-Hao Zhang, Nadine Aubry, Zhi-Hua Chen, Wei-Tao Wu, Sha Sha
-
- Published online by Cambridge University Press:
- 20 May 2019, pp. 305-331
-
- Article
- Export citation
-
The three-dimensional flow characteristics of the compressible vortex ring generated by under-expanded circular jets with two typical pressure ratios, i.e.
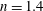 $n=1.4$ (moderate) and 4.0 (high), are investigated numerically with the use of large-eddy simulations. Our results illustrate that these two pressure ratios correspond to different shock structures (shock cell and Mach disc, respectively) within the jet. These two typical types of flow structures and characteristics are discussed and validated with experiments, and the different generation mechanisms of the secondary vortex rings are compared. Moreover, detailed information about the evolution of the secondary vortex ring, primary vortex ring and turbulence transition features, including the radial and azimuthal modes, is investigated. The geometric features and mixing effects of the jets are also explored.
$n=1.4$ (moderate) and 4.0 (high), are investigated numerically with the use of large-eddy simulations. Our results illustrate that these two pressure ratios correspond to different shock structures (shock cell and Mach disc, respectively) within the jet. These two typical types of flow structures and characteristics are discussed and validated with experiments, and the different generation mechanisms of the secondary vortex rings are compared. Moreover, detailed information about the evolution of the secondary vortex ring, primary vortex ring and turbulence transition features, including the radial and azimuthal modes, is investigated. The geometric features and mixing effects of the jets are also explored.
Transition to convection in single bubble diffusive growth
- Álvaro Moreno Soto, Oscar R. Enríquez, Andrea Prosperetti, Detlef Lohse, Devaraj van der Meer
-
- Published online by Cambridge University Press:
- 20 May 2019, pp. 332-349
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
We investigate the growth of gas bubbles in a water solution at rest with a supersaturation level that is generally associated with diffusive mass transfer. For
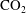 $\text{CO}_{2}$ bubbles, it has been previously observed that, after some time of growing in a diffusive regime, a density-driven convective flow enhances the mass transfer rate into the bubble. This is due to the lower density of the gas-depleted liquid which surrounds the bubble. In this work, we report on experiments with different supersaturation values, measuring the time
$\text{CO}_{2}$ bubbles, it has been previously observed that, after some time of growing in a diffusive regime, a density-driven convective flow enhances the mass transfer rate into the bubble. This is due to the lower density of the gas-depleted liquid which surrounds the bubble. In this work, we report on experiments with different supersaturation values, measuring the time 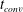 $t_{conv}$ it takes for convection to dominate over the diffusion-driven growth. We demonstrate that by considering buoyancy and drag forces on the depleted liquid around the bubble, we can satisfactorily predict the transition time. In fact, our analysis shows that this onset does not only depend on the supersaturation, but also on the absolute pressure, which we corroborate in experiments. Subsequently, we study how the depletion caused by the growth of successive single bubbles influences the onset of convection. Finally, we study the convection onset around diffusively growing nitrogen
$t_{conv}$ it takes for convection to dominate over the diffusion-driven growth. We demonstrate that by considering buoyancy and drag forces on the depleted liquid around the bubble, we can satisfactorily predict the transition time. In fact, our analysis shows that this onset does not only depend on the supersaturation, but also on the absolute pressure, which we corroborate in experiments. Subsequently, we study how the depletion caused by the growth of successive single bubbles influences the onset of convection. Finally, we study the convection onset around diffusively growing nitrogen 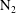 $\text{N}_{2}$ bubbles. As
$\text{N}_{2}$ bubbles. As 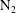 $\text{N}_{2}$ is much less soluble in water, the growth takes much longer. However, after waiting long enough and consistent with our theory, convection still occurs as for any gas–liquid combination, provided that the density of the solution sufficiently changes with the gas concentration.
$\text{N}_{2}$ is much less soluble in water, the growth takes much longer. However, after waiting long enough and consistent with our theory, convection still occurs as for any gas–liquid combination, provided that the density of the solution sufficiently changes with the gas concentration.
Scattering of gravity waves by a periodically structured ridge of finite extent
- Agnès Maurel, Kim Pham, Jean-Jacques Marigo
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 350-376
-
- Article
- Export citation
-
We study the propagation of water waves over a ridge structured at the subwavelength scale using homogenization techniques able to account for its finite extent. The calculations are conducted in the time domain considering the full three-dimensional problem to capture the effects of the evanescent field in the water channel over the structured ridge and at its boundaries. This provides an effective two-dimensional wave equation which is a classical result but also non-intuitive transmission conditions between the region of the ridge and the surrounding regions of constant immersion depth. Numerical results provide evidence that the scattering properties of a structured ridge can be strongly influenced by the evanescent fields, a fact which is accurately captured by the homogenized model.
Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows
- R. Baidya, W. J. Baars, S. Zimmerman, M. Samie, R. J. Hearst, E. Dogan, L. Mascotelli, X. Zheng, G. Bellani, A. Talamelli, B. Ganapathisubramani, N. Hutchins, I. Marusic, J. Klewicki, J. P. Monty
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 377-400
-
- Article
- Export citation
-
Streamwise velocity and wall-shear stress are acquired simultaneously with a hot-wire and an array of azimuthal/spanwise-spaced skin friction sensors in large-scale pipe and boundary layer flow facilities at high Reynolds numbers. These allow for a correlation analysis on a per-scale basis between the velocity and reference skin friction signals to reveal which velocity-based turbulent motions are stochastically coherent with turbulent skin friction. In the logarithmic region, the wall-attached structures in both the pipe and boundary layers show evidence of self-similarity, and the range of scales over which the self-similarity is observed decreases with an increasing azimuthal/spanwise offset between the velocity and the reference skin friction signals. The present empirical observations support the existence of a self-similar range of wall-attached turbulence, which in turn are used to extend the model of Baars et al. (J. Fluid Mech., vol. 823, p. R2) to include the azimuthal/spanwise trends. Furthermore, the region where the self-similarity is observed correspond with the wall height where the mean momentum equation formally admits a self-similar invariant form, and simultaneously where the mean and variance profiles of the streamwise velocity exhibit logarithmic dependence. The experimental observations suggest that the self-similar wall-attached structures follow an aspect ratio of
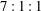 $7:1:1$ in the streamwise, spanwise and wall-normal directions, respectively.
$7:1:1$ in the streamwise, spanwise and wall-normal directions, respectively.
Horizontal diffusive motion of columnar vortices in rotating Rayleigh–Bénard convection
- D. Noto, Y. Tasaka, T. Yanagisawa, Y. Murai
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 401-426
-
- Article
- Export citation
-
In laboratory experiments, horizontal translational motion of columnar vortices formed in rotating Rayleigh–Bénard convection was investigated. Two types of measurements, vertical velocity fields and horizontal temperature fields, were conducted with water as the test fluid. Using particle image velocimetry, the vertical velocity fields determined the parameter range at which the quasi-two-dimensional columnar vortices emerged. Locally, the duration characteristics of the columns, evaluated with their vertical coherence, indicate the minimum time scale of translational motion of the vortices in the horizontal plane. Vortex tracking of the horizontal temperature fields over long observation periods (
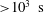 ${>}10^{3}~\text{s}$) was conducted using encapsulated thermochromic liquid crystal visualization. Two cylindrical vessels with different radii showed the emergence of the centrifugal effect in
${>}10^{3}~\text{s}$) was conducted using encapsulated thermochromic liquid crystal visualization. Two cylindrical vessels with different radii showed the emergence of the centrifugal effect in 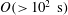 $O({>}10^{2}~\text{s})$ despite the small Froude number (
$O({>}10^{2}~\text{s})$ despite the small Froude number (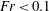 $Fr<0.1$). Further, in the horizontal plane the columnar vortices behaved in a random-walk-like diffusive motion. The statistically calculated mean-squared displacements indicated anomalous diffusive motion of the columns; displacement increasing with time as
$Fr<0.1$). Further, in the horizontal plane the columnar vortices behaved in a random-walk-like diffusive motion. The statistically calculated mean-squared displacements indicated anomalous diffusive motion of the columns; displacement increasing with time as 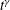 $t^{\unicode[STIX]{x1D6FE}}$ with
$t^{\unicode[STIX]{x1D6FE}}$ with 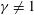 $\unicode[STIX]{x1D6FE}\neq 1$. We discuss the causes of this anomaly in both the instantaneous and long-term statistical data gathered from experimental observations over different time scales. The enclosure effect from the repulsion of up-welling and down-welling vortices ensures that vortices diffuse only little, resulting in a sub-diffusive (decelerated) motion
$\unicode[STIX]{x1D6FE}\neq 1$. We discuss the causes of this anomaly in both the instantaneous and long-term statistical data gathered from experimental observations over different time scales. The enclosure effect from the repulsion of up-welling and down-welling vortices ensures that vortices diffuse only little, resulting in a sub-diffusive (decelerated) motion 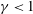 $\unicode[STIX]{x1D6FE}<1$ in
$\unicode[STIX]{x1D6FE}<1$ in 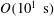 $O(10^{1}~\text{s})$. With this weak centrifugal contribution, the translational motion of the columns slowly accelerates in the radial direction and thereby yields a super-diffusive (accelerated) motion
$O(10^{1}~\text{s})$. With this weak centrifugal contribution, the translational motion of the columns slowly accelerates in the radial direction and thereby yields a super-diffusive (accelerated) motion 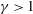 $\unicode[STIX]{x1D6FE}>1$ in
$\unicode[STIX]{x1D6FE}>1$ in 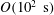 $O(10^{2}~\text{s})$.
$O(10^{2}~\text{s})$.
Control of crossflow-vortex-induced transition by unsteady control vortices
- Zhengfei Guo, Markus J. Kloker
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 427-449
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
The fundamental mechanisms of a hitherto unstudied approach to control the crossflow-induced transition in a three-dimensional boundary layer employing unsteady control vortices are investigated by means of direct numerical simulations. Using a spanwise row of blowing/suction or volume-force actuators, subcritical travelling crossflow vortex modes are excited to impose a stabilizing (upstream) flow deformation (UFD). Volume forcing mimics the effects of alternating current plasma actuators driven by a low-frequency sinusoidal signal. In this case the axes of the actuators are aligned with the wave crests of the desired travelling mode to maximize receptivity and abate the influence of other unwanted, misaligned modes. The resulting travelling crossflow vortices generate a beneficial mean-flow distortion reducing the amplification rate of naturally occurring steady or unsteady crossflow modes without invoking significant secondary instabilities. It is found that the stabilizing effect achieved by travelling control modes is somewhat weaker than that achieved by the steady modes in the classical UFD method. However, the energy requirements for unsteady-UFD plasma actuators would be significantly lower than for steady UFD because the approach makes full use of the inherent unsteadiness of the plasma-induced volume force with alternating-current-driven actuators. Also, the input control amplitude can be lower since unsteady crossflow vortex modes grow stronger in the flow.