1. Introduction
Ice flows towards the calving front of an ice shelf, where fracture processes cause ice to break off (Reference Cuffey and PatersonCuffey and Paterson, 2010). A long-standing problem in glaciology is to quantify the rate of calving, as this ultimately determines ice-shelf geometry. This problem has a wider significance because ice-shelf geometry affects forces acting across the grounding line. Some very strong (r 2 > 0.9) correlations (Reference AlleyAlley and others, 2008; Reference Cuffey and PatersonCuffey and Paterson, 2010) of calving rate with glaciological parameters have been obtained using data from a set of ice shelves with a wide range of characteristics. Their study, restricted to ice shelves where the position of the calving front is known to be stationary, took calving-front velocity as a surrogate for calving rate. The correlations show that frontal centre-line velocity, u f, varies almost linearly with the product of frontal centreline thickness, H f, width, W, and centre-line strain rate perpendicular to the calving front, ef = ∂u f/∂x, where x is in the direction of flow, i.e. u f ∞. WH f e f. The situation is potentially rather complex, since empirical efforts to relate calving rate to glaciological parameters face the problem that similar groups of parameters might define the rate of supply of ice to the calving front by viscous flow processes as well as the rate of calving of ice by fracture processes. Consequently, an empirical correlation of calving rate with glaciological parameters may actually inform about factors that control the rate of viscous supply of ice to the calving front. In particular, the correlations of Reference AlleyAlley and others (2008) do not contain oceanographic factors, suggesting that the relationships describe the process of viscous flow to the calving front and are not predictive of calving rate. Put against this is the fact that existent glaciological theory for confined shelf flow predicts an approximately fourth-power dependence of velocity on the shelf width (e.g. Reference Van der VeenVan der Veen, 1999) rather than the empirical linear dependence.
This paper presents a new analytical theory for ice velocity at the calving front, specifically relating it through a simple formula to ice thickness, strain rate and ice-shelf width. It is a boundary layer theory, making a specific statement about flow occurring near a boundary (in this case the calving front), where stress boundary conditions are imposed. In many cases, and it is true here, it is possible to produce a theory because the boundary conditions allow simplifications to be made. The present theory assumes a Glen rheology, is verified by numerical modelling of ice-shelf flows, and is shown to make predictions very similar to the observations of of Reference AlleyAlley and others (2008). This is argued to be a strong indication that their correlation of calving-front velocity, described above, arises from viscous flow processes.
The theory and associated calculations fall into three parts: two-dimensional (2-D) flow modelling; one-dimensional (1-D) transversely integrated modelling; and use of the 1-D theory to develop a boundary layer theory. While ice- shelf flows are 2-D, much progress in understanding them has been made by integrating across the flow, and solving or analysing the resulting 1-D equations (e.g. Reference BuddBudd, 1966; Reference Nick, Vieli, Howat and JoughinNick and others, 2009; Reference Van der Veen, Plummer and StearnsVan der Veen and others, 2011). This approximation rests on the assumption that the plan aspect (width to length) ratio of the ice shelf is small, but what is sufficiently ‘small’ has not yet been quantified. For the calving-front flow processes considered in this paper, it turns out that numerical modelling of ice shelves with plan aspect ratios of ~1 still results in quantitative features predicted by the 1-D transversely integrated theory. This means that a boundary layer theory, which assumes the upstream boundary to be distant, is a useful description of many ice shelves. In this boundary layer description, a further approximation about the magnitude of mass exchange at the calving front can be made. This allows us to derive a formula relating calving-front velocity to ice thickness, shelf width and strain rate. This boundary layer description is analogous to a theory for grounding line dynamics of basally resisted ice streams (Reference SchoofSchoof, 2007a, Reference Schoofb) which predicts velocity and flux at the grounding line and is indeed derived in a similarfashion. This paper considers horizontal shearing, while Schoof’s grounding line theory considers vertical shearing.
The most compelling result of the theory presented here is its ability to explain the empirical relationships of Reference AlleyAlley and others (2008). It is also a verification of our understanding of ice flow in a more general way, as it considers a population of ice shelves rather than modelling an individual ice shelf. The paper presents an explanation as to why the theory works in view of the non-inclusion of several apparently significant parameters, such as ice-rate factor, spatial variation in ice rheology and shelf aspect ratio. A further point of interest is that, since the theory is developed in a way that is analogous to grounding line stability analysis, its success provides significant underpinning to theories of marine ice-sheet instability. Moreover, the theory is also applicable to laterally resisted grounded ice streams (those with zero basal friction), and suggests the same basic stability properties as those derived for basally resisted streams by Reference SchoofSchoof (2007a, Reference Schoofb), which is itself qualitatively consistent with earlier ideas about marine ice-sheet instability (Reference HughesHughes, 1973; Reference WeertmanWeertman, 1974; Reference Thomas and BentleyThomas and Bentley, 1978).
The paper is organized as follows. Firstly, the mathematical theory is derived. It is a boundary layer theory describing flow at the downstream end of the shelf, assuming that the upstream end is sufficiently distant that details of the flow other than the input flux are not important. This assumption is then examined with numerical modelling, and shown to be a very useful assumption in practice. Thirdly, the results are used to investigate the dataset of Reference AlleyAlley and others (2008), using the hypotheses generated by the mathematical analysis.
2. Mathematical Basis
2.1. Governing equations
Here we present the field equations and boundary conditions for 2-D vertically integrated ice-shelf flow; give an outline of how the transversely integrated 1-D equations are obtained (referring to Appendix A); and also describe how stresssoftening can be introduced into the 1-D equations.
Consider a confined ice shelf, with zero horizontal velocities at the lateral boundaries, prescribed normal velocity at the inlet (the grounding line) and prescribed tractions at the outlet (calving front). Grounding line and calving front are taken to have fixed positions. We use a Cartesian coordinate system, Oxy, with x in the predominant direction of flow and y transverse. The flanks of the shelf are at y = ±Ω, where the constant is the ‘semiwidth’ and it is also convenient to denote the width W ≡ 2Ω. The horizontal velocity field is given by u = (u, v).
Define a tensor

where τ is the horizontal deviator stress and I is the unit matrix; the vertically integrated momentum balance equations are (Reference Morland, Van der Veen and OerlemansMorland, 1987; Reference MacAyealMacAyeal, 1989)
Where γ = (1 — ρ i/ρ w) ρ i g, H is the ice thickness, ρ i and ρ w are the densities of ice and water, respectively, and g is the acceleration due to gravity. Nabla is a 2-D operator in this paper.
On the calving front the stress boundary conditions are
where n and t are the horizontal normal and tangent vectors. In the numerical modelling, along the ice-shelf sides both u and v are set to zero, while at the upstream end (the grounding line) the longitudinal velocity and shear stress are specified using transversely integrated approximations (Eqn (A4)), discussed below and in Appendix A. The evolution of thickness is given by
where t is time, a is the net mass exchange, b is the surface accumulation/ablation rate and m the basal melting/freezing rate. We use a power-law constitutive relationship,
where A is the rate factor. Under the assumptions of incompressibility and zero vertical shear,
is the second invariant of the strain-rate tensor, e, whose horizontal components are defined by
n is the Glen exponent and a is a margin-softening factor applied near the margin to account for the ice here being softer than at the centre of the shelf. Along the centre line of the ice shelf, σ is taken to be 1.
The 1-D theory, which is used to compute the centre-line velocity, is based on an integration of the ice flow across the width of the ice shelf, resulting in a coupled set of force and mass conservation equations in the along-flow direction. The driving stress is balanced by the horizontal shear stresses from the ice-stream sides and by the along-flow transfer of longitudinal stresses. The boundary condition at the glacier calving terminus is given by the longitudinal stress that balances the difference between hydrostatic pressure of the ice and water. Formally, the theory is developed for shelves where the shelf semiwidth is much less than the length, but numerical calculations in Section 3.2 show that this condition is not very stringent, and the theory is in fact broadly applicable for ice bodies with plan aspect ratio (width/length) not significantly greater than unity.
In Appendix A, equations of force and mass balance (Eqn (A3)) for a transversely integrated shelf or perfectly slippery stream are developed. The 1-D theory deduces an approximate expression for uc, the centre-line velocity:

where subscript ‘c’ indicates consideration of the centreline value, Ω is the shelf semiwidth, τ c = τ xx (y = 0) is the centre-line longitudinal stress and τ l is the shear stress, τ xy (y = Ω), at the lateral margin. The equations of force and mass balance are
where ![]() at the centre line. This represents a standard set of equations used for simulations of ice shelves and streams. A typical upstream boundary condition is prescribed velocity or flux at the grounding line, while the downstream boundary condition at the calving front is
at the centre line. This represents a standard set of equations used for simulations of ice shelves and streams. A typical upstream boundary condition is prescribed velocity or flux at the grounding line, while the downstream boundary condition at the calving front is
where subscript ‘f’ implies evaluation of the centre-line value at the calving front.
A variant of Eqn (8a), which allows for the contribution of the longitudinal stress,τ xx , to the stress invariant, gives a slightly different expression for the velocity,
where P is defined in Eqn (A7) and λ = τ l /τ c is the ‘traction number’. This extension is similar in motivation to several recent ‘hybrid’ models dealing with vertically integrated membrane stress approximations (Reference BassisBassis, 2010; Reference Egholm, Knudsen, Clark and LesemannEgholm and others, 2011; Reference GoldbergGoldberg, 2011), but is not as complicated as any of these or the related ‘L1L2’ approximation (Reference Schoof and HindmarshSchoof and Hindmarsh, 2010).
The following two subsections deal with a solution of Eqns (9); the practical consequence of this is a simplification in the way the lateral shear stress at the calving front, τf, is computed, which allows us to construct special formulae for dynamics at the calving front. Readers not interested in the details of the solution procedure may wish to proceed directly to Section 2.4.
2.2. Similarity analysis
Here we carry out a scaling analysis, showing that the transversely integrated 1-D equations (Eqns (9)) are scale invariant under the additional assumption that a ≪ H c e c, which we specify by setting a = 0. The term H c e c is the thinning rate due to ice spreading. This allows us to establish scaling relationships between velocity, thickness, strain rate and width, which turn out to be very similar to the empirical correlations of Reference AlleyAlley and others (2008). The thinning rate at the calving front, H f e f, varies considerably in nature, having a value 0.025 m a-1 for H = 200 m, A =10-18 Pa-1/3 a-1, corresponding to a temperature of —30°C, to 4 m a-1 for H = 400 m, A = 10-17 Pa-1/3 a-1, corresponding to a temperature of —10°C. The assumption that allows us to carry out the similarity analysis thus holds for many, but not all, ice shelves, and we shall return to cases where it is not a good assumption.
We make the choice of scales
where asterisks indicate a scale magnitude and we define
We solve for the length scale, x * by defining

and use ![]() Eqn (11b) to find
Eqn (11b) to find
Using this with ![]() we obtain
we obtain
and substituting this into Eqn 11a2)and using this with Eqn (11d) and (11a1) we solve for λ*, to find
From these and Eqn (11b), the important scaling results
emerge, which show that ![]() scales with
scales with ![]() or, alternatively, with
or, alternatively, with ![]() These two forms are both very useful; the former in theoretical analyses, since fewer parameters are involved, the latter in observational comparisons, since measurements of e
c are available. These are very closely related to the calving-front velocity relationships (Eqns (15)) developed in Section 2.4, and this is the rationale for calling them ‘scaling relationships’.
These two forms are both very useful; the former in theoretical analyses, since fewer parameters are involved, the latter in observational comparisons, since measurements of e
c are available. These are very closely related to the calving-front velocity relationships (Eqns (15)) developed in Section 2.4, and this is the rationale for calling them ‘scaling relationships’.
Subsitution of Eqn (11) into Eqn (9) yields the dimension-less and scale-invariant equations
with boundary condition
where values with tildes are dimensionless. We therefore only have to solve Eqns (12) once for given parameters and use the scaling relationships to construct any other solution. It is convenient to think of the solution being parameterized by the thickness, H*, which determines ![]() as well as
as well as![]() ∂
x
H*, etc.
∂
x
H*, etc.
2.3. Evaluation of membrane correction term: a boundary layer solution
We now solve the 1-D equation set (Eqns (12)), which we only have to solve once for each value of n on the domain —∞ < x ≤ 0. The main purpose of this is to find the relationship between ![]() and
and ![]() ; recall that subscript ‘f’ indicates evaluation at the calving front. One way of doing this would be to solve Eqns (12) as a standard elliptic boundary problem. However, it can also be formulated in the following manner, which avoids dealing with the numerical problem of the infinite domain. We use a boundary layer approach, where we are saying that the flux does not change appreciably in a significant zone near the boundary.
; recall that subscript ‘f’ indicates evaluation at the calving front. One way of doing this would be to solve Eqns (12) as a standard elliptic boundary problem. However, it can also be formulated in the following manner, which avoids dealing with the numerical problem of the infinite domain. We use a boundary layer approach, where we are saying that the flux does not change appreciably in a significant zone near the boundary.
We use the fact that only one set of boundary conditions, ![]() , satisfies the existence conditions for a bounded solution (Reference SchoofSchoof, 2007b). Here we find an approximation to the unique couplet,
, satisfies the existence conditions for a bounded solution (Reference SchoofSchoof, 2007b). Here we find an approximation to the unique couplet, ![]() , that provides a bounded solution for
, that provides a bounded solution for  . The couplet is found by numerical integration of the ODE (ordinary differential equation) pair, Eqns (12), upstream from x = 0 starting from trial values of
. The couplet is found by numerical integration of the ODE (ordinary differential equation) pair, Eqns (12), upstream from x = 0 starting from trial values of ![]() . Without loss of generality we set
. Without loss of generality we set ![]() and vary
and vary ![]() . Numerical solutions
. Numerical solutions  diverge either to plus or minus infinity, and we aim to find an approximate value of
diverge either to plus or minus infinity, and we aim to find an approximate value of ![]() that divides the two cases and corresponds to the bounded solution. We present our results in terms of a parameter
that divides the two cases and corresponds to the bounded solution. We present our results in terms of a parameter

which allows us to write ![]() and, in dimensional units,
and, in dimensional units,
where τ lf is the lateral shear stress at the calving front. The number β is thus a correction to the ‘narrow shelf’ formula, applicable only at the calving front. The numerical solution for various n obtained with an ODE solver is shown in Table 1; for n = 3 and σ = 1, we find β ⋍ 0.91. Having used the scaling analysis to evaluate the membrane correction, there is little further to be gained by working in dimensionless units, and we now revert to physical units, using the constant β(n) to represent the membrane term correction.
Table 1. Solution parameters for the scale-free 1-D equation set (Eqns (12)) as a function of n. Section 2.3 explains the calculation and the relationship ![]()

2.4. Universal scaling relationships at the calving front
The developments in the preceding two subsections, and in particular Eqn (13), allow us to write the momentum equation (9a) at the calving front as
which applies in steady state only, and where β is a function of n only and presented in Table 1; β introduces the correction necessary to allow for the absence of the term 2∂(Hτc/∂x). We now derive a formula relating the calving front centre-line velocity to the thickness for the 1-D equation set, and show that it implies that thickness, slope, longitudinal stress and lateral shear stress at the calving front are all linearly related. We use the calving-front momentum Equation (14) and the continuity equation (9b), evaluated at the calving front, to eliminate ∂ x H f and obtain a relationship between velocity or flux and thickness at the calving front. Two equivalent forms are particularly useful:


where Eqn (15b) has used ![]() The first of the two relationships is used in this paper for comparison with observations, where estimates of e
f are available, while the second form is useful in theoretical analyses and for comparisons with numerical results. Note also that these are essentially scaling relationships. For a comparable with Hf ef a more accurate relationship is
The first of the two relationships is used in this paper for comparison with observations, where estimates of e
f are available, while the second form is useful in theoretical analyses and for comparisons with numerical results. Note also that these are essentially scaling relationships. For a comparable with Hf ef a more accurate relationship is

β in this case is slightly different from the value given in Table 1. Forms including the strain rate, e f, are advantageous for comparing with observations, which list strain rate; in addition the sensitivity to the poorly known rate factor, A, is low. The forms that relate velocity to thickness are more useful for stability analysis. A useful form for the flux, q f (volume discharge per unit width), is

Appendix B shows that the same algebraic process may be used to heuristically derive the boundary relationships for basally resisted streams, as given by Reference SchoofSchoof (2007a).
The scaling law is equivalent to a statement that the traction number, γ = τlf/τf, has a universal value at the calving front. To see this, we use the scaling relationship, Eqn (15a), with the relationships Eqn (8a), Eqn (9c) and ![]() to obtain the traction number at the calving front
to obtain the traction number at the calving front

When σ = 1, 1-D flows are specified by one parameter, n, and, as shown above, there is one universal solution for any given n. A solution obtained for one calving-front thickness may be rescaled to obtain the corresponding solution for any other thickness.
The traction number also defines the leading-order behaviour of rheological softening due to longitudinal extension for thin flows (Reference Schoof and HindmarshSchoof and Hindmarsh, 2010), and λ in this case is given by

which provides a nonlinear equation for λ. It is straightforward to show, starting from Eqn (A6), that the calving-front velocity given in Eqns (15) should be multiplied by P to account for rheological softening.
In Appendix C we show that the same scalings, with extensions for the lateral flow, hold for 2-D flows. This is a necessary condition for the scaling properties to hold in 2-D for a ≪ Hec . The caveat for both 1-D and 2-D theories is that the plan aspect ratio should not be too large. In section 3.1 we explore the quantitative accuracy of the scaling theory for 1-D and 2-D flows.
3. Assessment of Scaling Theory Accuracy
3.1. Boundary layer structure
A numerical example of 2-D confined ice-shelf flow is presented here. The focus is on the boundary layers, which are the areal zones where the flow in the interior of the shelf adjusts from its interior pattern to be consistent with the stress fields imposed at the boundary. This subsection also refers to Appendix D, which uses scaling principles to obtain estimates for boundary layer size. The scaling theory is a boundary layer theory, since it assumes the solution domain to be much longer than the boundary layer, and assumes the influence of upstream boundary conditions to be negligible. The following calculations examine this assumption quantitatively.
Numerical modelling of ice shelves firstly illustrates a boundary layer occurring in the longitudinal velocity field near the calving front, where ice flow accelerates in response to the force imbalance (Fig. 1a). This example is obtained from a 2-D flow model that uses the Morland-MacAyeal equations (Eqns (2-4)), run to steady state (|∂H/∂t| « |a|). The ice accelerates towards the calving front, with a parabolic cross-profile. Scaling arguments presented in Appendix D indicate that this boundary layer has length approximately equal to the width of the ice shelf.
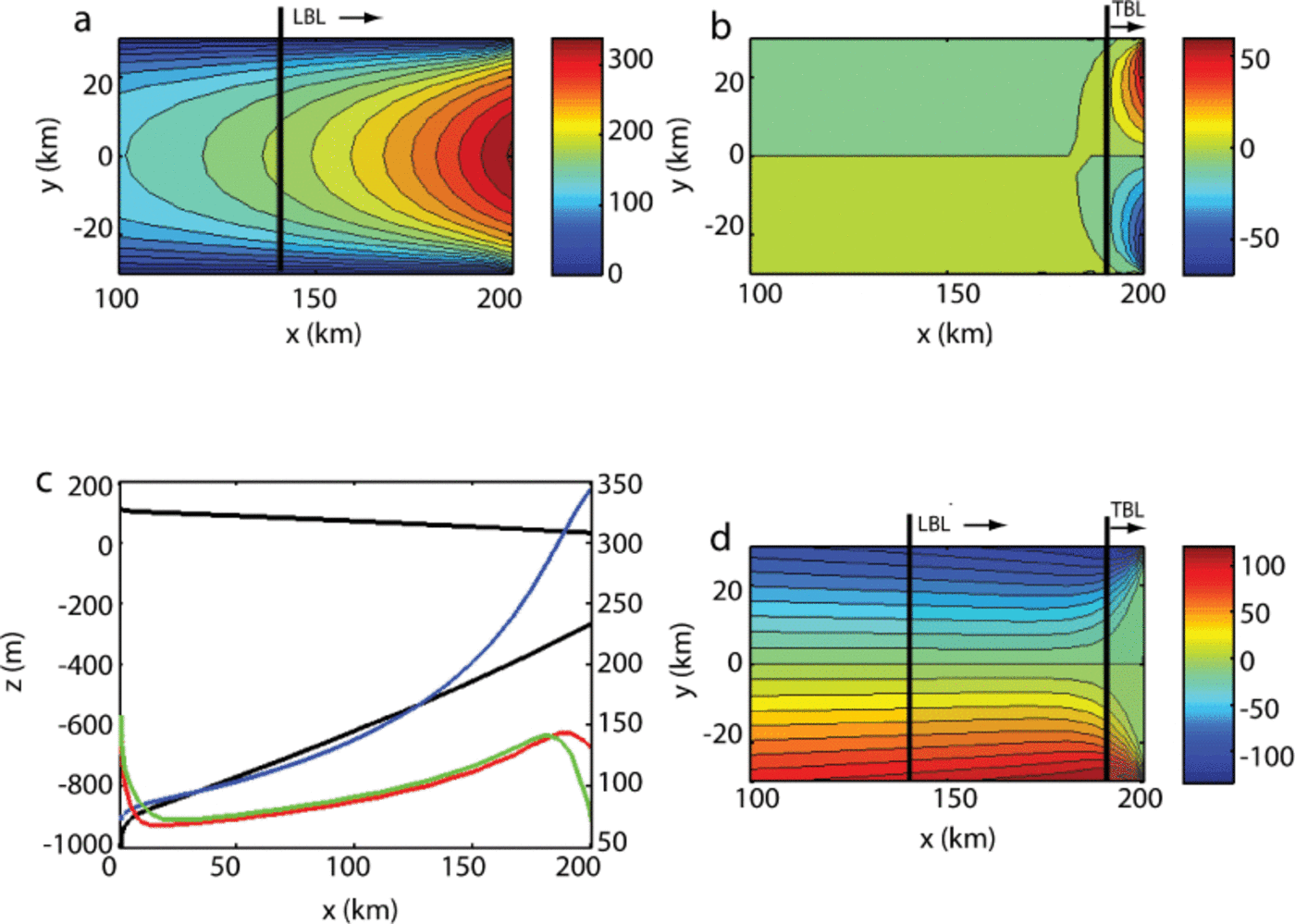
Fig. 1. Illustrations of boundary layers with numerical calculations. Flow is towards calving front on right; lateral margins have prescribed zero velocity, upstream end has prescribed longitudinal velocity and shear stress. Horizontal axes represent distance in kilometres along flow; in (a), (b) and (d) the vertical axis represents distance across the shelf. (a) Contours of longitudinal velocity fields (ma−1) showing acceleration over longitudinal boundary layer (LBL); (b) contours of transverse velocity fields (ma−1) showing acceleration over transverse boundary layer (TBL); (c) plots of ice geometry (m) (black; left axis) and velocity (ma−1) (blue), normal traction, S xx (kPa) (red), and twice longitudinal stress τ xx (kPa) (green) (right axis) (d) Contours of shear stress (kPa) showing decrease across transverse boundary layer. See Appendix D for details of prediction of boundary layer extent.
A second boundary layer, due to rapid changes in the shear stress which is zero at the calving front (Fig. 1d), exists in the shear stress and transverse velocity (Fig. 1b), which has length one-sixth of the width (Appendix D). At the front, the quantity ∂ y u is large, and the zero shear stress implies ∂ qx v to be large, and in consequence τ yy to increase rapidly near the calving front. In the main body of the flow (zones A and B), τ yy is much less than τ xx . Figure 1c shows centre-line plots of surface, s, base, b, velocity, u, and the quantities S xx and 2τ xx . The stress, S xx , reaches a maximum at the upstream end of the transverse boundary layer, before decreasing in the transverse boundary layer to its prescribed value, γH/2, at the calving front. In the transverse boundary layer, 2τ xx declines from being close to S xx when τ yy is small, to a value at the calving front where τ xx and τ yy are comparable in magnitude.
In these examples, the momentum balance and continuity equations are solved using pseudospectral methods, which can be regarded as finite-difference methods with spectral accuracy (Reference FornbergFornberg, 1996). The solution is on 31 × 21 nodes. Velocities and thickness are all solved on the same nodes, which are distributed according to the usual pseudospectral procedure of Chebyshev clustering. We used ρi = 900 kg m‒3, ρ w = 1000 kg m‒3, g = 9.8 m s–2, n = 3, σ = 1 and A = 3.2 × 10–18 Pa–3s–1, which corresponds to an ice temperature between —30 and —25°C.
Based on the numerical calculations, we present a sketch of the flow field structure (Fig. 2). In the main part of the flow (zone A) the traasverse sheaaing balances the gravitational drive (∂ y (HS xy ) ~ ρ i gH∂ x s). Nearer the front (zone B) the longitudinal stress gradient term, ∂ x S xx , increases, and the term ∂ x (HS xx ) can become as important as the other two terms in the force balance. Zone B is the longitudinal boundary layer. In zones C and Clat, the flow accommodates the fact that the shear stress is zero at the front. In zone C, ∂ x (HS xx ) ~ ρ i gH∂ x s, as the shear stress and its lateral gradient are small. However, in zone C there is still a transverse gradient in the longitudinal velocity, u, induced by flow from further upstream, which implies that ∂ y u is balanced by ∂ x v, since the shear strain rate is zero at the calving front. Zone C is the transverse boundary layer. The consequence of this is the establishment of a transverse flow at the calving front, with v flowing outfrom the centre towards the lateral margin. Near these margins, in zone Clat, both the velocity gradient and τyy reverse sign in order to accommodate the zero transverse velocity at the margin. In Appendix D, it is shown that the extent of the longitudinal boundary is the width of the flow, for both 1 -D (transversely integrated) and 2-D cases, while the longitudinal extent of the transverse boundary layer is one-sixth of the width. The equispacing of the contours in Figure 1d shows that the shear stress varies linearly with transverse position, as assumed in the 1-D derivation, well into the longitudinal boundary layer (zone B).

Fig. 2. Sketch of boundary layer structure. Zone A is where lateral shear stress gradients balance the longitudinal driving stress. In zone B the longitudinal driving stress is balanced by lateral shear stress gradients and longitudinal gradients in HS xx . In zone C the longitudinal driving stress is balanced by longitudinal gradients in HS xx , and the longitudinal gradient in shear stress establishes a strong transverse flow. In zone Clat, all terms play a role in the horizontal force balance.
3.2. Scaling relationships from numerical models of ice-shelf flow
We now examine the quantitative accuracy of the calving- front formulae for flows of finite length with nonzero accumulation, and in particular for 2-D flows with varying aspect ratio. Firstly, a transversely integrated 1-D numerical model is employed, using Eqns (9), again using a numerical technique based on pseudospectral techniques. The model is run to steady state, and the output flux at the calving front plotted against the ice thickness at the calving front. Calving-front velocity was varied by changing either the input flux or the net accumulation. The aspect ratio was varied both by altering shelf length and shelf width. Calving-front thicknesses of 200-400 m are produced with calving-front velocities ranging from <100ma-1 to >1000 m a-1. Parameters used are as for the example shown in Figure 2.
Figure 3 shows the results of numerical calculations with such a 1-D model, compared with the theoretical results, Eqn (15b), for the same 1-D governing equations, demonstrating that the predicted scaling relationship holds very well for these finite-domain calculations. The slight discrepancy seen at smaller thicknesses is due to the accumulation rate, a, becoming comparable in magnitude to the dynamic thinning, H f e f (Eqn (15c)).

Fig. 3. Correlations of computed centre-line velocity at calving front with thickness at same location. Lines are theoretical curves for velocity against thickness, the thin red one for β = 1, the thick black one for β appropriate for n = 3 given in Table 1, where β is the membrane stress correction term; circles are transversely integrated 1-D calculations, squares are 2-D calculations. (a) Series where output flux is varied by mean accumulation rate, with catchment area span of 500 km, and shelf length of 300 km, shelf width 60 km. (b) Series where output flux is varied by catchment area size, constant accumulation rate, shelf width 60 km. (c, d) Cases with shelf widths of 100 km (c) and 30 km (d). Velocity scaled by width 60 km to demonstrate that model results show the predicted linear correlation with width.
We also need to know whether the theory works for 2-D models, and at what ratio of width to length the theory starts to become inaccurate. Figure 3 also plots centre-line velocity against calving-front thickness obtained from the 2-D flow models used to generate Figure 1. The scaling relationship evidently holds for these flows as well, although the quantitative predictions of velocity are approximately twice as high as those from 1-D modelling. Plan aspect ratio (width to length) is also expected to affect the relation between velocity, width and thickness. Figure 4 shows that the scaling relationship holds well for aspect ratios of ~1 for 2-D flows, and is still accurate to ~10% even for aspect ratios of 2.

Fig. 4. Showing the effect of aspect ratio (width to length) on the scaling relationship. Black squares are calculations from 2-D flow shown in Figure 3, where aspect ratio is <1. Coloured squares are additional calculations with indicated aspect ratio, for 2-D flows, showing that at large aspect ratio the scaling relation breaks down.
Though not unexpected, it is worth understanding why the 2-D flows are faster than the 1-D flows for a given calving- front thickness. Rheological softening due to the effect of τxx in the invariant in the shear relationship (Eqn (10)) leads to a speed-up of 12-13% for several different cases, obtained (as before) by varying the input flux, accumulation and stream width. That the number should be constant is expected, as the rheological softening is controlled by the traction number, λ, which remains universal even with the physics of rheological softening (Eqn (18)). However, rheological softening does not account for all the speed-up.
Figure 1c shows that ∂
x
(HS
xx
) < 0 near the calving front. Here the confined shelf behaves like an unconfined shelf, as lateral resistance decreases towards the calving front. We can say that this leads to an effective boundary condition between zones B and C (Fig. 2) where ![]() In view of the numerical demonstration that the flows scale with H
f, it is extremely likely that the maximum value of Sxx
is proportional to H
f. Another way of looking at the difference between 1-D transversely integrated flows and 2-D flows is that the 1-D flow implicitly assumes the shear stress at the calving front varies linearly across the front, and this introduces a quantitative error in the normal deviatoric stresses. This means that the geometry of the ice front must play a role, as it will affect the shear stress distribution near the calving front; extending ice tongues are predicted to have a different coefficient in the velocity relationship corresponding to Eqn (15b). One might anticipate similar geometric effects will occur in basally resisted flows, where the vertically integrated forms assume that the shear stress at the grounding line increases linearly with depth, while in reality it will be affected by the presence or absence of an ice shelf.
In view of the numerical demonstration that the flows scale with H
f, it is extremely likely that the maximum value of Sxx
is proportional to H
f. Another way of looking at the difference between 1-D transversely integrated flows and 2-D flows is that the 1-D flow implicitly assumes the shear stress at the calving front varies linearly across the front, and this introduces a quantitative error in the normal deviatoric stresses. This means that the geometry of the ice front must play a role, as it will affect the shear stress distribution near the calving front; extending ice tongues are predicted to have a different coefficient in the velocity relationship corresponding to Eqn (15b). One might anticipate similar geometric effects will occur in basally resisted flows, where the vertically integrated forms assume that the shear stress at the grounding line increases linearly with depth, while in reality it will be affected by the presence or absence of an ice shelf.
4. Observational Verification of the Scaling Theory
The scaling theory predicts simple relationships between the ice velocity perpendicular to the ice front, the width of the shelf, its thickness and the strain rate perpendicular to the calving front. These relationships are markedly different from the standard ones mentioned above (Reference Van der VeenVan der Veen, 1999); the steady-state velocity relationship is ![]() (Eqn 15a). Given that n is generally held to lie between 3 and 4 (Reference Cuffey and PatersonCuffey and Paterson, 2010), this relationship is strikingly similar to the empirical correlation of Reference AlleyAlley and others (2008). The above form of the scaling relationship is useful for empirical comparisons. An equivalent form, useful for theoretical work, is
(Eqn 15a). Given that n is generally held to lie between 3 and 4 (Reference Cuffey and PatersonCuffey and Paterson, 2010), this relationship is strikingly similar to the empirical correlation of Reference AlleyAlley and others (2008). The above form of the scaling relationship is useful for empirical comparisons. An equivalent form, useful for theoretical work, is ![]() (Eqn 15b).
(Eqn 15b).
Given these new relationships, Figure 5 and Table 2 investigate further the correlations of u f with H f, e f and Ω obtained using previously published data (Reference AlleyAlley and others, 2008). The inclusion of strain rate and width is crucial to good matches. Cases 7-10, which exclude this combination, have the poorest correlations. Thickness is less important, but does, nevertheless, improve the fit. A good correlation is obtained with the parameter groups W and H f e f, with estimates of the indices close to that predicted by the scaling theory (cases 4 and 5, plotted in Fig. 5). Case 4 gives the predicted value of n/(n + 1) for n = 3.
Table 2. Indices for multiple regression of calving-front velocity, u f, against various combinations of thickness, H f, strain rate, e f, and ice-shelf semiwidth, Ω. Data taken from Reference AlleyAlley and others (2008). Quantity r 2 explains total variance explained by the correlation. Computed using Matlab® regress routine


Fig. 5. Correlations of observed calving-front velocity, u f, with glaciological parameters. Data taken from Reference AlleyAlley and others (2008). Left: u f/Ω regressed against (e f H f) giving a best-fit exponent of 0.98, case 5 in Table 2. Right: u f plotted against best-fit group Ω0.83(e f H f)0.75, case 4 in Table 2. (More details in Table 2.)
Width is easy to measure, while thickness may be contaminated by uncertainty about the mean density. Measuring the appropriate strain rate at the calving front is more difficult since the existence of the shorter transverse boundary layer (Figs 1 and 2) makes it more difficult to define exactly how ef should be measured. The parameters ignored in this calibration are the aspect ratio and temperature- dependent viscous rate factor, A. From a theoretical point of view, the correlation depends weakly (Eqn (15a)) on the unknown coefficient A (a factor of 2 between ice at —10°C and —30°C). Marginal softening (Reference Vieli, Payne, Shepherd and DuVieli and others, 2007; Reference Khazendar, Rignot and LarourKhazendar and others, 2011), which is not included among the observational parameters, is an expected occurrence, but there is also very low sensitivity to this in the empirical strain-rate form (Eqn (15b)) of the scaling relationship. The numerical experiments indicate only weak dependence on the aspect ratio when it is less than ~2. These low sensitivities to poorly quantified parameters permit the establishment of the very strong empirical correlations. The main unknown would appear to be the aspect ratio of the ice shelf. In fact, very few ice shelves with width/length ratio much greater than 1 exist, as embayments with such aspect ratios that contain ice shelves generally have ice rises located within them, that serve to decrease the effective aspect ratio.
Very good agreements between observed and predicted values of the proportionality coefficient,  are obtained in the scaling relationship (Eqn (15b)). For the scaling theory relationship, the coefficient of proportionality was estimated from the data as 0.023 ± 0.018 a3/4 m–7/4, assuming n = 3. This should be compared with apredicted value of 0.01 a3/4 m–7/4 with A = 10–17 Pa–3 a–1from Eqn (15a), corresponding to temperatures of —10°C. Numerical calculations in 2-D predict velocities roughly twice as large as those given by Eqn (15b), giving an estimate of the coefficient as 0.02 a3/4 m–7/4 at temperatures of — 10°C, with A = 10–17Pa–3a–1, and a smaller value of 0.01 a3/4 m–7/4 at temperatures of —30°C with A = 10–18 Pa–3 a–1.
are obtained in the scaling relationship (Eqn (15b)). For the scaling theory relationship, the coefficient of proportionality was estimated from the data as 0.023 ± 0.018 a3/4 m–7/4, assuming n = 3. This should be compared with apredicted value of 0.01 a3/4 m–7/4 with A = 10–17 Pa–3 a–1from Eqn (15a), corresponding to temperatures of —10°C. Numerical calculations in 2-D predict velocities roughly twice as large as those given by Eqn (15b), giving an estimate of the coefficient as 0.02 a3/4 m–7/4 at temperatures of — 10°C, with A = 10–17Pa–3a–1, and a smaller value of 0.01 a3/4 m–7/4 at temperatures of —30°C with A = 10–18 Pa–3 a–1.
A further point is the observation (Reference SandersonSanderson, 1979) that ice-shelf thickness gradients are observed to scale inversely with semiwidth; Sanderson explained this using a perfectly plastic approach. The scaling theory, and in particular the universality of the traction number expressed in Eqn (17b), shows that thickness gradient and width are inversely related, offering an alternative explanation for Sanderson’s observation.
5. Discussion
5.1. Ice shelves and the calving front
A major conclusion of this paper is that the apparent scaling relationship for calving (Reference AlleyAlley and others, 2008) is most likely to be a scaling law for viscous flow at the calving front. The theory works partly because the velocity is not sensitive to parameter uncertainty in the rheological properties of ice or to the aspect ratio, and partly because the theory is underpinned by very robust scale-invariance properties. A problem with the presentation of the empirical scaling relationships as a calving law was that it seemed to predict instability of calving-front position; a small retreat leads to thickening of the ice shelf, greater stresses and strain rates, and further retreat. In contrast, viscous supply stabilizes calving fronts. A small retreat leads to thickening, an increase in the ice velocity at the calving front and a re-establishment of the original position.
A likely significant feature is the way in which the stress configuration at the calving front affects fracture and calving. Two factors immediately suggest themselves; the first is the existence of a nonzero extensional stress parallel to the calving front. This is likely to induce fractures normal to the ice front, extending significant distances into the transverse boundary layer. A second point is that at the boundary the stress invariant is increased for τ yy = 0, despite the conditions S xx = γH/2 and τ xy = 0 (Appendix E), which must have implications for fracture where wave-induced stresses (e.g. Reference SergienkoSergienko, 2010) are of significance. This, and the fact that the traction number is universal, may provide some avenues for progress in understanding calving.
5.2. Implications for the stability of ice-sheet and ice-stream grounding lines
The scaling relationships also apply to ‘shelfy streams’, streams where all resistance comes from the side. For a flat bed, the driving stress is given by ρ i gH∂ x H, and one may follow the derivation of Eqns (15) and (16), replacing β by β/(1 — ρ i/ρ g) to obtain the flux/thickness relationship. The correction factor, (, is not exactly the same as given in Table 1, owing to the different bed slope. Equation (16) shows that flux across the grounding line is proportional to thickness to some quite high power, and forms the basis of stability arguments about the grounding line, as with basally resisted ice streams (Reference SchoofSchoof, 2007a). If the grounding line retreats along a reverse slope, the ice thickens and the flux increases, leading to a runaway instability. However, this is very much a partial answer, as most shelfy streams couple strongly with ice shelves, and the stability of the grounding line can only be understood through analysing the coupled behaviour of stream and shelf.
A particular concern regarding the accelerating mass loss from Antarctica (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011) is that it may, in part, be due to a grounding line instability. Despite increased theoretical understanding of the instability (Reference SchoofSchoof, 2007a), some clear links between changes in the ice geometry and acceleration of glaciers (Reference JenkinsJenkins and others, 2010), and laboratory evidence confirming our understanding of grounding lines (Reference Robison, Huppert and WorsterRobison and others, 2010), direct geophysical evidence for the theory underpinning grounding line dynamics is absent. The main problem is that the forces acting across the grounding line cannot be measured to the accuracy required. In contrast, these stresses are known very well for the calving front. The close links between the ideas behind this work and theories of grounding line behaviour that predict instability (Reference SchoofSchoof, 2007a; Reference Robison, Huppert and WorsterRobison and others, 2010) suggest that concerns regarding grounding line instability are securely founded. The numerous other effects discussed in the context of grounding line instability, primarily basal melting, serve to modulate the instability and, in the field, simply to obscure the essential processes.
5.3. Technical aspects
Since numerical results indicate that the 2-D flows scale with calving-front thicknesses, the flow patterns within the boundary layers shown in Figure 1 are universal. The linear dependence of shear stress on lateral position extends well into the longitudinal boundary layer, and only breaks down in the transverse boundary layer. This means that the 1-D transversely integrated approximation appears to work well down to length scales of around one-sixth of the ice-shelf or ice-stream width.
A point of interest lies in understanding how the main velocity changes from being proportional to Ωn + 1 upstream to being proportional to Ω at the calving front. To understand this, we note that the velocity relationship is ![]() In the main part of the flow (zone A, Fig. 2) we can differentiate with respect to x to obtain
In the main part of the flow (zone A, Fig. 2) we can differentiate with respect to x to obtain ![]() meaning that after using the continuity relationship,
meaning that after using the continuity relationship, ![]() we find ∂
x
H
c to be independent of the width in zone A. However, near the calving front, in zone B, ∂
x
u
f is determined by the boundary condition and thus solely by ice thickness among the variables. The kinematic condition gives
we find ∂
x
H
c to be independent of the width in zone A. However, near the calving front, in zone B, ∂
x
u
f is determined by the boundary condition and thus solely by ice thickness among the variables. The kinematic condition gives ![]() and the dependence of u
f on Ω becomes linear, as we now have
and the dependence of u
f on Ω becomes linear, as we now have ![]()
Some further points are: (1) transversely integrated ice- stream or ice-shelf models underestimate velocity by a factor of ~2, and (2) ice shelves with a width/length ratio less than ~1 have a universal traction number (shear stress to longitudinal stress ratio) at the calving front. The theory makes strong predictions that there should be strong lateral divergence at the calving front; it is not clear whether this has been observed.
It is worth reviewing the role of Appendixes C and D. Appendix D is a scale analysis of the equations without any assumption of steady state, and establishes the upstream extent of the boundary layers: one ice-shelf width for the longitudinal boundary layer, where Sxx adjusts from its interior value to the value set by the boundary conditions; and one-sixth of an ice-shelf width for the transverse boundary layer, where Sxz adjusts for similar reasons. Appendix C is a scaling based on the assumption of steady state, using the scale equivalence of the shear stress and the longitudinal stress, txx , to infer the scale invariance of the 2-D force-balance equations.
6. Concluding Points
A scaling theory for calving fronts has been developed, which shows two boundary layers exist, one for longitudinal momentum balance and one for transverse boundary layers. The boundary layers organize the flow in the ice shelf, and inform about how far upstream of the shelf boundary effects should be felt, which is of fundamental significance in understanding how stresses at the grounding line are determined. The scaling theory makes strong predictions about the relationship between calving-front velocity, ice thickness, strain rate and ice-shelf width. The accuracy of this theory has been validated by comparison with numerical calculations, and its applicability verified against a dataset collected with the aim of understanding calving. The theory implies that the correlation of calving rate with glaciological variables does not imply causation. Because it is a scaling relationship, the theory has universal aspects, in particular making a strong prediction about the relationship between the shear stress and longitudinal stress. These stresses are geometrically controlled and therefore measurable, even for unit plan aspect ratios.
Some geophysical verification has consequently been obtained for a mathematically similar boundary layer theory describing basally resisted grounding lines (Reference SchoofSchoof, 2007a), arising through the analogous nature of the shear flows involved. Further research into calving-front boundary layers will consequently deepen understanding of both calving- front and grounding-line boundary layers, as well as strengthen the predictive modelling of marine ice sheets (Reference Pollard and DeContoPollard and DeConto, 2009; Reference Katz and WorsterKatz and Worster, 2010). To understand calving, fundamental process approaches (Reference Amundson and TrufferAmundson and Truffer, 2010; Reference BassisBassis, 2011; Bassis and Walker, in press) and consideration of environmental factors (Reference Vaughan and DoakeVaughan and Doake, 1996; Reference Shepherd, Wingham, Payne and SkvarcaShepherd and others, 2003; Reference Benn, Warren and MottramBenn and others, 2007; Reference Bromirski, Sergienko and MacAyealBromirski and others, 2010) remain important.
Acknowledgements
This work was supported by funding from the Ice2sea programme from the European Union 7th Framework Programme, grant number 226375, Ice2sea contribution number 050, forming part of activities in Ice2sea Work- packages 2.1 and 5.3 and the British Antarctic Survey’s Polar Science for Planet Earth programme. I thank Jeremy Bassis and an anonymous reviewer for their detailed and thoughtful comments.
Appendix A. Derivation Of 1-D Transversely Integrated Shelf Equations
This 1-D approximation has not received the same attention from mathematicians as its vertical equivalent (e.g. Reference Baral, Hutter and GreveBaral and others, 2001; Reference Schoof and HindmarshSchoof and Hindmarsh, 2010), but a basic demonstration of its derivation as an asymptotic approximation is given by Reference HindmarshHindmarsh (2006). Expanded forms of the momentum equations (1) are given by
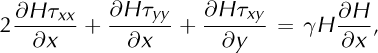

Following Reference Van der Veen, Plummer and StearnsVan der Veen (1999), 1-D transversely integrated flows are obtained by assuming the transverse shear stress varies linearly with transverse position, y, giving
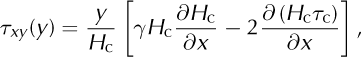
where the transversely meaned values of H and τ xx are approximated by their centre-line values, H c and
To compute the centre-line velocity, u c, we note that for the transversely integrated stream or shelf, the x-direction momentum balance is
where τ l = τxy (Ω). Integration of the shear relationship,

gives the expression for u c, the x-direction centre-line velocity

where σ is a margin-softening factor. Combining Eqns (A2) gives the standard form

The upstream boundary conditions used in the 2-D modeling are given by
with u c given by Eqn (A2d).
Under the assumption that shear stress varies linearly with transverse distance, we may write

where τl is the shear stress at the lateral margin and η = y/Ω, which may be rewritten as

and where we have also defined
Since, by definition,
we arrive at an algebraic equation for ω as a function of η, the normalized distance from the ice-sheet centre,
The solution for ω is used in the equation for lateral shearing, again using the assumption that shear stress varies linearly across the ice shelf,

and following a transverse integration we find
and the rheological softening parameter is

This can be solved iteratively in numerical solutions of the 1-D equation set. The standard form for the centre-line velocity may be retrieved by setting P ≡ 1. The hybridization used here is not as complex as the L1L2 approximation of Reference HindmarshHindmarsh (2004) and Reference SchoofSchoof and Hindmarsh (2010), and further work is needed to investigate the scaling properties of this and other hybrid formulation
Appendix B. Calving-Front Scaling Relationships and Relation to Schoof Grounding Line Formula
Here we show how the algebraic technique deriving flux formulae may also be used to derive the Schoof flux formula for basally resisted ice streams. Considerthe momentum and mass conservation for a basally resisted ice stream in plane flow with bed slope much smaller than thickness gradient,

where C is a drag coefficient. We assume the horizontal stress gradient terms are small and, eliminating ∂ x H, we obtain

and for small a the Schoof flux formula follows:

Appendix C. Conditions For 2-D Flows to be Scale-Free
Our aim here is to show that, in principle, the 2-D equations can be scaled to depend on only one parameter, H *. (This was done in Section 2.2 for the 1-D equations.) For algebraic simplicity we adopt a slightly more general scaling, allowing the x-direction length scale to be free. Let the scale for the thickness at the calving front be H* and choose as scales
where x
* is a longitudinal length scale of interest, which in practice will be the x-length scale of one of the boundary layers; we do not need to specify x* now. We assume that δ is a constant independent of Ω. We then use ![]() in Eqn (9a) to obtain the dimensionless scale-invariant form for the momentum balance equation
in Eqn (9a) to obtain the dimensionless scale-invariant form for the momentum balance equation

with tildes denoting dimensionless variables. A scale- invariant form also exists for the continuity equation that motivates the choice of scales
substitution of these in the continuity equation yields a scale- invariant form when a ≪ H∂
x
u
c. The scale invariance arises from the fact that the shear stress scale, ![]() is defined by H*, which is a result of the boundary layer theory through the universality of the traction number.
is defined by H*, which is a result of the boundary layer theory through the universality of the traction number.
We now consider the 2-D flows and make the choice of scales
The relationship for ∂
y
v* is consistent with the choice of scale for ![]() The fact that ∂
y
v* is independent of Ω implies that v, like u, scales with Ω, which is necessary for scale invariance from a kinematical point of view. This, and the fact that
The fact that ∂
y
v* is independent of Ω implies that v, like u, scales with Ω, which is necessary for scale invariance from a kinematical point of view. This, and the fact that ![]() must also do so. With these choices of scales, the 2-D momentumbalance equations (A1) become
must also do so. With these choices of scales, the 2-D momentumbalance equations (A1) become


which are scale invariant, holding for any combination of H* and Ω. The choices that ![]() and ∂y
H
* scale with H
* are therefore consistent with the 1-D scaling. It is straightforward to see that the continuity equation,
and ∂y
H
* scale with H
* are therefore consistent with the 1-D scaling. It is straightforward to see that the continuity equation,
is scale invariant under these same conditions. In consequence,scaling considerations demonstrate that the calvingfrontboundary layers of 2-D flows have the same scaling relationship as the 1-D flows, leading to the same condition of flows being parameterized by the calving-front thickness. At first sight, it is slightly puzzling that τ yy* and ∂ y v∗ donot tend to zero as the shelf becomes infinitely wide. The whole analysis, however, is based on the idea that the lateralmargins play a significant role. The longitudinal velocity,u, increases with width, and this results in the transversevelocity and horizontal stress not decreasing in value.
Appendix D. Boundary Layer Scale Estimates
Here we obtain expressions for the horizontal extent of the two boundary layers. In the 1-D transversely integrated form, only one boundary layer exists, in the region where τ xx changes from its interior value to its frontal value, set by the boundary condition. Letting asterisked quantities represent scale magnitudes, and letting L∗ represent the unknown longitudinal extent of boundary layer, we write scale versions of the left-hand side of Eqn (9a)

to find

The longitudinal boundary layer has extent roughly equal to the width, W = 2Ω, of the stream. The quantity  is close to unity, while the sensitivity to any margin-softening factor, σ, is small for n = 3.
is close to unity, while the sensitivity to any margin-softening factor, σ, is small for n = 3.
In 2-D, there are two frontal boundary layers in narrow ice shelves. One of these arises for identical reasons to the one just derived for the transversely integrated case. The second boundary layer arises from the flow in the interior (zones A and B) being close to a simple shear, with one of the planes aligned with the direction of flow. This implies a nonzero tangential traction on a vertical plane across the ice stream. However, at the calving front, the shear stress in the plane parallel to the front must be zero, so there must be a large term, (∂H τxy )/∂ x near the calving front. Figure 1 confirms this suggestion.
An analysis for the x-momentum balance gives the boundary layer length as similar to the width of the shelf. Ignoring the drive term, γH∂ x H, and the small transverse stress, the x-direction momentum balance equation (A1a) becomes

and replacing quantities with their asterisked scale magnitudes

so that ![]() Using
Using
where νis the viscosity, we find L
* = 2Ω and ![]() In fact, Eqn (17a) makes a stronger statement regarding the ratio
In fact, Eqn (17a) makes a stronger statement regarding the ratio ![]() , which can be evaluated and is very close to unity.
, which can be evaluated and is very close to unity.
The transverse boundary layer is more difficult to analyse, and we restrict attention to the longitudinal extent of zone C, and assume (as is demonstrated by numerical solutions) that the transverse gradients in thickness are small, implying that the transverse driving force and transverse thickness gradients are small. Then, expanding Eqn (A1b) and dropping terms involving ∂ y H, we find

We can also use the normal stress condition at the calving front, S xx = γH/2, to write
and use these two last expressions to eliminate τ yy , obtaining

which, when replaced by scale magnitudes, is

where D
* is the longitudinal extent of the transverse boundary layer. Then, using ![]()
the 6 stemming ultimately from the definition of the stress tensor S.
Appendix E. Stress Invariant At Calving Front
The stress invariant at the front, where τ xy = 0, is given by
and ![]() from the boundary condition,
from the boundary condition,  is the stress for an infinitely wide ice shelf, we find
is the stress for an infinitely wide ice shelf, we find

with minimum value 1 at μ = 1. Thus, nonzero τ yy causes an increase in the stress invariant near the calving front, compared with the plane flow situation, despite the constraint imposed by the boundary condition.











