Introduction
Over the last two decades the movement of glaciers and ice sheets has engendered many studies both theoretical and experimental. The linear deformation law (ideal viscosity in which strain-rate
Only three alternatives have hitherto been adopted:
-
i. Zero velocity at the bedrock contact. This is the hypothesis adopted by Weinberg in 1906 and Somigliana in 1925 and more recently again by Reference NyeNye (1965). Since the drillings by Blümcke and Hess on the Hintereisferner it has been known that this hypothesis is not in general exact. In fact slip over the bedrock constitutes practically all of the movement of rapid glaciers, whether these are temperate valley glaciers in steep zones (e.g. the Mer de Glace in the chaos of the Géant ice fall; speed 440 to 830 m/year; thickness 30 to 50 m), or whether they are distributary glaciers from a large ice sheet. These latter being cold except in a basal layer a few metres or tens of metres thick (Reference LliboutryLliboutry, 1966), the deformation in the body of the glacier is much reduced. The observed velocities of several kilometres per year (Reference Carbonell and BauerCarbonell and Bauer, 1961) come practically exclusively from sliding.
-
ii. Constant and uniform friction. This is the condition imposed by the mechanics of perfect plasticity. As introduced by Orowan and Nye in 1951 it led to interesting approximate results; thus on a flat bed the profile of an ice sheet is parabolic and independent of the accumulation. We note that it is also usable for a glacier with a semi-circular transverse profile assuming that the velocities are parallel. The problem then possesses axial symmetry (cylindrical).
-
iii. Friction an increasing function of velocity of sliding alone. f = Cu 1/m where f is the frictional force per unit area, u is the sliding velocity, m is a positive number, and C is a constant (or rather is characteristic of the bedrock, depending on its roughness, but one supposes this to be uniform). If we now combine this with the relation

which relates the frictional force with the density of ice ρ, the acceleration due to gravity g, the glacier thickness h, and the surface slope α, a law which is valid whenever the longitudinal stress is uniform, we obtain the relation

A law
In 1957 Reference WeertmanWeertman (1957) reached such a law theoretically with m = (n+1)/2 ≈ 2. This boundary condition was adopted by Nye for his important theoretical studies on glacier fluctuations. It should be noted that although it is traditionally cited in English publications, Weertman’s law has never been experimentally verified, any more than Nye’s theory which uses it. Certain qualitative conclusions drawn from it, such as the existence of kinematic waves, do not constitute proofs; they can be obtained with other boundary conditions. In fact up to now these two authors have cited each other for the basis of their theories!
Since 1958 the present author has shown (Reference LliboutryLliboutry, 1958[a], Reference Lliboutry[b], Reference Lliboutry1959) that the introduction of two new factors into Weertman’s theory leads to a completely different law of friction.
-
a. The ice may separate from the bed downstream from a protuberance, this cavitation being facilitated by the existence of subglacial water at a pressure p (in this paper p will represent the absolute pressure of this water and not its excess pressure above atmospheric pressure).
-
b. If there are a succession of bumps wide compared with their height, the friction of the glacier may, because of this cavitation, reduce and tend to zero at high velocities. This succession of bumps is essential as without it, even with cavitation, one returns essentially to the same law of friction as without cavitation (Reference WeertmanWeertman, 1964[a]; Reference LliboutryLliboutry, 1965).
In this paper this theory of cavitation is corrected, improved and completed: (a) we make a better calculation of the stresses and heat flux; (b) we extend the calculation for any cavitation (hitherto only a limiting case has been given); (c) we show that for a given velocity above a certain value the friction is maximum for two sizes of bumps; our old calculation, following that of Weertman, did not give the maximum but an intermediate minimum; (d) we estimate the value of the interstitial pressure p, hitherto indeterminate; (e) we improve the model of the bedrock.
We finally arrive at a very complicated law of friction, but it can be more or less simplified in order to tackle definite problems. This leads to boundary conditions that we can call (iv), (v) and (vi):
-
(iv) As a first approximation, Coulomb’s law of solid friction (Reference Bowden and TaborBowden and Tabor, 1956), but in the presence of an interstitial pressure. The friction is proportional to the resultant pressure N, which depends on h but is independent of velocity.
-
(v) As a second approximation, a law including a term in
and a term in . This law allows us to study kinematic waves.
. This law allows us to study kinematic waves.
-
(vi) Finally, the complete law, necessary in cases which depart from the usual situation, such as the slip of the tongue of the Allalingletscher, cause of the Mattmark disaster.
Before developing this theory of subglacial cavitation, we examine its experimental basis, and then record the exact timetable of previous theories and compare their results. My ideas have been presented in English by Weertman in an incomplete and erroneous form, and their fundamental difference not made clear.
1. The Facts Needing Explanation
1.1 Fluctuations in sliding velocity
Measurements made in the ablation zone of valley glaciers by Lütschg, Elliston, and others (reported by Reference LliboutryLliboutry, 1965, p. 624–26) show that the velocity can double in June when the melt water is most abundant. Other observations show that rain-water can play the same role.
On certain glaciers, careful survey measurements made at six-hourly intervals have shown erratic fluctuations in velocity (cf. Reference LliboutryLliboutry, 1965, p. 626–27). Those of Reference MillecampsMillecamps (1956[a], Reference Millecamps[b]) in particular show a somewhat regular jerky movement, which inevitably makes one think of a “stick—slip” movement. This suggests that friction for large velocities of sliding (kinetic friction) is lower than friction for slow or zero velocities of sliding (“quasi-static” friction).
Other increases in velocity of sliding follow with a certain delay after a series of years of high specific balance. A kind of flood wave forms which advances more rapidly than the ice. Nye and Weertman have applied their theory to the study of such waves, without having obtained quantitative verifications. In certain cases it seems that one has observed flood waves much more rapid than this theory predicts (cf. Reference LliboutryLliboutry, 1965, p. 628–30).
1.2 Subglacial mechanisms
Subglacial cavities below protuberances of the bed have often been observed, even under 46 m of ice at Vesl-Skautbreen or 50 m of ice at the Grindelwaldgletscher (observations of McCall and of Carol reported in Reference LliboutryLliboutry, 1965, p. 640–42). Near the snout they become the rule and help explain the “crag and tail” features (Reference LliboutryLliboutry, 1965, p. 703 and planches LXII–LXIII). The existence of such cavities filled with water under a variable pressure allows us to explain subglacial quarrying (Reference LliboutryLliboutry, 1962). Periodic capture of these water pockets by the glacier allows us to explain the formation of stratified bottom moraine (Reference LliboutryLliboutry, 1964[a], Reference Lliboutry1965, p. 688–89).
The existence of subglacial water which is not cut off and which is maintained at a pressure different from the hydrostatic pressure due to the overlying ice has been observed during glacier soundings which have penetrated to bedrock. According to Reference ReynaudReynaud (1959), on the Glacier d’Argentières (Mont Blanc massif), in thermal bore holes, the water level dropped very rapidly when bedrock was reached at depths between 190 and 236 m—proof that water can flow beneath the glacier. Then the water level stabilized at 60 to 80 m below the surface. The mean pressure of ice on the bedrock was therefore ρgh = 18.5±2 bar, that of the water p = 14.5±2 bar.
According to Reference MathewsMathews (1964), the bottom of a mine reached the South Leduc Glacier in British Columbia at 160 m below the surface of the glacier (at its centre the glacier reached a depth of 270 m). The pressure of interstitial water at the bottom of the mine rose during the summers of 1961 and 1962 to about 42 m of water (ρgh = 14 bar, p = 4.2 bar). A closer inspection of the pressure record shows that, following a period of strong melting or heavy rain, the pressure rises temporarily a great deal: it reached 130 m of water one day in June 1962. In January 1963 the pressure remained at 63 m. In February it rose temporarily, then fell to 35 m, some ice dam presumably having given way. At the same time the sliding velocity must have varied considerably, to judge by the two values given by Mathews: 25.5 m/year (measured over 35 days) and 34.6 m/year (measured over 17 days). It is unfortunate that the author does not give the surface slope, which is needed to calculate the friction, and that he did not register the velocity of sliding by a recording gauge. His measurements are nevertheless very valuable and must be generalized.
The uniqueness of the hydraulic system under the Glacier d’Argentières has been proved by injection of potassium dichromate. One can also quote the old measurements of Vallot and Vallot (1900) on the Mer de Glace: the subglacial stream was only 1.8 times slower than an open stream of the same slope; this proves the non-existence, in this case at least, of a large volume of liquid water in the body of the glacier.
1.3 The detached fragments of the Allalingletscher
The Allalingletscher in the Saas-Fée valley (Valais, Switzerland) descends a relatively gentle slope from 4190 m to 2850 m, then flows down a much steeper slope of polished rocks. As far back as records go, and until 1944, it reached a flatter region at the bottom of the valley and its snout was supported there, but, following an exceptional retreat occurring principally between 1944 and 1947, the snout rose to the middle of the slope, 600 m uphill. It thus formed a very thin layer of ice (less than 25 m thick, average about 12 m), a site for dramatic phenomena exclusively due to sliding (the horizontal shearing within so thin a layer of ice is completely negligible).
Following the Mattmark catastrophe, studies have been made by the Versuchsanstalt für Wasserbau and Erdbau of the Eidgenössischen Technische Hochschule, Zürich, by the Elektrowatt company (chief contractors for the Mattmark dam), and by the author as expert commissioned by the examining magistrate at Visp. Unfortunately because of the enquiry being conducted, it is at present impossible to publish the reports made, and only facts well known publicly, such as those reported for example by Reference VivianVivian (1966) can be used.
The layer of ice which separated as an avalanche on 30 August 1965, and buried 88 workmen employed in the construction of the Mattmark dam, had a surface area of about 100 000 m2 and a volume of 1.2×106 m3. Immediately after the catastrophe it was noticed that further uphill another similar layer of the glacier, of surface area about 60 000 m2 had detached itself from the main body and was advancing rapidly. Between this layer and the rest of the glacier, rock appeared along a growing fracture. The mean speed of the most rapid part of the layer went through a maximum between the 16th and 22nd day after the catastrophe (4.4 m/day). Two months after the catastrophe, the velocity had become very uniform in the layer and had fallen to 1.0 m/day. Röthlisberger and the author independently came to the conclusion that a similar phenomenon had occurred on the tongue of the Allalingletscher as had occurred on the Muldrow Glacier and others (Reference PostPost, 1960).
During this time, since 25 August, there had been neither melting nor rain, only snowfalls. No water came out from beneath the front of the layer. The cold (which, penetrating down crevasses must have reached the bedrock at many places) had considerably reduced the outflow of the small glacier streams.
-
i. The avalanching of the glacier tongue on a very uniform slope seems to prove that the kinetic friction is lower than the quasi-static friction and does not increase considerably with velocity. This is in agreement with my views, and contrary to Weertman’s theories (Reference WeertmanWeertman, 1957, Reference Weertman1964[a]).
-
ii. The avalanche sliding of the 30 August, and also the very rapid sliding which took place in September, do not seem to be related to an overall water layer (which makes us reject the hypothesis of Reference WeertmanWeertman (1962)).
-
iii. One can have high-speed sliding of an ice layer with friction on the bedrock significantly less than 1 bar. This can only be explained on Weertman’s theory if one allows an exceptionally small roughness of the bed.
-
iv. This high-speed sliding of an isolated layer of ice sometimes seems to be stable, which contradicts my 1965 theory (Reference LliboutryLliboutry, 1965, p. 642–52). In effect up to now we have thought that during rapid sliding stability has been assured by the contiguous parts of the glacier up- or down-stream, but here the intense crevassing of this very thin layer of ice has made it practically free and independent of the neighbouring parts.
2. Comparison Between Earlier Theories due to Weertman and the Present Author
2.1 Historial survey of the theories (the dates are those when the manuscripts were submitted to editors)
1944. Reference KoechlinKoechlin (1944) seems to have been the first person to attempt to find the theoretical friction per unit area of a glacier on its bedrock f. To do that he envisaged obstacles of height a, separated by a distance λ, and a compressive strength of the ice σ c. His friction law can be written simply if we introduce the roughness r = a/λ, as f = rσ c. This law is analogous to Coulomb’s law of solid friction in the sense that the sliding velocity does not enter, but differs from Coulomb’s law in that the normal pressure of the ice on the bedrock does not enter.
1956. Reference WeertmanWeertman (1957), combining the melting and refreezing on two opposite faces of a protuberance of the bedrock and plastic flow around the protuberance, found a pseudo-viscous flow law in which the friction f increased with sliding velocity u according to
where n is the exponent in Glen’s flow law for ice. From this one deduces a relation giving u as a function of the thickness of the glacier for a given slope of the form u = kh (n+1)/2. The weakest point in this theory is that it supposes that the ice behind the obstacle is subjected to a tensile stress of
16 July 1958. In the study of a flood wave on the Mer de Glace (Reference LliboutryLliboutry, 1958[b]), I found a static friction (later called “quasi-static”) of 1.8 bar, and a dynamic friction of 1.0 bar. In this way I explained the jerky movements observed by Reference MillecampsMillecamps (1956[a], Reference Millecamps[b]).
21 July 1958. I considered cavities down-stream from protuberances filled with water at an unknown pressure (Reference LliboutryLliboutry, 1958[a]). Together with Weertman’s two processes, called A (melting and refreezing) and B (plasticity without cavitation), one must now consider a third process C (plasticity with cavitation). I did not know how to estimate the corresponding friction f c except for protuberances very wide compared with their height and in the limiting case of very significant cavitation. It was found that f c in this case varies as
independent of the speed of sliding u. (In this expression p was the pressure in the water above atmospheric pressure, which in this article is called p–H.)
1959. I elaborated my theory in detail (Reference LliboutryLliboutry, 1959), correcting a calculating error, this gave me f c = Cu −1/(n+2) but did not modify the conclusions concerning the total friction f 0. For the value of p I always had to fall back on hypotheses.
1961. Reference ScheideggerScheidegger (1961, p. 268–72) presented the two theories, again correcting the error in the 1958 paper, although he referred to the 1959 paper and not to the 1958 one.
September 1962. At the Obergurgl symposium, Reference WeertmanWeertman (1962) criticized the hypothesis of the formation of fixed subglacial cavities. To do that he replaced the protuberances very wide compared with their height that I had envisaged by protuberances practically as wide as they are high, and he does not consider at all the existence of water filling the cavities. It was only after modifying my theory very profoundly that he was able to refute it.
Elsewhere in the same paper he considers a film of liquid water between ice and rock, supposing it to stretch continuously from one extremity of the glacier to the other. In order to explain catastrophic slidings he admits that, when a glacier flood wave arrives, the friction rises to about 2 bars and this thickens the water film until it reaches some millimetres in thickness. If one accepts that at the scale of millimetres the roughness is of the order of only about
2 October 1963. Reference Kamb and LaChapelleKamb and LaChapelle (1964) reported laboratory experiments in which there is sliding by melting and refreezing more rapid than that predicted by Weertman. They did not mention my theory. The article appeared in June 1964.
27 January 1964. I corrected Weertman’s calculation of melting and refreezing (Reference LliboutryLliboutry, 1964[a]). The temperature variations are three times larger, and the ice encloses liquid water. This leads to sliding by process A ten times faster, and seems to explain the results of Kamb and LaChapelle.
6 February 1964. In a letter to the Editor of Nature published on 4 April (Reference LliboutryLliboutry, 1964[b]), I explained catastrophic glacier advances using my theory of sliding, into which I introduced modifications. It is processes A and C which are in competition, not processes B and C. As a result of this the total friction, instead of being independent of velocity varies as u −1 (if we take n = 3).
14 February 1964. Reference WeertmanWeertman (1964[a]) improved his theory of 1957, envisaging in his turn the appearance of subglacial cavities. He supposed that the pressure in them is atmospheric pressure. This gives a different and smaller friction, but still proportional to u 2/(n+1). He also attempted to improve his calculation, and to do that introduced protuberances of different size, but limited to definite sizes in a geometric progression (…, Λ/100, Λ/10, Λ, 10Λ, 100Λ, …). No information is given on the distribution law of size; Weertman simply adds the corresponding frictions, which implicitly implies that he superposes the two sorts of protuberances instead of juxtaposing them as he does (implicitly again) in his 1957 theory. However whatever model he has in mind he immediately abandons it again to return to a continuous distribution of protuberances. This is not stated in the text, but without it, it would be absurd to envisage protuberances of a size A inversely proportional to the sliding velocity (Reference WeertmanWeertman, 1964[a], equation (8a)), as the sliding velocity can itself vary continuously.
In this paper Weertman again criticizes a theory which he attributes to me, but which is only a bad caricature of mine. He considers my mechanism C as a limiting case of his theory, whereas he ought rather compare it with the hypothesis he put forward in 1962 to explain catastrophic advances (swamping the little protuberances). He was at that time unaware of my two notes, which were in press.
This article appeared in October 1964. I had received preprints, but I thought it sufficiently secondary not to be worth modifying the corresponding chapter in my book, which was already edited.
1 May 1964. Reference WeertmanWeertman (1964[b]) gave his explanation of the experimental results of Reference Kamb and LaChapelleKamb and LaChapelle (1964).
22 May 1964. I sent to Masson & Cie., printers, the manuscript of chapters 12 to 18 of my Traité de Glaciologie (Reference LliboutryLliboutry, 1965). The galley proofs of chapter 16, including the details of the new version of my theory, were returned corrected to Masson on 8 September 1964. (An error in the calculations, which does not modify the result qualitatively, was corrected at the end of March 1965.) AIthough Tome II of the Traité appeared in the bookshops only on 14 December 1965, the theories of Reference WeertmanWeertman (1964[a]) and mine were thus worked out separately and independently.
25 February 1966. At a meeting of the Section de Glaciologie of the Société Hydro-technique de France, I presented a part of the present theory. The friction is calculated for any degree of cavitation whatsoever, the bed is considered as consisting of many superposed sinusoidal oscillations.
The first term comes from process B, the second term is that introduced in 1958, the third is that introduced in 1964.
22 February 1966. At the same time Weertman submitted to the editor of the Journal of Glaciology a criticism of my theory of 1965 (Reference WeertmanWeertman, 1967) and sent me a preprint. The principal accusation is still that it is incomplete, the pressure in the subglacial cavities not being given by the theory. Weertman will not agree that this variable can be an independent variable, a function of the amount of liquid water circulating in the subglacial hydraulic system, as is explained on p. 648 of the Traité de Glaciologie. He also puts forward the idea of a superposition of large and small sine waves, but does not make any calculations with this model.
9 March 1966. During a glaciological meeting at Zürich I reported new improvements to my theory. Using certain conditions that are generally true, p can be expressed as a function of h, which allows us to relate the rate of sliding to the thickness of the glacier. This question was reconsidered, and my law modified, in June 1966.
2.2 Relation between notations

In what follows the notation will follow that of Reference LliboutryLliboutry (1965).
2.3 Sliding in the absence of cavitation
Sliding by simultaneous melting and refreezing over obstacles of height a, width b and length l separated by distance λ is given by

According to Weertman α ≈ 1, whereas according to Reference LliboutryLliboutry (1965)

as a result of heat exchange with liquid water included in the ice.
With Weertman’s model of the bedrock (a ≈ b ≈ l), it follows that α ≈ 3.5. For very wide obstacles, which according to the present theory control the movement (a = r λ, b = λ, l = λ/2), this equation leads to

A direct calculation using a sinusoidal profile leads to

which is of the same order of magnitude. The values found in this way for the sliding velocity v A are much lower than with the cube-shaped bedrock protuberances of Weertman; a twentieth if
Now let us compare the sliding velocities due to plasticity. According to Weertman, when no cavity is formed down-stream of the obstacle,

In my theory I had the following differences from Weertman: (a) I considered that it was the widest protuberances (b ≈ λ) that controlled the movement, and (b) that ice deformed for a distance λ/4 from the bedrock, and not just by a distance a (this would be rigorously true for a perfectly plastic material and a longitudinal bed profile that was saw-toothed). This led to

To reconcile this with Weertman’s formula one would have to put

As Weertman puts a ≈ b ≈ l ≈ r λ, with n = 3,
In this case as well I obtained a sliding velocity much lower than Weertman’s; a fortieth if
For sliding without cavitation, Weertman finds Reference Weertman(1964[a], equation (8b))

with
Thus for n = 3

With

Numerically, u = 80 m/year for
My theory (Reference LliboutryLliboutry, 1965), on the other hand, leads to

that is to say Weertman’s value multiplied by 4√2k 2 r/3π 2.
Even with Weertman’s values (k = 2.31 and
2.4 Sliding with cavitation
Contrary to what one might think from fig. 16.20 of Lliboutry (1965, p. 645), it is not the first hypothesis of Reference WeertmanWeertman (1962) that has to be compared with my “process C”, but the second hypothesis of the same paper. I considered in effect a swamping of the protuberances, more effective the larger the velocity, a swamping which reduces the friction.
According to Reference WeertmanWeertman (1962, p. 36, equation (10))

where μ is the viscosity of water (= 5.7×10−16 bar year) and x is the distance from the head of the glacier. If n = 3 this reduces to

or, if C is inserted as a constant which only depends on the properties of water and ice,
In the theory in Reference LliboutryLliboutry (1965, p. 652, equation (37) with the values of C A and C C given on p. 651) one would have on the contrary

In this paper we shall see that, under certain conditons, (ρgh−p) = N is proportional to ρgh = f/α. One is then led to
Thus instead of being strongly dependent on the roughness of the bed, the sliding velocity is independent of it. This is much more logical because when the hollows are full of water their depth does not affect the sliding.
3. Sliding due to Plasticity on the Sinusoidal Model.
3.1 Friction in a sinusoidal model in the absence of separation between ice and rock
Let us first calculate the friction for a glacier bed which has only got bumps of one size regularly spaced and wide compared with their height (the term “bumps” used by skiers for the obstacles they have to overcome on pistes seems to me more appropriate than “protuberances”).
We can suppose that the flow of ice around such an obstacle takes place in a vertical plane, that is to say we treat it as a plane problem. The friction is then practically the same if the bumps are arranged irregularly, or if they are aligned in rows perpendicular to the flow, giving to the model of the bedrock chosen the appearance of a wash-board.
It is evidently completely inadmissible to introduce in such a wash-board model the little transverse trenches extending from one side of the glacier to the other. The figure published in Reference LliboutryLliboutry (1959, p. 256 and reproduced by Reference ScheideggerScheidegger (1961, p. 268) explains sufficiently clearly that the flow may be plane even if the bumps retain a finite width.
We now make a calculation for a well-defined angular frequency ω = 2π/λ and look for the corresponding friction f ω We then envisage the real bed where all frequencies are present. We therefore adopt as longitudinal bed profile
The bumps considered here are perfectly smooth and only support normal forces. It is only the asymmetry of the forces, the fact that they are larger on the uphill faces, that, when considered on the large scale, appears as a uniform friction.
In this section we are only envisaging plastic deformation of the ice without introducing supplementary sliding due to melting and refreezing. For this plastic deformation we adopt Glen’s law with n = 3, that is to say with the effective shear variables
If the principal stresses are σ 1, σ 2 = σ 1, and σ 3, and the corresponding strains

For temperate glacier ice B has the value 0.164 bar−1 year−3, but for ice very much riddled with liquid water such as is found very close to the bed of a glacier one may perhaps have much larger values, the more so if transient creep is important.
In the absence of separation we can suppose that the normal pressure that the ice exerts on the bedrock fluctuates sinusoidally about a mean value (ρgh cos α+H) with a phase difference of λ/4 compared with the relief (see Fig. 1)

Fig. 1. Pressure of ice against rock in the absence of cavitation. Vertical hatching where there is excess pressure. Horizontal hatching where pressure is reduced
On a scale large compared with the wavelength, we get the friction

or, putting a/λ = r (the roughness for the frequency ω)
There are two ways of calculating Δσ, the excess pressure on the uphill faces or the depression of pressure on the downhill ones:
-
i. We can say that under the action of an average value of, |σ 1−σ 3| equal to 2Δσ/π, the ice rises to a height a while flowing over the uphill face, that is to say in a distance of
(in Reference LliboutryLliboutry (1965) the factor of 2/π was omitted). Then we can estimate the zone within which |σ 1−σ 3| continues to have a high value as λ/4, by analogy with the case of perfect plasticity. It then follows that, if we put v for the rate of sliding

or

-
ii. Alternatively we can say that under the action of a maximum value of |σ 1−σ 3| equal to Δσ, the bottom layer of ice acquires a maximum inclination with respect to the x-axis equal to πa/λ. The velocity parallel to the x-axis being approximately v, that parallel to the z-axis must be

If we now suppose that the principal compression is always produced within a thickness λ/4, then
(5)
and it follows that
(6)
These two methods are not equivalent because the flow law of ice is not linear. The two values they lead to for the friction differ by a factor of

In the metre–bar–year system of units, and with B = 0.17 we obtain

3.2 Relation between cavitation and friction on the sinusoidal model
An important improvement to my earlier theories which is introduced here is the calculation of the friction for any degree of cavitation, approximating to a realistic hypothesis: the ice separates from the rock at the point with coordinates (x c, z c) and recontacts the bed at the point with coordinates (X c, Z c), as shown in Figure 2. We will suppose that the recontact point is situated on the tangent at the point of separation.

Fig. 2. Calculation of friction fω on the sinusoidal model for any cavitation
The cavitation will be defined by a parameter s, the ratio of the area where the ice effectively touches bedrock to the total area. The roughness a/λ being by supposition small, we can write
On the other hand X c and x c are related by the equation

which, using Equation (8) leads to

On the other hand, when there is cavitation, the normal pressure on the bedrock is no longer given by (3), as the cavities under the ice are filled with water at pressure p. This pressure p can be at most equal to the total pressure exerted by the ice and the atmosphere (ρgh cos α due to the glacier and H due to the atmosphere), otherwise the glacier will float. It may drop (at least for transient states following on some increase that occurs in velocity) down to the saturated vapour pressure of water at 0°C., i.e. practically zero. In this latter case the glacier adheres to the rock by suction. For the moment we will assume that this pressure p is given; the factors which determine it will be discussed in section 7. Following a suggestion of Reference HaefeliHaefeli (1966), this pressure p will be called the interstitial pressure, by analogy with that considered in rock mechanics.
We now put for σ 3 the following expression (Fig. 3)


Fig. 3. Pressure of ice against rock when there is cavitation. Compare with Figure 1
This expression reduces to Equation (3) when cavitation ceases (x c = X c = λ/4). Continuity dictates that
According to (8),

P will be determined by the fact that the component parallel to the z-axis must on average be equal to the sum of the pressure of the ice ρgh cos α and of the atmosphere H. As we have supposed that a ≪ λ, this means that to the second order in r

Whence, putting

The x component of the pressure σ 3 gives the mean friction f ω corresponding to a sinusoidal bedrock. The constant term p present throughout leads to

and there remains, putting

The second term of the integral can be transformed using the formula

If we replace X c by x c + λ(1−s), and

Transforming the differences between two cosines, we finally obtain the reduced friction

In this expression ωx c is given by Equation (9). A table of values is given as Table I below, and the function Φ (s) is plotted in Figure 4.

Fig. 4. Reduced friction as a function of cavitation on the sinusoidal model
Table I. Values of the Reduced Friction ϕ for Various Values of the Cavitation Parameter S

Cavitation begins when the friction f reaches the value f 0. The new and remarkable fact is that before it decreases the friction begins by increasing. It exceeds f 0 by some 33 per cent for a cavitation of about a half (s = 0.48).
When s is near to unity (incipient cavitation), putting 1−s = Φ, Equation (9) leads to
The logarithmic derivative of ϕ

now reduces to

When s is near to zero (intense cavitation), Equation (9) leads to
and Equation (14) to
The friction in relation to the area effectively in contact, f ω /s becomes equal to 2πf 0. It becomes independent of the velocity as though the ice were perfectly plastic.
Note that for s very small, Equation (12) gives P ≈ 3N/π 2 s 3. Putting x = λ−(s λ/2)+x′, we finally find in the area of actual contact a parabolic variation of the excess pressure

3.3 Cavitation as a function of the sliding velocity when only plasticity is present
In Reference LliboutryLliboutry (1965), the first calculation of section 3.1 was applied to the case of strong cavitation, replacing the whole bump by its summit alone. In doing this I introduced an error which is more and more important the larger the cavitation becomes. When the ice only touches a tiny summit of the bump, according to this reasoning the stresses are only increased for a tiny region above. However the stresses near the point of contact becomes infinitely great as the area of contact becomes infinitely small, and it is impossible for a stress to be extremely large in an extremely tiny volume, since the space derivatives cannot become infinite. An extremely large stress spreads into all the surrounding space.
It would therefore be better to make the calculation considering the situation on the roofs of the cavities, where the stresses never tend to infinity. Furthermore, the closure of a circular hole in ice is a problem for which Reference NyeNye (1953) has given an exact solution, so that we are not dealing with the completely unknown.
To estimate the slope of the roof, we again suppose that the stresses retain the same magnitude for a distance λ/4 above the roof. The principal stresses in this region are
Thus |σ 1−σ 3| = N, and the flow law for ice, Equation (2), gives us the rate at which ice descends towards the bedrock
The horizontal velocity of the ice is v, and the slope of the roofs of the cavities ω/v. Let us equate this slope to that at the point of separation,

Now if we put

Or, numerically, if we put B = 0.17 bar−3 year−1:
v 0 is the velocity at which cavitation begins, and the friction f 0 corresponds to it. Equation (6) can therefore be written more simply in terms of reduced variables as
when v ≥ v 0
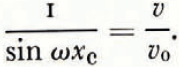
sin ωx c, being related to s by Equation (9) the problem is solved, but the analytic expression f ω (v) is not simple. The values of the reduced velocity V = v/v 0 for various values of the parameter determining the cavitation s are given in Table II. Together with Table I this gives Φ(v/v 0), shown in Figure 5. The same function is shown plotted logarithmically in Figure 6, together with s, which is plotted as the interrupted curve.

Fig. 5. The variation fω (friction on the sinusoidal model) as a function of sliding velocity v when sliding is due solely to plasticity.
Table II. Values of the Reduced Velocity V for Various Values of the Cavitation Parameter S

In the early stages of cavitation (s = 1−Φ) Equations (21) and (15) tell us that
and hence that dV/dΦ ≈ 4π 2 Φ/9. However according to Equation (16) dΦ/dΦ = 8π 2 Φ/9, thus we deduce that

The logarithmic derivative of Φ(v/v 0), i.e. the slope of the solid curve in Figure 6, thus increases suddenly from

Fig.6. Approximate expressions for fω when the sliding is solely due to plasticity.
For s very small, ωx c ≈ s 2 = v 0/v.Thus

and

so that

or, numerically, in the system of units metre-bar-year and putting, B ≈ 0.17,
For high velocities f ω decreases as
4. Sliding due to Pressure Melting on the Sinusoidal Model
4.1 Heat sources and heat transfer at the bottom of a glacier
The increase of stress on the uphill side of obstacles, the cause of the frictional force, does not only cause the plastic deformation and sliding calculated above; it also causes the ice to melt above the obstacle, and so produces a supplementary sliding. It is the amount of heat arriving at the uphill face which allows the ice to melt and so determines the sliding. This heat can have several origins:
-
i. Geothermal heat reaching the ice by conduction;
-
ii. Heat produced by the plastic deformation in the basal layers;
-
iii. Heat liberated by liquid water refreezing on the downhill faces of the bumps or on the roofs of subglacial cavities.
It is easy to see that the first two terms are negligible. Thus for (ii) the heat produced by plastic deformation is
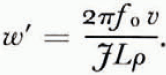
But JLρ = 3000 bar, whereas f 0 is of the order of 1 bar. This melting therefore makes the ice descend towards the rock at a speed of only w′ = v/500, whereas it moves forward with the velocity v.
As for heat transfer, this can happen in several ways:
-
i. By conduction through the rock or through the ice;
-
ii. By solid convection, the ice which has been cooled on the uphill face of a bump being replaced by warmer ice;
-
iii. By liquid convection, as a film of water circulates from the upstream face to the downstream face carrying calories with it;
-
iv. By simultaneous melting and refreezing, thanks to the liquid water content existing in the ice.
Process (i) is much more important than processes (ii) and (iii). The heat flux transported per unit area in unit time by conduction is K dθ/dx, or about 2K Δgθ/λ if Δθ is the temperature difference between the uphill and downhill faces. The heat transport by convection in the solid will be cρvΔθ where c is the heat capacity of ice and ρ its density. Their ratio is cρv λ/2K = v λ/76 if v is expressed in metres per year and λ in metres. This is very small except for big protuberances, protuberances for which sliding by melting and refreezing is in any case negligible.
As for the water film, its outflow per unit width is ρva (or of the order of ρva in the cavitation case). It thus transports c′ρvaΔθ calories where c′ is the heat capacity of water. Expressed as a fraction of the conduction term, it is of order c′ρva λ/2K. This is equally negligible for small bumps. Also this water which finds itself at a temperature below the melting point under the pressure p when it enters the cavity, only freezes in very small amounts at the actual point of entry.
As for process (iv), it hardly enters at all in the absence of cavitation, as the intense lamination of the basal ice facilitates the removal of liquid water: Reference CarolCarol (1947) observed its exudation against the rock. Thus more intergranular water should disappear above the bumps than reappears below and the process cannot take place. On the other hand, when there is cavitation, it is possible that heat transfer by melting and refreezing of intergranular water may occur. In effect the refreezing which takes place downhill against the rock may isolate liquid water from the rock, and, in a discontinuous but uninterrupted way, pockets of liquid water may be trapped in the ice as shown in Figure 7.

Fig. 7. Flow of ice in the absence of plasticity with a bedrock of sinusoidal profile. a. Without cavitation. b. With strong cavitation
4.2 State of the problem
We shall calculate the sliding v′ due to simultaneous melting and refreezing, all plasticity being excluded. We shall see that this case occurs when the size a of the obstacles is sufficiently small. With this mechanism we can also have or not have cavitation, but the cavitation will not be regular as in the case of plastic deformation. The refrozen ice which forms against the rock can only leave it intermittently as suggested in Figure 7b. The model adopted in section 3.2 and represented in Figure 3 is only an average, idealized case, and the Equations (8) to (12) derived there can in this case only be considered as approximate estimates of the average value. However we can still say that the mean friction f 0 always has a maximum equal to 1.33 f 0 for s = 0.48.
On the other hand Equations (6) and (7) and the whole of section 3.3 concerned with sliding velocities are not valid at all in this case. In particular, separation occurs at a velocity v′0, and no longer at v 0 as given by Equation (19).
To obtain the sliding velocity one has to calculate the heat flux which flows from the faces with lower pressure to those with higher pressure, and then write down that the volume of ice melted per unit width and time is equal to the sliding velocity multiplied by the height of the obstacle.
We note that, for protuberances of given transverse cross-section, the sliding will be a minimum when the width is large compared with the height. In effect in this case the heat has to flow in vertical planes, whereas for narrow protuberances heat can converge from both sides to the uphill face. Thus it is protuberances wide compared with their height which most oppose the flow and which therefore have to be considered in our calculations. This remark is the justification for continuing to restrict consideration to the plane problem.
4.3 Sliding by melting and refreezing in the absence of cavitation
We shall again consider our bedrock model having a longitudinal profile of sinusoidal shape
where C is 0.0074°C/bar.
In the rock θ satisfies the equation
At infinity in the downward direction (|z| = +∞), θ = 0, and on the bedrock θ has the value given above. The problem to be solved is thus a classical Dirichlet equation. For small roughnesses the bed can be considered as occurring at z = 0, and the solution is
Above the bed, in the temperate ice, the temperature no longer satisfies Laplace’s equation; thanks to infinitesimal melting and refreezing it adjusts itself to the variations of stress, which are not harmonic because the flow law of ice is not linear. However to obtain an order of magnitude we can consider the same variation.
The heat flux arriving per unit width between the points x and x+dxi;

where K i is the thermal conductivity of ice and K b that of bedrock.
From this the resulting melting per unit time, measured perpendicular to the surface, is

We note that the slope of the bedrock is also proportional to sin ωx. The resultant sliding is thus

where Q has been written for the total heat arriving on the uphill face. The stresses are unaffected, and therefore the friction is unaffected as well.
The friction is given by (4), so Equation (27) can be written

In particular, cavitation begins when the pressure in the centre of the downhill faces, (H+ρgh cos α−Δσ) reaches the value p, that is to say for Δσ = N The corresponding sliding velocity is v′0 given by

Numerically in the metre-bar-year system, K i = 0.0053 cal/cm deg sec = 16.8 Mcal/m deg year, Lρ = 71 Mcal/m3, C = 7.4×10−3 deg/bar, so K i C/Lρ = 1.75×10−3 m−2/bar year. If we suppose K b ≈ K i, Equation (29) reduces to
The friction corresponding to v′0 is
4.4 Sliding by melting and refreezing with cavitation
When cavitation appears, the pressure of the ice against the rock varies according to a more complicated law given by Equation (10) and shown on Figure 3. With a convenient choice of origin

To solve the Dirichlet problem which arises from the temperature distribution, this variation has to be broken down into a Fourier series. Some distance from the bedrock only the fundamental component matters, and its amplitude Δσ is given by

P is given by Equation (12). Whence, talking account of Equation (14).


With this new value of Δσ, the above calculation is always valid at a certain distance above the bedrock. When, however, we approach it, the lines of heat flux are perturbed, but, except perhaps for extreme cavitations, the total amount of heat going into the zone with over-pressure is not altered.
The cavitation only reaches the uphill sides if ωX c π, or, taking account of Equation (8), if
We find that s ≥ 0.628. The condition can also be written
Equation (27) remains valid, with the modified value of Δσ. Equation (28) is replaced by

and Equation (30) by
When sin (πs−ωx c ) sin πs, the ice only touches part of the uphill face. The irregularity to be overcome is then
Equation (28) in this case has therefore to become

or, in terms of reduced variables,

In order to suppress a discontinuity, it is better to use Equation (33) for s ≤ 0.5 instead of s ≤ 0.628.
Table III. Values of Reduced Friction Φ and Reduced Velocity V′ for Various Values of the Cavitation Parameter S

If s is very small,



or, numerically,
Figure 8 shows some approximate laws which will be useful later.

Fig. 8. Approximate expressions for fω when the sliding is solely due to pressure melting
5 Total Sliding on the Sinusoidal Model
5.1 Addibility of sliding velocities
In previous papers I have calculated the total sliding, which in this paper will be called u, by adding the sliding due to plasticity (here called v and not v B or v c according to whether there is cavitation or not) and the sliding due to pressure melting (here called v′ and not v A), i.e.
Reference WeertmanWeertman (1964[a]) has done the same addition, but it is not obvious a priori that this procedure is correct, as we are dealing with non-linear phenomena. We will therefore examine the question a little more deeply.
It is possible to reason as follows: The uphill surface of a bump is an “ablation area”. Flow lines terminate there, a flux of ice disappears (it becomes a flux of water which flows to the other side as a very thin water film). The downhill surface of the bump is an “accumulation area”. An ice flow appears there; flow lines are created. Everything therefore occurs as if the bottom layers of ice passed through the bump, that is to say as if its height were less by δ (cf. Figure 9, where the model of the bumps that has been taken is not sinusoidal but the kind considered by Weertman). In fact this is so from the point of view of the flow but not from the point of view of the stresses, which are just as high as before, since they do not simply have to enable the ice to get over an irregularity (a−δ), but also have to squeeze the bottom layer, of thickness δ, until it can cover the whole original surface of the bump.

Fig. 9. Flow of ice round a Weertman protuberance when plasticity and pressure melting act simultaneously
A simple and correct argument is the following.
At the middle of the downhill surface of a bump, whether there is cavitation or not, the ice moves downward at a velocity w due to plasticity, whose magnitude is given by the following equation deduced from Equation (5):
and a velocity w′ due to melting, whose magnitude is given by Equation (26) as

But Δσ is related to the friction by Equation (31)

In this equation we must put
For a given friction f ω we therefore have

When the two processes act simultaneously the roofs of cavities descend at a velocity (w+w′). The sliding velocity must then be (v+v′) which was what we wanted to prove.
5.2 Total sliding in the absence of cavitation
Adding the velocities of sliding given by Equations (20) and (30) we get the total velocity
In order to obtain reduced variables, let us introduce the two quantities u ⋆ and a ⋆, independent of a and defined by the equations
or


Numerically, in the metre–bar–year system, and putting K b ≈ K i and B = 0.17,
Equation (38) can now be written

It is easy to trace contours of the surface Φ(u,a). It is convenient to take reduced Iogarithmic coordinates for u and a. Putting log (u/u ⋆) = X and log (a/a ⋆) = Y (using logarithms to base 10), the contours satisfy the equation
Corresponding curves with Φ = constant shown on Figure 10 are all constructed from the limiting curve for Φ = 1

Fig. 10. Friction on the sinusoidal model fω as a function of the total sliding velocity u and the amplitude of the bumps a. Curves of fω/f0 = Φ= constant
by a simple displacement.
With increasing velocity cavitation appears (Φ = 1) first at the point X = 1, Y = 1. Put another way, when u reaches the value u ⋆ (i.e. as we shall see, for a velocity of some metres per year), separation begins in places on the bed where the undulations have amplitude a ⋆ (i.e. as we shall see, some centimetres).
The ice cannot succeed in detaching itself from the largest bumps, as the stresses are not large enough. Melting and refreezing ensure that the smallest bumps and protuberances mould themselves into the ice.
5.3 Total sliding with cavitation
When there is cavitation, if plasticity alone occurs, Equation (21) shows us that v/v 0 is a universal function (i.e. one in which no other parameter enters) of Φ, which we shall call V(Φ)
If pressure melting alone occurred, we would have

We shall call this universal function V′(Φ) (note that it is not the derivative of V(Φ)!). We can now write
or, using the quantities u ⋆ and a ⋆ defined above,

or, in logarithmic coordinates,
Curves of equal reduced friction can be constructed from Equation (44) by a displacement
Table IV. Parameters Determining the Curve Relating Reduced Sliding Velocity and Reduced Amplitude for Various Values of the Cavitation Parameter S and Reduced Friction Φ

Finally, then, the surface f ω (u,a) has the shape of an embankment or an esker with a bend in it. The crest runs horizontally (Fig. 10). Towards the right, in the region of high cavitation, the surface goes down again in a sort of cwm, instead of continuing to increase as it would in the case of Weertman’s bedrock model.
6. Friction with a More Realistic Model of the Bedrock
6.1 Bedrock formed by juxtaposing zones with sinusoidal profiles
First let us consider, as I have implicitly done in my earlier papers, a bedrock formed by a large number of individual areas randomly placed, each one of which has a pure sinusoidal profile (a mosaic of washboards). Let us suppose the roughness r to be the same for all of them. We can then define each element by the amplitude of its undulations a = r λ = 2πr/ω.
We will consider that the size of the individual areas is sufficiently small that the sliding velocity u is the same for them all. The friction f ω will be different for each area. On the scale of the glacier we will observe an average value

dS/dω, being the distribution law of the areas of the different regions, a law about which one can make various hypotheses.
In my earlier papers this difficulty was evaded; I assumed a uniform distribution of areas between two not very well defined limits, i.e. that dS/dω is a constant. In doing this I followed Weertman, who had also made the same assumption implicitly. As such a hypothesis is far from being certain, the rough argument given by Reference WeertmanWeertman (1957) seems quite adequate. This consists in saying that we only take account of bumps on which the friction is a maximum.
We are thus led to make a section of the surface f ω (u,a) which we studied above and which is shown in Figure 10, along a line of constant u. Such a section is shown in Figure 11. The resulting curve has a single maximum for u ≤ 2.75u ⋆ or thereabouts, but has two maxima for u > 2.75u ⋆.

Fig. 11. The function Φ(a) for different values of the sliding velocity u. (Sections of the surface of Figure 10 by surfaces of u = constant)
Provided there is no cavitation, the sliding velocity is the sum of the two velocities given by Equations (7′) and (29′). In the metre–bar–year system

If u is fixed

The maximum (df ω = 0) is given by ∂u/∂a = 0. In this way we get the value of a at the maximum as

This law remains valid until u = u ⋆ = 0.63N 2/100r, at which point it gives
For still higher velocities, the curve has two maxima. One corresponds to a sliding almost entirely due to plasticity, the other to a sliding almost entirely due to melting and refreezing. When the two mechanisms are of equal importance, the friction on the contrary passes through a minimum. To calculate it we must extract v(f ω ,a) and v′(f ω ,a) from the approximate formulae given in Figures 6 and 8, add them to obtain u and minimize as below.
Thus for s < 0.07, the asymptotic laws lead, in the metre–bar–year system, to
This minimum value of the friction was taken to be the maximum value by Reference LliboutryLliboutry (1965), a mistake due to using only the limiting laws for v and v′, without studying the form of the whole surface f ω (u,a). In reality the friction will be practically equal to the value at the maxima
The maximum corresponding to plasticity occurs for a value of v 0 such that u = 2v 0. From Equation (19′) we can read off a 0, the corresponding value of a. In the metre–bar–year system
The maximum corresponding to melting and refreezing occurs for a value of v′0 such that u = 1.7v′0. It follows from Equation (29′) that a must have the value
Let us take as an example, to fix our thinking, a fast-flowing alpine glacier with a depth h = 150 m, sliding at a velocity u = 80 m/year on a bedrock of roughness r = 0.075. We shall see that a plausible value of the resulting pressure is N = 7 bar. From Equations (41′) and (42′) it follows that u ⋆ = 4.25 m/year and a ⋆ = 0.023m. As u ≫ u ⋆ we find ourselves in the situation considered above. The friction is a maximum and has the value 2.1rN = 1.10. bar for the two scales a 0 = 0.88 m and a′0 = 1.05mm. However it is not reasonable to take as a model of the bedrock a mosaic of washboards with some 1000 times larger than the others! The bumps 1 mm high, corresponding to rock grains, will not be situated at the side of rocks 1 m high, but on these rocks. We must therefore superimpose our sine curves instead of juxtaposing them.
6.2 Correction terms in the friction and stability of flow
When one examines a longitudinal profile of bedrock on a map at a scale of 1:5000 for example, one can often approximate its shape to a sine curve of amplitude a = A and wavelength λ = Λ as a first approximation. Thus for the Allalingletscher in the part uncovered by the avalanche of 30 August 1965, according to unpublished profiles obtained by the E.T.H. Zürich, A = 15 m, Λ = 200 m. Under the Glacier du Tacul, some 200 to 400 m thick at its centre, M. Vallon (private communication) found A = 60 m and Λ = 800 m. In the first case A was of the same order of magnitude as the layer of ice, in the second it is 5 times smaller. Doubtless these are extreme cases. (Strangely in both cases r = A/Λ = 0.075.)
The study of the dynamics of a glacier which is wide compared with its depth can be made at two scales. We shall call these the “overall view” and the “detailed view”.
-
a. Overall view. We here consider the layer of ice as a whole sliding on a flat bed, the sine curve we have been discussing being part of the bumps on this bed. If the thickness of the glacier and the longitudinal strain-rate vary throughout the zone under study around a mean value without a systematic variation either up and down the glacier nor across the glacier, we can consider the flow to be a Nye flow as defined in Reference LliboutryLliboutry (1965, 65, p. 576). In the equation of equilibrium
(52)the two first terms average to zero, hence, by integrating across the whole thickness of the glacier, τ xz against the bedrock, which is practically equal to the friction per unit area on the bedrock f is given by (53)(This equation will not be true, for example, at the edge of a steep-walled glacier.)
(53)(This equation will not be true, for example, at the edge of a steep-walled glacier.)
-
b. Detailed view. The bumps and crests with amplitude A locally modify the stresses, and this modification is still important at the surface of the glacier. If one studies the dynamics of a glacier at the scale of some hundreds of metres to one kilometre, one observes, going down-glacier, variations in σ x . (This was observed for example by Reference NyeNye (1959) and his co-workers on Odinsbreen.) Integration of Equation (52) then leads, for the plane problem (τ xy negligible) to

Furthermore, on the detailed view, the slope of the bedrock β differs from that of the surface α. The components of the force which the bedrock applies to the glacier per unit area are

The friction is thus
(54)
Thus near the front in a zone where the flow is compressive (σ x −σ z > 0) and where the glacier is getting thinner (α−β > 0), the third term becomes important. It may however happen that, for f to have an acceptable value, sinα must be negative, that is to say on the detailed view the surface slope may change sign near the front over distances much larger than the thickness of the layer of ice. (This phenomenon has been observed in Antarctica, e.g. by Reference ShumskiyShumskiy (1966)). When one adopts this detailed view and Equation (54), we must not retain in our bedrock model the large-scale sine curve (A, Λ). It is with respect to this sine curve that we define bumps of the bedrock.
In the model of a bedrock consisting of superimposed sine curves and for high rates of sliding the two ways of thinking lead to the same result. The condition at the lower limit is that the value of f deduced from the stresses in the body of the glacier is equal to f deduced from processes occurring at the bed.
The sine curve (A, Λ) leads to a term in
In order that the equilibrium of the glacier should be stable, it is necessary that if a fortuitous cause makes the speed of sliding increase momentarily, the friction should increase as a result. If the friction decreases, the resultant force acting on the glacier is in the downhill direction, it will accelerate more and more and become an avalanche. We therefore write this condition
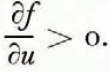
6.3 Bedrock formed by the superposition of several sine curves
A bedrock model sufficiently near to reality but still accessible to theory can be obtained by superposing several sine curves of the same roughness r = a i /λ i , but whose amplitudes a 1, a 2, …, ai , … and whose wavelengths λ 1, λ 2, …, λ i , … vary in geometrical progression. The first sine curve (a = A) can be determined from bedrock profiles obtained by seismic sounding and is therefore not arbitrary; the arbitrary features are that a i / λ i is constant and a i /a i +1 is constant and the value given to this constant. Common sense tells us that it ought to lie between 10 and 100, and we shall adopt 101.5 = 31.6.
The sine curve with a 1 = Atherefore has bumps on it of height a 2 = A/101.5, that is to say of the order of a metre. These carry little bumps of height a 3 = A/103, that is to say several centimetres, and these latter will have asperities of height a 4 = A/104.5, In general it is unnecessary to go any further as the later sine curves will have amplitudes lower than the thickness δ of the subglacial water film and do not cause any friction.
After having calculated u ⋆ and a ⋆ with the help of Equations (41′) and (42′), we can calculate log(u/u ⋆) = X and log(a i /a ⋆) = ϒ i , and plot the corresponding points M1, M2, …, Mi, on the surface Φ(X, ϒ). This has been done in Figure 12 for the case where. N ≈ 7 bars, u ≈ 80 m/year, A ≈ 40 m, and r ≈ 0.075. Figure 12 also shows the approximate expressions for Φ and s from Figures 6 and 7.

Fig. 12. Approximate formulae which allow us to calculate the friction
The total friction on the bedrock will be obtained by adding the frictions for each sine curve, i.e. f 1, f 2, f 3, …, but we must take into account in calculating fi that only the area where, on the larger scales, the ice is in effective contact with the bedrock should be used. If we use si for the value of si on a profile of amplitude ai , the friction is therefore
The study of the total friction as a function of the two variables u and N for different values of the parameters A and r characteristic of the bed can only be done by computer. One can however attempt to find approximate algebraic laws using the approximate expressions of Figure 12. Thus for alpine glaciers the two first points often fall in the top left-hand part of the diagram, corresponding to plastic deformation without cavitation, s 1 = s 2 = 1. We then obtain

The point M3 (corresponding to a = A/1000) is in the upper zone where the valid approximate law is

s 3 ≫ 1 so that the fourth term is negligible and we obtain the approximate law
But such a law is only valid in a quite restricted region; as u varies from 0 to infinity, according to Equation (57) f should vary from +∞ to −∞ passing through a minimum. However, in reality for very low velocities there is no cavitation and f tends to 0 with u; for very high velocities there is cavitation everywhere and f also tends to 0, passing through a maximum. Equation (57) is therefore only of use to give an approximate value of f, and at best of ∂f/∂u, but seems to give a quite false ∂2 f/∂u 2.
The f(u) given by Equation (57) is shown in Figure 13. It is a function that remains for a long time near to its minimum value

Fig. 13. Friction f as a function of the sliding velocity u for a given resultant pressure N
which occurs at
For alpine glaciers which slide rapidly on their beds we can therefore say that to a first approximation the friction is given by Equation (58). This is Coulomb’s law of solid friction in the presence of an interstitial pressure; the normal pressure H + ρgh cos α is replaced by the resultant pressure N.
6.4 Stability of the flow on the above model
If Coulomb’s law were rigorously valid, ∂f/∂u = 0, and a glacier would be in neutral equilibrium; it could slide at any speed without either accelerating or decelerating. In practice ∂f/∂u, on the overall view, must be always slightly positive, since glaciers are in general stable and ice avalanches are a rare phenomenon. If Equation (57) is valid, for ∂f/∂u to be positive u would have to be greater than u m. But for Equation (57) to be valid, it is necessary that cavitation does not appear behind second order bumps, that is to say sliding by melting and refreezing over these bumps is negligible, u < v 0 where
Above this value, f2 ceases to increase, and soon begins to decrease. As this term dominates in f, ∂f/∂u becomes negative and the glacier becomes unstable again.
With our chosen model of the rock bed (and assuming that this heuristic treatment contains no gross errors), glacier flow is only stable between two limits. One must have
If the sliding becomes less than the lower limit, it falls irreversibly to a very low value. If it exceeds the upper limit it increases irreversibly, and a catastrophic advance or ice avalanche results.
The study of actual glaciers does not contradict this hypothesis, and even seems to support it. With B = 0.17 year−1 bar−3, A = 15 to 40 m, N = 4 to 7 bars and r = 0.1 to 0.07, we find acceptable values of u.
Now let us look at the case of the detached fragment of the tongue of the Allalingletscher. ρgh cos αwas of order 2 bars and N was even smaller. The representative points for the different sine curves occur far to the right on Figure 12, in the zone where ∂f/∂u < 0, that is to say in unstable flow. The fact that this detached fragment did not form part of an avalanche as another fragment had on 30 August shows that in this case something new has occurred, and that the theory must be modified. The new fact is the collapse of the subglacial cavities. Those corresponding to M1 would be some 200 in long, and those to m2 some 6 m long, whereas the layer of ice is only 15 m thick. The first ones could never form, nor could many of the second; the glacier would break into pieces and then reform. Cavitation disappears, and we again take for f 1, and possibly for f 2, the equation
6.5 Suggestions for the improvement of the bedrock model
The laws of friction depend essentially on the bedrock model adopted, and all future progress in the theory depends above all on making quantitative field studies of the morphology of glacier beds. Unfortunately the few mathematical studies of such profiles made hitherto are not of much use for our present problem.
Reference Stone and DugundjiStone and Dugundji (1965) have surveyed a limited longitudinal profile and studied its level with respect to the horizontal Z(x) for 0 ≤ x ≤ L. To do this they double it by symmetry Z(−x) = Z(x), and then decompose it as a Fourier series for the symmetrical profile of length 2L which results. A smooth inclined plane would thus turn into a saw-tooth and hence give an infinite number of harmonics!
Reference Jaeger and SchuringJaeger and Schuring (1966) perform a true spectral analysis (decomposition by a Fourier integral, and not by a Fourier series), but still take a horizontal plane for reference, and not a surface that follows the general slope of the terrain. Furthermore the band of frequencies they study is too narrow; between the largest wavelengths they can reveal and the smallest the ratio is only 102 or 103 whereas it ought to be 106 or 107.
Once we possess such a spectral analysis, we could tell which were the wavelength regions most represented in the bedrock, choose four or five such bands, (λ 1, λ′1), (λ 2,λ′2), …, (λ i ,λ′ i ), …, which were quite distinct and far from one another, and neglect all wavelengths outside these bands.
The profile obtained if we consider only one of these bands, that is to say only the λ in the interval (λ i ,λ′ i ) constitutes a “pseudo-sine curve” to replace the perfect sine curve (a i , λ i ) of the theory above. This pseudo-sine curve will appear as a succession of bumps of irregular amplitude and length (Fig. 14). This will mean that the ice will always impinge on an appreciable part of some bumps which are larger than those that preceded them, such as bumps numbered 3 or 8. But on the other hand bumps immediately behind, such as those numbered 4, 6 and 7, may be completely overridden for quite moderate speeds. We may hope that these two facts will to some extent compensate and that the law relating the slope of the roofs of the cavities (−m = −πr sin ωx c ) to the fraction of the bedrock effectively in contact with the ice s will remain approximately valid. But this is by no means certain, and so I suggest the following experiment:

Fig. 14. Cavitation with a “pseudo-sine curve”
One dark night one should illuminate the surface of a glacier bed recently uncovered by a glacier with glancing illumination. The projected rays should be directed in the direction of movement of the glacier, and make an angle m with the general slope of the bedrock. By means of a vertical photograph one can planimeter the illuminated surfaces and so measure the real ice—rock contact area (that we have called s) when ice descends downhill from its protuberances with a slope m. In this way the law relating s(m) can be found. In this experiment λ i will be the length of the zone photographed, λ′ i the minimum length of illuminated patches below which one cannot planimeter them.
It is worth noting that even if studies of this type have not yet been made on Earth, they have already been carried out on the Moon. The length of the shadows photographed by the Surveyor satellite, or the variation of brilliance of the lunar surface as a function of phase angle, allow us to determine s(m). But even if the lunar relief contains “cirques”, it would seem to be ruled out that these are a glacial relief!Footnote *
7. Evaluation of the Resultant Pressure N
7.1 Thickness of the subglacial water film
Heat flow through the Earth melts about 5 mm of ice per year at the bottom of a temperate glacier, and the heat produced by plastic deformation in the basal layers melts a further few centimetres. (This latter melting takes place within the ice, but the water produced is continuously exuded towards the rock.) In this way a film of subglacial water is formed which can completely swamp the smallest bumps and can thicken into cavities below the medium-sized bumps. In the steady state this interstitial water is connected with the subglacial streams which form what we call the subglacial hydraulic system of the glacier. These streams are fed principally from the glacier surface by water which descends moulins. Following a period of enhanced melting or of heavy rain, the pressure may increase in the subglacial channels, and the direction of flow of the interstitial water might even reverse. Even though we lack direct observations on this water film, these conclusions seem reasonably certain as the subglacial hydraulic system is an experimental fact. (Let us recall that according to Reference WeertmanWeertman (1962) the water film is continuous from the bergschrund at the top of the glacier down to the snout, getting thicker all the time.)
Weertman estimates the loss of pressure head per unit length to be ρg sin α (α being as before the angle between surface angle and the horizontal). This would only be true if the bedrock were horizontal. In reality the loss of pressure through the water film must depend on the distance D that the water has to flow and the pressure head H w in the subglacial hydraulic system. Here we envisage only the case when the subglacial hydraulic system is at atmospheric pressure and when there is no cavitation. The pressure in the water film (which is simply the mean value of the normal pressure σ 3 envisaged in paragraph 3.1) drops from a value p M to H over a distance D. To simplify the situation let us suppose that the lines of flow in the water film are parallel. The mean value of the hydrostatic pressure in the film is thus
The loss of pressure per unit length of the water film is thus (2ρgh cos α)/D, and the volume lost per unit width of film

where δ is the thickness of the water film and μ. the viscosity of water at 0°C. If x is the distance from the point where the pressure is p M, the heat produced by the friction is xuf, that due to geothermal heat is negligible. The amount of water produced is thus
Equating these two expressions for the outflow and remembering that f = ρgh sin α, we finally obtain

The average value of

Numerically with μ =5.7×10−6 bar year and JLρ ′ = 3340 bars:

Even if D is 100 m and u 100 m/year,
7.2 Evaluation of the pressure HW in the subglacial hydraulic system
There are three possible cases, which lead to three different laws for p and thus for f(u).
-
i. Subglacial hydraulic system at atmospheric pressure H. This will be the case for mountain glaciers when the slope of the bedrock is important and excluding periods producing large quantities of water.
-
ii. Subglacial hydraulic system being filled. This will be the case for the same glaciers with an inclined bed during periods producing large quantities of water or sufficiently far from the snout. In this case in the given region of the glacier the pressure in the hydraulic system, H w, increases with depth according to the laws of hydrostatics
(62)
where ρ′g is the specific gravity of water, h the depth of the glacier, and h w the depth of water in the “wells”, i.e. in the moulins. This latter quantity is not well defined, and varies from time to time. To simplify the situation we may consider it to be equal to the depth of the crevasses and therefore constant.
-
iii. Flooded subglacial hydraulic system. This case is like the previous one but with (h−h W) equal to a constant ζ. It occurs in overdeepened zones in which the water cannot escape unless it gets over a sill (ζ is therefore the height difference between this sill and the bedrock, as in Figure 15a). This case will also occur for glaciers ending in the sea or a lake (ζ is then the height of the bedrock compared with sea-level or lake level, as in Fig. 15b). We therefore write
(63)

Fig. 15. Case when the subglacial hydraulic system is under pressure. a. An overdeepened zone. b. Near a calving front
7.3 Estimation of the interstitial pressure p and the resultant pressure N
The bumps envisaged in the present theory of cavitation, although wide compared with their height, are not infinitely wide. Cavities down-glacier from bumps cover a finite area, of the order of λ 2. Water is continually accumulating there, so they must have some outflow. (Without this the cavitation would continually increase, and the friction would drop to zero, as has been shown by recent experiments of Reference BrepsonBrepson (1966).) These outflows cannot connect with the up-glacier faces of the bumps, where there is a significant overpressure of the ice, but at the sides in regions where ice pressure is near to its average value.
In the steady state in order that water formed beneath the glacier can be drained out, the subglacial cavities must be grouped like a string of beads, with the interstitial pressures continuously decreasing (Fig. 16). The minimum pressure, at the end of the string, will be that appropriate to the subglacial hydraulic system, i.e. H w To find the maximum pressure, imagine the outflows to be too large and the drop of pressure between the successive cavities too small. Ice will flow to close such outflows and to increase the pressure drops. This process will stop when, at the top of the string, H+ρgh cos α = p. Along the string of beads, in the steady state, we therefore have

Fig. 16. String of subglacial cavities flowing into a subglacial stream
The mean value of p will therefore be
where κ is a factor which depends on the network of beads and subglacial channels;
From this we deduce a mean value of the resultant pressure N which enters to the first order in the expression for the friction.
Case (a). H W = H.
This was suggested as a hypothesis, without justification, by Reference Hubbert and RubeyHubbert and Rubey (1959).
Case (b). H W given by Equation (62).
This relation only remains valid if h w ≤ h ≤ h w ρ′/(ρ′−ρ cos α) or (as cos α ≈ 1 and ρ≈0.89)
If h < h w Equation (65) is valid; if h > 9h w the glacier is floated by the water which accumulates at the bottom of the glacier.
Case (c). H W given by Equation (63).
provided h> ρ′ζ/ρ cos α, without which the glacier is floated. When N does not enter to the first order, its appropriate mean value will be given by similar expressions but with different values of κ.
It is obvious that these approximate calculations do not take account of transient phenomena which can occur in the hydraulic system and the subglacial cavities when there is an advance or retreat of the glacier (such as the “suction effect” already mentioned).
7.4 Slope of a glacier with the Coulomb friction law
Using the value of N estimated in this way in the approximation given by Equation (58) (the Coulomb friction law), we obtain a friction directly proportional to the thickness h. As we also know that, on the overall view, f and h are related by Equation (53), it follows that there is a direct relation between h and α.
Case (a). (Sloping bedrock, subglacial channels at atmospheric pressure.) Here
Thus if κ = 0.58 and r = 0.075, tanα≈0.12. We are dealing with an average slope of the glacier. Ice falls or the snout region must be studied from the detailed view; these questions will be discussed in a later paper.
Case (c). (Overdeepened regions, glaciers ending in water.) In this case

The slope is less than in the preceding case. It becomes zero at the actual front, where h = ρ′ζ/ρ (the glacier begins to float, and as a result calves icebergs with the aid of the tide).
These results are in qualitative agreement with the facts. It is thus suggested that the mean slope of a glacier which is sliding rapidly on its bed gives some idea of the roughness at the scale of λ 2 (bumps of the order of magnitude of a metre).
7.5 Kinematic waves in case (a) using Equation (57) for the friction
Our interest in the overall view is that it allows us to study kinematic waves. If we put on one side case (b) (subglacial hydraulic system being filled), a case which only occurs for a short period each year, the interstitial pressure p (or the resultant pressure N) cease to be independent variables. The friction deduced for processes occurring at the bed of the glacier is only a function of u, h and α. But we have also seen that on the overall view (and on that alone), the friction deduced from the equilibrium of the glacier, Equation (53), only depends on h and α. Eliminating the friction, it follows that u is a function solely of h and α.
This is the condition for us to be able to write an equation with perturbations, and to speak of kinematic waves. When the velocity due to deformation within the body of the glacier is negligible compared with the sliding velocity, the speed of kinematic waves of material flow can be written (see e.g. Reference LliboutryLliboutry, 1965, p. 737–41)
and their diffusion coefficient
Unfortunately we have not obtained any simple law for f (u, N), but have had to content ourselves with the approximations given above. The first approximation (f independent of u) is very simple—it leads to a glacier reacting like a solid block, without any wave propagation. We must therefore use the second approximation (Equation (57)), which is only valid in a restricted region. Here we limit ourselves to discussing case (a), the study of case (c) being left for a later paper. Equations (53), (57) and (65) lead to
Whence

Only the positive root corresponds to a stable equilibrium. We note that the surface slope, tan α, must be greater than the limiting value given by Equation (68), which is a first approximation for it.
In the region where the approximation given by Equation (57) is valid, the sliding velocity u is therefore proportional to h 3. (This simple law recalls that of Weertman, with m = n instead of

∂u/∂α tends to infinity as tanα approaches its limiting value 2.72rκ. The diffusion of kinematic waves will therefore always be very marked in zones with strong sliding.
It is thus not the existence of kinematic waves travelling about four times faster than the ice, but their extremely rapid diffusion, which can be adduced as an argument in favour of the present theory.
Conclusion
The reader will, I hope, excuse this long and complicated theory, since natural phenomena are not simple. As Paul Valéry said “Tout ce qui est simple est faux” (everything simple is untrue). But he added “Tout ce qui est complexe est inutilisable” (everything complex is unusable). I hope I have demonstrated an exception; the laws of friction found are in the end simple, and depend on only a few parameters.
This general theory of cavitation throws light on several important factors about which we are extremely ill informed. Until they have been studied better, it is useless to develop the theory further.
-
a. It would be desirable to make spectral analyses of rock beds over a very wide range of wavelengths (106 to 107).
-
b. The interstitial pressure at the bottom of a glacier ought to be measured; to do this it would be sufficient to bore completely through a glacier, put a pressure measuring device at the bottom, and close up the hole.
-
c. The conditions under which a subglacial cavity would collapse when the glacier thickness is too small ought to be determined.
-
d. The rheological properties of ice saturated with water (not only its steady-state creep but also transient creep) are practically unknown.
This theory shows us, among other things, the difficulty there is in getting plastic deformation of temperate ice in the laboratory. When the specimen is not very large in size, it is always melting and refreezing processes which predominate. Experiments at present being made by M. Brepson in my laboratory show that the enormous viscometer containing specimens weighing 20 kg is hardly large enough.
Finally this theory should also suggest work to theorists, as the boundary condition at the bottom of the glacier which we have found is not one of the three conditions usually used.
In finishing it is a pleasure to thank Dr. J. W. Glen for having accepted responsibility for the translation of this paper into English.
































