Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T23:00:33.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Piezoelectric polymer thin films with architected cuts

Published online by Cambridge University Press:  14 February 2018

Lichen Fang ,
Jing Li ,
Zeyu Zhu ,
Santiago Orrego  and
Sung Hoon Kang Open the ORCID record for Sung Hoon Kang [Opens in a new window]
Lichen Fang
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA; and Hopkins Extreme Materials Institute, Johns Hopkins University, Baltimore, Maryland 21218, USA
Jing Li
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA; Hopkins Extreme Materials Institute, Johns Hopkins University, Baltimore, Maryland 21218, USA; and Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology, Wuhan, Hubei 430070, China
Zeyu Zhu
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA; and Hopkins Extreme Materials Institute, Johns Hopkins University, Baltimore, Maryland 21218, USA
Santiago Orrego
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA; and Hopkins Extreme Materials Institute, Johns Hopkins University, Baltimore, Maryland 21218, USA
Sung Hoon Kang*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA; and Hopkins Extreme Materials Institute, Johns Hopkins University, Baltimore, Maryland 21218, USA
*
a)Address all correspondence to this author. e-mail: shkang@jhu.edu
Get access

Abstract

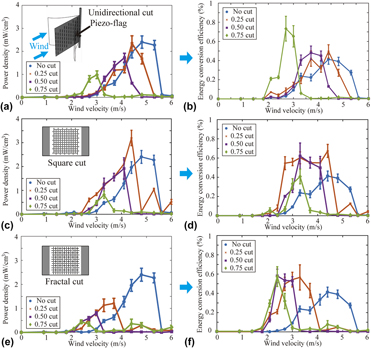
Introducing architected cuts is an attractive and simple approach to tune mechanical behaviors of planar materials like thin films for desirable or enhanced mechanical performance. However, little has been studied on the effects of architected cuts on functional materials like piezoelectric materials. We investigated how architected cut patterns affect mechanical and piezoelectric properties of polyvinylidene fluoride thin films by numerical, experimental, and analytical studies. Our results show that thin films with architected cuts can provide desired mechanical features like enhanced compliance, stretchability, and controllable Poisson’s ratio and resonance frequency, while maintaining piezoelectric performance under static loadings. Moreover, we could observe maximum ∼30% improvement in piezoelectric conversion efficiency under dynamic loadings and harvest energy from low frequency (<100 Hz) mechanical signals or low velocity (<5 m/s) winds, which are commonly existing in ambient environment. Using architected cuts doesn't require changing the material or overall dimensions, making it attractive for applications in self-powered devices with design constraints.

Keywords

polymerfilmpiezoelectric
Type
Invited Articles
Information
Journal of Materials Research , Volume 33 , Issue 3: Focus Issue: Architected Materials , 14 February 2018 , pp. 330 - 342
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Christopher Spadaccini

References

REFERENCES

Valdevit, L., Jacobsen, A.J., Greer, J.R., and Carter, W.B.: Protocols for the optimal design of multi-functional cellular structures: From hypersonics to micro-architected materials. J. Am. Ceram. Soc. 94, 1–20 (2011).CrossRefGoogle Scholar
Lakes, R.: Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040 (1987).CrossRefGoogle ScholarPubMed
Choi, J.B. and Lakes, R.S.: Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Fract. 80, 73–83 (1996).CrossRefGoogle Scholar
Lowe, A. and Lakes, R.S.: Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 19, 157–167 (2000).Google Scholar
Martz, E.O., Lakes, R.S., Goel, V.K., and Park, J.B.: Design of an artificial intervertebral disc exhibiting a negative Poisson’s ratio. Cell. Polym. 24, 127–138 (2005).CrossRefGoogle Scholar
Greaves, G.N., Greer, A.L., Lakes, R.S., and Rouxel, T.: Poisson’s ratio and modern materials. Nat. Mater. 10, 823–837 (2011).CrossRefGoogle ScholarPubMed
Osanov, M. and Guest, J.K.: Topology optimization for architected materials design. Annu. Rev. Mater. Res. 46, 211–233 (2016).CrossRefGoogle Scholar
Schaedler, T.A. and Carter, W.B.: Architected cellular materials. Annu. Rev. Mater. Res. 46, 187–210 (2016).CrossRefGoogle Scholar
Bertoldi, K.: Harnessing instabilities to design tunable architected cellular materials. Annu. Rev. Mater. Res. 47, 51–61 (2017).CrossRefGoogle Scholar
Lakes, R.S.: Negative-Poisson’s-ratio materials: Auxetic solids. Annu. Rev. Mater. Res. 47, 63–81 (2017).CrossRefGoogle Scholar
Overvelde, J.T.B., Weaver, J.C., Hoberman, C., and Bertoldi, K.: Rational design of reconfigurable prismatic architected materials. Nature 541, 347–352 (2017).CrossRefGoogle ScholarPubMed
Reis, P.M., Jaeger, H.M., and van Hecke, M.: Designer matter: A perspective. Extreme Mech. Lett. 5, 25–29 (2015).CrossRefGoogle Scholar
Bertoldi, K., Reis, P.M., Willshaw, S., and Mullin, T.: Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 22, 361–366 (2010).CrossRefGoogle ScholarPubMed
Kim, K., Ju, J., and Kim, D.M.: Porous materials with high negative Poisson’s ratios—A mechanism based material design. Smart Mater. Struct. 22, 084007 (2013).CrossRefGoogle Scholar
Virk, K., Monti, A., Trehard, T., Marsh, M., Hazra, K., Boba, K., Remillat, C.D.L., Scarpa, F., and Farrow, I.R.: SILICOMB PEEK kirigami cellular structures: Mechanical response and energy dissipation through zero and negative stiffness. Smart Mater. Struct. 22, 084014 (2013).CrossRefGoogle Scholar
Taylor, M., Francesconi, L., Gerendas, M., Shanian, A., Carson, C., and Bertoldi, K.: Low porosity metallic periodic structures with negative Poisson’s ratio. Adv. Mater. 26, 2365–2370 (2014).CrossRefGoogle ScholarPubMed
Jiang, Y. and Li, Y.: 3D printed chiral cellular solids with amplified auxetic effects due to elevated internal rotation. Adv. Eng. Mater. 19, 1600609 (2017).CrossRefGoogle Scholar
Cho, Y., Shin, J.H., Costa, A., Kim, T.A., Kunin, V., Li, J., Lee, S.Y., Yang, S., Han, H.N., Choi, I.S., and Srolovitz, D.J.: Engineering the shape and structure of materials by fractal cut. Proc. Natl. Acad. Sci. U. S. A. 111, 17390–17395 (2014).CrossRefGoogle ScholarPubMed
Shan, S., Kang, S.H., Raney, J.R., Wang, P., Fang, L., Candido, F., Lewis, J.A., and Bertoldi, K.: Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301 (2015).CrossRefGoogle ScholarPubMed
Restrepo, D., Mankame, N.D., and Zavattieri, P.D.: Phase transforming cellular materials. Extreme Mech. Lett. 4, 52–60 (2015).CrossRefGoogle Scholar
Liu, J., Gu, T., Shan, S., Kang, S.H., Weaver, J.C., and Bertoldi, K.: Harnessing buckling to design architected materials that exhibit effective negative swelling. Adv. Mater. 28, 6619–6624 (2016).CrossRefGoogle ScholarPubMed
Shan, S.C., Kang, S.H., Wang, P., Qu, C.Y., Shian, S., Chen, E.R., and Bertoldi, K.: Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Adv. Funct. Mater. 24, 4935–4942 (2014).CrossRefGoogle Scholar
Javid, F., Wang, P., Shanian, A., and Bertoldi, K.: Architected materials with ultra-low porosity for vibration control. Adv. Mater. 28, 5943–5948 (2016).CrossRefGoogle ScholarPubMed
Raney, J.R., Nadkarni, N., Daraio, C., Kochmann, D.M., Lewis, J.A., and Bertoldi, K.: Stable propagation of mechanical signals in soft media using stored elastic energy. Proc. Natl. Acad. Sci. U. S. A. 113, 9722–9727 (2016).CrossRefGoogle ScholarPubMed
Shan, S., Kang, S.H., Zhao, Z., Fang, L., and Bertoldi, K.: Design of planar isotropic negative Poisson’s ratio structures. Extreme Mech. Lett. 4, 96–102 (2015).CrossRefGoogle Scholar
Tang, Y.C., Lin, G.J., Han, L., Qiu, S.G., Yang, S., and Yin, J.: Design of hierarchically cut hinges for highly stretchable and reconfigurable metamaterials with enhanced strength. Adv. Mater. 27, 7181–7190 (2015).CrossRefGoogle ScholarPubMed
Sodano, H.A., Inman, D.J., and Park, G.: A review of power harvesting from vibration using piezoelectric materials. Shock Vib. Digest 36, 197–206 (2004).CrossRefGoogle Scholar
Toprak, A. and Tigli, O.: Piezoelectric energy harvesting: State-of-the-art and challenges. Appl. Phys. Rev. 1, 031104 (2014).CrossRefGoogle Scholar
Rajabi, A.H., Jaffe, M., and Arinzeh, T.L.: Piezoelectric materials for tissue regeneration: A review. Acta Biomater. 24, 12–23 (2015).CrossRefGoogle ScholarPubMed
Hwang, G-T., Park, H., Lee, J-H., Oh, S., Park, K-I., Byun, M., Park, H., Ahn, G., Jeong, C.K., No, K., Kwon, H., Lee, S-G., Joung, B., and Lee, K.J.: Self-powered cardiac pacemaker enabled by flexible single crystalline PMN-PT piezoelectric energy harvester. Adv. Mater. 26, 4880–4887 (2014).CrossRefGoogle ScholarPubMed
Lee, K.Y., Gupta, M.K., and Kim, S.W.: Transparent flexible stretchable piezoelectric and triboelectric nanogenerators for powering portable electronics. Nano Energy 14, 139–160 (2015).CrossRefGoogle Scholar
Hwang, G.T., Kim, Y., Lee, J.H., Oh, S., Jeong, C.K., Park, D.Y., Ryu, J., Kwon, H., Lee, S.G., Joung, B., Kim, D., and Lee, K.J.: Self-powered deep brain stimulation via a flexible PIMNT energy harvester. Energ. Environ. Sci. 8, 2677–2684 (2015).CrossRefGoogle Scholar
Fan, F.R., Tang, W., and Wang, Z.L.: Flexible nanogenerators for energy harvesting and self-powered electronics. Adv. Mater. 28, 4283–4305 (2016).CrossRefGoogle ScholarPubMed
Wang, X., Niu, S., Yi, F., Yin, Y., Hao, C., Dai, K., Zhang, Y., You, Z., and Wang, Z.L.: Harvesting ambient vibration energy over a wide frequency range for self-powered electronics. ACS Nano 11, 1728–1735 (2017).CrossRefGoogle Scholar
Orrego, S., Shoele, K., Ruas, A., Doran, K., Caggiano, B., Mittal, R., and Kang, S.H.: Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 194, 212–222 (2017).CrossRefGoogle Scholar
Smith, W.A.: Optimizing electromechanical coupling in piezocomposites using polymers with negative Poisson’s ratio. Proc. IEEE 1, 661–666 (1991).Google Scholar
Iyer, S., Alkhader, M., and Venkatesh, T.A.: Electromechanical behavior of auxetic piezoelectric cellular solids. Scr. Mater. 99, 65–68 (2015).CrossRefGoogle Scholar
Li, Q., Kuang, Y., and Zhu, M.L.: Auxetic piezoelectric energy harvesters for increased electric power output. AIP Adv. 7, 015104 (2017).CrossRefGoogle Scholar
Qi, Z., Campbell, D.K., and Park, H.S.: Atomistic simulations of tension-induced large deformation and stretchability in graphene kirigami. Phys. Rev. B 90, 245437 (2014).CrossRefGoogle Scholar
Blees, M.K., Barnard, A.W., Rose, P.A., Roberts, S.P., McGill, K.L., Huang, P.Y., Ruyack, A.R., Kevek, J.W., Kobrin, B., Muller, D.A. and McEuen, P.L.: Graphene kirigami. Nature 524, 204–207 (2015).CrossRefGoogle ScholarPubMed
Grima, J.N. and Evans, K.E.: Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 19, 1563–1565 (2000).CrossRefGoogle Scholar
Supplementary material: File

Fang et al. supplementary material

Fang et al. supplementary material 1

Download Fang et al. supplementary material(File)
File 3.8 MB