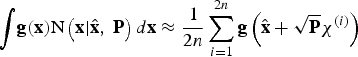1. INTRODUCTION
Underwater vehicles are used for a wide range of applications, including underwater mapping, oceanographic and bathymetric surveys and repair and inspection of subsea infrastructures in the oil and gas industries (Kinsey et al., Reference Kinsey, Eustice and Whitcomb2006; Leonard et al., Reference Leonard, Bennett, Smith and Feder1998). The traditional approach for navigation of underwater vehicles is dead reckoning (DR) (Brokloff, Reference Brokloff1997; Kinsey and Whitcomb, Reference Kinsey and Whitcomb2007). In the two-dimensional DR approach, the current position is calculated knowing the previous position and measurements of the velocity and heading (Groves, Reference Groves2008; Titterton and Weston, Reference Titterton and Weston2004; Hide et al., Reference Hide, Moore, Hill and Park2006). In underwater navigation, the velocity of the vehicle is measured using a Doppler Velocity Log (DVL) and the heading measurement is provided by a compass. Because the DVL needs at least three beams to measure the bottom track velocity, it would malfunction under conditions of large roll and pitch. Furthermore, the DVL's ping rate is generally slow (3–7 Hz) and dependency of the DVL signal on the acoustic environment causes the DVL to occasionally be unavailable (Farrell, Reference Farrell2008). The other disadvantage of the DR approach arises from the inaccuracy of the velocity data caused by internal biasing errors, external random errors and also error in heading measurement which causes the position error to grow with time due to the error in transformation of the velocity from body frame to navigation frame and time integration of the velocity signal (Jalving et al., Reference Jalving, Gade and Hagen2003).
A Strap-down Inertial Navigation System (SINS) estimates position, velocity, and orientation of the vehicle using the signals measured by an Inertial Measurement Unit (IMU) and is based on the dead-reckoning principle (Pitman, Reference Pitman1962; Britting, Reference Britting1971; Moore et al., Reference Moore, Hill, Norris, Hide, Park and Ward2008). The IMU is composed of a triad of orthogonal accelerometers and gyroscopes. Due to different noise sources in accelerometers and gyroscopes, and the successive time integration of the acceleration, the position error increases with time (Jekeli, Reference Jekeli2001; Grewal et al., Reference Grewal, Weill and Andrews2007; Atia et al., Reference Atia, Karamat and Noureldin2014). In order to bound the error growth, the SINS is used together with other navigation aids. In an underwater integrated navigation system, it is common to use auxiliary sensors such as the DVL, compass, depth meter, Global Positioning System (GPS) and Acoustic Positioning System (APS) to reduce the position error. Systems with several beacons mounted on a surface vessel have largely been superseded by Ultra-Short Baseline (USBL) systems. These use a single-phase array transponder on the ship that enables direction to be measured as well as range (Kinsey et al., Reference Kinsey, Eustice and Whitcomb2006; Stutters et al., Reference Stutters, Liu, Tiltman and Brown2008; Paull et al., Reference Paull, Saeedi, Seto and Li2014).
Over the last decade, numerous papers have utilised these sensors for underwater vehicle navigation (Yun et al., Reference Yun, Bachmann, McGhee and Whalen1999; Larsen, Reference Larsen2000; McEwen et al., Reference McEwen, Thomas, Weber and Psota2005; Kussat et al., Reference Kussat, Chadwell and Zimmerman2005; Jo and Choi, Reference Jo and Choi2006; Lee et al., Reference Lee, Jun, Kim, Lee, Aoki and Hyakudome2007; Miller et al., Reference Miller, Farrell, Zhao and Djapic2010; Hegrenaes and Hallingstad, Reference Hegrenaes and Hallingstad2011; Shabani et al., Reference Shabani, Gholami and Davari2015). Due to unavailability of GPS signals under the water, it is not possible to correct the SINS output using GPS data (Grenon et al., Reference Grenon, An, Smith and Healey2001; Marco and Healey, Reference Marco and Healey2001). APS are alternative approaches for aiding the SINS in underwater applications. However, since these types of system utilise several beacons to be either installed on the sea floor or mounted to a surface vessel, their operation range is restricted. In addition, the calibration and alignment of the beacons are time consuming and installation and maintenance of such systems are expensive (Stutters et al., Reference Stutters, Liu, Tiltman and Brown2008; Grenon et al., Reference Grenon, An, Smith and Healey2001). In order to perform independent underwater navigation, the use of on board auxiliary sensors, such as depth meter, DVL and compass are indispensable. Such sensors may be used to correct the SINS output without the need to use sources outside the vehicle.
In the strap-down underwater integrated navigation system, the DVL plays a critical role in bounding the SINS drift. However, over time intervals where the DVL is unavailable, the position error of the SINS increases quickly with time. Thus, due to a nonlinear dynamic system, the type of prediction algorithm becomes increasingly important. The prevalent method for incorporating the SINS output and the auxiliary signals is the Kalman filter (Grewal and Andrews, Reference Grewal and Andrews2008; Brown and Hwang, Reference Brown and Hwang1997; Bar-Shalom et al., Reference Bar-Shalom, Lee and Kirubarajan2001). In the last decade, in many cases, indirect filtering has been utilised for correcting the drift of the SINS output in underwater integrated navigation systems (Larsen, Reference Larsen2000; Jo and Choi, Reference Jo and Choi2006; Lee et al., Reference Lee, Jun, Kim, Lee, Aoki and Hyakudome2007; Miller et al., Reference Miller, Farrell, Zhao and Djapic2010; Hegrenaes and Hallingstad, Reference Hegrenaes and Hallingstad2011; Zhao and Gao, Reference Zhao and Gao2004).
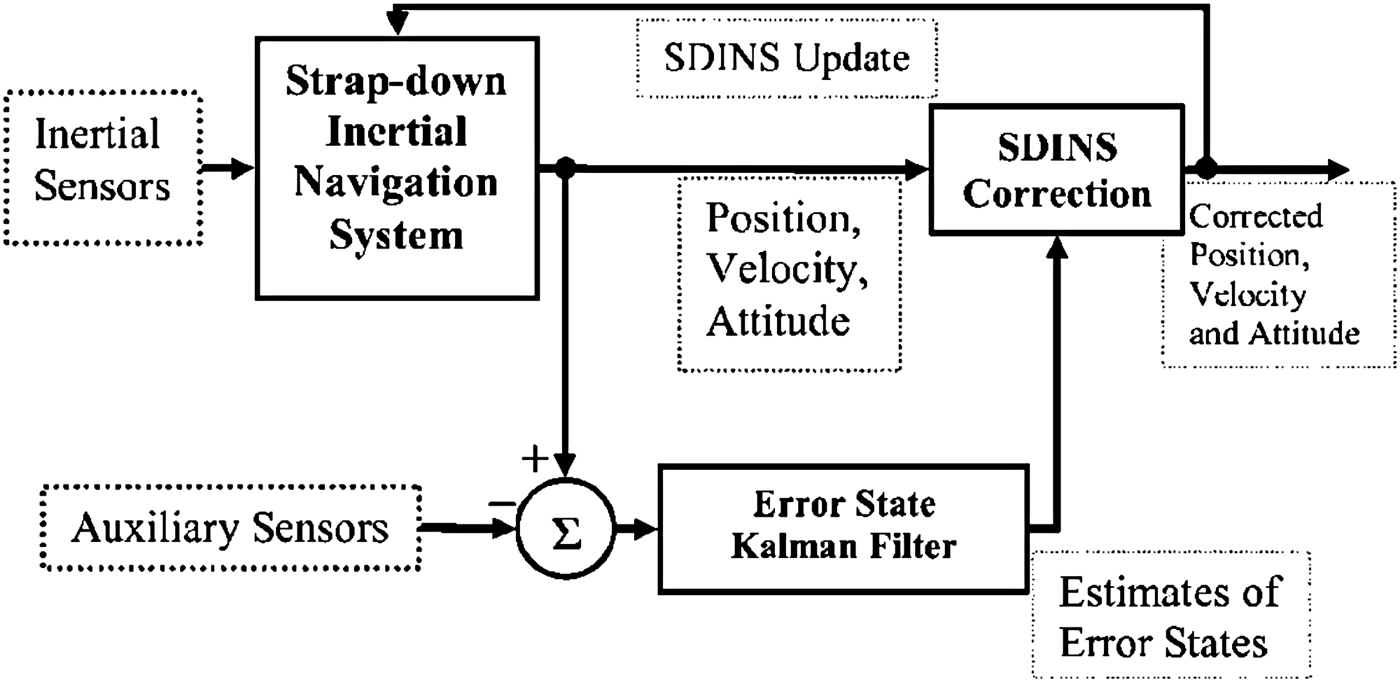
In this structure, as shown in Figure 1, differences between SINS outputs and auxiliary measurements are used by the Error State Kalman Filter (ESKF) to estimate the errors of position, velocity and orientation. Finally, the SINS outputs are corrected by the estimated errors. In this structure, the corrected state is fed back into the SINS to update it (Maybeck, Reference Maybeck1979; Farrell and Barth, Reference Farrell and Barth1999). Due to strong nonlinearity of the dynamic and measurement equations in the underwater integrated navigation system, linearization of these equations using the first order term of the Taylor series expansion leads to a substantial error in the estimates of error states and covariance matrix (Arasaratnam, Reference Arasaratnam2009; Van der Merwe, Reference Van der Merwe2004). Therefore, first order linearization in the ESKF causes the performance of the system to degrade, which can give rise to errors in the estimated position. In order to mitigate the errors caused by first order linearization employed by the ESKF, we are required to use a nonlinear filtering approach. To solve the linearization problem, the unscented filter was proposed to more accurately estimate the mean and covariance of the system's state (Julier and Uhmann, Reference Julier and Uhmann1997; Reference Julier and Uhmann2004). In the unscented filter, it is not required to linearize the nonlinear dynamic and measurement models through Jacobian derivations. Instead, by using the unscented transform, a set of deterministically selected sigma points is used which completely capture the true mean and covariance of the random vector. Then, these sigma points are propagated through the nonlinear functions. This algorithm captures the mean and covariance accurately to the three-order term of the Taylor series expansions for arbitrary nonlinear functions (Julier et al., Reference Julier, Uhmann and Durrant-Whyte2000; Wan and Van der Merwe, Reference Wan and Van Der Merwe2000). Arasaratnam and Haykin (Reference Arasaratnam and Haykin2009) proposed the Cubature Kalman Filter (CKF) where the third order spherical cubature integration rule was used for estimating the mean and covariance of the system's state. In their paper, they claimed that the cubature integration method is more accurate than the unscented filter. However, Sarkka (Reference Sarkka2013) showed that the CKF is a special case of the unscented filter by choosing the special values of the UKF's scaling parameters.

Figure 1. Indirect filtering.
For more accurately estimating the mean and covariance matrix of the navigation system's state and also preventing divergence of the filter, we propose a strap-down integrated navigation system using an unscented-based filtering approach for underwater applications.
Research on the unscented-based underwater integrated navigation system is scarce. Foss and Meland (Reference Foss and Meland2007) implemented the unscented filter for combining measurements from different sensors for an underwater vehicle and utilised numerical simulations for testing it. Yoon et al. (Reference Yoon, Yoon, Choi and Lee2003) proposed a location estimation algorithm where the GPS and Inertial Navigation System (INS) signals were combined by the UKF. In another study (Benzerrouk et al., Reference Benzerrouk, Salhi and Nebylov2013), an adaptive cubature INS/GNSS integrated navigation system was presented for aerospace applications and evaluated in simulations. Gao et al. (Reference Gao, Zhang and Wang2014) also proposed a SINS-BeiDou-DVL integrated navigation system based on a CKF for marine applications and its performance was examined through numerical simulations.
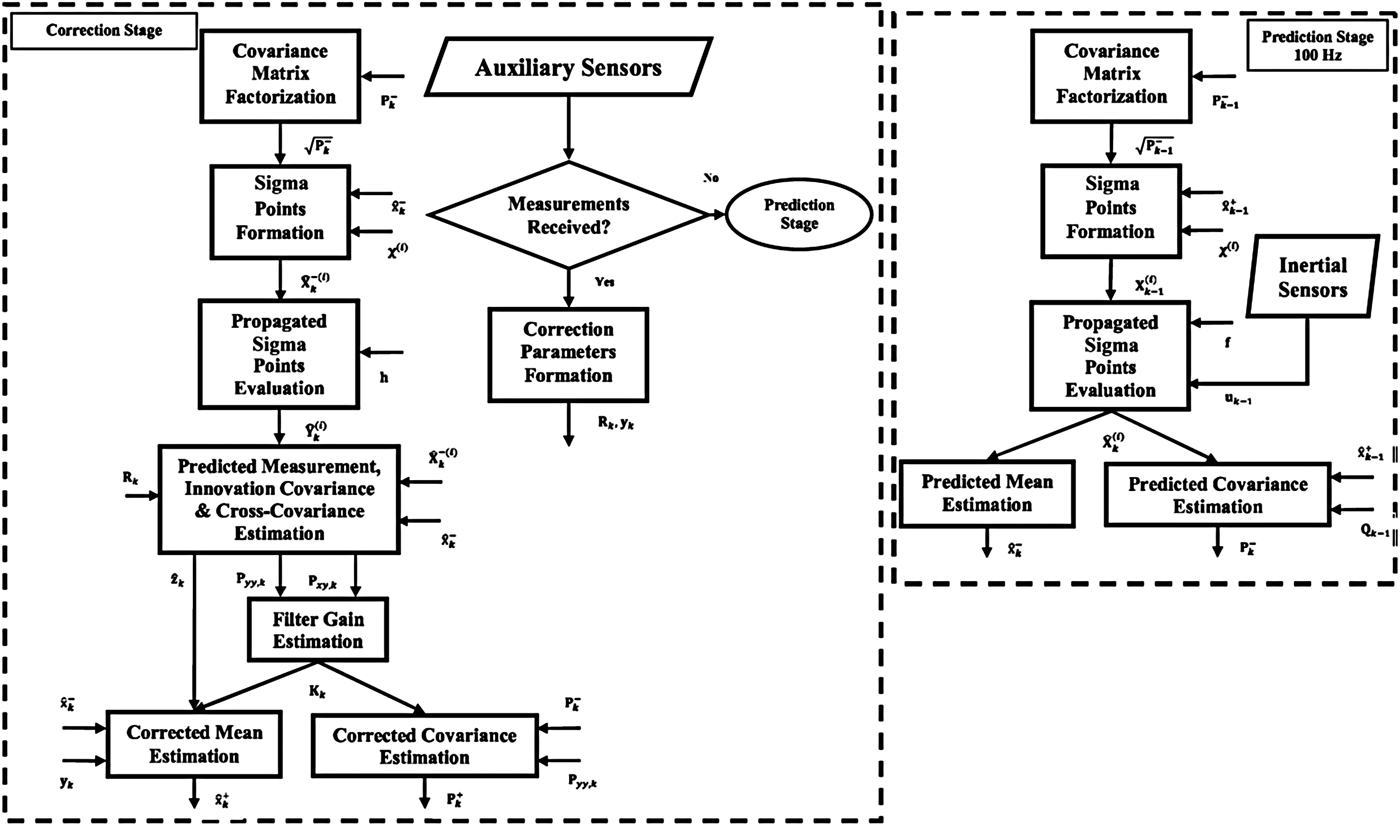
To the best of our knowledge, this paper presents the first experimental evaluation of an unscented filtering-based SINS for underwater vehicles. In the proposed algorithm, a nonlinear equation for the DVL measurement model is derived. Consequently, both the dynamic and the measurement equations for implementing the filter are nonlinear. In order to utilise the nonlinear capabilities of the unscented algorithm, the integration navigation system is implemented in a direct approach (Figure 2) (Maybeck, Reference Maybeck1979; Farrell and Barth Reference Farrell and Barth1999), where the total states of the system are used instead of error states. In this approach, unlike the indirect structure where the SINS and the prediction stage of the Kalman Filter (KF) are implemented into two distinct blocks, these two functions are merged and the correction stage of the filter operates asynchronously.

Figure 2. Direct filtering.
In addition, to exploit the unscented filter in the integrated navigation system, the roll and pitch signals computed from the accelerometer measurements are also used as auxiliary signals. Although, from a theoretical point of view, the processing of the same measurements in both prediction and correction stages is not completely correct, this technique works well in practice (Georgy et al., Reference Georgy, Karamat, Iqbal and Noureldin2011). Since GPS is not available underwater and DVL also have dropouts, this technique can limit the drift in the roll and pitch signals estimated from the gyroscopes, which, in turn, is the main origin of the growth of the position error (Skog and Handel, Reference Skog and Handel2009). The performance of the SINS/DVL integration system is investigated via a lake test in a surface vessel and compared with a similar system implemented by the ESKF. In Section 4, we show that the proposed algorithm estimates the output state more accurately than the prevalent ESKF structure.
The structure of this paper is as follows. After the Introduction, in Section 2, the equations related to the unscented filter are reviewed. In Section 3, the implemented system is described and related equations are derived. In Section 4, the performance of the designed system is evaluated using the results of the experimental tests. Finally, conclusions are presented in Section 5.
2. UNSCENTED INTEGRATION METHOD
Due to nonlinearity of the dynamic equations of navigation, the general form of a continuous time non-linear state space model (Simon, Reference Simon2006) may expressed as:
Where x is the total state vector of the system which is given as follows:
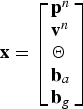 $${\bf x} = \left[ {\matrix{ {{\bf p}^n} \hfill \cr {{\bf v}^n} \hfill \cr \Theta \hfill \cr {{\bf b}_a} \hfill \cr {{\bf b}_g} \hfill \cr}} \right]$$
$${\bf x} = \left[ {\matrix{ {{\bf p}^n} \hfill \cr {{\bf v}^n} \hfill \cr \Theta \hfill \cr {{\bf b}_a} \hfill \cr {{\bf b}_g} \hfill \cr}} \right]$$![]() ${\bf p}^n = [L\comma\ l\comma\ Z]^T $ is the position vector of the vehicle in the navigation frame which includes the latitude, longitude, and the depth of the vehicle relative to the water surface.
${\bf p}^n = [L\comma\ l\comma\ Z]^T $ is the position vector of the vehicle in the navigation frame which includes the latitude, longitude, and the depth of the vehicle relative to the water surface. ![]() ${\bf v}^n = [v_N\comma\ v_E\comma\ v_D ]^T $ is the velocity vector resolved in the navigation frame which is included in the north velocity, east velocity, and down velocity. Θ = [ϕ, θ, ψ]T is the orientation vector of the body frame with respect to navigation frame (North, East, and Down directions).
${\bf v}^n = [v_N\comma\ v_E\comma\ v_D ]^T $ is the velocity vector resolved in the navigation frame which is included in the north velocity, east velocity, and down velocity. Θ = [ϕ, θ, ψ]T is the orientation vector of the body frame with respect to navigation frame (North, East, and Down directions). ![]() ${\bf b}_a = [b_{ax}\comma\ b_{ay}\comma\ b_{az} ]^T $ is the vector of the accelerometer bias and
${\bf b}_a = [b_{ax}\comma\ b_{ay}\comma\ b_{az} ]^T $ is the vector of the accelerometer bias and ![]() ${\bf b}_g = [b_{gx}\comma\ b_{gy}\comma\ b_{gz} ]^T $ is the vector of the gyroscope bias. The inertial sensors' biases are modelled as a random walk plus a random constant (Maybeck, Reference Maybeck1979; Farrell, Reference Farrell2008):
${\bf b}_g = [b_{gx}\comma\ b_{gy}\comma\ b_{gz} ]^T $ is the vector of the gyroscope bias. The inertial sensors' biases are modelled as a random walk plus a random constant (Maybeck, Reference Maybeck1979; Farrell, Reference Farrell2008):
Where ηa and ηg are Gaussian white noise vectors with variances ![]() $\sigma _{b_a} ^2 {\bf I}$ and
$\sigma _{b_a} ^2 {\bf I}$ and ![]() $\sigma _{b_g} ^2 {\bf I}$, respectively. Throughout, the symbol N represents the normal distribution and I is the identity matrix.
$\sigma _{b_g} ^2 {\bf I}$, respectively. Throughout, the symbol N represents the normal distribution and I is the identity matrix.
f is the system nonlinear function which describes the dynamic behaviour of the system. G is the dynamic noise distribution. The control input u is given by:
Where ![]() ${\bf f}^b = [\,f_x\comma\ f_y\comma\ f_z ]^T $ and
${\bf f}^b = [\,f_x\comma\ f_y\comma\ f_z ]^T $ and ![]() ${\bf \omega} _{ib}^b = [\,p\comma\ q\comma\ r]^T $ are the specific force and angular rate of the IMU relative to inertial frame, resolved in the IMU frame respectively, measured by the inertial sensors (Farrell, Reference Farrell2008; Groves, Reference Groves2008). w, in Equation (1), is the process noise due to uncertainty in the control inputs and is modelled in the KF as a Gaussian white noise vector with zero mean and a Power Spectral Density (PSD)
${\bf \omega} _{ib}^b = [\,p\comma\ q\comma\ r]^T $ are the specific force and angular rate of the IMU relative to inertial frame, resolved in the IMU frame respectively, measured by the inertial sensors (Farrell, Reference Farrell2008; Groves, Reference Groves2008). w, in Equation (1), is the process noise due to uncertainty in the control inputs and is modelled in the KF as a Gaussian white noise vector with zero mean and a Power Spectral Density (PSD) ![]() ${\bf Q}_c $, which may be expressed as follows:
${\bf Q}_c $, which may be expressed as follows:
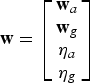 $${\bf w} = \left[ {\matrix{ {{\bf w}_a} \cr {{\bf w}_g} \cr {{\bf \eta} _a} \cr {{\bf \eta} _g} \cr}} \right]$$
$${\bf w} = \left[ {\matrix{ {{\bf w}_a} \cr {{\bf w}_g} \cr {{\bf \eta} _a} \cr {{\bf \eta} _g} \cr}} \right]$$
Where ![]() ${\bf w}_a = [w_{ax}\comma\ w_{ay}\comma\ w_{az} ]^T $ and
${\bf w}_a = [w_{ax}\comma\ w_{ay}\comma\ w_{az} ]^T $ and ![]() ${\bf w}_g = [w_{gx}\comma\ w_{gy}\comma\ w_{gz} ]^T $ are random noise components of the accelerometers and gyroscopes in x, y and z directions of the IMU axes, respectively and
${\bf w}_g = [w_{gx}\comma\ w_{gy}\comma\ w_{gz} ]^T $ are random noise components of the accelerometers and gyroscopes in x, y and z directions of the IMU axes, respectively and ![]() ${\bf Q}_c $ is a diagonal matrix as follows:
${\bf Q}_c $ is a diagonal matrix as follows:
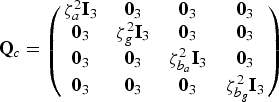 $${\bf Q}_c = \left( {\matrix{ {\zeta _a^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {\zeta _g^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {\zeta _{b_a} ^2 {\bf I}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {\zeta _{b_g} ^2 {\bf I}_3} \cr}} \right)$$
$${\bf Q}_c = \left( {\matrix{ {\zeta _a^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {\zeta _g^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {\zeta _{b_a} ^2 {\bf I}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {\zeta _{b_g} ^2 {\bf I}_3} \cr}} \right)$$
Where ζ a, ζ g, ![]() $\zeta _{b_a} $ and
$\zeta _{b_a} $ and ![]() $\zeta _{b_g} $ are the root power spectral density of the accelerometers' noise, gyroscopes' noise, accelerometers' bias and gyroscopes' bias, respectively. I3 and 03 are the 3 × 3 unit and zero matrices, respectively. Assuming that the noise characteristics of all accelerometers and all gyroscopes in x, y and z directions of the IMU axes are equal (Groves, Reference Groves2008; Niu et al., Reference Niu, Nasser, Goodall and El-Sheimy2007):
$\zeta _{b_g} $ are the root power spectral density of the accelerometers' noise, gyroscopes' noise, accelerometers' bias and gyroscopes' bias, respectively. I3 and 03 are the 3 × 3 unit and zero matrices, respectively. Assuming that the noise characteristics of all accelerometers and all gyroscopes in x, y and z directions of the IMU axes are equal (Groves, Reference Groves2008; Niu et al., Reference Niu, Nasser, Goodall and El-Sheimy2007):
Where σ a is the standard deviation of the accelerometer's noise, σ g is the standard deviation of the gyroscope's noise, dt is the sampling time of inertial sensors, ![]() $\sigma _{b_a} $ and
$\sigma _{b_a} $ and ![]() $\sigma _{b_g} $ are the standard deviations of the accelerometer and gyroscope bias, respectively and
$\sigma _{b_g} $ are the standard deviations of the accelerometer and gyroscope bias, respectively and ![]() $\tau _{b_a} $ and
$\tau _{b_a} $ and ![]() $\tau _{b_g} $ are their correlation time. In this paper, the specifications of the inertial sensors provided by manufacturers are used to determine the system noise PSDs (Groves, Reference Groves2008).
$\tau _{b_g} $ are their correlation time. In this paper, the specifications of the inertial sensors provided by manufacturers are used to determine the system noise PSDs (Groves, Reference Groves2008).
In the proposed approach, the auxiliary measurements of the system are a nonlinear combination of the states which are corrupted with noise. This can be given in terms of the total states of the system by the following equation:
Where y is the measurement vector of the system that is defined as follows:
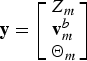 $${\bf y} = \left[ {\matrix{ {Z_m} \cr {{\bf v}_m^b} \cr {\Theta _m} \cr}} \right]$$
$${\bf y} = \left[ {\matrix{ {Z_m} \cr {{\bf v}_m^b} \cr {\Theta _m} \cr}} \right]$$
Where Z m is the auxiliary signal of depth, ![]() ${\bf v}_m^b = [v_x\comma\ v_y\comma\ v_z ]^T $ are the measurements of the DVL in the body frame, and Θm = [ϕ m, θ m, ψ m]T are the auxiliary signals of orientation. The roll and pitch measurements are computed by the accelerometer signals and heading measurement is provided by a compass.
${\bf v}_m^b = [v_x\comma\ v_y\comma\ v_z ]^T $ are the measurements of the DVL in the body frame, and Θm = [ϕ m, θ m, ψ m]T are the auxiliary signals of orientation. The roll and pitch measurements are computed by the accelerometer signals and heading measurement is provided by a compass.
h, in Equation (6), is the measurement model function and v represents the measurement noise which is assumed to be a zero mean, Gaussian white-noise process with known covariance matrix R.
The discrete-time form of the Equations (1) may be expressed by:
Where xk and uk are the total state vector of the system and the control input at discrete time k, respectively. qk is the process noise with covariance matrix Qk at time step k (Jekeli, Reference Jekeli2001; Farrell, Reference Farrell2008):
The discrete-time form of the Equations (10) may be given by the following equation:
Where yk is the measurement vector of the system at discrete time k. rk is the measurement noise vector with covariance matrix Rk at time step k. In many navigation applications, due to being independent, the individual components of the measurement noise vector, Rk are considered as a diagonal matrix (Groves, Reference Groves2008; Grewal and Andrews, Reference Grewal and Andrews2008).
The unscented filter can be derived as an approximation of the general Gaussian filter. In order to construct the Gaussian filter, the moment matching approximations are used and also the filtering distribution is assumed as Gaussian (Arasaratnam, Reference Arasaratnam2009; Sarkka, Reference Sarkka2013).
Where ![]() ${\hat{\bf x}}_k $ and Pk are the mean and the covariance of the Gaussian distribution, respectively.
${\hat{\bf x}}_k $ and Pk are the mean and the covariance of the Gaussian distribution, respectively.
The prediction stage of the Gaussian filter with additive noise is given as follows:
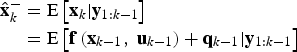 $$\eqalign{{\hat{\bf x}}_k^ - & = {\rm E}\left[ {{{\bf x}_k}\vert{{\bf y}_{1:k - 1}}} \right] \cr & = {\rm E}\left[ {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) + {{\bf q}_{k - 1}} \vert {{\bf y}_{1:k - 1}}} \right]} $$
$$\eqalign{{\hat{\bf x}}_k^ - & = {\rm E}\left[ {{{\bf x}_k}\vert{{\bf y}_{1:k - 1}}} \right] \cr & = {\rm E}\left[ {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) + {{\bf q}_{k - 1}} \vert {{\bf y}_{1:k - 1}}} \right]} $$Since qk−1 is zero-mean Gaussian, we get
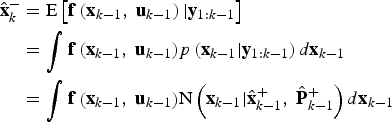 $$\eqalign{{\hat{\bf x}}_k^ - & = {\rm E}\left[ {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)\vert{{\bf y}_{1:k - 1}}} \right] \cr & = \int {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)} p\left( {{{\bf x}_{k - 1}}\vert{{\bf y}_{1:k - 1}}} \right)d{{\bf x}_{k - 1}} \cr & = \int {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)} {\rm N}\left( {{{\bf x}_{k - 1}}\vert{\hat{\bf x}}_{k - 1}^ + \comma\ {\hat{\bf P}}_{k - 1}^ + } \right)d{{\bf x}_{k - 1}}}$$
$$\eqalign{{\hat{\bf x}}_k^ - & = {\rm E}\left[ {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)\vert{{\bf y}_{1:k - 1}}} \right] \cr & = \int {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)} p\left( {{{\bf x}_{k - 1}}\vert{{\bf y}_{1:k - 1}}} \right)d{{\bf x}_{k - 1}} \cr & = \int {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right)} {\rm N}\left( {{{\bf x}_{k - 1}}\vert{\hat{\bf x}}_{k - 1}^ + \comma\ {\hat{\bf P}}_{k - 1}^ + } \right)d{{\bf x}_{k - 1}}}$$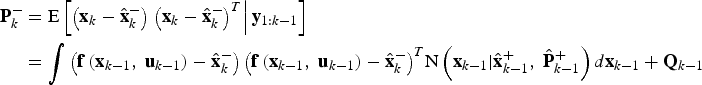 $$\eqalign{{\bf P}_k^ - & = {\rm E}\left[ {\left( {{{\bf x}_k} - {\hat{\bf x}}_k^ - } \right)\left. {{{\left( {{{\bf x}_k} - {\hat{\bf x}}_k^ - } \right)}^T}} \right\vert{{\bf y}_{1:k - 1}}} \right] \cr & = {\int {\left( {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) - {\hat{\bf x}}_k^ - } \right)\left( {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) - {\hat{\bf x}}_k^ - } \right)} ^T}{\rm N}\left( {{{\bf x}_{k - 1}}\vert{\hat{\bf x}}_{k - 1}^ + \comma\ {\hat{\bf P}}_{k - 1}^ + } \right)d{{\bf x}_{k - 1}} + {{\bf Q}_{k - 1}}} $$
$$\eqalign{{\bf P}_k^ - & = {\rm E}\left[ {\left( {{{\bf x}_k} - {\hat{\bf x}}_k^ - } \right)\left. {{{\left( {{{\bf x}_k} - {\hat{\bf x}}_k^ - } \right)}^T}} \right\vert{{\bf y}_{1:k - 1}}} \right] \cr & = {\int {\left( {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) - {\hat{\bf x}}_k^ - } \right)\left( {{\bf f}\left( {{{\bf x}_{k - 1}}\comma\ {{\bf u}_{k - 1}}} \right) - {\hat{\bf x}}_k^ - } \right)} ^T}{\rm N}\left( {{{\bf x}_{k - 1}}\vert{\hat{\bf x}}_{k - 1}^ + \comma\ {\hat{\bf P}}_{k - 1}^ + } \right)d{{\bf x}_{k - 1}} + {{\bf Q}_{k - 1}}} $$
Where E is the expectation operator, ![]() ${\hat{\bf x}}_k^ - $ and
${\hat{\bf x}}_k^ - $ and ![]() ${\bf P}_k^ - $ are the predicted mean and covariance of the Gaussian filter at the time step k.
${\bf P}_k^ - $ are the predicted mean and covariance of the Gaussian filter at the time step k.
Similarly to the prediction stage, the correction stage of the Gaussian filter is expressed by:
Where ![]() ${\hat {\bf z}}_k $ is the predicted measurement, Pyy,k is the innovation covariance, Pxy,k is the cross-covariance matrix, Kk is the filter gain matrix and
${\hat {\bf z}}_k $ is the predicted measurement, Pyy,k is the innovation covariance, Pxy,k is the cross-covariance matrix, Kk is the filter gain matrix and ![]() ${\hat {\bf x}}_k^ + $ and
${\hat {\bf x}}_k^ + $ and ![]() ${\bf P}_k^ + $ are the corrected mean and covariance of the Gaussian filter at the time step k, respectively.
${\bf P}_k^ + $ are the corrected mean and covariance of the Gaussian filter at the time step k, respectively.
The moment matching formulation makes possible the utilisation of the numerical approaches like the cubature integration methods for computing the multi-dimensional integrals of the form ![]() ${\int} {{\bf g}({\bf x}){\rm N}\left( {{\bf x}\vert{\hat {\bf x}}\comma\ {\bf P}} \right)d{\bf x}} $, where g(x) is an arbitrary nonlinear function.
${\int} {{\bf g}({\bf x}){\rm N}\left( {{\bf x}\vert{\hat {\bf x}}\comma\ {\bf P}} \right)d{\bf x}} $, where g(x) is an arbitrary nonlinear function.
It can be shown that the computation of the aforementioned integral may be accomplished using the third order spherical cubature rule as follows (Arasaratnam, Reference Arasaratnam2009; Sarkka, Reference Sarkka2013):
• Calculate the 2n cubature or sigma points by:
(25)Where n is the dimension of the state vector and ei is an n-component unit vector in the direction of coordinate axis i. In general, χ (i) is generated as follows: $$\chi ^{(i)} = \left\{ {\matrix{ {\sqrt n {\bf e}_i \comma\quad} & {i = 1\comma \ldots\comma\, n} \cr { - \sqrt n {\bf e}_{i - n} \comma\quad} & {i = n + 1\comma \ldots\comma\, 2n} \cr}} \right.$$(26)
$$\chi ^{(i)} = \left\{ {\matrix{ {\sqrt n {\bf e}_i \comma\quad} & {i = 1\comma \ldots\comma\, n} \cr { - \sqrt n {\bf e}_{i - n} \comma\quad} & {i = n + 1\comma \ldots\comma\, 2n} \cr}} \right.$$(26) $$\chi ^{(i)} = \left\{ {\left( {\matrix{ {\sqrt n} \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\left( {\matrix{ 0 \hfill \cr {\sqrt n} \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\ldots\comma \left( {\matrix{ 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr {\sqrt n} \hfill \cr}} \right)\comma\left( {\matrix{ { - \sqrt n} \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\left( {\matrix{ 0 \hfill \cr { - \sqrt n} \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\ldots\comma \left( {\matrix{ 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr { - \sqrt n} \hfill \cr}} \right)} \right\}$$
$$\chi ^{(i)} = \left\{ {\left( {\matrix{ {\sqrt n} \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\left( {\matrix{ 0 \hfill \cr {\sqrt n} \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\ldots\comma \left( {\matrix{ 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr {\sqrt n} \hfill \cr}} \right)\comma\left( {\matrix{ { - \sqrt n} \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\left( {\matrix{ 0 \hfill \cr { - \sqrt n} \hfill \cr 0 \hfill \cr \vdots \hfill \cr 0 \hfill \cr}} \right)\comma\ldots\comma \left( {\matrix{ 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr \vdots \hfill \cr { - \sqrt n} \hfill \cr}} \right)} \right\}$$• Compute the integral by:
(27) $${\int} {{\bf g}({\bf x}){\rm N}\left( {{\bf x} \vert {\hat {\bf x}}\comma\ {\bf P}} \right)d{\bf x} \approx \displaystyle{1 \over {2n}}\sum\limits_{i = 1}^{2n} {{\bf g}\left( {{\hat {\bf x}} + \sqrt {\bf P} \chi ^{(i)}} \right)}} $$
$${\int} {{\bf g}({\bf x}){\rm N}\left( {{\bf x} \vert {\hat {\bf x}}\comma\ {\bf P}} \right)d{\bf x} \approx \displaystyle{1 \over {2n}}\sum\limits_{i = 1}^{2n} {{\bf g}\left( {{\hat {\bf x}} + \sqrt {\bf P} \chi ^{(i)}} \right)}} $$
Where the square root of the matrix P(![]() $\sqrt {\bf P} = {\bf C}$) can be calculated by solving the Cholesky decomposition equation
$\sqrt {\bf P} = {\bf C}$) can be calculated by solving the Cholesky decomposition equation ![]() ${\bf P} = {\bf CC}^T $ for a symmetric, nonnegative definite matrix (Grewal and Andrews, Reference Grewal and Andrews2008).
${\bf P} = {\bf CC}^T $ for a symmetric, nonnegative definite matrix (Grewal and Andrews, Reference Grewal and Andrews2008).
3. INTEGRATED NAVIGATION SYSTEM EQUATIONS
In this section, the system and measurement equations for the total states of navigation are derived and the procedure of the designed system is described.
3.1. The system equations
The system nonlinear functions f described in Equation (1) are given as follows (Farrell, Reference Farrell2008; Britting, Reference Britting1971):
Where
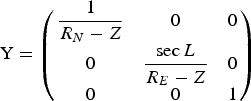 $${\rm Y} = \left( {\matrix{ {\displaystyle{1 \over {R_N - Z}}} & 0 & 0 \cr 0 & {\displaystyle{{\sec L} \over {R_E - Z}}} & 0 \cr 0 & 0 & 1 \cr}} \right)$$
$${\rm Y} = \left( {\matrix{ {\displaystyle{1 \over {R_N - Z}}} & 0 & 0 \cr 0 & {\displaystyle{{\sec L} \over {R_E - Z}}} & 0 \cr 0 & 0 & 1 \cr}} \right)$$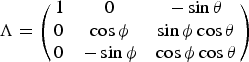 $$\Lambda = \left( {\matrix{ 1 & 0 & { - \sin \theta} \cr 0 & {\cos \phi} & {\sin \phi \cos \theta} \cr 0 & { - \sin \phi} & {\cos \phi \cos \theta} \cr}} \right)$$
$$\Lambda = \left( {\matrix{ 1 & 0 & { - \sin \theta} \cr 0 & {\cos \phi} & {\sin \phi \cos \theta} \cr 0 & { - \sin \phi} & {\cos \phi \cos \theta} \cr}} \right)$$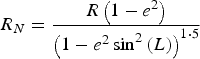 $$R_N = \displaystyle{{R\left( {1 - e^2} \right)} \over {\left( {1 - e^2 \sin ^2 \left( L \right)} \right)^{1\cdot5}}} $$
$$R_N = \displaystyle{{R\left( {1 - e^2} \right)} \over {\left( {1 - e^2 \sin ^2 \left( L \right)} \right)^{1\cdot5}}} $$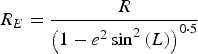 $$R_E = \displaystyle{R \over {\left( {1 - e^2 \sin ^2 \left( L \right)} \right)^{0\cdot5}}} $$
$$R_E = \displaystyle{R \over {\left( {1 - e^2 \sin ^2 \left( L \right)} \right)^{0\cdot5}}} $$ The variables R N, RE, R, e and Ω represent the meridian radius of curvature, the transverse radius of curvature, the length of the semi-major axis, the major eccentricity of the ellipsoid of the Earth, and the Earth's angular rate, respectively (Titterton and Weston, Reference Titterton and Weston2004). ![]() ${\bf C}_b^n $ is the transformation matrix from body to navigation axes which may be expressed by the following equation:
${\bf C}_b^n $ is the transformation matrix from body to navigation axes which may be expressed by the following equation:
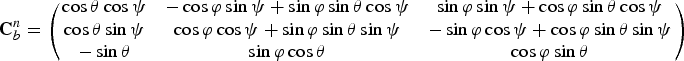 $${\bf C}_b^n = \left( {\matrix{ {\cos \theta \cos \psi} & { - \cos \varphi \sin \psi + \sin \varphi \sin \theta \cos \psi} & {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi} \cr {\cos \theta \sin \psi} & {\cos \varphi \cos \psi + \sin \varphi \sin \theta \sin \psi} & { - \sin \varphi \cos \psi + \cos \varphi \sin \theta \sin \psi} \cr { - \sin \theta} & {\sin \varphi \cos \theta} & {\cos \varphi \sin \theta} \cr}} \right)$$
$${\bf C}_b^n = \left( {\matrix{ {\cos \theta \cos \psi} & { - \cos \varphi \sin \psi + \sin \varphi \sin \theta \cos \psi} & {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi} \cr {\cos \theta \sin \psi} & {\cos \varphi \cos \psi + \sin \varphi \sin \theta \sin \psi} & { - \sin \varphi \cos \psi + \cos \varphi \sin \theta \sin \psi} \cr { - \sin \theta} & {\sin \varphi \cos \theta} & {\cos \varphi \sin \theta} \cr}} \right)$$fb represents the specific force in body axes. ![]() ${\bf \omega} _{ie}^n $ is the angular rate of the Earth expressed in the navigation frame.
${\bf \omega} _{ie}^n $ is the angular rate of the Earth expressed in the navigation frame. ![]() ${\bf \omega} _{en}^n $ represents the angular rate of the navigation frame with respect to the Earth-fixed frame. gn and g are the gravity vector in the navigation frame and the Earth gravity constant, respectively.
${\bf \omega} _{en}^n $ represents the angular rate of the navigation frame with respect to the Earth-fixed frame. gn and g are the gravity vector in the navigation frame and the Earth gravity constant, respectively. ![]() ${\bf \omega} _{nb}^b $ is the angular rate of the vehicle with respect to the navigation frame.
${\bf \omega} _{nb}^b $ is the angular rate of the vehicle with respect to the navigation frame. ![]() ${\bf \omega} _{ib}^b = [p\comma\ q\comma\ r]^T $ is the angular rate of the vehicle. The gravity g is computed by the following equation (Titterton and Weston, Reference Titterton and Weston2004):
${\bf \omega} _{ib}^b = [p\comma\ q\comma\ r]^T $ is the angular rate of the vehicle. The gravity g is computed by the following equation (Titterton and Weston, Reference Titterton and Weston2004):
Where
3.2. The measurement equations
In this section, the measurement equations used in this paper, including the depth, velocity, roll, pitch, and heading are derived.
The measurement equation of the depth meter and its measurement noise variance are defined by:
Where ν z and ![]() $\sigma _z^2 $ is the measurement noise and the measurement noise variance of the depth meter, respectively.
$\sigma _z^2 $ is the measurement noise and the measurement noise variance of the depth meter, respectively.
The relationship between the DVL's measurements and the states of the velocity may be expressed by the following nonlinear equation:
This equation can be expressed in component form as follows:
Where C ij is the element in the ith row and the jth column of the transformation matrix from body frame to navigation frame (i.e. ![]() ${\bf C}_n^b $), [v N, v E, v D] is the north, east and down velocity components and
${\bf C}_n^b $), [v N, v E, v D] is the north, east and down velocity components and ![]() $\nu _v = \left[ {\nu _{v_x}\comma\ \nu _{v_y}\comma\ \nu _{v_z}} \right]$ is the measurement noise vector of the DVL.
$\nu _v = \left[ {\nu _{v_x}\comma\ \nu _{v_y}\comma\ \nu _{v_z}} \right]$ is the measurement noise vector of the DVL.
It can be shown that the covariance matrix of the DVL measurements caused by instrumental noise is given by (Gilcoto et al., Reference Gilcoto, Jones and Farina-Busto2009):
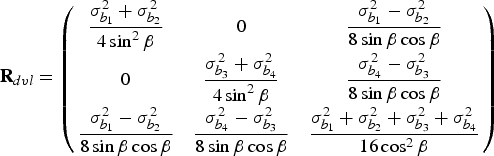 $${\bf R}_{dvl} = \left( {\matrix{ {\displaystyle{{\sigma _{b_1} ^2 + \sigma _{b_2} ^2} \over {4\sin ^2\beta}}} & 0 & {\displaystyle{{\sigma _{b_1} ^2 - \sigma _{b_2} ^2} \over {8\sin \beta \cos \beta}}} \cr 0 & {\displaystyle{{\sigma _{b_{3}} ^2 + \sigma _{b_4} ^2} \over {4\sin ^2 \beta}}} & {\displaystyle{{\sigma _{b_4} ^2 - \sigma _{b_3} ^2} \over {8\sin \beta \cos \beta}}} \cr {\displaystyle{{\sigma _{b_1} ^2 - \sigma _{b_2} ^2} \over {8\sin \beta \cos \beta}}} & {\displaystyle{{\sigma _{b_4} ^2 - \sigma _{b_3} ^2} \over {8\sin \beta \cos \beta}}} & {\displaystyle{{\sigma _{b_1} ^2 + \sigma _{b_2} ^2 + \sigma _{b_3} ^2 + \sigma _{b_4} ^2} \over {16\cos ^2 \beta}}} \cr}} \right)$$
$${\bf R}_{dvl} = \left( {\matrix{ {\displaystyle{{\sigma _{b_1} ^2 + \sigma _{b_2} ^2} \over {4\sin ^2\beta}}} & 0 & {\displaystyle{{\sigma _{b_1} ^2 - \sigma _{b_2} ^2} \over {8\sin \beta \cos \beta}}} \cr 0 & {\displaystyle{{\sigma _{b_{3}} ^2 + \sigma _{b_4} ^2} \over {4\sin ^2 \beta}}} & {\displaystyle{{\sigma _{b_4} ^2 - \sigma _{b_3} ^2} \over {8\sin \beta \cos \beta}}} \cr {\displaystyle{{\sigma _{b_1} ^2 - \sigma _{b_2} ^2} \over {8\sin \beta \cos \beta}}} & {\displaystyle{{\sigma _{b_4} ^2 - \sigma _{b_3} ^2} \over {8\sin \beta \cos \beta}}} & {\displaystyle{{\sigma _{b_1} ^2 + \sigma _{b_2} ^2 + \sigma _{b_3} ^2 + \sigma _{b_4} ^2} \over {16\cos ^2 \beta}}} \cr}} \right)$$
Where ![]() $\sigma _{b_i} ^2 $ is the variance of the radial velocity along the beam i (i = 1,2,3,4). It may be assumed that the radial velocity variances are equal which yields:
$\sigma _{b_i} ^2 $ is the variance of the radial velocity along the beam i (i = 1,2,3,4). It may be assumed that the radial velocity variances are equal which yields:
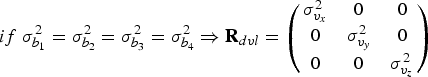 $$if\;\sigma _{b_1} ^2 = \sigma _{b_2} ^2 = \sigma _{b_3} ^2 = \sigma _{b_4} ^2 \Rightarrow {\bf R}_{dvl} = \left( {\matrix{ {\sigma _{v_x} ^2} & 0 & 0 \cr 0 & {\sigma _{v_y} ^2} & 0 \cr 0 & 0 & {\sigma _{v_z} ^2} \cr}} \right)$$
$$if\;\sigma _{b_1} ^2 = \sigma _{b_2} ^2 = \sigma _{b_3} ^2 = \sigma _{b_4} ^2 \Rightarrow {\bf R}_{dvl} = \left( {\matrix{ {\sigma _{v_x} ^2} & 0 & 0 \cr 0 & {\sigma _{v_y} ^2} & 0 \cr 0 & 0 & {\sigma _{v_z} ^2} \cr}} \right)$$
Where ![]() $\sigma _{v_x} ^2 $,
$\sigma _{v_x} ^2 $, ![]() $\sigma _{v_y} ^2 $, and
$\sigma _{v_y} ^2 $, and ![]() $\sigma _{v_z} ^2 $ are the variance of the DVL's measurements along its body frame.
$\sigma _{v_z} ^2 $ are the variance of the DVL's measurements along its body frame.
The measurement model of the roll and pitch may be given by:
Where ϕ m and θ m are the auxiliary signals of the roll and pitch computed from the accelerometer's signals. Under circumstances where the vehicle is stationary or moves at a constant velocity (or cruising conditions), the only acceleration acting on the vehicle is the acceleration due to gravity (Grenon et al., Reference Grenon, An, Smith and Healey2001; Groves, Reference Groves2008; Farrell, Reference Farrell2008). Therefore, the roll and pitch signals may be computed by the following equations:
Where f x and f y are the accelerations acting on the vehicle along the forward and starboard directions measured by the accelerometers. When the following logical condition is true, the roll and pitch measurements are used in the correction stage of the integration filter (Farrell, Reference Farrell2008):
Where T f and T ω are determined by trial and error. The symbol ![]() $\Vert\cdot\Vert$ denotes the norm of a vector.
$\Vert\cdot\Vert$ denotes the norm of a vector.
Although, in theory, the roll and pitch signals are correlated to each other, as stated in Equation (56), one can assume that these signals are independent for small pitch angles:
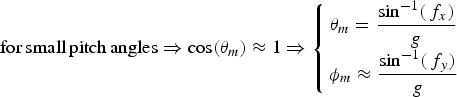 $${\rm for}\,{\rm small}\,{\rm pitch}\,{\rm angles} \Rightarrow \cos (\theta _m ) \approx 1 \Rightarrow \left\{ {\matrix{ {\theta _m = \displaystyle{{\sin ^{ - 1} (\,f_x )} \over g}} \cr {\phi _m \approx \displaystyle{{\sin ^{ - 1} (\,f_y )} \over g}} \cr}} \right.$$
$${\rm for}\,{\rm small}\,{\rm pitch}\,{\rm angles} \Rightarrow \cos (\theta _m ) \approx 1 \Rightarrow \left\{ {\matrix{ {\theta _m = \displaystyle{{\sin ^{ - 1} (\,f_x )} \over g}} \cr {\phi _m \approx \displaystyle{{\sin ^{ - 1} (\,f_y )} \over g}} \cr}} \right.$$This type of manoeuvre is performed in many marine applications, including the test conducted for this paper. Therefore, the measurement noise matrix for the signals of the roll and pitch is assumed to be diagonal as follows:
Where ![]() $\sigma _\varphi ^2 $ and
$\sigma _\varphi ^2 $ and ![]() $\sigma _\theta ^2 $ are the variance of the signals of the roll and pitch, respectively. These quantities are calculated in terms of the variance of the acceleration signals according to Equation (58).
$\sigma _\theta ^2 $ are the variance of the signals of the roll and pitch, respectively. These quantities are calculated in terms of the variance of the acceleration signals according to Equation (58).
The measurement equation of the compass and its measurement noise variance are defined by:
Where ![]() $\sigma _\psi ^2 $ is the variance of the compass measurement.
$\sigma _\psi ^2 $ is the variance of the compass measurement.
3.3. Data integration
3.3.1. The prediction stage
In the prediction stage of the unscented filter, for each time step of inertial sensors, the total state of the system ![]() ${\hat {\bf x}}^ - $ and covariance of the state
${\hat {\bf x}}^ - $ and covariance of the state ![]() ${\bf P}^ - $ are predicted using Equations (12) and (13) and the unscented based integration method given by Equations (20)–(22).
${\bf P}^ - $ are predicted using Equations (12) and (13) and the unscented based integration method given by Equations (20)–(22).
In order to execute the prediction stage, the system equations can be expressed in component form as follows:
Where
And
Where C ij is the element in the ith row and the jth column of the transformation matrix that is given by Equation (35).
3.3.2. The correction stage
Since auxiliary sensors are asynchronous or sampled at different rates, the correction stage is also executed asynchronously. Operating in asynchronous mode means that when measurements from one or more of the auxiliary sensors are received at time step k, the measurement parameters associated with those sensors (yk and Rk) are formed, and then the correction equations of the unscented filter are executed. In the event that none of the auxiliary sensors are available, the correction stage will not be executed. In this case, the filter continues to operate without correction using the prediction stage. The total state of the navigation and its covariance matrix are predicted with sampling frequency of inertial sensors according to Equations (12) and (13) with or without the correction stage.
On receiving of a new auxiliary signal yk, the navigation state ![]() ${\hat {\bf x}}^ + $ and its associated covariance matrix
${\hat {\bf x}}^ + $ and its associated covariance matrix ![]() ${\bf P}^ + $ at time step k are corrected using Equations (14)–(19) and the unscented-based integration method expressed by Equations (20)–(22).
${\bf P}^ + $ at time step k are corrected using Equations (14)–(19) and the unscented-based integration method expressed by Equations (20)–(22).
In the best case, where all of the auxiliary sensors are available, the measurement vector y and the matrix R are given as follows:
 $${\bf R} = \left[ {\matrix{ {\sigma _z^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & {\sigma _{v_x} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & {\sigma _{v_y} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _{v_z} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\phi ^2} \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\theta ^2} \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\psi ^2} \hfill \cr}} \right]$$
$${\bf R} = \left[ {\matrix{ {\sigma _z^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & {\sigma _{v_x} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & {\sigma _{v_y} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _{v_z} ^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\phi ^2} \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\theta ^2} \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\sigma _\psi ^2} \hfill \cr}} \right]$$The dimensions of the correction parameters are determined based on the number of received auxiliary sensors. When one of the sensors is not received, the matrices associated with that sensor, which was given in Section 3.2, are removed from the correction parameters. The measurement noise matrix, R, is determined by stationary measurements of the auxiliary sensors. However, due to external factors such as environmental vibration, the effective noise levels may be changed. Therefore, in order to obtain the optimal estimates, it is required to tune R (Groves, Reference Groves2008). The flowchart of the unscented based integrated navigation system is illustrated in Figure 3.

Figure 3. Strap-down integrated navigation system based on unscented based integration method.
4. EXPERIMENTAL RESULTS
In order to evaluate the performance of the proposed system, a lake test was accomplished. An instrumented vessel was utilised for the experiments as shown in Figure 4. The instruments used in the test include a fibre optic gyro IMU assembled by Sepahan Electronic Inc. with model Sarmad2, a DVL made by Jay Technology Inc., model IR/BQN_01 and a GPS receiver (NovAtelOEMV-1) installed on the vessel according to Figure 5. The GPS receiver is a single-frequency GPS receiver and its measurements were used only for position initialisation and reference purposes.

Figure 4. Instrumented vessel for experiments.

Figure 5. Instruments mounted on the vessel.
To evaluate the proposed approach, the inertial signals are incorporated with measurements of the DVL, depth meter, roll and pitch angles. The position estimated by the proposed approach is compared with a position reference. In order to have an accurate position reference, two similar GPS receivers were used as a simple differential GPS. The first GPS receiver was installed at the origin point and the second one on the vessel and the position reference was calculated by subtracting smoothed data of the two GPS receivers. Our measurements showed that the accuracy of the calculated position reference was lower than 2 metres. As shown in Figure 5, a stand was used for holding the DVL under the water. The specifications of the instruments used can be found in Table 1 (Novatel, 2010).
Table 1. Instrument specifications.

In this paper, a trajectory composed of both the pseudo-sinusoid manoeuvres and the approximately straight track is used to show the performance of the designed system. The signals measured by the instruments are logged by a computer carried by the vessel and then post-processing of the collected data is carried out in the laboratory. To verify the accuracy of the proposed system, its estimated position is compared with that of the ESKF-based integrated navigation system (Lee et al., Reference Lee, Jun, Kim, Lee, Aoki and Hyakudome2007; Miller et al., Reference Miller, Farrell, Zhao and Djapic2010; Shabani et al., Reference Shabani, Gholami, Davari and Emami2013).
According to Equations (8) and (9) and parameters given in Table 1, the matrix Qc is considered as follows:
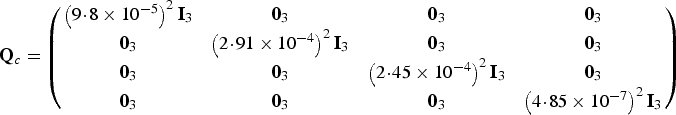 $${\bf Q}_c = \left( {\matrix{ {\left( {9\!\cdot\!8 \times 10^{ - 5}} \right)^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {\left( {2\!\cdot\!91 \times 10^{ - 4}} \right)^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {\left( {2\!\cdot\!45 \times 10^{ - 4}} \right)^2 {\bf I}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {\left( {4\!\cdot\!85 \times 10^{ - 7}} \right)^2 {\bf I}_3} \cr}} \right)$$
$${\bf Q}_c = \left( {\matrix{ {\left( {9\!\cdot\!8 \times 10^{ - 5}} \right)^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {\left( {2\!\cdot\!91 \times 10^{ - 4}} \right)^2 {\bf I}_3} & {{\bf 0}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {\left( {2\!\cdot\!45 \times 10^{ - 4}} \right)^2 {\bf I}_3} & {{\bf 0}_3} \cr {{\bf 0}_3} & {{\bf 0}_3} & {{\bf 0}_3} & {\left( {4\!\cdot\!85 \times 10^{ - 7}} \right)^2 {\bf I}_3} \cr}} \right)$$The measurement covariance matrix is also considered as follows:
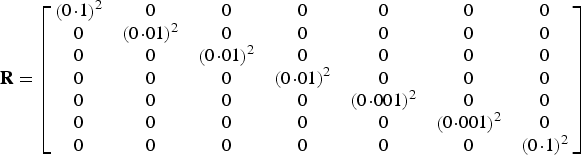 $${\bf R} = \left[ {\matrix{ {\left( {0\!\cdot\!1} \right)^2} & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!001} \right)^2} & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!001} \right)^2} & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!1} \right)^2} \cr}} \right]$$
$${\bf R} = \left[ {\matrix{ {\left( {0\!\cdot\!1} \right)^2} & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & {\left( {0\!\cdot\!01} \right)^2} & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!001} \right)^2} & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!001} \right)^2} & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & {\left( {0\!\cdot\!1} \right)^2} \cr}} \right]$$In Figure 6, the estimated positions in the horizontal (e.g. north and east) direction are shown. Figure 7 also shows the absolute error curves. Absolute error is expressed as the absolute value of the difference between the reference and estimated positions. In Figures 8 and 9, the curves of the estimated position absolute errors in the directions of the east and north are depicted, respectively. These curves are defined as the absolute value of the difference between the estimated position in the east (or north) direction and the GPS position in that direction.

Figure 6. Estimated positions.

Figure 7. Estimation error.

Figure 8. Estimated position errors in the east direction.

Figure 9. Estimated position errors in the north direction.
Based on these results, the positions estimated by both approaches pursue the reference position with a bounded error. However, due to utilising the more accurate integration method in the proposed navigation system, its estimation error is less than that of the ESKF approach.
In this paper, the Root Mean Square Error (RMSE) and the relative error criteria are used for quantitatively evaluating the performance of the system which is calculated as follows:
Where R i and E i are the reference and estimated position along the corresponding axis. In this test where the vessel travelled approximately 4897 metres for nearly 42 minutes, the RMSE values of the position estimated by the proposed system and ESKF approach are 4·3 m and 6·5 m and relative errors are 0·09% and 0·13% of the travelled distance, respectively. The maximum position error for the proposed system is 9·3 m, while this value for the ESKF approach is 16·1 m. The RMSE values of the estimated position in the directions of the east and north for the proposed system are 3·26 m and 2·8 m, whereas these values for ESKF approach are 3·95 m and 5·2 m. Therefore, in accordance with the obtained results, the unscented-based integrated navigation system estimates the vehicle position more accurately than the conventional ESKF approach. The results obtained from the practical test for travelled trajectory are summarised in Table 2.
Table 2. Performance comparison of the proposed system and conventional ESKF approach.

5. CONCLUSIONS
The conventional approach for combining SINS information and the auxiliary data in underwater navigation is the ESKF. In this approach, the errors in the position, velocity and orientation are estimated using the difference between SINS outputs and the auxiliary measurements and the KF operates based on the set of the INS error propagation equations derived from the first order approximation of the Taylor series expansion of the system dynamic and measurement equations. In this paper, in order to reduce the first order linearization effect on the estimation accuracy, an integrated navigation system for underwater applications is designed using unscented filtering. In the proposed system, the total state nonlinear dynamic and measurement models are used and the mean and covariance matrix of the navigation state, whether in the prediction or correction stage, are estimated using the unscented-based integration algorithm. The lake test results show that the proposed approach improves the system performance compared with the conventional ESKF approach.