Article contents
APPROXIMATELY MULTIPLICATIVE MAPS FROM WEIGHTED SEMILATTICE ALGEBRAS
Published online by Cambridge University Press: 17 June 2013
Abstract
We investigate which weighted convolution algebras 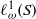 ${ \ell }_{\omega }^{1} (S)$, where
${ \ell }_{\omega }^{1} (S)$, where 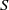 $S$ is a semilattice, are AMNM in the sense of Johnson [‘Approximately multiplicative functionals’, J. Lond. Math. Soc. (2) 34(3) (1986), 489–510]. We give an explicit example where this is not the case. We show that the unweighted examples are all AMNM, as are all
$S$ is a semilattice, are AMNM in the sense of Johnson [‘Approximately multiplicative functionals’, J. Lond. Math. Soc. (2) 34(3) (1986), 489–510]. We give an explicit example where this is not the case. We show that the unweighted examples are all AMNM, as are all 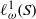 ${ \ell }_{\omega }^{1} (S)$ where
${ \ell }_{\omega }^{1} (S)$ where 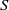 $S$ has either finite width or finite height. Some of these finite-width examples are isomorphic to function algebras studied by Feinstein [‘Strong Ditkin algebras without bounded relative units’, Int. J. Math. Math. Sci. 22(2) (1999), 437–443]. We also investigate when
$S$ has either finite width or finite height. Some of these finite-width examples are isomorphic to function algebras studied by Feinstein [‘Strong Ditkin algebras without bounded relative units’, Int. J. Math. Math. Sci. 22(2) (1999), 437–443]. We also investigate when 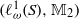 $({ \ell }_{\omega }^{1} (S), { \mathbb{M} }_{2} )$ is an AMNM pair in the sense of Johnson [‘Approximately multiplicative maps between Banach algebras’, J. Lond. Math. Soc. (2) 37(2) (1988), 294–316], where
$({ \ell }_{\omega }^{1} (S), { \mathbb{M} }_{2} )$ is an AMNM pair in the sense of Johnson [‘Approximately multiplicative maps between Banach algebras’, J. Lond. Math. Soc. (2) 37(2) (1988), 294–316], where 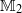 ${ \mathbb{M} }_{2} $ denotes the algebra of
${ \mathbb{M} }_{2} $ denotes the algebra of 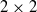 $2\times 2$ complex matrices. In particular, we obtain the following two contrasting results: (i) for many nontrivial weights on the totally ordered semilattice
$2\times 2$ complex matrices. In particular, we obtain the following two contrasting results: (i) for many nontrivial weights on the totally ordered semilattice 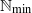 ${ \mathbb{N} }_{\min } $, the pair
${ \mathbb{N} }_{\min } $, the pair 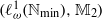 $({ \ell }_{\omega }^{1} ({ \mathbb{N} }_{\min } ), { \mathbb{M} }_{2} )$ is not AMNM; (ii) for any semilattice
$({ \ell }_{\omega }^{1} ({ \mathbb{N} }_{\min } ), { \mathbb{M} }_{2} )$ is not AMNM; (ii) for any semilattice 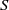 $S$, the pair
$S$, the pair 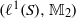 $({\ell }^{1} (S), { \mathbb{M} }_{2} )$ is AMNM. The latter result requires a detailed analysis of approximately commuting, approximately idempotent
$({\ell }^{1} (S), { \mathbb{M} }_{2} )$ is AMNM. The latter result requires a detailed analysis of approximately commuting, approximately idempotent 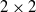 $2\times 2$ matrices.
$2\times 2$ matrices.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by




