Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T12:03:28.762Z Has data issue: false hasContentIssue false
  • English
  • Français

CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  21 December 2016

HENG HUAT CHAN ,
LIUQUAN WANG  and
YIFAN YANG
HENG HUAT CHAN
Affiliation:
Department of Mathematics, National University of Singapore, Singapore 119076, Singapore email matchh@nus.edu.sg
LIUQUAN WANG*
Affiliation:
Department of Mathematics, National University of Singapore, Singapore 119076, Singapore email wangliuquan@u.nus.edu
YIFAN YANG
Affiliation:
Department of Applied Mathematics, National Chiao Tung University, Hsinchu 300, Taiwan email yfyang@math.nctu.edu.tw
*
✉wangliuquan@u.nus.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 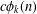$c\unicode[STIX]{x1D719}_{k}(n)$ denote the number of $k$-colored generalized Frobenius partitions of $n$. Recently, new Ramanujan-type congruences associated with 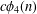$c\unicode[STIX]{x1D719}_{4}(n)$ were discovered. In this article, we discuss two approaches in proving such congruences using the theory of modular forms. Our methods allow us to prove congruences such as 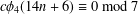$c\unicode[STIX]{x1D719}_{4}(14n+6)\equiv 0\;\text{mod}\;7$ and Seller’s congruence 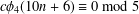$c\unicode[STIX]{x1D719}_{4}(10n+6)\equiv 0\;\text{mod}\;5$.

Keywords

congruencesgeneralized Frobenius partitionstheta functionseta-products

MSC classification

Primary: 05A17: Partitions of integers
Secondary: 11P83: Partitions; congruences and congruential restrictions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 157 - 176
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., Generalized Frobenius Partitions, Memoirs of the American Mathematical Society, 301 (American Mathematical Society, Providence, RI, 1984).CrossRefGoogle Scholar
Baruah, N. D. and Sarmah, B. K., ‘Congruences for generalized Frobenius partitions with 4 colors’, Discrete Math. 311 (2011), 1892–1902.Google Scholar
Berndt, B. C., Number Theory in the Spirit of Ramanujan (American Mathematical Society, Providence, RI, 2006).Google Scholar
Bruinier, J. H., van der Geer, G., Harder, G. and Zagier, D., The 1-2-3 of Modular Forms (Springer, Berlin–Heidelberg, 2008).Google Scholar
Chan, H. H. and Chua, K. S., ‘Representations of integers as sums of 32 squares’, Ramanujan J. 7 (2003), 79–89.Google Scholar
Chan, H. H. and Lewis, R. P., ‘Partition identities and congruences associated with the Fourier coefficients of the Euler products’, J. Comput. Appl. Math. 160 (2003), 69–75.Google Scholar
Diamond, F. and Shurman, J., A First Course in Modular Forms (Springer, New York, 2005).Google Scholar
Eichhorn, D. and Ono, K., ‘Congruences for partition functions’, in: Proc. Conf. in Honor of Heini Halbertstam, Vol. 1 (Birkhäuser, Boston, 1996), 309–321.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic relations for overpartitions’, J. Combin. Math. Combin. Comput. 53 (2005), 65–73.Google Scholar
Koblitz, N., Introduction to Elliptic Curves and Modular Forms (Springer, New York, 1984).Google Scholar
Lin, B. L. S., ‘New Ramanujan type congruences modulo 7 for 4-colored generalized Frobenius partitions’, Int. J. Number Theory 10 (2014), 637–639.CrossRefGoogle Scholar
Ono, K., The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and q-Series, CBMS Regional Conference Series in Mathematics, Vol. 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Rankin, R. A., Modular Forms and Functions (Cambridge University Press, Cambridge, 1977).Google Scholar
Sellers, J. A., ‘An unexpected congruence modulo 5 for 4-colored generalized Frobenius partitions’, J. Indian Math. Soc. (2013), 97–103; Special volume to commemorate the 125th birth anniversary of Srinivasa Ramanujan.Google Scholar
Sturm, J., On the Congruence of Modular Forms, Springer Lecture Notes in Mathematics, 1240 (Springer, Berlin–New York, 1984), 275–280.Google Scholar
Treneer, S., ‘Congruences for the coefficients of weakly holomorphic modular forms’, Proc. Lond. Math. Soc. 93 (2006), 304–324.Google Scholar
Wang, L., ‘Another proof of a conjecture by Hirschhorn and Sellers on overpartitions’, J. Integer Seq. 17 (2014), Article 14.9.8.Google Scholar
Wang, L., ‘New congruences for partitions where the odd parts are distinct’, J. Integer Seq. 18 (2015), Article 15.4.2.Google Scholar
Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis, 4th edn (Cambridge University Press, Cambridge, 1966).Google Scholar
Zhang, W. and Wang, C., ‘An unexpected Ramanujan-type congruence modulo 7 for 4-colored generalized Frobenius partitions’, Ramanujan J., doi:10.1007/s11139-015-9770-0.Google Scholar