Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T19:23:58.416Z Has data issue: false hasContentIssue false
  • English
  • Français

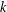$k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE

Part of: Singularities Local theory

Published online by Cambridge University Press:  30 April 2019

NAVEED HUSSAIN ,
STEPHEN S.-T. YAU  and
HUAIQING ZUO Open the ORCID record for HUAIQING ZUO [Opens in a new window]
NAVEED HUSSAIN
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, PR China e-mail: hnw15@mails.tsinghua.edu.cn
STEPHEN S.-T. YAU*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, PR China
HUAIQING ZUO
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, PR China e-mail: hqzuo@mail.tsinghua.edu.cn
*
e-mail: yau@uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 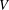$V$ be a hypersurface with an isolated singularity at the origin defined by the holomorphic function 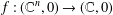$f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$. The Yau algebra 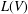$L(V)$ is defined to be the Lie algebra of derivations of the moduli algebra 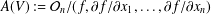$A(V):={\mathcal{O}}_{n}/(f,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{n})$, that is, 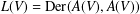$L(V)=\text{Der}(A(V),A(V))$. It is known that 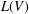$L(V)$ is finite dimensional and its dimension 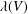$\unicode[STIX]{x1D706}(V)$ is called the Yau number. We introduce a new series of Lie algebras, that is, 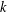$k$th Yau algebras 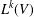$L^{k}(V)$, 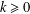$k\geq 0$, which are a generalization of the Yau algebra. The algebra $L^{k}(V)$ is defined to be the Lie algebra of derivations of the 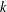$k$th moduli algebra 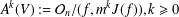$A^{k}(V):={\mathcal{O}}_{n}/(f,m^{k}J(f)),k\geq 0$, that is, 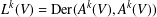$L^{k}(V)=\text{Der}(A^{k}(V),A^{k}(V))$, where $m$ is the maximal ideal of 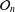${\mathcal{O}}_{n}$. The 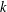$k$th Yau number is the dimension of 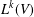$L^{k}(V)$, which we denote by 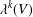$\unicode[STIX]{x1D706}^{k}(V)$. In particular, 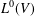$L^{0}(V)$ is exactly the Yau algebra, that is, 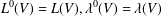$L^{0}(V)=L(V),\unicode[STIX]{x1D706}^{0}(V)=\unicode[STIX]{x1D706}(V)$. These numbers 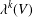$\unicode[STIX]{x1D706}^{k}(V)$ are new numerical analytic invariants of singularities. In this paper we formulate a conjecture that 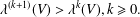$\unicode[STIX]{x1D706}^{(k+1)}(V)>\unicode[STIX]{x1D706}^{k}(V),k\geq 0.$ We prove this conjecture for a large class of singularities.

Keywords

derivationLie algebraisolated singularityYau algebra

MSC classification

Primary: 14B05: Singularities
Secondary: 32S05: Local singularities
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 1 , February 2021 , pp. 94 - 118
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by F. Larusson

Both S. Yau and H. Zuo were supported by NSFC Grant 11531007 and the start-up fund from Tsinghua University. H. Zuo was also supported by NSFC Grant 11771231 and the Tsinghua University Initiative Scientific Research Program.

References

Arnold, V. I., Gusein-Zade, S. M. and Varchenko, A. N., Singularities of Differential Maps, 2nd edn, Vol. 1 (MCNMO, Moskva, 2004).Google Scholar
Benson, M. and Yau, S. S.-T., ‘Lie algebras and their representations arising from isolated singularities: computer method in calculating the Lie algebras and their cohomology’, in: Complex Analytic Singularities, Advanced Studies in Pure Mathematics, 8 (North-Holland, Amsterdam, 1987), 3–58.CrossRefGoogle Scholar
Benson, M. and Yau, S. S.-T., ‘Equivalence between isolated hypersurface singularities’, Math. Ann. 287 (1990), 107–134.CrossRefGoogle Scholar
Block, R., ‘Determination of the differentiably simple rings with a minimal ideal’, Ann. of Math. (2) 90 (1969), 433–459.CrossRefGoogle Scholar
Chen, B., Chen, H., Yau, S. S.-T. and Zuo, H., ‘The non-existence of negative weight derivations on positive dimensional isolated singularities: generalized Wahl conjecture’, J. Differential Geom. to appear.Google Scholar
Chen, B., Hussain, N., Yau, S. S.-T. and Zuo, H., ‘Variation of complex structures and variation of Lie algebras II: new Lie algebras arising from singularities’, J. Dierential Geom. to appear.Google Scholar
Chen, H., Xu, Y.-J. and Yau, S. S.-T., ‘Nonexistence of negative weight derivation of moduli algebras of weighted homogeneous singularities’, J. Algebra 172 (1995), 243–254.CrossRefGoogle Scholar
Chen, H., Yau, S. S.-T. and Zuo, H., ‘Non-existence of negative weight derivations on positively graded Artinian algebras’, Trans. Amer. Math. Soc. to appear.Google Scholar
Ebeling, W. and Takahashi, A., ‘Strange duality of weighted homogeneous polynomials’, Compos. Math. 147 (2011), 1413–1433.CrossRefGoogle Scholar
Greuel, G.-M., Lossen, C. and Shustin, E., Introduction to Singularities and Deformations, Springer Monographs in Mathematics (Springer, Berlin, 2007).Google Scholar
Hussain, N., ‘Survey on derivation Lie algebras of isolated singularities’, Methods Appl. Anal. to appear.Google Scholar
Hussain, N., Yau, S. S.-T. and Zuo, H., ‘On the derivation Lie algebras of fewnomial singularities’, Bull. Aust. Math. Soc. 98(1) (2018), 77–88.CrossRefGoogle Scholar
Hussain, N., Yau, S. S.-T. and Zuo, H., ‘On the new k-th Yau algebras of isolated hypersurface singularities’, Math. Z. to appear. Published online (16 March 2019).Google Scholar
Mather, J. and Yau, S. S.-T., ‘Classification of isolated hypersurface singularities by their moduli algebras’, Invent. Math. 69 (1982), 243–251.CrossRefGoogle Scholar
Milnor, J. and Orlik, P., ‘Isolated singularities defined by weighted homogeneous polynomials’, Topology 9 (1970), 385–393.CrossRefGoogle Scholar
Saito, K., ‘Quasihomogene isolierte Singularitäten von Hyperflächen’, Invent. Math. 14 (1971), 123–142.CrossRefGoogle Scholar
Seeley, C. and Yau, S. S.-T., ‘Variation of complex structures and variation of Lie algebras’, Invent. Math. 99 (1990), 545–565.CrossRefGoogle Scholar
Xu, Y.-J. and Yau, S. S.-T., ‘Micro-local characterization of quasi-homogeneous singularities’, Amer. J. Math. 118(2) (1996), 389–399.Google Scholar
Yau, S. S.-T., ‘Continuous family of finite-dimensional representations of a solvable Lie algebra arising from singularities’, Proc. Natl Acad. Sci. USA 80 (1983), 7694–7696.CrossRefGoogle ScholarPubMed
Yau, S. S.-T., ‘Milnor algebras and equivalence relations among holomorphic functions’, Bull. Amer. Math. Soc. (N.S.) 9 (1983), 235–239.CrossRefGoogle Scholar
Yau, S. S.-T., ‘Criterions for right–left equivalence and right equivalence of holomorphic germs with isolated critical points’, Proc. Sympos. Pure Math. 41 (1984), 291–297.CrossRefGoogle Scholar
Yau, S. S.-T., ‘Solvable Lie algebras and generalized Cartan matrices arising from isolated singularities’, Math. Z. 191 (1986), 489–506.CrossRefGoogle Scholar
Yau, S. S.-T., ‘Solvability of Lie algebras arising from isolated singularities and nonisolatedness of singularities defined by sl (2, ℂ) invariant polynomials’, Amer. J. Math. 113 (1991), 773–778.Google Scholar
Yau, S. S.-T. and Zuo, H., ‘Derivations of the moduli algebras of weighted homogeneous hypersurface singularities’, J. Algebra 457 (2016), 18–25.CrossRefGoogle Scholar
Yau, S. S.-T. and Zuo, H., ‘A sharp upper estimate conjecture for the Yau number of a weighted homogeneous isolated hypersurface singularity’, Pure Appl. Math. Q. 12(1) (2016), 165–181.CrossRefGoogle Scholar
Yu, Y., ‘On Jacobian ideals invariant by reducible sl (2; C) action’, Trans. Amer. Math. Soc. 348 (1996), 2759–2791.CrossRefGoogle Scholar