Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T13:28:13.001Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LOOMIS–SIKORSKI THEOREM FOR 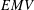$EMV$-ALGEBRAS

Part of: Boolean algebras (Boolean rings) Distributive lattices Modular lattices, complemented lattices

Published online by Cambridge University Press:  23 August 2018

ANATOLIJ DVUREČENSKIJ  and
OMID ZAHIRI
ANATOLIJ DVUREČENSKIJ
Affiliation:
Mathematical Institute, Slovak Academy of Sciences, Štefánikova 49, SK-814 73 Bratislava, Slovakia Depart. Algebra Geom., Palacký Univer. 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic email dvurecen@mat.savba.sk
OMID ZAHIRI*
Affiliation:
University of Applied Science and Technology, Tehran, Iran email zahiri@protonmail.com
*
✉om.zahiri@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An EMV-algebra resembles an MV-algebra in which a top element is not guaranteed. For 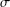$\unicode[STIX]{x1D70E}$-complete 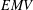$EMV$-algebras, we prove an analogue of the Loomis–Sikorski theorem showing that every 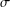$\unicode[STIX]{x1D70E}$-complete 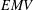$EMV$-algebra is a 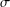$\unicode[STIX]{x1D70E}$-homomorphic image of an 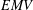$EMV$-tribe of fuzzy sets where all algebraic operations are defined by points. To prove it, some topological properties of the state-morphism space and the space of maximal ideals are established.

Keywords

MV-algebraidempotent elementEMV-algebra𝜎-complete EMV-algebraEMV-clanEMV-tribestate-morphismidealfilterhull-kernel topologythe Loomis–Sikorski theorem

MSC classification

Primary: 06C15: Complemented lattices, orthocomplemented lattices and posets
Secondary: 06D35: MV-algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 2 , April 2019 , pp. 200 - 234
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is grateful for support from grants APVV-16-0073, VEGA no. 2/0069/16 SAV and GAČR 15-15286S.

References

Barbieri, G. and Weber, H., ‘Measures on clans and on MV-algebras’, in: Handbook of Measure Theory, Vol. II (ed. Pap, E.) (Elsevier Science, Amsterdam, 2002), 911–945.Google Scholar
Belluce, L. P., ‘Semisimple algebras of infinite valued logic and bold fuzzy set theory’, Can. J. Math. 38(6) (1986), 1356–1379.Google Scholar
Chang, C. C., ‘Algebraic analysis of many valued logics’, Trans. Amer. Math. Soc. 88(2) (1958), 467–490.Google Scholar
Cignoli, R., D’Ottaviano, I. M. L. and Mundici, D., Algebraic Foundations of Many-Valued Reasoning (Springer Science and Business Media, Dordrecht, 2000).Google Scholar
Conrad, P. and Darnel, M. R., ‘Generalized Boolean algebras in lattice-ordered groups’, Order 14(4) (1997), 295–319.Google Scholar
Di Nola, A. and Russo, C., ‘The semiring-theoretic approach to MV-algebras’, Fuzzy Sets and Systems 281 (2015), 134–154.Google Scholar
Dvurečenskij, A., ‘Loomis–Sikorski theorem for 𝜎-complete MV-algebras and ℓ-groups’, J. Aust. Math. Soc. 68(2) (2000), 261–277.Google Scholar
Dvurečenskij, A., ‘Pseudo MV-algebras are intervals in ℓ-groups’, J. Aust. Math. Soc. 72(3) (2002), 427–446.Google Scholar
Dvurečenskij, A. and Pulmannová, S., New Trends in Quantum Structures (Kluwer Academic Publishers, Dordrecht, Ister Science, Bratislava, 2000).Google Scholar
Dvurečenskij, A. and Zahiri, O., ‘On EMV-algebras’, Preprint, 2017, arXiv:1706.00571.Google Scholar
Galatos, N. and Tsinakis, C., ‘Generalized MV-algebras’, J. Algebra 283 (2005), 254–291.Google Scholar
Georgescu, G. and Iorgulescu, A., ‘Pseudo MV-algebras’, Mult.-Valued Logic 6(1–2) (2001), 95–135.Google Scholar
Goodearl, K. R., Partially Ordered Abelian Groups with Interpolation, Matematical Surveys and Monographs, 20 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Kelley, J. L., General Topology, Van Nostrand, Toronto 1957, Graduate Texts in Mathematics (reprinted by Springer, New York, 1975).Google Scholar
Loomis, L. H., ‘On the representation of 𝜎-complete Boolean algebras’, Bull. Amer. Math. Soc. (N.S.) 53(8) (1947), 757–760.Google Scholar
Luxemburg, W. A. J. and Zaanen, A. C., Riesz Spaces, Vol. 1 (North-Holland Publishers, Amsterdam, London, 1971).Google Scholar
Mundici, D., ‘Interpretation of AF C ∗ -algebras in Łukasiewicz sentential calculus’, J. Funct. Anal. 65(1) (1986), 15–63.Google Scholar
Mundici, D., ‘Tensor products and the Loomis–Sikorski theorem for MV-algebras’, Adv. Appl. Math. 22(2) (1999), 227–248.Google Scholar
Sikorski, R., ‘On the representation of Boolean algebras as fields of sets’, Fundam. Math. 35(1) (1948), 247–258.Google Scholar
Stone, M. H., ‘Applications of the theory of Boolean rings to general topology’, Trans. Amer. Math. Soc. 41(3) (1937), 375–481.Google Scholar
Stone, M. H., ‘Topological representations of distributive lattices and Brouwerian logics’, Časopis pro pěstování matematiky a fysiky 67(1) (1938), 1–25.Google Scholar