Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-20T01:46:51.874Z Has data issue: false hasContentIssue false
  • English
  • Français

ON INVOLUTIONS AND INDICATORS OF FINITE ORTHOGONAL GROUPS

Part of: Linear algebraic groups and related topics Representation theory of groups Combinatorics

Published online by Cambridge University Press:  30 May 2018

GREGORY K. TAYLOR  and
C. RYAN VINROOT
GREGORY K. TAYLOR
Affiliation:
Department of Mathematics, Statistics, and Computer Science (MC249), University of Illinois at Chicago, 851 South Morgan Street, Chicago, IL 60680-7045, USA email gtaylo9@uic.edu
C. RYAN VINROOT*
Affiliation:
Department of Mathematics, College of William and Mary, P. O. Box 8795, Williamsburg, VA 23187-8795, USA email vinroot@math.wm.edu
*
✉vinroot@math.wm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the numbers of involutions and their relation to Frobenius–Schur indicators in the groups 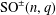$\text{SO}^{\pm }(n,q)$ and 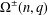$\unicode[STIX]{x1D6FA}^{\pm }(n,q)$. Our point of view for this study comes from two motivations. The first is the conjecture that a finite simple group 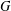$G$ is strongly real (all elements are conjugate to their inverses by an involution) if and only if it is totally orthogonal (all Frobenius–Schur indicators are 1), and we observe this holds for all finite simple groups 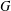$G$ other than the groups 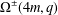$\unicode[STIX]{x1D6FA}^{\pm }(4m,q)$ with 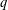$q$ even. We prove computationally that for small 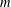$m$ this statement indeed holds for these groups by equating their character degree sums with the number of involutions. We also prove a result on a certain twisted indicator for the groups 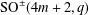$\text{SO}^{\pm }(4m+2,q)$ with 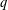$q$ odd. Our second motivation is to continue the work of Fulman, Guralnick, and Stanton on generating functions and asymptotics for involutions in classical groups. We extend their work by finding generating functions for the numbers of involutions in 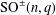$\text{SO}^{\pm }(n,q)$ and 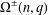$\unicode[STIX]{x1D6FA}^{\pm }(n,q)$ for all 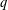$q$, and we use these to compute the asymptotic behavior for the number of involutions in these groups when 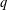$q$ is fixed and $n$ grows.

Keywords

orthogonal groups over finite fieldsFrobenius–Schur indicatorsinvolutionsgenerating functionsasymptotic enumeration

MSC classification

Primary: 20G40: Linear algebraic groups over finite fields
Secondary: 20C33: Representations of finite groups of Lie type 05A15: Exact enumeration problems, generating functions 05A16: Asymptotic enumeration
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 3 , December 2018 , pp. 380 - 416
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Andrews, G., The Theory of Partitions, Encyclopedia of Mathematics and its Applications, 2 (Addison-Wesley, Reading, MA, 1976).Google Scholar
Bagiński, C., ‘On sets of elements of the same order in the alternating group A n ’, Publ. Math. Debrecen 34(3–4) (1987), 313–315.Google Scholar
Barry, M. J. J., ‘Schur indices and 3 D 4(q 3), q odd’, J. Algebra 117(2) (1988), 522–524.Google Scholar
Brauer, R., Representations of Finite Groups, Lectures on Modern Mathematics, 1 (Wiley, New York, 1963), 133–175.Google Scholar
Bump, D. and Ginzburg, D., ‘Generalized Frobenius–Schur numbers’, J. Algebra 278(1) (2004), 294–313.Google Scholar
Cabanes, M. and Enguehard, M., Representation Theory of Finite Reductive Groups, New Mathematical Monographs (Cambridge University Press, Cambridge, 2004).Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups, Maximal Subgroups and Ordinary Characters for Simple Groups, With Computational Assistance from J. G. Thackray (Clarendon Press, Oxford, 1985).Google Scholar
Djoković, D. Ž., ‘Product of two involutions’, Arch. Math. (Basel) 18 (1967), 582–584.Google Scholar
Dye, R. H., ‘On the conjugacy classes of involutions of the simple orthogonal groups over perfect fields of characteristic two’, J. Algebra 18 (1971), 414–425.Google Scholar
Ellers, E. W. and Nolte, W., ‘Bireflectionality of orthogonal and symplectic groups’, Arch. Math. (Basel) 39 (1982), 113–118.Google Scholar
Fulman, J., Guralnick, R. and Stanton, D., ‘Asymptotics of the number of involutions in finite classical groups’, J. Group Theory 20(5) (2017), 871–902.Google Scholar
Fulman, J. and Vinroot, C. R., ‘Generating functions for real character degree sums of finite general linear and unitary groups’, J. Algebraic Combin. 40(2) (2014), 387–416.Google Scholar
Gal’t, A. A., ‘Strongly real elements in finite simple orthogonal groups’, Sib. Math. J. 51(2) (2010), 193–198.Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.8.7; 2017 (http://www.gap-system.org).Google Scholar
Gow, R., ‘Products of two involutions in classical groups of characteristic 2’, J. Algebra 71(2) (1981), 583–591.Google Scholar
Gow, R., ‘Real representations of the finite orthogonal and symplectic groups of odd characteristic’, J. Algebra 96(1) (1985), 249–274.Google Scholar
Grove, L. C., Classical Groups and Geometric Algebra, Graduate Studies in Mathematics, 39 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Isaacs, I. M., Character Theory of Finite Groups, Pure and Applied Mathematics, 69 (Academic Press, New York, 1976).Google Scholar
James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and its Applications, 16 (Addison-Wesley, Reading, MA, 1981).Google Scholar
Kaur, D. and Kulshrestha, A., ‘Strongly real special 2-groups’, Comm. Algebra 43(3) (2015), 1176–1193.Google Scholar
Kawanaka, N. and Matsuyama, H., ‘A twisted version of the Frobenius–Schur indicator and multiplicity-free representations’, Hokkaido Math. J. 19(3) (1990), 495–508.Google Scholar
Kleidman, P. and Liebeck, M., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambdridge, 1990).Google Scholar
Knüppel, F. and Thomsen, G., ‘Involutions and commutators in orthogonal groups’, J. Austral. Math. Soc. 65(1) (1998), 1–36.Google Scholar
Kolesnikov, S. G. and Nuzhin, Y. N., ‘On strong reality of finite simple groups’, Acta Appl. Math. 85(1–3) (2005), 195–203.Google Scholar
Lübeck, F., Character degrees and their multiplicities for some groups of Lie type of rank ${<}$ 9, http://www.math.rwth-aachen.du/∼Frank.Luebeck/chev/DegMult/index.html.Google Scholar
Lux, K., Schaeffer Fry, A. and Vinroot, C. R., ‘Strong reality properties of normalizers of parabolic subgroups in finite Coxeter groups’, Comm. Algebra 40(8) (2012), 3056–3070.Google Scholar
Odlyzko, A., ‘Asymptotic enumeration methods’, in: Handbook of Combinatorics, Vol. 2 (Elsevier, New York, 1995).Google Scholar
Ohmori, J., ‘On the Schur indices of characters of finite reductive groups in bad characteristic cases’, Osaka J. Math. 40(4) (2003), 1011–1019.Google Scholar
Rämö, J., ‘Strongly real elements of orthogonal groups in even characteristic’, J. Group Theory 14(1) (2011), 9–30.Google Scholar
Schaeffer Fry, A. A. and Vinroot, C. R., ‘Real classes of finite special unitary groups’, J. Group Theory 19(5) (2016), 735–762.Google Scholar
Tiep, P. H. and Zalesski, A. E., ‘Real conjugacy classes in algebraic groups and finite groups of Lie type’, J. Group Theory 8(3) (2005), 291–315.Google Scholar
Turull, A., ‘The Schur indices of the irreducible characters of the special linear groups’, J. Algebra 235(1) (2001), 275–314.Google Scholar
Vdovin, E. P. and Gal’t, A. A., ‘Strong reality of finite simple groups’, Sib. Math. J. 51(4) (2010), 610–615.Google Scholar
Vinroot, C. R., ‘Twisted Frobenius–Schur indicators of finite symplectic groups’, J. Algebra 293(1) (2005), 279–311.Google Scholar
Vinroot, C. R., ‘Character degree sums and real representations of finite classical groups of odd characteristic’, J. Algebra Appl. 9(4) (2010), 633–658.Google Scholar
Vinroot, C. R., ‘Real representations of symplectic groups over fields of characteristic two’, Internat. Math. Res. Notices, to appear.Google Scholar
Wall, G. E., ‘On the conjugacy classes in the unitary, orthogonal and symplectic groups’, J. Austral. Math. Soc. 3 (1962), 1–62.Google Scholar
Wonenburger, M., ‘Transformations which are products of two involutions’, J. Math. Mech. 16 (1966), 327–338.Google Scholar