Article contents
REPRESENTATION THEOREMS FOR NORMED ALGEBRAS
Published online by Cambridge University Press: 17 June 2013
Abstract
We show that for a normal locally-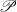 $\mathscr{P}$ space
$\mathscr{P}$ space 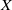 $X$ (where
$X$ (where 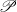 $\mathscr{P}$ is a topological property subject to some mild requirements) the subset
$\mathscr{P}$ is a topological property subject to some mild requirements) the subset 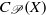 ${C}_{\mathscr{P}} (X)$ of
${C}_{\mathscr{P}} (X)$ of 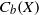 ${C}_{b} (X)$ consisting of those elements whose support has a neighborhood with
${C}_{b} (X)$ consisting of those elements whose support has a neighborhood with 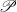 $\mathscr{P}$, is a subalgebra of
$\mathscr{P}$, is a subalgebra of 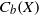 ${C}_{b} (X)$ isometrically isomorphic to
${C}_{b} (X)$ isometrically isomorphic to 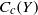 ${C}_{c} (Y)$ for some unique (up to homeomorphism) locally compact Hausdorff space
${C}_{c} (Y)$ for some unique (up to homeomorphism) locally compact Hausdorff space 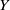 $Y$. The space
$Y$. The space 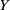 $Y$ is explicitly constructed as a subspace of the Stone–Čech compactification
$Y$ is explicitly constructed as a subspace of the Stone–Čech compactification 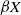 $\beta X$ of
$\beta X$ of 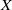 $X$ and contains
$X$ and contains 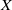 $X$ as a dense subspace. Under certain conditions,
$X$ as a dense subspace. Under certain conditions, 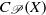 ${C}_{\mathscr{P}} (X)$ coincides with the set of those elements of
${C}_{\mathscr{P}} (X)$ coincides with the set of those elements of 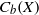 ${C}_{b} (X)$ whose support has
${C}_{b} (X)$ whose support has 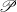 $\mathscr{P}$, it moreover becomes a Banach algebra, and simultaneously,
$\mathscr{P}$, it moreover becomes a Banach algebra, and simultaneously, 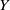 $Y$ satisfies
$Y$ satisfies 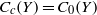 ${C}_{c} (Y)= {C}_{0} (Y)$. This includes the cases when
${C}_{c} (Y)= {C}_{0} (Y)$. This includes the cases when 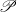 $\mathscr{P}$ is the Lindelöf property and
$\mathscr{P}$ is the Lindelöf property and 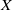 $X$ is either a locally compact paracompact space or a locally-
$X$ is either a locally compact paracompact space or a locally-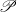 $\mathscr{P}$ metrizable space. In either of the latter cases, if
$\mathscr{P}$ metrizable space. In either of the latter cases, if 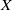 $X$ is non-
$X$ is non-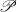 $\mathscr{P}$, then
$\mathscr{P}$, then 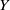 $Y$ is nonnormal and
$Y$ is nonnormal and 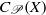 ${C}_{\mathscr{P}} (X)$ fits properly between
${C}_{\mathscr{P}} (X)$ fits properly between 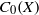 ${C}_{0} (X)$ and
${C}_{0} (X)$ and 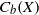 ${C}_{b} (X)$; even more, we can fit a chain of ideals of certain length between
${C}_{b} (X)$; even more, we can fit a chain of ideals of certain length between 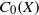 ${C}_{0} (X)$ and
${C}_{0} (X)$ and 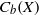 ${C}_{b} (X)$. The known construction of
${C}_{b} (X)$. The known construction of 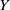 $Y$ enables us to derive a few further properties of either
$Y$ enables us to derive a few further properties of either 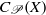 ${C}_{\mathscr{P}} (X)$ or
${C}_{\mathscr{P}} (X)$ or 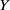 $Y$. Specifically, when
$Y$. Specifically, when 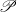 $\mathscr{P}$ is the Lindelöf property and
$\mathscr{P}$ is the Lindelöf property and 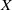 $X$ is a locally-
$X$ is a locally-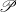 $\mathscr{P}$ metrizable space, we show that
$\mathscr{P}$ metrizable space, we show that 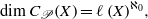 $$\begin{eqnarray*}\dim C_{\mathscr{P}}(X)= \ell \mathop{(X)}\nolimits ^{{\aleph }_{0} } ,\end{eqnarray*}$$
$$\begin{eqnarray*}\dim C_{\mathscr{P}}(X)= \ell \mathop{(X)}\nolimits ^{{\aleph }_{0} } ,\end{eqnarray*}$$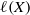 $\ell (X)$ is the Lindelöf number of
$\ell (X)$ is the Lindelöf number of 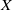 $X$, and when
$X$, and when 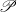 $\mathscr{P}$ is countable compactness and
$\mathscr{P}$ is countable compactness and 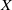 $X$ is a normal space, we show that
$X$ is a normal space, we show that 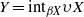 $$\begin{eqnarray*}Y= {\mathrm{int} }_{\beta X} \upsilon X\end{eqnarray*}$$
$$\begin{eqnarray*}Y= {\mathrm{int} }_{\beta X} \upsilon X\end{eqnarray*}$$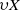 $\upsilon X$ is the Hewitt realcompactification of
$\upsilon X$ is the Hewitt realcompactification of 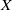 $X$.
$X$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 6
- Cited by




