Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-24T02:25:07.038Z Has data issue: false hasContentIssue false
  • English
  • Français

TILING BRANCHING MULTIPLICITY SPACES WITH GL${}_{2} $ PATTERN BLOCKS

Part of: Algebraic combinatorics Linear algebraic groups and related topics

Published online by Cambridge University Press:  10 April 2013

SANGJIB KIM
SANGJIB KIM*
Affiliation:
Department of Mathematics, Ewha Womens University, Seoul 120-750, South Korea
*
sangib@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study branching multiplicity spaces of complex classical groups in terms of 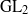${\mathrm{GL} }_{2} $ representations. In particular, we show how combinatorics of 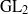${\mathrm{GL} }_{2} $ representations are intertwined to make branching rules under the restriction of 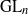${\mathrm{GL} }_{n} $ to 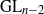${\mathrm{GL} }_{n- 2} $. We also discuss analogous results for the symplectic and orthogonal groups.

Keywords

classical groupsrepresentationsbranching rules

MSC classification

Secondary: 20G05: Representation theory 05E10: Combinatorial aspects of representation theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 3 , June 2013 , pp. 362 - 374
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Fulton, W. and Harris, J., ‘Representation theory: a first course’, in: Readings in Mathematics, Graduate Texts in Mathematics, 129 (Springer, New York, 1991).Google Scholar
Gelfand, I. M. and Tsetlin, M. L., ‘Finite-dimensional representations of the group of unimodular matrices’, Dokl. Akad. Nauk SSSR (N.S.) 71 (1950), 825–828.Google Scholar
Goodman, R. and Wallach, N. R., Symmetry, Representations, and Invariants, Graduate Texts in Mathematics, 255 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Kim, S., ‘Distributive lattices, affine semigroups, and branching rules of the classical groups’, J. Combin. Theory Ser. A 119 (6) (2012), 1132–1157.CrossRefGoogle Scholar
Kim, S. and Yacobi, O., ‘A basis for the symplectic group branching algebra’, J. Algebraic Combin. 35 (2) (2012), 269–290.CrossRefGoogle Scholar
King, R. C., ‘Branching rules for classical Lie groups using tensor and spinor methods’, J. Phys. A 8 (1975), 429–449.CrossRefGoogle Scholar
Koike, K. and Terada, I., ‘Young diagrammatic methods for the restriction of representations of complex classical Lie groups to reductive subgroups of maximal rank’, Adv. Math. 79 (1) (1990), 104–135.CrossRefGoogle Scholar
Molev, A. I., ‘Gelfand–Tsetlin bases for classical Lie algebras’, in: Handbook of Algebra, Vol. 4 (Elsevier/North-Holland, Amsterdam, 2006), 109–170.CrossRefGoogle Scholar
Proctor, R. A., ‘Young tableaux, Gelfand patterns, and branching rules for classical groups’, J. Algebra 164 (2) (1994), 299–360.CrossRefGoogle Scholar
Wallach, N. and Yacobi, O., ‘A multiplicity formula for tensor products of ${\mathrm{SL} }_{2} $ modules and an explicit ${\mathrm{Sp} }_{2n} $ to ${\mathrm{Sp} }_{2n- 2} \times {\mathrm{Sp} }_{2} $ branching formula’, in: Symmetry in Mathematics and Physics, Contemporary Mathematics, 490 (American Mathematical Society, Providence, RI, 2009), 151–155.CrossRefGoogle Scholar
Whippman, M. L., ‘Branching rules for simple Lie groups’, J. Math. Phys. 6 (1965), 1534–1539.CrossRefGoogle Scholar
Yacobi, O., ‘An analysis of the multiplicity spaces in branching of symplectic groups’, Selecta Math. (N.S.) 16 (4) (2010), 819–855.CrossRefGoogle Scholar