Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marzo, Jordi
Nitzan, Shahaf
and
Olsen, Jan-Fredrik
2012.
Sampling and interpolation in de Branges spaces with doubling phase.
Journal d'Analyse Mathématique,
Vol. 117,
Issue. 1,
p.
365.
Mengestie, Tesfa
2014.
Compact Carleson measures from sparse sequences.
Rocky Mountain Journal of Mathematics,
Vol. 44,
Issue. 1,
Baranov, A.
Dumont, A.
Hartmann, A.
and
Kellay, K.
2015.
Sampling, interpolation and Riesz bases in small Fock spaces.
Journal de Mathématiques Pures et Appliquées,
Vol. 103,
Issue. 6,
p.
1358.
Baranov, Anton
Belov, Yurii
and
Borichev, Alexander
2015.
Spectral synthesis in de Branges spaces.
Geometric and Functional Analysis,
Vol. 25,
Issue. 2,
p.
417.
Mengestie, Tesfa
2015.
Volterra Type Integral Operators and Composition Operators on Model Spaces.
Journal of Function Spaces,
Vol. 2015,
Issue. ,
p.
1.
Isaev, K. P.
2017.
On unconditional exponential bases in weighted spaces on interval of real axis.
Lobachevskii Journal of Mathematics,
Vol. 38,
Issue. 1,
p.
48.
Isaev, Konstantin Petrovich
and
Yulmukhametov, Rinad Salavatovich
2017.
О безусловных базисах из воспроизводящих ядер в пространствах типа Фока.
Функциональный анализ и его приложения,
Vol. 51,
Issue. 4,
p.
50.
Baranov, A.
Hartmann, A.
and
Kellay, K.
2017.
Geometry of reproducing kernels in model spaces near the boundary.
Journal of Mathematical Analysis and Applications,
Vol. 447,
Issue. 2,
p.
971.
Isaev, K. P.
and
Yulmukhametov, R. S.
2017.
On unconditional bases of reproducing kernels in Fock-type spaces.
Functional Analysis and Its Applications,
Vol. 51,
Issue. 4,
p.
283.
Varolin, Dror
2018.
Bergman interpolation on finite Riemann surfaces. Part I: asymptotically flat case.
Journal d'Analyse Mathématique,
Vol. 136,
Issue. 1,
p.
103.
Isaev, K. P.
Lutsenko, A. V.
and
Yulmukhametov, R. S.
2019.
Generating Functions for Bases in Hilbert Spaces of Entire Functions.
Journal of Mathematical Sciences,
Vol. 241,
Issue. 6,
p.
718.
Isaev, K. P.
and
Yulmukhametov, R. S.
2019.
On Hilbert Spaces of Entire Functions with Unconditional Bases of Reproducing Kernels.
Lobachevskii Journal of Mathematics,
Vol. 40,
Issue. 9,
p.
1283.
Kellay, K.
and
Omari, Y.
2020.
Riesz Bases of Reproducing Kernels in Small Fock Spaces.
Journal of Fourier Analysis and Applications,
Vol. 26,
Issue. 1,
Isaev, Konstantin Petrovich
and
Yulmukhametov, Rinad Salavatovich
2020.
Geometry of radial Hilbert spaces with unconditional bases of reproducing kernels.
Ufa Mathematical Journal,
Vol. 12,
Issue. 4,
p.
55.
Isaev, K. P.
Trunov, K. V.
and
Yulmukhametov, R. S.
2020.
Equivalent Norms in Hilbert Spaces with Unconditional Bases of Reproducing Kernels.
Journal of Mathematical Sciences,
Vol. 250,
Issue. 2,
p.
310.
Isaev, K. P.
and
Yulmukhametov, R. S.
2021.
On a Sufficient Condition for the Existence of Unconditional Bases of Reproducing Kernels in Hilbert Spaces of Entire Functions.
Lobachevskii Journal of Mathematics,
Vol. 42,
Issue. 6,
p.
1154.
Isaev, K. P.
Lutsenko, A. V.
and
Yulmukhametov, R. S.
2021.
Necessary Condition for the Existence of Unconditional Bases of Reproducing Kernels for Hilbert Spaces of Entire Functions.
Journal of Mathematical Sciences,
Vol. 257,
Issue. 5,
p.
662.
Omari, Youssef
2021.
Complete interpolating sequences for small Fock spaces.
Journal of Functional Analysis,
Vol. 281,
Issue. 5,
p.
109064.
Isaev, K. P.
Lutsenko, A. V.
and
Yulmukhametov, R. S.
2022.
Unconditional Bases of Reproducing Kernels for Fock Spaces with Nonradial Weights.
Journal of Mathematical Sciences,
Vol. 260,
Issue. 6,
p.
748.
Isaev, K. P.
and
Yulmukhametov, R. S.
2022.
Riesz bases of normalized reproducing kernels in Fock type spaces.
Analysis and Mathematical Physics,
Vol. 12,
Issue. 1,




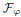 with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(
with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(