Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T01:40:46.070Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE WELL-POSEDNESS OF PARABOLIC EQUATIONS OF NAVIER–STOKES TYPE WITH $\mathit{BMO}^{-1}$ DATA

Part of: Incompressible viscous fluids Harmonic analysis in several variables

Published online by Cambridge University Press:  27 April 2015

Pascal Auscher  and
Dorothee Frey
Pascal Auscher
Affiliation:
Univ. Paris-Sud, Laboratoire de Mathématiques, UMR 8628 du CNRS, F-91405 Orsay, France (pascal.auscher@math.u-psud.fr; dorothee.frey@univ-nantes.fr)
Dorothee Frey
Affiliation:
Univ. Paris-Sud, Laboratoire de Mathématiques, UMR 8628 du CNRS, F-91405 Orsay, France (pascal.auscher@math.u-psud.fr; dorothee.frey@univ-nantes.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a strategy making extensive use of tent spaces to study parabolic equations with quadratic nonlinearities as for the Navier–Stokes system. We begin with a new proof of the well-known result of Koch and Tataru on the well-posedness of Navier–Stokes equations in 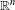$\mathbb{R}^{n}$ with small initial data in 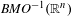$\mathit{BMO}^{-1}(\mathbb{R}^{n})$. We then study another model where neither pointwise kernel bounds nor self-adjointness are available.

Keywords

Navier–Stokes equationstent spacesmaximal regularityHardy spaces

MSC classification

Primary: 76D05: Navier-Stokes equations 42B37: Harmonic analysis and PDE 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 5 , November 2017 , pp. 947 - 985
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auscher, P., Regularity theorems and heat kernel for elliptic operators, J. Lond. Math. Soc. (2) 54(2) (1996), 284–296.CrossRefGoogle Scholar
Auscher, P., On necessary and sufficient conditions for L p -estimates of Riesz transforms associated to elliptic operators on ℝ n and related estimates, Mem. Amer. Math. Soc. 871 (2007), xviii+75 pp.Google Scholar
Auscher, P., Change of angle in tent spaces, C. R. Math. Acad. Sci. Paris 349(5–6) (2011), 297–301.Google Scholar
Auscher, P. and Axelsson, A., Remarks on maximal regularity, in Progress in Nonlinear Differential Equations and their Applications vol. 80, pp. 45–55 (Birkhäuser/Springer Basel AG, Basel, 2011).Google Scholar
Auscher, P., Duong, X. T. and McIntosh, A., Boundedness of Banach space valued singular integral operators and Hardy spaces, unpublished manuscript, 2002.Google Scholar
Auscher, P., Hofmann, S., Lacey, M., McIntosh, A. and Tchamitchian, P., The solution of the Kato square root problem for second order elliptic operators on ℝ n , Ann. of Math. (2) 156(2) (2002), 633–654.Google Scholar
Auscher, P., Kriegler, C., Monniaux, S. and Portal, P., Singular integral operators on tent spaces, J. Evol. Equ. 12(4) (2012), 741–765.Google Scholar
Auscher, P., McIntosh, A. and Russ, E., Hardy spaces of differential forms on Riemannian manifolds, J. Geom. Anal. 18(1) (2008), 192–248.CrossRefGoogle Scholar
Auscher, P., Monniaux, S. and Portal, P., The maximal regularity operator on tent spaces, Commun. Pure Appl. Anal. 11(6) (2012), 2213–2219.Google Scholar
Auscher, P., van Neerven, J. and Portal, P., Conical stochastic maximal L p -regularity for 1⩽p < ∞ , Math. Ann. 359(3–4) (2014), 863–889.CrossRefGoogle Scholar
Auscher, P. and Stahlhut, S., A priori estimates for boundary value elliptic problems via first order systems, preprint, 2014, arXiv:1403.5367 [math.CA].Google Scholar
Auscher, P. and Tchamitchian, P., Square root problem for divergence operators and related topics, Astérisque 249 (1998).Google Scholar
Auscher, P. and Tchamitchian, P., Espaces critiques pour le système des équations de Navier–Stokes incompressibles, preprint, 1999, arXiv:0812.1158 [math.AP].Google Scholar
Bahouri, H. and Gallagher, I., The heat kernel and frequency localized functions on the Heisenberg group, in Progress in Nonlinear Differential Equations and their Applications vol. 78, pp. 17–35 (Birkhäuser Boston, Inc., Boston, MA, 2009).Google Scholar
Bourgain, J. and Pavlović, N., Ill-posedness of the Navier–Stokes equations in a critical space in 3D, J. Funct. Anal. 255(9) (2008), 2233–2247.CrossRefGoogle Scholar
Coifman, R. R., Meyer, Y. and Stein, E. M., Some new function spaces and their applications to harmonic analysis, J. Funct. Anal. 62 (1985), 304–335.CrossRefGoogle Scholar
Coulhon, T. and Duong, X. T., Maximal regularity and kernel bounds: observations on a theorem by Hieber and Prüss, Adv. Differential Equations 5(1–3) (2000), 343–368.CrossRefGoogle Scholar
Dubois, S., What is a solution to the Navier–Stokes equations?, C. R. Math. Acad. Sci. Paris 335(1) (2002), 27–32.CrossRefGoogle Scholar
Duoandikoetxea, J., Fourier analysis, in Graduate Studies in Mathematics vol. 29 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Duong, X. T. and Robinson, D. W., Semigroup kernels, Poisson bounds, and holomorphic functional calculus, J. Funct. Anal. 142(1) (1996), 89–128.Google Scholar
Fefferman, C. L. and Stein, E. M., H p spaces of several variables, Acta Math. 129 (1972), 137–193.Google Scholar
Furioli, G., Lemarié-Rieusset, P.-G. and Terraneo, E., Unicité dans L 3(ℝ3) et d’autres espaces fonctionnels limites pour Navier–Stokes, Rev. Mat. Iberoam. 16(3) (2000), 605–667.Google Scholar
Giga, Y., Solutions for semilinear parabolic equations in L p and regularity of weak solutions of the Navier–Stokes system, J. Differential Equations 62(2) (1986), 186–212.Google Scholar
Haak, B. H. and Kunstmann, P. C., On Kato’s method for Navier–Stokes equations, J. Math. Fluid Mech. 11(4) (2009), 492–535.Google Scholar
Hofmann, S., Lacey, M. and McIntosh, A., The solution of the Kato problem for divergence form elliptic operators with Gaussian heat kernel bounds, Ann. of Math. (2) 156(2) (2002), 623–631.CrossRefGoogle Scholar
Hofmann, S. and Mayboroda, S., Hardy and BMO spaces associated to divergence form elliptic operators, Math. Ann. 344(1) (2009), 37–116.Google Scholar
Hofmann, S., Mayboroda, S. and McIntosh, A., Second order elliptic operators with complex bounded measurable coefficients in L p , Sobolev and Hardy spaces, Ann. Sci. Éc. Norm. Supér. (4) 44(5) (2011), 723–800.Google Scholar
Hytönen, T., van Neerven, J. and Portal, P., Conical square function estimates in UMD Banach spaces and applications to H ∞ -functional calculi, J. Anal. Math. 106 (2008), 317–351.Google Scholar
Hytönen, T. and Rosén, A., On the Carleson duality, Ark. Mat. 51(2) (2013), 293–313.Google Scholar
Iwabuchi, T. and Nakamura, M., Small solutions for nonlinear heat equations, the Navier–Stokes equation, and the Keller-Segel system in Besov and Triebel–Lizorkin spaces, Adv. Differential Equations 18(7–8) (2013), 687–736.Google Scholar
Koch, H. and Lamm, T., Geometric flows with rough initial data, Asian J. Math. 16(2) (2012), 209–235.Google Scholar
Koch, H. and Lamm, T., Parabolic equations with rough data, preprint, 2013, arXiv:1310.3658 [math.AP].Google Scholar
Koch, H. and Tataru, D., Well-posedness for the Navier–Stokes equations, Adv. Math. 157(1) (2001), 22–35.Google Scholar
Lemarié-Rieusset, P. G., Recent developments in the Navier–Stokes problem, in Chapman & Hall/CRC Research Notes in Mathematics vol. 431 (Chapman & Hall/CRC, Boca Raton, FL, 2002).Google Scholar
Lemarié-Rieusset, P. G. and Marchand, F., Solutions auto-similaires non radiales pour l’équation quasi-géostrophique dissipative critique, C. R. Math. Acad. Sci. Paris 341(9) (2005), 535–538.Google Scholar
Liu, W. and Röckner, M., Local and global well-posedness of SPDE with generalized coercivity conditions, J. Differential Equations 254(2) (2013), 725–755.CrossRefGoogle Scholar
Mitrea, M. and Monniaux, S., On the analyticity of the semigroup generated by the Stokes operator with Neumann-type boundary conditions on Lipschitz subdomains of Riemannian manifolds, Trans. Amer. Math. Soc. 361(6) (2009), 3125–3157.Google Scholar
Mitrea, M. and Monniaux, S., The nonlinear Hodge–Navier–Stokes equations in Lipschitz domains, Differ. Integral Equ. 22(3–4) (2009), 339–356.Google Scholar
Mitrea, M. and Taylor, M. E., Navier–Stokes equations on Lipschitz domains in Riemannian manifolds, Math. Ann. 321(4) (2001), 955–987.CrossRefGoogle Scholar
de Simon, L., Un’applicazione della theoria degli integrali singolari allo studio delle equazioni differenziali lineare astratte del primo ordine, Rend. Sem. Mat. Univ. Padova 34 (1964), 205–223.Google Scholar
Taylor, M. E., Incompressible fluid flows on rough domains, in Progress in Nonlinear Differential Equations and their Applications vol. 42, pp. 320–334 (Birkhäuser, Basel, 2000).Google Scholar
Triebel, H., Theory of function spaces, in Monographs in Mathematics vol. 78 (Birkhäuser Verlag, Basel, 1983).Google Scholar
Yoneda, T., Ill-posedness of the 3D-Navier–Stokes equations in a generalized Besov space near BMO -1 , J. Funct. Anal. 258(10) (2010), 3376–3387.Google Scholar