Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T09:26:54.063Z Has data issue: false hasContentIssue false
  • English
  • Français

On the lengths of Koszul homology modules and generalized fractions

Published online by Cambridge University Press:  24 October 2008

N. T. Cuong  and
N. D. Minh
N. T. Cuong
Affiliation:
Hanoi Institute of Mathematics, P.O. Box 631, Bo Ho, 10.000 Hanoi, Vietnam
N. D. Minh
Affiliation:
Hanoi Institute of Mathematics, P.O. Box 631, Bo Ho, 10.000 Hanoi, Vietnam
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout this paper, let A be a Noetherian local ring with maximal ideal m and M a finitely generated A-module with d = dimAM ≥ 1. Denote by N the set of all positive integers.

Let x = (x1, …, xd) be a system of parameters (s.o.p) for M and let

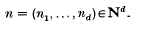
We consider the following two problems: (i) When is the length of Koszul homology

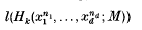
a polynomial in n for all k = 0, …, d and n1; …, nd sufficiently large (n ≫ 0)?

(ii) Is the length of the generalized fractio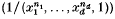n in 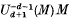a polynomial in n for n ≫ 0?

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 1 , July 1996 , pp. 31 - 42
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Auslander, M. and Buchsbaum, D. A.. Codimension and multiplicity. Ann. Math. 68 (1958), 625–657.CrossRefGoogle Scholar
[2]Cuong, N. T.. On the length of the powers of systems of parameters in local ring. Nagoya Math. J. 120 (1990), 77–88.CrossRefGoogle Scholar
[3]Cuong, N. T.. On the dimension of the non-Cohen-Macaulay locus of local ring admitting dualizing complexes. Math. Proc. Cambridge Phil. Soc. (2) 109 (1991), 479–488.CrossRefGoogle Scholar
[4]Cuong, N. T.. On the least degree of polynomials bounding above the differences between lengths and multiplicities of certain systems of parameters in local rings. Nagoya Math. J. 125 (1992), 105–114.CrossRefGoogle Scholar
[5]Cuong, N. T.. The theory of polynomial types and p-standard ideals in local rings and applications, preprint.Google Scholar
[6]Cuong, N. T., Schenzel, P. and Trung, N. V.. Verallgemeinerte Cohen-Macaulay Moduln. Math. Nach. 85 (1978), 57–75.Google Scholar
[7]Garcla Roig, J- I.. On polynomial bounds for the Koszul homology of certain multiplicity systems. J. London Math. Soc. (2) 34 (1986), 411–416.CrossRefGoogle Scholar
[8]Goto, S. and Yamagishi, K.. The theory of unconditional strong d-sequences and modules of finite local cohomology, preprint.Google Scholar
[9]Kaplansky, I.. Commutative rings (Allyn and Bacon, 1970).Google Scholar
[10]Kirby, D.. Artinian modules and Hilbert polynomials. Quart. J. Math. Oxford (2) 24 (1973), 47–57.CrossRefGoogle Scholar
[11]MacDonald, I. G.. Secondary representation of modules over a commutative ring. Sympos. Math. 11 (1973), 23–43.Google Scholar
[12]Matsumura, H.. Commutative algebra. Second Edition (Benjamin, 1980).Google Scholar
[13]Schenzel, P.. Cohomological annihilators. Math. Proc. Cambridge Phil. Soc. 91 (1982), 345–350.CrossRefGoogle Scholar
[14]Sharp, R. Y. and Hamieh, M. A.. Lengths of certain generalized fractions. J. Pure Appl. Algebra 38 (1985), 323–336.CrossRefGoogle Scholar
[15]Sharp, R. Y. and Zakeri, H.. Modules of generalized fractions. Mathematika 29 (1982), 32–41.CrossRefGoogle Scholar
[16]Sharp, R. Y. and Zakeri, H.. Local cohomology and modules of generalized fractions. Mathematika 29 (1982), 296–306.CrossRefGoogle Scholar
[17]Sharp, R. Y. and Zakeri, H.. Generalized fractions and the monomial conjecture. J. Algebra 92 (1985), 380–388.CrossRefGoogle Scholar
[18]Trung, N. V.. Toward a theory of generalized Cohen–Macaulay modules. Nagoya Math. J. 102 (1986), 1–49.CrossRefGoogle Scholar